A very limited role of tropospheric chlorine as a sink of the greenhouse gas methane

Unexpectedly large seasonal phase differences between CH₄ concentration and its ¹³C ∕ ¹²C isotopic ratio and their inter-annual variations observed in southern hemispheric time series have been attributed to the Cl + CH₄ reaction, in which ¹³CH₄ is discriminated strongly compared to OH + CH₄, and have provided the only (indirect) evidence of a hemispheric-scale presence of oxidative cycle-relevant quantities of tropospheric atomic Cl. Our analysis of concurrent New Zealand and Antarctic time series of CH₄ and CO mixing and isotope ratios shows that a corresponding ¹³C ∕ ¹²C variability is absent in CO. Using the AC-GCM EMAC model and isotopic mass balancing for comparing the periods of presumably high and low Cl, it is shown that variations in extra-tropical Southern Hemisphere Cl cannot have exceeded 0.9 × 10³ atoms cm⁻³. It is demonstrated that the ¹³C ∕ ¹²C ratio of CO is a sensitive indicator for the isotopic composition of reacted CH₄ and therefore for its sources. Despite ambiguities about the yield of CO from CH₄ oxidation (with this yield being an important factor in the budget of CO) and uncertainties about the isotopic composition of sources of CO (in particular biomass burning), the contribution of Cl to the removal of CH₄ in the troposphere is probably much lower than currently assumed.

1 Introduction

Compared to the troposphere's main oxidant OH (hydroxyl radical), the role of Cl (atomic chlorine) for CH₄ is small. A recently published detailed model-based estimate attributes ∼ 2.6 % of methane's photochemical tropospheric loss to Cl (Hossaini et al., 2016). Because this loss constitutes only a small term in the methane budget, it might be deemed irrelevant. Nevertheless, growing spatial and temporal coverage in CH₄ observational data allows for top-down estimates of changes in the source–sink budget to the order of ∼ 1 %. Moreover, considering that the photochemical sink is the dominant and best-known term in the global methane budget, it makes sense to improve our calculations. The grateful aspect of this endeavour clearly is that one does not need an accurate estimate of Cl as a global tropospheric sink of CH₄ as such. It would already be helpful to have independent estimates of the upper limit for this interesting sink of CH₄, whose rise in the Anthropocene thus far has contributed one-fifth to global warming.

Irrespective of the implications for the CH₄ budget, it stands to reason to fully understand tropospheric Cl and its chemistry in different air masses, from marine boundary layer air to strongly polluted air masses, and several studies address these complex processes. It is also clear that the budget of a species as fickle as atomic chlorine is hard to determine in general terms (which forms a less grateful aspect of “assessing chlorine”). Nevertheless, a new effort – in assessing chlorine's role on a larger than regional scale, on the basis of trace gas measurements, may be useful.

Even more so than for OH, estimates of the abundance of Cl atoms are chiefly based on indirect evidence. Direct measurements of OH concentrations ([OH]) are difficult and rare, and for [Cl] this is even much more so. Therefore, the method (by choice or opportunity) is indirect. Not only are indirect measurements easier, the use of trace gases that react with OH and Cl also has the advantage that space- and time-averaged estimates are obtainable. In this case, one can select for instance two hydrocarbons, one of which has a comparatively high reactivity to Cl. The change in ratio between the two hydrocarbon concentrations gives information on [Cl] relative to [OH].

Using stable isotope ratio information offers another such indirect method. The intrinsic advantage here is that one can use a single trace gas, a single hydrocarbon, or even the much studied greenhouse gas CH₄ itself. Although the rate coefficient for the reaction of OH with ¹²CH₄ is only ∼ 4 ‰ faster than that with ¹³CH₄ (Saueressig et al., 2001), for Cl + CH₄ the difference is much larger (Saueressig et al., 1995; Crowley et al., 1999), viz. 63–75 ‰ (at the range of tropospheric temperatures). Broadly speaking, the presence of ¹³C-enriched CH₄ points to reaction with Cl. If this were not enough, one could measure the D ∕ H ratio of CH₄ and obtain additional valuable information because of the large isotope fractionation (KIE, kinetic isotope effect, formerly and still expressed using the kinetic fractionation constant ε= α−1) and the differences between the KIEs for ¹³C and D. A recent paper (Whitehill et al., 2017) reports changes in the clumped isotopic composition of CH₄ in reaction with Cl based on laboratory experiments, raising hope that clumped isotope measurements (which are very difficult) may in an additional way assist to further assess the role of Cl in the oxidation of CH₄ in the atmosphere.

An advantage is that the “stable isotope method” in principle removes the uncertainty about the variability induced by having to use two different trace gas species, each of which may have an independent, variable source. Routinely overlooked is another (principle) advantage of stable isotope analysis offered in the case of atmospheric CH₄ → CO conversion, namely measurement of the isotopic composition of the reaction product CO. Even though variations in [CO] may not be resolvable due to the large spatio-temporal variability of its sources and sink, its ¹³C ∕ ¹²C ratio may well tell a clearer story. This is the added advantage of the stable isotope method (we note that the lifetime of ¹⁴C is sufficiently long to render much of what is stated to also apply to this well-known radioisotope, but there are complications on which we cannot dwell here).

In this way the presence of Cl during Antarctic ozone hole conditions could be inferred in an independent fashion (Brenninkmeijer et al., 1996). Not only did the CH₄ inventory become slightly enriched in ¹³C due to the large KIE in Cl + CH₄, the CO ensuing from CH₄ resulted in strong depletions in the background ¹³CO. There are at least three reasons for the strong isotope depletion. First, CO concentrations are low in the stratosphere and the in situ produced CO had a large impact. Second, the ¹³C content of CH₄ is characteristically low due to its chiefly bacterial origin. Third, and this is an important point mentioned above, the ¹³C KIE for Cl + CH₄ happens to be very large. The combination of these effects renders the stable isotope analysis of CO a sensitive indicator. Dealing with tropospheric Cl, the same principle has been applied during springtime tropospheric ozone depletion events in the Arctic. Short-term bursts of free Cl could be inferred from concomitant decreases in δ¹³C(CO) within a per mil¹ range (Röckmann et al., 1999).

We record that there also is a removal of CO by reaction with Cl atoms, with the rate constant typically being 6 times smaller than that of CO + OH. Given this very low rate coefficient and the low Cl ∕ OH ratio, only an extremely large KIE in the CO + Cl reaction could impact significantly on δ¹³C of the CO inventory. In contrast, the rate constant for CH₄ + Cl is typically 20 times larger than that for CH₄ + OH. Cl is not expected to play a significant role in atmospheric CO removal, except possibly at polar sunrise (Hewitt et al., 1996) and in some stratospheric chemistry analyses (see, for example, Müller et al., 1996; Sander et al., 2011b). None of a few of papers on tropospheric CO thus mentions Cl as a sink for CO because of its negligible share; fortunately, because the reaction product is not so nice.

In this brief account we cannot do justice to all tropospheric Cl-related papers in the literature and we refer to the recent model-based paper by Hossaini et al. (2016) and references therein. In comparison with OH, which is recycled in about two of three reactions in the troposphere (Lelieveld et al., 2016), the role of recycling of Cl is lower and not well known. The presence of Cl in the marine boundary layer has been inferred using hydrocarbon measurements (early study by Parrish et al., 1993) and likewise during polar sunrise (Jobson et al., 1994), Cl₂ has been measured in situ in coastal air (Spicer et al., 1998) and in the Arctic (Liao et al., 2014). ClNO₂, which is an important precursor, has been measured (Osthoff et al., 2008 and Thornton et al., 2010), also by Young et al. (2012), although they found no Cl fingerprint in hydrocarbon ratios.

Recently, Baker et al. (2016) inferred the presence of Cl in pollution outflow from continental Asia using hydrocarbon measurements on air samples collected at cruise altitude by the CARIBIC Lufthansa Airbus aircraft observatory. Before that, Baker et al. (2011) had likewise inferred that Cl is formed in an emission plume of the Eyjafjallajökull volcano probed by the same CARIBIC A340 aircraft. All these and other publications discuss the presence of Cl in a variety of tropospheric environments wrestling with the complexity of its chemistry and paucity of experimental data.

The additional importance of revisiting the role of Cl radicals in the present atmosphere actually surfaces in the reconstruction and understanding of the budget of CH₄ in the past. Changes in the tropospheric burden of CH₄ that occurred in the past (last glacial maximum to present) are due to changes in CH₄ sources and to a minor degree to changes in OH chemistry (Levine et al., 2011b). One would a priori expect δ¹³C(CH₄) to provide additional information on source changes, as it did for immediate past changes (Schaefer et al., 2016), were it not the case that large changes in Cl abundance may well have affected the δ¹³C(CH₄) record (Levine et al., 2011a). If this is indeed the case, changes in Cl abundance in the past may have not affected the CH₄ budget itself significantly, but may have invalidated to a certain degree the δ¹³C(CH₄) isotope method for determining changes in sources (biogenic vs. biomass burning).

We turn our attention to a paradox concerning today's tropospheric Cl, namely: if the presence of tropospheric Cl could be inferred from ¹³C isotope enrichment in CH₄, why is this effect not visible as concurrent isotope depletion in CO? Or, more explicitly stated, if the δ¹³C(CO) isotope method for Cl detection works well for the austral polar stratosphere in spring (Brenninkmeijer et al., 1996) and for the polar sunrise in the Arctic (Röckmann et al., 1999), why not so for the troposphere, or does it? Is a clear negative signal in δ¹³C(CO) indeed absent, and if so, does this absence allow us to cap estimates of tropospheric Cl levels?

2 Data analysis

2.1 Chlorine in the Southern Hemisphere

Because the budgets of CH₄ and CO in the Southern Hemisphere (SH) are less complicated than in the Northern Hemisphere, as is shown by their compact regular seasonal cycles at remote observatories², and because long records of CO and CH₄ including isotopic data are available, we focus on the Southern Hemisphere. In the SH evidently the emphasis is on Cl generated in the marine boundary layer (MBL).

We first revisit the information on Cl based on δ¹³C measurements of CH₄. Initially, mixing ratio and δ¹³C(CH₄) values for shipboard collected air samples in the Pacific pointed to a large apparent sink isotope fractionation (“apparent” KIE) of 12–15 ‰ – well in excess of the aforementioned 4 ‰ from OH + CH₄ – which led to the conjecture that a fraction of CH₄ is removed in the MBL by Cl atoms which discriminate strongly against ¹³CH₄ (Lowe et al., 1999; Allan et al., 2001). Following several publications exploring this effect, Allan et al. (2007) (hereinafter referred to as A07) using global modelling and observational data from the extratropical Southern Hemisphere (ETSH), confirmed a large apparent KIE and could estimate a global marine boundary layer based Cl sink for CH₄ averaging at 25 Tg(CH₄) yr⁻¹.

Given this number, a first-order estimate of the accompanying response of δ¹³C of CO to the production of CO from Cl + CH₄ can be made. Assuming a 100 % yield of CO from OH + CH₄ (and likewise Cl + CH₄), the 25 Tg yr⁻¹ CH₄ sink corresponds to a Cl-based annual CO production of 44 Tg yr⁻¹, which is ∼ 1.8 % of the total CO budget. By using a δ¹³C value of CO of −28 ‰ (annual tropospheric average), that of CH₄ of −48 ‰ and a KIE of 70 ‰, (Cl + CH₄) causes a negative shift in δ¹³C(CO) of about 1.6 ‰. Considering that the lifetime of CO is much shorter than that of CH₄ and that Cl is concentrated in the MBL, the local and/or seasonal effect on δ¹³C(CO) would be even larger.

Unfortunately, a negative shift in δ¹³C(CO) is unwelcome in attempts to close the SH CO budget using δ¹³C. As Manning et al. (1997) have pointed out, budget closure is only possible when the yield of CO from CH₄ + OH (denoted hereinafter as λ) is assumed to be merely about 0.7. In other words, even without incorporating the formation of CO from Cl + CH₄, the CH₄-derived ¹³C-depleted fraction of CO (which is high in the ETSH at above 40 %) appeared to be too dominant and had to be reduced by assuming lower yields of CO from CH₄. Soon thereafter, Bergamaschi et al. (2000) also encountered this problem in a 3-D inverse modelling study using the isotopic composition of CO and could best reconcile data and model by reducing λ to about 0.86. They do mention that incorporating CO from Cl + CH₄ would require λ values as low as 0.71. Platt et al. (2004), who discuss mechanisms for the production of Cl in the marine boundary layer, also allude to the necessity to have to reduce the assumed CO yield of OH + CH₄.

One difficult feature of the δ¹³C(CH₄)-based Cl estimate was a large inter-annual variability that could not be explained. A07 identified two periods of different Cl abundance in the ETSH, namely 1994–1996, with MBL values of 28 × 10³ atoms cm⁻³ (high-Cl period, “HC”) and 1998–2000 with much lower values, viz. 9 × 10³ atoms cm⁻³ (low-Cl period, “LC”). The nearly 3-fold drop in the resulting Cl + CH₄ sink rate (37 to 13 Tg(CH₄) yr⁻¹, or 6.4 to 2.2 % of the total, respectively) inferred from δ¹³C(CH₄) for the two periods is not discernible in the simultaneous δ¹³C(CO) record (see Sect. 2.2).

Later, Lassey et al. (2011) investigated the apparent KIE in detail and found that it can differ markedly from both the seasonal and mass-balanced KIEs. In other words, the apparent KIE derived from the seasonal changes in [CH₄] and δ¹³C(CH₄) values appeared not to properly represent the respective effects of the two KIEs. The implication is that the inferred very large range of [Cl] may be in error, and the absence of a corresponding signal in δ¹³C(CO) is in that respect an experimental confirmation. Below we will go into detail.

2.2 Observations in the ETSH

We scrutinise the mixing and ¹³C ∕ ¹²C ratios of CH₄ and CO in the MBL air at Baring Head, New Zealand (41.41^∘ S, 174.87^∘ E, 85 m a.s.l., denoted hereinafter “BHD”) and at Scott Base, Antarctica (77.80^∘ S, 166.67^∘ E, 184 m a.s.l., denoted “SCB”)³ provided by the National Institute of Water and Atmospheric Research (NIWA, 2010). Examined in the A07 study on CH₄, these data are the result of laboratory analyses of large air samples collected on a monthly to weekly basis. The collection strategy (using wind direction, CO₂ mixing ratio temporal stability and back-trajectory analysis) allows air masses that represent background ETSH air to be selected. Established over two decades, these time series confer the longest continuous records of ¹³CH₄ and ¹³CO observations to date. The reported overall uncertainties of the CH₄ mixing ratio and δ¹³C do not exceed ±0.3 % (about ±5 nmol mol⁻¹) and ±0.05 ‰ (Lowe et al., 1991). For CO, the respective uncertainties are ±4 % ∕ ±0.2 ‰ (prior to 1994, Brenninkmeijer, 1993) and ±7 % ∕ ±0.8 ‰ (since 1994, NIWA, 2010). The CO records from BHD and SCB exhibit small variations in annual (minimum-to-maximum) span and no significant long-term trend in both mixing and isotope ratios throughout 1990–2005 (see Gromov, 2013, Sect. 4.1.1). In contrast to this, the concomitant [CH₄] values have increased on average by about 5 % within the same period, which is consistent with other observational records (Lassey et al., 2010). It can be concluded that such augmentation of atmospheric burden of the major (and largely depleted in ¹³C) in situ sources of CO remains statistically indiscernible in the ETSH δ¹³C(CO) record, because of more perceptible variations caused by changes in sink and/or the other (foremost biomass burning) sources of CO.

We subsequently regard the statistics of the two subsets of observational data falling into the HC and LC periods, as shown in Fig. 1. For testing the robustness of our comparison against the timing of the air sampling, we “bootstrap” the data by selecting only the pairs of CH₄ ∕ CO samples collected within 1-week windows (shown with solid boxes in Fig. 1). This operation has virtually no effect on CO distributions, as its statistic is smaller (total of 116 and 88 samples at BHD and SCB, respectively) and controls the sub-sampling of the datasets. For CH₄, no effect is noted either, with an exception of significant (i.e. exceeding measurement uncertainty) changes to the “bootstrapped” median CH₄ mixing ratio at BHD, which is some 6 nmol mol⁻¹ lower during the HC. This is an indication that the CO sampling times are likely to be more representative for background air. Overall, we conclude that the CH₄ and CO datasets reflect variations in the composition of the same background air. Contrary to CH₄, there is no perceptible reduction in seasonal variations of mixing and isotope ratios of CO at SCB throughout the HC period.

To determine the significance of observed changes in CO using sufficient statistics, we derive quasi-annual averages (QAAs) of CO mixing ∕ isotope ratio averages representing the HC, LC and long-term periods (all data and from 1994 onwards). For the correct temporal weighting of the samples, we first calculated quasi-monthly averages and their variances, which then contributed equally to the QAA. Table 1 lists the results along with the number of samples used in the calculation. Note that there are about twice as many outliers⁴ in the entire BHD record (3.8 %) compared to those in the SCB (2.2 %), which suggests that the estimated difference between the HC and LC averages (HC − LC, denoted Δ) is probably more influenced by regional sources at BHD. Except for δ¹³C(CO) at SCB (with considerable significance of Δ being negative, p value of 0.79), we conclude that all CO QAAs emerge as statistically indistinguishable, also when compared to the long-term averages. For CO mixing ratios, the Cl-driven difference should amount up to 1.2 nmol mol⁻¹ (conservatively assuming up to 50 % of CO derived from CH₄ oxidation changed by 4.2 %), which is 2.5–3 times smaller than the errors in Δ. At both stations, the Δ values indicate changes to the atmospheric reservoir involving ¹³C-depleted CO, but in opposite directions (i.e. a removal at BHD – which contradicts A07 – and an addition at SCB). It is important to note that the CO + OH sink alters atmospheric CO in a similar fashion (i.e. the remaining CO burden becomes enriched in ¹³C).

Table 1 Statistics on quasi-annual average (QAA) mixing and isotope ratios of CO observed and simulated at BHD and SCB.

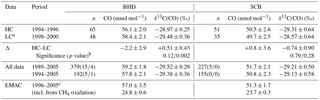
Notes: Values in parentheses are the number of outliers (mild/extreme; see the footnote 4); the latter were excluded from the calculation of the long-term (up to 2005) averages. Quoted are standard errors of quasi-annual averages (±1σ). ^a Time-interpolated value is used for February (no samples are available at SCB during the LC period). ^b The p value is estimated for the null hypothesis that Δ of δ¹³C(CO) QAA is below $\mathrm{0}/-\mathrm{2}\mathit{\sigma }$ (left-tail test). ^c The aggregate of the emission inventories used in the simulation correspond closest to 2000 (see details in Gromov et al., 2017).

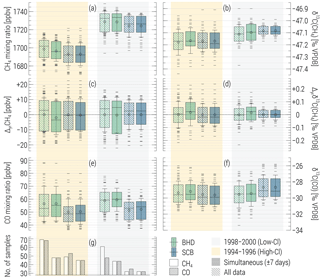
Figure 1 Statistics on the CH₄ and CO mixing and ¹³C ∕ ¹²C ratios observed at Baring Head (BHD) and Scott Base (SCB) throughout the high-Cl (HC, orange shaded) and low-Cl (LC, grey shaded) periods hypothesised by Allan et al. (2007) (see text for details). Panels (c, d) show statistics on the anomalies with respect to the annual averages (denoted with “Δ_yr”). Panel (g) displays the number of samples in each subset. The full time series of the data are shown in the Supplement (Fig. S2). Boxes and whiskers present the median and interquartile ranges and ±1σ (of the population) of the data. Circles and minus symbols denote the averages and samples falling outside ±1σ. Solid boxes denote the subset of data when CH₄ and CO samples were taken simultaneously (up to 7 days apart); hatched boxes refer to all data.

2.3 EMAC model

For extending the interpretation of observed ETSH CO, we resort to the results of simulations performed with the ECHAM5/MESSy Atmospheric Chemistry (EMAC) general circulation model (Jöckel et al., 2010). EMAC includes all relevant processes (atmospheric transport, calculation of chemistry kinetics, photolysis rates, trace gas emissions, etc.) for simulating the current global atmospheric state. The set-up we use resembles that of the EMAC evaluation study (MESSy Development Cycle 2, Jöckel et al., 2010) and is augmented with kinetic tagging tools (Gromov et al., 2010). These allow direct quantification of the CO component stemming from CH₄ oxidation (and as corollary provide λ) by following the carbon (C) exchanges through all intermediates (shown in Supplement Fig. S1) within a comprehensive chemistry mechanism simulated by the MECCA sub-model (Module Efficiently Calculating the Chemistry of the Atmosphere, Sander et al., 2011a). The emission set-up contains only the standard emissions and precursors of Cl and yields average MBL Cl concentrations in the order of 10¹–10² atoms cm⁻³ (see the detailed simulated budgets in the Supplement, Table S1). These results are in line with MBL [Cl] of (0.5–2) × 10² atoms cm⁻³ obtained by Hossaini et al. (2016) in a similar model set-up (ORG2).

The QAAs of [CO] simulated in EMAC for the period 1996–2005 in the grid boxes enclosing the locations of BHD and SCB are also given in Table 1. Despite the spatial and temporal averaging used (∼ 2.8^∘ horizontal grid cell size at the T42L31ECMWF resolution, weekly averages), model QAAs match observations well and have similar uncertainties (resulting from monthly means variation; the observed and simulated seasonalities are shown in the Supplement, Fig. S3). Due to longer lifetimes of CO and CH₄ in the well-mixed ETSH and, more importantly, their synchronous sink and production via OH, we expect much lower (factor ∼ 1∕5 compared to that of the total CO) variation in the CH₄-derived [CO] component. The fraction of the latter (denoted γ, see Table 2) is proportional to the average tropospheric λ of 93 % (diagnosed simulated value). Depending on the zonal domain, Cl atoms in EMAC initiate (0.15–0.25) % of CH₄ sink in the troposphere. The fraction of CH₄ removed in the ETSH (43 Tg(C) yr⁻¹) is minor compared to that in the tropics (271 Tg(C) yr⁻¹). About 13 % of tropospheric sink occurs in the boundary layer.

Additionally, we simulate the sink-effective ¹³C enrichment in CO (denoted η_c) resulting from the ¹²C-preferential CO + OH reaction and removal of the CH₄ → CO chain intermediates (dry or wet deposition, when γ < 1), convoluted with atmospheric mixing and transport. The corresponding η_c value at a given space–time point denotes how much higher the δ¹³C of airborne CO is compared to the case when sink KIEs were absent⁵. Altogether, values of γ and η_c at the stations and domain-wise integrals of CH₄ sink (S) and λ (listed in Table 2) are used in the calculations that follow now.

2.4 Sensitivity of δ¹³C(CO) to the CH₄ + Cl sink

Using the observational and model data, we attempt to estimate the sensitivity of δ¹³C(CO) at a given station to supposed inter-annual changes in the Cl-initiated CH₄ sink. The QAA of δ¹³C(CO) (denoted δ_c) can be approximated as a two-component mixture of CH₄- and non-CH₄-derived CO sources augmented by the effective sink enrichment:

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}_{\mathrm{c}}\cong (\mathrm{1}-\mathit{\gamma }){\mathit{\delta }}_{\mathrm{n}}+\mathit{\gamma }({\mathit{\delta }}_{\mathrm{m}}-{\mathit{\epsilon }}_{\mathrm{m}})+{\mathit{\eta }}_{\mathrm{c}}.\end{array}$$

We refer the reader to Table 2 for the explanation of the parameters and their values. In essence, we account for the fractionations induced in atmospheric sinks (η_c in CO and ε_m in CH₄) and mix the sources in the proportion defined by γ. Exemplifying the estimate from A07, SH Cl changes should cause ε_m to drop from 15 ‰ to 7 ‰ between the HC and LC, rendering δ¹³C of the carbon from CH₄ arriving to CO of −62.2 ‰ and −54.2 ‰, respectively. By rearranging Eq. (1) we derive the non-CH₄ CO source δ¹³C signature δ_n (see Table 2). Since there are virtually no surface sources of CO south of 40^∘ S in the ETSH (see, for example, Gromov et al., 2017, Sect. 3.4), the difference in δ_n at BHD and SCB could be driven only by poleward ¹³C enrichment of the non-CH₄ in situ sources (e.g. oxidation of higher hydrocarbons) and/or a stronger (than simulated in EMAC) zonal gradient in η_c. Note that the station-wise δ_n discrepancy scales with the ε_m value, although not strongly: at ε_m of OH sink KIE (3.9 ‰) it reduces from (2.2 ± 2.1) ‰ to (1.5 ± 2.2) ‰. In a statistical sense, the derived δ_n values reflect the same underlying source signature (p value is 0.31).

Table 2 Parameters used in calculus.

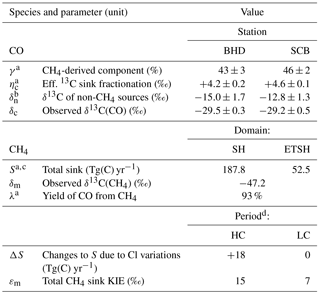
Notes: Quoted QAAs and standard errors (±1σ); the latter are omitted for the components contributing to δ_c and δ_n errors insignificantly. ^a Estimate based on EMAC results. ^b Derived at ε_m= 11 ‰ (average of the LC and HC periods). ^c Includes the LC Cl sink term from A07 (9.7 Tg(C) yr⁻¹). For the SH, the sum of the ETSH and halved intra-tropical integrals is taken. ^d Estimates from A07.

Using Eq. (1) to define δ_c in the HC and LC periods, one obtains its sensitivity (Δδ_c) to changes in the CH₄ + Cl sink (ΔS) and in the total sink KIE (Δε_m)⁶:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{\mathit{\delta }}_{\mathrm{c}}=({\mathit{\lambda }}_{\mathrm{a}}/\mathit{\lambda }{)}^{\mathrm{LC}}\mathit{\gamma }(({\mathit{\delta }}_{\mathrm{m}}{-}^{\mathrm{HC}}{\mathit{\epsilon }}_{\mathrm{m}}-{\mathit{\delta }}_{\mathrm{n}})\mathit{\mu }-\mathrm{\Delta }{\mathit{\epsilon }}_{\mathrm{m}}).\end{array}$$

Here superscripts indicate the period the values are taken for, Δ denotes the HC − LC difference (same as in Sect. 2.2 above) and $\mathit{\mu }=\mathrm{\Delta }S{/}^{\mathrm{LC}}S$ is the change in the total CH₄ sink S relative to the LC conditions. The value of S represents the tropospheric column of a given domain, i.e. we assume that ΔS is distributed homogeneously over the SH or ETSH. Formulated using γ, Eq. (2) allows the projection of the results for the alternative CO yield value λ_a (different from that obtained in EMAC), as our simulations confirm that λ directly proportionates γ and S in the tropospheric column (but not in the MBL). Furthermore, Δδ_c is derived under the assumption of constancy of η_c and δ_n values. Whilst for η_c such is likely the case (judging by the very similar observed CO mixing ratios, and hence lifetimes, during HC and LC), for the latter an upper limit of ±1 ‰ can be put from the typical variation in the δ¹³C of the underlying sources (see Gromov et al., 2017, Table 5). This is lower than the uncertainty associated with δ_n values derived here (cf. Table 2); we discuss the range of δ_n values required to concomitantly mask the changes in δ_c below.

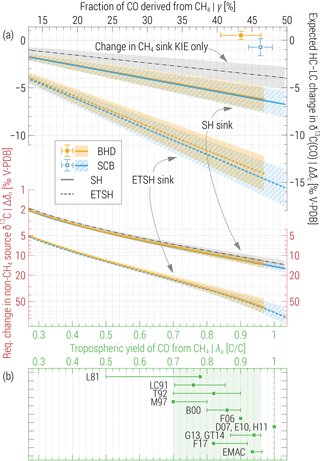
Figure 2 (a) Top: expected CH₄ + Cl sink-driven changes to δ¹³C(CO) between HC and LC periods at the ETSH stations (Δδ_c) as a function of CH₄-derived CO fraction (γ, top axis) resulting from assumed yield values (λ_a, bottom axis, approximate). Large symbols denote the observed (ordinate) and simulated (abscissa, EMAC) values. Thick lines present Δδ_c values calculated using Eq. (2) assuming that hypothesised changes to the CH₄ + Cl sink occur within the entire SH (solid) and ETSH only (dashed). Thin dashed–dotted lines exemplify the effect due to mere changes in CH₄ sink KIE (Δε_m). Bottom: average augmentation to the non-CH₄ sources signature (Δδ_n) required to compensate Δδ_c at the respective values and domains (note the different axis shown in red). Errors bars and areas denote ±1σ of the annual means and derived estimates. See Sects. 2.4 and 3 for details. (b) Tropospheric yield of CO from CH₄ oxidation reckoned in the current and previous studies. Symbols (error bars) denote the best (range of) estimates or the global (domain) averages. Abbreviations refer to the following: L81 – Logan et al. (1981), LC91 – Lelieveld and Crutzen (1991), T92 – Tie et al. (1992), M97 – Manning et al. (1997), B00 – Bergamaschi et al. (2000), F06 – Folberth et al. (2006), D07 – Duncan et al. (2007), E10 – Emmons et al. (2010), H11 – Hooghiemstra et al. (2011), G13 – Gromov (2013), GT14 – Gromov and Taraborrelli, MPI-C (unpublished results using EMAC, 2014), F17 – Franco et al. (2018), EMAC – current study.

Figure 2a shows the values of Δδ_c, calculated for different stations and domains, as a function of γ (implicitly scaling with arbitrarily chosen yield value λ_a). Very large changes are expected for the ETSH, where μ is about 4 times that in the SH. Importantly, the ^LCS value includes the Cl sink term from A07 (which is ∼ 29 times greater than the total tropospheric CH₄ + Cl sink simulated in EMAC); hence, we receive the “lowest sensitivity” for the case when the Cl sink is added up to (instead of partly replacing) the other CH₄ sinks, e.g. that via OH. Alternatively, Δδ_c will additionally intensify by −0.2 ‰ and −(1.8–2.1) ‰ in the SH and ETSH, respectively. By setting μ= 0 in Eq. (2), we quantify the contribution of the CH₄ sink KIE (which increases by Δε_m) only. Independent from the assumptions on the Cl sink domain and magnitude, it demonstrates the effect of lowering of δ¹³C of C arriving to CO from CH₄ and accounts for one-third to two-thirds of the total Δδ_c value (cf. Fig. 2, thin dashed–dotted line).

Finally, we estimate the equivalent increase in the δ¹³C value of the non-CH₄ sources (Δδ_n) that would be required to mask the depleting effect of a hypothetical CH₄ + Cl sink increase. We subtract Eq. (1) written for the HC and LC and solve it assuming Δδ_c= 0 (notation from Eq. 2 is kept):

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }{\mathit{\delta }}_{\mathrm{n}}={\displaystyle \frac{({\mathit{\delta }}_{\mathrm{n}}-({\mathit{\delta }}_{\mathrm{m}}{-}^{\mathrm{LC}}{\mathit{\epsilon }}_{\mathrm{m}}\left)\right)\mathit{\mu }+(\mathrm{1}+\mathit{\mu })\mathrm{\Delta }{\mathit{\epsilon }}_{\mathrm{m}}}{\left(\right({\mathit{\lambda }}_{\mathrm{a}}/\mathit{\lambda }{)}^{\mathrm{LC}}\mathit{\gamma }{)}^{-\mathrm{1}}-(\mathrm{1}+\mathit{\mu })}}.\end{array}$$

Averages of Δδ_n at BHD and SCB are plotted in the lower panel of Fig. 2a, respectively. Similar to Δδ_c, Δδ_n scales with the assumed domain and CH₄ input to CO, albeit stronger, because δ_n is closer to the δ¹³C of the total CO source (δ_c−η_c) compared to that for CH₄ (δ_m−ε_m). Thus, if we accept the EMAC-suggested tropospheric CO yield in the SH of λ= 93 %, Cl-driven changes to the δ¹³C(CO) at BHD and SCB are expected to be of at least −(5.8–6.3) ‰ between the LC and HC, unless these are masked by unrealistic concurrent increases in δ¹³C of the non-CH₄ sources of about +(11.6–13.5) ‰. If one assumes the CH₄ + Cl sink changes only within the ETSH, these estimates scale to −(13.1–14.5) ‰ and +(46–61) ‰, respectively. It is important to note that we gauge the expected changes to the annual averages of δ¹³C(CO), which do integrate seasonal variations. The latter are observed at merely ±1.5 ‰ (cf. Figs. 1 and S2) and should also increase strongly, if the Cl sink has a similar seasonal variation to that of OH (although A07 used a seasonal cycle based on dimethyl-sulfide-related species in the SH, which has a shorter summer maximum).

3 Discussion

The photochemical yield of CO from CH₄ constitutes a major factor of uncertainty in the CO budget. Modelling studies to date agreed on values of λ≥ 0.7 (see the overview in Fig. 2b). Several recent studies (see D07, E10 and H11) suggest, however, that λ is close to unity and by doing so contradict findings of ¹³CO-inclusive studies (see M97, B00 and G13). Assuming that λ < 0.7 or that λ ∼ 1 would be in conflict with basic principles, i.e. photochemical kinetics and dry and wet removal processes affecting the intermediates of the CH₄ → CO chain, or their erroneous implementation in the global atmospheric models.

Our estimates of Δδ_c bear the uncertainty of the assumed λ value; nonetheless, they affirm that even if only 70 % of reacted CH₄ molecules yield CO, at least one-third of the changes to the δ¹³C signature of this source (that is, (δ_m+ε_m) times 0.7) should be expressed in the ETSH δ¹³C(CO). Since δ_m changed by about +0.1 ‰ between the HC and LC periods (cf. Fig. 1b), we conclude that ε_m could not change by more than +2 ‰ in the SH as well (with this estimate being lower for λ above 0.7)⁷. Furthermore, statistically significant non-zero Δδ_c values (p value of 0.01) should appear at very low λ, viz. above 0.05 (ETSH sink) and 0.12 (SH sink, respectively). We regard these two atmospheric domains because observations in the well-mixed ETSH may not single out the actual location of the Cl + CH₄ sink: The large part of sink-driven variations in the mixing ratio and δ¹³C of CH₄ and CO is merely transported into the ETSH from the tropics, where almost three-quarters of the total CH₄ sink and accompanying CO production is expected (see Table S1 for EMAC results, also Gromov, 2013, Sect. 6.2.3). Accordingly, Hossaini et al. (2016) also assign a major fraction of the CH₄ + Cl sink to the lower latitudes. If such were not the case (i.e. if varying Cl + CH₄ sink were confined to the ETSH), the estimated effect on δ¹³C(CO) would be roughly twice that reckoned for the SH, i.e. extreme values.

There are a few remarks on the usability of the method used by A07, in addition to the thorough theoretical enquiry by Lassey et al. (2011). Evidence, or at least indications, for Cl in the ETSH is based on the [CH₄] vs. δ¹³C(CH₄) Lissajous (a.k.a. phase) diagrams being ellipses in the case of seasonal cycles. The slope of their major axis gives the “apparent” KIE, from which the ratio Cl ∕ OH can be inferred when the individual KIEs are known. Clearly, Cl was not assessed on the basis of the annual average value of δ¹³C(CH₄) but on the basis of its seasonal cycle, which is small. Using annual averages, however, is still impeded by perceptible long-term trends in [CH₄] and δ¹³C(CH₄), which neither A07 (who consider the final 8 equilibrated years of the 40-year spin-up simulations) nor Lassey et al. (2011) (who use a rather idealised model) have accounted for. For example, presence and asynchronous evolution of [CH₄] and δ¹³C(CH₄) long-term trends could result in different mixing and transport of CH₄ isotopologues compared to that resulting from trend-free simulated seasonal variations. We note that while observed [CH₄] growth is similar throughout both HC and LC periods, such is not the case for δ¹³C(CH₄), which does not increase in the LC (cf. Fig. S2a, c and, in particular, the seasonal time series fits for CH₄ at the NIWA website⁸). Furthermore, the latter is likely a global signal of the 2000–2007 intermittent stop in tropospheric CH₄ growth, which manifested itself in δ¹³C earlier than in mixing ratios and terminated with the reversed ¹³C ∕ ¹²C trend (see, for example, Nisbet et al., 2016). Currently available observational data do not allow unambiguous attribution of this global phenomenon to one or several causes proposed (Turner et al., 2017), however.

Our incomplete information about the ¹³C isotopic composition of CH₄ sources presently prevents a Cl-induced input into the annual average value of δ¹³C(CH₄) being singled out, even though it should be perceptible (about +1.5 ‰, assuming for the sake of matter a 2.5 % Cl sink). The corresponding negative shift in δ¹³C(CO) is about 1.6 ‰ (estimated in Sect. 2.1). In this respect, δ¹³C(CH₄) and δ¹³C(CO) are equally sensitive to Cl. Because oxidation of CH₄ is a main source of CO in the ETSH, and the isotopic composition of atmospheric CH₄ is better known than that of its sources, it may well be that variation in the annual average value of δ¹³C(CO) is a more useful variable for estimating [Cl]. The relatively long lifetime and small seasonality in sources result in weak seasonal cycles of mixing ratio and δ¹³C in CH₄. In contrast, the seasonal cycle of δ¹³C(CO) is dominated by the large difference in isotopic composition of its sources, with the main driver being the switch between CO from CH₄ oxidation and that of the other sources. Since the presence of Cl makes CH₄ oxidation an even more ¹³C-depleted source, the impact of CH₄ oxidation on CO in the ETSH peaks and may render the seasonal amplitude (in particular summer minima) of δ¹³C(CO) a sensitive indicator for Cl. Unfortunately, deficit of observational data (large uncertainties due to insufficient statistics) currently hinder such application.

A fundamental problem remains that the ETSH δ¹³C(CO) budget cannot be closed even when a Cl sink is excluded, unless a CO yield from CH₄ of 0.7–0.86 is assumed (Manning et al., 1997; Bergamaschi et al., 2000). Yields below unity leave, however, the possibility that a positive fractionation in the removal of the CH₄ → CO intermediates may be at play. Using λ= (0.7–0.86) and γ= 0.3 for the troposphere, one calculates that an average KIE of (11–33) ‰ should escort the removal of intermediates in order to offset the Cl input to δ¹³C(CO). This estimate is 3–8 times higher than current parameterisations suggest (about 4 ‰, see Gromov, 2013, Sect. 6.2.4) and is even higher in the SH, where γ is above 0.4. Another complication is potentially present because one cannot exclude that the room temperature laboratory data for the ¹³C KIE for CO+OH reaction are not applicable to the bulk of the troposphere, even though the reaction itself is little temperature- but mostly pressure-dependent (see Gromov, 2013, Sect. 6.1.4). The unbalanced ¹³C(CO) budget may then be the consequence of underestimating the CO sink KIE in the models, despite adequate estimates of the sources' ¹³C ∕ ¹²C ratios.

4 Conclusions

We emphasise the value of long-term observations of CO isotopic composition, especially at locations like Scott Base (Antarctica), where influence of local sources is smallest and the fraction of photochemically produced CO is largest. In combination with modelling (e.g. EMAC), δ¹³C(CO) allows monitoring for intra-annual changes in the carbon isotopic composition of CH₄-derived CO, namely the δ¹³C value of reacted CH₄ modified by the total sink KIE (ε_m). Within the range of probable λ values (0.7–0.93), we are able to cap the potential changes in ε_m by +(2.0–1.5) ‰ between 1994–1996 and 1998–2000 in the ETSH, which contrasts the +8 ‰ derived by Allan et al. (2007). Conversely, δ¹³C(CO) may also be employed for “top-down” estimates of δ¹³C values of CH₄ sources, provided the ε_m is equilibrated on a scale of a tropospheric CH₄ lifetime. This could be achieved in a differential mixing model (also known as the “Keeling” plot) contrasting small variance in CH₄-derived [CO] and δ¹³C and largely varying input from other CO sources (e.g. biomass burning).

We conclude that δ¹³C(CO) is particularly sensitive to the CH₄ + Cl sink. Its temporal variations, if they exist, may allow an independent “bottom-up” [Cl] proxy to be calibrated, e.g. emissions of Cl simulated in process-based models. For example, changes in observed δ¹³C(CO) at SCB (see Table 1) allow variations of the Cl-driven sink of CH₄ not larger than (1.5 ${\mathit{\lambda }}_{\mathrm{a}}^{-\mathrm{1}})$ % of its total (assuming the yield λ_a of CO from CH₄). Projecting this figure onto EMAC results (Table S1, zonal tropospheric integrals) implies that variations in mean ETSH chlorine abundance should have not exceeded Δ[Cl] = (0.9 ${\mathit{\lambda }}_{\mathrm{a}}^{-\mathrm{1}})\times {\mathrm{10}}^{\mathrm{3}}$ atoms cm⁻³ between 1994–1996 and 1998–2000. Regarding the fact that Manning et al. (1997) and Bergamaschi et al. (2000) could only close the SH ¹³C(CO) budget assuming λ values of 0.7 and 0.86, which are within the generally accepted range, it is unlikely that tropospheric Cl is as high as assumed in the literature.

Although invoking isotopic information is often like opening a can of worms (scientists' favourite diet), relevant conclusions emerge. Lassey et al. (2011) exposed shortcomings of the phase diagram method; we show here, using a low- and high-Cl scenario, that unrealistic yield values of CO from CH₄ oxidation (λ below 0.12 in the SH) and/or implausible increases in the δ¹³C of non-CH₄ sources of CO (exceeding +7 ‰ at realistic λ≥ 0.7) would have to be assumed to explain the absence of concurrent inter-annual variations in δ¹³C(CO) in the ETSH. This constitutes an independent, observation-based evaluation of [Cl] variations envisaged by Allan et al. (2007), from which we conclude that such variations are extremely unlikely. Concerning estimates of background levels of Cl, even attributing 1 % of the total tropospheric sink of CH₄ to Cl aggravates the non-trivial problem of balancing the global ¹³C(CO) budget. It follows that the role of tropospheric Cl as a sink of CH₄ oxidation (see, for example, Saunois et al., 2016, and references therein) is seriously overestimated.

Appendix A: Derivations

Below we detail the derivation of Eqs. (2) and (3). The former is obtained by writing Eq. (1) for the HC and LC periods.

$$\begin{array}{ll}{\displaystyle }& {}^{\mathrm{HC}}{\mathit{\delta }}_{\mathrm{c}}\left(\mathrm{1}{-}^{\mathrm{HC}}\mathit{\gamma }\right){\mathit{\delta }}_{\mathrm{n}}{+}^{\mathrm{HC}}\mathit{\gamma }\left({\mathit{\delta }}_{\mathrm{m}}{-}^{\mathrm{HC}}{\mathit{\epsilon }}_{\mathrm{m}}\right)+{\mathit{\eta }}_{\mathrm{c}},\\ {\displaystyle }& {}^{\mathrm{LC}}{\mathit{\delta }}_{\mathrm{c}}\left(\mathrm{1}{-}^{\mathrm{LC}}\mathit{\gamma }\right){\mathit{\delta }}_{\mathrm{n}}{+}^{\mathrm{LC}}\mathit{\gamma }\left({\mathit{\delta }}_{\mathrm{m}}{-}^{\mathrm{LC}}{\mathit{\epsilon }}_{\mathrm{m}}\right)+{\mathit{\eta }}_{\mathrm{c}},\end{array}$$

and subtracting these to yield the respective change to δ_c:

$${}^{\mathrm{HC}}{\mathit{\delta }}_{\mathrm{c}}{-}^{\mathrm{LC}}{\mathit{\delta }}_{\mathrm{c}}={(}^{\mathrm{HC}}\mathit{\gamma }{-}^{\mathrm{LC}}\mathit{\gamma }\left)\right({\mathit{\delta }}_{\mathrm{m}}-{\mathit{\delta }}_{\mathrm{n}}){-}^{\mathrm{HC}}{\mathit{\gamma }}^{\mathrm{HC}}{\mathit{\epsilon }}_{\mathrm{m}}{+}^{\mathrm{LC}}{\mathit{\gamma }}^{\mathrm{LC}}{\mathit{\epsilon }}_{\mathrm{m}}.$$

Note that γ is proportional to the product (λ⋅S) and hence increases by (1 + ΔS ∕ ^LCS) during the HC period. Thus, using

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{\mu }=\mathrm{\Delta }S{/}^{\mathrm{LC}}S,\\ {\displaystyle }& {}^{\mathrm{HC}}\mathit{\gamma }{/}^{\mathrm{LC}}\mathit{\gamma }=(\mathrm{1}+\mathit{\mu }),\\ {\displaystyle }& {\displaystyle }\mathrm{\Delta }{\mathit{\epsilon }}_{\mathrm{m}}{=}^{\mathrm{HC}}{\mathit{\epsilon }}_{\mathrm{m}}{-}^{\mathrm{LC}}{\mathit{\epsilon }}_{\mathrm{m}},\end{array}$$

and factoring with respect to ^LCγ, one obtains:

$${\displaystyle }\mathrm{\Delta }{\mathit{\delta }}_{\mathrm{c}}{\equiv }^{\mathrm{HC}}{\mathit{\delta }}_{\mathrm{c}}{-}^{\mathrm{LC}}{\mathit{\delta }}_{\mathrm{c}}{=}^{\mathrm{LC}}\mathit{\gamma }\left(\right({\mathit{\delta }}_{\mathrm{m}}{-}^{\mathrm{HC}}{\mathit{\epsilon }}_{\mathrm{m}}-{\mathit{\delta }}_{\mathrm{n}})\mathit{\mu }-\mathrm{\Delta }{\mathit{\epsilon }}_{\mathrm{m}}).$$

Finally, the value of Δδ_c can be projected for any arbitrary yield value λ_a (different to λ obtained in EMAC and used in our calculations) by scaling the value of ^LCγ with λ_a ∕ λ, which yields Eq. (2).

Derivation of Eq. (3) is done in a similar fashion, i.e. equating the right-hand sides of Eq. (1) written for HC and LC periods (assuming that δ_c does not change):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\mathrm{1}{-}^{\mathrm{LC}}\mathit{\gamma }\right){\mathit{\delta }}_{\mathrm{n}}{+}^{\mathrm{LC}}\mathit{\gamma }\left({\mathit{\delta }}_{\mathrm{m}}{-}^{\mathrm{LC}}{\mathit{\epsilon }}_{\mathrm{m}}\right)=\\ {\displaystyle }& {\displaystyle }=\left(\mathrm{1}{-}^{\mathrm{LC}}\mathit{\gamma }\right(\mathrm{1}+\mathit{\mu }\left)\right)({\mathit{\delta }}_{\mathrm{n}}+\mathrm{\Delta }{\mathit{\delta }}_{\mathrm{n}})\\ {\displaystyle }& {\displaystyle }{+}^{\mathrm{LC}}\mathit{\gamma }(\mathrm{1}+\mathit{\mu })({\mathit{\delta }}_{\mathrm{m}}-{(}^{\mathrm{LC}}{\mathit{\epsilon }}_{\mathrm{m}}+\mathrm{\Delta }{\mathit{\epsilon }}_{\mathrm{m}})).\end{array}$$

Rearranging the above expression for Δδ_n (required change in δ_n sought) and factoring with respect to ^LCγ yields the following:

$${\displaystyle }\mathrm{\Delta }{\mathit{\delta }}_{\mathrm{n}}={\displaystyle \frac{({\mathit{\delta }}_{\mathrm{n}}-({\mathit{\delta }}_{\mathrm{m}}{-}^{\mathrm{LC}}{\mathit{\epsilon }}_{\mathrm{m}}\left)\right)\mathit{\mu }+(\mathrm{1}+\mathit{\mu })\mathrm{\Delta }{\mathit{\epsilon }}_{\mathrm{m}}}{{(}^{\mathrm{LC}}\mathit{\gamma }{)}^{-\mathrm{1}}-(\mathrm{1}+\mathit{\mu })}},$$

where ^LCγ can be further modulated by λ_a ∕ λ to account for an arbitrary yield value, as shown in Eq. (3).