the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical note: Evaluation of the simultaneous measurements of mesospheric OH, HO2, and O3 under a photochemical equilibrium assumption – a statistical approach
Mikhail Y. Kulikov
Anton A. Nechaev
Mikhail V. Belikovich
Tatiana S. Ermakova
Alexander M. Feigin
This Technical Note presents a statistical approach to evaluating simultaneous measurements of several atmospheric components under the assumption of photochemical equilibrium. We consider simultaneous measurements of OH, HO2, and O3 at the altitudes of the mesosphere as a specific example and their daytime photochemical equilibrium as an evaluating relationship. A simplified algebraic equation relating local concentrations of these components in the 50–100 km altitude range has been derived. The parameters of the equation are temperature, neutral density, local zenith angle, and the rates of eight reactions. We have performed a one-year simulation of the mesosphere and lower thermosphere using a 3-D chemical-transport model. The simulation shows that the discrepancy between the calculated evolution of the components and the equilibrium value given by the equation does not exceed 3–4 % in the full range of altitudes independent of season or latitude. We have developed a statistical Bayesian evaluation technique for simultaneous measurements of OH, HO2, and O3 based on the equilibrium equation taking into account the measurement error. The first results of the application of the technique to MLS/Aura data (Microwave Limb Sounder) are presented in this Technical Note. It has been found that the satellite data of the HO2 distribution regularly demonstrate lower altitudes of this component's mesospheric maximum. This has also been confirmed by model HO2 distributions and comparison with offline retrieval of HO2 from the daily zonal means MLS radiance.
- Article
(8000 KB) - Full-text XML
- BibTeX
- EndNote
A prominent feature of atmospheric photochemical systems is the presence of a large number of chemical components with short lifetimes and concentrations close to stable photochemical equilibrium at every instant. The condition of balance between their sources and sinks is described by a system of algebraic equations. This system can be used to determine characteristics of hard-to-measure atmospheric species through other measurable components, evaluate results of remote or in situ measurements, estimate reaction rates usually known with significant uncertainty, and to understand processes and chemical reactions that influence the variability in the most important atmospheric components, e.g., ozone, in the geographical region of interest.
This approach has found the following wide applications:
-
In 3-D chemical transport models that include a large set of physical and chemical processes with a broad spectrum of spatio-temporal scales. In particular, the chemical family concept is widely used for simulating gas-phase photochemistry of the lower and middle atmosphere (e.g., Douglass et al., 1989; Kaye and Rood, 1989; Rasch et al., 1995), when transport is taken into account only for the concentration of a chemical family, while relative concentrations of the constituent fast components are calculated from the instantaneous stable equilibrium condition. Complemented with Henry's law (e.g., Djouad et al., 2003; Tulet et al., 2006) in multiphase models, this approach markedly saves calculation time and increases the overall stability of the numerical scheme. Moreover, use of the photochemical equilibrium condition to simulate fast component dynamics reduces the phase space dimension of box models significantly (e.g., Kulikov and Feigin, 2014), allowing a comprehensive analysis of nontrivial nonlinear dynamic properties of various atmospheric photochemical systems (e.g., Feigin and Konovalov, 1996; Feigin et al., 1998; Konovalov et al., 1999; Konovalov and Feigin, 2000; Kulikov et al., 2012).
-
In investigations of the chemistry of the surface layer and free troposphere in different regions (over megalopolises, in rural areas, in the mountains, over the seas) based on measurements of nitrogen species, peroxy radicals, ozone, aerosols, and other components aimed at understanding processes impacting the surface ozone formation and air quality. The equilibrium condition is most frequently used for nitrogen species. For example, Chameides (1975) proposed a model for determining the vertical distribution of odd nitrogen, in which the HNO3 profile could be deployed to retrieve profiles of five other components (NO, NO2, NO3, N2O5, and HNO2) from their photochemical equilibrium condition. In the paper by Stedman et al. (1975), the equation for NO2 equilibrium that accounted only for the main source and sink of this component was applied to determine the photodissociation constant J(NO2). A more accurate equation for the NO2 equilibrium was used by Crawford et al. (1996) and Koike et al. (1996) to determine NO2∕NO partitioning and NOx, allowing for, in particular, an investigation of the spatial distribution of NOx∕NOy over the Pacific.
Nighttime equilibrium in the NO2-NO3-N2O5 system is used to determine surface layer N2O5 concentration, equilibrium constant of this system, equilibrium partitioning between NO3 and N2O5, and loss coefficients of NO3, N2O5, and NOx (Martinez et al., 2000; Brown et al., 2003; Crowley et al., 2010; McLaren et al., 2010; Benton et al., 2010; Sobanski et al., 2016).
Platt et al. (1979) used the CH2O photochemical equilibrium condition to analyze results of simultaneous measurement of CH2O, O3, and NO2 and to identify mechanisms of CH2O formation over rural areas and in maritime air. In the papers by Ko et al. (2003), Cantrell et al. (2003), and Penkett et al. (1997, 1998) algebraic expressions derived from equilibrium conditions for H2O2, peroxy radicals, and nitrogen species were used to determine equilibrium values of peroxide concentration, total peroxy radical level, and NO∕NO2 ratio, and to diagnose the ozone production and loss levels in a clean or polluted troposphere.
-
In stratospheric chemistry studies, including determination of a critical parameter in catalytic cycles of ozone destruction in the polar stratosphere. In particular, the equilibrium condition for ClO and Cl2O2 along with the measurement data of daytime and nighttime concentrations of these components in the polar stratosphere are used to evaluate the temperature dependence of the ClO concentration, reaction constants determining the ClO + ClO + M ↔ Cl2O2 + M equilibrium, and the photolysis rate of Cl2O2 (Ghosh et al., 1997; Avallone et al., 2001; Solomon et al., 2002; Stimpfle et al., 2004; von Hobe et al., 2005, 2007; Berthet et al., 2005; Butz et al., 2007; Kremser et al., 2011; Sumińska-Ebersoldt et al., 2012; Wetzel et al., 2012).
Pyle et al. (1983) proposed a method for derivation of the OH concentration from satellite infrared measurements of NO2 and HNO3 using a simple algebraic relation following from the equilibrium condition for HNO3. Algorithms for retrieving distributions of OH and HO2 from the satellite measurement data of O3, NO2, H2O, HNO3 by LIMS/Nimbus-7 and UARS with the help of algebraic models following from the photochemical equilibrium of Ox, HOx, and HNO3 components were proposed by Pyle and Zavody (1985) and Pickett and Peterson (1996). It is also noteworthy that similar models are widely used for calculating concentrations of components with a short lifetime (e.g., O(1D) and OH) and subsequently evaluating vertical distributions of eddy diffusivity from measurements of trace gas concentration profiles (e.g., see Massie and Hunten, 1981).
Kondo et al. (1988) made use of the photochemical equilibrium between NO and NO2 for understanding diurnal variations in NO concentration measured during aircraft flights. In the paper by Webster et al. (1990) simultaneous in situ balloon-borne measurements of NO, NO2, HNO3, O3, and N2O and the photochemical equilibrium condition for various nitrogen components were used to determine OH, N2O5, and NOy concentrations. A similar approach was employed by Kawa et al. (1990), who obtained NO2, N2O5, ClNO3, HNO3, and OH concentrations from aircraft measurements of NO, ClO, and O3 concentrations. Hauchecorne et al. (2010) found that NO3 concentration measured by GOMOS/ENVISAT positively correlates with temperature at altitudes up to 45 km in the region where NO3 is in chemical equilibrium with O3. Funke et al. (2005) used NO and NO2 stable-state photochemistry to verify correctness of the new approach of retrieving distributions of those components from MIPAS/ENVISAT measurement data. Marchand et al. (2007) proposed a method to retrieve the temperature distribution in the stratosphere between 30 and 40 km from O3 and NO3 measurements by GOMOS with the help of a simple equation derived from the nighttime NO3 chemical equilibrium.
-
In investigations of the chemistry of Ox-HOx components and atmospheric glows in the mesosphere to lower thermosphere (MLT) area. In particular, Kulikov et al. (2006, 2009a) proposed algorithms for the simultaneous retrieval of O, H, HO2, and H2O from joint OH and O3 satellite measurement, in which the assumption of photochemical equilibrium of O3, OH, and HO2 was utilized. For several decades the assumption of the photochemical equilibrium of ozone (PEO) was widely used to determine distributions of atomic oxygen and atomic hydrogen at altitudes of the MLT via satellite and rocket measurements of ozone concentration and airglow emissions (e.g., Evans and Llewellyn, 1973; Good, 1976; Pendleton et al., 1983; McDade et al., 1985; McDade and Llewellyn, 1988; Evans et al., 1988; Thomas, 1990; Llewellyn et al., 1993; Llewellyn and McDade, 1996; Mlynczak et al., 2007, 2013a, b, 2014; Smith et al., 2010; Siskind et al., 2008, 2015). Russell and Lowe (2003) applied PEO to infer the seasonal and global climatology of atomic oxygen using WINDII/UARS. PEO was deployed to investigate hydroxyl emission mechanisms, morphology, and variability in the MLT region (Marsh et al., 2006; Xu et al., 2010, 2012; Kowalewski et al., 2014). Mlynczak and Solomon (1991, 1993) and Mlynczak et al. (2013b) used the equilibrium assumption to derive exothermic chemical heat. The PEO assumption was employed for studying the mesospheric OH* layer response to gravity waves (Swenson and Gardner, 1998). In ultimately theoretical works, e.g., Grygalashvyly et al. (2014) and Grygalashvyly (2015), PEO was used to derive the dependence of excited hydroxyl layer concentration and altitude on atomic oxygen and temperature. In the paper by Sonnemann et al. (2015) it was used to analyze annual variations of the OH* layer. Moreover, PEO is frequently applied implicitly, when authors are equating the nighttime loss of ozone in the reaction with atomic hydrogen and production of ozone by a 3-body reaction of molecular and atomic oxygen (e.g., Nikoukar et al., 2007).
In the present Technical Note we demonstrate how the photochemical equilibrium condition of several atmospheric components may be employed to statistically validate data of their simultaneous measurements, particularly in the case when measurement error is large.
We consider the simultaneous photochemical daytime equilibrium of OH, HO2, and O3 at the altitudes of the mesosphere. We have derived a simplified algebraic equation
describing the relationship between local concentrations of the components at the altitudes of 50–100 km. The only parameters of the equation are temperature, neutral density, local zenith angle, and constants of eight reactions. A one-year simulation of the mesosphere and lower thermosphere based on a 3-D chemical-transport model shows that the discrepancy between the calculated evolution of the components and the equilibrium value given by the equation does not exceed 3–4 % in the full range of altitudes independent of season or latitude.
We have developed a statistical Bayesian evaluation technique for simultaneous measurement of OH, HO2, and O3 based on the mentioned equilibrium equation taking into account the measurement error. The first results of its application to MLS/Aura data (Wang et al., 2015a, b; Schwartz et al., 2015) are presented. It is found that the satellite data of the HO2 distribution regularly demonstrate lower altitudes of this component's mesospheric maximum. These results confirm the ones obtained via the offline retrieval of HO2 from the MLS primary data (Millán et al., 2015).
This Technical Note is structured as follows. A 3-D chemical transport model is briefly described in Sect. 2. In Sect. 3, a simplified algebraic relationship between the equilibrium concentrations of OH, HO2, and O3 is derived and verified by 3-D simulations. Section 4 presents the method of statistical evaluation of simultaneous data of OH, HO2, and O3. The results of applying the method to MLS/Aura data are presented in Sect. 5. The last section contains a discussion of the results followed by concluding remarks.
For our calculations we used the global 3-D chemical transport model (CTM) of the middle atmosphere developed by the Leibniz Institute of Atmospheric Physics (IAP; e.g., Berger, 1994; Ebel et al., 1995; Kremp et al., 1999; Berger and von Zahn, 1999; Hartogh et al., 2004, 2011; Sonnemann et al., 1998, 2006, 2007). It was designed particularly for investigation of the spatio-temporal structure of phenomena in the MLT region and specifically in the extended mesopause region. The grid-point model extends from the ground up to the middle thermosphere (0–150 km; 118 pressure-height levels). The horizontal resolution amounts to 5.625∘ latitudinally and 5.625∘ longitudinally. The chemical module described in numerous papers (e.g., Sonnemann et al., 1998; Körner and Sonnemann, 2001; Grygalashvyly et al., 2009, 2011, 2012) consists of 19 constituents, 49 chemical reactions, and 14 photo-dissociation reactions (see Table 1). The reaction rates used in the model are taken from Burkholder et al. (2015). The temperature-dependent reaction rates are calculated online; thus, they are sensitive to small temperature fluctuations. We make use of the pre-calculated dissociation rates (Kremp et al., 1999).
The evolution of the components of the HOx (H, OH, HO2, H2O2) and NOx (N, NO, NO2, NO3) families is calculated using the chemical family concept proposed by Shimazaki (Shimazaki, 1985). This is done because of the presence of short-lived components among these families, with lifetimes much shorter than those of the families themselves, which imposes significant restrictions on the value of the CTM's integration step. For example, the daytime lifetimes of OH and HO2 above 70 km are about 1 s or less, while the lifetime of the HOx family is about 104 s or more. Therefore, when calculating these components individually it is necessary to set the CTM's integration step to be much less than 1 s. In our work, the Shimazaki technique is applied for calculating the evolution of each component of the HOx and NOx families. We emphasize that this technique does not explicitly use the steady-state approximation for the components, instead it utilizes the approach based on an implicit Euler scheme (see Shimazaki, 1985). This allows for increasing the integration step of the CTM significantly without loss of accuracy in calculating the short-lived components. In our work the integration time is chosen to be 9 s.
The model includes 3-D advective and vertical diffusive transport (turbulent and molecular). Three-dimensional fields of temperature and winds are taken from the Canadian Middle Atmosphere Model (CMAM) for the year 2000 (de Grandpre et al., 2000; Scinocca et al., 2008). We use the Walcek scheme (Walcek and Aleksic, 1998; Walcek, 2000) for advective transport and the implicit Thomas algorithm as described in Morton and Mayers (1994) for diffusive transport. The vertical eddy diffusion coefficient is based on the results by Lübken (1997).
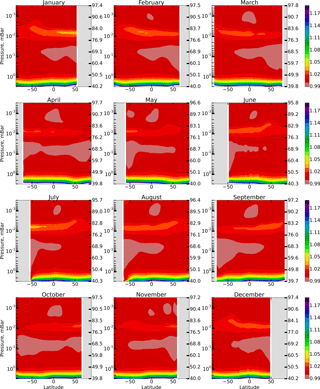
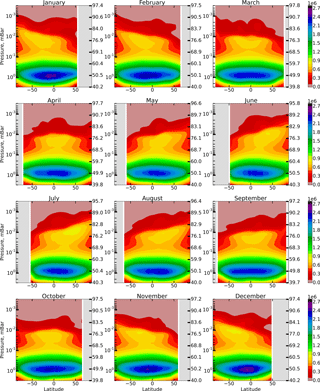
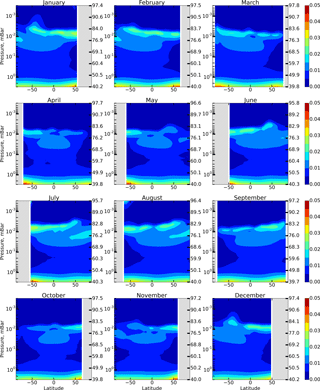
We calculate the annual variation in spatio-temporal distributions of OH, HO2, and O3 and constructed distributions of the F(OH, HO2,O3) function introduced in Sect. 1. To remove transitional regions that correspond to sunset and sunrise, we only take into account periods of local time with the solar zenith angle χ<85∘. The obtained results are presented in the model coordinates, so the pressure-height levels are used for the vertical axes. In addition, the approximate altitudes are shown in the figures of Sect. 1, calculated for a given month utilizing averaged temperature profiles of the model and hydrostatic equilibrium.
The daytime balance of OH concentration at mesospheric altitudes is determined by the following primary reactions (Brasseur and Solomon, 2005):
The daytime balance of the HO2 concentration is
The daytime balance of the O3 concentration is
Expressions for local concentrations of OH, HO2, and O3 in the photochemical equilibrium are written in the form
where ki are the corresponding reaction constants from Burkholder et al. (2015).
We eliminate O and H from Eqs. (1)–(3) and derive an expression depending only on OH, HO2, and O3.
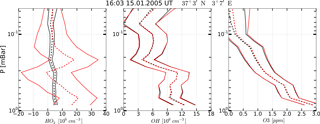
Figure 4Example of OH, HO2, and O3 vertical profiles measured (red curves) on 15 January 2005 at 16:03 UT, 37∘3′ N, 3∘7′ E and corresponding retrieved profiles (black curves). Solid curves: boundaries of the 65 % confidence intervals, dashed curves: medians.
Almost everywhere in the mesosphere and lower thermosphere (with the exception of 85–95 km, see Kulikov et al., 2017) the photodissociation is the main ozone sink, i.e., . Therefore, in the zero order approximation, Eq. (3) can be simplified and the concentration of atomic oxygen can be defined in terms of ozone concentration:
Making use of Eq. (4) we can derive, from Eq. (2), an expression for the concentration of H in terms of concentrations of OH, HO2, and O3:
By substituting this equation and Eq. (4) into Eq. (1) we obtain an expression relating OH, HO2, and O3:
Figure 1 shows height–latitude cross-sections of for each month (in this section angle brackets denote monthly averaged zonal mean values). The gray area corresponds to χ>85∘. One can see that Eq. (6) is most accurate within the 50–76 km range and above 86 km, where %. The difference reaches 3–4 % in the region between 76 and 86 km. The altitude of this region has an annual variation with a maximum deviation in the winter hemisphere. Below 50 km the value of increases up to 1.2 at 40 km, thus below the stratopause Eq. (6) no longer describes the simultaneous photochemical equilibrium of OH, HO2, and O3. Note that these components remain short-lived below 50 km (with the lifetimes of about 102–103 s; Brasseur and Solomon, 2005) depending on height and duration of daylight. However, for a quantitative description of their daytime equilibrium, it is necessary to include additional reactions involving, in particular, the components of the NOx family.
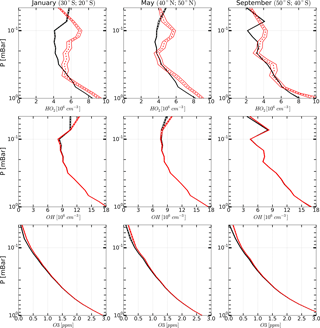
Figure 5Examples of monthly averaged zonal mean vertical profiles of OH, HO2, and O3 measured (red curves) in January, May, and March 2005 and corresponding retrieved profiles (black curves). Solid curves: boundaries of the 65 % confidence intervals, dashed curves: medians.
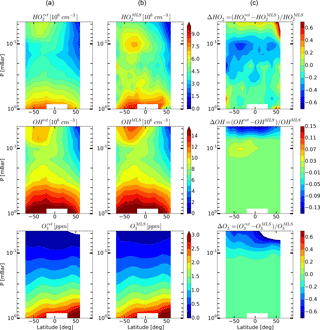
Figure 6Daytime monthly averaged zonal mean retrieved (a) and measured (b) distributions of HO2, OH, and O3 and their relative difference (c) in January 2005.
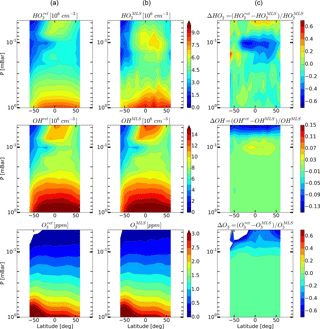
Figure 7Daytime monthly averaged zonal mean retrieved (a) and measured (b) distributions of HO2, OH, and O3 and their relative difference (c) for May 2005.
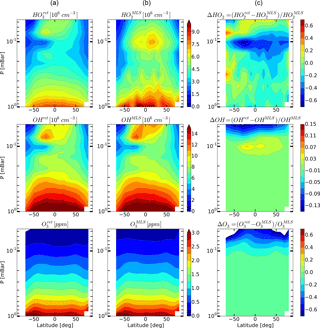
Figure 8Daytime monthly averaged zonal mean retrieved (a) and measured (b) distributions of HO2, OH, and O3 and their relative difference (c) for September 2005.
Note also that Eqs. (1) and (6) take into account only the main daytime source of OH (POH) specified by reactions (R18), (R14), and (R21):
These reactions run “inside” the HOx (H, OH, HO2, H2O2) family and do not perturb its total concentration. The height–latitude cross-sections of for each month are presented in Fig. 2.
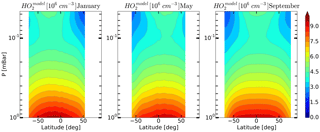
Figure 9Daytime monthly averaged zonal mean model distributions of HO2 for January, May, and September.
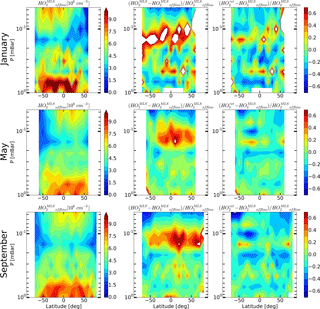
Figure 10Daytime mean monthly averaged distributions of HO2 retrieved by Millán et al. (2015) and relative differences and .
The next important daytime source of OH is specified by reactions (R59) and (R7) involving H2O, the main source for the HOx family:
Figure 3 shows height–latitude cross-sections of for each month. Comparing Figs. 1 and 3, we conclude that the previously indicated 3–4 % deviation of from 1 in the region between 76 and 86 km is largely due to the neglect of these reactions.
Another source of OH is sporadically activated during charged particle precipitation events and exists for a relatively short time (several days). Solar proton events (SPEs) perturb the ionic composition in the mesosphere and the upper stratosphere considerably and trigger a whole cascade of reactions involving ions, neutral components, and their clusters (e.g., O ⋅ H2O). This leads to an additional (to reactions R59 and R7) conversion of H2O molecules into OH and H (Solomon et al., 1981). The maximum of the OH production rate ( induced by SPE is located in the polar latitudes in the region of 60–80 km and, as a rule, does not exceed 2×103 cm−3 s−1 (Jackman et al., 2011, 2014). It can be seen from Fig. 2 that at these latitudes and altitudes the ratio does not exceed 1–2 %, even for the maximum values of . This means that the impact of on Eq. (6) is of the same order of smallness as in the case of reactions (R59) and (R7); hence, it may be neglected. A similar conclusion can be made for other reactions from Table 1, not accounted for by Eq. (6), including the ones involving NOx in both quiet and perturbed conditions in the mesosphere.
The proposed method is based on the statistical Bayesian procedure described in the works by Kulikov et al. (2009b) and Nechaev et al. (2016). It was originally developed for retrieving trace gas concentrations in the mesosphere from ground-based and satellite measurements of other mesospheric components. With respect to the considered evaluation problem, this procedure consists of three steps: (i) constructing a conditional probability density function (PDF) of OH, HO2, and O3 concentration values at each altitude z in the selected interval assuming that there is certain measurement data of these components and the algebraic relationship (6) is valid; ii) calculating the first moments of this distribution, i.e., expected value and dispersion of each component using the Metropolis–Hastings algorithm (Chib and Greenberg, 1995) for multidimensional integration; (iii) comparing the obtained results with the initial measurement data.
For constructing posterior PDF it is convenient to introduce vector , whose components are the retrieved values of chemical species concentrations at a certain altitude z, and vector composed of experimentally measured values of the components of vector u, , where ξj is a random error of measuring the jth component of vector u at the altitude z. It is assumed that
-
random variables ξj are distributed normally with densities
-
ξj are mutually independent:
where Wξ(ξ) is the total PDF of all ξj;
-
dispersions σj in Eq. (7), that are expected error values, are assumed to be known a priori (in our case they are provided by the MLS retrieval algorithm along with measured data).
Then the probability to observe vector x is given by the conditional PDF
where δ (...) is the delta function.
The prior relationship of HO, O, and OHret concentrations (Eq. 6) can be written as . Integrating the left-hand side of Eq. (9) with the conditional PDF of the variable u3:
yields a likelihood function of the model
According to Bayes' theorem, the posterior function, i.e., the probability density of latent variables u1 and u2, under the condition that x is observed, is defined by the expression
in which Papr(u1,u2) defines the prior PDF of u1 and u2.
The retrieved value of the latent variable is hereinafter understood as the mean value of the function in Eq. (11):
Its dispersion defines the uncertainty in the retrieval:
where the angle brackets denote averaging in the sense of Eq. (12).
We used the latest version (v4.2) of the MLS “standard” product (Livesey et al., 2017) for trace gas concentrations and temperature T within the 1–0.046 mbar pressure interval, where all data are suitable for scientific applications (Wang et al., 2015a, b; Schwartz et al., 2015). We took the daytime data when the solar zenith angle χ<80∘ for January, May, and September 2005. All data were appropriately screened. “Pressure”, “estimated precision”, “status flag”, “quality”, “convergence”, and “clouds” fields were taken into account. HO2 data were seen as the day-minus-night difference as prescribed by the MLS data guidelines (Livesey et al., 2017). Following Pickett et al. (2008), each daytime profile of this component measured on a given day at a latitude Lat, a profile resulting from averaging the nighttime profiles of HO2, measured on the same day in the latitude range of Lat ± 5∘, was subtracted. This operation eliminates systematic biases affecting HO2 retrievals, but limits the studied latitude range to the one where MLS observes both daytime and nighttime data.
The integrals in Eqs. (12)–(13) were calculated at every pressure level p for each set of simultaneously measured vertical profiles OHMLS(p), HO, O, TMLS(p), , , and . The vertical profiles , , , , , and were found at each point of the globe along the satellite track. Numerical integration was performed by a Monte Carlo method. For each pressure level, a sample of about 5×105 pairs of random variable values distributed with normalized probability density given by Eq. (11) with was generated with the help of the Metropolis–Hastings algorithm (Chib and Greenberg, 1995). In this case, the statistical moments in Eqs. (12)–(13) were determined by summation over the sample.
A typical example of retrieved profiles HO, O, and OHret (black curves) in comparison with the measured HO, O, and OHMLS (red curves) is given in Fig. 4. First of all, note that statistics of the retrieved data are in satisfactory agreement with the initial measurement of OH and O3 concentrations, but not of HO2. The error of satellite measurement, , greatly exceeds the uncertainty in the retrieval, , so at some altitudes the values of (red dashed curves) do not fall within the corresponding intervals . Second, the results of a single measurement of all three components and their retrieved values have considerable uncertainties relative to their means within the whole interval of altitudes. Therefore, the observed and retrieved data should be compared using the commonly accepted approach (e.g., Pickett et al., 2008) of averaging large ensembles of profiles within certain latitude and time ranges, or zones. It is supposed that the noise of satellite measurement instruments is delta-correlated, so that random values corresponding to each single measured or retrieved profile are statistically independent. In this case the dispersion of a measured or retrieved zonal mean profile is determined by summation
where N is the number of measured or retrieved profiles within the zone and is the dispersion of the kth measured or retrieved profile.
The range of latitudes covered by the satellite trajectory was divided into 17 bins 10∘ each. About 3000 single profiles of each chemical component fall into one bin during a month of MLS/Aura observations. Therefore, the resulting uncertainties due to measurement noise in OH, HO2, and O3 concentration profiles (both measured and retrieved) averaged over such ensembles are significantly lower (about one and a half orders of magnitude) than the uncertainties in individual profiles. Examples of such profiles for January, May, and September 2005 are presented in Fig. 5. One can see that the indicated uncertainties are now small enough to make clear conclusions about the extent to which the observed and retrieved profiles agree by comparing their averaged values only, i.e., , , and and , , and .
Figures 4–6 show monthly averaged zonal mean pressure–latitude cross-sections of , , and as well as similar characteristics for OH and O3 concentration profiles for three months of the year 2005. First, clearly, the distributions of and are in good qualitative and quantitative agreement with the initial MLS/Aura measurement data at lower altitudes, below ∼ 0.07 and 0.1 mbar, correspondingly. At higher altitudes, the distributions of reproduce all the main structural features of , but the retrieved OH concentration has lower values than the observed one with a relative difference ΔOH reaching ∼ 15 % at the top. The distribution of above 0.1 mbar, in turn, differs considerably from , both in quantity and quality, and ΔO3 locally reaches 50–60 % and more. Second, for all months there are significant qualitative and quantitative differences between and , the most noticeable one being location of the mesospheric maximum of this component's concentration. According to the observations it is close to 0.1 mbar, while the retrieved data demonstrate the altitudes of about ∼ 0.046 mbar or higher. Our analysis of the applied method of statistical evaluation demonstrates that the higher position of this maximum in the distributions of is influenced by the OHMLS data in which the mesospheric maximum (see Figs. 6–8) is also located notably higher than 0.1 mbar.
On the basis of the data presented in Sect. 5 we can conclude that, upon the whole, simultaneous OH, HO2 and O3 satellite measurements poorly satisfy the photochemical equilibrium condition. This bias is most prominent for the HO2 component. We can conjecture that a possible explanation for the bias is the significant systematic error in HO2 measurements, particularly at the height of the mesospheric maximum. This assumption is supported by the calculation of the HO2 distributions with the use of our 3-D chemical transport model (see Fig. 9). It can be seen that the mesospheric maximum of HO2 in these months, as well as of the distributions lies above 0.046 mbar.
Moreover, new data on the HO2 distributions were recently obtained from the MLS measurements. Millán et al. (2015) performed the offline retrieval of daily zonal means of HO2 profiles using averaged MLS radiances measured in 10∘ latitude bins. Averaged spectra have a better signal-to-noise ratio, which removes many of the limitations of the MLS standard product for HO2. In particular, the upper boundary of the altitude region in which daytime data are suitable for scientific use has reached 0.0032 mbar, and the “day-minus-night” correction is not needed at altitudes above 1 mbar. Comparison with various experimental and model data has shown that the offline retrieval reproduces the basic properties of the HO2 distribution in the mesosphere relatively well (at least qualitatively; Millán et al., 2015).
The offline retrieval product, the alternative data set of daytime HO2, has recently become publicly available at https://mls.jpl.nasa.gov (last access: 26 May 2018). Figure 10 shows the monthly averaged zonal means of the offline retrieval data ( and relative differences with retrieved and MLS standard product data and , correspondingly. Figure 10 represents the same time periods as Figs. 6–8. It is worth noting that the distributions depicted in Fig. 10 represent significantly different amounts of data. The data sets for May and September include 31 and 27 days of measurements, respectively, whereas the January data set encompasses only 4 days. The latter makes the graphs in the first row in Fig. 10 noisier than the others. One can see that the results of the offline HO2 retrieval show the same features as the results of our evaluation technique in comparison to the standard MLS retrieval, i.e., the height of mesospheric HO2 maximum is notably higher. We can conclude that the distributions of better match than , although some quantitative discrepancy between and also exists. Note that this may be due to systematic errors in the distributions, which cannot be excluded within the framework of the introduced technique. For a detailed qualitative and quantitative comparison of and , one should modify the method so that a statistical evaluation of the OHMLS and O standard products, and the data of the offline HO2 retrieval, could be conducted within the framework of a single procedure with no account for the HO distributions. This modification is under way and will be presented elsewhere.
The proposed method for statistical evaluation of mesospheric species measurements can be readily generalized to other atmospheric photochemical systems that contain short-lived components (see Introduction). It may also be modified for assessing hard-to-measure chemical components, characteristics of atmospheric processes (like wind speed or turbulent diffusion rate), or poorly known reaction rates.
Inquiries about the data used in this paper can be addressed to Mikhail Belikovich (belikovich@ipfran.ru).
The authors declare that they have no conflict of interest.
This work was carried out within the framework of the state assignment of IAP
RAS (project 0035-2014-0033) and was supported partially by the Russian
Foundation for Basic Research (project no. 17-05-01142).
Edited by: Patrick Jöckel
Reviewed by: two anonymous referees
Avallone, L. M. and Toohey, D. W.: Tests of halogen photochemistry using in situ measurements of ClO and BrO in the lower polar stratosphere, J. Geophys. Res., 106, 10411–1042, https://doi.org/10.1029/2000JD900831, 2001.
Benton, A. K., Langridge, J. M., Ball, S. M., Bloss, W. J., Dall'Osto, M., Nemitz, E., Harrison, R. M., and Jones, R. L.: Night-time chemistry above London: measurements of NO3 and N2O5 from the BT Tower, Atmos. Chem. Phys., 10, 9781–9795, https://doi.org/10.5194/acp-10-9781-2010, 2010.
Berger, U.: Numerische Simulation klimatologischer Prozesse und thermische Gezeiten in der mittleren Atmosphäre, Thesis, Univ. Cologne, Germany, 1994.
Berger, U. and von Zahn, U.: The two-level structure of the mesopause: A model study, J. Geophys. Res., 104, 22083–22093, 1999.
Berthet, G., Ricaud, P., Lefevre, F., Le Flochmoen, E., Urban, J., Barret, B., Lautie, N., Dupuy, E., De La Noe, J., and Murtagh, D.: Nighttime chlorine monoxide observations by the Odin satellite and implications for the ClO/Cl2O2 equilibrium, Geophys. Res. Lett., 32, L11812, https://doi.org/10.1029/2005GL022649, 2005.
Brasseur, G. and Solomon, S.: Aeronomy of the Middle Atmosphere, 644 pp., 3rd edition, Springer, The Netherlands, 2005.
Brown, S. S., Stark, H., Ryerson, T. B., Williams, E. J., Nicks Jr., D. K., Trainer, M., Fehsenfeld, F. C., and Ravishankara, A. R.: Nitrogen oxides in the nocturnal boundary layer: Simultaneous in situ measurements of NO3, N2O5, NO2, NO, and O3, J. Geophys. Res., 108, ACH18-1–ACH18-11, https://doi.org/10.1029/2002JD002917, 2003.
Burkholder, J. B., Sander, S. P., Abbatt, J., Barker, J. R., Huie, R. E., Kolb, C. E., Kurylo, M. J., Orkin, V. L., Wilmouth, D. M., and Wine, P. H.: Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 18, JPL Publication 15-10, Jet Propulsion Laboratory, Pasadena, available at: http://jpldataeval.jpl.nasa.gov (last access: 26 May 2018), 2015.
Butz, A., Bosch, H., Camy-Peyret, C., Dorf, M., Engel, A., Payan, S., and Pfeilsticker, K.: Observational constraints on the kinetics of the ClO-BrO and ClO-ClO ozone loss cycles in the Arcticwinter stratosphere, Geophys. Res. Lett., 34, L05801, https://doi.org/10.1029/2006GL028718, 2007.
Cantrell, C. A., Mauldin, L., Zondlo, M., Eisele, F., Kosciuch, E., Shetter, R., Lefer, B., Hall, S., Campos, T., Ridley, B., Walega, J., Fried, A., Wert, B., Flocke, F., Weinheimer, A., Hannigan, J., Coffey, M., Atlas, E., Stephens, S., Heikes, B., Snow, J., Blake, D., Blake, N., Katzenstein, A., Lopez, J., Browell, E. V., Dibb, J., Scheuer, E., Seid, G., and Talbot, R.: Steady state free radical budgets and ozone photochemistry during TOPSE, J. Geophys. Res., 108, TOP9-1–TOP9-22, https://doi.org/10.1029/2002JD002198, 2003.
Chameides, W.: Tropospheric odd nitrogen and the atmospheric water vapor cycle, J. Geophys. Res., 84, 4989–4996, https://doi.org/10.1029/JC080i036p04989, 1975.
Chib, S. and Greenberg, E.: Understanding the Metropolis-Hastings Algorithm, The American Statistician, 49, 327–335, https://doi.org/10.2307/2684568, 1995.
Crawford, J., Davis, D., Chen, G., Bradshaw, J., Sandholm, S., Gregory, G., Sachse, G., Anderson, B., Collins, J., Blake, D., Singh, H., Heikes, B., Talbot, R., and Rodriguez, J.: Photostationary state analysis of the NO2-NO system based on airborne observations from the western and central North Pacific, J. Geophys. Res., 101, 2053–2072, https://doi.org/10.1029/95JD02201, 1996.
Crowley, J. N., Schuster, G., Pouvesle, N., Parchatka, U., Fischer, H., Bonn, B., Bingemer, H., and Lelieveld, J.: Nocturnal nitrogen oxides at a rural mountain-site in south-western Germany, Atmos. Chem. Phys., 10, 2795–2812, https://doi.org/10.5194/acp-10-2795-2010, 2010.
de Grandpre, J., Beagley, S. R., Fomichev, V. I., Griffioen, E., McConnell, J. C., Medvedev, A. S., and Shepherd., T. G.: Ozone climatology using interactive chemistry: Results from the Canadian Middle Atmosphere Model, J. Geophys. Res.-Atmos., 105, 26475–26491, https://doi.org/10.1029/2000JD900427, 2000.
Djouad, R., Michelangeli, D. V., and Gong, W.: Numerical solution for atmospheric multiphase models: Testing the validity of equilibrium assumptions, J. Geophys. Res., 108, ACH1-1–ACH1-13, https://doi.org/10.1029/2002JD002969, 2003.
Douglass, A. R., Jackman, C. H., and Stolarski, R. S.: Comparison of model results transporting the odd nitrogen family with results transporting separate odd nitrogen species, J. Geophys. Res., 94, 9862–9872, https://doi.org/10.1029/JD094iD07p09862, 1989.
Ebel, A., Berger, U., and Krueger, B. C.: Numerical simulations with COMMA, a global model of the middle atmosphere, SIMPO Newsletter, 12, 22–32, 1995.
Evans, W. F. J. and Llewellyn, E. J.: Atomic hydrogen concentrations in the mesosphere and the hydroxyl emissions, J. Geophys. Res., 78, 323–326, https://doi.org/10.1029/JA078i001p00323, 1973.
Evans, W. F. J., McDade, I. C., Yuen, J., and Llewellyn, E. J.: A rocket measurement of the O2 infrared atmospheric (0-0) band emission in the dayglow and a determination of the mesospheric ozone and atomic oxygen densities, Can. J. Phys., 66, 941–946, https://doi.org/10.1139/p88-151, 1988.
Feigin, A. M. and Konovalov, I. B.: On the possibility of complicated dynamic behavior of atmospheric photochemical systems: Instability of the Antarctic photochemistry during the ozone hole formation, J. Geophys. Res., 101, 26023–26038, https://doi.org/10.1029/96JD02011, 1996.
Feigin, A. M., Konovalov, I. B., and Molkov, Ya. I.: Towards understanding nonlinear nature of atmospheric photochemistry: Essential dynamic model of the mesospheric photochemical system, J. Geophys. Res., 103, 25447–25460, https://doi.org/10.1029/98JD01569, 1998.
Funke, B., Lopez-Puertas, M., von Clarmann, T., Stiller, G. P., Fischer, H., Glatthor, N., Grabowski, U., Hopfner, M., Kellmann, S., Kiefer, M., Linden, A., Mengistu Tsidu, G., Milz, M., Steck, T., and Wang, D. Y.: Retrieval of stratospheric NOx from 5.3 and 6.2 mm nonlocal thermodynamic equilibrium emissions measured by Michelson Interferometer for Passive Atmospheric Sounding (MIPAS) on Envisat, J. Geophys. Res., 110, D09302, https://doi.org/10.1029/2004JD005225, 2005.
Ghosh, S., Pyle, J. A., and Good, P.: Temperature dependence of the ClO concentration near the stratopause, J. Geophys. Res., 102, 19207–19216, https://doi.org/10.1029/97JD01099, 1997.
Good, R. E.: Determination of atomic oxygen density from rocket borne measurements of hydroxyl airglow, Planet. Space Sci., 24, 389–395, doi.org/10.1016/0032-0633(76)90052-0, 1976.
Grygalashvyly, M.: Several notes on the OH* layer, Ann. Geophys., 33, 923–930, https://doi.org/10.5194/angeo-33-923-2015, 2015.
Grygalashvyly, M., Sonnemann, G. R., and Hartogh, P.: Long-term behavior of the concentration of the minor constituents in the mesosphere – A model study, Atmos. Chem. Phys., 9, 2779–2792, https://doi.org/10.5194/acp-9-2779-2009, 2009.
Grygalashvyly, M., Becker, E., and Sonnemann, G. R.: Wave mixing effects on minor chemical constituents in the MLT region: Results from a global CTM driven by high-resolution dynamics, J. Geophys. Res., 116, D18302, https://doi.org/10.1029/2010JD015518, 2011.
Grygalashvyly, M., Becker, E., and Sonnemann, G. R.: Gravity wave mixing and effective diffusivity for minor chemical constituents in the mesosphere/lower thermosphere, Space Sci. Rev., 168, 333–362, https://doi.org/10.1007/s11214-011-9857-x, 2012.
Grygalashvyly, M., Sonnemann, G. R., Lübken, F.-J., Hartogh, P., and Berger, U.: Hydroxyl layer: Mean state and trends at midlatitudes, J. Geophys. Res.-Atmos., 119, 12391–12419, https://doi.org/10.1002/2014JD022094, 2014.
Hartogh, P., Jarchow, C., Sonnemann, G. R., and Grygalashvyly, M.: On the spatiotemporal behavior of ozone within the upper mesosphere/mesopause region under nearly polar night conditions, J. Geophys. Res., 109, D18303, https://doi.org/10.1029/2004JD004576, 2004.
Hartogh, P., Sonnemann, G. R., Grygalashvyly, M., and Jarchow, Ch.: Ozone trends in mid-latitude stratopause region based on microwave measurements at Lindau (51.66∘ N, 10.13∘ E), the ozone reference model, and model calculations, Adv. Space Res., 47, 1937–1948, https://doi.org/10.1016/j.asr.2011.01.010, 2011.
Hauchecorne, A., Bertaux, J. L., Dalaudier, F., Keckhut, P., Lemennais, P., Bekki, S., Marchand, M., Lebrun, J. C., Kyrölä, E., Tamminen, J., Sofieva, V., Fussen, D., Vanhellemont, F., Fanton d'Andon, O., Barrot, G., Blanot, L., Fehr, T., and Saavedra de Miguel, L.: Response of tropical stratospheric O3, NO2 and NO3 to the equatorial Quasi-Biennial Oscillation and to temperature as seen from GOMOS/ENVISAT, Atmos. Chem. Phys., 10, 8873–8879, https://doi.org/10.5194/acp-10-8873-2010, 2010.
Jackman, C. H., Marsh, D. R., Vitt, F. M., Roble, R. G., Randall, C. E., Bernath, P. F., Funke, B., López-Puertas, M., Versick, S., Stiller, G. P., Tylka, A. J., and Fleming, E. L.: Northern Hemisphere atmospheric influence of the solar proton events and ground level enhancement in January 2005, Atmos. Chem. Phys., 11, 6153–6166, https://doi.org/10.5194/acp-11-6153-2011, 2011.
Jackman, C. H., Randall, C. E., Harvey, V. L., Wang, S., Fleming, E. L., López-Puertas, M., Funke, B., and Bernath, P. F.: Middle atmospheric changes caused by the January and March 2012 solar proton events, Atmos. Chem. Phys., 14, 1025–1038, https://doi.org/10.5194/acp-14-1025-2014, 2014.
Kawa, S. R., Fahey, D. W., Solomon, S., Brune, W. H., Proffitt, M. H., Toohey, D. W., Anderson Jr., D. E., Anderson, L. C., and Chan, K. R.: Interpretation of aircraft measurements of NO, ClO, and O3 in the lower stratosphere, J. Geophys. Res., 95, 18597–18609, https://doi.org/10.1029/JD095iD11p18597, 1990.
Kremp, C., Berger, U., Hoffmann, P., Keuer, D., and Sonnemann, G. R.: Seasonal variation of middle latitude wind fields of the mesopause region – a comparison between observation and model calculation, Geophys. Res. Lett., 26, 1279–1282, 1999.
Kaye, J. A. and Rood, R. B.: Chemistry and transport in a three-dimensional stratospheric model: Chlorine species during a simulated stratospheric warming, J. Geophys. Res., 94, 1057–1083, https://doi.org/10.1029/JD094iD01p01057, 1989.
Ko, M., Hu, W., Rodriguez, J. M., Kondo, Y., Koike, M., Kita, K., Kawakami, S., Blake, D., Liu, S., and Ogawa, T.: Photochemical ozone budget during the BIBLE A and B campaigns, J. Geophys. Res., 107, BIB 8-1–BIB 8-16, https://doi.org/10.1029/2001JD000800, 2002.
Koike, M., Kondo, Y., Kawakami, S., Singh, H. B., Ziereis, H., and Merrill, J. T.: Ratios of reactive nitrogen species over the Pacific during PEM-West A, J. Geophys. Res., 101, 1829–1851, https://doi.org/10.1029/95JD02728, 1996.
Konovalov, I. B. and Feigin, A. M.: Toward an understanding of the nonlinear nature of atmospheric photochemistry: Origin of the complicated dynamic behaviour of the mesospheric photochemical system, Nonlin. Processes Geophys., 7, 87–104, https://doi.org/10.5194/npg-7-87-2000, 2000.
Konovalov, I. B., Feigin, A. M., and Mukhina, A. Y.: Toward understanding of the nonlinear nature of atmospheric photochemistry: Multiple equilibrium states in the high-latitude lower stratospheric photochemical system, J. Geophys. Res., 104, 8669–8689, https://doi.org/10.1029/1998JD100037, 1999.
Körner, U. and Sonnemann, G. R.: Global 3D-modeling of water vapor concentration of the mesosphere/mesopause region and implications with respect to the NLC region, J. Geophys. Res.-Atmos., 106, 9639–9651, https://doi.org/10.1029/2000JD900744, 2001.
Kowalewski, S., von Savigny, C., Palm, M., McDade, I. C., and Notholt, J.: On the impact of the temporal variability of the collisional quenching process on the mesospheric OH emission layer: a study based on SD-WACCM4 and SABER, Atmos. Chem. Phys., 14, 10193–10210, https://doi.org/10.5194/acp-14-10193-2014, 2014.
Kremser, S., Schofield, R., Bodeker, G. E., Connor, B. J., Rex, M., Barret, J., Mooney, T., Salawitch, R. J., Canty, T., Frieler, K., Chipperfield, M. P., Langematz, U., and Feng, W.: Retrievals of chlorine chemistry kinetic parameters from Antarctic ClO microwave radiometer measurements, Atmos. Chem. Phys., 11, 5183–5193, https://doi.org/10.5194/acp-11-5183-2011, 2011.
Kulikov, M. Yu. and Feigin, A. M.: Automated construction of the basic dynamic models of the atmospheric photochemical systems using the RADM2 chemical mechanism as an example, Radiophys. Quantum Electron., 57, 478–487, https://doi.org/10.1007/s11141-014-9530-9, 2014.
Kulikov, M. Y., Feigin, A. M., and Sonnemann, G. R.: Retrieval of the vertical distribution of chemical components in the mesosphere from simultaneous measurements of ozone and hydroxyl distributions, Radiophys. Quantum Electron., 49, 683–691, https://doi.org/10.1007/s11141-006-0103-4, 2006.
Kulikov, M. Yu., Feigin, A. M., and Sonnemann, G. R.: Retrieval of water vapor profile in the mesosphere from satellite ozone and hydroxyl measurements by the basic dynamic model of mesospheric photochemical system, Atmos. Chem. Phys., 9, 8199–8210, https://doi.org/10.5194/acp-9-8199-2009, 2009a.
Kulikov, M. Y., Mukhin, D. N., and Feigin, A. M.: Bayesian strategy of accuracy estimation for characteristics retrieved from experimental data using base dynamic models of atmospheric photochemical systems, Radiophys. Quantum Electron., 52, 618–626, https://doi.org/10.1007/s11141-010-9171-6, 2009b.
Kulikov, M. Yu., Vadimova, O. L., Ignatov, S. K., and Feigin, A. M.: The mechanism of non-linear photochemical oscillations in the mesopause region, Nonlin. Processes Geophys., 19, 501–512, https://doi.org/10.5194/npg-19-501-2012, 2012.
Kulikov, M. Y., Belikovich, M. V., Grygalashvyly, M., Sonnemann, G. R., Ermakova, T. S., Nechaev, A. A., and Feigin, A. M.: Daytime ozone loss term in the mesopause region, Ann. Geophys., 35, 677–682, https://doi.org/10.5194/angeo-35-677-2017, 2017.
Livesey, N. J., Read, W. G., Wagner, P. A., Frovideaux, L., Lambert, A., Manney, G. L., Millan, L. F., Pumphrey, H. C., Santee, M. L., Schwartz, M. J., Wang, S., Fuller, R. A., Jarnot, R. F., Knosp, B. W., and Martinez, E.: Earth Observing System (EOS) Aura Microwave Limb Sounder (MLS) Version 4.2 Level 2 data quality and description document, JPL D-33509, JPL publication, USA, 2017.
Llewellyn, E. J. and McDade, I. C.: A reference model for atomic oxygen in the terrestrial atmosphere, Adv. Space Res., 18, 209–226, https://doi.org/10.1016/0273-1177(96)00059-2, 1996.
Llewellyn, E. J., McDade, I. C., Moorhouse, P., and Lockerbie, M. D.: Possible reference models for atomic oxygen in the terrestrial atmosphere, Adv. Space Res., 13, 135–144, https://doi.org/10.1016/0273-1177(93)90013-2, 1993.
Lübken, F. J.: Seasonal variation of turbulent energy dissipation rates at high latitudes as determined by in situ measurements of neutral density fluctuations, J. Geophys. Res., 102, 13441–13456, 1997.
Marchand, M., Bekki, S., Lefevre, F., and Hauchecorne, A.: Temperature retrieval from stratospheric O3 and NO3 GOMOS data, Geophys. Res. Lett., 34, L24809, https://doi.org/10.1029/2007GL030280, 2007.
Marsh, D. R., Smith, A. K., Mlynczak, M. G., and Russell III, J. M.: SABER observations of the OH Meinel airglow variability near the mesopause, J. Geophys. Res., 111, A10S05, https://doi.org/10.1029/2005JA011451, 2006.
Martinez, M., Perner, D., Hackenthal, E.-M., Kulzer, S., and Schultz, L.: NO3 at Helgoland during the NORDEX campaign in October 1996, J. Geophys. Res., 105, 22685–22695, https://doi.org/10.1029/2000JD900255, 2000.
Massie, S. T. and Hunten, D. M.: Stratospheric eddy diffusion coefficients from tracer data, J. Geophys. Res., 86, 9859–9868, https://doi.org/10.1029/JC086iC10p09859, 1981.
McDade, I. C. and Llewellyn, E. J.: Mesospheric oxygen atom densities inferred from night-time OH Meinel band emission rates, Planet. Space Sci., 36, 897–905, https://doi.org/10.1016/0032-0633(88)90097-9, 1988.
McDade, I. C., Llewellyn, E. J., and Harris, F. R.: Atomic oxygen concentrations in the lower auroral thermosphere, Adv. Space Res., 5, 229–232, https://doi.org/10.1016/0273-1177(85)90379-5, 1985.
McLaren, R., Wojtal, P., Majonis, D., McCourt, J., Halla, J. D., and Brook, J.: NO3 radical measurements in a polluted marine environment: links to ozone formation, Atmos. Chem. Phys., 10, 4187–4206, https://doi.org/10.5194/acp-10-4187-2010, 2010.
Millán, L., Wang, S., Livesey, N., Kinnison, D., Sagawa, H., and Kasai, Y.: Stratospheric and mesospheric HO2 observations from the Aura Microwave Limb Sounder, Atmos. Chem. Phys., 15, 2889–2902, https://doi.org/10.5194/acp-15-2889-2015, 2015.
Mlynczak, M. G. and Solomon, S.: Middle atmosphere heating by exothermic chemical reactions involving odd-hydrogen species, Geophys. Res. Lett., 18, 37–40, https://doi.org/10.1029/90GL02672, 1991.
Mlynczak, M. G. and Solomon, S.: A detailed evaluation of the heating efficiency in the middle atmosphere, J. Geophys. Res., 98, 10517–10541, https://doi.org/10.1029/93JD00315, 1993.
Mlynczak, M. G., Marshall, B. T., Martin-Torres, F. J., Russell III, J. M., Thompson, R. E., Remsberg, E. E., and Gordley, L. L.: Sounding of the Atmosphere using Broadband Emission Radiometry observations of daytime mesospheric O2(1D) 1.27 µm emission and derivation of ozone, atomic oxygen, and solar and chemical energy deposition rates, J. Geophys. Res., 112, D15306, https://doi.org/10.1029/2006JD008355, 2007.
Mlynczak, M. G., Hunt, L. A., Mast, J. C., Marshall, B. T., Russell III, J. M., Smith, A. K., Siskind, D. E., Yee, J.-H., Mertens, C. J., Martin-Torres, F. J., Thompson, R. E., Drob, D. P., and Gordley, L. L.: Atomic oxygen in the mesosphere and lower thermosphere derived from SABER: Algorithm theoretical basis and measurement uncertainty, J. Geophys. Res., 118, 5724–5735, https://doi.org/10.1002/jgrd.50401, 2013a.
Mlynczak, M. G., Hunt, L. H., Mertens, C. J., Marshall, B. T., Russell III, J. M., López-Puertas, M., Smith, A. K., Siskind, D. E., Mast, J. C., Thompson, R. E., and Gordley, L. L.: Radiative and energetic constraints on the global annual mean atomic oxygen concentration in the mesopause region, J. Geophys. Res.-Atmos., 118, 5796–5802, https://doi.org/10.1002/jgrd.50400, 2013b.
Mlynczak, M. G., Hunt, L. A., Marshall, B. T., Mertens, C. J., Marsh, D. R., Smith, A. K., Russell, J. M., Siskind, D. E., and Gordley, L. L.: Atomic hydrogen in the mesopause region derived from SABER: Algorithm theoretical basis, measurement uncertainty, and results, J. Geophys. Res., 119, 3516–3526, https://doi.org/10.1002/2013JD021263, 2014.
Morton, K. W. and Mayers, D. F.: Numerical Solution of Partial Differential Equations, Cambridge University Press, 1994.
Nechaev, A. A., Ermakova, T. S., and Kulikov, M. Y.: Determination of the Trace-Gas Concentrations at the Altitudes of the Lower and Middle Mesosphere from the Time Series of Ozone Concentration, Radiophys. Quantum Electron., 59, 546–559, https://doi.org/10.1007/s11141-016-9722-6, 2016.
Nikoukar, R., Swenson, G. R., Liu, A. Z., and Kamalabadi, F.: On the variability of mesospheric OH emission profiles, J. Geophys. Res., 112, D19109, https://doi.org/10.1029/2007JD008601, 2007.
Pendleton, W. R., Baker, K. D., and Howlett, L. C.: Rocket-based investigations of O(3P), O2(a1Δg) and OH*(ν=1,2) during the solar eclipse of 26 February1979, J. Atmos. Terr. Phys., 45, 479–491, https://doi.org/10.1016/S0021-9169(83)81108-8, 1983.
Penkett, S. A., Monks, P. S., Carpenter, L. J., Clemitshaw, K. C., Ayers, G. P., Gillett, R. W., Galbally, I. E., and Meyer, C. P.: Relationships between ozone photolysis rates and peroxy radical concentrations in clean marine air over the Southern Ocean, J. Geophys. Res., 102, 12805–12817, https://doi.org/10.1029/97JD00765, 1997.
Penkett, S. A., Reeves, C. E., Bandy, B. J., Kent, J. M., and Richer, H. R.: Comparison of calculated and measured peroxide data collected in marine air to investigate prominent features of the annual cycle of ozone in the troposphere, J. Geophys. Res., 103, 13377–13388, https://doi.org/10.1029/97JD02852, 1998.
Platt, U., Perner, D., and Pätz, H. W.: Simultaneous measurement of atmospheric CH2O, O3, and NO2 by differential optical absorption, J. Geophys. Res., 84, 6329–6335, 10.1029/JC084iC10p06329, 1979.
Pyle, J. A. and Zavody, A. M.: The derivation of hydrogen containing radical concentrations from satellite data sets, Q. J. Roy. Meteorol. Soc., 111, 993–1012, https://doi.org/10.1002/qj.49711147005, 1985.
Pyle, J. A., Zavody, A. M., Harries, J. E., and Moffat, P. H.: Derivation of OH concentration from satellite infrared measurements of NO2 and HNO3, Nature, 305, 690–692, https://doi.org/10.1038/305690a0, 1983.
Pickett, H. M. and Peterson, D. B.: Comparison of measured stratospheric OH with prediction, J. Geophys. Res., 101, 16789–16796, https://doi.org/10.1029/96JD01168, 1996.
Pickett, H. M., Drouin, B. J., Canty, T., Salawitch, R. J., Fuller, R. A., Perun, V. S., Livesey, N. J., Waters, J. W., Stachnik, R. A., Sander, S. P., Traub, W. A., Jucks, K. W., and Minschwaner, K.: Validation of Aura Microwave Limb Sounder OH and HO2 measurements, J. Geophys. Res., 113, D16S30, https://doi.org/10.1029/2007JD008775, 2008.
Rasch, P. J., Boville, B. A., and Brasseur, G. P.: A three-dimensional general circulation model with coupled chemistry for the middle atmosphere, J. Geophys. Res., 100, 9041–9071, https://doi.org/10.1029/95JD00019, 1995.
Russell, J. P. and Lowe, R. P.: Atomic oxygen profiles (80–94 km) derived from Wind Imaging Interferometer/Upper Atmospheric Research Satellite measurements of the hydroxyl airglow: 1. Validation of technique, J. Geophys. Res., 108, ACH5-1–ACH5-8, https://doi.org/10.1029/2003JD003454, 2003.
Schwartz, M., Froidevaux, L., Livesey, N., and Read, W.: MLS/Aura Level 2 Ozone (O3) Mixing Ratio V004, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), https://doi.org/10.5067/AURA/MLS/DATA2017, 2015.
Scinocca, J. F., McFarlane, N. A., Lazare, M., Li, J., and Plummer, D.: The CCCma third generation AGCM and its extension into the middle atmosphere, Atmos. Chem. Phys., 8, 7055–7074, https://doi.org/10.5194/acp-8-7055-2008, 2008.
Shimazaki, T.: Minor Constituents in the Middle Atmosphere, D. Reidel, Norwell, Mass., USA, 444 pp., 1985.
Siskind, D. E., Marsh, D. R., Mlynczak, M. G., Martin-Torres, F. J., and Russell III, J. M.: Decreases in atomic hydrogen over the summer pole: Evidence for dehydration from polar mesospheric clouds?, Geophys. Res. Lett., 35, L13809, https://doi.org/10.1029/2008GL033742, 2008.
Siskind, D. E., Mlynczak, M. G., Marshall, T., Friedrich, M., and Gumbel, J.: Implications of odd oxygen observations by the TIMED/SABER instrument for lower D region ionospheric modeling, J. Atmos. Sol. Terr. Phys., 124, 63–70, https://doi.org/10.1016/j.jastp.2015.01.014, 2015.
Smith, A. K., Marsh, D. R., Mlynczak, M. G., and Mast, J. C.: Temporal variations of atomic oxygen in the upper mesosphere from SABER, J. Geophys. Res., 115, D18309, https://doi.org/10.1029/2009JD013434, 2010.
Sobanski, N., Tang, M. J., Thieser, J., Schuster, G., Pöhler, D., Fischer, H., Song, W., Sauvage, C., Williams, J., Fachinger, J., Berkes, F., Hoor, P., Platt, U., Lelieveld, J., and Crowley, J. N.: Chemical and meteorological influences on the lifetime of NO3 at a semi-rural mountain site during PARADE, Atmos. Chem. Phys., 16, 4867–4883, https://doi.org/10.5194/acp-16-4867-2016, 2016.
Solomon, P., Connor, B., Barrett, J., Mooney, T., Lee, A., and Parrish, A.: Measurements of stratospheric ClO over Antarctica in 1996–2000 and implications for ClO dimer chemistry, Geophys. Res. Lett., 29, 3-1–3-4, https://doi.org/10.1029/2002GL015232, 2002.
Solomon, S., Rusch, D. W., Gerard, J.-C., Reid, G. C., and Crutzen, P. J.: The effect of particle precipitation events on the neutral and ion chemistry of the middle atmosphere. 2. Odd hydrogen, Planet. Space Sci., 29, 885–892, 1981.
Sonnemann, G., Kremp, C., Ebel, A., and Berger, U.: A three-dimensional dynamic model of minor constituents of the mesosphere, Atmos. Environ., 32, 3157–3172, https://doi.org/10.1016/S1352-2310(98)00113-7, 1998.
Sonnemann, G. R., Grygalashvyly, M., Hartogh, P., and Jarchow, C.: Behavior of mesospheric ozone under nearly polar night conditions, Adv. Space Res., 38, 2402–2407, https://doi.org/10.1016/j.asr.2006.09.011, 2006.
Sonnemann, G. R., Hartogh, P., Jarchow, C., Grygalashvyly, M., and Berger, U.: On the winter anomaly of the night-to-day ratio of ozone in the middle to upper mesosphere in middle to high latitudes, Adv. Space Res., 40, 846–854, https://doi.org/10.1016/j.asr.2007.01.039, 2007.
Sonnemann, G. R., Hartogh, P., Berger, U., and Grygalashvyly, M.: Hydroxyl layer: trend of number density and intra-annual variability, Ann. Geophys., 33, 749–767, https://doi.org/10.5194/angeo-33-749-2015, 2015.
Swenson, G. R. and Gardner, C. S.: Analytical models for the responses of the mesospheric OH* and Na layers to atmospheric gravity waves, J. Geophys. Res., 103, 6271–6294, https://doi.org/10.1029/97JD02985, 1998.
Stedman, D. H., Chameides, W., and Jackson, J. O.: Comparison of experimental and computed values for J(NO2), Geophys. Res. Lett., 2, 22–25, https://doi.org/10.1029/GL002i001p00022, 1975.
Stimpfle, R. M., Wilmouth, D. M., Salawitch, R. J., and Anderson, J. G.: First measurements of ClOOCl in the stratosphere: The coupling of ClOOCl and ClO in the Arctic polar vortex, J. Geophys. Res., 109, D03301, https://doi.org/10.1029/2003JD003811, 2004.
Sumińska-Ebersoldt, O., Lehmann, R., Wegner, T., Grooß, J.-U., Hösen, E., Weigel, R., Frey, W., Griessbach, S., Mitev, V., Emde, C., Volk, C. M., Borrmann, S., Rex, M., Stroh, F., and von Hobe, M.: ClOOCl photolysis at high solar zenith angles: analysis of the RECONCILE self-match flight, Atmos. Chem. Phys., 12, 1353–1365, https://doi.org/10.5194/acp-12-1353-2012, 2012.
Thomas, R. J.: Atomic hydrogen and atomic oxygen density in the mesosphere region: Global and seasonal variations deduced from Solar Mesosphere Explorer near-infrared emissions, J. Geophys. Res., 95, 16457–16476, https://doi.org/10.1029/JD095iD10p16457, 1990.
Tulet, P., Grini, A., Griffin, R. J., and Petitcol, S.: ORILAM-SOA: A computationally efficient model for predicting secondary organic aerosols in three-dimensional atmospheric models, J. Geophys. Res., 111, D23208, https://doi.org/10.1029/2006JD007152, 2006.
von Hobe, M., Grooß, J.-U., Müller, R., Hrechanyy, S., Winkler, U., and Stroh, F.: A re-evaluation of the ClO/Cl2O2 equilibrium constant based on stratospheric in-situ observations, Atmos. Chem. Phys., 5, 693–702, https://doi.org/10.5194/acp-5-693-2005, 2005.
von Hobe, M., Salawitch, R. J., Canty, T., Keller-Rudek, H., Moortgat, G. K., Grooß, J.-U., Müller, R., and Stroh, F.: Understanding the kinetics of the ClO dimer cycle, Atmos. Chem. Phys., 7, 3055–3069, https://doi.org/10.5194/acp-7-3055-2007, 2007.
Walcek, C. J.: Minor flux adjustment near mixing ratio extremes for simplified yet highly accurate monotonic calculation of tracer advection, J. Geophys. Res., 105, 9335–9348, 2000.
Walcek, C. J. and Aleksic, N. M.: A simple but accurate mass conservative, peak preserving, mixing ratio bounded advection algorithm with Fortran code, Atmos. Environ., 32, 3863–3880, 1998.
Wang, S., Pickett, H., Livesey, N., and Read, W.: MLS/Aura Level 2 Hydroperoxy (HO2) Mixing Ratio V004, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), https://doi.org/10.5067/AURA/MLS/DATA2013, 2015a.
Wang, S., Livesey, N., and Read, W.: MLS/Aura Level 2 Hydroxyl (OH) Mixing Ratio V004, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), https://doi.org/10.5067/AURA/MLS/DATA2018, 2015b.
Webster, C. R., May, R. D., Toumi, R., and Pyle, J. A.: Active nitrogen partitioning and the nighttime formation of N2O5 in the stratosphere: Simultaneous in situ measurements of NO, NO2, HNO3, O3, and N2O using the BLISS diode laser spectrometer, J. Geophys. Res., 95, 13851–13866, https://doi.org/10.1029/JD095iD09p13851, 1990.
Wetzel, G., Oelhaf, H., Kirner, O., Friedl-Vallon, F., Ruhnke, R., Ebersoldt, A., Kleinert, A., Maucher, G., Nordmeyer, H., and Orphal, J.: Diurnal variations of reactive chlorine and nitrogen oxides observed by MIPAS-B inside the January 2010 Arctic vortex, Atmos. Chem. Phys., 12, 6581–6592, https://doi.org/10.5194/acp-12-6581-2012, 2012.
Xu, J., Smith, A. K., Jiang, G., Gao, H., Wei, Y., Mlynczak, M. G., and Russell III, J. M.: Strong longitudinal variations in the OH nightglow, Geophys. Res. Lett., 37, L21801, https://doi.org/10.1029/2010GL043972, 2010.
Xu, J., Gao, H., Smith, A. K., and Zhu, Y.: Using TIMED/SABER nightglow observations to investigate hydroxyl emission mechanisms in the mesopause region, J. Geophys. Res., 117, D02301, https://doi.org/10.1029/2011JD016342, 2012.
- Abstract
- Introduction
- Model and calculations
- Daytime photochemical equilibrium of OH, HO2, and O3 at the altitudes of the mesosphere
- Method of statistical evaluation of simultaneous measurement of OH, HO2, and O3
- MLS/Aura data evaluation and results
- Discussion and conclusion
- Data availability
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Model and calculations
- Daytime photochemical equilibrium of OH, HO2, and O3 at the altitudes of the mesosphere
- Method of statistical evaluation of simultaneous measurement of OH, HO2, and O3
- MLS/Aura data evaluation and results
- Discussion and conclusion
- Data availability
- Competing interests
- Acknowledgements
- References