The influence of internal variability on Earth's energy balance framework and implications for estimating climate sensitivity

Our climate is constrained by the balance between solar energy absorbed by the Earth and terrestrial energy radiated to space. This energy balance has been widely used to infer equilibrium climate sensitivity (ECS) from observations of 20th-century warming. Such estimates yield lower values than other methods, and these have been influential in pushing down the consensus ECS range in recent assessments. Here we test the method using a 100-member ensemble of the Max Planck Institute Earth System Model (MPI-ESM1.1) simulations of the period 1850–2005 with known forcing. We calculate ECS in each ensemble member using energy balance, yielding values ranging from 2.1 to 3.9 K. The spread in the ensemble is related to the central assumption in the energy budget framework: that global average surface temperature anomalies are indicative of anomalies in outgoing energy (either of terrestrial origin or reflected solar energy). We find that this assumption is not well supported over the historical temperature record in the model ensemble or more recent satellite observations. We find that framing energy balance in terms of 500 hPa tropical temperature better describes the planet's energy balance.

1 The problem

When an energy imbalance is imposed, such as by adding a greenhouse gas to the atmosphere, the climate will shift in such a way to eliminate the energy imbalance. This process is embodied in the traditional linearized energy balance equation:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }R=F+\mathit{\lambda }{T}_{\mathrm{S}},\end{array}$$

where the forcing F is an imposed energy imbalance, T_S is the global average surface temperature, and λ relates changes in T_S to a change in net top-of-atmosphere (TOA) flux (Gregory et al., 2002; Dessler and Zelinka, 2014). R is the resulting TOA flux imbalance from the combined forcing and response. All quantities are deviations from an equilibrium base state, usually the pre-industrial climate. Equilibrium climate sensitivity (hereafter ECS, the equilibrium warming in response to a doubling of CO₂) is equal to $-F_{\mathrm{2}\times {\mathrm{CO}}_{\mathrm{2}}}/\mathit{\lambda }$, where $F_{\mathrm{2}\times {\mathrm{CO}}_{\mathrm{2}}}$ is the forcing from doubled CO₂.

Many investigators (e.g., Gregory et al., 2002; Annan and Hargreaves, 2006; Otto et al., 2013; Lewis and Curry, 2015; Aldrin et al., 2012; Skeie et al., 2014; Forster, 2016) have used Eq. (1) combined with estimates of R, F, and T_S to estimate λ:

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }\mathit{\lambda }=\mathrm{\Delta }(R-F)/\mathrm{\Delta }{T}_{\mathrm{S}},\end{array}$$

where Δ indicates the change between the start of the historical period (usually the mid- to late 19th century) and a recent period. These calculations result in values of λ near −2 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ and appear to rule out ECS larger than ∼ 4 K (Stevens et al., 2016). The substantial likelihood of an ECS below 2 K implied by these calculations led the IPCC Fifth Assessment Report to extend their lower bound on likely values of ECS to 1.5 K (Collins et al., 2013).

We test this energy balance methodology through a perfect model experiment consisting of an analysis of a 100-member ensemble of runs of the Max Planck Institute Earth System Model, MPI-ESM1.1. This is the latest coupled climate model from the Max Planck Institute for Meteorology and consists of the ECHAM6.3 atmosphere and land model coupled to the MPI-OM ocean model. The atmospheric resolution is T63 spectral truncation, corresponding to about 200 km, with 47 vertical levels, whereas the ocean has a nominal resolution of about 1.5^∘ and 40 vertical levels. MPI-ESM1.1 is a bug-fixed and improved version of the MPI-ESM used during the fifth phase of the Coupled Model Intercomparison Project (CMIP5; Giorgetta et al., 2013) and nearly identical to the MPI-ESM1.2 model being used to provide output to CMIP6, except that the historical forcings are from the MPI-ESM. Each of the 100 members simulates the years 1850–2005 (Fig. 1) and uses the same evolution of historical natural and anthropogenic forcings. The members differ only in their initial conditions – each starts from a different state sampled from a 2000-year control simulation.

We calculate effective radiative forcing F for the ensemble by subtracting top-of-atmosphere flux R in a run with climatological sea surface temperatures (SSTs) and a constant pre-industrial atmosphere from average R from an ensemble of three runs using the same SSTs but the time-varying atmospheric composition used in the historical runs (Hansen et al., 2005; Forster et al., 2016). The three-member ensemble begins with perturbed atmospheric states. We estimate $F_{\mathrm{2}\times {\mathrm{CO}}_{\mathrm{2}}}$ using the same approach in a set of fixed-SST runs in which CO₂ increases at 1 % per year, which yields a $F_{\mathrm{2}\times {\mathrm{CO}}_{\mathrm{2}}}$ value of 3.9 W m⁻².

We calculate λ using Eq. (2) for each ensemble member, producing values ranging from −1.88 to −1.01 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (5–95 % range −1.63 to −1.17 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$), with an ensemble median of −1.43 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (Fig. 2a). In this calculation, Δ(R−F) and ΔT_S are the average difference between the first and last decade of each run. The spread in λ depends to some extent on how the calculation is set up – if one used the difference between the averages of the first and last 20 years, for example, the range in λ declines from 0.87 to 0.48 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$. Using longer averaging periods does not further decrease the range.

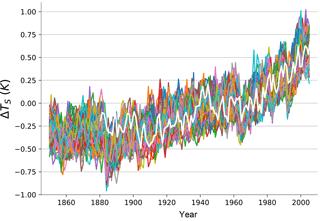
Figure 1 Plot of annual and global average surface temperature from the 100 members of the MPI-ESM1.1 ensemble (colored lines), along with the GISTEMP measurements (Hansen et al., 2010) (white line). Temperatures are referenced to the 1951–1980 average.

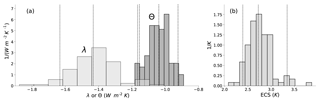
Figure 2 Probability density functions (PDFs) of (a) λ (lighter) and Θ (darker) and (b) ECS derived from the members of the MPI-ESM1.1 historical ensemble. The vertical lines are the 5th, 50th, and 95th percentile of each distribution.

We also calculate ECS = $-F_{\mathrm{2}\times {\mathrm{CO}}_{\mathrm{2}}}/\mathit{\lambda }$ for each ensemble member, producing values ranging from 2.08 to 3.87 K (5–95 % range 2.39 to 3.34 K) (Fig. 2b), with an ensemble median of 2.72 K. Thus, our analysis shows that λ and ECS estimated from the historical record can vary widely simply due to internal variability. Given that we have only a single realization of the 20th century, we should not consider estimates based on the historical period to be precise – even with perfect observations. This supports previous work that also emphasized the impact of internal variability on estimates of λ and ECS (Huber et al., 2014; Andrews et al., 2015; Zhou et al., 2016; Gregory and Andrews, 2016).

Previous researchers have questioned whether the historical record provides an accurate measure of λ and ECS, and we can check this by comparing the ensemble values to ECS estimates from a 2×CO₂ run of the MPI-ESM1.2, which is physically very close to MPI-ESM1.1. An abrupt 2×CO₂ run yields an ECS of 2.93 K in response to an abrupt doubling of CO₂ (estimated by regressing years 100–1000 of a 1000-year run) – 8 % larger than the ensemble median. This is in line with the 10 % difference in ECS estimated by Mauritsen and Pincus (2017) to arise from the average CMIP5 model time-dependent feedback but smaller than suggested in other recent studies of ECS in transient climate runs (e.g., Armour, 2017; Proistosescu and Huybers, 2017).

Thus, there are a number of issues that need to be considered when interpreting estimates of λ and ECS derived from the historical period. In addition to the precision and accuracy issues discussed above, it also includes the large and evolving uncertainty in forcing over the 20th century (Forster, 2016), different forcing efficacies of greenhouse gases and aerosols (Shindell, 2014; Kummer and Dessler, 2014), and geographically incomplete or inhomogeneous observations (Richardson et al., 2016).

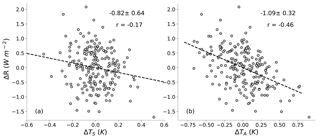
Figure 3 Scatterplot of monthly anomalies of ΔR vs. (a) global average surface temperature ΔT_S and (b) tropical average 500 hPa temperature ΔT_A. Observations cover the period March 2000–July 2017, and anomalies are deviations from the mean annual cycle. ΔR and temperature time series are detrended to account for forcing. The dashed lines are ordinary least-squares fits; the slope, 5–95 % confidence interval, and correlation coefficient are shown on each panel. Confidence intervals account for autocorrelation of the time series (Santer et al., 2000).

2 Why are estimates using the traditional energy balance approach imprecise?

In this section, we explain the physical process by which internal variability leads to the large spread in λ and ECS estimated from the ensemble. We begin by observing that Eqs. (1) and (2) parameterize R−F in terms of global average surface temperature, T_S. In model runs with strong forcing driving large warming, such as abrupt 4×CO₂ simulations, there is indeed a strong correlation between these variables (e.g., Gregory et al., 2004). However, because R−F in such runs is dominated by a monotonic trend, correlations will exist with any geophysical field that also exhibits a monotonic trend, regardless of whether there is a physical connection between the fields. Thus, one should not take the correlation between R−F and T_S in these runs as proving causality.

If T_S is a good proxy for the response R−F, we would expect to also see a correlation in measurements dominated by interannual variations. Observational data allow us to test this hypothesis. We use observations of R from the Clouds and the Earth's Radiant Energy System (CERES) Energy Balanced and Filled product (ed. 4) (Loeb et al., 2018), which cover the period March 2000 to July 2017. Our sign convention throughout the paper is that downward fluxes are positive. Temperatures come from the European Centre for Medium-Range Weather Forecasts (ECMWF) Interim Re-Analysis (ERA-Interim) (Dee et al., 2011). We assume forcing changes linearly over this time period and account for it by detrending ΔR and ΔT anomaly time series using a linear least-squares fit to remove the long-term trend.

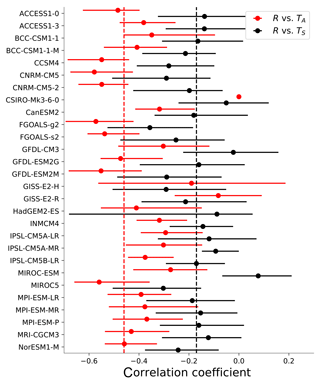
Figure 4 Correlation coefficients between ΔR and temperature in CMIP5 control runs: black and red symbols represent the correlation with ΔT_S and ΔT_A, respectively. The dot is the average of the correlation coefficients from the 17-year segments of the model run; the bars indicate the maximum and minimum values from the control run. The dashed lines are the corresponding correlation coefficients from the CERES regressions in Fig. 3.

These data show that ΔR is poorly correlated with ΔT_S in response to interannual variability (Fig. 3a), as has been noted many times in the literature; see, e.g., Sect. 5 of Forster (2016). In particular, the low correlation coefficient tells us that ΔT_S explains little of the variance in ΔR. Using explicit estimates of forcing or other temperature data sets (e.g., MERRA-2) yields the same result.

Global climate models that submitted output to CMIP5 (Taylor et al., 2012) also show this poor correlation. To demonstrate this, we have calculated the correlation coefficient between ΔT_S and ΔR in CMIP5 pre-industrial control runs (these are runs for which forcing F=0). To facilitate comparison with the CERES data, as well as avoid any issues with long-term drift in the control runs, we break each run into 17-year segments to match the length of the CERES data and calculate the correlation coefficient of monthly anomalies of ΔR and ΔT_S for each segment. Figure 4 shows that the correlation between ΔR and ΔT_S in the models is similar to that from the CERES analysis.

Recent work provides an explanation: the response of Δ(R−F) to a particular ΔT_S is determined not only by the global average magnitude but also by the pattern of warming (Armour et al., 2013; Andrews et al., 2015; Gregory and Andrews, 2016; Zhou et al., 2016, 2017; Andrews and Webb, 2018). During El Niño cycles that dominate the observations in Fig. 3, the spatial pattern of warm and cool regions changes, leading to responses in Δ(R−F) that do not scale cleanly with ΔT_S – something Stevens et al. (2016) refer to as “pattern effects”.

To demonstrate how this also generates the spread in λ in the model ensemble (Fig. 2a), we calculate the local response λ_r in three equal-area regions (90–19.4^∘ S, 19.4^∘ S–19.4^∘ N, 19.4–90^∘ N). We define λ_r as the regional analog to λ (Eq. 2):

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }{\mathit{\lambda }}_{\mathrm{r}}=\mathrm{\Delta }(R-F{)}_{\mathrm{r}}/\mathrm{\Delta }{T}_{\mathrm{S},\mathrm{r}},\end{array}$$

where the “r” subscript indicates a regional average value.

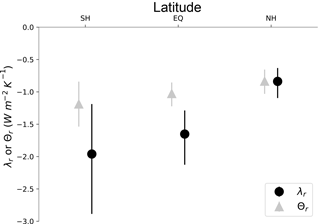
Figure 5 λ_r and Θ_r calculated as regional average Δ(R−F) divided by regional average temperature (ΔT_S for λ and ΔT_A for Θ). The regions are 90–19.4^∘ S (SH), 19.4^∘ S–19.4^∘ N (EQ), and 19.4–90^∘ N (NH). The values are calculated for each member of the 100-member ensemble; the solid symbols are the ensemble average, while the bars show the 5–95 % range.

We find that λ_r varies between the regions (Fig. 5). This means that different ensemble members with similar global average ΔT_S but different patterns of surface warming produce different values of global average Δ(R−F), thereby leading to spread in the estimated λ among the ensemble members. We also see strong variability in λ_r within each region, suggesting that how the warming is distributed within the region also drives some of the spread in estimated λ in the ensemble.

This explanation is consistent with analyses showing that λ changes during transient runs as the pattern of surface temperature evolves (Senior and Mitchell, 2000; Armour et al., 2013; Andrews et al., 2015; Gregory and Andrews, 2016; Stevens et al., 2016). In our model ensemble, however, the pattern changes are caused by internal variability rather than differing regional heat capacities that cause some regions to warm more slowly than others during forced warming.

3 A better way to describe energy balance

Our analysis demonstrates limitations of the conventional energy balance framework (Eq. 1). It has been previously noted that ΔR correlates better with tropospheric temperatures than ΔT_S (Murphy, 2010; Spencer and Braswell, 2010; Trenberth et al., 2015). Other analyses have also stressed the importance of atmospheric temperatures – through its influence on lapse rate – as providing a fundamental control on the planet's energy budget (Zhou et al., 2016; Ceppi and Gregory, 2017). Based on this, we test a new energy balance framework constructed using the temperature of the tropical atmosphere:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }R-F=\mathrm{\Theta }{T}_{\mathrm{A}},\end{array}$$

where T_A is the tropical average (30^∘ N–30^∘ S) 500 hPa temperature and Θ relates this quantity to R−F. R and F are the same global average quantities they were in Eq. (1). ECS can be expressed in terms of Θ:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }\text{ECS}=-{\displaystyle \frac{\mathrm{\Delta }{F}_{\mathrm{2}\times {\mathrm{CO}}_{\mathrm{2}}}}{\mathrm{\Theta }}}{\displaystyle \frac{\mathrm{\Delta }{T}_{\mathrm{S}}}{\mathrm{\Delta }{T}_{\mathrm{A}}}},\end{array}$$

where ΔT_S and ΔT_A are the equilibrium changes in these quantities in response to doubled CO₂. The CMIP5 ensemble average ratio ΔT_S∕ΔT_A is 0.86 ± 0.10 (±1σ), where Δ represents the average difference between the first and last decades of the abrupt 4×CO₂ runs.

Support for Eq. (4) can be found in the observations: ΔR shows a tighter correlation with ΔT_A than with ΔT_S in observations (Fig. 3a vs. Fig. 3b). CMIP5 models also show this (Fig. 4). Given that the slope of these plots can be taken as estimates of Θ and λ, the tighter correlation leads to more accurate estimates of Θ than λ, both in absolute and relative terms.

Turning to the model ensemble, we next demonstrate that Θ is a more precise metric than λ. We do this by calculating Θ [$=\mathrm{\Delta }(R-F)/\mathrm{\Delta }{T}_{\mathrm{A}}$] in each ensemble member, yielding values ranging from −1.18 to −0.89 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (5–95 % range −1.16 to −0.92 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$), with an ensemble median of −1.04 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (Fig. 2a). There is clearly less variability in Θ among the ensemble members than for λ. This reflects less variability in the regional response Θ_r ($=\mathrm{\Delta }(R-F{)}_{\mathrm{r}}/\mathrm{\Delta }{T}_{\mathrm{A},\mathrm{r}}$) than in λ_r (Fig. 5), as well as less variability within the regions. We therefore conclude that interannual variability has less of an impact on Θ than λ.

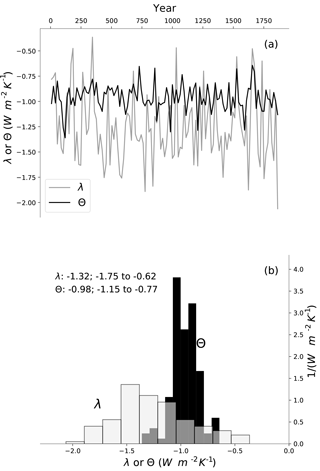
Figure 6 (a) Time series of λ (gray) and Θ (black) estimated in a 17-year sliding window of a 2000-year control run of the MPI-ESM1.1. (b) PDFs of the time series in (a). Median and 5–95 % confidence interval for each distribution are displayed on the plot.

We can also reproduce this in a 2000-year control run (a run with fixed pre-industrial boundary conditions) of the MPI-ESM1.1 model. Figure 6 shows λ calculated in a sliding 17-year window and confirms significant temporal variability in λ. We can similarly calculate Θ, and the figure shows that temporal variability in Θ is substantially smaller.

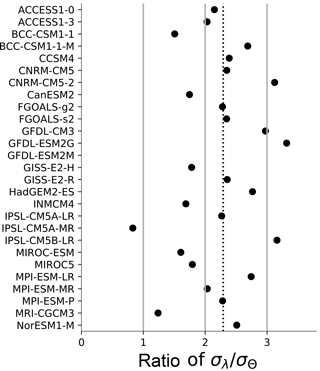
Figure 7 The standard deviation (SD) of the λ time series divided by the SD of the Θ time series. Each time series is calculated from 17-year segments of CMIP5 control runs. The dotted line is the ensemble average.

This result is also reproduced in the CMIP5 control models. Figure 7 plots the standard deviation (SD) of each CMIP5 model's set of short-term λ divided by the SD of that model's set of short-term Θ (as described previously, we calculate time series of short-term λ and Θ values for each model by regressing anomalies in a 17-year sliding window of the control runs). All of the models fall above 1, demonstrating that there is less variability in the Θ time series than in the λ time series in every climate model. This confirms that Θ is more robust with respect to internal variability than λ. It also suggests that Θ estimated from the satellite data (Fig. 3) should be considered a better estimate of the climate system's long-term value than λ estimated from the same data set.

As far as accuracy goes, we can compare Θ in the ensemble over the historical period to Θ in response to much larger warming. The ensemble median of Θ from the historic period (Fig. 2), −1.04 ± 0.01 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (5–95 % confidence interval), is close to the value obtained from an analysis of the first 150 years of an abrupt 4×CO₂ run of the same model, Θ = −1.03 ± 0.04 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$, as well as Θ calculated from all 2600 years of this run, Θ = −1.00 ± 0.01 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (values from the 4×CO₂ runs are all obtained using the Gregory method (Gregory et al., 2004) using annual average R and temperatures). On the other hand, λ changes substantially in the 4×CO₂ run as the climate warms: λ = −1.36 ± 0.07 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ when calculated from the first 150 years, but λ = −0.95 ± 0.01 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ from all 2600 years of that run.

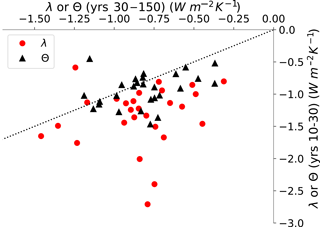
Figure 8 Scatterplot of λ₁₀₋₃₀ vs. λ₃₀₋₁₅₀ (red circles) in CMIP5 abrupt 4×CO₂ runs, as well as Θ₁₀₋₃₀ vs. Θ₃₀₋₁₅₀ (black triangles) in the same models. Each point represents one model. The dotted line is the 1:1 line. The subscripts (10–30, 30–150) indicate the years of the run from which the values are calculated.

We can verify this result in the CMIP5 abrupt 4×CO₂ ensemble. It has been previously demonstrated that plots of R−F vs. T_S do not trace straight lines as the climate warms (Andrews et al., 2015; Rugenstein et al., 2016; Rose and Rayborn, 2016; Armour, 2017), so λ and ECS calculated in a single model run may depend on the portion of the run selected. In the CMIP5 abrupt 4×CO₂ ensemble, for example, average λ calculated by regressing years 10–30 (λ₁₀₋₃₀) is more negative than λ calculated from years 30–150 (λ₃₀₋₁₅₀) by 0.49 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (Fig. 8).

Several explanations for this have been advanced, most prominently that λ is a function of the pattern of surface warming (Senior and Mitchell, 2000; Armour et al., 2013; Andrews et al., 2015; Gregory and Andrews, 2016; Zhou et al., 2016; Stevens et al., 2016). Using Θ largely eliminates this pattern effect: Θ₁₀₋₃₀ and Θ₃₀₋₁₅₀ have an average difference of 0.13 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ for the CMIP5 ensemble (Fig. 8). Thus, we find additional evidence that Θ tends to be similar for different amounts and patterns of warming.

The lack of curvature in the Θ calculations means there is curvature in the relation between T_A and T_S in the models. Thus, the pattern effect's impact on ECS calculations shifts from λ in the traditional framework to the ΔT_S∕ΔT_A term in Eq. (4). This also emphasizes the need to improve our understanding of the factors that control ΔT_S∕ΔT_A, as well as how future patterns of surface warming will evolve.

There are several plausible reasons why T_A may control R better than T_S. It seems likely that several of the feedbacks – e.g., lapse rate, water vapor, or longwave cloud – should be more strongly influenced by atmospheric temperatures than T_S. More recently, it has been shown that atmospheric temperatures also play a key role in regulating low clouds (Zhou et al., 2016, 2017), thereby influencing the shortwave cloud feedback. This is also consistent with Ceppi and Gregory (2017), who identified a dependence of ECS on atmospheric stability in models. We have not further investigated this – ultimately, our use of T_A in Eq. (4) is based on observations (Murphy, 2010; Spencer and Braswell, 2010; Trenberth et al., 2015) that it correlates well with R. Other metrics, such as global average atmospheric temperature, work almost as well. Clearly, further investigations on how to best describe the Earth's energy balance are warranted.

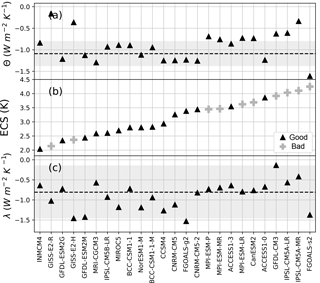
Figure 9 (a) Θ from individual CMIP5 control runs. The dotted line is the estimate from CERES observations; the gray region is the 5–95 % confidence band. (b) ECS from each CMIP5 model, estimated from the first 150 years of abrupt 4×CO₂ runs using the Gregory method (Gregory et al., 2004). “Good” models are those whose Θ agrees with observations in (a); “bad” models are those whose Θ does not. (c) Same as (a) but for λ.

Finally, one of our ultimate goals for this revised framework is to help produce better estimates of ECS. We are working on a detailed analysis of ECS based on this framework, which is presently in review (Dessler and Forster, 2018), but we briefly show here how the advantages of the revised energy balance framework may be leveraged to do this. Figure 9a shows Θ calculated from control runs of 25 CMIP5 models. To calculate Θ in the control runs, we break each control run into 17-year segments and calculate monthly anomalies of ΔR and ΔT_A during each segment. Then, we calculate Θ for each segment as the slope of the regression of ΔR vs. ΔT_A for that segment. Thus, for each control run, we generate a large number of estimates of Θ. The value in Fig. 9a is the average of these individual values.

Figure 9b shows the ECS of these models, calculated from the first 150 years of the abrupt 4×CO₂ runs using the Gregory method. If we assume that models with more accurate simulation of short-term Θ produce more accurate estimates of ECS (Brown and Caldeira, 2017; Wu and North, 2002), then we can use Fig. 9a and b to constrain ECS. We find that the 15 models whose average short-term Θ falls within the uncertainty of Θ estimated from CERES observations have ECS values ranging from 2.0 to 3.9 K, with an average of 2.9 K. This excludes many of the highest-ECS models, a result consistent with other analyses (Cox et al., 2018; Lewis and Curry, 2015).

It would not have been possible to draw this conclusion with the conventional energy balance framework. Figure 9c shows the comparison between λ from the control runs (calculated the same way Θ was calculated) and CERES observations. Because of the much larger uncertainty in the observational estimate of short-term λ, almost all models fall within the observational range, thereby prohibiting any constraint on the ECS range.

It may also be possible to use the relation between short-term and long-term Θ as an emergent constraint to convert short-term observations to the long-term response. There is some scatter in the relation in the CMIP5 ensemble, however, so more analysis of how these are related is likely required before ECS can be constrained in this way.

4 Conclusions

We have estimated ECS in each of a 100-member climate model ensemble using the same energy balance constraint used by many investigators to estimate ECS from 20th-century historical observations. We find that the method is imprecise – the estimates of ECS range from 2.1 to 3.9 K (Fig. 2), with some ensemble members far from the model's true value of 2.9 K. Given that we only have a single ensemble of reality, one should recognize that estimates of ECS derived from the historical record may not be a good estimate of our climate system's true value.

The source of the imprecision relates to the construction of the traditional energy balance equation (Eq. 1). In it, the response of TOA net flux (R−F) is parameterized in terms of global average surface temperature (T_S). Recent research has suggested that the response is not just determined by the magnitude of T_S but also includes other factors, such as the pattern of T_S (e.g., Armour et al., 2013; Andrews et al., 2015; Gregory and Andrews, 2016; Zhou et al., 2017) or the lapse rate (e.g., Zhou et al., 2017; Ceppi and Gregory, 2017; Andrews and Webb, 2018). As a result, two ensemble members with the same ΔT_S can have different climate responses, Δ(R−F), leading to spread in the inferred λ.

The lack of a direct relationship between T_S and radiation balance suggests that it may be profitable to investigate alternative formulations. We test parameterizing the response in terms of 500 hPa tropical temperature (Eq. 4) and find that it is superior in many ways. Ultimately, how investigators describe the energy balance of the planet will depend on the problem and the available data. The surface temperature is indeed special, so the traditional framework may be preferred for some problems. But investigators may find that the alternatives are superior for certain problems, for instance constraining Earth's climate sensitivity.