the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Impact of aerosols on ice crystal size
Kuo-Nan Liou
Jonathan H. Jiang
Qinbin Li
Rong Fu
Lei Huang
Xiaohong Liu
Xiangjun Shi
Hui Su
Cenlin He
The interactions between aerosols and ice clouds represent one of the largest uncertainties in global radiative forcing from pre-industrial time to the present. In particular, the impact of aerosols on ice crystal effective radius (Rei), which is a key parameter determining ice clouds' net radiative effect, is highly uncertain due to limited and conflicting observational evidence. Here we investigate the effects of aerosols on Rei under different meteorological conditions using 9-year satellite observations. We find that the responses of Rei to aerosol loadings are modulated by water vapor amount in conjunction with several other meteorological parameters. While there is a significant negative correlation between Rei and aerosol loading in moist conditions, consistent with the “Twomey effect” for liquid clouds, a strong positive correlation between the two occurs in dry conditions. Simulations based on a cloud parcel model suggest that water vapor modulates the relative importance of different ice nucleation modes, leading to the opposite aerosol impacts between moist and dry conditions. When ice clouds are decomposed into those generated from deep convection and formed in situ, the water vapor modulation remains in effect for both ice cloud types, although the sensitivities of Rei to aerosols differ noticeably between them due to distinct formation mechanisms. The water vapor modulation can largely explain the difference in the responses of Rei to aerosol loadings in various seasons. A proper representation of the water vapor modulation is essential for an accurate estimate of aerosol–cloud radiative forcing produced by ice clouds.
- Article
(4386 KB) - Full-text XML
-
Supplement
(1209 KB) - BibTeX
- EndNote
Aerosols are known to interact with clouds and hence affect Earth's radiative balance, which represents the largest uncertainty in global radiative forcing from pre-industrial time to the present (IPCC, 2013). The interactions between aerosols and liquid as well as mixed-phase clouds have been extensively studied (Rosenfeld et al., 2014; Seinfeld et al., 2016; Zhao et al., 2017b); however, much less attention has been paid to ice clouds, among which cirrus clouds are globally distributed and present at all latitudes and seasons with a global cloud cover of about 30 % (Wylie et al., 1994, 2005). Ice clouds, formed with various types of aerosols serving as ice nucleating particles (INPs) (Murray et al., 2012; Hoose and Möhler, 2012), act as a major modulator of global radiation budget and hence climatic parameters (e.g., temperature and precipitation) by reflecting solar radiation back to space (solar albedo effect, cooling) and by absorbing and re-emitting long-wave terrestrial radiation (greenhouse effect, warming); the balance between the two is dependent on ice cloud properties, particularly ice crystal size (Liou, 2005; Waliser et al., 2009; Fu and Liou, 1993). Limited estimates (IPCC, 2013; Liu et al., 2009; Fan et al., 2016) have shown that the global aerosol–cloud radiative forcing produced by ice clouds can be very significant but highly uncertain, ranging from −0.67 to 0.70 W m−2. For reference purposes, the best estimate of global aerosol–cloud radiative forcing produced by all cloud types is −0.45 W m−2 (90 % confidence interval [−1.2, 0 W m−2]) according to the Intergovernmental Panel on Climate Change (IPCC) (Fig. TS.6 in IPCC, 2013).
The substantial uncertainty in aerosol–ice cloud radiative forcing arises largely from a poor understanding of the aerosol effects on ice cloud properties, in particular ice crystal effective radius (Rei), a key parameter determining ice clouds' net radiative effect (Fu and Liou, 1993). Very limited observational studies (Jiang et al., 2008, 2011; Su et al., 2011; Chylek et al., 2006; Massie et al., 2007) have investigated the response of Rei to aerosol loadings. Most of them (Jiang et al., 2008, 2011; Su et al., 2011) found that polluted clouds involved smaller Rei than clean clouds, in agreement with the classical “Twomey effect” for liquid clouds (Twomey, 1977), which states that more aerosols can result in more and smaller cloud droplets and hence larger cloud albedo. In contrast, a couple of studies over the Indian Ocean (Chylek et al., 2006; Massie et al., 2007) reported that Rei is roughly unchanged (Massie et al., 2007) or larger (Chylek et al., 2006) during more polluted episodes. It has been shown that increased aerosols (and thus INPs) lead to enhanced heterogeneous nucleation, which is associated with larger and fewer ice crystals as compared to the homogeneous nucleation counterpart (DeMott et al., 2010; Chylek et al., 2006). However, the reasons for disagreement among various studies and the controlling factors for different aerosol indirect effects are yet to be explored; therefore, the sign and magnitude of the overall aerosol effects remain in question.
With the objective to resolve the substantial uncertainty, we systematically investigate the effects of aerosols on Rei of two types of ice clouds under different meteorological conditions using 9-year continuous satellite observations from 2007 to 2015. The study region is East Asia and its surrounding areas (15–55∘ N, 70–135∘ E; Fig. S1 in the Supplement), where aerosol loadings can range from small to extremely large values in different locations and time periods and aerosol types are varied (Wang et al., 2017; Zhao et al., 2017a).
2.1 Sources of observational data
We obtain collocated aerosol/cloud measurements primarily from MODIS (Moderate Resolution Imaging Spectroradiometer) on board the Aqua satellite and CALIPSO (Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations), as summarized in Table S1 in the Supplement.
We acquire aerosol optical depth (AOD) retrievals at 550 nm from the level 2 MODIS aerosol product (MYD04, Collection 6) at a resolution of 10 km × 10 km. The accuracy of AOD (denoted by τ) retrievals has been estimated to be about ±(0.05+0.15τ) over land and ±(0.03+0.05τ) over ocean (Levy et al., 2010; Remer et al., 2005). Similarly, we obtain cloud effective radius (equivalent to Rei in the case of ice phase) and cloud phase determined by the “cloud optical property” algorithm from the level 2 MODIS cloud product (MYD06, Collection 6) at a 1 km × 1 km resolution (Platnick et al., 2015). The MYD06 product provides an estimate of the uncertainty in Rei for each pixel, which takes into account a variety of error sources including (1) instrument calibration, (2) atmospheric corrections, (3) surface spectral reflectance, and (4) forward radiative transfer model, e.g., the size distribution assumption (Platnick et al., 2015). The pixel-level Rei uncertainties for the samples used in this study are 6.41 ± 4.97 % (standard deviation). In the subsequent analysis (Sect. 3.1–3.3) we use mean Rei within certain AOD bins, and the uncertainties are smaller than those for individual pixels. Also, we focus on Rei changes in response to aerosol loading instead of absolute Rei values. For these reasons, the Rei uncertainty ranges are much smaller than the magnitude of Rei trends depicted in this study (see Figs. 1 and 3). We note that the current uncertainty evaluation has not considered the assumptions of ice crystal habit (shape), which will be discussed in Sect. 3.4. Stein et al. (2011) compared the MODIS Rei data with the “DARDAR” retrieval product (Delanoe and Hogan, 2008, 2010) based on CloudSat and CALIPSO measurements. The default DARDAR retrievals of Rei are mostly larger than MODIS's values, which is partly attributable to different assumptions of ice crystal habit in these two products. When the DARDAR retrievals are adjusted to mimic the MODIS assumption of ice crystal habit, the joint distribution of individual Rei retrievals has its peak close to the ratio of 1 between the two products, indicating a much better agreement (Stein et al., 2011). Nevertheless, the overall shape of the distributions indicates that the MODIS retrievals mostly lie between 10 and 50 µm, while the DARDAR retrievals, corrected for the crystal habit assumption, mostly lie between 10 and 80 µm. Hong and Liu (2015) reveal that the large Rei values in DARDAR retrievals are predominantly associated with large cloud optical thickness (> 3.0, particularly > 20). In this study, however, we focus on ice-only clouds (mostly cirrus clouds), which typically have an optical thickness less than 5.0 (see Fig. 2). For this reason, the agreement in Rei between MODIS and DARDAR could be better for the type of cloud used in our analysis.
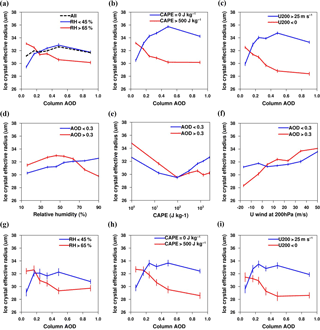
Figure 1Influence of aerosols on ice crystal effective radius (Rei) of ice clouds modulated by meteorological conditions. (a–c) Changes in Rei with AOD for different ranges of (a) RH100−440 hPa, (b) CAPE, and (c) U200. (d–f) Changes in Rei with (d) RH100−440 hPa, (e) CAPE, and (f) U200 for different ranges of AOD. (g–i) The same as (a–c) but for the profiles with dust aerosols only. The meteorological parameters and AOD are divided into three and two ranges containing similar numbers of data points, respectively; the curves for the medium meteorological range are not shown. The error bars denote the standard errors () of the bin average, where σ is the standard deviation and N is the sample number. The influences of other meteorological parameters are shown in Fig. S2. The total number of samples used in this figure is 5.68×104.
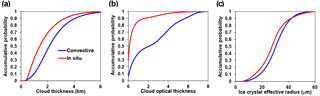
Figure 2Accumulative probability distribution of the properties of two ice cloud types: (a) cloud thickness, (b) cloud optical thickness, and (c) Rei.
The CALIPSO satellite flies behind Aqua by about 75 s and carries CALIOP (Cloud-Aerosol Lidar with Orthogonal Polarization), a dual-wavelength near-nadir polarization lidar (Winker et al., 2007). CALIOP has the capability to determine the global vertical distribution of aerosols and clouds. In this study, we make use of the CALIPSO level 2 merged aerosol and cloud layer product (05kmMLay, version 4.10) with an along-track resolution of 5 km and a high vertical resolution of 30–60 m below 20.2 km. The variables we employ for the investigation include aerosol/cloud layer numbers, layer base temperature, layer top/base height, layer aerosol/cloud optical depth, feature classification flags (containing the flags of “cloud type” and “aerosol type”), and two quality control (QC) flags, named the cloud aerosol discrimination (CAD) score and extinction QC (Atmospheric Science Data Center, 2012).
To examine the impact of meteorological conditions on aerosol–Rei relations, we also obtain vertically resolved pressure, relative humidity (RH), and temperature from the CALIPSO aerosol profile product (05kmAPro, version 4.10) and middle cloud layer temperature (Tmid) from the CALIPSO 05kmMLay product (version 4.10). The other meteorological parameters (see Table S1) are collected from the NCEP's Final Analysis reanalysis data (ds083.2), which are produced at a resolution every 6 h. Since Aqua and CALIPSO satellites overpass the study areas between 05:00 and 08:00 UTC, the ds083.2 datasets at 06:00 UTC are utilized.
2.2 Processing of observational data
In the analysis, we identify a CALIPSO profile layer at 5 km resolution as ice cloud when its cloud type is cirrus or its layer base temperature is colder than −35 ∘C. Previous studies (Mace et al., 2001, 2006; Kramer et al., 2016) have distinguished two major types of ice clouds characterized by distinct formation mechanisms: ice clouds generated from deep convection (convection-generated ice clouds) and those generated in situ due to updraft caused by frontal systems, gravity waves, or orographic waves (in situ ice clouds). Considering that the impact of aerosols could differ according to formation processes, we separate these two ice cloud types using CALIPSO data and a similar approach to that developed by Riihimaki and McFarlane (2010). First, we group ice cloud profiles at 5 km resolution into objects using the criteria that neighboring ice cloud profiles must vertically overlap (the base of the higher cloud layer is lower than the top of the lower cloud layer) and be separated by no more than one profile horizontally (i.e., distance ≤ 5 km). Only single-layer ice cloud objects with valid quality assurance (QA) flags (20 ≤ CAD score ≤ 100, Extinction QC ) are accepted in this study. We subsequently classify ice cloud objects into three types, i.e., convection-generated, in situ, and other ice clouds, according to their connection to other clouds. The criteria to determine whether two clouds are connected are consistent with those used to group ice cloud objects; i.e., the neighboring profiles must vertically overlap and be horizontally separated by no more than 5 km. Convection-generated ice clouds consist of ice cloud objects that are connected to larger clouds that include deep convective cloud profiles (i.e., the cloud type flag is deep convection). An ice cloud object is classified as in situ if at least 95 % of a cloud consists of a single ice cloud object which is at least 25 km (i.e., five profiles) in the horizontal direction, and none of the remaining profiles are of the deep convection type. The remaining ice cloud objects are categorized as the “other” type. We should be cautious that the convection-generated and in situ ice clouds may not be perfectly separated using the approach described above. For example, the in situ ice clouds identified here could include convectively detrained objects, which are no longer connected with their parent deep convection, and convectively detrained objects whose parent deep convective clouds do not overlap with CALIPSO's track. The convection-generated ice clouds may also be contaminated by some in situ formed ice cloud objects that happen to be spatially connected to deep convection. However, the classification scheme appears to be reasonable, as indicated by the distinct properties of the two ice cloud types shown in Sect. 3.2.
We then match collocated MODIS/Aqua and CALIPSO observations by averaging retrieved AOD and Rei from MODIS level 2 products (MYD04 and MYD06) within 30 and 5 km radii of each 5 km ice cloud profile from CALIPSO, respectively. The averaging is done to achieve near-simultaneous aerosol and cloud measurements since AOD observations from MODIS are missing under cloudy conditions. As AOD variation has a large spatial length scale of 40–400 km (Anderson et al., 2003), it is averaged within a larger radius than that of Rei to increase the number of data points with valid AOD observations. The average Rei is calculated based on the pixels with cloud phase of ice and Rei uncertainty smaller than 100 %. Apart from the column AOD, we also need to obtain AOD of the aerosol layers mixed with ice cloud layers as in situ ice clouds are primarily affected by aerosols at the ice cloud height. For this purpose, we use the CALIPSO 05kmMLay product to select the aerosol layers which have valid QA flags (−100 ≤ CAD score ≤ −20, Extinction QC ; Huang et al., 2013) and are vertically less than 0.25 km away from the ice cloud layer following Costantino and Breon (2010). The AOD of these aerosol layers are averaged within a 30 km radius of ice cloud profiles. The meteorological parameters from the NCEP datasets (ds083.2) are matched to the CALIPSO resolution by determining which NCEP grid contains a certain CALIPSO 5 km profile. Finally, we eliminate profiles with column AOD > 1.5 to reduce the potential effect of cloud contamination (Wang et al., 2015).
Convection-generated ice clouds are generated by convective updraft originating from the lower troposphere and are therefore affected by aerosols at various altitudes, whereas in situ ice clouds are primarily dependent on aerosols near the cloud height. For this reason, we use column AOD and layer AOD mixed with ice clouds as proxies for aerosols interacting with convection-generated and in situ ice clouds, respectively. We also investigate the overall effect of aerosols on all types of ice clouds. In this case, column AOD is used as a proxy for aerosol loading affecting ice clouds following a number of previous studies (Jiang et al., 2011; Massie et al., 2007; Ou et al., 2009). The rationale is that the MODIS-detected AOD generally shows a close correlation to the MLS (Microwave Limb Sounder)-observed CO concentration in ice clouds (Jiang et al., 2008, 2009), which in turn correlates well with the aerosol loading mixed with clouds in accordance with both aircraft measurements and atmospheric modeling (Jiang et al., 2009; Li et al., 2005; Clarke and Kapustin, 2010). After the preceding screening, about 2.73×104, 1.09×104, and 5.68×104 profiles are used to analyze the relationships between column/layer AOD and Rei of convection-generated, in situ, and all types of ice clouds. The available profiles for in situ ice clouds are fewer in number because aerosols mixed with ice clouds are often optically thin or masked by clouds and hence may not be fully detected by CALIPSO.
2.3 Cloud parcel model simulation
To support the key findings (i.e., the water vapor modulation of Rei–aerosol relations) from satellite observations and elucidate the underlying physical mechanisms, we perform model simulations using a cloud parcel model, which was originally developed by Shi and Liu (2016) and updated in this study to incorporate immersion nucleation. The model mimics formation and evolution of in situ ice clouds in an adiabatically rising air parcel. The model's governing equations that describe the evolution of temperature, pressure, and mass mixing ratio, number concentration, and size of ice crystals can be found in Pruppacher and Klett (1997). The main microphysical processes considered include homogeneous nucleation and two modes of heterogeneous nucleation (deposition and immersion nucleation), depositional growth, sublimation, and sedimentation. The rate of homogeneous nucleation of supercooled sulfate droplets is calculated based on the water activity of sulfate solution (Shi and Liu, 2016). The dry sulfate aerosol is assumed to follow a log-normal size distribution with a geometric mean radius of 0.02 µm. The deposition nucleation on externally mixed dust (deposition INP) and immersion nucleation of coated dust (immersion INP) are parameterized following the work of Kuebbeler et al. (2014); the critical ice supersaturation ratios are 10 % (T≤220 K) or 20 % (T>220 K) for the former and 30 % for the latter. Anthropogenic INPs are not included in the cloud parcel model following recent studies (Shi and Liu, 2016; Kuebbeler et al., 2014). This is because (1) ice nucleation experiments for black carbon show contradicting results (Hoose and Möhler, 2012), and (2) ice nucleation parameterizations for anthropogenic aerosol constituents other than black carbon have not been adequately developed under ice cloud conditions due to limited experimental data. Also, we find that the relationships between Rei and loadings of dust aerosols are similar to those between Rei and loadings of all aerosols (Sect. 3.1). As such, we argue that the general pattern of simulation results would remain unchanged if more INPs were incorporated. The accommodation coefficient of water vapor deposition on ice crystals is assumed to be 0.1 (Shi and Liu, 2016). The sedimentation velocity of ice crystals is parameterized following Ikawa and Saito (1991). The model neglects some ice microphysical processes such as aggregational growth of ice crystals. Although aggregational growth can affect the concentration and size of ice crystals, its effects should be relatively small in terms of the response of Rei to aerosol loading since this process is not strongly dependent on aerosols.
We conduct two groups of numerical experiments with different available water amount for ice formation, denoted by initial water vapor mass mixing ratios (pv). Each group is comprised of 100 sub-groups with initial sulfate number concentrations increasing linearly from 5 to 500 cm−3. The concentration ratios of externally mixed dust (deposition INP), coated dust (immersion INP), and sulfate (not INP) are prescribed values of for all experiments since INPs represent only 1 in 103 to 106 of ambient particles (Fan et al., 2016). In each sub-group, we conduct 100 1 h experiments driven by different vertical velocity spectra following the approach described by Shi and Liu (2016). The vertical air motions at a 10 s resolution were retrieved from Millimeter Wave Cloud Radar (MMCR) observations at a site located in the Southern Great Plains (SGP; 36.6∘ N, 97.5∘ W) for a 6 h period (Shi and Liu, 2016). For each of the 100 experiments, we randomly sample a 1 h time windows from the 6 h vertical velocity retrievals, subtract the arithmetical mean, and adjust the standard deviation to 0.25 m s−1. A constant large-scale updraft velocity of 0.02 m s−1 is subsequently added to the sampled vertical velocity spectra to drive the parcel model. The initial pressure and temperature for all experiments are set at 250 hPa and 220 K, respectively.
The model assumes that the air parcel has no mass or energy exchange with the environment except for sedimentation of ice crystals, which is not realistic. For example, the outburst of homogeneous nucleation in an air parcel can quickly exhaust supersaturation and take water vapor from surrounding parcels. To conceptually mimic this process, we have divided the 100 experiments within a sub-group into 10 combinations, each consisting of 10 experiments. It is assumed that the air parcels in the same combination can exchange water vapor and reach equilibrium. Consequently, the occurrence of homogeneous nucleation in one parcel will suppress the homogeneous nucleation in the connected parcels due to the depletion of water vapor.
The ice crystal number concentration (Ni) and Rei at the end of the experiments are used to construct the aerosol–cloud relationships. The Ni for a given aerosol number concentration (i.e., a sub-group of experiments) is calculated using an arithmetical mean of the 100 experiments, while Rei is calculated from mean Ni and mean ice volume: Rei= (mean volume/mean )1∕3.
3.1 Relationships between Rei and aerosols modulated by meteorology
In this section we discuss the impact of aerosols on Rei, with both ice cloud types lumped together, based on satellite data (Fig. 1). The aerosol effects on individual ice cloud types will be discussed in the next section. The dashed line in Fig. 1a shows the overall changes in Rei with AOD. Rei generally increases with increasing AOD for a moderate AOD range (< 0.5), and it decreases slightly for higher AOD. This relationship is attributable to complex interactions between meteorological conditions and microphysical processes, which will be detailed below.
Having shown overall response of Rei to AOD, we investigate whether the responses are similar under different meteorological conditions. We plot the Rei–AOD relationships separately for different ranges of meteorological parameters, as shown in Figs. 1a–c and S2. Included in the analysis are most meteorological parameters that can potentially affect ice cloud formation and evolution, including the relative humidity averaged between 100 and 440 hPa (RH100−440 hPa), convective available potential energy (CAPE) which is an indicator of convective strength, middle cloud layer temperature (Tmid), wind speed and direction at ice cloud height and at surface, vertical velocity below and at ice cloud height, and vertical wind shear. For some meteorological parameters, e.g., vertical wind shear and vertical velocity at 300/500 hPa, the curve shapes are similar for different meteorological ranges. However, for RH100−440 hPa, CAPE, and the U component of wind speed at 200 hPa (U200), the curve shapes vary significantly according to different ranges (Fig. 1a–c). As illustrated by RH100−440 hPa and CAPE, Rei decreases significantly with increasing AOD for high RH100−440 hPa (> 65 %) or CAPE (> 500 J kg−1) following the rule of the Twomey effect. In contrast, for low RH100−440 hPa (< 45 %) or CAPE (0 J kg−1), Rei generally increases sharply with AOD; an exception is that at a large AOD range (> 0.5), a further increase in AOD could decrease Rei slightly. To the best of our knowledge, the strong dependency of Rei–AOD relationships on meteorological conditions for ice clouds has been demonstrated for the first time.
These correlations, however, may not be necessarily attributed to aerosols. It is theoretically possible that certain meteorological parameters lead to simultaneous changes in both AOD and ice cloud properties and produce a correlation between these two parameters. To rule out this possibility, we examine the responses of AOD to the above-mentioned meteorological parameters (Fig. S3) and find that AOD does not serve as proxy for them since it varies by less than 0.2 in response to variation in any meteorological parameter. Furthermore, we bin observed Rei according to RH100−440 hPa, CAPE, and U200, for different ranges of AOD (Fig. 1d–f). Using RH100−440 hPa as an example, a larger AOD corresponds to smaller Rei for a given RH100−440 hPa within the larger RH100−440 hPa range, whereas an increase in AOD enlarges Rei for a given RH100−440 hPa within the smaller RH100−440 hPa range. Similar results are found for CAPE and U200 (Fig. 1d–f), demonstrating the role of aerosols in altering Rei under the same meteorological conditions. Moreover, the cloud contamination in AOD retrieval (Kaufman et al., 2005) or aerosol contamination in cloud retrieval (Brennan et al., 2005) is not likely to lead to observed Rei–AOD correlations because the retrieval biases cannot explain the opposite correlations under different meteorological conditions. Therefore, we conclude that both the positive and negative correlations between AOD and Rei are primarily attributed to the aerosol effect. This causality is also supported by numerical simulations using a cloud parcel model to be described in Sect. 3.4. Furthermore, we find that the three meteorological parameters which pose the strongest impact on Rei–AOD relationships (RH100−440 hPa, CAPE, and U200) are closely correlated with each other, with correlation coefficients between each two exceeding ±0.5 and p value less than 0.01 (Table S2). In fact, all these three parameters are closely related to the amount of water vapor available for ice cloud formation. It is obvious that RH100−440 hPa is an indicator of water vapor amount. CAPE represents convective strength and hence water vapor lifted to ice cloud heights; U200 is the zonal wind at 200 hPa as opposed to the meridional wind, and denotes the origin of air mass such as moist Pacific Ocean (negative U200, easterly wind) or dry inland continent (positive U200, westerly wind). Therefore, water vapor amount is likely a key factor which modulates the observed impact of aerosols on Rei.
The proposed mechanism for the water vapor modulation is that a different water vapor amount substantially alters the relative significance of different ice nucleation modes, thereby resulting in different Rei–AOD relationships. Specifically, ice crystals form via two primary pathways: homogeneous nucleation of liquid cloud droplets (or supercooled solution particles) below about −35 ∘C and heterogeneous nucleation triggered by INPs (IPCC, 2013; DeMott et al., 2010). INPs possess surface properties favorable to lowering the ice supersaturation ratio required for freezing (IPCC, 2013; DeMott et al., 2010); therefore, the onset of heterogeneous nucleation is generally easier and earlier in rising air parcels. Under moist conditions (high RH100−440 hPa, high CAPE, or negative U200), an air parcel could experience a longer time duration for supersaturation development, increasing the odds of exceeding the supersaturation threshold for homogeneous ice nucleation. Therefore, homogeneous nucleation dominates in this case, and more aerosols could give rise to more numerous and smaller ice crystals, which is in connection with the Twomey effect for liquid clouds. Under dry conditions, however, the earlier onset of heterogeneous nucleation can strongly compete with and possibly prevent homogeneous nucleation involving more abundant liquid droplets or solution particles (IPCC, 2013; DeMott et al., 2010). Therefore, more aerosols (and hence more INPs) are expected to lead to a higher fraction of ice crystals produced by heterogeneous nucleation comprising of fewer and larger ice crystals. This is known as the “negative Twomey effect” as first described by Kärcher and Lohmann (2003). At a very large AOD range (> 0.5), heterogeneous nucleation dominates, and a further increase in aerosols would decrease Rei due to the formation of more smaller ice crystals. These proposed mechanisms will be supported and elaborated on using model simulations in Sect. 3.4.
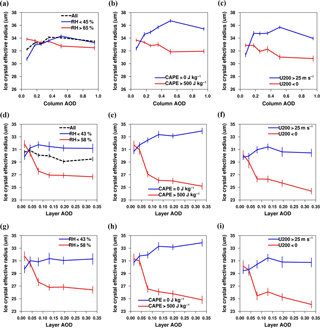
Figure 3Changes in Rei of convection-generated and in situ ice clouds with aerosols. (a–c) Changes in Rei of convection-generated ice clouds with AOD for different ranges of (a) RH100−440 hPa, (b) CAPE, and (c) U200. (d–f) Changes in Rei of in situ ice clouds with layer AOD for different ranges of (d) RH100−440 hPa, (e) CAPE, and (f) U200. (g–i) The same as (d–f) but for the profiles with dust aerosols only. The meteorological parameters are divided into three ranges containing similar numbers of data points, and the curves for the medium range are not shown. Note that we use column AOD and layer AOD mixed with ice clouds as proxies for aerosols interacting with convection-generated and in situ ice clouds, respectively. The definition of error bars is the same as in Fig. 1. The total numbers of samples used for convection-generated and in situ ice clouds are 2.73×104 and 1.09×104, respectively.
Here an inherent assumption is that INP concentration is roughly proportional to, or at least positively correlated with AOD. Considering that INPs only account for a small fraction of ambient aerosols, we may not take this assumption for granted. Here we plot the Rei–AOD relations using only the cases in which the aerosol type (a flag contained in the feature classification flags of CALIPSO) is dust (Fig. 1g–i), and find that the water modulation effect is very similar to the preceding results (i.e., Fig. 1a–c). In addition to column AOD, we also find similar dependences of Rei on layer AOD (mixed with in situ ice clouds) for all aerosols and for dust only (see Fig. 3d–i). Since specific components of dust aerosols have been known as effective INPs (Murray et al., 2012; Hoose and Möhler, 2012), the similar Rei–AOD relations of dust and of all aerosols support the proposed mechanisms for water vapor modulation to some extent.
3.2 Rei–aerosol relationships for two types of ice clouds
Considering that distinct formation mechanisms of convection-generated and in situ ice clouds may lead to different aerosol effects, we distinguish these two ice cloud types based on their connection to deep convection (Sect. 2.2). In the study region, the convection-generated, in situ, and other ice clouds account for 44.9, 52.4, and 2.7 % of all ice cloud profiles, respectively. Figure 2 illustrates the accumulative probability distribution of cloud thickness, cloud optical thickness (COT), and Rei of the two ice cloud types. The cloud thickness and COT of convection-generated ice clouds are remarkably larger than those of in situ ice clouds because more water is transported to the upper troposphere in the formation process of the former type, consistent with numerous aircraft measurement results (e.g., Kramer et al., 2016; Luebke et al., 2016; Muhlbauer et al., 2014). The Rei of convection-generated ice clouds is slightly larger than that of in situ ice clouds, which has also been reported in a number of aircraft campaigns (Luebke et al., 2016; Kramer et al., 2016). The larger Rei in convection-generated ice clouds is attributed to larger water amount and the fact that they are produced by convection emerging from lower altitude. Below the −35 ∘C isotherm, ice crystals stem only from heterogeneous nucleation, which tends to produce larger ice crystals compared to the homogeneous nucleation counterpart (Luebke et al., 2016).
Figure 3 shows the impact of aerosols on Rei under different meteorological conditions for convection-generated and in situ ice clouds, respectively. As described in Sect. 2.2, we use column AOD and layer AOD mixed with ice clouds as proxies of aerosols interacting with convection-generated and in situ ice clouds, respectively. The most impressive feature from these figures is that the meteorology modulation remains in effect for either of the two ice cloud types, such that Rei generally decreases with AOD under high RH100−440 hPa/high CAPE/negative U200 conditions, whereas the reverse is true under low RH100−440 hPa/low CAPE/positive U200 conditions. Similar to Sect. 3.1, we also demonstrate that the Rei–aerosol relationships are primarily attributed to the aerosol effect by illustrating the role of aerosols in altering Rei under the nearly constant meteorological conditions (Fig. S4). For example, a larger AOD is associated with a smaller Rei for a given RH100−440 hPa within the larger RH100−440 hPa range, while an increase in AOD leads to a larger Rei for a given RH100−440 hPa within the smaller RH100−440 hPa range. These results illustrate that the meteorology modulation of aerosol effects on Rei is valid regardless of ice cloud formation mechanisms.
A closer look at Fig. 3 shows that noted differences exist between the Rei–aerosol relationships for the two ice cloud types. For convection-generated ice clouds, a weak negative correlation (but that is still statistically significant at the 0.01 level) between Rei and AOD is found under moist conditions, while a strong positive correlation is found under dry conditions. Note that at a large AOD range (> 0.5) under dry conditions, a further increase in AOD could slightly reduce Rei because of the Twomey effect when heterogeneous nucleation prevails. For in situ ice clouds, however, weaker positive and stronger negative correlations are shown under dry and moist conditions, respectively. As a result, overall Rei slightly increases with aerosol loading for convection-generated ice clouds, but it slightly decreases for in situ clouds.
These differences are again linked to the distinct formation mechanisms of the two ice cloud types. As the formation mechanism of convection-generated ice clouds is quite complex, we first briefly review major pathways of ice crystal formation in convection-generated clouds. On the one hand, ice crystals are produced by heterogeneous freezing of liquid droplets at temperatures larger than about −35 ∘C or possibly by homogeneous freezing of liquid droplets at about −35 ∘C (Kramer et al., 2016). The ice crystals are then lifted to the temperature range < −35 ∘C and are considered to be ice clouds (Kramer et al., 2016). On the other hand, an additional freezing of solution particles (in contrast to liquid droplets in the former case) may occur in the presence of “preexisting ice” if the updraft is sufficiently strong. The freezing mechanism is likely homogeneous nucleation since INPs have already been consumed (Kramer et al., 2016). Such additional freezing events do not occur easily and hence make less important contributions to ice crystal budget (Luebke et al., 2016) since the preexisting ice suppresses supersaturation and prevents the threshold for homogeneous nucleation from being reached (Shi et al., 2015). In this study, “homogeneous nucleation” refers to the freezing of liquid droplets near the −35 ∘C isotherm as well as the freezing of solution particles below −35 ∘C. The former could be important for ice formation because any liquid droplets would be homogeneously nucleated when they are lifted to the −35 ∘C isotherm. Evidence for homogeneous droplet freezing has been frequently observed in deep convective clouds and convection-generated cirrus clouds (Twohy and Poellot, 2005; Heymsfield et al., 2005; Rosenfeld and Woodley, 2000; Choi et al., 2010). In particular, liquid droplets are frequently observed to supercool to temperatures approaching −35 ∘C and even below, and at slightly colder temperature only ice is found, which serves as strong evidence for homogeneous droplet freezing (Rosenfeld and Woodley, 2000; Choi et al., 2010). Even if the occurrence frequency of homogeneous droplet freezing is low, its contribution to ice number concentration and Rei may still be substantial in view of the fact that numerous ice crystals can be produced in a single homogeneous nucleation event.
Obviously, convection-generated ice clouds are influenced by aerosols at various heights, which presumably contain many more INPs than the thin upper tropospheric aerosol layers in the case of in situ ice clouds. In addition, the heterogeneously formed ice crystals in convective clouds are able to grow before being lifted to −35 ∘C isotherm where homogeneous nucleation bursts, giving rise to a larger difference between the ice crystal sizes produced by heterogeneous and homogeneous nucleation as compared to in situ ice clouds. For these reasons, under dry conditions, the increase in Rei with aerosol loading, which is due to the transition from homogeneous-dominated to heterogeneous-dominated regimes, would be much more pronounced for convection-generated ice clouds.
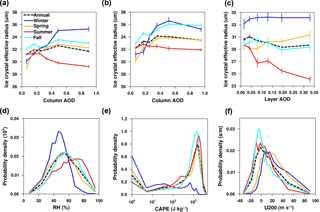
Figure 4Changes in Rei with AOD and the probability distribution of selected meteorological parameters as a function of season. (a–c) Changes in Rei with AOD as a function of season for (a) all ice clouds, (b) convection-generated ice clouds, and (c) in situ ice clouds. (d–f) The probability distribution of (d) RH100−440 hPa, (e) CAPE, and (f) U200 as a function of season. Definitions of season are as follows: Winter – December, January, and February; Spring – March, April, and May; Summer – June, July, and August; Fall – September, October, and November. The definition of error bars is the same as in Fig. 1. The total numbers of samples used are 5.68×104 (a, d–f), 2.73×104 (b), and 1.09×104 (c).
In moist conditions, homogeneous nucleation could dominate for both ice cloud types as described in Sect. 3.1, but the mass fraction of homogeneously formed ice crystals is smaller for convection-generated ice clouds than that for in situ ice clouds, leading to a weaker decline in Rei with aerosols. Alternatively, for convection-generated ice clouds, ice multiplication, a microphysical process in which collision between ice particles and large supercooled droplets rapidly produces many secondary ice particles in strong updrafts (Lawson et al., 2015; Koenig, 1965, 1963), could also play a remarkable role in ice formation. Its role could be important only under moist conditions where cloud droplets may grow to large sizes required for ice multiplication (Lawson et al., 2015; Koenig, 1965, 1963). The onset of ice multiplication may suppress or even prevent homogeneous nucleation from occurring. In the situation dominated by ice multiplication, the relatively flat response of Rei to AOD in the case of convection-generated ice clouds can also be explained since ice multiplication is supposed to be stronger at lower AODs, which favors the formation of large cloud droplets. Whether the ice formation under moist conditions is dominated by homogeneous nucleation or ice multiplication is clearly dependent on environmental conditions such as updraft velocity, water vapor, cloud height and thickness, etc.; this is a subject requiring further research.
3.3 Seasonal variations in Rei–aerosol relationships
Furthermore, we find that the meteorological modulation can largely explain differences in Rei–AOD relationships as a function of season. Figure 4a shows that the Rei–AOD relationships are dramatically different associated with season, such that Rei decreases significantly with increasing AOD in summer (June, July, and August), while Rei increases rapidly in winter (December, January, and February). Figure 4d–f illustrate the probability distribution functions (PDFs) of RH100−440 hPa, CAPE, and U200 in different seasons (the area under any PDF equals 1.0). The overlapping area of PDFs in summer and winter represents the degree of difference in meteorological conditions between these two seasons. We find that meteorological conditions are significantly distinct in summer and winter in terms of RH100−440 hPa, CAPE, and U200, as indicated by relatively small overlapping areas (< 0.6) for these three parameters. The RH100−440 hPa and CAPE tend to be higher, and U200 tends to be more negative in summer. Moreover, the shapes of Rei–AOD curves in summer and winter highly resemble those under high-RH100−440 hPa/high-CAPE/negative-U200 and low-RH100−440 hPa/low-CAPE/positive-U200 conditions, respectively (see Fig. 1a–c), which demonstrates that the discrepancy in meteorological conditions between winter and summer can, to a large extent, explain the distinct Rei–AOD relationships in these two seasons.
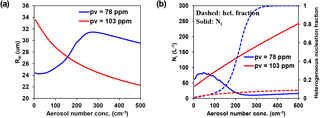
Figure 5Simulated changes in (a) Rei and (b) ice crystal number concentration (Ni) and the fraction of ice crystal number produced by heterogeneous nucleation (het.) as a function of the total aerosol number concentration. Simulations are conducted for two initial water vapor mass mixing ratios (pv), an indicator of available water amount for ice formation. The ratios of externally mixed dust (deposition INP), coated dust (immersion INP), and sulfate (not INP) are prescribed values of in all experiments.
With regard to different ice cloud types, the percentages of ice cloud profiles that are the convection-generated type are 38.2, 48.1, 51.4, and 39.1 % in winter, spring, summer, and fall, respectively. The corresponding percentages for in situ ice clouds are 57.0, 49.6, 47.0, and 58.2 %, respectively. Figure 4b and c show that, for both ice cloud types, the Rei–aerosol curves in summer and winter are largely similar to those under moist and dry conditions (Fig. 3), indicating that the seasonal variations in Rei–aerosol relations for both ice cloud types are largely attributable to the meteorology modulation. For convection-generated ice clouds, in winter, spring and fall, Rei generally increases when AOD < 0.5, characteristic of homogeneous nucleation being overtaken by heterogeneous nucleation, while Rei decreases slightly when AOD > 0.5 in accordance with heterogeneous nucleation and increasing INP concentrations. In summer, Rei shows a weak decreasing trend with AOD, which could be explained by the domination of homogeneous nucleation or ice multiplication as described in Sect. 3.2. For in situ ice clouds, a sharp decline in Rei with AOD is observed in summer, attributed to the Twomey effect when homogeneous nucleation prevails. The trends in other seasons are rather weak (although an increase is noticed in winter at low layer AOD). A probable reason is that each season consists of varying meteorological conditions (Fig. 4d–f). As shown in Fig. 3d–f, the decreasing trends in Rei under moist conditions are strong, while the increasing trends under dry conditions are relatively weak. Even if the occurrence frequency of dry conditions is large in a season, say winter, the integration of all meteorological conditions may still yield a relatively flat Rei–aerosol relationship. Another possible reason is that the correlation of INP concentration and layer AOD could be weak in some physical conditions.
3.4 Modeling support for the water vapor modulation
We have shown that the Rei–aerosol relationships are modulated by meteorological conditions, particularly water vapor amount. To support the observed relationships and our proposed physical mechanisms, we perform model simulations as described in Sect. 2.3 and summarize the results in Fig. 5.
Figure 5a reveals that the simulated patterns of Rei–aerosol relationships under different water vapor amounts agree fairly well with the corresponding observed patterns (Fig. 1a–c). Specifically, with an adequate water vapor supply (pv = 103 ppm), Rei decreases significantly with aerosol concentrations (Twomey effect). Under dry conditions (pv = 78 ppm), Rei increases noticeably with small to moderate aerosol concentrations (negative Twomey effect) and decreases slightly with further aerosol increase. A deeper analysis of the simulation results supports our proposed mechanism (Sect. 3.1) that the competition between different ice nucleation modes is the key to explain the water vapor modulation. With an adequate water vapor supply (pv = 103 ppm), the onset of deposition and immersion nucleation consumes only a small fraction of water vapor due to the small INP population. Considerable supersaturation remains. After further updraft movement, homogeneous nucleation is triggered and occurs spontaneously over a higher and narrow ice supersaturation range (140–160 %). Therefore, homogeneous nucleation acts as the dominant ice formation pathway, as indicated by the very small number fraction (< 10 %) of heterogeneously formed ice crystals, shown in Fig. 5b. In this case, more aerosols are associated with the formation of more numerous and smaller ice crystals, consistent with the simulation results of Liu and Penner (2005). With an inadequate water vapor supply (pv = 78 ppm), Fig. 5b reveals that the number fraction of heterogeneously formed ice crystals increases dramatically from < 1 % to ∼ 95 % when aerosol number concentrations increase from 5 to ∼ 300 cm−3 (the INP number concentrations increase proportionally). Obviously, the occurrence of heterogeneous nucleation could consume a considerable fraction of water vapor such that the remaining supersaturation is quite low and would require extremely strong updraft to uphold the homogeneous nucleation threshold. When aerosol loading increases, homogeneous nucleation is gradually suppressed and reduced to a minimum. Since the outburst of homogeneous nucleation generally produces more ice crystals at a smaller size compared with the heterogeneous counterpart, an increasing fraction of heterogeneous nucleation would result in fewer ice crystals with a larger average size (negative Twomey effect). At larger aerosol loading (300–500 cm−3), a further aerosol increase slightly reduces Rei in accordance with heterogeneous nucleation and the Twomey effect (all INPs are consumed in this aerosol concentration range).
The current cloud parcel model simulates the environmental conditions and physical processes for in situ ice clouds. For convection-generated ice clouds, the competition between homogeneous and heterogeneous nucleation may explain the observed Rei–aerosol relations, especially under dry conditions; however, the formation of this ice cloud type involves additional complex physical processes. As described in Sect. 3.2, ice multiplication, together with heterogeneous nucleation, may play an important role and dominate the ice formation in moist conditions. Furthermore, ice crystals in convection-generated ice clouds are formed primarily by the freezing of liquid droplets rather than nucleation on solution particles. The simulation of the aerosol impact on convection-generated ice clouds calls for more sophisticated models and future investigations.
As a simplified model, the simulation results of the cloud parcel model may not be quantitatively compared with the observational data. In satellite data analysis, we used column/layer AOD and RH100−440 hPa (or CAPE, U200) as proxies for aerosol loading related to ice clouds and overall available water amount in the upper atmosphere, respectively. However, the cloud parcel model only tracks the aerosol number concentration and water vapor within a single air parcel. It is clear that a direct and quantitative comparison between satellite observations and model results requires the development of a 3-D atmospheric model and analysis, a difficult task for further investigation in the future. Although the indices are not exactly the same, we submit that the simulated dependency of Rei on aerosols could be used to qualitatively interpret the observed relationships because the indices used in satellite analysis (AOD and RH100−440 hPa) and parcel model (aerosol number concentration and water vapor mixing ratio) are closely correlated with each other and the meteorological parameters and aerosol concentration ranges used in the simulations are representative of typical in situ ice clouds.
Finally, a factor that could potentially induce changes in satellite-retrieved Rei but has not been considered is the habit of ice crystals. Based on previous studies (Bailey and Hallett, 2009; Lawson et al., 2006; Lynch et al., 2002), the habit of ice crystals is dependent on a number of factors, among which the most important one is temperature, followed by ice supersaturation ratio. In this study we focus on Rei changes with aerosol loading, for which temperature does not appear to have a noticeable effect. For supersaturation ratio, the formation of ice crystals under moist conditions is dominated by homogeneous nucleation; therefore, the ice supersaturation ratio surrounding ice crystals is usually very low and the ice habit is not likely to change significantly with aerosol loading. Under drier conditions, however, heterogeneous nucleation gradually takes over homogeneous nucleation with aerosol loading increase. Subsequently, the supersaturation ratio surrounding ice crystals would become higher, possibly leading to changes in ice crystal habit. Considering that a single habit (i.e., aggregated column) is assumed in the Collection 6 MODIS retrieval algorithm (Platnick et al., 2015), ice habit changes could possibly induce changes in the satellite-retrieved Rei. However, this retrieval bias should not change our major conclusion about the aerosol impact on ice crystal size, which has been supported by the cloud parcel modeling used in this study. The quantitative assessment of the impact of ice crystal habit on satellite retrievals of Rei is a very complicated and difficult task that merits further study.
In this study, we investigate the effects of aerosols on Rei under different meteorological conditions using 9-year satellite observations. We find that the responses of Rei to aerosol loadings are modulated by water vapor amount in conjunction with several other meteorological parameters, and the responses vary from a significant negative correlation (Twomey effect) to a strong positive correlation (negative Twomey effect). Simulations using a cloud parcel model indicate that the water vapor modulation works primarily by altering the relative importance of different ice nucleation modes. The water vapor modulation holds true for both convection-generated and in situ ice clouds, though the sensitivities of Rei to aerosols differ noticeably between these two ice cloud types due to distinct formation mechanisms. The water vapor modulation can largely explain the different responses of Rei to aerosol loadings in various seasons.
Rei is a key parameter determining the relative significance of the solar albedo (cooling) effect and the infrared greenhouse (warming) effect of ice clouds; the variation of Rei could change the sign of ice clouds' net radiative effect (Fu and Liou, 1993). Aerosols have strong and intricate effects on Rei through their indirect effect. We provide the first and direct evidence that the competition between the Twomey effect and negative Twomey effect is controlled by certain meteorological parameters, primarily water vapor amount. Consequently, the first aerosol indirect forcing, defined as the radiative forcing due to aerosol-induced changes in Rei under a constant ice water content (IPCC, 2013; Penner et al., 2011), would change from positive to negative between high and low RH ranges, implying that the water vapor modulation could play an important role in determining the sign, magnitude, and probably seasonal and regional variations of aerosol–ice cloud radiative forcings. An adequate and accurate representation of this modulation in climate models will undoubtedly induce changes in the magnitude and sign of the current estimate of aerosol–ice cloud radiative forcing. Finally, although this study focuses on East Asia, we anticipate that the present findings might be generalized to other regions as well in view of the fact that the aerosol loadings in East Asia usually span a larger range than other regions due to substantial emissions (Zhao et al., 2017a; Wang et al., 2014) and that the aerosol effects on ice cloud properties are particularly pronounced at low and moderate aerosol loadings (Figs. 1, 3, 4).
The data that are needed to evaluate the results and conclusions are provided in the main text and in the Supplement. Additional related data will be available upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-1065-2018-supplement.
The authors declare that they have no conflict of interest.
Research work contained in this paper has been supported by NSF grants AGS
1660587 and 1701526, and NASA ROSES ACMAP, CCST, and TASNPP grants. Xiaohong
Liu's work is supported by the Climate Model Development and Validation
Activity funded by the Office of Biological and Environmental Research in the
US Department of Energy Office of Science. We also acknowledge the support of
the Joint Institute for Regional Earth System Science and Engineering at the
University of California, Los Angeles, and the Jet Propulsion Laboratory,
California Institute of Technology, under contract with
NASA.
Edited by: Qiang Fu
Reviewed by: two anonymous referees
Anderson, T. L., Charlson, R. J., Winker, D. M., Ogren, J. A., and Holmen, K.: Mesoscale variations of tropospheric aerosols, J. Atmos. Sci., 60, 119–136, https://doi.org/10.1175/1520-0469(2003)060<0119:Mvota>2.0.Co;2, 2003.
Atmospheric Science Data Center: CALIPSO Quality Statements Lidar Level 2 Cloud and Aerosol Layer Products Version Releases: 3.01, 3.02, available at: https://eosweb.larc.nasa.gov/PRODOCS/calipso/Quality_Summaries/CALIOP_L2LayerProducts_3.01.html (last access: 1 October 2016), 2012.
Bailey, M. P. and Hallett, J.: A Comprehensive Habit Diagram for Atmospheric Ice Crystals: Confirmation from the Laboratory, AIRS II, and Other Field Studies, J. Atmos. Sci., 66, 2888–2899, https://doi.org/10.1175/2009jas2883.1, 2009.
Brennan, J. I., Kaufman, Y. J., Koren, I., and Li, R. R.: Aerosol-cloud interaction-misclassification of MODIS clouds in heavy aerosol, IEEE T. Geosci. Remote, 43, 911–915, https://doi.org/10.1109/Tgrs.2005.844662, 2005.
Choi, Y. S., Lindzen, R. S., Ho, C. H., and Kim, J.: Space observations of cold-cloud phase change, P. Natl. Acad. Sci. USA, 107, 11211–11216, https://doi.org/10.1073/pnas.1006241107, 2010.
Chylek, P., Dubey, M. K., Lohmann, U., Ramanathan, V., Kaufman, Y. J., Lesins, G., Hudson, J., Altmann, G., and Olsen, S.: Aerosol indirect effect over the Indian Ocean, Geophys. Res. Lett., 33, L06806, https://doi.org/10.1029/2005gl025397, 2006.
Clarke, A. and Kapustin, V.: Hemispheric aerosol vertical profiles: Anthropogenic impacts on optical depth and cloud nuclei, Science, 329, 1488–1492, https://doi.org/10.1126/science.1188838, 2010.
Costantino, L. and Breon, F. M.: Analysis of aerosol-cloud interaction from multi-sensor satellite observations, Geophys. Res. Lett., 37, L11801, https://doi.org/10.1029/2009GL041828, 2010.
Delanoe, J. and Hogan, R. J.: A variational scheme for retrieving ice cloud properties from combined radar, lidar, and infrared radiometer, J. Geophys. Res., 113, D07204, https://doi.org/10.1029/2007JD009000, 2008.
Delanoe, J. and Hogan, R. J.: Combined CloudSat-CALIPSO-MODIS retrievals of the properties of ice clouds, J. Geophys. Res., 115, D00H29, https://doi.org/10.1029/2009JD012346, 2010.
DeMott, P. J., Prenni, A. J., Liu, X., Kreidenweis, S. M., Petters, M. D., Twohy, C. H., Richardson, M. S., Eidhammer, T., and Rogers, D. C.: Predicting global atmospheric ice nuclei distributions and their impacts on climate, P. Natl. Acad. Sci. USA, 107, 11217–11222, https://doi.org/10.1073/pnas.0910818107, 2010.
Fan, J. W., Wang, Y., Rosenfeld, D., and Liu, X. H.: Review of Aerosol–Cloud Interactions: Mechanisms, Significance, and Challenges, J. Atmos. Sci., 73, 4221–4252, 2016.
Fu, Q. and Liou, K. N.: Parameterization of the Radiative Properties of Cirrus Clouds, J. Atmos. Sci., 50, 2008–2025, https://doi.org/10.1175/1520-0469(1993)050<2008:Potrpo>2.0.Co;2, 1993.
Heymsfield, A. J., Miloshevich, L. M., Schmitt, C., Bansemer, A., Twohy, C., Poellot, M. R., Fridlind, A., and Gerber, H.: Homogeneous ice nucleation in subtropical and tropical convection and its influence on cirrus anvil microphysics, J. Atmos. Sci., 62, 41–64, https://doi.org/10.1175/jas-3360.1, 2005.
Hong, Y. L. and Liu, G. S.: The Characteristics of Ice Cloud Properties Derived from CloudSat and CALIPSO Measurements, J. Climate, 28, 3880–3901, https://doi.org/10.1175/jcli-d-14-00666.1, 2015.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
Huang, L., Jiang, J. H., Tackett, J. L., Su, H., and Fu, R.: Seasonal and diurnal variations of aerosol extinction profile and type distribution from CALIPSO 5-year observations, J. Geophys. Res.-Atmos., 118, 4572–4596, https://doi.org/10.1002/jgrd.50407, 2013.
Ikawa, M. and Saito, K.: Description of a Non-hydrostatic Model Developed at the Forecast Research Department of the MRI, Meteorological Research Institute, Tsukuba, Ibaraki, Japan, available at: http://www.mri-jma.go.jp/Publish/Technical/DATA/VOL_28/28_en.html (last access: 30 June 2017), 1991.
IPCC: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 1535 pp., 2013.
Jiang, J. H., Su, H., Schoeberl, M. R., Massie, S. T., Colarco, P., Platnick, S., and Livesey, N. J.: Clean and polluted clouds: Relationships among pollution, ice clouds, and precipitation in South America, Geophys. Res. Lett., 35, L14804, https://doi.org/10.1029/2008gl034631, 2008.
Jiang, J. H., Su, H., Massie, S. T., Colarco, P. R., Schoeberl, M. R., and Platnick, S.: Aerosol–CO relationship and aerosol effect on ice cloud particle size: Analyses from Aura Microwave Limb Sounder and Aqua Moderate Resolution Imaging Spectroradiometer observations, J. Geophys. Res., 114, D20207, https://doi.org/10.1029/2009jd012421, 2009.
Jiang, J. H., Su, H., Zhai, C., Massie, S. T., Schoeberl, M. R., Colarco, P. R., Platnick, S., Gu, Y., and Liou, K.-N.: Influence of convection and aerosol pollution on ice cloud particle effective radius, Atmos. Chem. Phys., 11, 457–463, https://doi.org/10.5194/acp-11-457-2011, 2011.
Kärcher, B. and Lohmann, U.: A parameterization of cirrus cloud formation: Heterogeneous freezing, J. Geophys. Res., 108, 4402, https://doi.org/10.1029/2002jd003220, 2003.
Kaufman, Y. J., Koren, I., Remer, L. A., Rosenfeld, D., and Rudich, Y.: The effect of smoke, dust, and pollution aerosol on shallow cloud development over the Atlantic Ocean, P. Natl. Acad. Sci. USA, 102, 11207–11212, https://doi.org/10.1073/pnas.0505191102, 2005.
Koenig, L. R.: The glaciating behavior of small cumulonimbus clouds, J. Atmos. Sci., 20, 29–47, https://doi.org/10.1175/1520-0469(1963)020<0029:tgbosc>2.0.co;2, 1963.
Koenig, L. R.: Drop freezing through drop breakup, J. Atmos. Sci., 22, 448–451, https://doi.org/10.1175/1520-0469(1965)022<0448:dftdb>2.0.co;2, 1965.
Krämer, M., Rolf, C., Luebke, A., Afchine, A., Spelten, N., Costa, A., Meyer, J., Zöger, M., Smith, J., Herman, R. L., Buchholz, B., Ebert, V., Baumgardner, D., Borrmann, S., Klingebiel, M., and Avallone, L.: A microphysics guide to cirrus clouds – Part 1: Cirrus types, Atmos. Chem. Phys., 16, 3463–3483, https://doi.org/10.5194/acp-16-3463-2016, 2016.
Kuebbeler, M., Lohmann, U., Hendricks, J., and Kärcher, B.: Dust ice nuclei effects on cirrus clouds, Atmos. Chem. Phys., 14, 3027–3046, https://doi.org/10.5194/acp-14-3027-2014, 2014.
Lawson, R. P., Baker, B., Pilson, B., and Mo, Q. X.: In situ observations of the microphysical properties of wave, cirrus, and anvil clouds. Part II: Cirrus clouds, J. Atmos. Sci., 63, 3186–3203, https://doi.org/10.1175/jas3803.1, 2006.
Lawson, R. P., Woods, S., and Morrison, H.: The Microphysics of Ice and Precipitation Development in Tropical Cumulus Clouds, J. Atmos. Sci., 72, 2429–2445, https://doi.org/10.1175/jas-d-14-0274.1, 2015.
Levy, R. C., Remer, L. A., Kleidman, R. G., Mattoo, S., Ichoku, C., Kahn, R., and Eck, T. F.: Global evaluation of the Collection 5 MODIS dark-target aerosol products over land, Atmos. Chem. Phys., 10, 10399–10420, https://doi.org/10.5194/acp-10-10399-2010, 2010.
Li, Q. B., Jiang, J. H., Wu, D. L., Read, W. G., Livesey, N. J., Waters, J. W., Zhang, Y. S., Wang, B., Filipiak, M. J., Davis, C. P., Turquety, S., Wu, S. L., Park, R. J., Yantosca, R. M., and Jacob, D. J.: Convective outflow of South Asian pollution: A global CTM simulation compared with EOS MLS observations, Geophys. Res. Lett., 32, L14826, https://doi.org/10.1029/2005gl022762, 2005.
Liou, K. N.: Cirrus clouds and climate in McGraw-Hill Yearbook of Science and Technology, McGraw-Hill Professional, New York, USA, 2005.
Liu, X. H. and Penner, J. E.: Ice nucleation parameterization for global models, Meteorol. Z., 14, 499–514, https://doi.org/10.1127/0941-2948/2005/0059, 2005.
Liu, X. H., Penner, J. E., and Wang, M. H.: Influence of anthropogenic sulfate and black carbon on upper tropospheric clouds in the NCAR CAM3 model coupled to the IMPACT global aerosol model, J. Geophys. Res., 114, D03204, https://doi.org/10.1029/2008jd010492, 2009.
Luebke, A. E., Afchine, A., Costa, A., Grooß, J.-U., Meyer, J., Rolf, C., Spelten, N., Avallone, L. M., Baumgardner, D., and Krämer, M.: The origin of midlatitude ice clouds and the resulting influence on their microphysical properties, Atmos. Chem. Phys., 16, 5793–5809, https://doi.org/10.5194/acp-16-5793-2016, 2016.
Lynch, D. K., Sassen, K., Starr, D., and Stephens, G.: Cirrus, Oxford University Press, New York, USA, 2002.
Mace, G. G., Clothiaux, E. E., and Ackerman, T. P.: The composite characteristics of cirrus clouds: Bulk properties revealed by one year of continuous cloud radar data, J. Climate, 14, 2185–2203, https://doi.org/10.1175/1520-0442(2001)014<2185:tccocc>2.0.co;2, 2001.
Mace, G. G., Benson, S., and Vernon, E.: Cirrus clouds and the large-scale atmospheric state: Relationships revealed by six years of ground-based data, J. Climate, 19, 3257–3278, https://doi.org/10.1175/jcli3786.1, 2006.
Massie, S. T., Heymsfield, A., Schmitt, C., Muller, D., and Seifert, P.: Aerosol indirect effects as a function of cloud top pressure, J. Geophys. Res., 112, D06202, https://doi.org/10.1029/2006JD007383, 2007.
Muhlbauer, A., Ackerman, T. P., Comstock, J. M., Diskin, G. S., Evans, S. M., Lawson, R. P., and Marchand, R. T.: Impact of large-scale dynamics on the microphysical properties of midlatitude cirrus, J. Geophys. Res.-Atmos., 119, 3976–3996, https://doi.org/10.1002/2013JD020035, 2014.
Murray, B. J., O'Sullivan, D., Atkinson, J. D., and Webb, M. E.: Ice nucleation by particles immersed in supercooled cloud droplets, Chem. Soc. Rev., 41, 6519–6554, https://doi.org/10.1039/c2cs35200a, 2012.
Ou, S. S. C., Liou, K. N., Wang, X. J., Hansell, R., Lefevre, R., and Cocks, S.: Satellite remote sensing of dust aerosol indirect effects on ice cloud formation, Appl. Optics, 48, 633–642, https://doi.org/10.1364/AO.48.000633, 2009.
Penner, J. E., Xu, L., and Wang, M. H.: Satellite methods underestimate indirect climate forcing by aerosols, P. Natl. Acad. Sci. USA, 108, 13404–13408, https://doi.org/10.1073/pnas.1018526108, 2011.
Platnick, S., King, M. D., and Meyer, K. G.: MODIS cloud optical properties: user guide for the collection 6 level-2 MOD06/MYD06 product and associated level-3 datasets, available at: https://modis-images.gsfc.nasa.gov/_docs/C6MOD06OPUserGuide.pdf (last access: 15 October 2017), 2015.
Pruppacher, H. R. and Klett, J. D.: Microphysics of Cloud and Precipitation, Springer, New York, USA, 1997.
Remer, L. A., Kaufman, Y. J., Tanre, D., Mattoo, S., Chu, D. A., Martins, J. V., Li, R. R., Ichoku, C., Levy, R. C., Kleidman, R. G., Eck, T. F., Vermote, E., and Holben, B. N.: The MODIS aerosol algorithm, products, and validation, J. Atmos. Sci., 62, 947–973, https://doi.org/10.1175/Jas3385.1, 2005.
Riihimaki, L. D. and McFarlane, S. A.: Frequency and morphology of tropical tropopause layer cirrus from CALIPSO observations: Are isolated cirrus different from those connected to deep convection?, J. Geophys. Res., 115, D18201, https://doi.org/10.1029/2009jd013133, 2010.
Rosenfeld, D. and Woodley, W. L.: Deep convective clouds with sustained supercooled liquid water down to −37.5 ∘C, Nature, 405, 440–442, https://doi.org/10.1038/35013030, 2000.
Rosenfeld, D., Andreae, M. O., Asmi, A., Chin, M., de Leeuw, G., Donovan, D. P., Kahn, R., Kinne, S., Kivekas, N., Kulmala, M., Lau, W., Schmidt, K. S., Suni, T., Wagner, T., Wild, M., and Quaas, J.: Global observations of aerosol-cloud-precipitation-climate interactions, Rev. Geophys., 52, 750–808, https://doi.org/10.1002/2013RG000441, 2014.
Seinfeld, J. H., Bretherton, C., Carslaw, K. S., Coe, H., DeMott, P. J., Dunlea, E. J., Feingold, G., Ghan, S., Guenther, A. B., Kahn, R., Kraucunas, I., Kreidenweis, S. M., Molina, M. J., Nenes, A., Penner, J. E., Prather, K. A., Ramanathan, V., Ramaswamy, V., Rasch, P. J., Ravishankara, A. R., Rosenfeld, D., Stephens, G., and Wood, R.: Improving our fundamental understanding of the role of aerosol-cloud interactions in the climate system, P. Natl. Acad. Sci. USA, 113, 5781–5790, https://doi.org/10.1073/pnas.1514043113, 2016.
Shi, X. and Liu, X.: Effect of cloud-scale vertical velocity on the contribution of homogeneous nucleation to cirrus formation and radiative forcing, Geophys. Res. Lett., 43, 6588–6595, https://doi.org/10.1002/2016GL069531, 2016.
Shi, X., Liu, X., and Zhang, K.: Effects of pre-existing ice crystals on cirrus clouds and comparison between different ice nucleation parameterizations with the Community Atmosphere Model (CAM5), Atmos. Chem. Phys., 15, 1503–1520, https://doi.org/10.5194/acp-15-1503-2015, 2015.
Stein, T. H. M., Delanoe, J., and Hogan, R. J.: A Comparison among Four Different Retrieval Methods for Ice-Cloud Properties Using Data from CloudSat, CALIPSO, and MODIS, J. Appl. Meteorol. Clim., 50, 1952–1969, https://doi.org/10.1175/2011jamc2646.1, 2011.
Su, H., Jiang, J. H., Lu, X. H., Penner, J. E., Read, W. G., Massie, S., Schoeberl, M. R., Colarco, P., Livesey, N. J., and Santee, M. L.: Observed Increase of TTL Temperature and Water Vapor in Polluted Clouds over Asia, J Climate, 24, 2728–2736, https://doi.org/10.1175/2010JCLI3749.1, 2011.
Twohy, C. H. and Poellot, M. R.: Chemical characteristics of ice residual nuclei in anvil cirrus clouds: evidence for homogeneous and heterogeneous ice formation, Atmos. Chem. Phys., 5, 2289–2297, https://doi.org/10.5194/acp-5-2289-2005, 2005.
Twomey, S.: Influence of pollution on shortwave albedo of clouds, J. Atmos. Sci., 34, 1149–1152, https://doi.org/10.1175/1520-0469(1977)034<1149:tiopot>2.0.co;2, 1977.
Waliser, D. E., Li, J. L. F., Woods, C. P., Austin, R. T., Bacmeister, J., Chern, J., Del Genio, A., Jiang, J. H., Kuang, Z. M., Meng, H., Minnis, P., Platnick, S., Rossow, W. B., Stephens, G. L., Sun-Mack, S., Tao, W. K., Tompkins, A. M., Vane, D. G., Walker, C., and Wu, D.: Cloud ice: A climate model challenge with signs and expectations of progress, J. Geophys. Res., 114, D00A21, https://doi.org/10.1029/2008JD010015, 2009.
Wang, F., Guo, J. P., Zhang, J. H., Huang, J. F., Min, M., Chen, T. M., Liu, H., Deng, M. J., and Li, X. W.: Multi-sensor quantification of aerosol-induced variability in warm clouds over eastern China, Atmos. Environ., 113, 1–9, https://doi.org/10.1016/j.atmosenv.2015.04.063, 2015.
Wang, J. D., Zhao, B., Wang, S. X., Yang, F. M., Xing, J., Morawska, L., Ding, A. J., Kulmala, M., Kerminen, V. M., Kujansuu, J., Wang, Z. F., Ding, D. A., Zhang, X. Y., Wang, H. B., Tian, M., Petaja, T., Jiang, J. K., and Hao, J. M.: Particulate matter pollution over China and the effects of control policies, Sci. Total Environ., 584, 426–447, https://doi.org/10.1016/j.scitotenv.2017.01.027, 2017.
Wang, S. X., Zhao, B., Cai, S. Y., Klimont, Z., Nielsen, C. P., Morikawa, T., Woo, J. H., Kim, Y., Fu, X., Xu, J. Y., Hao, J. M., and He, K. B.: Emission trends and mitigation options for air pollutants in East Asia, Atmos. Chem. Phys., 14, 6571–6603, https://doi.org/10.5194/acp-14-6571-2014, 2014.
Winker, D. M., Hunt, W. H., and McGill, M. J.: Initial performance assessment of CALIOP, Geophys. Res. Lett., 34, L19803, https://doi.org/10.1029/2007gl030135, 2007.
Wylie, D. P., Menzel, W. P., Woolf, H. M., and Strabala, K. I.: 4 Years of Global Cirrus Cloud Statistics Using Hirs, J. Climate, 7, 1972–1986, https://doi.org/10.1175/1520-0442(1994)007<1972:Fyogcc>2.0.Co;2, 1994.
Wylie, D. P., Jackson, D. L., Menzel, W. P., and Bates, J. J.: Trends in global cloud cover in two decades of HIRS observations, J. Climate, 18, 3021–3031, https://doi.org/10.1175/Jcli3461.1, 2005.
Zhao, B., Jiang, J. H., Gu, Y., Diner, D., Worden, J., Liou, K. N., Su, H., Xing, J., Garay, M., and Huang, L.: Decadal-scale trends in regional aerosol particle properties and their linkage to emission changes, Environ. Res. Lett., 12, 054021, https://doi.org/10.1088/1748-9326/aa6cb2, 2017a.
Zhao, B., Liou, K. N., Gu, Y., Li, Q. B., Jiang, J. H., Su, H., He, C. L., Tseng, H. L. R., Wang, S. X., Liu, R., Qi, L., Lee, W. L., and Hao, J. M.: Enhanced PM2.5 pollution in China due to aerosol-cloud interactions, Sci. Rep.-UK, 7, 4453, https://doi.org/10.1038/s41598-017-04096-8, 2017b.





