Technical note: General formulation for the distribution problem – prognostic assumed probability density function (PDF) approach based on the maximum-entropy principle and the Liouville equation

A general formulation for the distribution problem is presented, which is applicable to frequency distributions of subgrid-scale variables and hydrometeor size distributions, as well as to probability distributions characterizing data uncertainties. The general formulation is presented based upon two well-known basic principles: the maximum-entropy principle and the Liouville equation. The maximum-entropy principle defines the most likely general distribution form if necessary constraints are specified. This paper proposes to specify these constraints as the output variables to be used in a host model. Once a general distribution form is defined, the problem of the temporal evolution of the distribution reduces to that of predicting a small number of parameters characterizing it. This paper derives prognostic equations for these parameters from the Liouville equation. The developed formulation, which is applicable to a wide range of atmospheric modeling problems, is specifically applied to the condensation growth of cloud droplets as a demonstration.

1 Introduction

The present paper considers the distribution problem in a general manner. Regarding the problems of distributions, at least three examples are identified in atmospheric sciences.

The first and perhaps most obvious example is the problem of determining the distribution of a variable over a domain as a distribution density function (DDF). Typically, the domain corresponds to a grid box in a numerical simulation, and the obtained distribution is used for calculating subgrid-scale characteristics that are required by a host model. This problem may be called the subgrid-scale distribution problem. A specific application of this problem is the determination of the fractional area occupied by clouds within a grid box (Sommeria and Deadorff, 1977; Mellor, 1977; Bougeault, 1981; Le Treut and Li, 1991; Bechtold et al., 1992, 1995; Richard and Royer, 1993; Bony and Emanuel, 2001; Golaz et al., 2002; Tompkins, 2002). Arguably all subgrid-scale processes may be represented under this subgrid-scale distribution framework (cf. Yano, 2016).

The second example is the size distribution of hydrometeor particles (condensed water, ice species, etc.). Information on particle size distributions (PSDs) is crucial for predicting various conversion processes from one hydrometeor type to another as well as for evaluating fall-out rates of those hydrometeors (cf. Khain et al., 2015; Khain and Pinsky, 2018). The rates of all these processes depend sensitively on the hydrometeor particle size.

The third and perhaps most abstract example of the distribution is the probability. The notion of probability appears in many aspects of the atmospheric sciences (e.g., Yano and Manzato, 2022). Here, we especially keep in mind applications to data assimilation, in which data uncertainties are measured by probability distributions (cf. Wikle and Berliner, 2007).

The present paper considers all three of these problems under a single framework. It is possible to consider these three qualitatively different problems together because the time evolution of all these distributions can, in principle, be predicted by similar equations. The time evolution of both the subgrid-scale distribution (DDF) and the probability density function (PDF) is predicted by the Liouville equation (cf. Sect. 3.5). Here, it is hard to overemphasize the clear difference between them; to put it simply, distribution and probability are distinctively different concepts. Unfortunately, in the literature, both are often referred to as PDFs. We follow this custom to some extent, but we will add “DDF” in parentheses whenever it is not cumbersome. Thus, though these two problems deal with different types of distributions, both are governed by the same equation. The time evolution of PSDs is, fundamentally, described by the stochastic-collection equation by adding additional tendency terms to it (cf. Sect. 3.6). Though its form is not identical to the Liouville equation, it can still be considered in an analogous manner. Thus, it becomes possible to deal with these three different problems under a single framework.

All three of these problems also suffer from the same difficulty: direct use of these fundamental equations (Liouville and stochastic-collection) turns out to be very expensive computationally. In data assimilation, an ensemble-forecast method is adopted as an alternative, but the difficulty of generating a statistically large enough ensemble remains. Thus a numerically more efficient method must be sought in order to make them practically useful. This difficulty has been, so far, addressed separately in these three problems. The originality of the present work is to simply point out that all three of these computational problems can be considered under a common framework.

In the subgrid-scale distribution problem, a main strategy is to assume a simple distribution form that is specified by a small number of parameters, sometimes termed “PDF parameters”. The PDF parameter values, and hence the distribution itself, evolve with time as conditions change from, say, overcast cloud to cumulus cloud. Hence the time evolution of the PDF parameters must be predicted. Typically, this is done by first predicting a set of moments of the distribution and then inverting the set to solve for the PDF parameters. This general approach can be called an assumed-PDF method. One of the earliest applications of the idea to turbulence is by Lockwood and Naguib (1975). See also an early review by Pope (1979).

A main strategy in cloud microphysics is to integrate the full information over all the possible particle sizes. Thus, the distribution problem becomes implicit. This approach is called bulk. However, for performing integrals over particle size, we need to assume a certain distribution form, which is typically exponential or the gamma distribution. In this manner, we see a clear link of the “bulk” microphysical approaches to the “assumed-PDF” approach.

In data assimilation, typically, a decision is made to focus only on the mean, variance, and some covariances of a probability distribution. As a result, a full probability is not explicitly considered. Here, typically, an “assumed PDF” is Gaussian.

For overviews on how these three problems are constructed using the distributions, we refer to Machulskaya (2015) for the subgrid-scale distribution problem; Seifert and Beheng (2001, 2006), Khain et al. (2015), and Khain and Pinsky (2018) for microphysics; and Bannister (2017), Jazwinski (1970), and Carrassi et al. (2018) for the data assimilation. Among those three problems, the role of probability may be least obvious in data assimilation, especially for those who only consult the final formulation of the standard variational principle. Here, we specifically refer to Sect. 2 of Carrassi et al. (2018), in which a more formal formulation in terms of the probability is presented.

The purpose of this study is to present a more coherent and self-contained formulation for the distribution problems under the framework of those assumed-PDF approaches in a general sense. The assumed-PDF approaches solve only about half of the whole problem. There are still two major issues to be resolved: (i) the choice of an assumed-PDF form and (ii) methodologies for evaluating the time evolution of the introduced PDF parameters efficiently. The present study proposes the solutions to those two major issues. Currently, there is no clear guiding principle for the first issue (cf. Sect. 3.2.2). The second issue is currently dealt with by relating the PDF parameters and moments to each other, but the conversion from moments to parameters is not guaranteed to be simple or analytic (cf. Sect. 3.2.1). By addressing these two major issues in the distribution problem, the present study generalizes the formulation for the existing assumed-PDF approaches developed for the subgrid-scale distribution problem into more general distribution problems. By doing so, the present study links the subgrid-scale distribution problem to the distribution problem more generally, as found in, for example, cloud microphysics and data assimilation. Conversely, the generalized formulation of the present study reduces to the existing assumed-PDF approaches by introducing additional approximations and assumptions (cf. Sect. 5.4).

Here, these two questions are addressed separately in this study in Sects. 4 and 5, respectively. Thus, those two methodologies can also be adopted independently if desired. Yet, the present study suggests that the most coherent formulation for the assumed-PDF approaches can be developed by adopting both methodologies together.

In this manner, the present work also constitutes an effort to develop a unified and coherent formulation for subgrid-scale representations (Yano, 2016; Yano et al., 2014, 2018). Readers are encouraged to refer to them for the authors' general perspectives on the subgrid-scale representations, but see further Yano (2015a, b). Refer especially to Yano (2016) for general discussions of the subgrid-scale distribution problem. Keep in mind that the subgrid-scale representation problem is considered exclusively from the perspective of DDF in the present study but without excluding the possibilities of alternative approaches as discussed in Yano (2016). More generally, the fundamental research, as pursued in the present study, is extremely crucial for the improvement of subgrid-scale parameterizations (Yano et al., 2014). Even the current operational numerical forecasts, which are based on a premise of high-resolution cloud modeling, may break down without such fundamental research to support them (Yano et al., 2018).

The paper begins in the next section by introducing a basic governing equation system that is adopted throughout the paper to construct the general formulation for the distribution problems. As seen therein, the adopted governing equation is general enough that the formulation of the present study can be applied to more or less any problems that can be expected in atmospheric sciences. Section 3 reviews our basic knowledge about the distribution problem. The moment concept is first introduced in Sect. 3.1 because it is so central in the current approaches. The basic idea of the assumed-PDF approach is outlined in Sect. 3.2, where its basic problems are also pointed out. The maximum-entropy principle, which defines the form for the most likely general distribution under given constraints, is introduced in Sect. 3.3, and its applications are further discussed in Sect. 3.4. The Liouville equation is introduced in Sect. 3.5, and the stochastic-collection equation is separately introduced in Sect. 3.6.

Both the maximum-entropy principle and the Liouville equation play key roles in the present study, albeit in different manners, in resolving the two aforementioned major issues. The first issue is addressed by taking the maximum entropy as a guiding principle. A key open question here is the precise conditions to be posed under this principle in order to define a PDF (DDF). A standard procedure is to take what we already know as a specified condition of a system (e.g., total kinetic energy of an ideal-gas system). An original argument of the present paper is to propose to constrain the form of the PDF (DDF), instead, by the quantities that are required, for example, for purpose of predictions (e.g., cloud fractions, precipitation rate) in modeling. This argument is developed in Sect. 4 by discussing the contrasts between the standard statistical problems and those typically addressed in atmospheric sciences. The second issue is addressed in Sect. 5 by deriving a general form from the Liouville equation of prognostic equations for predicting the time evolution of the PDF parameters introduced under an assumed PDF. The derived general formulation is applied to the illustrative example of the condensation growth of cloud droplets in Sect. 6. The paper is concluded in Sect. 7.

It is emphasized that this work presents a new formulation by addressing the two aforementioned major problems in the assumed-PDF approaches, rather than solving any specific problems. For this reason, the basic style is to present basic principles first in a straight and concise manner. We choose this style for ease of referring to formulations, especially based on the fact that the presented formulation can be applied to almost any distribution problems in atmospheric sciences. Specific examples are gradually introduced so that a more concrete picture of the methodology gradually emerges. Readers who would like to see a concrete example first are suggested to go to Sect. 6 directly and read backwards. Also for this reason, the governing equation system to be considered in the present study is introduced in a standalone manner separately in the next section so that the range of applicability of the present study to various atmospheric problems should become immediately clear. Along the lines of generality intended in the present study, all the equations are presented in nondimensional forms, setting the various physical constants to unity for convenience, throughout the paper.

2 Governing equation system

Many physical variables, say ϕ, of the atmospheric flows are advective; thus they are governed by an equation of the following form:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial \mathit{\varphi }}{\partial t}}=-\mathit{v}\cdot \mathrm{\nabla }\mathit{\varphi }+F.\end{array}$$

Here, v is the velocity and F designates all the tendencies (source) contributing to the variable, ϕ, apart from the advection as represented as the first term on the right-hand side. The source, F, generally depends on the variable, ϕ, and also possibly on time t and space. For instance, in a cloud macrophysical application, ϕ is the liquid water content or the number density of liquid droplets with a particular radius. Equations (2.9), (2.10), and (2.11) of Machulskaya (2015) are examples of the equations of the form of Eq. (1) considered in the context of the DDF problem. Yano et al. (2005) and Yano (2016) show that the basic formulations for the subgrid-scale parameterizations can be reproduced by simply examining this general form (Eq. 1). More specifically, Yano (2014) shows that all the essential, basic standard formulas for the mass-flux convection parameterization can be reproduced from a general governing equation, Eq. (1).

With an ultimate application to the systems described by governing equations of the form of Eq. (1) in mind, for ease of the deductions in the following, the present study focuses on a case with no spatial dependence in the above:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{d}\mathit{\varphi }}{\mathrm{d}t}}=F.\end{array}$$

Yet, in spite of this restriction, and without arguing for any general physical relevance, it may also be worthwhile to emphasize that the source term, F, in Eq. (2) includes any types of physical processes that are locally defined. Most of the microphysical processes, for example, fall into this category. More importantly, this restriction does not have any serious consequences because the final general formulation for predicting the assumed-PDF parameters in Sect. 5.1 is very easily generalized to the cases with spatial dependence (cf. Sect. 5.3).

To maintain the generality of the formulation, the term, F, is left unspecified in considering the time evolution of various types of distributions in Sect. 5. As a result, the formulations presented in the following, especially our key result given by Eqs. (50a) and (50b), are applicable to any types of physics. All we have to do is to specify the form, F, as required in applications. As a specific example, the source term is set to $F=\mathrm{1}/r$ in Sect. 6 (cf. Eq. 76a) in considering the condensation growth of a droplet with a radius, r. We also examine the behavior of systems with mathematically simple forms for F in Sect. 5.5 as well as in Appendix C. Keep in mind that in Eq. (1), the source term, F, can be space dependent, say, involving spatial derivatives. However, in considering Eq. (2) in the following, this possibility will be excluded for ease of analysis. Furthermore, in the present study, the source term, F, is assumed to be deterministic, except for the case of the Brownian motion considered in Sect. 4.4.

Throughout the study, only the cases with a single variable, ϕ, are considered explicitly for the economy of presentation. However, when multiple variables are involved in a problem, as is typically the case in any realistic applications, the only modification required is to replace the scalar, ϕ, by a vector. Examples with systems with multiple dimensions are presented in Yano (2024). Probably, a more serious restriction in the following development of the formulation is in considering only the cases with no spatial dependence. However, as it turns out, the generalization of the final formulation to the spatially dependent cases with Eq. (1) is fairly straightforward, as discussed in Sect. 5.3.

In the present work, we proceed with the hypothesis that the physics of a system is already completely known in the form of Eq. (2) with a forcing term, F, completely specified. In practical applications, this hypothesis is satisfied by specifying all the terms in a system in a closed form, as parameterizations, if required. Especially, in applying the general formulation of the present study to the subgrid-scale distribution problems, this hypothesis means that we know the governing equation system of the small scale to be parameterized fully; cf. Sect. 4.3 for further discussions. In this spirit, for example, Yano (2014) proceeds with a hypothesis that we know perfectly the equations for the cloud-resolving modeling and reconstructs the standard mass-flux-based convection parameterization based on this hypothesis. In the same way, the present method solves a subgrid-scale distribution problem assuming that we know the full equations for all the scales of a system. As is going to be seen, for this reason, we do not need any turbulence closures (cf. Mellor, 1973; Mellor and Yamada, 1974) in the present formulation.

3 Basic principles

The purpose of this section is to summarize well-known basic principles for describing PDFs (DDFs).

3.1 Distributions and moments

Let a PDF (DDF) for a variable, ϕ, be denoted by p(ϕ). Moments, 〈ϕⁿ〉 ($n=\mathrm{1},\mathrm{2},\mathrm{\dots }$),¹ can be constructed from a given distribution, p, by

$$\begin{array}{}\text{(3)}& \langle {\mathit{\varphi }}^n\rangle =\int {\mathit{\varphi }}^{n}p\mathrm{d}\mathit{\varphi }.\end{array}$$

Here, an unspecified integral range may be taken from −∞ to +∞ with many of the physical variables, but some physical variables are semi-positive definite (e.g., temperature, mixing ratios). In the latter case, the integral range above must be from 0 to +∞.

The series of moments may be interpreted analogously to the Taylor series, in the sense that it constrains a function. However, unlike the latter, there is no closed analytical formula for reconstructing the original distribution from a given series of moments: although a series of moments can be derived from a given distribution in a straightforward manner, the reverse is hardly the case. This is in spite of the extensive literature on the subject (e.g., Daniels, 1954; Butler, 2007; Dang and Xu, 2019). On the other hand, the usefulness of the moments for describing the turbulent flows can hardly be overemphasized (e.g., Stull, 1988; Garratt, 1992) either.

3.2 Assumed PDF (DDF)

3.2.1 General formulation

The basic idea of an assumed-PDF (DDF) approach is to introduce a generic form of PDF (DDF) characterized by a few free parameters, say λ_i ($i=\mathrm{0},\mathrm{\dots },N$, where N is kept as small as possible), but in such a manner that the distribution of a variable of concern can be represented:

$$\begin{array}{}\text{(4a)}& p=p(\mathit{\varphi },{\mathit{\lambda }}_{\mathrm{0}},{\mathit{\lambda }}_{\mathrm{1}},\mathrm{\dots },{\mathit{\lambda }}_N).\end{array}$$

Here, λ₀ will be used to designate a constant factor for a normalization of a distribution throughout the paper whenever the assumed-PDF formulation is discussed in a general manner. On the other hand, p₀ will be adopted for the normalization factor whenever a specific PDF form is discussed; the latter choice is consistent with the fact that notations different than λ_i (i≠0) are also often adopted for the other assumed-PDF parameters.

Importantly, the distribution, p, is related to the cumulative probability, P, by

$$\begin{array}{}\text{(4b)}& p=\mathrm{d}P/\mathrm{d}\mathit{\varphi },\end{array}$$

where P is more precisely defined as the probability that the variable ϕ^′ is less than a specified value ϕ; i.e., $P=P({\mathit{\varphi }}^{\prime }<\mathit{\varphi })$.

Examples of distributions taking the form of Eq. (4a) are discussed in subsequent subsections (e.g., Eqs. 24 and 25, setting p₀=λ₀ therein). Once the functional form of a distribution is constrained by Eq. (4a), the problem of determining the distribution p(ϕ), which must be defined for every value of ϕ, reduces to that of determining a given finite set of parameters {λ_i}, which evolve with time by following the evolution of the distribution. However, keep in mind that the parameters {λ_i} should not depend on ϕ for obvious reasons. Note that {*} indicates a set of parameters throughout the paper.

Here, it is important to remember that an assumed-PDF form is only an approximation; to state this fact more emphatically, it may be better to state it as

$$\begin{array}{}\text{(4c)}& p=p(\mathit{\varphi },{\mathit{\lambda }}_{\mathrm{0}},{\mathit{\lambda }}_{\mathrm{1}},\mathrm{\dots },{\mathit{\lambda }}_N)+\mathit{\epsilon },\end{array}$$

with ε designating the possible error under this approximation. Yet, in the following deductions, this error term is mostly neglected, except for couple of exceptions where it is added as a reminder.

A major exception to the above rule is when the assumed PDF is an exact solution of the original equation, and when the initial PDF follows the assumed form, there is no error. We may further expect that the error remains small even if the initial PDF does not follow the assumed form. Otherwise, there is no way that an assumed-PDF form can predict the evolution of a distribution in any accurate manner.

The parameters {λ_i} defining the distribution (Eq. 3) may be determined, for example, from a known set of moments, 〈ϕⁿ〉; i.e.,

$$\begin{array}{}\text{(5)}& {\mathit{\lambda }}_i={\mathit{\lambda }}_i\left(\mathit{\right\{}\langle {\mathit{\varphi }}^n\rangle \mathit{\left\}}\right).\end{array}$$

The prognostic equations for these moments, or diagnostic approximations of these equations, are, in turn, known from, e.g., the turbulence theories for the system (Eq. 1) in the context of the subgrid-scale distribution problem; thus the problem is closed in this manner. That is the current basic strategy of the assumed-PDF (DDF) approach (Larson, 2022).

However, there are problems with this strategy. First, the functional form of a PDF (DDF), p(ϕ,{λ_i}), must somehow be prescribed. However, no clear principle has been identified. A main thread of this paper is to use the maximum-entropy principle (cf. Sect. 3.3) for this purpose. The second problem is the difficulty of deriving a closed expression (Eq. 5) for defining the PDF (DDF) parameters from a given set of moments. Here, it is straightforward to compute the moments from a given PDF (DDF); thus we can readily write this down as

$$\begin{array}{}\text{(6)}& \langle {\mathit{\varphi }}^n\rangle =\langle {\mathit{\varphi }}^n\rangle \left(\mathit{\right\{}{\mathit{\lambda }}_i\mathit{\left\}}\right).\end{array}$$

However, inverting Eq. (6) into Eq. (5) is often not at all trivial due to the nonlinearity in the former, and PDF parameters are defined only in an implicit manner from a set of moments. See Eq. (6) of Milbrandt and Yau (2005) for example. Often extra assumptions and approximations are required to make this inversion possible (cf. Machulskaya, 2015). Alternatively, an iterative procedure can be adopted in order to invert a given set of moments and deduce the PDF parameter values (e.g., Lewellen and Yoh, 1993). The difficulty of the inversion is exacerbated by predicting more (higher-order) moments and also by moving to multivariate PDFs. In Sect. 5, we will show, by more explicitly invoking the Liouville equation as introduced in Sect. 3.5, how a prognostic set of equations for {λ_i} can be written down explicitly. These equations are closed in the sense that no further inversion is required.

3.2.2 Choice of assumed-distribution forms

In current assumed-PDF (DDF) approaches in the context of the subgrid-scale distribution problem, distribution forms to be adopted are chosen in a rather subjective manner, mostly based on computational convenience. For this reason, one popular choice is double Gaussian, i.e., a sum of 2 Gaussians, for the purpose of representing a skewness (e.g., Larson et al., 2002; Fitch, 2019; Naumann et al., 2013). Although those studies show some fits to distributions obtained from either observation or large-eddy simulations as support, we should not consider that double-Gaussian distributions have been verified by data; no objective comparisons with alternative possible distributions have been made.

On the other hand, observations suggest that the hydrometeor PSD follows an exponential distribution in the size (Marshall and Palmer, 1948). However, Yano et al. (2016) point out the difficulty of identifying the best fit for the PSDs observationally from various exponential distribution forms that are derived from the maximum-entropy principle (cf. Sect. 3.3): it is indeed not possible to verify in any convincing manner that any of those fit the observations better than the others, although it is possible to discuss different values of errors of those fittings.

3.3 Maximum-entropy principle: derivation

3.3.1 Derivation

To address the first issue of the choice of PDF (DDF) form, we take the maximum entropy as a guiding principle. It must be emphasized that this is merely a mathematical principle. Here, the guiding principle suggests that it is not any physical principle but merely a principle that guides a choice of an assumed-PDF form. Note especially that Boltzmann's entropy, which takes a mathematically identical form, can be derived by physical reasoning. However, it should not be confused with the information entropy in general. From a physical point of view, although the principle is plausible, there is no guarantee that it actually works. For this reason, we adopt this principle merely as a guide for identifying a necessary assumed form of a PDF (DDF). Such a guiding principle is useful when there is no other principle for choosing an assumed distribution. This principle should not be interpreted as a hypothesis either because it suggests that the guiding principle may be disproved by experiments. Here, the success of a guiding principle may vary from case to case. However, so long as this principle is used with caution, we expect that it remains useful for choosing a PDF form.

The maximum-entropy principle asks the question of what the “most likely” distribution of a variable is under a given set of “constraints” (cf. Eq. 12 below). It simply argues that the “most likely” distribution is a distribution that is actually realized in a given system. The argument of this principle is simple and appealing enough to gain extensive application (cf. Kapur, 1989), notably in the statistical description of geophysical flows (e.g., Robert and Sommeria, 1991; Verkley and Lynch, 2009; Verkley, 2011; Verkley et al., 2016). For this reason, the present study also invokes this principle. See Yano (2019) for further implications of this principle, as well as for further references of applications in atmospheric sciences and many other disciplines.

Here, “most likely” is defined in terms of the number of possible combinations for a given state of a variable (cf. Eq. 8 below). We develop the idea for a discrete system first for ease of explanation. Thus, we assume a variable, ϕ, takes m values, say, designated by ϕ_i ($i=\mathrm{1},\mathrm{\dots },m$). For instance, in a cloud macrophysics application, ϕ might represent the liquid water content, whose values might be binned into m categories (0 to 1 g kg⁻¹, 1 to 2 g kg⁻¹, etc.). Let us assume that the total number of data (e.g., measurements, model outputs) is n and, among them, n_i takes a value ϕ_i ($i=\mathrm{1},\mathrm{\dots },m$). For instance, we might sample a cloud n times, each time drawing a value of liquid water content, and we might denote the number of samples that fall into the ith bin by n_i. Thus, the frequency distribution of the variable, ϕ, is given by

$$\begin{array}{}\text{(7)}& p_i=n_i/n,\end{array}$$

with $i=\mathrm{1},\mathrm{\dots },m$.

The total number of possible combinations for realizing this distribution is

$$\begin{array}{}\text{(8)}& W={\displaystyle \frac{n\mathrm{!}}{n_{\mathrm{1}}\mathrm{!}\mathrm{\dots }{n}_m\mathrm{!}}}.\end{array}$$

By applying a logarithm to the above and also applying Stirling's formula,

$$\begin{array}{}\text{(9)}& \log n\mathrm{!}=n\log n+O\left(n\right),\end{array}$$

which is valid in the asymptotic limit of n→∞; for every integer involved in the definition of W, we can approximate

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\mathrm{1}}{n}}\log W\simeq -\sum _{i=\mathrm{1}}^m{p}_i\log p_i.\end{array}$$

The right-hand side of Eq. (10) is the information entropy (Shannon, 1948), which we shall refer to as “entropy” for short.² Thus, the problem of maximizing the number of possible combinations reduces to that of maximizing the entropy, and it leads to the notion of the maximum-entropy principle.

The most extreme case of this distribution is when ϕ always takes only a particular value, say ϕ_j; thus p_i=δ_ij, using Kronecker's delta. In this case, there is no possibility of reshuffling the data; thus W=1 and the entropy is zero. Qualitatively, as a variable is more widely distributed, the entropy becomes larger.

A continuous version of the entropy is

$$\begin{array}{}\text{(11)}& -\int p\log p\mathrm{d}\mathit{\varphi },\end{array}$$

where p=p(ϕ). However, some subtleties will be remarked upon later in Sect. 3.4.1.

In applying the maximum-entropy principle, here, we suppose that the distribution is constrained by L conditions given by

$$\begin{array}{}\text{(12)}& \int G_l(p,\mathit{\varphi })\mathrm{d}\mathit{\varphi }=C_l\end{array}$$

for $l=\mathrm{1},\mathrm{\dots },L$. Here, $G_l(p,\mathit{\varphi })=p{\mathit{\sigma }}_l\left(\mathit{\varphi }\right)$, σ_l(ϕ) denotes functions of ϕ (they define the constraints by Eq. 12), and C_l denotes known constants. See Sect. 3.4.2 for specific examples (cf. Eq. 22) and Yano et al. (2016) for physical considerations of choices. Also keep in mind that a distribution is normalized by

$$\begin{array}{}\text{(13)}& \int p\mathrm{d}\mathit{\varphi }=\mathrm{1}.\end{array}$$

The normalization can be considered a special case of the constraints (Eq. 12) with G₀=p and C₀=1 by extending the above series to l=0. Note that, exceptionally, when the PSDs are considered, C₀ must be equal to the total particle number density.

Thus, the most likely distribution is obtained by maximizing Eq. (11) under the constraints (Eq. 12) with $l=\mathrm{0},\mathrm{\dots },L$. This goal is accomplished by applying a variational principle, as defined by following a standard notation (cf. Chap. 2, Goldstein et al., 2002):

$$\begin{array}{}\text{(14)}& \mathit{\delta }\left[-\int p\log p\mathrm{d}\mathit{\varphi }-\sum _{l=\mathrm{0}}^m{\mathit{\lambda }}_l^{\prime }\int G_l(p,\mathit{\varphi })\mathrm{d}\mathit{\varphi }\right]=\mathrm{0},\end{array}$$

with Lagrange multipliers, ${\mathit{\lambda }}_l^{\prime }$. The above variation reduces to

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{\displaystyle \frac{\mathit{\delta }}{\mathit{\delta }p}}& \left[\int p\log p\mathrm{d}\mathit{\varphi }+\sum _{l=\mathrm{0}}^L{\mathit{\lambda }}_l^{\prime }\int G_l(p,\mathit{\varphi })\mathrm{d}\mathit{\varphi }\right]\mathit{\delta }p\\ & =\int \left[\log p+\sum _{l=\mathrm{0}}^L{\mathit{\lambda }}_l{\displaystyle \frac{\partial G_l}{\partial p}}\right]\mathrm{d}\mathit{\varphi }\mathit{\delta }p=\mathrm{0},\end{array}\end{array}$$

where the multipliers are re-set to

$$\begin{array}{}\text{(16)}& {\mathit{\lambda }}_l=\left\{\begin{array}{ll}\mathrm{1}+{\mathit{\lambda }}_{\mathrm{0}}^{\prime }& l=\mathrm{0},\\ {\mathit{\lambda }}_l^{\prime }& l\ne \mathrm{0}.\end{array}\right.\end{array}$$

Noting that $\partial G_{\mathrm{0}}/\partial p=\mathrm{1}$ and $\partial G_l/\partial p={\mathit{\sigma }}_l\left(\mathit{\varphi }\right)$ ($l=\mathrm{1},\mathrm{\dots },L$) and further re-setting p₀ to equal $e^{-{\mathit{\lambda }}_{\mathrm{0}}}$, the most likely distribution under these constraints is

$$\begin{array}{}\text{(17)}& p=p_{\mathrm{0}}\exp \left[-\sum _{l=\mathrm{1}}^L{\mathit{\lambda }}_l{\mathit{\sigma }}_l\left(\mathit{\varphi }\right)\right].\end{array}$$

Here the constants, p₀ and λ_l are determined from the constraints (Eq. 12 and 13) by directly substituting the distribution form (Eq. 17) into them. This is the basic premise of the maximum-entropy principle: a distribution of a variable, ϕ, is completely determined from only L constraints if they are chosen properly. These L constraints determine L parameters, {λ_j}, that characterize the distribution. Recall that whenever the general assumed-PDF formulation is discussed, we further re-set λ₀ to equal p₀ (cf. Eq. 44a).

3.3.2 Technical remarks

A rather ostensible limitation of the general result (Eq. 17) from the maximum-entropy principle is that it does not include the possibility of a distribution zero at the zero value, as is the case with many semi-positive definite atmospheric variables, in any obvious manner. However, this simply stems from the fact that results from the maximum entropy are not exact: this principle is based on an approximate logarithmic expression of the number, W, of possible combinations under an asymptotic limit of n→∞ (cf. Eq. 9). In this respect, this principle may be considered a special case of the large-deviation principle (e.g., Touchette, 2009): it can elucidate only a predominant exponential dependence as seen in Eq. (17). A possible additional subdominant algebraic dependence is kept implicit because such a weak dependency drops out in the given asymptotic approximation. Thus, if required, an algebraic dependence of, say, ϕ^μ can be multiplied on this distribution without contradicting the given result (Eq. 17). Here, μ is an unspecified free positive parameter. This slight generalization ensures the condition p(0)=0 as required for many atmospheric variables. See further discussions in Sect. 3.4.3 and further mathematical background in Guiasu (1977).

3.4 Maximum-entropy principle: examples

In order to understand the general distribution given by Eq. (17) above better, this sub-section considers some special cases. Implications of the maximum-entropy principle are also remarked upon.

3.4.1 Homogeneous distribution

The simplest case for consideration is one without any constraints (i.e., L=0). Then Eq. (17) simply reduces to a homogeneous distribution:

$$\begin{array}{}\text{(18)}& p=p_{\mathrm{0}}.\end{array}$$

This means that a variable, ϕ, has an equal chance of having every possible value when there is nothing to constrain ϕ.

However, there are a few difficulties in applying this conclusion to arbitrary physical variables. First, a distribution of a variable must be bounded from both below and above in order to apply this distribution. Second, the conclusion depends on the choice of a physical variable. This is realized by noting that any physical variable, ϕ, can be transformed into another, φ, by assuming a relation, for example,

$$\begin{array}{}\text{(19)}& \mathit{\varphi }={\mathit{\phi }}^{\mathit{\alpha }},\end{array}$$

with a constant α, and then the distribution is transformed by a relation

$$\begin{array}{}\text{(20)}& p\left(\mathit{\varphi }\right)\mathrm{d}\mathit{\varphi }=\mathit{\alpha }{\mathit{\phi }}^{\mathit{\alpha }-\mathrm{1}}p\left({\mathit{\phi }}^{\mathit{\alpha }}\right)\mathrm{d}\mathit{\phi }.\end{array}$$

Here, recall the definition of the distribution, p, given by Eq. (4b).

Thus, although the system may represent a homogeneous distribution in terms of a particular variable, ϕ, it is no longer homogeneously distributed in terms of another related variable, φ. This is a contradiction because a constant distribution is obtained for a transformed variable, φ, when the maximum-entropy principle is directly applied to the latter. In this case, the original variable, ϕ, no longer follows a constant probability according to the relation of Eq. (20).

The source of this ambiguity, i.e., the result from the maximum-entropy principle depending on the choice of the distribution variable (ϕ or φ), stems from the fact that in translating a discrete expression for entropy (Eq. 10) into a continuous version (Eq. 11), it is assumed that a variable, ϕ, takes discrete values defined by a constant increment, $\mathrm{\Delta }\mathit{\varphi }=({\mathit{\varphi }}_m-{\mathit{\varphi }}_{\mathrm{1}})/(m-\mathrm{1})$, over an interval, [ϕ₁,ϕ_m]:

$$\begin{array}{}\text{(21)}& {\mathit{\varphi }}_i={\mathit{\varphi }}_{\mathrm{1}}+(i-\mathrm{1})\mathrm{\Delta }\mathit{\varphi },\end{array}$$

with $i=\mathrm{1},\mathrm{\dots },m$. Then Eq. (11) is obtained from the right-hand side of Eq. (10) by multiplying Δϕ on the latter and taking a limit of m→∞. Conversely, Eq. (11) can be approximated by the right-hand side of Eq. (10) multiplied by Δϕ with the discretization (Eq. 21). Note that ambiguity with an arbitrary algebraic factor is also consistent with the nature of the maximum-entropy principle that is valid only in an asymptotic sense, as already suggested in Sect. 3.3.2.

3.4.2 Constraints by moments

When a variable is constrained by the first L moments, general constraints (Eq. 12) reduce to

$$\begin{array}{}\text{(22)}& \int {\mathit{\varphi }}^{l}p\mathrm{d}\mathit{\varphi }=C_l,\end{array}$$

with C_l being a value of the lth moment with σ_l=ϕ^l. The general distribution (Eq. 17) reduces to

$$\begin{array}{}\text{(23)}& p=p_{\mathrm{0}}\exp \left[-\sum _{l=\mathrm{1}}^L{\mathit{\lambda }}_l{\mathit{\varphi }}^l\right].\end{array}$$

In particular, when a system is constrained only by a mean (i.e., L=1), the distribution reduces to an exponential distribution,

$$\begin{array}{}\text{(24)}& p=p_{\mathrm{0}}\exp [-{\mathit{\lambda }}_{\mathrm{1}}\mathit{\varphi }],\end{array}$$

i.e., the probability of the first occurrence of an event under a Poisson process, and when a system is also constrained by a variance (i.e., L=2), it reduces to a Gaussian distribution,

$$\begin{array}{}\text{(25)}& p=p_{\mathrm{0}}\exp [-{\mathit{\lambda }}_{\mathrm{2}}(\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}],\end{array}$$

with a slight reconfiguration of the general form (Eq. 23). Here, the mean is given by 〈ϕ〉 with λ₁=2λ₂〈ϕ〉. These results are consistent with our common usage of these distributions: when only a mean (e.g., waiting time) is of concern, an exponential distribution can be adopted. When a variance is also of interest, a Gaussian distribution is the most convenient.

3.4.3 Gamma distribution

Note that general distribution forms obtained from the maximum-entropy principle, as seen by Eqs. (17) and (23), always take an exponential form without any algebraic factor. However, in many atmospheric applications, a distribution with an algebraic dependence is observed. The best example would be the gamma distribution, which is commonly adopted for representing PSDs in cloud microphysics (e.g., Khain et al., 2015). Furthermore, the gamma distribution is a favorable choice for representing various semi-positive definite variables (e.g., water vapor, mixing ratios of various microphysical water species) as argued by Bishop (2016).

The issue may be commented on from three perspectives. First, it is important to keep in mind the asymptotic nature of the maximum-entropy principle, which is derived under an asymptotic limit of n→∞. As noted in Sect. 3.3.2, for this reason, the maximum-entropy principle is best understood as a special application of the large-deviation principle, which is designed to express only the dominant exponential dependence, and a remaining subdominant algebraic dependence is left implicit. From this perspective, the gamma distribution can be interpreted to be a straight generalization of an exponential distribution, obtained by multiplying an arbitrary, subdominant algebraic factor.

A way of deriving the gamma distribution more explicitly is as a consequence of a transformation of a distribution variable, as discussed in Sect. 3.4.1. By setting a new variable to be φ, a transformed distribution can contain an algebraic factor as shown by Eq. (20). Lastly, it is in fact possible to obtain an algebraic dependence from the maximum-entropy principle simply by setting one of the constraints to be σ_l=log ϕ. The physical meaning of such a constraint is not immediately clear, but it is a question that may be worthy of further investigation. When the constraints are chosen to be σ₁=log ϕ and σ₂=ϕ, then a gamma distribution is obtained.

3.5 Liouville equation

When a system is governed by an equation of the form of Eq. (2), as introduced in Sect. 2, the Liouville equation,

$$\begin{array}{}\text{(26)}& {\displaystyle \frac{\partial p\left(\mathit{\varphi }\right)}{\partial t}}=-{\displaystyle \frac{\partial Fp\left(\mathit{\varphi }\right)}{\partial \mathit{\varphi }}},\end{array}$$

describes the time evolution of a distribution density, p(ϕ), of a given physical variable, ϕ. Note that so long as the original full physics is exactly described by Eq. (2) in a deterministic manner, with F as a continuous function of ϕ, the associated evolution of the probability distribution density is also exactly described by Eq. (26). See Yano and Ouchtar (2017) for a very concise derivation. Generalization for the multiple-variable case is accomplished straightforwardly by replacing ϕ and F by vectors. See, e.g., Risken (1984) for systems with stochasticity. More general formulations for the partial differential equation (PDE) systems are presented, e.g., as Eq. (15) in Larson (2004), with a full derivation given by, e.g., Pope (1985) and Klimenko and Bilger (1999).

In spite of its advantage in directly evaluating the time evolution of a given distribution, the Liouville equation is unfortunately rarely adopted in the studies of atmospheric sciences (e.g., Ehrendorfer, 1994a, b, 2006; Yano and Ouchtar, 2017; Garret, 2019; Hermoso et al., 2020) due to its prohibitive computational cost. An efficient computation methodology, which may make much wider application possible, will be presented in Sect. 5. The result can easily be generalized to a PDE system, as outlined in Sect. 5.3.

3.6 PSD equation

A prognostic equation for a PSD, n(r), of hydrometeors can be considered in an analogous manner to the Liouville equation, but it differs in the detail (cf. Khain et al., 2015). A PSD, being considered at a single macroscopic point, is advected, and also a source term, S, does not generally take a flux divergence form:

$$\begin{array}{}\text{(27)}& {\displaystyle \frac{\partial n\left(r\right)}{\partial t}}+{\mathrm{\nabla }}_h\cdot n\left(r\right)\mathit{u}+{\displaystyle \frac{\partial (w-w_{\mathrm{t}}(r\left)\right)n\left(r\right)}{\partial z}}=S\left(r\right).\end{array}$$

Here, r is the particle size, u the horizontal velocity, w the vertical velocity, and w_t(r) the terminal velocity of the particle with the size r. The source term may furthermore be separated into two distinctive processes, collision processes, S_col, and non-collision processes, S_loc, namely the growth and the reduction (e.g., evaporation) processes of the individual particles:

$$\begin{array}{}\text{(28a)}& S\left(r\right)=S_{\text{col}}\left(r\right)+S_{\text{loc}}\left(r\right).\end{array}$$

The collision term may take the form

$$\begin{array}{}\text{(28b)}& \begin{array}{rl}{S}_{\text{col}}\left(m\right)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{\mathrm{0}}{\overset{m}{\int }}n\left(m^{\prime }\right)n(m-m^{\prime })K(m^{\prime },m-m^{\prime })\mathrm{d}{m}^{\prime }\\ & -\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}n\left(m\right)n\left(m^{\prime }\right)K(m,m^{\prime })\mathrm{d}{m}^{\prime },\end{array}\end{array}$$

setting the particle masses to be m=m(r) and $m^{\prime }=m\left(r^{\prime }\right)$. Here, $K(m,m^{\prime })$ is the collision kernel between the particles of the masses, m and m^′. Also note S_col(r)dr=S_col(m)dm. The first and the second terms on the right-hand side above represent gain and loss, respectively, for a given particle size. The collision process prevents Eq. (27) from being reduced to the Liouville equation because this process makes the source, F, discontinuous as a function of the particle size. Nevertheless, Eq. (27) can be treated in an analogous manner to the Liouville equation (Eq. 26) by replacing the right-hand side of Eq. (26), $-(\partial p(\mathit{\varphi })F/\partial \mathit{\varphi })$, by the tendency of PSD as given in Eq. (27). Furthermore, the PSD equation (Eq. 27) reduces to the Liouville equation when the advection and the collision effects can be neglected, as seen in Sect. 6.

4 Applications to atmospheric processes

In applying the statistical principles discussed in the last section to atmospheric problems, some additional considerations are required due to differences from typical statistical problems. This section discusses those differences. Our discussions may be rather abstract and philosophical. However, we believe that they provide insights into critical issues of atmospheric modeling that are often overlooked. Our discussions lead to a principle for choosing distribution constraints in atmospheric problems, as required for the maximum-entropy principle, which we call the output-constrained distribution principle.

There are, namely, three important differences in the atmospheric applications from standard statistical applications. Those are discussed in the following three subsections.

4.1 Static or non-static, diagnostic or prognostic

First, statistics or, more precisely, mathematical statistics is fundamentally static and diagnostic: methodologies of statistics and probability (e.g., hypothesis testing, probabilities with a binomial system) as found in standard textbooks (e.g., Feller, 1968; Wonnacott and Wonnacott, 1969; Jaynes, 2003; Gregory, 2005) do not involve any time-dependent problems. Extensive time-dependent statistical models in the literature belong to statistical mechanics and stochastic modeling rather than to mathematical statistics. This fundamentally static nature of the statistics is also reflected upon in more modern statistic theories; for example a standard textbook on deep learning (Goodfellow et al., 2016) does not address any time-dependent problems. Very symbolically, the notion of “updating” a prior distribution in Bayesian probability theories (e.g., Bernardo and Smith, 1997), contrary to its connotation, involves not a concept of time but just an update of our knowledge within a fixed time.

This is a rather stark contrast to the atmospheric system, which continuously evolves with time: we are inherently interested in forecasts. Allegorically speaking, there is no time to update the priors with the atmospheric system because, as soon as information is updated, the original prior is already obsolete because the system itself has changed. Still allegorically speaking, the best we can do is to update (in a meteorological sense but not in a statistical sense) the priors themselves with time. In other words, in describing the atmospheric processes, the key issue is to predict the time evolution of the probability and the statistics: atmospheric problems are fundamentally non-static and prognostic.

The data assimilation problem falls in the middle of the two. As in any other atmospheric problem, the prediction of the evolution of the data uncertainty is a key aspect of data assimilation. At the same time, the statistical update of data by incorporating observational information is another key aspect of the data assimilation. In the present study, the focus is exclusively on the first aspect.

4.2 Output-constrained distribution principle

Second, in many statistical applications as well as in standard equilibrium statistical mechanics, as summarized by Jaynes (1978), a final aim is to know a distribution of a given variable. For this goal, the integrated quantities are inputs to a problem that constrains a distribution. Under these constraints, we define the most likely distribution from the maximum-entropy principle.

However, in atmospheric modeling, knowing a distribution itself, though it may be of theoretical interest, is not an ultimate aim. It is merely a means of obtaining certain integrated quantities (e.g., microphysical tendencies, grid-box-averaged quantities, standard deviation error measures) for a modeling purpose. For this goal, a precise form of a distribution is not of interest, but it must be just accurate enough for providing these required final outputs. This is a very different problem compared to the problems in standard equilibrium statistical mechanics. Here, we must clearly recognize that these are two different problems: although a more accurate distribution may help to evaluate the required statistical quantities more accurately, there should be a way of making the latter more accurate without making the former more accurate than necessary.

This observation leads to an interesting possibility for constructing a prescribed PDF (DDF) form in atmospheric-science applications: take the necessary outputs rather than the available inputs as constraints. Thus, for example, if the purpose is to know a mean value (e.g., a waiting time), take an exponential distribution (Eq. 24). If the purpose is to know a variance (e.g., a standard deviation error in temperature measurements), take a Gaussian distribution (Eq. 25). We propose to call these output-constrained distributions. Note that an assumed PDF obtained under this principle may provide a poor fit to the actual distribution. Our basic argument here is that, nevertheless, an assumed PDF will work reasonably well for the purpose of estimating the required output values (i.e., “constraints”) because the given distribution is obtained from the maximum-entropy principle by taking those required outputs as the constraints.

The proposed re-interpretation is consistent with a basic requirement for an assumed-PDF form: if we need to fit a PDF to L statistical variables, L parameters must be introduced. This is not the case with a popular approach of introducing an assumed double-Gaussian distribution for the sake of representing the skewness of an actual distribution (e.g., Larson et al., 2002; Fitch, 2019; Naumann et al., 2013): the number of parameters of an assumed PDF becomes greater than that of required outputs. For example, with a single variable, a double-Gaussian distribution introduces five parameters when only three outputs are required (mean, variance, skewness). In contrast, the proposed principle suggests how to choose a distribution that contains the minimum number of parameters compatible with the required number of outputs. Here, we invoke the maximum-entropy principle for this purpose.

A current standard approach of updating the PDF parameters is from some moments (e.g., mean, variance) of variables. The output-constrained distribution principle dictates the need to update those parameters using the actual output variables that are required for a host model or quantities that are crucial for predicting the evolution of the system of concern. This rather philosophical statement poses an important practical question of, for example, whether it is optimal to choose the radar reflectivity as a third constraint in bulk microphysics.

Here, the notion of “output variables that are required for a host model” is more specifically relevant to the subgrid-scale distribution for a parameterization. Recall that the goal of a parameterization is to provide not every detail of subgrid-scale processes but only the so-called apparent sources, Q₁ and Q₂, i.e., tendencies of the temperature and moisture due to the subgrid-scale processes (cf. Yanai et al., 1973), and only as grid-scale averages. All the other details are only for the purpose of a consistent calculation of the subgrid-scale processes. In the case of the clouds microphysics with explicit cloud modeling (thus the cloud processes themselves are not “parameterized”), certain variables must be passed over to different components of the model, which plays the role of “host model” in this context. For example, the mixing ratios of clouds and rain, q_c and q_r, must be counted for an accurate definition of the buoyancy in the momentum equation. Some radiation schemes require inputs of the mean radius of the cloud and rain droplets, r_c and r_p, although they are typically not prognostic variables of the cloud microphysics. Those variables are considered to be the “necessary variables (outputs) for the host model”. Thus, especially in the context of the cloud microphysics, the “necessary variables (outputs)” should be clearly distinguished from the prognostic variables in the cloud microphysics. The case of data assimilation is more subtle because there is neither a host model nor other model components to which information must be passed. Yet, for operational purposes, we are not interested in knowing the full shape of the probability distribution of a variable in order to quantify the uncertainty. In traditional assimilation formulations, we merely ask for the standard deviation errors/uncertainties in variables; those are considered the “necessary outputs” for the data assimilation.

4.3 Availability of input data

A third major difference of atmospheric problems compared to standard statistical problems is the availability of input data (e.g., initial constraints). Regarding the latter, we assume a situation whereby available input data (information) are rather limited. For example, the Maxwell–Boltzmann distribution is derived by assuming that only the total energy is known. It is rarely asked how to obtain more information so that, for example, a higher-order correction to the Maxwell–Boltzmann distribution can be obtained. A limited amount of information is the given starting point.

On the other hand, in atmospheric problems, available information is rather unlimited, or at least, we believe that we can obtain more data by either modeling or observation if necessary. In other words, the input data are rather unconstrained. For the subgrid-scale distributions, more explicit models such as cloud-resolving models (CRMs) or large-eddy simulations (LESs) can be used at will for any detailed simulations for the subgrid-scale processes of concern, especially with enhancements of computing power. Such an abundance of information tends to obscure the basic idea of statistical description. The same issue can also be identified from the perspective of the assumed-PDF (DDF) approach: we can take as many moments as required in principle. The only issues are the computational cost and accuracy benefit.

In other words, in principle, the number of available inputs is less limited in atmospheric problems. Thus, if this available information is simply adopted as constraints for defining the most likely distribution under the maximum-entropy principle, the number of distribution parameters can arbitrarily be increased to get as accurate a distribution as desired. This consideration also strengthens the argument of the last subsection. In the context of the assumed-PDF (DDF) approach, a number of “constraints” (e.g., moments) must be decided in such a manner that required outputs can be evaluated in a sufficiently accurate manner. In other words, the problem must be constrained by required outputs rather than by available inputs; that is the essence of the output-constrained distribution principle.

4.4 Validation: diffusion problem

Over the last two subsections (Sect. 4.2 and 4.3), arguments have been developed for re-interpreting the maximum-entropy principle in such a manner that the actual variables required as outputs are to be adopted as “constraints” for determining a distribution. Recall that the output-constrained distribution principle is proposed merely as a guiding principle for choosing an assumed form for distributions; thus we do not expect that those chosen distribution forms can make any perfect predictions. Nevertheless, it would be helpful to quantify the degrees of the accuracy of predictions; that is the purpose of this subsection.

Thus, this subsection tests the proposed output-constrained distribution principle by taking, as an example, a one-dimensional diffusion equation:

$$\begin{array}{}\text{(29)}& \left({\displaystyle \frac{\partial }{\partial t}}-{\displaystyle \frac{{\partial }^{\mathrm{2}}}{\partial x^{\mathrm{2}}}}\right)p=\mathrm{0},\end{array}$$

with a diffusion coefficient set to unity for simplicity. When a system evolves purely under white-noise forcing, as in the case of Brownian motion, the prognostic equation for the distribution, p, reduces to this form. Also note that Eq. (29) is a special case of the Fokker–Planck equation.

Let us assume that we are interested in predicting only a mean and a variance for the position, x, of the distribution, p. In other words, the required outputs for our problem are only a mean, 〈x〉, and a variance, 〈(x−〈x〉)²〉. In this case, the output-constrained distribution principle suggests that it suffices to take a Gaussian distribution; say

$$\begin{array}{}\text{(30)}& p(x,t)=p_{\mathrm{0}}\left(t\right)e^{-{\mathit{\lambda }}_{\mathrm{2}}\left(t\right)(x-\langle x\rangle (t){)}^{\mathrm{2}}}.\end{array}$$

Note that in this particular case, the adopted distribution form also corresponds to an exact solution of the system (Eq. 29).

The time dependence of the parameters, λ₂(t) and 〈x〉(t), introduced in the above solution (Eq. 30) can be derived by directly substituting Eq. (30) into Eq. (29); cf. Sect. 5.7.When the initial conditions are given by

$$\begin{array}{}\text{(31a)}& {\displaystyle }\langle x\rangle {|}_{t=\mathrm{0}}& {\displaystyle }=\langle x{\rangle }_{\mathrm{0}},\text{(31b)}& {\displaystyle }\langle (x-\langle x\rangle {)}^{\mathrm{2}}\rangle {|}_{t=\mathrm{0}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\lambda }}^{*}}},\end{array}$$

the time evolution of the distribution (Eq. 30) is given by

$$\begin{array}{}\text{(32)}& \begin{array}{rl}p(x,t)& ={\displaystyle \frac{\mathrm{1}}{(\mathrm{1}+\mathrm{4}{\mathit{\lambda }}^{*}t{)}^{\mathrm{1}/\mathrm{2}}}}{\left({\displaystyle \frac{{\mathit{\lambda }}^{*}}{\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{2}}\\ & \times \exp \left[-{\displaystyle \frac{{\mathit{\lambda }}^{*}(x-\langle x{\rangle }_{\mathrm{0}}{)}^{\mathrm{2}}}{\mathrm{1}+\mathrm{4}{\mathit{\lambda }}^{*}t}}\right].\end{array}\end{array}$$

Here, the distribution, p, is also normalized so that its integral over the whole domain becomes unity, and the time evolution of the mean and the variance is given by

$$\begin{array}{ll}\text{(33a)}& {\displaystyle }\langle x\rangle & {\displaystyle }=\langle x{\rangle }_{\mathrm{0}},{\displaystyle }\langle (x-\langle x\rangle {)}^{\mathrm{2}}\rangle & {\displaystyle }={\displaystyle \frac{\mathrm{1}+\mathrm{4}{\mathit{\lambda }}^{*}t}{\mathrm{2}{\mathit{\lambda }}^{*}}}\\ \text{(33b)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\lambda }}^{*}}}+\mathrm{2}t.\end{array}$$

Note that the mean is a constant with time in the diffusion problem if the initial condition is Gaussian, whereas the variance increases linearly with time.

The basic idea behind the output-constrained distribution principle is to define a PDF in such a manner that the required output variables (mean and variance here) can be evaluated most effectively with the minimum possible parameters. Fitting an actual distribution under an assumed-PDF form is not a goal. To test the workings of this principle, we consider two examples in which we set both the initial mean and the variance of the output-constrained distribution (Eq. 32) to be equal to those of an actual initial distribution and compare the evolutions of means and variances of both distributions.

4.4.1 Example 1: double-Gaussian distribution

As a first example, we take an initial distribution consisting of two Gaussian distributions:

$$\begin{array}{}\text{(34)}& \begin{array}{rl}p(x,t=\mathrm{0})=& {\mathit{\alpha }}_{\mathrm{1}}{\left({\displaystyle \frac{{\mathit{\mu }}_{\mathrm{1}}}{\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{2}}{e}^{-{\mathit{\mu }}_{\mathrm{1}}(x-x_{\mathrm{1}}{)}^{\mathrm{2}}}\\ & +{\mathit{\alpha }}_{\mathrm{2}}{\left({\displaystyle \frac{{\mathit{\mu }}_{\mathrm{2}}}{\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{2}}{e}^{-{\mathit{\mu }}_{\mathrm{2}}(x-x_{\mathrm{2}}{)}^{\mathrm{2}}}.\end{array}\end{array}$$

Here, two Gaussians are centered as x=x₁ and x₂, respectively. By a normalization condition, we may set

$$\begin{array}{}\text{(35a)}& {\mathit{\alpha }}_{\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{2}}=\mathrm{1}.\end{array}$$

We may further set

$$\begin{array}{}\text{(35b)}& {\mathit{\alpha }}_{\mathrm{1}}{x}_{\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{2}}{x}_{\mathrm{2}}=\mathrm{0}\end{array}$$

so that the initial mean is 〈x〉=0.

It is immediately seen that the time evolution of this system is given by

$$\begin{array}{}\text{(36)}& \begin{array}{rl}p(x,t)& ={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{1}}}{(\mathrm{1}+\mathrm{4}{\mathit{\mu }}_{\mathrm{1}}t{)}^{\mathrm{1}/\mathrm{2}}}}{\left({\displaystyle \frac{{\mathit{\mu }}_{\mathrm{1}}}{\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{2}}{e}^{-{\mathit{\mu }}_{\mathrm{1}}(x-x_{\mathrm{1}}{)}^{\mathrm{2}}/(\mathrm{1}+\mathrm{4}{\mathit{\mu }}_{\mathrm{1}}t)}\\ & +{\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{2}}}{(\mathrm{1}+\mathrm{4}{\mathit{\mu }}_{\mathrm{2}}t{)}^{\mathrm{1}/\mathrm{2}}}}{\left({\displaystyle \frac{{\mathit{\mu }}_{\mathrm{2}}}{\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{2}}{e}^{-{\mathit{\mu }}_{\mathrm{2}}(x-x_{\mathrm{2}}{)}^{\mathrm{2}}/(\mathrm{1}+\mathrm{4}{\mathit{\mu }}_{\mathrm{2}}t)}.\end{array}\end{array}$$

Here, the mean remains a constant with time, thus 〈x〉=0, and evolution of the variance is given by

$$\begin{array}{ll}{\displaystyle }\langle x^{\mathrm{2}}\rangle & {\displaystyle }={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{1}}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{1}+\mathrm{4}{\mathit{\mu }}_{\mathrm{1}}t}{{\mathit{\mu }}_{\mathrm{1}}}}+{\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{2}}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{1}+\mathrm{4}{\mathit{\mu }}_{\mathrm{2}}t}{{\mathit{\mu }}_{\mathrm{2}}}}\\ \text{(37)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left({\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{1}}}{{\mathit{\mu }}_{\mathrm{1}}}}+{\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{2}}}{{\mathit{\mu }}_{\mathrm{2}}}}\right)+\mathrm{2}t.\end{array}$$

We can evaluate the statistical evolution of this system by an output-constrained distribution (i.e., a single-Gaussian distribution) by setting the initial mean and variance to be identical. Thus, we obtain 〈x〉₀=0 and

$$\begin{array}{}\text{(38)}& {\mathit{\lambda }}^{*}={\left({\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{1}}}{{\mathit{\mu }}_{\mathrm{1}}}}+{\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{2}}}{{\mathit{\mu }}_{\mathrm{2}}}}\right)}^{-\mathrm{1}}\end{array}$$

in Eq. (32). Substitution of Eq. (38) into Eq. (33b) shows that this single-Gaussian model can predict the time evolution of both the mean (rather trivially) and the variance of a two-Gaussian system perfectly.

Note that in this case, a single Gaussian hardly fits a double-Gaussian distribution in any good approximation, especially when two Gaussians are well separated from each other. However, if our interest is merely to predict a variance, then in this example a single-Gaussian approximation perfectly serves the purpose, being consistent with a proposed re-interpretation of the maximum-entropy principle. This example may appear to be rather too special and artificial. Nevertheless, it makes the case well that for predicting a limited number of statistical quantities satisfactorily, accurately predicting the evolution of the whole distribution is not necessarily a requirement.

4.4.2 Example 2: a skewed Gaussian distribution

The second example is a skewed initial distribution given by

$$\begin{array}{}\text{(39)}& p(x,t=\mathrm{0})={\left({\displaystyle \frac{\mathit{\lambda }}{\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{2}}(\mathrm{1}+\mathit{\alpha }x)e^{-\mathit{\lambda }{x}^{\mathrm{2}}}.\end{array}$$

Here, a constant parameter, α, controls the skewness of this distribution. This example examines how well an assumed Gaussian distribution predicts the statistics when an actual distribution is not Gaussian.

The time evolution of this system is solved by, for example, a Fourier transform method, as summarized in Appendix A. The final answer is

$$\begin{array}{}\text{(40)}& \begin{array}{rl}p(x,t)=& {\displaystyle \frac{\mathrm{1}}{(\mathrm{1}+\mathrm{4}\mathit{\lambda }t{)}^{\mathrm{1}/\mathrm{2}}}}\left[\mathrm{1}+{\displaystyle \frac{\mathit{\alpha }x}{(\mathrm{1}+\mathrm{4}\mathit{\lambda }t{]}^{\mathrm{2}}}}\right]\\ & \times {\left({\displaystyle \frac{\mathit{\lambda }}{\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{2}}\exp \left[-{\displaystyle \frac{\mathit{\lambda }{x}^{\mathrm{2}}}{\mathrm{1}+\mathrm{4}\mathit{\lambda }t}}\right].\end{array}\end{array}$$

From this solution, the time evolution of mean and variance is readily evaluated as

$$\begin{array}{}\text{(41a)}& {\displaystyle }\langle x\rangle & {\displaystyle }={\displaystyle \frac{\mathit{\alpha }}{\mathrm{2}\mathit{\lambda }(\mathrm{1}+\mathrm{4}\mathit{\lambda }t)}},\text{(41b)}& {\displaystyle }\langle (x-\langle x\rangle {)}^{\mathrm{2}}\rangle & {\displaystyle }={\displaystyle \frac{\mathrm{1}+\mathrm{4}\mathit{\lambda }t}{\mathrm{2}\mathit{\lambda }}}\left[\mathrm{1}-{\displaystyle \frac{{\mathit{\alpha }}^{\mathrm{2}}}{\mathrm{2}\mathit{\lambda }(\mathrm{1}+\mathrm{4}\mathit{\lambda }t{)}^{\mathrm{3}}}}\right].\end{array}$$

“Fit” to this problem under the assumed single-Gaussian distribution is given by

$$\begin{array}{}\text{(42a)}& {\displaystyle }\langle x{\rangle }_{\mathrm{0}}& {\displaystyle }={\displaystyle \frac{\mathit{\alpha }}{\mathrm{2}\mathit{\lambda }}},\text{(42b)}& {\displaystyle }{\mathit{\lambda }}^{*}& {\displaystyle }=\mathit{\lambda }{\left(\mathrm{1}-{\displaystyle \frac{{\mathit{\alpha }}^{\mathrm{2}}}{\mathrm{2}\mathit{\lambda }}}\right)}^{-\mathrm{1}}.\end{array}$$

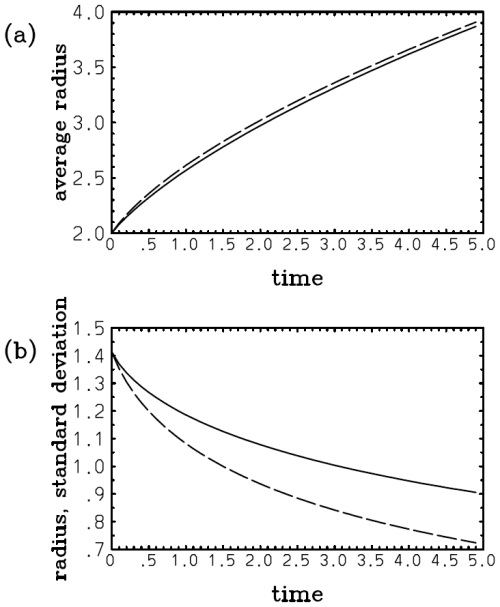
In this case, the assumed PDF fails to predict a gradual shift of the mean to the origin from an initial position (cf. Eqs. 41a and 42a; Fig. 1a). This discrepancy is hardly a surprise because an assumed-PDF evolution is not expected to predict an evolution of an actual distribution in any perfect manner. However, the growth of the deviation of the variance with the assumed single-Gaussian distribution (Eq. 42b; Fig. 1b, long dash) from the real value (Eq. 41b; Fig. 1b, solid) is relatively slow, and an underestimate is only 25 % even at λt=10 with a relatively large nondimensional skewness parameter (i.e., $\mathit{\alpha }/{\mathit{\lambda }}^{\mathrm{1}/\mathrm{2}}=\mathrm{0.5}$) assumed.

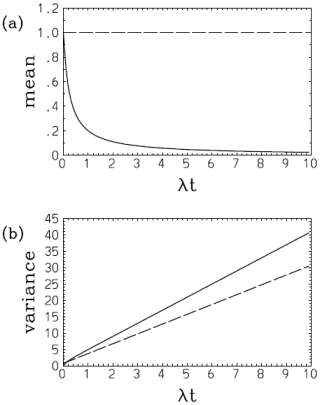
Figure 1 Plots of (a) $\mathrm{2}\mathit{\lambda }\langle x\rangle /\mathit{\alpha }$ and (b) 2λ〈(x−〈x〉)²〉 with an initial skewed Gaussian distribution (Eq. 39) with $\mathit{\alpha }/{\mathit{\lambda }}^{\mathrm{1}/\mathrm{2}}=\mathrm{0.5}$: exact (solid) and with a single-Gaussian approximation (long dash). Note that in panel (a), although the exact mean (solid) decreases to zero with time, the assumed Gaussian solution (long dash) totally fails to predict this tendency. Nevertheless, the prediction of the variance (b) with the assumed Gaussian (long dash) is still qualitatively correct, even though a tendency for underestimation compared to the exact value (solid) may be noted.

5 Liouville equation constrained by an assumed PDF

As emphasized in the last section, in principle, a full physical system, as given by Eq. (2) in the present study, is known in atmospheric problems; thus it also prompts us to exploit the Liouville equation (Eq. 26) in predicting the time evolution of a distribution. The next question is how it can be exploited efficiently. The output-constrained distribution principle introduced in the last section provides half of the answer to this question: adopt a distribution form that is defined from the maximum-entropy principle but taking the required outputs for the host model as the “constraints”, 〈σ_l〉 ($l=\mathrm{1},\mathrm{\dots },n$). As a result, a distribution with a finite number of parameters, {λ_i}, is obtained. Thus, the problem of defining the time evolution of a continuous distribution function reduces to that of describing the time evolution of a finite number of parameters {λ_i(t)}. The remaining half of the question is how to actually calculate the time evolution of {λ_i} directly by a set of ordinary differential equations. The present section addresses this remaining half. Importantly, the formulation presented in this section does not rely on the output-constrained distribution (maximum-entropy) principle. Rather, it can be applied to any form of assumed PDFs.

The first key step required for this procedure is, as just suggested, to replace the time derivative, $\partial p/\partial t$, of the distribution by time derivatives, ${\dot{\mathit{\lambda }}}_l$, of the PDF parameters. This is simply accomplished by taking a chain rule to the time derivative, noting that the time dependence in the distribution (Eq. 4a) arises solely from the parameters, {λ_i}:

$$\begin{array}{}\text{(43)}& {\displaystyle \frac{\partial p}{\partial t}}=\sum _{i=\mathrm{0}}^N{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}{\dot{\mathit{\lambda }}}_i.\end{array}$$

A specific example of this procedure is given by Eq. (55) below, which can also be performed either more directly or using Eq. (43) explicitly.

5.1 General formulation

This subsection derives a prognostic set of equations for the PDF parameters {λ_l} in a general manner. The derivation is repeated in Sect. 5.5 by taking the exponential distribution as an example so that the basic idea can be seen in a more concrete manner.

We assume a distribution in a general form (Eq. 4a) assuming that a distribution is defined by N+1 free parameters λ_i ($i=\mathrm{0},\mathrm{\dots },N$). Here, we assume that λ₀ is a constant factor that is required for normalizing the distribution, as already noted when introducing the assumed distribution in a general form by Eq. (4a); thus

$$\begin{array}{}\text{(44a)}& p\propto {\mathit{\lambda }}_{\mathrm{0}}\end{array}$$

or

$$\begin{array}{}\text{(44b)}& {\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_{\mathrm{0}}}}={\displaystyle \frac{p}{{\mathit{\lambda }}_{\mathrm{0}}}}.\end{array}$$

Substitution of Eq. (44b) into Eq. (43) leads to

$$\begin{array}{}\text{(45)}& {\displaystyle \frac{\partial p}{\partial t}}=p{\displaystyle \frac{{\dot{\mathit{\lambda }}}_{\mathrm{0}}}{{\mathit{\lambda }}_{\mathrm{0}}}}+\sum _{i=\mathrm{1}}^N{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}{\dot{\mathit{\lambda }}}_i.\end{array}$$

The replacement of the left-hand side of Eq. (45) by that of the right-hand side is the key step of reducing the problem of the evolution of a distribution, p, as a whole to that of the fixed number of parameters, λ_i ($i=\mathrm{1},\mathrm{\dots },N$).

The time evolution of this distribution is constrained in two ways: first, by a normalization condition (Eq. 13) and, second, by the Liouville equation (Eq. 26). The normalization condition (Eq. 13) can also be cast into a prognostic form by taking the time derivative:

$$\begin{array}{}\text{(46)}& {\displaystyle \frac{\partial }{\partial t}}\int p\mathrm{d}\mathit{\varphi }=\mathrm{0},\end{array}$$

with the normalization (Eq. 13) introduced as an initial condition. Note that in cases with PSDs, the right-hand side of Eq. (13) must be replaced by ${\dot{C}}_{\mathrm{0}}$, with C₀ standing for the total particle number density. Thus, the following reduction must also be modified accordingly.

When the integral range is fixed with time, the time derivative can be moved inside the integral, operating only on the distribution, p, in Eq. (46). Further substituting the formula for the time derivative (45), we obtain

$$\begin{array}{}\text{(47)}& {\displaystyle \frac{{\dot{\mathit{\lambda }}}_{\mathrm{0}}}{{\mathit{\lambda }}_{\mathrm{0}}}}=-\sum _{i=\mathrm{1}}^N\left[\int {\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}\mathrm{d}\mathit{\varphi }\right]{\dot{\mathit{\lambda }}}_i.\end{array}$$

The Liouville equation (Eq. 26) also reduces from Eq. (45) to

$$\begin{array}{}\text{(48)}& p{\displaystyle \frac{{\dot{\mathit{\lambda }}}_{\mathrm{0}}}{{\mathit{\lambda }}_{\mathrm{0}}}}+\sum _{i=\mathrm{1}}^N{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}{\dot{\mathit{\lambda }}}_i+{\displaystyle \frac{\partial }{\partial \mathit{\varphi }}}\left(pF\right)=\mathrm{0},\end{array}$$

and furthermore, by substituting Eq. (47) into the above, to

$$\begin{array}{}\text{(49a)}& \sum _{i=\mathrm{1}}^N\left[{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}-p\int {\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}\mathrm{d}\mathit{\varphi }\right]{\dot{\mathit{\lambda }}}_i+{\displaystyle \frac{\partial }{\partial \mathit{\varphi }}}\left(pF\right)=\mathrm{0}.\end{array}$$

Equation (49a) is the key result of the present study because it constitutes a prognostic equation for evaluating the time evolution of {λ_i}. Note that when the same procedure is applied to the diffusion equation (Eq. 29), by replacing $\partial pF/\partial \mathit{\varphi }$ by $-{\partial }^{\mathrm{2}}p/\partial {\mathit{\varphi }}^{\mathrm{2}}$, it reduces to a set of ordinary differential equations for λ₂ and 〈x〉, as shown in Sect. 5.4.1. As in the case with the diffusion equation, more generally, when the assumed-PDF form constitutes an exact solution of a given system, Eq. (49a) is separated out into the ϕ and λ_i dependencies, and the latter dependencies can be solved separately, independent of the distribution variable, ϕ. This point can be understood directly from the fact that Eq. (49a) is equivalent to the original Liouville equation (Eq. 26) under the given assumed-PDF form.

However, because the assumed PDF generally constitutes merely an approximation of a true distribution, ϕ dependence in Eq. (49a) cannot be separated out in a general case; thus this equation cannot be solved in any consistent manner merely in terms of the assumed-PDF parameters, {λ_i}. The consequence of the approximate nature of the assumed PDF in Eq. (49a) is more explicitly seen by substituting Eq. (4c) into Eq. (26):

$$\begin{array}{}\text{(49b)}& \sum _{i=\mathrm{1}}^N\left[{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}-p\int {\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}\mathrm{d}\mathit{\varphi }\right]{\dot{\mathit{\lambda }}}_i+{\displaystyle \frac{\partial }{\partial \mathit{\varphi }}}\left(pF\right)=\mathcal{E},\end{array}$$

with ℰ suggesting a possible error. We should keep well in mind that this very last fact does not change regardless of the manner in which we attempt to predict the evolution of a distribution by an assumed PDF. In other words, Eq. (49a) itself is not defective, but the difficulty here is a simple consequence of the assumed-PDF approach, which attempts to solve the evolutions of distributions by assuming the forms that are not actual solutions.

Thus, the next goal is to derive a closed set of equations, not depending on ϕ, from Eq. (49a) in order to solve a set of distribution parameters, {λ_i}, in a consistent manner. For this purpose, we need to remove the ϕ dependence from Eq. (49a). An only option that we can see is to simply integrate it over ϕ. Here, a goal is to obtain N differential equations for λ_i ($i=\mathrm{1},\mathrm{\dots },N$) by removing ϕ dependence. For this purpose, we apply a set of weights, σ_l ($l=\mathrm{1},\mathrm{\dots },N$), to Eq. (49a) and integrate them over ϕ. Here, the weight, σ_l, is an unspecified function of ϕ but independent of {λ_i}. After integration in ϕ, we obtain

$$\begin{array}{}\text{(50a)}& \textcolor{red}{}\end{array}$$

for $l=\mathrm{1},\mathrm{\dots },N$. As a result, we obtain N ordinary differential equations for N unknowns. The set of Eq. (50a) is linear in terms of ${\dot{\mathit{\lambda }}}_i$; thus it can be inverted in principle, and the tendencies, ${\dot{\mathit{\lambda }}}_i$, can explicitly be evaluated. Here, keep in mind that Eq. (50a) is valid only approximately; thus it may be more emphatically stated as

$$\begin{array}{}\text{(50b)}& \begin{array}{rl}\sum _{i=\mathrm{1}}^N& \left[\int {\mathit{\sigma }}_l{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}\mathrm{d}\mathit{\varphi }-\int {\mathit{\sigma }}_{l}p\mathrm{d}\mathit{\varphi }\int {\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}\mathrm{d}\mathit{\varphi }\right]{\dot{\mathit{\lambda }}}_i\\ & =-\int {\mathit{\sigma }}_l{\displaystyle \frac{\partial }{\partial \mathit{\varphi }}}\left(pF\right)\mathrm{d}\mathit{\varphi }+{\mathcal{E}}_l,\end{array}\end{array}$$

with ℰ_l suggesting an associated error. Note further that the right-hand side of Eq. (50a) can be re-written as

$$\begin{array}{}\text{(51)}& \int {\mathit{\sigma }}_l{\displaystyle \frac{\partial }{\partial \mathit{\varphi }}}\left(pF\right)\mathrm{d}\mathit{\varphi }=-\int pF{\displaystyle \frac{\partial {\mathit{\sigma }}_l}{\partial \mathit{\varphi }}}\mathrm{d}\mathit{\varphi }\end{array}$$

by an integration by parts, assuming that pF vanishes at the edges of the integral range. Realize that the key step introduced in the formulation here is to predict the PDF parameters, {〈λ_l〉(t)}, by Eq. (50a). In this manner, we circumvent the principal difficulty of the current assumed-PDF approaches of inverting the relations of Eq. (6) into the form of Eq. (5). Now, the major remaining open question with this procedure is the choice of the weights, {σ_l}, which is the issue to be addressed next.

5.2 Choice of the weights, {σ_l}

Here, the most appropriate choice of the weights, {σ_l}, becomes immediately clear by noting that the left-hand side of Eq. (50a) corresponds to a temporal tendency, $\mathrm{d}\langle {\mathit{\sigma }}_l\rangle /\mathrm{d}t$, of the “averaged” weight:

$$\begin{array}{}\text{(52a)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\langle {\mathit{\sigma }}_l\rangle =\int {\mathit{\sigma }}_l{\displaystyle \frac{\partial p}{\partial t}}\mathrm{d}\mathit{\varphi }=\sum _{i=\mathrm{0}}^N\left[\int {\mathit{\sigma }}_l{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}\mathrm{d}\mathit{\varphi }\right]{\dot{\mathit{\lambda }}}_i,\end{array}$$

where the last expression reduces to the left-hand side of Eq. (50a) with the help of Eq. (47). Thus, symbolically, Eq. (50a) is equivalent to

$$\begin{array}{}\text{(52b)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\langle {\mathit{\sigma }}_l\rangle =\langle F_{{\mathit{\sigma }}_l}\rangle ,\end{array}$$

with $F_{{\mathit{\sigma }}_l}$ the source term that defines the tendency of σ_l. By the deduction from Eq. (52a), we can conclude that Eq. (50a) predicts the time evolution of 〈σ_l〉, as given by Eq. (52b), where

$$\begin{array}{}\text{(52c)}& \langle {\mathit{\sigma }}_l\rangle =\int p{\mathit{\sigma }}_l\mathrm{d}\mathit{\varphi }.\end{array}$$

It also follows that if {〈σ_l〉} is chosen as the outputs to be used in the host model, by following the output-constrained distribution principle (cf. Sect. 4.2), Eq. (50a) predicts those required outputs consistently under a given assumed PDF (DDF), being equivalent for solving Eq. (52b). Thus, we choose {σ_l} to be the same as in the constraints of Eq. (12) with G_l=pσ_l and L=N.

A standard choice following the assumed-PDF (DDF) approach is to set σ_l=ϕ^l. This procedure is equivalent to time-integrating the moments for predicting {λ_i}. Equation (50a) or (52b) further reduces to a diagnostic method based on moments typically adopted in the subgrid-scale assumed-PDF formulations, when {〈σ_l〉} is taken as moments, and also a diagnostic limit is taken. As already emphasized in introducing the governing equation (Eq. 2) of the system in Sect. 2, the source term, F, includes all the physics associated with a variable, ϕ. A multi-variable extension is also straightforward. Thus, in principle, this formulation can be applied to any assumed-PDF approaches, including those in cloud microphysics and data assimilation.

In subsequent subsections, more specific versions of Eq. (50a) for various assumed-PDF forms are presented, as a demonstration that this general formulation can actually be used. These results can readily be used as receipts for applying the formulation to any physical problems under given assumed-PDF forms, once the source term, F, is specified. However, as a detour, in the next subsection, we first discuss the generalization of the formulation introduced into the PDE system, and in Sect. 5.4, we discuss its link to the existing assumed-PDF approaches and the bulk microphysics.

5.3 Generalization to the PDE system (Eq. 1)

The discussion of the last subsection suggests that the derivation of the prognostic equations for the assumed-PDF parameters in the one-dimensional dynamical system (Eq. 2) can be generalized into partial differential equation (PDE) systems, described by Eq. (1), in a relatively straightforward manner.

First note that in a PDE system, the time derivative on the right-hand side of Eq. (52a) is replaced by a partial time derivative:

$$\begin{array}{}\text{(53a)}& {\displaystyle \frac{\partial }{\partial t}}\langle {\mathit{\sigma }}_l\rangle =\int {\mathit{\sigma }}_l{\displaystyle \frac{\partial p}{\partial t}}\mathrm{d}\mathit{\varphi }=\sum _{i=\mathrm{0}}^N\left[\int {\mathit{\sigma }}_l{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}\mathrm{d}\mathit{\varphi }\right]{\dot{\mathit{\lambda }}}_i.\end{array}$$

Note next that a time-evolution equation for σ_l can be derived from the basic governing equation (Eq. 1) by taking a chain rule:

$$\begin{array}{}\text{(53b)}& {\displaystyle \frac{\partial {\mathit{\sigma }}_l}{\partial t}}={\displaystyle \frac{\partial {\mathit{\sigma }}_l}{\partial \mathit{\phi }}}{\displaystyle \frac{\partial \mathit{\phi }}{\partial t}}={\displaystyle \frac{\partial {\mathit{\sigma }}_l}{\partial \mathit{\phi }}}(-\mathit{v}\cdot \mathrm{\nabla }\mathit{\varphi }+F).\end{array}$$

Thus,

$$\begin{array}{}\text{(53c)}& F_{{\mathit{\sigma }}_l}={\displaystyle \frac{\partial {\mathit{\sigma }}_l}{\partial \mathit{\phi }}}(-\mathit{v}\cdot \mathrm{\nabla }\mathit{\varphi }+F),\end{array}$$

and with the help of Eq. (53c), the PDE version of Eq. (52b) becomes

$$\begin{array}{}\text{(53d)}& {\displaystyle \frac{\partial }{\partial t}}\langle {\mathit{\sigma }}_l\rangle =\langle F_{{\mathit{\sigma }}_l}\rangle .\end{array}$$

By combining Eqs. (53a) and (53d), the prognostic set of equations for ${\dot{\mathit{\lambda }}}_i$ is given by

$$\begin{array}{}\text{(53e)}& {\displaystyle \frac{\partial }{\partial t}}\langle {\mathit{\sigma }}_l\rangle =\sum _{i=\mathrm{0}}^N\left[\int {\mathit{\sigma }}_l{\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_i}}\mathrm{d}\mathit{\varphi }\right]{\dot{\mathit{\lambda }}}_i=\langle F_{{\mathit{\sigma }}_l}\rangle .\end{array}$$

Keep in mind that ${\dot{\mathit{\lambda }}}_i$ in the above designates the partial time derivative. The generality of the final result (Eq. 53e) would not be necessary to emphasize.

5.4 Link to the existing assumed-PDF approaches and the bulk microphysics

The formulation presented in the last three subsections constitutes a generalization of the existing assumed-PDF approaches in the following manner. Recall that with the help of Eq. (52a), the general equation (Eq. 50a) can be more symbolically be written as Eq. (52b). Here, keep in mind that a spatial dependence of variables with Eq. (1) can also be taken into account by simply replacing the time derivative on the left-hand side by a partial derivative (cf. Eq. 53d). Also keep in mind the possibilities of generalizations in the systems with multiple variables (cf. Yano, 2024), though they remain implicit here. In this manner, Eq. (52b) constitutes a general form of governing equations considered in the existing assumed-PDF approaches, as more specifically presented by, e.g., Eqs. (3.1)–(3.10) in Larson (2022).

The first generalization to be noted is the fact that 〈σ_l〉 can be of any output variables as required by a host model so long as σ_l is properly defined as functions of dependent variables. Also note that the integral range in definition (Eq. 12) can be taken in any manner, although such a full generalization itself is left for future studies (cf. Yano, 2024). Thus, for example, a cloud fraction can also be introduced as one of the output variables of the form, 〈σ_l〉, under this definition. On the other hand, the existing assumed-PDF approaches, rather arbitrarily, restrict these statistical variables, 〈σ_l〉, to being moments (e.g., Golaz et al., 2002). The formulation introduced here demonstrates that this restriction is not necessary, but a very wide range of choices can be made for 〈σ_l〉.

Furthermore, the existing assumed-PDF approaches perform time integrals of the statistical variables, 〈σ_l〉, by Eq. (52b). Note that with some variables, Eq. (52b) is solved diagnostically by setting the left-hand side to be zero (cf. Larson, 2022). After updating 〈σ_l〉, the PDF parameters, {λ_l}, are diagnosed from the given set of {〈σ_l〉} from the following relations:

$$\begin{array}{}\text{(54)}& \langle {\mathit{\sigma }}_j\rangle =\langle {\mathit{\sigma }}_j\rangle \left(\mathit{\right\{}{\mathit{\lambda }}_l\mathit{\left\}}\right)\end{array}$$

for $j=\mathrm{1},\mathrm{\dots }N$. As already discussed in Sect. 3.2.1, the inversion of {〈σ_l〉} to {λ_l} is not always easy.

The introduced general formulation, in turn, shows that the left-hand side of Eq. (52b) or Eq. (53d) can be replaced by the left-hand side of Eq. (50a) or Eq. (53a); thus the problem directly reduces to the prognoses of the PDF parameters of a given distribution. As a result, there is no longer a need to perform a cumbersome inversion. This modification greatly facilitates the computational procedure. Note especially that when the same set of moments is taken for {〈σ_l〉}, with identical assumed-PDF forms, the present formulation is perfectly equivalent to an existing assumed-PDF model apart from the fact that the PDF parameters, {λ_l}, instead of the moment set, {〈σ_l〉}, are directly predicted.

Another strength of the present formulation is in more explicitly showing that the right-hand side of Eq. (52b) or Eq. (53d) can also be totally expressed in terms of the PDF parameters. As a result, there is no longer a need to introduce further closures to the assumed-PDF formulation, as also noted by Golaz et al. (2002). However, this last rather obvious point is not always recognized, and some assumed-PDF approaches often introduce additional closures to close their formulations (e.g., Fitch, 2019; Naumann et al., 2013).

The standard formulations in the bulk microphysics (cf. Milbrandt and Yau, 2005, and the references therein) are to adopt the mixing ratio, q; the total number density, N_T; and the radar reflectivity, Z, as the prognostic variables, with the order to be adopted with decreasing truncations. Under the present formulation, neglecting multiplication factors, q and Z correspond to setting σ₁=r³ and σ₂=r⁶, respectively, whereas N_T is predicted in a standalone manner by separating out the number density, n, into the two components by setting n=N_Tp. More or less the same remarks follow for them with further flexibilities in the formulation by re-writing it in terms of a general form of Eq. (52b) or Eq. (53d). Probably, most importantly, the choice of the radar reflectivity, Z, as a “constraint” can be questioned from the point of view of the output-constrained distribution principle (cf. Sect. 4.2): though the reflectivity, Z, may be a useful variable to compare with the observation, it is not directly required in any microphysical tendencies within a model.³

5.5 Application 1: exponential distribution

In this subsection, we repeat the general derivation presented in Sect. 5.1 by taking the exponential distribution (Eq. 24 with λ₀=p₀) as an example. Here, we immediately obtain $\partial p/\partial {\mathit{\lambda }}_{\mathrm{0}}=p/{\mathit{\lambda }}_{\mathrm{0}}$, $\partial p/\partial {\mathit{\lambda }}_{\mathrm{1}}=-p\mathit{\varphi }$, and

$$\begin{array}{}\text{(55)}& {\displaystyle \frac{\partial p}{\partial t}}=p{\displaystyle \frac{{\dot{\mathit{\lambda }}}_{\mathrm{0}}}{{\mathit{\lambda }}_{\mathrm{0}}}}-p\mathit{\varphi }{\dot{\mathit{\lambda }}}_{\mathrm{1}}.\end{array}$$

The normalization condition (Eq. 46) is obtained by integrating the above equation with respect to ϕ:

$$\begin{array}{}\text{(56a)}& {\displaystyle \frac{{\dot{\mathit{\lambda }}}_{\mathrm{0}}}{{\mathit{\lambda }}_{\mathrm{0}}}}\int p\mathrm{d}\mathit{\varphi }-{\dot{\mathit{\lambda }}}_{\mathrm{1}}\int p\mathit{\varphi }\mathrm{d}\mathit{\varphi }=\mathrm{0}.\end{array}$$

Noting that $\int p\mathrm{d}\mathit{\varphi }=\mathrm{1}$ and $\int p\mathit{\varphi }\mathrm{d}\mathit{\varphi }\equiv \langle \mathit{\varphi }\rangle =\mathrm{1}/{\mathit{\lambda }}_{\mathrm{1}}$, it reduces to

$$\begin{array}{}\text{(56b)}& {\displaystyle \frac{{\dot{\mathit{\lambda }}}_{\mathrm{0}}}{{\mathit{\lambda }}_{\mathrm{0}}}}-{\displaystyle \frac{{\dot{\mathit{\lambda }}}_{\mathrm{1}}}{{\mathit{\lambda }}_{\mathrm{1}}}}=\mathrm{0},\end{array}$$

which can be immediately integrated into

$$\begin{array}{}\text{(56c)}& {\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{0}}}{{\mathit{\lambda }}_{\mathrm{1}}}}=\text{const}.\end{array}$$

That is the constraint under the normalization condition. Alternatively, the normalization condition can be obtained directly by performing an integral of the distribution analytically:

$$\begin{array}{}\text{(56d)}& {\mathit{\lambda }}_{\mathrm{0}}={\mathit{\lambda }}_{\mathrm{1}}.\end{array}$$

Substitution of Eq. (56b) into Eq. (55), in the same manner as that of Eq. (47) into Eq. (48), makes the right-hand side dependent only on λ₁. Substituting this final expression into the Liouville equation (Eq. 26), we obtain

$$\begin{array}{}\text{(57a)}& p\left({\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{1}}}}-\mathit{\varphi }\right){\dot{\mathit{\lambda }}}_{\mathrm{1}}+{\displaystyle \frac{\partial }{\partial \mathit{\varphi }}}\left(pF\right)=\mathrm{0}.\end{array}$$

Here, this equation contains ϕ dependence; thus it cannot be directly used to predict λ₁.

We remove the ϕ dependence from Eq. (57a) by multiplying a weight σ₁ that depends only on ϕ and integrating it by ϕ over $[\mathrm{0},+\mathrm{\infty }]$. We choose the weight σ₁=ϕ because the exponential distribution is to be used for predicting the mean value, based on an argument in Sect. 4.2.

Thus,

$$\begin{array}{}\text{(57b)}& \left[{\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{1}}}}\langle \mathit{\varphi }\rangle -\langle {\mathit{\varphi }}^{\mathrm{2}}\rangle \right]{\dot{\mathit{\lambda }}}_{\mathrm{1}}-\langle F\rangle =\mathrm{0},\end{array}$$

or by further noting $\langle \mathit{\varphi }\rangle =\mathrm{1}/{\mathit{\lambda }}_{\mathrm{1}}$ and $\langle {\mathit{\varphi }}^{\mathrm{2}}\rangle =\mathrm{2}/{\mathit{\lambda }}_{\mathrm{1}}^{\mathrm{2}}$,

$$\begin{array}{}\text{(58a)}& {\dot{\mathit{\lambda }}}_{\mathrm{1}}=-{\mathit{\lambda }}_{\mathrm{1}}^{\mathrm{2}}\langle F\rangle .\end{array}$$

This equation states that when there is a positive mean source, 〈F〉>0, the slope of the distribution becomes gentler by transporting it to larger values, whereas a mean sink (negative source) steepens the distribution. The above equation can readily be solved analytically, and we obtain

$$\begin{array}{}\text{(58b)}& {\mathit{\lambda }}_{\mathrm{1}}\left(t\right)={\left[{\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{1}}\left(\mathrm{0}\right)}}+\underset{\mathrm{0}}{\overset{t}{\int }}\langle F\rangle \mathrm{d}t\right]}^{-\mathrm{1}}.\end{array}$$

The significance of the above result may be best interpreted by re-writing it for the mean value:

$$\begin{array}{}\text{(58c)}& \langle \mathit{\varphi }\rangle ={\mathit{\lambda }}_{\mathrm{1}}(t{)}^{-\mathrm{1}}=\langle \mathit{\varphi }\rangle {\mathrm{|}}_{t=\mathrm{0}}+\underset{\mathrm{0}}{\overset{t}{\int }}\langle F\rangle \mathrm{d}t.\end{array}$$

This is the consistent evolution of the mean state under the assumed exponential distribution.

Here, the weight, σ₁=ϕ, has been chosen above in a manner consistent with the fact that the exponential distribution has been derived from the maximum-entropy principle, taking the mean as the constraint. Yet, the general formulation presented in Sect. 5.1 can be used to predict any constraint defined by the weight, σ₁, consistently with time under a given assumed distribution. Thus, a natural question to ask is, how is the evolution of the PDF parameter, λ₁, sensitive to the choice of the weight, σ₁, for the constraint? To address this question, we now set the weight to be σ₁=ϕⁿ more generally with an unspecified integer, n. In this case, we evaluate the evolution of the assumed distribution (Eq. 24) in such a manner that 〈ϕⁿ〉 evolves consistently. As a result, the prediction of the evolution of the parameter, λ₁, is modified to achieve the best prediction of 〈ϕⁿ〉 for a specified particular n with the consequence of causing the prediction of the other moments to deteriorate. Especially, when we set n≠1, the prediction of the mean value is no longer optimized by the constraint with σ₁=ϕⁿ.

Consequently, instead of Eqs. (58b) and (58c), we obtain

$$\begin{array}{}\text{(59a)}& {\displaystyle }{\mathit{\lambda }}_{\mathrm{1}}\left(t\right)& {\displaystyle }={\left[{\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{1}}^n\left(\mathrm{0}\right)}}+{\displaystyle \frac{n}{n\mathrm{!}}}\underset{\mathrm{0}}{\overset{t}{\int }}\langle F{\mathit{\varphi }}^{n-\mathrm{1}}\rangle \mathrm{d}t\right]}^{-\mathrm{1}/n},\text{(59b)}& {\displaystyle }\langle {\mathit{\varphi }}^n\rangle & {\displaystyle }=\langle {\mathit{\varphi }}^n\rangle {\mathrm{|}}_{t=\mathrm{0}}+n\underset{\mathrm{0}}{\overset{t}{\int }}\langle F{\mathit{\varphi }}^{n-\mathrm{1}}\rangle \mathrm{d}t,\end{array}$$

noting that $\langle {\mathit{\varphi }}^n\rangle =n\mathrm{!}/{\mathit{\lambda }}_{\mathrm{1}}^n$. In this case, Eq. (59b) presents a consistent evolution of 〈ϕⁿ〉.

Keep in mind that the solution of Eq. (59a) is implicit when F itself also depends on ϕ. A more explicit solution can be derived by setting it more specifically as, say, F=ϕ^m. Solving an equivalent equation to Eq. (57b), we find

$$\begin{array}{}\text{(59c)}& {\mathit{\lambda }}_{\mathrm{1}}\left(t\right)=\left({\mathit{\lambda }}_{\mathrm{1}}^{m-\mathrm{1}}\right(\mathrm{0})-{\mathit{\gamma }}_{m}t{)}^{\mathrm{1}/(m-\mathrm{1})},\end{array}$$

where

$$\begin{array}{}\text{(59d)}& {\mathit{\gamma }}_m=(m-\mathrm{1})(n+m-\mathrm{1})\mathrm{!}/n\mathrm{!}\end{array}$$

when m≠1.

It is clear that the parameter, λ₁, qualitatively changes with a different “rate”, γ_m, of evolution with the varying n; thus the evolution of the assumed PDF is sensitive to the choice of the weight, σ₁. It also follows that a proper choice of σ₁ is crucial to ensure that an output, 〈σ₁〉, of a particular interest is consistently predicted. A simple way to achieve this consistency is to solve a prognostic equation for 〈σ₁〉 in terms of λ₁. The general formulation presented in Sect. 5.1 is constructed in this manner.

Here, however, there is a serious problem with the above solution (Eq. 59c): the exponential distribution continuously flattens with time, and the distribution becomes totally homogeneous at $t={\mathit{\lambda }}_{\mathrm{1}}^{m-\mathrm{1}}\left(\mathrm{0}\right)/{\mathit{\gamma }}_m$; then λ₁=0, and the solution breaks down beyond this point with λ₁ becoming a complex number. Such a collapse of the distribution is a dramatic example of suggesting an inherent limitation of the assumed-PDF approach. Figure 2 plots the obtained time series of λ₁ with m=0, 2, 3, 4 in panels (a)–(d) with the weight exponents n=1 (solid), n=2 (long dash), and n=3 (short dash). It is seen that the discrepancy of the solution with different weights, σ₁, is exacerbated rapidly as a higher-order dependence of F on ϕ (i.e., with the increasing m: Fig. 2b–d). The exception is the case with m=0, where γ₀=0; thus this singularity is avoided (Fig. 2a). Here, we set the initial condition as λ₁(0)=1. This is equivalent to normalizing the PDF parameter and the time into ${\mathit{\lambda }}_{\mathrm{1}}/{\mathit{\lambda }}_{\mathrm{1}}\left(\mathrm{0}\right)$ and ${\mathit{\lambda }}_{\mathrm{1}}^{\mathrm{1}-m}\left(\mathrm{0}\right)t$, respectively.

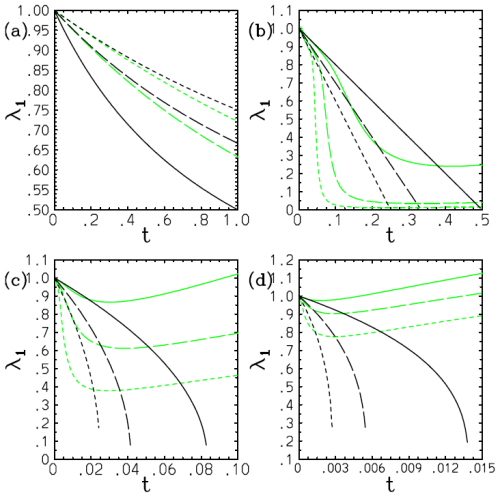
Figure 2 Plot of the obtained time series of λ₁ with m=0 (a), 2 (b), 3 (c), and 4 (d) with the weight exponents n=1 (solid), n=2 (long dash), and n=3 (short dash). The values of λ₁ evaluated from 〈ϕⁿ〉 obtained using the exact solutions are further overlaid by green curves.

The values of λ₁ evaluated from 〈ϕⁿ〉 with the exact solutions in Appendix B are further overlaid by green curves with further discussions concerning the exact solutions referred to therein. In the case with m=0, we find satisfactory agreement of the PDF parameter, λ₁, between the solution (Eq. 59c) and the exact results (Fig. 2a). However, due to the singularities discussed above with m≥2, the diagnosed solution (Eq. 59c) rapidly deviates from the exact results (Fig. 2b–d).

The case with m=1 must be considered separately, and in this case we find, for all n values,

$$\begin{array}{}\text{(59e)}& {\mathit{\lambda }}_{\mathrm{1}}\left(t\right)={\mathit{\lambda }}_{\mathrm{1}}\left(\mathrm{0}\right)e^{-t}.\end{array}$$

As it turns out, this is an exact solution of the evolution of the system, as shown in Appendix B.

5.6 Application 2: Gaussian distribution

The second application is the Gaussian distribution, especially because this is a standard distribution assumed in data assimilation. The Gaussian distribution is also often assumed in subgrid-scale distribution problems. Here, the simplest case with a single variable is considered, as given by Eq. (25). Here, p₀=λ₀, and we take the mean value, $\langle \mathit{\varphi }\rangle =-\mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}/{\mathit{\lambda }}_{\mathrm{1}}$, to be a PDF parameter in place of λ₁. From a normalization condition,

$$\begin{array}{}\text{(60)}& p_{\mathrm{0}}={\left({\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{2}}}{\mathit{\pi }}}\right)}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

This diagnostic relation can be used to update the distribution constant p₀ in place of updating it by integrating Eq. (47).

We further note that

$$\begin{array}{}\text{(61a)}& {\displaystyle \frac{\partial p}{\partial \langle \mathit{\varphi }\rangle }}& {\displaystyle }=\mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}(\mathit{\varphi }-\langle \mathit{\varphi }\rangle )p,\text{(61b)}& {\displaystyle \frac{\partial p}{\partial {\mathit{\lambda }}_{\mathrm{2}}}}& {\displaystyle }=-(\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}p.\end{array}$$

By substituting these expressions into Eq. (50a), we obtain

$$\begin{array}{}\text{(62)}& {\displaystyle }\begin{array}{rl}& \mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}\dot{\langle \mathit{\varphi }\rangle }[\langle {\mathit{\sigma }}_l(\mathit{\varphi }-\langle \mathit{\varphi }\rangle )\rangle -\langle {\mathit{\sigma }}_l\rangle \langle \mathit{\varphi }-\langle \mathit{\varphi }\rangle \rangle ]\\ & +{\dot{\mathit{\lambda }}}_{\mathrm{2}}[-\langle {\mathit{\sigma }}_l(\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}\rangle +\langle {\mathit{\sigma }}_l\rangle \langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}\rangle ]=〈F{\displaystyle \frac{\partial {\mathit{\sigma }}_l}{\partial \mathit{\varphi }}}〉.\end{array}\end{array}$$

Note that an integration by parts is applied to the last term in Eq. (50a) to obtain the right-hand side above. Note also that $\langle \mathit{\varphi }-\langle \mathit{\varphi }\rangle \rangle =\mathrm{0}$, and thus

$$\begin{array}{}\text{(63)}& \begin{array}{rl}& \mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}\dot{\langle \mathit{\varphi }\rangle }\langle {\mathit{\sigma }}_l(\mathit{\varphi }-\langle \mathit{\varphi }\rangle )\rangle \\ & +{\dot{\mathit{\lambda }}}_{\mathrm{2}}[-\langle {\mathit{\sigma }}_l(\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}\rangle +\langle {\mathit{\sigma }}_l\rangle \langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}\rangle ]=〈F{\displaystyle \frac{\partial {\mathit{\sigma }}_l}{\partial \mathit{\varphi }}}〉.\end{array}\end{array}$$

Recall that the Gaussian distribution is obtained from the maximum-entropy principle when a system is constrained by the mean and the variance; thus we set ${\mathit{\sigma }}_{\mathrm{1}}=\mathit{\varphi }-\langle \mathit{\varphi }\rangle$ and ${\mathit{\sigma }}_{\mathrm{2}}=(\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}$ in the above. With l=1, we obtain

$$\begin{array}{}\text{(64a)}& \mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}\rangle \dot{\langle \mathit{\varphi }\rangle }-\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{3}}\rangle {\dot{\mathit{\lambda }}}_{\mathrm{2}}=\langle F\rangle \end{array}$$

and, with l=2,

$$\begin{array}{}\text{(64b)}& \begin{array}{rl}& \mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{3}}\rangle \dot{\langle \mathit{\varphi }\rangle }\\ & +[-\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{4}}\rangle +\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}{\rangle }^{\mathrm{2}}]{\dot{\mathit{\lambda }}}_{\mathrm{2}}=\\ & \mathrm{2}\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle )F\rangle .\end{array}\end{array}$$

Note that the Gaussian distribution is not skewed; thus $\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{3}}\rangle =\mathrm{0}$. Also note the relations

$$\begin{array}{}\text{(65a)}& {\displaystyle }\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}\rangle & {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}}},\text{(65b)}& {\displaystyle }\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{4}}\rangle & {\displaystyle }=\mathrm{3}\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}{\rangle }^{\mathrm{2}}.\end{array}$$

By substituting these relations into Eqs. (64a) and (64b), we obtain the final results:

$$\begin{array}{}\text{(66a)}& {\displaystyle }\dot{\langle \mathit{\varphi }\rangle }& {\displaystyle }=\langle F\rangle ,\text{(66b)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{2}}}}\right)& {\displaystyle }=\mathrm{4}\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle )F\rangle .\end{array}$$

Equation (66a) simply means that the mean value evolves by following a tendency defined by the mean source, whereas Eq. (66b) suggests that the distribution is more dispersed when a more positive source is found away from the mean value.

5.7 Diffusion problem

The diffusion equation (Eq. 29) considered in Sect. 4.4 is a particular problem that can be solved exactly by the Gaussian distribution (Eq. 25). We note that the diffusion equation (Eq. 29), re-setting x=ϕ here, is obtained from the Liouville equation (Eq. 26) by setting the forcing to be an operator, $F=-\partial /\partial \mathit{\varphi }$. As a result, the general formulation presented so far can directly be applied to the diffusion equation: by substituting the derivative relations (Eqs. 61a and b) into Eq. (49a) and also noting that

$$\begin{array}{}\text{(67)}& {\displaystyle \frac{{\partial }^{\mathrm{2}}p}{\partial {\mathit{\varphi }}^{\mathrm{2}}}}=[-\mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}+\mathrm{4}{\mathit{\lambda }}_{\mathrm{2}}^{\mathrm{2}}(\mathit{\varphi }-\langle \mathit{\varphi }\rangle {)}^{\mathrm{2}}]p,\end{array}$$

we obtain

$$\begin{array}{}\text{(68)}& \begin{array}{rl}& \mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}(\mathit{\varphi }-\langle \mathit{\varphi }\rangle )\langle \dot{\mathit{\varphi }}\rangle \\ & -\left[(\mathit{\varphi }-\langle \mathit{\varphi }\rangle {]}^{\mathrm{2}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\lambda }}_{\mathrm{2}}}}\right][{\dot{\mathit{\lambda }}}_{\mathrm{2}}+\mathrm{4}{\mathit{\lambda }}_{\mathrm{2}}^{\mathrm{2}}]=\mathrm{0}.\end{array}\end{array}$$

Note that the same can also be obtained by directly substituting Eq. (25) into Eq. (29). The above equation can be solved for the two parameters, 〈ϕ〉 and λ₂, independently of ϕ by setting

$$\begin{array}{}\text{(69a)}& {\displaystyle }\langle \dot{\mathit{\varphi }}\rangle & {\displaystyle }=\mathrm{0},\text{(69b)}& {\displaystyle }{\dot{\mathit{\lambda }}}_{\mathrm{2}}+\mathrm{4}{\mathit{\lambda }}_{\mathrm{2}}^{\mathrm{2}}& {\displaystyle }=\mathrm{0}.\end{array}$$

The same pair as the above is more directly obtained by substituting 〈F〉=0 and $\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle )F\rangle =-\mathrm{1}$ into Eqs. (66a) and (66b). Solving for Eqs. (69a) and (69b), we arrive at the solution (Eq. 32).

5.8 Application 3: gamma distribution

The third example to consider is the gamma distribution (cf. Sect. 3.4.3):

$$\begin{array}{}\text{(70a)}& p=p_{\mathrm{0}}{\mathit{\varphi }}^{\mathit{\mu }}{e}^{-\mathit{\lambda }\mathit{\varphi }},\end{array}$$

where

$$\begin{array}{}\text{(70b)}& p_{\mathrm{0}}={\displaystyle \frac{{\mathit{\lambda }}^{\mathit{\mu }+\mathrm{1}}}{\mathrm{\Gamma }(\mathit{\mu }+\mathrm{1})}}\end{array}$$

from the normalization condition. Recall that the gamma function, Γ(x), is defined by

$$\begin{array}{}\text{(70c)}& \mathrm{\Gamma }\left(x\right)=\underset{\mathrm{0}}{\overset{+\mathrm{\infty }}{\int }}{\mathit{\xi }}^{x-\mathrm{1}}{e}^{-\mathit{\xi }}\mathrm{d}\mathit{\xi }.\end{array}$$

We note the expressions for the derivatives by the distribution parameters:

$$\begin{array}{}\text{(71a)}& {\displaystyle \frac{\partial p}{\partial \mathit{\mu }}}& {\displaystyle }=p\log \mathit{\varphi },\text{(71b)}& {\displaystyle \frac{\partial p}{\partial \mathit{\lambda }}}& {\displaystyle }=-\mathit{\varphi }p.\end{array}$$

By substituting these two expressions into Eq. (50a), we obtain

$$\begin{array}{}\text{(72)}& \begin{array}{rl}\dot{\mathit{\mu }}[\langle {\mathit{\sigma }}_l\log \mathit{\varphi }\rangle & -\langle {\mathit{\sigma }}_l\rangle \langle \log \mathit{\varphi }\rangle ]+\dot{\mathit{\lambda }}[-\langle {\mathit{\sigma }}_l\mathit{\varphi }\rangle +\langle {\mathit{\sigma }}_l\rangle \langle \mathit{\varphi }\rangle ]=\\ & 〈F{\displaystyle \frac{\partial {\mathit{\sigma }}_l}{\partial \mathit{\varphi }}}〉\end{array}\end{array}$$

for l=1, 2. As before, we set σ₁=ϕ and σ₂=ϕ². We note especially

$$\begin{array}{}\text{(73a)}& {\displaystyle }\langle \mathit{\varphi }\log \mathit{\varphi }\rangle & {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathit{\lambda }}}\left[\right(\mathit{\mu }+\mathrm{1})\langle \log \mathit{\varphi }\rangle +\mathrm{1}],\text{(73b)}& {\displaystyle }\langle {\mathit{\varphi }}^{\mathrm{2}}\log \mathit{\varphi }\rangle & {\displaystyle }={\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}^{\mathrm{2}}}}\left[\right(\mathit{\mu }+\mathrm{1}\left)\right(\mathit{\mu }+\mathrm{2})\langle \log \mathit{\varphi }\rangle +\mathrm{2}\mathit{\mu }+\mathrm{3}].\end{array}$$

Thus, with l=1 and 2, respectively, we obtain

$$\begin{array}{}\text{(74a)}& {\displaystyle \frac{\dot{\mathit{\mu }}}{\mathit{\lambda }}}-(\mathit{\mu }+\mathrm{1}){\displaystyle \frac{\dot{\mathit{\lambda }}}{{\mathit{\lambda }}^{\mathrm{2}}}}& {\displaystyle }=\langle F\rangle ,\text{(74b)}& {\displaystyle \frac{\mathrm{2}\mathit{\mu }+\mathrm{3}}{{\mathit{\lambda }}^{\mathrm{2}}}}\dot{\mathit{\mu }}-{\displaystyle \frac{\mathrm{2}(\mathit{\mu }+\mathrm{2})(\mathit{\mu }+\mathrm{1})}{{\mathit{\lambda }}^{\mathrm{3}}}}\dot{\mathit{\lambda }}& {\displaystyle }=\mathrm{2}\langle \mathit{\varphi }F\rangle .\end{array}$$

By combining Eqs. (74a) and (74b), we obtain the equations for the tendencies of the two PDF parameters as

$$\begin{array}{}\text{(75a)}& {\displaystyle }\dot{\mathit{\mu }}& {\displaystyle }=\mathrm{2}\mathit{\lambda }\left[\right(\mathit{\mu }+\mathrm{2})\langle F\rangle -\mathit{\lambda }\langle \mathit{\varphi }F\rangle ],\text{(75b)}& {\displaystyle }\dot{\mathit{\lambda }}& {\displaystyle }={\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{2}}}{\mathit{\mu }+\mathrm{1}}}\left[\right(\mathrm{2}\mathit{\mu }+\mathrm{3})\langle F\rangle -\mathrm{2}\mathit{\lambda }\langle \mathit{\varphi }F\rangle ].\end{array}$$

6 Demonstration: condensation growth of cloud droplets

The general formulation for directly predicting the evolution of the assumed-PDF (DDF) parameters was presented in the last section. The purpose of this section is to demonstrate the steps of this formulation by taking the condensation growth of cloud droplets as an example. The output-constrained distribution introduced in Sect. 4.2 is also invoked in choosing a distribution form. It is known that the size, r, of a cloud droplet grows with a rate proportional to $\mathrm{1}/r$ under a fixed state of super-saturation (cf. Chap. 6, Rogers and Yau, 1989). Thus, by setting a proportionality constant to unity, the governing equation (Eq. 2) of this system becomes

$$\begin{array}{}\text{(76a)}& \dot{r}={\displaystyle \frac{\mathrm{1}}{r}},\end{array}$$

with ϕ=r and $F=\mathrm{1}/r$. In this case, p(r) becomes a number density of drops with a radius r, or PSD. Here, we normalize the PSD with Eq. (13).

The system of Eq. (76a) can be solved analytically, and the general solution is

$$\begin{array}{}\text{(76b)}& r\left(t\right)=(r_{\mathrm{0}}+\mathrm{2}t{)}^{\mathrm{1}/\mathrm{2}},\end{array}$$

with r₀ being the initial condition. Consequently, when an initial distribution of droplets is given by

$$\begin{array}{}\text{(77)}& p(r,t=\mathrm{0})=p_{\mathrm{0}}\left(r\right),\end{array}$$

its subsequent evolution is defined by

$$\begin{array}{}\text{(78a)}& p(r,t)\mathrm{d}r=p_{\mathrm{0}}\left(r_{\mathrm{0}}\right)\mathrm{d}{r}_{\mathrm{0}}\end{array}$$

by following the chain rule of Eq. (20). Here, the initial condition, $r_{\mathrm{0}}=r\left(\mathrm{0}\right|r,t)$, is related to the droplet size, r, at the time t by

$$\begin{array}{}\text{(78b)}& r_{\mathrm{0}}=r\left(\mathrm{0}\right|r,t)=(r^{\mathrm{2}}-\mathrm{2}t{)}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

From Eq. (78b), we find $\mathrm{d}{r}_{\mathrm{0}}/\mathrm{d}r=r/r_{\mathrm{0}}$, and by substituting this final result into Eq. (77), we obtain

$$\begin{array}{}\text{(78c)}& p=(r/r_{\mathrm{0}})p_{\mathrm{0}},\end{array}$$

but $p(r,t)=\mathrm{0}$ for r²(t)<2t. In this manner, the problem of time evolution of the droplet distribution under the condensation growth is solved analytically.

As a specific initial distribution, we set

$$\begin{array}{}\text{(79)}& p(r,t=\mathrm{0})={\displaystyle \frac{{\mathit{\lambda }}^{\mathit{\mu }+\mathrm{1}}}{\mathrm{\Gamma }(\mathit{\mu }+\mathrm{1})}}{r}^{\mathit{\mu }}{e}^{-\mathit{\lambda }r},\end{array}$$

with μ=1 and λ=1. The exact time evolution following this initialization, which obeys Eq. (78a) or (78c), is shown in Fig. 3a with varying curves for t=0–4 with an interval of Δt=1. The whole distribution moves with time to larger sizes, r, as seen in Fig. 3a, because of condensational growth, as expected, but it is also associated with the squeezing tendency by the factor, $r/r_{\mathrm{0}}$, with time, as predicted from the analytical solution (Eq. 78c). The rate of squeezing is larger towards the smaller r₀ and forms a shockwave front at the peak at the minimum droplet size,

$$\begin{array}{}\text{(80)}& r=(\mathrm{2}t{)}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

The peak also sharpens with time, as it moves to larger values with time. The pronounced narrowing tendency of the distribution with time is well known in the literature. Remarkably, it leads to a decrease in the standard deviation with time as seen below.

Figure 3 Time evolution of the cloud-droplet size distribution under condensation growth with the curves corresponding to t=0 (solid) to t=4 (double-chain dash) with an interval of Δt=1: (a) exact result and (b) when a gamma distribution is assumed. Note that the whole distribution moves to a larger droplet size with time.

In the following, the two assumed PSDs are considered for demonstrations of the general formulation of the last section.

6.1 Gamma distribution

Considering the fact that our example is a microphysical problem, the most natural choice to consider is the gamma distribution (Eq. 70a), as a commonly adopted distribution in microphysics (cf. Sect. 3.4.3). A general formulation for this case is presented in Sect. 5.7. The only additional information required is to note $\langle F\rangle =\mathit{\lambda }/\mathit{\mu }$ and 〈rF〉=1 with the system (Eq. 76a), recalling the definition (Eq. 52c) for the angle bracket, and also $F=\mathrm{1}/r$. Substituting them, Eqs. (75a) and (75b) are solved by the fourth-order Runge–Kutta method with a time step of 10⁻² and the initial condition given by μ=1 and λ=1. The result is shown in Fig. 3b with the same curves as in Fig. 3a. Obviously, it is not possible to reproduce the shockwave structure at the minimum size (Eq. 80) by a gamma distribution. However, it is still remarkable that an overall evolution of the size distribution is reasonably reproduced.

The result here is especially remarkable because the computation of the evolution of the distribution involves only time integrations of two parameters, μ and γ; then the full distribution is automatically determined from the assumed gamma distribution form. In a standard approach of directly evaluating the evolution of a distribution by integrating Eq. (26) with time, we need to introduce a number of values for r that we wish to evaluate. For example, in Fig. 2a and b, 100 points are used for plotting the distribution curves for each time. Furthermore, for numerically integrating the Liouville equation (Eq. 26), we need to take r large enough so that we can set p=0 as the boundary condition at the largest r: this requirement further increases the number of points required for the computation by, say, a factor of 10. In standard bin microphysics, 30 points are considered the minimum (cf. Khain et al., 2015). The assumed-PDF (DDF) approach adopted here enables us to compute the same only with the two parameters, instead of many bins for r.

To verify the prediction of statistics, Fig. 4 plots the time evolutions of (a) the average size, 〈r〉, and (b) the standard deviation, $\langle (r-\langle r\rangle {)}^{\mathrm{2}}{\rangle }^{\mathrm{1}/\mathrm{2}}$ with $\langle r\rangle =(\mathit{\mu }+\mathrm{1})/\mathit{\lambda }$ and $\langle (r-\langle r\rangle {)}^{\mathrm{2}}\rangle =(\mathit{\mu }+\mathrm{1})/{\mathit{\lambda }}^{\mathrm{2}}$. Here, the exact evolutions are shown in solid curves, whereas the approximate predictions with the assumed gamma distribution are shown by long-dash curves. Keep in mind that from the point of view of the maximum-entropy principle, the gamma distribution is designed to predict only a mean value properly. An additional algebraic correction factor is not the result of any “constraint” from the point of view of the large-deviation principle (cf. Sect. 3.3.2). These predictions are accurate only under limits of an assumed distribution. In fact, the prediction of the mean (Fig. 4a) is almost perfect, although that of the standard deviation deviates noticeably from the actual evolution with time (Fig. 4b).

Figure 4 Time evolutions of (a) the average size, 〈r〉, and (b) the standard deviation, $\langle (r-\langle r\rangle {)}^{\mathrm{2}}{\rangle }^{\mathrm{1}/\mathrm{2}}$, of droplets undergoing condensation growth. Here, exact evolutions are shown in solid curves, whereas the predictions with the assumed gamma distribution are shown by long-dash curves.

6.2 Exponential distribution

We further simplify the assumed distribution into an exponential so that there is only a single parameter, λ₁, in the distribution (cf. Eq. 57a). In this case, the assumed distribution no longer fits the actual evolution initiated with a gamma distribution (Eq. 79) as r→0.

Here, we face a technical problem for adopting the exponential distribution for this system because the integral for 〈F〉 diverges due to a singularity of the source, F, at r=0. To avoid this problem, we set λ₁ of the exponential distribution in such a manner that it gives the same mean size, 〈r〉, as the gamma distribution given by Eq. (79) (i.e., ${\mathit{\lambda }}_{\mathrm{1}}=\mathit{\lambda }/(\mathrm{1}+\mathit{\mu })$), and then we adopt a formula, $\langle F\rangle =\mathit{\lambda }/\mathit{\mu }$, directly from the gamma distribution. Thus, $\langle F\rangle =(\mathrm{1}+\mathit{\mu }){\mathit{\lambda }}_{\mathrm{1}}/\mathit{\mu }$. Here, μ is kept the same as the initial condition of the distribution (Eq. 79). Under this assumption, the time integral of Eq. (58a) can be performed, and the evolution of the mean size can be evaluated by Eq. (58c). Evolution of the standard deviation is also evaluated as $\mathrm{1}/{\mathit{\lambda }}_{\mathrm{1}}$.

These results are shown in Fig. 5 in the same format as in Fig. 4; the evolution of the standard deviation (long-dash curve in panel b) now becomes totally opposite to the actual tendency (solid curve). However, the evolution of the mean size is still predicted in a consistent manner overall with panel (a). The results are simply consistent with the assertion in Sect. 4.2 that if the sole purpose of using a distribution is to predict the evolution of a mean, the exponential distribution is sufficient for the purpose. Here, this assertion is supported to a reasonable extent, even though an actual distribution does not fit the exponential distribution at all.

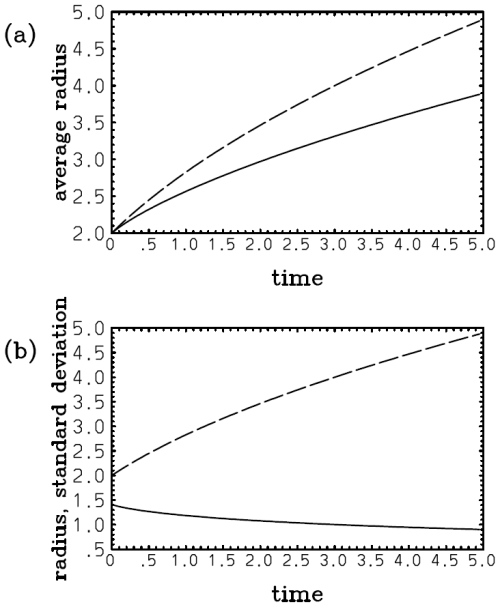
Figure 5 The same as in Fig. 3 but long-dash curves are when an exponential distribution is assumed for prediction.

Appendix C presents further demonstrative mathematical examples.

7 Conclusions and discussions

Distribution problems are identified in various contexts of atmospheric sciences: subgrid-scale distribution, the size distribution of hydrometeors, and probabilities in data assimilation. Considering the dispersed literature on those three distribution problems, the present paper has tried to set up a general perspective for all the distribution problems. As noted in the introduction, the majority of approaches in the distribution problems are based on a framework, which can be termed “assumed PDF”, in which a distribution to be simulated is approximated by a distribution form characterized only by a few free parameters (cf. Golaz et al., 2002).

The present work has attempted to answer the basic questions of how such a simple assumed PDF can be best chosen and how the evolution of those PDF parameters can be evaluated consistently. To address these basic questions, it is important to realize that not every statistical aspect of any distribution can be predicted by the assumed-PDF approaches either accurately or consistently. More specifically, the number of statistical variables (but not limited to simple moments) that can be consistently predicted by an assumed-PDF approach cannot exceed the number of assumed-PDF parameters introduced by the given assumed PDF. Thus, the best that we can accomplish under an assumed-PDF approach is to predict the same number of statistical variables as that of the assumed-PDF free parameters. The proposed formulation in the present study is designed exactly to accomplish this best.

The present study next notes (Sect. 4.2) that in many atmospheric applications, a given host model does not require using the full form of a distribution as an output from a distribution model, but, instead, it requires only a limited number of statistical quantities that correspond to the physical variables of interest in the host model (e.g., domain-averaged total condensed water, cloud fraction) as outputs. Thus, the most desirable formulation would be to predict the evolution of those statistical outputs required in a given host model consistently. The final general formulation presented in Sect. 5.1 is constructed exactly by following this receipt: the time evolution of the assumed-PDF parameters, {λ_l}, is evaluated by Eq. (50a), which is equivalent to solving the prediction (Eq. 52b) for the required model outputs, {〈σ_l〉}, in terms of {λ_l}.

Probably, the most novel aspect of the present study is in deriving equations for the assumed-PDF parameters and predicting them directly. This proposed alternative approach can overcome difficulties of the current standard method that requires a difficult mapping between the moments of the PDF (mean, variance, skewness, etc. of overall PDF) and the PDF parameters (e.g., mean of each Gaussian component in a double-Gaussian PDF; cf. Lewellen and Yoh, 1993; Machulskaya, 2015; Milbrandt and Yau, 2005). Furthermore, by introducing a re-interpretation of the maximum-entropy principle (cf. Sect. 3.3) in Sect. 4.2, we propose to adopt those required statistical outputs as “constraints” to define the assumed-PDF form for a given problem to resolve the common problem of how to choose it, which is usually done rather arbitrarily. The paper has also emphasized that approaches of trying to choose a distribution form based on analyses of observational or simulation data found in the literature lack objectivity (cf. Sect. 3.2.2).

In the present study, the possible model outputs and constraints have been limited to much simpler statistical quantities of the form, {〈σ_l〉}. However, generalizations to those physically more significant variables, such as the domain-averaged total condensed water and the cloud fraction, are conceptually straightforward. For example, the cloud fraction can formally be defined in terms of the DDF, p(q_t), of the total water, q_t, as

$$\begin{array}{}\text{(81)}& \underset{q^{*}}{\overset{+\mathrm{\infty }}{\int }}p\left(q_{\mathrm{t}}\right)\mathrm{d}{q}_{\mathrm{t}},\end{array}$$

where q^* is the saturated moisture at a given height. Following a similar line of argument to that presented in Sect. 5, a prognostic equation for the cloud fraction, as defined above, can be derived by integrating Eq. (49a) over the range of $[q^{*},+\mathrm{\infty }]$, although a full derivation is left for a future paper. Alternatively, a prognostic equation for the consistent DDF parameters can more directly be derived from the prognostic equation for the cloud fraction (Eq. 81), to be written down similarly to Eq. (52b). A consistent assumed-distribution form can also be derived by introducing the integral (81) as a constraint for the maximum-entropy principle.

An obvious consequence of this formulation is that the evolution of the PDF (DDF) would be predicted differently by choosing the weights, {σ_l}, differently. However, this consequence should not be considered an inherent shortcoming of the present formulation. Rather, one should realize that this is the fundamental limitation of the assumed-PDF (DDF) approach: it cannot predict every statistic of a distribution accurately, as already emphasized. Simply, a different choice of the set, {σ_l}, predicts a different set of statistical outputs, {〈σ_l〉}, consistently. This point has been explicitly demonstrated in Sect. 5.5. Thus, our best advice is to choose {〈σ_l〉} to be those weights actually required by the host model so that they are actually predicted consistently under a given assumed-PDF form.

The present work is built upon the solid basis of two well-known mathematical and physical principles: (1) the maximum-entropy principle, which guides the determination of the most likely distribution of a problem, and (2) the Liouville equation, which predicts the time evolution of distributions. The stochastic-collection equation for the hydrometeor size distribution can also be treated in an analogous manner to the Liouville equation. However, adopting these two basic principles in practical atmospheric problems is not quite straightforward, and we face two major difficulties: first, application of the maximum-entropy principle to the atmospheric problems is not straightforward because it is often not obvious how to identify the physical constraints required for determining a distribution (cf. Yano et al., 2016). Second, though the Liouville equation permits us to perform a prediction of distributions in a formal manner, for both DDF and PDF, its direct use would entail enormous numerical cost. We have addressed these two difficulties by adopting a simple distribution form containing only a small number of parameters so that its evolution with time can be predicted only in terms of those parameters. In principle, the formulations presented in this study are applicable to any atmospheric model in a straightforward manner, albeit with required coding and testing, because the term, F, for the physical tendency in the Liouville Eq. (26) is left unspecified in presenting the general formulations. This straightforwardness includes no need to introduce any extra closure, say, based on a turbulence model, for example as is partially the case with CLUBB (Cloud Layers Modified By Binormals; Golaz et al., 2002; Larson and Golaz, 2005; Larson et al., 2019), so that higher-order moments can be expressed in terms of the moments considered under a given truncation of the system.

As a demonstrative example with a specified F, the paper has considered the condensational growth of cloud droplets. A rather unusual feature of this demonstration can be found in comparing its performance with an exact numerical result: the flexibility of the proposed formulation permits us to do this very easily. Additional mathematical demonstrative examples are found in Appendix C. Further examples with further elaborations of the methodology are also found in the study by Yano (2024). We also anticipate that fuller applications of the developed formulation are still to follow, especially because the only way to evaluate the accuracy of the method is to directly compare the results with more accurate sophisticated evaluations, as presented in Sects. 5.5 and 6 and Appendix C herein as well in Yano (2024). Yet, it is hoped that this simple example provides a concrete idea about how to use this general formulation and that readers can already apply the formulation to their own problems.

Two relatively distinct steps are involved in the present formulation: (1) determination of the PDF form based on the output-constrained distribution principle, as a re-interpretation of the maximum-entropy principle, and (2) prognostic equations for the PDF parameters derived from the Liouville equation. Thus, whenever new types of the output “constraints” are introduced into a problem, new types of general PDF forms must first be derived based on step 1. Next, new sets of prognostic equations must be derived based on step 2. Alternatively, two steps can be adopted separately. For example, the evolution of a PDF form defined under the output-constrained distribution principle can be evaluated by a more traditional assumed-PDF approach based on moments. Conversely, currently existing assumed-PDF schemes can be re-written based on step 2 but without changing the assumed-PDF forms.

The general formulation for the distribution problem presented here constitutes, first of all, a natural extension of the existing assumed-PDF (DDF) approaches for the subgrid-scale distributions as discussed in Sect. 5.3. The work further suggests that the same general formulation is also applicable to other distribution problems, including cloud microphysics and data assimilation. Extensive further general possibilities of the proposed formulation are yet to be fully explored. For example, constraints introduced by Eq. (12) have assumed a fixed integral range. On the other hand, for example, the cloud-fraction problem needs to take an integral with respect to the total water above the saturation value (cf. Eq. 81), which changes with time, as an output. It requires a further generalization of the formulation (e.g., with Eq. 47).

The overall accuracy of predicting the required outputs (“constraints”) by the proposed prognostic PDF formulation is emphasized, except for the case where the evolution of the assumed-PDF parameters presents singularities. Such undesirable behaviors stem from a highly truncated PDF form under the assumed-PDF formulation. When a multi-dimension system is considered as in Yano (2024), the evolution of the PDF parameters can even become chaotic with the given system behaving chaotically when the evolution of the distribution itself is statistically stable. We need to face this inherent limitation of the assumed-PDF approach with a limited number of PDF parameters.

Furthermore, there is a key issue left unaddressed: the performance of integrals denoted by 〈…〉 throughout the paper. In the present study, all the integrals of the problem have been performed analytically, apart from those including an unspecified physical-tendency term, F. Performing the latter integrals in general, especially with a complex physical-tendency term, is, however, not trivial. The most flexible approach currently available is Monte Carlo integration (e.g., Gentle, 2003; Larson and Schanen, 2013). However, this approach is numerically rather expensive and hardly considered an ultimate answer. A key to the success of the prognostic assumed-PDF formulation presented herein, especially our key result, Eq. (50a), is to perform those integrals in an efficient manner, albeit possibly with a numerical aide. The integral problems in general can be greatly facilitated by adopting Laplace's method in asymptotic expansion and more specifically by invoking Watson's lemma (cf. Chap. 6, Bender and Orszag, 1978), considering the fact that more or less all the types of distributions of interest here take the form of an exponential decay away from the maximum. In particular, all these integrals reduce to a form of an asymptotic expansion in terms of gamma functions if a Taylor expansion of a subdominant contribution is possible. The more strongly a distribution is peaked, the fewer terms required.

Another aspect that has not been explicitly taken into account is stochasticity; its potential importance in atmospheric modeling can hardly be overemphasized (cf. Berner et al., 2017). Formulations already exist for taking stochasticity into account as a generalization of the Liouville equation (cf. Risken, 1984).

Appendix A: Mathematical details of Sect. 4.4.2

We apply a Fourier integral

$$\begin{array}{}\text{(A1)}& p(x,t)=\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}\stackrel{\mathrm{̃}}{p}(k,t)e^{ikx}\mathrm{d}k\end{array}$$

to the diffusion problem (Eq. 29). The Fourier transform for (Eq. A1) is given by

$$\begin{array}{}\text{(A2)}& \stackrel{\mathrm{̃}}{p}(k,t)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}p(x,t)e^{-ikx}\mathrm{d}x.\end{array}$$

Thus, the initial condition is transformed into

$$\begin{array}{}\text{(A3)}& \stackrel{\mathrm{̃}}{p}(k,t=\mathrm{0})={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}(\mathrm{1}+\mathit{\alpha }x)e^{-\mathit{\lambda }{x}^{\mathrm{2}}-ikx}\mathrm{d}x.\end{array}$$

The transform of the first term is straightforward, and

$$\begin{array}{}\text{(A4)}& \begin{array}{rl}\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}{e}^{-\mathit{\lambda }{x}^{\mathrm{2}}-ikx}\mathrm{d}x& =e^{-k^{\mathrm{2}}/\mathrm{4}\mathit{\lambda }}\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}{e}^{-\mathit{\lambda }(x+ik/\mathrm{2}\mathit{\lambda }{)}^{\mathrm{2}}}\mathrm{d}x\\ & =\left({\displaystyle \frac{\mathit{\pi }}{\mathit{\lambda }}}\right)e^{-k^{\mathrm{2}}/\mathrm{4}\mathit{\lambda }}.\end{array}\end{array}$$

For performing the second term in the transform (Eq. A3), we note the following relation:

$$\begin{array}{}\text{(A5)}& \begin{array}{rl}x{e}^{-\mathit{\lambda }(x+ik/\mathrm{2}\mathit{\lambda }{)}^{\mathrm{2}}}=& -{\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\lambda }}}{\displaystyle \frac{\partial }{\partial x}}{e}^{-\mathit{\lambda }(x+ik/\mathrm{2}\mathit{\lambda }{)}^{\mathrm{2}}}\\ & +{\displaystyle \frac{ik}{\mathrm{4}{\mathit{\lambda }}^{\mathrm{2}}}}{e}^{-\mathit{\lambda }(x+ik/\mathrm{2}\mathit{\lambda }{)}^{\mathrm{2}}}.\end{array}\end{array}$$

Finally, in performing the inverse Fourier transform (Eq. A1), we re-factorize the exponent by noting

$$\begin{array}{}\text{(A6)}& \begin{array}{rl}{k}^{\mathrm{2}}& \left(t+{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\lambda }}}\right)-ikx=\\ & \left(t+{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\lambda }}}\right)\left[k-{\displaystyle \frac{ix}{\mathrm{2}}}{\left(t+{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\lambda }}}\right)}^{-\mathrm{1}}\right]\\ & +{\displaystyle \frac{x^{\mathrm{2}}}{\mathrm{4}}}{\left(t+{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\lambda }}}\right)}^{-\mathrm{1}}.\end{array}\end{array}$$

Appendix B: Exact solutions of the problem in Sect. 5.5

The problem of the system with F=ϕ^m in Sect. 5.5 can be solved analytically, and the evolution of the PDF can also be solved in a closed form by following the methodology of Sect. 6; the resulting solution of the PDF is

$$\begin{array}{}\text{(B1)}& p(\mathit{\varphi },t)=p\left({\mathit{\varphi }}_{\mathrm{0}}\right(\mathit{\varphi },t),t=\mathrm{0}){\displaystyle \frac{\mathrm{d}{\mathit{\varphi }}_{\mathrm{0}}}{\mathrm{d}\mathit{\varphi }}},\end{array}$$

where ${\mathit{\varphi }}_{\mathrm{0}}={\mathit{\varphi }}_{\mathrm{0}}(\mathit{\varphi },t)$ is an initial condition that leads to a state, ϕ, at time, t.

Once an explicit PDF form is given, numerical integrals further provide the required moments, 〈ϕⁿ〉. As a minor technicality, the actual integral is performed with respect to ϕ₀ after transforming ϕ into ϕ₀ because the distribution tends to stretch to larger values increasingly with time, and we need to increase the upper limit of the integral with respect to ϕ accordingly. The variable transformation allows us to stretch the integral range with respect to ϕ automatically by simply performing the integral over the same range with respect to ϕ₀. Once a moment, 〈ϕⁿ〉, for a given n is obtained, a consistent exponent, λ₁, can be evaluated by the formula

$$\begin{array}{}\text{(B1a)}& {\mathit{\lambda }}_{\mathrm{1}}={\left[{\displaystyle \frac{n\mathrm{!}}{\langle {\mathit{\varphi }}^n\rangle }}\right]}^{\mathrm{1}/n}\end{array}$$

by invoking the fact that the moments are given by

$$\begin{array}{}\text{(B1b)}& \langle {\mathit{\varphi }}^n\rangle ={\displaystyle \frac{n\mathrm{!}}{{\mathit{\lambda }}_{\mathrm{1}}^n}}\end{array}$$

under an assumption of the exponential distribution. The parameter, λ₁, estimated from Eq. (B1a) is added as green curves in Fig. 2.

The following subsections discuss the exact solutions for the specific choice of the power, m, that is required to accomplish those steps.

B1 When m=0

The system simply reduces to $\dot{\mathit{\varphi }}=\mathrm{1}$, which is solved as $\mathit{\varphi }={\mathit{\varphi }}_{\mathrm{0}}+t$. It follows that ${\mathit{\varphi }}_{\mathrm{0}}=\mathit{\varphi }-t$ and $\mathrm{d}{\mathit{\varphi }}_{\mathrm{0}}/\mathrm{d}\mathit{\varphi }=\mathrm{1}$. By substituting those relations into Eq. (B1), we find

$$\begin{array}{}\text{(B2)}& p(\mathit{\varphi },t)=\left\{\begin{array}{ll}{\mathit{\lambda }}_{\mathrm{1}}{e}^{-{\mathit{\lambda }}_{\mathrm{1}}(x-t)}& x\ge t,\\ \mathrm{0}& x<t.\end{array}\right.\end{array}$$

From this distribution, the moments can be readily evaluated analytically, and the first three moments are given by

$$\begin{array}{}\text{(B3a)}& {\displaystyle }\langle \mathit{\varphi }\rangle & {\displaystyle }={\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{1}}\left(\mathrm{0}\right)}}+t,\text{(B3b)}& {\displaystyle }\langle {\mathit{\varphi }}^{\mathrm{2}}\rangle & {\displaystyle }=\mathrm{2}\left({\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{1}}^{\mathrm{2}}\left(\mathrm{0}\right)}}+{\displaystyle \frac{t}{{\mathit{\lambda }}_{\mathrm{1}}\left(\mathrm{0}\right)}}+{\displaystyle \frac{t^{\mathrm{2}}}{\mathrm{2}}}\right),\text{(B3c)}& {\displaystyle }\langle {\mathit{\varphi }}^{\mathrm{3}}\rangle & {\displaystyle }=\mathrm{6}\left({\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{1}}^{\mathrm{3}}\left(\mathrm{0}\right)}}+{\displaystyle \frac{t}{{\mathit{\lambda }}_{\mathrm{1}}^{\mathrm{2}}\left(\mathrm{0}\right)}}+{\displaystyle \frac{t^{\mathrm{2}}}{\mathrm{3}{\mathit{\lambda }}_{\mathrm{1}}\left(\mathrm{0}\right)}}+{\displaystyle \frac{t^{\mathrm{3}}}{\mathrm{27}}}\right).\end{array}$$

The values of λ₁ obtained from the above results can directly be compared with those obtained by setting m=0 in Eqs. (59c) and (59d):

$$\begin{array}{}\text{(B4)}& {\mathit{\lambda }}_{\mathrm{1}}={\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{1}}\left(\mathrm{0}\right)}}+{\displaystyle \frac{t}{n}},\end{array}$$

with varying n. The assumed formulation can predict the consistent value of λ₁ with the constraint of σ₁=ϕⁿ up to O(t), in general, and the agreement is perfect especially with n=1.

B2 When m=1

In this case, we find

$$\begin{array}{}\text{(B5a)}& {\displaystyle }\mathit{\varphi }& {\displaystyle }={\mathit{\varphi }}_{\mathrm{0}}{e}^t,\text{(B5b)}& {\displaystyle }{\mathit{\varphi }}_{\mathrm{0}}& {\displaystyle }=\mathit{\varphi }{e}^{-t},\text{(B5c)}& {\displaystyle \frac{\mathrm{d}{\mathit{\varphi }}_{\mathrm{0}}}{\mathrm{d}\mathit{\varphi }}}& {\displaystyle }=e^{-t}.\end{array}$$

From these relations, we find that this system evolves exactly as prescribed by Eq. (59e), maintaining the exponential distribution.

B3 When m>1

In this case, the exact solution of the system is

$$\begin{array}{}\text{(B6)}& \mathit{\varphi }=[{\mathit{\varphi }}_{\mathrm{0}}^{-(m-\mathrm{1})}-(m-\mathrm{1})t{]}^{-\mathrm{1}/(m-\mathrm{1})},\end{array}$$

and it follows that

$$\begin{array}{}\text{(B7a)}& {\displaystyle }{\mathit{\varphi }}_{\mathrm{0}}& {\displaystyle }=[{\mathit{\varphi }}^{-(m-\mathrm{1})}+(m-\mathrm{1})t{]}^{-\mathrm{1}/(m-\mathrm{1})},\text{(B7b)}& {\displaystyle \frac{\mathrm{d}{\mathit{\varphi }}_{\mathrm{0}}}{\mathrm{d}\mathit{\varphi }}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{{\mathit{\varphi }}^m}}[{\mathit{\varphi }}^{-(m-\mathrm{1})}+(m-\mathrm{1})t{]}^{-m/(m-\mathrm{1})}.\end{array}$$

By substituting Eqs. (B7a) and (B7b) into Eq. (B1), an explicit form of the PDF evolution is obtained.

Note that the solution (Eq. B6) becomes singular at $t={\mathit{\varphi }}^{-(m-\mathrm{1})}/(m-\mathrm{1})$ with the tendency of $\mathit{\varphi }\to +\mathrm{\infty }$. Due to this tendency, the distribution increasingly presents a longer tail with time with an increasingly significant deviation from an exponential distribution. This tendency is also aggravated with the increasing n; thus the estimate of λ₁ based on the constraint, σ₁=ϕⁿ, also deteriorates faster with time with increasing n (cf. Eqs. 59c and 59d), as seen in Fig. 2.

Appendix C: Further demonstrative examples

This appendix further compares between the exact and assumed-PDF solutions by taking three simple dynamical systems, and their basic behaviors can be inferred from the forcing forms. These comparisons follow on from a demonstration of the assumed-PDF approach taking a simple physical system in Sect. 6 and further expose basic characteristics of the assumed-PDF solutions.

As simple dynamical systems, we consider the following three forms of forcing:

• (i)

  $F=-\mathit{\varphi }$: the only stable fixed point of this system is ϕ=0, and the system approaches this fixed point regardless of the initial condition, ϕ₀, with $\mathit{\varphi }={\mathit{\varphi }}_{\mathrm{0}}{e}^{-t}$.

• (ii)

  $F=\mathit{\varphi }(\mathit{\varphi }-\mathrm{1})$: the system consists of a stable fixed point at ϕ=0 and an unstable fixed point at ϕ=1. Every initial point below ϕ=1 exponentially approaches ϕ=0, and every initial point above ϕ=1 exponentially approaches infinity with time. An explicit solution is

  $$\begin{array}{}\text{(C1)}& \mathit{\varphi }={\displaystyle \frac{{\mathit{\varphi }}_{\mathrm{0}}}{{\mathit{\varphi }}_{\mathrm{0}}-({\mathit{\varphi }}_{\mathrm{0}}-\mathrm{1})e^t}},\end{array}$$

  with ϕ₀ being the initial condition.

• (iii)

  $F=-\mathit{\varphi }(\mathit{\varphi }-\mathrm{1})(\mathit{\varphi }-\mathrm{2})$: the system consists of two stable fixed points at ϕ=0 and 2 and an unstable fixed point at ϕ=1. Every initial point below and above ϕ=1 exponentially approaches ϕ=0 and 2, respectively. An explicit solution is

  $$\begin{array}{}\text{(C2a)}& \mathit{\varphi }=\mathrm{1}\pm (\mathrm{1}-A{e}^{-\mathrm{2}t}{)}^{-\mathrm{1}/\mathrm{2}},\end{array}$$

  where

  $$\begin{array}{}\text{(C2b)}& A={\displaystyle \frac{{\mathit{\varphi }}_{\mathrm{0}}({\mathit{\varphi }}_{\mathrm{0}}-\mathrm{2})}{({\mathit{\varphi }}_{\mathrm{0}}-\mathrm{1}{)}^{\mathrm{2}}}}\end{array}$$

  and the sign in the solution is chosen by the sign of ϕ₀−1.

We examine the evolution of these systems by initializing the distribution as Gaussian of the form (Eq. 25) with $\langle \mathit{\varphi }\rangle {\mathrm{|}}_{t=\mathrm{0}}=\mathrm{1}$ and ${\mathit{\lambda }}_{\mathrm{1}}{\mathrm{|}}_{t=\mathrm{0}}=\mathrm{10}$. Here, the initial peak of the distribution is taken to be sharp enough so that we can focus on the evolution of the system initialized in the vicinity of x=1. The assumed peak point is not a stable fixed point with any of those systems, and it is more precisely an unstable fixed point with the latter two systems. Thus, the evolution is expected to be away from the given initial peak in all these three cases.

The exact evolutions of those three systems with this initial distribution can be derived using the following relations:

$$\begin{array}{}\text{(C3)}& {\displaystyle }\text{(i)}{\displaystyle }{\displaystyle }{\mathit{\varphi }}_{\mathrm{0}}=\mathit{\varphi }{e}^t,\mathrm{d}{\mathit{\varphi }}_{\mathrm{0}}/\mathrm{d}\mathit{\varphi }=e^t.\end{array}$$

$$\begin{array}{}\text{(C4a)}& {\displaystyle }\text{(ii)}& {\displaystyle }& {\displaystyle }{\mathit{\varphi }}_{\mathrm{0}}& {\displaystyle }={\displaystyle \frac{\mathit{\varphi }}{\mathit{\varphi }-(\mathit{\varphi }-\mathrm{1})e^{-t}}},\text{(C4b)}& {\displaystyle }& {\displaystyle }& {\displaystyle \frac{\mathrm{d}{\mathit{\varphi }}_{\mathrm{0}}}{\mathrm{d}\mathit{\varphi }}}& {\displaystyle }={\displaystyle \frac{e^{-t}}{(\mathit{\varphi }-(\mathit{\varphi }-\mathrm{1})e^{-t}{)}^{\mathrm{2}}}}.\end{array}$$

$$\begin{array}{}\text{(C5a)}& {\displaystyle }\text{(iii)}& {\displaystyle }& {\displaystyle }{\mathit{\varphi }}_{\mathrm{0}}& {\displaystyle }=\mathrm{1}\pm (\mathrm{1}-B{e}^{\mathrm{2}t}{)}^{-\mathrm{1}/\mathrm{2}},\text{(C5b)}& {\displaystyle }& {\displaystyle }& {\displaystyle \frac{\mathrm{d}{\mathit{\varphi }}_{\mathrm{0}}}{\mathrm{d}\mathit{\varphi }}}& {\displaystyle }=\mathrm{1}\pm (\mathrm{1}-B{e}^{\mathrm{2}t}{)}^{-\mathrm{3}/\mathrm{2}}{e}^{\mathrm{2}t},\end{array}$$

with

C5c$$\begin{array}{}\text{(C5c)}& {\displaystyle }& {\displaystyle }& {\displaystyle }B={\displaystyle \frac{\mathit{\varphi }(\mathit{\varphi }-\mathrm{2})}{(\mathit{\varphi }-\mathrm{1}{)}^{\mathrm{2}}}}.\end{array}$$

The exact evolutions of the distributions are obtained by substituting these relations into Eq. (B1).

Evolution of a distribution under the assumed PDF (i.e., Gaussian) is evaluated in terms of the evolutions of the two PDF parameters, 〈ϕ〉 and λ₁, as given by Eqs. (66a) and (66b). For this purpose, the following relations for the three systems are invoked:

$$\begin{array}{}\text{(C6a)}& {\displaystyle }\text{(i)}& {\displaystyle }& {\displaystyle }\langle F\rangle & {\displaystyle }=-\langle \mathit{\varphi }\rangle ,\text{(C6b)}& {\displaystyle }& {\displaystyle }& {\displaystyle }\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle )F\rangle & {\displaystyle }=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\lambda }}}.\end{array}$$

$$\begin{array}{}\text{(C7a)}& {\displaystyle }\text{(ii)}& {\displaystyle }& {\displaystyle }\langle F\rangle & {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\lambda }}}+F(\langle \mathit{\varphi }\rangle ),\text{(C7b)}& {\displaystyle }& {\displaystyle }& {\displaystyle }\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle )F\rangle & {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\lambda }}}(\mathrm{3}\langle \mathit{\varphi }\rangle -\mathrm{1}).\end{array}$$

$$\begin{array}{}\text{(C8a)}& {\displaystyle }\text{(iii)}& {\displaystyle }& {\displaystyle }\langle F\rangle & {\displaystyle }=-{\displaystyle \frac{\mathrm{3}}{\mathrm{2}\mathit{\lambda }}}(\langle \mathit{\varphi }\rangle -\mathrm{1})+F(\langle \mathit{\varphi }\rangle ),\text{(C8b)}& {\displaystyle }& {\displaystyle }& {\displaystyle }\langle (\mathit{\varphi }-\langle \mathit{\varphi }\rangle )F\rangle & {\displaystyle }=-\left[{\displaystyle \frac{\mathrm{3}}{\mathrm{2}{\mathit{\lambda }}^{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{1}}{\mathit{\lambda }}}(\mathrm{3}\langle \mathit{\varphi }{\rangle }^{\mathrm{2}}-{\displaystyle \frac{\mathrm{9}}{\mathrm{2}}}\langle \mathit{\varphi }\rangle +\mathrm{1})\right].\end{array}$$

Figures C1–C3 show the obtained evolutions of the distributions for those three systems, respectively. In each figure, the upper and lower frames, (a) and (b), respectively, show the results for the exact computations and with the assumed PDFs (Gaussian). Here, the intervals for the plots are set as Δt=0.6, 0.2, and 0.3 for those three cases, respectively. Different intervals are chosen for the ease of following the sequence of the evolution of the distributions for all three cases visually.

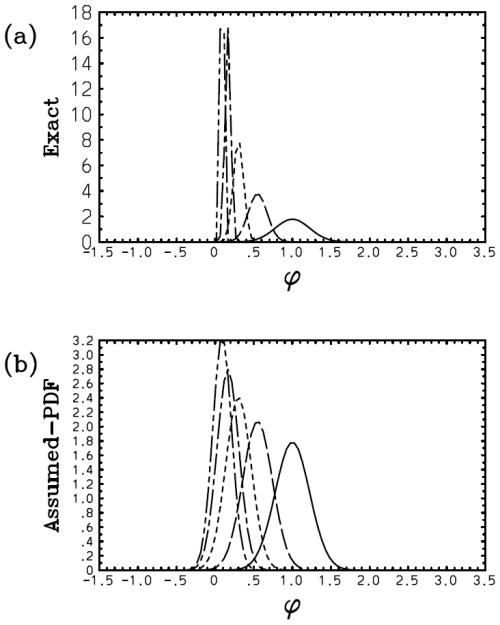
Figure C1 Evolution of the distribution for model i with the interval of Δt=0.6, with the initial distribution given by the solid line for (a) the exact solution and (b) the assumed Gaussian distribution, shown with the varying types of curves. In both cases, the distribution peak moves towards smaller values with time.

With the first dynamical system (i), the distribution peak moves towards ϕ=0, a stable fixed point of the system, with both exact and assumed-PDF-based calculations, as seen in Fig. C1. The exact evolution (Fig. C1a) presents a strong tendency towards the sharpening of the peak as well. This sharpening tendency is substantially weaker with the assumed-PDF calculation (Fig. C1b).

With the second system (ii), the distribution tends to spread with time in both directions, towards the two stable fixed points at ϕ=0 and $\mathit{\varphi }\to +\mathrm{\infty }$. Both calculations present an expected spreading tendency of the distribution with time but in different manners. The exact calculation (Fig. C2a) shows that the distribution peak moves to a smaller ϕ with time but, at the same time, with a tendency for a long tail to stretch towards a larger ϕ. However, the calculation with the assumed Gaussian distribution cannot reproduce the tendency of the distribution to be skewed with time by design. The assumed-PDF calculation (Fig. C2b), instead, shows that the distribution spreads by moving the peak towards a larger ϕ with time. The tendency of spread is less dramatic, too.

Figure C2 The same as Fig. C1 but for model ii with the interval of Δt=0.2. The peak moves towards smaller and larger values with the exact and assumed distributions with this model, respectively.

With the third dynamical system (iii), the system initialized in the vicinity of the unstable fixed point, ϕ=1, tends to evolve towards either of the two stable fixed points at ϕ=0 and 2. As a result, as the exact calculation shows (Fig. C3a), an initial distribution that peaked at ϕ=1 splits into the two peaks centered close to those two stable fixed points with time. Of course, it is not possible to reproduce such a tendency by assuming a Gaussian distribution as an assumed form. Thus, under the assumed-PDF calculation (Fig. C3b), we only see a tendency for the distribution to gradually spread with time. One may also get an impression that the rate of spread of the distribution is not sufficient enough to reproduce a drastic tendency towards the two peaks in exact calculation.

Figure C3 The same as Fig. C1 but for model iii with the interval of Δt=0.4. The distribution peak monotonously decreases with time in both cases.

From the overview so far, it is clear that the assumed-PDF approach can reproduce the actual evolution of the distribution in a manner that is less satisfactory even qualitatively. However, as emphasized in the main text, the purpose of the assumed PDF is not to predict the evolution of the whole distribution. Its purpose is solely limited to reproducing limited statistics that are specified under the output-constrained distribution principle. More specifically, under the given specific assumed-PDF formulation with the Gaussian, the sole goal is to predict the mean and the variance consistently. Thus, the main question to be addressed is how those statistics have been predicted.

To address this question, Fig. C4a and b plot the time series of the mean and the standard deviation, respectively, with the assumed-PDF (black) and exact (green) calculations. The curves for models i, ii, and iii are shown by the solid, long-dash, and short-dash curves, respectively. Here, the assumed PDF predicts the means of models i and iii perfectly. The predictions of the standard deviations of these two models are overall consistent with the exact results, although the predicted tendencies are less pronounced than the exact results, especially with model i. On the other hand, the agreement of the evolution of the standard deviation with model iii (short dash) is still rather remarkable, considering the fact that the assumed PDF does not reproduce an overall evolution of the distribution even qualitatively. This provides another example, in addition to the case of Sect. 4.4.1, demonstrating that it is not indispensable to fit the distribution quantitatively well to obtain a realistic prediction of a required statistics.

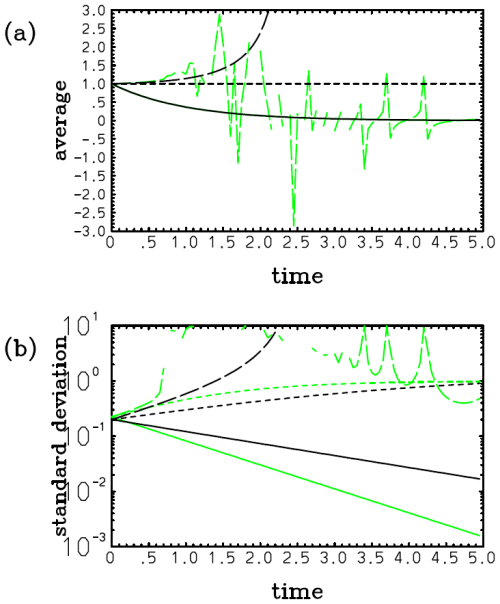
Figure C4 Statistics of the dynamical systems under consideration: the (a) average and (b) standard deviation for models i (solid), ii (long dash), and iii (short dash). Black curves are the results with the assumed PDF, and green ones are the results from direct integrals of the exact solutions. Here, the results of the means for models i and iii with the assumed PDF agree perfectly with the exact results.

In the case with model ii, the calculations with the exact distribution have their own problem: the numerical integral of the distribution is extremely sensitive to the integral range and the total number of points used. In Fig. C4, the integral is performed over the range of −49 to 51 with 10⁴ points with respect to ϕ₀. Examination of those sensitivities shows that the overall behavior of the curve (long-dash line in green) is still correct, although the random-looking oscillatory behavior sensitively changes with the integral range and the number of points adopted. This inherent difficulty fundamentally stems from the fact that the distribution increasingly presents a long tail towards the positive direction with time, as seen in Fig. C2a. This tendency is reflected by the singularities in Eqs. (C4a) and (C4b) that lead to a more direct difficulty in the integrals.

Comparing the curves (long-dash line) for the model ii with the exact (green) and assumed-PDF (black) calculations, we conclude that the assumed-PDF approach can predict the tendencies of the statistics (mean and variance) only up to t≃0.5, but beyond that point, the actual evolution begins to dramatically deviate from the monotonously increasing tendencies predicted by the assumed-PDF method. The former shows that, due to the shift of the peak towards the smaller values with time, both the average and the standard deviation begin to decrease after t≃0.5. This later transition simply fails to be captured by the assumed-PDF solution. Here, the singularities in Eqs. (C4a) and (C4b) lead to a divergence of both the mean and the standard deviations in finite time.