the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The role of interfacial tension in the size-dependent phase separation of atmospheric aerosol particles
Ryan Schmedding
Atmospheric aerosol particles span orders of magnitude in size. In ultrafine particles, the energetic contributions of surfaces and interfaces to the Gibbs energy become significant and increase in importance as particle diameter decreases. For these particles, the thermodynamic equilibrium state depends on size, composition, and temperature. Various aerosol systems have been observed to undergo liquid–liquid phase separation (LLPS), impacting equilibrium gas–particle partitioning, modifying physicochemical properties of the particle phases, and influencing cloud droplet activation. Numerous laboratory experiments have characterized the onset relative humidity of LLPS in larger aerosol particles and macroscopic bulk systems. However, in sufficiently small particles, the interfacial tension between two liquid phases constitutes an energetic barrier that may prevent the formation of an additional liquid phase. Determining said small-size limit is a key question.
We introduce a predictive droplet model based on the Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients (AIOMFAC) model. This model enables size-dependent computations of surface and interfacial tension effects on bulk–surface partitioning within phase-separated and single-phase particles. We evaluate four approaches for computing interfacial tension in multicomponent droplets, including a new method introduced in this work. Of the approaches tested, Antonov's rule best matches observed liquid–liquid interfacial tensions in highly immiscible mixtures, while a modified Butler equation fits well in more miscible systems. We find that two approaches substantially lower the onset relative humidity of LLPS for the studied systems.
- Article
(4192 KB) - Full-text XML
-
Supplement
(635 KB) - BibTeX
- EndNote
Atmospheric aerosols and their interactions with clouds and radiation are a major source of uncertainty in global climate models (IPCC, 2014). The condensed particle phase component of an aerosol, henceforth referred to as aerosol particles or “aerosols”, varies in composition regionally and with time (Jimenez et al., 2009). Organic compounds contribute a substantial mass fraction to the total condensed material within ambient aerosols. Organic-rich particles can be emitted directly (primary organic aerosols) or formed from gas-phase reactions involving volatile organic compounds (VOCs). Aerosols which contain substantial amounts of secondary organic compounds are often referred to as secondary organic aerosols (SOAs). For complete lists of abbreviations, symbols, and their meanings, please refer to Tables S1 and S2 in the Supplement. SOA mixed with inorganic species such as dissolved aqueous electrolytes form the majority of fine-mode aerosols in many regions of the world (Zhang et al., 2007). Therefore, understanding the properties of aerosol particles is important for better constraints on global air quality and climate models and related future climate projections.
The effects of a population of aerosol particles on weather and climate depend on the collective properties of the particles. Two properties which have been the focus of numerous studies are the number of condensed phases present in an aerosol particle and the morphology of the particle, i.e., whether said particle is of spherical or nonspherical shape or consists of a combination of smaller three-dimensional structures (Kucinski et al., 2019; Ohno et al., 2023). Liquid–liquid phase separation (LLPS) has been observed in numerous laboratory-generated and atmospheric aerosols, with many particles of varying compositions splitting into two distinct phases in contact with one another (Marcolli and Krieger, 2006; You et al., 2012; Ciobanu et al., 2009; Bertram et al., 2011; Freedman, 2017). More recently, the presence of three liquid phases within single aerosol particles has been observed in laboratory mimics of urban aerosols (Huang et al., 2021; Kucinski et al., 2019). The unique composition of each liquid phase present in a particle determines a range of the physicochemical properties of those phases and/or a particle overall. These properties include the hygroscopicity and related equilibrium water content, surface tension, viscosity, acidity, and ionic strength, all of which may vary as a function of environmental (thermodynamic) conditions and phase-specific composition (Lilek and Zuend, 2022; Gervasi et al., 2020; Schmedding and Zuend, 2023; Kleinheins et al., 2023). Organic-rich phases may exhibit atmospherically relevant physical properties similar to that of an aqueous electrolyte-containing phase or properties which are quite different from those of the aqueous ion-rich phase (Li et al., 2021; Chan et al., 2006). These properties may affect the growth and aging of aerosol particles by limiting the reactive uptake of species such as isoprene-derived epoxydiols or N2O5 (Gaston et al., 2014; Schmedding et al., 2020). Aerosol–cloud interactions can also be affected by the presence of liquid–liquid phase separation in aerosol particles, especially so if LLPS persists to high relative humidity (RH) values (Ovadnevaite et al., 2017; Malek et al., 2023). The reduction in droplet surface tension typically caused by an enrichment of organics at the gas–particle surface and the coupled simultaneous modification to the bulk-phase composition due to bulk–surface partitioning have competing effects on the water vapor saturation ratio and minimum dry particle size necessary for cloud droplet activation. This can ultimately lead to a substantial shift in the critical saturation ratio and diameter necessary for the activation of aerosol particles into cloud droplets (Ruehl et al., 2016; Ovadnevaite et al., 2017; Davies et al., 2019; Schmedding and Zuend, 2023).
Beyond changes to the physicochemical properties of aerosol particles stemming from the formation of distinct condensed phases within a particle, the three-dimensional (3-D) morphology of a particle may be modified. Homogeneously mixed particles assume a spherical shape under equilibrium conditions due to the impact of surface tension. In the case of a phase-separated particle, deviations from sphericity are possible (Kwamena et al., 2010; Gorkowski et al., 2020). Some LLPS particles still form an overall spherical structure with an organic-rich shell (phase β) covering an inorganic-rich core (phase α). Other, more complex, structures are possible, such as a partially engulfed morphology, wherein the particle is no longer radially symmetric or perfectly spherical. In a partially engulfed particle, phase β does not spread completely over phase α and leaves a portion of phase α exposed (Kwamena et al., 2010; Reid et al., 2011; Ciobanu et al., 2009; Song et al., 2012, 2013; Shiraiwa et al., 2013). Such particle geometries interact with radiation differently than their core–shell counterparts (Lang-Yona et al., 2010). It has also been observed that LLPS particles composed of 3-methylglutaric acid and ammonium sulfate, which have a core–shell morphology at higher RH, form partially engulfed particles at lower RH (Lam et al., 2021). Should additional condensed phases be present beyond the simplest two-phase case, various combinations of spherical shells and partially engulfing phases are possible (Huang et al., 2021), leading to geometric structures which may be highly complex. Under equilibrium conditions, the sequence of these phases in terms of the innermost to outermost phase of the particle is determined by the configuration which minimizes the overall Gibbs energy of the particle. Usually, this results in arrangements that favor placing the phases with higher hypothetical gas–liquid surface tensions closer to the center of the particle, while those with lower surface tensions are closer to or at the gas–particle boundary.
Analogous to the surface between a gas phase and a condensed phase, the interface between two condensed phases, particularly two liquid phases, might experience a similar phenomenon with respect to the enrichment and depletion of different compounds (Hua et al., 2016). Note that hereafter in this article “surface” refers to a gas–liquid phase boundary and that “interface” refers to the boundary between two condensed (liquid) phases. There have been several attempts to quantify the relative contribution of the liquid–liquid (LL) interface between two condensed phases to the overall energy of a particle and whether bulk-phase depletion plays a role at the LL interface. Until recently, it has been assumed that the energetic contributions from LL interfacial tension in typical aerosol particles are negligible for particles with diameters larger than approximately 100 nm for which the Kelvin effect is also relatively minor (Russell and Ming, 2002; Zuend et al., 2010). Despite this, recent studies have found that the contribution of a LL interface to the Gibbs energy of a particle may have a small but not insignificant effect on the RH at which the particle will undergo LLPS upon dehydration (Ohno et al., 2023).
In order to better understand the role of interfacial tension and its interaction with phase separation and particle morphologies, predictive models of interfacial tension and associated phase composition changes are necessary. Different approaches have been considered for the prediction of liquid–liquid interfacial tension; a brief overview is presented in the following, with additional theory and methods discussed in Sect. 2.
The simplest approximation for the interfacial tension between two phases α and β, σαβ, is by taking the absolute difference of the hypothetical gas–liquid surface tensions of the two phases (σα and σβ) when each is considered in isolation,
Equation (1) is known as Antonov's rule (Antonov, 1907). While Eq. (1) may be a good first-order approximation of the interfacial tension for some systems, it is an empirical estimation method and not thermodynamically rigorous (Makkonen and Kurkela, 2018; Winter, 1995). A distinct approach for determining the interfacial tension between two liquid phases was proposed by Girifalco and Good (1957):
where ϕ is a system-dependent interaction/correction parameter. It has been shown that ϕ may be constrained by the following inequality:
The value of ϕ can be defined in the case of binary systems with molecules 1 and 2 of approximately equal size and spherical shape in a hexagonal arrangement as
where d is the equilibrium distance between the two molecules denoted in the subscript (Girifalco and Good, 1957). In the case of binary systems with molecules of unequal sizes or shapes, the value of ϕ could be approximated by the following equation:
where V is the molar volume of molecule 1 or 2, respectively (Girifalco and Good, 1957). Qualitatively, ϕ is described as being lower in systems where the primary molecular interactions are different, e.g., dispersion forces in phase β and hydrogen bonding in phase α (Girifalco and Good, 1957).
Note that in the case of a single well-mixed phase, where σαβ=0, ϕ=1 . In the limiting case where , Eq. (2) reduces to Eq. (1). However, the utility of this equation for systems with more than two components or with compounds that are soluble in both phases remains an open question (Makkonen and Kurkela, 2018). Equation (2) was further refined to
where σα,disp and σβ,disp are the contributions from dispersion forces to the surface tensions of phases α and β, respectively (Fowkes, 1962, 1963). Of course, such a model relies on accurate constraints on the dispersive and nondispersive contributions to the surface energies per unit area of both phases, thus limiting the utility of this approach.
As mentioned above, some atmospheric aerosol systems have been observed to undergo LLPS for particles with large diameters, yet particles of the same or similar composition may not undergo LLPS should their diameters be substantially smaller (Kucinski et al., 2019; Freedman, 2020; Ott and Freedman, 2020; Ohno et al., 2023). Indeed, it is thought that at sufficiently small diameters, the high surface-area-to-volume ratios of atmospheric aerosol particles lead to a sufficient energetic barrier from the combined effects of surface and interfacial tensions such that the formation of an additional phase is inhibited (Ohno et al., 2023; Freedman, 2020). It should be noted that the effect of aerosol composition, particularly the presence of different inorganic electrolytes, complicates size-dependent LLPS; for example, Ott and Freedman (2021) report that particles containing sodium cations are phase-separated down to smaller sizes than similar particles which contain ammonium cations.
In summary, at the boundary between two distinct phases there exists an energetic penalty. In the case of a gas–liquid boundary, this penalty is often referred to as the surface tension. A similar tension exists at the boundary between two liquid phases. If the gas–liquid interface can be thought of as a finite-depth region, with a distinct composition from the adjacent liquid phase beneath it, then there must exist an interfacial tension at this boundary as well. The sum of this interfacial tension and the surface tension at the gas–liquid boundary form the measurable surface tension that can be observed directly. Numerous methods have been proposed to determine the interfacial tension between two liquid phases using thermodynamic theory, semiempirical approaches, and system-specific fits. The sum of the three energetic interfacial contributions leads to differences in the total Gibbs energy for a well-mixed or phase-separated particle. Greater differences in Gibbs energy occur in particles with higher surface/interfacial-area-to-volume ratios. Such differences in Gibbs energy may be sufficiently large that they lead to reductions in the onset RH of LLPS or even the complete suppression of LLPS. To our knowledge, no predictive model exists that accounts for the coupled feedbacks of aerosol particle size and three-dimensional morphology on the conditions under which a particle will separate into two (or more) liquid phases or remain homogeneously mixed. As such, we present a thermodynamic framework for exploring and quantifying size-dependent LLPS in aerosol particles.
2.1 Modeling interfacial tension between two liquid phases
In the case of a closed thermodynamic system with two or more liquid phases, the Gibbs energy at constant temperature and pressure can be expressed as follows:
Here, and are the chemical potential and molar amount of species j in phase ϕ. σι is the surface or interfacial tension at phase boundary ι, and Aι is the area of phase boundary ι. τ represents the energetic contribution of a three-phase boundary line, sometimes referred to as the line tension, and l is the length of the three-phase boundary line. Note that a three-phase boundary line will only exist in a particle with a partially engulfed morphology or when particles are deposited on a substrate for analysis in laboratory experiments. Furthermore, given that measured and predicted line energy contributions in complex systems are thought to be orders of magnitude lower than those from LL interface contributions, energetic contributions from the τl term are usually assumed to be negligible (Amirfazli and Neumann, 2004).
Schmedding and Zuend (2023) developed an approach for predicting the equilibrium surface tension of a single-liquid-phase droplet with a finite-depth Guggenheim interface of radial thickness δs. Guggenheim interfaces are an alternative approach to the classical Gibbsian treatment of interfaces, the latter treating them as infinitely thin two-dimensional surfaces located at the point where the excess concentration of some species in the system, typically the solvent, is zero (Gibbs, 1906). Guggenheim interfaces instead treat the surface of a solution as a thermodynamically distinct region from the bulk liquid phase beneath it and the gas phase above it (Guggenheim, 1940). Such a definition allows for more flexibility in defining the location of the interface and its extent and composition, as well as accounting for the feedback of bulk–surface partitioning on the bulk composition in small droplets. Their approach employed the Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients (AIOMFAC) model (Zuend et al., 2008, 2011; Yin et al., 2022) to calculate activity coefficients in the surface and bulk phases of an aerosol particle for application in the Butler equation:
Here, σi is the surface tension of the droplet as predicted by the right-hand-side expression based on component i, is the surface tension of i in the pure-component case at the same pressure and temperature, R is the universal gas constant, T is the temperature, and 𝒜i is the partial molar area of i which depends on the surface phase geometry.
is the mole-fraction-based activity of i in the surface phase, and is the mole-fraction-based (or molality-based, in the case of inorganic electrolytes) activity of i in the liquid bulk phase. can be calculated as the product of the concentration of species i, either in mole fraction or molality as previously mentioned, and the activity coefficient, γi, at a given temperature on the associated composition scale. For a surface phase represented by a concentric shell on a spherical droplet core, 𝒜i is defined as
where A is the outer surface phase area, and denotes the molar amount and molar volume of i, respectively, in the finite-depth surface phase. rp is the particle radius, i.e., the outer radius of the surface phase, and δs is the radial thickness of the surface. For a derivation of Eq. (9), see Schmedding and Zuend (2023).
Under equilibrium conditions, the surface tensions computed via Eq. (8) for all k components in solution must be equal, such that
While the structure of a gas–liquid interface may be best represented by a thin yet finite depth surface phase to account for bulk–surface partitioning, the structure of a LL interface may be more easily represented by a two-dimensional (2-D) dividing surface. The latter is the case since the absolute material and density gradients across LL interfaces are much smaller than across a gas–liquid surface. Therefore, unlike the approach to bulk–surface partitioning described in Schmedding and Zuend (2023), there is no depletion from phase α or phase β to the LL interface between them as the tightly coupled partitioning between phases α and β accounts for the depletion of either phase with respect to the LL interface. Note, however, that modifications to the equilibrium partitioning of components between the two liquid phases due to the presence of the interface can be accounted for. This 2-D LL interface treatment has the added benefit of simplifying the approach used to determine the interfacial tension as the interplay between partitioning and nonideal mixing may be greatly simplified in the liquid–liquid interface.
Returning to the approach of Schmedding and Zuend (2023), which utilized Eq. (8) to predict surface tension, we now extend the same approach to account for the boundary between two liquid phases. For a LL interface, Eq. (8) must be modified, since the reference state surface tension values () are inherently different from those found at the gas–liquid surface. At a gas–liquid boundary, is assumed to be the surface tension of a droplet of pure component i. Analogously, for LL interfaces, is assumed to be the interfacial tension that exists between two molecular layers of pure component i. Because the compositions of the two layers of i are identical in the LL reference state case – a hypothetical interface – any molecule present at this reference LL interface would not experience an additional energetic penalty. Therefore, in the case of a LL interface,
Consequently, in the case of a LL interface, Eq. (8) simplifies to (Bahramian and Danesh, 2005, 2004)
Note that for a 2-D LL interface . Analogous to Eq. (9), the interfacial tension values determined via Eq. (11) for individual components must match at equilibrium, i.e.,
An approach developed by Bahramian and Danesh (2004) utilized lattice theory and suggested that the activity coefficients present in a LL interface (γαβ) can be approximated by the geometric mean of the activity coefficients in the liquid phases α and β on either side of the interface:
However, they note that the choice of for the exponent in this case is determined by the configuration of molecules present in the interfacial region. This approach was also later expanded by Wang and Anderko (2013) to account for the effect of electrolyte species in mixed organic–inorganic systems with good agreement to experimental data. Therefore, in this study, the geometric mean approach for activity coefficients was chosen as one option for multicomponent aerosol systems containing mixtures of water, organic species, and electrolytes.
If the assumption of Eq. (13) is used and recalling that under equilibrium conditions and , Eq. (11) can be rearranged to the following form (Bahramian and Danesh, 2004, 2005):
This leads to a single unknown variable, σαβ, which must be the same for all species such that the criteria given by Eq. (12) are satisfied. Thus, the interfacial tension value can be numerically solved in a direct manner rather than relying on a more complex bulk–interface partitioning algorithm (unlike the case for bulk–surface partitioning). It should be noted that the behavior of electrolyte species in solution may require more complex treatments of their impacts on interfacial tension (Wang and Anderko, 2013). However, many of these treatments rely on semiempirical relationships fitted to experimental data, thus reducing their predictive power and flexibility. As such, in this approach we assume that electrolyte components (here as neutral cation–anion combinations) can be treated in the same manner as water and the organic components.
2.2 Alternative models of interfacial tension
In order to determine the importance of a rigorous treatment of interfacial energetic contributions in aerosol particles and the resulting geometric morphologies, we introduce the following approaches, allowing for a quantitative comparison (see Sect. 3). A first option is a model which allows for LLPS and bulk–surface partitioning but assumes that the LL interface is a 2-D dividing surface with an energetic contribution of 0 (labeled as the “no IFE” approach).
A more thorough treatment includes assuming a 2-D LL interface with the interfacial tension value estimated by the difference in (hypothetical) gas–liquid surface tensions of the organic phase and the aqueous phase (Eq. 1) (Antonov's rule). One caveat of this treatment is that it renders determining whether a particle is of core–shell or partially engulfed morphology impossible. This is because of a known inconsistency of Antonov's rule with the constraints imposed by the triangle inequality necessary for calculating the contact angles among the phases (Binyaminov et al., 2021). As a similar option, Eq. (2) can be employed as a semiempirical representation of the LL interfacial tension. This Girifalco–Good equation can be tuned with a single, system-specific parameter ϕ to improve agreement with pertinent experimental data.
Antonov (1907)Girifalco and Good (1957)Bahramian and Danesh (2005)Table 1Summary of interfacial tension treatments used for the interfaces between phases α and β as well as between the surface phase and the liquid bulk phase just beneath it.

A final semiempirical approach for the LL interfacial tension is based on a modified version of the approach of Bahramian (2024), who stated that . In this case, we treat the composition of the interfacial layer as the weighted average of the compositions of a monolayer of phase α and β on either side of the 2-D dividing plane such that
Here, vi is the effective volume fraction of i in phase α, phase β, or the two (mono)layers of α and β immediately adjacent to the interfacial dividing plane (the hypothetical interfacial bilayer). η is defined as the value that satisfies the criteria that and η>0 in order to satisfy the criteria of Bahramian (2024). A reference energetic contribution value for this bilayer system can be estimated by
Given , the energetic contributions from either phase at the liquid–liquid interface may be estimated by applying Antonov's rule separately to each monolayer adjacent to the interface, such that
Note that the superscript vf refers to the volume-fraction-weighted mean of pure-component values. The sum of these two energetic contributions yields the effective interfacial tension at the liquid–liquid interface:
It is important to note that an interface also exists between the exterior surface phase (which we treat as a 3-D Guggenheim interfacial phase) and the interior bulk of a particle (see Fig. 1 for details). This interface, henceforth referred to as the bulk–surface interface, can be treated in much the same way as the liquid–liquid interface between phases α and β using any of the approaches outlined in Table 1. This “ls” interface contributes an additional energetic term, which scales with σls, to the overall Gibbs energy of the particle in addition to the interfacial tension contribution that scales with σαβ . While the energetic contribution from this boundary is likely small, it cannot be neglected categorically, since differences in composition between the surface phase and the adjacent bulk phase may become significant, especially at higher RH at which the particle is well-mixed or when phases α and β are similar in composition. At intermediate and lower relative humidities in the presence of LLPS, the compositions of phases α and β tend to be more distinct from each other. Under those conditions, it is likely that the α–β LL interface plays a larger role than the bulk–surface interface (see Fig. 3). The area of the bulk–surface interface can be calculated as follows:
The value of σls can be calculated using the same approaches as for σαβ. For consistency, we always apply the same method to both interfaces for a given case. Refer to Table 1 for a summary of the various interfacial tension approaches applied in this work.
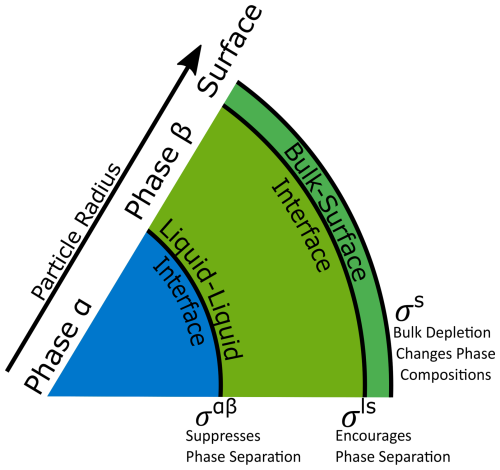
Figure 1Schematic of phase and interface configurations considered in this study. In a liquid–liquid phase-separated aerosol particle with two liquid phases α and β, there exist two energetic penalties (σαβ and σls) due to interfaces between the condensed phases. There is also an energetic penalty at the gas–particle surface (σs). The interplay between these three energetic contributions has an effect on the composition of particle phases and, via gas–particle partitioning, as well as the aerosol system overall.
An important feature of σls is that it cannot be fully disentangled from σs as expanding the surface of a solution droplet will expand both the boundary at the gas–liquid interface as well as the boundary between the bulk phase and the surface phase. Therefore, the expression for the chemical potential of the surface phase as described in Schmedding and Zuend (2023) must be modified slightly when accounting for this additional interface. An exception is the case of a pure-component droplet, in which case σls=0.
The following equations define the component-specific and interface-aware chemical potentials in the surface phase and an adjacent liquid bulk phase (Aston and Herrington, 1991):
Equation (21) describes the chemical potential of components (i) in a liquid bulk phase when additionally accounting for the contributions of i to the 2-D LL interfacial energy per unit amount of substance of the ls interface. Equations (20) and (21) may be combined under equilibrium conditions () while assuming (defining) that . This leads to a coupled expression for the surface tension at the gas–liquid interface:
Note that σs is now defined as ; when σls is negligible, . An alternative mathematically equivalent option is to fold the effect of a LL interface into adjusted bulk-phase activities (), as described in Sect. 2.3.
2.3 Coupled vapor–liquid–liquid and bulk–surface equilibrium calculation
Using the coupled vapor–liquid–liquid equilibrium modeling approach of Zuend et al. (2010) and Zuend and Seinfeld (2012), for a given overall condensed-phase composition, a bulk liquid–liquid equilibrium (LLE) calculation is first performed while ignoring any adjustments due to bulk–surface equilibrium (BSE). This provides an initial guess in the form of a condensed-phase equilibrium state for a given particle composition. Given the overall composition and particle size, an initial guess for the surface composition of the entire particle and the associated BSE problem can be generated using the initial guess algorithm of Schmedding and Zuend (2023). Rather than fully depleting species out of phase β or α, it is assumed that both phases contribute material proportionally to the total amount of surface molecules, ns, such that
where is the fraction of neutral component j in phase α, is the fraction of j in phase β, εj is the ratio of j in the surface phase to the total amount of j in the particle phase or , and is the total amount of species j in the liquid phases plus the surface phase while excluding any amount of species j in the gas phase. Similarly, for electrolyte component el, the contributions from phases α and β can be written as follows:
where is the maximum fraction of species el, which may partition into phase α. Returning to the uncoupled or “BSE-free” calculation, these initial guess values are used for a second liquid–liquid equilibrium calculation for the interior bulk of the particle. Once a value of σαβ is obtained, the energetic impact of the interface can be represented as an additional contribution to each component's chemical potential. In practice, this is equivalent to expressing the interfacial tension effect as an adjustment factor to the activities of components of phase α in the following form:
Likewise, in order to accurately capture the equilibrium partial pressures, pi, of gas-phase species over the curved droplet surface and thus the equilibrium number concentration of gas-phase molecules, , the activities of each component in the particle must be scaled by the Kelvin effect as follows:
Here, is the equilibrium saturation ratio, and rp is the overall particle or droplet radius. The droplet's equilibrium RH (equal to Sw) is calculated using . In the case where the gas–particle partitioning of organic species is allowed, the gas-phase quantity of species i (per m3 of air), , is given by
where VG denotes the unit gas-phase volume (1 m3).
At this point, for a given overall droplet composition and temperature and with initial guesses established for both the liquid–liquid equilibrium phase compositions (if predicted to be present) as well as the bulk–surface equilibrium and associated surface tension and interfacial tensions, we can proceed to solve the fully coupled interior phase partitioning problem of a single droplet of given size. In our present proof-of-concept implementation, which is not optimized for best computational performance, we approach this as a nested interior problem to the overall gas–particle partitioning solution as qualitatively described in the following. We run a modified version of the BSE algorithm of Schmedding and Zuend (2023) to solve the Butler equation iteratively while updating the interfacial tensions and LLE state and phase compositions. In practice, the modification is to embed the LLE refinement method by Zuend and Seinfeld (2013) to solve the LLE problem within each iteration of the parent BSE algorithm while accounting for adjusted amounts available for phases α and β (due to changes in bulk–surface partitioning) and using interfacial-tension-adjusted activities for the components in phases α and β. This means that during each iteration within the LLE solver (and hence also within the BSE solver), the interfacial tensions are updated with the selected method (e.g., Antonov's rule or Girifalco–Good), and the normalized Gibbs energy of mixing of the droplet is updated as well. This procedure allows for a numerical solution of these coupled systems of equations within a single particle, and in conjunction with the vapor–liquid equilibrium solver (the outermost nesting level), the full equilibration of the gas phase with a population of (monodisperse) particles within a unit volume of air. It also allows for an initially assumed LLPS state (for the corresponding bulk system) to disappear if it becomes unfavorable due to bulk–surface partitioning and interfacial tension impacts on adjusted component activities.
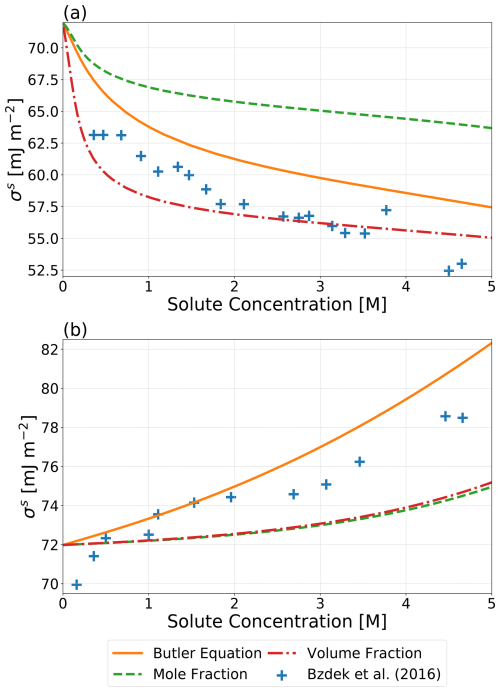
Figure 2Predicted σs values using an approach based on the Butler equation by Schmedding and Zuend (2023), a surface phase volume-fraction-weighted mean of pure-component surface tensions, and a surface phase mole-fraction-weighted mean of pure-component surface tensions as a function of solute concentration for binary systems of (a) water and glutaric acid and (b) water and NaCl. The cross symbols show measurements based on the optical tweezer method by Bzdek et al. (2016) at 298 K. Surface phase compositions were calculated using the Butler equation with the assumption that . Bulk–surface partitioning calculations were performed, assuming a water-free particle diameter of 5000 nm.
In summary, a coupled system of nonlinear algebraic equations needs to be solved, the solution of which must fulfill the necessary condition that the interface-corrected activities () are equivalent across all phases at equilibrium. These corrected activities can be employed along with the relative molar amounts in each phase to determine the change in Gibbs energy due to mixing and interfaces per mole of particulate matter (GPM) for a given particle radius, rp. The following expanded equation is employed:
where represents the moles of j in the particulate matter (any condensed phase), and . Note that this equation only applies to a monodisperse aerosol population.
3.1 Interfacial and surface tensions
Throughout this study, we presume that both σαβ and σls can be determined using one of the introduced methods. Several of those methods rely on the assumption that hypothetical gas–liquid surface tensions of the phases involved can be estimated based on a weighted average of the pure-component surface tensions, . A complete list of all for the components of the systems examined in this work can be found in Table S3. Also reported in Table S3 are the organic-to-inorganic dry mass ratio (OIR) values for each system. In order to explore the validity of this assumption, volume-fraction-based and mole-fraction-based approaches for estimating the surface tension are compared to experimental surface tension data. Figure 2 shows the predicted surface tensions using the aforementioned weighted average approaches based on the composition of the surface and bulk phases as determined by the bulk–surface partitioning treatment of Schmedding and Zuend (2023) along with the more thermodynamically rigorous treatment of surface tension from that same work. It is shown that all three approaches can reasonably approximate the measured surface tensions of the finite-volume droplets, with the volume-fraction-based approach performing better than the mole-fraction-based approach for the water and glutaric acid system. Both weighted average approaches give similar results for the aqueous NaCl system.
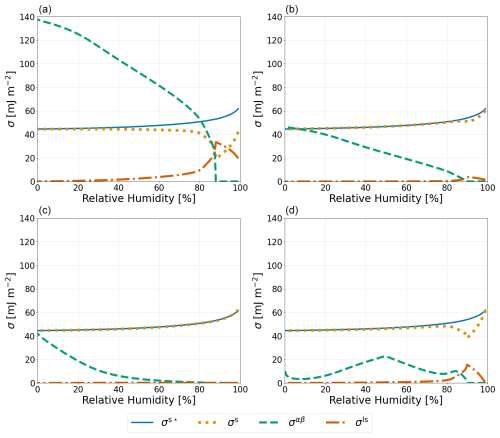
Figure 3Predicted values of σs⋆, which represents the measurable effect of expanding a finite-depth surface phase as defined in Eq. (23); σs; σαβ; and σls (see legend) for a particle of 1000 nm dry diameter composed of water–PEG-400–ammonium sulfate at T=298 K. σαβ and σls were calculated using (a) Antonov's rule (Eq. 1), (b) the Girifalco–Good equation (Eq. 2), (c) the Butler equation with geometric mean activity coefficients (Eq. 14), and (d) the weighted mean interfacial composition approach (Eq. 18).
To compare the relative magnitudes of the different approaches laid out in this work, a 1000 nm dry diameter water–PEG-400–ammonium sulfate system was modeled with each of the four approaches described in Sect. 2.1 and 2.2. The potential crystallization (efflorescence) of ammonium sulfate at lower RH was ignored in our model calculations, hence rendering predictions for RH rather hypothetical but allowing us to perform and interpret calculations over a wide range in electrolyte concentrations. Shown in Fig. 3 are the values of σαβ, σls, σs, and σs⋆ for each of the aforementioned approaches. Antonov's rule (Eq. 1, panel A) leads to the largest predicted values of σαβ and σls along with the smallest σs. The other three approaches have minimal effects on σs, except near the onset of phase separation. In these panels of Fig. 3, when viewed from high to low RH, the onset of LLPS is the reason for the visible and related kinks in the σls and σs curves, as well as the more obvious onset of nonzero σαβ values. The weighted mean interfacial composition approach (Eq. 18) (panel D) exhibits unique behavior with a local maximum of σαβ at ∼ 50 % RH and a local minimum at ∼ 10 % RH. Such behavior may be caused by the compositions of phases α and β becoming more similar as water is removed from the system and other organic species become dominant as solvents.
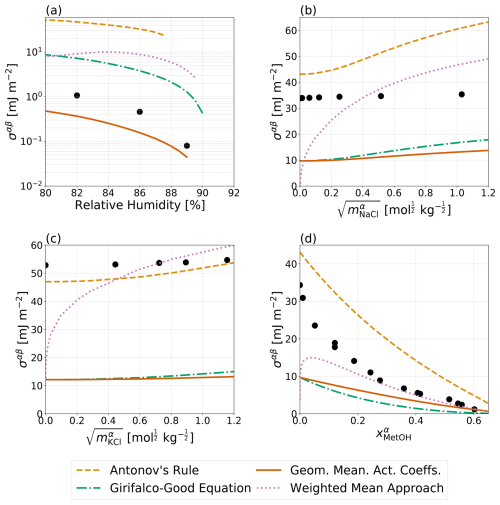
Figure 4Predicted σαβ values (curves) compared to measurements (solid circles). The x-axis scales correspond to those used in the experimental data references. Data and predictions for all systems are for T=298 K. (a) A water–PEG-400–ammonium sulfate system with experimental data by Song et al. (2013), (b) a water–benzene–sodium chloride system (Harkins and Humphery, 1915), (c) a water–dodecane–potassium chloride system (Aveyard and Saleem, 1976), and (d) a water–benzene–methanol system (Pliskin and Treybal, 1966; Paul and De Chazal, 1967). The four distinct parameterizations for interfacial tension from Table 1 are shown (except for the no IFE case). The pure-component surface tensions of organic components can be found in Table S3.
Given the lack of interfacial tension data for atmospherically relevant aerosol systems, it is difficult to compare any of the approaches laid out in this work to direct measurements for validation. However, Song et al. (2013) reported interfacial tension values near the onset of liquid–liquid phase separation for a bulk water–PEG-400–ammonium sulfate system. Shown in Fig. 4a are these measurements in comparison to Antonov's rule (Eq. 1), the Girifalco–Good equation (Eq. 2), the Butler equation with geometric mean activity coefficients (Eqs. 11 and 13), and the weighted mean approach developed in this work (Eq. 18). For this system, which only included measurements near the onset of phase separation, Butler equation with geometric mean activity coefficients (Eq. 11) best matches the measured interfacial tension followed by the Girifalco–Good equation (Eq. 2), while Antonov's rule (Eq. 1) performs most poorly. It should be noted that adjusting the value of ϕ in the Girifalco–Good equation (Eq. 2) may lead to a better match with measured data; however, use of such adjusted parameters requires refitting of ϕ for each specific system and thus reduces the predictive power and application of the model. Figure 4b shows the predicted interfacial tensions from a water–benzene–sodium chloride system along with bulk solution measurements as a function of sodium chloride concentration in the salt-rich aqueous phase. In this case, none of the models described in this work are capable of reasonably matching the measurements, with Antonov's rule (Eq. 1) performing the best and the other approaches yielding substantially lower interfacial tensions, including at zero NaCl content. Similarly, Fig. 4c, shows measured and predicted interfacial tensions for a water–dodecane–potassium chloride system as a function of the aqueous-phase electrolyte molality. In this case, Antonov's rule (Eq. 1) performs the best of the various approaches and is capable of closely matching the measured interfacial tension at high electrolyte concentrations, while all of the other approaches fail to capture the measured behavior. Finally, measurements of an electrolyte free system of water–benzene–methanol is shown in Fig. 4d. At high methanol mole fractions, the measured interfacial tensions are most similar to those predicted by the weighted mean interfacial composition approach (Eq. 18), while the Butler equation with geometric mean activity coefficients (Eq. 11) approach underpredicts the interfacial tension but performs the second best. At low methanol content, Antonov's rule (Eq. 1) is again the best method for this nearly completely phase-separated system (as in Fig. 4b). In order to better understand the importance of in determining the value of σαβ and σls, predictions corresponding to those shown in Fig. 4 were performed with adjustments to and ; those are shown in Fig. S1 in the Supplement. Briefly, minor adjustments to lead to better agreement between the Girifalco–Good equation (Eq. 2) and measured data from the water–PEG-400–ammonium sulfate system in panel A. In panels B and C, there is better agreement between Antonov's rule (Eq. 1) and the water–benzene–sodium chloride system and the water–dodecane–potassium chloride system with the adjustments to . However, in panel D, Antonov's rule (Eq. 1) performs more poorly for the interfacial tension in comparison to measurements for the water–benzene–methanol, assuming the same values of benzene and methanol as those in panels b and c of Fig. S1.
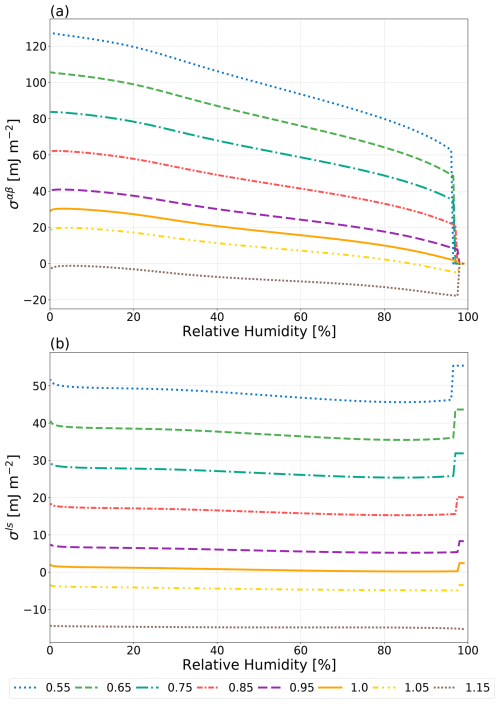
Figure 5The effect of varying ϕ (see legend) on σαβ of a water–suberic acid–ammonium sulfate particle with a water-free diameter of 1000 nm as predicted by the Girifalco–Good approach (Eq. 2). ϕmin=0.55 and ϕmax=1.15 as reported by Harris and Byers (1989).
The Girifalco–Good equation (Eq. 2) contains a single semiempirical fit parameter, ϕ, which grants it some degree of flexibility at the expense of predictive power. Harris and Byers (1989) reported that fitted values of ϕ lie between approximately 0.55 and 1.15 for many systems. Note that, as previously in Sect. 1, it is assumed that ϕ=1 when an interface-free LLE calculation predicts a homogeneously mixed particle. If this were not the case, then nonzero interfacial tension values between two identical phases would be possible. Thus, ϕ is allowed to deviate from its default value of 1.0 when the interface-free LLE calculation predicts phase separation. Shown in Fig. 5 are the values of the predicted LL interfacial tensions when ϕ is varied over the range of 0.55 to 1.15 for a water–suberic acid–ammonium sulfate system. Values of ϕ greater than 1 can produce unrealistically small σαβ values (including negative interfacial tensions), while ϕ<1 increases σαβ values. Overall, the tested range in values of ϕ from 0.55 to 1 results in a relatively wide range of physically feasible outcomes for the shown system, e.g., spanning about 70 mJ m−2 in σαβ at 80 % RH. Hence, optimizing this parameter for a specific system could be a successful approach for achieving a close match to measurements, especially if a composition dependence is also considered. However, such a tuning approach is inconsistent with a typical goal in atmospheric aerosol modeling, namely, that of developing generally predictive methods (here of interfacial tension) applicable to a wide range of multicomponent aerosol systems and independent of any experimental data required for specific tuning purposes.
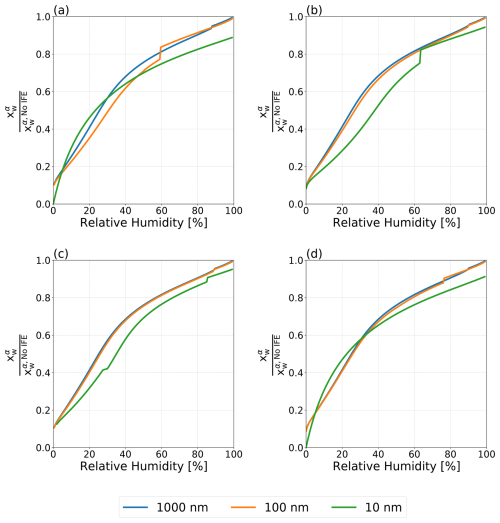
Figure 6Normalized mole fraction of water in the aqueous phase α for water–PEG-400–ammonium sulfate particles with dry diameters ranging from 10 to 1000 nm at T=298 K. (a) Antonov's rule (Eq. 1), (b) the Girifalco–Good equation (Eq. 2), (c) the Butler equation with geometric mean activity coefficient treatment (Eq. 11), and (d) the weighted mean interfacial composition approach (Eq. 18). Kinks in the curves are indicative of the onset of LLPS.
3.2 Size-dependent phase separation in core–shell aerosols
Figure 6 shows the predicted and normalized mole fraction of water in the ammonium sulfate-rich phase α () for water–PEG-400–ammonium sulfate particles using the four treatments for interfacial tension laid out in this work. (see Figs. S2 and S3 in the Supplement for the plots corresponding to the normalized mole fractions of PEG-400 and ammonium sulfate in phase α). In order to better understand the role of interfacial energy in terms of its feedback on particle phase compositions, the shown mole fractions are normalized by those predicted by the no IFE treatment for the same conditions. Even at RH values above the onset of LLPS, where only σls affects the composition of the single liquid phase (α) present, there is a reduction in the concentration of water relative to the no IFE case. That is, the values of are consistently ≤ 1.0, indicating a reduction in the relative water content of phase α when σαβ and σls are accounted for. This indicates that interfacial tension effects in aerosols are not only important for shifting the onset in LLPS or for cloud droplet activation, but also impact the equilibrium compositions of the various particle phases, unlike in macroscopic bulk systems (for which the no IFE case is a better proxy). At lower RH values, the difference in composition is more pronounced, as all four approaches lead to differences of an order of magnitude from the interfacial energy-free treatment. With each approach, there was also a noticeable dependence on particle dry diameter. For the 10 nm particles, these differences in composition are most substantial, while the 1000 nm particle and the 100 nm particle behaved more similarly to one another. In Fig. 6a, the 10 nm particle exhibits complete suppression of LLPS, across the entire RH range. However, all other interfacial tension treatments lead to LLPS in a certain RH range, as marked by the sudden change (kinks) in with decreasing RH.
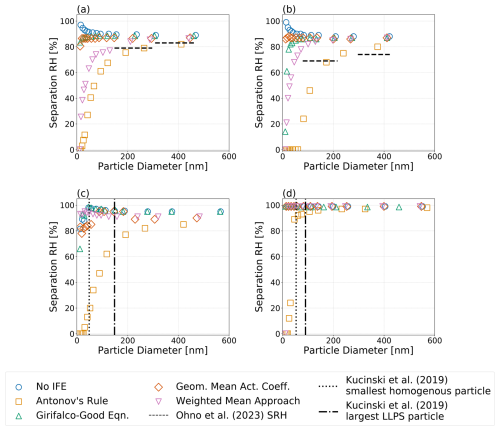
Figure 7Predicted equilibrium separation RH versus particle wet diameter for particles of the same dry composition but different choices of interfacial tension treatment; see legend. Systems shown are the following: (a) water–PEG-300–ammonium sulfate, (b) water–1,2,6-hexanetriol–ammonium sulfate, (c) water–CSOA-with-succinic acid–ammonium sulfate, and (d) water–α-pinene-SOA–ammonium sulfate. (a, b) Dashed horizontal lines indicate measured equilibrium separation RH values by Ohno et al. (2023). (c, d) Vertical lines show the observed largest homogeneous and the smallest phases-separated particles, respectively, as determined by Kucinski et al. (2019). All calculations were performed at 298 K.
Figure 7 shows the equilibrium water vapor saturation ratio (i.e., RH) corresponding to the onset of liquid–liquid phase separation (also denoted as SRH) for (a) a water–PEG-300–ammonium sulfate system; (b) a water–1,2,6-hexanetriol–ammonium sulfate system, both corresponding to systems examined by Ohno et al. (2023); (c) a 12-component complex SOA surrogate mixture (CSOA) with succinic acid mixed with water and ammonium sulfate; and (d) a water–α-pinene-SOA–ammonium sulfate system. Systems (c) and (d) correspond to those studied experimentally by Kucinski et al. (2019). The α-pinene SOA surrogate system used here for the model predictions is based on the components and relative compositions tabulated by Rastak et al. (2017). Shown for each system are the impacts of the four interfacial tension estimation approaches on the separation RH of LLPS: σαβ=0, Eq. (1), the Girifalco–Good equation (Eq. 2), and Butler equation with geometric mean activity coefficients (Eq. 11). For all systems, applying Eq. (1) led to the most substantial reductions in the onset RH of LLPS, with noticeable decreases in the separation RH occurring in particles with wet diameters between approximately 100 and 250 nm. In the case where σαβ=0, our model predicts an increase in the separation RH for small particle sizes, caused mostly by an increase in effective equilibrium RH at small particle diameters due to the Kelvin effect. It should also be noted that the consideration of nonzero σls encourages the occurrence of LLPS and shifts the onset of LLPS in smaller particles to higher RH values as compared to particles with the same initial composition but a larger dry diameter. Indeed, relative to said larger particles, there is a slight increase in the separation RH values in the sub-100 nm (wet diameter) size range for the water–PEG-300–ammonium sulfate system, while a more noticeable decrease in separation RH is predicted for particles with diameters <20 nm. In comparison to observations of size-dependent LLPS behavior, Antonov's rule (Eq. 1) is the only approach that is consistently capable of suppressing phase separation to below 20 % RH for small wet diameters (likely reported as complete suppression in measurements) for all of the systems shown. The application of Antonov's rule (Eq. 1) also leads to measurable decreases in the onset RH of LLPS even for relatively large particle wet diameters (>200 nm), in agreement with the experimental data reported by Ohno et al. (2023) and Kucinski et al. (2019). Indeed, for the α-pinene SOA system shown in Fig. 7d, only Antonov's rule (Eq. 1) leads to a notable size dependence in the LLPS onset RH. The corresponding values of σαβ at the onset of LLPS are shown in Fig. S4, and the water-free OIRs are listed in Table S3. For treatments which predict stronger size dependencies on the separation RH, there is less agreement between σαβ at the onset of LLPS for the weighted mean interfacial composition approach (Eq. 18). This is due to the fact that the predicted σαβ exhibits a local minimum at low RH values (see Fig. 3d). The location of such a local minimum is a function of particle size; thus, smaller particles may undergo LLPS at RHs below the RH which minimizes σαβ.
Figure S4 shows the value of σαβ at the SRH for the systems shown in Fig. 7. For all systems, σαβ at the SRH is lower for larger particles and begins to increase with decreasing particle size. This is due to the fact that these particles experience a decrease in the SRH and therefore the compositions of phases α and β become more distinct at the SRH. However, it should be noted that for very small particles the value of σαβ at the SRH begins to decrease. Said trend is most clear when Antonov's rule (Eq. 1) is applied. This decreasing trend suggests that the compositional differences between liquid phases at very small sizes and low RH become less distinct as the overall water content of the particle is low. Such a trend may be responsible for the behavior shown in Fig. 7b and c, wherein the smallest particles do not neatly decrease in SRH with respect to particle size; indeed, the competing effects among σαβ, σls, and lead to weaker decreases in SRH and in the case of panel C and either the Girifalco–Good equation (Eq. 2) or the Butler equation with geometric mean activity coefficient treatment (Eq. 11), a plateauing effect with a local maximum and then a continued decrease in SRH. However, this effect is small relative to the overall decrease in SRH with decreasing particle size.
Figure S5 shows the same systems as in Fig. 7 but with the assumption that σls=0. For the more extreme treatments of σαβ, such as with Antonov's rule (Eq. 1) or the weighted mean interfacial composition approach (Eq. 18), the exclusion of σls has a negligible impact on the size-dependent SRH. However, if σls=0 and a less extreme treatment of σαβ, such as the Girifalco–Good equation (Eq. 2) or the Butler equation with geometric mean activity coefficient treatment (Eq. 11), are used, then there is a positive increase in the SRH that is very similar to the no IFE case. It is also important to note that the local maximum behavior discussed in Fig. 7 is still present and thus cannot be attributed to the presence or absence of σls. Employing either the Girifalco–Good equation (Eq. 2) or the Butler equation with geometric mean activity coefficient treatment (Eq. 11) yields quantitatively similar LLPS behavior. This suggests that the Girifalco–Good equation (Eq. 2) may serve as a good approximation of a more thermodynamically rigorous treatment for the LL interface – at least for qualitatively similar systems to the ones studied in this work.
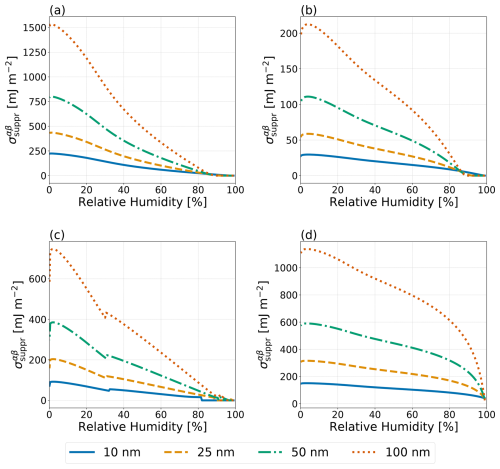
Figure 8Predicted hypothetical σαβ values necessary to completely suppress phase separation in the no IFE case () as a function of RH for particles with dry diameters of 10, 25, 50, and 100 nm (see legend) at T=298 K. Systems as in Fig. 7: (a) water–PEG-300–ammonium sulfate, (b) water–1,2,6-hexanetriol–ammonium sulfate, (c) water–CSOA-with-succinic acid–ammonium sulfate, and (d) water–α-pinene-SOA–ammonium sulfate.
For particles of less than 100 nm in (wet) diameter, the hypothetical minimum LL interfacial tension necessary to fully suppress LLPS, , was calculated based on the difference between the predicted molar Gibbs energy of the phase-separated solution and that of the homogeneous solution in the no IFE case. These values are shown in Fig. 8 for the systems from Fig. 7. Both the water–PEG-300–ammonium sulfate and the water–1,2,6-hexanetriol–ammonium sulfate systems exhibited weaker size dependence for than the water–CSOA-with-succinic acid–ammonium sulfate system or the water–α-pinene-SOA–ammonium sulfate system. At low RH (<30%), both of these SOA-proxy systems required large () values to inhibit LLPS, even in the ultrafine size regime. As expected, at RH levels near the onset of phase separation, very small values of σαβ already exceed in the case of all systems. However, the systems shown in Fig. 8 do not include any feedback from the inclusion of σls treatments. The different treatments for σls lead to differences in the composition of the particle before the onset of phase separation and, as such, may lead to modifications to the value of for the systems shown. The comparison and size effects shown in Fig. 8 mainly serve the purpose of demonstrating that a size dependence exists, yet complete suppression of LLPS in the RH range from 40 % to 80 % is energetically rather difficult (at least when assuming that AIOMFAC reasonably represents the molecular interactions).
The approaches for predicting LL interfacial tension described and tested in this work can produce a broad range of values for the system under, otherwise, the same conditions. For mixtures in which there is a higher degree of mutual solubility among components preferring either phase α or β (e.g., the water–PEG-300–ammonium sulfate, water–PEG-400–ammonium sulfate, water–1,2,6-hexanetriol–ammonium sulfate, and the water–benzene–methanol systems), the Girifalco–Good equation and the Butler equation with geometric mean activity coefficients (Eq. 14) agree well with previously reported experimental data. In the case of systems with more complete phase separation (such as the water–benzene–NaCl system and the water–dodecane–KCl system), Antonov's rule (Eq. 1) appears to be an appropriate method. It is important to note that such systems exhibiting nearly complete phase separation are not necessarily representative of atmospherically relevant systems that may be found in ambient mixtures of water, SOA, and inorganic ions (Zuend et al., 2011).
The inclusion of interfacial energy corrections mapped onto the chemical activities of components in affected particles can be important for the resulting equilibrium particle phase compositions, even for larger particles, as shown in Fig. 6. The effects are more pronounced for smaller particles; however, the magnitude of the change in composition in comparison to the no IFE case is approximately the same for the four approaches of interfacial energy prediction discussed in this work.
Despite better agreement with interfacial tension measurements, the application of the Girifalco–Good (Eq. 2) equation and the Butler equation with geometric mean activity coefficient treatment (Eq. 11) does not agree well with observed separation relative humidities as a function of particle size. Indeed, Antonov's rule (Eq. 1) is the only approach which consistently predicts size-limited phase separation for the systems examined in this work. Importantly, the application of Antonov's rule (Eq. 1) to the systems examined in Ohno et al. (2023) leads to relatively good agreement with the observed size-dependent reduction in separation RH for both the water–PEG-300–ammonium sulfate and the water–1,2,6-hexanetriol–ammonium sulfate systems. We note that the no IFE simulations lead to higher separation relative humidities for larger particles in both cases. However, in the case of the water–PEG-300–ammonium sulfate system, Ohno et al. (2023) discuss limiting the upper bound of the explored RH range in their experiments to 83 % to avoid issues with condensation in their setup.
For the complex SOA system with ammonium sulfate analyzed by Kucinski et al. (2019), the application of Antonov's rule (Eq. 1) leads to a predicted reduction in SRH; however, only particles with diameters below 20 nm exhibited complete suppression of phase separation. Likewise, the α-pinene SOA surrogate system only exhibited complete suppression of LLPS for particles with diameters below 15 nm. For this system, the components were based on those generated by the Master Chemical Mechanism for a specific ozonolysis case study (Rastak et al., 2017); therefore, most of the used values were not available from measurements, and we assumed a value of 35 mJ m−2 for those organic products. It is possible that better constraints on these values may lead to larger σαβ values, which are capable of further suppressing LLPS at higher relative humidities. However, for this system the interfacial tension required to suppress LLPS becomes quite high as the RH decreases. It is therefore unlikely that realistic interfacial tensions of typically less than 100 mJ m−2 will completely inhibit LLPS across the full RH range for all but the smallest ultrafine particles.
The energetic contributions of the LL interface and the bulk–surface interface have competing effects on a particle's internal mixing state. If an energetic contribution from the LL interface is included and the bulk–surface interface is neglected, then particles may exhibit decreases in SRH. However, if both contributions are included and we assume that the same treatment is used for both interfaces (e.g., the Girifalco–Good equation, Eq. 2), then particles with smaller diameters phase separate at the same or higher relative humidities than larger particles in all but the most extreme cases of interfacial tension. This is likely due to the fact that in a particle in which phase separation is suppressed (compared to the macroscopic bulk case), the composition of the surface will be more distinct from that of the interior bulk, leading to a larger energetic contribution at the bulk–surface interface. Given that the area of the bulk–surface interface must inherently always be larger than the αβ LL interface, a comparable bulk–surface LL interface value would lead to a larger total energetic contribution per particle. Thus, in many cases it becomes favorable even for an ultrafine particle to form a LLPS and thereby substantially lower σls while introducing a nonzero σαβ.
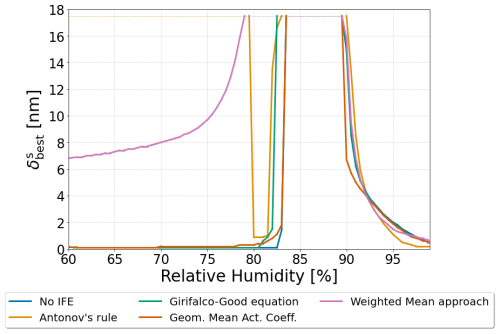
Figure 9The δs value corresponding to the overall minimum in Gibbs energy of a 250 nm dry diameter particle for each interfacial tension treatment. The particle was composed of water, 1,2,6-hexanetriol, and ammonium sulfate with a 2:1 organic-to-inorganic dry mass ratio. δs values between 0.1–17.5 nm were tested.
The inclusion of surface energy, liquid–liquid interface, and bulk–surface interface may also lead to a more complete picture regarding the structure of the surface phase. Thicker 3-D surface phases of larger corresponding δs values typically imply higher surface energy contributions. However, surfaces with thicker δs values tend to be of compositions that are more similar to the interior bulk of the particle. This would reduce the energetic penalties from the bulk–surface interface and inhibit phase separation by increasing depletion of species out of the interior bulk of the particle to the surface phase. Likewise, the opposite effects likely would occur in a particle with a surface that has a small δs value. The particle would have a lower surface energy coupled with a higher bulk–surface LL interfacial tension and reduced inhibition of LLPS. To explore this trade-off quantitatively, we have run a range of predictions during which δs was allowed to vary from 0.1 to 17.5 nm in surface thickness, and we evaluated the resulting normalized Gibbs energy of the system. Simulations were not conducted above δs>17.5 nm as this would represent an extreme case wherein the volume of the surface could become substantially greater than the volume of phase β. Figure 9 shows the determined optimum values of δs for a water–1,2,6-hexanetriol–ammonium sulfate particle with a water-free diameter of 250 nm as a function of RH. For this system, the optimum δs value () is calculated for the various interfacial tension options for σαβ and σls compared throughout this work: the no IFE case, Antonov's rule (Eq. 1), the Girifalco–Good equation (Eq. 2), the Butler equation with geometric mean activity coefficients (Eq. 14), and the weighted mean interfacial composition approach (Eq. 18). As the relative humidity is decreased, the thickness of increases near the onset of LLPS. Values of remain high and then decrease in all cases. In the case of the weighted mean interfacial composition approach (Eq. 18), the decrease in is more gradual at lower RH. The application of Antonov's rule (Eq. 1) leads to unique behavior among the different methods tested, due to its suppression of LLPS when δs is large. This causes to return to large values at lower RHs, which forces the particle to form a single bulk phase with a very thick surface phase. Such behavior is due to the particle trying to minimize compositional differences across phases α and β and the surface by increasing the material present in the surface phase. The relative changes in with decreasing RH near the onset of phase separation are similar in magnitude for the no IFE case, the Girifalco–Good equation, the Butler equation with geometric mean activity coefficient treatment (Eq. 11), and the weighted mean interfacial composition approach. Such behavior suggests that the inclusion of bulk–surface partitioning is more important for determining the structure of the surface phase than the inclusion of σls. At RH values further below the onset of LLPS, becomes much smaller again for the no IFE case, the Girifalco–Good equation, the the Butler equation with geometric mean activity coefficient treatment (Eq. 11), approaching the physical limit of a three-dimensional surface phase () in agreement with Schmedding and Zuend (2023). This is likely due to the fact that the energetic contributions of σαβ are much larger than those of σls and that lower values of δs correspond to lower values of σs⋆. The results reported by Schmedding and Zuend (2023), which did not account for the energetic penalty of the bulk–surface interface, found that thinner surfaces are more energetically favorable for well-mixed particles. The inclusion of this interfacial contribution suggests that the most favorable surface thickness is dynamic; typically favoring a thin surface phase in dilute aqueous droplets. Moreover, in some cases a thicker surface is preferred to a thinner one, especially close to the onset of LLPS. This could suggest a potential mechanism wherein LLPS may occur initially as a form of bulk–surface partitioning with a gradual thickening of the surface phase before an additional distinct bulk-phase forms. It is possible that such behavior may be responsible for some of the observed size-limited phase separation behavior reported in previous studies, since, with limited depth resolution in an experiment, it is difficult to distinguish between a thick surface phase that is enriched in organic species and a thin, organic-rich phase β in particles in which such a configuration for the surface may be favorable.
Atmospheric aerosol particles may exhibit liquid–liquid phase separation (e.g., You et al., 2014; Huang et al., 2021). Recent observations have noted that some aerosol systems may exhibit size-dependent LLPS wherein smaller particles undergo LLPS under more extreme conditions (e.g., substantially lower RH) than large particles. This study aims to explore the interactions between phase separation, bulk–surface partitioning, and LL interfaces in aerosol particles through the extension of a previously developed bulk–surface partitioning model which now includes the coupling with a liquid–liquid phase separation model. Various treatments for the energetic contribution of LL interfaces are explored. For systems with greater miscibility among the solution components, the Girifalco–Good equation and the Butler equation more accurately reproduce measured interfacial tensions. For systems exhibiting increased immiscibility among components, Antonov's rule performs better than the other approaches. The inclusion of LL interfacial tension terms and bulk–surface partitioning leads to a predicted lowering of the separation RH of LLPS in many systems. This reduction in the separation RH was most pronounced for particles with wet diameters below 50–70 nm. The weighted mean composition approach and Antonov's rule led to the largest decreases in the predicted separation RH for all of the systems examined in this work. For the smallest particle sizes studied (10–50 nm in wet diameter), these two approaches led to substantial suppression of LLPS to below 40 % RH (around the efflorescence RH of ammonium sulfate) or complete inhibition of LLPS. An energetic contribution from the LL boundary between the surface phase and its adjacent bulk phase was considered in this work. This interfacial tension contribution is shown to be at its maximum near the separation RH, where the difference in composition between the surface and bulk phases is greatest.
While numerous studies have examined LLPS in larger particles and macroscopic bulk solutions, studies on LLPS in submicron-sized particles are scarce (Kucinski et al., 2019; Ohno et al., 2023; Ott and Freedman, 2020, 2021). For small particles, it can be difficult to experimentally distinguish between a surface phase of more than monolayer thickness phase and a thin bulk phase in a core–shell configuration, since the minimum required thickness to call a surface layer a “regular” liquid phase rather than a multilayer surface is a matter of perspective. The interplay of bulk–surface partitioning, interfacial tensions, and LLPS hint at the difficulties in conducting measurements on nanoparticles. Measurements of size-dependent particle properties in the submicron range should be contactless. Contact with the particle (surface) will change the surface-area-to-volume ratio, may generate additional interfaces, induce bulk–surface partitioning feedbacks, and indirectly influence the targeted particle properties. The applicability of measurements performed on macroscopic systems for microscopic droplets needs to be considered carefully. Most LL interfacial tension measurements are made using bulk solution techniques; therefore, caution is warranted when extrapolating these data to sub-100 nm particles for which deviations from bulk solution are pronounced. This study highlights the interest in additional measurements covering sub-100 nm particles to provide guidance for constraining model parameters. This work represents a step towards more physically realistic representations of aerosol particles accounting for LL interfaces and size-dependent LLPS behavior. While offering options for interfacial tension treatment, this model remains predictive and broadly applicable in its design. It will allow for a predictive treatment of particles in the ultrafine aerosol regime and aids in connecting measurements taken on larger particles to their smaller counterparts.
The interfacial tension at the αβ interface and the surface energies of phases α and β may be used to predict if a particle's equilibrium morphology is core–shell or partially engulfed. Because partially engulfed morphologies require additional considerations, these morphological questions are a direction for future studies.
The experimental data and model outputs underlying all figures shown are provided in the Supplement. The size-dependent phase separation code is available upon request from the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-25-327-2025-supplement.
RS performed model development and simulations, visualized model outputs, and wrote the manuscript. AZ conceived the project, assisted with model development and theory, cowrote the manuscript, was responsible for supervision, and secured funding for the work.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This research has been supported by the Natural Sciences and Engineering Research Council of Canada (grant no. RGPIN-2021-02688), the Fonds de recherche du Québec – Nature et technologies (grant no. 314186), and Environment and Climate Change Canada (grant no. GCXE20S049).
This paper was edited by Stefania Gilardoni and reviewed by two anonymous referees.
Amirfazli, A. and Neumann, A.: Status of the three-phase line tension: a review, Adv. Colloid Interfac., 110, 121–141, https://doi.org/10.1016/j.cis.2004.05.001, 2004. a
Antonov, G. N.: Sur la tension superficielle à la limite de deux couches, J. Chim. Phys., 5, 372–385, https://doi.org/10.1051/jcp/1907050372, 1907. a, b
Aston, M. S. and Herrington, T. M.: The effect of added electrolyte on surface pressure/area per molecule isotherms, J. Colloid Interfac. Sci., 141, 50–59, 1991. a
Aveyard, R. L. and Saleem, S. M.: Interfacial tensions at alkane-aqueous electrolyte interfaces, J. Chem. Soc. Faraday T., 72, 1609–1617, https://doi.org/10.1039/F19767201609, 1976. a
Bahramian, A.: Unlocking the Secrets of Liquid-Liquid Interfaces and Phase Equilibria: Exploring the Interplay of Critical Composition, Interfacial Tension, and Mutual Solubility, Langmuir, 40, 4684–4701, https://doi.org/10.1021/acs.langmuir.3c03344, 2024. a, b
Bahramian, A. and Danesh, A.: Prediction of liquid-liquid interfacial tension in multi-component systems, Fluid Phase Equilibr., 221, 197–205, https://doi.org/10.1016/j.fluid.2004.04.012, 2004. a, b, c
Bahramian, A. and Danesh, A.: Prediction of liquid-vapour surface tension in multi-component systems, Fluid Phase Equilibr., 236, 156–161, https://doi.org/10.1016/j.fluid.2005.07.016, 2005. a, b, c
Bertram, A. K., Martin, S. T., Hanna, S. J., Smith, M. L., Bodsworth, A., Chen, Q., Kuwata, M., Liu, A., You, Y., and Zorn, S. R.: Predicting the relative humidities of liquid-liquid phase separation, efflorescence, and deliquescence of mixed particles of ammonium sulfate, organic material, and water using the organic-to-sulfate mass ratio of the particle and the oxygen-to-carbon elemental ratio of the organic component, Atmos. Chem. Phys., 11, 10995–11006, https://doi.org/10.5194/acp-11-10995-2011, 2011. a
Binyaminov, H., Abdullah, F., Zargarzadeh, L., and Elliott, J. A. W.: Thermodynamic Investigation of Droplet-Droplet and Bubble-Droplet Equilibrium in an Immiscible Medium, J. Phys. Chem. B, 125, 8636–8651, https://doi.org/10.1021/acs.jpcb.1c02877, 2021. a
Bzdek, B. R., Power, R. M., Simpson, S. H., Reid, J. P., and Royall, C. P.: Precise, contactless measurements of the surface tension of picolitre aerosol droplets, Chem. Sci., 7, 274–285, https://doi.org/10.1039/C5SC03184B, 2016. a
Chan, M. N., Lee, A. K. Y., and Chan, C. K.: Responses of Ammonium Sulfate Particles Coated with Glutaric Acid to Cyclic Changes in Relative Humidity: Hygroscopicity and Raman Characterization, Environ. Sci. Technol., 40, 6983–6989, https://doi.org/10.1021/es060928c, 2006. a
Ciobanu, V. G., Marcolli, C., Krieger, U. K., Weers, U., and Peter, T.: Liquid-Liquid Phase Separation in Mixed Organic/Inorganic Aerosol Particles, J. Phys. Chem. A, 113, 10966–10978, https://doi.org/10.1021/jp905054d, 2009. a, b
Davies, J. F., Zuend, A., and Wilson, K. R.: Technical note: The role of evolving surface tension in the formation of cloud droplets, Atmos. Chem. Phys., 19, 2933–2946, https://doi.org/10.5194/acp-19-2933-2019, 2019. a
Fowkes, F. M.: Determination of interfacial tensions, contact angles, and dispersion forces in surfaces by assuming additivity of intermolecular interactions in surfaces, J. Phys. Chem., 66, 382–382, https://doi.org/10.1021/j100808a524, 1962. a
Fowkes, F. M.: Additivity of intermolecular forces at interfaces. I. determination of the contribution to surface and interfacial tensions of dispersion forces in various liquids, J. Phys. Chem., 67, 2538–2541, https://doi.org/10.1021/j100806a008, 1963. a
Freedman, M. A.: Phase separation in organic aerosol, Chem. Soc. Rev., 46, 7694–7705, https://doi.org/10.1039/C6CS00783J, 2017. a
Freedman, M. A.: Liquid-Liquid Phase Separation in Supermicrometer and Submicrometer Aerosol Particles, Accounts of Chem. Res., 53, 1102–1110, https://doi.org/10.1021/acs.accounts.0c00093, 2020. a, b
Gaston, C. J., Thornton, J. A., and Ng, N. L.: Reactive uptake of N2O5 to internally mixed inorganic and organic particles: the role of organic carbon oxidation state and inferred organic phase separations, Atmos. Chem. Phys., 14, 5693–5707, https://doi.org/10.5194/acp-14-5693-2014, 2014. a
Gervasi, N. R., Topping, D. O., and Zuend, A.: A predictive group-contribution model for the viscosity of aqueous organic aerosol, Atmos. Chem. Phys., 20, 2987–3008, https://doi.org/10.5194/acp-20-2987-2020, 2020. a
Gibbs, J. W.: Thermodynamics, vol. 1, Longmans, Green and Company, 1906. a
Girifalco, L. A. and Good, R. J.: A Theory for the Estimation of Surface and Interfacial Energies. I. Derivation and Application to Interfacial Tension, J. Phys. Chem., 61, 904–909, https://doi.org/10.1021/j150553a013, 1957. a, b, c, d, e
Gorkowski, K., Donahue, N. M., and Sullivan, R. C.: Aerosol Optical Tweezers Constrain the Morphology Evolution of Liquid-Liquid Phase-Separated Atmospheric Particles, Chem, 6, 204–220, https://doi.org/10.1016/j.chempr.2019.10.018, 2020. a
Guggenheim, E.: The thermodynamics of interfaces in systems of several components, T. Faraday Soc., 35, 397–412, https://doi.org/10.1039/TF9403500397, 1940. a
Harkins, W. D. and Humphery, E. C.: The Surface-Tension at the Interface Between Two Liquids, P. Natl. Acad. Sci. USA, 1, 585–590, https://doi.org/10.1073/pnas.1.12.585, 1915. a
Harris, M. T. and Byers, C. H.: An advanced technique for interfacial tension measurement in liquid- liquid systems, Tech. rep., https://doi.org/10.2172/5172058, 1989. a, b
Hua, X., Bevan, M. A., and Frechette, J.: Reversible Partitioning of Nanoparticles at an Oil-Water Interface, Langmuir, 32, 11341–11352, https://doi.org/10.1021/acs.langmuir.6b02255, 2016. a
Huang, Y., Mahrt, F., Xu, S., Shiraiwa, M., Zuend, A., and Bertram, A. K.: Coexistence of three liquid phases in individual atmospheric aerosol particles, P. Natl. Acad. Sci. USA, 118, e2102512118, https://doi.org/10.1073/pnas.2102512118, 2021. a, b, c
Intergovernmental Panel on Climate (IPCC): Summary for Policymakers, Cambridge University Press, Cambridge, 1–30, ISBN 9781107057999, https://doi.org/10.1017/CBO9781107415324.004, 2014. a
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., null null, Dunlea, J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of Organic Aerosols in the Atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009. a
Kleinheins, J., Shardt, N., El Haber, M., Ferronato, C., Nozière, B., Peter, T., and Marcolli, C.: Surface tension models for binary aqueous solutions: a review and intercomparison, Phys. Chem. Chem. Phys., 25, 11055–11074, https://doi.org/10.1039/D3CP00322A, 2023. a
Kucinski, T. M., Dawson, J. N., and Freedman, M. A.: Size-Dependent Liquid-Liquid Phase Separation in Atmospherically Relevant Complex Systems, J. Phys. Chem. Lett., 10, 6915–6920, https://doi.org/10.1021/acs.jpclett.9b02532, 2019. a, b, c, d, e, f, g, h
Kwamena, Buajarern, J., and Reid, J. P.: Equilibrium Morphology of Mixed Organic/Inorganic/Aqueous Aerosol Droplets: Investigating the Effect of Relative Humidity and Surfactants, J. Phys. Chem. A, 114, 5787–5795, https://doi.org/10.1021/jp1003648, 2010. a, b
Lam, H. K., Xu, R., Choczynski, J., Davies, J. F., Ham, D., Song, M., Zuend, A., Li, W., Tse, Y.-L. S., and Chan, M. N.: Effects of liquid–liquid phase separation and relative humidity on the heterogeneous OH oxidation of inorganic–organic aerosols: insights from methylglutaric acid and ammonium sulfate particles, Atmos. Chem. Phys., 21, 2053–2066, https://doi.org/10.5194/acp-21-2053-2021, 2021. a
Lang-Yona, N., Abo-Riziq, A., Erlick, C., Segre, E., Trainic, M., and Rudich, Y.: Interaction of internally mixed aerosols with light, Phys. Chem. Chem. Phys., 12, 21–31, https://doi.org/10.1039/B913176K, 2010. a
Li, W., Teng, X., Chen, X., Liu, L., Xu, L., Zhang, J., Wang, Y., Zhang, Y., and Shi, Z.: Organic Coating Reduces Hygroscopic Growth of Phase-Separated Aerosol Particles, Environ. Sci. Technol., 55, 16339–16346, https://doi.org/10.1021/acs.est.1c05901, 2021. a
Lilek, J. and Zuend, A.: A predictive viscosity model for aqueous electrolytes and mixed organic–inorganic aerosol phases, Atmos. Chem. Phys., 22, 3203–3233, https://doi.org/10.5194/acp-22-3203-2022, 2022. a
Makkonen, L. and Kurkela, J.: Another look at the interfacial interaction parameter, J. Colloid Interfac. Sci., 529, 243–246, https://doi.org/10.1016/j.jcis.2018.06.015, 2018. a, b
Malek, K., Gohil, K., Olonimoyo, E. A., Ferdousi-Rokib, N., Huang, Q., Pitta, K. R., Nandy, L., Voss, K. A., Raymond, T. M., Dutcher, D. D., Freedman, M. A., and Asa-Awuku, A.: Liquid-Liquid Phase Separation Can Drive Aerosol Droplet Growth in Supersaturated Regimes, ACS Environmental Au, 3, 348–360, https://doi.org/10.1021/acsenvironau.3c00015, 2023. a
Marcolli, C. and Krieger, U. K.: Phase Changes during Hygroscopic Cycles of Mixed Organic/Inorganic Model Systems of Tropospheric Aerosols, J. Phys. Chem. A, 110, 1881–1893, https://doi.org/10.1021/jp0556759, 2006. a
Ohno, P. E., Brandão, L., Rainone, E. M., Aruffo, E., Wang, J., Qin, Y., and Martin, S. T.: Size Dependence of Liquid-Liquid Phase Separation by in Situ Study of Flowing Submicron Aerosol Particles, J. Phys. Chem. A, 127, 2967–2974, https://doi.org/10.1021/acs.jpca.2c08224, 2023. a, b, c, d, e, f, g, h, i, j
Ott, E.-J. E. and Freedman, M. A.: Inhibition of Phase Separation in Aerosolized Water-Soluble Polymer-Polymer Nanoparticles at Small Sizes and the Effects of Molecular Weight, J. Phys. Chem. B, 124, 7518–7523, https://doi.org/10.1021/acs.jpcb.0c06535, 2020. a, b
Ott, E.-J. E. and Freedman, M. A.: Influence of Ions on the Size Dependent Morphology of Aerosol Particles, ACS Earth and Space Chemistry, 5, 2320–2328, https://doi.org/10.1021/acsearthspacechem.1c00210, 2021. a, b
Ovadnevaite, J., Zuend, A., Laaksonen, A., Sanchez, K. J., Roberts, G., Ceburnis, D., Decesari, S., Rinaldi, M., Hodas, N., Facchini, M. C., Seinfeld, J. H., and O'Dowd, C.: Surface tension prevails over solute effect in organic-influenced cloud droplet activation, Nature, 546, 637–641, https://doi.org/10.1038/nature22806, 2017. a, b
Paul, G. W. and De Chazal, L. M.: Interfacial tensions in ternary liquid-liquid systems, J. Chem. Eng. Data, 12, 105–107, https://doi.org/10.1021/je60032a033, 1967. a
Pliskin, I. and Treybal, R. E.: Interfacial Tensions in Two-Liquid-Phase Ternary Systems, J. Chem. Eng. Data, 11, 49–52, https://doi.org/10.1021/je60028a013, 1966. a
Rastak, N., Pajunoja, A., Acosta Navarro, J. C., Ma, J., Song, M., Partridge, D. G., Kirkevåg, A., Leong, Y., Hu, W. W., Taylor, N. F., Lambe, A., Cerully, K., Bougiatioti, A., Liu, P., Krejci, R., Petäjä, T., Percival, C., Davidovits, P., Worsnop, D. R., Ekman, A. M. L., Nenes, A., Martin, S., Jimenez, J. L., Collins, D. R., Topping, D., Bertram, A. K., Zuend, A., Virtanen, A., and Riipinen, I.: Microphysical explanation of the RH-dependent water affinity of biogenic organic aerosol and its importance for climate, Geophys. Re. Lett., 44, 5167–5177, https://doi.org/10.1002/2017GL073056, 2017. a, b
Reid, J. P., Dennis-Smither, B. J., Kwamena, N.-O. A., Miles, R. E. H., Hanford, K. L., and Homer, C. J.: The morphology of aerosol particles consisting of hydrophobic and hydrophilic phases: hydrocarbons, alcohols and fatty acids as the hydrophobic component, Phys. Chem. Chem. Phys., 13, 15559–15572, https://doi.org/10.1039/C1CP21510H, 2011. a
Ruehl, C. R., Davies, J. F., and Wilson, K. R.: An interfacial mechanism for cloud droplet formation on organic aerosols, Science, 351, 1447–1450, https://doi.org/10.1126/science.aad4889, 2016. a
Russell, L. M. and Ming, Y.: Deliquescence of small particles, J. Chem. Phys., 116, 311–321, https://doi.org/10.1063/1.1420727, 2002. a
Schmedding, R. and Zuend, A.: A thermodynamic framework for bulk–surface partitioning in finite-volume mixed organic–inorganic aerosol particles and cloud droplets, Atmos. Chem. Phys., 23, 7741–7765, https://doi.org/10.5194/acp-23-7741-2023, 2023. a, b, c, d, e, f, g, h, i, j, k, l, m
Schmedding, R., Rasool, Q. Z., Zhang, Y., Pye, H. O. T., Zhang, H., Chen, Y., Surratt, J. D., Lopez-Hilfiker, F. D., Thornton, J. A., Goldstein, A. H., and Vizuete, W.: Predicting secondary organic aerosol phase state and viscosity and its effect on multiphase chemistry in a regional-scale air quality model, Atmos. Chem. Phys., 20, 8201–8225, https://doi.org/10.5194/acp-20-8201-2020, 2020. a
Shiraiwa, M., Zuend, A., Bertram, A. K., and Seinfeld, J. H.: Gas-particle particle partitioning of atmospheric aerosols: interplay of physical state, non-ideal mixing and morphology, Phys. Chem. Chem. Phys., 15, 11441–11453, https://doi.org/10.1039/C3CP51595H, 2013. a
Song, M., Marcolli, C., Krieger, U. K., Zuend, A., and Peter, T.: Liquid-liquid phase separation and morphology of internally mixed dicarboxylic acids/ammonium sulfate/water particles, Atmos. Chem. Phys., 12, 2691–2712, https://doi.org/10.5194/acp-12-2691-2012, 2012. a
Song, M., Marcolli, C., Krieger, U. K., Lienhard, D. M., and Peter, T.: Morphologies of mixed organic/inorganic/aqueous aerosol droplets, Faraday Discuss., 165, 289–316, https://doi.org/10.1039/C3FD00049D, 2013. a, b, c
Wang, P. and Anderko, A.: Modeling Interfacial Tension in Liquid-Liquid Systems Containing Electrolytes, Ind. Eng. Chem. Rese., 52, 6822–6840, https://doi.org/10.1021/ie303460c, 2013. a, b
Winter, A.: Antonow's rule 85 years later, Heterogeneous Chem. Rev., 2, 269–308, 1995. a
Yin, H., Dou, J., Klein, L., Krieger, U. K., Bain, A., Wallace, B. J., Preston, T. C., and Zuend, A.: Extension of the AIOMFAC model by iodine and carbonate species: applications for aerosol acidity and cloud droplet activation, Atmos. Chem. Phys., 22, 973–1013, https://doi.org/10.5194/acp-22-973-2022, 2022. a
You, Y., Renbaum-Wolff, L., Carreras-Sospedra, M., Hanna, S. J., Hiranuma, N., Kamal, S., Smith, M. L., Zhang, X., Weber, R. J., Shilling, J. E., Dabdub, D., Martin, S. T., and Bertram, A. K.: Images reveal that atmospheric particles can undergo liquid-liquid phase separations, P. Natl. Acad. Sci. USA, 109, 13188–13193, https://doi.org/10.1073/pnas.1206414109, 2012. a
You, Y., Smith, M. L., Song, M., Martin, S. T., and Bertram, A. K.: Liquid–liquid phase separation in atmospherically relevant particles consisting of organic species and inorganic salts, Int. Rev. Phys. Chem., 33, 43–77, https://doi.org/10.1080/0144235X.2014.890786, 2014. a
Zhang, Q., Jimenez, J. L., Canagaratna, M. R., Allan, J. D., Coe, H., Ulbrich, I., Alfarra, M. R., Takami, A., Middlebrook, A. M., Sun, Y. L., Dzepina, K., Dunlea, E., Docherty, K., DeCarlo, P. F., Salcedo, D., Onasch, T., Jayne, J. T., Miyoshi, T., Shimono, A., Hatakeyama, S., Takegawa, N., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Williams, P., Bower, K., Bahreini, R., Cottrell, L., Griffin, R. J., Rautiainen, J., Sun, J. Y., Zhang, Y. M., and Worsnop, D. R.: Ubiquity and dominance of oxygenated species in organic aerosols in anthropogenically-influenced Northern Hemisphere midlatitudes, Geophys. Res. Lett., 34, 13, https://doi.org/10.1029/2007GL029979, 2007. a
Zuend, A. and Seinfeld, J. H.: Modeling the gas-particle partitioning of secondary organic aerosol: the importance of liquid-liquid phase separation, Atmos. Chem. Phys., 12, 3857–3882, https://doi.org/10.5194/acp-12-3857-2012, 2012. a
Zuend, A. and Seinfeld, J. H.: A practical method for the calculation of liquid-liquid equilibria in multicomponent organic-water-electrolyte systems using physicochemical constraints, Fluid Phase Equilibr., 337, 201–213, https://doi.org/10.1016/j.fluid.2012.09.034, 2013. a
Zuend, A., Marcolli, C., Luo, B. P., and Peter, T.: A thermodynamic model of mixed organic-inorganic aerosols to predict activity coefficients, Atmos. Chem. Phys., 8, 4559–4593, https://doi.org/10.5194/acp-8-4559-2008, 2008. a
Zuend, A., Marcolli, C., Peter, T., and Seinfeld, J. H.: Computation of liquid-liquid equilibria and phase stabilities: implications for RH-dependent gas/particle partitioning of organic-inorganic aerosols, Atmos. Chem. Phys., 10, 7795–7820, https://doi.org/10.5194/acp-10-7795-2010, 2010. a, b
Zuend, A., Marcolli, C., Booth, A. M., Lienhard, D. M., Soonsin, V., Krieger, U. K., Topping, D. O., McFiggans, G., Peter, T., and Seinfeld, J. H.: New and extended parameterization of the thermodynamic model AIOMFAC: calculation of activity coefficients for organic-inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups, Atmos. Chem. Phys., 11, 9155–9206, https://doi.org/10.5194/acp-11-9155-2011, 2011. a, b





