Correction of ERA5 temperature and relative humidity biases by bivariate quantile mapping for contrail formation analysis

Aviation contributes to global emissions of carbon dioxide, aerosol particles, water vapor (WV), and other compounds. WV promotes the formation of condensation trails (contrails), which are known for their net warming effect on the climate. Contrail formation is often estimated using the Schmidt–Appleman criterion (SAc) together with meteorological data from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 atmospheric reanalysis model. We compare ERA5 output of temperature and relative humidity in the upper troposphere and lower stratosphere with 5 years of In-service Aircraft for a Global Observing System (IAGOS) observations over the North Atlantic. Good agreement was found for the temperature fields, with a maximum bias of −0.4 K (200 hPa level), while larger biases were found for relative humidity of up to −5.5 % (250 hPa level). Using original ERA5 data, conditions prone to contrail formation occurred 50.3 % and 7.9 % of the time for non-persistent and persistent contrails, respectively, while 44.0 % and 12.1 % were flagged in the IAGOS data. We propose a multivariate quantile mapping (QM) correction to remove systematic biases by post-processing ERA5 temperature and relative humidity fields with respect to contrail formation. The QM correction was applied to post-process ERA5 data, reducing the temperature bias to less than 0.1 K and the relative humidity bias to less than −1.5 %, resulting in 44 % and 10.9 % of the data points now being flagged for non-persistent and persistent contrail formation, respectively. Our bias correction generalizes well compared to the IAGOS observations. How it generalizes outside the IAGOS regions remains to be investigated.

1 Introduction

Aviation contributes to global climate warming (Lee et al., 2021). The total contribution by aviation is commonly split into two parts. One fraction is directly attributable to carbon dioxide (CO₂) and is well quantified. For the year 2018, aviation was estimated to be responsible for 2.5 % to 2.6 % of global CO₂ emissions (Friedlingstein et al., 2019; Lee et al., 2021; Boucher et al., 2021). The other contributing fraction to aviation-induced climate change comes from byproducts resulting from fossil fuel combustion, like nitrogen oxides (NO_x), sulfur dioxide (SO₂), and aerosol particles. Furthermore, the combustion of all fuels, regardless of whether they are fossil or synthetic, leads to the emission of water vapor (WV) as long as they contain hydrogen.

The effects of WV have received increasing attention in recent years as the emitted WV in engine exhaust allows and triggers the formation of condensation trails, also called contrails (Schumann, 1996; Kärcher, 2018). Optically thin cirrus and contrails are known to have a net warming effect on the climate (Burkhardt and Kärcher, 2011; Schumann et al., 2015; Lee et al., 2021). The influence of a perturbation, e.g., clouds, aerosols, or gases, on the Earth's atmosphere and its radiative transfer is quantified by the radiative forcing (RF). By definition, RF is defined as the difference in the net irradiance at the top of atmosphere under perturbed and unperturbed conditions (Ramanathan et al., 1989). Effective radiative forcing (ERF) additionally includes the radiative impact of adjustments in the troposphere and stratosphere (Bickel et al., 2020). The aviation-induced global CO₂-related ERF is estimated to be around 30 mW m⁻² (Boucher et al., 2021). Contrail RF is estimated to be stronger, at about 60 mW m⁻², but is subject to much larger uncertainties (Burkhardt and Kärcher, 2011).

Contrail formation depends on the ambient conditions, which have to be sufficiently cold and moist. The thresholds of temperature, below which a contrail forms, and relative humidity, above which a contrail can form, are estimated with the Schmidt–Appleman criterion (SAc, Schmidt, 1941; Appleman, 1953). For a contrail to be persistent (with the common meaning that is has a lifetime longer than 10 min), the ambient air has to fulfill the SAc and must also be supersaturated with respect to ice. When these criteria are fulfilled and persistent contrails have formed, they can remain for hours, spread, merge, and increase the total cirrus cloud cover. Employing climate simulations and analyzing satellite observations, Burkhardt and Kärcher (2011) and Quaas et al. (2021) estimated an increase in total cloud cover due to contrail formation of 6 % to 10 % in the midlatitudes of the Northern Hemisphere, where most of the flights occur.

To lower the climate impact of aviation it is important to reduce CO₂ as well as non-CO₂ effects. An approach to minimize non-CO₂ effects is active flight rerouting to avoid areas where contrails are likely to form and persist, which would require accurate numerical weather predictions. A useful prerequisite is to identify and document flight levels and regions of the Earth's atmosphere that are particularly prone to contrail formation. Such a statistical database might be obtained by ground-based or satellite observations. Ground-based observations, such as those performed by Schumann et al. (2013), used a rooftop camera to infer cirrus properties and contrail occurrence. However, this approach is limited to a single location or a few locations over land-covered areas. Alternatively, satellite observations provide a top-down view with the required global coverage but come with some drawbacks (Meyer et al., 2002; Minnis et al., 2013). Depending on the sensor and the satellite platform, the temporal or spatial resolutions are often insufficient to detect young contrails with low cloud optical thickness (Kärcher et al., 2009). Furthermore, satellite observations, similarly to ground-based observations, can be compromised by underlying cloud layers between the surface and the cirrus. High spatial resolution is provided by in situ measurement during dedicated measurement campaigns, during which contrails are directly probed and contrail properties are investigated. Such measurement campaigns, for instance by Krämer et al. (2009, 2020) and Voigt et al. (2017), are rare. Furthermore, they may lack spatial representation by targeting specific atmospheric features as well as cloud conditions, which may bias the results (Petzold et al., 2020). The In-service Aircraft for a Global Observing System (IAGOS;  Petzold et al., 2015) data set differs from field campaigns in that it covers large areas of North America, the North Atlantic, and Europe, which have now been sampled for around 2 decades, including its predecessor Measurement of OZone and water vapour on Airbus In-service airCraft (MOZAIC;  Marenco et al., 1998; Petzold et al., 2017). Still, the coverage is limited to the current flight tracks.

Assessing contrail occurrence more systematically or over a larger domain requires a modeling approach that can be interactive or online. Interactive contrail models are typically implemented in climate models (e.g., Bock and Burkhardt, 2016) by simulating ice-supersaturated regions and calculating contrail cirrus cover based on aircraft emission inventories. Offline contrail models, such as CoCiP (Schumann, 2012), use meteorological fields to analysis contrail formation and evolution to contrail cirrus. However, the assessment strongly relies on the accurate representation in the model of the temperature and humidity fields at high altitudes, as well as that of ice cloud amount and microphysical properties. Offline models such as CoCiP require meteorological data, e.g., temperature and humidity, as input. A well-established data set of meteorological data is provided by ERA5 (Hersbach et al., 2020), which stems from a state-of-the-art global modeling system of the European Centre for Medium-Range Weather Forecasts (ECMWF) and a large number of observational data streams. The ERA5 output is based on simulations with a specific, constant version of the Integrated Forecasting System (IFS) of ECMWF. Thus, the ERA5 data set from 1940 to the present can provide some insight into trends in the Earth's atmosphere. Previous studies have shown that the IFS scheme and the associated data assimilation are able to represent the temperature field well, as verified by radiosonde and satellite observations (Dyroff et al., 2015; Carminati et al., 2019). Higher uncertainties with respect to IAGOS observations were found in the reanalysis of relative humidity, which is generally challenging due to the high temporal and spatial variability of WV. Specific issues have been identified in the upper troposphere and lower stratosphere, as well as with the general representation of ice supersaturation. For example, Bland et al. (2021) compared radiosonde observations with the operational ECMWF IFS weather forecast and identified a lower-stratosphere moist bias in specific humidity. Similarly, Krüger et al. (2022) compared measurements from a differential absorption lidar with ECMWF ERA5 reanalysis data (on a relative tropopause coordinate) and identified a small moist bias in the specific humidity in the upper troposphere that increases to a moderate to significant moist bias in the lower stratosphere. Contrarily, studies that compared water vapor concentrations and ice supersaturation in ERA-Interim and ERA5 with aircraft in situ observations found that conditions of ice supersaturation are not frequent enough in those reanalysis products, suggesting a dry bias in relative humidity (Dyroff et al., 2015; Gierens et al., 2020; Reutter et al., 2020; Schumann et al., 2021). Consequently, there is no consensus on whether ECMWF reanalysis products are subject to a moist or dry bias in the upper troposphere. It is noted that in situ aircraft observations are potentially biased in terms of spatial sampling because aircraft typically avoid deep convective clouds and the outflow of such clouds. However, cirrus clouds are typically not avoided (Petzold et al., 2020), and therefore a potential sampling issue with respect to cirrus clouds is not expected to play more than a minor role.

Comparing and bias-correcting ERA5 with IAGOS is important because (i) IAGOS data have been shown to be reliable, (ii) IAGOS samples temperature and relative humidity at exactly at the locations and pressure levels that are relevant to aviation studies, and (iii) ERA5 is often used for the analysis of potential contrail formation. It is important to stress that we do not seek to make a universally applicable correction of humidity in ERA5 but rather provide a corrected humidity to enable better estimates of contrail occurrence. Relying on IAGOS data allows us to do so exactly at the locations and pressure levels that are relevant for aviation studies.

To mitigate the dry bias in relative humidity under conditions close to ice supersaturation in ERA-Interim and ERA5, studies have applied either multiplication factors (Schumann and Graf, 2013; Schumann et al., 2015) or parameterized corrections (Teoh et al., 2022a). However, these proposed corrections consider neither the temperature dependence of humidity nor the spatial variations in the relative humidity bias, particularly at different pressure levels. In this study we propose a correction for ERA5 data that is based on a bivariate quantile mapping (QM), which is a standard method of model bias correction (Cannon et al., 2015; Cannon, 2016, 2018). The QM method allows the removal of biases based on the statistical distributions of an observed and modeled quantity, for example temperature and relative humidity, with the aim of better estimating the contrail formation potential in air traffic regions. Here, the QM is trained on 3.5 years of IAGOS observations and collocated ERA5 data of temperature and relative humidity. The QM method is then applied to 5.5 years of ERA5 data and compared with IAGOS. Subsequently, we determine the impact of the correction on the estimation of non-persistent and persistent contrails with respect to IAGOS. In the case of false classifications the underlying differences in simulated and observed temperature and relative humidity are determined to identify systematic shortcomings in ERA5.

The QM correction aims to remove possible temperature and humidity biases in ERA5 post-processed data to better estimate the contrail formation potential beyond the common locations of the IAGOS flight tracks. The advantage of such a correction is that ERA5 data away from the IAGOS flight tracks can be used to estimate the large-scale contrail formation potential, thus providing a broader perspective on potential contrail formation in space and time over the Atlantic. Potential applications include the study of temporal and spatial patterns of contrail formation and the development of rerouting options based on statistical distributions of contrail formation potential.

Subsequent to this Introduction, Sect. 2 describes the data and methods used in this study. After that the results are presented in Sect. 3 and summarized in Sect. 4. Appendices A–C provide detailed information about the IAGOS data analysis.

2 Data and methods

2.1 In-service Aircraft for a Global Observing System

In-service Aircraft for a Global Observing System (IAGOS;  Petzold et al., 2015) is a framework of commercial aircraft equipped with a set of sensors for in situ measurements of meteorological conditions, trace gas concentrations, and cloud properties. Since 2015, all aircraft within the IAGOS framework have been equipped with the “Package 1” (P1) instrument system that includes a backscatter cloud probe (BCP) to measure the particle number concentration N_ice and a dedicated sensor (ICH; Helten et al., 1999) that measures temperature T_P1 and relative humidity r_P1. The BCP is a single-particle backscattering optical spectrometer to detect cloud particles with sizes between 5 and 75 µm. Light with 658 nm wavelength is emitted by a light-emitting diode and directed through a quartz window to the outside of the aircraft fuselage. The light is focused on a narrow range of 4 cm that represents the target area. Cloud particles within the focus backscatter the radiation to a sensor. The intensity of the radiation is proportional to the size, the refractive index, and the shape of the particles as well as the angle under which the particles were hit by the beam. Directly from these measurements the particle size and the particle number concentration N can be derived. More details on the BCP can be found in Beswick et al. (2014). Measurements of N are used to separate in-cloud ($N\ge \mathrm{0.015}{\mathrm{cm}}^{-\mathrm{3}}$) and cloud-free measurements ($N<\mathrm{0.001}{\mathrm{cm}}^{-\mathrm{3}}$) following the thresholds given by Petzold et al. (1997). For intermediate conditions, where $\mathrm{0.001}\le N<\mathrm{0.015}{\mathrm{cm}}^{-\mathrm{3}}$, the measurements cannot be clearly attributed to in-cloud or cloud-free conditions, so they are assigned to the intermediate category (Petzold et al., 2017; Sanogo et al., 2024).

The ICH package is comprised of a capacitive sensor (Humicap-H, Vaisala, Finland) for measurements of relative humidity (defined over liquid water) and a collocated PT-100 platinum sensor for temperature measurements. Both sensors are mounted within a model 102 BX housing of Rosemount Inc. (Aerospace Division, USA) to minimize heating from solar radiation and thermodynamic effects. The recorded data are post-processed by the IAGOS consortium to correct the raw data following Helten et al. (1998) and Boulanger et al. (2018, 2020). Hereby an “in-flight calibration method” (IFC) correcting an offset drift during the course of the deployment period is applied (Smit et al., 2008; Petzold et al., 2017).

Post-processed data of T_P1 and r_P1 are stored every 4 s. However, the response time $t_{\mathrm{1}}-\mathrm{1}/e$ of a sensor is an important characteristic as it directly affects the measurements. $t_{\mathrm{1}}-\mathrm{1}/e$ is commonly defined as the time that is required by a sensor to adapt to $\mathrm{1}-\frac{\mathrm{1}}{e}=\mathrm{0.6}\stackrel{\mathrm{‾}}{\mathrm{3}}$ of an abrupt change in the measured quantity. The temperature sensor is characterized by a response time $t_{\mathrm{1}}-\mathrm{1}/e$ of 4 s and an accuracy of ±0.5 K. The IAGOS humidity sensor is characterized by an average uncertainty of ±6 %. Including uncertainties from sensor calibration and data post-processing, the uncertainty ranges between 5 % and up to 10 % and increases with decreasing temperature (Helten et al., 1998). The humidity sensor's response time $t_{\mathrm{1}}-\mathrm{1}/e$ was determined to be 1 s at 293 K and increases to several minutes at 233 K (Neis et al., 2015). $t_{\mathrm{1}}-\mathrm{1}/e$ of the relative humidity sensor increases due to reduced molecular diffusion into and out of the sensor's polymer substrate. In a first-order approximation, the distance between two IAGOS measurements of T_P1 and r_P1 is 0.96 km at a cruise speed of 240 m s⁻¹. However, $t_{\mathrm{1}}-\mathrm{1}/e$ of the relative humidity sensor averages these measurements over a distance that ranges between 15 km (253 K) and 50 km (233 K) at cruise altitude.

IAGOS measurements in the lower stratosphere that are typically characterized by low values of relative humidity (≈ r_P1 < 10 %) are subject to a moist bias. This moist bias is a nonlinear function of the relative humidity and requires a multidimensional regression correction that is currently under development (Konjari et al., 2022). Therefore, this known moist bias in IAGOS is not corrected in our analysis and it should be kept in mind that subsequent differences between ERA5 and IAGOS for low values of relative humidity may also be attributable to artifacts in the IAGOS measurements. However, since the focus of this analysis is to investigate contrail formation and persistence, only high values of relative humidity are relevant. Consequently, the moist bias for low relative humidity values in the IAGOS observations has little impact on our analysis.

In this study, we use only the IAGOS measurements that fulfill the following criteria:

• IAGOS quality flag of T_P1 and r_P1 is “good” and “limited”

• Measurements are located between 30° N and 70° N and between 110° W and 30° E

• Measurements are between 325 and 150 hPa

• r_P1 (with respect to liquid water) is between 0 % and 100 %

While IAGOS has been operated for many years, the global horizontal and vertical coverage remains heterogeneous. Figure 1 shows a density plot of all IAGOS measurements from January 2015 to June 2021 fulfilling the above criteria. Due to the history of IAGOS and the contributing airlines, the highest measurement density is found across the North Atlantic domain (Fig. 1, green, 65–5° W). A slightly reduced density is found over North America (Fig. 1, red, 105–65° W) and Europe (Fig. 1, blue, 5° W–30° E), particularly towards the western and eastern boundaries of the respective boxes. Outside of the boxes, the coverage is lower, and therefore we focus our analysis on these three domains. These domains also follow the selection from Petzold et al. (2020).

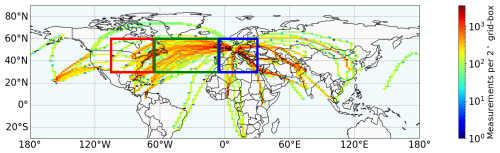
Figure 1 Number of measurements per 2° × 2° grid box of analyzed IAGOS measurements for the time from January 2015 to June 2021. The measurements are filtered for data quality and pressure levels. This study uses measurements in three boxes: United States (US, red), North Atlantic (NA, green), and continental Europe (EU, blue). Longitude coordinates of the bounding boxes are selected to follow Petzold et al. (2020).

Figure 2a–e show the total numbers of measurements per pressure level (p level) and the fractions attributable to the three sub-domains, which can also be understood as a proxy for the altitude distribution of commercial air traffic in the North Atlantic corridor. The largest number of samples (35.3 %) is found at the 200 hPa level (Fig. 2d). Slightly fewer samples are obtained at the 225 hPa level (Fig. 2c) with 32.0 % and at the 250 hPa level (Fig. 2b) with 26.5 %. Contributions from p levels 300 and 175 hPa are small at 2.5 % and 3.3 %, respectively. Due to the typical flight profiles (for an example see Fig. 10 in Petzold et al., 2015) the majority of measurements at low p levels (Fig. 2e) are sampled over Europe, where aircraft reach their maximum cruising altitude when returning to their main hubs. For intermediate p levels, the fraction of samples over the North Atlantic is largest compared to the EU and US domain (Fig. 2c), while for the highest p levels the EU domain dominates again (Fig. 2a), corresponding to where the majority of IAGOS-contributing airlines have their main hubs.

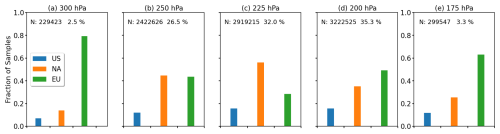
Figure 2 (a–e) Fraction of analyzed IAGOS observations by pressure level separated by sub-domain (see Table 1). The total number of samples per pressure level and the fraction with respect to the total sample size are indicated at the top.

Table 1 ERA5 pressure levels (in hPa) and pressure ranges used to collocate the IAGOS observations.

The measurement density is a function of longitude, latitude, and p level. In addition, the sampling is biased, i.e., by avoiding severe weather and by avoiding or favoring specific atmospheric circulation patterns, such as the jet stream (Petzold et al., 2020). The North Atlantic flight tracks (routes typically used by aircraft to cross the Atlantic) are selected on a daily basis to avoid (westbound) or take advantage (eastbound) of the jet stream. This might cause a bias in the sampling of certain atmospheric conditions that might be associated with the jet stream and midlatitude storm activity (Pasquier et al., 2019).

2.2 ERA5

Meteorological data are obtained from the ECMWF Copernicus Climate Data Store (ECMWF CDS, 2021) using output of the high-resolution component (HRES, T639) of ERA5 (Hersbach et al., 2020). The maximal spatial resolution on the Cartesian grid with 0.25° × 0.25° and maximal temporal resolution of 1 h are used. We make use of the full vertical resolution with a 50 hPa spacing between 350 and 300 hPa and a 25 hPa spacing between 300 and 150 hPa. Along-track temperature T_ERA, relative humidity r_ERA, and cloud fraction CF_ERA are extracted using the nearest-neighbor method, i.e., selecting the ERA5 grid points that are temporally and spatially (horizontally and vertically) closest to the IAGOS observations. Thus spatial and temporal interpolation of relative humidity is not done because the relative humidity depends on the underlying temperature and absolute humidity field, which are both related through the Clausius–Clapeyron relationship. Due to the exponential nature of the Clausius–Clapeyron equation, linear interpolation, for example, could lead to incorrect values of relative humidity.

The ERA5 data set was generated with the ECMWF Integrated Forecasting System (IFS) Cycle 41r2, which was operational in 2016. Within ERA5 the relative humidity is provided with respect to liquid water or ice depending on T_ERA of the grid box. In general, relative humidity (unitless) is defined as the ratio of the water vapor pressure e(T) to the saturation water vapor pressure e_sat(T) as

$$\begin{array}{}\text{(1)}& r={\displaystyle \frac{e}{e_{\mathrm{sat}}\left(T\right)}}.\end{array}$$

In ERA5, e_sat(T) is given by

$$\begin{array}{}\text{(2)}& e_{\mathrm{sat}}\left(T\right)=\mathit{\alpha }\cdot e_{\mathrm{sat},\mathrm{l}}\left(T\right)+(\mathrm{1}-\mathit{\alpha })\cdot e_{\mathrm{sat},\mathrm{i}}\left(T\right),\end{array}$$

with e_sat,l(T) and e_sat,i(T) the saturation water vapor pressure over liquid water and ice, respectively. e_sat,l(T) and e_sat,i(T) are given by

$$\begin{array}{}\text{(3)}& e_{\mathrm{sat}}\left(T\right)=a_{\mathrm{1}}\cdot \exp \left\{a_{\mathrm{3}}\cdot \left({\displaystyle \frac{T-T_{\mathrm{0}}}{T-a_{\mathrm{4}}}}\right)\right\},\end{array}$$

with a₁ = 611.21 Pa, a₃ = 17.502, and a₄ = 32.19 K for liquid water and a₁ = 611.21 Pa, a₃ = 22.587, and a₄ =  −0.7 K over ice; in both cases T₀ is 273.16 K (Buck, 1981; Alduchov and Eskridge, 1996; ECMWF, 2020). The scaling factor α in Eq. (2) is a piecewise linear function of temperature T determined by

$$\begin{array}{}\text{(4)}& \mathit{\alpha }=\left\{\begin{array}{lll}\mathrm{0}& \text{for}& T<T_{\mathrm{ice}}\\ \frac{T-T_{\mathrm{ice}}}{T_{\mathrm{0}}-T_{\mathrm{ice}}}& \text{for}& T_{\mathrm{ice}}\le T<T_{\mathrm{0}}\\ \mathrm{1}& \text{for}& T_{\mathrm{0}}\le T,\end{array}\right.\end{array}$$

with T_ice = 250.16 K and T₀ = 273.16 K. For consistency and comparability with IAGOS all extracted values of relative humidity are converted to be defined solely over liquid water (α=1) or ice (α=0) and are subsequently referred to as r_ERA and r_ERA,ice, respectively. For consistency, IAGOS relative humidity defined over liquid water is labeled with r_P1 and defined over ice with r_P1,ice.

The fixed (Cartesian) grid resolution of 0.25° of ERA5 does not correspond to a constant longitudinal grid box size in kilometers, which instead depends on the latitude. Considering the three sub-domains between 30 and 70° N, the spatial resolution of one ERA5 grid box ranges between 24 km (30° N) and 14 km (70° N). Therefore, we assume an average grid box size of 19 km. However, it should be noted that ERA5 is a spectral model with an internal Gaussian resolution of around 31 km and, thus the effective resolution is coarser than the Cartesian grid resolution (Hersbach et al., 2020). While the IAGOS relative humidity measurements are already smoothed due to the response time of the relative humidity sensor, we additionally smooth the IAGOS measurements by applying a Gaussian filter to account for the mismatch in spatial resolution between IAGOS and ERA5. The standard deviation σ of a Gaussian filter is approximated with

$$\begin{array}{}\text{(5)}& \mathit{\sigma }={\displaystyle \frac{k-\mathrm{1}}{\mathrm{6}}},\end{array}$$

which can be regarded as an approximation for a Gaussian distribution, as 3σ includes 99.7 % of the Gaussian distribution. k is the window length of the smoothing filter and achieved by setting σ = 3 based on the assumption of an average cruise speed of around 240 m s⁻¹ and a resulting segment length (distance between two measurements) of around 1 km.

2.2.1 In-cloud representation of supersaturation in ERA5

Previous studies have shown that the upper troposphere is frequently supersaturated with respect to ice under cloud-free (Gierens et al., 1999; Petzold et al., 2020) as well as cloudy conditions (Spichtinger et al., 2004; Dekoutsidis et al., 2023). While ice supersaturation (ISS) in cloud-free conditions is represented in state-of-the-art numerical weather models, they currently lack an appropriate representation of ISS under cloudy conditions. Often, ISS is clipped to r_ice = 100 %, applying the so-called “saturation adjustment” (McDonald, 1963). This adjustment is also applied in the IFS ice cloud microphysical scheme. The adjustment is a necessity because of a missing diagnostic variable that would track the time-dependent in-cloud saturation (Tompkins et al., 2007). As a consequence of the adjustment, all available “excess” water vapor, which is beyond the threshold, is deposited on existing ice particles within one time step, forcing r_ice back to 100 %. The adjustment approach proved to be suitable for most atmospheric conditions (Gierens et al., 1999; Tompkins et al., 2007; Lamquin et al., 2009). However, the use of ERA5 relative humidity data, which are subject to adjustment in the context of contrail formation analysis, leads to an underestimation of ice-supersaturated regions (ISSRs) in the upper troposphere (Gierens et al., 2020).

To compensate for the relative humidity dry bias in ERA5 for contrail detection applications, r_ERA,ice values are sometimes scaled by multiplication factors between 0.8 and 0.9, particularly in Schumann and Graf (2013) and Schumann et al. (2015). An updated scaling method was proposed by Teoh et al. (2022a, T22 hereafter) that enhances r_ERA,ice > 100 % and reduces r_ERA,ice < 100 % by a factor which depends on the original r_ERA,ice. Within our study, we use T22-corrected values of r_ERA,ice as a benchmark.

2.3 Quantile mapping

In this study we propose using a quantile mapping (QM) method to remove the lack of ISS in ERA5. QM is a correction method that it is frequently used to correct model biases in comparison to observations in a way that imposes the observed statistical distribution (Maraun et al., 2010; Maraun, 2012; Cannon et al., 2015; Cannon, 2018). Within our study, the QM technique is applied to ERA5 data and IAGOS measurements, which are regarded as the reference. Subsequently, we provide a brief overview of the mathematical concept of QM for which we follow the notations from Cannon et al. (2015) and Cannon (2018).

The basis of QM algorithms is to consider cumulative distribution functions (CDFs), F_o,h and F_m,h, of the observed (x_o,h) and simulated (x_m,h) quantity, respectively. The CDFs describe the probability that the value of a quantity (or random variable) x, for example temperature or relative humidity, has a value that is less than or equal to x. In our case x_o,h represents the IAGOS T_P1 or r_P1 measurements and x_m,h the corresponding along-track data from ERA5. The subscript “h” commonly refers to historical data, which can also be understood as training data. The training data make use of IAGOS measurements from January 2018 to June 2021, as this period was considered to be stable in the IAGOS post-processing. Based on the relationship of F_o,h and F_m,h, the biased model output x_m,p(t) at any given time t is corrected. The corrected value is represented by ${\widehat{x}}_{\mathrm{m},\mathrm{p}}\left(t\right)$ (Cannon et al., 2015; Cannon, 2018). This is written in mathematical notation as

$$\begin{array}{}\text{(6)}& {\widehat{x}}_{\mathrm{m},\mathrm{p}}\left(t\right)=F_{\mathrm{o},\mathrm{h}}^{-\mathrm{1}}\mathit{\left\{}{F}_{\mathrm{m},\mathrm{h}}\right[x_{\mathrm{m},\mathrm{p}}\left(t\right)\left]\mathit{\right\}}.\end{array}$$

Equation (6) therefore couples a (potentially biased) model output to the most likely value that is observed in reality by the convolution of F_m,h and $F_{\mathrm{o},\mathrm{h}}^{-\mathrm{1}}$. The QM technique is applied to the entire reference period from January 2015 to June 2021, which includes but exceeds the training period. The periods were chosen to (a) verify the general applicability of the bivariate QM correction method with the same data set and to (b) validate the stability of the bias correction in years outside the training period.

Equation (6) describes the basic QM bias correction that depends only on one variable. Here, we propose a bivariate QM version for T_ERA and r_ERA,ice as the bias between ERA5 and IAGOS might depend on latitude. Such a multivariate QM is similar to the suggested versions by Cannon (2016), Cannon (2018), or François et al. (2020).

For the temperature bias correction, F_o,h and F_m,h are determined at each p level and for two latitude bands. The latitude bands are defined by the outer boundaries of the investigated area with 30 and 70° N, with the split center point given by the 50th percentile of the measurements per pressure level. Thus $F_{\mathrm{o},\mathrm{h}}(p,\mathrm{\Phi })$ and $F_{\mathrm{m},\mathrm{h}}(p,\mathrm{\Phi })$ are determined for different classes of pressure p and latitude Φ. $F_{\mathrm{o},\mathrm{h}}(p,\mathrm{\Phi })$ and $F_{\mathrm{m},\mathrm{h}}(p,\mathrm{\Phi })$ span a temperature range from 190 and 273 K. Similarly, r_ice is corrected with $F_{\mathrm{o},\mathrm{h}}(p,\mathrm{\Phi },T)$ and $F_{\mathrm{m},\mathrm{h}}(p,\mathrm{\Phi },T)$, which are calculated for each p level, two latitude bands Φ, and five temperature bins. As above, T ranges from 190 to 273 K with five temperature bins defined by 20th percentile steps so that each temperature bin contains an equal number of observations at each p level and latitude bin. Consequently, $F_{\mathrm{o},\mathrm{h}}(p,\mathrm{\Phi },T)$ and $F_{\mathrm{m},\mathrm{h}}(p,\mathrm{\Phi },T)$ are calculated for a total of 80 bins. A visualization of the resulting CDFs of temperature and relative humidity is given in Appendix A.

The presented version of the QM correction assumes a time-invariant bias between the model and observations. On the model side, we assume that the ERA5 data set is constant in time, since it is generated only with the IFS Cycle 41r2 and therefore has the same implementation of the dynamical core and cloud microphysics representation. However, there may be some changes in the quantity and quality of observations feeding into the ERA5 data assimilation system. The IAGOS reference observations may also vary over time due to changes in instrument calibration and maintenance procedures. The temporal consistency of IAGOS relative humidity measurements was investigated by means of monthly climatologies. A constant bias in temperature and relative humidity between ERA5 and IAGOS was found. IAGOS relative humidity measurements from the year 2017 are an exception, when IAGOS observations tend towards elevated relative humidity observations with respect to the other years, while the bias in temperature remained constant (see Appendix B). Biases between IAGOS, ERA5, and corrected ERA5 were further separated for their dependencies on latitude and longitude. While the bias in the temperature was found to be independent of longitude and latitude, the bias in relative humidity was smallest in North America and increased towards continental Europe (see Appendix C).

2.4 Schmidt–Appleman criterion, potential contrail formation, and contrail persistence

To allow for contrail formation the ambient air must be sufficiently cold and moist. The formation is typically estimated using relative humidity r_crit and a critical temperature T_crit threshold that is derived from the Schmidt–Appleman criterion (SAc;  Appleman, 1953). The SAc is based solely on thermodynamic principles and has been determined to be a valid approximation, although it does not provide information on the fate of the contrail, which is a more complicated function of the ambient conditions but also the interactions of the vortex phase with the environment. The SAc is a necessary but insufficient criterion for persistent contrails. For contrails to be persistent (lifetime > 10 min), the ambient air must be additionally supersaturated with respect to ice (r_ice > 100 %) in so-called ice-supersaturated regions (ISSRs). However, even under slightly subsaturated conditions contrails can form, but the persistence is uncertain. In weakly subsaturated conditions the dissipation of ice crystals is slow and, hence contrails can remain for hours (Li et al., 2023). Within this study, we use the revised version of the SAc, following Schumann (1996) and Rap et al. (2010). Calculations are performed for kerosene with a fuel specific energy of 𝒬 = 43.2 MJ kg⁻¹ and an emission index of water of EI${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ = 1.25. The overall propulsion efficiency η is set to a typical value of 0.3 (Rap et al., 2010). For details on the SAc and equations used to calculate T_crit and r_crit the reader is referred to Wolf et al. (2023).

The SAc and the requirement for ice supersaturation separate the water vapor–pressure–temperature diagram (see Fig. 2 in Wolf et al., 2023) in four different areas. The first area represents conditions where the ambient air fulfills the SAc but is subsaturated with respect to ice. In our study, contrails that form under these conditions are regarded as non-persistent and are labeled as non-persistent contrails (NPCs). Within the second area the SAc is fulfilled and ambient air is additionally supersaturated with respect to ice, and persistent contrails (PCs) can form. The third area is treated as a special case, in which the ambient air does not fulfill the SAc but is ice-supersaturated. Contrails that might have formed under conditions “R1-NPC” or “R2-PC” and that are mixed in area 3 may persist and spread. Therefore, area 3 can be understood as a potential “reservoir” (R) for contrails (Wolf et al., 2023). The SAc and the ISS threshold are used to flag the IAGOS measurements and the along-track ERA5 for NPC, PC, and R conditions. Samples that belong to none of these three categories are flagged as “no contrails” (NoC).

3 Results

3.1 Distributions of temperature and relative humidity from ERA5 and IAGOS

In a first step, along-track temperature and relative humidity from January 2015 to June 2021 from IAGOS and ERA5 are compared in terms of probability density functions (PDFs), mean values, and mean difference (MD). The performances of the QM correction and the T22 correction are further quantified by the root mean square error (RMSE), the mean absolute error (MAE), the mean square error, and the mean difference (MD). The analysis is limited to p levels 250, 225, and 200 hPa, representing the most frequented p levels (Fig. 2b–d).

Beginning with the temperature distributions, Fig. 3 (first column) shows that at p levels 200 and 225 hPa, measured T_P1 and simulated T_ERA agree well in terms of the MD (dashed lines) and the overall shape of the distributions. Only minor deviations in the MD of −0.4 K (200 hPa) and −0.1 K (225 hPa) are found, with a negative MD suggesting that ERA5 is colder than observed on average (T_ERA < T_P1; see Fig. 3, second column). After the bias correction, the MD is reduced at all p levels to below 0.1 K, and the shape of the PDFs of $T_{\mathrm{ERA}}^{\mathrm{cor}}$ is also adjusted to better match the distributions of T_P1 (Fig. 3, second column).

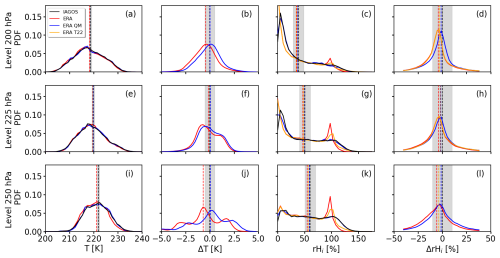
Figure 3 Probability density functions (PDFs) of temperature T (in K) and relative humidity r_ice with respect to ice (in %) from IAGOS (black), ERA5 (red), and bias-corrected ERA5 data (blue). From top to bottom, rows represent pressure levels 200, 225, and 250 hPa. The first column shows PDFs of temperature from IAGOS T_P1, ERA5 T_ERA, and the bias-corrected ERA5 $T_{\mathrm{ERA}}^{\mathrm{cor}}$. The second column presents the absolute difference of T_ERA and $T_{\mathrm{ERA}}^{\mathrm{cor}}$ with respect to T_P1. Columns three and four are the same as columns one and two but for relative humidity r_ice. In addition, bias-corrected $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{T}\mathrm{22}}$ using the correction method after T22 is given in orange. Differences are calculated by subtracting the IAGOS reference from the model output. In each plot, the median values of the distributions are indicated by the dashed vertical lines, with the black line indicating the IAGOS data. For reference, the average measurement uncertainties for T_P1 and r_ERA,ice with ±0.5 K and ±10 % are indicated around mean T_P1 and r_ERA,ice, respectively.

Relative humidity is plotted in the third column of Fig. 3. The distributions of r_ice are bimodal, although the two modes have different magnitudes. The bimodal shape in the PDFs of upper-air r_ice matches previous studies, e.g., Ruzmaikin et al. (2014), who used satellite observations from the Atmospheric Infrared Sounder (AIRS). The first mode at low r_ice is caused by dry atmospheric conditions related to dry-air intrusions from the stratosphere into the upper troposphere, e.g., behind frontal zones (Browning, 1997), and flight sections within the lower stratosphere. The second mode at r_ice = 100 % is related to regions of high humidity or measurements inside clouds. With the general decrease in absolute humidity and possible intrusion of dry air from the stratosphere, the first mode becomes more and more pronounced with decreasing p, while the second mode flattens and almost vanishes.

Comparing the PDFs of r_ERA,ice and r_P1,ice minor differences are found for the first mode. However, larger differences appear for the second mode at r_ice = 100 %, where the occurrence frequency of large r_ERA,ice well exceeds r_P1,ice, while r_ERA,ice > 100 % is underrepresented. The PDF of r_ERA,ice close to 100 % is characterized by a triangular shape, while the distribution of r_P1,ice is smaller in magnitude, broader in width, and skewed towards r_P1,ice > 100 %. Furthermore, at all p levels, mean r_ERA,ice (red line, column three in Fig. 3) is generally shifted to lower values compared to mean r_P1,ice (black line). This indicates a lack of ISSR in ERA5 that is expected from its use of saturation adjustment (Sect. 2.2.1). The resulting MDs are determined to be −4.3 % (200 hPa), −3.8 % (225 hPa), and −5.5 % (250 hPa).

Smoothing the IAGOS data, as explained in Sect. 2.2, leads to mean values of T_P1 and r_P1,ice for the native and the smoothed data that are similar by 0.1°C and 1 %, respectively. As smoothing did not change the mean values significantly, the differences in the PDFs of ERA5 and IAGOS, as well as the bias in mean r_ERA,ice compared to r_P1,ice, cannot be attributed to differences in the spatial resolutions. However, the smoothing of the IAGOS data leads to a reduction in the variability as well as in the extreme values in measured T_P1 and r_P1,ice (not shown here).

To correct for the lack of ISS, i.e., the mismatch in the PDFs (Fig. 3, third column), the QM technique is applied. After the QM correction the MDs are reduced by almost half to −1.3 % (200 hPa), −1.5 % (225 hPa), and −0.9 % (250 hPa), which indicates a remaining slight dry bias in r_ERA,ice compared to IAGOS as the MD remains negative (see Fig. 5j). However, the QM correction leads to an adjustment of all PDFs such that the shape of the PDFs of corrected $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ matches the IAGOS observations. For comparison, we apply the T22 correction that only partly removes the relative humidity dry bias, resulting in MDs between −3.7 % (250 hPa) and −2.0 % (225 hPa) (see Fig. 3, fourth column, and Fig. 5j). Furthermore, differences in the second mode in relation to the IAGOS observations remain as the T22 correction only scales values above a certain threshold, which primarily shifts the bulk of data points from 100 % to higher r_ice. An overview of the original and corrected mean T and r_ice is given in Table 2.

Table 2 Mean values of temperature T and relative humidity r_ice from IAGOS and ERA5 calculated from the original and the corrected values using the QM correction and the scaling from T22. The data include filtered measurements from January 2015 to June 2021. Values in parentheses are the differences relative to IAGOS.

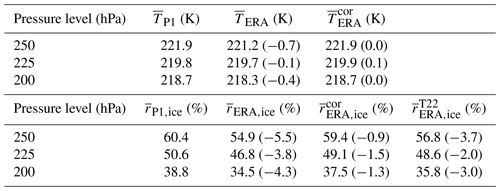
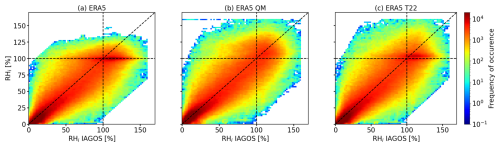
Figure 4 (a–c) Bidimensional histogram of original r_ERA,ice (a), QM-corrected $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ (b), and T22-corrected $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{T}\mathrm{22}}$ (c) as a function of IAGOS-observed r_P1,ice. Relative humidity is binned in intervals of 2 %. r_ice is given as relative humidity with respect to ice. Pressure levels 250, 225, and 200 hPa are combined. Perfect agreement is indicated by the dashed diagonal line, and ice saturation is indicated by the dashed horizontal and vertical lines.

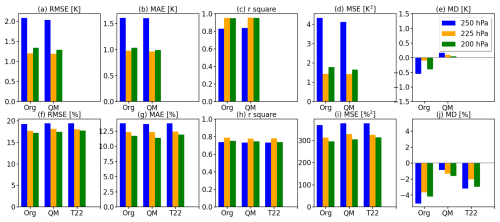
Figure 5 Bar plots of (a, f) root mean square error (RMSE), (b, g) mean absolute error (MAE), (c, h) R² score, (d, i) mean square error (MSE), and (e, j) mean difference (MD) of ERA5 against IAGOS. The first row shows metrics for T and the second row for r_ice. The first set of bars represents the original ERA5 output (label Org), while the second set represents the data set after the quantile mapping correction (label QM). In the second row a third set of bars indicates the T22 correction. The metrics are calculated for pressure levels of 250 (blue), 225 (orange), and 200 hPa (green).

The individual PDFs of r_ice are used to compile joined two-dimensional (2D) histograms that are shown in Fig. 4a–c. In general, the frequency distribution of r_ERA,ice and r_P1,ice follows the diagonal line of “ideal” agreement (Fig. 4a). However, the distribution is slightly shifted to below the 1:1 line, indicating a lower r_ERA,ice and therefore drier conditions in ERA5 compared to the IAGOS observations. Particularly striking is the elongated feature of the r_ERA,ice distribution positioned close to 100 % (second mode) and a flattening for r_ERA,ice > 130 % as a result of the saturation adjustment. Gierens et al. (2020) presented a similar comparison of r_ice between ERA5 and IAGOS, providing only a scatter plot and not a density distribution. They found a strong scattering around the 1:1 line and described the distribution as “scattered all over the place”, with poor agreement among r_ERA,ice and r_P1,ice. While we agree that the distributions in Fig. 4a–c are subject to scattering, the majority of the points (red to dark-red colors) show a reasonable alignment along the 1:1 line. For the individual pressure fields of 250, 225, and 200 hPa, R² scores of 0.74, 0.79, and 0.75 are determined, respectively (see also Fig. 5h).

After the application of the QM correction the alignment with the 1:1 line is improved (see Fig. 4b). As expected from Fig. 3, the artificially pronounced second mode in r_ERA,ice is removed in $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ and the distribution extends further towards r_ice > 130 %, better representing the conditions observed by IAGOS. The QM correction leads to R² values of 0.73, 0.78, and 0.75 at 250, 225, and 200 hPa, respectively, that are similar to the uncorrected ones (see also Fig. 5h).

For reference, the T22-corrected r_ice is compared with observed r_P1,ice and shown in Fig. 4c. The scaling of the T22 method enhances r_ice values that are close to or above 100 % and shifts the elongated feature towards higher r_ice but does not eliminate it. For this correction R² values of 0.73 (250 hPa), 0.78 (225 hPa), and 0.74 (200 hPa) are calculated. So this type of correction leads to a small decrease in the R² score compared to the original ERA5 data.

To quantify the performance and the impact of the QM method, five metrics are calculated, namely the root mean square error (RMSE), the mean absolute error (MAE), the R² score, the mean square error (MSE), and the mean deviation (MD). This set of metrics has been selected to account for the different sensitivity of the metrics to outliers.

The top row in Fig. 5 visualizes the calculated metrics for the temperature. In general, the 250 hPa p level is characterized by the largest RMSE of 2.1 K, MAE of 1.6 K, and MSE of 4.3 K² in relation to the other p levels, which is explained by the enhanced natural variability in the temperature field with increasing p level. A larger natural variability leads to larger differences among the IAGOS measurements and the nearest ERA5 values. At the 225 and 200 hPa levels, in a more stratified atmosphere, the RMSE, MAE, and MSE are generally lower and similar for both p levels with values around 1.2 K, 1 K, and 1.5 K², respectively. The QM correction leads to a minimal increase in the R² score at all p levels, while RMSE, MAE, and MSE increase unnoticeably. However, as expected and as demonstrated before, the MD is significantly reduced.

Similarly, the bottom row in Fig. 5 visualizes the calculated metrics for the original, QM-corrected, and T22-corrected r_ice against the IAGOS observations. As for the temperature, the RMSE, MAE, and MSE are largest for the 250 hPa p level, followed by the 225 and 200 hPa p levels. At all p levels, the QM and T22 corrections lead to a constant or marginally increased RMSE, MAE, and MSE, while the R² score remains almost constant. The increase in RMSE, MAE, and MSE appears counterintuitive from the results shown in Fig. 4, with an improvement in the mean values and the distributions. However, both correction methods are purely statistical and do not remove differences in the temperature and relative humidity of individual data points. Instead singular data points might be falsely adjusted by the QM correction, which then creates outliers to which the RMSE and MSE respond very sensitively, thus the large RMSE and MSE for relative humidity. In contrast, MAE is less susceptible to outliers.

3.2 Distribution of relative humidity under cloud-free and in-cloud conditions

The IFS ISS adjustment partly depends on the ERA5 cloud fraction CF_ERA as only cloud-containing grid boxes are clipped in r_ice (Tompkins et al., 2007). The effect of CF_ERA on the distribution of r_ice is investigated by separating $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ by using thresholds of CF_ERA < 0.2 (cloud-free), 0.2, ≦ CF_ERA < 0.8 (intermediate), and 0.8, ≦ CF_ERA <= 1 (cloudy). Accordingly, IAGOS measurements of r_P1,ice are separated for cloud-free, intermediate, and in-cloud measurements using the cloud particle number concentration N as described in Sect. 2.1. This is only a subset of the IAGOS data used in this study because BCP data are not always available for these flights. Data from pressure levels 250, 225, and 200 hPa are considered here.

Figure 6a shows PDFs of r_ice from IAGOS (black), ERA5 (red), and QM-corrected ERA5 (blue). The data are filtered separately for conditions, where IAGOS measures outside of clouds or where ERA5 indicates almost cloud-free conditions (CF ≦ 0.2). This category includes 88.3 % of the ERA5 data and 97.7 % of the IAGOS data. For cloud-free conditions, the distributions of r_ice < 60 % are similar to the one presented Fig. 3c, g, and k. As expected, the three PDFs of IAGOS, ERA5, and QM-corrected ERA5 are characterized by a peak towards small r_ice, which is attributed to measurements and ERA5 output with dry conditions. Differences in the PDFs appear when r_ice approaches 100 %, where the probability of occurrence in r_P1,ice is higher compared to r_ERA,ice. This resembles the scatter plot in Fig. 4a, where r_ERA,ice systematically tends toward smaller r_ice. Recall that IAGOS is subject to a slight moist bias in relative humidity under conditions with low absolute humidity that are often encountered in the lower stratosphere (see Sect. 2.1). It can be seen in Fig. 6a that the QM correction has only a limited impact on $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$. This is due to the nature of, and is an advantage of, the QM technique, which respects the probability of occurrence by giving less weight to rare conditions (logarithmic y scale). For cloud-free or almost cloud-free conditions mean values for r_P1,ice, r_ERA,ice, and $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ of 28.9 %, 30.1 %, and 38 % were determined.

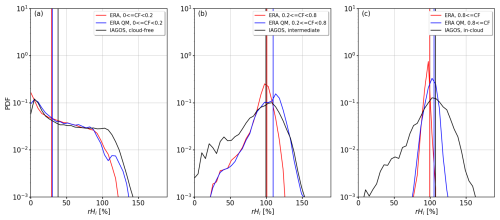
Figure 6 (a–c) Probability density functions of relative humidity r_ice with respect to ice (in %) from IAGOS (black), original ERA5 (red), and corrected ERA5 (blue) using quantile mapping. Panels (a), (b), and (c) show the PDFs separated for cloud-free, intermediate, and in-cloud conditions, respectively. Mean values of the distributions are indicated by the vertical lines.

PDFs of r_ice of intermediate values are shown in Fig. 6b. This category includes 7.3 % of the ERA5 data and 1.3 % of the IAGOS data. Within this category it is not clear whether an ERA5 data point should be considered cloudy or cloud-free. The same is the case for IAGOS measurements. The shape of the PDFs changed compared to Fig. 6a, as the shape is now dominated by a peak in r_ice between 90 % and 100 %. The shape of r_P1,ice from IAGOS reveals the largest variability (width of the distribution), partly due to the intermediate detection of in-cloud and cloud-free conditions. QM-corrected values of $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ lead to a distribution where the left tail resembles the distribution from the original data r_ERA,ice, while the right tail approaches the distribution of r_P1,ice. Under intermediate cloud conditions the QM correction skews the distribution to the right, which leads to a mean of $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ = 109.3%. For r_ERA,ice and r_P1,ice mean values of 100.9 % and 99.4 % are determined, respectively. The improved representation of r_ERA,ice in the intermediate category is particularly important, as NPC and PC formation is relevant from a radiative perspective in cloud-free or almost cloud-free air.

Figure 6c shows PDFs of r_ice when CF_ERA is larger than 0.8, i.e., where an ERA5 data point has a high probability of being considered cloudy, or when IAGOS measurements are from inside of clouds. This category includes 4.4 % of the ERA5 data and 0.9 % of the IAGOS data. The relatively limited number of samples (< 1 %) from within clouds causes a less robust PDF compared to the PDF based on measurements conducted outside of clouds. This difference might be due to the fact that, compared to research aircraft measurements, the backscatter cloud probe misses clouds with N smaller than its detection limit of N = 0.001 cm⁻³ (Beswick et al., 2014; Petzold et al., 2017). All three distributions of r_ice are narrower compared to the cloud-free or intermediate conditions, with r_P1,ice being broadest. This is partly due to the larger natural variability in the IAGOS measurements compared to the ERA5 simulations of r_ERA,ice. The distribution of r_ERA,ice is centered between 75 % and 100 % with a steep slope on either side. Particularly towards r_ERA,ice of 100 % the cutoff of r_ERA,ice for in-cloud conditions is prominent, which is not represented in r_P1,ice. The QM correction slightly broadens the distribution of $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ towards values above 100 %. The bias in r_ERA,ice under cloudy conditions is reduced, resulting in a mean $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ of 105.6 %. This is closer to the measured mean r_IAGOS,ice of 107.6 % compared to the original output of r_IAGOS,ice with a mean of 99.6 %. In addition, the distribution of QM-corrected $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ is slightly broadened but does not resemble IAGOS and better agrees with measurements from, e.g., Krämer et al. (2016, 2020) and Li and Groß (2022), who reported in-cloud r_ice between 90 % and 110 % due to the slow sublimation or growth of ice particles in cloudy conditions.

3.3 Along-track contrail formation potential and the effect of applied corrections

Along-track time series of uncorrected and corrected ERA5 data and IAGOS measurements are flagged for non-persistent contrail (NPC), persistent contrail (PC), and reservoir (R) conditions using the method described in Sect. 2.4. All data points not belonging to any of the categories are flagged for no contrail formation (NoC). Considering all data points from January 2015 to June 2021 at p levels 250–200 hPa, it is found that 44 % of the IAGOS observations show potential for NPC formation. PCs appear to be less frequent with about 12.1 %, and R conditions are rare with an occurrence of only 1.2 %. Using the original along-track ERA5 output, the contrail formation potential for NPC, PC, and R is estimated to be 50.3 %, 7.9 %, and 0.8 %, respectively. Due to the dry bias in relative humidity and the clipping of r_ERA,ice at 100 % the NPC category is enhanced in ERA5 at the expense of the PC category compared to the IAGOS measurements.

For reference, Teoh et al. (2020) (see Table 1 therein) estimated that 18.4 % of the flights form contrails (i.e., at least one contrail section during a flight), with only 7.4 % of the total analyzed flight distance leading to contrails. While there is reasonable agreement in the occurrence of contrails, we identified more than twice the chance of forming non-persistent contrails. There are two main potential sources of disagreement. First, the account of aircraft characteristics is different. The estimates of our study solely rely on the SAc including constant values for fuel properties (specific heat capacity Q) and the overall propulsion efficiency η given in Sect. 2.4. Contrarily, the more elaborate method by Teoh et al. (2020) uses a fleet data set that includes flight-specific information on aircraft engine type, thrust settings during flight stages, and estimates of black carbon (soot) emissions. This information was ingested into the contrail cirrus prediction model CoCiP from Schumann (2012) to determine contrail formation and the related radiative effect. It is noted that CoCiP only considers flight sections to be a contrail when a certain contrail radiative effect is exceeded; i.e., the ice particle number is larger than 10³ m⁻³ and the cirrus optical thickness is larger than 10⁻⁶ (Schumann, 2012). Thus, the results from Teoh et al. (2020) consider the potential for contrail formation, actual aircraft emissions, the synoptic conditions, and the contrail radiative effect. For our approach, with the IAGOS data set, no such aircraft performance data are available. Secondly, the way flight distance is counted as contrail-forming is different between the two studies. In our study, the SAc accounts only for thermodynamic properties.

Subsequently, the impact of corrected $T_{\mathrm{ERA}}^{\mathrm{cor}}$ and $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ on the along-track classification of NPC, PC, and R is investigated. The individual contributions of T and r are separated by applying the QM correction separately to T and r. The scaling method from T22 is shown as a benchmark.

Applying the QM correction only to T_ERA leads to a reduction in the fraction of NPC from 50.3 % to 47.8 % and for PC from 7.9 % to 7.7 %, respectively. The correction increases the mean $T_{\mathrm{ERA}}^{\mathrm{cor}}$ (ambient temperature), allowing fewer ERA5 samples to pass the T and r_ice thresholds for NPC and PC formation. Consequently, the fraction of NoC or R conditions increases, where supersaturation is reached but the SAc is not fulfilled. The remaining differences in the distributions of NPC, PC, and R between the T_ERA-only corrected and the IAGOS measurements indicate that temperature correction alone is insufficient to better represent NPC and PC (see Table 3).

Table 3 Fractions of measurement points (in %) labeled as non-persistent, persistent, and no contrail formation, as well as reservoir conditions. The results using the scaling method after Teoh et al. (2022b) are labeled with T22.

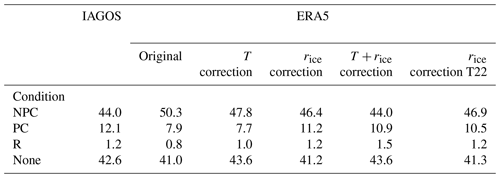
Applying the QM correction only to r_ERA,ice reduces the frequency of NPC to 46.3 %. At the same time the number of PCs increases to 11.4 % and R conditions are slightly increased to 1.2 %. Thus, this correction leads to an increase in PC, mostly at the expense of the NPC category. This is simply because of the higher mean $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ and correspondingly more samples that pass the thresholds given by the SAc. Compared to the T_ERA-only correction, the r_ERA,ice-only correction has the largest impact on the categorization and is, therefore, the main driver of potential misclassification and needs to be correctly represented.

The scaling-based T22 correction is most similar to the QM correction of r_ERA,ice only. After the T22 correction, 46.9 % of the samples were identified as NPC, which is slightly above the IAGOS reference and similar to the estimated occurrence after the QM r_ERA,ice-only correction. With the T22 correction, PC and R conditions are found in 10.5 % and 1.2 % of the cases, which is also comparable to the result from the QM r_ERA,ice-only correction.

Applying the QM correction to both T_ERA and r_ERA,ice results in a decrease in NPC to 44.0 %, which corresponds to the occurrence of NPC that is found in the IAGOS data set and is below the original ERA5 data. It is also slightly lower than after the QM r_ERA,ice-only correction. This is due to the simultaneous correction of T and r_ERA,ice as some samples become too warm to form contrails. PC conditions are found in 10.9 % of the samples, which is slightly less compared to the QM correction of r_ERA,ice. The frequency of R conditions and NoC increase slightly. It is found that the combined correction of T_ERA and r_ERA,ice leads to the best agreement with the IAGOS observations. While the improvement is primarily caused by the correction of r_ERA,ice, it is emphasized that T also has to be corrected as the calculation of r_ERA,ice depends on the underlying temperature field. The conversion of specific humidity to relative humidity and the conversion between relative humidity with respect to ice and liquid water via the saturation curves become very sensitive to T when approaching low temperatures that exist at typical flight levels; see, e.g., Ambaum (2020).

For a detailed understanding of how the QM correction modifies the classification of NPC, PC, R, and NoC, the redistribution among the contrail categories is determined by tracking the classification before and after the corrections. The distributions have to be interpreted qualitatively as the statistics include a potential yearly variation. Figure 7a–d show the contribution of the pre-correction categories to the classification after applying a specific correction method.

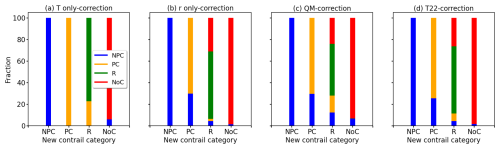
Figure 7 (a–d) Redistributed fractions (in %) of original ERA5 contrail classification with respect to the classification after applying the T-only correction, the r-only correction, the QM correction, and the correction after T22, respectively. The original classifications of non-persistent contrails (NPCs) are given in blue, persistent contrails (PCs) are given in orange, reservoir conditions (R) are colored in green, and samples that do not allow for contrail formation (NoC) are given in red.

For example, Fig. 7a shows that the majority of the QM T_ERA-only corrected ERA5 samples that are now classified as NPC were already NPC before the correction. Only a minority of the new NPC samples were previously identified as PC or belonged to the NoC category before. The QM T_ERA-only correction does not significantly affect the PC category but leads to the largest redistribution in the R category. Due to the increase in mean T_ERA, previous PC-flagged samples now contribute 21 % to the R category. However, the proportion of R conditions relative to the total number of samples is small and thus the overall relevance is small. Similarly, samples previously classified as NPCs contribute little to the NoC category.

Similar to Fig. 7a, the QM r_ERA,ice-only correction, given in Fig. 7b, and the T22 correction, given in Fig. 7d, lead to only minor changes in the NPC category. In the case of the QM r_ERA,ice-only correction the newly flagged samples in the R category are composed of samples that already belong to the R category (62.5 %) or the NoC category (31.3 %). In the case of the T22 correction a similar pattern is found but with an additional share of previously flagged PC samples (7.0 %). Both corrections show similar patterns for the newly formed PC category, which now consist of about of 75 % and 25 % of former PC and NPC data points, respectively.

The QM correction, shown in Fig. 7c, is a superposition of the QM T_ERA-only and QM r_ERA,ice-only correction. No redistribution within the NPC category is found. The R category is subject to the strongest redistribution but keeping in mind that the R category represents the smallest proportion of all data points. The newly formed PC category now consists of 29 % and 71 % of former NPC and PC data points, respectively.

3.4 Analysis of collocated contrail formation potential from ERA5 and IAGOS

Beyond the comparison of bulk statistics, the collocated temporal and spatial along-track representation of NPC and PC in ERA5 are validated against IAGOS observations using a confusion matrix, where we consider NPC, PC, R, and NoC conditions to be single binary events.

A confusion matrix is a table that is used to visualize the classification performance of an algorithm (see Table 4 for a schematic for a binary event). In our case the classification is based on (i) the IAGOS observations and (ii) the ERA5 data. Perhaps persistent contrails form only in a minority of situations, so we computed the equitable threat score (ETS;  Mason, 2012) following the reasoning of Gierens et al. (2020) given in Appendix A of their paper. The ETS can be regarded as equal to the four entries of the contingency table when the total number of samples is sufficiently large (Hogan et al., 2010; Gierens et al., 2020), which is the case considering our data set. The ETS ranges between 0 for random relations and 1 for perfect correlation and is calculated on the basis of true positive (TP), true negative (TN), false positive (FP), and false negative (FN) by

$$\begin{array}{}\text{(7)}& \mathrm{ETS}={\displaystyle \frac{\mathrm{TP}-r}{\mathrm{TP}+\mathrm{FN}+\mathrm{FP}-r}},\end{array}$$

with

$$\begin{array}{}\text{(8)}& r={\displaystyle \frac{(\mathrm{TP}+\mathrm{FP})\cdot (\mathrm{TP}+\mathrm{FN})}{(\mathrm{TP}+\mathrm{FP}+\mathrm{FN}+\mathrm{TN})}}.\end{array}$$

Table 4 Schematic contingency table for a binary event. Adapted from Stephenson (2000).

The ETS is calculated for the original and corrected ERA5 data against IAGOS estimates (see Table 5 and Fig. 8).

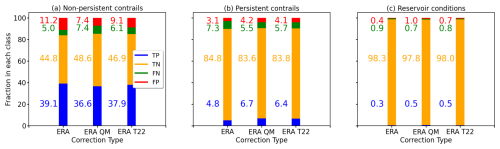
Figure 8 Fraction of true positive (TP), true negative (TN), false positive (FP), and false negative (FN) results from ERA5 data classifications based on IAGOS observations (reference) for (a) non-persistent contrails, (b) persistent contrails, and (c) reservoir conditions. ERA5 data that are compared in their original form are labeled as“ERA”, data after the QM correction are labeled as “ERA cor2d”, and data using the correction after Teoh et al. (2022b) are labeled as “ERA T22”.

Table 5 Equitable threat score (ETS) calculated from the confusion matrix between IAGOS (reference) and the original ERA5 as well as the corrected ERA5 output.

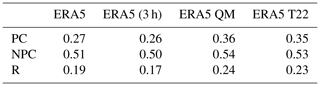
Statistics based on a confusion matrix like the one given in Table 4 are a tough test for ERA5 because even small spatial or temporal errors in the temperature or humidity fields can lead to misclassifications. To estimate the effect of a possible pattern shift, we use the 3-hourly (3 h) ERA5 data on T_ERA and r_ERA,ice. Evaluating the NPC and PC formation as well as the R condition with the confusion matrix between IAGOS and the coarsened ERA5 (3 h), the ETS remains almost constant. This indicates that the sensitivity of the confusion matrix and the ETS to temporal and spatial decorrelations that occur within 3 h is low. In addition, the differences in ETS between the original ERA5 and the 3-hourly ERA5 data provide a reference for estimating the impact of the corrections in relation to temporal–spatial mismatches. Thus, differences in the calculated ETS that are larger than that reference are truly due to incorrect values of T_ERA and r_ERA,ice.

The application of the QM correction modifies the distributions of temperature and relative humidity in such a way that PC conditions are correctly detected more frequently, resulting in an increase in ETS from 0.27 to 0.36. Similarly, for the NPC and R categories an increase in ETS from 0.51 to 0.54 and 0.19 to 0.24, respectively, is observed. Thus, the QM correction leads to an improvement across all categories. The QM correction appears to be most effective for the PC category, which is also the most relevant category considering the longevity and the potential radiative effects of contrails. Similar improvements in the contrail estimation are observed for the T22 correction. For all categories, an increase in the ETS is observed compared to the original ERA5 data. The T22-correction-related ETS values are comparable to those of the QM correction and are listed in Table 5. Based on the original ERA5 data, an ETS of 0.27 and 0.51 is calculated for PC and NPC conditions, respectively. For reference, we provide values obtained by Gierens et al. (2020), who compared ERA5 with MOZAIC measurements. Gierens et al. (2020) compared MOZAIC data and ERA5 for individual months, while we calculate the ETS on the basis of several years. Therefore, the ETS values from Gierens et al. (2020) are subject to significant monthly variations. For comparability, the ETS values from Gierens et al. (2020), given for the months of January, April, July, and October in their Table 1, were used to calculate mean ETS of 0.12 and 0.74 for PC and NPC conditions, respectively. Evaluating the contingency tables by means of ETS, it can be concluded that the QM correction and the T22 correction lead to a better estimation of all contrail types compared to the original ERA5 data. Compared to the mean values calculated from Gierens et al. (2020) we found a lower performance of uncorrected and corrected ERA5 for the NPC category, while there is a better performance for the PC category, especially after the QM correction and the T22 correction.

3.5 Disentangling classification with respect to temperature and relative humidity

Even after QM correction, about 16 % of the NPC and 11.5 % of the PC observation–measurement pairs are classified as “false positive” and “false negative”. The sensitivity study using 3-hourly ERA5 data showed that this is unrelated to spatial mismatches but is rather due to actual deviations in temperature and relative humidity between IAGOS and ERA5. Subsequently, we aim to quantify the mean differences in temperature and relative humidity that remained after the QM correction and that contribute to the misclassification of potential contrail formation. Within the following section all ERA5 values are QM-corrected.

The along-track samples from IAGOS and ERA5 are categorized by a contingency table with the categories NoC, NPC, and PC, taking IAGOS as the reference. The created contingency table is visualized in the legend of Fig. 9. The diagonal elements of the contingency table represent combinations of IAGOS and ERA5 that agree in terms of contrail occurrence, while all off-diagonal values are incorrectly classified. For each of the nine contingency table combinations the corresponding mean differences in the temperature,

$$\begin{array}{}\text{(9)}& \stackrel{\mathrm{‾}}{\mathrm{\Delta }T}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{T}_{\mathrm{ERA}\mathrm{5},\mathrm{i}}-T_{\mathrm{IAGOS},\mathrm{i}},\end{array}$$

and relative humidity,

$$\begin{array}{}\text{(10)}& {\stackrel{\mathrm{‾}}{\mathrm{\Delta }r}}_{\mathrm{ice}}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{r}_{\mathrm{ERA}\mathrm{5},\mathrm{ice},\mathrm{i}}-r_{\mathrm{IAGOS},\mathrm{ice},\mathrm{i}},\end{array}$$

are calculated, with n the number of data points in each category. Figure 9a–c present the 2D space spanned by $\stackrel{\mathrm{‾}}{\mathrm{\Delta }T}$ and $\stackrel{\mathrm{‾}}{\mathrm{\Delta }r}$ for each of the contingency table combinations at p levels 250, 225, and 200 hPa, respectively. In the following, a notation of “A–B” with $\mathrm{A},\mathrm{B}\in \{\mathrm{NoC},\mathrm{NPC},\mathrm{PC}\}$ is used as an abbreviation for the classification of A from IAGOS and B in ERA5. For example, a notation of “NPC–PC” means a combination of IAGOS NPC conditions and ERA5 PC conditions.

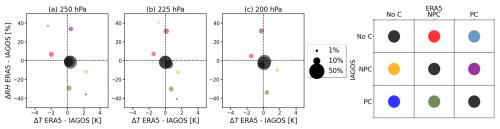
Figure 9 (a–c) Mean difference in temperature T (in K) and relative humidity r_ice (in %) between IAGOS and ERA5 corrected by quantile mapping for three pressure levels: from left to right, 250, 225, and 200 hPa. Colored dots represent a combination of mean ΔT and Δr for one of the nine categories of the contingency table (right). The area of the dots is proportional to the fraction of measurement–simulation pairs with respect to the total number per pressure level. Colors indicate the classification using the legend shown in the right-hand panel with the following categories: no contrail formation (NoC), non-persistent contrails (NPCs), and persistent contrails (PCs).

In general, $\stackrel{\mathrm{‾}}{\mathrm{\Delta }T}$ and ${\stackrel{\mathrm{‾}}{\mathrm{\Delta }r}}_{\mathrm{ice}}$ are similar at all three p levels; the three p levels are discussed simultaneously and the fraction of each category compared to the total number of samples is given for the middle layer at 225 hPa. A total of 81.9 % of the observation–model combinations are correctly categorized and represented along the contingency table diagonal. As expected, corresponding $\stackrel{\mathrm{‾}}{\mathrm{\Delta }T}$ and ${\stackrel{\mathrm{‾}}{\mathrm{\Delta }r}}_{\mathrm{ice}}$ (black dots) are close to the origin.

Contrarily, the off-diagonal groups are mostly located in the top-left and lower-right quadrants. Misclassifications for PC–NPC (green, 4.5 %) and NPC–PC (violet, 5.4 %) are mostly due to errors in ${\stackrel{\mathrm{‾}}{\mathrm{\Delta }r}}_{\mathrm{ice}}$. Samples in the PC–NPC group (green) were incorrectly categorized due to relative humidity that is too low in ERA5, while the NPC–PC samples (violet) were too moist. But of course, since r_ice depends on T, misclassifications are also caused by errors in T, even if they do not dominate in these cases.

Misclassifications for the combinations NoC–NPC (red, 3.7 %) and NPC–NoC (yellow, 1.9 %) are mostly due to errors in T. For NoC–NPC and NPC–NoC, $T_{\mathrm{ERA}}^{\mathrm{cor}}$ was colder or warmer than T_P1, respectively.

Least frequent are the misclassifications NoC–PC (light blue, 0.3 %) and PC–NoC (dark blue, 0.5 %). These two groups are subject to the largest $\stackrel{\mathrm{‾}}{\mathrm{\Delta }T}$ and ${\stackrel{\mathrm{‾}}{\mathrm{\Delta }r}}_{\mathrm{ice}}$. Samples in these categories were only found at the 250 and 225 hPa p level, while PC–NoC (dark blue) is not found at the 200 hPa level. It is likely that data points in the two categories result from small-scale variations captured by IAGOS that are not represented by ERA5 due to temporal and spatial resolution.

It is worth identifying whether the misclassification in ERA5 with respect to IAGOS is most often due to biases in temperature or in humidity. Focusing on the PC estimation using ERA5, the primary reason for a misclassification after the correction is the deviation in r_ice. This is shown by the proximity of the violet and green dots to the y axis (small ΔT), while the differences in r_ice are larger than ±20 %. Hence, the underestimation (green dot) or overestimation (violet dot) of potential contrail formation is primary related to the underlying humidity field in ERA5.

4 Summary

In this study we proposed a temperature and relative humidity correction method for ERA5 based on a bivariate quantile mapping (QM) technique to better estimate the contrail formation potential. The QM correction was trained on 3.5 years of IAGOS observations and collocated ERA5 data of T_ERA and r_ERA,ice. The QM correction was then applied to 5.5 years of ERA5 data and compared with IAGOS. The target region covers the eastern United States, the North Atlantic, and continental Europe, spanning 30 to 70° N and 110° W to 30° E for pressure (p) levels 250 to 200 hPa, where the majority of IAGOS observations are available (93.8 %).

Parallel to the IAGOS data post-processing and the calculation of cumulative distribution functions (CDFs) for the QM correction, the along-track biases in temperature and relative humidity between ERA5 and IAGOS were analyzed. In general, biases in temperature and relative humidity are characterized by a dependence on p level, with the largest differences typically for the lowest p level at 200 hPa. Biases were further separated for their dependencies on latitude and longitude. While the cold bias in temperature with respect to IAGOS was found to be independent of longitude and latitude, the dry bias in relative humidity with respect to IAGOS was smallest in North America and increased towards continental Europe. The temporal consistency of IAGOS relative humidity measurements was investigated by means of monthly climatologies. A constant dry bias in relative humidity in ERA5 with respect to IAGOS was found. IAGOS relative humidity measurements from the year 2017 are an exception, when IAGOS observations tend towards elevated relative humidity observations with respect to the other years, while the bias in temperature remained constant.

Using the bivariate QM correction, the cold bias in T_ERA was reduced from −0.7, −0.1, and −0.4 K at p levels 250, 225, and 200 hPa, respectively, to below 0.1 K at all p levels. The dry bias in relative humidity was reduced from −5.5 %, −3.8 %, and −4.3 % to −0.9 %, −1.5 %, and −1.3 % at 250, 225, and 200 hPa, respectively. While a slight dry bias compared to IAGOS remains, a significant improvement in terms of the probability density functions (PDFs) of the relative humidity distribution is achieved. PDFs of corrected relative humidity are almost identical in shape to the PDFs determined from the IAGOS observations. A previously existing artificial peak at r_ERA,ice = 100 % in the PDFs of ERA5, which is caused by the saturation adjustment in ERA5, was removed. Consequently, corrected values of $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ better represent the actual conditions in terms of mean value and frequency of occurrence.

Subsequently, the impact of the QM correction on the detection and classification of NPC, PC, and R with respect to IAGOS was evaluated. Measurements from IAGOS and along-tack ERA5 data were flagged for NPC, PC, R, and NoC conditions. Based on the original ERA5 data set, 50.3 %, 7.9 %, and 0.8 % of all data points were identified as NPC, PC, and R, respectively. Compared to the IAGOS estimates of 44.0 %, 12.1 %, and 1.2 % for NPC, PC, and R, an overestimation of NPC and underestimation of PC were identified in ERA5. After the ERA5 QM correction, 44.0 %, 10.9 %, and 1.5 % of the samples were identified as NPC, PC, and R conditions, indicating a general improvement of the contrail estimation with respect to the original ERA5 data. Using a parameterized relative humidity correction from Teoh et al. (2022a), used here as a reference for comparison, led to 46.9 %, 10.5 %, and 1.2 % of NPC, PC, and R conditions, respectively, which is comparable to the performance from the QM correction.

The temporal and spatial estimation of NPC, PC, and R in ERA5 with respect to IAGOS was assessed with a contingency table. Based on the contingency table the equitable threat score (ETS) was calculated. The largest improvement is found for the PC category with an increase in ETS from 0.27 to 0.36. Smaller improvements were found for the NPC and the R category, with an increase in ETS from 0.51 to 0.54 and 0.2 to 0.24, respectively.

The contingency table further revealed that 81.9 % of the data samples were coherently flagged in IAGOS and ERA5 after QM correction. In these cases almost no biases in temperature and relative humidity between IAGOS and ERA5 remain. The remaining 18.1 % of the data points, which were incorrectly classified for NPC, PC, and R conditions by ERA5, are caused by remaining biases in temperature and relative humidity of varying magnitude. The misclassifications were insensitive to the applied correction method. False classifications of NPC as PC were primarily dominated by a relative humidity bias, while false classifications of NPC as NoC were dominated by a bias in the temperature. However, the majority of misclassifications were caused by combinations of temperature and relative humidity biases, with ERA5 either being cold–moist or a warm–dry biased compared to IAGOS. Furthermore, the relative humidity bias between IAGOS and ERA5 was found to depend on the temperature. As a result, the QM correction leads to an estimation of NPC, PC, and R in ERA5 that is comparable to the distribution identified in the IAGOS observations. Overall, the presented QM correction allows removing the systematic bias in temperature and relative humidity in ERA5 using IAGOS as a reference. Therefore, the method can be applied to ERA5 data to estimate the contrail formation potential away from IAGOS flight tracks under the constraint that the correction is applied to grid points within a specified domain between 105° W and 30° E and from 30 to 70° N. This provides a broader perspective on potential contrail formation in space and time over the Atlantic region. This allows the study of temporal and spatial patterns of contrail formation over the North Atlantic region to develop statistically based rerouting options.

Appendix A: Cumulative distribution functions for quantile mapping

Here we provide an example for calculated cumulative distribution functions (CDFs) of relative humidity r defined with respect to ice. IAGOS CDFs (F_o,h) and ERA CDFs (F_m,h) are calculated on the basis of the observed IAGOS relative humidity (x_o,h) and simulated along-track ERA5 relative humidity (x_m,h), respectively, following the description in Sect. 2.3. Figure A1 shows F_o,h (dashed lines) and F_m,h (solid lines) for individual pressure (p) levels between 350 and 200 hPa. As described in Sect. 2.3 the full domain (specified in Sect. 2.1) is subdivided into two latitude bands. The split point is determined by the 50th percentile at each p level such that both latitude bands contain equal numbers of data points. For legibility, only CDFs of the northernmost latitude band are shown here. The selection is arbitrary and conclusions are transferable between the two bands.

Table A1 Notations.

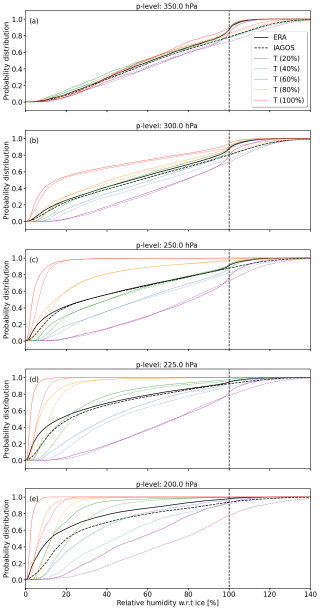
Figure A1 (a–e) Cumulative distribution functions (CDFs) F of relative humidity with respect to ice (in %). CDFs from ERA5 F_m,h and IAGOS F_o,h are given by solid and dashed lines, respectively. The black lines represent F_o,h and F_m,h that depend on p level and latitude Φ. Color-coded are F_m,h and F_o,h that additionally consider five temperature bins with bin sizes defined by 20^th percentiles.

The black lines in Fig. A1 indicate F_o,h and F_m,h from the quantile mapping (QM) approach that considers only the p-level dependence and the latitude band. For the majority of the p levels, F_o,h and F_m,h are similar in shape. An exception is r between 100 % and 110 % at levels 350 ≤ p ≤ 250 hPa, where F_m,h (ERA5) shows a dominant mode, while F_o,h (IAGOS) remains flat. The mode in F_m,h is a superposition of two effects. While the peak is of natural origin, as reported by Krämer et al. (2016, 2020), it is also caused by the saturation adjustment in ERA5 (see Sect. 2.2.1). This mode becomes less prominent with decreasing p as the atmosphere gets drier with altitudes, so supersaturation is less likely. Simultaneously, the differences between F_o,h and F_m,h increase for r < 20 %, where both F_o,h and F_m,h are further characterized by a steep slope. The largest effect in this regard is found at the 200 hPa p level, where F_m,h contains a larger fraction of high relative humidity values compared to F_o,h, indicating an underestimation of r that is not attributable to the saturation adjustment. For example, 50 % of the ERA relative humidity values are smaller than around 15 %, while the respective value for IAGOS is around 22 %, indicating a general dry bias unrelated to the saturation adjustment.

The color-coded lines in Fig. A1 represent the bivariate QM approach, where r is additionally separated for five temperature (T) bins that are defined by 20 % steps. F_m,h and F_o,h that result from the bivariate QM reveal a strong dependence on T, which becomes visible in the deviating shapes of F_m,h and F_o,h at a constant p level and latitude band. The systematic order of the colored lines further indicates that T bins with low T (0–20th percentile, violet lines) are mostly dominated by high relative humidity values, while bins with higher T (80–100th percentile, red lines) are dominated by low r. The CDFs with lower T are generally flat with a continuous slope, while T bins with higher temperatures are dominated by a steep slope for r < 10 %, particularly for p < 250 hPa. However, for the bivariate QM correction the actual shape of F_m,h and F_o,h is less relevant than the difference. These differences between F_m,h and F_o,h increase with decreasing p level. The importance of considering the T dependence is further highlighted by the fact that the simpler univariate QM approach (black) and related F_m,h and F_o,h do not consider the shape and the shape difference required to adequately correct r under different ambient conditions, particularly with a decreasing p level.

Appendix B: Temporal consistency in temperature and relative humidity of IAGOS and ERA5

Applying the quantile mapping (QM) correction in the presented form requires a time-invariant bias in temperature (T) and relative humidity (r_ice) between IAGOS and ERA5. The bias between the two might vary due to variations in the instrument calibration procedure or changes in the sampling distribution due to seasonal flight schedules.

We tested for time invariance by calculating mean values of T and r_ice from ERA5 as well as IAGOS over all samples for each month spanning January 2015 to June 2021 at p levels of 250, 225, and 200 hPa.

Figure B1a shows that monthly mean T_ERA (red) and T_P1 (black) agree well, which is expected from the small bias presented in Fig. 3. Furthermore, the monthly mean difference between T_P1 and T_ERA, given in Fig. B1b, remains constant with values around −0.5 K and a maximum of −1 K, except for some individual spikes. Figure B1b also shows that QM-corrected $T_{\mathrm{ERA}}^{\mathrm{cor}}$ (blue) better matches T_P1, which is indicated by maximum differences of ±0.5 K.

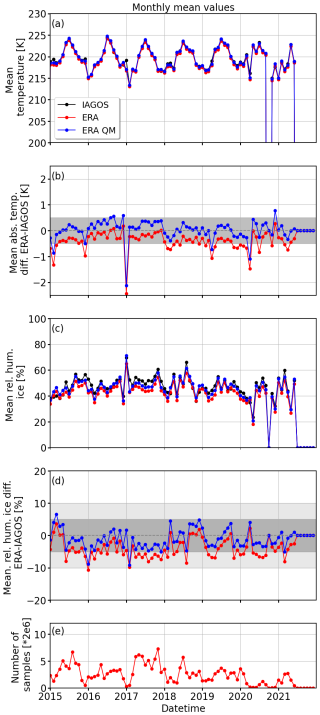
Figure B1 (a) Time series of monthly mean temperature (in K) from IAGOS (black), ERA5 (red), and corrected ERA5 (blue). (b) Time series of temperature difference (in K) from ERA5 minus IAGOS (red) as well as corrected ERA5 minus IAGOS (blue). Panels (c) and (d) are similar to (a) and (b) but for relative humidity with respect to ice r_ice in percent. (e) Total number of samples available to calculate the monthly mean.

Similarly, Fig. B1c shows monthly mean of r_P1,ice (black), original ERA5 r_ERA,ice (red), and QM-corrected ERA5 $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ (blue) ranging between 40 % and 50 % for the majority of the period. An exception is the period after 2020, which is due to low data availability (see Fig. B1e). Figure B1c illustrates that r_ERA,ice (red) follows r_P1,ice (black) with an offset between 3 % and up to −12 % that has been shown before (fourth column in Fig. 3). Like for the temperature correction, Fig. B1d clearly shows that the QM correction increases mean $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ such that the bias between ERA5 and IAGOS is reduced, bringing the monthly means of $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ closer to 0.

Even though the bias Δr_ice = r_ERA,ice − r_P1,ice remains fairly constant for the majority of the presented time series, the differences are particularly pronounced for the years 2016 and 2017. However, their temperature bias ΔT = T_ERA − T_P1 remains constant (Fig. B1b), which suggests that changes in the sampling, e.g., due to modified aircraft operations, are not the cause but the known grounding problem of IAGOS acquisition in this time period (see Sanogo et al., 2024).

In the absence of alternative observations to compare against IAGOS, we turn to the interannual variation in r_ice to confirm that relative humidity measurements for the years 2016 and 2017 are anomalous. Multiyear monthly climatological means of r_ERA,ice and r_P1,ice are calculated spanning the years 2015 to 2021. Using uncorrected r_ERA,ice as the reference, anomalies of r_P1,ice, r_ERA,ice, and $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ are determined by subtracting the monthly mean of an individual year from the multiyear monthly climatological mean. Figure B2 shows mean anomalies of r_P1,ice that range from −11.9 % (2017) to 0.8 % (2020). Similarly, mean anomalies of r_ERA,ice range between −4.2 % (2017) and 5.5 % (2020). The mean anomalies between ERA5 and IAGOS are largest for the year 2016 and particularly 2017; the difference between the anomalies for the year 2017 exceeds all other years with a value of −6.8 %. Slightly smaller mean anomaly differences between ERA5 and IAGOS are found for the years 2016 of −4.7 % and 2020 of −4.7 %. Therefore, the year 2017 and parts of 2016 are special cases compared to the other years in terms of anomalies during which r_P1,ice is likely biased towards values that are too moist.

Figure B2 (a–g) Anomalies of relative humidity from ERA5 r_ERA,ice (red), corrected ERA5 $r_{\mathrm{ERA},\mathrm{ice}}^{\mathrm{cor}}$ (blue), and IAGOS r_P1,ice (black) with respect to the multiyear r_ERA,ice for January 2015 to June 2021. Differences are given in units of relative humidity.

Appendix C: Latitudinally and longitudinally dependent deviations in temperature and relative humidity between ERA5 and IAGOS

The bias between IAGOS and ERA5 might depend on the geographic position, e.g., due to characteristic spatial distributions of water vapor in the atmosphere. Such spatially dependent biases in T and r_ice between ERA5 and IAGOS are identified by calculating mean differences for bins of 10° in latitude and longitude at p levels 300, 250, 225, and 200 hPa. The calculations include all samples from the years 2015 to 2021 and from within the defined sub-domain (30–70° N, 105° W–30° E).

First, the longitudinal variation in ΔT is analyzed (Fig. C1a). In general, a tendency toward more negative ΔT is found for decreasing p levels, reaching a maximum at the 200 hPa p level, where ΔT mostly reaches values of up to −2 K. Large ΔT at 200 hPa westwards of 80° must be cautiously interpreted due to the low number of available samples in this pressure level and longitude bin (see Fig. C1e). The generally negative ΔT indicates that the mean temperature from ERA5 is predominantly lower than measured by IAGOS. ΔT at pressure levels 250 hPa (green) and 225 hPa (red) is almost constant over the entire longitude range, with ΔT being smaller than −0.5. An exception is the 300 hPa level, where ΔT exceeds −0.5 K and reaches values of up to −1 K east of 50° W. Separating ΔT for latitudes between 30 and 70° N does not reveal any latitudinal dependencies. An exception is the 200 hPa p level, where ΔT increases towards the Equator and reaches up to −1.7 K at 30° N.

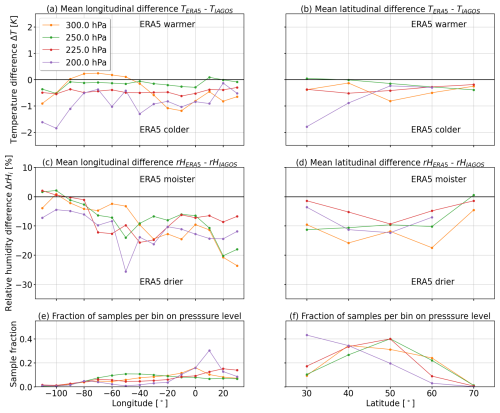
Figure C1 (a–b) Temperature difference ΔT (in K) between ERA5 and IAGOS as a function of longitude and latitude, respectively. (c–d) Same as the top row but for the difference in relative humidity r_ice (in %). Pressure levels of 300, 250, 225, and 200 hPa are indicated in orange, green, red, and purple, respectively. (e–f) Fraction of available samples per longitude or latitude bin with respect to the total number of samples per pressure level.

Similar to T, the longitudinal and latitudinal dependence of r_ice is analyzed (see Fig. C1c, d). In general, Δr_ice increase from the west, with Δr_ice around 0 %, towards the east, reaching Δr of up to −25 % at the 300 and 250 hPa p levels. No systematic offset among the p levels is found. While Δr_ice is largest at the 200 hPa level at 110° W, Δr_ice is among the smallest levels at 30° E. Conversely, Δr_ice is small at the 250 hPa level at 110° W and is the second-largest Δr_ice at 30° E. Similar to T, separating Δr_ice by latitude does not show strong latitudinal sensitivity, with the smallest values between −10 % and −4 % at the 225 and 200 hPa p levels. The largest Δr_ice values, of up to Δr_ice = −25 %, are found at the 300 hPa level, particularly between 40 and 60° N.

Separating biases in T and r clearly shows the necessity of considering the p level in the QM correction. In contrast, binning by latitude appears to be of minor importance, which relaxes the requirement for more than two bins in the proposed QM correction. In contrast, the dependency of r_ice on the longitude is much more pronounced and would require individual cumulative distribution functions but could not be considered in the QM correction as dividing the data into three sub-domains would lead to insufficient data in rarely sampled combinations of T and p.