Homogeneous ice nucleation in adsorbed water films: a theoretical approach

Ice nucleation plays a critical role in cloud formation and atmospheric processes, influencing precipitation and climate. In this study, we present a theoretical approach for describing homogeneous ice nucleation within adsorbed water films on insoluble substrates and suggest that it may be a mechanism for deposition ice nucleation with non-porous ice nuclei that induce ice premelting. Our theory is based on the Frenkel–Halsey–Hill (FHH) adsorption model, which characterizes the substrate–adsorbate interaction, and the classical nucleation theory of homogeneous freezing, which describes the probability of ice formation. We use the theory to model the melting point (MP), critical ice nucleus size, and nucleation rates as functions of adsorbed water film thickness and substrate properties. Our results indicate that the melting point depression can be as much as 5 K on hydrophilic substrates when the thickness of the water film is 1 nm. The onset temperature for homogeneous ice nucleation (235 K for cloud droplets) can shift 1–2 K lower in adsorbed films. At temperatures below 235 K, the humidity at which ice nucleation occurs is determined by the condition that the adsorbed water film must be thick enough to accommodate the critical ice nucleus. Comparisons of calculated relative humidity conditions with experimental ice nucleation data for silica particles show promising agreement, validating the FHH model as a framework for describing deposition ice nucleation in the atmosphere.

1 Introduction

Atmospheric ice nucleation can occur via homogeneous or heterogeneous freezing of cloud droplets or aqueous aerosols or via deposition of water vapor onto surfaces of solid, insoluble ice nuclei (Pruppacher and Klett, 1997). Despite its importance for the evolution of clouds and precipitation, many aspects of ice nucleation processes remain poorly understood even after a century of research (Laaksonen and Malila, 2021). During the recent decade, the suggestion that ice nucleation from deposition may involve adsorption or pore condensation followed by a freezing mechanism (Welti et al., 2014; Marcolli, 2014) has led to the question of how the size of the system, for example, pore dimensions or film thickness, affects the homogeneous nucleation of supercooled water (Marcolli, 2020). In confined geometries, the chemical potential of water differs from that of bulk water. Furthermore, the critical ice nucleus must fit within the system dimensions. There have been conflicting molecular simulation results regarding ice nucleation in free-standing water films (that is, films in contact only with their own vapor) with thicknesses in the nanometer range, with some studies finding increasing homogeneous nucleation rates (Haji-Akbari and Debenedetti, 2017) and other studies finding decreasing homogeneous nucleation rates (Lü et al., 2013; Haji-Akbari et al., 2014) with decreasing film thickness. Hayton et al. (2024) recently suggested that the discrepancies can be reconciled by accounting for the intermolecular potential truncation applied in the various studies. Their own simulations indicated that homogeneous ice nucleation remains bulk-like down to a film thickness of about 3.5 nm. In the atmosphere, water films do not exist as separate entities, but multilayer water films (i.e., films consisting of more than one monolayer) can adsorb on the surfaces of atmospheric aerosols at sufficiently high relative humidities.

Deposition ice nucleation was originally treated within the classical nucleation theory framework by Fletcher (1959) as vapor molecules depositing directly into the crystalline phase without an intermediate liquid-like state. However, because of the much smaller critical radius of ice in liquid compared to in vapor, the formation of a critical ice nucleus is much more likely due to fluctuations in the supercooled liquid rather than an ensemble of vapor molecules depositing on a surface almost simultaneously and in such a configuration that they are immediately able to form a hexagonal crystal. From this perspective, freezing of adsorbed films on non-porous, insoluble aerosols would seem to be a more likely route to deposition ice nucleation than the direct vapor-to-ice mechanism. Indeed, our recent molecular dynamics simulations (Roudsari et al., 2024) have shown that a water film with a thickness of just four monolayers can freeze on silver iodide surfaces at a temperature of 253 K.

The Frenkel–Halsey–Hill (FHH) adsorption activation theory (Sorjamaa and Laaksonen, 2007) has been successfully used to describe cloud drop formation on various types of insoluble particles (Kumar et al., 2011). In this work, we use FHH theory as a framework to derive the chemical potentials of adsorbed water and ice and use them to describe the thermodynamics of ice nucleation in supercooled water films. Theoretical predictions are compared to laboratory measurements on ice nucleation induced by silica particles.

2 Theory

2.1 Multilayer adsorption

We model multilayer adsorption on insoluble substrates using the FHH theory (Frenkel, 1946; Halsey, 1948; Hill, 1952), which contains two parameters (A(T) and B) that must be determined experimentally. These parameters can be obtained by measuring adsorption isotherms (which show the amount of adsorbed gas or vapor on solid surfaces as a function of saturation ratio at constant temperature) (Halsey, 1948; Laaksonen, 2015) or by conducting cloud drop formation experiments (Kumar et al., 2011). These measurements are usually made at or close to room temperature, whereas our aim is to derive a theory of the freezing of adsorbed films at temperatures tens of degrees below room temperature. We therefore start by considering the temperature dependence of multilayer adsorption, which can be derived starting from the Clausius–Clapeyron equation (e.g., Kanagy, 1950). At any constant number of adsorbed monolayers N, the difference of the logarithms of equilibrium saturation ratios S₁ and S₂ at temperatures T₁ and T₂ is

$$\begin{array}{}\text{(1)}& \ln S_{\mathrm{2}}-\ln S_{\mathrm{1}}={\displaystyle \frac{\mathrm{\Delta }{L}_{\mathrm{A}}}{k}}\left({\displaystyle \frac{\mathrm{1}}{T_{\mathrm{1}}}}-{\displaystyle \frac{\mathrm{1}}{T_{\mathrm{2}}}}\right),\end{array}$$

where $\mathrm{\Delta }{L}_{\mathrm{A}}=L_{\mathrm{A}}-L_{\mathrm{V}}$ (L_A is the heat of adsorption and L_V is the heat of vaporization of liquid water) and k is the Boltzmann constant.

We model multilayer adsorption using the FHH adsorption isotherm. The isotherm can be written as

$$\begin{array}{}\text{(2)}& \ln S=-A\left(T\right)N^{-B},\end{array}$$

where A(T) and B are constants describing the molecular interaction between the first adsorbed monolayer and the adsorbent and the rate of decay of the interaction as a function of film thickness, respectively. In previous work (Laaksonen et al., 2020), the temperature dependence of the isotherm was not considered, since the calculations were done for room temperature. However, in the original form of the FHH isotherm, derived assuming the Lennard-Jones (LJ) intermolecular potential, the A(T) parameter is in fact temperature-dependent. We can now rewrite Eq. (2) in a similar form to Eq. (1):

$$\begin{array}{}\text{(3)}& \ln S_{\mathrm{2}}-\ln S_{\mathrm{1}}=\left(A\right(T_{\mathrm{1}})-A(T_{\mathrm{2}}\left)\right)N^{-B}.\end{array}$$

The temperature dependence of adsorption obtained from the FHH model should be in agreement with the more general Eq. (1) based on the Clausius–Clapeyron relation. We therefore assume the following specific temperature dependence for the parameter A(T):

$$\begin{array}{}\text{(4)}& A\left(T\right)=A^{\prime }/\left(kT\right),\end{array}$$

where A^′ is a temperature-independent constant. Inserting Eq. (4) into Eq. (3), we obtain

$$\begin{array}{}\text{(5)}& \ln S_{\mathrm{2}}-\ln S_{\mathrm{1}}=\left({\displaystyle \frac{A^{\prime }}{k}}\right)\left({\displaystyle \frac{\mathrm{1}}{T_{\mathrm{1}}}}-{\displaystyle \frac{\mathrm{1}}{T_{\mathrm{2}}}}\right)N^{-B}.\end{array}$$

Comparing Eq. (5) with Eq. (1), we have $A^{\prime }{N}^{-B}=\mathrm{\Delta }{L}_{\mathrm{A}}$.

When an adsorbed film forms on an aerosol particle, Eq. (2) alone is not sufficient to calculate the equilibrium saturation ratio. The curvature of the particle induces a Kelvin effect that increases the vapor pressure of the film. To account for the Kelvin effect, Eq. (1) can be extended (Sorjamaa and Laaksonen, 2007) to

$$\begin{array}{}\text{(6)}& \ln S=-A\left(T\right)N^{-B}+{\displaystyle \frac{\mathrm{2}{\mathit{\gamma }}_{\mathrm{w}}{v}_{\mathrm{w}}}{kTR}},\end{array}$$

where γ_w is the air–water surface tension, v_w is the molecular volume of water, and R is the radius from the center of the aerosol particle (assumed spherical) to the surface of the adsorbed film. Denoting the radius of the dry aerosol particle by R_p, the thickness of the film equals R−R_p and the number of adsorbed monolayers is

$$\begin{array}{}\text{(7)}& N={\displaystyle \frac{R-R_{\mathrm{p}}}{d}},\end{array}$$

where d is the thickness of an adsorbed monolayer.

2.2 Freezing of bulk water

We treat the freezing of adsorbed water using the classical nucleation theory (CNT). The homogeneous nucleation rate of ice in bulk water is given by (Laaksonen and Malila, 2021)

$$\begin{array}{}\text{(8)}& J_{\mathrm{hom}}=C\exp {\displaystyle \frac{-\mathrm{16}\mathit{\pi }{v}_i^{\mathrm{2}}{\mathit{\gamma }}_{\mathrm{iw}}^{\mathrm{3}}}{\mathrm{3}kT\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}^{\mathrm{2}}}},\end{array}$$

where C is a kinetic prefactor, v_i is the molecular volume of ice, γ_iw is the interfacial tension between water and ice, and Δμ_iw denotes the chemical potential difference between ice and water. The radius of the critical ice nucleus in water is given by

$$\begin{array}{}\text{(9)}& R_{\mathrm{iw}}^{*}={\displaystyle \frac{\mathrm{2}{v}_{\mathrm{i}}{\mathit{\gamma }}_{\mathrm{iw}}}{\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}}}.\end{array}$$

The chemical potential difference is usually approximated by

$$\begin{array}{}\text{(10)}& \mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}\approx kT\ln \left({\displaystyle \frac{e_{\mathrm{w}}}{e_{\mathrm{i}}}}\right),\end{array}$$

where e_w and e_i denote the equilibrium vapor pressures of bulk water and ice, respectively.

2.3 Chemical potential of adsorbed water

When the mother phase of nucleating ice is adsorbed water instead of bulk water, the chemical potential of the liquid phase is equal to that of its equilibrium vapor (pressure P and saturation ratio over ice $S_{\mathrm{i}}=P/e_{\mathrm{i}}$), and the chemical potential difference between bulk ice and adsorbed liquid can be expressed as

$$\begin{array}{}\text{(11)}& \mathrm{\Delta }{\mathit{\mu }}_{\mathrm{ia}}\approx kT\ln S_{\mathrm{i}}.\end{array}$$

If bulk ice is taken to be the stable state, then freezing should not occur at P<e_i. However, adsorbed ice films obviously can exist at subsaturation (just as adsorbed multilayer water films can exist at relative humidity below 100 %; e.g., McCafferty and Zettlemoyer, 1971; Pashley and Kitchener, 1979; Ibrahim et al., 2018; Viisanen et al., 2024), and a transition from a supercooled liquid film to an ice film through nucleation must be possible when the temperature is below the melting point (MP) of the ice film, even if the pressure of the vapor in equilibrium with the film is below e_i. Thin films of hexagonal ice have been created in the laboratory by vapor adsorption at low temperatures (<140 K; Thürmer and Nie, 2013), by heating adsorbed glassy ice films that transition to hexagonal ice (Leist et al., 2003), and by letting thicker ice overlayers on mineral surfaces sublimate until a thin film is left (Yeşilbaş and Boily, 2016).

We postulate that the stable reference state for a supercooled liquid film containing a given number of water molecules at temperature T is, instead of bulk ice, a film consisting of hexagonal ice that has the same number of molecules as the water film. The chemical potential difference between liquid and ice films with a fixed number of water molecules $n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ can be expressed by the FHH theory. The equilibrium for a liquid film is given by

$$\begin{array}{}\text{(12)}& \ln S_{\mathrm{w}}=\ln {\displaystyle \frac{P_{\mathrm{w}}}{e_{\mathrm{w}}}}=-A_{\mathrm{w}}{N}_{\mathrm{w}}^{-B_{\mathrm{w}}}.\end{array}$$

Here, P_w is the pressure of water vapor in equilibrium with the adsorbed film. For the ice film, we write

$$\begin{array}{}\text{(13)}& \ln S_{\mathrm{i}}=\ln {\displaystyle \frac{P_{\mathrm{i}}}{e_{\mathrm{i}}}}=-A_{\mathrm{i}}{N}_{\mathrm{i}}^{-B_{\mathrm{i}}},\end{array}$$

where we have left out the argument (T) from A_w and A_i for convenience. Now,

$$\begin{array}{}\text{(14)}& n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{\Omega }{N}_{\mathrm{w}}{\displaystyle \frac{d_{\mathrm{w}}}{v_{\mathrm{w}}}}=\mathrm{\Omega }{N}_{\mathrm{i}}{\displaystyle \frac{d_{\mathrm{i}}}{v_{\mathrm{i}}}},\end{array}$$

where Ω is the surface area covered by the film and v_w and v_i and d_w and d_i are the molecular volumes and monolayer thicknesses, respectively, of water and ice. Thus,

$$\begin{array}{}\text{(15)}& N_{\mathrm{i}}=\left({\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{i}}}{{\mathit{\sigma }}_{\mathrm{w}}}}\right)N_{\mathrm{w}},\end{array}$$

with σ_i and σ_w denoting the cross-sections of water and ice on the surface of the adsorbent ($\mathit{\sigma }=v/d$). The monolayer thickness of water is taken to be d_w=2.84 Å, which corresponds to a cross-section of σ_w=10.5 Ų (McClellan and Harnsberger, 1967). For the monolayer thickness of ice, we use half of the intermolecular distance along the vertical direction (c axis) of the hexagonal unit cell from molecular dynamics simulations, d_i=3.63 Å (Roudsari et al., 2024), which is in good agreement with temperature-dependent lattice parameter measurements from neutron diffraction (Fortes, 2018). Note that the cross-section of ice σ_i≈8.9 Ų is smaller than σ_w.

To be able to calculate the freezing nucleation rate in adsorbed water, we need an equation for the chemical potential difference between adsorbed water and adsorbed ice, which we denote by Δμ_A. By subtracting Eq. (13) from Eq. (12) and rearranging the terms, we obtain

$$\begin{array}{}\text{(16)}& \mathrm{\Delta }{\mathit{\mu }}_{\mathrm{A}}\approx kT\ln {\displaystyle \frac{P_{\mathrm{w}}}{P_{\mathrm{i}}}}=kT\left[\ln {\displaystyle \frac{e_{\mathrm{w}}}{e_{\mathrm{i}}}}+A_{\mathrm{i}}{N}_{\mathrm{i}}^{-B_{\mathrm{i}}}-A_{\mathrm{w}}{N}_{\mathrm{w}}^{-B_{\mathrm{w}}}\right].\end{array}$$

The vapor pressures of the liquid and the ice films are equal at the melting point of the ice film, which can therefore be found by locating the temperature at which Δμ_A=0 (see Figs. 4 and 5). We note that, for this requirement to be fulfilled, the sum of the last two terms on the right-hand side of the above equation must be negative. This imposes restrictions on the values that the set of FHH parameters ($A_{\mathrm{i}},A_{\mathrm{w}},B_{\mathrm{i}},B_{\mathrm{w}}$) can have. For example, because the FHH parameters describe molecular interactions between the adsorbate and the adsorbent, it is likely that the parameter values do not change much due to a phase transition of the adsorbate, and, indeed, this seems to be the case for water on graphite (Lbadaoui-Darvas et al., 2023). However, setting A_i=A_w and B_i=B_w would cause the melting point of an adsorbed film not to decrease below the melting point of bulk water but to increase above it, since N_w>N_i for a fixed $n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$.

Although the FHH parameters cannot be exactly the same for water and ice, we can gain some insight from the derivation by Hill (1952) of the FHH theory for molecules interacting via the LJ potential. The LJ value for B depends only on the intermolecular potential and is exactly 3. Therefore, it does not change with the solidification of LJ liquid. Likewise, A(T) depends on the LJ potential parameters but also on the densities of the adsorbate and the adsorbent and therefore changes when a phase transition takes place. If we make the assumption that $B_{\mathrm{i}}=B_{\mathrm{w}}=B$, which, at least for water on graphite, is not far from true (Lbadaoui-Darvas et al., 2023), then we must have $A_{\mathrm{i}}<A_{\mathrm{w}}({\mathit{\sigma }}_{\mathrm{i}}/{\mathit{\sigma }}_{\mathrm{w}}{)}^{-B}$ in order for Δμ_A to change sign at some temperature below 273.15 K. This can be seen when inserting Eqs. (10), (15) into Eq. (16):

$$\begin{array}{}\text{(17)}& \mathrm{\Delta }{\mathit{\mu }}_{\mathrm{A}}\approx \mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}+kT{N}_w^{-B}\left[A_{\mathrm{i}}({\mathit{\sigma }}_{\mathrm{i}}/{\mathit{\sigma }}_{\mathrm{w}}{)}^{-B}-A_{\mathrm{w}}\right].\end{array}$$

We next derive a relation between the A parameters of ice and water starting from an intermediate expression of Hill (1952) for “LJ water” and an adsorbent (subscript a) surface:

$$\begin{array}{}\text{(18)}& kT\ln S=(N_{\mathrm{w}}{d}_{\mathrm{w}}{)}^{-\mathrm{3}}\left(C_{\mathrm{w}}-C_{\mathrm{a}}\right).\end{array}$$

The constants C_w and C_a are given by

$$\begin{array}{}\text{(19)}& C_{\mathrm{w}}={\displaystyle \frac{\mathit{\pi }{\mathit{ϵ}}_{\mathrm{w}}{\mathit{\varsigma }}_{\mathrm{w}}^{\mathrm{6}}}{\mathrm{3}{v}_{\mathrm{w}}}};C_{\mathrm{a}}={\displaystyle \frac{\mathit{\pi }{\mathit{ϵ}}_{\mathrm{a}}{\mathit{\varsigma }}_{\mathrm{a}}^{\mathrm{6}}}{\mathrm{3}{v}_{\mathrm{a}}}},\end{array}$$

where ϵ_w and ς_w are the LJ energy and length parameters for water–water interactions, respectively; ϵ_a and ς_a are the LJ parameters for water-adsorbent interactions; and v_a is the molecular volume of the adsorbent. Rearranging and equating Eq. (18) with Eq. (2), the FHH equation (with B=3) gives an expression for the FHH parameter A_w:

$$\begin{array}{}\text{(20)}& A_{\mathrm{w}}={\displaystyle \frac{\mathrm{1}}{kT{d}_{\mathrm{w}}^{\mathrm{3}}}}\left(C_{\mathrm{a}}-C_{\mathrm{w}}\right).\end{array}$$

We can now write a similar equation for A_i:

$$\begin{array}{}\text{(21)}& A_{\mathrm{i}}={\displaystyle \frac{\mathrm{1}}{kT{d}_{\mathrm{i}}^{\mathrm{3}}}}\left(C_{\mathrm{a}}-C_{\mathrm{i}}\right),\end{array}$$

where $C_{\mathrm{i}}=C_{\mathrm{w}}(v_{\mathrm{w}}/v_{\mathrm{i}})$ (note that the LJ parameters are the same for water and ice). By eliminating the term C_a from the pair of equations and inserting Eq. (19), we get

$$\begin{array}{}\text{(22)}& A_{\mathrm{i}}=A_{\mathrm{w}}{\left({\displaystyle \frac{d_{\mathrm{w}}}{d_{\mathrm{i}}}}\right)}^{\mathrm{3}}+{\displaystyle \frac{\mathit{\pi }{\mathit{ϵ}}_{\mathrm{w}}{\mathit{\varsigma }}_{\mathrm{w}}^{\mathrm{6}}}{\mathrm{3}kT{d}_{\mathrm{i}}^{\mathrm{3}}}}(v_{\mathrm{w}}^{-\mathrm{1}}-v_{\mathrm{i}}^{-\mathrm{1}}).\end{array}$$

When the FHH theory was first derived, it was soon discovered that it rarely works for the adsorption of real gases or vapors (nitrogen, water) with B=3 but works surprisingly well if B is treated as an adjustable parameter (Halsey, 1948; Hill, 1952). We thus replace exponent 3 in Eq. (22) by B and have

$$\begin{array}{}\text{(23)}& A_{\mathrm{i}}=A_{\mathrm{w}}{\left({\displaystyle \frac{d_{\mathrm{w}}}{d_{\mathrm{i}}}}\right)}^B+{\displaystyle \frac{\mathit{\pi }{\mathit{ϵ}}_{\mathrm{w}}{\mathit{\varsigma }}_{\mathrm{w}}^{B+\mathrm{3}}}{\mathrm{3}kT{d}_{\mathrm{i}}^B}}\left(v_{\mathrm{w}}^{-B/\mathrm{3}}-v_{\mathrm{i}}^{-B/\mathrm{3}}\right).\end{array}$$

In doing so, we have made some approximations; for example, the LJ potential is spherically symmetric, whereas water molecules are not; therefore their true intermolecular potential function is not spherically symmetric either. Figure 1 shows A_i as a function of A_w at two different temperatures for B values between 1 and 5 calculated using Eq. (23). We use the LJ parameters of Kulmala (1988) that are based on water's critical properties: ${\mathit{ϵ}}_{\mathrm{w}}=\mathrm{440.3}\cdot k$ and ς_w=0.31 nm. The viscosity-based LJ energy and length parameters for water that can be found in the table of Poling et al. (2001) (along with values for other molecular species) are somewhat different from these; however, the exact values of the parameters have only a very minor effect on the numerical results, as the second term on the right-hand side of Eq. (23) is small compared to the first term.

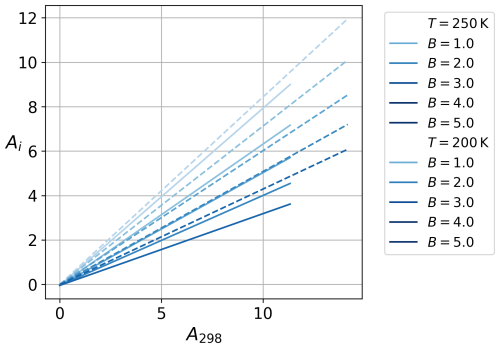
Figure 1 The variations in A_i (ice interaction) with respect to A_w (water interaction) under varying conditions of B at T=200 K (dashed line) and T=250 K (solid line).

Inserting Eq. (23) in Eq. (17) leads to

$$\begin{array}{}\text{(24)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{A}}& \approx \mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}+kT{N}_w^{-B}\left\{A_{\mathrm{w}}\left[{\left({\displaystyle \frac{v_{\mathrm{w}}}{v_{\mathrm{i}}}}\right)}^B-\mathrm{1}\right]\right.\\ & \left.+{\displaystyle \frac{\mathit{\pi }{\mathit{ϵ}}_{\mathrm{w}}{\mathit{\varsigma }}_{\mathrm{w}}^{B+\mathrm{3}}}{\mathrm{3}kT{d}_{\mathrm{w}}^B}}{\left({\displaystyle \frac{v_{\mathrm{w}}}{v_{\mathrm{i}}}}\right)}^B(v_{\mathrm{w}}^{-B/\mathrm{3}}-v_{\mathrm{i}}^{-B/\mathrm{3}})\right\}.\end{array}\end{array}$$

In this way, we have reduced the number of parameters of our system from four (A_w, B_w, A_i, B_i) in Eq. (16) to two (A_w, B) in Eq. (24). Note that B remains the same for liquid water and ice because it depends only on the intermolecular potential.

2.4 Homogeneous ice nucleation in adsorbed water

We make the assumption that all other variables except the chemical potential difference are the same for adsorbed and bulk water. We thereby obtain expressions for the homogeneous nucleation rate and the radius of the critical nucleus in adsorbed water simply by replacing Δμ_iw in Eqs. (8) and (9) with Δμ_A:

$$\begin{array}{}\text{(25)}& {\displaystyle }{J}_{\mathrm{hom},\mathrm{A}}=J_{\mathrm{hom}}\left({\displaystyle \frac{\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}^{\mathrm{2}}}{\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{A}}^{\mathrm{2}}}}\right),\text{(26)}& {\displaystyle }{R}_{\mathrm{iA}}^{*}=R_{\mathrm{iw}}^{*}\left({\displaystyle \frac{\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}}{\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{A}}}}\right).\end{array}$$

The homogeneous nucleation rate of bulk water is calculated using the parameterizations for the chemical potential difference, the interfacial tension between ice and water, and the ice density (to calculate the molecular volume of ice) given by Espinosa et al. (2018) (see Appendix A2). Using these parameterizations with Eq. (7) produces nucleation rates that are in good agreement with the experimental results on homogeneous freezing of water droplets. However, the parameterization of Espinosa et al. for the chemical potential difference yields a water saturation line, which differs significantly from other parameterizations found in the literature (e.g., Hyland and Wexler, 1983; Wagner and Pruss, 2002; Murphy and Koop, 2005; Kalova, 2022). We therefore use the chemical potential difference, ice density, and ice–water interfacial tension expressions of Espinosa et al. only in calculations of the nucleation rate. In all other calculations, we use equations for the properties of water and ice given in Appendix A1.

The above equations hold for water films on flat surfaces, but, with curved surfaces, the chemical potential should in principle be modified because of the increase in the internal pressure of a droplet caused by surface tension, which is greater for smaller droplets (the Laplace effect). This could be done, for example, using equations for chemical potential as a function of pressure (Nĕmec, 2013; Marcolli, 2020). However, we restrict our calculations to water films on relatively large particles (diameter 100 nm or more) so that the omission of the Laplace pressure effect should not produce much error.

3 Experiment

3.1 Substance characterization

Silica (silicon dioxide, SiO₂) powder is used in this work as a test substance for comparison of experimental deposition ice nucleation with model calculations. The powdered silica sample was prepared by grinding fused silica beads (Sigma-Aldrich, 4-20 mesh) with a planetary mill for 10 min at 300 rpm. For determining the particle size distribution, the powder was dry-dispersed using a magnetic stirrer and a directed airflow to agitate the powder. Figure 2a shows the resulting particle size distribution measured with a scanning mobility particle sizer (SMPS; 3938 TSI).

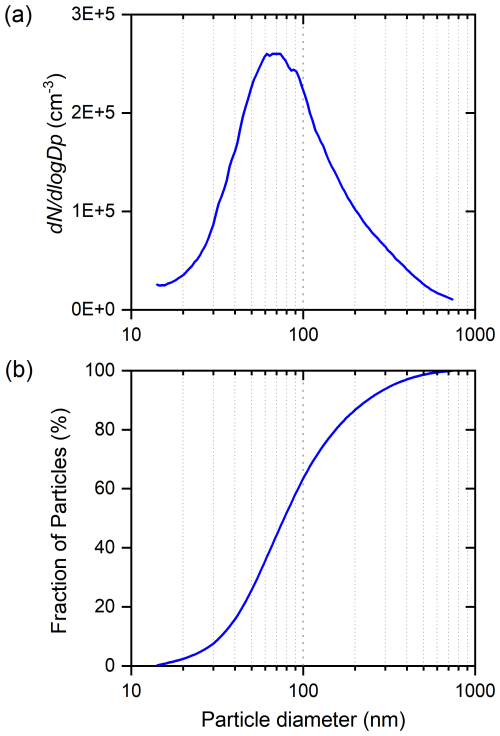
Figure 2 (a) Size distribution of SiO₂ powder measured with an SMPS. (b) The corresponding cumulative size distribution.

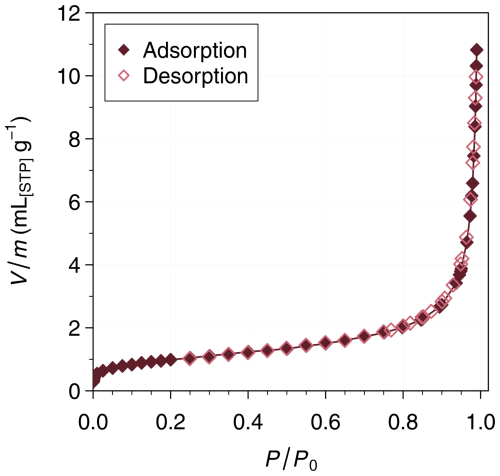
Nitrogen adsorption isotherms showing the amount of adsorbed N₂ as a function of saturation ratio were measured at 77.3 K with a Belsorp MAX II automatic gas adsorption instrument (Microtrac MRB). The absence of hysteresis in the nitrogen adsorption isotherm measurements (Fig. 3) indicates that the analyzed sample is non-porous.

Figure 3 Nitrogen adsorption (solid symbols) and desorption (open symbols) isotherms for non-porous silica as a function of the nitrogen saturation ratio ($P/P_{\mathrm{0}}$) at the boiling point of liquid nitrogen. The volume of adsorbed nitrogen is expressed per gram of sample at standard conditions.

3.2 SPIN measurements

Ice nucleation experiments were conducted with a modified version of the SPectrometer for Ice Nuclei (SPIN; DMT) described in Welti et al. (2020). SPIN is a continuous flow diffusion chamber type of experiment in which the test particles are exposed for a duration of approximately 10 s to constant temperature and relative humidity. The test particles were dry-dispersed by agitating the powder with a magnetic stirrer in the same way as for the size distribution measurement. The concentration of test particles introduced into SPIN is monitored using a condensation particle counter (CPC; Airmodus A20). Ice nucleation is detected by the growth of ice crystals using an optical particle counter at the exit of the chamber. The ratio of ice crystals to total particles in an experiment is reported as an activated fraction. The data points shown in this work (Sect. 4.4) are averaged from three separate experimental runs into 1 °C bins. The error bars are calculated as root-sum-squared errors based on instrumental uncertainties of temperature and humidity and on the standard deviation of the individual data points used in the averaging.

4 Results and discussion

4.1 Melting point temperature

At the phase boundary, the melting temperature is defined by the condition of zero chemical potential difference between the adsorbed ice and the liquid film, which corresponds to equality of their equilibrium vapor pressures (P_w=P_i, Eq. 16). This condition of standard phase equilibrium allows calculation of the melting temperature as a function of film thickness for each pair of A_w and B. Note that the A_w values shown below refer to 298 K and are denoted by A₂₉₈; the values of A_w for liquid water at other temperatures are obtained from Eq. (4), and the A_i values for ice are obtained from Eq. (23).

Figure 4 illustrates the variation in vapor pressure with temperature for different interaction parameters. Panel (a) shows the results for A₂₉₈=4.0 and B=1.0, while panel (b) presents the results for A₂₉₈=3.0 and B=2.0. The liquid water film thicknesses considered are 1.5 and 3.0 nm (the latter value corresponds to about 10 monolayers; thicker films are occasionally seen in adsorption measurements at high saturation ratios but are quite rare). The intersection points of the vapor pressure curves for water and ice, shown in Fig. 4, correspond to the melting point temperatures. The results indicate that thicker liquid water films exhibit higher melting point temperatures compared to thinner films. Furthermore, stronger interaction parameters (higher A_w, lower B) result in lower melting point temperatures.

Figure 5 illustrates the temperature of the melting point as a function of the thickness of the film for parameters A₂₉₈ and B ranging from 1.0 to 4.0. Panel (a) shows results for A₂₉₈=1.0, panel (b) shows results for A₂₉₈=2.0, panel (c) shows results for A₂₉₈=3.0, and panel (d) shows results for A₂₉₈=4.0. Each curve shows a clear trend where the melting point temperature increases with film thickness before leveling off asymptotically to the bulk water melting point at higher thicknesses. Figure 5 clearly shows the impact of the strength of the interaction between the adsorbent substrate and water, which is greater at higher values of A₂₉₈, and the range of the interaction into the water layers, which is greater at lower values of B. Note that the blue curves in the two lower panels (panels c and d) of Fig. 5 are probably unrealistically hydrophilic compared to atmospherically relevant mineral aerosols (Kumar et al., 2011). The model thus indicates that the melting point could be decreased by up to about 5 K in 1 nm thick water films on atmospheric particles. For comparison, similar freezing-point depression is caused by 5–10 weight percent of sodium chloride in aqueous solution. Furthermore, the melting points may be reduced in films with a thickness of several nanometers when the parameter B has values between 1 and 2. At higher values of B, the model surfaces are hydrophobic enough so that the films must be thinner than 3 to 4 nm for any noticeable decrease in the melting point.

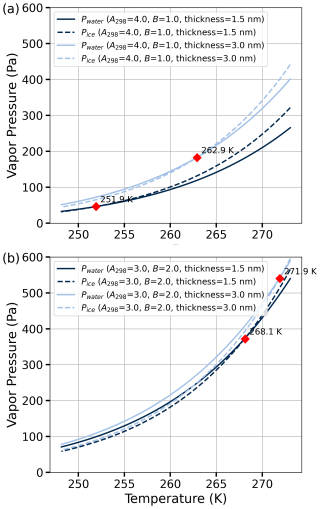
Figure 4 The two panels illustrate the temperature-dependent vapor pressure for adsorbed water and ice, calculated using Eqs. (9) and (13). The intersection points (red diamonds) of the vapor pressure curves for water and ice (Δμ_A=0, Eq. 16) indicate the melting point temperatures. Panel (a) corresponds to parameter values A₂₉₈=4.0 and B=1.0, evaluated for thicknesses of 1.5 and 3.0 nm. Panel (b) shows the same analysis for A₂₉₈=3.0 and B=2.0, also evaluated for thicknesses of 1.5 and 3.0 nm.

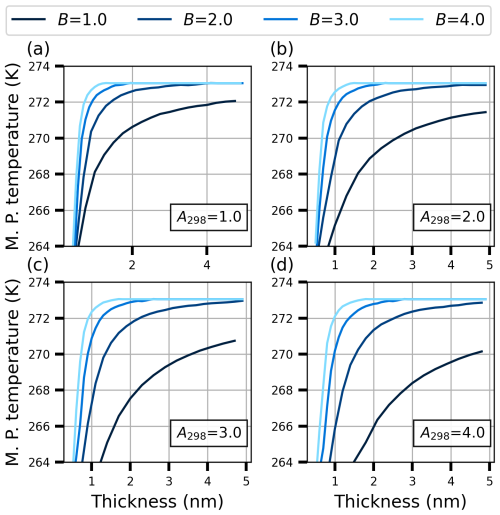
Figure 5 Melting point (MP) temperature as a function of film thickness (nm) for varying values of parameter A₂₉₈ (1.0, 2.0, 3.0, and 4.0) and parameter B (1.0, 2.0, 3.0, and 4.0). Panels (a)–(d) show the influence of increasing A₂₉₈ on the melting point. The effect of different B values is shown in each panel.

4.2 Nucleation rate (J)

Homogeneous nucleation rates are obtained based on Eq. (25) for different water film thicknesses and varying A_w and B parameters, which characterize the molecular interactions in the FHH model. The chemical potential difference Δμ_A, present in the denominator of Eq. (25), is influenced by these A_w and B parameters, directly affecting nucleation rates. Furthermore, the number of water monolayers (N_w) also plays a critical role in determining Δμ_A and consequently the nucleation rate. The film thickness is equal to N_w⋅d_w. For example, a film of 1 nm thickness consists of the equivalent of 3.5 layers of adsorbed water. The combined effect of film thickness and molecular interaction parameters is captured in the nucleation rate profile seen in panels (a) and (b) of Fig. 6.

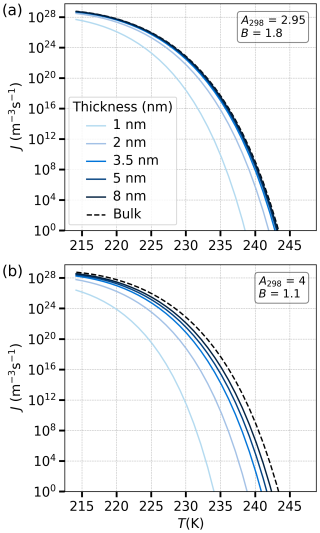
Figure 6 Comparison of nucleation rates J (${\mathrm{m}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$) as a function of temperature T for different parameter sets. Panel (a) shows results for systems with A₂₉₈=2.95 and B=1.8, while panel (b) displays results for A₂₉₈=4 and B=1.1. Each curve corresponds to nucleation rates under different film thicknesses ranging from 1 to 8 nm and a bulk system case (dashed line). The nucleation rate is presented on a logarithmic scale.

In both panels of Fig. 6, the nucleation rate decreases rapidly with increasing temperature, and thinner films experience more suppression of nucleation compared to thicker ones. The lightest-blue curve in each panel, which corresponds to thinner films (1 nm), shows a much lower nucleation rate than the darkest-blue curve, which represents the thicker 8 nm film. The darkest-blue curves are much closer to the bulk nucleation rate, reflecting the transition from surface-controlled nucleation behavior in thin films to bulk-like behavior in thicker films. When comparing panel (a) and panel (b), it is clear that, for stronger molecular interaction, represented by higher A_w and lower B values (panel b, A₂₉₈=4 and B=1.1), nucleation rates are generally lower across the temperature range. This suggests that increasing A while decreasing B results in stronger suppression of nucleation, particularly in thinner films. In contrast, lower A_w and higher B values (panel a, A₂₉₈=2.95 and B=1.8) result in higher nucleation rates, especially in thicker films. This is consistent with the molecular dynamics simulations of Hayton et al. (2024), who observed that homogeneous ice nucleation in free-standing thin water films exhibited bulk-like behavior even at very small length scales.

4.3 Critical radius

The radius of the critical nucleus in the adsorbed water film and the bulk water is calculated using Eqs. (26) and (9), respectively. The ratio of these radii is shown in panels (a) and (b) of Fig. 7 for different A_w and B and thicknesses of the water film. Panel (a) of Fig. 7 shows the results for A₂₉₈=2.95 and B=1.8, while panel (b) corresponds to A₂₉₈=4 and B=1.1, covering a range of film thicknesses from 1 to 8 nm. In both panels, the thinner water films exhibit a higher ratio of critical nucleus radii compared to thicker films, especially at lower temperatures. For example, the 1 and 2 nm films show significantly larger ratios compared to the other curves, indicating that the critical nucleus radius in adsorbed water becomes notably larger than in bulk water for thinner films. This suggests that, for thin films, adsorption has a stronger effect on suppressing nucleation by increasing the critical nucleus size.

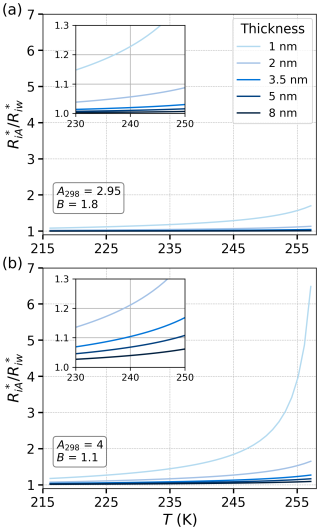
Figure 7 The ratio $R_{\mathrm{iA}}^{*}/R_{\mathrm{iw}}^{*}$, representing the radius of critical nucleus in adsorbed water ($R_{\mathrm{iA}}^{*}$) to the radius of the critical nucleus in a homogeneous case ($R_{\mathrm{iw}}^{*}$) as a function of temperature T(K). Note that, according to Eq. (26), $R_{\mathrm{iA}}^{*}/R_{\mathrm{iw}}^{*}=\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}/\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{A}}$. The curves correspond to different values of the parameters A₂₉₈ and B (FHH isotherm) and film thicknesses. The zoomed-in insets highlight the behavior in the temperature range from 230 to 250 K. The results show that smaller film thicknesses lead to a more pronounced increase in the critical nucleus size ratio as temperature rises, indicating greater sensitivity to temperature changes in systems with thinner adsorbed water layers.

The inset in each panel zooms in on the temperature range between 230 and 250 K to highlight the behavior near the onset of homogeneous freezing. In both panels, the ratio of critical radii approaches unity at lower temperatures, particularly for thicker films (5 and 8 nm). Panels (a) and (b) of Figs. 6 and 7 indicate that, for thicker films, the nucleation behavior of adsorbed water films becomes increasingly similar to that of the bulk water, especially below the onset temperature of homogeneous freezing around 235 K. Panel (b), with A₂₉₈=4 and B=1.1, shows a higher increase in the critical radius ratio at lower temperatures, suggesting that higher interaction values (larger A_w, smaller B) cause a greater deviation from the nucleation behavior of bulk water.

4.4 Critical supersaturations for ice nucleation

Figure 8 shows the variation in critical supersaturation with respect to ice (given as relative humidity (RH${}_{\mathrm{ice}}^{*}$)) as a function of temperature, calculated using two different expressions for equilibrium vapor pressure over water. In panel (a), the equilibrium vapor pressure is calculated using the equation of Murphy and Koop (2005), while panel (b) uses the expression for the equilibrium water vapor pressure given by Wagner and Pruss (2002). Both equations are given in Appendix A1. Above 235 K, the vapor pressures obtained from these two expressions are almost equal, but they deviate at lower temperatures in the “no man's land”, where vapor pressures of supercooled water cannot be measured directly. In our calculations, we assume adsorbed water to be frozen when the nucleation probability is

$$\begin{array}{}\text{(27)}& P=\mathrm{1}-\exp (-J_{\mathrm{hom},\mathrm{A}}{V}_{\mathrm{A}}\mathit{\tau })\ge \mathrm{0.01},\end{array}$$

where V_A denotes the volume of adsorbed water on a single ice nucleus and the time τ is taken to be equal to the residence time in the SPIN instrument, which is 10 s. The criterion represented by Eq. (27) corresponds to a 1 % activated fraction of aerosols as measured by SPIN.

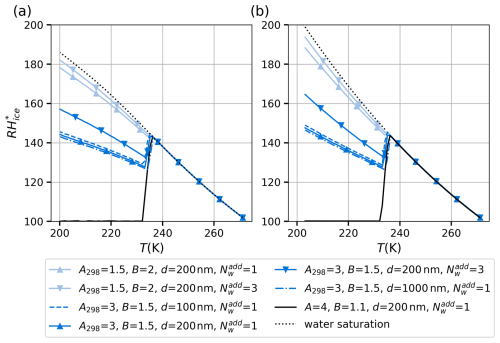
Figure 8 Comparison of critical relative humidity with respect to ice (RH${}_{\mathrm{ice}}^{*}$) as a function of temperature (T) for different parameter sets. Panel (a) uses the water saturation model from Murphy and Koop (2005), while panel (b) applies the expression for equilibrium water vapor pressure given by Wagner and Pruss (2002). Each line represents different combinations of the parameters A₂₉₈ and B and the number of additional water monolayers ($N_{\mathrm{w}}^{\mathrm{add}}$) separating the critical nucleus from the adjacent surface or the vapor phase. The dashed lines show the sensitivity to particle radius (R_p).

Panels (a) and (b) of Fig. 8 display several curves corresponding to different parameterizations of the FHH adsorption model, which describes multilayer adsorption of water onto a substrate. Ice nucleation is likely to occur homogeneously rather than heterogeneously on surfaces that can induce ice premelting (Qiu and Molinero, 2018). Surface-adjacent water can be strongly bound to the substrate and can thereby be hindered to rearrange into an ice-like lattice structure (Barahona, 2018, and references therein). On such surfaces, there will be at least one layer of liquid-like water between the surface and the critical ice nucleus. Furthermore, one or more liquid-like layers could separate the ice nucleus from the vapor phase. To test the influence of additional layers not involved in the formation of the critical nucleus, we require that the thickness of the adsorbed layer be equal to the diameter of the critical ice nucleus plus one to three monolayers of water for ice nucleation to become possible. The number of additional monolayers is indicated by $N_{\mathrm{w}}^{\mathrm{add}}$ in the legend of panels (a) and (b) of Fig. 8. The FHH parameters A_w and B and the number of additional monolayers ($N_{\mathrm{w}}^{\mathrm{add}}$) separating the critical nucleus from the substrate or surrounding vapor phase vary between the curves, and these differences affect the supersaturation required for ice nucleation. Note that we subtract the volume of the additional monolayers from V_A in Eq. (27); this volume depends, of course, on whether the additional monolayers are adjacent to the surface of the adsorbent particle (which we assume in the calculations) or if they are at the liquid–vapor interface. However, in practice, subtracting the additional volume from V_A has very little effect on the numerical results because the nucleation rate is a very steep function of temperature. The dotted black line in both panels of Fig. 8 represents the water saturation line, indicating the RH_ice at which water condenses. Initially, as the temperature decreases, the criterion of Eq. (27) is not fulfilled below water saturation. The temperature at which freezing occurs is seen as a steep drop in the relative humidity (RH${}_{\mathrm{ice}}^{*}$) line from the water saturation line. There is some variation in the exact temperature at which the separation of the critical supersaturation RH${}_{\mathrm{ice}}^{*}$ from the water saturation line occurs, which is due to the variability in the nucleation rate and the adsorbed volume between the different FHH models at a given temperature and humidity. However, as the nucleation rate increases very steeply in the vicinity of 233 K, the variation in the separation temperature remains quite small. Once the separation of RH${}_{\mathrm{ice}}^{*}$ from the water saturation line has occurred, the lines level off or start to increase again. These turns are caused by two different limiting factors. Firstly, the thickness of the adsorbed water film must be large enough to accommodate the critical ice nucleus plus $N_{\mathrm{w}}^{\mathrm{add}}$. If the critical nucleus size did not change with temperature, the curves would be parallel to the water saturation line because the amount of adsorbed water is almost constant at a fixed relative humidity (with respect to liquid water) within a temperature range of 10–20 K. However, the size of the critical nucleus decreases with temperature, bending the curves away from the water saturation line.

It should be noted that the slopes of our theoretical curves below 235 K are impacted not only by the saturation vapor pressure equation used in the calculations but also by the temperature dependencies of surface and interfacial tensions and density of water and by the temperature dependence of the A_w parameter. All these temperature dependencies are uncertain, and it would be interesting to perform a sensitivity study in the future using experimental ice nucleation results as a constraint.

Finally, with the curves leveling off very close to ice saturation (solid black lines), the limiting factor is not the thickness of the adsorbed layer, as, in these cases, the adsorbed layer is thick enough to accommodate the critical ice nucleus already below ice saturation. Rather, the limitation in these cases is similar to that in the activation of insoluble cloud condensation nuclei to cloud droplets (Sorjamaa and Laaksonen, 2007); the ice particle must overcome a Köhler-type maximum created by competition between the FHH and Kelvin terms (cf. Eq. 6 for ice adsorption) for rapid growth to ensue. In other words, ice clusters can only grow freely in ice-supersaturated conditions.

4.5 Comparison of theory and experiment

Figure 9 compares the results of our model calculations with the experimental data for silica (SiO₂). We chose silica as the ice-nucleating material because it is likely that heterogeneous freezing does not occur on premelting-inducing silica surfaces (David et al., 2019). As seen in Fig. 9, several research groups have measured ice nucleation on silicas, and there is quite a lot of variability among the results. In addition to experimental errors, we believe that an important reason for the scatter of the results is the large physical and chemical variability in different types of silicas. Silica can be either crystalline or amorphous and porous or non-porous. The surface chemistry of silica varies depending on how it has been manufactured and whether it has been treated thermally (calcinated) and/or hydrated. Bare silica surfaces are rather hydrophobic, but contact with water induces the formation of surface silanol (SiOH), siloxide (SiO⁻), and siloxane (Si-O-Si) groups. Silanol and siloxide are hydrophilic, whereas siloxane is hydrophobic. For example, silicas produced chemically from solutions of low pH and calcinated silicas tend to be hydrophobic (Warring et al., 2016).

The predictions of the model of RH${}_{\mathrm{ice}}^{*}$ as a function of temperature, shown as different lines, were generated using two different values of B and two to four additional layers $N_{\mathrm{w}}^{\mathrm{add}}$ of surface-adjacent water, or layers at the liquid–vapor interface that do not participate in ice nucleation. The experimental data shown in pink and green represent literature data, while the black data represent the experimental results of our laboratory. It should be mentioned that the silica particle sizes are variable, whereas, in our model calculations, we set the particle size to 550 nm. The size distribution of the silica used in our experiments (Fig. 2a) peaks at about 70 nm; however, it is unlikely that particles smaller than 100 nm have contributed to the 1 % activated fraction. Furthermore, the 1 % fraction of the particles that activate at the critical supersaturation are likely to be the largest particles; 1 % of the particles are larger than about 550 nm (see the cumulative size distribution in Fig. 2b). Above 100 nm, the model size dependence is quite weak; the vertical bar in Fig. 9 indicates how much the critical supersaturation lines would shift up if the particle size was 100 nm and down if the particle size was 1000 nm (see also dashed blue curves in Fig. 8). According to the model, 50 nm particles with the same FHH parameters would nucleate ice at RH${}_{\mathrm{ice}}^{*}=\mathrm{151}\mathit{\%}$. The model lines generated with our model fit the experimental data (black circles) very well, suggesting that the model accurately captures the RH${}_{\mathrm{ice}}^{*}$ behavior of silica particles over a range of temperatures. At temperatures below 235 K, the experimental slope appears steeper than the individual theoretical lines; however, the measurement uncertainties are quite large at the lowest temperatures.

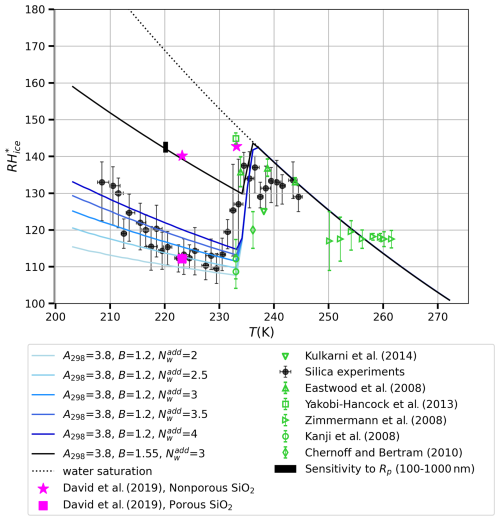
Figure 9 Comparison of relative humidity with respect to ice (RH_ice) as a function of temperature (T) for various experimental studies and model outputs. The water saturation curve was calculated using the expression for equilibrium vapor pressure given by Wagner and Pruss (2002). The vertical bar on the black curve reflects the theoretical model's sensitivity of RH_ice to particle radius (R_p from 100 to 1000 nm). Error bars on the data points indicate experimental uncertainties reported in the respective studies.

Zimmermann et al. (2008) reported the temperature of ice formation and the corresponding supersaturation for the deposition ice nucleation on silica particles at 250–265 K, represented by right-facing green triangles in Fig. 9. They found an almost constant RH${}_{\mathrm{ice}}^{*}$ of 117 %; however, the error bars of the data points extend to the water saturation line. In the study by Eastwood et al. (2008), the onset conditions of deposition ice nucleation for quartz at 233–246 K are reported to occur close to water saturation, as indicated by upward-facing green triangles. The onset humidity conditions of Kanji et al. (2008) at 233 K are close to our model predictions, while those of Yakobi-Hancock et al. (2013) and Chernoff and Bertram (2010) appear to detach from the water saturation line at temperatures a few degrees warmer than our model prediction. The pink square and two stars indicate the experimental data of David et al. (2019), representing data for porous silica and for non-porous silica, respectively. Interestingly, the data point for porous silica coincides with our own experiments and with model predictions for hydrophilic silica with the FHH parameters A₂₉₈=3.8 and B=1.2, while the data points for non-porous silica correspond to model prediction for more hydrophobic silica with A₂₉₈=3.8 and B=1.55. For comparison, Kumar et al. (2011) obtained A₂₉₈=2.95 and B=1.36 from cloud drop formation experiments with silica particles; as their B value is between the two modeled values and A₂₉₈ is not markedly different from the model value either (the model is much more sensitive to B than to A₂₉₈), we believe that the modeled values are reasonable. Our interpretation is that the calcinated silicas used by David et al. (2019) are hydrophobic and that the non-calcinated silica used in our experiments is hydrophilic. If experiments were performed for silica that is as hydrophilic as that used in our experiments but also porous, the resulting critical supersaturation would likely be below that of the data point (pink square) of David et al. (2019).

One factor in the promising agreement of our model with the experimental data, especially at lower temperatures (below 235 K), is the incorporation of the equilibrium vapor pressure equation derived by Wagner and Pruss (2002). This equation improved the performance of our model relative to the vapor pressure equation of Murphy and Koop (2005) by making the critical supersaturation curves somewhat steeper (see Fig. 8). However, as discussed in the previous subsection, the temperature dependencies of a number of variables that affect the slopes remain uncertain, especially below 235 K. These uncertainties should be diminished in order to obtain a better understanding of the agreement (or disagreement) between experiments and theory. In addition, experiments should be repeated using monodisperse aerosols with a few different dry sizes.

5 Conclusions

In this study, we extended the FHH adsorption theory to model homogeneous ice nucleation in supercooled water films adsorbed on insoluble substrates. We derived theoretical equations for the chemical potential in adsorbed water that allow the prediction of homogeneous ice nucleation on the basis of classical nucleation theory. Our theoretical approach captures the complex relationship between molecular interactions, described by the FHH parameters A_w and B and the thickness of the film in determining the conditions of ice nucleation. We showed that the melting point, critical nucleus size, and nucleation rates are influenced by the thickness of the water film, with thinner films exhibiting the largest effects on the conditions for ice nucleation because of stronger adsorbate–substrate interactions. The model was validated against experimental data for silica particles. The critical relative humidity with respect to ice (RH${}_{\mathrm{ice}}^{*}$) predicted for the onset of nucleation as a function of temperatures agrees well with both our laboratory results and previous studies. It should be noted that the equilibrium vapor pressure equation derived by Wagner and Pruss (2002) improved the agreement with the experimental data, especially at temperatures below 235 K. These findings emphasize the importance of the adsorption of a multilayer water film in the deposition ice nucleation process on insoluble aerosols in the atmosphere. By providing a detailed description of how ice nucleation in these systems varies with film thickness and substrate interactions, this work offers insights into ice cloud formation. Future studies could explore refinements of the FHH model to include additional complexities, such as the impact of surface curvature and chemical heterogeneity, or use the model to describe heterogeneous freezing within adsorbed water films.

Appendix A: Parameterizations used in the computations

A1 Water and ice properties

T denotes absolute temperature (K), and T_c is the temperature in degrees centigrade. The density of liquid water (Marcolli, 2017) (g cm⁻³) is

$$\begin{array}{}\text{(A1)}& \begin{array}{rl}{\mathit{\rho }}_w=& \mathrm{1.8643535}-\mathrm{0.0725821489}T+\mathrm{2.5194368}\cdot {\mathrm{10}}^{-\mathrm{3}}{T}^{\mathrm{2}}\\ & +\mathrm{4.9000203}\cdot {\mathrm{10}}^{-\mathrm{5}}{T}^{\mathrm{3}}+\mathrm{5.860253}\cdot {\mathrm{10}}^{-\mathrm{7}}{T}^{\mathrm{4}}\\ & -\mathrm{4.5055151}\cdot {\mathrm{10}}^{-\mathrm{9}}{T}^{\mathrm{5}}+\mathrm{2.2616353}\cdot {\mathrm{10}}^{-\mathrm{11}}{T}^{\mathrm{6}}\\ & -\mathrm{7.3484974}\cdot {\mathrm{10}}^{-\mathrm{14}}{T}^{\mathrm{7}}+\mathrm{1.4862784}\cdot {\mathrm{10}}^{-\mathrm{16}}{T}^{\mathrm{8}}\\ & -\mathrm{1.6984748}\cdot {\mathrm{10}}^{-\mathrm{19}}{T}^{\mathrm{9}}+\mathrm{8.3699379}\cdot {\mathrm{10}}^{-\mathrm{23}}{T}^{\mathrm{10}}.\end{array}\end{array}$$

The density of ice (Pruppacher and Klett, 1997) (kg m⁻³) is

$$\begin{array}{}\text{(A2)}& {\mathit{\rho }}_{\mathrm{i}}=\mathrm{916.7}-\mathrm{0.175}{T}_{\mathrm{c}}-\mathrm{0.0005}{T}^{\mathrm{2}}.\end{array}$$

The molecular volumes of water and ice are given by

$$\begin{array}{}\text{(A3)}& v_{\mathrm{w}}\left(T\right)={\displaystyle \frac{M_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{w}}\left(T\right)N_{\mathrm{A}}}}\end{array}$$

and

$$\begin{array}{}\text{(A4)}& v_{\mathrm{i}}\left(T\right)={\displaystyle \frac{M_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{i}}\left(T\right)N_{\mathrm{A}}}},\end{array}$$

where M_w is the molecular mass of water and N_A is Avogadro's number.

The equilibrium vapor pressure of liquid water by Murphy and Koop (2005) (Pa) is

$$\begin{array}{}\text{(A5)}& \begin{array}{rl}{e}_{\mathrm{w}}=& \exp \mathit{\{}\mathrm{54.842763}-\mathrm{6763.22}/T-\mathrm{4.21}\ln (T)\\ & +\mathrm{0.000367}T+\tanh \left[\mathrm{0.0415}\right(T-\mathrm{218.8}\left)\right]\\ & [\mathrm{53.878}-\mathrm{1331.22}/T-\mathrm{9.44523}\ln (T)\\ & +\mathrm{0.014025}T\left]\mathit{\right\}}.\end{array}\end{array}$$

The equilibrium vapor pressure of liquid water by Wagner and Pruss (2002) (Pa) is

$$\begin{array}{}\text{(A6)}& \begin{array}{rl}{e}_{\mathrm{w}}=& P_{\mathrm{c}}\exp \left[T_{\mathrm{c}}{T}^{-\mathrm{1}}\right(-\mathrm{7.85951783}\mathit{\tau }+\mathrm{1.84408259}{\mathit{\tau }}^{\mathrm{1.5}}\\ & -\mathrm{11.7866497}{\mathit{\tau }}^{\mathrm{3}}+\mathrm{22.6807411}{\mathit{\tau }}^{\mathrm{3.5}}\\ & -\mathrm{15.9618719}{\mathit{\tau }}^{\mathrm{4}}+\mathrm{1.80122502}{\mathit{\tau }}^{\mathrm{7.5}}\left)\right].\end{array}\end{array}$$

Here, $\mathit{\tau }=\mathrm{1}-T{T}_{\mathrm{c}}^{-\mathrm{1}}$, and the critical temperature and pressure are T_c=647.096 K and P_c=22.064 MPa.

The equilibrium vapor pressure of hexagonal ice (Murphy and Koop, 2005) (Pa) is

$$\begin{array}{}\text{(A7)}& \begin{array}{rl}{e}_i& =\exp [\mathrm{9.550426}-\mathrm{5723.265}/T+\mathrm{3.53068}\ln (T)\\ & -\mathrm{0.00728332}T].\end{array}\end{array}$$

The surface tension of water (Hrubý et al., 2014) (N m⁻¹) is

$$\begin{array}{}\text{(A8)}& \begin{array}{rl}{\mathit{\gamma }}_{\mathrm{w}}& =\mathrm{0.2358}(\mathrm{1}-T/\mathrm{647.096}{)}^{\mathrm{1.256}}[\mathrm{1}-\mathrm{0.625}(\mathrm{1}\\ & -T/\mathrm{647.096}\left)\right].\end{array}\end{array}$$

Interfacial tension between liquid water and hexagonal ice (N m⁻¹) is calculated using the Antonoff rule:

$$\begin{array}{}\text{(A9)}& {\mathit{\gamma }}_{\mathrm{iw}}={\mathit{\gamma }}_i-{\mathit{\gamma }}_{\mathrm{w}},\end{array}$$

where the ice–vapor interfacial tension is obtained from

$$\begin{array}{}\text{(A10)}& {\mathit{\gamma }}_i=\mathrm{0.1364}-\mathrm{0.00015}T.\end{array}$$

This relation, with the temperature dependence of Hale and Plummer (1974), returns the experimental value of 0.98 N m⁻¹ at 255.85 K (Boinovich and Emelyanenko, 2014).

A2 Parameterizations used in nucleation rate calculations

The pre-exponential factor of nucleation rate of ice in bulk water (Espinosa et al., 2018) (${\mathrm{m}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$) is

$$\begin{array}{}\text{(A11)}& C=\exp (\mathrm{91.656}+\mathrm{0.11729}{T}_{\mathrm{c}}+\mathrm{0.00081401}{T}_{\mathrm{c}}^{\mathrm{2}}).\end{array}$$

The chemical potential difference between water and ice used in the calculation of the nucleation rate (Espinosa et al., 2018) (J mol⁻¹) is

$$\begin{array}{}\text{(A12)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{iw}}& (\mathrm{0.00035032}-\mathrm{0.0046013}{T}_{\mathrm{c}}-\mathrm{2.3187}\\ & \times {\mathrm{10}}^{-\mathrm{5}}{T}_{\mathrm{c}}^{\mathrm{2}}+\mathrm{6.9536}\times {\mathrm{10}}^{-\mathrm{8}}{T}_{\mathrm{c}}^{\mathrm{3}})/\mathrm{4184}.\end{array}\end{array}$$

The density of hexagonal ice used in the calculation of the nucleation rate (Espinosa et al., 2018) (g cm⁻³) is

$$\begin{array}{}\text{(A13)}& {\mathit{\rho }}_{\mathrm{i}}=\mathrm{0.906}-\mathrm{0.14}\times {\mathrm{10}}^{-\mathrm{3}}{T}_{\mathrm{c}}.\end{array}$$

The interfacial tension between liquid water and hexagonal ice used in the calculation of the nucleation rate (Espinosa et al., 2018) (N m⁻¹) is

$$\begin{array}{}\text{(A14)}& \begin{array}{rl}{\mathit{\gamma }}_{\mathrm{iw}}& =(\mathrm{29.986}+\mathrm{0.25559}{T}_{\mathrm{c}}-\mathrm{0.0010465}{T}_{\mathrm{c}}^{\mathrm{2}}\\ & -\mathrm{4.6503}\times {\mathrm{10}}^{-\mathrm{6}}{T}_{\mathrm{c}}^{\mathrm{3}}+{\mathrm{2.9065}}^{\times }{\mathrm{10}}^{-\mathrm{7}}{T}_{\mathrm{c}}^{\mathrm{4}})/\mathrm{1000}.\end{array}\end{array}$$

Appendix B: List of variables

Table B1 List of symbols used in the article.