Secondary ice production – no evidence of efficient rime-splintering mechanism

Mixed-phase clouds are essential for Earth’s weather and climate system. Ice multiplication via secondary ice production (SIP) is thought to be responsible for the observed strong increase in ice particle number concentration in mixed-phase clouds. In this study, we focus on the rime splintering also known as the Hallett–Mossop (HM) process, which still lacks physical and quantitative understanding. We report on an experimental study of rime splintering conducted in a newly developed setup under conditions representing convective mixed-phase clouds in the temperature range of −4 to −10 °C. The riming process was observed with high-speed video microscopy and infrared thermography, while potential secondary ice (SI) particles in the super-micron size range were detected by a custom-built ice counter. Contrary to earlier HM experiments, where up to several hundreds of SI particles per milligram of rime were found at −5 °C, we found no evidence of productive SIP, which fundamentally questions the importance of rime splintering. Further, we could exclude two potential mechanisms suggested to be the explanation for rime splintering: the freezing of droplets upon glancing contact with the rimer and the fragmentation of spherically freezing droplets on the rimer surface. The break-off of sublimating fragile rime spires was observed to produce very few SI particles, which is insufficient to explain the large numbers of ice particles reported in earlier studies. In the transition regime between wet and dry growth, in analogy to phenomena of the deformation of drizzle droplets upon freezing, we also observed the formation of spikes on the rimer surface, which might be a source of SIP.

1 Introduction

Ice formation in mixed-phase clouds affects cloud radiative properties; impacts cloud electricity, precipitation formation, and cloud lifetime; and is therefore essential for Earth's weather and climate systems. Primary ice particles are formed by ice-nucleating particles (INPs) catalyzing the nucleation process or via homogeneous freezing at temperatures below around −38 °C. In situ and remote sensing measurements of the ice crystal number concentration (ICNC) in mixed-phase clouds occasionally demonstrate a strong discrepancy between the ICNC and INP concentrations of 1 to 4 orders of magnitude at moderate supercooling (Hobbs, 1969; Hobbs and Rangno, 1985, 1990; Mossop, 1985b; Hogan et al., 2002; Crosier et al., 2011; Crawford et al., 2012; Heymsfield and Willis, 2014; Lawson et al., 2015; Taylor et al., 2016; Lasher-Trapp et al., 2016; Huang et al., 2017; Ladino et al., 2017; O'Shea et al., 2017; Korolev et al., 2020; Luke et al., 2021; Ramelli et al., 2021; Li et al., 2021). Such a discrepancy could be explained by secondary ice production (SIP) processes increasing the total ice particle number concentration by the multiplication of pre-existing ice particles (Field et al., 2017; Korolev and Leisner, 2020; Chisnell and Latham, 1976; Connolly et al., 2006; Sun et al., 2010; Crawford et al., 2012; Yano et al., 2016; Sullivan et al., 2018; Sotiropoulou et al., 2020; Georgakaki et al., 2022). The newest studies suggest that SIP is the dominant ice formation process in mixed-phase clouds (Zhao and Liu, 2021; Zhao et al., 2023). According to Korolev and Leisner (2020), SIP might proceed according to the following mechanisms: (a) droplet fragmentation during freezing (Takahashi and Yamashita, 1977; Wildeman et al., 2017; Lauber et al., 2018; Keinert et al., 2020; Kleinheins et al., 2021), (b) rime splintering, (c) fragmentation during ice–ice particle collisions (Vardiman, 1978; Takahashi et al., 1995; Grzegorczyk et al., 2023), (d) ice fragmentation due to thermal shock (Dye and Hobbs, 1968; King and Fletcher, 1976b), (e) ice fragmentation due to sublimation (Oraltay and Hallett, 1989; Dong et al., 1994; Bacon et al., 1998), and (f) ice fragmentation due to the activation of INPs in transient supersaturation (e.g., Prabhakaran et al., 2020). Yet another SIP mechanism occurring during the break-up of freezing droplets on impact with smaller ice particles, suggested by Phillips et al. (2018), was supported experimentally by James et al. (2021). None of these proposed SIP mechanisms has been sufficiently characterized so far.

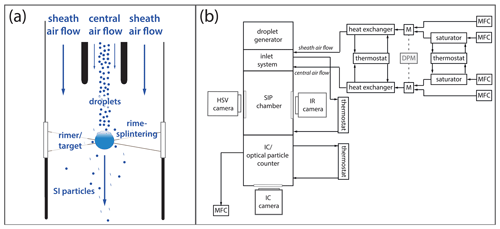
Figure 1 (a) A sketch of the SIP chamber. (b) A schematic of IDEFIX with a flow conditioning system, droplet generator, inlet system, SIP chamber with a high-speed video (HSV) camera, infrared (IR) thermography system, and ice counter (IC). (M: turbulent mixing chamber, DPM: dew point mirror, MFC: mass flow controller.)

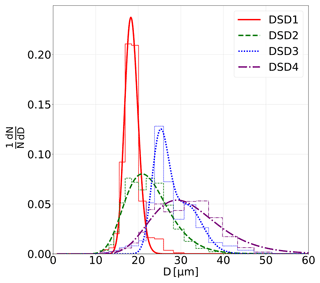
Figure 2 Normalized number size distributions of four different droplet populations used in the IDEFIX experiments (DSD1–DSD4), including measurements (bar graph) and respective log-normal fits (curves and parameters are given in Table 1).

The most widely accepted SIP mechanism is the Hallett–Mossop (HM) or, more generally, the rime-splintering process (Hallett and Mossop, 1974; Mossop and Hallett, 1974), which suggests that the secondary ice (SI) particles are produced upon riming of a large ice particle (called rimer). Riming results from droplet–ice collisions as the ice particle falls through a cloud of supercooled droplets. Rime splintering was identified in laboratory experiments to be active in a narrow air temperature range of between −3 and −8 °C (Hallett and Mossop, 1974). They found a maximum SIP rate of around 350 SI particles per milligram of accreted rime at near −5 °C and at a rimer velocity of 2.7 m s⁻¹. Similar results were obtained by Mossop in the follow-up experiments (Mossop, 1976, 1985a). Therefore, the temperature range from −3 to −8 °C is often referred to as the “Hallett–Mossop temperature regime”. Heymsfield and Mossop (1984) highlighted the importance of the rimer surface temperature, which can be higher than the air temperature due to the latent heat of crystallization released upon the freezing of accreted droplets (Heymsfield and Mossop, 1984). Generally, the freezing of a supercooled water droplet can be subdivided into three stages (Macklin and Payne, 1967). In the initial freezing or recalescence stage, ice dendrites rapidly grow through the droplet starting from the nucleation site, and the latent heat released during the phase transition causes the temperature of the droplet to rise to the melting point of water (0 °C) (Macklin and Payne, 1967; Pruppacher and Klett, 2010; Korolev and Leisner, 2020). In the subsequent second freezing stage, where the remaining liquid water freezes, the droplet temperature stays at 0 °C, as heat dissipation to the environment via heat conduction balances the latent heat of crystallization. After freezing is completed, the droplet cools down to the temperature of the environment. The freezing of a small droplet upon collision with a larger ice particle follows the same pathway but with a (100 times) higher rate of latent heat removal through the water–ice boundary, so that the temperature of the droplet may not reach the melting point at all. However, if the droplet mass accretion rate is high, the rimer surface temperature could rise to the melting point of water, signifying the transition from the dry-growth to the wet-growth regime (Schumann–Ludlam limit, Schumann, 1938; Ludlam, 1958; Pruppacher and Klett, 2010). The wet-growth regime is thought to inhibit rime splintering (Bader et al., 1974; Pruppacher and Klett, 2010; Korolev and Leisner, 2020; and references therein). Following the initial experiments by Hallett and Mossop, a connection between the droplet size distribution (DSD) and the rate of SIP due to rime splintering has been identified in the later experimental studies. In particular, the efficiency of rime splintering was found to be the highest if droplets smaller than 12 µm and larger than 24 µm in diameter were present at the same time (Hallett and Mossop, 1974; Mossop, 1978a, 1985a). The rimer velocity also seems to be a relevant parameter for rime splintering, with reported maximum SIP rates observed between 2 and 6 m s⁻¹ (Mossop, 1976, 1985a; Saunders and Hosseini, 2001). Despite plentiful evidence of the rime-splintering SIP from laboratory experiments and in situ observations, the mechanism responsible for the release of SI splinters is still debated. Several mechanisms have been proposed that might cause SIP during riming based on the release of stresses due to the mechanical action (shedding), pressure or thermal gradients during riming, freezing initiation of a droplet that makes glancing contact with the rimer, or detachment of frail ice needles by sublimation (Mossop, 1976; Choularton et al., 1980; Dong and Hallett, 1989).

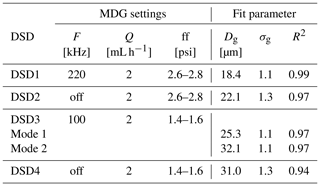
Table 1 MDG settings frequency, F; liquid flow rate, Q; and flow focusing pressure difference, ff, resulting in four different droplet size distributions, DSD1–4, which were found to be log-normally distributed by applying $\frac{\mathrm{1}}{N}\frac{\mathrm{d}N}{\mathrm{d}D}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}\mathit{\pi }}\ln {\mathit{\sigma }}_{\mathrm{g}}}\exp \left(-\frac{(\ln D-\ln D_{\mathrm{g}}{)}^{\mathrm{2}}}{\mathrm{2}\ln {{\mathit{\sigma }}_{\mathrm{g}}}^{\mathrm{2}}}\right)$. Given are the geometric mean diameter, D_g, and the geometric standard deviation factor, σ_g, of the log-normal distributions fitted to DSD1–4 (Fig. 2). For DSD3, a bimodal fit was applied and the relative fraction of modes 1 and 2 is 0.7 and 0.2, respectively. The goodness of fit is described by the coefficient of determination, R².

Two types of experimental methods have been applied to study rime splintering in a laboratory by either using a single fixed ice grain simulating realistic graupel (Brownscombe and Hallett, 1967; Aufdermaur and Johnson, 1972; Bader et al., 1974) or mimicking falling rimers by large, rotating ice-covered metal rods in a cloud simulation chamber filled with supercooled droplets produced by steam from a boiler (Hallett and Mossop, 1974; Mossop, 1976, 1985a; Saunders and Hosseini, 2001). In the following discussion, we refer to HM-type experiments corresponding to the latter case. For all of these experimental methods, the conditions regarding temperature, DSD, and impact velocity were mostly comparable to those encountered in the atmosphere. However, information about droplet–rimer collision rates and rimer surface temperature is often missing. Simultaneous microscopic observation of the riming surface in an airflow and the detection of SI particles have not been performed to date. In many cases, the existence of background ice particles in the simulation chamber led to large uncertainties in determined SIP rates. Difficulties in controlling the experimental conditions have apparently been responsible for the low replicability of the measured SIP rates that have been reported to be in the range from 0 to 8000 SI particles per milligram of rime at similar conditions (Korolev and Leisner, 2020). It is remarkable that a significant number of SI particles is reported mainly from the HM-type experiments using large rimer surfaces and steam generation of cloud droplets, with the exception of the study by Latham and Mason (1961). In the latter study, however, the presence of carbon dioxide probably caused the high number of splinters (Korolev and Leisner, 2020).

The overview of the previous experimental results indicates the necessity to revisit the rime-splintering experiments under better-controlled conditions and with improved measuring techniques. For this purpose, the new laboratory experiment, IDEFIX (Ice Droplets splintEring on FreezIng eXperiment), was set up, allowing for the direct observation of the riming process on the surface of a fixed graupel particle with high-speed video microscopy and infrared thermography, while detecting the SI particles with a newly developed ice counter.

2 Ice Droplets splintEring on FreezIng eXperiment (IDEFIX)

The experimental setup IDEFIX has been developed to study SIP resulting from riming on a qualitative and quantitative level for atmospheric representative and well-controlled conditions. In IDEFIX, riming is simulated by exposing a fixed large ice particle (diameter ≈ 1 mm) to a stream of supercooled water droplets carried by an airflow. The rimer was produced by freezing a drop of 1 µL deionized water placed on the intersection of two carbon fibers with a thickness of about 6 µm (Fig. 1a). The airflow velocity corresponds to the terminal fall velocity of a graupel grain of 1 mm in diameter, which is approximately 1 m s⁻¹. IDEFIX provides thermodynamic and flow conditions and allows for the visualization of the riming process, measurement of the graupel surface temperature, and quantification of the production rate of the SI particles.

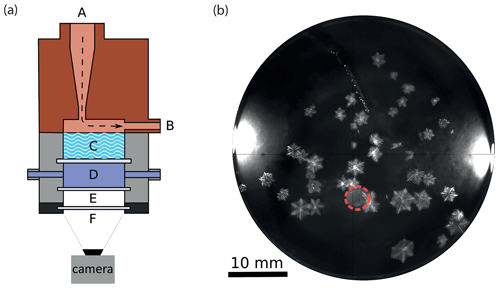
Figure 3 Ice counter (IC) used to detect the SI particles via impaction on a supercooled sucrose solution. In panel (a), a cross section of the IC is shown including the inlet (A), outlet (B), sucrose bath (C), flow-through chamber with cooling liquid (D), thermal isolation cell with two transparent windows (E), and camera setup (F). The entire IC housing is cooled by ethanol flowing through the chamber (D) and the copper housing body (not shown). In panel (b), an example of ice crystals in the supercooled sucrose solution is given. The bright spots on the left and right side are the LED lights installed in (C) for illumination. A Pt100 temperature sensor is immersed in the sucrose solution to measure its temperature. The nozzle position is marked by the dashed red circle.

Table 2 IDEFIX parameter space for SIP experiments.

2.1 Experimental setup

IDEFIX consists of a pre-conditioning system, a droplet generator, an inlet system, the SIP chamber, and the SI particle detection system (Fig. 1b). IDEFIX is fed with two airflows (i.e., the central and the sheath airflows), each independently conditioned with respect to temperature, humidity, and flow rate. Thereto, particle-free dry ar and humidified air (Nafion saturator; Gasmet) are mixed in turbulent mixing chambers and subsequently cooled to the required temperature inside the heat exchangers controlled by a thermostat (FP50; JULABO). In the experiments described here, the central and the sheath airflows have the same temperature.

The central and the sheath airflows are isokinetically combined in an inlet system upstream of the SIP chamber. Flow conditions inside the SIP chamber are laminar. For a subset of experiments simulating higher droplet impact velocities, the central airflow was increased by up to factor of 3. The supercooled droplets, generated by a droplet generator, are injected into the central airflow in the inlet system. Upon entering the SIP chamber, the droplets are supercooled for approx. 5 s and in thermal equilibrium with the airflow, as the thermal relaxation time of 20 µm droplets is on the order of 20 ms. The temperatures of the inlet and the metal walls of the SIP chamber are controlled by a thermostat (F25; JULABO). The inner diameter of the SIP chamber (17 mm) was chosen to minimize the potential losses of SI particles to the walls by the impaction of splintered SI particles. As the worst-case scenario, we consider a 20 µm diameter particle ejected from the rimer surface at 10 m s⁻¹. In this case, the stopping distance is about 7 mm. Downstream of the SIP chamber, either an optical particle counter, welas^® (welas^®1000; Palas^®), or the newly developed ice particle counter is installed to determine the DSD or the total number of SI particles, respectively.

In this study, the airflow temperature varied in the range of between −4 and −10 °C and the airflow velocity of between 1 and 3 m s⁻¹. Due to the systematic temperature deviation at the rimer position of around +1 K, the water vapor saturation with respect to ice is 90 %. Water vapor emitted by evaporating water droplets contributes less than 1 % RH and can be neglected.

2.2 Droplet generation and size distributions

A monodisperse droplet generator (MDG; model 1530; TSI^®) is used for generating droplets with different size distributions. In the MDG, the mechanical vibration of the nozzle combined with aerodynamic focusing produces a jet of deionized water droplets (details are described in Duan et al., 2016). The DSD and total droplet number can be controlled by adjusting the liquid flow rate, vibration frequency, and the focusing airflow rate. To study the impact of different droplet sizes on the efficiency of rime-splintering SIP, four different MDG settings were used, and the resulting DSDs were measured with an optical particle counter, welas^®. The MDG settings and parameters of the log-normal fits of the DSDs are given in Table 1 and shown in Fig. 2.

As the droplets produced by the MDG are intrinsically charged, two bipolar corona discharges operating at 50 Hz with an alternating voltage of 5 kV were used to partly neutralize the droplets prior to entering the inlet system. This has significantly improved the stability of droplet generation.

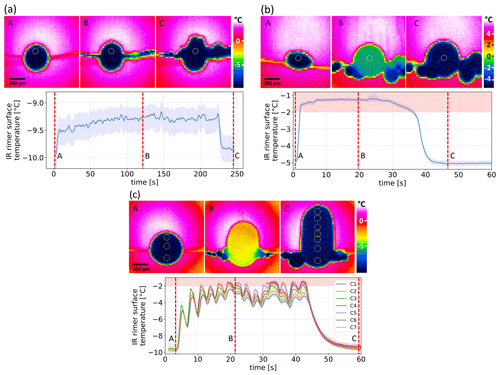
Figure 4 Sequence of IR images before (A), during (B), and after (C) riming (a, b) and the time series of the average rimer surface temperature measured within circles of 150–200 µm in diameter close to the rimer top in the IR images for the dry- (a), wet- (b), and transitional-growth regime (c). In example (c), several measurement circles (C1–C7, numbered from bottom to top) were applied. The red-shaded areas mark the IR temperature region of the water melting point according to calibration measurements. Please note the different scales of the color bars.

Figure 5 HSV image sequence of individual droplet–rimer collisions with airflow velocity of 1 m s⁻¹ at −5 °C and droplet diameter D=16.5 µm (a), −7 °C and D=20 µm (b), and −10 °C and D=18.5 µm (c) in the dry-growth regime.

Figure 6 Macroscopic view of the graupel surface structure in a matured stage grouped according to temperature and the prevailing growth regime. In all cases, the airflow velocity was set to 1 m s⁻¹.

2.3 Riming observation

For microscopic and thermal observation of the riming process a high-speed video (HSV) camera (Phantom Veo 710L; HS Vision) and an infrared (IR) camera (ImageIR 7340; InfraTec GmbH) were used. The HSV camera was operated with a 10× microscopic objective (Plan Apo; Mitutoyo) in the transmitted illumination. This setup allowed for an exposure time of 2 µs, a focal depth of about 200 µm, and a pixel resolution of about 2 µm. The field of view (FOV) and the recording time varied according to the selected frame rate. For low frame rates in the range of 100–1000 fps, the maximum frame size was 1280 × 800 pixels corresponding to the FOV of 3.5 × 1.6 mm. With this setting, it was possible to observe the evolving rimer surface structure over a time period of several seconds. In order to record individual droplet–rimer collisions with high frame rates (up to 70 000 fps), the maximum frame size was reduced to 256 × 256 pixels (FOV of 0.5 × 0.5 mm).

The IR camera was operated with a 2× germanium macroscopic lens and provided measurements of the rimer temperature with an accuracy of ±1 K based on the factory calibration in the temperature range from −30 to 300 °C, as described in Kleinheins et al. (2021). In the IR calibration experiment (Sect. S3 in the Supplement), the rimer surface of true temperature 0 °C was found to appear 1.4 ± 0.6 K colder in the IR measurements. This offset, which can be attributed to the presence of Ge windows and proximity of chamber walls, should be kept in mind when considering the diagrams showing the IR temperature values. The IR video sequences have been recorded at a frame rate of 25 fps.

2.4 Ice particle detection

To count the SI particles, a custom-built ice counter (IC) is installed downstream of the SIP chamber of IDEFIX. The cross section of the IC is shown in Fig. 3a. SI particles and droplets carried by the airflow are directed to the surface of a sucrose solution (Merck™; 42.85 wt %) kept at a temperature just below its melting point. As the sucrose solution is slightly supercooled, impinging ice crystals slowly grow to optically detectable sizes, whereas liquid droplets dissolve in the solution upon contact. The melting point for this sucrose concentration was determined experimentally to be −5.0 °C, and the solution was kept at −5.7 °C throughout the experiments. The method of using a supercooled sugar solution for ice crystal detection was first introduced by Bigg (1957) and has been popular for detecting ice crystals in laboratory experiments (e.g., Mason and Maybank, 1960; Aufdermaur and Johnson, 1972; Kolomeychuk et al., 1975). By heating the sugar solution above the melting point, ice crystals melt, and a new experimental cycle can be started without the need to exchange the sucrose solution. The sucrose bath is illuminated from above with two white LEDs, and the ice crystals floating on the surface of the sucrose solution are observed with a video camera (Photonfocus MV1-D2080-160-G2) through the transparent windows of the cooling cell from below. An example of ice crystals grown in the IC bath is shown in Fig. 3b. The impaction probability of an ice crystal on the surface of the sucrose solution is higher for larger ice crystals and higher flow velocity. The flow in the IC is accelerated through a nozzle of 3.5 mm diameter at the end of the conical flow tube connected to the SIP chamber (see Fig. 3a). At this nozzle size and a total airflow rate of 12.35 L min⁻¹, the impaction cutoff aerodynamic diameter of 2 µm has been found experimentally. However, taking into account that secondary ice crystals are exposed to subsaturated conditions with respect to ice and sublimate on their way to the IC, the 2 µm cutoff diameter at the collision point corresponds to an initial ice particle diameter of 3.3 µm released in the vicinity of the rimer. Details of the IC characterization experiments can be found in Sect. S1 in the Supplement. To ensure that there are no background counts, every experiment was preceded and followed by a blank test, where a rimer was situated in the SIP chamber and exposed to a droplet-free airflow for at least about 2 min. Only the experiments where no ice appeared in the IC sucrose solution are considered valid.

3 Results and discussion

3.1 Riming

3.1.1 Growth regimes

Riming experiments were conducted with four different droplet populations, as described in the experimental section. For each DSD, the respective collision rates have been calculated, as described in the Supplement (see Sect. S2), and can be found in Table 2 together with the relevant experimental parameters. Depending on the settings (DSD1–4; see Fig. 2), three different riming regimes were observed at IDEFIX: (a) dry-growth, (b) wet-growth, (c) and transitional-growth. Examples of the characteristic time series of the rimer surface temperature before, during, and after riming are given in Fig. 4.

Dry growth was observed for low mass collision rates associated with DSD1 and DSD2. In all experiments with these settings, the rimer surface temperature increased by a constant value of about 0.3 to 2 K during riming, as shown in Fig. 4a. After riming, the rimer surface temperature returns to the environment temperature. In the wet-growth regime (Schumann, 1938) resulting from high mass collision rates, the latent heat released by the freezing of continuously colliding droplets cannot be removed rapidly enough by heat dissipation and sublimation so that the surface temperature of the rimer rises to the melting point of water (see heat balance model of a riming particle in Sect. S2.1 in the Supplement) and a liquid layer forms at the graupel surface (Fig. 4b). In the cases where the collision rate varied with time, the rimer surface temperature was observed to oscillate between the melting point and a lower temperature. We describe this as the transitional-growth regime (see Fig. 4c). The wet-growth and transitional-growth regimes were occasionally observed with DSD3 and DSD4.

3.1.2 Microscopic structure of rime

In the dry-growth regime, the structure of rime is independent of the collision rate because the individual droplets colliding with the rimer freeze completely before the next droplet arrives. In the experiments described here, the inter-arrival time between two consecutive droplets hitting the same spot on the rimer surface was between 0.4 and 0.6 s, as calculated with Eq. 11 in Sect. S4 in the Supplement. This is significantly longer than the time of individual droplets freezing, which was calculated to be between 0.01 and 0.04 s (Eqs. 11, 12 in Sect. S4 in the Supplement), assuming that the freezing droplets on the ice surface at a temperature between −10 and −5 °C have a semi-spherical-cap geometry, respectively.

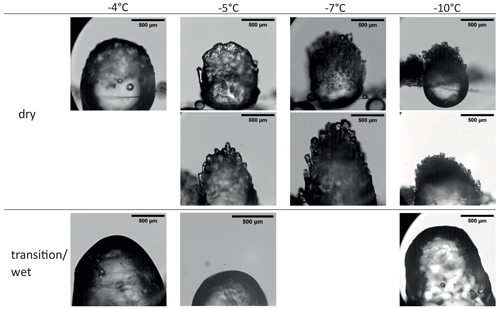
Upon collision with the rimer surface, a droplet starts spreading to assume the equilibrium shape determined by the surface energy relationship between the ice, water, and gas phases. However, the spreading is counteracted by freezing, which is also initiated at the moment of contact. Contrary to the freezing rate, the spreading rate does not depend on the temperature in the range of between −3 and −8 °C; the final shape of an accreted droplet is therefore defined by the time required to halt the spreading. The HSV records taken at −5, −7, and −10 °C in Fig. 5 show different shapes of accreted droplets. At −10 °C, the accreted frozen droplets retain their quasi-hemispherical shape with an apparent contact angle of between 80 and 120°. Multiple frozen droplets are forming narrow ice spicules at this temperature. At temperatures above −10 °C, droplets spread to flat lentil shapes with apparent contact angles of about 30° ± 10°, forming thick rime columns.

The tendency to freeze in spherical shapes upon droplet accretion at lower temperatures was also observed by Macklin and Payne (1968, 1969) and Dong and Hallett (1989). The microscopic photographs of rime structures by Griggs and Choularton (1986) also show preferential formation of fragile ice needles with decreasing temperature.

During riming in the transitional-growth or wet-growth regime, a dense ice particle with a smooth surface was formed at all investigated temperatures (Fig. 6, lower panel). In these growth regimes, the characteristic inter-arrival time is about 0.10 s and is close to the freezing time of water droplets in the size range of 30–50 µm in diameter for the investigated temperature range in the IDEFIX experiments (approx. 0.08–0.23 s at −5 °C). Hence, larger accreted droplets are still partially liquid when the next droplets arrive at the same spot. This leads to continuous wetting of the rimer surface, thus impeding the growth of rime spires.

3.2 Rime splintering

Out of 30 valid IDEFIX experiments with droplet–rimer mass collision rates in the range of between 1.6 $\times {\mathrm{10}}^{-\mathrm{3}}$ and 16 $\times {\mathrm{10}}^{-\mathrm{3}}$ mg mm⁻² s⁻¹, only in six experiments were potential SIP events identified by observing ice particles in the IC (see Table 3). A detailed overview of the valid rime-splintering experiments, as well as HSV and IC images of the experiments with potential SIP, is given in Table S3 and Fig. S7 in Sect. S5 in the Supplement. In two experiments at −5 °C, ice particles were counted with the IC during riming, whereby no co-occurring SIP was seen in the high-speed video recordings. There were also four experiments at −7 and −10 °C, in which one or two individual ice crystals were detected in the IC several minutes after riming. Among these four cases, sublimation-induced break-off of a rime spire was observed twice with the HSV camera. An example of a rime spire bending down before its final break-off, which was documented after about 10 min of sublimation, is shown in Fig. 7.

Table 3 Number of valid IDEFIX experiments in total and where ice crystals were detected in the IC (potential SIP) during or after riming for all experimental temperatures. The number of cases in the different growth regimes is given in parentheses. In case of potential SIP, the number of detected ice crystals and the prevailing growth regime during the experiment are given as well. Further details can be found in Table S3 in the Supplement.

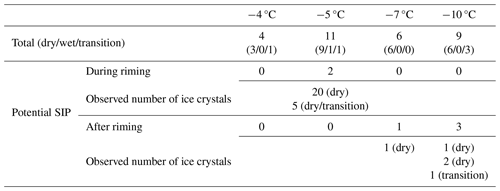
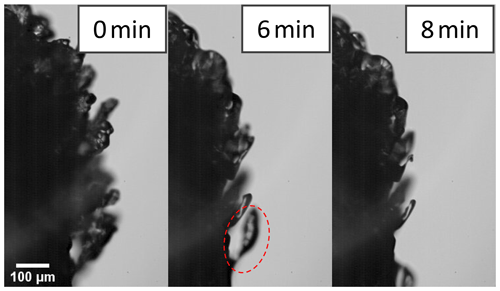
Figure 7 High-speed image sequence of sublimating rime spires on the surface of a graupel particle at −10 °C in an ice-subsaturated environment with airflow velocity of 1 m s⁻¹ after riming. After about 8 min of sublimation, the encircled rime spire was observed to bend down before it finally broke off 2 further minutes later.

The cases for which ice crystals were observed in the IC during riming could not be reproduced in other experiments conducted under the same conditions. We therefore conclude that no efficient and reproducible SIP was observed during riming experiments with IDEFIX within the investigated parameter range (see Table 2). In all potential SIP cases, the number of ice crystals detected in the IC was well below the values expected on the basis of the original HM experiments (Hallett and Mossop, 1974; Mossop, 1976, 1985a) in the temperature range of −3 to −8 °C. In their experiments, up to 300–350 SI particles per milligram of rime were observed at around −5 °C for rimer velocities in the range of 2–4 m s⁻¹ and accretion rates on the order of 10⁻⁴ mg mm⁻² s⁻¹ (Mossop, 1985a). To summarize all SIP experiments in the dry-growth regime at −5 °C, the number of detected ice crystals account for a maximum of 7.6 SI particles per milligram. Note that this derived SIP rate is determined by one out of five experiments (Table 3). We acknowledge the possibility that all SI crystals generated via rime splintering were considerably smaller than the 3.3 µm diameter and therefore could not be detected. The possible reasons for inefficient SIP in our experiments are summarized at the end of this section. In the following, we discuss the individual mechanisms potentially underlying the rime-splintering SIP (illustrated in Fig. 8) based on our microscopic observation of riming events in more detail.

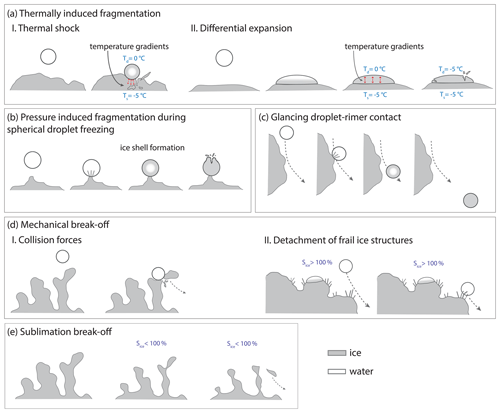
Figure 8 Schematic illustration of different mechanisms proposed to explain the rime-splintering SIP mechanism (a–d). A proposed mechanism, where riming leads indirectly to SIP is sketched in panel (e). In panel (a), temperature gradients are indicated with red arrows. The ice surface has an exemplary temperature of $T_{\mathrm{s}}=-\mathrm{5}$ °C just like the incident supercooled droplet. During freezing upon impact, the droplet temperature (T_d) increases to up to 0 °C. Schematic II in panel (a) is adapted from the simplistic conceptual model and the observation of a shattered droplet from Dong and Hallett (1989, Figs. 12 and 13 therein). Panel (b) is adopted from a camera observation of splintering due to ice shell fragmentation of a spherically shaped accreted droplet, presented in Choularton et al. (1980, Fig. 2c therein). In schematic II in panel (d), saturation with respect to ice (S_ice) has to be over 100 % to enable depositional growth of frail ice structures on the rimer surface. In an ice-subsaturated environment (e), sublimation can lead to the fragmentation of rime spires previously grown on the graupel surface.

Splintering during the freezing of an accreted droplet. This mechanism suggests that the SI particles are produced as a result of the fragmentation of the ice shell forming around a freezing droplet (Mossop, 1976; Choularton et al., 1980; Griggs and Choularton, 1983) in analogy to the shattering of droplets freezing in free fall (Kleinheins et al., 2021; Lauber et al., 2018; Keinert et al., 2020). As an ice shell forms around the freezing droplet, the pressure in the liquid water trapped inside increases considerably (up to 240 bar; Kleinheins et al., 2021). If pressure-induced stress exceeds tensile strength of ice, pressure is released by elastic deformation followed by the fragmentation of the ice shell. An illustrative case of pressure-induced fragmentation and splintering of a droplet accreted on a surface covered with ice at −7 °C was observed by Choularton et al. (1980, Fig. 2c therein) and is shown schematically in Fig. 8b.

The formation of an ice shell enclosing a freezing droplet requires the spherically symmetrical removal of the latent heat of crystallization through the droplet surface facilitated, for example, by ventilation and droplet rotation in free fall. A stationary droplet accreted on the surface of a rimer could form an ice shell only if the heat flux through the contact surface were comparable with that of diffusion and convective heat removal through the air. This could be the case if the freezing droplet were connected to the rimer by a thin neck formed, for example, by a smaller frozen droplet present at the point of contact (Choularton et al., 1980; Emersic and Connolly, 2017).

Observations obtained with IDEFIX and reported in previous studies by Dong and Hallett (1989) and Emersic and Connolly (2017) have shown that the droplets tend to spread upon impact on smooth and rough ice surfaces at a temperature above −10 °C. This clearly contradicts the hypothesis of the pressure-induced fragmentation of the ice shell forming around the freezing droplet accreted to the rimer surface. Below −7 °C, there is a distinct tendency of the accreted droplets to freeze in a spherical shape. However, in our experiments with IDEFIX, no SIP during riming was observed at −10 °C. To this effect, Griggs and Choularton (1983) speculated that at such low temperatures, the ice shell of an accreted freezing droplet might be too strong for cracking. This contradicts the observation of Kleinheins et al. (2021), who reported pressure release events in freezing droplets down to the temperature of −25 °C for much larger droplets.

Even if the ice shell is not forming around the freezing droplet, the latent heat released during freezing can induce thermal gradients at the droplet–ice interface and thus lead to differential thermal expansion of ice, which could result in fragmentation of the freezing accreted droplet or the underlying ice structure, as illustrated in Fig. 8aI and aII, respectively. A detailed review of these thermal shock mechanisms is given in Korolev and Leisner (2020) and references therein.

Although the dry-growth regime would have offered suitable conditions, no evidence was found for such SIP mechanisms associated with thermal shock (Koenig, 1963; King and Fletcher, 1976a) or shear stress release (Dong and Hallett, 1989) in IDEFIX experiments. Even if a large fraction of SI particles generated in this way were smaller than 3.3 µm in diameter and had detection probabilities less than 50 %, considering sublimation effects on the way to the IC, we would expect that due to the high number of droplet collisions at IDEFIX (on the order of 2000 per experiment), at least a few SI particles would have been detected with the IC.

Droplet freezing induced by glancing contact with rimer surface. Illustrated in Fig. 8c, it can be considered an SIP mechanism (Mossop, 1976). According to our statistical estimation, about 2 to 17 droplets per second are passing near the rimer surface at a distance smaller than the median droplet diameter of 20–30 µm (a concept described in Wang, 2013). Based on this estimation, multiple frozen droplets should have been observed in the IC as their size would ensure their efficient impaction on the surface of the sucrose solution. As we do not observe continuous SIP, droplets experiencing glancing contact with the rimer surface are always accreted by the surface or do not freeze upon glancing contact with ice. On the rare occasion when a droplet on a glancing trajectory was in the focal plane of the imaging optics, we have observed droplet coalescence with the rimer surface (Fig. 9). The preferential accretion of grazing droplets is affirmed by the results of Emersic and Connolly (2017).

Figure 9 Glancing collision of a droplet of 20 µm in diameter, resulting in accretion to the rimer surface at −7 °C and 1 m s⁻¹. The arrow illustrates the trajectory of the droplet.

Break-off of frail ice structures due to mechanical action or sublimation. This is another potential SIP associated with riming. Fragile ice formations such as chains of frozen droplets or towers on the rimer surface (also called rime spires) or ice needles preferentially growing by vapor deposition on the rimer surface at around −5 °C in an ice- and water-supersaturated environment (Libbrecht, 2017) are suggested to be a further potential source of SI particles associated with rime-splintering SIP (Macklin, 1960; Bader et al., 1974; Mossop, 1976). Those fragile ice structures may break off upon collisions with droplets or other ice particles (Mossop et al., 1974), as illustrated in Fig. 8dI and dII. Neither the detachment of frail ice needles nor the mechanical break-off from rime spires was observed in IDEFIX in the investigated parameter space. Even at −10 °C, the more fragile rime spires are mechanically stable. Experiments by Griggs and Choularton (1986) showed that rime spires are unlikely to break off due to sheer force of air motion alone and that relative velocities of above 60 m s⁻¹ are required in order for this to occur. Deposition growth of ice needles could not be observed at IDEFIX as the flow around the rimer is slightly subsaturated with respect to ice.

Sublimation break-off of rime spires can take place in ice-subsaturated conditions and thus might be a mechanism for SIP (Mossop and Hallett, 1974; Oraltay and Hallett, 1989). Thereby, the thinner parts of a rime spire or other fragile ice structures sublimate faster compared to thicker ice structures, leading to ice particle separation and consequently to ice multiplication (Fig. 8e). Sublimational break-off was described for pristine ice crystals with aspect ratios larger than three favorable and rimed ice particles (Dong and Hallett, 1989; Dong et al., 1994; Bacon et al., 1998; Korolev and Leisner, 2020). Very few cases of rime spire break-off due to sublimation were observed in IDEFIX after riming at −7 and −10 °C (see Table 3).

Generally, fragmentation by sublimation can be thought of as a separate SIP process from rime splintering (Korolev and Leisner, 2020) since riming plays only an indirect role, leading to a finely structured graupel surface dominated by frail rime spires in the dry-growth regime. Based on the argument of Korolev and Leisner (2020) and Korolev et al. (2020) that small ice fragments in a subsaturated cloud environment are more likely to fully sublimate before they return to a cloud zone supersaturated with respect to ice, it might be unlikely that this mechanism is important in atmospheric clouds. In contrast, Deshmukh et al. (2022) could theoretically derive a significant contribution of SIP due to sublimation also taking graupel into account. It is conceivable that the mechanism may be important in regions near the cloud edge where entrainment of dry air occurs, as discussed earlier by Bacon et al. (1998).

To discuss the possible reasons for why no efficient SIP has been observed in the IDEFIX experiments in contrast to earlier HM-type experiments (Mossop et al., 1974; Mossop, 1976, 1978a, 1985a; Saunders and Hosseini, 2001), we compare the details of experimental setups. In the IDEFIX riming experiments, (i) the geometrical cross-sectional area of the rimer is about 1000 times smaller than in the HM-type setup, (ii) the droplet populations contained almost no droplets smaller than 12 µm in diameter, (iii) the mass collision rates are a factor of 10 to 100 higher than in the original HM experiments, and (iv) the airflow in IDEFIX is not supersaturated with respect to ice. Nevertheless, the IDEFIX setup reproduces most of the processes that were previously thought to be responsible for SIP via riming splintering.

(i) Although, in IDEFIX, the rimer has a realistic graupel size of roughly 1 mm in diameter, the rimer was unrealistically large in the previous HM-type experiments, where cylindrical metal rods (e.g., 30 cm × 0.24 cm) were used as a rimer (Hallett and Mossop, 1974; Mossop, 1976, 1985a; Saunders and Hosseini, 2001). Such a large riming surface would allow for the observation of effects that are statistically less frequent. In more detail, the observation can be explained by SIP as either a continuous process producing low numbers of SI particles over the whole period of riming or a random burst event producing a high number of SI particles. In the second case, a rime-splintering event could be rare but produce a high number of SI particles – for example, if a rimer has to undergo multiple sublimation–deposition growth cycles to develop frail dendrites that can easily break off. To detect such events, significantly higher accretion rates, longer observation times, or a larger number of rimers need to be investigated. For the IDEFIX conditions, the accretion rate cannot be increased without undergoing a transition from dry to wet growth. Longer observation times of the IDEFIX riming rates or multiple rimers are not feasible with IDEFIX. Consequently, to be able to detect rare but efficient events, a different experimental setup would be required.

(ii) Only the IDEFIX setting with DSD2 contained droplets smaller than 12 µm. In that case, the concentration ratio of small accreted droplets compared to droplets larger than 24 µm was 0.05. This is lower than the concentration ratios from 0.1 to 2.0 (or higher) used in HM experiments, in which the efficiency of rime splintering was found to correlate with the accretion rate of droplets smaller than 12 µm and larger than 24 µm in diameter. Different droplet size distributions were tested in the HM-type experiments (e.g., Mossop and Hallett, 1974; Mossop, 1976, 1978a, b, 1985a; Heymsfield and Mossop, 1984; Saunders and Hosseini, 2001), but to our knowledge, a negative control test excluding droplets smaller than around 12 µm in diameter was not conducted. The described correlation supported the hypothesis that spherical freezing might occur when a large droplet is accreted onto an already frozen small accreted droplet, leading to spherical freezing and ice shell fragmentation (Griggs and Choularton, 1983; Mossop, 1978a, 1985a). Although the influence of small droplets on rime splintering cannot be excluded, our observations indicate that a larger droplet accreting on a smaller ice structure on the rimer surface would spread instead of freezing as a spherical droplet. This is demonstrated by the case displayed in Fig. 10, where a droplet of 25 µm in diameter spreads over a narrow elevated ice structure with a characteristic length of 12  µm at −7 °C rather than freezing spherically. Similar observations have been reported by Emersic and Connolly (2017) (Fig. 7a, b therein), where the spreading of two droplets with diameters of 30 µm on a frozen droplet cap of about 11 µm in diameter was observed at rimer temperatures of −7 to −8 °C. Harris-Hobbs and Cooper (1987) presented a parameterization (HHC parameterization) relating the SIP rates and the droplet size distribution featuring droplets smaller than 13 µm and larger than 24 µm (flat DSD). This parameterization is based on the results of HM-type experiments in support of the hypothetical mechanism of the spherical freezing of larger droplets landing on top of smaller ones (Choularton et al., 1978, 1980). Since small droplets were present in only one of our experiments at −5 °C, the HHC parameterization would have predicted no SIP or just a few particles for DSD2, which we, however, have not observed (see the reviewer comment by P. Connolly, 2024, and our response). While we do not doubt the true nature of the correlation between the flat shape of the droplet size distribution and high SIP rates observed in the HM-type experiments, we have found no evidence supporting the underlying physical mechanism. We thus conclude that the correlation between the presence of small droplets and the high SIP rates in the HM-type experiments has to be based on a different physical mechanism rather than a hypothetical spherical freezing of larger droplets landing on top of smaller droplets. Thus, the HHC parameterization is applicable only to the experiments that closely reproduce the HM-type SIP experimental settings and cannot be used for interpretation and even less as an explanation of our negative results.

Figure 10 Counterexample to spherical droplet freezing on a small ice structure. Collision of a 25 µm in diameter droplet with a 12 µm wide ice neck at −7 °C and 1 m s⁻¹.

(iii) The IDEFIX mass collision rates in the dry-growth regime are a factor of 10 higher compared to those reported by Mossop (1985a). However, the characteristic time of individual droplet freezing is always much shorter than the characteristic inter-arrival time of colliding droplets (see Sect. 3.1.2). Thus, in the dry-growth regime, the rimer surface is completely frozen and in thermal equilibrium between the two consequent droplets colliding at the same site. From this point of view, the actual collision rate is not affecting the SIP efficiency as long as the growth regime remains dry. The accretion rate is only relevant for the statistical quantification of the number of SI particles produced per milligram of rime.

(iv) In contrast to the HM-type experiments where droplets were produced by a steam generator, the humidified airflow in IDEFIX was slightly subsaturated with respect to ice. Therefore, no depositional growth of ice on the rimer surface could be observed. It should be noted, however, that for the frail ice structures (dendrites, needles, columns, or prisms) to grow to the size where they could be detached upon collision with a droplet (Fig. 8dII), a significant amount of time is required. In the middle of the HM SIP temperature interval (−5 °C) and at water saturation, an ice needle needs about 5 s to reach a length of 10 µm. During this time, the growing ice crystal would experience, on average, more than 10 collision events with a liquid droplet under IDEFIX conditions (see the discussion in Sect. 3.1) and between 0 and 2 collisions in a former HM-type experiment (considering accretion rates given in Mossop, 1985a). Thus, an ice crystal growing via the deposition of water vapor at water saturation has no chance of reaching the size where it could be mechanically detached under IDEFIX experimental conditions and only a slight chance under conditions present in the past HM-type experiments. Therefore, it remains an open question as to whether the detachment of frail ice structures growing on the rimer surface via water vapor deposition could be an explanation for the high number of SI particles observed in previous HM-type experiments, as suggested by Mossop (1976). Note, however, that in a real atmospheric cloud, firstly, depositional ice growth is faster due to the lower gas pressure and, secondly, a falling graupel could experience strong variations in the accretion rate so that the frail ice structures might have time to develop.

We therefore conclude that, in spite of the difference between the experimental conditions of HM-type experiments and IDEFIX, the majority of the mechanisms (see points i to iii) supposedly underlying the effective SIP are not supported by our observations. The role of frail ice structures growing on the rimer surface via water vapor deposition remains an open question.

Figure 11 IDEFIX observations of ice spicule formation during transitional growth (a–c, e) and of ascending air bubbles within a liquid channel inside an ice target (d) at −10 °C.

Previous HM-type experiments were limited to riming in the dry-growth regime, because the formation of a liquid layer during wet growth is thought to inhibit suitable conditions for rime splintering (Pruppacher and Klett, 2010; Korolev and Leisner, 2020). Interestingly, at −5 °C, one of the equivocal cases indicating a potential SIP mechanism was observed during riming in the transitional-growth regime. Occasionally, small ice spicules (about 20 µm in length) would grow out of the freezing rimer surface after transition from the wet-growth to the dry-growth regime caused by fluctuation in collision rates at −10 °C. Such ice spicule growth is illustrated in Fig. 11a–c, e. We hypothesize that liquid water becomes entrapped in the pockets under the ice shell on the rimer surface during a change in the growth regime from (local) wet to dry, causing internal pressure buildup and the spicule formation. Although no ice particles were detected in the IC in any of these cases, ice spicule formation could be a source of SI particles in analogy to SIP during the freezing of large droplets. A similar case of spicule formation during wet growth has been described only once before in Macklin (1960). We also observed gas bubbles appearing on the surface of ice shell of the frozen rimer after transition from the wet-growth to the dry-growth regime (Fig. 11d), indicating that the transitional-growth regime could be more important for rime-splintering SIP than previously recognized.

Rotation is required to form naturally appearing graupel. In the IDEFIX experimental setup, the rimer is fixed by two crossing carbon fibers, excluding the random movement and precession that a natural graupel particle experiences during free fall. According to the timescale considerations given above, local microphysical processes on the rimer surface should not depend on the collision rate in the dry-growth regime. Moreover, a free-falling graupel collects supercooled cloud droplets on the side which is exposed to airflow, similarly to the IDEFIX conditions. It is also unlikely that the centrifugal force could cause break-off of fragile structures. Jayaratne and Grigos (1991) have found that centripetal acceleration of 9 g is needed to break off the ice structures. This leads us to the conclusion that missing rotation or random movement has no influence on the rime-splintering mechanism per se.

4 Summary and conclusion

The Ice Droplets splintEring on FreezIng eXperiment (IDEFIX) was designed to investigate the physical mechanisms underlying ice multiplication during the riming of an ice particle falling through a cloud of supercooled droplets. In IDEFIX, the experimental conditions were selected to closely represent the environment within a mixed-phase convective cloud with respect to rimer size, ambient temperature, settling velocity, and droplet size range. IDEFIX was focused on understanding the potential SIP mechanisms during riming on the microscopic scale, allowing for the observation of single droplet–ice accretion events with high temporal and spatial resolution. To achieve this goal, the riming process was observed with high-speed video microscopy and IR thermography. The detection of SI particles was carried out using a custom-built ice counter based on the inertial deposition and subsequent growth of SI particles in a supercooled sucrose solution. Therewith, SI particles with initial diameters larger than approx. 3 µm could be reliably detected.

No evidence of a productive rime-splintering SIP was found during dry and wet graupel growth, in contrast to the reports on the previous HM-type experiments, where several hundreds of SI particles per milligram of rime were detected at −5 °C. From our observations, we conclude the following:

• The fragmentation of droplets freezing on top of smaller accreted droplets (Griggs and Choularton, 1983) can most likely be ruled out as the mechanism responsible for the effective ice multiplication during rime splintering.

• The freezing of droplets upon glancing contact with the rimer (Mossop, 1976) was not observed.

• We found no indication of the SIP mechanisms associated with the transient thermal gradient around a freezing droplet (King and Fletcher, 1976b; Dong and Hallett, 1989).

• Sublimational break-off of frail rime spires at −7 and −10 °C has been observed in the ice-subsaturated environment but could not account for expected high numbers of SI particles under typical HM conditions (Hallett and Mossop, 1974).

The fact that the results from earlier HM-type experiments are not reproduced in this study can be explained in several ways. First, the number of SI particles observed in the earlier experiments could have been overestimated due to less-controlled experimental conditions. This would imply that the HM SIP process is not as efficient in the mixed-phase clouds as it was assumed before. Second, the rime-splintering SIP can occur as a random chain of rare burst events producing a high number of SI particles instead of being a continuous process producing low numbers of SI particles over the whole period of riming. A different type of experiment is required to address this issue. Finally, the SI particles produced in IDEFIX could always be significantly smaller than the detection limit of the ice counter (approx. 3 µm in diameter). As IDEFIX is operated below ice saturation, submicron ice particles would sublimate completely or escape detection in the ice counter. This would imply that the actual SIP mechanism underlying the HM process could not be detected in IDEFIX. As sublimational break-off produces larger SI particles easily detectable in IDEFIX, and the spherical freezing of riming droplets and droplets freezing upon glancing contact with graupel could be excluded as potential mechanisms based on our observations, the nature of the alleged SIP mechanism behind the HM ice multiplication process remains unveiled.

In the transitional regime between dry and wet rimer growth (Schumann–Ludlam limit), pressure-induced rimer surface deformation has been observed. In analogy to droplets shattering upon freezing, such deformations could be indicative of SIP during pressure release events. Given that variation between high and low accretion rates might facilitate the growth and sublimation of frail ice dendrites which could be detached upon collision with a droplet or ice particle, the role of temperature and humidity fluctuations in the clouds provides a new vantage point to the rime-splintering ice multiplication mechanisms. At the very least, this observation points towards the possibility that rime-splintering SIP does not necessarily occur during riming in the dry-growth regime only, as has been assumed so far. However, further experiments on riming at the Schumann–Ludlam limit would be needed to assess the frequency of surface deformation occurrence and its SIP potential.

To summarize, the number of ice crystals detected in IDEFIX experiments is much too low to explain the rapid glaciation observed in convective and frontal clouds. It is therefore likely that other SIP mechanisms (review given in Korolev and Leisner, 2020) such as droplet shattering upon freezing, SIP due to ice–ice collisions, ice fragmentation during thermal shock, fragmentation during sublimation, and activation of INPs in transient supersaturation in the wake of a freezing droplet or hail have to be considered to explain the ice enhancement in mixed-phase clouds. In rapidly changing cloud conditions where no individual SIP mechanism can prevail for a long time, a combination or cascading chain of several SIP mechanisms is more likely to be the case.