Water activity and surface tension of aqueous ammonium sulfate and D-glucose aerosol nanoparticles

Water activity (a_w) and interfacial energy or surface tension (σ) are key thermodynamic parameters to describe the hygroscopic growth of atmospheric aerosol particles and their ability to serve as cloud condensation nuclei (CCN), thus influencing the hydrological cycle and climate. Due to size effects and complex mixing states, however, these parameters are not well constrained for nanoparticles composed of organic and inorganic compounds in aqueous solution.

In this study, we determined a_w and σ by differential Köhler analysis (DKA) of hygroscopic growth measurement data for aerosol particles smaller than 100 nm composed of aqueous ammonium sulfate (AS), D-glucose (Gl), and their mixtures. High-precision measurements of hygroscopic growth were performed at relative humidities (denoted RH) ranging from 2.0 % to 99.6 % with a high-humidity tandem differential mobility analyzer (HHTDMA) in three complementary modes of operation: hydration, dehydration, and restructuring. The restructuring mode (hydration followed by dehydration) enabled the transformation of initially irregular particles into compact globules and the determination of mass equivalent diameters. The HHTDMA-derived growth factors complemented by DKA allows for determination of water activity and surface tension from dilute to highly supersaturated aqueous solutions that are not accessible with other methods. Thus, for mixed AS / Gl nanoparticles with mass ratios of 4:1 and 1:1, the upper limit of solute mass fraction (X_s) was 0.92 and 0.98, respectively.

For pure AS and Gl, the DKA-derived a_w is in good agreement with electrodynamic balance and bulk measurement data. For AS particles, our a_w data also agree well with the Extended Aerosol Inorganics Model (E-AIM III) over the entire concentration range. In contrast, the UNIFAC model as a part of AIOMFAC (Zuend et al., 2011) was found to overestimate a_w in aqueous Gl particles, which can be attributed to unaccounted intermolecular interactions.

For mixed AS and Gl nanoparticles, we observed a non-monotonic concentration dependence of the surface tension that does not follow the predictions by modeling approaches constructed for mixed inorganic/organic systems. Thus, AS / Gl particles with a 1:1 mass ratio exhibited a strong decrease of σ with increasing solute mass fraction, a minimum value of 56.5 mN m⁻¹ at X_s≈0.5, and a reverse trend of increasing σ at higher concentrations. We suggest that D-glucose molecules surrounded by ammonium sulfate ions tend to associate, forming non-polar aggregates, which lowers the surface tension at the air–droplet interface.

We analyzed the uncertainty in the DKA-derived water activity and surface tension, related to the instrumental errors as well as to the morphology of the nanoparticles and their phase state. Our studies have shown that under optimal modes of operation of HHTDMA for moderate aqueous concentrations, the uncertainty in a_w and σ does not exceed 0.2 %–0.4 % and 3 %–4 %, respectively, but it increases by an order of magnitude in the case of highly concentrated nanodroplet solutions.

1 Introduction

Water uptake of aerosol particles is among the central issues of current research into atmospheric and climate processes (Pöschl, 2005; Andreae and Rosenfeld, 2008). Water activity and surface tension (interfacial energy) are key thermodynamic parameters of classical Köhler theory, which describes the hygroscopic growth of particles and their ability to serve as cloud condensation nuclei (CCN) (Swietlicki et al., 2008; Prisle et al., 2011; Forestieri et al., 2018; Ruehl et al., 2016; Ovadnevaite et al., 2017; Davies et al., 2019). Bulk methods, such as pendant drop tensiometry (Anastasiadis et al., 1987; Topping et al., 2007; Shapiro et al., 2009), electrodynamic balance (EDB), and optical tweezers operating with super-micrometric particles are mainly used to determine a_w and σ (Tang et al., 2019; Bzdek et al., 2020). The applicability of these methods to nanoparticles is limited because the water uptake, gas–particle and bulk–surface partitioning, and related phase transitions (deliquescence, efflorescence) depend on particle size (Biskos et al., 2006a, b; Prisle et al., 2010; Djikaev et al., 2001; Cheng et al., 2015). To bridge the gap between experimental and modeling results for bulk materials and nanoparticles, a new method called differential Köhler analysis (DKA) was developed recently (Cheng et al., 2015). This method allows for determination of the water activity and surface tension of supersaturated aqueous solutions based on hygroscopic growth measurement of nano-sized droplets. Recently, Lei et al. (2023) used the DKA method to estimate water activity of the levoglucosan and D-glucose aerosol nanoparticles using nano-HTDMA (hygroscopicity tandem differential mobility analyzer) in the size range of 6–100 nm with RH below 90 %. These results show a good agreement of the DKA-derived water activity with the earlier experimental data and E-AIM. However, no DKA-based surface tension data were reported in that study.

Atmospheric aerosol particles are mainly a mixture of organic and inorganic components. The interaction of organic–inorganic species in aqueous solutions affects both bulk (Raoul effect) and surface (Kelvin effect) properties of nanoparticles. In order to estimate these effects independently, model approximations for a_w or σ are introduced (Li and Lu, 2001; Tuckermann, 2007; Prisle et al., 2010; Petters and Petters, 2016; Ruehl et al., 2016; Ovadnevaite et al., 2017; Forestieri et al., 2018; Davies et al., 2019; Schmedding and Zuend, 2023; and references therein). However, it is difficult to verify the validity of these approximations with respect to the nanodroplets accounting for the bulk–surface partitioning and liquid–liquid separation effects. The advantage of the DKA method is precisely that it allows for simultaneous determination of the bulk and surface characteristics of nanodroplets in the wide concentration range, including a highly supersaturated solution. This provides a new opportunity for validation of the theoretical approaches used for both a_w and σ in the pure and mixed organic–inorganic aerosols. In addition to pure substances, the DKA method is applied here to derive the water activity and surface tension of two-component particles comprising ammonium sulfate and D-glucose with mass ratios of 4:1 and 1:1. Both components are surface inactive and highly water soluble.

The DKA data were obtained from the measurements of hygroscopic growth factors with a high-humidity tandem differential mobility analyzer (HHTDMA) for aerosol particles with diameters in the range of 17–100 nm at relative humidity (RH) of 2.0 %–99.6 %. The high precision of growth factor measurements in the wide particle size and RH range allows for determination of the water activity and surface tension from dilute to highly supersaturated aqueous solutions under conditions that are not accessible to other methods.

We analyze and discuss our nanoparticle measurement results with respect to those obtained with bulk experimental methods and thermodynamic models. In addition, our HHTDMA measurements provide information about particle restructuring in response to water vapor adsorption at low and intermediate RH levels (Mikhailov et al., 2009, 2021), which enable the determination of mass equivalent diameters for the investigated nanoparticles as well as uncertainty analyses and refinements of the DKA-derived thermodynamic parameters at subsaturation and supersaturation conditions.

2 Material and methods

2.1 Aerosol generation

The investigated aerosols were produced by nebulizing an aqueous solution of pure ammonium sulfate (99.9 % pure, ChemCruz) and D-glucose (99.55 % pure, Fisher) at ∼0.01 % weight concentration or their mixture with $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{4}:\mathrm{1}$ and 1:1 weight ratios.

2.2 HHTDMA setup and modes of operation

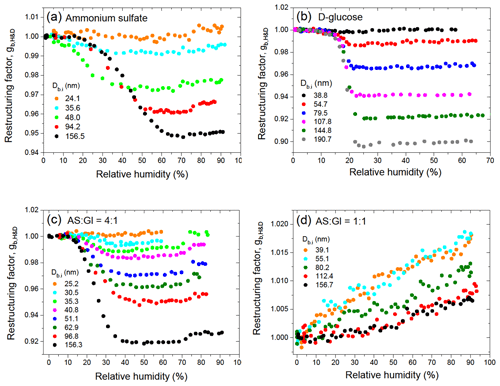
The hygroscopic properties of size-selected aerosol particles were measured in the 2.0 %–99.6 % RH range with a high-humidity tandem differential mobility analyzer (HHTDMA) (see Mikhailov and Vlasenko, 2020; Mikhailov et al., 2021). Throughout the whole relative humidity range, the absolute uncertainty of RH is less than 0.5 %, and the relative growth factor uncertainty due to RH and instrumental errors does not exceed 1 %. A detailed calculation of growth factor uncertainty is described in Mikhailov and Vlasenko (2020) (Sect. 2.5). Three operation modes are available using this HHTDMA instrument: hydration and dehydration (H&D) (also called restructuring mode), hydration, and dehydration. The H&D mode was used to determine the optimal RH range in which initial irregular particles transform into compact globules.

Inorganic and organic aerosol particles as well as their mixtures restructure upon humidification below their deliquescence (Mikhailov et al., 2020). Irregular envelope shape and porosity cause a discrepancy between the mobility-equivalent and mass-equivalent particle diameters that limits precision of the mobility-diameter-based hygroscopicity tandem differential mobility analyzer (HTDMA) (Gysel et al., 2004; Mikhailov et al., 2020). To account for restructuring, we used the minimum mobility particle diameter, D_b,H&D,min, obtained in the H&D HHTDMA mode as an approximation of mass-equivalent diameter of the dry solute particle, D_s (i.e., D_s=D_b,H&D,min). The size-dependent restructuring factor was calculated as follows: $g_{\text{b,H\&D}}=D_{\text{b,RH}}/D_{\text{b,i}}$, where D_b,i and D_b,RH are the initial mobility particle diameter and that measured at RH of aerosol preconditioning, respectively (Mikhailov et al., 2021, Supplement S3). The description of the particle restructuring mechanism is beyond the scope of this work. It will be considered in detail in the next paper.

In this study, the H&D mode was in situ coupled with a conventional hydration or dehydration mode. In the combined modes, the initial monodisperse dry particles were first led through the preconditioning section where they underwent microstructural transformation, by means of humidification in the 2 %–90 % RH range (Nafion humidifier) and drying (Nafion dryer followed by a silica gel diffusion dryer). At the same time, the aerosol and sheath flow in the second differential mobility analyzer was below 3 % RH (Mikhailov et al., 2020, 2021, Supplement S3). The preconditioning RH at which the particles reached their minimum diameter, D_b,H&D;min, was then kept constant throughout the standard hydration or dehydration experiment. The mobility-equivalent particle growth factor, g_b, was calculated as the ratio of the mobility-equivalent diameter, D_b, measured after conditioning (hydration, dehydration) to the minimum mobility diameter, D_b;H&D;min, observed in the H&D mode:

$$\begin{array}{}\text{(1)}& g_{\mathrm{b}}={\displaystyle \frac{D_{\mathrm{b}}}{D_{\text{b,H\&D,min}}}}.\end{array}$$

3 Thermodynamic models

3.1 Differential Köhler analysis (DKA)

The basis of the DKA method (Cheng et al., 2015) is the Köhler equation which describes the equilibrium relative humidity, s_w, over a spherical droplet as a function of a_w, σ, and the mass equivalent diameter D_b:

$$\begin{array}{}\text{(2)}& s_{\mathrm{w}}={\displaystyle \frac{\text{RH}}{\mathrm{100}}}=a_{\mathrm{w}}\exp \left({\displaystyle \frac{\mathrm{4}\mathit{\sigma }{\mathit{\nu }}_{\mathrm{w}}}{RT{D}_{\mathrm{b}}}}\right)=a_{\mathrm{w}}\exp \left({\displaystyle \frac{\mathrm{4}\mathit{\sigma }{\mathit{\nu }}_{\mathrm{w}}}{RT{D}_{\mathrm{s}}{g}_{\mathrm{b}}}}\right),\end{array}$$

where v_w is the partial molar volume of water, R is the universal gas constant, and T is the temperature. D_b in Eq. (2) is often replaced by the product of D_s and g_b; that is, $g_{\mathrm{b}}=D_{\mathrm{b}}/D_{\mathrm{s}}$. The logarithmic form of Eq. (2) is

$$\begin{array}{}\text{(3)}& \ln s_{\mathrm{w}}=\ln a_{\mathrm{w}}\left(g_{\mathrm{b}}\right)+{\displaystyle \frac{A}{D_{\mathrm{s}}}}\mathit{\sigma }\left(g_{\mathrm{b}}\right),\end{array}$$

where $A=\mathrm{4}{\mathit{\upsilon }}_{\mathrm{w}}/RT{g}_{\mathrm{b}}$. From Eq. (3) it follows that a_w and σ can be obtained as the fitting parameters for the s_w(D_s) dependence with the same g_b. Obviously, the larger the number of experimental values of D_s that are used for the fitting, the more accurately a_w and σ can be estimated. This study utilized four sizes for ammonium sulfate and eight sizes for D-glucose and its mixture with ammonium sulfate in the D_s range 17–100 nm, where the Kelvin curvature effect has a significant impact on particle hygroscopicity. We used the Levenberg–Marquardt algorithm (implemented in Origin 9.0) to find a_w and σ in the iterative procedure with standard fitting error as a measure of their uncertainty. It should be noted that fitting of the experimental s_w(D_s) dependences over the entire set of dry diameters significantly improves the reliability of the DKA-derived a_w and σ as compared to the original approach, where these quantities were calculated in pairs for available dry diameters (Cheng et al., 2015; Lei et al., 2023).

According to Eq. (3), DKA assumes that water activity and surface tension depend on g_b only (i.e., concentration). However, in the case of bulk–surface partitioning, both water activity and surface tension may also depend on D_s. To minimize this effect, we used surface inactive compounds. Previous studies on the example of NaCl and (NH₄)₂SO₄ nanoparticles have shown that the size effect is negligible for such compounds (Bahadur and Russell, 2008; Cheng et al., 2015, Supplement).

3.2 HHTDMA-derived activity coefficients

In a binary system at a constant temperature and pressure, the water activity, a_w, and the solute activity, a_s, are related by the Gibbs–Duhem equation (Prausnitz et al., 1999):

$$\begin{array}{}\text{(4)}& x_{\mathrm{s}}\mathrm{d}\ln a_{\mathrm{s}}=-x_{\mathrm{w}}\mathrm{d}\ln a_{\mathrm{w}},\end{array}$$

where x_w and x_s are the mole fractions of water and solute, respectively. According to Robinson and Stokes (1970), the water activity and molal osmotic coefficient of solute, Φ_s, for the real solution are related by

$$\begin{array}{}\text{(5)}& \ln a_{\mathrm{w}}=-{\displaystyle \frac{{\mathit{\nu }}_{\mathrm{s}}{m}_{\mathrm{s}}{\mathrm{\Phi }}_{\mathrm{s}}{M}_{\mathrm{w}}}{\mathrm{1000}}},\end{array}$$

where ν_s and m_s are the stoichiometric dissociation number and molality of the solute (mol kg⁻¹ of water), and M_w is the molecular mass of water (g mol⁻¹). For electrolyte solution in the molality scale,

$$\begin{array}{}\text{(6)}& a_{\mathrm{s}}=a_{\pm }^{{\mathit{\nu }}_{\mathrm{s}}}=({\mathit{\gamma }}_{\pm }{m}_{\pm }{)}^{{\mathit{\nu }}_{\mathrm{s}}}={\mathit{\gamma }}_{\pm }^{v_{\mathrm{s}}}{m}_{\mathrm{s}}({\mathit{\nu }}_{+}^{{\mathit{\nu }}_{+}}{\mathit{\nu }}_{-}^{{\mathit{\nu }}_{-}}).\end{array}$$

ν₊ and ν₋ are the numbers of positive and negative ions produced upon dissociation of the solute (${\mathit{\nu }}_{\mathrm{s}}={\mathit{\nu }}_{+}+{\mathit{\nu }}_{-}$); and m_±, γ_±, and a_± are the mean molality, activity coefficient, and activity of the solute. For ammonium sulfate with ν_s=3 and non-dissociating D-glucose with ν_s=1 from Eq. (6) it follows that

$$\begin{array}{}\text{(7)}& a_{\text{AS}}={\mathrm{4}}^{\mathrm{1}/\mathrm{3}}{m}_{\text{AS}}{\mathit{\gamma }}_{\pm }^{\mathrm{3}}\text{ and }{a}_{\text{Gl}}=\mathit{\gamma }{m}_{\text{Gl}}.\end{array}$$

Combining Eqs. (4)–(6) gives (Prausnitz et al., 1999)

$$\begin{array}{}\text{(8)}& \mathrm{d}\ln {\mathit{\gamma }}_{\pm }=\mathrm{d}{\mathrm{\Phi }}_{\mathrm{s}}+{\displaystyle \frac{\mathrm{1}}{m_{\mathrm{s}}}}({\mathrm{\Phi }}_{\mathrm{s}}-\mathrm{1})\mathrm{d}{m}_{\mathrm{s}}.\end{array}$$

Integration from m_s=0 to the solution of interest yields

$$\begin{array}{}\text{(9)}& \ln {\mathit{\gamma }}_{\pm }={\mathrm{\Phi }}_{\mathrm{s}}-\mathrm{1}+\underset{\mathrm{0}}{\overset{m}{\int }}{\displaystyle \frac{{\mathrm{\Phi }}_{\mathrm{s}}-\mathrm{1}}{m_{\mathrm{s}}}}\mathrm{d}{m}_{\mathrm{s}}.\end{array}$$

The integral in Eq. (9) was evaluated numerically by plotting values of $({\mathrm{\Phi }}_{\mathrm{s}}-\mathrm{1})/m_{\mathrm{s}}$ against m_s.

3.3 Surface tension models

The DKA-derived σ of pure AS and Gl aqueous solutions and their mixtures were compared with the model of Li and Lu (2001) and Dutcher et al. (2010). These models were moderately successful at representing the surface tensions of aqueous solutions of some soluble salts and their mixtures with organic compounds (Topping et al., 2007). The model by Dutcher et al. (2010) expresses the surface tension (σ) in terms of the surface tension of pure water (σ_w) and that of a hypothetical molten salt (σ_s):

$$\begin{array}{}\text{(10)}& \ln \mathit{\sigma }=x_{\mathrm{w}}\ln {\mathit{\sigma }}_{\mathrm{w}}+x_{\mathrm{s}}\ln {\mathit{\sigma }}_{\mathrm{s}},\end{array}$$

where x_w and x_s are the mole fractions of water (w) and salt (s). It is assumed that the surface tension of a solution at different temperatures is described by $\mathit{\sigma }={\mathit{\sigma }}_{\mathrm{w}}+x_{\mathrm{s}}{F}_{\text{ws}}\left(T\right)$, with $F_{\text{ws}}\left(T\right)=a_{\text{ws}}+b_{\text{ws}}T$, where a_ws and b_ws are fitted parameters. At very high salt concentrations, a similar relationship is used: $\mathit{\sigma }={\mathit{\sigma }}_{\mathrm{s}}+x_{\mathrm{w}}{F}_{\text{sw}}\left(T\right)$ with $F_{\text{sw}}\left(T\right)=a_{\text{sw}}+b_{\text{sw}}T$. The two above expressions can be applied to express the surface tension over the entire concentration range:

$$\begin{array}{}\text{(11)}& \begin{array}{rl}\ln \mathit{\sigma }\left(T\right)=& x_{\mathrm{w}}\ln \left({\mathit{\sigma }}_{\mathrm{w}}\right(T)+x_{\mathrm{s}}{F}_{\text{ws}}(T\left)\right)\\ & +x_{\mathrm{s}}\ln \left({\mathit{\sigma }}_{\mathrm{s}}\right(T)+x_{\mathrm{w}}{F}_{\text{sw}}(T\left)\right).\end{array}\end{array}$$

Equation (11) was used to calculate σ of ammonium sulfate particles at T=298 K with parameters σ_w=72.0 mN m⁻¹, σ_s=185.0 mN m⁻¹, $a_{\text{ws}}=a_{\text{sw}}=\mathrm{0}$, b_ws=0.366 $\mathrm{mN}{\mathrm{m}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$, and $b_{\text{sw}}=-\mathrm{0.289}$ $\mathrm{mN}{\mathrm{m}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$ as suggested by Dutcher et al. (2010). The Li and Lu (2001) surface tension model includes a Langmuir-type adsorption isotherm and a term dependent on the activity of dissolved solid. For an aqueous solution with one solute, this model yields

$$\begin{array}{}\text{(12)}& \mathit{\sigma }={\mathit{\sigma }}_{\mathrm{w}}+RT{\mathrm{\Gamma }}_{\mathrm{s}}^{w\mathrm{0}}\ln {\displaystyle \frac{\mathrm{1}}{\mathrm{1}+K_{\mathrm{s}}{a}_{\mathrm{s}}}},\end{array}$$

where ${\mathrm{\Gamma }}_{\mathrm{s}}^{w\mathrm{0}}$ is the saturated surface excess of solute (s), and K_s is the adsorption equilibrium constant of solute (s). For multi-component systems, Li and Lu (2001) proposed two approaches. The first approach, referred to as LiLu (1), implies that there is no interaction or competing adsorption between species at the interface:

$$\begin{array}{}\text{(13)}& \mathit{\sigma }={\mathit{\sigma }}_{\mathrm{w}}+RT\sum _{i-\mathrm{1}}^k{\mathrm{\Gamma }}_i^{w\mathrm{0}}\ln {\displaystyle \frac{\mathrm{1}}{\mathrm{1}+K_i{a}_i}}.\end{array}$$

The second approach, that we refer to as LiLu (2), considers the interacting and competing adsorption between species in the interface for mixed aqueous systems at higher concentrations. This yields another expression for the surface tension of mixed solutions:

$$\begin{array}{}\text{(14)}& \mathit{\sigma }={\mathit{\sigma }}_{\mathrm{w}}+RT\sum _{i-\mathrm{1}}^k{\mathrm{\Gamma }}_i^{w\mathrm{0}}\ln \left(\mathrm{1}-{\displaystyle \frac{K_i{a}_i}{\mathrm{1}+{\sum }_i{K}_i{a}_i}}\right).\end{array}$$

We also compared the DKA–derived σ with simpler approximations, including those describing a supersaturated solution. Thus, for a ammonium sulfate solution, we used the parameterization by Pruppacher and Klett (1997):

$$\begin{array}{}\text{(15)}& \mathit{\sigma }\left(\mathrm{N}{\mathrm{m}}^{-\mathrm{1}}\right)=\mathrm{0.072}+{\displaystyle \frac{\mathrm{2.34}\times {\mathrm{10}}^{-\mathrm{2}}\times X_{\mathrm{s}}}{\mathrm{1}-X_{\mathrm{s}}}},\end{array}$$

where X_s is the mass fraction of solute. This parameterization is expected to be valid up to X_s≈0.8. For the concentration dependence of surface tension of an aqueous D-glucose solution, the linear function given by Aumann et al. (2010) was chosen:

$$\begin{array}{}\text{(16)}& \mathit{\sigma }\left(\mathrm{mN}{\mathrm{m}}^{-\mathrm{1}}\right)={\mathit{\sigma }}_{\mathrm{w}}+{\displaystyle \frac{\mathrm{\Delta }\mathit{\sigma }}{\mathrm{\Delta }C}}C,\end{array}$$

where C is the molarity concentration (mol L⁻¹) and $\mathrm{\Delta }\mathit{\sigma }/\mathrm{\Delta }C=\mathrm{1.29}$ (mN m⁻¹/mol L⁻¹) with upper limit of C being 3.5 mol L⁻¹ (m_Gl=6.0 mol kg⁻¹).

4 Experimental results and discussion

4.1 Particle restructuring due to humidification

Figure 1 illustrates the restructuring of aerosol particles in the H&D mode. Both pure and mixed particles restructure with increasing RH, wherein this effect is strongest for the largest diameters. Interestingly, mixed AS / Gl particles with a mass ratio of 4:1 undergo strong restructuring with g_b,H&D less than 1 (Fig. 1c), whereas AS / Gl particles with a mass ratio of 1:1 show no structural change (Fig. 1d). For these particles, the restructuring factor g_b,H&D is larger than 1 and increases with RH, indicating that initial particles are compact and spherical (i.e., $D_{\text{b,i}}=D_{\text{b,H\&D,min}}=D_{\mathrm{s}}$) (Mikhailov et al., 2020). The size-dependent increase in g_b,H&D (Fig. 1c) is due to a residual water film on the particle surface after dehydration in the H&D mode. The higher values of $\mathrm{d}{g}_{\text{b,H\&D}}/\mathrm{d}\text{RH}$ observed for particles with smaller diameters support this assumption. Since the H&D mode is in situ coupled with a conventional hydration or dehydration mode, the observed D_b,H&D,min values at specified RH were directly used to calculate the growth factor using Eq. (1). This has made it possible to eliminate the uncertainty in the growth factor caused by irregular particle morphology, which is as high as 5 % or more for particles with D_b,i>70 nm.

Figure 1 RH-dependent restructuring of ammonium sulfate (a), D-glucose (b), and their mixture with mass ratio $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{4}:\mathrm{1}$ (c) and $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{1}:\mathrm{1}$ (d) obtained in the H&D mode as a function of particle size.

4.2 Size-dependent growth factors

Figure 2 shows the size-dependent growth factors of pure and mixed particles observed upon dehydration in the HHTDMA mode, calculated using Eq. (1). The dehydration branch was used because it allows us to determine a_w and σ over a wide concentration range, including highly concentrated droplet solutions. Note that, in contrast to pure ammonium sulfate and its 4:1 mixture with D-glucose, in the case of pure D-glucose (Fig. 2b) and mixed AS / Gl particles with a mass ratio of 1:1 (Fig. 2d), the growth factors obtained in the hydration and dehydration modes are identical over the whole range of relative humidity (Fig. S1 in the Supplement). As expected, due to the Kelvin effect, for the same g_b the equilibrium values of s_w (or RH) for smaller particles shift towards higher values (Eq. 2). This is clearly visible for all particles measured at RH above 70 % (inserts in Fig. 2). For ammonium sulfate particles, this pattern is valid also for highly concentrated solutions up to efflorescence RH (ERH ∼30 %) (Fig. 3a). However, in the cases of D-glucose (Fig. 3b) and AS / Gl (1:1) mixed particles (Fig. 3d), this pattern is not obvious. Moreover, in the case of AS / Gl (4:1) particles, the values of s_w for small particles are lower than for large particles (Fig. 3c), in contrast to the behavior of pure ammonium sulfate (Fig. 3a). The measurement data in Fig. 3b and d also demonstrate that for D-glucose and AS / Gl (1:1) particles in the vicinity of RH≈48 % the g_b(RH) dependence has an inflection point (derivative $\mathrm{d}{g}_{\mathrm{b}}/\mathrm{d}\text{RH}$ has extremum; see the insert in Fig. 3b and d), indicating a distinct water sorption mechanism and hence a different phase state of the particles before and after this RH point. Most likely, at low RH, D-glucose and AS / Gl (1:1) mixed particles are in the semi-solid amorphous state; the increase in humidity over glassy amorphous particles leads to a moisture-induced phase transition that occurs at a “glass transition relative humidity” of RH_g≈48 % (Mikhailov et al., 2009).

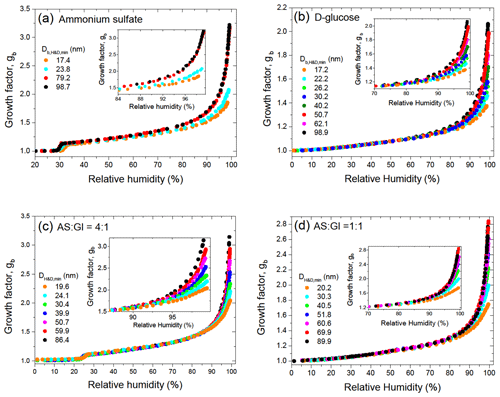
Figure 2 Size-dependent growth factors, g_b, of ammonium sulfate (a), D-glucose (b), and their mixture with mass ratios $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{4}:\mathrm{1}$ (c) and $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{1}:\mathrm{1}$ (d) obtained in the dehydration HHTDMA mode.

Continued water uptake converts the amorphous particles into concentrated solution droplets. Due to the very low molecular diffusivity of glasses, the uptake of water vapor by glassy aerosol particles is limited to surface adsorption, whereas above RH_g the particles are in a viscous liquid state and absorb water in the particle bulk. Differences in water sorption mechanisms may explain why the growth factors of small particles at low RH are higher than for larger particles. At RH below RH_g with the same water adsorption layer, the water film contribution to g_b will be higher for small particles. For example, at a water layer thickness of 0.56 nm (i.e., two monolayers of water molecules), g_b for aerosol particles of 19 and 100 nm are 1.031 and 1.006, respectively. This pattern is clearly seen for AC/Gl (1:1) particles with compact initial structures (i.e., D_b,i=D_H&D,min, and g_b=g_H&D) for which the growth factor of large particles at the same RH is lower than that for small particles (Fig. 1d). Note also that moisture-induced transformation from the semi-solid state to the solute state can occur gradually within a certain RH range (Mikhailov et al., 2009). All these features in the water uptake by amorphous particles at high concentrations (low growth factor values) lead to additional uncertainties when using the DKA method.

4.3 DKA-derived a_w and a_s for single-component aqueous solution

The DKA-derived water activity for ammonium sulfate and D-glucose aerosol particles are shown in Fig. 4a and b, respectively. More information on the DKA calculation can be found in Sect. S1 in the Supplement. The estimated uncertainty of a_w for pure species is shown in Fig. S2 in the Supplement. The a_w values for ammonium sulfate (Fig. 4a) agree well with electrodynamic balance (EDB) measurements by Tang and Munkelwitz (1994), Clegg et al. (1995), and Chan et al. (1992) and are almost identical to the DKA-derived a_w values previously reported by Cheng et al. (2015) and Extended Aerosol Inorganic Model (E-AIM III) of Wexler and Clegg (2002), including highly concentrated aqueous solutions. In general, the DKA-derived water activities obtained for pure ammonium sulfate particles reproduce the literature data well.

Figure 4b shows the DKA-derived a_w values of D-glucose aerosol particles. Our data are consistent with the EDB measurements by Peng et al. (2001) up to X_Gl∼0.8. The observed divergence of the water activity at X_Gl>0.8 may be due to kinetic limitations in highly viscous semi-solid amorphous particles (Mikhailov et al., 2009), which prevail in EDB experiments with micrometer-sized particles. As noted in Sect. 4.2 and shown in Fig. 3d at $\text{RH}={\text{RH}}_{\mathrm{g}}\sim \mathrm{48}$ %, particles undergo moisture-induced phase transition where semi-solid particles become concentrated solution droplets. This RH value is very close to a_w∼49 %, below which a strong deviation between DKA- and EDB-derived a_w is observed (Fig. 4b). If this is the case, the DKA-derived a_w here is closer to the real a_w.

At the same time, the DKA-derived a_w values differ from those predicted by the AIOMFAC model (Zuend et al., 2008), with a maximum deviation of 6 % at X_Gl∼0.7. The discrepancy between measured and AIOMFAC-predicted a_w values for carbohydrates has been noted previously and is attributed to relatively strong intramolecular interactions due to several polar groups in close proximity, not accounted for by the UNIFAC model within the AIOMFAC framework (Zuend et al., 2011).

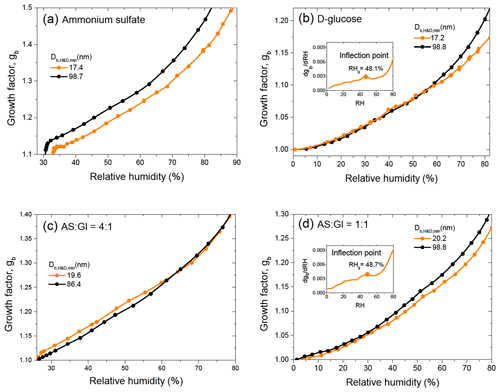
Figure 3 Growth factor, g_b, of ammonium sulfate (a), D-glucose (b), and their mixture with mass ratios $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{4}:\mathrm{1}$ (c) and $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{1}:\mathrm{1}$ (d) at low RH values for minimum and maximum sizes. The inserts (b and d) show derivative $\mathrm{d}{g}_{\mathrm{b}}/\mathrm{d}\text{RH}$ with inflection point RH_g. The instrumental error in RH_g does not exceed the symbol size.

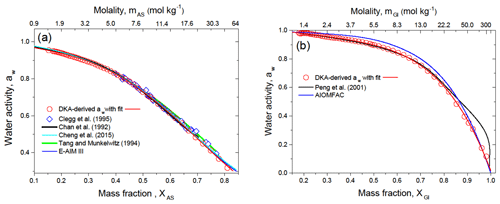
Figure 4 DKA-derived water activity, a_w, of ammonium sulfate (a) and D-glucose (b) aqueous solution at 298 K in comparison with literature data as a function of mass fraction and molality. The red line in panels (a) and (b) is a polynomial fit to all DKA data of a_w. The best fit coefficients are listed in Table S1.

The multicomponent surface tension model of Li and Lu (2001) is based on the activity of the solute. To take advantage of this model, we calculated the activity coefficients of single solutes by numerical integration of Eq. (9) and then, using Eq. (7), their activities (see Sect. S2 in the Supplement for more details). The calculation results are shown in Fig. 5 in comparison with literature data. One can see that the ammonium sulfate activity is in good agreement with E-AIM (Fig. 5a) up to X_AS=0.75 (m_AS=22.7 mol kg⁻¹). At higher X_AS values, there is a discrepancy between our data and the model data. This discrepancy is most likely due to the uncertainty in DKA-derived a_w in concentrated ammonium sulfate aqueous solutions (Fig. S2) and uncertainty in assessment of the integral Eq. (9) in the asymptotic region (m_s→0) (Lakhanpal and Conway, 1960).

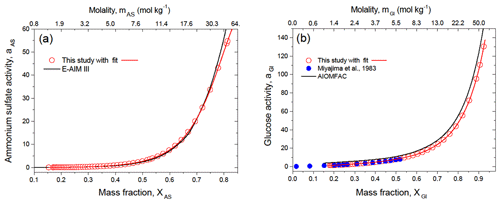
Figure 5 Solute activity of ammonium sulfate (a) and D-glucose (b) in water at 298 K together with literature data as a function of mass fraction and molality. The red line in panels (a) and (b) are polynomial function with fitting parameters listed in Table S2.

Figure 5b shows the DKA-based activity of D-glucose. One can see that these values are in agreement with bulk measurements by Miyajima et al. (1983), obtained by the isopiestic method (blue symbols) available up to X_Gl=0.52 (m_Gl=6.0 mol kg⁻¹). At the same time, a systematic deviation is observed between our results and the AIOMFAC model. As previously noted, the UNIFAC as a part of the AIOMFAC model does not match well with D-glucose and other carbohydrates, owing to strong intramolecular interactions of the polar groups in close proximity.

In general, the DKA-derived water activity and activity of ammonium sulfate and D-glucose in aqueous solutions reproduce the literature data well. For future applications, we fitted DKA-derived a_w and a_s for single solutes with a polynomial function. The obtained fitting parameters are listed in Tables S1 and S2 in the Supplement.

4.4 Surface tension of the single solute solution droplet

Figure 6 shows the DKA-derived surface tension of ammonium sulfate and D-glucose aqueous solution droplets as a function of solute activity. For future use, we fit our data with the Li and Lu (2001) model (Eq. 12). The resulting values of ${\mathrm{\Gamma }}_{\mathrm{s}}^{w\mathrm{0}}$ and K_s together with the a_s fitting interval are listed in Table S3 in the Supplement. The negative ${\mathrm{\Gamma }}_{\mathrm{s}}^{w\mathrm{0}}$ values obtained for both ammonium sulfate and glucose solution droplets indicate that a negative adsorption occurs on the interface between the vapor and liquid phases, leading to surface tensions increasing with concentration, which is typical for surface-inactive compounds (Tuckermann, 2007; Aumann et al., 2010).

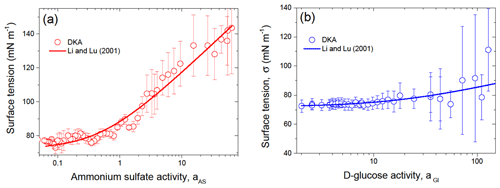
Figure 6 Surface tension of ammonium sulfate (a) and D-glucose (b) aqueous solution droplets as a function of solute activity. The line in panels (a) and (b) is the model of Li and Lu (2001) (Eq. 12), with the best-fit parameters listed in Table S3.

For comparison with the literature data, in Fig. 7 we plotted the DKA surface tension in more accessible concentration scales, i.e., in mass fraction and molality. Figure 7a shows that the DKA-derived σ for ammonium sulfate solution is in agreement, within uncertainty, with the empirical approximation of Pruppacher and Klett (1997) and also consistent with the Dutcher et al. (2010) model up to X_AS≈0.5 (m_AS=7.6 mol kg⁻¹). Above this value, the difference between DKA data and those by Dutcher et al. (2010) gradually increases with increasing concentration. This difference is due to the fact that model parameters used in Dutcher et al. (2010) (Sect. 3.3) are only valid for a concentration of ammonium sulfate not exceeding X_AS=0.43 (m_AS=5.69 mol kg⁻¹), although the model structure allows for calculation of σ in the concentration range from dilute solution to molten salt (Eq. 11). Figure 7b shows the DKA-derived σ for D-glucose solution droplets as a function of mass fraction or molality together with the literature data. It can be seen that the DKA data are consistent with bulk measurements reported by Aumann et al. (2010). In the X_Gl range of 0.24 to 0.52, the average deviation between DKA-derived and literature σ is 2 %.

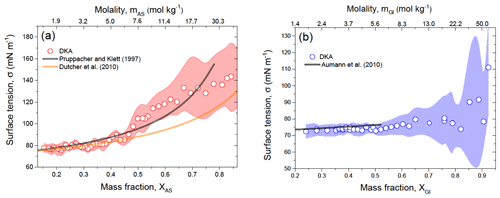
Figure 7 DKA-derived surface tension of ammonium sulfate (a) and D-glucose (b) solution droplets as a function of mass fraction and molality in comparison with literature. The shaded area in panels (a) and (b) indicates uncertainty in the DKA retrieval σ.

Note that the uncertainty in the DKA-retrieval parameters is strongly influenced by of the accuracy of s_w (or RH) and g_b determination. At low g_b (highly concentrated solutions) when $\mathrm{\Delta }{g}_{\mathrm{b}}/\mathrm{\Delta }{s}_{\mathrm{w}}$ is small, the uncertainty in the DKA-derived a_w and σ increases with decreasing g_b. In addition, phase state ambiguity and associated kinetic limitations can provide additional uncertainties. As an example, Fig. S3 in the Supplement shows experimental s_w(D_s) dependences at low and high growth factors for D-glucose aerosol particles and corresponding uncertainties in the DKA-derived a_w and σ.

4.5 DKA-derived a_w and σ for mixed ammonium sulfate and D-glucose aerosol particles

In the absence of solute–solute interactions (“separate solutes”), the corresponding relationship for the water activity of the mixture is $a_{\mathrm{w}}={\prod }_i{a}_{\mathrm{w},i}$, where a_w,i is the water activity of a pure aqueous solution of i at the same concentration as in the mixture (Mikhailov et al., 2004; Clegg and Seinfeld, 2006). Within this approach, referred to as “separate solute water activity” (SSWA), the water activity of mixed particles containing ammonium sulfate and D-glucose can be expressed as

$$\begin{array}{}\text{(17)}& a_{\mathrm{w}}=a_{\text{w,AS}}{a}_{\text{w,Gl}}.\end{array}$$

Figure 8 shows the DKA-derived water activity of the mixed AS / Gl particles with a mass ratio of 4:1 (a) and 1:1 (b), as well as results of the AIOMFAC and SSWA models. One can see that the DKA-derived a_w and both models are consistent up to X_s∼0.3. A further increase in concentration is accompanied by a significant deviation of the model a_w values, both among themselves and from the DKA-derived a_w. It appears that the SSWA approximation underestimates the specific interactions between ions and molecules in the droplet volume (higher a_w), whereas the AIOMFAC model overestimates them (lower a_w), especially in concentrated solutions.

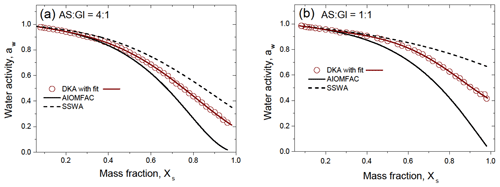
Figure 8 Water activity of the aqueous solution of the mixed ammonium sulfate and D-glucose with mass ratio $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{4}:\mathrm{1}$ (a) and $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{1}:\mathrm{1}$ (b) compared to model data as a function of the mass fraction of the solute, X_s. The red line in panels (a) and (b) are polynomial function with fitting parameters listed in Table S1. SSWA denotes separate solute water activity (Eq. 17).

Figure 9 shows the DKA-retrieved surface tension of the mixed AS / Gl particles with mass ratios of 4:1 (a) and 1:1 (b), compared to the Li and Lu (2001) model. Both approaches, i.e., LiLu (1) and LiLu (2), do not match well with the HHTDMA–DKA-based σ. This discrepancy is especially pronounced for the mixed particles with an AS / Gl mass ratio of 1:1 (Fig. 9b). A slight lowering of the surface tension compared to that of water is already noticeable for a 4:1 mixture (Fig. 9a). The $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{1}:\mathrm{1}$ mixture (Fig. 9b) shows more significant surface tension depression, which is not a monotonic function of concentration. At X_s≈0.5, the σ reaches a minimum of 56.5 ± 3.0 mN m⁻¹ (22 % reduction compared to pure water) and increases again with concentration. Further increase in surface tension with concentration is the result of solidification of aerosol particles. According to Eq. (10) at X_s→1, σ tends to the surface tension of molten state, σ_s, which for AS and Gl is 185 mN m⁻¹ (Dutcher et al., 2010) and 150.9 mN m⁻¹ (Docoslis et al., 2000), respectively. Thus, at X_s=1 the mole-fraction-weighted value of σ for $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{4}:\mathrm{1}$ and 1:1 is 179 and 170 mN m⁻¹, respectively, which reasonably agrees with the DKA-derived σ at high X_s values (Fig. 9a and b).

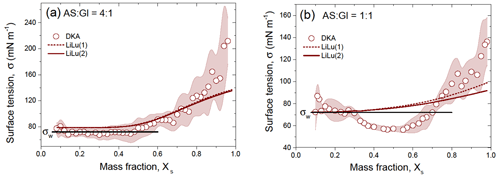
Figure 9 DKA-derived surface tension of the aqueous solution of the mixed ammonium sulfate and D-glucose with mass ratio $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{4}:\mathrm{1}$ (a) and $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{1}:\mathrm{1}$ (b) together with Li and Lu (2001) model (LiLu (1) – Eq. (13) and LiLu (2) – Eq. (14)) as a function of mass fraction of the solute, X_s. The shaded area in panels (a) and (b) indicates the uncertainty in the DKA retrieval σ, the black line is the surface tension of pure water σ_w=72.0 mN m⁻¹.

Note that the decrease in surface tension observed in Fig. 9b and its subsequent increase with concentration is reproduced in repeated measurements (see Fig. S4 in the Supplement). Most likely the reduction in surface tension at moderate concentrations is caused by the salting out effect (Setschenow, 1889; Kiss et al., 2005; Marcolli and Krieger, 2006; Frosch et al., 2011; Wang et al., 2014; Lin et al., 2020; Bzdek et al., 2020) and results from the interaction between ammonium sulfate ions and D-glucose molecules, facilitating the association of initially surface-inactive hydrophilic organic molecules into surface-active hydrophobic associates (quasi-macromolecules). Docoslis et al. (2000) analyzed the difference between polysaccharides (dextran, Ficoll) and their surface-inactive constituents (sucrose, glucose). They concluded that the contrasting results are caused by the differences in polar intermolecular reactivities of the monomeric and polymeric glucides. The singly dissolved monomeric sugars contribute strongly to the polar (Lewis acid–base) free energy of cohesion through the multiple interactions between their freely available electron donors and acceptors, through mutual interactions as well as through interactions with the surrounding water dipoles. However once covalently polymerized, these polysaccharides have lost the strong bipolarity of the monomeric sugar molecules. It can thus be assumed that, in an aqueous AS / Gl system, ${{\mathrm{NH}}_{\mathrm{4}}}^{+}$ and ${{\mathrm{SO}}_{\mathrm{4}}}^{\mathrm{2}-}$ ions effectively neutralize the bipolarity of the monomeric D-glucose molecules, facilitating their association into less-polar aggregates with reduced σ values, which are more readily accommodated at the air–droplet interface. Obviously, this mechanism is more pronounced for mixed $\text{AS\hspace{0.17em}:\hspace{0.17em}Gl}=\mathrm{1}:\mathrm{1}$ particles (Fig. 9b) than for their 4:1 mixture (Fig. 9a), due to the higher D-glucose content (by a factor of 2.5).

5 Summary and conclusions

In this study, the DKA method was applied to derive water activities and surface tension of pure ammonium sulfate and D-glucose as well as their mixtures with mass ratios of 4:1 and 1:1 based on shape-corrected hygroscopic growth factors for particles with diameter of 17–100 nm in the relative humidity range of 2.0 %–99.6 %. The obtained a_w and σ values for pure ammonium sulfate and D-glucose droplet solution are in good agreement with the bulk measurements in the available concentration range for bulk methods. The DKA method was employed for the first time to determine a_w and σ of AS / Gl mixed particles. Our data show that for dilute and moderate solution concentrations (X_s<0.3), the SSWA and AIOMFAC models are in agreement with the DKA-derived a_w. However, the discrepancy between the model and our data increases rapidly with increasing solution concentration, with SSWA underestimating DKA data, while AIOMFAC overestimates it. Both ammonium sulfate and D-glucose are surface-inactive compounds with a positive $\mathrm{\Delta }\mathit{\sigma }/\mathrm{\Delta }C$ slope, indicating negative solute adsorption. Interestingly, mixing them together leads to positive adsorption and reduction in surface tension at the air–surface interface (i.e., the AS / Gl mixture becomes a surface-active compound due to salting out). We suggest that AS ions neutralize polar groups of D-glucose, helping them to combine into less-polar aggregates with reduced σ values at the air–surface interface.

The error analysis showed that there are some factors affecting the accuracy of a_w and σ determined by the DKA method. One of them is the irregular morphology of the initial nanoparticles, which leads to a size-dependent error in g_b. Other factors are mainly characteristic of highly concentrated nanodroplet solutions, such as the large uncertainty of g_b and ambiguity of the phase state. Both small growth factor changes at low RH and the different mechanisms of water uptake (surface adsorption vs. bulk absorption) lead to an increased uncertainty in the DKA-derived values of a_w and σ. Thus, for D-glucose aerosol particles at RH near RH_g=48 % and g_b=1.08 (X_Gl=0.85; m_Gl=32.4 mol kg⁻¹), the relative uncertainty in a_w is 3.5 % and in σ it is 41.2 %, respectively.

As mentioned above, DKA assumes that thermodynamic parameters depend only on concentration and are independent of particle size. Good agreement of DKA-derived a_w and σ with the literature data showed that, for particles in the size range of 20–100 nm, this approach is acceptable for single-component solutions of AS and Gl as well as their mixtures, at least at moderate concentrations. Additional HHTDMA–DKA studies are needed to evaluate the accuracy of this approximation for nanoparticles containing surface-active molecules. We plan to conduct such studies to compare the DKA-derived a_w and σ with available experimental data and models that account for size-dependent bulk–surface partitioning.