Impact of acidity and surface-modulated acid dissociation on cloud response to organic aerosol

Acid dissociation of the organic aerosol fraction has the potential to impact cloud-activating properties by altering aqueous-phase H⁺ concentrations and water activity but is currently overlooked in most atmospheric aerosol models. We implemented a simple representation of organic acid dissociation in the aerosol–chemistry–climate box model ECHAM6.3–HAM2.3 and investigated the impact on aerosol-forming aqueous sulfur chemistry, cloud droplet number concentrations, and the shortwave radiative effect. Many atmospheric organic acids are also surface-active and may be strongly adsorbed at the surface of small aqueous droplets. The degree of dissociation has recently been observed for several atmospheric surface-active organics with Brönsted acid character to be significantly shifted in the surface, compared to the bulk aqueous solution. In addition to the well-known bulk acidity, we therefore introduced an empirical account of this surface-modulated dissociation to further explore the potential impact on aerosol climate effects. Malonic acid and decanoic acid were used as proxies for atmospheric organic aerosols of different surface-active and acid strengths. Both acids were found to yield sufficient hydrogen ion concentrations from dissociation in an aqueous droplet population to strongly influence aqueous aerosol sulfur chemistry, leading to enhanced cloud droplet number concentrations and a cooling shortwave radiative effect. Further considering the surface modulation of organic acid dissociation, the impact on cloud microphysics was smaller than according to the well-known bulk solution acidity but still significant. Our results show that organic aerosol acid dissociation can significantly influence predictions of aerosol and cloud droplet formation and aerosol–cloud–climate effects and that, even for a well-known bulk solution phenomenon such as acidity, it may be important to also consider the specific influence of surface effects when surface-active acids comprise a significant fraction of the total organic aerosol mass.

1 Introduction

Atmospheric aerosols are an important contributor to Earth’s climate. They may either absorb or reflect heat and sunlight, directly affecting Earth’s energy budget (IPCC, 2013; Masson-Delmotte et al., 2021). Aerosols also contribute to the global climate through indirect effects where they serve as the necessary seeds for cloud formation (Twomey, 1977; Lohmann and Lesins, 2002). The chemical composition of aerosols is complex and includes numerous organic and inorganic species (O'Dowd et al., 2004; Putaud et al., 2010; Murphy et al., 2006). Organic compounds have been reported to comprise approximately 20 %–50 % of the total aerosol mass at mid-latitude regions (Saxena and Hildemann, 1996; Putaud et al., 2004) and a much higher proportion (approximately 90 %) in tropical forests (Andreae and Crutzen, 1997; Roberts et al., 2001; Kanakidou et al., 2005). Significant amounts of organic aerosols (approximately 70 % of the total aerosol mass) are also reported in the middle troposphere (Huebert et al., 2004). Despite their abundance and importance, the organic fraction is the least understood component of atmospheric aerosols and the uncertainty around organic aerosols, and their interaction with clouds remains one of the largest overall sources of uncertainty in climate projections (IPCC, 2013; Seinfeld et al., 2016; Legg, 2021). The size, chemical composition, and phase state of organic aerosol (OA) are known to directly impact its cloud droplet formation potential (Hallquist et al., 2009; McFiggans et al., 2006) and the radiative effect of clouds (Turnock et al., 2019). However, climate models often have a limited representation of OA processes and properties, such as acidity and surface activity of the organic components (Kanakidou et al., 2005; Prisle et al., 2012a; Freedman et al., 2018; Pye et al., 2020), which contribute to the overall uncertainty in predictions of OAs and their interactions with clouds.

Organic aerosols contain a substantial fraction of species exhibiting Brönsted acid character (Jacob, 1986; Millet et al., 2015; Keene and Galloway, 1984; Chebbi and Carlier, 1996; Chen et al., 2021b; Angelis et al., 2012; Mochizuki et al., 2016; Wu et al., 2020; Kawamura et al., 1985). The concentrations of acidic species in aqueous aerosols directly affect the aerosol pH by modifying the H⁺ concentrations within the aerosol (Pye et al., 2020; Ault, 2020). This pH affects the dissociation of individual acidic species with significant consequences for aerosol chemistry (Hung et al., 2018; Wang et al., 2018) and phase state (Liu et al., 2019). For example, pH-dependent sulfur oxidation (Liu et al., 2020) and salt formation by acidic or basic OA (Yli-Juuti et al., 2013) can each lead to significant mass formation and alter the overall chemical composition of aerosols. The chemical form (protonated or deprotonated) of acidic OA and contributions to the number of solute species in the aqueous aerosol phase can strongly affect water activity and condensation–evaporation equilibrium (Prisle, 2006; Prisle et al., 2008; Frosch et al., 2011; Michailoudi et al., 2019).

Many atmospheric organic acids also exhibit surface activity in aqueous solutions, such as aqueous aerosols and cloud droplets (Prisle, 2024). Surface-active organics (surfactants) have been reported in atmospheric aerosols from many different regions and environments (Gérard et al., 2016; Petters and Petters, 2016; Nozière et al., 2017; Kroflič et al., 2018; Gérard et al., 2019a). Surfactants adsorb at the aqueous surface, leading to enhanced surface concentrations compared to the interior (bulk) of a solution. In microscopic and submicron-sized aerosols and droplets, the surface adsorption can result in significant redistribution of surface-active OA mass from the bulk to the surface phase, so-called bulk–surface partitioning, as a consequence of the very high ratio of surface area (A) to bulk volume (V) in these size ranges (Prisle et al., 2008, 2010b). For spherical droplets of diameter D_wet=0.1, 1, and 10 µm, $A/V=\mathrm{6}/D_{\mathrm{wet}}$ is 60, 6, and 0.6 µm⁻¹, respectively (Prisle, 2021). Thermodynamic calculations have shown that for aerosol particles containing surfactant fatty acids and their salts, organosulfates, di- and polycarboxylic acids, and complex fulvic acids, a large fraction of the surface-active OA is partitioned to the surface during major parts of hygroscopic growth and cloud droplet activation (Prisle et al., 2010b, 2011; Hansen et al., 2015; Malila and Prisle, 2018; Lin et al., 2018, 2020; Prisle, 2021; Vepsäläinen et al., 2022, 2023). Consequently, the chemical and physical state of the surface may significantly contribute to determining the overall aerosol properties (Prisle et al., 2012b; Bzdek et al., 2020; Prisle, 2021, 2024).

Highly surface sensitive synchrotron radiation excited X-ray photoelectron spectroscopy (XPS) measurements have been used to investigate the acid–base speciation of surface-active atmospheric Brönsted acids and bases in the surface region of aqueous solutions (Prisle et al., 2012b; Werner et al., 2018; Öhrwall et al., 2015). In these experiments, the protonated form of each conjugate pair was found at an extraordinarily large fraction, compared to that expected from their acidity and the bulk solution pH. Werner et al. (2018) observed a shift in the degree of protonation for simple mono-carboxylic acids at the surface in dilute aqueous solutions (50 mM butyric or pentanoic acid) corresponding to activating cloud droplets. The acid–base equilibrium in the surface was shifted systematically across a very wide range of solution pH, overall corresponding to an apparent shift in pK_a on the order of 1–2 pH units, compared to the well-known bulk acidity, for each of the acids. Shifts in surface protonation degree of similar magnitude were also previously observed using XPS for dilute aqueous solutions of 10–25 mM decanoate/decanoic acid (Prisle et al., 2012b), 0.1 M propanoate/propanoic acid, and 0.1 M octanoate/octanoic acid (Öhrwall et al., 2015) at near-neutral pH. XPS measurements on aqueous solutions of succinic acid, a moderately surface-active dicarboxylic acid, over a range of concentrations from 0.05–0.5 M and solution pH from 2.0–12.9 also indicated a shifted acid–base equilibrium in the surface compared to the bulk, where the protonated form showed a considerably higher propensity to reside in the aqueous surface region than its conjugate deprotonated form (Werner et al., 2014a). These observations are further supported by experiments by Wellen et al. (2017), who used surface tension titration and infrared reflection absorption spectroscopy to obtain pH-dependent aqueous surface tension of nonanoic and decanoic acids at their aqueous solution surfaces. They inferred that the so-called surface pK_a was greater than the well-known bulk pK_a by 1 pH unit for nonanoic acid and 2 pH units for decanoic acid, suggesting that the organic acid dissociation response to a given aqueous bulk pH is different in the surface, compared to the bulk.

The general behavior of acidic compounds at the aqueous interface is still not well constrained (Saykally, 2013). Petersen and Saykally (2005, 2008) observed an enhanced surface concentration of hydronium ions in aqueous solutions of hydroiodic acid, alkali iodides, and alkali hydroxides using second harmonic generation spectroscopy experiments. This was in contrast to previous macroscopic bubble and droplet experiments, which were interpreted to indicate that hydroxide ions were enhanced at the air–water interface (Graciaa et al., 1995; Takahashi, 2005; Karraker and Radke, 2002; Creux et al., 2007). Enami et al. (2010) also made similar observations of enhanced hydronium ions in the surface of trimethylamine solutions using electrospray mass spectrometry. Recently, Gong et al. (2023) used stimulated Raman scattering microscopy to observe enhanced concentrations of sulfate and bisulfate anions, with bisulfate being more surface enriched than sulfate, in the surface of 2.9 µm aerosol droplets generated from an aqueous solution with 300 mM NaHSO₄ and 50 mM Na₂SO₄ at the same pH. They interpret this as an enhancement of acidity, with an approximately 3-fold increase in the hydrogen ion concentration, at the droplet edge, compared to the center of the droplet. Previous observations by Margarella et al. (2013) on the dissociation of sulfuric acid at the water interface, using liquid-jet photoelectron spectroscopy, have also reported that the ratio of bisulfate-to-sulfate anions was higher in the surface region.

In this work, we use an aerosol–chemistry–climate box model to investigate the potential impact on aerosol-forming aqueous-phase sulfur chemistry, cloud droplet activation, and aerosol–cloud–climate parameters of organic acid dissociation in aqueous aerosols and its additional surface modulation for surfactant acidic OA. Very few studies have previously addressed the dissociation of organic components in aerosols in relation to cloud chemistry and microphysics (Tilgner et al., 2021a; Angle et al., 2021). Tilgner et al. (2021a) compiled a kinetic data set to study the implications of varying aerosol acidity for the oxidation of the protonated and deprotonated forms of atmospheric organic acids with aqueous-phase oxidants, such as OH radicals, NO₃ radicals, or O₃. They showed that acidity strongly affects the chemical processing of dissociating organic compounds but did not provide a direct correlation between organic dissociation and cloud activation. Angle et al. (2021) measured the pH of freshly emitted (nascent) sea spray aerosol using a Micro-Orifice Uniform Deposit Impactor (MOUDI) and impacting the aerosols onto colorimetric pH strips. They found that the pH of nascent sea spray aerosols was approximately 4 pH units lower than that of sea water. The dissociation of organic acids in the aerosols is proposed as a possible factor contributing to the low nascent sea spray aerosol pH. Angle et al. (2021) note that for a nascent sea spray aerosol with a diameter of 200 nm and surface layer of palmitic acid, only 4.4 % acid dissociation would be required to lower the aerosol pH from 8 to 2. However, they do not provide any details on how the organic acid dissociation would affect the aerosol properties. To the best of our knowledge, the organic acid dissociation in aqueous aerosols, let alone accounting for its surface-specific modulation, has never been studied in the context of a cloud activation model.

2 Methods

We first introduce an account of well-known organic acid dissociation in bulk aqueous solution and then augment it with a simple empirical representation to further include surface-driven suppression of dissociation according to observations from XPS measurements. We use ECHAM6.3–HAM2.3 (here referred to as HAMBOX), which is a box model version of the aerosol–chemistry–climate model ECHAM–HAMMOZ (Tegen et al., 2019), to calculate the total aerosol population sulfate mass and cloud droplet number concentrations (CDNCs) for an air parcel and the shortwave radiative effect (RE) from cloud formation, as examples of key processes taking place in aqueous organic aerosols and droplets. The impact of organic aerosol bulk acidity and surface-modulated suppressed dissociation on aerosol sulfur chemistry and cloud microphysics is assessed by comparing to predictions for identical conditions without accounting for organic acid dissociation. The simulation time for all calculations was 1 h, with 1 s time steps.

2.1 Aerosol module in HAMBOX

HAMBOX uses the SALSA2.0 aerosol module (Kokkola et al., 2018), where the aerosol size distribution is calculated using the sectional approach (Jacobson, 2005) and represented using 10 size bins i. Here, we group the 10 size bins into four sub-ranges: nucleation (i=1 and 2) with mean particle diameter, $\stackrel{\mathrm{‾}}{d_{\mathrm{p}}}=\mathrm{56}$ nm; Aitken (i=3, 4 and 5) with $\stackrel{\mathrm{‾}}{d_{\mathrm{p}}}=\mathrm{160}$ nm; accumulation (i=6, 7 and 8) with $\stackrel{\mathrm{‾}}{d_{\mathrm{p}}}=\mathrm{485}$ nm, and coarse (i=9 and 10) with $\stackrel{\mathrm{‾}}{d_{\mathrm{p}}}=\mathrm{1.85}$ µm. The initial number concentration in each sub-range (Table 1) used for all HAMBOX simulations is representative of clean environments, such as European villages (Tunved et al., 2005, 2008). As a property of the sectional approach, when particles grow or shrink out of the boundaries of their size bins, they are redistributed to new size bins, and the new aerosol size distribution is calculated at each simulation time step.

Table 1 Initial aerosol number concentration in each size sub-range used in HAMBOX–SALSA2.0, representative of clean environments (Tunved et al., 2005, 2008).

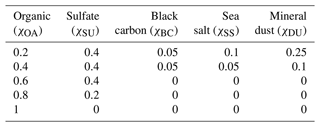
A sulfur chemistry module (Feichter et al., 1996a) is coupled to the aerosol growth module in SALSA2.0. At each time step, the sulfur chemistry module feeds the calculated sulfate mass fraction in the aerosol population into the growth module, which undergoes an aerosol redistribution and feeds back the new aerosol size distribution and chemical composition to the sulfur chemistry module. The aerosol chemical composition in SALSA2.0 is represented by the model compound classes “sulfate” (SU), “organic aerosol” (OA), “sea salt” (SS), “black carbon” (BC), and “mineral dust” (DU). Of these model compounds, sulfate, organic aerosol, and sea salt constitute the soluble species and are considered internally mixed in each size bin of the aerosol population. Black carbon and mineral dust are insoluble species which are externally mixed in each size bin with the soluble species, as described by Kokkola et al. (2018). We consider five different initial conditions with different OA mass fractions ${\mathit{\chi }}_{\mathrm{OA}}=\mathit{\{}\mathrm{0.2},\mathrm{0.4},\mathrm{0.6},\mathrm{0.8},\mathrm{1}\mathit{\}}$ to represent different environments where OA has been reported in varying concentrations. For example, in boreal forest environments, the OA mass fraction is reported to be around 0.6 (Äijälä et al., 2019) and in marine environments around 0.2 (O'Dowd et al., 2004). χ_OA=1 is a hypothetical extreme where we consider OA to comprise the entire aerosol phase. The initial mass fractions of all aerosol model compounds in these five conditions are shown in Table 2.

The sulfur chemistry module is used to calculate the aqueous-phase secondary sulfate mass from oxidation of sulfur dioxide in the aerosol population based on varying hydrogen ion concentration in the aqueous aerosol, considering no organic acid dissociation, organic acid dissociation according to well-known bulk acidity, and surface-modulated organic acid dissociation (Sect. 2.3 below).

Table 2 Initial aerosol mass fractions of all model compounds in the five different environmental scenarios considered.

2.2 Cloud microphysics in HAMBOX

From the total aerosol mass and composition, the resulting cloud droplet number concentrations and consequent shortwave radiative effect are calculated with the HAMBOX cloud microphysics module. The HAMBOX cloud microphysics used in this work includes the calculation of critical supersaturation (S_i) and activated fraction (n_i) for each aerosol size bin i. A detailed description of the parameterizations and equations used to calculate these cloud activation factors is available from Abdul-Razzak (2002) and Abdul-Razzak et al. (1998) and briefly summarized here.

First, the maximum critical supersaturation for the air parcel is calculated as

$$\begin{array}{}\text{(1)}& S_{max}={\displaystyle \frac{S_{\mathrm{e}}}{{\left[\mathrm{0.5}{\left(\frac{\mathit{\varsigma }}{\mathit{\eta }}\right)}^{\mathrm{3}/\mathrm{2}}+{\left(\frac{S_{\mathrm{e}}^{\mathrm{2}}}{\mathit{\eta }+\mathrm{3}\mathit{\zeta }}\right)}^{\mathrm{3}/\mathrm{4}}\right]}^{\mathrm{1}/\mathrm{2}}}},\end{array}$$

where η is the surface tension correction factor; ζ is the correction factor for the Kelvin term in the Köhler curve (for details, see Eqs. (5) and (6) in Abdul-Razzak and Ghan, 2002); and S_e is the effective critical supersaturation for the air parcel,

$$\begin{array}{}\text{(2)}& S_{\mathrm{e}}^{\mathrm{2}/\mathrm{3}}={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^I{N}_i}{{\sum }_{i=\mathrm{1}}^I{N}_i/S_i^{\mathrm{2}/\mathrm{3}}}}.\end{array}$$

Here, I=10 is the total number of aerosol size bins, N_i is the number of particles in each bin i, and S_i is the critical supersaturation for each bin, given by

$$\begin{array}{}\text{(3)}& S_i=\exp \left({\displaystyle \frac{A}{D_{\mathrm{wet}}}}-{\displaystyle \frac{B}{D_{\mathrm{wet}}^{\mathrm{3}}-d_{\mathrm{p}}^{\mathrm{3}}}}\right)-\mathrm{1},\end{array}$$

where D_wet and d_p are droplet and dry particle diameters, respectively. The terms A and B are calculated as

$$\begin{array}{}\text{(4)}& A={\displaystyle \frac{\mathrm{4}{M}_{\mathrm{w}}{\mathit{\sigma }}_{\mathrm{w}}}{RT{\mathit{\rho }}_{\mathrm{w}}}},B={\displaystyle \frac{\mathrm{6}{n}_{\mathrm{s}}{M}_{\mathrm{w}}}{\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}}},\end{array}$$

where M_w=0.018 kg mol⁻¹ is the molecular weight of water; σ_w=0.073 N m⁻¹ is the surface tension of pure water; ρ_w=1000 kg m⁻³ is the density of water; R=8.314 $\mathrm{J}{\mathrm{K}}^{-\mathrm{1}}{\mathrm{mol}}^{-\mathrm{1}}$ is the ideal gas constant; T=293 K is the temperature; and n_s is the number of moles of solute obtained from the mass fractions of soluble species χ_OA, χ_SU, and χ_SS.

With the maximum supersaturation of the air parcel, cloud droplet activation in each bin is determined by comparing S_max with S_il and S_iu (the lower and upper critical supersaturation bounds of the bin). The number of activated particles in each size bin i is given by

$$\begin{array}{}\text{(5)}& n_i=\mathrm{0},\mathrm{if}{S}_{max}<S_{\mathrm{il}},\end{array}$$

$$\begin{array}{}\text{(6)}& n_i={\displaystyle \frac{\log (S_{max}/S_{\mathrm{il}})}{\log (S_{\mathrm{iu}}/S_{\mathrm{il}})}},\mathrm{if}{S}_{\mathrm{il}}\le S_{max}\le S_{\mathrm{iu}},\end{array}$$

and

$$\begin{array}{}\text{(7)}& n_i=\mathrm{1},\mathrm{if}{S}_{\mathrm{iu}}<S_{max}.\end{array}$$

S_il and S_iu are obtained using Eq. (3) for the diameters of the smallest (d_il) and largest (d_iu) particles in each size bin. The average activated fraction for all size bins is then calculated by

$$\begin{array}{}\text{(8)}& n={\displaystyle \frac{\sum n_i}{\sum N_i}}.\end{array}$$

The total number of activated particles is given by the cloud droplet number concentration, which is calculated using the number of activating particles within each size bin, as

$$\begin{array}{}\text{(9)}& \mathrm{CDNC}=\sum _{i=\mathrm{1}}^I{N}_i{n}_i.\end{array}$$

The CDNC calculated using Eq. (9) considering organic bulk acidity and surface-modulated organic acid dissociation is denoted by CDNC_HA and the change with respect to the reference condition of no organic acid dissociation (CDNC₀) is

$$\begin{array}{}\text{(10)}& \mathrm{\Delta }\mathrm{CDNC}={\displaystyle \frac{{\mathrm{CDNC}}_{\mathrm{HA}}-{\mathrm{CDNC}}_{\mathrm{0}}}{{\mathrm{CDNC}}_{\mathrm{0}}}}.\end{array}$$

We estimate the change in shortwave radiative effect (RE) from including organic bulk acidity and surface-modulated organic acid dissociation, respectively, using the method given by Bzdek et al. (2020). The change in cloud-top albedo at constant cloud liquid water content (LWC=0.03 g m⁻³, Zheng and Ming, 2022) is calculated from ΔCDNC as

$$\begin{array}{}\text{(11)}& \mathrm{\Delta }a=\mathrm{LWC}(\mathrm{1}-\mathrm{LWC})\mathrm{\Delta }\mathrm{CDNC}/\left(\mathrm{3}\mathrm{CDNC}\right).\end{array}$$

The shortwave radiative effect is then calculated as

$$\begin{array}{}\text{(12)}& \mathrm{RE}\approx -F_{\mathrm{0}}{E}_{\mathrm{LWC}}{T}_{\mathrm{LWC}}^{\mathrm{2}}\mathrm{\Delta }a,\end{array}$$

where F₀=340 W m⁻² is the incoming solar flux at the top of the atmosphere; E_LWC=0.3 is the fractional coverage of different types of clouds; and T_LWC=0.76 is the transmittance of the atmosphere at visible wavelengths, which is assumed to be constant for all simulations.

For all HAMBOX cloud microphysics calculations, we assume a constant cloud temperature of 271 K, cloud pressure of 101 kPa, cloud fraction of 0.3, saturation ratio of gas-phase water of 0.3, and updraft velocity of 0.3 m s⁻¹, consistent with Tegen et al. (2019).

2.3 Sulfur chemistry in HAMBOX

We use the aqueous sulfur chemistry module of Feichter et al. (1996b), with modifications described below, to calculate the aqueous-phase secondary sulfate concentration $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ in the aerosol population formed from the oxidation of SO₂ by H₂O₂ and O₃ in aqueous droplets. The reaction rate for the H₂O₂ oxidation pathway can be written as

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\partial }{\partial t}}{\left[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\right]}^{\prime \prime }={\displaystyle \frac{k_{\mathrm{4}}\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\right]\left[{\mathrm{SO}}_{\mathrm{2}}\right]}{\left[{\mathrm{H}}^{+}\right]+\mathrm{0.1}}},\end{array}$$

where the rate constant k₄ is calculated by

$$\begin{array}{}\text{(14)}& k_{\mathrm{4}}=\mathrm{8}\times {\mathrm{10}}^{\mathrm{4}}\exp \left(-\mathrm{3650}\left({\displaystyle \frac{\mathrm{1}}{T}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{298}}}\right)\right),\end{array}$$

where T is the cloud temperature = 271 K. Equation (13) is known to be pH-insensitive (Liu et al., 2020) and is used in this work to determine the aqueous secondary sulfate concentration from the H₂O₂ oxidation for simulations where organic acid dissociation is not considered.

To calculate $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ from the H₂O₂ oxidation pathway accounting for pH dependency arising from organic bulk acidity, we follow the procedure given by Liu et al. (2020), which is valid for pH>2. Here, we use the general acid catalysis reaction mechanism, where SO₂ in an aqueous environment exists as the ${\mathrm{HSO}}_{\mathrm{3}}^{-}$ anion and reacts with H₂O₂ in the presence of an organic acid (HA) catalyst, which acts as a proton donor (Maaß et al., 1999; McArdle and Hoffmann, 1983). Briefly, the overall reaction mechanism is represented as

$$\begin{array}{}\text{(R1)}& {\mathrm{HSO}}_{\mathrm{3}}^{-}+{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\rightleftharpoons {\mathrm{HOOSO}}_{\mathrm{2}}^{-}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}$$

and

$$\begin{array}{}\text{(R2)}& {\mathrm{HOOSO}}_{\mathrm{2}}^{-}+\mathrm{HA}\to \mathrm{2}{\mathrm{H}}^{+}+{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+{\mathrm{A}}^{-}.\end{array}$$

The rate expression for (R1)–(R2) is

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{\partial }{\partial t}}{\left[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\right]}^{\prime \prime }=\left(k+{\displaystyle \frac{k_{\mathrm{HA}}\left[\mathrm{HA}\right]}{\left[{\mathrm{H}}^{+}\right]}}\right)K_{\mathrm{a}\mathrm{1}}\left[{\mathrm{SO}}_{\mathrm{2}}\right]\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\right],\end{array}$$

where K_a1 is the thermodynamic dissociation constant (corresponding to the first acid dissociation constant as defined for organic acids in Reaction R4 below) of H₂SO₃, and k is a constant derived from the reaction rate coefficient and the thermodynamic equilibrium constants. k_HA is the overall rate constant for the general acid catalysis mechanism approximated by $\log k_{\mathrm{HA}}=-\mathrm{0.57}$(pK_a)+6.83 (Liu et al., 2020; Drexler et al., 1991). This approximation for k_HA in relation to the pK_a of an organic acid was derived by Liu et al. (2020) for an ionic strength of I=0.5 mol kg⁻¹. Therefore, we assume this same ionic strength for aqueous droplets in all our calculations.

The secondary sulfate concentration from O₃ oxidation is given by

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{\partial }{\partial t}}{\left[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\right]}^{\prime \prime }=\left(k_{\mathrm{51}}+{\displaystyle \frac{k_{\mathrm{52}}}{\left[{\mathrm{H}}^{+}\right]}}\right)\left[{\mathrm{O}}_{\mathrm{3}}\right]\left[{\mathrm{SO}}_{\mathrm{2}}\right],\end{array}$$

where rate constants k₅₁ and k₅₂ are calculated from

$$\begin{array}{}\text{(17)}& k_{\mathrm{51}}=\mathrm{4.39}\times {\mathrm{10}}^{\mathrm{11}}\exp \left({\displaystyle \frac{-\mathrm{4131}}{T}}\right)\end{array}$$

and

$$\begin{array}{}\text{(18)}& k_{\mathrm{52}}=\mathrm{2.56}\times {\mathrm{10}}^{\mathrm{3}}\exp \left({\displaystyle \frac{-\mathrm{996}}{T}}\right).\end{array}$$

Sulfate concentrations thus calculated in the aqueous-phase sulfur chemistry module are distributed to pre-existing aerosol size bins in SALSA2.0.

When no organic aerosol acid dissociation (“no diss”) is considered, the default H⁺ concentration in HAMBOX is denoted by [H⁺]₀ and obtained from water and aqueous-phase sulfate concentrations as

$$\begin{array}{}\text{(19)}& {\left[{\mathrm{H}}^{+}\right]}_{\mathrm{0}}={\left[{\mathrm{H}}^{+}\right]}_{\mathrm{initial}}+{\displaystyle \frac{{\left[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\right]}_{\mathrm{sol}}}{\mathrm{LWC}\times {\mathrm{MW}}_{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}}},\end{array}$$

where LWC is the cloud liquid water content (in [g m⁻³]), ${\mathrm{MW}}_{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}$ is the molar weight of the sulfate anion, and the soluble sulfate concentration $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}_{\mathrm{sol}}$ is obtained from the summation of soluble sulfate (obtained from χ_SU, Table 2) in all bins. ${\left[{\mathrm{H}}^{+}\right]}_{\mathrm{initial}}=\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{6}}$ mol L⁻¹ is the hydrogen ion concentration obtained from the cloud pH=5, which is assumed to be uniform for all size bins and consistent with the pH of warm low-lying tropospheric clouds (Pye et al., 2020). For all simulations in the sulfur chemistry module, we assume [SO₂], [H₂O₂], and [O₃] in cloud are fixed at 5, 1, and 50 ppb, respectively (Tilgner et al., 2021b).

We introduce organic acid dissociation to the sulfur chemistry module by modifying Eq. (19) to obtain the total hydrogen ion concentration in the aerosol population as

$$\begin{array}{}\text{(20)}& {\left[{\mathrm{H}}^{+}\right]}_{\mathrm{tot}}={\left[{\mathrm{H}}^{+}\right]}_{\mathrm{initial}}+{\displaystyle \frac{{\left[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\right]}_{\mathrm{sol}}}{\mathrm{LWC}\times {\mathrm{MW}}_{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}}}+{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{HA}},\end{array}$$

where [H⁺]_HA is the concentration of the hydrogen ions dissociated by the acidic organic aerosol components. The calculated [H⁺]_tot is then used to obtain the aqueous-phase secondary sulfate concentration in the aerosol population from SO₂ oxidation by H₂O₂ (Eq. 15) and O₃ (Eq. 16), for varying conditions of organic acid dissociation. The sulfate concentrations thus obtained give a modified sulfate mass fraction (χ_SU, Sect. 2.1 and Table 2) in the entire aerosol population.

2.4 Organic acid dissociation

We assume the entire OA fraction is comprised of an organic acid and consider two different acids, malonic acid (a diprotic acid) and decanoic acid (a monoprotic acid), as examples of important organic aerosol components in the atmosphere (Yassaa et al., 2001; Narukawa et al., 2002; Mochida et al., 2003; Graham et al., 2003; Cheng et al., 2004; Li and Yu, 2005; Tedetti et al., 2006) with different well-known aqueous bulk acidity and prominent examples of moderately and strongly surface-active organic species, respectively (Vepsäläinen et al., 2022, 2023). The acid dissociation constants for aqueous bulk solutions are here denoted as p$K_a^{\mathrm{bulk}}$ to distinguish the well-known bulk dissociation behavior from surface-modulated dissociation introduced in Sect. 2.4.3 below. The molecular weight (MW), density (ρ), and bulk acid constants for decanoic and malonic acids used in our calculations are given in Table 3. For the monoprotic decanoic acid, p$K_a^{\mathrm{bulk}}$ is the reported first pK_a readily available from the literature, whereas for the diprotic malonic acid, p$K_a^{\mathrm{bulk}}$ is taken as the sum of the first and second pK_a reported in the literature (same as β in Eq. 29 below). The dissociation behavior of monoprotic and diprotic acids in similar aqueous environments differ greatly, and we use different kinetic equations to describe both treatments of organic bulk and surface-modulated acid dissociation, presented in Sects. 2.4.1, 2.4.2, and 2.4.3.

2.4.1 Monoprotic acids

The dissociation of a monoprotic organic acid (HA) in aqueous solution is represented by the equilibrium

$$\begin{array}{}\text{(R3)}& \mathrm{HA}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\rightleftharpoons {\mathrm{A}}^{-}+{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+},\end{array}$$

where H⁺ from the dissociation of the organic acid is considered to be fully hydrated, such that the concentration of H₃O⁺ is equivalent to the concentration of hydrogen ions from dissociation of HA. The equilibrium acid dissociation constant is

$$\begin{array}{}\text{(21)}& K_{\mathrm{a}}={\displaystyle \frac{a_{{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}}{a}_{{\mathrm{A}}^{-}}}{a_{\mathrm{HA}}}},\end{array}$$

where $a_{{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}},a_{{\mathrm{A}}^{-}}$, and a_HA are the activities of H₃O⁺ cations, A⁻ anions, and HA molecules, respectively. Equation (21) can be approximated in terms of the molar concentrations and ideal-dilute molar-concentration-based activity coefficients (γ_i) of each species i as

$$\begin{array}{}\text{(22)}& K_a={\displaystyle \frac{\left[{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right]\left[{\mathrm{A}}^{-}\right]}{\left[\mathrm{HA}\right]}}{\displaystyle \frac{{\mathit{\gamma }}_{{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}}{\mathit{\gamma }}_{{\mathrm{A}}^{-}}}{{\mathit{\gamma }}_{\mathrm{HA}}}}.\end{array}$$

Since a monoprotic acid HA has only one ionizable hydrogen in Eq. (22),

$$\begin{array}{}\text{(23)}& \left[{\mathrm{A}}^{-}\right]=\left[{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right],\mathrm{and}\left[\mathrm{HA}\right]=[\mathrm{HA}{]}_{\mathrm{tot}}-\left[{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right],\end{array}$$

where [HA]_tot is the total concentration of the organic acid.

The acid dissociation degree α is defined as

$$\begin{array}{}\text{(24)}& \mathit{\alpha }={\displaystyle \frac{\left[{\mathrm{A}}^{-}\right]}{[\mathrm{HA}{]}_{\mathrm{tot}}}}={\displaystyle \frac{\left[{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right]}{[\mathrm{HA}{]}_{\mathrm{tot}}}}.\end{array}$$

Combining Eqs. (22) and (24) and approximating $\frac{{\mathit{\gamma }}_{{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}}{\mathit{\gamma }}_{{\mathrm{A}}^{-}}}{{\mathit{\gamma }}_{\mathrm{HA}}}$ with the mean activity coefficient γ_±,

$$\begin{array}{}\text{(25)}& K_{\mathrm{a}}=[\mathrm{HA}{]}_{\mathrm{tot}}\left({\displaystyle \frac{{\mathit{\alpha }}^{\mathrm{2}}}{\mathrm{1}-\mathit{\alpha }}}\right){\mathit{\gamma }}_{\pm }^{\mathrm{2}}.\end{array}$$

For a highly dilute solution (e.g., [HA]_tot<0.001 mol L⁻¹), ${\mathit{\gamma }}_{\pm }^{\mathrm{2}}\approx \mathrm{1}$ and Eq. (25) can be written as

$$\begin{array}{}\text{(26)}& \mathit{\alpha }={\displaystyle \frac{-K_{\mathrm{a}}+\sqrt{K_{\mathrm{a}}^{\mathrm{2}}+\mathrm{4}{K}_{\mathrm{a}}\times [\mathrm{HA}{]}_{\mathrm{tot}}}}{\mathrm{2}[\mathrm{HA}{]}_{\mathrm{tot}}}}.\end{array}$$

With [HA]_tot known from χ_OA and other properties of the aerosol population, the hydrogen ion concentration from organic acid dissociation [H⁺]_HA is obtained as [H₃O⁺] in Eq. (24) by

$$\begin{array}{}\text{(27)}& [{\mathrm{H}}^{+}{]}_{\mathrm{HA}}=\left[{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right]=\mathit{\alpha }[\mathrm{HA}{]}_{\mathrm{tot}},\end{array}$$

where the acid dissociation degree α is given by Eq. (26).

2.4.2 Diprotic acids

For a diprotic organic acid (H₂A), the dissociation of H⁺ ions in an aqueous solution can be considered to occur in two stages,

$$\begin{array}{}\text{(R4)}& {\mathrm{H}}_{\mathrm{2}}\mathrm{A}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\rightleftharpoons {\mathrm{HA}}^{-}+{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\end{array}$$

and

$$\begin{array}{}\text{(R5)}& {\mathrm{HA}}^{-}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\rightleftharpoons {\mathrm{A}}^{\mathrm{2}-}+{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}.\end{array}$$

The dissociation constant for (R4) is the first dissociation constant of the diprotic acid, denoted as K_a1, and the dissociation constant for (R5) is the second dissociation constant of the diprotic acid, denoted as K_a2. The overall dissociation constant of H₂A is

$$\begin{array}{}\text{(28)}& \mathit{\beta }=K_{\mathrm{a}\mathrm{1}}{K}_{\mathrm{a}\mathrm{2}},\end{array}$$

and, therefore,

$$\begin{array}{}\text{(29)}& \mathrm{p}\mathit{\beta }=\mathrm{p}{K}_{\mathrm{a}\mathrm{1}}+\mathrm{p}{K}_{\mathrm{a}\mathrm{2}}.\end{array}$$

Using similar assumptions as for the monoprotic acid, for a highly dilute solution, the acid dissociation degree α for a diprotic acid can be derived as

$$\begin{array}{}\text{(30)}& \mathit{\alpha }={\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\beta }[{\mathrm{H}}_{\mathrm{2}}\mathrm{A}{]}_{\mathrm{tot}}+\mathrm{2}}},\end{array}$$

where [H₂A]_tot is the total concentration of the diprotic acid. Analogously to the case of a monoprotic acid, the hydrogen ion concentration from dissociation of a diprotic organic acid [H⁺]_HA is given by

$$\begin{array}{}\text{(31)}& [{\mathrm{H}}^{+}{]}_{\mathrm{HA}}=\left[{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right]=\mathit{\alpha }[{\mathrm{H}}_{\mathrm{2}}\mathrm{A}{]}_{\mathrm{tot}},\end{array}$$

where the acid dissociation degree α is now given by Eq. (30).

2.4.3 Surface-modulated organic acid dissociation

We now introduce a simple empirical representation of the shift in organic acid dissociation previously observed in surface-sensitive XPS experiments. Werner et al. (2018) found that the surface-specific dissociation state of surface-active mono-carboxylic acids was significantly suppressed in dilute aqueous solutions across a very wide range of solution pH=2–12. Similar suppressed dissociation states were also found for other mono- and dicarboxylic acids of both stronger and weaker surface activity, in aqueous solutions closer to neutral pH (Prisle et al., 2012b; Werner et al., 2014b; Öhrwall et al., 2015). The shifted dissociation states are attributed to both increased concentrations of the surface-active organic acids in the surface and increased non-ideality (higher activity coefficients) of the charged deprotonated conjugate species A⁻ and hydronium ions, compared to the neutral molecular acid HA, in the organic-rich air–solution interfacial region (Werner et al., 2018; Prisle, 2024). From Eq. (22), this corresponds to an apparent shift of the acid pK_a at the surface,

$$\begin{array}{}\text{(32)}& {\mathrm{pK}}_{\mathrm{a}}={\mathrm{pK}}_{\mathrm{a}}^{\mathrm{bulk}}+\log \left({\displaystyle \frac{{\mathit{\gamma }}_{{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}}{\mathit{\gamma }}_{{\mathrm{A}}^{-}}}{{\mathit{\gamma }}_{\mathrm{HA}}}}\right),\end{array}$$

compared to the well-known bulk acidity p$K_a^{\mathrm{bulk}}$ obtained for dilute aqueous solutions, where all activity coefficients are assumed to be ideal, γ_i=1 (Prisle, 2024).

The dissociation states observed with XPS are broadly consistent with a magnitude of the apparent shift in pK_a of $\log \left(\frac{{\mathit{\gamma }}_{{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}}{\mathit{\gamma }}_{{\mathrm{A}}^{-}}}{{\mathit{\gamma }}_{\mathrm{HA}}}\right)=\mathrm{1}$–2 pH units across the surface titration curve (Prisle, 2024). Here we introduce the effect of surface-modulated acid dissociation by shifting the well-known bulk pK_a of each organic acid according to these shifts of the surface titration curves. We consider two magnitudes of this apparent shift, covering the range of experimental observations from XPS. For a monoprotic acid, we consider p$K_a={\mathrm{pK}}_{\mathrm{a}}^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a={\mathrm{pK}}_{\mathrm{a}}^{\mathrm{bulk}}+\mathrm{2}$, where p$K_a^{\mathrm{bulk}}$ is the well-known pK_a of the organic acid in aqueous bulk solution. To represent the surface shifted dissociation of both carboxylic groups in a diprotic acid, we increase both the first and second acid constant, by 1 or 2 pH units, to similarly obtain p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$. Here we refer to the shifted pK_a values as the surface-modulated apparent pK_a. However, we strongly emphasize that the pK_a, which is an intrinsic property of each organic acid in bulk aqueous solution, is not itself changed. Only the dissociation responses of the organic acids to a given pH of the solution (here, the cloud pH) are changed in the surface (Prisle, 2024).

For both mono- and diprotic acids, the values used for surface-modulated apparent pK_a are given in Table 3. For each pK_a, the corresponding acid dissociation degree α is calculated for the monoprotic acid using Eq. (26) and for the diprotic acid using Eq. (30). The value for α decreases with increasing pK_a, such that the increased apparent pK_a values represent suppressed dissociation of the organic acid in the surface. The surface modulation of organic dissociation is most pronounced in a range of several pH units around the bulk pK_a. At very low and very high pH, the surface dissociation states collapse onto the well-known bulk solution dissociation behavior (Werner et al., 2018; Prisle, 2024). For both the organic acids used here, the p$K_a^{\mathrm{bulk}}$ is within a few pH units of the cloud pH.

Although we implement the effect of surface-modulated acid dissociation as a consequence of simultaneous surface activity of the organic acid, we do not explicitly consider the bulk–surface partitioning of organic acids in our calculations. Our simple empirical representation by shifting the apparent pK_a for the organic acid corresponds to assuming that the overall dissociation state in aqueous aerosols and droplets is described by the surface-modulated properties. This is closely representative of aerosols and droplets where the majority of organic aerosol components are partitioned to the aqueous surface, as a consequence of strong organic surface activity or high $A/V$ in the microscopic and submicron size ranges (Prisle, 2021, 2024). In real atmospheric aerosol and droplet mixtures of both surface-active and more water-soluble OA, organic species will be partially partitioned to the surface, and the overall dissociation state should be described as a combination of both well-known bulk acidity and surface-modulated states. The present simple empirical representation therefore gives an upper bound of the potential effects of surface-modulated acid dissociation according to the previous observations from XPS experiments.

When surface-modulated organic acid dissociation is considered, these properties are assumed to remain consistent throughout the 1 h simulations. Prisle et al. (2008) and Prisle (2021) estimated that surface adsorption of typical atmospheric surfactants equilibrates within a timescale of a second in micron-sized droplets. Lin et al. (2020) investigated the impact of surface adsorption dynamics on surfactant effects in cloud droplet activation and found that different dynamic effects nearly cancel out at every time step. Noziere et al. (2014) assumed that both the bulk and surface reach a state of reasonable equilibrium with respect to organic adsorption at the aqueous surface within approximately 495 s. Therefore, we consider this assumption to be a reasonable first approximation.

Table 3 Properties of the organic acids used in calculations of acid dissociation, including molecular properties (MW and ρ), well-known bulk solution acidity (pK_a1, pK_a2, and p$K_a^{\mathrm{bulk}}$), and surface-modulated dissociation properties (implemented as p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$).

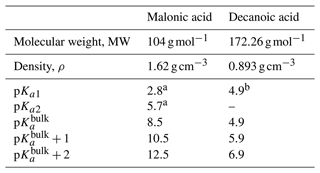
^a Stahl and Wermuth (2002). ^b Martell and Smith (1974).

2.4.4 The van't Hoff factor for organic dissociation

Aqueous-phase dissociation also influences the available amount of solute species in aerosol particles and droplets, affecting the calculations of water activity and critical supersaturation (Sect. 2.2). The molar amount of available solute n_s is calculated in SALSA2.0 from the molar amounts of all the internally mixed soluble species as

$$\begin{array}{}\text{(33)}& n_{\mathrm{s}}=i_{\mathrm{SU}}{n}_{\mathrm{SU}}+i_{\mathrm{OA}}{n}_{\mathrm{OA}}+i_{\mathrm{SS}}{n}_{\mathrm{SS}},\end{array}$$

where the n_SU, n_OA, and n_SS are the molar amounts of sulfate, organic aerosol, and sea salt, respectively, derived from the initial aerosol mass fractions given in Table 2, and i_SU, i_OA, and i_SS are the corresponding van't Hoff factors for each soluble species. In SALSA2.0, the sulfate and sea salt are considered to be fully dissociated, such that i_SU=3 and i_SS=2. By default, organic aerosol is not considered as dissociated and i_OA=1.

To include effects of organic acid dissociation, i_OA is calculated with consideration of the acid dissociation degree α (from Eqs. 26 and 30) as

$$\begin{array}{}\text{(34)}& i_{\mathrm{OA}}=\mathrm{1}+\mathit{\alpha }(n_{\mathrm{ions}}-\mathrm{1}),\end{array}$$

where n_ions=2 for the monoprotic acid and n_ions=3 for the diprotic acid is the number of ions formed from one formula unit of the organic acid. The total available molar amount of solute (n_s, Eq. 33) is thus modified by organic acid dissociation according to i_OA from Eq. (34) and reflected in the Raoult term B (Eq. 4), which changes the critical supersaturation S_i for each aerosol size bin. The van't Hoff factor is calculated for each pK_a using Eq. (34). The dissociation degrees and van't Hoff factors for the no organic dissociation (no diss), organic acid dissociation according to bulk acidity (p$K_a^{\mathrm{bulk}}$), and surface-modulated suppressed organic acid dissociation (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$), for all the OA mass fractions considered here, are given in the Supplement (Table S1).

3 Results and discussions

We present the results of HAMBOX simulations for sulfur chemistry, cloud microphysics, and aerosol–cloud–climate effects, considering organic acid bulk acidity (p$K_a^{\mathrm{bulk}}$), surface-modulated suppressed organic acid dissociation (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and 2), and no organic acid dissociation (no diss). Simulations were carried out assuming the entire OA fraction (Table 2) is composed of either malonic acid or decanoic acid. Results of sulfur chemistry calculations are presented in terms of total hydrogen ion concentration [H⁺]_tot and secondary sulfate concentration $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ in the aerosol population. The consecutive effect on cloud-activating properties is then presented in terms of change in cloud droplet number concentration ΔCDNC and cloud radiative effect RE predicted for bulk and surface-modulated suppressed dissociation of the organic acids, compared to no organic dissociation.

3.1 Aqueous aerosol hydrogen ion concentration

Figure 1 shows the total hydrogen ion concentration [H⁺]_tot calculated with HAMBOX (Eq. 20) in the aqueous aerosol population with sizes between D_wet=0.317–40 µm after 1 h of simulation time, as a function of varying pK_a, corresponding to representations of bulk (p$K_a^{\mathrm{bulk}}$) and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and 2) organic acid dissociation, considering the OA fraction as malonic acid (panels a, b) or decanoic acid (panels c, d), for varying initial mass fraction of organic aerosol (${\mathit{\chi }}_{\mathrm{OA}}=\mathit{\{}\mathrm{0.2},\mathrm{0.4},\mathrm{0.6},\mathrm{0.8},\mathrm{1}\mathit{\}}$ in blue, purple, pink, orange, and yellow, respectively). The hydrogen ion concentration for no organic dissociation (no diss, Eq. 19) is also shown as a black line. As expected, [H⁺]_tot does not change with pK_a when organic acid dissociation is not accounted for, whereas a significant increase is observed for both malonic and decanoic acids when organic acid dissociation is considered. The total hydrogen ion concentration is highest when organic acid dissociation is considered according to p$K_a^{\mathrm{bulk}}$ and decreases for all χ_OA values as acid dissociation is increasingly suppressed according to the surface-modulated apparent p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$.

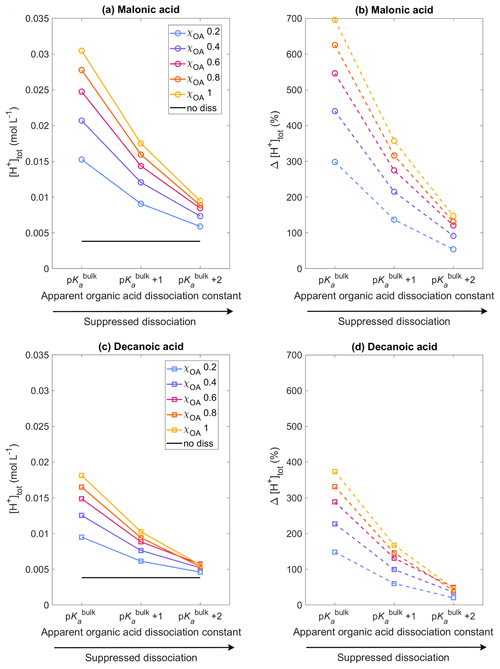
Figure 1 Aqueous aerosol total hydrogen ion concentration, [H⁺]_tot, calculated from Eq. (20) with the sulfur chemistry module of HAMBOX in the aqueous aerosol population with sizes between D_wet=0.317–40 µm, after 1 h of simulation time, assuming five different initial organic mass fractions ${\mathit{\chi }}_{\mathrm{OA}}=\mathit{\{}\mathrm{0.2},\mathrm{0.4},\mathrm{0.6},\mathrm{0.8},\mathrm{1}\mathit{\}}$, denoted by blue, purple, pink, orange, and yellow, respectively (see also Table 2), with varying pK_a corresponding to representations of bulk (p$K_a^{\mathrm{bulk}}$) and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and 2) organic acid dissociation. (a, b) All OA is assumed to be malonic acid, and (c, d) all OA is assumed to be decanoic acid. Simulations without accounting for organic acid dissociation are represented by no diss and (b) and (d) show the relative change in total hydrogen ion concentration Δ[H⁺]_tot calculated from Eq. (35) for each of the acid dissociation conditions with respect to no diss.

The relative change in total hydrogen ion concentration with respect to the no diss condition

$$\begin{array}{}\text{(35)}& \mathrm{\Delta }{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{tot}}={\displaystyle \frac{{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{tot}}-\left[{\mathrm{H}}^{+}\right]{}_{\mathrm{0}}}{\left[{\mathrm{H}}^{+}\right]{}_{\mathrm{0}}}}\times \mathrm{100}\end{array}$$

is shown for malonic and decanoic acids in panels (b) and (d), respectively, of Fig. 1. For malonic acid with p$K_a^{\mathrm{bulk}}$, $\mathrm{\Delta }[{\mathrm{H}}^{+}{]}_{\mathrm{tot}}=\mathrm{298.5}$ % at the lowest OA mass fraction χ_OA=0.2 % and 696 % for the highest OA mass fraction χ_OA=1. Under the surface-modulated suppressed organic acid dissociation condition p$K_a^{\mathrm{bulk}}+\mathrm{1}$, Δ[H⁺]_tot decreases to 137 % and 357 % for χ_OA=0.2 and χ_OA=1, respectively. On further suppression of organic acid dissociation according to p$K_a^{\mathrm{bulk}}+\mathrm{2}$, Δ[H⁺]_tot further decreases to 54 % and 148 %, respectively, at these OA mass fractions. For decanoic acid organic aerosol, the total hydrogen ion concentration at p$K_a^{\mathrm{bulk}}$ increases by 148% with respect to no diss for χ_OA=0.2 and by 374 % for χ_OA=1. At p$K_a^{\mathrm{bulk}}+\mathrm{1}$, Δ[H⁺]_tot decreases to 61 % and 168 %, respectively, and at p$K_a^{\mathrm{bulk}}+\mathrm{2}$ further to 20 % and 47 % for χ_OA=0.2 and 1, respectively. Therefore, even considering the stronger surface-modulated suppression of organic acid dissociation with p$K_a^{\mathrm{bulk}}+\mathrm{2}$, the total hydrogen ion concentration in the aqueous aerosol is still 20 %–47 % higher than no diss for decanoic acid and 54 %–148 % higher for malonic acid, depending on the initial organic aerosol mass fraction.

The results shown in Fig. 1 and in the following are obtained for a constant ionic strength of I=0.5 mol kg⁻¹. Ionic strength is a bulk solution phenomenon and not expected to affect surface adsorbed organic acids, which can be considered a (partially) liquid–liquid separated phase (Prisle et al., 2010a), to the same degree as in the bulk solution. Therefore, the number of hydrogen ions dissociated by the organic acid ([H⁺]_HA, Eq. 20) is expected to depend on I mainly for the bulk solution condition and potentially to some extent for the surface-modulated conditions. The total hydrogen ion concentration ([H⁺]_tot, Eq. 20) in the aerosol population is shown in Fig. S1 of the Supplement for malonic acid as the OA, considering χ_OA=0.4 and 0.6, and for varying ionic strengths $I=\mathit{\{}\mathrm{0.5},\mathrm{1},\mathrm{3},\mathrm{5}\mathit{\}}$ mol kg⁻¹.

The total hydrogen ion concentration decreases with increasing ionic strength, as expected. For χ_OA=0.4, [H⁺]_tot is approximately 270 % greater for p$K_a^{\mathrm{bulk}}$ than without consideration of dissociation (no diss) at I=5 mol kg⁻¹. For the surface-modulated dissociation condition at the same ionic strength and organic aerosol mass fraction, [H⁺]_tot is approximately 120 % greater for p$K_a^{\mathrm{bulk}}+\mathrm{1}$ compared to no diss. Even for the more strongly suppressed dissociation corresponding to p$K_a^{\mathrm{bulk}}+\mathrm{2}$, [H⁺]_tot is approximately 45 % higher than without dissociation. Therefore, for $I=\mathit{\{}\mathrm{0.5},\mathrm{1},\mathrm{3},\mathrm{5}\mathit{\}}$ mol kg⁻¹, the total hydrogen ion concentration in the aqueous aerosol has significant contribution from organic acid dissociation. Similar analysis for varying ionic strength considering the OA as decanoic acid was not immediately possible, due to lack of data on the variation of pK_a with I for aqueous decanoic acid solutions. However, measurements of pK_a for acetic acid in aqueous solutions with varying ionic strength were reported by Cohn et al. (1928). The total hydrogen ion concentration for varying ionic strengths in the aqueous aerosol is shown for acetic acid as the OA in Fig. S2 of the Supplement. For acetic acid as the OA, organic acid dissociation considering $I=\mathit{\{}\mathrm{0.02},\mathrm{0.2},\mathrm{1},\mathrm{4}\mathit{\}}$ mol kg⁻¹ results in approximately 270 %–380 % higher [H⁺]_tot than without acid dissociation. Both acetic acid (pK_a=4.76, Goldberg et al., 2002) and decanoic acid (pK_a=4.9, Martell and Smith, 1974) are straight-chain monocarboxylic acids with comparable bulk acidity, and their aqueous dissociation properties are expected to be similar. Therefore, variation in I is expected to result in similar [H⁺]_tot in the aqueous aerosol when the OA is decanoic acid as for acetic acid.

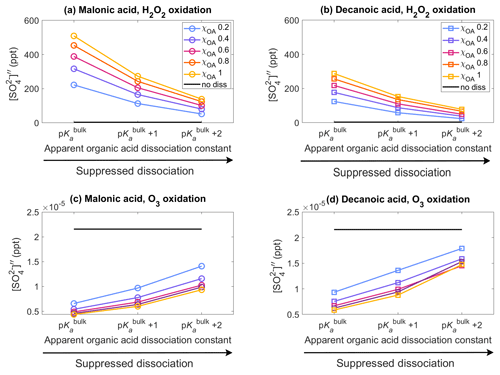
Figure 2 Aqueous aerosol secondary sulfate concentrations $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ from oxidation of SO₂ by H₂O₂ (panels a, b, Eqs. 15 and 13) and O₃ (panels c, d, Eq. 16), for malonic acid (panels a, c) and decanoic acid (panels b, d), with varying pK_a corresponding to representations of bulk (p$K_a^{\mathrm{bulk}}$) and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and 2) organic acid dissociation, in the aqueous aerosol population with sizes between D_wet=0.317–40 µm, calculated in the sulfur chemistry module of HAMBOX with five different initial organic mass fractions ${\mathit{\chi }}_{\mathrm{OA}}=\mathit{\{}\mathrm{0.2},\mathrm{0.4},\mathrm{0.6},\mathrm{0.8},\mathrm{1}\mathit{\}}$, denoted by blue, purple, pink, orange, and yellow, respectively (Table 2), after 1 h of simulation time. Simulations without accounting for organic acid dissociation are represented by no diss (black curves).

3.2 Aqueous aerosol sulfate concentration

Figure 2 shows the aqueous-phase secondary sulfate concentrations $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ from oxidation of SO₂ by H₂O₂ and O₃ (Sect. 2.3) in the aqueous aerosol population with sizes between D_wet=0.317–40 µm, after 1 h of simulation time, for varying acid pK_a corresponding to representations of bulk (p$K_a^{\mathrm{bulk}}$) and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$) organic dissociation, assuming five different initial organic mass fractions ${\mathit{\chi }}_{\mathrm{OA}}=\mathit{\{}\mathrm{0.2},\mathrm{0.4},\mathrm{0.6},\mathrm{0.8},\mathrm{1}\mathit{\}}$, denoted by blue, purple, pink, orange, and yellow, respectively, and considering the OA fraction as malonic acid (panels a, c) or decanoic acid (panels b, d). The secondary sulfate concentration obtained from simulations without consideration of organic acid dissociation (no diss, black line) is shown for reference. The relative changes in the sulfate concentration compared to no diss ($\mathrm{\Delta }[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$) for both oxidation pathways are given in Fig. S3 in the Supplement.

The sulfate concentration from H₂O₂ oxidation (panels a, b) increases drastically for both organic acids when organic acid dissociation is accounted for. From Eq. (15), it may seem that sulfate concentration should decrease with increasing [H⁺]_tot, but the reverse is observed in Fig. 2. This is a property of the general acid-catalyzed mechanism, where the pK_a-dependent rate constant k_HA offsets the decrease in $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ caused by increased [H⁺]_tot concentration. These results are in line with Liu et al. (2020), who suggested the general acid-catalyzed H₂O₂ oxidation to explain “missing” sulfate during severe haze episodes. The oxidation of SO₂ by O₃ (panels c, d) follows a straightforward dependence on [H⁺]_tot (Eq. 16), where increased hydrogen ion concentration results in decreased $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$, compared to the no diss condition.

For malonic acid, H₂O₂ oxidation shows an increase in aqueous-phase secondary sulfate concentration compared to no diss (Fig. 2a), with $\mathrm{\Delta }[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ ranging from 6434 %–14876 % at p$K_a^{\mathrm{bulk}}$ with increasing χ_OA (Supplement Fig. S3a). With surface-modulated suppressed organic acid dissociation, $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ decreases compared to p$K_a^{\mathrm{bulk}}$. The lowest $\mathrm{\Delta }[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ is predicted for p$K_a^{\mathrm{bulk}}+\mathrm{2}$ at χ_OA=0.2. But even here, $\mathrm{\Delta }[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }=\mathrm{1432}$ %, which is a strong increase compared to no diss. Similar trends are found for the H₂O₂ oxidation with decanoic acid (Fig. 2b), where the highest $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ is obtained for p$K_a^{\mathrm{bulk}}$, with $\mathrm{\Delta }[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ ranging from 3557 %–8367 % with increasing χ_OA (Supplement Fig. S3b). The lowest $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ predicted for decanoic acid as the OA is seen for the stronger surface-modulated suppression of organic acid dissociation at p$K_a^{\mathrm{bulk}}+\mathrm{2}$ and χ_OA=0.2, as expected, with $\mathrm{\Delta }[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }=\mathrm{598}$ %. The aqueous-phase secondary sulfate concentration from O₃ oxidation of SO₂ (Fig. 2c) decreases by 70 %–80 % compared to no diss for malonic acid as the OA at p$K_a^{\mathrm{bulk}}$, with increasing χ_OA (Supplement Fig. S3c). The decrease is smaller for surface-modulated suppressed acid dissociation, as expected, with $\mathrm{\Delta }[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }=\mathrm{35}$ %–55 % for the more strongly suppressed dissociation at p$K_a^{\mathrm{bulk}}+\mathrm{2}$. For decanoic acid as the OA (Fig. 2d), a similar trend is seen for $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ from O₃ oxidation, where the decrease in aqueous-phase secondary sulfate concentration is in the range of $\mathrm{\Delta }[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }=\mathrm{20}$ %–75 % for bulk and surface-modulated suppressed dissociation (Supplement Fig. S3d). Therefore, H₂O₂ oxidation of SO₂ results in a far greater increase in $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ in the aerosol population than the decrease in $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ from the O₃ oxidation of SO₂, compared to “no diss”.

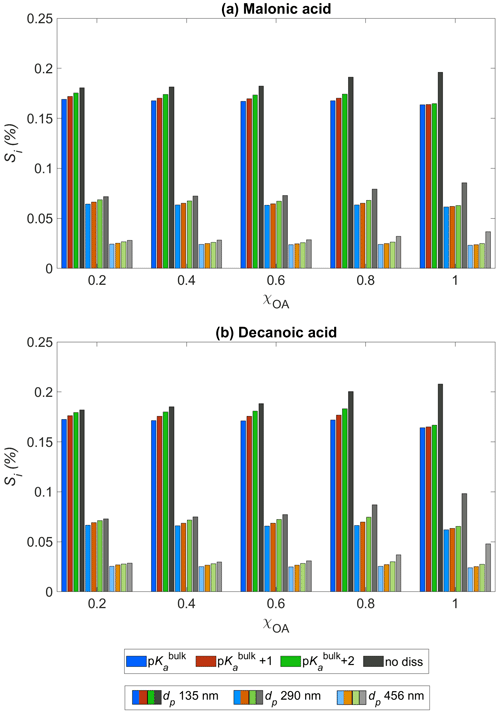
Figure 3 Critical supersaturation S_i as a function of the initial organic aerosol mass fraction χ_OA for (a) malonic acid and (b) decanoic acid, for three initial dry particle sizes, d_p = 135 nm (darkest shade), 290 nm (lighter shade), and 456 nm (lightest shade), and pK_a representing bulk (p$K_a^{\mathrm{bulk}}$, in blue) and surface (p$K_a^{\mathrm{bulk}}+\mathrm{1}$, in orange, and p$K_a^{\mathrm{bulk}}+\mathrm{2}$, in green) organic acid dissociation. Simulations without accounting for organic acid dissociation are represented by no diss (black and grey bars).

These results show how the increase in [H⁺]_tot from organic acid dissociation in terms of [H⁺]_HA results in significant increases in predicted $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ in the aqueous aerosol, compared to when organic acid dissociation is not accounted for. As expected, the effect is smaller when organic dissociation is suppressed according to surface-modulated pK_a, but even for the stronger suppression considered here, the effect is 1432 %–4000 % and 598 %–2500% with increasing χ_OA, for malonic and decanoic acid organic aerosol, respectively. We see that the effect of acid dissociation is larger for H₂O₂ oxidation, suggesting that this pathway is more sensitive to inclusion of organic aerosol acidity and dissociation effects.

3.3 Activation of droplets

Figure 3 shows the critical supersaturation S_i (Eq. 3) predicted with HAMBOX for initial organic mass fractions ${\mathit{\chi }}_{\mathrm{OA}}=\mathit{\{}\mathrm{0.2},\mathrm{0.4},\mathrm{0.6},\mathrm{0.8},\mathrm{1}\mathit{\}}$, obtained for three dry particle sizes, d_p = 135 nm (darkest shade), 290 nm (lighter shade), and 456 nm (lightest shade), with pK_a represented by bulk (p$K_a^{\mathrm{bulk}}$) and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$) organic acid dissociation, considering the OA fraction as malonic acid (panel a) or decanoic acid (panel b). Results from simulations with the no diss condition (black bars) are also shown in both panels for each dry particle size. The dry particle sizes chosen here fall in the accumulation sub-range of size bins. We choose these dry particle sizes to investigate the critical supersaturation as particles in the accumulation size range have been shown to be the most effective in CDNC production (Patel and Jiang, 2021).

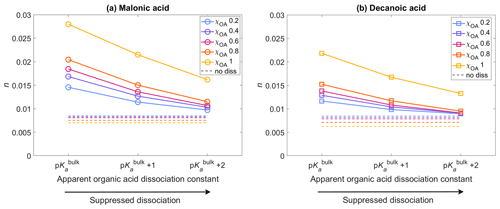
Figure 4 The average activated fraction, n, of the aerosol population with droplet sizes between D_wet=0.317–40 µm, after 1 h of simulation time, for five different initial organic mass fractions ${\mathit{\chi }}_{\mathrm{OA}}=\mathit{\{}\mathrm{0.2},\mathrm{0.4},\mathrm{0.6},\mathrm{0.8},\mathrm{1}\mathit{\}}$, denoted by blue, purple, pink, orange, and yellow, respectively (see also Table 2), calculated for varying pK_a corresponding to representations of bulk (p$K_a^{\mathrm{bulk}}$) and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and 2) organic acid dissociation, and considering the entire OA fraction as (a) malonic acid and (b) decanoic acid. The average activated fraction in the no diss condition is shown as dashed lines in corresponding colors for each χ_OA.

The redistribution of aerosol sizes caused by the increased sulfate concentrations affects the calculation of the droplet size D_wet (Eq. 3). Therefore, S_i is affected by bulk (p$K_a^{\mathrm{bulk}}$) and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$) acid dissociation of the OA. We see that for both organic acids considered, the increased secondary sulfate concentrations in the aqueous aerosols, compared to no diss, are sufficient to significantly decrease S_i for all χ_OA at each of the three dry particle sizes considered. As expected, the decrease in S_i is smaller when surface-modulated suppressed acid dissociation is considered, compared to simulations considering bulk acidity of OA. For decanoic acid as the OA (panel b), the difference between S_i calculated for bulk and surface-modulated pK_a is larger than for malonic acid as the OA (panel a), especially for the larger dry particle sizes (lightest shade) and higher organic mass fractions, χ_OA=0.6–1. This suggests that S_i from consideration of decanoic acid dissociation is more susceptible to changes in the surface-modulated pK_a than for malonic acid, especially at higher d_p and χ_OA. While decanoic acid is the more surface-active of the two organic acids considered, because our simple empirical representation does not explicitly account for surface adsorption, this effect is caused here by the differences in bulk and apparent surface-modulated pK_a with respect to the aerosol pH. As the organic mass fraction increases, the difference in S_i between all pK_a conditions and no diss increases for both organic acids.

The calculated S_i in each size bin also includes any changes in aerosol water activity due to increased organic van't Hoff factor from organic acid dissociation (Eq. 34, Sect. 2.4.4). We see that for both organic acids, the water activity is sufficiently reduced, even for the surface-modulated suppressed acid dissociation, to significantly decrease S_i, compared to no diss. It is well established that aerosol critical supersaturation typically increases with increasing OA mass fraction, due to the higher hygroscopicity of organic aerosol components compared to other soluble species, such as inorganic salts (Svenningsson et al., 2006). However, Fig. 3 shows that organic acid dissociation can partially counter this increase in S_i. This effect is smaller if surface-modulated suppression of organic acid dissociation is considered, which is expected to be more relevant for smaller particles and droplets, due to their high ratio of surface area to bulk volume, and for aerosol populations with higher fractions of surface-active OA (Prisle, 2021).

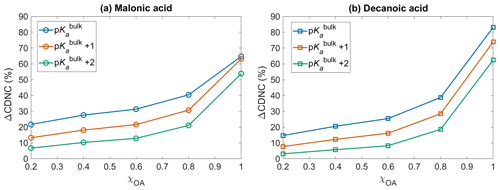
Figure 5 The change in cloud droplet number concentration ΔCDNC (Eq. 10) with respect to no diss, as a function of initial organic mass fractions χ_OA, considering the OA fraction as (a) malonic acid OA and (b) decanoic acid OA, assuming organic acid dissociation according to bulk (p$K_a^{\mathrm{bulk}}$, blue) and surface-modulated properties (p$K_a^{\mathrm{bulk}}+\mathrm{1}$, orange, and p$K_a^{\mathrm{bulk}}+\mathrm{2}$, green).

Figure 4 shows the activated fraction n (Eq. 8) of the aerosol population, with droplet sizes between D_wet=0.317–40 µm, averaged for all aerosol size bins, calculated for initial organic mass fractions ${\mathit{\chi }}_{\mathrm{OA}}=\mathit{\{}\mathrm{0.2},\mathrm{0.4},\mathrm{0.6},\mathrm{0.8},\mathrm{1}\mathit{\}}$, denoted by blue, purple, pink, orange, and yellow, respectively (Table 2), with pK_a representing bulk (p$K_a^{\mathrm{bulk}}$) and surface (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$) organic acid dissociation, considering the OA fraction as malonic acid (panel a) or decanoic acid (panel b). The average activated fractions for simulations not considering organic acid dissociation (no diss) are shown as dashed lines in corresponding colors for each χ_OA, approximately 0.006–0.008 for both organic acids. The inclusion of organic acid dissociation effects results in higher activated fractions than no diss for both organic acids, with malonic acid dissociation resulting in a greater n than decanoic acid, for the same χ_OA and pK_a. This is expected, as malonic acid is a stronger acid with lower p$K_a^{\mathrm{bulk}}$ and [H⁺]_tot from malonic acid dissociation under the same conditions is higher than for decanoic acid. The maximum activated fraction is observed for p$K_a^{\mathrm{bulk}}$ with n=0.014–0.027 for malonic acid as the OA and n=0.012–0.021 for decanoic acid as the OA. For surface-modulated suppressed organic acid dissociation according to p$K_a^{\mathrm{bulk}}+\mathrm{1}$, the activated fraction decreases to 0.011–0.021 and 0.010–0.016 for malonic and decanoic acid OA, respectively. As expected, the stronger surface-modulated acid dissociation suppression according to p$K_a^{\mathrm{bulk}}+\mathrm{2}$ further decreases the activated fraction, but n is still higher than for no diss (0.009–0.016 and 0.009–0.013 for malonic and decanoic acid OA, respectively). For both organic acids, the activated fraction also increases with increasing χ_OA, which is expected as the [H⁺]_tot increases with increasing χ_OA (Fig. 1). For both organic acids, [H⁺]_tot is sufficiently high to lead to a decrease in S_i that translates into an increased activated fraction for both bulk and surface-modulated suppressed organic acid dissociation conditions, with a smaller effect for the suppressed acid dissociation, as expected.

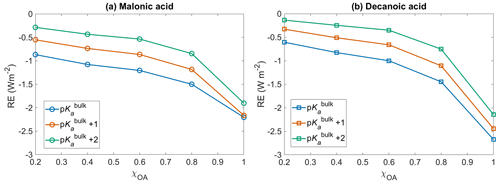
Figure 6 Short wave radiative effect (RE, Eq. 12) with respect to no diss for (a) malonic acid and (b) decanoic acid OA, for varying initial organic mass fractions χ_OA, assuming organic dissociation according to bulk acidity (p$K_a^{\mathrm{bulk}}$, blue) and surface-modulated organic acid dissociation (p$K_a^{\mathrm{bulk}}+\mathrm{1}$, orange, and p$K_a^{\mathrm{bulk}}+\mathrm{2}$, green).

3.4 Cloud droplet number concentration

Figure 5 shows the change in cloud droplet number concentration ΔCDNC (Eq. 10) with respect to no diss, as a function of the initial organic mass fraction χ_OA, considering the entire OA fraction as malonic acid (panel a) and decanoic acid (panel b), for varying pK_a corresponding to representations of bulk (p$K_a^{\mathrm{bulk}}$, in blue), and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$, in orange, and p$K_a^{\mathrm{bulk}}+\mathrm{2}$, in green) organic acid dissociation. A significant enhancement in CDNC is seen for both malonic and decanoic acid, compared to when no organic acid dissociation is considered (no diss). Similar trends are seen for both acids, where p$K_a^{\mathrm{bulk}}$ shows the highest CDNC enhancement compared to no diss. This is expected based on the calculated [H⁺]_tot (Fig. 1) and $[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}{]}^{\prime \prime }$ (Fig. 2) from the bulk organic acidity and surface-modulated suppressed organic acid dissociation and consequent critical supersaturation (S_i, Fig. 3) from both organic acids. For p$K_a^{\mathrm{bulk}}$ and decanoic acid as the OA, ΔCDNC ranges from 14.7 % to 83.1 % with increasing χ_OA. For malonic acid as the OA, the ΔCDNC is smaller, ranging from 21.7 % to 64.7 % for corresponding χ_OA considering bulk acidity p$K_a^{\mathrm{bulk}}$. Under surface-modulated suppressed organic acid dissociation p$K_a^{\mathrm{bulk}}+\mathrm{1}$, the CDNC enhancement is less than that obtained from p$K_a^{\mathrm{bulk}}$, ranging from 7.7 % to 73.9 % for decanoic acid and 13.3 % to 63.1 % for malonic acid. For the stronger surface-modulated acid dissociation suppression p$K_a^{\mathrm{bulk}}+\mathrm{2}$, ΔCDNC is 3.1 % to 62.5 % for decanoic acid as the OA and 6.7 % to 53.9 % for malonic acid as the OA, with increasing χ_OA.

The CDNC enhancement upon including OA acid dissociation is caused by the change in aerosol size distribution due to the increased sulfate concentrations, which shifts the distribution towards larger particles, which are more effective in CDNC production (Hudson and Da, 1996; McFiggans et al., 2006). Since size plays a significant role in cloud droplet nucleating ability of aerosol particles (Dusek et al., 2006), the effect of organic acid dissociation on cloud response will be different depending on whether bulk or surface-modulated properties are used to describe the organic aerosol, and from Fig. 5 we see that this difference is significant for both malonic and decanoic acid OA under the simulation conditions. The aerosol size distribution after 1 h of simulation time, with and without including the sulfur chemistry module, is given in the Supplement (Figs. S4 and S5) for both organic acids, assuming initial organic mass fraction χ_OA=0.8. The aerosol size distribution is shown for varying pK_a values, corresponding to representations of bulk (p$K_a^{\mathrm{bulk}}$) and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and 2) organic acid dissociation, together with the no acid dissociation condition. Without organic acid dissociation, the size distribution is almost the same after 1 h for simulations with and without activating the sulfur chemistry module, for both organic acids. For bulk acidity p$K_a^{\mathrm{bulk}}$, the aerosol size distribution at 1 h is significantly different from the no diss size distribution. The change is smaller for the suppressed organic acid dissociation conditions p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and p$K_a^{\mathrm{bulk}}+\mathrm{2}$. However, even for the stronger suppressed dissociation the change in aerosol size distribution is sufficient to yield ΔCDNC by 6.7 %–53.8 % and 3.1 %–62.4 % for malonic acid and decanoic acid as the OA, respectively, compared to no diss.

3.5 Shortwave radiative effect

Figure 6 shows the shortwave radiative effect RE (Eq. 12) with respect to no diss, as a function of initial organic mass fractions χ_OA=0.2–1, considering the entire OA fraction as malonic acid (panel a) or decanoic acid (panel b), for varying pK_a corresponding to representations of bulk (p$K_a^{\mathrm{bulk}}$, in blue), and surface-modulated (p$K_a^{\mathrm{bulk}}+\mathrm{1}$, in orange, and p$K_a^{\mathrm{bulk}}+\mathrm{2}$, in green) organic acid dissociation. The inclusion of organic acid dissociation leads to a cooling effect for both organic acids, compared to no diss. Considering organic acid dissociation with bulk properties (p$K_a^{\mathrm{bulk}}$), a larger cooling effect is observed for both acids, ranging from −0.6 to −2.7 W m⁻² for decanoic acid and −0.86 to −2.2 W m⁻² for malonic acid, as χ_OA increases from 0.2 to 1. The effect is smaller when surface-modulated suppression of acid dissociation is considered but still significant compared to no diss. For malonic acid as the OA, the range of RE extends from −0.5 to −2.2 W m⁻² for p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and from −0.3 to −1.6 W m⁻² for the more strongly suppressed organic acid dissociation p$K_a^{\mathrm{bulk}}+\mathrm{2}$. For decanoic acid as the OA, the range of RE varies from −0.3 to −2.4 W m⁻² for p$K_a^{\mathrm{bulk}}+\mathrm{1}$ and from −0.1 to −2.1 W m⁻² for p$K_a^{\mathrm{bulk}}+\mathrm{2}$.

The effects of OA acid dissociation on cloud droplet number concentrations and radiative effect without considering the changes in the aqueous aerosol sulfur chemistry are shown in Fig. S6 of the Supplement. Here, the effects of organic acid dissociation arise from modification of the van't Hoff factor i_OA (Eq. 34), reflected as changes in the Raoult term B (Eq. 4) and consequently S_i (Eq. 3). The ΔCDNC and RE in Fig. S6 are therefore independent of the increased [H⁺]-driven sulfate concentrations in the aqueous aerosol and instead reflect the change in water activity due to the dissociation of the organic acid and consequent increase in the number of available moles of solute n_s (Eq. 33). Considering OA acid dissociation effects in the water activity exclusively, malonic acid OA shows <0.5 % ΔCDNC with respect to no diss for all representations of organic acid dissociation. For decanoic acid OA, ΔCDNC with respect to no diss is slightly higher (≈1%), especially for bulk acidity p$K_a^{\mathrm{bulk}}$ and higher χ_OA. The resulting RE with respect to no diss is within a range between 0 and −0.01 W m⁻² for malonic acid as the OA and 0 to −0.05 W m⁻² for decanoic acid as the OA.

3.6 Discussion

Our results show that acid dissociation of organic aerosols, exemplified with malonic and decanoic acid as common atmospheric moderately strong acids, can influence aqueous-phase sulfur chemistry to significantly impact the cloud shortwave radiative effect. Surface modulated suppressed acid dissociation of OA can further change the concentration of hydrogen ions in aqueous aerosol from what is immediately expected from the bulk acidity and aerosol pH. Under these surface-modulated conditions, the effects of organic acid dissociation on cloud properties are reduced but still significant. Since many components in atmospheric OA are both acidic and surface-active, this may be important to represent in large-scale models. Furthermore, the impact of OA acid dissociation on cloud-activating properties via aqueous-phase aerosol sulfur chemistry is significantly stronger than by changing the aerosol water activity and will be strongly underestimated if only effects on water activity are considered.

The increased hydrogen ion concentration in aqueous aerosols as a result of OA acid dissociation leads to enhanced sulfate mass from oxidation of SO₂ by H₂O₂. Increased sulfate concentrations could potentially lead to enhanced formation of organosulfur compounds within the aerosols. Organosulfur compounds form in the atmosphere through heterogeneous reactions between volatile organic compounds and inorganic aerosol sulfate and can comprise over 15 % of the secondary organic aerosol mass (Hettiyadura et al., 2019; Chen et al., 2021a; Bruggemann et al., 2020; Riva et al., 2019). These organosulfur compounds could further increase OA mass and affect the resulting cloud droplet number concentrations. Organosulfates have been shown to exhibit acidic properties and primarily exist in the deprotonated form under atmospheric pH conditions (Fankhauser et al., 2022). Organosulfates are also known to be surface-active in aqueous solutions (Hansen et al., 2015; Prisle et al., 2010b, 2011; Lin et al., 2018; Malila and Prisle, 2018). Therefore, the mechanisms of both organic acid dissociation and its surface modulation studied here for atmospheric carboxylic acids could also apply to organosulfate aerosols, potentially affecting cloud droplet activation in a similar manner.

Bulk–surface partitioning in aqueous aerosols can be seen as a form of (potentially second order) liquid–liquid phase separation (Prisle, 2024). Phase separation of organic aerosols and its impact on cloud-activating properties of aerosol particles have been widely studied (Reid et al., 2018; Freedman, 2017; You et al., 2014). The partitioning of surface-active aerosol components occurs between the bulk and surface phases due to differences in composition and affinity for each phase. The suppression of organic acid dissociation considered here is exactly a consequence of the increased concentration of surface-active organic acid in the surface phase. Liquid–liquid phase separation in the bulk phase would effectively create two separate solutions with different compositions and ensuing properties. The modulation of organic acid dissociation could be taken into account separately for these phases, based on their individual concentrations, following analogous schemes as described by Prisle et al. (2010a).

Our results suggest that organic acid dissociation should be considered for accurate predictions of OA chemistry and cloud microphysics in the atmosphere. The specific magnitude of predictions with the present box model implementation may not be immediately representative of analogous simulations with full 3D aerosol–chemistry–climate models, due to their greater complexity and numerous coupled processes. For example, the effect of potential surface-modulated suppressed dissociation will further depend on aerosol surface activity and is expected to be especially relevant for smaller droplet sizes. However, as we have used a box model version of ECHAM–HAMMOZ, implementation of the OA acid dissociation mechanisms considered here will follow analogous strategies for the full model. The box model simulations contribute insights into the detailed mechanisms of OA acid dissociation and its impact on aerosol chemistry and cloud formation, and our present results provide a first assessment of the potential significance for resulting aerosol–cloud–climate parameters under conditions similar to those examined here.

4 Conclusions

We investigated the effects of organic aerosol acid dissociation on total hydrogen ion concentration in aqueous aerosols and the impact on resulting secondary sulfate aerosol mass, cloud droplet number concentration, and aerosol shortwave radiative effect, using the aerosol–chemistry–climate box model ECHAM6.3–HAM2.3 (HAMBOX). Simulations were carried out considering the entire OA to comprise organic acid and we used malonic and decanoic acid as proxies for atmospheric OA with different aqueous acidity and surface activity. Dissociation of organic acids was considered in three scenarios: (1) the current standard of no dissociation, (2) following well-known bulk solution acidity given by the reported acid constant p$K_a^{\mathrm{bulk}}$, and (3) accounting for a surface-modulated suppression of dissociation as observed in recent laboratory experiments.

Our results show that organic acid dissociation increases hydrogen ion concentrations in the aqueous aerosol phase, as expected. This leads to strongly increased secondary sulfate aerosol mass, which in turn decreases the critical supersaturation for cloud droplet activation and yields a higher activated aerosol fraction than if OA acid dissociation is not considered. The cloud response is observed as enhanced cloud droplet number concentration and a strong shortwave radiative effect of clouds. The effects of organic acid dissociation are greatest when considering the bulk acidity of OA but still significant even when potential surface-modulated suppression of dissociation is also included.

As many atmospheric organic aerosol components are acidic (Pye et al., 2020), their dissociation can have significant impacts on cloud properties. This work highlights the importance of including such organic acid dissociation effects in large scale atmospheric models. We suspect that, combined with the high surface area to bulk volume ratio and bulk–surface partitioning in small droplets (Bzdek et al., 2020; Prisle, 2021), the effects of organic dissociation and potential size-dependent surface-modulated acid dissociation could be significant in explaining some knowledge gaps about organic aerosol formation and acidity in atmospheric aerosols. OA acid dissociation could be particularly relevant in explaining discrepancies of atmospheric models with observations for polluted environments (Lee et al., 2013), where organic mass fraction is usually high, and the organic acid dissociation effects could become very significant. Many of these organic aerosol acids may also be surface-active in aqueous solutions (Gérard et al., 2019b), such as haze and activating cloud droplets, and therefore corrections to account for surface-modulated suppression of organic acid dissociation may also be necessary.