Estimating the concentration of silver iodide needed to detect unambiguous signatures of glaciogenic cloud seeding

Detecting an unambiguous radar reflectivity signature is vital for investigating cloud-seeding impacts. The radar reflectivity change attributed to seeding depends on both the cloud conditions and the concentration of silver iodide (AgI) particles. In this study, the reflectivity change induced by glaciogenic seeding using different AgI particle concentrations is investigated under various cloud conditions using a 1D ice growth model coupled with an AgI nucleation parameterization. In addition, an algorithm is developed to estimate the minimum AgI particle concentration needed for a measurable glaciogenic cloud-seeding signature, assuming there is sufficient supercooled liquid water. The results show that the 1D model captures the ice growth habit compared to available observations and yields an unambiguous reflectivity change that is consistent with 3D model simulations and previous observational studies. Simulations indicate that seeding at a temperature of about −15 °C has the highest probability of detecting the radar seeding signature. This finding is consistent with the fact that the seeding temperature was about −15 °C or slightly warmer in most documented cases of unambiguous seeding signatures. Using the 1D model, 2500 numerical experiments are conducted, and the outputs are used to develop a parameterization to estimate the AgI particle concentration needed to detect an unambiguous seeding signature. Application of this parameterization to a real case suggests that seeding between −21 and −11 °C may possibly produce unambiguous seeding signatures and that seeding at about −15 °C requires the lowest AgI particle concentration. Seeding at warmer temperatures in precipitating clouds requires an extremely high amount of AgI and a very high content of supercooled liquid water. The results shown in this study deepen our understanding of the relationship between AgI particle concentration and radar seeding signatures under different cloud conditions. The parameterization can be used in operational seeding-based decision-making regarding the optimal amount of AgI dispersed.

1 Introduction

Glaciogenic seeding using dry ice or silver iodide (AgI) is the primary technique for enhancing precipitation in mixed-phase stratiform clouds (Rauber et al., 2019). The scientific principle is that plenty of supercooled liquid water exists in mixed-phase clouds, whereas the concentration of natural ice-nucleating particles is low, which limits the amount of liquid water that can be converted to precipitation naturally (Geerts and Rauber, 2022). Introducing more ice crystals through glaciogenic seeding can enhance the Wegener–Bergeron–Findeisen (WBF) process, which means that ice grows at the expense of liquid water, leading to more precipitating snow crystals (Jing et al., 2015). Investigating the impact of seeding on clouds and precipitation has always been vital in this research field (Rasmussen et al., 2018; Rauber et al., 2019; Geerts and Rauber, 2022). However, seeding signatures are often obscured by the large variability in natural precipitation. For decades, scientists have made great efforts to detect unambiguous seeding signatures in field measurements (e.g., French et al., 2018; Rauber et al., 2019; Wang et al., 2021; Zaremba et al., 2024).

The first unambiguous observational evidence of precipitation enhancement induced by cloud seeding was reported by Hobbs et al. (1981). In their study, dry ice was used to seed a non-precipitating stratiform cloud. A Ka-band cloud radar showed a clear enhancement in the radar reflectivity factor (Z_e​​​​​​​) after seeding, suggesting the formation of ice plumes. In 1990, Deshler et al. (1990) reported another case with evident precipitation enhancement based on radar measurements. Seeding produced echoes of 3–10 dBZ in non-precipitating clouds. After this case study, unambiguous seeding signatures in stratiform clouds were rarely documented for more than 20 years, especially in cases in which AgI was used; one exception was Huggins (2007), who used a scanning Ka-band radar to depict the impact of ground-based AgI seeding. Similarly, Jing et al. (2015, 2016) and Jing and Geerts (2015) showed seeding effects based on X-band radar reflectivity data collected during the 2011–2012 AgI Seeding Cloud Impact Investigation (ASCII; Geerts et al., 2013), but these studies analyzed differences in composite radar reflectivity (SEED minus NOSEED) rather than instantaneous reflectivity scans. Recently, in three cases from the 2017 project “Seeded and Natural Orographic Wintertime clouds: the Idaho Experiment” (SNOWIE; Tessendorf et al., 2019), an unambiguous airborne seeding signature was detected using radar and airborne in situ measurements. In all three cases described in French et al. (2018) and Friedrich et al. (2021), the natural precipitation was weak, the ice concentrations in clouds were low (< 1 L⁻¹), and AgI seeding near the cloud tops produced a significant enhancement in ice water content (IWC) and surface precipitation, as well as an increase in the reflectivity factor (Z_e) of 10–30 dBZ after seeding, detected by an X-band radar. Enhancements in radar reflectivity of 10–30 dBZ induced by AgI seeding have also been reported in recent years from other regions (e.g., Dong et al., 2020, 2021; Yue et al., 2021; Wang et al., 2021), and in some cases, parts of the cloud regions were completely glaciated after seeding (Wang et al., 2024). Recently, by seeding supercooled stratus clouds with an uncrewed aerial vehicle, Henneberger et al. (2023) provided new observational evidence of precipitation enhancement at temperatures as high as −5 °C. An unambiguous seeding signature was detected using in situ and ground-based remote sensing instruments when the background noise was low.

However, despite the successful case studies shown above, most field experiments failed to detect a seeding signature. For example, there were 18 intensive operation periods involving airborne seeding in SNOWIE, but a clear seeding signature was observed only in three of them (Geerts and Rauber, 2022). In general, airborne seeding of elevated layers of liquid water is more likely to correspond to radar-detectable than ground-based seeding because scanning radars cannot detect impacts very close to the ground, especially over complex terrain (due to beam blockage). In any event, most field measurements before SNOWIE showed no clear signatures of glaciogenic cloud seeding, though statistical analyses in randomized seeding experiments suggested precipitation enhancements of 3 %–17 %, and in some cases, the precipitation enhancement reached up to 57 % (e.g., Geerts et al., 2013; Pokharel et al., 2014; Jing et al., 2015; Jing and Geerts, 2015; Jing et al., 2016). In these studies, the evidence in individual radar scans is insufficient for determining whether the seeding is ineffective or the seeding signature is undetectable (Zaremba et al., 2024). We may conclude that the cloud conditions are not optimal or that the AgI concentration is too low to produce a signature greater than the natural variability. The efficiency of cloud seeding depends on the cloud conditions. Previous studies suggest that for optimal seeding conditions, supercooled liquid water must be present in the cloud (Geerts and Rauber, 2022), the cloud depth above −5 °C should be deeper than 400 m for ice growth (Manton and Warren, 2011), the seeding temperature should be lower than −8 °C (Breed et al., 2014), and the concentrations of natural ice crystals should be low (Jing et al., 2016). However, thermodynamic and microphysical conditions vary significantly in a cloud and differ substantially among different clouds. It is also possible that seeding is effective but not radar-detectable because the natural concentration of snow particles dominates the radar signal (Zaremba et al., 2024). Seeding under different conditions and using different AgI particle concentrations may result in different seeding signatures. It would be helpful in seeding operations if we could quickly estimate which region has the optimal seeding conditions and how much AgI is needed for an unambiguous seeding signature.

The purpose of this study is to develop an algorithm to estimate how much AgI is needed to detect the signature of glaciogenic cloud seeding. The basic idea is that Z_e is determined by ice crystal size and concentration and that the WBF process is the major ice growth mechanism in mixed-phase stratiform clouds. Since there are sophisticated theories and well-developed parameterizations for ice diffusional growth, we can model the Z_e values induced by cloud seeding. By conducting multiple sensitivity experiments under various cloud conditions, we can develop a parameterization that reveals the relationships between AgI particle concentrations and the Z_e values induced by cloud seeding, and using this parameterization, we can estimate the AgI particle concentration needed to produce a Z_e value greater than the natural variability. The algorithm and the results presented in this study can be used to improve the efficiency of cloud-seeding operations.

The rest of the paper is organized as follows. Section 2 describes the ice nucleation and the ice growth model. An evaluation of the model, a discussion of the model results, and a parameterization for AgI particle concentration are developed in Sect. 3. In Sect. 4, this parameterization is applied to a real case. The conclusions and discussion are presented in Sect. 5.

2 Modeling ice nucleation and growth

In this study, we use a one-dimensional (1D) model of ice nucleation and growth to simulate the growth trajectory of ice crystals. Similar models have been used in previous studies to investigate ice microphysics (Chen and Lamb, 1994; Korolev and Field, 2008) and to retrieve ice properties using radar measurements (Zhang et al., 2014). In addition, we incorporate an AgI nucleation parameterization (Xue et al., 2013a, b) into the model to simulate ice generation caused by cloud seeding. Using this model, we can estimate the IWC and Z_e values produced by cloud seeding in mixed-phase stratiform clouds with relatively weak turbulence.

2.1 Parameterization of AgI nucleation

To model ice nucleation through AgI particles, we follow the parameterization described in Xue et al. (2013a). This parameterization was originally developed based on cloud chamber experiments from DeMott (1995) and Meyers et al. (1995). Four ice nucleation modes are considered. For deposition nucleation, which is valid when the saturation ratio with respect to ice is greater than 1.04 and the temperature is colder than 268.2 K, the fraction of seeded AgI that can nucleate ice is expressed as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{F}_{\mathrm{dep}}& =a\left(S_{\mathrm{i}}-\mathrm{1}\right)+b\left({\displaystyle \frac{\mathrm{273.16}-T}{T_{\mathrm{0}}}}\right)+c(S_{\mathrm{i}}-\mathrm{1}{)}^{\mathrm{2}}\\ & +d{\left({\displaystyle \frac{\mathrm{273.16}-T}{T_{\mathrm{0}}}}\right)}^{\mathrm{2}}+e(S_{\mathrm{i}}-\mathrm{1}{)}^{\mathrm{3}},\end{array}\end{array}$$

where T₀=10 K, $a=-\mathrm{3.25}\times {\mathrm{10}}^{-\mathrm{3}}$, $b=\mathrm{5.39}\times {\mathrm{10}}^{-\mathrm{5}}$, $c=\mathrm{4.35}\times {\mathrm{10}}^{-\mathrm{2}}$, $d=\mathrm{1.55}\times {\mathrm{10}}^{-\mathrm{4}}$, and $e=-\mathrm{0.07}$. S_i is the saturation ratio with respect to ice.

The fraction of AgI that can nucleate ice through condensation-freezing nucleation, which applies when temperatures are colder than 268.66 K, can be calculated using

$$\begin{array}{}\text{(2)}& F_{\mathrm{cdf}}=a{\left({\displaystyle \frac{\mathrm{268.66}-T}{T_{\mathrm{0}}}}\right)}^{\mathrm{3}}(S_{\mathrm{w}}-\mathrm{1}{)}^{\mathrm{2}},\end{array}$$

where a=900. S_w is the saturation ratio with respect to water.

The third mode is contact freezing, which is minor compared to the other nucleation mechanisms. This mode is given by

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{F}_{\mathrm{ctf}}& =F_{\mathrm{scav}}\left[a+b\left(S_{\mathrm{i}}-\mathrm{1}\right)+c{\left(S_{\mathrm{i}}-\mathrm{1}\right)}^{\mathrm{2}}+d{\left(S_{\mathrm{i}}-\mathrm{1}\right)}^{\mathrm{3}}\right.\\ & \left.+e{\left(S_{\mathrm{i}}-\mathrm{1}\right)}^{\mathrm{4}}+f{\left(S_{\mathrm{i}}-\mathrm{1}\right)}^{\mathrm{5}}+g(S_{\mathrm{i}}-\mathrm{1}{)}^{\mathrm{6}}\right],\end{array}\end{array}$$

where a=0.0878, b=23.7947, c=52.3167, d=2255.4484, e=568.3257, f=2460.4234, and g=263.1248. F_scav is the fraction of the total number of AgI particles scavenged by cloud droplets (Caro et al., 2004). Contact freezing is valid when S_i>1.058 and T<269.2 K.

And the last mode is immersion freezing, which is valid for temperatures colder than 268.2 K. This mode is expressed as

$$\begin{array}{}\text{(4)}& F_{\mathrm{imf}}=a{F}_{\mathrm{imm}}{\left({\displaystyle \frac{\mathrm{268.2}-T}{T_{\mathrm{0}}}}\right)}^b,\end{array}$$

where a=0.0274 and b=3.3. F_imm is the fraction of AgI particles that are immersed in cloud droplets but not nucleated. Based on the equations above, we can calculate the concentration of ice generated through cloud seeding at a given AgI particle concentration. For simplicity, this 1D model does not incorporate the 3D turbulent dispersion of AgI particles. In each numerical experiment, seeding is performed at a given temperature (height), and seeding takes place only at the beginning of each run. The total AgI particle concentration decreases with each time step (1 s) due to continuous ice nucleation. The nucleated ice crystals that form at the seeding level are either columnar or plate-like, depending on the background temperature, and they remain that way as they descend to the surface.

2.2 Growth of ice crystals

In mixed-phase stratiform clouds with relatively weak turbulence, the WBF process, during which ice grows at the expense of liquid water, is the most important mechanism for ice growth. Therefore, if there is sufficient liquid water in the cloud, diffusional growth contributes the most to ice mass and size. However, it should be noted that the WBF process is not always valid; if the updraft is strong enough, the cloud will become supersaturated with respect to water, leading to the simultaneous growth of droplets and ice crystals. Korolev (2007) showed that the WBF process only applies in weak downdrafts and weak updrafts; therefore, we emphasize that the model used here only applies to stratiform clouds with weak turbulence. In fact, even weak turbulence may occasionally result in supersaturation with respect to water, and radiative cooling at the cloud top reduces stability, resulting in weak vertical motions at the cloud top that may also enhance supersaturation. These factors are not considered and could, in part, contribute to the model uncertainties in the results shown in Sect. 3. In addition to the WBF process, we also consider the riming process, but the model does not incorporate aggregation or secondary-ice-production (SIP) mechanisms, such as the rime-splintering process and the shattering of freezing drops, which may alter ice particle size distributions and radar reflectivity (Yang et al., 2024b). By not including these processes, the model may underestimate reflectivity in conditions where aggregation is a dominant growth mechanism or in clouds with either abundant supercooled water or high ice crystal concentrations as a result of SIP.

According to Mason (1953), the diffusional-growth rate of an ice crystal is given by

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}m}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{4}\mathit{\pi }C\left(S_{\mathrm{i}}-\mathrm{1}\right)f_{\mathrm{v}}}{L_{\mathrm{d}}^{\mathrm{2}}/K{R}_{\mathrm{v}}{T}_{\mathrm{a}}^{\mathrm{2}}+\mathrm{1}/D_{\mathrm{v}}{\mathit{\rho }}_{\mathrm{s}}}},\end{array}$$

where R_v is the specific gas constant for vapor, L_d is the latent heat of deposition, K is the thermal conductivity of air, T_a is the ambient temperature, D_v is the diffusion coefficient of vapor, ρ_s is the density of saturated vapor, and S_i is the saturation ratio with respect to ice (which depends on the liquid phase and temperature). Moreover, f_v is the ventilation factor, expressed as

$$\begin{array}{}\text{(6)}& f_{\mathrm{v}}=\left\{\begin{array}{ll}\mathrm{1}+\mathrm{0.14}{X}^{\mathrm{2}},& X<\mathrm{1}\\ \mathrm{0.86}+\mathrm{0.28}X,& X\ge \mathrm{1}\end{array}\right.,\end{array}$$

where $X={\mathit{Sc}}^{\mathrm{1}/\mathrm{3}}{\mathit{Re}}^{\mathrm{1}/\mathrm{2}}$, with Sc representing the Schmidt number and Re representing the Reynolds number (Hall and Pruppacher, 1976).

In Eq. (5), the capacitance (C) reveals the shape of the ice crystals, which is dependent on temperature and supersaturation. Many laboratory experiments have investigated the shapes of ice crystals during diffusional growth (e.g., Fukuta and Takahashi, 1999; Bailey and Hallett, 2009). Typically, plate-like ice crystals (hexagonal plates, sectored plates, dendrites, etc.) form at temperatures warmer than −4 °C and at temperatures between −8 and −22 °C, whereas column-like ice crystals (columns, needles, etc.) form at temperatures between −4 and −8 °C (Fukuta and Takahashi, 1999). At temperatures colder than −22 °C, ice crystals could be either columns or plates (Bailey and Hallett, 2009). Based on laboratory experiments, Chen and Lamb (1994) developed a parameterization of C. For plate-like ice crystals,

$$\begin{array}{}\text{(7)}& {\displaystyle }C={\displaystyle \frac{a\mathit{\epsilon }}{{\sin }^{-\mathrm{1}}\mathit{\epsilon }}},\text{(8)}& {\displaystyle }\mathit{\epsilon }=\sqrt{\mathrm{1}-c^{\mathrm{2}}/a^{\mathrm{2}}}=\sqrt{\mathrm{1}-{\mathit{\varphi }}^{\mathrm{2}}},\end{array}$$

and for column-like ice crystals,

$$\begin{array}{}\text{(9)}& {\displaystyle }C={\displaystyle \frac{c\mathit{\epsilon }}{\ln \left[\left(\mathrm{1}+\mathit{\epsilon }\right)\mathit{\varphi }\right]}},\text{(10)}& {\displaystyle }\mathit{\epsilon }=\sqrt{\mathrm{1}-a^{\mathrm{2}}/c^{\mathrm{2}}}=\sqrt{\mathrm{1}-{\mathit{\varphi }}^{-\mathrm{2}}},\end{array}$$

where a and c are the particle radii along the a and c axes, respectively. For plate-like ice crystals, the a axis is longer than the c axis, while for column-like particles, the c axis is longer. Moreover, $\mathit{\varphi }=c/a$ is the aspect ratio of the ice crystal. The change in the surface volume of the ice crystal is expressed as

$$\begin{array}{}\text{(11)}& \mathrm{d}V={\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{dep}}}}\mathrm{d}m,\end{array}$$

where ρ_dep is the mass density at the time of deposition. Chen and Lamb (1994) showed that ρ_dep (g cm⁻³) can be expressed using

$$\begin{array}{}\text{(12)}& {\mathit{\rho }}_{\mathrm{dep}}=\mathrm{91}\exp \left[-\mathrm{3}{\displaystyle \frac{max\left(\mathrm{\Delta }\mathit{\rho }-\mathrm{0.05},\mathrm{0}\right)}{\mathrm{\Gamma }\left(T\right)}}\right],\end{array}$$

where Δρ is the excess vapor density. Γ(T) is the inherent growth ratio of ice, which is parameterized based on data from multiple laboratory experiments (Harrington et al., 2019):

$$\begin{array}{}\text{(13)}& \mathrm{\Gamma }\left(T\right)={\displaystyle \frac{\mathrm{d}c}{\mathit{\varphi }\mathrm{d}a}}.\end{array}$$

The initial ice particle is assumed to be spherical. The volume can be expressed as

$$\begin{array}{}\text{(14)}& {\displaystyle }V={\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathit{\pi }{a}^{\mathrm{2}}c={\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathit{\pi }{a}^{\mathrm{3}}\mathit{\varphi },\text{(15)}& {\displaystyle }\mathrm{d}\ln V=\mathrm{3}\mathrm{d}\ln a+\mathrm{d}\ln \mathit{\varphi }.\end{array}$$

The differential representation of ϕ is given by

$$\begin{array}{}\text{(16)}& {\displaystyle }\begin{array}{rl}\mathrm{d}\mathit{\varphi }& ={\displaystyle \frac{\mathrm{1}}{a}}\mathrm{d}c-{\displaystyle \frac{c}{a^{\mathrm{2}}}}\mathrm{d}a=\left({\displaystyle \frac{\mathrm{d}c}{\mathrm{d}a}}-\mathit{\varphi }\right)\mathrm{d}\ln a\\ & =\mathit{\varphi }\left(\mathrm{\Gamma }-\mathrm{1}\right)\mathrm{d}\ln a,\end{array}\text{(17)}& {\displaystyle \frac{\mathrm{d}\mathit{\varphi }}{\mathit{\varphi }}}={\displaystyle \frac{\mathrm{d}V}{V}}\left({\displaystyle \frac{\mathrm{\Gamma }-\mathrm{1}}{\mathrm{\Gamma }+\mathrm{2}}}\right).\end{array}$$

Based on the equations above, we can estimate the changes in ϕ, a, and c over time as follows:

$$\begin{array}{}\text{(18)}& {\displaystyle }\mathit{\varphi }\left(t+\mathrm{\Delta }t\right)=\mathit{\varphi }\left(t\right){\left[{\displaystyle \frac{V\left(t\right)+\mathrm{d}V}{V\left(t\right)}}\right]}^{\left(\mathrm{\Gamma }-\mathrm{1}\right)\left(\mathrm{\Gamma }+\mathrm{2}\right)},\text{(19)}& {\displaystyle }a\left(t+\mathrm{\Delta }t\right)={\left[{\displaystyle \frac{\mathrm{3}}{\mathrm{4}\mathit{\pi }}}{\displaystyle \frac{V\left(t\right)+\mathrm{d}V}{\mathit{\varphi }\left(t+\mathrm{\Delta }t\right)}}\right]}^{\mathrm{1}/\mathrm{3}},\text{(20)}& {\displaystyle }c\left(t+\mathrm{\Delta }t\right)=\mathit{\varphi }\left(t+\mathrm{\Delta }t\right)\times a\left(t+\mathrm{\Delta }t\right).\end{array}$$

Although diffusional growth is the most important mechanism for ice growth in mixed-phase stratiform clouds, accretional growth (riming) is also considered in the model. According to Heymsfield (1982), the mass growth rate due to riming can be parameterized as

$$\begin{array}{}\text{(21)}& {\displaystyle \frac{\mathrm{d}{m}_R}{\mathrm{d}t}}=A{V}_{\mathrm{t}}E\left(Dd\right)\mathrm{LWC},\end{array}$$

where A is the particle cross-sectional area normal to the fall; V_t is the terminal fall velocity of ice crystals; LWC refers to the liquid water content, estimated assuming adiabatic-cloud conditions; and E(Dd) is the collection efficiency between an ice crystal with a diameter of D and a droplet with a diameter of d. For simplicity, we assume a droplet diameter of 10 µm, which is a typical size for droplets in continental clouds (Wallace and Hobbs, 2006; Wang et al., 2021).

To account for the impact of turbulence on the growth of ice crystals, we use a Gaussian normal distribution with a zero-mean vertical air velocity and a standard deviation of 0.75 m s⁻¹. A similar method has been used in previous studies (e.g., Korolev and Field, 2008; Zhang et al., 2014). The vertical velocity of an ice crystal is the sum of the particle's terminal fall velocity and vertical air velocity. As the ice crystals fall from the seeding level, the temperature below the seeding level is calculated using a lapse rate of 5.5 K km⁻¹, and the pressure is calculated using the hydrostatic equation. Sensitivity tests using lapse rates of 5 and 6 K km⁻¹ reveal minor differences in the modeled results of the ice mass.

2.3 Terminal velocity of ice crystals

The terminal velocity of an ice crystal depends on its mass, size, and habits, as well as on the ambient air density. In the present study, we follow a method developed by Heymsfield and Westbrook (2010) to estimate the terminal velocity (V_t) of ice crystals, which has been evaluated against observations (Heymsfield and Westbrook, 2010; Zhang et al., 2014), as follows:

$$\begin{array}{}\text{(22)}& V_{\mathrm{t}}={\displaystyle \frac{\mathit{\eta }\mathit{Re}}{{\mathit{\rho }}_{\mathrm{air}}D}},\end{array}$$

where η is the dynamical viscosity and D is the maximum size of the projection of the particle perpendicular to the direction of fall. According to Böhm (1992), D=2a for a plate, $D=\mathrm{2}\sqrt{ac}$ for column, and D=2r for a sphere. Re is the Reynolds number, given by

$$\begin{array}{}\text{(23)}& \mathit{Re}={\displaystyle \frac{{\mathit{\delta }}_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{4}}}\left(\mathrm{1}+{\displaystyle \frac{\mathrm{4}\sqrt{X^{\ast }}}{{\mathit{\delta }}_{\mathrm{0}}^{\mathrm{2}}\sqrt{C_{\mathrm{0}}}}}\right),\end{array}$$

where C₀=0.35 and δ₀=8.0.

$$\begin{array}{}\text{(24)}& X^{\ast }={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{air}}}{{\mathit{\eta }}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{8}mg}{A_r^k}},\end{array}$$

where the value of k is 0.5, according to Heymsfield and Westbrook (2010), and A_r is the ratio of the projected area (A) of the particle to the area of the external circle, expressed as

$$\begin{array}{}\text{(25)}& A_r=A/\left[\left(\mathit{\pi }/\mathrm{4}\right)D^{\mathrm{2}}\right].\end{array}$$

Following Harrington et al. (2013), for plate-like particles,

$$\begin{array}{}\text{(26)}& A=\mathit{\pi }{a}^{\mathrm{2}}{\left({\mathit{\rho }}_{\mathrm{i}}/{\mathit{\rho }}_{\mathrm{bi}}\right)}^{\mathrm{2}},\end{array}$$

and for columnar particles,

$$\begin{array}{}\text{(27)}& A=\mathit{\pi }ac,\end{array}$$

where ρ_i is the density of the ice crystal and ρ_bi is the bulk density of solid ice (0.91 g cm⁻³). The ice shape (plate-like or column-like) is assumed to remain unchanged with height as the ice falls.

2.4 Calculation of the IWC and Z_e

In this model, we assume that the initial ice size distribution follows the modified gamma distribution (Mace et al., 1998):

$$\begin{array}{}\text{(28)}& N_{\mathrm{i}}\left(D\right)=N_X\exp \left(\mathit{\alpha }\right)\left({\displaystyle \frac{D}{D_X}}\right)\exp \left(-{\displaystyle \frac{D\mathit{\alpha }}{D_X}}\right),\end{array}$$

where D_X=10 µm and α=2. Sensitivity tests using different values for these coefficients will be shown later (Fig. 3). N_i is the ice concentration per unit of length, while N_X is the number concentration per unit of length at the functional maximum and is determined by the ice nucleation induced by AgI. This initial size distribution is partitioned into 80 bins with isometric radius intervals, and we loop through all the bins to simulate the growth of ice crystals with different initial sizes. Based on the modeled ice mass and size, we can calculate the IWC and Z_e as follows:

$$\begin{array}{}\text{(29)}& {\displaystyle }\mathrm{IWC}=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}m\left(D\right)N_{\mathrm{i}}\left(D\right)\mathrm{d}D,\text{(30)}& {\displaystyle }{Z}_{\mathrm{e}}=N_{\mathrm{i}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}f\left(D_{\mathrm{m}}\right)D_{\mathrm{m}}^{\mathrm{6}}\mathrm{d}D,\end{array}$$

where D_m is the melted-ice diameter, f(D_m) is the normalized ice size distribution, and N_i is the ice concentration. In the present study, Z_e is calculated assuming Rayleigh scattering; thus, the radar signal is more sensitive to the size of the particles. For radars with shorter wavelengths, such as the W-band cloud radar, the signal may be sensitive to ice concentration. In SNOWIE, both W-band and X-band radars were used. The W-band radar observed clear Z_e enhancement near the seeding level, while the X-band radar detected weak Z_e in the ice plume near the seeding level, which increased downwind toward the surface (Friedrich et al., 2021). We will show that the modeled results (Sect. 3) are consistent with the observed Z_e profile using the X-band radar.

In turbulent clouds, ice crystals may disperse horizontally over time, resulting in a reduced ice concentration. In the 1D model, we can estimate the change in N_i(D) by solving the 1D dispersion equation as follows:

$$\begin{array}{}\text{(31)}& {\displaystyle \frac{\partial N_{\mathrm{i}}}{\partial t}}=\mathit{\nu }{\displaystyle \frac{{\partial }^{\mathrm{2}}{N}_{\mathrm{i}}}{\partial x^{\mathrm{2}}}},\end{array}$$

where ν is the turbulent kinematic-diffusion coefficient and depends on the turbulent intensity. In mixed-phase stratiform clouds with relatively simple dynamics, ν is typically smaller than 10 m⁻² s⁻¹ (Pinsky et al., 2018). In clouds with strong wind shear or embedded convections, ν could be larger, and the ice growth trajectory could be much more complicated. Therefore, we emphasize again that the model described here only applies to stratiform clouds with relatively weak turbulence. In the present study, the value of ν is randomly selected between 1 and 10 m⁻² s⁻¹. In clouds with strong turbulence or embedded convection, the microphysics and dynamics are much more complicated (Yang et al., 2016a, b).

3 Model results

3.1 Examples of ice microphysics from the 1D model

First, we evaluate the growth of a single ice crystal simulated using the 1D model. Figure 1 compares the modeled mass and size of a single ice crystal with the laboratory experiments from Takahashi et al. (1991). The laboratory experiments were conducted at various temperatures under standard atmospheric pressure. The initial ice crystal is assumed to be spherical and has a radius of approximately 4 µm. In the model simulation, we use the same thermodynamic conditions and initial ice size as in the laboratory experiments (Eq. 28 is used instead of Fig. 1). It can be seen in the figure that the modeled results are fairly consistent with the observations. The mass growth rate has two peaks, at −15 or −6 °C, and is at its highest at −15 °C. The ice crystal formed at −15 °C is plate-like, and the one formed at −6 °C is column-like (Eqs. 7–10 in Sect. 2.2). After 25 min, the mass of the ice crystal grown at −15 °C is about an order of magnitude greater than that grown at −20 °C. The sizes along different axes depend on the shape of the ice crystals. At −6 °C, the ice crystal is column-like, meaning the c axis is the largest, while at −15 °C, the a axis is the largest as the ice crystal is plate-like. The ice size can rapidly increase from 4 µm to more than 1 mm within 20 min at −15 and −6 °C. At temperatures lower than −20 °C, the ice growth habit is less sensitive to temperature. In general, the uncertainty in the modeled ice mass and size is less than 20 % compared to the observation. This gives us the confidence needed to use the model to estimate ice growth.

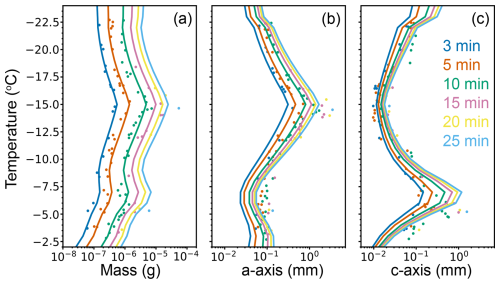
Figure 1 (a) Growth of the mass of a single ice crystal as a function of time at different temperatures under standard atmospheric pressure. The dots correspond to laboratory experiments conducted by Takahashi et al. (1991), and the curves are from model simulations. Panels (b) and (c) are similar to panel (a) but are for the a axis and c axis, respectively.

According to Fig. 1, it is expected that a detectable seeding signature is more probable at −15 °C or colder temperatures. To investigate the seeding signature at a given height, it is necessary to explore how ice concentration, IWC, and Z_e change vertically as the ice crystals fall from the seeding level. Figure 2 shows the vertical profiles of ice concentration, IWC, and Z_e for seeding temperatures of −15, −18, and −20 °C (at seeding heights of 5, 5.6, and 6 km altitude, respectively). The results are obtained using 10 numerical experiments for each seeding temperature. The model runs for 60 min in each experiment. The shaded area indicates the 20th–80th percentile range, and the solid lines represent the mean profiles. The uncertainties are due to the random numbers used to model the turbulence effect. Seeding at a relatively low temperature results in a higher ice concentration, and ice concentration decreases with height. For an AgI particle concentration of 35 cm⁻³, the ice concentrations are 10 times lower. Regardless of the AgI particle concentration, it can be seen that the vertical variations in IWC and Z_e are consistent. Below 4.8 km altitude, IWC and Z_e values are at their greatest when the seeding temperature is −15 °C and at their lowest when the seeding temperature is −20 °C. Although more ice can be nucleated through AgI at lower temperatures, its mass growth is much slower than that of ice initiated at −15 °C, leading to lower IWC and Z_e values, which are more sensitive to size than concentration. The vertical variations in IWC and Z_e are also related to the terminal fall velocity of ice crystals with different shapes. Ice crystals initiated at −20 °C are of a similar scale along the a axis and c axis; thus, the ice particles are more spherical compared to the plate-like ice crystals initiated at −15 °C. The plate-like ice crystals have a low terminal velocity, meaning they can remain at temperatures near −15 °C for a relatively long time, resulting in a substantial increase in ice mass and size. However, the ice particles initiated at −20 °C have a higher terminal velocity when they fall through the −15 °C level. Based on the results shown in Figs. 1 and 2, it is suggested that seeding at a temperature of −15 °C can provide a higher probability of detecting the seeding signature using radar. This conclusion is interestingly consistent with the fact that the seeding temperature was about −15 °C (or slightly warmer in non-precipitating clouds) in many of the cases with unambiguous seeding signatures detected (e.g., French et al., 2018; Yue et al., 2021; Wang et al., 2024), while at colder or warmer seeding temperatures in precipitating clouds, no clear seeding signature was observed.

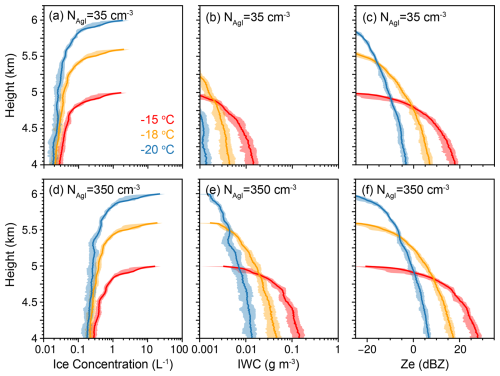
Figure 2 Vertical profiles of (a, d) ice concentration, (b, e) IWC, and (c, f) Z_e from simulations with different seeding temperatures and AgI particle concentrations of (a–c) 35 cm⁻³ and (d–f) 350 cm⁻³. The results were derived from 10 numerical experiments for each seeding temperature. The shaded area captures the 20th–80th percentile range, and the solid lines represent the mean profiles.

In the model, we assume that there is sufficient supercooled liquid water and a continuous water supply. However, in real clouds, this is not always true, and there is often an upper limit to the LWC in clouds. This would certainly affect ice growth and the Z_e profiles. We conducted several sensitivity tests with a seeding temperature of −15 °C, including different upper limits for the LWC (assuming no continuous liquid water supply; Fig. 3a), different time durations for ice growth (Fig. 3b), and different AgI particle concentrations for a limited LWC (Fig. 3c). It can be seen in the figure that for a model time of 90 min, Z_e decreases with decreasing LWC (Fig. 3a). For a given LWC of 0.2 g m⁻³, ice nucleation and growth over a longer time would consume more liquid water, leading to lower Z_e values (Fig. 3b), which would mean that ice formed later on would lack sufficient liquid water and vapor for growth. For a given LWC and temporal duration, a higher AgI concentration does not always produce larger Z_e values (Fig. 3c); ice crystals may compete for the limited liquid water and suppress the ice crystal size. In addition, we conducted sensitivity tests with different turbulent-dispersion coefficients and different initial ice particle size distributions (Fig. 3d–f). These are also sources of uncertainty in the model, though the Z_e profile is less sensitive to these factors compared to LWC. These results provide us with a better understanding of how modeled ice mass and Z_e may vary due to different environmental conditions.

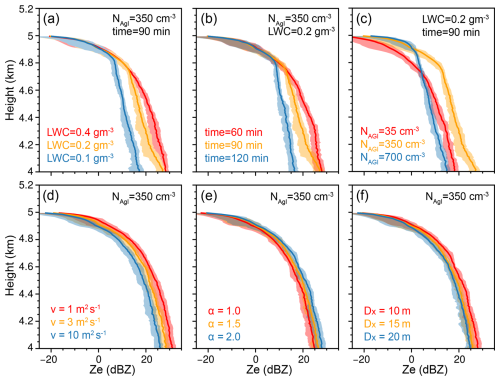
Figure 3 Vertical profiles of Z_e simulations using different (a) upper limits of LWC, (b) temporal durations for ice growth, (c) AgI particle concentrations with limited LWC, (d) turbulent kinematic-diffusion coefficients, and (e, f)​​​​​​​ coefficients in the initial ice particle size distributions. Seeding is performed at −15 °C in all the experiments.

3.2 Comparison to the 3D model simulation

To further evaluate the 1D ice growth model, it is compared with a 3D large-eddy simulation (LES) of stratiform clouds observed on 1 January 2022 in northern China. The cloud was originally shallow, with a depth of approximately 600 m. The cloud top temperature was approximately −16 °C (Wang et al., 2024). This cloud was seeded at around −15 °C, and evident Z_e enhancement was detected by radar after seeding (Wang et al., 2024). The cloud was almost entirely liquid before seeding, and the seeded area quickly glaciated within an hour. More details of the measurements can be found in Wang et al. (2024). In this study, we use the LES mode of the Weather Research and Forecasting (WRF) model, employing periodic boundaries to simulate the cloud. The solid lines in Fig. 4 show the initial profiles of temperature, potential temperature, the vapor mixing ratio, and wind velocity above the ground level. Adiabatic liquid water content (LWC) is assumed in the cloud, and the wind shear in the cloud layer (dark shaded area in Fig. 4) is relatively weak. To evaluate the performance of the 1D model in simulating deeper clouds, we modified the temperature and vapor-mixing-ratio data (dashed lines) to allow for the formation of a deep saturated layer. The modeled cloud has a base height of 1.3 km altitude and a top height of 2.9 km altitude (shaded area in Fig. 4). The initial LWC increases from 0 to 0.2 g m⁻³ from the cloud base to the top, and it rapidly decreases to 0 g m⁻³ above 2.9 km altitude.

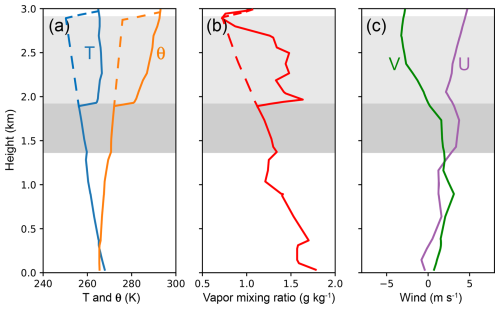
Figure 4 The initial profiles of (a) temperature and potential temperature (θ), (b) the vapor mixing ratio, and (c) the u and v components of the wind field. The solid lines indicate the original sounding data used for the shallow cloud, and the dashed lines indicate the modified data used for the deep case. The dark shaded area (1.3–1.9 km altitude) indicates the shallow-cloud layer, and the light shaded area (1.3–2.9 km altitude) indicates the deep-cloud layer.​​​​​​​

In the experiment for the shallow cloud, the model has a horizontal resolution of 50 m, and the domain size is 10 km × 10 km × 4 km. In the deep-cloud experiment, the same horizontal resolution and size are used, but in the vertical dimension, we extend the depth to 5 km. In both experiments, 180 vertical levels are used to resolve the vertical structure of the cloud. A ±0.1 K temperature perturbation is added at the cloud base to initiate turbulence. A spin-up time of 30 min is used (Yang et al., 2024a), and the ice process is turned off during the spin-up time. Seeding is conducted for 30 min along a straight line (with a length of 10 km in the longitudinal direction) at 1.8 km altitude (−15 °C) for the shallow case and at 2.6 km altitude (−21 °C) for the deep case. We tested two different AgI particle concentrations (35 and 350 cm⁻³) in the simulations. The physics schemes used in the simulation include the revised MM5 surface layer scheme (Jiménez et al., 2012); the Noah land surface model (Tewari et al., 2004); the Rapid Radiative Transfer Model (Mlawer et al., 1997); and the Fast Spectral Bin Microphysics scheme (Khain et al., 2004), which can explicitly simulate more complicated microphysics than the 1D model. Cumulus and boundary layer parameterizations are turned off in the LES. The cloud condensation nuclei (CCN) concentration is expressed by $N_{\mathrm{CCN}}=N_{\mathrm{0}}{S}_{\mathrm{w}}^k$, where N₀ refers to the CCN concentration at a supersaturation level of 1 %, S_w represents the supersaturation with respect to water (expressed as a percentage), and k is the slope of the CCN size distribution. For continental China, Qu et al. (2017) suggested that N₀ = 4000 and k = 0.9. The warm-rain process is not possible with such a high aerosol concentration and weak wind shear in the cloud since collision–coalescence cannot be initiated. Since the observation suggests that the cloud is entirely liquid before seeding, the natural ice nucleation process is turned off in the model. Thus, ice crystals are only generated due to cloud seeding. Similar to the 1D model, the AgI nucleation parameterization is from Xue et al. (2013a).

Figure 5a–d shows Z_e values, cloud water, and ice mixing ratios corresponding to 30 min after seeding in the 3D LES model for the shallow case. Ice crystals, which are initially nucleated near the cloud top, can rapidly grow and fall out of the cloud within 30 min. With a lower AgI concentration (35 cm⁻³), the ice mixing ratio is lower than 0.06 g kg⁻¹ after 30 min, while at a higher AgI particle concentration (350 cm⁻³), the modeled ice mixing ratio exceeds 0.15 g kg⁻¹. Since the cloud is entirely liquid in areas unaffected by seeding, the seeding signature can be clearly identified once the ice plume forms, using either in situ measurements or remote sensing measurements (Wang et al., 2024; French et al., 2018). A higher ice mixing ratio implies a higher radar reflectivity. As shown in Fig. 5a, at a lower AgI particle concentration (35 cm⁻³), the maximum Z_e value near the cloud base 30 min after seeding is approximately 10 dBZ, while at a higher AgI particle concentration (350 cm⁻³), Z_e exceeds 20 dBZ. Z_e is relatively small near the cloud top and increases from the cloud top to the base. Below the cloud base, Z_e decreases due to ice sublimation. The magnitude of Z_e in the core of seeding plumes (5–30 dBZ) is fairly consistent with observational studies in which cloud seeding was operated at −15 °C (Wang et al., 2021; French et al., 2018), indicating that the LES model can capture the characteristics of ice growth habits. The ice concentration in such a shallow cloud, with top temperatures as warm as −15 °C, is typically low (Zhang et al., 2014), resulting in weak Z_e in the natural cloud. Z_e attributed to cloud seeding (Fig. 5) is large enough to be detected by operational weather radars.

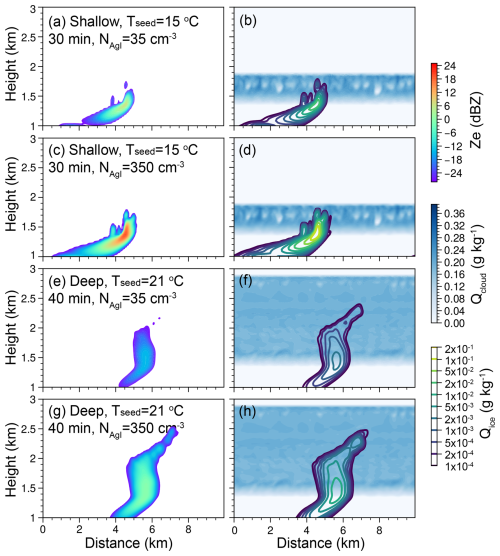
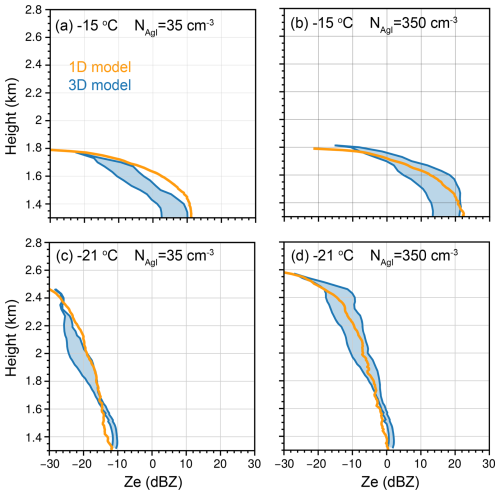
Figure 5 Cross sections of (a) Z_e (rainbow shading) and (b) both the liquid water mixing ratio (blue shading) and the ice mixing ratio (contours), obtained from the 3D LES for the shallow case using an AgI particle concentration of 35 cm⁻³. Seeding is performed at 1.8 km altitude (−15 °C). Panels (c) and (d) are similar to panels (a) and (b) but depict an AgI particle concentration of 350 cm⁻³. Panels (e)–(h) are similar to panels (a)–(d) but depict the deep case, employing a seeding level at 2.6 km altitude (−21 °C). T_seed: seeding-level temperature. Q_cloud: cloud water mixing ratio. Q_cloud: ice water mixing ratio.

For the deeper case, as seen in Fig. 5e–f, the modeled Z_e and IWC values are much lower than those for the shallow case because seeding was performed at a temperature of −21 °C. We present the results from 40 min after seeding because the ice crystals needed more time to reach the cloud base in this case than in the shallow case. In general, Z_e and IWC values increase from the seeding level toward the cloud base, and the maximum Z_e value is only −10 (1 dBZ) for an AgI particle concentration of 35 (350 cm⁻³). These low values are often smaller than those of the signals of natural precipitation. This conclusion is consistent with Fig. 2; therefore, both the 1D model and the 3D model suggest a high ice growth rate at −15 °C and a lower ice growth rate at colder temperatures.

Figure 6 compares the radar reflectivity from the 1D model simulation with that from the 3D model simulation. The left and right boundaries of each blue-shaded area indicate the 95th percentile and the maximum Z_e value from the 3D model, respectively. As shown in the figure, the 1D model is generally consistent with the 3D model, and the oversimplified dynamics do not change the magnitude and vertical variation in Z_e. Near the cloud base, an AgI concentration of 35 cm⁻³ leads to a maximum reflectivity of 11 dBZ (Fig. 6a), and Z_e increases to 21 dBZ as the AgI concentration increases to 350 cm⁻³ (Fig. 6b). This magnitude is similar for both the 1D and 3D models. Therefore, the 1D model is valid for investigating the vertical variation in Z_e below the seeding level. Although the 1D model is consistent with the 3D model in the cases presented here, it should be noted that uncertainties are inevitably present when modeling Z_e in both models. Improving the ice nucleation and growth parameterizations in the models is vital for the purpose of this study. Previous observational studies have shown that the ice nucleation efficiency of AgI particles varies across different experiments (Marcolli et al., 2016), and recently, Ramelli et al. (2024), using in situ and remote sensing measurements, showed that ice growth rates exhibit large variations in seeded clouds, indicating that in real clouds, the dynamics and microphysics are complicated. Such observational datasets are useful for evaluating and improving ice growth models (Omanovic et al., 2024).

Figure 6 Vertical profiles of Z_e simulated using the 1D and 3D models with AgI particle concentrations of (a, c) 35 cm⁻³ and (b, d) 350 cm⁻³, respectively. The left and right boundaries of the blue-shaded area indicate the 95th percentile and the maximum Z_e value from the 3D model, respectively.

3.3 Parameterizing the AgI concentration needed to detect unambiguous seeding signatures

Since the 1D model can simulate the growth habit of ice crystals reasonably well, we conducted 2500 numerical experiments with a variety of seeding temperatures (−30 to −7 °C), seeding pressures (350–850 hPa), AgI particle concentrations at the seeding level (1–10⁶ cm⁻³), and depths from the seeding level (i.e., the vertical distances between the seeding levels and target levels, where we aim to detect unambiguous seeding signatures; 500–4000 m). We include very high AgI particle concentrations at the seeding level in the experiments because it is helpful to have a large parameter space to constrain the parameterization. In addition, in many observational studies, normal AgI particle concentrations (10–1000 cm⁻³) are insufficient for detecting the seeding signature, though AgI particle concentrations with a magnitude of 10⁵–10⁶ cm⁻³ are probably not possible in reality. Again, it should be noted that we assume there is sufficient supercooled liquid water in the cloud. Figure 7 shows modeled Z_e values (colored) at the target levels as a function of different seeding temperatures, AgI particle concentrations, and depths from the seeding level. Statistically, we can see that both temperature and AgI particle concentrations have important impacts on the seeding impacts. The modeled Z_e values are relatively high at −15 °C, with higher AgI particle concentrations. Clouds with cold top temperatures can be either shallow or deep, and at a given seeding temperature, the modeled Z_e values increase with depth (similar to the Z_e profiles in Fig. 2). Cloud top pressure also influences the growth rate of ice crystals, but its impact is minor compared to that of other factors.

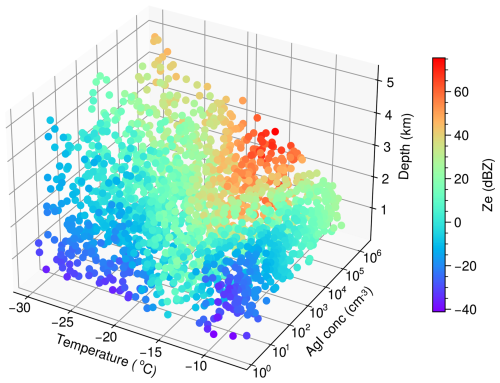
Figure 7 Modeled Z_e values (colored dots) at target levels for different seeding temperatures, AgI concentrations, and cloud depths from the seeding level, all based on data from 1000 numerical experiments using the 1D model. AgI conc: AgI concentration.

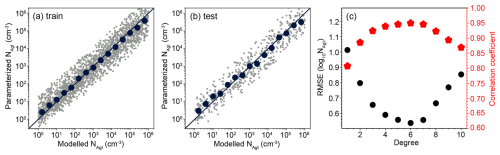
Figure 8 (a) Scatter plot of parameterized and modeled AgI particle concentrations. The gray dots represent the results from the 2000 numerical experiments used for training, and the dark-blue dots are binned averages. The parameterization is developed using a polynomial regression with a degree of 6. (b) Similar to panel (a) but for the 500 experiments used for the test. (c) RMSEs and correlation coefficients between the parameterized and modeled AgI concentrations for different polynomial degrees used in the regression of training data.

Using the results from the 2500 numerical experiments, we parameterize the AgI particle concentration that is needed to detect the seeding signature. We train the data using polynomial regression based on 2000 experiments randomly selected from all simulations, and we then test the parameterization using the remaining 500 experiments. The inputs are seeding-level temperature (T_seed), seeding-level pressure (P_seed), cloud depth from the seeding level (D_seed), and Z_e attributed to seeding at the target level (Z_{e_target}). The output is the AgI particle concentration at the seeding level (N_AgI).

$$\begin{array}{}\text{(32)}& N_{\mathrm{AgI}}=f\left(T_{\mathrm{seed}},P_{\mathrm{seed}},D_{\mathrm{seed}},Z_{\mathrm{e}\mathrm{\_}\mathrm{target}}\right)\end{array}$$

Thus, for a given cloud, we can decide how much AgI is needed to seed at different heights to produce a radar signal exceeding the natural variability at the target level. Figure 8a compares the modeled and parameterized AgI particle concentrations using the training data. Generally, the data points lie along the 1 : 1 line, and this works well for the test data (Fig. 8b), indicating that the parameterization can reasonably reveal the relationships between AgI particle concentrations and Z_e under different cloud conditions. In the polynomial regression used for Fig. 8a, a degree of 6 (i.e., the maximum power for the input variables) is used. We also tested different degree values in the regression, as shown in Fig. 8c. A degree of 6 gives the smallest root mean square error (RMSE) and the highest correlation coefficient between the modeled and parameterized AgI particle concentrations. The correlation coefficient increases as the degree increases from 1 to 6. For degrees larger than 6, the polynomial regression becomes overfitted.

4 Application to a real case

4.1 Radar observations

In this section, the parameterization is applied to a mixed-phase stratiform cloud with moderate natural precipitation (0.2–0.3 mm h⁻¹). The purpose is to estimate the concentration of AgI that is needed to detect the seeding signature in this case. Figure 9 shows the temperature profile and Z_e values measured by a Ka-band cloud radar. The cloud was observed in the region of Hulun Buir, northeastern China, on 3 August 2023. It formed during the passage of a warm front (near z = 1.7 km in Fig. 9a). The cloud was stratiform and deep, with a top temperature of about −25 °C. The freezing level was at about 4.2 km altitude. It can be seen that there are large natural variabilities in observed Z_e values. Above the freezing level, the largest Z_e value is about 15 dBZ, and the average Z_e value is 4 dBZ.

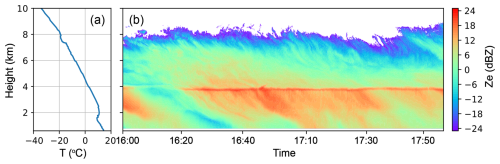
Figure 9 (a) Temperature profile measured by a radiosonde and (b) Z_e measured by a Ka-band cloud radar for a stratiform cloud observed in the region of Hulun Buir, northeastern China, on 3 August 2023. Times are provided in local time (LT).

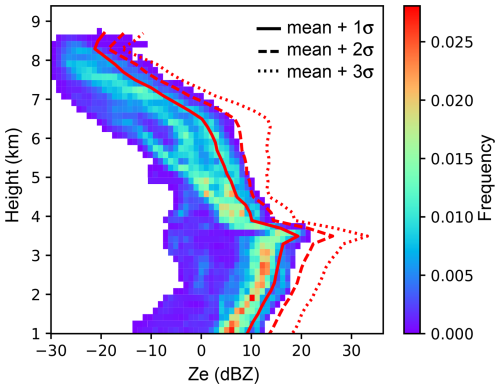
To determine the AgI particle concentration, firstly, we need to choose a threshold for Z_e induced by cloud seeding; i.e., seeding-induced Z_e values should be higher than this threshold so that composite Z_e values (combining natural and seeding Z_e) can exceed the natural variability after seeding. Figure 10 shows a contoured frequency-by-altitude diagram (CFAD) of observed Z_e values. The solid red line indicates the average Z_e value plus 1 standard deviation, and the dashed line indicates the mean plus 2 standard deviations. These two thresholds are probably still not large enough if seeding is performed in regions with relatively high values of natural Z_e (e.g., at 16:40 LT), but they may be fine if seeding is conducted at 16:10 LT, when values of natural Z_e are low. To better detect the seeding signature, a larger value of Z_e is necessary, such as the mean plus 3 standard deviations (dotted line), which well exceeds the maximum value of natural Z_e.

Figure 10 CFAD of Z_e observed by the Ka-band radar for the period shown in Fig. 9b. The solid, dashed, and dotted lines indicate the mean Z_e value plus 1, 2, or 3 standard deviation(s), respectively.

4.2 AgI concentrations needed to detect the seeding signature

Figure 11 shows the AgI particle concentrations needed at different heights (−22 to −7 °C) to detect Z_e values attributed to seeding above the freezing level (4.2 km altitude), assuming there is sufficient supercooled liquid water to support ice growth. We test three different thresholds for seeding-induced Z_e values (5.9, 11.2, and 16.7 dBZ). These values correspond to composite Z_e values (mean values of natural Z_e and seeding-induced Z_e) of 8, 12, and 17 dBZ above the freezing level (see the three red lines in Fig. 10). It is expected that more AgI is needed to obtain larger Z_e values, but the vertical variations in the three profiles of AgI particle concentration are very similar (Fig. 11). The required AgI concentration is lowest at about 7.3 km altitude (−15 °C), where 20 cm⁻³ of AgI is sufficient for cloud seeding to induce a composite Z_e value exceeding 17 dBZ. Therefore, seeding at this level provides the highest probability of detecting the seeding signature. However, airborne seeding at −15 °C is not always possible because of flight limitations (e.g., airframe icing). Seeding at colder or warmer temperatures may also exceed the Z_e threshold if the AgI particle concentration is high enough; however, since a normal AgI concentration in cloud-seeding operations has a magnitude of 10–1000 cm⁻³, it is unlikely that seeding below 6.5 km altitude will yield a detectable seeding signal near the freezing level in this case.

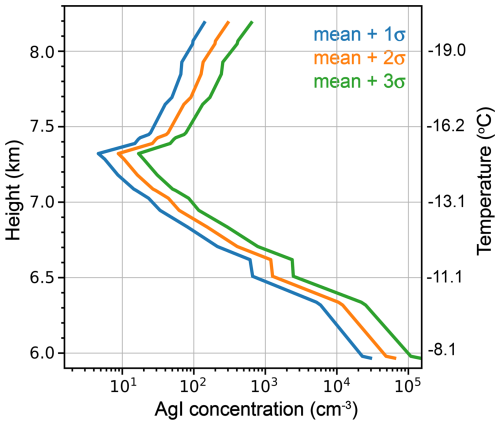
Figure 11 Profiles of AgI concentrations needed to detect seeding signatures at the freezing levels for different Z_e anomaly thresholds.

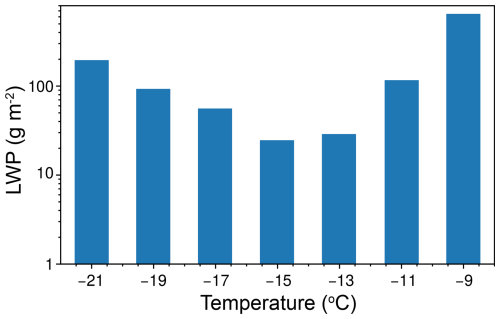
In precipitating clouds, the presence of natural ice would diminish the detectability of the seeding signature because both natural and seeded ice crystals would compete for the supercooled liquid water. We do not consider the interaction between seeded and natural ice in the 1D model because we assume that there is sufficient supercooled liquid water for their growth, and aggregation between natural and seeded ice is expected to further enhance the ice crystal size, which is favorable for seeding-signature detection. Therefore, we are able to apply the parameterization to a precipitating cloud; at the very least, it provides a threshold of AgI particle concentration that is needed to detect unambiguous seeding signatures. However, the assumption of sufficient liquid water is not always valid, especially when the natural ice concentration is high. Figure 12 shows the liquid water path (LWP) between the seeding level and the target level (4.2 km altitude) needed to support the growth of ice at different seeding temperatures. Seeding at −15 °C consumes the least liquid water, i.e., less than 30 g m⁻². The LWP in this cloud, observed by a microwave radiometer, was mostly larger than 300 g m⁻². However, both rainwater and cloud water contribute to the LWP, meaning we do not have direct measurements of the LWC in clouds. Accordingly, it is not known whether there is sufficient water for ice growth when seeding occurs at temperatures between −21 and −11 °C. Seeding at temperatures warmer than −10 °C requires much more liquid water due to the high AgI particle concentration; therefore, the size of ice crystals and Z_e may be even smaller, as suggested by the model. Previous observational studies suggest that the LWP in shallow mixed-phase stratiform clouds often exhibits a value lower than 100 g m⁻² (Zhang et al., 2014). Such a low LWP value prevents the growth of ice crystals if the ice concentration is high. In addition, if there is no continuous supply of liquid water (e.g., in orographic updrafts), seeding can cause complete cloud glaciation in the seeded region (Dong et al., 2021).

Figure 12 The LWP needed to support the growth of ice for different seeding temperatures between the seeding level and the target level.

5 Discussion and conclusions

In this study, IWC and Z_e values induced by glaciogenic seeding using different AgI particle concentrations under various cloud conditions are investigated using a 1D ice growth model coupled with an AgI nucleation parameterization. In addition, an algorithm is developed to estimate the AgI particle concentration that is needed to detect the signature of glaciogenic cloud seeding. This algorithm, which is a parameterization that links AgI particle concentrations to Z_e values induced by seeding, is developed based on multiple numerical experiments using the 1D model. The main conclusions are as follows:

1. The 1D model captures the characteristics of ice growth habits compared to laboratory experiments, and the modeled IWC and Z_e values are consistent with the 3D LES model. However, the evaluation was conducted using only two case studies, meaning further model validation is needed in the future, especially with regard to field measurements.

2. Since ice crystals exhibit their highest growth rate at −15 °C, IWC and Z_e values induced by cloud seeding at −15 °C are larger than those induced by seeding at colder temperatures. Therefore, a radar seeding signature is most likely to be detected at a temperature of about −15 °C. This finding is consistent with the fact that the seeding temperature was about −15 °C or slightly warmer in most documented cases of unambiguous seeding signatures.

3. A higher AgI particle concentration leads to higher Z_e values, assuming all other parameters are equal. Both the 1D and 3D models suggest that for an AgI particle concentration of 35 cm⁻³, Z_e values induced by cloud seeding range from 10–20 dBZ, and for an AgI particle concentration of 350 cm⁻³, Z_e values range from 20–30 dBZ, as long as sufficient liquid water is available.

4. Using the 1D model, 2500 numerical experiments were conducted under various cloud conditions and at various AgI particle concentrations. Statistical analysis based on the model data indicates that AgI particle concentrations and temperature are the major factors controlling IWC and Z_e values at the target level. The depth from the seeding level also influences IWC and Z_e values as a deeper cloud provides a longer path for ice growth.

5. Based on data from the 2500 numerical experiments, a parameterization is developed using polynomial regression to estimate the minimum AgI particle concentration needed to detect the signature of glaciogenic cloud seeding, assuming there is sufficient liquid water for ice growth. The seeding temperature, pressure, Z_e values, and cloud depth from the seeding level are used as inputs to train the parameterization, and the AgI particle concentration is the output.

6. Application of this parameterization to a real case with natural precipitation suggests that seeding at about −15 °C requires the least amount of AgI to obtain a seeding signature exceeding the natural variability. Seeding at slightly colder or warmer temperatures may also produce a detectable signature but requires more AgI and supercooled liquid water. Seeding impact at temperatures warmer than −10 °C is unlikely to be detected in this case because it requires an extremely high concentration of AgI and an LWP exceeding 600 g m⁻². However, for non-precipitating clouds, seeding at temperatures warmer than −10 °C may produce detectable seeding signatures.

This study has several limitations:

• The results shown here only apply to mixed-phase stratiform clouds with relatively simple dynamics because we assumed relatively weak turbulence in the model. In clouds with stronger turbulence or convection, ice growth trajectories are more complicated; thus, a 3D model has to be used to investigate the seeding-induced signature under various ambient conditions (Xue et al., 2022; Hua et al., 2024).

• AgI released pyrotechnically from point sources on the ground or in the air (burn-in-place or ejectable flares, rockets, etc.) vary greatly in concentration. In fact, AgI particle concentrations in 3D models are typically depicted on a log scale rather than a linear scale (e.g., Xue et al., 2013b, 2022). Therefore, seeding operators have little control over AgI concentrations. However, as AgI disperses from a point source in the boundary layer or cloud turbulence, our study shows that it may cross a “sweet spot” where, under given cloud conditions, the seeding impact is optimally detectable.

• The parameterization developed in this study applies to airborne cloud seeding. For ground-based seeding, which is often used for orographic clouds, the AgI particles are mixed into clouds mainly through boundary layer turbulence. Boundary layer convection and a hydraulic jump in the lee may enhance the vertical dispersion of AgI particles (Jing et al., 2016). Therefore, to investigate ice nucleation and growth, it is important to resolve the vertical dispersion of AgI particles (Xue et al., 2013b), which is not considered in the 1D model presented in this study. The high-resolution LES model is a better choice for modeling the impact of ground-based cloud seeding (Xue et al., 2013b; Chu et al., 2014).

• In our study, it is expected that cloud seeding accounts for most of the ice mass in the seeding plume. The best radar seeding signatures come from clouds with no or very weak natural precipitation (Friedrich et al., 2020). In reality, natural snowfall may contribute significantly. It is difficult to quantitatively separate the precipitation attributed to cloud seeding from natural precipitation. Nevertheless, unambiguous seeding signatures in precipitating clouds can still be useful in studying the chain of physics of cloud seeding.

• The 1D model does not thermodynamically constrain the LWC available for glaciogenic seeding. With a limited LWC, a larger AgI concentration may reduce the radar reflectivity enhancement because more, but smaller, ice crystals will form compared to when a lower AgI concentration is used. Such a constraint is captured in a 3D model.

In short, the results shown in this study deepen our understanding of the relationships between AgI particle concentrations and Z_e under different cloud conditions. The parameterization has limitations, but it can be useful in seeding operations for providing a quick estimation of how much AgI particle concentration is needed to obtain an unambiguous seeding signature.