The impact of aerosol on cloud water: a heuristic perspective

Aerosol–cloud interactions modulate the role of clouds in Earth's climate. We derive, evaluate, and apply a simple model to understand aerosol-mediated cloud water adjustments in stratocumulus based on only two prognostic equations for the integrated cloud water L and droplet number concentration N. The model is solved numerically and analytically and agrees well with documented large-eddy-simulation data and satellite retrievals. A tight relationship between adjustments at low and high N is found, revealing the influence of non-precipitation processes (primarily entrainment) on adjustments in precipitating clouds. Furthermore, it is shown that adjustments in non-precipitating clouds tend to be positively biased by external L or N perturbations, while adjustments in precipitating clouds are barely susceptible. By deliberately reducing the complexity of the underlying system, this study constitutes a way forward to facilitate process-level understanding of cloud water adjustments.

1 Introduction

By constituting the nuclei on which cloud droplets form, aerosol substantially shapes the microphysical composition of clouds, their optical properties, and hence their role in Earth's climate. One important example is the ability of clouds to reflect incident solar radiation back to space, causing a negative (cooling) influence on Earth's radiation budget. While aerosol tends to increase cloud reflectance, this and other aerosol–cloud–climate interactions are only marginally understood (e.g., Boucher et al., 2013; Forster et al., 2021).

One metric to quantify aerosol–cloud–climate interactions is the susceptibility of the shortwave cloud albedo A to changes in the cloud droplet number concentration N (e.g., Platnick and Twomey, 1994). This susceptibility can be expressed as

$$\begin{array}{}\text{(1)}& S\equiv {\displaystyle \frac{\mathrm{d}\ln \left(A\right)}{\mathrm{d}\ln \left(N\right)}}={\displaystyle \frac{\mathrm{1}-A}{\mathrm{3}}}\left[\mathrm{1}+{\displaystyle \frac{\mathrm{5}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{d}\ln \left(L\right)}{\mathrm{d}\ln \left(N\right)}}\right],\end{array}$$

where the term $(\mathrm{1}-A)/\mathrm{3}\ge \mathrm{0}$ represents the fairly well understood increase in A with N at constant cloud water, commonly referred to as the Twomey effect (Twomey, 1974, 1977). This study will address the considerably less understood cloud water adjustments $\mathrm{d}\ln \left(L\right)/\mathrm{d}\ln \left(N\right)$ in the bracketed term. Depending on how the vertically integrated cloud water L changes with N, cloud water adjustments can increase, decrease, or even change the sign of S.

In earlier years, cloud water adjustments were mainly thought to be related to precipitation suppression, i.e., the increasingly less efficient production of precipitation by smaller cloud droplets, resulting in larger L for higher N, causing a larger S than anticipated from the Twomey effect alone (e.g., Albrecht, 1989). Later, it was recognized that the mixing of clouds with their environment (entrainment) increases for higher N, which causes L to decrease, resulting in a smaller or even negative S (e.g., Wang et al., 2003; Ackerman et al., 2004; Bretherton et al., 2007; Glassmeier et al., 2021). Together, these effects result in an increase in L for lower N, followed by a decrease for higher N. The commensurately more nuanced influence of cloud water adjustments on S has been retrieved from satellite observations of shallow cumulus and stratocumulus clouds (e.g., Gryspeerdt et al., 2019).

Large-eddy simulations (LESs) have become the primary tool to gain process-level understanding of cloud water adjustments. While LES estimates stem from the high-resolution representation of the underlying dynamics and cloud microphysics, they tend to be valid only for limited spatial domains and specific initial and boundary conditions (e.g., Ackerman et al., 2009; Glassmeier et al., 2021). On the other hand, satellite observations have become increasingly useful for an integrated view of aerosol–cloud–climate interactions, sampling a wealth of real-world data, but also for the inherent co-variability of aerosol and meteorology that confounds process-level understanding (e.g., Gryspeerdt et al., 2019; Mülmenstädt et al., 2024).

Aiming to combine the aforementioned integrated view with process-level insights, this paper will develop a heuristic model for cloud water adjustments in stratocumulus, a crucial cloud type in Earth's radiation budget (e.g., Wood, 2012). The foundations of this model will be laid out in Sect. 2, and it will be applied in Sect. 3. Basic sensitivities to model parameters are analyzed in Sect. 4. Section 5 addresses the variability of cloud water adjustments in externally perturbed systems, presenting a way forward to use this study's results when interpreting observed cloud water adjustment. The paper is summarized and concluded in Sect. 6.

2 Model formulation

The heuristic model is formulated using ideas that originated from satellite retrievals by Gryspeerdt et al. (2019) and the LES modeling by Hoffmann et al. (2020): their works showed that cloud water adjustments can be separated into two distinct regimes, which are dominated by precipitation at low N and thermodynamics at high N, respectively. Here, thermodynamics comprises the effects of entrainment, radiative cooling, and surface fluxes on L. Thus, we will refer to the underlying processes in those regimes as driven by precipitation or thermodynamics in the following. Moreover, we introduce the shorthand,

$$\begin{array}{}\text{(2)}& m\equiv {\displaystyle \frac{\mathrm{d}\ln \left(L\right)}{\mathrm{d}\ln \left(N\right)}},\end{array}$$

for the change in L with N. The optional subscripts h and l indicate limits for high and low N, respectively. The ∞ subscript marks (potentially prescribed) steady states.

The effects of precipitation and thermodynamics on the temporal change in L are represented as

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}L}{\mathrm{d}t}}& =-c_{\mathrm{1}}{\displaystyle \frac{L^{\mathrm{3}/\mathrm{2}}}{N}}+{\displaystyle \frac{L_{\mathrm{\infty },\mathrm{h}}\left(N\right)-L}{{\mathit{\tau }}_{\mathrm{t}}}}\\ & =-{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{L}{{\mathit{\tau }}_{\mathrm{p}}(L,N)}}+{\displaystyle \frac{L_{\mathrm{\infty },\mathrm{h}}\left(N\right)-L}{{\mathit{\tau }}_{\mathrm{t}}}},\end{array}\end{array}$$

whose terms will be described next. All variables, parameters, and derived parameters used in the heuristic model are summarized in Table 1.

The first term on the right-hand side of Eq. (3) represents a precipitation sink. The employed expression relates the cloud base rain rate to L and N. We express the precipitation sink by introducing a precipitation timescale

$$\begin{array}{}\text{(4)}& {\mathit{\tau }}_{\mathrm{p}}={\left|{\displaystyle \frac{\mathrm{d}}{\mathrm{d}L}}\left(-c_{\mathrm{1}}{\displaystyle \frac{L^{\mathrm{3}/\mathrm{2}}}{N}}\right)\right|}^{-\mathrm{1}}={\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{\mathrm{1}}{c_{\mathrm{1}}}}{\displaystyle \frac{N}{L^{\mathrm{1}/\mathrm{2}}}},\end{array}$$

where the term in parentheses is a more common representation of the cloud base rain rate, which has been assessed observationally and theoretically (e.g., Van Zanten et al., 2005; Kostinski, 2008). It has been argued that the exponents of L and N depend on the assumed sedimentation velocity and hence droplet size (Feingold et al., 2013). For simplicity, these dependencies are neglected here, as is evaporation below the cloud base.

The second term on the right-hand side of Eq. (3) depicts the charge/discharge to the thermodynamic carrying capacity of the system L_∞,h, which can also be interpreted as a steady-state L at high N, whose existence has been discussed by Hoffmann et al. (2020). For a given N, this term can be a sink to the L budget due to an excess in entrainment warming and drying, causing the cloud to evaporate ($L>L_{\mathrm{\infty },\mathrm{h}}$), or a source driven by longwave radiative cooling, leading to more condensation ($L<L_{\mathrm{\infty },\mathrm{h}}$), while the effect of surface fluxes is usually small (see Fig. 2 in Hoffmann et al., 2020). The timescale associated with this process is given by τ_t. The thermodynamic carrying capacity is derived from Eq. (2) and expressed as

$$\begin{array}{}\text{(5)}& L_{\mathrm{\infty },\mathrm{h}}=L_{\mathrm{0}}{\left({\displaystyle \frac{N}{N_{\mathrm{0}}}}\right)}^{m_{\mathrm{\infty },\mathrm{h}}},\end{array}$$

where m_∞,h determines how L_∞,h changes with N, while L₀ and N₀ are constant parameters.

Many studies (Fig. 1 in Glassmeier et al., 2021) have determined m_∞,h, and hence L_∞,h, for high N, which excludes the effects of precipitation present at low N. Here, L_∞,h is applied to all N with the same m_∞,h. This idea is motivated by the insight that the temporal change in L due to thermodynamics (entrainment, radiative cooling, and surface fluxes) exhibits a sensitivity to N that seems independent of the presence of precipitation. This was initially shown in Fig. 3 of Hoffmann et al. (2020) but is recreated in a more useful way in the Supplement (Fig. S1). Thus, the same adjustment of thermodynamic processes at high N (i.e., m_∞,h) is assumed to persist for low N. Specifically, $m_{\mathrm{\infty },\mathrm{h}}<\mathrm{0}$ due to the increase in entrainment with N (Wang et al., 2003; Ackerman et al., 2004; Bretherton et al., 2007).

The model parameters have been chosen to match the ensemble LES modeling of Glassmeier et al. (2021), who studied cloud water adjustments in stratocumulus clouds. They determined τ_t=9 h and $m_{\mathrm{\infty },\mathrm{h}}=-\mathrm{0.64}$ using an emulator. Based on their Fig. 3a, we selected $L_{\mathrm{0}}=\mathrm{90}\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}$ and $N_{\mathrm{0}}=\mathrm{100}{\mathrm{cm}}^{-\mathrm{3}}$ to match their L_∞ for high N and derived $c_{\mathrm{1}}=\mathrm{7600}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{kg}}^{-\mathrm{1}/\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ to match their L_∞ for low N. Note that this set of parameters should be seen as one potential realization of cloud water adjustments. The sensitivity to these parameters will be analyzed in Sect. 4. Note that to fit the aforementioned ensemble LESs, c₁ is about half the value observed by Van Zanten et al. (2005), necessary to account for the subadiabaticity of L naturally included in observations but not captured in Eq. (3). Further, note that the thermodynamic charge/discharge in Eq. (3) is driven by the linear difference $L_{\mathrm{\infty },\mathrm{h}}-L$, without further justification. A model driven by the logarithmic difference $\ln \left(L_{\mathrm{\infty },\mathrm{h}}\right)-\ln \left(L\right)$ does not align well with the ensemble LES modeling of Glassmeier et al. (2021) but is briefly discussed in the Supplement (Sect. S1 and Fig. S2).

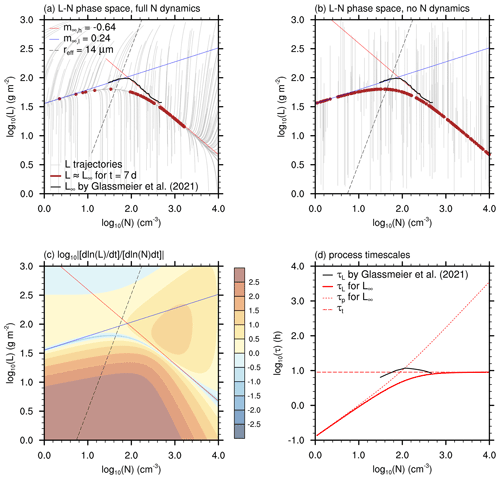
Figure 1 Panel (a) and (b) show trajectories of individual simulations (gray lines) in an L–N phase space with and without N dynamics, respectively. Brown dots indicate the location of simulations after 7 d. The quotient of the relative motion in L and N directions is shown in panel (c). These panels are overlaid with the corresponding ensemble LES reference by Glassmeier et al. (2021) (thick black line), the slopes $m_{\mathrm{\infty },\mathrm{l}}=\mathrm{0.24}$ and $m_{\mathrm{\infty },\mathrm{h}}=-\mathrm{0.64}$ (blue and red lines, respectively), and the 14 µm cloud top effective droplet radius (dashed black line). Panel (d) shows the process timescales τ_t, τ_p and τ_L (red lines), as well as ensemble LES reference by Glassmeier et al. (2021) (black line).

For completeness, a prognostic equation for N, loosely based on Baker and Charlson (1990), is solved. The expression

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathrm{d}N}{\mathrm{d}t}}=c_{\mathrm{2}}N\left(-c_{\mathrm{1}}{\displaystyle \frac{L^{\mathrm{3}/\mathrm{2}}}{N}}\right)-c_{\mathrm{3}}{N}^{\mathrm{2}}+S_{\mathrm{N}}\end{array}$$

combines sinks of N by precipitation (first term on the right-hand side) and Brownian coagulation (second term), as well as a source S_N (third term) that could represent, e.g., the emission of sea spray. Here, we choose $c_{\mathrm{3}}={\mathrm{10}}^{-\mathrm{15}}{\mathrm{m}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$ (e.g., Seinfeld and Pandis, 2016) and $c_{\mathrm{2}}=\mathrm{3}{\mathrm{m}}^{\mathrm{2}}{\mathrm{kg}}^{-\mathrm{1}}$, which can be considered the upper limit for c₂ (Wood, 2006). Nonetheless, the effect of precipitation scavenging steered by c₂ on the steady-state behavior of L is small, as we will show next.

Table 1 The first block states variables predicted by the heuristic model, the second parameters prescribed for the heuristic model, and the third derived parameters used in the heuristic model.

3 An initial assessment

Results from integrating Eqs. (3) and (6) for 7 d with a time step Δt=1 min are shown in Fig. 1a. The source S_N has been neglected for simplicity. In total, 250 simulations are conducted, with initial L and N randomly placed between 1 and 1000 g m⁻², as well as 1 and 100 000 cm⁻³, while only results for $N\le \mathrm{10}\mathrm{000}{\mathrm{cm}}^{-\mathrm{3}}$ are shown. Note that while $N<\mathrm{10}{\mathrm{cm}}^{-\mathrm{3}}$ are frequently observed in stratocumulus, they tend to not exhibit $N>\mathrm{1000}{\mathrm{cm}}^{-\mathrm{3}}$ (e.g., Wood, 2012). This discrepancy is irrelevant to this study that focuses on the change of L with N, i.e., the slope m, which is constant for such high N, as we will see below.

The individual simulations (gray lines in Fig. 1a) show substantial motion in the L direction, while motion in the N direction is only relevant at low $N<\mathrm{100}{\text{cm}}^{-\mathrm{3}}$ due to precipitation scavenging and at high $N>\mathrm{1000}{\text{cm}}^{-\mathrm{3}}$ due to Brownian coagulation. Although S_N=0 and hence $\text{d}N/\text{d}t<\mathrm{0}$ everywhere in the phase space, a stable population of simulations persists between these limits for at least the 7 d of simulated time considered (brown dots). (Baker and Charlson (1990) showed how the consideration of a S_N>0 could offset the losses in N, causing N_∞ steady states.) In the L direction, these simulations approach a steady-state L_∞ that agrees well with the ensemble LES reference by Glassmeier et al. (2021) (black line) and especially its slopes m_h and m_l toward high and low N. As we will show below, these slopes agree well with the heuristic model's steady-state slopes $m_{\mathrm{\infty },\mathrm{h}}=-\mathrm{0.64}$ and $m_{\mathrm{\infty },\mathrm{l}}=\mathrm{0.24}$ (red and blue lines, respectively). The only notable difference to the LES reference is the more gentle transition between the two slopes, which might be due to the continuous representation of precipitation in Eq. (3), while the process of autoconversion, i.e., the initiation of precipitation, is a discontinuous process that only allows precipitation to form once a certain droplet size is exceeded (Kessler, 1969). This threshold is illustrated by the dashed black line indicating a cloud top effective droplet radius of 14 µm that is often used to discriminate precipitating from non-precipitating clouds and scales with $(L/N^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{6}}$ (e.g., Gerber, 1996; Goren et al., 2019).

Solving only Eq. (3), i.e., without the N dynamics considered by Eq. (6), the steady-state L_∞ exhibits very similar features to the previously discussed solution (Fig. 1b). Most importantly, the slopes and hence the cloud water adjustments agree, which is why N dynamics are neglected in the following. A reason for the apparent independence of cloud water adjustments from N dynamics is shown in Fig. 1c, which shows the relative motion of the system, $\left|\left[\mathrm{d}\ln \right(L)/\mathrm{d}t]/\left[\mathrm{d}\ln \right(N)/\mathrm{d}t]\right|=\left|\mathrm{d}\ln \left(L\right)/\mathrm{d}\ln \left(N\right)]\right|$. Relative changes in L exceed changes in N almost everywhere in the phase space (warm colors). Changes in N dominate primarily around the steady state (cold colors), where $\mathrm{d}L/\mathrm{d}t=\mathrm{0}$ per definition. Brownian coagulation widens this region around the steady state for high N, while precipitation scavenging creates another region where N dynamics dominate at low N but for L≫L_∞. Although precipitation scavenging is often reported for low N with potential implications for cloud water adjustments (e.g., Gryspeerdt et al., 2022), the L_∞ values investigated here are too small to be affected by stronger N dynamics, thus allowing us to neglect them for now. Future work might want to include a prognostic equation for the cloud fraction, which tends to be smaller than unity for low N, resulting in higher in-cloud L than predicted by Eq. (3) and thus stronger precipitation scavenging by Eq. (6).

To further understand the steady-state behavior of L and its slope m, we investigate $\mathrm{d}L/\mathrm{d}t=\mathrm{0}$ of Eq. (3) analytically. A few algebraic rearrangements yield

$$\begin{array}{}\text{(7)}& L_{\mathrm{\infty }}=L_{\mathrm{\infty },\mathrm{h}}{\left(\mathrm{1}+c_{\mathrm{1}}{\mathit{\tau }}_{\mathrm{t}}{\displaystyle \frac{L_{\mathrm{\infty }}^{\mathrm{1}/\mathrm{2}}}{N}}\right)}^{-\mathrm{1}}=L_{\mathrm{\infty },\mathrm{h}}{\left(\mathrm{1}+{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{t}}}{{\mathit{\tau }}_{\mathrm{p}}}}\right)}^{-\mathrm{1}}.\end{array}$$

The term in parentheses describes the deviation of L_∞ from L_∞,h due to precipitation, and its strength depends on the ratio of the process timescales τ_t and τ_p. Figure 1d shows the N dependence of τ_t; τ_p; and the timescale of all L processes, ${\mathit{\tau }}_{\mathrm{L}}={\left({\mathit{\tau }}_{\mathrm{t}}^{-\mathrm{1}}+{\mathit{\tau }}_{\mathrm{p}}^{-\mathrm{1}}\right)}^{-\mathrm{1}}$, in the steady state. While τ_t (long-dashed red line) is constant as prescribed, a strong increase in τ_p (short-dashed red line) with N is shown, indicating that precipitation only affects L_∞ for sufficiently small N. Thus, τ_L (continuous red line) follows τ_p for low N and τ_t for high N. τ_L from the ensemble of LESs of Glassmeier et al. (2021) (black line) captures this behavior only partially, which might be related to the difficulty in determining multiple derivatives from LES data. Note that we introduce $N\approx \mathrm{100}{\mathrm{cm}}^{-\mathrm{3}}$ as the boundary between the precipitation- and thermodynamics-dominated and hence low and high N parts of the phase space, as it corresponds to the L_∞ inflection point in the heuristic model and LES ensemble data of Glassmeier et al. (2021) (Fig. 1a and b).

The logarithmic derivative of Eq. (7) with respect to ln (N) gives

$$\begin{array}{}\text{(8)}& m_{\mathrm{\infty }}={\displaystyle \frac{m_{\mathrm{\infty },\mathrm{h}}}{\mathrm{1}+\frac{{\mathit{\tau }}_{\mathrm{t}}}{{\mathit{\tau }}_{\mathrm{p}}}}}+{\displaystyle \frac{\frac{\mathrm{2}}{\mathrm{3}}\left(m_{\mathrm{\infty },\mathrm{h}}+\mathrm{1}\right)}{\mathrm{1}+\frac{{\mathit{\tau }}_{\mathrm{p}}}{{\mathit{\tau }}_{\mathrm{t}}}}},\end{array}$$

with more details provided in the Supplement (Sect. S2). m_∞ shows that for τ_t≪τ_p ($N\gg \mathrm{100}{\mathrm{cm}}^{-\mathrm{3}}$), thermodynamics dominate cloud water adjustments via m_∞,h. For τ_p≪τ_t ($N\ll \mathrm{100}{\mathrm{cm}}^{-\mathrm{3}}$), m_∞ approaches

$$\begin{array}{}\text{(9)}& m_{\mathrm{\infty },\mathrm{l}}={\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}(m_{\mathrm{\infty },\mathrm{h}}+\mathrm{1}),\end{array}$$

which combines the effects of thermodynamic adjustments, m_∞,h, with a precipitation adjustment of $\mathrm{2}/\mathrm{3}$. This behavior is captured well in Fig. 1a and b, where the slopes $m_{\mathrm{\infty },\mathrm{h}}=-\mathrm{0.64}$ (red line) and $m_{\mathrm{\infty },\mathrm{l}}=\mathrm{0.24}$ (blue line) overlap with the model data.

Additionally, the relationship (Eq. 9) constitutes a way to assess the consistency of cloud water adjustments derived for low and high N. Strictly speaking, the m_∞,h derived from m_∞,l via Eq. (9) only represents the thermodynamic adjustments at low N, while the thermodynamic adjustments at high N might differ. Nonetheless, the cloud water adjustments of m_l=0.21 and $m_{\mathrm{h}}=-\mathrm{0.64}$ determined from the ensemble of LESs by Glassmeier et al. (2021) agree well with Eq. (9). Deviations from Eq. (9) can indicate aerosol–meteorology co-variability commonly found in maritime and continental air masses (e.g., Brenguier et al., 2003) but absent in the LESs of Glassmeier et al. (2021) by design. Moreover, deviations can hint at changes in the sensitivity of thermodynamic processes to N, e.g., the stabilizing effect of evaporating precipitation on boundary-layer dynamics and hence entrainment at low N, which naturally vanishes for higher N due to decreasing precipitation (e.g., Nicholls, 1984; Caldwell et al., 2005; Wood, 2007; Hoffmann et al., 2023).

4 Sensitivity to model parameters

Now, the dependence of model (3) on the parameters τ_t, c₁, L₀, and m_∞,h is tested in Fig. 2a to d, showing L after 7 d of integration as a function of N. The dependence on N₀ is neglected here, as it is analogous to L₀ via its influence on L_∞,h. If τ_t, c₁, L₀ or m_∞,h is not varied, their aforementioned default is used. The default case is indicated by gray dots, while setups with varied parameters are highlighted by colored dots. Time stepping and initialization follow the previously outlined procedure.

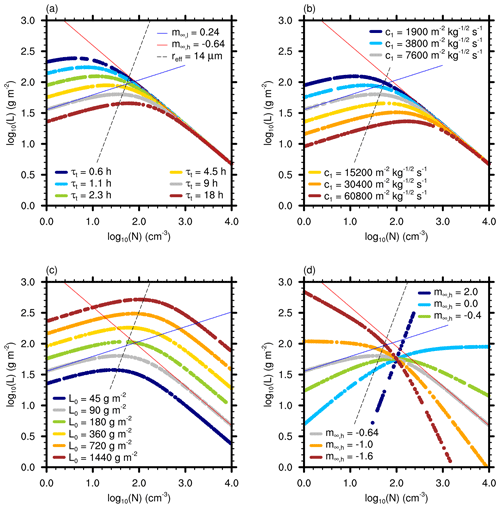
Figure 2 L after 7 d as a function of N for variations in (a) τ_t, (b) c₁, (c) L₀, and (d) m_∞,h (colored dots). The default configuration is differentiated by gray dots. Plots are overlaid with $m_{\mathrm{\infty },\mathrm{l}}=\mathrm{0.24}$ and $m_{\mathrm{\infty },\mathrm{h}}=-\mathrm{0.64}$ (blue and red lines) and the 14 µm cloud top effective droplet radius (dashed black line).

Figure 2a shows that shorter τ_t force L to follow L_∞,h for lower N compared to the default case. The commensurately higher L at low N is caused by a faster recharge of precipitation losses by thermodynamics, while L at high N is unchanged. As expected from Eq. (8), m_h and m_l approach the slopes m_∞,h and m_∞,l for all τ_t. However, the transition between m_h and m_l is shifted depending on the ratio ${\mathit{\tau }}_{\mathrm{p}}/{\mathit{\tau }}_{\mathrm{t}}$. A similar influence is visible from variations in the precipitation constant c₁, which determines the strength of precipitation losses at small N (Fig. 2b). Note that the value of c₁ closest to the observations by Van Zanten et al. (2005) (yellow dots) results in stronger precipitation losses than in the ensemble LESs of Glassmeier et al. (2021) (gray dots).

L changes proportionally to L₀ for all N, with its slopes matching m_∞,l and m_∞,h as before (Fig. 2c). For all L₀, the maximum L agrees well with the cloud top effective droplet radius of 14 µm (dashed line), marking the transition between precipitating and non-precipitating clouds. Note that this is not the case for the previously discussed sensitivities on τ_t and c₁ (Fig. 2a and b). This indicates that the usefulness of the cloud top effective radius threshold for separating the precipitating and non-precipitating branches of L depends on τ_t and c₁.

The sensitivity to m_∞,h is displayed in Fig. 2d. As indicated by Eq. (8), the slopes for high and low N are commensurate with the prescribed values m_∞,h and the resultant m_∞,l. Nonetheless, we would like to highlight a few interesting values that m_∞,h may assume, even though $m_{\mathrm{\infty },\mathrm{h}}>\mathrm{0}$ is likely unphysical due to the negative impact of increased entrainment on L at higher N. For $m_{\mathrm{\infty },\mathrm{h}}=\mathrm{2.0}$ (dark-blue dots), cloud water adjustments are the same for all N ($m_{\mathrm{\infty },\mathrm{l}}=m_{\mathrm{\infty },\mathrm{h}}$), while any $m_{\mathrm{\infty },\mathrm{h}}>\mathrm{2.0}$ will result in $m_{\mathrm{\infty },\mathrm{l}}<m_{\mathrm{\infty },\mathrm{h}}$. Coincidentally, $m_{\mathrm{\infty },\mathrm{h}}=\mathrm{2.0}$ matches the slope of the effective radius (dashed line). If $m_{\mathrm{\infty },\mathrm{h}}=-\mathrm{1.0}$ (orange dots), cloud water adjustments vanish at low N ($m_{\mathrm{\infty },\mathrm{l}}=\mathrm{0}$), while they vanish at high N for $m_{\mathrm{\infty },\mathrm{h}}=\mathrm{0.0}$ (light-blue dots). Sufficiently strong negative cloud water adjustments can offset the Twomey effect and thus cause a decrease in cloud albedo with increasing N, i.e., S<0 according to Eq. (1). Obviously, $m_{\mathrm{\infty },\mathrm{h}}<-\mathrm{0.4}$ (green dots) causes negative S for high N, but $m_{\mathrm{\infty },\mathrm{h}}<-\mathrm{1.6}$ (brown dots) establishes negative S for all N by also guaranteeing that $m_{\mathrm{\infty },\mathrm{l}}<-\mathrm{0.4}$.

5 A perturbed system

Building on the previous analysis of the unperturbed steady-state behavior of the model (Eq. 3), we would now like to understand its susceptibility to external perturbations in N and L. N perturbations exist at various temporal and spatial scales, covering highly localized aerosol emissions such as ship tracks to phenomena on regional scales like volcanic eruptions. At the same time, these perturbations might exhibit correlations with L.

In this study, perturbations are modeled as a Bernoulli process and are applied with the probability $\mathrm{\Delta }t/{\mathit{\tau }}_{\mathrm{prt}}$ evaluated for every time step of the model. Here, τ_prt is the perturbation timescale, which is varied from 20 min to 2 weeks. If a perturbation takes place, ln (N) is modified by adding a Δln (N)_prt=ξσ_prt, where ξ is a normally distributed random number with zero mean and unity standard deviation, modified by σ_prt=0.5, 1.0, or 2.0. At the same time, a Δln (L)=m_prtΔln (N)_prt is added to ln (L), with $m_{\mathrm{prt}}=-\mathrm{1.0}$, 0.0, or 1.0 to introduce correlations in the perturbation. Note that τ_prt, σ_prt, and m_prt are chosen to elucidate the general sensitivity of the system and not to match a realistic case. However, the resultant variability is similar to satellite retrievals (e.g., Gryspeerdt et al., 2019) if sufficiently slow perturbations are applied (Fig. S3). We use the default model parameters described above. Time stepping and initialization follow the previously outlined procedure. No N dynamics other than the perturbation are considered. Results are averaged over the last 2 d of the 7 d simulations. In total, 100 000 simulations are executed for each configuration.

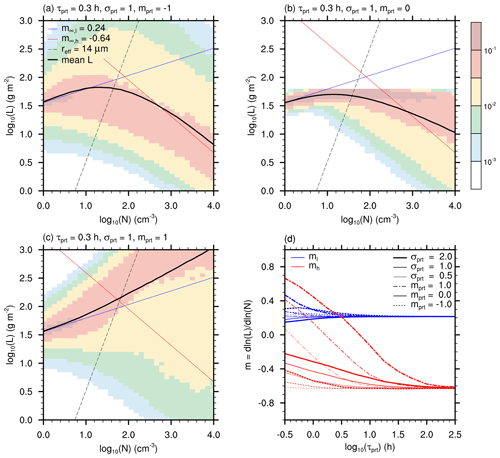
Figure 3 Joint L–N histograms (opaque colors) and mean ln (L) (thick black line) for perturbations in L and N for τ_prt=0.3 h, σ_prt=1.0 with (a) $m_{\mathrm{prt}}=-\mathrm{1}$, (b) 0.0, and (c) 1.0. Plots are overlaid with $m_{\mathrm{\infty },\mathrm{l}}=\mathrm{0.24}$ and $m_{\mathrm{\infty },\mathrm{h}}=-\mathrm{0.64}$ (blue and red lines) and the 14 µm cloud top effective droplet radius (dashed black line). Note that the histograms are normalized such that the integral over each N column yields 1 (Gryspeerdt et al., 2019). Panel (d) shows the fitted slopes m_l (blue lines) and m_h (red lines) for σ_prt=0.5 (thin lines), 1.0 (medium lines), and 2.0 (thick lines) and $m_{\mathrm{prt}}=-\mathrm{1.0}$ (dashed lines), 0.0 (continuous lines), and 1.0 (dash-dotted lines).

Figure 3a to c show example distributions of L and N for $m_{\mathrm{prt}}=-\mathrm{1.0}$, 0.0, and 1.0, respectively, with the same σ_prt=1.0 and τ_prt=0.3 h for all cases. The short τ_prt has been chosen to highlight some processes that are more subtle at larger τ_prt (see also Fig. S3 for τ_prt=10 h). For high N, one sees that the variability in L for a given N is proportional to the difference between m_prt and m_∞,h, which determines the time required for thermodynamics to counter a perturbation in L. Because thermodynamic charge/discharge is linear in L and the perturbations are applied in ln (L) space, more time is required to deplete a positive L perturbation than a negative. This asymmetric response results in slightly higher mean L (black lines) than in the unperturbed case, and adjustments appear less negative than the prescribed ($m_{\mathrm{h}}>m_{\mathrm{\infty },\mathrm{h}}$).

A similar effect is also visible for low N. As long as L is sufficiently affected by the perturbation ($m_{\mathrm{prt}}=-\mathrm{1.0}$ and 1.0, Fig. 3a and c), larger L values are possible due to the aforementioned asymmetric response by thermodynamics to the perturbation. However, precipitation removes positively perturbed L more efficiently for lower N than for larger, causing adjustments to appear more positive than in the unperturbed case ($m_{\mathrm{l}}>m_{\mathrm{\infty },\mathrm{l}}$). For perturbations in N only (m_prt=0.0, Fig. 3b), the mean L increases more gently than in the unperturbed cases, which results in $m_{\mathrm{l}}<m_{\mathrm{\infty },\mathrm{l}}$. This is due to stronger precipitation for negative N perturbations, removing any excess in L more quickly than thermodynamics can increase L for positive N perturbations.

Figure 3d shows m_l (blue lines) and m_h (red lines) as a function of τ_p. The slopes have been determined by linear regression from the mean ln (L), using the respective ranges $\mathrm{1}{\mathrm{cm}}^{-\mathrm{3}}<N<\mathrm{5}{\mathrm{cm}}^{-\mathrm{3}}$ and $\mathrm{1000}{\mathrm{cm}}^{-\mathrm{3}}<N<\mathrm{10}\mathrm{000}{\mathrm{cm}}^{-\mathrm{3}}$, which have been chosen to minimize the influence of the transition zone between the slopes.

The strongest impact of perturbations on m_h (red lines) is visible for m_prt=1.0, and it scales with σ_prt as one would expect. Interestingly, all tested perturbations cause $m_{\mathrm{h}}>m_{\mathrm{\infty },\mathrm{h}}$, but it is expected that more strongly negative perturbations ($m_{\mathrm{prt}}\ll -\mathrm{1.0}$) could cause a $m_{\mathrm{h}}<m_{\mathrm{\infty },\mathrm{h}}$. Nonetheless, the influence of perturbations vanishes for τ_prt≫τ_t, i.e., when thermodynamic charge/discharge becomes faster than the perturbation. Similarly, m_l (blue lines) is not affected when τ_prt≫τ_p. Because τ_p≪τ_t for low N (see Fig. 1d), m_l is much less susceptible to perturbations than m_h. Overall, m_l is closer to $m_{\mathrm{\infty },\mathrm{l}}=\mathrm{0.24}$ than m_h to $m_{\mathrm{\infty },\mathrm{h}}=-\mathrm{0.64}$ for most tested configurations. Thus, m_l might constitute a way to constrain the unperturbed m_∞,h via Eq. (9), while m_h might not necessarily enable conclusions on m_∞,h as long as perturbations cannot be ruled out.

6 Summary and conclusions

Understanding aerosol–cloud interactions is crucial for constraining the effects of aerosols on the climate. In this study, a heuristic model to understand aerosol-mediated cloud water adjustments in stratocumulus has been derived, evaluated, and applied. The model has been developed to predict the evolution of cloud water path L as a function of the cloud droplet number concentration N. Although the concurrent evolution in N can have an impact on the evolution of L (e.g., Gryspeerdt et al., 2022), it has been neglected for most of this study, and N has been considered a mere parameter. The reason for this is that the relatively small steady-state L to which the system converged does not enable substantial changes in N by precipitation scavenging.

For the evolution of L, two processes have been considered: (i) the removal of L by precipitation and (ii) changes in L by thermodynamics, i.e., the integrated effect of entrainment, radiation, and surface fluxes. The analytical and numerical analysis of the prognostic equation for L shows that it represents the development of two distinct slopes $m=\mathrm{d}\ln \left(L\right)/\ln \left(N\right)$. One is dominated by precipitation at low N and the other by thermodynamics at high N, which is in agreement with previous studies using satellite retrievals (e.g., Gryspeerdt et al., 2019) and large-eddy simulations (LESs) (e.g., Hoffmann et al., 2020; Glassmeier et al., 2021). The study finds that these slopes are intimately related via

$$m_{\mathrm{l}}={\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}(m_{\mathrm{h}}+\mathrm{1}),$$

showing that precipitation adjustments at low N, i.e., m_l, are partially controlled by the thermodynamic adjustments dominating at high N, i.e., m_h. Thus, this relationship implicitly assumes the same thermodynamic adjustments m_h for all N.

The slopes determined from an ensemble of LESs (Glassmeier et al., 2021) obey the aforementioned relationship between m_l=0.21 and $m_{\mathrm{h}}=-\mathrm{0.64}$ well. However, this LES ensemble did not include aerosol–meteorology co-variability by design and hence justifies the use of the same thermodynamic adjustments m_h for all N. Observed values for m_l are between 0.1 and 0.4 (e.g., Christensen and Stephens, 2011; Gryspeerdt et al., 2019; Possner et al., 2020), which would require m_h to vary between −0.9 and −0.4 to follow the aforementioned relationship. But these values only barely overlap with the observed range for m_h between −0.2 and −0.4 (e.g., Christensen and Stephens, 2011; Gryspeerdt et al., 2019; Possner et al., 2020). This discrepancy indicates stronger thermodynamic adjustments at low N that transition into weaker thermodynamic adjustments at high N, suggesting that m_h should be a function of N. Note that any piecewise constant m_h obeys the aforementioned relationship with m_l, making it possible to use different m_h for low and high N in the proposed framework.

Aerosol–meteorology co-variability could be an explanation for this N dependency. However, we would like to emphasize that this aerosol–meteorology co-variability does not have to be exogenous (e.g., differences in continental and maritime air, e.g., Brenguier et al., 2003) but could be created by the analyzed system endogenously (e.g., the stabilizing effect of evaporating precipitation on boundary-layer dynamics and hence entrainment, e.g., Nicholls, 1984; Caldwell et al., 2005; Wood, 2007; Hoffmann et al., 2023). Quantifying the influence of aerosol–meteorology co-variability on the relationship between m_l and m_h constitutes an interesting way to continue this study and to deepen process-level understanding of aerosol–cloud–climate interactions.

Another explanation for the weaker observed m_h is external perturbations affecting N and L. Our results show that thermodynamic adjustments are sensitive to perturbations with timescales of a few tens of hours or less, causing m_h to be weaker than in unperturbed simulations, i.e., to be closer to the aforementioned observations, while m_l is barely affected (cf. Fig. 3d).

To constrain the role of aerosols and clouds in the climate system, these perturbations and their biases have to be given due consideration. At the same time, eliminating the effects of perturbations is similarly important for a deeper process-level understanding of cloud water adjustments. Simple models like the one developed here seem to be a useful approach to condense the wealth of theoretical, modeling, and observational knowledge gained so far. Together, this strengthens the need to combine top-down and bottom-up approaches to advance our understanding of aerosol–cloud–climate interactions (e.g., Mülmenstädt and Feingold, 2018; Glassmeier et al., 2019).