The impact of quasi-biennial oscillation (QBO) disruptions on diurnal tides over the low- and mid-latitude mesosphere and lower thermosphere (MLT) region observed by a meteor radar chain

A quasi-biennial oscillation (QBO) disruption is a very rare phenomenon in which QBO westward wind is temporarily interrupted by the occurrence of a band of westward wind in the tropical stratosphere. This phenomenon is important as it could greatly affect the global atmospheric circulation, especially in the mesosphere. Past observational and modelling studies have shown the QBO varying mesospheric diurnal tide, but the mechanism is still not fully understood. In this study, we report on the strong response of mesospheric diurnal tides to the two QBO disruptions that occurred in 2015–2016 and 2019–2020 and their possible mechanisms. The diurnal tidal winds are observed by a meteor radar chain, consisting of meteor radars located at Kunming (25.6° N, 103.8° E), Wuhan (30.5° N, 114.2° E), Mengcheng (33.4° N, 116.5° E), Beijing (40.3° N, 116.2° E), and Mohe (53.5° N, 122.3° E) in China. These observations provide clear evidence that mesospheric diurnal tides are unusually weakened (by ∼ −6 m s⁻¹) during these QBO disruptions, over Kunming, Wuhan, Mengcheng, and Beijing. Using the Specific Dynamics version of the Whole Atmosphere Community Climate Model with thermosphere and ionosphere extension (SD-WACCM-X) and the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 (ERA5) dataset, the analysis indicates that the QBO wind affects mid-latitude mesospheric diurnal tides by modulating both the solar radiative absorption by subtropical stratospheric ozone (∼ 5 to 0.5 hPa) and the tidal–gravity wave interaction in the mesosphere (∼ 60 to 100 km). Thus, these unexpected QBO disruptions provide an opportunity to better understand the coupling between climate change and middle-atmospheric dynamics.

1 Introduction

Atmospheric tides are global-scale atmospheric oscillations with periods that are the harmonics of a solar day (Chapman and Lindzen, 1970). The diurnal tides (24 h period) are dominant modes that have been extensively studied. Numerous studies have reported interannual variabilities in diurnal tides (Pancheva et al., 2020; Davis et al., 2013; Hagan et al., 1999; Laskar et al., 2016; Lieberman et al., 2004; Lieberman, 1997; He et al., 2024). The interannual variability in these tides is mainly attributed to the 11-year solar cycle (Sun et al., 2022), the El Niño–Southern Oscillation (ENSO; Cen et al., 2022; Lieberman et al., 2007), and the quasi-biennial oscillation (QBO; Davis et al., 2013; Hagan et al., 1999; Laskar et al., 2016; Salinas et al., 2023).

The QBO in the tropical stratosphere is the dominant mode of interannual variability in the zonal mean zonal wind in the pressure range of 5–100 hPa; it consists of the descent of alternating eastward and westward winds with a period of approximately 20–30 months (Ebdon, 1960; Reed et al., 1961; Andrews et al., 1987). Theory states that the tropical stratospheric QBO is driven by upward propagating equatorial planetary waves and gravity waves (GWs) via momentum deposition (Lindzen and Holton, 1968; Plumb and McEwan, 1978; Baldwin et al., 2001). The QBO can strongly modulate stratospheric dynamic processes such as the ozone transport from tropical to high-latitude regions (Hampson and Haynes, 2006; Holton and Tan, 1980); in addition to the stratosphere, the QBO modulates deep convection in the troposphere (Collimore et al., 2003) and the Madden–Julian oscillation (Zhang and Zhang, 2018) as well as the propagation of atmospheric tides (Davis et al., 2013; Hagan et al., 1999; Laskar et al., 2016), planetary waves (Andrews et al., 1987), and GWs (Geller et al., 2016). By modulating the atmospheric waves that propagate vertically from the troposphere to the mesosphere, the QBO signature can reach higher altitudes and play a significant role in middle-atmospheric dynamics. For example, the QBO is clearly evident in low-latitude mesospheric winds (e.g., Vincent et al., 1998) and OH (∼ 85 km) and OI (∼ 96 km) nightglows (e.g., Reid et al., 2014), and the impact of the QBO on atmospheric tides is an important dynamic process.

In the past, several studies have reported the QBO variabilities of tides in the mesosphere and lower thermosphere (MLT) region. Vincent et al. (1998) reported a clear QBO-like variability in diurnal tides over Adelaide (35° S, 138° E) observed by long-term medium-frequency (MF) radars. Using the numerical spectral model (NSM), Mayr and Mengel (2005) suggested that the interannual variability in mesospheric diurnal tides is generated by the QBO possibly due to the momentum deposition of GWs. Using meteor-radar-based winds over Andenes (69° N, 16° E) and Juliusruh (54° N, 13° E), Laskar et al. (2016) reported that mesospheric semidiurnal tides are enhanced during the QBO eastward phase (QBOE) and suppressed during the QBO westward phase (QBOW). These authors suggested that the filtering effect of the QBO zonal wind on planetary waves and the interaction between tides and planetary waves imprint the QBO signature on mesospheric tides. Pramitha et al. (2021) suggested that the QBO variation in mesospheric diurnal tides at low latitudes is associated with ozone variability at the QBO scale. There are three primary theories to explain the observed QBO signature in mesospheric diurnal tides. These are based on GW momentum deposition, filtering effect of the zonal mean flow, and stratospheric ozone heating. However, existing observational evidence cannot conclusively support these conjectures, so the mechanism of this process is still unclear.

During the 2015–2016 winter, a very rare phenomenon occurred in the tropical stratosphere in the form of the temporarily interrupted QBO eastward wind by a band of developing westward wind; this phenomenon is called the QBO disruption (Osprey et al., 2016; Newman et al., 2016; Coy et al., 2017; Kang et al., 2020; He et al., 2022). Several studies suggested that this phenomenon is forced by anomalously enhanced westward equatorial Rossby waves (Osprey et al., 2016; Newman et al., 2016). Barton and McCormack (2017) suggested that an extreme El Niño event induces the QBO disruption by weakening the lower stratospheric subtropical westward jet. Pramitha et al., 2021) first reported a clearly disrupted QBO signature in low-latitude mesospheric diurnal tides observed by Tirupati (13.63° N, 79.4° E) meteor radar. However, the extreme El Niño event during November 2015–January 2016 also suppressed the mesospheric diurnal tides (e.g., Cen et al., 2022); therefore, the impact of the disrupted QBO on mesospheric diurnal tides is still poorly understood.

Unexpectedly, the QBO was interrupted again in the 2019–2020 winter with lower El Niño anomalies (Li et al., 2023; Kang and Chun, 2021; Kang et al., 2022), providing a valuable opportunity to further understand the connection between stratospheric QBO disruptions and mesospheric diurnal tides. In addition, the stratospheric QBO can strongly modulate global circulation from the tropics to the poles, but there are few reports on how QBO disruptions affect the mid-latitude mesospheric dynamics. In this regard, this study reports the impacts of the 2015–2016 and 2019–2020 QBO disruptions on mid-latitude mesospheric diurnal tides observed by a meteor radar chain, consisting of five meteor radars located at Kunming (25.6° N, 103.8° E), Wuhan (30.5° N, 114.2° E), Beijing (40.3° N, 116.2° E), and Mohe (53.5° N, 122.3° E). The ERA5 reanalysis dataset and the Specific Dynamics version of the Whole Atmosphere Community Climate Model with thermosphere and ionosphere extension (SD-WACCM-X) simulations are also used to determine the possible mechanism responsible for the connection between tropical stratospheric QBO disruptions and mid-latitude mesospheric diurnal tides. Section 2 provides the data and methods employed in this study; Sect. 3 presents the results; and the discussion and conclusions are provided in Sects. 4 and 5, respectively.

2 Data and methodology

2.1 Meteor radars

Meteor radars are used to calculate the horizontal wind over Mohe, Beijing, Mengcheng, Wuhan, and Kunming. Table 1 summarizes the basic system parameters, geographic coordinates, and observational time periods for the meteor radars used in this study. Figure 1 presents the geographic locations of these meteor radars and the variability in the QBO magnitude with latitude. These meteor radars are from the ATRAD meteor detection radar (MDR) series (Li et al., 2018; Holdsworth et al., 2004; Yi et al., 2019; Zhou et al., 2022). The meteor radars located at Mohe, Beijing, and Wuhan belong to the Institute of Geology and Geophysics, Chinese Academy of Sciences (IGGCAS), which is a part of the Chinese Meridian Project and STERN (the Solar-Terrestrial Environment Research Network). The Mengcheng meteor radar is run by the University of Science and Technology of China. The Kunming meteor radar is run by the Kunming Electro-magnetic Environment Observation and Research Station.

Table 1 Geographic locations, operation frequencies and observational time periods of the meteor radars used in this study.

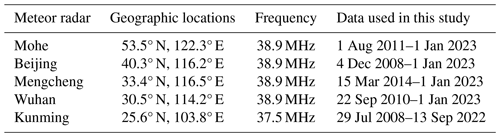
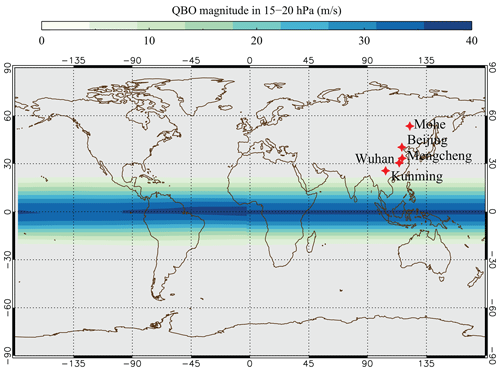
Figure 1 The QBO magnitude (m s⁻¹) averaged in the pressure level range of 15–20 hPa during 2000–2014 according to ERA5 reanalysis. Before calculating the QBO magnitude, the monthly mean zonal wind is derived by removing seasonal variations and the semiannual oscillation (SAO). The red stars mark the locations of the five radars used in this study.

Meteor radar operation and analysis for these radars are described by Holdsworth et al. (2004), and the interested reader is directed there. All five radars are used to measure horizontal winds and sample in the altitude region from 70 to 110 km. The temporal and altitudinal resolutions are 1 h and 2 km, respectively. Because of missing horizontal wind data in the altitude ranges of 70–76 km and 100–110 km, only the observed horizontal winds in the altitude range of 78–98 km are analyzed in this study.

2.2 SD-WACCM-X

SD-WACCM-X is a comprehensive numerical model based on the Community Earth System Model version 1 (CESM1) framework (Hurrell et al., 2006) and is designed to investigate the coupling among chemistry, radiation, and dynamics and their impact on the Earth's climate system (Neale et al., 2013). The SD-WACCM-X version 2.1 simulation from the surface up to ∼ 50 km is nudged from Modern-Era Retrospective analysis for Research and Applications version 2 (MERRA-2) data.

In this study, the monthly SD-WACCM-X simulation is used to obtain the mesospheric wind diurnal tides, heating sources of these tides, and GW drag on zonal wind; these heating sources in the SD-WACCM-X are exported as temperature tendencies due to the solar heating rate, solar radiative absorption by water vapor, and ozone. The GW drag on the zonal wind in the SD-WACCM-X is exported as zonal wind tendencies due to total GW drag, and the tropical stratospheric zonal mean zonal wind in the SD-WACCM-X output is also used to present the QBO signature in tropical stratospheric GWs.

2.3 ERA5 reanalysis

ERA5 is the fifth-generation reanalysis dataset from the ECMWF. It provides several improvements compared to ERA-Interim, as detailed by Hersbach and Dee (2016). The analysis is produced at a 1 h time step using a significantly more advanced 4D-Var assimilation scheme. Its horizontal resolution is approximately 31 km, and atmospheric variables are calculated at 137 pressure levels (Hersbach et al., 2020). The data for the 1979–2022 period were released in 2023. In this study, the monthly ozone concentration in model levels is used to analyze the possible excitation sources of mesospheric diurnal tides.

2.4 Approach for tidal decomposition

The series of hourly zonal and meridional winds are performed by least-squares fitting in a 3 d sliding window with a 1 d time step to decompose the amplitudes and phases of various tidal components, including diurnal, semidiurnal, and terdiurnal tides. The screening conditions for the fitting are as follows: if the valid data rate within the window is less than half of the total or span less than two-thirds of their phase, the data within this window cannot be used for subsequent calculation. Otherwise, the 3 d wind data remain eligible for analysis. Then, a least-squares fitting method, as described by Baumgarten and Stober (2019), is performed on the hourly wind data for each 3 d window throughout the series to decompose the diurnal tides as follows:

$$\begin{array}{}\text{(1)}& u\left(\mathrm{z},\mathrm{t}\right)=u_{\mathrm{0}}\left(z\right)+\sum _{n=\mathrm{1}}^{\mathrm{3}}{a}_n\left(z\right)\sin \left({\displaystyle \frac{\mathrm{2}\mathit{\pi }n}{T}}t\right)+b_n\left(z\right)\cos \left({\displaystyle \frac{\mathrm{2}\mathit{\pi }n}{T}}t\right),\end{array}$$

where u represents either zonal or meridional wind, z represents altitude, t represents time, n represents temporal wavenumber, T equals 24 h, and u₀ represents mean zonal or mean meridional wind.

3 Results

3.1 Meteor radars observations

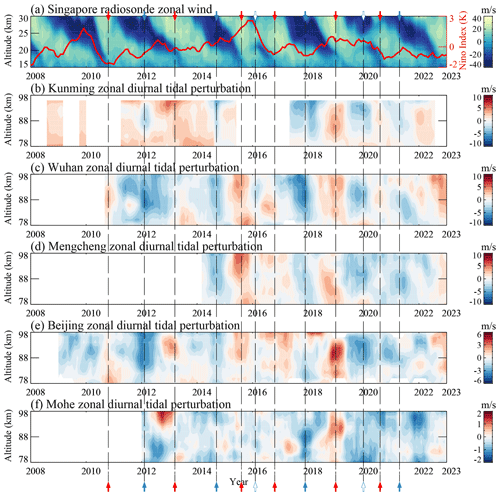
Figure 2a presents the zonal wind in the pressure level range of 100–10 hPa observed by the Singapore radiosonde (1° N, 104° E), which reveals the normal pattern of the QBO with alternately descending westward and eastward wind with a period of approximately 20–30 months. This characteristic QBO zonal wind pattern is disrupted in 2015–2016 and 2019–2020, as highlighted by the dashed lines in Fig. 2a. During the two QBO disruptions, the descending eastward wind is interrupted by a localized westward wind near the pressure level of 40 hPa, resulting in split equatorial westerly jets. In this study, we focus on the strong impacts of the recent QBO disruptions on mid-latitude MLT diurnal tides.

Figure 1b–f present the meridional diurnal tidal amplitude perturbations over Kunming, Wuhan, Mengcheng, Beijing, and Mohe, respectively. Considering that the response of QBO to tidal amplitudes in the zonal wind component are weaker than in the meridional wind component, meridional diurnal tides are primarily considered in this study, and the zonal diurnal tidal amplitude perturbations observed by these meteor radars are shown in Fig. A1. To show the connection between diurnal tides and the stratospheric QBO, diurnal tidal perturbations are derived by removing seasonal variations and the 11-year solar cycle variations. Diurnal tidal perturbations over Kunming, Wuhan, Mengcheng, and Beijing are very similar to the variability in the QBO zonal wind, while the diurnal tides over Mohe do not exhibit a clear QBO signature. Diurnal tidal perturbations are enhanced during QBOE, and those are suppressed during QBOW. However, during 2015–2017 and 2019–2021, diurnal tides in the MLT region are unusually weakened when the eastward wind is interrupted by a localized westward wind near 40 hPa. The tidal responses to the QBO disruptions were remarkably similar over Beijing, Mengcheng, and Wuhan (∼ 30–40° N). In contrast, the diurnal tides observed by the Kunming meteor radar (∼ 25° N) primarily respond to the QBO disruption above 80 km. This suggests that the impact of the QBO disruptions on mesospheric diurnal tides might differ between the subtropical region and in the mid-latitude region.

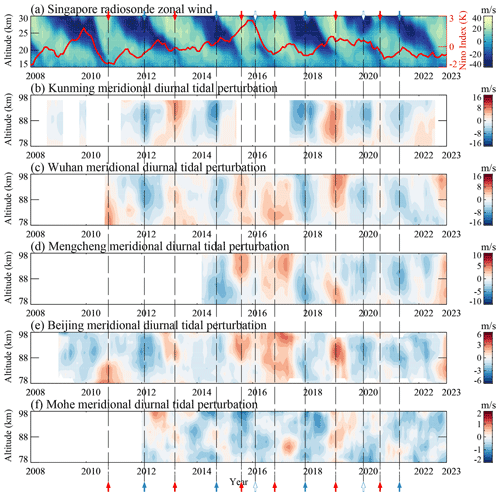
Figure 2 (a) The QBO zonal wind observed by the Singapore radiosonde for the 100–10 hPa pressure levels (∼ 15–30 km). The red curve indicates the Niño 3.4 index. (b–f) The meridional diurnal tidal amplitude perturbations observed from meteor radars over (b) Kunming, (c) Wuhan, (d) Mengcheng, (e) Beijing, and (f) Mohe in the altitude range from 78 to 98 km during 2008–2023. These tidal perturbations are derived by removing the seasonal variations and 11-year solar cycle variations. Note that the color bar values are different. The dashed lines represent QBOE and QBOW. The red and solid blue arrows denote QBOE and QBOW, respectively. The blue hollow arrows denote the two QBO disruptions in winters of 2015–2016 and 2019–2020.

In the past, numerous studies have reported the QBO signature in mesospheric diurnal tides (Davis et al., 2013; Hagan et al., 1999; Laskar et al., 2016; Vincent et al., 1998; Mayr and Mengel, 2005; Ern et al., 2014, 2023; Salinas et al., 2023). However, the features and mechanism of mesospheric tides during QBO disruptions are still poorly understood. The ENSO, as the dominant interannual variation in the tropical troposphere (Yulaeva and Wallace, 1994), can also affect mesospheric diurnal tides (Cen et al., 2022; Lieberman et al., 2007). Cen et al. (2022) suggested that El Niño events suppress mesospheric diurnal tides in the boreal winter, including the winter of 2015–2016. Figure 2a presents the Niño 3.4 index (red curve) during 2008–2023. The Niño 3.4 index reached a temperature anomaly of 2.57 K during the winter of 2015–2016, while it reached 0.74 K during the winter of 2019–2020. As shown in Fig. 2a–c, the negative mesospheric tidal perturbations during the winter of 2015–2016 exhibit weaker intensity compared to those during the winter of 2019–2020. This pattern contrasts with the Niño 3.4 index, suggesting that the negative tidal perturbations observed during QBO disruptions are not linked to the ENSO. Therefore, the negative tidal perturbations observed during winters of 2015–2016 and 2019–2020 are likely associated with the QBO disruptions.

3.2 ERA5 ozone variability

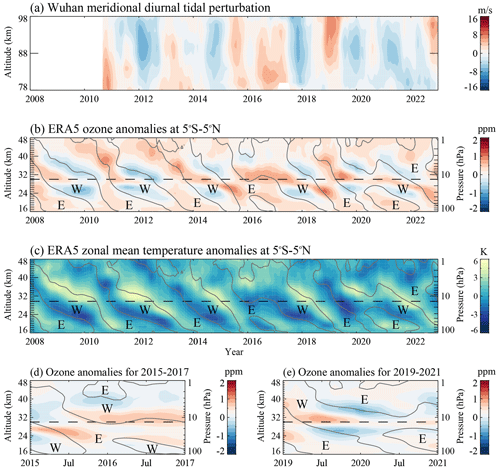
Figure 3 (a) The meridional diurnal tidal amplitude perturbations observed from the meteor radar over Wuhan in the altitude range from 78 to 98 km during 2008–2023. (b) The monthly mean anomalies of the ozone mixing ratio from ERA5 reanalysis (contour fill plots; ppm meaning 10⁻⁶ kg kg⁻¹) averaged between 5° S and 5° N in the altitude range of 20–60 km. The solid grey lines indicate the zero-wind lines of monthly averaged zonal mean zonal wind (E: eastward wind, W: westward wind). (c) As in panel (b) but for zonal mean temperature. The anomalies are derived by removing the seasonal variations and 11-year solar cycle variations. The dashed lines denote the altitude of 30 km.

Considering that QBOs dominate the stratospheric dynamics in the equatorial region and the major tidal heating source in the stratosphere is the solar radiative absorption by ozone molecules, the possible QBO impact on ozone concentrations may cause a QBO signature in stratospheric solar radiative heating. In this study, the ERA5 ozone concentration is used to explore the QBO impact on ozone variability and the relationship between ozone variability and observed diurnal tides. Figure 3 presents the anomalies in the ozone concentration and QBO in the tropical stratosphere (5° S–5° N). The ozone variability is associated with the stratospheric QBO wind (solid grey lines in Fig. 3b) and the mid-latitude mesospheric diurnal tidal perturbations (Fig. 3a).

As shown in Fig. 3b, the tropical stratospheric ozone is strongly modulated by a QBO-related variability, primarily within the altitude range of 20–50 km. The ozone concentration reaches the minimum value within the altitude range of ∼ 22–28 km and ∼ 30–40 km, respectively, as the zonal mean zonal wind turns westward within the altitude range of ∼ 20–35 km (as shown in Fig. 3d). When the zonal mean zonal wind at altitudes ranging from ∼ 20–35 km is dominated by eastward wind, the ozone concentration reaches the maximum value within the altitude of ∼ 22–28 km and ∼ 32–45 km, respectively. In the lower stratosphere (∼ 22–28 km), positive (negative) ozone anomalies propagate downward in the similar form of zonal mean eastward (westward) wind shears. This behavior aligns with the zonal mean positive (negative) temperature anomalies as depicted in Fig. 3c. In the upper stratosphere (above ∼ 30 km), the phase of ozone anomalies is almost opposite to the phase of QBO winds and temperature. During the QBO disruptions, both layers of ozone anomalies exhibit negative values accordingly in winters of 2015–2016 and 2019–2020 as shown in Fig. 3d and e.

In the tropical lower stratosphere, the ozone variability is primarily determined by transport due to the relatively longer chemical lifetime of the ozone molecule and stronger vertical gradient in this area. In the tropical upper stratosphere, the ozone variability is modulated by both the transport and the photochemistry process. In the tropical stratosphere, when the QBO wind shear is eastward (westward), the air becomes warm (cooling) due to thermal wind balance (Fig. 3c; Baldwin et al., 2001). In the lower stratosphere, the QBO-related temperature differences induce a downward (upward) meridional circulation (Gray and Chipperfield, 1990), resulting in the increasing (reduced) ozone and nitrous oxide (N₂O) concentration (Salawitch et al., 2005; Park et al., 2017). N₂O is the primary source of the NO_x species and NO_x is the major sink of ozone in the middle stratosphere (Salawitch et al., 2005). Thus, in the upper stratosphere, the phase of ozone anomalies is opposite to the phase of the QBO-related temperature due to chemical control by NO_x (Park et al., 2017). As a result of alternating descending pattern of QBO winds, the phase of ozone anomalies in the upper stratosphere is approximately coherent with QBO wind at ∼ 20 hPa. Besides, the solar radiative absorption by the ozone molecule in the upper stratosphere is also the major heating sources of the diurnal tides (Hagan et al., 1999; Vichare and Rajaram, 2013), and the ozone variability in the upper stratosphere is in a coherent manner with the mesospheric diurnal tides. Thus, the ozone variability in the upper stratosphere is primarily focused on in this study.

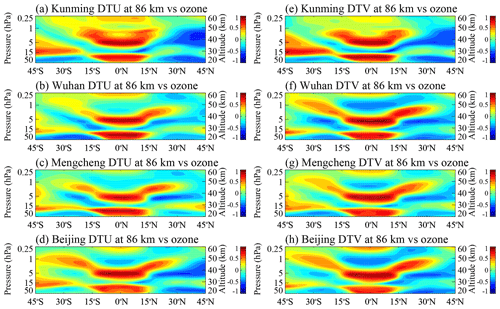
Figure 4 (a–d) Correlations between the anomalies in the ozone concentration in 45° S–45° N in the altitude range of 20–60 km and zonal diurnal tidal amplitudes at 86 km observed by meteor radars over (a) Kunming, (b) Wuhan, (c) Mengcheng, and (d) Beijing, respectively. (e–h) As in panels (a–d) but for meridional diurnal tides.

To investigate the connection between QBO-related ozone variability and mesospheric diurnal tides, Fig. 4a–h present the correlation between the ozone variability and diurnal tidal perturbations in both wind components observed by meteor radars. As shown in Fig. 4, although the latitudinal differences in these tidal observations are significant, ranging from ∼ 25 to ∼ 40° N, the region with a strong correlation between ozone and these tides remains relatively unchanged. A portion of the ozone correlated with tides is located at nearly 30 hPa in the tropical lower stratosphere of approximately 10° S–10° N, and another portion is situated at nearly 5 hPa in the ∼ 10° S–10° N tropical upper stratosphere, extending toward the subtropical region (∼ 15–30° N) as the altitude increases up to ∼ 0.5 hPa.

The correlation analysis suggests that the interannual oscillation of ozone in the tropical lower stratosphere and subtropical upper stratosphere are in phase with the interannual oscillation of diurnal tides over the low- and mid-latitude MLT region. As shown above, dominant variability in the diurnal tides over low- and mid-latitude MLT region and the ozone concentration in the tropical lower and upper stratosphere is tied to the QBO. Interestingly, the region of QBO-related ozone variability in the upper stratosphere is not limited in the tropical region but extends toward the subtropical region (∼ 30° N), with the altitude range increasing from ∼ 30–40 km to ∼ 40–50 km. In addition to the interannual variability, the relationship between the response of the upper stratospheric ozone and mesospheric diurnal tides to the QBO disruptions also deserves to be discussed.

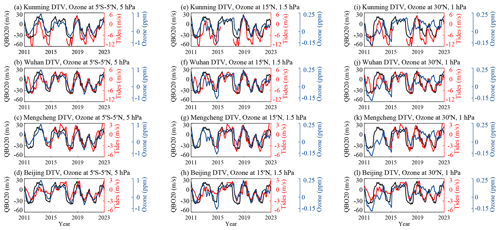
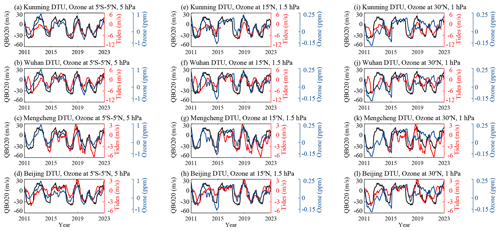
Figure 5 (a–d) Comparative analysis of the meridional diurnal tides observed by meteor radars (red) over (a) Kunming, (b) Wuhan, (c) Mengcheng, and (d) Beijing, with the QBO wind observed by Singapore radiosonde at 20 hPa (QBO20, black) and ozone concentration anomalies derived by ERA5 reanalysis (blue) at 5° S–5° N and 5 hPa, respectively. (e–h) As in panels (a–d) but for ozone anomalies at 15° N and 1.5 hPa. (i–l) As in panels (a–d) but for ozone anomalies at 30° N and 1 hPa. The anomalies in the ozone concentration are derived by removing the seasonal variations and 11-year solar cycle variability.

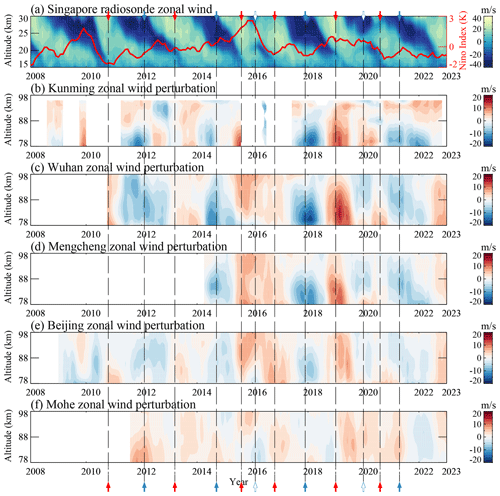
To show the QBO signature and QBO disruptions impacts on ozone variability, Fig. 5a–h present the ozone anomalies in the tropical upper stratosphere (5° S–5° N, 5 hPa), subtropical upper stratosphere (∼ 15° N, 1.5 hPa), and low-latitude upper stratosphere (∼ 30° N, 1 hPa). The comparison between ozone variability and zonal tidal amplitudes is shown in Fig. A2. As shown in Fig. 5a–d, the meridional diurnal tides at 86 km over Kunming, Wuhan, Mengcheng, and Beijing as well as the ozone variabilities at 5° S–5° N, and 5 hPa are all strongly consistent with the QBO wind at 20 hPa. As shown in Fig. 5e–h, the ozone variability at 15° N, and 1.5 hPa also exhibits a significant QBO signature, which is associated with the QBO wind at 20 hPa and with mesospheric diurnal tides. Furthermore, during the winters of 2015–2016 and 2019–2020, a simultaneous reduction in the zone concentration was observed in both the tropical and the subtropical stratosphere. This decreases, along with the attenuation of the mesospheric tides, exhibited a significant alignment with the temporary westward QBO wind pattern. However, as shown in Fig. 5i–l, the ozone variability at 30° N and 1 hPa show consistency with the mesospheric diurnal tides in the time period of 2011–2018 and 2023, but this is different during 2019–2022. Compared with the ozone in the subtropical region (∼ 15° N) and in the tropical region (5° S–5° N), this result implies that the interannual variations in mesospheric diurnal tides are more likely induced by the subtropical ozone (∼ 15° N) variability rather than the ozone in the low-latitude region (∼ 30° N).

Of course, statistically significant correlations between two parameters cannot imply their interdependency. Considering that the ozone heating responsible for exciting diurnal tides primarily occurs at altitudes between ∼ 40–50 km (Fig. A3; Hagan et al., 1999; Vichare and Rajaram, 2013), ozone concentration variabilities at nearly 30 hPa in the tropical stratosphere are less likely to be the cause of the QBO signature in mesospheric diurnal tides. The connection between QBO-related ozone at ∼ 5–0.5 hPa (∼ 35–50 km) and the QBO signature in mesospheric diurnal tides needs further analysis via a comprehensive numerical model, such as SD-WACCM-X. QBO impacts on the tidal excitation are explored in Sect. 4.

3.3 SD-WACCM-X simulations

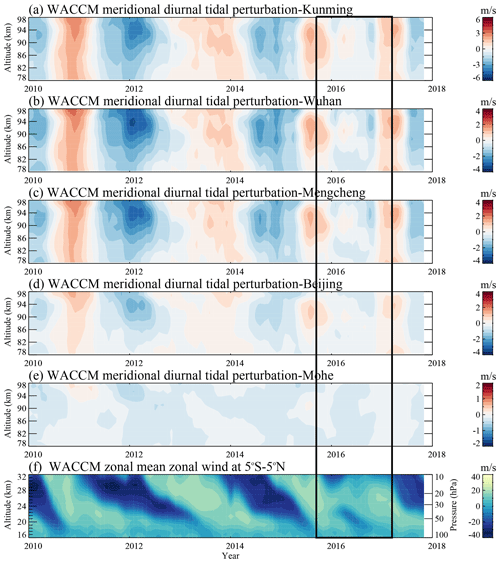
Figure 6 (a–e) The meridional diurnal tidal amplitude perturbations derived by SD-WACCM-X over (a) Kunming, (b) Wuhan, (c) Mengcheng, (d) Beijing, and (e) Mohe in the altitude range from 78 to 98 km during 2010–2018. These tidal perturbations are derived by the same methodology as in Fig. 2. Note that the color bar values are different. (f) The zonal mean zonal wind derived by SD-WACCM-X averaged in 5° S–5° N in the pressure levels of 100–10 hPa during 2010–2018. The rectangular box highlights the QBO disruptions in the winter of 2015–2016.

To further consider the mechanism of disrupted QBO impacts on tides, the diurnal tides in zonal and meridional components over the locations of these five meteor radars are simulated by SD-WACCM-X in the altitude ranging from 78 to 98 km. Figure 6 presents the SD-WACCM-X simulations for the meridional diurnal tidal perturbations during 2010–2018 over the locations of Kunming, Wuhan, Mengcheng, Beijing, and Mohe. WACCM tidal perturbations are deseasonalized by the same methodology to remove the seasonal variations and the 11-year solar cycle variability as on the meteor radar observations. Figure 6f presents the tropical zonal mean zonal wind simulated by WACCM modelling. Compared to the zonal wind observed by the Singapore radiosonde (Fig. 2a), WACCM modelling could simulate the QBO wind and the QBO disruption in the winter of 2015–2016 well. As shown in Fig. 6, the mid-latitude mesospheric diurnal tides derived by WACCM over Kunming, Wuhan, Mengcheng, and Beijing are also greatly weakened during the 2015–2016 QBO disruption. Similarly, the QBO signature can be clearly identified in the diurnal tidal perturbations over Kunming, Wuhan, Mengcheng, and Beijing during the simulated time period that the mesospheric diurnal tides are enhanced during QBOE and suppressed during QBOW.

However, compared to meteor radar observations, the QBO signature in diurnal tides simulated by WACCM is ∼ 3 m s⁻¹ over Kunming and weaker than the observation value of ∼ 6 m s⁻¹. Also, the time period during which the diurnal tides are weakened during the QBO disruption in the WACCM output is longer than that observed by meteor radars. Stober et al. (2021) and Zhou et al. (2022) have compared the mesospheric tides observed by meteor radars and simulated by WACCM modelling and discussed the agreements and deviations of the seasonal variations in mean winds and tides. Their results also suggested that the meteor-radar-observed diurnal tidal amplitudes are usually greater than those simulated by WACCM. The tidal difference between observations and modelling simulations primarily depends on tidal forcing in the troposphere and stratosphere (Ortland, 2017), propagation, and interaction with GWs (Stober et al., 2021). These differences indicate that these processes are still unclear in the QBO modulation; nevertheless, WACCM simulations could still be used to explore the mechanism of QBO modulation considering that disrupted QBO signatures are clearly identified in WACCM diurnal tides.

4 Discussion

4.1 Tidal forcing and propagation

Diurnal tides are primarily excited by solar radiative absorption by water vapor in the troposphere, ozone molecules in the stratosphere, and oxygen molecules in the thermosphere. According to tidal theory, heating rates of solar radiative absorption by water vapor in the upper troposphere and ozone molecules in the stratosphere are responsible for mesospheric diurnal tidal forcing. Thus, we examine the perturbation of the diurnal solar heating source simulated by WACCM modelling in the altitude range of 0–100 km, which potentially contributes to the positive diurnal tidal anomalies in the stratosphere during QBOE and negative diurnal tidal anomalies during QBOW.

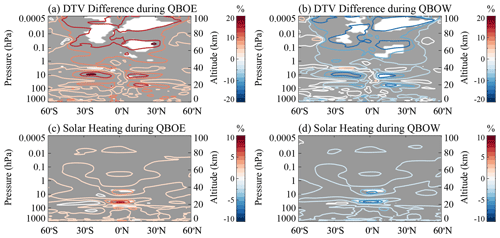
Figure 7 (a) Anomalous percentage variances of the meridional diurnal tides in the latitudinal range of 60° S–60° N during QBOE. (b) As in panel (a) but during QBOW. (c) As in panel (a), but for the solar radiative heating. (d) As in panel (b), but during QBOW. The solid red lines denote the positive response, while the solid blue lines denote the negative response. The white regions denote 95 % significance according to the Monte Carlo test; the grey area indicates where the response is insignificant at the 95 % level according to the Monte Carlo test. Note that the color bar values are different.

Figure 7a and b present the anomalous percentage variances of the WACCM meridional diurnal tides averaged in 100–120° E during QBOE and QBOW, respectively. During QBOE, the meridional diurnal tides are greatly enhanced by ∼ 20 % in the MLT region (80–100 km) from 45° S to 45° N; the diurnal tides are also significantly positive in the altitude range of ∼ 50–80 km from 5 to 30° N and in the altitude range of 20–40 km from 5 to 25° N. During QBOW, the diurnal tides are suppressed by ∼ 20 % in the same region. The altitudinal and latitudinal variabilities in these regions with significantly positive responses suggest that the QBO signature in diurnal tides over the mid-latitude MLT region may propagate from the tropical and/or subtropical stratosphere. The tidal response to the QBO in the WACCM simulation is consistent with that observed by meteor radars, so the WACCM simulation is expected to be used to explore the process of QBO modulations on mesospheric diurnal tides.

As shown in Fig. 7c and d, the solar radiative heating rates are significantly positive (∼ 10 %) in the tropical region (∼ 10° S–10° N) at ∼ 5 and ∼ 30 hPa during QBOE and negative (∼ −10 %) in the same region during QBOW. The region where the solar heating rates strongly respond to QBO extends to mid-latitudes, with the altitude increasing from ∼ 5 to ∼ 0.1 hPa, although this extended area is not significant at the 95 % level. At the altitude of the strong response region at ∼ 5–0.1 hPa, tidal forcing is primarily solar radiative absorption by ozone molecules. Notably, the QBO-related solar heating variability is approximately in the same region as the QBO-related ozone variability in the upper stratosphere, indicating that the QBO affects the tidal heating source in the stratosphere via modulating the solar radiative absorption by ozone molecules. According to the relationship between ozone variability at ∼ 5–0.5 hPa and QBO-related tidal perturbations in the mid-latitude MLT region, the possible mechanism is as follows.

During QBOE, the dominant eastward zonal wind descends in the tropical stratosphere, and a warm region develops at the location of maximum vertical wind shear via thermal wind balance (Baldwin et al., 2001). As the tropical lower stratosphere becomes warmer and the tropical upper stratosphere cooler at the same time, the infrared cooling to space is relatively enhanced below ∼ 30 km and is relatively suppressed above ∼ 30 km, resulting in a downward poleward motion in the tropical stratosphere; because the phase of induced secondary circulation in the high-latitude region is reversed, this process is also opposite in the high-latitude region. This meridional circulation induced by the QBO eastward winds is opposite to the Brewer–Dobson circulation (BD circulation; Butchart, 2014), hindering the transport of ozone and other molecules such as N₂O towards the polar region (Andrews et al., 1987; Baldwin et al., 2001; Park et al., 2017; Pramitha et al., 2021). This results in the accumulation of a relatively large ozone amounts in the tropical lower stratosphere. In the tropical upper stratosphere, the ozone peaks are slightly reduced, but the largely reduced NO_x peaks due to less N₂O eventually increase the ozone concentration. The increased ozone concentration in the subtropical upper stratosphere excites stronger diurnal tides via higher solar radiative absorption. As the tides propagate upward to the mid-latitude MLT region, the QBO signature is impressed onto the diurnal tides. During QBOW, the meridional circulation induced by QBO westward winds is shown in Fig. 8b. The meridional circulation and the process during QBOW are opposite to them during QBOE, causing the weakening of diurnal tides in the mid-latitude region.

Both recent QBO disruptions occur in the winter. In normal winters, the stratosphere is forced by BD circulation, in which the upward northward motion is in the tropical stratosphere and the downward motion is in the boreal mid-latitude stratosphere. In the winter, during the QBO disruption events, the descending eastward wind in the tropical stratosphere is interrupted by a temporary westward wind at ∼ 20 km induced by the variations in the equatorial planetary waves, extratropical Rossby waves, and gravity waves (Osprey et al., 2016; Kang et al., 2020; Kang and Chun, 2021). The meridional circulations during the QBO disruption events are also changed due to the variation in the stratospheric dynamics (as shown in Fig. 8c and d). During the 2015–2016 QBO disruption, the direction of the anomalous meridional residual circulation is similar to during QBOW, but is weaker and unsymmetrical with the Equator, resulting in the slight reduction in the ozone concentration. During the 2019–2020 QBO disruption, the anomalous meridional residual circulation shows an upward motion in the tropical stratosphere, which also induces the negative ozone anomalies (Diallo et al., 2022). The negative ozone anomalies indicate the reduction in solar radiative heating (as shown in Fig. A4), resulting in the slight weakening of the mesospheric diurnal tides in the low- and mid-latitude MLT region during the QBO disruption events.

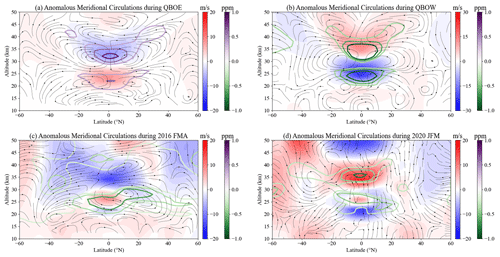
Figure 8 (a–d) Latitude versus altitude sections of the zonal mean zonal wind perturbations (shading), the anomalies of zonal mean ozone concentration (contours) and the anomalous meridional residual mean circulation (streamlines) derived by the ERA5 reanalysis during (a) QBOE, (b) QBOW, (c) February to April in 2016 (FMA 2016), and (d) January to March in 2020 (JFM 2020). The wind perturbations, ozone anomalies, and anomalous meridional circulations are derived by removing the seasonal variations and 11-year solar cycle variations. The vertical winds are multiplied by 100. Note that the color bar values are different.

4.2 Effect of gravity wave forcing

In addition to the solar radiative heating and tidal propagation, the mesospheric diurnal tides are also affected by the interaction with GWs (Liu and Hagan, 1998; Li et al., 2009; Stober et al., 2021). GWs are the dominant driving force of MLT dynamic processes (Liu et al., 2009; Sato et al., 2009; John and Kumar, 2012; Stober et al., 2023, 2024) and can greatly modulate tidal amplitude and phase (Walterscheid, 1981; Lu et al., 2009; Li et al., 2009; Liu and Hagan, 1998). However, the effect of GWs on diurnal tides is still not fully understood due to limited MLT observation with high temporal resolution and the current model accuracy, which cannot fully resolve both small-scale GWs and tides.

In WACCM simulations, the GW driving force is represented by a parameterization, and the tropospheric sources are interactive and primarily triggered by convection and flow rather than orography in the tropics (Beres et al., 2015). As tropical GWs propagate upward to the tropopause and lower stratosphere, these GWs and other equatorial waves, including Kelvin waves, mixed Rossby-gravity waves, and equatorial Rossby waves, jointly drive the pattern of QBO circulation (Baldwin et al., 2001; Holton and Tan, 1980; Lindzen and Holton, 1968; Geller et al., 2016; Mayr and Mengel, 2005; Ern et al., 2014, 2023). During QBO disruptions, the tropical GWs are also suggested to be associated with the temporary westward jet that interrupted the QBO eastward wind at ∼ 50 hPa (Barton and McCormack, 2017; Li et al., 2023; He et al., 2022; Kang et al., 2020; Kang and Chun, 2021). Considering the interaction between GWs and QBO winds in the tropical stratosphere, GWs propagating upward to the mesosphere will likely be modulated by the QBO as the wind phase of the QBO varies. Hereafter, these GWs may have contributed to the QBO signature in the mid-latitude mesospheric diurnal tides and the temporary weakening of diurnal tides during QBO disruptions.

Figure 9a presents the QBO variabilities of the GW drag on zonal wind in the tropical stratosphere derived via the WACCM simulation. The equatorial zonal GW drag in the altitude range of ∼ 20–40 km is closely related to the zonal wind shears and zero wind lines of the QBO. The zonal GW drag is positive during the QBO zonal wind reversal from westward to eastward winds; the zonal GW drag is negative as the QBO zonal wind shifts from eastward to westward wind. In particular, a strong negative zonal GW drag of approximately −0.6 m s⁻¹ d⁻¹ occurs at nearly 12 hPa during the 2015–2016 QBO disruption after the time when the eastward wind turns into westward wind.

As the GWs propagate upward to the upper stratosphere and mesosphere, the QBO amplitude rapidly diminishes to less than 5 m s⁻¹ near the stratopause after which the dominant mode of zonal wind becomes the semiannual oscillation (SAO; e.g., Baldwin et al., 2001). The GWs in the tropical mesosphere exhibit a much lower QBO signature due to the strong interaction between the GWs and the SAO in zonal flow. In the altitude range of ∼ 60–100 km, the QBO-related varying GWs primarily dominate the mid- and high-latitude mesosphere, and these GWs produce a QBO-related zonal wind (as shown in Fig. A5) known as the mesospheric QBO (e.g., Baldwin et al., 2001). Similarly, the anomalies during QBO disruptions can be clearly classified in the MLT background zonal wind. Above all, the QBO signature and anomalies during QBO disruptions are strongly imprinted on the mesospheric GWs. In this section, we focus on the effect of GW forcing on the amplitudes of diurnal tides (DT–GW forcing). The approach to calculate the DT–GW forcing is shown in Appendix A (Liu et al., 2013).

Figure 9b and c present the anomalies of mesospheric DT–GW forcing parameterized in the WACCM simulation in the altitude range of 60–100 km during QBOE and QBOW, respectively. The GWs enhance diurnal tides in the boreal (∼ 70–90 km) and austral (∼ 60–80 km) subtropical mesosphere during QBOE, while they suppress the diurnal tides in the same region during QBOW. The magnitude is slightly greater in the austral mesosphere (∼ 4 m s⁻¹ d⁻¹) than in the boreal mesosphere (∼ 2 m s⁻¹ d⁻¹) due to the apparent hemispheric asymmetry of convective activities. The QBO signature in mesospheric DT–GW forcing is consistent with the QBO signature in mesospheric diurnal tides, indicating that GWs could be a factor that enables the tropical stratospheric QBO to modulate mid-latitude MLT diurnal tides.

During usual winters (Fig. 9d), The GWs enhance diurnal tides (∼ 4 m s⁻¹ d⁻¹) in the boreal mid-latitude mesosphere (∼ 70–90 km) and suppress diurnal tides in astral mid-latitude mesosphere (∼ 60–80 km). The time period of 2016 February–April is when the Singapore eastward wind at 30 hPa reaches a minimum during the 2015–2016 QBO disruption. As shown in Fig. 9e, the GWs dampen the diurnal tides in the boreal mid-latitude MLT (∼ 80–100 km) during FMA 2016. During the same time period, the DT–GW forcing is positive in the boreal subtropical lower mesosphere (∼ 70–80 km) and at high altitudes above ∼ 100 km. The area of negative DT–GW forcing corresponds well with the altitude range where the diurnal tides respond strongly to the QBO disruption observed by meteor radars; the region of positive GW forcing corresponds to the altitude range where the QBO disruption signature in diurnal tides is weak. For example, at lower altitudes, the diurnal tides observed by Kunming meteor radar respond to the QBO disruption only above 82 km, possibly because the DT–GW forcing derived by WACCM has the opposite effect on the diurnal tides in the altitude range of ∼ 70–80 km.

The modulation by GWs of the mesospheric diurnal tides can explain the latitudinal and altitudinal differences in the tidal response to the QBO disruption. Although the observational evidence for DT–GW forcing is still lacking, from the analysis of this WACCM simulation and ERA5 reanalysis, the QBO signature and anomalies associated with QBO disruptions to mesospheric diurnal tides can result from both perturbations to the tidal generation in the stratosphere and perturbations to the tidal–GW interaction in the MLT region.

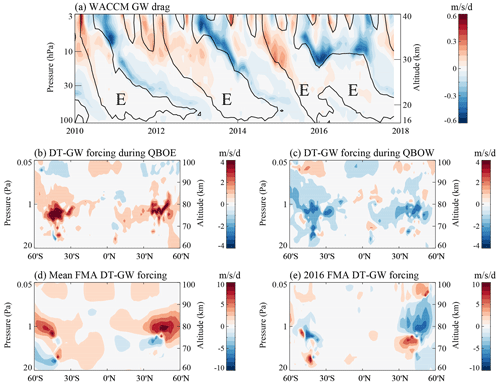
Figure 9 (a) Altitude–year cross sections of 5° S–5° N averaged total zonal GW drag in the altitude range of 15–40 km during 2010–2018 derived by WACCM simulation. The solid black lines indicate zero zonal mean zonal wind averaged in 5° S–5° N. (b–c) The anomalies of the GW forcing on the mesospheric diurnal tides in the altitude range of 60–100 km during QBOE (b) and during QBOW (c). (d) Composite year mean of DT–GW forcing derived by WACCM simulation during FMA. (e) As in panel (d) but for DT–GW forcing during FMA 2016. Note that the values of color bars are different in panels (a), (b, c), and (d, e).

5 Conclusions

In this paper, the impact of QBO disruptions on diurnal tides over the mid-latitude MLT region is investigated using a meteor radar chain observation of MLT horizontal winds. The meteor radar chain consists of five meteor radars located at Kunming (25.6° N, 103.8° E), Wuhan (30.5° N, 114.2° E), Mengcheng (33.4° N, 116.5° E), Beijing (40.3° N, 116.2° E), and Mohe (53.5° N, 122.3° E). The zonal and meridional diurnal tides in the MLT region are strongly modulated by the stratospheric QBO during 2009–2023 over Kunming, Wuhan, and Beijing. The diurnal tides over the low- and mid-latitude MLT region are positive during QBOE and negative during QBOW and are dampened during recent QBO disruptions (by ∼ 6 m s⁻¹).

Possible mechanisms have been discussed to explain the impact of the QBO and the recent QBO disruptions on diurnal tides over the low- and mid-latitude MLT region being: (1) the impact of QBO wind on the sources of tidal heating in the stratosphere and its upward propagation and (2) the impact of QBO wind on the interaction between tides and GWs in the mesosphere. These mechanisms are, respectively, explained as follows.

As the solar radiative heating by ozone is one of the main exciting sources of diurnal tides (Hagan et al., 1999; Vichare and Rajaram, 2013; Pramitha et al., 2021), the stratospheric ozone variability response to stratospheric QBO and recent QBO disruptions is investigated. The ozone mixing ratio increases during QBOE and decreases during QBOW and during the recent QBO disruptions in the tropical and subtropical stratosphere (∼ 35–50 km). During normal QBO, the QBO-induced secondary meridional residual circulations modulate the ozone anomalies and further affect the amplitudes of the mesospheric diurnal tides. During both QBO disruptions, the temporary westward jet induces the anomalous tropical upwelling of the Brewer–Dobson circulation and slightly reduces the ozone in the tropical and subtropical upper stratosphere, resulting in the weakening of the mesospheric diurnal tides. This lasted for a few months over the low- and mid- latitudes. However, the response of mesospheric diurnal tides is ∼ 20 %, and the response of ozone variability is ∼ 10 %, which implies that the impact of ozone on mesospheric diurnal tides may not be the only mechanism in the QBO-tidal connection.

In the mesosphere, the diurnal tidal variability is also strongly affected by interactions with GWs (Li et al., 2009; Cen et al., 2022). The GW forcing on diurnal tides is positive during QBOE and negative during QBOW and the recent QBO disruptions. This result indicates that GWs tend to dampen the MLT diurnal tides during QBOW and QBO disruptions. In addition, the difference in DT–GW forcing during QBO disruption between the low and mid-latitudes can explain the differences of the diurnal tidal response to the QBO disruption between Kunming and Mengcheng/Beijing. This tidal–GW interaction may be one of the main mechanisms of the mesospheric diurnal tidal response to QBO disruptions. However, the parameterized GW in the SD-WACCM-X simulation is still not satisfactory enough to reflect real observations. Further investigation is necessary, with more detailed GW observations or with GW simulations in higher-resolution models.

These results suggest that the QBO disruptions can greatly affect mid-latitude mesospheric diurnal tides by modulating tidal heating excitations in the stratosphere and the tidal–GW interaction in the upper mesosphere. Here, the MLT tide plays a significant role in understanding the coupling between tropical climate changes and mid-latitude mesospheric dynamics. As the influence of tides and GWs propagates upward to the E region, the unusual disrupted QBO signature may be found in the ionosphere, and this unexpected phenomenon will likely affect global communications. This finding provides a valuable opportunity to explore the complex and important coupling between climate change and middle atmospheric dynamics.

Appendix A: Approach to calculate the gravity wave forcing on diurnal tides

In principle, the zonal wind diurnal tides can be written as

$$\begin{array}{}\text{(A1)}& u^{\prime }\left(t\right)=A\cos \left(\mathrm{\Omega }(t-\mathit{\varphi })\right),\end{array}$$

where A and ϕ are the amplitude and phase of the diurnal tides, respectively, and $\mathrm{\Omega }=\mathrm{2}\mathit{\pi }/\mathrm{24}$ h represents rotational angular velocity of the Earth.

Figure A1 The same as Fig. 2 but for zonal diurnal tidal amplitude perturbations.

The zonal tidal tendency in time can be written as

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}{\displaystyle \frac{\partial u^{\prime }}{\partial t}}& =A\cdot \mathrm{\Omega }\cdot \cos \left(\mathrm{\Omega }(t-\mathit{\varphi })+{\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}\right)\\ & =A\cdot \mathrm{\Omega }\cdot \cos \left(\mathrm{\Omega }(t-(\mathit{\varphi }-\mathrm{6}\left)\right)\right).\end{array}\end{array}$$

The phase of that tidal tendency leads the tide itself by 6 h. To evaluate the effect of GW forcing on diurnal tidal amplitudes (Yang et al., 2018; Cen et al., 2022), the DT–GW forcing can be calculated as

$$\begin{array}{}\text{(A3)}& \begin{array}{rl}{\mathrm{GW}}_{\mathrm{forcing}}& =\partial a_{\mathrm{DT}}/\partial t={\mathrm{GW}}_{\mathrm{drag}}\mathrm{\Delta }\mathit{\phi }\\ & ={\mathrm{GW}}_{\mathrm{drag}}\cos \left(\mathrm{\Omega }\left({\mathit{\varphi }}_{\mathrm{GW}}-({\mathit{\varphi }}_{\mathrm{DT}}-\mathrm{6})\right)\right),\end{array}\end{array}$$

where a_DT and ϕ_DT are the amplitude and phase of the diurnal tide, respectively. GW_drag and ϕ_GW are the amplitude and phase of the diurnal variation of the GW drag on background horizontal winds, respectively.

The purpose of modifying GW drag (Δφ) is to introduce the phase relationship between GW drag and the temporal tendency of diurnal tides. As the GW drag is in phase with the temporal tendency of diurnal tides, the Δφ is positive and GWs enhance the tides; if the phases are opposite, the Δφ is negative and GWs dampen diurnal tides.

However, Eq. (A3) holds only when the GW forcing is small relative to the frequency of the tides (1/24 h; Liu et al., 2013). When the GW acceleration is large, the observed diurnal tides are modulated significantly in both amplitude and phase. Considering to the relationship between the equivalent Rayleigh friction (ERF) and the effects on the amplitude and phase of the diurnal tide, which is given by (McLandress, 2002; Liu et al., 2013)

$$\begin{array}{}\text{(A4)}& \partial a_{\mathrm{DT}}/\partial t=-a_{\mathrm{DT}}\mathrm{Re}\left(\mathit{\gamma }\right),\partial {\mathit{\varphi }}_{\mathrm{DT}}/\partial t=\mathrm{Im}\left(\mathit{\gamma }\right),\end{array}$$

where γ denotes the ERF. In order to calculate the more accurate effect of the GW forcing on the diurnal tide, the method described by Liu et al. (2013) is used in this study. The ERF with respect to the tide without GW forcing γ₀ is expressed as (Liu et al., 2013)

$$\begin{array}{}\text{(A5)}& {\mathit{\gamma }}_{\mathrm{0}}={\displaystyle \frac{\mathit{\gamma }}{\mathrm{1}-i\mathit{\gamma }/\mathrm{\Omega }}}.\end{array}$$

Considering Eq. (A4), the effect of the GW forcing on the diurnal tidal amplitude can be estimated by

$$\begin{array}{}\text{(A6)}& \partial a_{\mathrm{DT}}/\partial t=-a_{\mathrm{DT}}\mathrm{Re}\left({\mathit{\gamma }}_{\mathrm{0}}\right).\end{array}$$

Figure A2 The same as Fig. 5 but for zonal diurnal tides. DTU: zonal diurnal tides.

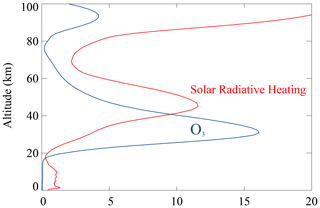
Figure A3 The altitude profiles of ozone concentration (ppm; blue curve) and solar radiative heating (×10 mW kg⁻¹; red curve) at 5° S–5° N in the altitude range of 0–100 km derived by SD-WACCM-X simulations.

Figure A4 (a–d) Comparative analysis of the zonal diurnal tidal perturbations derived from SD-WACCM-X (red) at 86 km over (a) Kunming, (b) Wuhan, (c) Mengcheng, and (d) Beijing with the QBO wind observed by Singapore radiosonde at 30 hPa (black) and solar radiative heating rates derived from SD-WACCM-X (blue) at 5° S–5° N, 5 hPa, respectively. (e–h) As in panel (a–d) but for meridional diurnal tides.

Figure A5 The same as Fig. 2 but for the interannual variation in the background zonal winds.