Precipitation in the mountains of Central Asia: isotopic composition and source regions

Over 900 event-based precipitation samples were collected in 2019–2021 in the Tien Shan and its foothills and analysed using cavity ring-down spectroscopy. δD and δ¹⁸O values were highest in summer and lowest in winter, and annual cycles of deuterium excess (d-excess) varied between sites, reflecting local conditions. The δ¹⁸O and δD values increased from north to south in all seasons except autumn, and latitude was a statistically significant predictor of δ¹⁸O and δD in the overall data set, along with elevation in winter and elevation and longitude in autumn. Elevation was a significant predictor of d-excess in all seasons, and local air temperature was a more important control over δ¹⁸O and δD than precipitation depth. Local meteoric water lines were derived using seven regression methods applied to non-weighted and weighted precipitation. Non-weighted ordinary least squares regression and reduced major axis regression methods are recommended overall, except for summer when the precipitation-weighted least squares regression should be used, particularly in the south. Atmospheric back-trajectory and mixing-model analyses were applied in combination to identify air mass source regions and their relative contribution to precipitation. Recycled moisture from irrigated land in the Amu Darya and Syr Darya basins and from the study catchments accounted for 29 %–71 % of precipitation, depending on the site and season. In the Chon Kyzyl-Suu catchment, local re-evaporation from Issyk-Kul accounted for up to 85 % of precipitation. These findings highlight the importance of moisture from terrestrial sources, especially irrigated land, for the formation of precipitation in the Tien Shan.

1 Introduction

Atmospheric precipitation is the primary water source that contributes to river runoff in the mountains of Central Asia (CA), both directly and by sustaining seasonal snowpack and glaciers, whose meltwater maintains dry-season river flow. In CA, precipitation is characterised by strong spatial variability due to large changes in elevation, from approximately 400 to 7000 m above sea level (a.s.l.) over relatively short distances and the mountain ridge and valley positions in relation to the moisture-bearing flow (Lydolph, 1977; Aizen et al., 1997). Longer-term changes and interannual precipitation variability affect all components of CA water resources (Shahgedanova, 2002; Jin et al., 2012; Aizen et al., 2017), and there is strong evidence for a decline in glacier area and negative glacier mass balance (Kutuzov and Shahgedanova, 2009; Farinotti et al., 2015; Severskiy et al., 2016; Kapitsa et al., 2020). These changes are attributed to the observed air temperature increase and to prolonged negative precipitation anomalies observed in the 1970s–1980s (Shahgedanova et al., 2018; Hoelzle et al., 2019). Projections from the Coupled Model Intercomparison Project Phase 6 (CMIP6) show an increase in annual precipitation in high mountain regions, with variation between regions and seasons – especially over the plains and foothills, and uncertainty remains about how these changes will be offset or enhanced by changes in evaporation and atmospheric circulation (Jiang et al., 2020). These uncertainties are amplified in impact assessments using glacier mass balance, hydrological, water resource, and crop models. To reduce the uncertainties in the precipitation projections, a better understanding of precipitation sources and moisture cycling, of the links between changes in atmospheric circulation and precipitation, and of the precipitation response to climatic warming is needed (Kaser et al., 2010; Immerzeel et al., 2020; Viviroli et al., 2020).

Analysis of the isotopic composition of precipitation has been used to investigate precipitation sources and moisture cycling (Yoshimura, 2015; Putman et al., 2019; Jasechko, 2019), as the stable isotopes of hydrogen and oxygen describe water fractionation due to evaporation, transportation and condensation, and precipitation. The ratios of heavy (¹⁸O) to light (¹⁶O) isotopes of oxygen (δ¹⁸O) and deuterium (D) to light hydrogen (¹H) and the relationship between δD and δ¹⁸O in precipitation at the global scale, known as the global meteoric water line (GMWL) and approximated by Eq. (1), have been widely applied in hydrometeorology since the 1960s (Craig, 1961; Craig and Gordon, 1965):

$$\begin{array}{}\text{(1)}& \mathit{\delta }\mathrm{D}=\mathrm{8}\times {\mathit{\delta }}^{\mathrm{18}}\mathrm{O}+\mathrm{10}.\end{array}$$

Rozanski et al. (1993) investigated δD and δ¹⁸O relationships using the data from the Global Network of Isotopes in Precipitation (GNIP) sites and suggested that local meteoric water lines (LMWLs) provide a better representation of isotopic composition of regional precipitation because they depend on latitude, continentality, altitude, and regional climatic anomalies. Relationships between GMWL and LMWLs help identify regional characteristics and processes affecting precipitation (Wang et al., 2018; Putman et al., 2019). LMWLs are typically used together with the deuterium excess (d-excess). Equation (2) was developed by Dansgaard (1964) to define d-excess and is used to characterise moisture sources:

$$\begin{array}{}\text{(2)}& \text{d-excess}=\mathit{\delta }\mathrm{D}-(\mathrm{8}\times {\mathit{\delta }}^{\mathrm{18}}\mathrm{O}).\end{array}$$

The global average d-excess of precipitation is 10 ‰. In general, moisture recycling increases d-excess values, and higher d-excess in precipitation signifies the addition of re-evaporated moisture from continental basins, while lower values signify moisture originating from the oceans. This difference makes it possible to distinguish precipitation originating over distant oceanic sources and more local sources in the continental interiors (Araguás-Araguás et al., 2000; Pang et al., 2011; Aemisegger et al., 2014; Bershaw, 2018), particularly when d-excess is used in conjunction with atmospheric back-trajectory analysis (Wang et al., 2017, 2019; Bershaw, 2018). Sub-cloud evaporation in a warm and dry air column reduces d-excess (Friedman et al., 1962), and d-excess of cloud condensate may be substantially different from the d-excess of precipitation samples collected at ground level (Froehlich et al., 2008), especially in arid regions (Juhlke et al., 2019). Isotopic composition and d-excess can also change with altitude (Bershaw, 2018; Natali et al., 2022; Yang et al., 2023) in response to sub-cloud evaporation; variations in distances travelled by a raindrop; and the transition from upwind slope, where lower temperature and higher humidity suppress evaporation as orographic precipitation forms, to downwind rain shadow. While the sub-cloud evaporation and a longer distance travelled by a raindrop from the cloud base to the surface are known to decrease d-excess values, the rain shadow effect results in higher d-excess. Consequently, d-excess serves as a valuable proxy for not only identifying precipitation sources but also tracking changes in air mass moisture along its pathway.

While the use of stable isotopes in hydrometeorology increases globally (Yoshimura, 2015; Aggarwal et al., 2016; Jasechko, 2019), knowledge about the isotopic composition of precipitation in CA (defined here as Kazakhstan (KZ), Kyrgyzstan (KG), Tajikistan (TJ), Turkmenistan, and Uzbekistan (UZ)) is limited. Currently, the GNIP database contains only seven measurements of δD and δ¹⁸O from the precipitation samples collected in Tashkent, Uzbekistan (IAEA/WMO, 2015). This contrasts extensive measurements in the Chinese Tien Shan (Pang et al., 2011; Wang et al., 2016b, 2018; Chen et al., 2021), where the Chinese Network of Isotopes in Precipitation (CHNIP) became operational in 2004 (Liu et al., 2014; Zhang and Wang, 2018).

The lack of CA precipitation isotope data prevents LMWL development and limits our understanding and the quantification of the regional contributions to precipitation. In contrast to the Chinese Tien Shan, where event-based precipitation samples have been analysed (Pang et al., 2011; Wang et al., 2016b, 2018; Chen et al., 2021), in CA, isotopic compositions from ice cores taken from the Inylchek (Tien Shan) and Fedchenko (Pamir) glaciers have only been used to characterise moisture sources and regional atmospheric circulation patterns (Aizen et al., 1996, 2004, 2009; Kreutz et al., 2003). Moisture sources for the Inylchek glacier were established broadly as the Atlantic Ocean, Mediterranean Sea, and Black Sea on the basis of δ¹⁸O analysis combined with the catalogue of weather types (Aizen et al., 2004), whilst most precipitation over the Pamir was found to have originated in the Atlantic (Aizen et al., 2009). The dominant moisture sources for the western Pamir were identified as the Mediterranean and Caspian seas, which was further evidenced by high d-excess values of 20 ‰ measured in snow and ice cores (Bershaw, 2018). However, according to the event-based precipitation and trajectory analyses, d-excess in the western Pamir was lower at 13 ‰, leading to the conclusion that the Mediterranean contributed approximately 20 % of the total moisture (Juhlke et al., 2019). This discrepancy may be due to the uncertainty in linking ice core samples to moisture trajectories or because regional source signals are altered in CA along the long moisture transportation routes (Bershaw, 2018).

The overall aim of the work is to determine the air mass source regions and trajectories of the precipitation falling over the northern Tien Shan with the purpose of improving our knowledge of this aspect of the regional link between precipitation and water resources. To achieve the overall aim there are four objectives: (i) evaluate the spatial and temporal variations in the isotopic composition of precipitation; (ii) quantify the relationship between δ¹⁸O and δD and location, air temperature, and precipitation depth; (iii) derive LMWLs; and (iv) establish a relationship between variations in isotopic composition of precipitation and air mass origin. Objectives (i), (ii), and (iii) are set to help better understand the atmospheric and geographical controls on precipitation isotope ratio variability in space and over time. The derivation of LMWLs (objective iii) has the benefit of aiding the future assessment of the relative contributions of different water sources to streamflow, groundwater recharge, and isotope mass balance studies. We combined a backward trajectory analysis with isotope data to explore the utility of the latter for determining the relative contribution of different air mass source regions to the regional mountain precipitation. To achieve the objectives and hence the overall aim, water stable isotopes were measured in precipitation samples taken between 2019 and 2021 by the Central Asia Research and Adaptation Water Network (CARAWAN) in five catchments located predominantly in the mountains (Fig. 1).

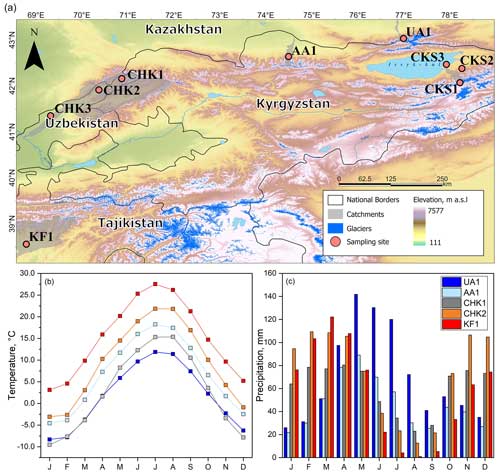
Figure 1 (a) Study area and locations of the sampling sites. Site numbering and details are given in Table 1. A digital elevation model (DEM) derived from the Shuttle Radar Topography Mission (SRTM) is used as the background (available at https://dwtkns.com/srtm30m/, last access: 22 October 2024). Glacier outlines are from the Global Land Ice Measurements from Space (GLIMS) database (Consortium, 2017). National borders and waterbodies are from the Esri ArcGIS Hub. (b) Mean monthly temperature and (c) mean monthly precipitation in the 1980–2015 period.

2 Data and methods

2.1 Study area and sampling programme

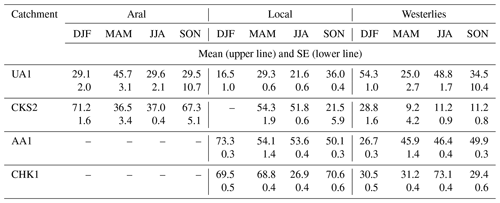
Precipitation samples were collected in five river catchments: Ulken Almaty (UA), Ala-Archa (AA), Chon Kyzyl-Suu (CKS), and Chirchik (CHK) in the Tien Shan and Kofarnihon (KF) in the Pamir-Alay (Fig. 1a). CKS is located on the shores of Issyk-Kul, the largest freshwater mountain lake in CA. Issyk-Kul does not freeze in winter. There is a smaller lake, which freezes in winter, in proximity to the UA1 site. There were eight sampling sites, six of which in the mountains between 1255 and 3277 m a.s.l. and two in the foothills at lower elevations (Table 1).

Table 1 Characteristics of sampling sites (Fig. 1a) and details of the sampling programme. N is the number of samples.

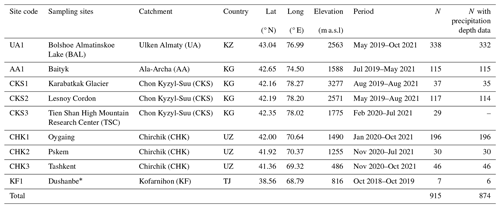
^* Cumulative monthly precipitation.

In the UA, AA, and CKS catchments in the north of the region, the Köppen climate classification is subarctic and tundra in the high mountains and changing to humid continental climate in the middle mountains and to the semi-arid grassland steppe as elevation decreases. In the CHK and KF catchments in the south, the Köppen climate classification changes with elevation from subarctic in the high mountains to humid continental and then to a Mediterranean climate and to semi-arid grasslands and desert on the plains. The region is characterised by the strong seasonal and altitudinal changes in temperature and precipitation (Fig. 1b, c). In the foothills, mean July temperatures reach 24–26 °C and mean January temperatures vary between approximately −10 °C in the north and 5 °C in the south of the region. Annual precipitation ranges between 100 mm a⁻¹ in the deserts of Uzbekistan and south-western Kazakhstan to 1200 a⁻¹ mm in the mountains. The location of the major mountain ranges is an important control over precipitation, and, while the outer ranges receive high precipitation during the wet season, intermontane basins are arid (Lydolph, 1977; Aizen et al., 1997). Precipitation increases in October when regional atmospheric circulation is dominated by the westerly flow. Across most of the region, precipitation maxima occur in spring, in March–April in the south and April–May in the north. At higher elevations in the northern Tien Shan, precipitation peaks between May and July (Fig. 1c). In winter, the northern part of the region is dominated by the Siberian anticyclone and precipitation is low.

The event-based precipitation samples (n= 908) and meteorological data (daily air temperature; depth, type, and duration of event-based precipitation) were collected between 2019 and 2021 (Table 1). Seven samples of cumulative monthly precipitation were collected in Dushanbe using a Palmex rain sampler (http://www.rainsampler.com/portfolio-page/rain-sampler-rs1/, last access: 28 August 2023).

The event-based precipitation samples were collected using the standard Tretyakov precipitation gauges (Yang et al., 1995) immediately after the precipitation events by trained meteorological observers, who were ever present at the sites for the duration of the study period. A comparison of the ability of different types of precipitation collectors to prevent evaporation and associated fractionation showed that the use of this type of gauge is acceptable in isotope hydrology, especially when used in regions with temperate to semi-arid climates and when the time between the precipitation occurrence and sample collection is short (i.e. days) (Michelsen et al., 2018). The rainfall samples were filtered using 0.2 µm filters at the sampling sites and were stored in 2 mL glass vials with screw caps pre-washed several times with the filtered rainwater. The snowfall samples were melted at room temperature, filtered using 0.2 µm filters, and placed in the 2 mL glass vials. To avoid evaporation, all vials were sealed with Parafilm M (Bemis Company, USA, part no. PM-992) and stored at 4 °C.

The samples were analysed using a Picarro isotopic water analyser (L2120-i) with measurement precision of ±0.6 ‰ and ±0.2 ‰ for δD and δ¹⁸O, respectively. The sample analysis procedures and quality were certified by the International Atomic Energy Agency (IAEA) through the completion of a round-robin test using samples supplied by IAEA and according to the procedure and criteria outlined in Wassenaar et al. (2021). The error propagation for d-excess was calculated according to Natali et al. (2022) using the error values of ±0.2 ‰ for δ¹⁸O and ±0.6 ‰ for δD, resulting in a total uncertainty value of ±2.5 ‰.

The samples were injected into the analyser seven times sequentially, and the first three measurements were discarded to avoid any memory effect from the previous samples. The remaining four measurements were checked for consistency using the criterion of standard deviation not exceeding 1.5 ‰ and 0.15 ‰ for δD and δ¹⁸O, respectively. The final values were calculated as means of the four valid measurements. If four measurements satisfying these conditions were not obtained, the samples were re-measured and the average of at least three valid measurements was recorded (52 samples). The isotopic ratios were recorded using delta notation in per mille (‰) relative to Vienna Standard Mean Ocean Water (VSMOW):

$$\begin{array}{}\text{(3)}& \mathit{\delta }=\left({\displaystyle \frac{R_{\mathrm{sample}}}{R_{\mathrm{standard}}}}-\mathrm{1}\right)\times \mathrm{1000}\mathrm{‰},\end{array}$$

where R_sample and R_standard are the isotope ratios ²H $/$ ¹H or ¹⁸O $/$ ¹⁶O of the samples and the standard, respectively. Two primary standards, VSMOW and Standard Light Antarctic Precipitation (SLAP), and two secondary standards were used. The secondary standards were (i) Tuyuksu snow meltwater (TSMW) collected from the Tuyuksu glacier (43.04° N, 77.08° E; 3780 m a.s.l.) located in proximity to the UA1 site with δD of −122.0 ‰ and δ¹⁸O of −17.2 ‰ and (ii) commercially available spring water (SW) with δD of −55.0 ‰ and δ¹⁸O of −8.5 ‰.

2.2 Quantifying links between the isotopic composition of precipitation, the geographical location, and local meteorological conditions

Stepwise regression was used to determine the relationship between the isotopic composition of precipitation, latitude and longitude, and elevation. The δ¹⁸O and δD values derived from all event-based samples collected at the individual sampling sites located between 38.56–43.04° N, 68.79–76.99° E, and 486–3277 m a.s.l. (Table 1) were the response variables.

The effects of surface air temperature and precipitation depth on mean monthly values of δ¹⁸O and δD were examined using linear regression and the method of Dansgaard (1964). The latter suggested that a difference between isotopic ratios of δ¹⁸O averaged over warm (May–October) and cold (November–April) periods are indicative of a control by either local temperature or precipitation amount over isotopic ratios. Positive values of the δ¹⁸O difference are typical of high- and middle-latitude continental regions and indicate a strong surface air temperature control over the isotopic composition of precipitation.

2.3 Local meteoric water line (LMWL)

There are two approaches to defining LMWLs. The first approach assigns equal weighting to all data points regardless of the amount of precipitation they represent and is used to evaluate the atmospheric and hydrometeorological processes controlling the isotopic composition of precipitation. However, samples obtained from smaller precipitation events tend to have lower d-excess due to the sub-cloud evaporation, leading to sample enrichment in comparison to samples obtained from heavy-precipitation events which are more depleted (Hughes and Crawford, 2012; Crawford et al., 2014). To overcome this problem and to represent hydrologically significant precipitation, which is important for local hydrological applications, weighted precipitation is used. This method requires data on precipitation depth (Table 1). Both approaches were used for comparison and to produce recommendations on the LMWL development in the study region considering that precipitation depth may not be available in other projects.

Ordinary least squares regression (OLSR) was used to define LMWLs from the unweighted samples (n= 915; Table 1). Precipitation depth was recorded for 874 samples (Table 1) that were used in the precipitation-weighted analysis. Six regression methods were applied to the event-based precipitation samples: three non-weighted (OLSR, reduced major axis regression (RMA), and major axis regression (MA)) and three precipitation-weighted (precipitation-weighted least squares regression (PWLSR), precipitation-weighted reduced major axis regression (PWRMA), and precipitation-weighted major axis regression (PWMA)) (Hughes and Crawford, 2012; Crawford et al., 2014). The Local Meteoric Water Line Freeware (available at http://openscience.ansto.gov.au/collection/879, last access: 28 August 2024) was used in all calculations. The software calculates the following parameters: slope of regression line (a); standard deviation of the slope (sa); intercept of regression line (b); standard deviation of the intercept (sb); average value of the sum of the squared errors of three methods, either OLSR, RMA, or MA, or three precipitation-weighted regressions; and root mean sum of squared errors (RMSSE), which allows inter-comparison of different regression methods. The proximity of the RMSSE values to 1.0 was used as an indicator of the method suitability for the analysed data set. The t test was applied to evaluate the statistical significance of a difference between OLSR and every other regression method.

2.4 Back-trajectory modelling and cluster analysis using HYSPLIT

To evaluate the controls of atmospheric circulation over the isotopic composition of precipitation and characterise its geographical sources, δ¹⁸O, δD, and d-excess values were used in conjunction with the three-dimensional atmospheric back-trajectory analysis. The HYSPLIT model (Version 5.2.0) using the Global Data Assimilation System (GDAS) meteorological data sets with a horizontal resolution of 1° (Draxler and Rolph, 2013; Stein et al., 2015; Rolph et al., 2017) was used. HYSPLIT was run for each precipitation event registered at UA1, CKS2, AA1, and CHK1 (Table 1) using the latitude, longitude, and elevation of the sites as input parameters. All sites were located between 1255 and 2571 m a.s.l. The use of site elevation as a starting point is justified because, in the region, most moisture in the air column is contained between 1500 and 3000 m a.s.l. where the lifting condensation level is positioned and where precipitation forms (Chen et al., 2024; Zongxing et al., 2016). The length of integration was 120 h because uncertainty in the calculation of trajectories increases with time afterwards (Draxler and Rolph, 2013). The global median value of the water vapour residence time in the atmosphere is estimated as approximately 5 d (120 h) although several studies estimate it as 8–10 d (Van Der Ent and Tuinenburg, 2017).

In line with previous studies (Jorba et al., 2004; Wu et al., 2015; Pérez et al., 2015; Bagheri et al., 2019; Kostrova et al., 2020) and to comply with the HYSPLIT cluster analysis function requirements, single trajectories were calculated instead of trajectory ensembles, potentially introducing uncertainty. The starting time of each back trajectory was defined as the hour closest to the start of precipitation event. The median duration of precipitation events was 240 min. A comparison between trajectories calculated for the start and the end of precipitation events exceeding 660 min (90th percentile) was performed. The differences between the coordinates of their point of origin were within the HYSPLIT resolution.

The generated back trajectories were grouped using cluster analysis based on minimising the distance and maximising the difference between clusters with distinct trajectories (Dorling et al., 1992). The HYSPLIT 5.2.0 built-in cluster analysis function (available at https://www.ready.noaa.gov/HYSPLIT_hytrial.php, last access: 28 August 2024) was used to derive clusters for the UA1, CKS2, AA1, and CHK1 sites. Total spatial variance (TSV), defined as sum of the spatial variances of all clusters, was used to determine the optimal number of clusters. The percentage of change in TSV was plotted against the number of clusters, and the first large increase in the change in TSV was taken as an indicator of the final number of clusters (Wilks, 1995; Kostrova et al., 2020).

Isotopic ratios and d-excess values were initially analysed for the clusters generated for each site and season. However, many trajectory clusters generated for different sites were similar (e.g. the “West” cluster was generated for each site; see Fig. 6 later in the text). Splitting the data by season for each site resulted in a small number of members in each cluster. To overcome this problem, similar trajectory clusters from different sites were merged. Some of the clusters included data from all sites (e.g. West), while others were limited to a smaller number of sites. Isotopic ratios and d-excess were averaged by cluster and meteorological seasons. Analysis of variance (ANOVA) and pairwise t tests were used to test whether the differences between δ¹⁸O, δD, and d-excess values attributed to different clusters were significant at the 95 % confidence level.

2.5 Quantifying relative contributions of the trajectory sources to total precipitation

The proportional contributions of the trajectory sources to the total precipitation were quantified using a linear mixing model whereby two isotopic signatures (δ¹⁸O and δD) enable partitioning of the total precipitation between three sources (Phillips and Gregg, 2001). Fractional contributions were calculated using Eqs. (4) and (5) (Phillips and Gregg, 2001):

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathit{\delta }}_P=f_{\mathrm{A}}{\mathit{\delta }}_{\mathrm{A}}+f_{\mathrm{B}}{\mathit{\delta }}_{\mathrm{B}}+f_{\mathrm{C}}{\mathit{\delta }}_{\mathrm{C}},\text{(5)}& {\displaystyle }{f}_{\mathrm{A}}+f_{\mathrm{B}}+f_{\mathrm{C}}=\mathrm{1},\end{array}$$

where f_A, f_B, and f_C are fractional contributions of different trajectory groups to local precipitation; δ_A, δ_B, and δ_C are isotopic values of each group by season; and δ_P is the seasonal mean isotopic value for all precipitation events during the sampling period. The software IsoError Version 1.04 (available at http://www.epa.gov/eco-research, last access: 28 August 2024) (Phillips and Gregg, 2001) was used to apply the mixing model.

The mixing model was limited to a maximum of three contributing trajectory sources (Eqs. 4–5), but up to five clusters of back trajectories were identified. The number of clusters was reduced to form three trajectory groups for different seasons using the following criteria: (i) direction of travel, (ii) distance travelled, and (iii) whether local circulation trajectories remained within the catchment boundaries. Clusters 1, 2, and 3 were merged to form a single (West) group because, despite the differences in directions, they were associated with the long-distance transport along the peripheries of depressions originating over the Atlantic. The statistical significance of differences between δ¹⁸O, δD, and d-excess values associated with different groups was assessed using ANOVA.

3 Results

3.1 Seasonal and spatial variability in δD and δ¹⁸O

The descriptive statistics of δD and δ¹⁸O derived from the event-based precipitation at each catchment are summarised in Fig. 2 and the Supplement, Table S1 (where data are shown for each sampling site and for three types of precipitation: snow, rain, and mixed). The δ¹⁸O and δD means and standard deviations for all events between 2019 and 2021 were −8.6 ± 6.5 ‰ and −56.1 ± 50.1 ‰, respectively. Rain samples (n= 528) were characterised by higher mean δ¹⁸O and δD values of −4.9 ‰, and −28.1 ‰, respectively, whereas snow samples (n= 260) had lower mean δ¹⁸O and δD values of −15.4 ‰ and −110.7 ‰, respectively (Table S1). Variability in the snow sub-set was higher than in the rain sub-set, with standard deviations of ±5.5 ‰ (δ¹⁸O) and ±44.6 ‰ (δD) for snow and ±4.3 ‰ (δ¹⁸O) and ±30.0 ‰ (δD) for rain. The mixed-precipitation data set, based on 120 samples, showed intermediate values of δ¹⁸O of −9.7 ‰ and δD of −61.7 ‰; the values of standard deviations were lowest for δ¹⁸O in comparison with the rain and snow sub-sets and broadly the same as for rain for δD (Table S1).

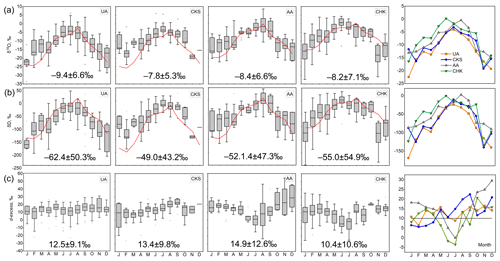
Figure 2 Box plots of (a) δ¹⁸O, (b) δD, and (c) d-excess in precipitation collected at the four catchments (see Fig. 1 and Table 1 for locations of catchments and the number of samples) between 2019 and 2021 (left panels) and mean monthly d-excess values (right panels). Precipitation was sampled at three sites in CHK and CKS, and data from all sites are included. Annual mean values ± standard deviation calculated for the 2019–2021 period are shown. The horizontal line in (c) (right panel) shows the global mean d-excess (10 ‰). The red lines in (a) and (b) (left panels) show data from the Waterisotopes Database (Bowen, 2022). The Waterisotopes Database data were averaged over all sampling locations in CKS and CHK.

Clear seasonal cycles were observed in δD and δ¹⁸O values in each catchment where isotopic ratios were higher in summer and lower in winter (Fig. 2a, b; Table S1). In the event-based precipitation samples, δ¹⁸O and δD values varied widely from −33.6 ‰ to 8.6 ‰ and from −258.8 ‰ to 45.2 ‰, respectively (Fig. 2a, b). Both δ¹⁸O and δD showed larger variability in those months when snow and mixed precipitation were observed, namely between November and March in the more southerly CHK catchment and in April–May and November in other catchments (Fig. 2a, b; Table S1). The CHK3 site (17 % of all CHK samples; two samples only in JJA) was located at 486 m a.s.l., enhancing the difference with other catchments and sites (Fig. 3). Between late spring and early autumn, the between-sample variability was reduced, and the standard deviations were lower except for the higher-elevation and more northerly catchments, i.e. UA and AA (Fig. 2a, b).

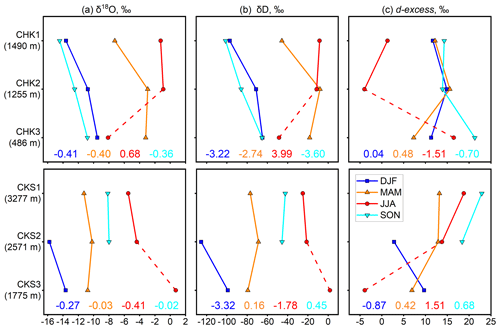
Figure 3 Changes with elevation in (a) δ¹⁸O, (b) δD, and (c) d-excess by season in CHK (upper panels) and CKS (bottom panels). Dashed lines indicate a small number of samples and low precipitation per event in CHK3 and CKS3. Numbers show seasonal values of elevational gradients (‰ (100 m)⁻¹).

The relationships between isotopic precipitation composition and latitude, longitude, and elevation were quantified by the following equations, derived using all available samples:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{18}}\mathrm{O}=\mathrm{36.3}-\mathrm{1.18}\mathrm{lat}+\mathrm{0.07}\mathrm{long}-\mathrm{0.00001}E,\text{(7)}& {\displaystyle }\mathit{\delta }\mathrm{D}=\mathrm{342}-\mathrm{10.75}\mathrm{lat}+\mathrm{0.73}\mathrm{long}-\mathrm{0.002}E,\end{array}$$

where lat is latitude (°), long is longitude (°), and E is elevation (m a.s.l.). Regression equations for four meteorological seasons are shown in Table S2. Latitude is the only statistically significant predictor of both δ¹⁸O and δD in the overall data set (p < 0.01), while relationships with longitude and elevation were not statistically significant. Elevation was the only significant predictor of δ¹⁸O and δD in winter (p < 0.05). Elevation and longitude were significant predictors in autumn (p < 0.05). Three sites with an elevation difference of more than 800 m a.s.l. in CHK and CKS allowed examination of elevation gradients in isotopic ratios and d-excess, which were calculated using the lowest and the highest sampling points for which data were available (Table 1). For both δ¹⁸O and δD, the gradients were highest in summer but not consistent between CKS and CHK (Fig. 3). Very few samples were available for the CHK3 (city of Tashkent) site located in the foothills, and isotopic ratios were not consistent with the high temperatures registered at this site.

The indices, derived from the application of the Dansgaard (1964) method, confirmed the links between isotopic ratios and temperature evident in Fig. 2. The indices were positive, ranging between 7.0 ‰ in CKS and 8.6 ‰ in UA (Table S3), therefore demonstrating a strong temperature effect and a lower influence of precipitation amount on isotopic ratios. For the whole data set, coefficients of determination for the event-based values of δD and δ¹⁸O and air temperature (measured at the sampling sites) were 0.56 and 0.54, respectively (Eqs. 8–9), ranging between 0.46 and 0.66 for the individual sampling sites (Table S4). Except CHK3, they were statistically significant at the 95 % confidence level. The δ¹⁸O and δD changed by 0.62 ‰ °C⁻¹ and 4.68 ‰ °C⁻¹, respectively, for the whole data set. The highest coefficients were obtained for the AA1 and CHK1 sites (0.66 and 0.64, respectively) and the lowest (0.27) for CHK3. The highest gradients were observed at CHK1 (0.74 ‰ °C⁻¹ and 5.50 % °C⁻¹) and the lowest at CHK3 (0.32 ‰ °C⁻¹ and 2.46 % °C⁻¹) (Table S4).

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{18}}\mathrm{O}=\mathrm{0.62}T-\mathrm{10.61},R^{\mathrm{2}}=\mathrm{0.56},p<\mathrm{0.01},\text{(9)}& {\displaystyle }\mathit{\delta }\mathrm{D}=\mathrm{4.68}T-\mathrm{71.64},R^{\mathrm{2}}=\mathrm{0.54},p<\mathrm{0.01},\end{array}$$

where T is air temperature (°C) at the sampling sites.

There was no statistically significant correlation between isotopic ratios and precipitation depth in the study region.

3.2 The d-excess variations over the region and elevation effects

The mean seasonal d-excess values for all samples were 12.5 ± 11.4 ‰ (DJF), 12.7 ± 7.8 ‰ (MAM), 10.0 ± 11.3 ‰ (JJA), and 16.6 ± 9.5 ‰ (SON) (Fig. 2c). In the AA and CHK catchments, minimum d-excess values were observed in June–July (when mean monthly values were negative), increasing in DJF (AA) and MAM and SON (CHK). In UA and CKS, seasonal cycles were less pronounced (UA) or different, with a maximum in August–September (CKS). In CKS, located on the shores of Issyk-Kul, d-excess was below 10 ‰ between January and April.

In spring, d-excess values above 10 ‰ were observed in all catchments (except CKS in March–April) and autumn–early winter in line with the occurrence of the wet season (Fig. 1). In the AA catchment, values of over 10 ‰ were observed between September and May. Values of more than 20 ‰, indicating strong re-evaporation, were evident between October and December in the AA catchment and in the individual months in the same period in CHK (October) and CKS (September, December). A particularly high mean monthly value, reaching 29.5 ‰, was recorded in the AA catchment in December although this calculation is based on seven samples (Table S1).

Figure 3 shows elevational profiles of d-excess. In CKS, d-excess values increased with elevation from −3.9 ‰ (n=3) at CKS3 located at 1755 m a.s.l. to 18.9 ‰ (n=28) at CKS1 (3277 m a.s.l.) in JJA. Similar altitudinal profiles were observed in MAM, albeit with a reduced gradient (6.9 ‰ and 13.2 ‰ at CKS3 and CKS1, respectively), and in SON, when data were available for the CKS2 (2571 m a.s.l.) and CKS1 sites only (Fig. 3c). In CHK, d-excess values changed little at the higher-elevation sites of CHK2 (1255 m a.s.l.) and CHK1 (1490 m a.s.l.) in DJF, MAM, and SON (between both seasons and sites). The largest seasonal variations occurred at the low-elevation (486 m a.s.l.) site of CHK3. The steepest elevational gradients were observed in JJA, when the mean seasonal d-excess declined from 16.5 ‰ (n=2) in CHK3 to a negative value of −3.9 ‰ (n=4) in CHK2. This trend was opposite to that of CKS. Similar but less pronounced gradients were observed in SON. The high d-excess values at CHK3 were not consistent with its low elevation, high air temperature observed during the precipitation events considered (29.8 °C) (Table S3), and small precipitation depth (on average 0.1 mm per event).

Analysis of the overall event-based data set showed that there were no significant geographical controls over d-excess. However, analysis of the seasonal sub-sets showed that elevation was a significant predictor of d-excess (p < 0.01) in all seasons. Longitude was a statistically significant predictor of d-excess in MAM (p < 0.05) and SON (p < 0.05) (Table S2).

3.3 LMWLs for the mountains of Central Asia

LMWLs were calculated using the whole data set and for the individual catchments (Tables S5–S9). The LMWL developed from the whole set of the event-based precipitation samples (Table 1; Fig. 4a) using the most common unweighted OLSR method (Sect. 2.3) was

$$\begin{array}{}\text{(10)}& \mathit{\delta }\mathrm{D}=\left(\mathrm{7.56}\pm \mathrm{0.05}\right){\mathit{\delta }}^{\mathrm{18}}\mathrm{O}+\left(\mathrm{8.65}\pm \mathrm{0.54}\right),R^{\mathrm{2}}=\mathrm{0.96}.\end{array}$$

The LMWL developed from 149 mean monthly averaged event-based samples values including the Dushanbe monthly cumulative precipitation samples (Fig. 4b) using the same regression method was

$$\begin{array}{}\text{(11)}& \mathit{\delta }\mathrm{D}=\left(\mathrm{7.6}\pm \mathrm{0.1}\right){\mathit{\delta }}^{\mathrm{18}}\mathrm{O}+\left(\mathrm{9.6}\pm \mathrm{1.2}\right),R^{\mathrm{2}}=\mathrm{0.97}.\end{array}$$

Figure 4 and Table S5 show the parameters of the derived regression equations. The slope and intercept values were lower (Eqs. 10–11; Fig. 4a–c) than those of the GMWL (Dansgaard, 1964). The 95 % confidence intervals in Eq. (10) were 7.6–9.7 for the intercept and 7.5–7.7 for the slope. The corresponding confidence intervals in Eq. (11) were 7.2–11.9 and 7.3–7.8. For the total study area, the slope changed from 6.1 ± 0.1 in JJA to 8.1 ± 0.1 in DJF and the intercept from 2.7 ± 0.7 in JJA to 13.8 ± 2.1 in DJF. The DJF slope and intercept values in OLSR LMWL, derived from 17 event-based samples, were lower in CKS than in other catchments, at 6.7 ± 0.5 and −12.1 ± 8.3, respectively (Fig. 4d). The slope value for DJF was close to that in JJA (in contrast to other catchments), indicating strong evaporation from the lake.

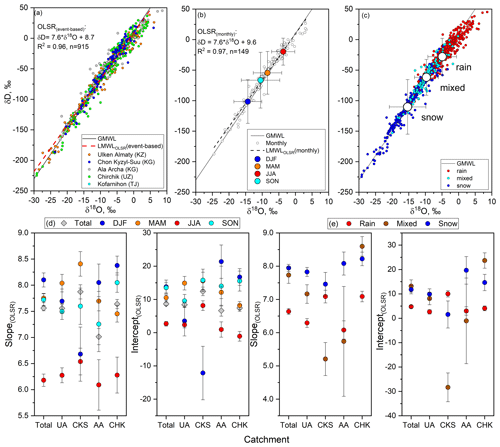
Figure 4 The upper panels show dual δD and δ¹⁸O plots for (a) the event-based samples for individual catchments, (b) monthly averaged values and seasonal means, and (c) different types of precipitation. The lower panels show the OLSR-based LMWL slopes and intercepts (d) using event-based data for each catchment by season and (e) by type of precipitation.

The performance of different regression methods was assessed using the RMSSEav statistics (Sect. 2.3). For all six methods, RMSSEav values were close to 1, indicating good performance; however, the best regression fit was obtained by the RMA and PWLSR methods for the non-weighted and weighted precipitation, respectively (Tables S6–S9). Generally, the weighted methods (PWLSR, PWRMA, and PWMA) generated steeper LMWL slopes than the non-weighted methods (OLSR, RMA, and MA). However, a t test, applied to assess the differences between the regression metrics generated by the six methods and OLSR, showed that results of the RMA method were not significantly different from OLSR (p > 0.05) when calculations were made for individual basins, seasons, and types of precipitation, with two exceptions as follows: (i) the event-based rain-only sub-set and (ii) all event-based samples combined across the region (Tables S5, S9). Parameters of the regression equations for each catchment, season, and precipitation type are shown in Tables S5–S9. Here, the outcomes from the OLSR and PWLSR methods are summarised.

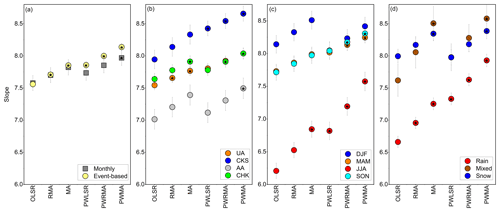
Figure 5 LMWL slopes derived from the regression equations developed using six methods (see Sect. 2.3 for abbreviations) (a) for the event-based and monthly data set for all samples across the region, (b) by catchment, (c) by season, and (d) by precipitation type for the event-based samples. Statistically significant values are marked with a star. The values of slopes and intercepts and the outcomes of t tests of between-method differences are presented in Tables S5–S9.

For the whole region, the slope values varied from 7.6 (monthly and event-based) OLSR to 7.7 (monthly) and 7.9 (event-based) using PWLSR (Fig. 5a). The performance of the methods varied between catchments (Fig. 5b). The largest between-method differences were observed in CKS (n= 149), with slope values ranging between 7.9 (OLSR) and 8.4 (PWLSR). Statistically significant differences between the non-weighted OLSR and the weighted PWLSR method were observed in AA and CHK because of the lower amounts of precipitation, especially in CHK in summer. In the UA and CKS sites, the differences were not significant. The slope values derived from the event-based precipitation data for SON (n= 138) and DJF (n= 168) did not vary significantly between the OLSR and PWLSR methods (Fig. 5c) while they were significantly different in MAM (n= 273) and JJA (n= 290). Larger differences were observed in JJA (n= 290) when slope values varied from 6.2 (OLSR) to 6.8 (PWLSR) (Fig. 6c). The similarly large differences characterised the rain sample sub-set (n= 514), with slope values ranging from 6.7 (OLSR) to 7.3 (PWLSR) (Fig. 5d).

3.4 Relationships between isotopic composition and precipitation provenance

Overall, 766 of the 5 d (120 h) back trajectories were generated for every precipitation event for four sampling points: UA1 (n= 338), CKS2 (n= 117), AA1 (n= 115), and CHK1 (n= 196) (Table 1). Overall, five clusters were identified: the northern part of Kazakhstan–southern Siberia (North – Cluster 1); south-eastern Europe, the Black Sea, and the Caspian Sea (West – Cluster 2); Iran and the eastern Mediterranean (South-West – Cluster 3); the lower reaches of the Syr Darya and Amu Darya and irrigated area around the Aral Sea (Aral – Cluster 4); and precipitation formed within the study catchments (Local – Cluster 5).

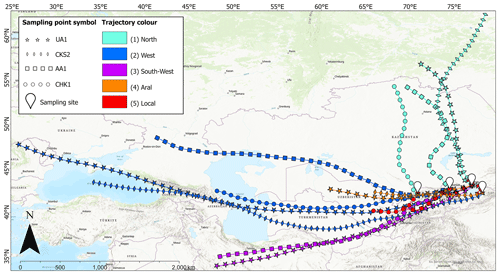
Figure 6 Trajectory clusters including mean back trajectories (as generated by HYSPLIT) for the original clusters for four sampling sites for the study period. Esri ArcGIS Pro World Topographic Map and World Hillshade are used as the background. Publisher's remark: please note that the above figure contains disputed territories.

Clusters 1 and 2 were identified at each site, accounting for 6 %–26 % and 5 %–19 % of all trajectories (Table 2; Fig. 7). The Cluster 1 trajectories were most frequent at UA1 and least frequent at CHK1 and were the most frequent group in JJA overall. In DJF, the Cluster 1 trajectories were registered only one and eight times at UA1 and CHK2 (Fig. 7). The Cluster 2 trajectories were most frequent at CHK1 and least frequent at UA1 (observed three times per season in MAM, JJA, and SON) and CKS2 (observed twice per season in DJF, JJA, and SON). The Cluster 3 trajectories originated in Iran, reaching UA1 and AA1 predominantly in DJF and MAM, but they were not observed at CHK1 and CKS2 (Fig. 7). While limiting trajectories to 120 h duration places their origin in Iran, the extension of their duration leads to the eastern Mediterranean, albeit with higher uncertainty. Clusters 1, 2, and 3 represented the long-distance moisture transport with mean trajectory lengths and standard deviations of 1738 ± 451, 3285 ± 1109, and 2652 ± 185 km, respectively. Trajectories from Clusters 1, 2, and 3 represented circulation along the peripheries of the low-pressure systems located north-west or west of the study region, and the differences between them were due to the latitudinal positions of the low-pressure system centres. Cluster 4 included shorter trajectories (1188 ± 237 km) to UA1 and CKS2 from the irrigated lands located along the Syr Darya and Amu Darya and the Aral Sea. This cluster accounted for 33 % and 44 % of all trajectories at UA1 and CKS2, respectively (Table 2; Fig. 6), with the highest frequency in MAM and JJA (Fig. 7). The lengths of the 5 d trajectories in Cluster 5, representing precipitation formed locally, varied between 292 km at CKS2 and 565 km at AA1, with a mean length of 438 ± 140 km. There is uncertainty about allocating trajectories to Clusters 4 and 5 at CHK1 because, although the Cluster 5 trajectories satisfied the allocation criteria, the lower part of the CHK catchment is irrigated and the Chirchik is a tributary of the Amu Darya. Trajectories of this cluster were observed at each site, accounting for 26 % (UA1) to 45 %–61 % (other sites) of all trajectories (Table 2).

Table 2 Frequency of trajectories by cluster and mean values (upper line) and standard deviation (lower line) of δ¹⁸O, δD, and d-excess ( ‰). C is cluster; SD is standard deviation; N is the number of trajectories corresponding to individual precipitation events and their proportion of the total for each site; Lat is latitude (° N) and Long is longitude (° E); D is distance from the trajectory source (120 h iteration) to the sampling point (km). The seasonal mean temperature (T) and total and mean precipitation (P) were derived for the days when precipitation samples were collected over the sampling period (Table 1) and averaged (summed) over trajectory clusters and seasons.

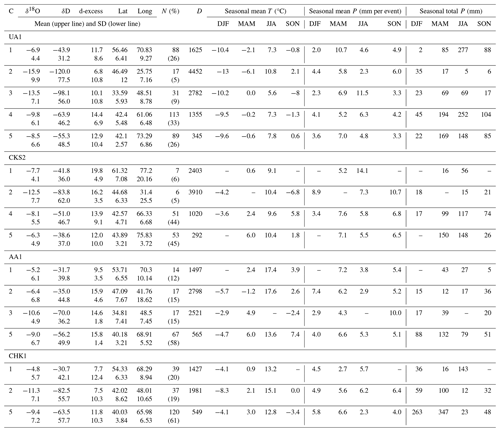
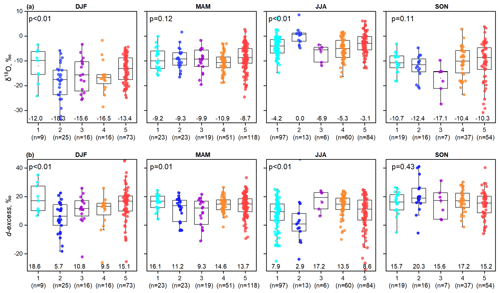
Figure 7 Seasonal values of (a) δ¹⁸O and (b) d-excess according to the trajectory clusters. Numbers along the x axes show the number of events in each group and season.

Isotopic ratios and d-excess values averaged over the trajectory clusters by site are shown in Table 2; the box plots are shown in Figs. S2 and S3. The between-cluster differences in δ¹⁸O were largest in JJA and DJF, while in MAM and SON (wet seasons; Fig. 1c), they were not statistically significant at the 95 % confidence level (Fig. 7). In DJF, isotopic ratios of Cluster 1 precipitation were less negative with a mean δ¹⁸O value of −12.01 ‰, while ratios associated with Cluster 2, representing the longest-distance transport from the west, were more negative, with a mean δ¹⁸O of −18.29 ‰ (Fig. 7a). However, less negative values of δ¹⁸O and δD were observed at AA1 in Cluster 2 (−6.4 ‰ and −35.0 ‰, respectively), where trajectories started over the East European Plain and crossed the deserts of western Kazakhstan. In JJA, the highest mean δ¹⁸O value of 0.01 ‰ characterised Cluster 2. The lowest mean δ¹⁸O values characterised Cluster 3 in both JJA and SON (−6.94 ‰ and −17.6 ‰, respectively). Cluster 5 was characterised by the highest in-cluster variability in δ¹⁸O. At UA1, AA1, and CHK2, Cluster 5 trajectories arrived predominantly from the south-west and corresponded to more negative isotopic values, while at CKS2, they arrived from the north-east and corresponded to higher isotopic ratios (Fig. 6; Table 2).

The between-cluster differences in d-excess were significant in all seasons except SON (Fig. 7b). In DJF, the lowest mean d-excess value (5.7 ‰) characterised Cluster 2 and the highest (18.6 ‰) characterised Cluster 1 (Fig. 7b). The highest mean JJA value of 17.2 ‰ characterised Cluster 3, arriving from Iran to UA1 and AA1. Cluster 4 trajectories originating over the irrigated lands in the Aral Sea basin had mean annual d-excess values of 14.4 ‰ and 13.9 ‰ at UA1 and CKS2 (Table 2). Cluster 5 was characterised by the highest variability in d-excess values (Fig. 7b).

3.5 Relative contributions of moisture sources to precipitation

The three components of the mixing model (Eq. 4) were (i) δ_A – precipitation formed inland over the Aral Basin (Cluster 4); (ii) δ_B – locally formed precipitation (Cluster 5); and (iii) δ_C – precipitation associated with the Atlantic depressions (merged Clusters 1–3; termed “Westerlies”), and δ_P was the mean seasonal value of the isotopic ratios (Fig. 8). Using UA1 in DJF as an example, the mean seasonal precipitation isotopic ratios (δ_P) were −134.5 ‰ for δD and −17.9 ‰ for δ¹⁸O, respectively. The three components of mixing-model isotopic ratios were δ_A (−121.6 ‰ for δD and −17.1 ‰ for δ¹⁸O), δ_B (−91.9 ‰ for δD and −12.7 ‰ for δ¹⁸O), and δ_C (−154.3 ‰ for δD and −19.9 ‰ for δ¹⁸O). At UA1, three groups of trajectories were registered in each season, and at CKS2 the same was the case in all seasons except DJF, when there was no precipitation associated with local trajectories. Only two groups – Local and Westerlies – were represented at AA1 and CHK2.

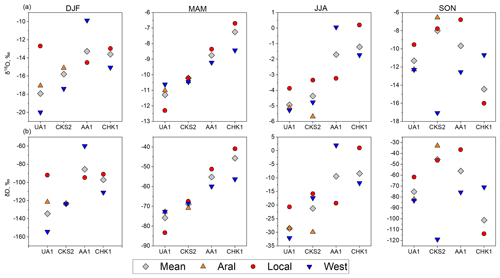
Figure 8 The values of (a) δ¹⁸O and (b) δD characterising seasonal precipitation (δ_P), precipitation originating over the Aral Basin (δ_A), locally formed precipitation (δ_B), and precipitation associated with the westerly transport (δ_C) for each basin.

The proportional contributions of the identified trajectory sources at different sites and seasons are shown in Table 3. The westerly flow was the main contributor to precipitation at UA1 in winter (54 %) and at UA1 and CHK2 in summer (49 % and 73 %, respectively). The Aral Basin contributed 46 % at UA1 in MAM and 71.2 % and 67.3 % at CKS2 in DJF and SON, respectively. In other seasons, the contribution from the Aral Basin varied between 29 % and 37 %. Contributions of the locally formed precipitation ranged from 16 % to 73 %, being particularly high at CKS2 in MAM and JJA, while the absence of a contribution from local sources in DJF was likely an artefact of the small number of samples (n= 7). Locally formed precipitation prevailed throughout the year at AA1 and at CHK2, except JJA.

Table 3 Proportional contributions of moisture sources (%) to precipitation and standard error (SE).

4 Discussion

4.1 Regional trends in isotopic ratios and d-excess

Clear seasonal cycles of δ¹⁸O and δD were observed in every catchment, with higher δ¹⁸O and δD values registered in summer and lower values in winter (Fig. 2), in line with the annual temperature cycle (Fig. 1b). The maximum enrichment occurred between June in the south (e.g. CHK) and in July–August further north, while the most negative values were registered between November and February (Fig. 2; Table S1). In the CKS catchment, the lake effect was evident in the cold season due to the contrast between an enhanced contribution of heavier water vapour from the lake and lighter vapour delivered by the cold air masses (Bowen et al., 2012; Xiao et al., 2017; Minder et al., 2020), resulting in the less negative isotopic ratios of precipitation (Fig. 2). Air temperature was a statistically significant predictor of δ¹⁸O and δD, but coefficients of determination of 0.46–0.66 implied that using air temperature as a proxy for isotopic signatures may lead to high uncertainty in the reconstructions of isoscapes in the mountains. Similar coefficients have been obtained for the Chinese Tien Shan (Wang et al., 2017, 2022), northern Kazakhstan (Yapiyev et al., 2020), and other high- and middle-latitude regions (Gat and Gonfiantini, 1981; Gat, 1996; Rozanski et al., 1993; Putman et al., 2019) although stronger links were reported by Kostrova et al. (2020) for south-eastern Siberia. The δ¹⁸O and δD values changed by 0.62 ‰ °C⁻¹ and 4.68 ‰ °C⁻¹, respectively, for the whole data set, which is consistent with the results for the upper Urumchi (alternatively Ürümqi) Basin in the Chinese Tien Shan (Pang et al., 2011). Temporal variability in isotopic ratios was stronger in winter, and this was also confirmed by a comparison of the snow and rain data sets (Table S1 and Fig. 4). In winter, day-to-day temperature fluctuations, associated with changing synoptic conditions, are stronger than in summer, with mean temperature changes between 2 consecutive days of 4 °C (Shahgedanova, 2002). There was no statistically significant link between isotopic ratios and event precipitation depth, even in the arid CHK catchment. Previous studies conducted in the neighbouring regions (Liu et al., 2014; Wang et al., 2018; Juhlke et al., 2019) and globally (Bowen, 2010; Bowen et al., 2019; Putman et al., 2019) also concluded that this correlation was weak.

The observed seasonal cycles of δ¹⁸O and δD were generally consistent with the global interpolation of precipitation isoscapes (Bowen and Revenaugh, 2003; Bowen et al., 2019), the global high-resolution isotope precipitation data (Terzer-Wassmuth et al., 2021), and results reported for the Chinese Tien Shan (Liu et al., 2014; Wang et al., 2019). However, the interpolations significantly underestimated isotopic ratios in the study region between October and March (Fig. 2a, b) due to the lack of data available to date. For example, the annual mean difference between measured ratios and those derived from the global database (Fig. 2) varied from −0.3 ‰ (CHK) to 4.8 ‰ (CKS) for δ¹⁸O and from −6.7 ‰ (CHK) to 37.4 (CKS) for δD but reached 10.1 ‰ (CKS) for δ¹⁸O and 52.5 ‰ (AA) for δD in winter (Figs. 2a, b; S1).

Seasonal variations in the importance of geographical predictors were observed due to the indirect effects of different moisture source regions, atmospheric disturbances, and changes in evaporation between summer and other seasons. In CA, spatial variability in δ¹⁸O and δD in precipitation in all seasons except autumn was characterised by an overall increase in isotopic ratios from north (UA) to south (CHK) (Table S1). The application of stepwise regression to the event-based data (Eqs. 6–7) showed that latitude was a statistically significant predictor of δ¹⁸O and δD in the overall CA data set. In the Chinese Tien Shan, mean isotopic ratios, measured at the mountain sites (between 1628 and 2458 m a.s.l., which is similar to the elevations of our sites), were less negative in the south-west and more negative in the north-east in JJA (Wang et al., 2016b). When combined, both data sets confirm this spatial trend, with mean JJA δ¹⁸O changing from −1.2 ‰ and −1.7 ‰ in CHK1 (70.64° E) and AA1 (74.50° E) to −10.1 ‰ (93.03° E) and −10.5 ‰ (94.42° E) in China. In CA, elevation was a significant predictor of δ¹⁸O and δD in winter and autumn, and longitude was a significant predictor in autumn and spring, when westerly flow dominates. In the Chinese Tien Shan, there was no clear spatial or elevational trend at the mountain sites in DJF (Wang et al., 2016b). The number of sites in our study was relatively small (Table 1), and CKS experienced lake effects. Both factors limited the performance of the regression model. Liu et al. (2014) used 29 sampling points in a similar analysis in northern China; Wang et al. (2016b) used 23 sites (although only 6 were in the mountains). The regression model can be improved in the future using isotopic data from a wider range of geographical locations, e.g. by combining data sets from CA and the Chinese Tien Shan and by including the newly established sites in the western Pamir, where sampling commenced in 2023.

Previous studies in the Chinese Tien Shan and in the western Pamir showed that the annual cycle of d-excess was opposite to those of δ¹⁸O and δD, with high (positive) values in the cold season and low (negative) values in summer (Pang et al., 2011; Wang et al., 2016b; Zhang and Wang, 2018; Juhlke et al., 2019). The JJA d-excess values in AA and CHK, calculated using unweighted precipitation, confirmed this conclusion, being as low as −3.5 ‰ and similar to d-excess values measured in Iran and Iraq (Juhlke et al., 2019). Low precipitation amounts and higher temperatures, especially at CHK, enhanced negative d-excess values in JJA. There was a clear distinction between the AA and CHK catchments located in the west (72–74.5° E; Table 1), which matched the wider regional pattern, and CKS (78° E) located in proximity to Issyk-Kul (Fig. 2c; Table S1), where the lake effect resulted in lower d-excess values which fell below 10 ‰ between January and April and increased to 20 ‰–22 ‰ in August–September (Fig. 2c). The annual d-excess cycle in UA in the north-east of the study area (43° N, 77° E) was less pronounced. This sampling site was located by a much smaller (∼0.8 km²) mountain lake which freezes in winter. While locations of sampling sites were to an extent defined by the practical aspects of long-term monitoring, the presence of lakes complicated analysis of geographical d-excess patterns.

The observed elevational profiles of d-excess were inconsistent between sites and seasons (Fig. 3), partly because precipitation events were not always observed on the same days at different sites in the same catchment but also because of the different local conditions. At CKS, d-excess increased with elevation in summer in line with the decreasing air temperature and the distance that raindrops travel between the cloud base and land surface (Natali et al., 2022). This is consistent with a broader pattern of elevational change and d-excess described by Bershaw (2018). In DJF, when the sub-cloud evaporation effect is absent (Fröhlich et al., 2001), d-excess values declined with elevation between the CKS2 and CKS3 sites. Lapse rates of d-excess were small in spring and autumn (wet seasons), likely due to the reduced sub-cloud evaporation and the occurrence of predominantly liquid precipitation at lower elevations and snow at CKS1 in spring. Thus, in CKS, d-excess values for snow and rain were 9.7 ‰ and 15.3 ‰, respectively (Table S1).

In CHK, low-intensity precipitation events dominated in JJA, with 86 % and 74 % precipitation events producing less than 10 and 5 mm, respectively. At the same time, air temperatures were high, even in the middle mountains where most samples were collected (Fig. 1; Table 1), leading to a strong sub-cloud evaporation effect. The lowest mean d-excess value of −3.9 ‰ was registered at CHK2 (1255 m a.s.l.) in JJA, increasing to an average of 1.3 ‰ at CHK1 (1490 m a.s.l.), which is similar to CKS (Fig. 3). However, the mean summer d-excess value of 16.5 ‰ in CHK3 (city of Tashkent, 486 m a.s.l.; derived from two precipitation events only) was inconsistent with the observed meteorological conditions. We suggest that Tashkent, located in the extensively irrigated foothills and featuring urban irrigation, may exhibit higher d-excess values in JJA (as well as SON) due to the contribution of water re-evaporated from the irrigated land. Similar oasis effects were reported by Wang et al. (2016a, b) and Zhang and Wang (2018); however, a larger number of samples is required for confirmation.

4.2 LMWLs

LMWLs were developed for the study area for the first time to complement those for the Chinese sector of the Tien Shan (Wang et al., 2018). Although isotopic ratios are controlled by equilibrium fractionation, in the arid regions, where significant evaporation of precipitation is observed, especially during events of light precipitation or virga, kinetic fractionation is important, resulting in the difference between the GMWL and LMWLs (Tian et al., 2007; Wang et al., 2018, 2019; Chen et al., 2021). In CA, the availability of the LMWLs enables quantification of the relative contributions of water sources, including precipitation, to runoff (Bowen et al., 2018; He et al., 2019) and calculation of lake mass balance (Yapiyev et al., 2020). Both tasks are relevant to adaptation policies in this water-deficient region.

Results obtained using monthly and event-based samples were close, indicating that either can be used to develop LMWLs in the region. Application of the standard OLSR method to the data from individual catchments and seasons showed that higher slope values were observed in winter and spring (7.6–8.4) when the air temperature was lower and relative humidity higher, and when precipitation peaked in spring. The lowest values (6.1–6.3) were observed in summer, suggesting strong evaporation and a contribution to precipitation from local recycled moisture (Fig. 4; Table S5). The CKS catchment featured strong seasonal variations with the lowest slope value of 6.6 in DJF, pointing at evaporation from Issyk-Kul, and the highest value of 8.4 in spring. The seasonal variations in the LMWL slope were consistent with those in the Chinese Tien Shan (Wang et al., 2018); however it is difficult to compare spatial variations in the LMWL slopes because of a limited number of sites used in this study. A clear north-to-south gradient for the LMWL slope was reported for the Chinese Tien Shan and adjacent regions, with the lowest values observed in the extremely arid Tarim Basin (Wang et al., 2018). In our study region, the lowest summer and annual values were observed in the AA rather than in the CHK catchment although AA is located in the northern part of the study area (albeit in the inner Tien Shan).

Previous studies (Hughes and Crawford, 2012; Liu et al., 2014; Wang et al., 2018) demonstrated that low summer precipitation contributes to uncertainty in modelling LMWLs. Whilst there was no statistically significant link between isotopic ratios and precipitation depth overall, the potential effects of low-intensity precipitation on summer isotopic ratios, especially in the more arid regions, warranted a comparison of different LMWL derivation methods using non-weighted and weighted precipitation. The methods using non-weighted precipitation generated similar results which were not significantly different from the OLSR although the best fit was obtained using RMA method (Tables S6–S9). The differences between methods based on weighted and non-weighted precipitation were small in all seasons except summer, when the largest difference was observed in (i) the AA and CHK catchments and (ii) the rain-only sub-set in all catchments (Fig. 5). The best fit was obtained using the PWLSR method (Tables S6–S9). In the Chinese Tien Shan, similar differences between methods based on weighted and non-weighted precipitation were observed in the southern Tarim Basin and the northern Junggar region (Wang et al., 2018). We recommend that the OLSR and RMA methods can be used in the mountains of CA, except for in the warm season when low rainfall depths are observed under high temperatures and the PWLSR method should be used.

4.3 Trajectory sources and d-excess

Synoptic-scale patterns of d-excess are used to characterise changes in moisture sources, but their interpretation is ambiguous, especially in CA where water vapour travels large distances (e.g. Clusters 1–3) and is affected by secondary fractionation processes (Bershaw, 2018). In this study, there were well-pronounced differences between the mean d-excess values associated with different trajectory sources in all seasons except SON. The highest d-excess values in JJA (17.2 ‰; Fig. 7b) were predictably associated with trajectories arriving from Iran and extending to the Mediterranean (if the iteration time exceeded 120 h), in line with the uniquely high d-excess values characterising this region (Bershaw, 2018). Trajectories arriving from the Black Sea were by contrast characterised by the lowest mean d-excess values in both JJA and DJF (Fig. 7b) because the Black Sea region is characterised by high relative humidity throughout the year. Mean values of d-excess associated with Siberian trajectories varied strongly between the highest in the data set in DJF (18.6 ± 10.3 ‰) and lower values in JJA (7.9 ± 10.6 ‰), in line with seasonal changes in temperature and humidity (Bershaw, 2018; Kostrova et al., 2020). Trajectories originating over the irrigated Aral Sea basin had a mean annual d-excess of 14.3 ± 7.6 ‰ and remained consistently high throughout the year, indicating the contribution of re-evaporated moisture to precipitation.

4.4 Precipitation provenance in Central Asia

The westerly airflow transporting the Atlantic moisture has been widely acknowledged as the main source of precipitation in CA based on studies of both climate (e.g. Shahgedanova, 2002) and isotope hydrology (e.g. Tian et al., 2007; Feng et al., 2013). This pathway was detected in all seasons; however, the mixing-model results (Table 3; Fig. 8) showed that inland recycled moisture, originating from both the irrigated land in the Aral Sea region and the study catchments, was the predominant source of precipitation in the study area. This conclusion is in agreement with Link et al. (2020), who showed that in Kyrgyzstan, the fraction of precipitation that originates from terrestrial sources reaches 61 %, making it 1 of the top 10 countries with the highest contributions from local terrestrial sources. Precipitation maxima in all catchments occur in MAM, except UA, where it peaks in May–July (Fig. 1). In MAM, precipitation associated with the local trajectories accounted for 52 %–54 % in CKS and AA, increasing to 69 % in CHK. The Aral Sea region contributed 46 % and 37 % in UA and CKS, respectively (Table 3). Precipitation associated with the local within-catchment trajectories made the largest contribution at CHK (70 %) and AA (73 %). We attributed the high contribution of local sources to continuing evapotranspiration on the plains of Uzbekistan, where temperatures remain mostly positive in winter. There was uncertainty about the separation of the locally formed precipitation from that which formed over the Aral Basin in CHK because the catchment is a part of the Aral Basin with extensive irrigation. The westerly group made the largest contribution in UA, located on the northernmost slope of the Tien Shan, in JJA (49 %) and DJF (54 %) and in AA in all seasons (46 %–50 %) except DJF.

The combined back-trajectory and mixing-model analysis has several limitations. Firstly, the performance of the mixing model depends on the differences in isotopic signatures between the trajectory clusters (Fig. 7) and groups (Fig. 8). This separation was less clear in MAM (Fig. 8), when the precipitation maximum is observed, increasing uncertainty in this season. Secondly, while the trajectory method determines the provenance of the air masses, it does not account for moisture uptake along the transportation routes. However, our results were consistent with Wang et al. (2017), who used back trajectories adjusted with specific humidity and showed that the terrestrial moisture evaporated from Europe and CA may be the main source of precipitation in the Chinese Tien Shan. The results were also consistent with the outcomes of moisture-tracking models. Tuinenburg et al. (2020) showed that evaporation recycling (defined as the fraction of evaporation that precipitates in the same river basin that it is evaporated from) reaches 30 %–40 % over the Tien Shan and its foothills. The annual mean of the distance which evaporated moisture travelled in a longitudinal direction is about 2–6° (Tuinenburg et al., 2020), which is consistent with the length of the local trajectories (Table 2). Application of a specific humidity-based model (e.g. Oza et al., 2022; Natali et al., 2023; Oza et al., 2022) would be a useful follow-on study to account for the history of moisture dynamics along the trajectories.

The third limitation was the discrepancy between the number of the identified trajectory clusters and the number of components in the mixing model imposed by the use of two tracers. To overcome this, Clusters 1, 2, and 3 were merged to form Group 1 – “Westerlies”. This problem did not affect the CKS and CHK catchments, where Group 1 was represented by a single cluster (Fig. S2 in the Supplement). In AA, clusters were merged to form Group 1 in MAM (Clusters 1 and 2 had six and two members, respectively) and SON (Clusters 1 and 2 had one and seven members, respectively). Five clusters were represented in the UA catchment only. However, there was clear seasonality in cluster occurrence at this site. The trajectory of a single precipitation event was assigned to Cluster 1 in DJF, and there was no statistically significant difference between Clusters 2 and 3 (p= 0.29) forming Group 1. By contrast, the difference between Groups 1, 2, and 3 was significant at the 93 % confidence level for δ¹⁸O (Fig. S2). In JJA, Group 1 included 61 events assigned to Cluster 1. The difference between Clusters 2 and 3 for δ¹⁸O was statistically significant (p= 0.03), but a small number of events (three and six, respectively) were assigned to these clusters. The difference with Cluster 1 was significant at the 91 % confidence level. In SON, Cluster 1 included 18 events, and the difference with Clusters 2 (n= 2) and 3 (n= 5) was not statistically significant (p= 0.13). Therefore, the uncertainty imposed by the limitation of the methodology is moderated by the seasonality of clusters at the UA catchment because a single cluster dominates in Group 1 in each season. In the future, this problem will be overcome using the electric conductivity of precipitation as an additional tracer in the mixing model.

The identified significant contribution of the local sources and of the extensively irrigated lower reaches of the Amu Darya and Syr Darya as well as of over 80 artificial reservoirs located in this region (Xenarios et al., 2019) to precipitation in the Tien Shan poses questions about the effects of both climate change, including the observed and projected increase in evaporation (Ren et al., 2022; Tuinenburg et al., 2020), and water management (Wei et al., 2013) on moisture cycling in CA. Regional evapotranspiration was previously shown to provide a significant input to precipitation, especially during dry periods in the arid and semi-arid regions globally (Miralles et al., 2016). Water evaporated from the irrigated land contributes to precipitation over the glacierised UA and CKS catchments (and possibly CHK), contributing to snow accumulation at high elevations in MAM, which is the main accumulation season in the region. This, in turn, sustains seasonal snowpack and glaciers providing water for irrigation. A modelling study by de Kok et al. (2018) suggested that increased irrigation in the Tarim Basin altered the precipitation regime in a way that favoured glacier growth in the Kunlun Shan, providing a partial explanation of the formation of the Karakorum–Kunlun–east Pamir anomaly (Farinotti et al., 2020). Our analysis of isotopic composition of precipitation shows that the same mechanism may operate in some regions of the Tien Shan.

5 Conclusions

An important achievement of this study is the development of an extensive isotopic database for the mountains of CA. These data have enabled the analysis of geographical, elevational, and temporal patterns in precipitation isotopic composition and of the attribution of precipitation to regional sources. Contributing these data to GNIP will improve the representation of the CA mountains in global high-resolution precipitation isoscape databases, especially in the cold season when the differences between modelled and measured ratios were highest. The advantages of the developed data set are (i) wide geographical coverage from the northern Tien Shan to the Gissar-Alay foothills, (ii) sampling at different elevations within two catchments because of the limited availability of such data globally, and (iii) the availability of event-based precipitation samples. The legacy of the programme is the installation of the Palmex rain samplers for the long-term collection of monthly precipitation samples for isotopic analysis in three catchments (Kishi Almaty, CKS, and CHK), including samplers at two elevations (700 and 3438 m a.s.l. and away from the lake in the neighbouring catchment of UA) in the Kishi Almaty catchment, which will support further investigation into elevational gradients in isotopic ratios and d-excess.

Clear annual cycles of δ¹⁸O and δD were identified, with maxima in summer and minima in winter at all sites, while annual d-excess cycles highlighted the effects of local conditions on precipitation formation. Both δ¹⁸O and δD values increase from north to south. These temporal and spatial patterns and the regression between air temperature and isotopic ratios showed that local air temperature controls the isotopic composition of precipitation. The relationships between δ¹⁸O and δD and geographical variables were quantified, though further investigation including a combined data set from CA and the Chinese Tien Shan will likely enhance result robustness.

LMWLs were developed for the whole region and for individual catchments and seasons. The use of weighted precipitation and the PWLSR method to derive LMWLs is recommended in JJA, especially in the southern part of the region, while unweighted precipitation can be used in other seasons and in the northern Tien Shan with OLSR and RMA methods.

For the first time, isotope data were used together with back trajectories to determine the contribution of different trajectory sources to precipitation. It was shown that the combined contribution of inland re-evaporated moisture from the irrigated land in the Aral Basin and local moisture recycling exceeded the contribution of the longer-distance transport associated with the westerlies. The model has several limitations, and the following improvements will be needed to confirm the initial findings: a longer sampling period enabling better separation between trajectory clusters, accounting for the history of moisture uptake along the transportation routes, and the application of additional tracers to increase the number of end-members in the mixing model. However, the identified contribution of re-evaporated moisture to regional precipitation highlights strong water loss and inefficient water management in CA. It also suggests that irrigation sustained by snowmelt and glacier melt and associated increases in evapotranspiration may benefit glacier mass balance, an issue which requires further investigation. Further work to improve the spatial density of sampling sites and increase the number of samples, especially in the inner Tien Shan and the Pamir, is also needed to confirm the findings.