Microphysical processes of super typhoon Lekima (2019) and their impacts on polarimetric radar remote sensing of precipitation

The complex precipitation microphysics associated with super typhoon Lekima (2019) and its potential impacts on the consistency of multi-source datasets and radar quantitative precipitation estimation were disentangled using a suite of in situ and remote sensing observations around the waterlogged area in the groove windward slope (GWS) of Yandang Mountain (YDM) and Kuocang Mountain, China. The main findings include the following: (i) the quality control processing for radar and disdrometers, which collect raindrop size distribution (DSD) data, effectively enhances the self-consistency between radar measurements, such as radar reflectivity (Z_H), differential reflectivity (Z_DR), and the specific differential phase (K_DP), as well as the consistency between radar, disdrometers, and gauges. (ii) The microphysical processes, in which breakup overwhelms coalescence in the coalescence–breakup balance of precipitation particles, noticeably make radar measurements prone to be breakup-dominated in radar volume gates, which accounts for the phenomenon where the high number concentration rather than the large size of drops contributes more to a given attenuation-corrected Z_H ($Z_{\mathrm{H}}^{\mathrm{C}}$) and the significant deviation of attenuation-corrected Z_DR ($Z_{\mathrm{DR}}^{\mathrm{C}}$) from its expected values (${\widehat{Z}}_{\mathrm{DR}}$) estimated by DSD-simulated Z_DR–Z_H relationships. (iii) The twin-parameter radar rainfall estimates based on measured Z_H ($Z_{\mathrm{H}}^{\mathrm{M}}$) and Z_DR ($Z_{\mathrm{DR}}^{\mathrm{M}}$), and their corrected counterparts $Z_{\mathrm{H}}^{\mathrm{C}}$ and $Z_{\mathrm{DR}}^{\mathrm{C}}$, i.e., R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$) and R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$), both tend to overestimate rainfall around the GWS of YDM, mainly ascribed to the unique microphysical process in which the breakup-dominated small-sized drops above transition to the coalescence-dominated large-sized drops falling near the surface. (iv) The improved performance of R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) is attributed to the utilization of ${\widehat{Z}}_{\mathrm{DR}}$, which equals physically converting breakup-dominated measurements in radar volume gates to their coalescence-dominated counterparts, and this also benefits from the better self-consistency between $Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$, and K_DP, as well as their consistency with the surface counterparts.

1 Introduction

Weather radars form the cornerstone of national weather warnings and forecast infrastructure in many countries. Doppler radar networks play an indispensable role in modern meteorological and hydrological applications, such as quantitative precipitation estimation (QPE), in support of the application of some hydrological models for water resource management, especially during high-impact weather events in urban environments (Chandrasekar et al., 2018; Cifelli et al., 2018; Chen and Chandrasekar, 2018). Although technological advances such as dual-polarization have tremendously improved weather radar applications in hydrometeorology remote sensing, it is still a challenge to incorporate complex precipitation dynamics and microphysics in an adaptive manner to optimize the quantitative applications of polarimetric radar measurements, including horizontal reflectivity Z_H, differential reflectivity Z_DR, copolar correlation coefficient ρ_HV, differential propagation phase Φ_DP, and its range derivative K_DP (specific differential phase). Traditional utilization of these measurements has only been able to extract some information on complex spatiotemporal precipitation variability.

In general, three main factors contribute to radar QPE uncertainties: radar measurement error, parameterization error of various radar–rain rate (R) relationships, and random error. In practical applications, it is crucial to consider these three factors as a whole to ensure radar rainfall estimates approximate the surface rainfall truth as much as possible. Among conventional radar QPE algorithms, those developed based on Z_H measurements are typical and are still in use today. For instance, an earlier version of the radar QPE algorithm in the National Oceanic and Atmospheric Administration (NOAA) Multi-Radar/Multi-Sensor System (MRMS) and its refined version both utilize multi-radar hybrid Z_H to derive the radar-based rainfall field (Zhang et al., 2011, 2016). The recent update of MRMS further incorporated specific attenuation (A_H) and K_DP to enhance the Z_H-based algorithm (Wang et al., 2019; Ryzhkov et al., 2022), and such an update can benefit from (i) the insensitivity of A_H to raindrop size distribution (DSD) variability (Ryzhkov et al., 2014); (ii) K_DP is a better indicator of rain rate and liquid water content (LWC, g m⁻³) than Z_H, since K_DP connects more tightly to the precipitation particle size distribution; and (iii) R(K_DP) and R(A_H) inherit the immunity of Φ_DP to miscalibration, attenuation, partial beam blockage, and wet radome effects (Park et al., 2005; Ryzhkov et al., 2014, 2022), which are hard to address when using Z_H for radar QPE, especially at higher frequencies such as C- and X-bands (Park et al., 2005; Matrosov, 2010; Frasier et al., 2013). However, since A_H and α are simultaneously derived, R(A_H) partly inherits the sensitivity of α to temperature (Ryzhkov et al., 2014), which occurs with the ascending altitude of the propagation of one radar beam. Multi-parameter radar QPE algorithms further integrate Z_DR with Z_H, K_DP, or A_H to infer more information about raindrop shape, such as the double-measurement algorithm R(Z_H, Z_DR), R(K_DP, Z_DR), and R(A_H, Z_DR) and the triple-measurement radar QPE algorithm as R(Z_H, Z_DR, K_DP) (Matrosov, 2010; Gosset et al., 2010; Schneebeli and Berne, 2012; Keenan et al., 2001; Chen et al., 2017; Gou et al., 2019b), but these algorithms all assume that Z_DR measurements are well calibrated and attenuation-corrected (Ryzhkov et al., 2005; Bringi et al., 2010).

In addition to radar measurements, disdrometer and rain gauge data are often used to determine the optimal parameters of radar-based QPE algorithms (Lee and Zawadzki, 2005; Tokay et al., 2005). For example, the MRMS system utilizes long-term Z_H and gauge rainfall measurements to obtain climatological Z–R relationships for each precipitation type (Zhang et al., 2011, 2016). In Gou et al. (2018, 2020), rain gauge measurements are used to dynamically adjust Z–R relationships to reflect the microphysical evolutions of precipitation systems. Nevertheless, the accuracy of meteorological gauge rainfall recordings is usually configured as 0.1 mm, and rain gauges may record less rainfall than reality due to debris blockage (tree leaves, insects, etc.) and the quick spinning of tipping buckets in a heavy shower situation. In addition, the surface wind may hinder some raindrops from falling into the tipping bucket, and the mechanical failures of the tipping bucket will record abnormally high or low rainfall, which introduces significant errors to the gauge network. Similarly, disdrometer measurements can be affected by strong winds and mixed-phase hydrometeors falling through the laser sampling area of the disdrometer, resulting in degraded quality of the DSD recordings (Tokay and Bashor, 2010). Since the DSD data collected by disdrometers are indispensable and sometimes are the only resources that can be used for precipitation microphysical analysis and the establishment of polarimetric radar rainfall relationships, meticulous quality control (QC) must be conducted on the disdrometer measurements (Friedrich et al., 2013).

Another issue that is important but rarely considered in radar QPE is the changing microphysics that occurs during the falling processes of precipitation particles between radar volume gates and surface ground, which is often indicated by inconsistent radar observations with their surface counterparts. The Z_H measurements in the melting layer (ML) of a stratiform rain system, which features falling melting snowflakes or ice crystals, usually need to be corrected for subsequent rainfall retrievals, especially when little rain is reported on the ground (Chen et al., 2020). A severe updraft may introduce a large Z_H and Z_DR column (Snyder et al., 2015; Carlin et al., 2017), while the surface rain gauge may record little or time-lagged rainfall, which is frequently perceived in the front of a squall line system or wind gust system. In addition, the contamination of mixed-phase hydrometeor particles on K_DP and A_H may lead to R(K_DP) and R(A_H) being overestimated (Gou et al., 2019b), and the falling wet hailstones may also contaminate radar-measured Z_H, K_DP, and A_H (Donavon and Jungbluth, 2007; Ryzhkov et al., 2014), leading to an overestimated hotspot on the derived rainfall field if such contaminations are not well addressed.

The complex microphysical variations mentioned above may coexist in a large-scale precipitation system such as a typhoon.

Before the polarimetric update, the impacts of the coexisting precipitation types on the radar QPE can be exploited through the vertical profile of reflectivity (VPR, Xu et al., 2008; Zhang et al., 2011, 2016). During the landfall of typhoon Hakui (2012), the VPR characteristics of coexisting tropical, convective, and stratiform rain account for the spatial precipitation variability (Gou et al., 2014). Super typhoon Lekima (2019) was the first super typhoon that landed on the eastern coast of Zhejiang after the polarimetric radar update, which provided an opportunity to exploit more microphysical signatures of the typhoon. Lekima landed on the coastal area of Chengnan town in Wen Ling (WL) city at 17:45 UTC, 9 August 2019, and the maximum wind near its center was about 52 m s⁻¹, which made it the strongest typhoon landing on the mainland of China in 2019. According to the statistics of the Chinese Meteorological Administration, Lekima was detained on land for 44 h; the affected area with rainfall measurements over 100 mm was about 361 000 km² during this period, and 19 national meteorological stations broke their historical daily rainfall recordings. During landfall, high waves were stirred up along the coastline, as depicted in Fig. 1a, and the landslide in Fig. 1b blocked the river and temporarily formed a dike with a sudden rise of the water level of the river before the collapse of the landslide dike, resulting in 22 casualties around this area. Waterlogging submerged the road network and many buildings in the urban area of Wen Ling (WL), Lin Hai (LH), Yu Huan (YH), and Xian Ju (XJ) in Taizhou (TZ) city (see Fig. 1c–f). Millions of people were evacuated from TZ city or were trapped in the disaster area. A total of 57 casualties were reported due to the landslides, floods, and waterlogging during the landfall of Lekima.

Figure 1 The disastrous situation in WZ and TZ due to the landfall of super typhoon Lekima: (a) high waves along the Wen Ling (WL) coast of TZ city; (b) landslide in the northern mountain area of Yong Jia (YJ) in WZ city; (c–f) serious waterlogging in WL, Lin Hai (LH), Yu Huan (YH), and Xian Ju (XJ) town of TZ city. Photo (a) is available at http://picture.youth.cn/qtdb/201908/t20190810_12036586.htm (last access: 15 January 2023). Photo (b) is available at https://baijiahao.baidu.com/s?id=1641647981934061656&wfr=spider&for=pc (last access: 15 January 2023). Photo (c) is available at https://new.qq.com/omn/20190810/20190810A0FZUT00.html?pc (last access: 15 January 2023). Photo (d) is available at https://new.qq.com/omn/20190828/20190828A0KGLT00.html (last access: 15 January 2023). Photo (e) is available at https://www.newssz.com/sz/2019/0818/94241-1/ (last access: 15 January 2023). Photo (f) is available at https://m.chinanews.com/wap/detail/undefined/zw/8925613.shtml (last access: 15 January 2023).

This paper investigates the microphysical characteristics of the typhoon-induced storm after its landfall, using observations from an S-band polarimetric radar deployed at Wenzhou (hereafter referred to as WZ-SPOL), six Thies disdrometers, and a local rain gauge network around the disaster area. So far, the reason for the significant convective asymmetries in the concentric eyewalls before its landfall has been ascribed to the phase locking of vortex Rossby waves (VRW), and the cloud and precipitation microphysics caused by this phase-locking VRW-triggered asymmetric convection have been revealed (Dai et al., 2021; Huang et al., 2022), mainly based on the WZ-SPOL radar and another Doppler weather radar in TZ city. The DSD differences in the eyewall and spiral rainbands based on surface disdrometer measurements have also been demonstrated (Bao et al., 2020). However, the microphysical processes inherent in Lekima after its landfall have not been thoroughly investigated.

The novel contributions of this paper are summarized as follows: (1) an enhanced QC procedure for disdrometer measurement is developed and analyzed through cross-comparison with rain gauge and WZ-SPOL radar measurements. (2) The microphysical process with overwhelming breakup over coalescence during the landfall of Lekima is revealed based on radar and surface disdrometers. (3) The impacts of dominant breakup and coalescence on radar QPE are investigated through an R(Z_H, Z_DR) estimator, and this algorithm integrates the expected Z_DR (i.e., ${\widehat{Z}}_{\mathrm{DR}}$) estimated from attenuation-corrected Z_H (i.e., $Z_{\mathrm{H}}^{\mathrm{C}}$) to mitigate the negative effects of the unique microphysical process, in which dominant breakup in the air transitioned to dominant coalescence near the surface around the GWS of YDM.

The remainder of this article is organized as follows: Sect. 2 introduces the study domain, hardware configuration, and data processing methodologies. Section 3 details the precipitation microphysics associated with Lekima (2019). The impacts of dominant collision–breakup or collision–coalescence on radar QPE performance are also quantified in Sect. 3. Section 4 summarizes the main findings of this study and suggests future directions in implementing this work in an operational environment.

2 Study domain and data processing

2.1 Study domain

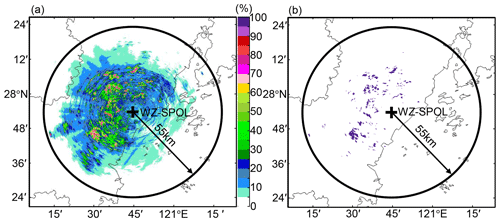
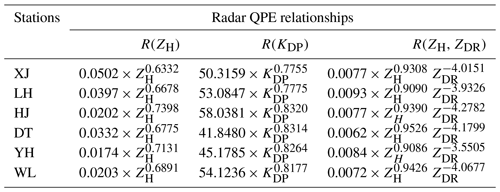
As shown in Fig. 2a, this paper focused on the north side of WZ city and the south side of TZ city. These two cities are both regional central cities of eastern China: WZ is an important trade city with more than nine million residents and an urban popularity density of 2900 km⁻². TZ is an important seaport city in southeastern China with six million residents and an urban popularity density of 688 km⁻². Historical typhoons have landed on the coastlines of these two cities, indicating the necessity and importance of monitoring typhoons coming into this area. With this aim, the S-band weather radar in WZ was upgraded to a polarimetric radar system in 2019 to enhance its precipitation-monitoring capability. The WZ-SPOL radar is deployed on a hill (735 m) near the coastline, as depicted in Fig. 2a. It sufficiently covers the flood and waterlogging disaster area caused by the landfall of Lekima. Two mountains lie between WZ and TZ, Kuocang Mountain (KCM) and Yandang Mountain (YDM). Although the mountainous terrain causes no serious beam blockage issues, the vertical gap between the radar beam center and the surface enlarges with ascending volume gates, as depicted in Fig. 2c. In addition, KCM and YDM both feature a typical groove topography, as indicated by the dashed lines in Fig. 2a, which benefits the assembling and uplifting of water vapor on the lower atmospheric layers.

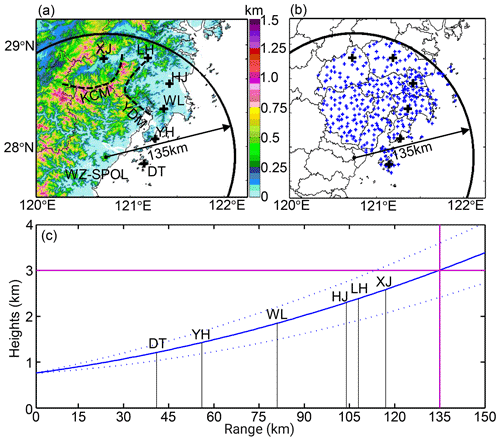
Figure 2 (a) Terrain elevation and disdrometer network around the WZ-SPOL radar (735 m), (b) rain gauge network around the disaster center area, and (c) the height of the radar beam shown as a function of measurement range in standard atmospheric conditions. The two dashed lines refer to the GWS of YDM and KCM. The black + in (a) and (b) refer to six national meteorological sites, and the blue + in (b) refers to regional meteorological sites. The solid and dotted blue curves in (c) refer to the height of the radar beam center and its radius boundaries, the vertical black lines mark the range distance of national meteorological stations (heights < 0.1 km) from the radar, and the two orthogonal purple lines refer to the altitude of 3 km and range of 135 km.

Six Thies laser-optical disdrometers have been deployed at the national meteorological stations around the target area since 2017 (see Figs. 2a and 1b). These include Xian Ju (XJ), Lin Hai (LH), Wen Ling (WL), Hong Jia (HJ), Yu Huan (YH), and Dong Tou (DT), and they provide particle size and terminal velocity (size–velocity) pairs with a 1 min time resolution. These size–velocity pairs are utilized to calculate rainfall intensity and to simulate dual-polarization radar measurements near the surface.

In addition, 356 tipping-bucket rain gauge stations (see Fig. 2b) are uniformly deployed around 10 towns that have suffered from landslide and waterlogging disasters within the coverage of a radius of 135 km from the WZ-SPOL radar. The time resolution of the gauge measurements is also configured as 1 min; if hourly gauge measurements are temporarily interrupted due to network issues, such as transmission congestion, these interrupted recordings will not be utilized. If we suppose that a gauge rainfall recording exceeds 1 mm, but the ratio between hourly gauge rainfall and any hourly radar estimates exceeds 10 (or less than 0.1 for the intercomparison), then this gauge measurement is suspected to be falsely reported and will not be used. This ratio (10, suggested in Marzen, 2004) is large enough to eliminate significant outliers but keep most other valuable gauge rainfall recordings.

2.2 Radar configuration and data processing

The WZ-SPOL radar adopts the simultaneous horizontal and vertical polarization mode. For the routine operations, the standard volume coverage pattern (VCP21) is configured, which has elevation angles including 0.5, 1.5, 2.4, 3.3, 4.3, 6.0, 9.9, 14.5, and 19.5^∘. The azimuthal radial resolution is set as 0.95^∘, and the range gate resolution is configured as 250 m for all elevation angles. Radar-measured Z_H, Z_DR, ρ_HV, as well as radial velocity (V_R) and Ψ_DP, are archived in the radar data acquisition (RDA) system and then transferred to the radar products generation system to produce some predefined standard radar products. QC processing for WZ-SPOL radar data is performed using the following steps:

• i.

  Ground clutter (GC) identification and mitigation.

  Two parts are included in this step. The clutter mitigation decision (CMD) algorithm (Hubbert et al., 2009) has been integrated into the RDA software to filter the ground clutters in real-time, but some residual static ground clutters (RSGC) still exist in the WZ-SPOL radar measurements at the 0.5^∘ elevation angle. To further eliminate the RSGC, the WZ-SPOL radar Z_H measurements on the 0.5^∘ elevation angle from August 2019 are utilized. The max number (N_max) of the pixel with Z_H > 0 dBZ within 55 km from the WZ-SPOL radar is 6981, and the observation number (N_obs) of each pixel within this range is normalized by dividing N_max. Then, an RSGC statistical map is derived, as shown in Fig. 3a, representing the relative frequency (freq. % of Z_H > 0 dBZ) within the coverage of the WZ-SPOL radar. In this map, the pixels with freq. > 50 % are deemed to be contaminated by the RSGC, and they form an RSGC mask in Fig. 3b to eliminate RSGC-contaminated Z_H and Z_DR at the 0.5^∘ elevation angle of the WZ-SPOL radar.

• ii.

  Ψ_DP processing.

  A nine-gate smoothing is first carried out to suppress the noise signals along the Ψ_DP range profile. Then, a procedure is executed to correct the aliased Ψ_DP based on the standard deviation of Ψ_DP in nine consecutive range gates (Wang and Chandrasekar, 2009), and 360^∘ are added to the aliased Ψ_DP to guarantee a monotonically increasing Ψ_DP range profile. In addition, the iterative filtering method in Hubbert and Bringi (1995) is used to filter the backscatter differential phase, and a zero-started filtered Φ_DP (${\mathrm{\Phi }}_{\mathrm{DP}}^{\mathrm{filter}}$) range profile is obtained by removing the initial phase of Φ_DP. The ${\mathrm{\Phi }}_{\mathrm{DP}}^{\mathrm{filter}}$ range profile is utilized to estimate K_DP through a linear fitting approach (Wang and Chandrasekar, 2009) with an additional non-negative constraint on K_DP.

• iii.

  Attenuation correction for Z_H.

  The ZPHI approach proposed by Bringi et al. (2001) is extended for correcting S-band Z_H measurements:

  $$\begin{array}{}\text{(1a)}& {\displaystyle }{A}_{\mathrm{H}}\left(r\right)={\displaystyle \frac{{\left[Z_{\mathrm{H}}^{\mathrm{M}}\right]}^b\left[{\mathrm{10}}^{\mathrm{0.1}b\mathit{\alpha }\mathrm{\Delta }\mathrm{\Phi }\left(r_{\mathrm{0}},r_m\right)}-\mathrm{1}\right]}{I\left(r_{\mathrm{0}},r_m\right)+\left[{\mathrm{10}}^{\mathrm{0.1}b\mathit{\alpha }\mathrm{\Delta }\mathrm{\Phi }\left(r_{\mathrm{0}},r_m\right)}-\mathrm{1}\right]I\left(r,r_m\right),}}\text{(1b)}& {\displaystyle }\mathrm{\Delta }{\mathrm{\Phi }}_{\mathrm{DP}}\left(r_{\mathrm{0}},r_m\right)={\mathrm{\Phi }}_{\mathrm{DP}}\left(r_m\right)-{\mathrm{\Phi }}_{\mathrm{DP}}\left(r_{\mathrm{0}}\right),\text{(1c)}& {\displaystyle }I\left(r_{\mathrm{0}},r_m\right)=\mathrm{0.46}b{\int }_{r_{\mathrm{0}}}^{r_m}\left[Z_{\mathrm{H}}^{\mathrm{M}}\right(r){]}^b\mathrm{d}s,\text{(1d)}& {\displaystyle }I\left(r,r_m\right)=\mathrm{0.46}b{\int }_r^{r_m}\left[Z_{\mathrm{H}}^{\mathrm{M}}\right(r){]}^b\mathrm{d}s,\text{(1e)}& {\displaystyle }{\mathrm{\Phi }}_{\mathrm{DP}}^{\mathrm{rec}}\left(r_{\mathrm{0}},r_m\right)=\mathrm{2}{\int }_{r_{\mathrm{0}}}^{r_m}{\displaystyle \frac{A_{\mathrm{H}}\left(s,\mathit{\alpha }\right)}{\mathit{\alpha }}}\mathrm{d}s,\text{(1f)}& {\displaystyle }C\left(r_{\mathrm{0}},r_m\right)={\int }_{r_{\mathrm{0}}}^{r_m}\left|{\mathrm{\Phi }}_{\mathrm{DP}}^{\mathrm{rec}}\left(s,\mathit{\alpha }\right)-{\mathrm{\Phi }}_{\mathrm{DP}}\right|\mathrm{d}s,\text{(1g)}& {\displaystyle }{Z}_{\mathrm{H}}^{\mathrm{C}}\left(r\right)=Z_{\mathrm{H}}^{\mathrm{M}}\left(r\right)+\mathrm{2}\underset{\mathrm{0}}{\overset{r}{\int }}{A}_{\mathrm{H}}\left(s,\mathit{\alpha }\right)\mathrm{d}s,\end{array}$$

  where $Z_{\mathrm{H}}^{\mathrm{M}}$ and $Z_{\mathrm{H}}^{\mathrm{C}}$ denote the measured and attenuation-corrected reflectivity, respectively; Φ_DP refers to the filtered differential phase; ${\mathrm{\Phi }}_{\mathrm{DP}}^{\mathrm{rec}}$ is a reconstructed differential phase through the ZPHI processing chain with an optimal coefficient α iteratively searched in the range [0.01, 0.12] by step 0.01 until the cost function C(r₀,r_m) of the difference between Φ_DP and ${\mathrm{\Phi }}_{\mathrm{DP}}^{\mathrm{rec}}$ in Eq. (1f) is minimized. The coefficient b is assumed to be 0.62 for the S-band (Ryzhkov et al., 2014).

  The ZPHI approach utilizes $Z_{\mathrm{H}}^{\mathrm{M}}$ and ΔΦ_DP in Eq. (1b) to calculate attenuation A_H. Here, it should be noted that three constraints are imposed on the ZPHI processing chain to ensure its practical performance, including a non-negative constraint on A_H, ρ_HV constraint on the range gate partitioning, and convergence constraint to avoid incorrect calculation termination (Gou et al., 2019a). Finally, $Z_{\mathrm{H}}^{\mathrm{M}}$ is corrected to $Z_{\mathrm{H}}^{\mathrm{C}}$ according to Eq. (1g).

• iv.

  Z_DR processing.

  The Z_DR offset is usually routinely obtained in zenith mode, with which near-zero Z_DR is anticipated in light rain scenarios, and then this offset is fed back to the RDA system to ensure slight Z_DR bias. Bringi et al. (2001) showed that all Z_DR values at the far side of one radial profile are expected to approximate 0 dB if the “intrinsic” Z_H is small enough (i.e., $Z_{\mathrm{H}}^{\mathrm{C}}$ < 20 dBZ) and attenuation-corrected Z_DR ($Z_{\mathrm{DR}}^{\mathrm{C}}$) should approximate to their ${\widehat{Z}}_{\mathrm{DR}}$ along the whole radial profile; thus, appropriate Z_DR bias adjustment may effectively help in such a Z_DR approximation. In this process, near-zero ${\widehat{Z}}_{\mathrm{DR}}$ is also anticipated for far-side volume gates containing ice crystals with $Z_{\mathrm{H}}^{\mathrm{C}}\mathit{<}\mathrm{20}$ dBZ. Here, the exponential Z_DR–Z_H relationship is established as Eq. (2a) based on the quality-controlled DSD datasets from all national meteorological stations (denoted as S₀) detailed in Sect. 2.3 and the analysis in Sect. 3.1. Therein, Z_H, Z_DR, and K_DP are simulated using the T-matrix method, assuming the raindrop aspect ratio in Brandes et al. (2002) at a temperature of 20 ^∘C. Then, the differential attenuation factor (A_DP) in Eq. (2b) is calculated by adjusting β to obtain $Z_{\mathrm{DR}}^{\mathrm{C}}$ according to Eq. (2c). The optimal β can be iteratively determined for A_DP by minimizing the differences between $Z_{\mathrm{DR}}^{\mathrm{C}}$ and ${\widehat{Z}}_{\mathrm{DR}}$ in Eq. (2d), along the whole radial range profile. Additional ΔZ_DR is also iteratively imposed on the whole range profile with a step of 0.1 dB to mitigate the residual Z_DR bias caused by miscalibration or wet radome effects. Then, $Z_{\mathrm{DR}}^{\mathrm{M}}$ is corrected by Eq. (2c) to $Z_{\mathrm{DR}}^{\mathrm{C}}$ through A_DP calculated by the optimal β. $Z_{\mathrm{DR}}^{\mathrm{C}}$ is utilized for the subsequent analysis and radar rainfall estimation:

  $$\begin{array}{}\text{(2a)}& {\displaystyle }{\widehat{Z}}_{\mathrm{DR}}\left(r\right)=\mathrm{1.3038}\times {\mathrm{10}}^{-\mathrm{4}}{Z}_{\mathrm{H}}(r{)}^{\mathrm{2.4508}},\text{(2b)}& {\displaystyle }{A}_{\mathrm{DP}}(r;\mathit{\beta })={\displaystyle \frac{\mathit{\beta }}{{\mathit{\alpha }}_{\mathrm{opt}}}}{A}_{\mathrm{H}}(r;{\mathit{\alpha }}_{\mathrm{opt}}),\text{(2c)}& {\displaystyle }{Z}_{\mathrm{DR}}^{\mathrm{C}}\left(r;\mathit{\beta }\right)=\mathrm{\Delta }{Z}_{\mathrm{DR}}+Z_{\mathrm{DR}}^{\mathrm{M}}\left(r\right)+\mathrm{2}{\int }_{\mathrm{0}}^r{A}_{\mathrm{DP}}\left(s,\mathit{\beta }\right)\mathrm{d}s,\text{(2d)}& {\displaystyle }{C}_{\mathrm{DR}}={\int }_{\mathrm{0}}^r\left|Z_{\mathrm{DR}}^{\mathrm{C}}\left(r;\mathit{\beta }\right)-{\widehat{Z}}_{\mathrm{DR}}\left(r\right)\right|\mathrm{d}r.\end{array}$$

Figure 3 (a) Statistics of pixels with Z_H > 0 dBZ within 55 km from the WZ-SPOL radar and (b) residual static ground clutter mask of the WZ-SPOL radar.

2.3 DSD data processing

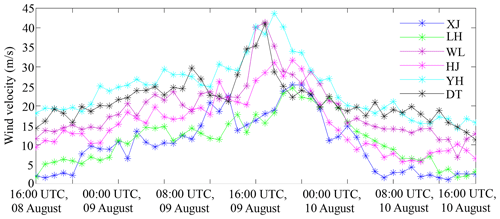
The Thies disdrometer measurements configured with 1 min sampling intervals collected between 00:00 UTC, 9 August 2019, and 00:00 UTC, 11 August 2019, are utilized. These measurements were variously affected by the strong winds, with the hourly maximum wind speed exceeding 20 m s⁻¹, as depicted in Fig. 4. Particularly, YH, WL, and DT suffered more seriously (> 40 m s⁻¹) after 16:00 UTC, 9 August 2019. Theoretically, the size–velocity measurements of raindrops, which are recorded by disdrometers in pairs, should be uniformly distributed as in the drop velocity model in Beard (1977), which can be represented as

$$\begin{array}{}\text{(3)}& V_{\mathrm{B}}\left(D_i\right)=\mathrm{9.65}-\mathrm{10.3}\times e^{-\mathrm{0.6}{D}_i},\end{array}$$

where D_i is the diameter of the ith size class (diameter interval) and V_B is estimated by D_i. However, real velocity measurement (V_M) of disdrometers may deviate seriously from V_B due to the strong wind effects. For instance, many size–velocity pairs at all six stations are biased with V_M < 0.5 V_B and distributed in all predefined size classes; more deviated size–velocity pairs of WL, YH, and DT are featured with V_M < 0.5 V_B in Fig. 5d–f than in XJ, LH, and HJ in Fig. 5a–c, which can also be ascribed to high wind speeds. Consequently, these size–velocity pairs need to be preprocessed, and the QC procedure utilized hereafter includes the following three steps:

• i.

  For wind-contaminated size–velocity pairs, if the V_M of the ith size class is located inside [0.5 V_B, 1.5 V_B] (enclosed by the blue lines in Fig. 5), the size–velocity pairs are deemed to agree well with Eq. (3) and will be kept; the other outliers will be eliminated.

• ii.

  For the potential hail (D_i > 5 mm) and graupel (D_i in [2 mm, 5 mm]), two size–velocity relationships listed in Friedrich et al. (2013) as

  $$\begin{array}{}\text{(4a)}& {\displaystyle }{V}_{\mathrm{H}}\left(D_i\right)=\mathrm{10.58}\times (\mathrm{0.1}{D}_i{)}^{\mathrm{0.267}},\text{(4b)}& {\displaystyle }{V}_{\mathrm{G}}\left(D_i\right)=\mathrm{1.37}\times (\mathrm{0.1}{D}_i{)}^{\mathrm{0.66}}\end{array}$$

  are selected to estimate the velocity of potential hail (V_H) and graupel (V_G) corresponding to D_i. The size–velocity pairs that fulfilled $\left|V_{\mathrm{B}}-V_{\mathrm{M}}\right|<\left|V_{\mathrm{H}}-V_{\mathrm{M}}\right|$ or $\left|V_{\mathrm{B}}-V_{\mathrm{M}}\right|<\left|V_{\mathrm{G}}-V_{\mathrm{M}}\right|$ will be kept, because they are more prone to raindrops; otherwise, these measurements are eliminated from the original dataset depicted in Fig. 5.

• iii.

  The residual contaminations, which the above-mentioned processing cannot directly eliminate due to their similar size–velocity characteristics to raindrops, need another analysis based on DSD-derived median volume diameter (D₀) and Z_DR. Larger Z_DR values are anticipated for melting solid particles than raindrops with similar diameters. The final QC processing result of the DSD dataset is presented in Sect. 3.1.

Figure 4 Time series of hourly maximum wind speed at the six national meteorological stations between 16:00 UTC, 8 August 2019, and 16:00 UTC, 10 August 2019.

3 Analysis and results

3.1 The consistency between multi-source data

3.1.1 The surface consistency between disdrometer and rain gauge

A DSD dataset is critical for establishing relationships between polarimetric radar variables for radar QPE algorithms. Disdrometers and rain gauges are usually deployed at the same meteorological site; although they sample the precipitation differently, their rainfall measurements in the same area should agree with each other. However, DSD-derived rainfall at six stations, directly calculated from the size–velocity pairs in Fig. 5 without any QC processing (denoted as R_M), all presented unrealistically large values: maximum R_M at LH, XJ, and HJ exceeded 200 mm that at DT exceeded 400 mm and that at WL and YH unbelievably exceeded 3×10³ and 10⁴ mm during typhoon Lekima. For convenient comparison of disdrometers with gauge rainfall series, R_M is rewritten as

$$\begin{array}{}\text{(5)}& R_{\mathrm{TM}}=\left\{\begin{array}{ll}{R}_{\mathrm{T}}+(R_{\mathrm{M}}-R_{\mathrm{T}})/C_{\mathrm{T}}& R_{\mathrm{M}}>R_{\mathrm{T}}\\ R_{\mathrm{M}}& R_{\mathrm{M}}\le R_{\mathrm{T}},\end{array}\right.\end{array}$$

where R_TM stands for the transformed rainfall value and R_T stands for a rainfall threshold that is set a little larger than the maximum hourly gauge rainfall. C_T is also manually set for each station, and C_T partly indicates that R_M is at least C_T times higher than gauge rainfall. The R_M part exceeding R_T can shrink into a limited range interval, and R_T and C_T serve for comparing R_M and DSD-derived rainfall after QC processing (denoted as R_QC) in the same figure, as depicted in Fig. 6. Accordingly, C_T of YH and WL in Fig. 6 is huge (800 and 500, ≥20 at the other stations). Meanwhile, DSD-derived maximum Z_H, Z_DR, K_DP, and R exceeded 85 dBZ, 5.5 dB, 1500 ^∘ km⁻¹, and 15000 mm h⁻¹, respectively (see Fig. 7a–c), and they are also abnormally larger than the final QC-processed counterparts (rectangles in Fig. 7a–c). If these unrealistic DSD-derived radar variables were directly utilized to establish the parameters of any radar QPE algorithm, an unrealistically overestimated radar rainfall field would be obtained. Afterward, the QC procedure in Sect. 2.3 is first imposed on the size–velocity pairs, and its performance and effectiveness are investigated through comparison with gauge rainfall recordings.

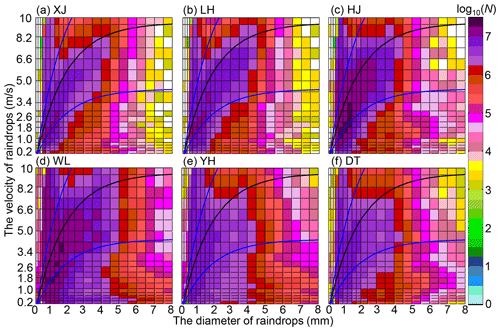
Figure 5 The original size–velocity dataset collected at (a) XJ, (b) LH, (c) HJ, (d) WL, (e) YH, and (f) DT. The black and blue lines refer to the fall speed V_B, 0.5 V_B, and 1.5 V_B calculated in Eq. (3).

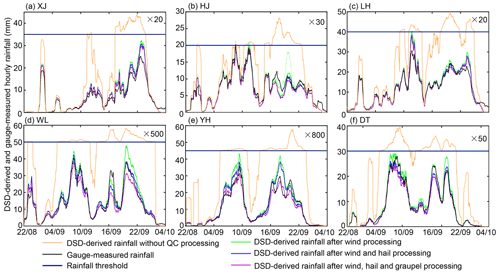
Figure 6 Time series of DSD-derived and gauge hourly rainfall. Panels (a)–(f) are obtained from XJ, HJ, LH, WL, YH, and DT, respectively, during 22:00 UTC, 8 August 2019, and 04:00 UTC, 10 August 2019. The number following × refers to C_T, and bold, dark blue straight lines indicate the threshold of R_T of each station according to Eq. (5). The green dotted line in (b) is conditioned by V_M∈ [0.4 V_B, 1.5 V_B], and other green solid lines are conditioned by V_M∈ [0.5 V_B, 1.5 V_B].

According to a visual comparison in Fig. 6, the severe overestimation of R_M at all six stations is reduced after processing wind effects, and a better approximation is noticeable at XJ, HJ, LH, and DT in Fig. 6a–c and e, where the extra hail and graupel processing hardly change the residual differences. In contrast, the R_QC time series at WL agrees well with its gauge rainfall recordings after the hail processing but is underestimated after extra graupel processing (see Fig. 6d). This implies that WL suffers from some solid particle contaminations. Still, these solid particles may melt and have similar size–velocity characteristics to raindrops, and their removal is responsible for the final underestimation of R_QC at WL after QC processing. YH also suffered from solid particle contaminations. During its peak rainfall recording period between 16:00 and 22:00 UTC, 9 August 2019, R_QC in Fig. 6e changes relatively less after the hail processing and still deviates largely from gauge rainfall recordings; conversely, R_QC better approximates gauge rainfall after the graupel processing. This indicates that the terminal velocity of these filtered particles is more prone to graupel (not deduced by size). Section 3.2.1 further verifies the falling solid particles.

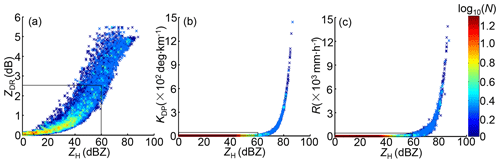
Figure 7 The scattergrams of DSD-derived polarimetric radar variables without QC processing: (a) Z_DR vs. Z_H, (b) K_DP vs. Z_H, (c) R vs. Z_H. The rectangles in (a–c) indicate the ranges of DSD-derived variables after final QC processing.

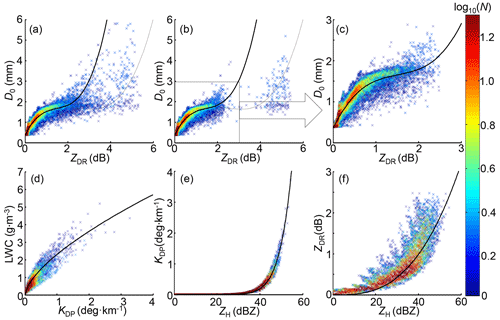
Figure 8 Scattergrams between polarimetric radar variables: (a) D₀ vs. Z_DR after eliminating wind contaminations. Panel (b) is based on (a) but after removing the hail and graupel contaminations further. Panel (c) is based on (b) but after further eliminating the residual graupel contaminations with Z_DR > 2.5 dB. Panels (d), (e), and (f) are LWC vs. K_DP, K_DP vs. Z_H, and Z_DR vs. Z_H based on the same dataset as (c). The thick black lines in (a)–(c) stand for Eq. (5); the thin black lines in (a) and (b) indicate the overfitted results, and the black curves in (d)-(f) stand for Eqs. (6), (7), and (2a), respectively.

These residual solid particles could result in a false relationship between D₀ and Z_DR. As shown in Fig. 8a, the fitted curve uniformly passed through the scattergram, representing an excellent fitting relationship between D₀ and Z_DR. However, as mentioned above, these DSD-derived D₀ and Z_DR still suffer from some solid particle contaminations after processing the wind effects. Even after hail and graupel processing, the scattergram in Fig. 8b still presents a significant overfitted relationship between D₀ and Z_DR. The scatters with Z_DR > 2.5 dB are related to melting solid particles with D₀ ranging from 1.5 to 4 mm, and some have raindrop-like sizes (< 2 mm). Finally, DSD-derived radar variables constrained by Z_DR < 2.5 dB are assumed to be contributed by pure raindrops, and they are utilized to fit the D₀–Z_DR, LWC–K_DP, and K_DP–Z_H relationships in Fig. 8c–e and the Z_DR–Z_H relationship in Eq. (2a) (see Fig. 8f):

$$\begin{array}{}\text{(6)}& {\displaystyle }\begin{array}{rl}{D}_{\mathrm{0}}& =\mathrm{0.2987}\times Z_{\mathrm{DR}}^{\mathrm{3}}-\mathrm{1.3229}\times Z_{\mathrm{DR}}^{\mathrm{2}}+\mathrm{2.1931}\times Z_{\mathrm{DR}}\\ & +\mathrm{0.3543},\end{array}\text{(7)}& {\displaystyle }\mathrm{LWC}=\mathrm{2.0949}\times K_{\mathrm{DP}}^{\mathrm{0.6889}},\text{(8)}& {\displaystyle }{K}_{\mathrm{DP}}=\mathrm{1.5473}\times {\mathrm{10}}^{-\mathrm{15}}\times Z_{\mathrm{H}}^{\mathrm{8.8365}}.\end{array}$$

Combining these relationships and another relationship between the normalized concentration of raindrops (N_w, in mm⁻¹ m⁻³), LWC, and the mean volume diameter of the drop size distribution (D_m, in mm) in Eqs. (9) and (10),

$$\begin{array}{}\text{(9)}& {\displaystyle }{N}_{\mathrm{w}}={\displaystyle \frac{{\mathrm{4}}^{\mathrm{4}}}{\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}}}{\displaystyle \frac{\mathrm{LWC}}{D_{\mathrm{m}}^{\mathrm{4}}}},\text{(10)}& {\displaystyle }{D}_{\mathrm{m}}={\displaystyle \frac{\mathrm{4}+\mathit{\mu }}{\mathrm{3.67}+\mathit{\mu }}}{D}_{\mathrm{0}},\end{array}$$

where ρ_w is the water density (1 g cm⁻³), high-resolution DSD parameter fields can be derived from WZ-SPOL radar measurements.

3.1.2 The self-consistency between radar measurements

The self-consistency can demonstrate the credibility of polarimetric radar measurements through scattergrams (Fig. 9). The scattergrams in Fig. 9b and d are obtained from all $Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$, and K_DP measurements described in Fig. 11. The ZHPI approach (Bringi et al., 2001) with more constraints described in Gou et al. (2019a) effectively mitigates the attenuation effects on Z_H and Z_DR of the WZ-SPOL radar. The spatial fields of $Z_{\mathrm{H}}^{\mathrm{M}}$ and $Z_{\mathrm{DR}}^{\mathrm{M}}$ are not presented (they will not be used for the subsequent analysis), but it is noticeable that radar-measured $Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$, and K_DP are not self-consistent before attenuation correction processing: it is obvious for $Z_{\mathrm{H}}^{\mathrm{M}}\mathit{>}\mathrm{40}$ dBZ and K_DP > 1 ^∘ km⁻¹ that K_DP–$Z_{\mathrm{H}}^{\mathrm{M}}$ scatters deviates positively from the theoretical K_DP–Z_H curve (Eq. 8 as depicted in Fig. 8e), indicating that larger reflectivity values are anticipated for these K_DP measurements. In addition, an overall deviation of $Z_{\mathrm{DR}}^{\mathrm{M}}$–$Z_{\mathrm{H}}^{\mathrm{M}}$ distribution in Fig. 9c from the theoretical Z_DR–Z_H curve (the black curve stands for Eq. 2a as depicted in Fig. 8f) addresses a non-negligible negative Z_DR bias before the differential attenuation correction. In contrast, the scattergram core areas in Fig. 9b and d (defined as log₁₀(N) > 1.6) exhibit more compact distribution along theoretical K_DP–Z_H and Z_DR–Z_H curves, demonstrating the effectiveness of the attenuation correction to enhance the self-consistency between $Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$, and K_DP.

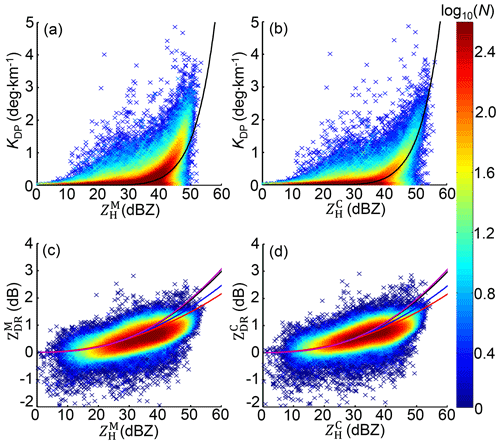
Figure 9 The scattergram between polarimetric measurements from the WZ-SPOL radar, (a) K_DP vs. $Z_{\mathrm{H}}^{\mathrm{M}}$, (b) K_DP vs. $Z_{\mathrm{H}}^{\mathrm{C}}$, (c) $Z_{\mathrm{DR}}^{\mathrm{M}}$ vs. $Z_{\mathrm{H}}^{\mathrm{M}}$, and (d) $Z_{\mathrm{DR}}^{\mathrm{C}}$ vs. $Z_{\mathrm{H}}^{\mathrm{C}}$. Measurements of all six stations derive the black curves; the blue, red, and purple curves in (c) and (d) stand for Eqs. (11a)–(11c) derived from S_I–S_III.

Radar measurements are feedback from drops in the air, but disdrometers collect DSD near the surface. In this sense, the comparison above also means that radar measurements tend to be more consistent with their surface counterparts after the correction. However, this does not mean that they completely agree; conversely, $Z_{\mathrm{DR}}^{\mathrm{C}}$ still deviates largely from ${\widehat{Z}}_{\mathrm{DR}}$ when reflectivity exceeds 35 dBZ in Fig. 9d. In addition, the time series in Fig. 10 shows that extremely large DSD-derived Z_H, Z_DR, and K_DP in Fig. 7 (time series not presented) have diminished, and they begin to approximate their radar-measured counterparts. The hail and graupel processing effectively improves the consistency between the gauge and disdrometer, as mentioned above; furthermore, DSD-derived Z_H and K_DP also simultaneously tend to better approximate radar-measured $Z_{\mathrm{H}}^{\mathrm{C}}$ and K_DP. Meanwhile, the residual differences between radar and DSD are still prominent in terms of Z_DR, and larger DSD-derived Z_DR than radar-measured $Z_{\mathrm{DR}}^{\mathrm{C}}$ occurs at WL and YH, indicating that larger-sized drops are collected by WL and YH than the radar volume gates above.

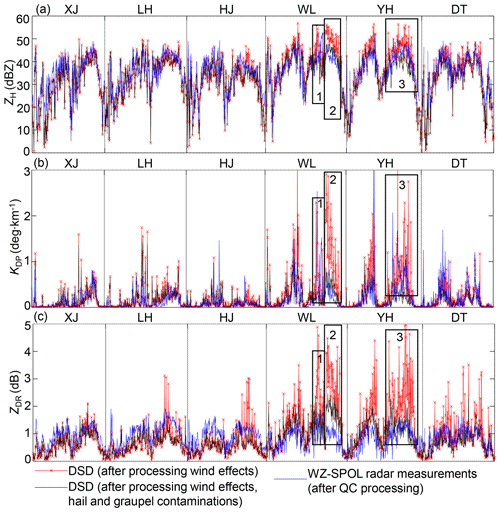
Figure 10 (a) Time series of radar-measured $Z_{\mathrm{H}}^{\mathrm{C}}$ and DSD-derived Z_H at the six meteorological stations shown in Fig. 6 during 22:00 UTC, 8 August 2019, and 04:00 UTC, 10 August 2019. (b) Similar to (a), but for radar-measured K_DP and DSD-derived K_DP. (c) Similar to (a), but for radar-measured $Z_{\mathrm{DR}}^{\mathrm{C}}$ and DSD-derived Z_DR.

Considering that Eq. (2a) is fitted based on S₀, and R_QC at WL agrees better with gauge rainfall if no graupel processing occurs, S₀ can be refined: S_I excludes large-sized drops by removing WL, S_II further excludes large-sized drops from WL and YH, and S_III re-includes more large-sized drops by adding the size–velocity pairs removed by graupel processing at WL. In this way, three new Z_DR–Z_H relationships are re-established as

$$\begin{array}{}\text{(11a)}& {\displaystyle }{\widehat{Z}}_{\mathrm{DR}}\left(r\right)=\mathrm{3.477}\times {\mathrm{10}}^{-\mathrm{4}}{Z}_{\mathrm{H}}(r{)}^{\mathrm{2.161}}\mathrm{DSD}\in S_{\mathrm{I}},\text{(11b)}& {\displaystyle }{\widehat{Z}}_{\mathrm{DR}}\left(r\right)=\mathrm{5.033}\times {\mathrm{10}}^{-\mathrm{4}}{Z}_{\mathrm{H}}(r{)}^{\mathrm{2.0383}}\mathrm{DSD}\in S_{\mathrm{II}},\text{(11c)}& {\displaystyle }{\widehat{Z}}_{\mathrm{DR}}\left(r\right)=\mathrm{1.0652}\times {\mathrm{10}}^{-\mathrm{4}}{Z}_{\mathrm{H}}(r{)}^{\mathrm{2.508}}\mathrm{DSD}\in S_{\mathrm{III}}.\end{array}$$

The further removal of the DT dataset from S_II will change the Z_DR–Z_H relationship in Eq. (11b) very little (data not presented). Although there is an uncertainty that large-sized drops may source either from melting solid particles or the collision–coalescence, more large-sized drops in S₀ and S_III make Eqs. (2a) and (11c) (higher ${\widehat{Z}}_{\mathrm{DR}}$ estimates) prone to the outcome of the dominant collision–coalescence process; conversely, more small-sized drops in S_II and S_III make Eqs. (11a) and (11b) prone to dominant collision–breakup. Resultantly, Eqs. (11a) and (11b) exhibit smaller Z_DR than that of Eqs. (2a) and (11c) for a given $Z_{\mathrm{H}}^{\mathrm{C}}$, which agrees well with the simulation result in Kumjian and Prat (2014). In Fig. 9d, radar-measured $Z_{\mathrm{DR}}^{\mathrm{C}}$ tends to be more consistent with Eqs. (11a) and (11b) for a given $Z_{\mathrm{H}}^{\mathrm{C}}$ than Eqs. (2a) and (11c) in the scattergram core area, and this $Z_{\mathrm{DR}}^{\mathrm{C}}$–$Z_{\mathrm{H}}^{\mathrm{C}}$ scattergram reflects that the governing collision–breakup processes in radar volume gates restrain the drop size increase due to the coalescence–breakup balance, which means $Z_{\mathrm{DR}}^{\mathrm{C}}$ does not grow similarly to coalescence-dominated volume gates.

3.2 Microphysics of the landfall of Lekima (2019)

When super typhoon Lekima landed on the eastern coast of China, several beneficial conditions for its evolution were perceived: (i) the severe interaction between the mountain and the typhoon caused terrain-enhanced precipitation, (ii) the wind speed shear (the bold black curves in Fig. 11a–d) with noticeable V_R differences benefited the strengthening development of convective storms, and (iii) the typhoon carried abundant warm moisture which can condensate if confronted with cold air. The characteristics of Lekima can be described based on $Z_{\mathrm{H}}^{\mathrm{C}}$: the outer and inner eyewalls were both featured with $Z_{\mathrm{H}}^{\mathrm{C}}\mathit{>}\mathrm{55}$ dBZ before landfall in Fig. 11e, indicating the enhanced convective development of the concentric eyewalls before its landfall; afterward, the inner eyewall was destroyed and merged with the outer eyewall into a convective storm with an enlarged area, with $Z_{\mathrm{H}}^{\mathrm{C}}\mathit{>}\mathrm{55}$ dBZ dwelling around the GWS of YDM (in Fig. 11f), and then the storm area with $Z_{\mathrm{H}}^{\mathrm{C}}\mathit{>}\mathrm{55}$ dBZ transitioned to the north GWS of YDM (in Fig. 11g) but strongly weakened when it passed over the mountain ridge between YDM and KCM (as depicted in Fig. 11h). More complex microphysical processes than these described also occurred during the landfall of Lekima.

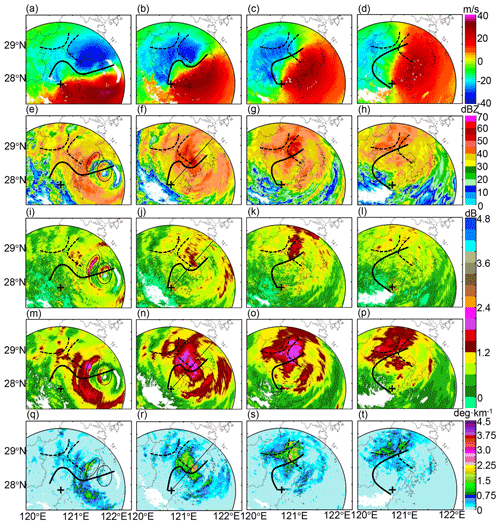
Figure 11 WZ-SPOL radar measurements during typhoon Lekima: (a)–(d) are Doppler velocity V_R at 16:01, 17:59, 20:02, and 22:00 UTC, 9 August 2019, respectively; (e)–(h), (i)–(l), (m)–(p), (q)–(t) are, respectively, $Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$, and K_DP simultaneously as (a–d). The solid black lines refer to wind shear deduced from V_R. The dashed black lines refer to the GWS of KCM and YDM, and + indicates the location of the WZ-SPOL radar. The ellipses in (e), (i), (m), and (q) indicate where hydrometeor size sorting occurred. The black lines along the radial profiles in (f), (j), (n), and (r) indicate the azimuthal angle shown in Fig. 18.

3.2.1 Polarimetric signatures of solid particles

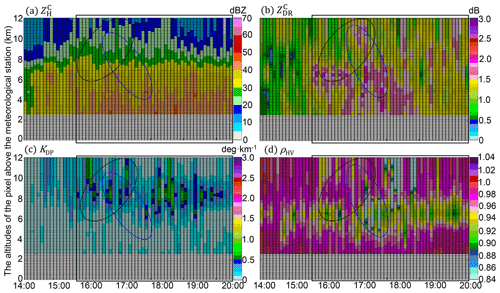
The time series of vertical polarimetric radar measurement (Figs. 12–17), which is constructed with an altitude resolution of 100 m based on the technique in Zhang et al. (2005), is chosen to describe the microphysical evolutions upon each station; DSD-derived radar measurements in Sect. 3.1 assist in interpreting what occurred near the surface. The combination of radar and DSD can effectively explain the potential microphysical processes in the vertical gap between the air and the surface.

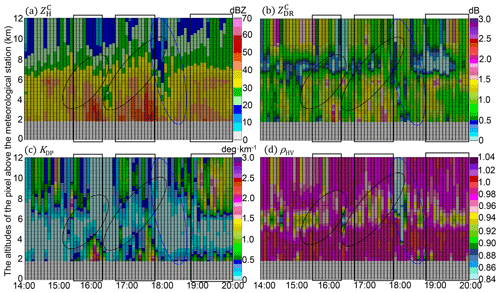
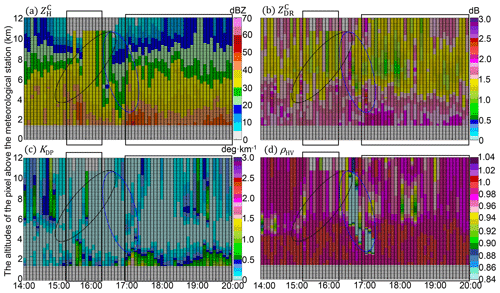
Figure 12 (a) Time series of vertical polarimetric radar variables upon the WL station between 14:00 UTC, 8 August 2019, and 20:00 UTC, 9 August 2019, (a) $Z_{\mathrm{H}}^{\mathrm{C}}$, (b) $Z_{\mathrm{DR}}^{\mathrm{C}}$, (c) K_DP, and (d) ρ_HV. The black rectangles indicate developing convective storms, the black ellipses surround the potential updrafts, and the blue ellipses surround the subsiding signatures of ice or mixed-phase particles.

The freezing level (FL) is significant in the vertical measurements (see Figs. 12, 14, and 17), and its altitude is about 7 km: the layers with near-zero $Z_{\mathrm{DR}}^{\mathrm{C}}$ measurements dominate above the FL, indicating the dominant dry snow aggregates ($Z_{\mathrm{H}}^{\mathrm{C}}\mathit{<}\mathrm{30}$ dBZ); ρ_HV is relatively weaker (< 0.98) below the FL, indicating the dominant mix-phase particles in the ML (near 6 km). In addition, the sustaining large K_DP (>1 ^∘ km⁻¹) upon WL and HJ (Figs. 12 and 14) after 18:00 UTC, 9 August 2019, (after landfall) indicates the high concentration of solid particles above the FL. In addition, the significant upward extension of $Z_{\mathrm{H}}^{\mathrm{C}}$ (> 40 dBZ) and $Z_{\mathrm{DR}}^{\mathrm{C}}$ (> 1 dB) columns marked with black rectangles indicate the developing convective storms; the black ellipses indicate potential updrafts coupled with the storm; the blue ellipses indicate subsiding signatures of falling solid particles deducing from gradual decreasing heights of ρ_HV < 0.98 over time. The convective storms are accompanied by abundant water content, as indicated by significant K_DP (> 0.5^∘ km⁻¹) columns extending upwards, which benefited the size increases of the falling solid particles. The microphysical processes of the solid particles differed at each station.

The WZ-SPOL radar initially measured similar Z_DR but larger Z_H and K_DP compared with DSD at the WL station (rectangle 1 in Fig. 10) before the landfall of Lekima, and more concentrated hydrometeors aloft accompanying the updrafts compared to the surface in this process account for this phenomenon, which is verified in the first rectangle of Fig. 12a and c. Furthermore, two consecutive severe updrafts passed over WL, one from the outer eyewall and the other from the inner eyewall, causing the significant upward extension of $Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$, and K_DP columns below the FL, as depicted in two black rectangles in Fig. 12. As illustrated in two black ellipses, some ice particles might ascend with the first updraft, then fall and melt in the time gap between two updrafts, with the signature of ρ_HV < 0.98 reaching the lowest layer of 1.8 km; they instantly suffered from another size increase process confronting the second updraft (in the second ellipse) and then fell with the subsiding signals of ρ_HV and $Z_{\mathrm{DR}}^{\mathrm{C}}$ (in the blue ellipse): $Z_{\mathrm{DR}}^{\mathrm{C}}\mathit{<}\mathrm{0.5}$ dB was sustained when ρ_HV gradually transitioned from ρ_HV < 0.84 around the FL to ρ_HV < 0.98 on the lowest layer, indicating the existence of some near-spherical but mixed-phase particles during this falling process. These solid particles partly account for the larger DSD-derived Z_DR near the surface than the WZ-SPOL radar (rectangle 2 in Fig. 10), but the coalescence of raindrops might also partly account for this DSD-derived larger Z_DR.

Similar updrafts occurred upon the YH station (rectangle 3 in Fig. 10), and the WZ-SPOL radar measured similar K_DP but weaker Z_H and Z_DR compared with DSD before the hail/graupel processing. Featuring with similar $Z_{\mathrm{H}}^{\mathrm{C}}$ extending upwards upon the YH station, large $Z_{\mathrm{DR}}^{\mathrm{C}}$ (> 1.2 dB) and weak K_DP (< 0.2 ^∘ km⁻¹) accompanied the updrafts with ρ_HV < 0.98 in the black ellipse of Fig. 13, indicating that dominant large-sized mixed-phase particles were developing around the ML. Then, in the blue ellipse, the subsiding signals of ρ_HV < 0.84 formed in Fig. 13d after 16:30 UTC and tended to decrease their heights over time; finally, they transitioned to ρ_HV > 0.98 on the top of the $Z_{\mathrm{DR}}^{\mathrm{C}}$ (> 2 dB) columns, attributing to the transformation of melting solid particles into big raindrops. Compared with surface DSD, the decrease in radar-measured $Z_{\mathrm{H}}^{\mathrm{C}}$ and K_DP reflects the reduction of LWC in the vertical gap; this LWC reduction did not contribute to the size increase of drops, because radar and DSD presented similar Z_DR. Another possible explanation is that some LWC is absorbed by the falling solid particles, contributing to the filtered Z_DR part in the hail/graupel processing.

Figure 13 The same as Fig. 12 but for the YH station.

Another solid particle falling occurred upon HJ, which is to the north of the landfall positions of Lekima. Even with the unnoticeable upward $Z_{\mathrm{H}}^{\mathrm{C}}$ enhancement between 17:00 and 18:00 UTC, 9 August 2019, as depicted in Fig. 14a, the large $Z_{\mathrm{DR}}^{\mathrm{C}}$ signals of the ML in Fig. 14b diminished due to the updraft, $Z_{\mathrm{DR}}^{\mathrm{C}}$ and K_DP both increased, and ρ_HV reduced steadily after 18:00 UTC above the FL in the black ellipses of Fig. 13b–d. Subsiding signals of ρ_HV < 0.84 also emerged after 18:00 UTC, resulting in the ρ_HV reduction from 0.98 to 0.96 on the lowest layer. Conditioning V_M by [0.5V_B, 1.5V_B] eliminated some size–velocity pairs of the solid particles at HJ, because solid precipitation particles have smaller terminal velocities than liquid particles. Conversely, the rising overestimation of R_QC by reconditioning V_M by [0.4 V_B, 1.5 V_B] in Fig. 6b (the dotted green line) further verified this possibility.

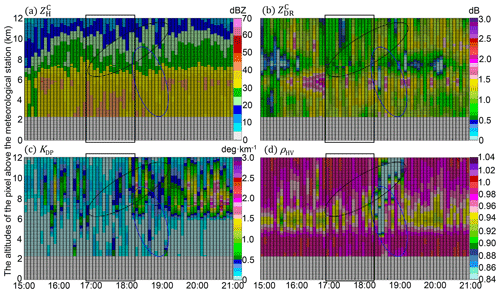
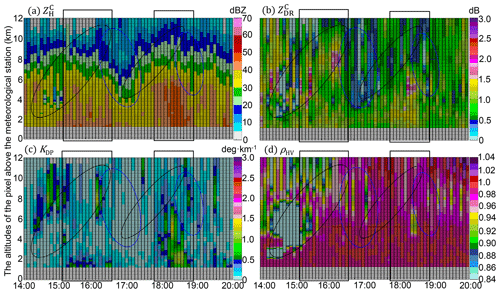
Figure 14 The same as Fig. 12 but for the HJ station between 15:00 UTC, 8 August 2019, and 21:00 UTC, 9 August 2019.

These common characteristics feature in HJ, DT, LH, and XJ in Figs. 14–17: K_DP (< 0.5 ^∘ km⁻¹) above the FL indicated a lower concentration of ice particles upon DT, LH, and XJ than upon the other three sites, which refrains the size increase of falling solid particles through the aggregation process; the insignificant $Z_{\mathrm{H}}^{\mathrm{C}}$ (< 45 dBZ) and K_DP (< 0.2 ^∘ km⁻¹) extending upwards reflect the relatively low concentration of hydrometeors below the ML upon HJ, LH, and XJ, which refrains the further size increases of melting ice particles in the warm rain environment. The exceptions in $Z_{\mathrm{DR}}^{\mathrm{C}}$ columns upon DT between 18:00 and 19:00 UTC in Fig. 15b were attributed to the falling melting ice particles upon an updraft with high LWC (K_DP > 1^∘ in Fig. 15c); those in LH between 18:00 and 19:00 UTC were attributed to the sustaining weak updrafts ($Z_{\mathrm{H}}^{\mathrm{C}}$ <45dBZ) but more concentrated ice particles above the FL. The deep ML (ρ_HV < 0.98) also features these stations, and this signature even extends down to the lowest layer of LH and HJ with $Z_{\mathrm{DR}}^{\mathrm{C}}\mathit{>}\mathrm{2}$ dB dwelling below the FL. In addition, most ice particles upon these four stations might have melted in the air before being collected by disdrometers near the surface, which effectively accounts for the small rainfall differences between disdrometers and rain gauges. However, the residual differences between radar and DSD are mainly related to the warm process of raindrops below the ML.

Figure 15 The same as Fig. 12 but for the DT station.

Figure 16 The same as Fig. 12 but for the LH station.

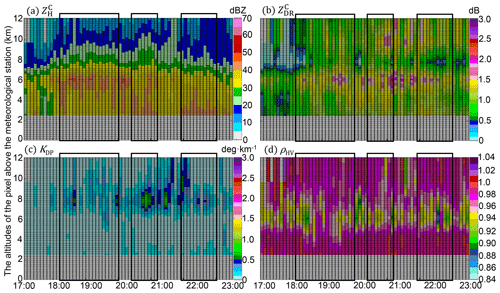
Figure 17 The same as Fig. 12 but for the XJ station between 15:00 UTC, 8 August 2019, and 21:00 UTC, 9 August 2019.

Figure 18 The WZ-SPOL radar along a radial profile (azimuth angle = 46^∘) at an elevation angle of 0.5^∘ at 17:59 UTC, 9 August 2019: (a) $Z_{\mathrm{H}}^{\mathrm{C}}$ and $Z_{\mathrm{H}}^{\mathrm{M}}$; (b) $Z_{\mathrm{DR}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$, and ${\widehat{Z}}_{\mathrm{DR}}$; and (c) Φ_DP, K_DP, and ρ_HV. This azimuth angle is marked in Fig. 11.

3.2.2 Polarimetric signatures of raindrops

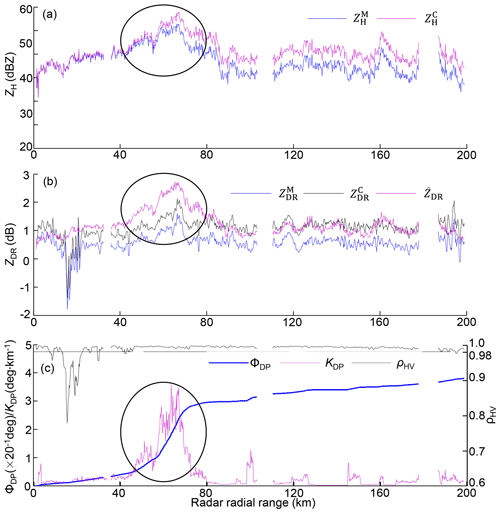
The deviation of $Z_{\mathrm{DR}}^{\mathrm{C}}$ from ${\widehat{Z}}_{\mathrm{DR}}$ is a non-negligible phenomenon during landfall of Lekima: underestimated $Z_{\mathrm{DR}}^{\mathrm{C}}$ in Fig. 11i–l compared with ${\widehat{Z}}_{\mathrm{DR}}$ in Fig. 11m–p emerged in areas with significant K_DP in Fig. 11q–t, which simultaneously emerged around the GWS of YDM. Apparently, $Z_{\mathrm{DR}}^{\mathrm{C}}$ cannot completely approximate ${\widehat{Z}}_{\mathrm{DR}}$ after correction; intrinsically, the microphysical composition issue, either dominant large-sized or small-sized raindrops filling in radar volume gates, resultantly determines final $Z_{\mathrm{DR}}^{\mathrm{C}}$–$Z_{\mathrm{H}}^{\mathrm{C}}$ distribution. One typical radial range profile in Fig. 18 is detailed to clarify this phenomenon. The ellipse-surrounded storm area contributes the most attenuation and differential attenuation with maximum ΔZ_H = 7.9 dBZ and ΔZ_DR = 0.645 dB, respectively, in Fig. 18a and b. Although the correction can result in enhanced consistency between Z_H and K_DP (see Sect. 3.1.2) and some $Z_{\mathrm{DR}}^{\mathrm{C}}$ have indeed partly approximated well to ${\widehat{Z}}_{\mathrm{DR}}$ (outside the ellipse in Fig. 18b), the other $Z_{\mathrm{DR}}^{\mathrm{C}}$ within the storm (in the ellipse) still have a residual Z_DR bias of about −1 dB. Additionally, ρ_HV ranging from 0.99 to 1 (in Fig. 15c) further indicates the dominance of pure liquid precipitation; high LWC and N_w can be deduced from Eqs. (8) and (9) (K_DP ≈ 3.5 ^∘ km⁻¹; ΔΦ_DP ≈ 68.5^∘ in Fig. 12c). Z_H is a composite integral of hydrometeors with different sizes and number concentrations, and Z_DR is sensitive to hydrometeor size; therefore, high concentrations of small-sized drops rather than large-sized drops contribute more to radar-measured $Z_{\mathrm{H}}^{\mathrm{C}}$ in radar volume gates. This unique composition resultantly causes an overestimated ${\widehat{Z}}_{\mathrm{DR}}$ estimated by $Z_{\mathrm{H}}^{\mathrm{C}}$, or conversely, underestimated $Z_{\mathrm{DR}}^{\mathrm{C}}$ compared with ${\widehat{Z}}_{\mathrm{DR}}$.

The hydrometeor size sorting (HSS) partly accounts for the position inconsistency between $Z_{\mathrm{H}}^{\mathrm{C}}$ and $Z_{\mathrm{DR}}^{\mathrm{C}}$, and it is significant in the rectangle-surrounded area of the inner eyewall, characterized by a maximum of $Z_{\mathrm{DR}}^{\mathrm{C}}$ in Fig. 12i on the significant upwind gradients of K_DP in Fig. 12q (Homeyer et al., 2021; Hu et al., 2020). Since $Z_{\mathrm{H}}^{\mathrm{C}}$ in Fig. 12e and K_DP in Fig. 12q are consistent with each other, the large ${\widehat{Z}}_{\mathrm{DR}}$ estimated by $Z_{\mathrm{H}}^{\mathrm{C}}$ also horizontally deviates from the area with large $Z_{\mathrm{DR}}^{\mathrm{C}}$. Differential sedimentation of hydrometeors of various sizes is the intrinsic reason for HSS (Feng and Bell, 2019), which is significant in the outer eyewall. The higher LWC (> 3 g m⁻³) features the outer eyewall as depicted in Fig. 16e; the area with large $Z_{\mathrm{DR}}^{\mathrm{C}}$ (> 2 dB) consists of dominant larger-sized drops with D₀ > 1.8 mm in Fig. 16a, but relatively lower concentration with log₁₀(N_w) > 4.4 in Fig. 16a than in its downwind area. Meanwhile, lower LWC (< 2 g m⁻³) features a cyclonical downwind area, but this area consists of dominant higher concentrated (log₁₀(N_w) > 4.4) small-sized drops (D₀ < 1.625 mm). However, HSS cannot account for the overall underestimation of $Z_{\mathrm{DR}}^{\mathrm{C}}$ when pixels with large $Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$, and K_DP coincide.

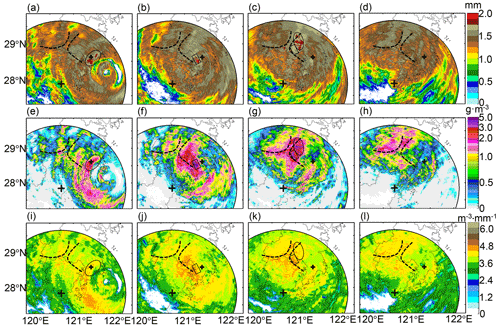
Figure 19 Radar-retrieved DSD parameters during typhoon Lekima: (a)–(d) are D₀ at 16:01, 17:59, 20:02, and 22:00 UTC, 9 August 2019, respectively; (e)–(h) and (i)–(l) are LWC and log₁₀(N_w), respectively, at the same time as (a)–(d). Two dashed lines refer to the GWS of YDM and KCM. The large + indicates the location of the WZ-SPOL radar site, and the little + indicates the location of the WL station.

The collision process in warm rain has three probable colliding outcomes: bounce, coalescence, and breakup. In one volume gate, bounce cannot change raindrop size and concentration; coalescence boosts the size increase, but breakup increases the concentration. The existence of large raindrops with D₀ > 1.8 mm around the GWS of YDM (in Fig. 19b and c) indeed back the occurrences of collision–coalescence processes, which corresponds to $Z_{\mathrm{DR}}^{\mathrm{C}}$ (> 1.8 dB in Fig. 11j and k). However, if the size increases contribute enough in one volume gate, $Z_{\mathrm{DR}}^{\mathrm{C}}$ might have well-approximated ${\widehat{Z}}_{\mathrm{DR}}$ in the storm area and agree better with $Z_{\mathrm{H}}^{\mathrm{C}}$. In addition, raindrops cannot continue increasing their size; spontaneous breakup (Srivastava, 1971) or collision–breakup due to vertical wind shear (i.e., Deng et al., 2019) co-occurs during the falling process of drops:

• i.

  The first evidence comes from the radar-measured $Z_{\mathrm{DR}}^{\mathrm{C}}$–$Z_{\mathrm{H}}^{\mathrm{C}}$ scattergram in Fig. 11d, and it tends to be more consistent with Z_DR–Z_H relationships dominated by small-sized drops related to the breakup, not large-sized drops related to the coalescence. This also agrees with the simulation results in Kumjian and Prat (2014).

• ii.

  The second natural phenomenon is the decreasing Z_DR downward in the lower atmospheric layers. Although some $Z_{\mathrm{DR}}^{\mathrm{C}}$ columns were indeed enhancing downward in Figs. 12–17, particularly in the time frames with significant updrafts with $Z_{\mathrm{H}}^{\mathrm{C}}$ extending upwards upon WL and YH, more time frames presented a dominant decreasing $Z_{\mathrm{DR}}^{\mathrm{C}}$ toward the ground, such as at DT, HJ, LH, and XJ.

• iii.

  The residual differences between radar and DSD are evident for the possible process in the vertical gap between radar volume gates and the surface. If dominant collision–coalescence occurred, DSD-derived Z_DR should be more significant than their radar counterparts in the air. However, the opposite is true at XJ, HJ, and LH, as depicted in Fig. 10. Meanwhile, DT exhibits similar Z_DR, Z_H, and K_DP to its radar counterparts after the landfall of Lekima, which is also evidence against the contribution from coalescence.

The collision–coalescence indeed occurs, but the breakup balances the size increase. This is evident in the evolutions of D₀ and N_w constrained by a given LWC, which is typical around the GWS of YDM. In Fig. 19c, g, and k, the identical LWC fill in the rectangle-surrounded and ellipse-surrounded regions; the latter exhibits larger D₀ (> 1.75 mm) but lower N_w with log₁₀(N_w) < 4.4; conversely, the former shows smaller D₀ (< 1.75 mm) but higher N_w with log₁₀ (N_w) > 4.4. Similar situations occurred in the two left columns in Fig. 19, and sparse large-sized D₀ is only prominent in a small area (in ellipse and rectangle); high N_w but small D₀ are features of the other parts of the typhoon. The LWC in one range gate will contribute not only to the size increase but also to the concentration, attributing to the balance between coalescence and breakup.

Combining the abovementioned observations, the overwhelming breakup of large-sized drops over coalescence firmly restrains the magnitudes of radar-measured $Z_{\mathrm{DR}}^{\mathrm{C}}$ for a given $Z_{\mathrm{H}}^{\mathrm{C}}$, accounting for the noticeable deviation of $Z_{\mathrm{DR}}^{\mathrm{C}}$ from ${\widehat{Z}}_{\mathrm{DR}}$ (in Fig. 11). Despite all this, collision–coalescence accompanied by the terrain-enhanced precipitation occurred when Lekima took high LWC (> 2 g m⁻³) and passed over YDM, as depicted in Fig. 19f and g, resulting in an overall LWC reduction around the GWS of KCM (i.e., Fig. 19g to h). During this period, D₀ and N_w simultaneously increased: D₀ increased by about 0.5 mm from Fig. 19a to D₀ > 1.5 mm in Fig. 19c; log₁₀ (N_w) increased about 0.4–0.8 from Fig. 19i to k, and these enhancements coincided well with the GWS of YDM. The gradual but insignificant enhancement persisted around the GWS of KCM, including an LWC increase by about 1 g m⁻³ (i.e., Fig. 19e–h), a diameter transition from D₀ < 1.25 mm to D₀ > 1.5 mm (i.e., Fig. 19a–d), and growth of log₁₀ (N_w) about 0.4 in sparse pixels (i.e., Fig. 19i–l), but this enhancement was relatively weaker than that around the GWS of YDM. This comparison indicates that extensive large-sized drops had formed and fallen around the GWS of YDM before Lekima moved to the north, which effectively accounts for the flood disasters. However, the utilization of radar-measured $Z_{\mathrm{DR}}^{\mathrm{C}}$ may not derive accurate radar rainfall fields.

3.3 Radar QPE analysis

3.3.1 The performances of radar QPE

Utilizing the DSD dataset from S₀, three primary radar rainfall rate relationships for R(Z_H), R(K_DP), and R(Z_H, Z_DR) are respectively established as

$$\begin{array}{}\text{(12a)}& {\displaystyle }R\left(Z_{\mathrm{H}}\right)=\mathrm{0.0544}\times Z_{\mathrm{H}}^{\mathrm{0.608}},\text{(12b)}& {\displaystyle }R\left(K_{\mathrm{DP}}\right)=\mathrm{45.0484}\times K_{\mathrm{DP}}^{\mathrm{0.7679}},\text{(12c)}& {\displaystyle }R\left(Z_{\mathrm{H}},Z_{\mathrm{DR}}\right)=\mathrm{0.0086}\times Z_{\mathrm{H}}^{\mathrm{0.9153}}{Z}_{\mathrm{DR}}^{-\mathrm{3.8606}}\end{array}$$

based on the standard weighted least squares nonlinear fitting method and DSD-derived radar variables (depicted in Fig. 20). In addition, $Z_{\mathrm{DR}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$, and ${\widehat{Z}}_{\mathrm{DR}}$ are integrated with Z_H to exploit the impacts of the above-mentioned microphysical process on radar QPE algorithms. The pixel-to-pixel linear average accumulation scheme is utilized to retrieve radar 6 h rainfall fields for these radar QPE estimators and is then evaluated independently by comparing gauge 6 h rainfall measurements through the absolute normalized mean error (E_NMA), root mean square error (E_RMS), and correlation coefficient (E_CC) as

$$\begin{array}{}\text{(13a)}& {\displaystyle }{E}_{\mathrm{NMA}}={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^n\mathrm{|}{r}_i-{\mathrm{g}}_i\mathrm{|}}{{\sum }_{i=\mathrm{1}}^n{\mathrm{g}}_i}}\times \mathrm{100}\mathrm{\%}\text{(13b)}& {\displaystyle }{E}_{\mathrm{RMS}}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n(r_i-{\mathrm{g}}_i{)}^{\mathrm{2}}}\text{(13c)}& {\displaystyle }{E}_{\mathrm{CC}}={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^n(r_i-\stackrel{\mathrm{‾}}{r})({\mathrm{g}}_i-\stackrel{\mathrm{‾}}{g})}{\sqrt{{\sum }_{i=\mathrm{1}}^n(r_i-\stackrel{\mathrm{‾}}{r}{)}^{\mathrm{2}}}\sqrt{{\sum }_{i=\mathrm{1}}^n({\mathrm{g}}_i-\stackrel{\mathrm{‾}}{g}{)}^{\mathrm{2}}},}}\end{array}$$

where r_i and g_i refer to radar rainfall estimates and gauge rainfall. The 6 h radar rainfall fields retrieved by R($Z_{\mathrm{H}}^{\mathrm{M}}$), R($Z_{\mathrm{H}}^{\mathrm{C}}$), R(K_DP), R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$), R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$), and R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) are derived in Fig. 21, as well as the scattergram between radar rainfall estimates and gauge rainfall measurements, depicted in Fig. 22, to reveal their practical performances around the disaster area.

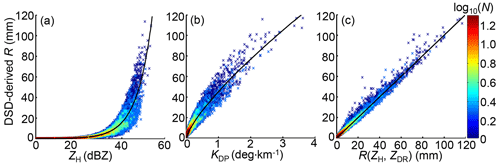
Figure 20 The scattergram of (a) DSD-derived R vs. Z_H, (b) DSD-derived R vs. K_DP, and (c) DSD-derived R vs. R estimated by fitted R(Z_H, Z_DR).

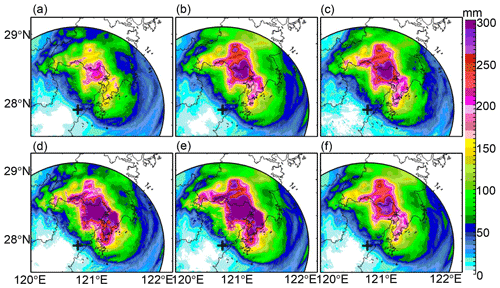
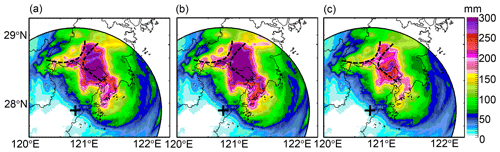
Figure 21 The 6 h rainfall estimates derived from (a) R($Z_{\mathrm{H}}^{\mathrm{M}}$), (b) R($Z_{\mathrm{H}}^{\mathrm{C}}$), (c) R(K_DP), (d) R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$), (e) R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$), and (f) R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) at 22:00 UTC, 9 August 2019. Two dashed lines refer to the GWS of YDM and KCM, and + refers to the WZ-SPOL radar site.

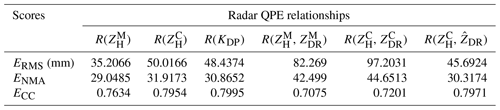
R($Z_{\mathrm{H}}^{\mathrm{M}}$) presents lower rainfall estimates in Fig. 21a than the other radar rainfall estimators in Fig. 21b–f, although they have similar rainfall center shapes. In terms of statistical scores in Table 1, R($Z_{\mathrm{H}}^{\mathrm{M}}$) does not perform the worst among all radar rainfall estimators. Its E_RMS, E_NMA, and E_CC even outperform R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$) by 57 %, 31.6 % and 7.9 %, and outperform R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$) by 63.8 %, 34.9 % and 6 %, respectively. However, its underestimation can easily be perceived from the scatters in Fig. 22a when rainfall recordings exceed 100 mm in the center rainfall area. This phenomenon can be ascribed to the attenuation on $Z_{\mathrm{H}}^{\mathrm{M}}$ caused by the highly concentrated hydrometeors in the storm during the landfall of Lekima.

Table 1 Evaluation scores of 6 h rainfall accumulations based on six radar QPE relationships.

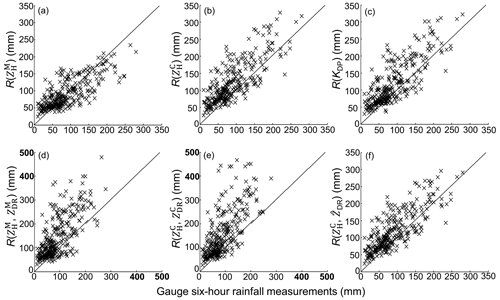
Figure 22 The scattergram of 6 h rainfall estimates from radar versus corresponding gauge rainfall measurements. The radar rainfall estimates are derived at 22:00 UTC, 9 August 2019, using (a) R($Z_{\mathrm{H}}^{\mathrm{M}}$), (b) R($Z_{\mathrm{H}}^{\mathrm{C}}$), (c) R(K_DP), (d) R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$), (e) R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$), and (f) R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$).

In contrast, R($Z_{\mathrm{H}}^{\mathrm{C}}$) in Fig. 21b presents higher rainfall estimates and R($Z_{\mathrm{H}}^{\mathrm{C}}$) mainly overestimates, since more scatters are distributed above the diagonal line (y=x) as depicted in Fig. 22b, and its E_CC outperforms that of R($Z_{\mathrm{H}}^{\mathrm{M}}$) by 4.2 %, even with larger E_NMA and E_NMA scores. The overestimation of R($Z_{\mathrm{H}}^{\mathrm{C}}$) in the rainfall center area conversely demonstrates the effectiveness of the attenuation correction based on the ZPHI approach, because the same R(Z_H) relationship is utilized for the rainfall retrieval; the only difference is the replacement of $Z_{\mathrm{H}}^{\mathrm{M}}$ with $Z_{\mathrm{H}}^{\mathrm{C}}$.

R(K_DP) in Fig. 21c presents a similar rainfall field structure to R($Z_{\mathrm{H}}^{\mathrm{C}}$). The scores of R(K_DP) are just a little superior to that of R($Z_{\mathrm{H}}^{\mathrm{C}}$) in Table 1, with its E_RMS, E_NMA, and E_CC outperforming that of R($Z_{\mathrm{H}}^{\mathrm{C}}$) by 3.1 %, 3.2 %, and 0.5 %, respectively. The scattergrams in Fig. 22b and c are also similar to each other, indicating that R(K_DP) and R($Z_{\mathrm{H}}^{\mathrm{C}}$) both overestimate, although R(K_DP) is less overestimated when rainfall recordings are less than 100 mm. Their similar performances can be attributed to the consistency between radar-measured K_DP and $Z_{\mathrm{H}}^{\mathrm{C}}$ measurements as described in Sect. 3.1.2.

R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$) and R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$) in Fig. 21d and e both present significantly higher estimates in the rainfall center area than the others, which results in severe overestimation according to the scattergrams in Fig. 22d and e. Furthermore, R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$) obtains the worst E_RMS and E_NMA scores of all radar rainfall estimators, and this can be explained based on the Z_H-related and Z_DR-related calculation items as demonstrated in Fig. 23: $Z_{\mathrm{H}}^{\mathrm{C}}$ obtains much higher rainfall estimates through Z_H-related items than $Z_{\mathrm{H}}^{\mathrm{M}}$. However, the calculation needs to be further adjusted through the Z_DR-related item: the larger Z_DR measurements correspond to fewer final rainfall estimates. A −0.5 dB Z_DR bias could result in relatively less rainfall adjustment, according to Fig. 23. The attenuation effects on $Z_{\mathrm{DR}}^{\mathrm{M}}$ make the corresponding rainfall calculation less adjusted, which can effectively account for the overestimation of R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$). However, the correction cannot make $Z_{\mathrm{DR}}^{\mathrm{C}}$ completely consistent with $Z_{\mathrm{H}}^{\mathrm{C}}$, but it is underestimated, as demonstrated in Sect. 3.1.2, which is related to the dynamic microphysical process described in Sect. 3.2.

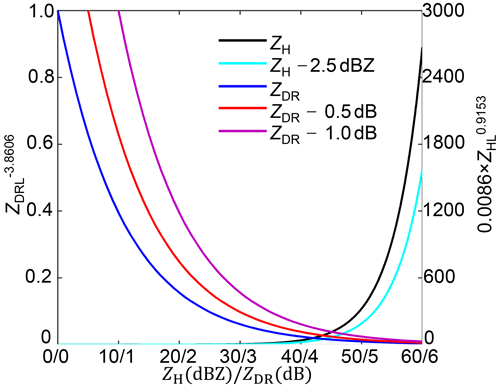
Figure 23 The contribution of Z_H-related and Z_DR-related terms in the R(Z_H, Z_DR) relationship with different Z_H and Z_DR biases. The R(Z_H, Z_DR) relationship is detailed in Eq. (12c). Z_HL and Z_DRL refer to Z_H and Z_DR at a linear scale.

The spatial texture of R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) in Fig. 21f presents slightly fewer rainfall estimates than R($Z_{\mathrm{H}}^{\mathrm{C}}$) and R(K_DP) in Fig. 21b and c, and the scattergram in Fig. 22f shows that R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) agrees better with the gauge rainfall than in Fig. 22b and c. R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) effectively reduces the overestimates and is obviously superior to R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$) and R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$). The E_RMS/E_NMA score of R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) is better than R($Z_{\mathrm{H}}^{\mathrm{C}}$) and R(K_DP), by $\mathrm{8.6}\mathit{\%}/\mathrm{5}\mathit{\%}$ and $\mathrm{5.7}\mathit{\%}/\mathrm{1.8}\mathit{\%}$, respectively, although its E_CC score is slightly worse by 0.2 % and 0.3 %. The superiority of R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) can also be apparently attributed to the incorporation of ${\widehat{Z}}_{\mathrm{DR}}$. ${\widehat{Z}}_{\mathrm{DR}}$ is not a real radar measurement; it is directly estimated from $Z_{\mathrm{H}}^{\mathrm{C}}$ from the theoretical DSD-derived Z_DR–Z_H relationship in Eq. (2a). ${\widehat{Z}}_{\mathrm{DR}}$ is naturally self-consistent with $Z_{\mathrm{H}}^{\mathrm{C}}$ and K_DP, since $Z_{\mathrm{H}}^{\mathrm{C}}$ and K_DP have agreed well with their DSD-derived counterparts regarding the K_DP–Z_H distributions and pixel-to-pixel comparisons in Sect. 3.1. The utilization of the DSD-derived Z_DR–Z_H relationship intrinsically assumes that composition in radar volume gates has a similar size and concentration to its surface counterparts; therefore, ${\widehat{Z}}_{\mathrm{DR}}$ can be seen as an equivalent radar variable. The replacement of $Z_{\mathrm{DR}}^{\mathrm{C}}$ with ${\widehat{Z}}_{\mathrm{DR}}$ is also equivalent to imposing the surface raindrop size and concentration on radar measurements. The relatively larger ${\widehat{Z}}_{\mathrm{DR}}$ than $Z_{\mathrm{DR}}^{\mathrm{C}}$ means a more significant adjustment can be performed for rainfall estimation using R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$), according to Fig. 23, and this also indicates that the anticipated giant raindrops had fallen around the GWS of YDM. Except for the simultaneous D₀ and N_w increases, the following alternative ${\widehat{Z}}_{\mathrm{DR}}$ indirectly verifies the dominant collision–coalescence around this area.

3.3.2 The impacts of microphysical processes on radar QPE

The consistency between radar and surface measurements is critical for radar QPE algorithms, but the microphysical process in the vertical gap between air and surface may worsen the practical performances of radar QPE. This is the case around the GWS of YDM: the primary outcome of the collision process transitions from a dominant breakup in the air to dominant coalescence near the surface due to the topographical enhancement. Using radar measurements on the lowest elevation angle to retrieve radar QPE implicitly assumes that they are representative of surface precipitation, but they are not in this situation; only R(Z_H), R(K_DP), and R(Z_H, Z_DR) relationships established based on the DSD dataset represent the feedback near the surface. Although R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) performs best, ${\widehat{Z}}_{\mathrm{DR}}$ can also be estimated by Eqs. (11a)–(11c). However, $Z_{\mathrm{DR}}^{\mathrm{C}}$ changes little if a smaller or larger ${\widehat{Z}}_{\mathrm{DR}}$ estimated by Eqs. (11a)–(11c) is imposed in the correction procedure, as $Z_{\mathrm{DR}}^{\mathrm{C}}$–$Z_{\mathrm{H}}^{\mathrm{C}}$ scattergrams shown in Fig. 24a–c. Furthermore, the corresponding three R(Z_H, Z_DR) relationships based on S_I–S_III can be established as

$$\begin{array}{}\text{(14a)}& {\displaystyle }R\left(Z_{\mathrm{H}},Z_{\mathrm{DR}}\right)=\mathrm{0.0088}\times Z_{\mathrm{H}}^{\mathrm{0.917}}{Z}_{\mathrm{DR}}^{-\mathrm{3.9203}}\mathrm{DSD}\in S_{\mathrm{I}},\text{(14b)}& {\displaystyle }R\left(Z_{\mathrm{H}},Z_{\mathrm{DR}}\right)=\mathrm{0.0085}\times Z_{\mathrm{H}}^{\mathrm{0.9222}}{Z}_{\mathrm{DR}}^{-\mathrm{4.0371}}\mathrm{DSD}\in S_{\mathrm{II}},\text{(14c)}& {\displaystyle }R\left(Z_{\mathrm{H}},Z_{\mathrm{DR}}\right)=\mathrm{0.0078}\times Z_{\mathrm{H}}^{\mathrm{0.9342}}{Z}_{\mathrm{DR}}^{-\mathrm{4.2321}}\mathrm{DSD}\in S_{\mathrm{III}}.\end{array}$$

The alternative utilization of S_I–S_III slightly changes the parameters of R(Z_H, Z_DR) with minor rainfall rate differences estimated by Eqs. (12c), (14a)–(14c). However, the impacts on ${\widehat{Z}}_{\mathrm{DR}}$ are non-negligible, particularly for a given $Z_{\mathrm{H}}^{\mathrm{C}}$ exceeding 35 dBZ, and smaller ${\widehat{Z}}_{\mathrm{DR}}$ means weaker adjustment for the Z_HL-related item, as depicted in Fig. 23.

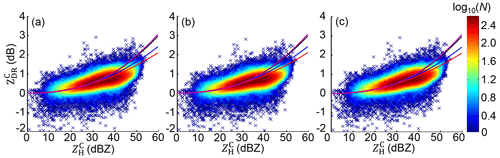
Figure 24 Scattergrams between $Z_{\mathrm{DR}}^{\mathrm{C}}$ and $Z_{\mathrm{H}}^{\mathrm{C}}$, utilizing ${\widehat{Z}}_{\mathrm{DR}}$ estimated by (a) Eq. (11a) (the blue curve), (b) Eq. (11b) (the red curve), and (c) Eq. (11c) (the purple curve). The black curve stands for Eq. (2a).

As in the analysis in Sect. 3.1.2, radar-measured $Z_{\mathrm{DR}}^{\mathrm{C}}$–$Z_{\mathrm{H}}^{\mathrm{C}}$ in volume gates tend to be more consistent with S_I and S_II, because breakup overwhelms in the coalescence–breakup balance, so if breakup still dominates when these drops further fall on the ground, R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}})$ estimated by Eqs. (14a) and (14b) should perform better than that estimated by Eq. (12c). However, in reality, their spatial fields in Fig. 25a and b and scattergrams in Fig. 26a and b conversely present a similar overestimation as R($Z_{\mathrm{H}}^{\mathrm{M}}$, $Z_{\mathrm{DR}}^{\mathrm{M}}$) and R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$), which contradict the anticipated results. Such a contradiction means ${\widehat{Z}}_{\mathrm{DR}}$ estimated by Eqs. (11a) and (11b) is not representative enough for surface precipitation. In contrast, R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) in Fig. 25c shows even lower rainfall estimates than that in Fig. 21f (obtained through Eq. 12c based on S₀), which can also be seen by comparing the scattergrams in Figs. 26c and 22f. In addition, when large-sized drops are gradually excluded from the DSD dataset for ${\widehat{Z}}_{\mathrm{DR}}$ and R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}})$, E_CC changes little in Table 2, whereas E_RMS and E_NMA both exhibit a monotonic increasing tendency, implying the non-negligible contribution of large-sized drops around the GWS of YDM.

Table 2 Evaluation scores of R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) calculated by different datasets^*.

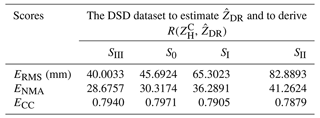
^* S_III includes more size–velocity pairs than S₀.

Figure 25 The same as Fig. 21, but (a)–(c) were calculated with Eqs. (14a)–(14c), respectively.

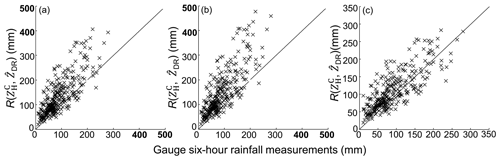
Figure 26 The scattergram of 6 h rainfall estimates from R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) versus corresponding gauge rainfall measurements at 22:00 UTC, 9 August 2019: (a)–(c) are, respectively, for results calculated using Eqs. (14a)–(14c).

The dominant breakup in the air but dominant coalescence around the GWS of YDM can be ascribed to the overshooting of radar beams and the topographical enhancement. In this sense, the utilization of ${\widehat{Z}}_{\mathrm{DR}}$ instead of $Z_{\mathrm{DR}}^{\mathrm{C}}$ equals a physical conversion of breakup-dominated outcome in one volume gate for a given $Z_{\mathrm{H}}^{\mathrm{C}}$ into their coalescence-dominated counterparts in an average sense. In this conversion process, consistency between radar-measured $Z_{\mathrm{H}}^{\mathrm{C}}$ and K_DP in the air and the surface counterparts (DSD-derived K_DP and Z_H) has been achieved, as indicated in Sect. 3.1.2, demonstrating the mass conservation characteristics of falling drops. Therefore, radar-measured $Z_{\mathrm{H}}^{\mathrm{C}}$ and K_DP around the GWS of YDM may change insignificantly, which makes it conducive for R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}})$ to obtain a better radar rainfall field.

Table 3 Radar QPE relationships at six different meteorological stations.

3.4 Discussion

The microphysical processes during the landfall of typhoon Lekima have been revealed based on the analysis of consistency between measurements from radar, disdrometers, and rain gauge networks. The cause of the flood disaster around the GWS of YDM, and its impacts on the practical performance of radar QPE algorithms have been investigated. Several critical issues should be considered for radar quantitative applications in future:

• i.

  High-quality DSD datasets could lay a solid foundation for microphysical analysis and polarimetric radar applications, but selecting representative datasets for different microphysical processes is critical to determine parameters for quantitative applications, such as the construction of relationships between Z_H, Z_DR, K_DP, and R. The size–velocity QC procedure could be deeply refined for radar QPE in cold seasons. So far, one-dimensional disdrometers (OTT or Thies) are the main facilities to collect DSD measurements in the national meteorological stations over China. However, both GWS areas in this article have no DSD measurements for directly revealing and validating the critical precipitation process in the typhoon center area. Furthermore, there are more similar GWS areas in south China, thus deploying some two-dimensional disdrometers in these vital target locations could be beneficial for future research.

• ii.

  The polarimetric radar measurements are indispensable for microphysical analysis and quantitative applications. In particular, Z_DR provides critical signatures for analyzing the collision process in this super typhoon event. Currently, more X-band polarimetric radar systems have been planned and/or deployed to fill the gap of operational S-band radar networks. Although Z_DR of S-,C-, and X-band radars is sensitive to drop size in different degrees, Z_DR biases in X-band radar measurements can be more serious in a super typhoon case due to radome attenuation. The correction methods of Z_H and Z_DR in this article could potentially be further refined for X-band applications.

• iii.

  The spatial variability of precipitation could be far more complex, and it is oversimplified to assert that convective or stratiform rainfall always exhibits breakup or coalescence (Kumjian and Prat, 2014). It is noticed that the practical performances of R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) rely on determining optimal ${\widehat{Z}}_{\mathrm{DR}}$ based on the representative DSD dataset of the microphysical process, which is the main limitation of R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$). R(K_DP) or R(A_H) are insensitive to such uncertainty, and they can outperform R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{DR}$) if they are further optimized. In addition, a single relationship between R and radar measurements might not be applicable to all range gates within the radar coverage, for example, R(Z_H), R(K_DP), and R(Z_H, Z_DR) relationships listed in Table 3 are different; therefore, the residual differences between radar estimates and gauge measurements are still significant for R($Z_{\mathrm{H}}^{\mathrm{C}}$), R(K_DP), and R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$). Merging radar with gauge measurements may partly reduce such differences if surface gauge rainfall bias caused by strong wind can be mitigated effectively.

• iv.

  The vertical gap between radar measurements and surface hinders deriving more optimal relationships and the complete vertical view of the microphysical processes, which are critical in precipitation events such as this super typhoon case. Sophisticated correction models are necessary to mitigate uncertainty caused by the vertical gap, such as the classical models for vertical extrapolation if only radar measurements on higher altitudes are available, either caused by complete beam blockage of mountainous terrain or the high altitudes of radar sites. Efficient implementation of the correction models requires prior knowledge of vertical microphysical precipitation variations. Still, the precipitation process should be determined to effectively match the model with radar measurements. In this typhoon case, the microphysical process is much more complicated, but if the coalescence–breakup balance of the collision process can be measured quantitatively and incorporated into radar QPE algorithms in the future, a more reasonable model can be established to enhance radar QPE performance.

4 Summary

This paper utilized a range of data, including observations from the WZ-SPOL radar, disdrometers, and gauge rainfall measurements, to analyze the microphysical processes during the landfall of Lekima (2019). The investigation focused on demonstrating the impacts of precipitation microphysics on the consistency of multi-source measurements and radar QPE performance. The main findings are summarized as follows:

• i.

  Measurements from radar, disdrometers, and rain gauges are more consistent after the QC processing, including attenuation correction of radar observations and wind and hail/graupel processing of size–velocity measurements from disdrometers.

• ii.

  The breakup overwhelms coalescence as the primary outcome of the collision process of raindrops, noticeably making radar-measured $Z_{\mathrm{DR}}^{\mathrm{C}}$–$Z_{\mathrm{H}}^{\mathrm{C}}$ be breakup-dominated, which accounts for that high drop concentration rather than large drop size contributes more to a given $Z_{\mathrm{H}}^{\mathrm{C}}$ and the residual deviation of $Z_{\mathrm{DR}}^{\mathrm{C}}$ from ${\widehat{Z}}_{\mathrm{DR}}$.

• iii.

  R($Z_{\mathrm{H}}^{\mathrm{C}}$) performs comparably well with R(K_DP) owing to attenuation correction, but R($Z_{\mathrm{H}}^{\mathrm{C}}$, $Z_{\mathrm{DR}}^{\mathrm{C}}$) performs worse with serious overestimation. This is related to the unique microphysical process around the GWS of YDM, in which the breakup-dominated small-sized drops in radar sampling volumes were located above the surface but coalescence-dominated large-sized drops were near the surface.

• iv.

  R($Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$) outperforms R($Z_{\mathrm{H}}^{\mathrm{C}}$) and R(K_DP) in terms of the E_RMS and E_NMA scores, and the utilization of ${\widehat{Z}}_{\mathrm{DR}}$ instead of $Z_{\mathrm{DR}}^{\mathrm{C}}$ is close to physically converting breakup-dominated measurements in radar range gates to coalescence-dominated counterparts, which boosts better self-consistency between $Z_{\mathrm{H}}^{\mathrm{C}}$, ${\widehat{Z}}_{\mathrm{DR}}$, and K_DP and their consistency with the surface counterparts derived from disdrometer measurements.

The complex precipitation microphysics may have other unknown impacts on the self-consistency of radar measurements and the consistency between multi-source datasets, which is still a challenge for future research. An in-depth understanding of such microphysical processes is critical for improving radar quantitative remote sensing of precipitation. Deployment of cost-effective zenith radar (X- or Ka-band) networks may be an effective complement of operational weather radar networks. Collaborative observations of various remote sensing facilities such as these can not only help to resolve more microphysical processes in the vertical gaps currently missed by scanning radars but also support the development of more reasonable models to mitigate the resulting application uncertainty, especially in complex terrain regions.