the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Reaction dynamics of P(4S) + O2(X3Σ−g) → O(3P) + PO(X2Π) on a global CHIPR potential energy surface of PO2(X2A1): implications for atmospheric modelling
Guangan Chen
Ximing Li
Linhua Liu
The reaction dynamics of P(4S) + O2(X) → O(3P) + PO(X2Π) are thought to be important in atmospheric and interstellar chemistry. Based on the state-of-the-art ab initio energy points, we analytically constructed a global potential energy surface (PES) for the ground-state PO2(X2A1) using the combined-hyperbolic-inverse-power-representation (CHIPR) method. A total of 6471 energy points were computed by the multireference configuration interaction method with the Davidson correction and aug-cc-pV5Z basis set. The analytical CHIPR PES reproduces ab initio energies accurately with a root-mean-square deviation of 91.5 cm−1 (or 0.262 kcal mol−1). The strongly bound valence region of the PES has complicated topographical features with multiple potential wells and barriers. The attributes of the important intermediates are carefully validated with our geometry optimization results, as well as previous experimental and computational results. Finally, the reaction probability, integral cross sections, and rate constants for P(4S) + O2(X) → O(3P) + PO(X2Π) are calculated using the quasi-classical trajectory and time-dependent wave packet methods. The trends of probability and integral cross section versus the collision energy can be divided into three stages, which are governed by the entrance barriers or exothermicity of the reaction. The rate constant demonstrates strong Arrhenius linear behaviour at relatively low temperatures but deviates from this pattern at high temperatures. The calculated cross sections and rate constants are helpful for modelling the phosphorus chemistry in atmospheric and interstellar media.
- Article
(7407 KB) - Full-text XML
-
Supplement
(329 KB) - BibTeX
- EndNote
Phosphorus (P) is one of the essential biogenic elements found in all known organisms. Its compounds are abundant in biological systems and greatly contribute to basic biological functions (Maciá, 2005). Much of the P on Earth's surface is locked up in mineral phosphate forms with fairly poor bioavailability, while the P compounds with low oxidation are generally more reactive and accessible for potential prebiotic chemistry (Todd, 2022) but unstable under terrestrial redox conditions (Pasek, 2008).
One source of P compounds with low oxidation on Earth's surface is interstellar dust particles (IDPs), which account for 99 % of the total amount of incoming extra-terrestrial material each year (Plane et al., 2018), containing P with about 8 % abundance (Lodders, 2003). The ablation of IDPs in the upper atmosphere of terrestrial planets delivers PO and P (Carrillo-Sánchez et al., 2020), a part of which might undergo a series of chemical processes to form bioavailable H3PO3 before reaching the Earth's surface. The corresponding P chemistry networks (Douglas et al., 2019, 2020; Plane et al., 2021) were predicted by electronic structure theory and given by
This suggests that meteor-ablated P is likely oxidized by the Reaction (R1) first. Hence, the dynamics study of Reaction (R1) will contribute to a deeper understanding of the chemical evolution of P and PO in the Earth's atmosphere.
Reaction R1 is also important in astrochemistry. For example, PO has been widely observed in the interstellar medium (ISM) (Tenenbaum et al., 2007; De Beck et al., 2013; Ziurys et al., 2018; Lefloch et al., 2016; Rivilla et al., 2020) and is considered to be the main reservoir for gas-phase P in the ISM (Ziurys et al., 2018; Rivilla et al., 2020). There is some evidence to suggest that PO was present in cometary ice before the birth of the Sun (Rivilla et al., 2020), and the comets possibly provided a major source of prebiotic phosphorus compounds (Maciá et al., 1997). Hence, investigation of the formation of PO is helpful for modelling its abundance in the ISM.
Given its important role in interstellar and atmospheric chemistry, Reaction (R1) was investigated in several experimental and theoretical studies (Douglas et al., 2019; Husain and Norris, 1977; Husain and Slater, 1978; Clyne and Ono, 1982; Henshaw et al., 1987; Gomes et al., 2022). Previous experiments presented its rate constants at a specified temperature of about 300 K (Husain and Norris, 1977; Husain and Slater, 1978; Clyne and Ono, 1982; Henshaw et al., 1987), and their values diverged by an order of magnitude. A recent experiment has determined the rate constants of P(4S) + O2 → O + PO at temperatures ranging from ∼200 to 750 K (Douglas et al., 2019). In the same work, the rate constants of P(4S) + O2(X) → O(3P) + PO(X2Π) were also computed using the Rice–Ramsperger–Kassel–Markus (RRKM) theory with the molecular geometry optimization at the B3LYP/aug-cc-pVQZ (AVQZ) level. Subsequently, the state-of-the-art ab initio method was used to predict the minimum energy path (MEP) of this reaction (Gomes et al., 2022), and the rate constants were computed by employing the standard transition-state theory (TST). These two theoretical rate constants reproduced the experimental results to some extent, and the difference between them came mainly from the predicted barrier heights. The limitation of the work by Douglas et al. (2019) is that the B3LYP method is not good at predicting the barrier heights (Zhao and Truhlar, 2008; Peverati and Truhlar, 2012). Also, the statistical RRKM and TST theories may fail due to unincluded non-statistical dynamics effects (Carpenter, 1998; Thomas et al., 2008), so a dynamics study for this reaction is required. Moreover, their analytical forms of the rate constants were obtained by fitting predictive data lower than 1000 K, so the fitted rate constants at high temperatures may not be accurate. Accurately modelling the rate constants of P(4S) + O2(X) → O(3P) + PO(X2Π) in a wide temperature range is desired, because the temperatures of ablation of IDPs could reach more than 2500 K.
The reactants P(4S) + O2(X) and products O(3P) + PO(X2Π) are connected to the lowest doublet and quartet states of PO2, in which the doublet state (X2A1) plays a major role in this reaction (Gomes et al., 2022). The molecular geometries and vibration frequencies of PO2(X2A1) have been well studied by several theoretical (Lohr, 1984; Kabbadj and Liévin, 1989; Jarrett-Sprague and Hillier, 1990; Cai et al., 1996; Francisco, 2002; Xianyi et al., 2008; Liang et al., 2013; Xu et al., 1996; Bauschlicher, 1999) and experimental (Cordes and Witschel, 1965; Davies and Thrush, 1968; Drowart et al., 1972; Verma and McCarthy, 1983; Kawaguchi et al., 1985; Hamilton, 1987; Qian et al., 1995; Lei et al., 2001; Lawson et al., 2011) methods. The recent measurement reported RPO=2.771 a0 and θOPO=135.3∘ with the C2v symmetry (Kawaguchi et al., 1985), along with the vibration frequencies of 1075.4, 397.3 and 1327.54 cm−1 for the symmetrical stretching (ω1) (Lei et al., 2001), bending (ω2) (Lei et al., 2001), and antisymmetric stretching (ω3) (Lawson et al., 2011), respectively. It is worth noting that the potential energy surface (PES) can yield physical insights into the reaction path, energy transfer, and structure of intermediates. The analytical form of a global PES modelled by ab initio energies can accurately predict the barrier height, and it is the first step toward molecular simulations, such as the reactive or non-reactive collisions and photodissociation within the system (Conway et al., 2020; Caridade et al., 2013; Schmidt et al., 2013). Therefore, a dynamics study carried out on such a PES is reliable, and the information including the reaction probability and integral cross section (ICS) can be well predicted. The first analytical PES of PO2(X2A1) was constructed using the B3P86/6-311G(3df, 3pd) energy points (Zeng and Zhao, 2012), but the dissociation energy was well beyond the experimental value, and the intermediates were not all predicted. For performing a high-precision dynamics study of the title reaction, it is necessary to develop a global PES of PO2(X2A1), in which the potential energies should be calculated with the state-of-the-art ab initio method, and the reaction path should be well reproduced and carefully validated.
This work aims to establish a global PES for the ground-state PO2(X2A1) so as to present a dynamics study on P(4S) + O2(X) → O(3P) + PO(X2Π). The state-of-the-art ab initio method was applied to calculate the potential energies of PO2(X2A1). The analytical PES was then generated using the combined-hyperbolic-inverse-power-representation (CHIPR) method (Varandas, 2013; Rocha and Varandas, 2020, 2021). The rate constants for the P(4S) + O2(X) → O(3P) + PO(X2Π) reaction at temperatures ranging below 5000 K were obtained using the quasi-classical trajectory (QCT) (Peslherbe et al., 1999; Li et al., 2014) and time-dependent wave packet (TDWP) (Zhang and Zhang, 1993, 1994) methods, and they were compared with available experimental and theoretical results. Moreover, the state-specified reaction probability and ICSs were provided in order to get a deeper understanding of this reaction.
All ab initio calculations of the ground-state PO2(X2A1) were carried out using the MOLPRO 2015 software package (Werner et al., 2020; Eckert et al., 1997) with the Cs (A′) symmetry point group. The Dunning-type aug-cc-pV5Z (AV5Z) basis set (Dunning et al., 2001; Martin and Uzan, 1998; Woon and Dunning, 1993) was applied. The calculation processes are as follows. Firstly, the Hartree–Fock (HF) method was used to obtain the single-configuration wave function of PO2(X2A1). The relevant multi-configuration wave functions were generated by the full-valence complete active space self-consistent field (CASSCF) method (Knowles and Werner, 1985) based on the HF wave function. Finally, the dynamics correlation energies were considered by the internally contracted multireference configuration-interaction method including the Davidson correction (MRCI(Q)) (Knowles and Werner, 1988; Werner and Knowles, 1988), in which the CASSCF wave functions were set as reference. In the CASSCF and MRCI(Q) calculations, 12 active molecular orbitals () involved 17 valence shell electrons, and the remaining 14 inner shell electrons were closed into 7 core orbitals (). A total of 6471 ab initio energy points were generated from two grids defined in Jacobi coordinates and six additional grids defined around the important intermediates. For example, the RA-BC, rBC, and γA-BC for the A-BC channel of an ABC molecule are defined as the distance of the A atom relative to the centre of mass of BC, the bond distance of BC, and the angle between RA-BC and rBC, respectively. In the P-O2 channel, the grids were defined by , , and . In the O-PO channel, the ranges were defined by , , and . The additional grids around the equilibrium geometry, local minimum, and transition states were constructed to be dense enough according to the geometry optimization (OPTG) (Eckert et al., 1997) results obtained from MOLPRO 2015 (Werner et al., 2020; Eckert et al., 1997).
According to the spin-spatial Wigner–Witmer correlation, the dissociation scheme of the ground-state PO2(X2A1) can be described by
The ground-state PO2(X2A1) dissociates adiabatically into O(3P) + PO(X2Π), P(4S) + O2(X), and P(4S) + O(3P) + O(3P). Assuming the energy of infinitely separated P(4S) + O(3P) + O(3P) atoms to be the zero point, the global adiabatic CHIPR PES of the ground-state PO2(X2A1) has the following many-body expansion (MBE) (Murrell et al., 1984; Varandas and Murrell, 1977) form:
where V(2) represents the two-body fragments represented by the diatomic potential energy curves (PECs) of O2(X) and PO(X2Π). V(3) is the three-body fragment. In the CHIPR method (Rocha and Varandas, 2020, 2021; Varandas, 2013), two-body fragments are given by
where ZA and ZB are the nuclear charges of atoms A and B, respectively. Ck represents expansion coefficients of an Lth-order polynomial, and y is the basis set consisting of the linear combination of R-dependent functions (see Eq. 4 shown below). For the AB2-type species like PO2, the CHIPR three-body fragment can be simplified to the following permutation symmetric form (Rocha and Varandas, 2020, 2021; Varandas, 2013):
where represents expansion coefficients for an Lth-order polynomial, and yp represents basis sets of coordinates (p=1, 2, 3) for the reference geometry, which are expressed in terms of the Mth-order distributed-origin contracted basis set (Rocha and Varandas, 2020, 2021):
where
and
are primitive bases. γp,α represents non-linear parameters, and represents the origin. The fitting process was carried out in the CHIPR 4.0 program (Rocha and Varandas, 2021). For more detailed descriptions of the CHIPR method, we refer the reader to the related manuals (Rocha and Varandas, 2020, 2021). In recent years, there has been a lot of global PESs constructed based on this method, such as H3 (Varandas, 2013), HO2 (Varandas, 2013), C3 (Rocha and Varandas, 2019a), C3H (Rocha and Varandas, 2019b), PH2 (Chen et al., 2022), NH2 (Li et al., 2022), Si2C (Li et al., 2023), and SiC2 (Rocha et al., 2022).
3.1 Two-body fragment
Based on Eq. (1), the PECs of the ground states O2(X) and PO(X2Π) were fitted to the CHIPR form of Eq. (2) to obtain the two-body fragments of the MBE potential of PO2(X2A1). The ab initio potential energies were calculated at the MRCI(Q) level of theory with the AV5Z basis set. For O2(X), D2h symmetry was chosen with the consideration of 10 active molecular orbitals (3 Ag + 1 B3u + 1 B2u + 3 B1u + 1 B2g +1 B3g) and 2 closed orbitals (1 Ag + 1 B1u), while 10 active molecular orbitals (6 A1 + 2 B1 + 2 B2) and 6 closed orbitals (4 A1 + 1 B1 + 1 B2) of C2v symmetry were applied for PO(X2Π). A total of 43 and 34 ab initio energy points were obtained for O2(X) and PO(X2Π), respectively.
During the fitting, the 4th-order contracted bases (Eq. 4) and 8th-order polynomial expression (Eq. 2) were applied for O2(X) and PO(X2Π). Figure 1a presents the final CHIPR PECs of O2(X) and PO(X2Π) with the root-mean-square deviations (RMSDs) of 2.05 and 1.85 cm−1, respectively. Figure 1b shows the deviations between ab initio energy points and the corresponding CHIPR energies, which are within ±6 cm−1. The obtained CHIPR PECs of O2(X) and PO(X2Π) reproduce well with the ab initio energy points and exhibit a smooth strongly bound valence region and reasonable dissociation behaviours. As shown in Table 1, the spectroscopic constants of our CHIPR PECs agree well with those of previous theoretical and experimental results. Hence, the CHIPR PECs of O2(X) and PO(X2Π) are reliable and can be used as two-body fragments to construct a global PES of PO2(X2A1). The analytic functions of the O2(X) and PO(X2Π) PECs are collected in the ready-to-use Fortran code in the Supplement.
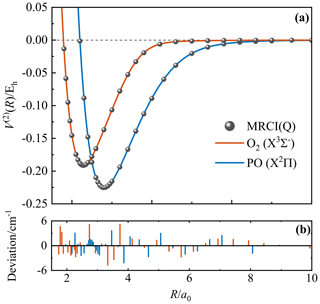
Figure 1(a) The PECs of O2(X) and PO(X2Π). The unit of potential energy is the atomic unit (hartree, Eh). Solid lines are the CHIPR PECs. Solid circles are ab initio energies. (b) The deviations between ab initio energy points and the corresponding CHIPR energies.
Table 1Spectroscopic constants of the CHIPR PECs of O2(X) and PO(X2Π), along with previous theoretical and experimental results.
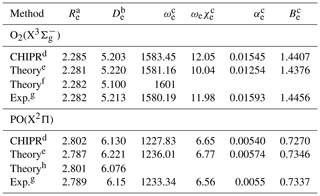
a The equilibrium geometry in unit of a0. b The dissociation energy in unit of eV. c The units of ωe, ωeχe, αe, and Be are cm−1. d The CHIPR PECs. e Results at the icMRCI(Q)/CBS(56) + CV + DK level (Liu et al., 2014, 2017). f Results at the CCSDT/AVQZ level (Sordo, 2001). g Ref. (Huber and Herzberg, 1979). h Results at the MRCI(Q)-r/aug-cc-wCV5Z level (Prajapat et al., 2017).
3.2 Three-body fragment
For the CHIPR PES of PO2(X2A1), the 4th-order contracted bases (Eq. 4) and 12th-order polynomial expression (Eq. 3) were used to fit the three-body fragment. The first trial of the fitted PES presented the complex topographical features around the reaction path, including the important intermediates of 1 global minimum (GM), 1 local minimum (LM), and 4 transition states (TSs). Then, the OPTG was carried out for these configurations, and the additional energy grids were calculated based on the OPTG results. During the subsequent fitting processes, the weights for the additional grids were set to be 5, and those for the remaining energy points were set to be 1. The final PES was constructed from 6471 ab initio energy points, covering an energy range up to 500 kcal mol−1 above the GM. Table 2 lists the RMSDs between the analytical CHIPR energies and ab initio energies in the indicated energy range above the GM and those for the additional energy grids. The GM, LM, and TSs of PO2(X2A1) were well reproduced by the CHIPR method with RMSDs lower than 25 cm−1. The total RMSD is 91.5 cm−1 (or 0.262 kcal mol−1), implying the high fitting accuracy and reliability of the CHIPR PES of PO2(X2A1). The whole PO2(X2A1) PES is collected in the ready-to-use Fortran code in the Supplement.
Table 2The root-mean-square deviations (RMSDs) in the indicated energy range above the GM and those for the additional energy grids.
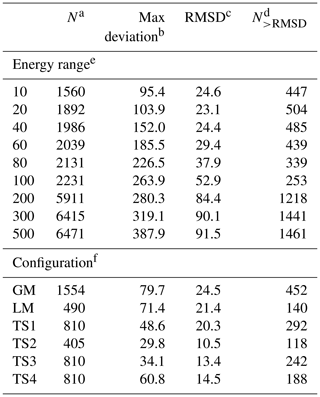
a The number of energy points in the corresponding range. b The maximum deviation in the corresponding range, cm−1. c The RMSD for the corresponding range, cm−1. d The number of energy points with a deviation larger than the RMSD. e The indicated energy range above the GM, kcal mol−1. f The additional energy grids.
Figures 2–4 display the topographical features and the relevant stationary points of the CHIPR PES for the ground-state PO2(X2A1). Table 3 compares the main attributes of the stationary points for the CHIPR PES with other theoretical and experimental results, including the interatomic distances for OO (R1) and PO (R2 and R3), the bond angle (θ) between R2 and R3, the vibration frequencies (symmetrical stretching ω1, bending ω2, and antisymmetric stretching ω3), and the potential energies (E) relative to the P(4S) + O(3P) + O(3P) asymptote. In particular, our OPTG results for GM, LM, TS1, TS2, TS3, and TS4 are also collected in Table 3, which are calculated at the MRCI(Q) level as implemented in MOLPRO 2015 (Werner et al., 2020). As shown in Table 3, the attributes of all the stationary points reproduced by the CHIPR method are very similar to the OPTG results.
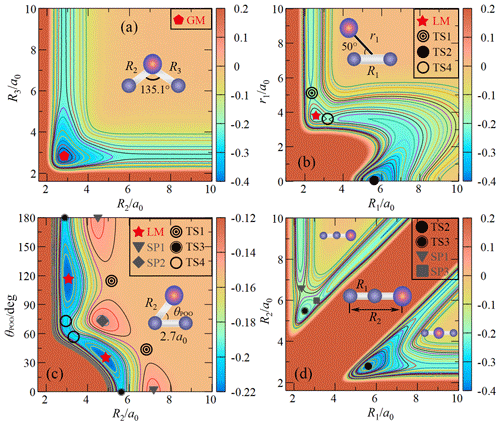
Figure 2(a) The contour plot for bond stretching in the OPO bending configuration with θ fixed at 135.1∘. Contours are equally spaced by 0.02 Eh, starting from −0.4 Eh. (b) The contour plot for the insertion of the P atom into the O2 fragment with the insertion angle of 50∘. Contours are equally spaced by 0.011 Eh, starting from −0.38 Eh. (c) The contour plot for P moving around one of the O atoms with R1 fixed at 2.7 a0. Contours are equally spaced by 0.006 Eh, starting from −0.4 Eh. (d) The contour plot for bond stretching of OOP colinear configuration. Contours are equally spaced by 0.01 Eh, starting from −0.4 Eh.
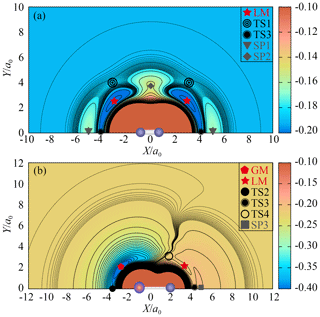
Figure 3(a) The contour plot for P moving around the centre of mass of O2 with R1 fixed at 2.285 a0. Contours are equally spaced by 0.011 Eh, starting from −0.22 Eh. Dashed areas are contours equally spaced by 0.0005 Eh, starting from −0.192 Eh. (b) The contour plot for O moving around the centre of mass of PO with R2 fixed at 2.788 a0. Contours are equally spaced by 0.013 Eh, starting from −0.41 Eh. Dashed areas are contours equally spaced by 0.0001 Eh, starting from −0.226 Eh.
Table 3Attributes of the global minimum (GM), local minimum (LM), transition state (TS) and second-order saddle (SP) of PO2(X2A1) CHIPR PES.
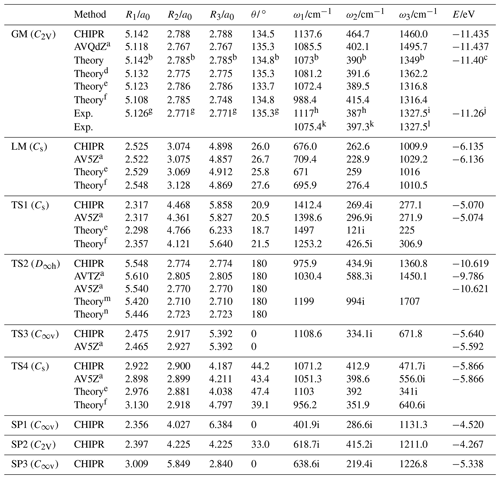
a Results from the geometry optimization (OPTG). b Results at the CCSD(T)/AVQZ level (Francisco, 2002). c Result at the CCSD(T)/(CBS + SO + DK + CV + ZPE) level (Bauschlicher, 1999). d Results at the CCSD(T)/AV5Z level (Liang et al., 2013). e Results at the B3LYP/AVQZ level (Douglas et al., 2019). f Results at the MRCI(Q)/AVTZ + d level (Gomes et al., 2022). g equilibrium geometry deduced from the observed rotational constants (Kawaguchi et al., 1985). h The vibrational frequencies from the laser-induced fluorescence spectrum (Hamilton, 1987). i Origin of the v3 fundamental band obtained from the infrared absorption spectrum (Qian et al., 1995). j The experimental atomization energy D0(PO2) (Drowart et al., 1972). k Vibration frequencies from fluorescence emission and laser fluorescence excitation spectra (Lei et al., 2001). l Term value of the v3 fundamental band obtained from laser absorption spectrum (Lawson et al., 2011). m Results at the SCF/3-21G* level (Kabbadj and Liévin, 1989). n Results at the SCF/6-31G* level (Lohr, 1984).
Figure 2a shows the topographical features of the PO2(X2A1) PES for the PO bond stretching from θ fixed at the equilibrium angle of 135.1∘. As shown in Fig. 2a, the GM of the CHIPR PES has a C2v symmetric configuration with bond lengths of R1=5.142 a0 and a0, which can be seen in Figs. 3b and 4 as well. The vibrational frequencies are computed to be 1137.6, 464.7, and 1460.0 cm−1 for ω1, ω2, and ω3, respectively. According to Table 3, these attributes of GM agree well with previous theoretical and experimental results, excepted that ω3 is slightly higher than experimental results and those calculated by the CCSD(T) method. Figure 2a presents the channel of an O atom dissociated from PO2(X2A1), and the corresponding dissociation energy De(O-PO) of the CHIPR PES is 5.305 eV, which is similar to the experiment value of 5.11 eV (Drowart et al., 1972) and the theoretical result of 5.24 eV at the CCSD((CBS + SO + DK + CV + ZPE) level (Bauschlicher, 1999). The dissociation energy of the P atom dissociated from PO2(X2A1) is predicted to be 6.23 eV, showing a good concordance of the predicted value of 6.15 eV at the CI/3-21G* level (Kabbadj and Liévin, 1989).
Figure 2b and c shows the entrance channel of P(4S) + O2(X) → O(3P) + PO(X2Π), i.e. the contour plots for the insertion of the P atom into the O2 fragment with the insertion angle of 50∘ and for P moving around one of the O atoms with R1 fixed at 2.7 a0, respectively. As illustrated in these two figures, the MEP of the entrance channel is connected by TS1, LM, and TS4 in turn, which is in accordance with the earlier prediction (Gomes et al., 2022; Douglas et al., 2019). The most important configuration for the reaction is the entrance barrier of TS1. The barrier height relative to the P(4S) + O2(X) asymptote was theoretically predicted to be 0.032 eV at the B3LYP/AVQZ level (Douglas et al., 2019) and 0.158, 0.142, and 0.137 eV at the MRCIAVXdZ (X=T, Q, 5) levels (Gomes et al., 2022), respectively. Our CHIPR PES is fitted by the energies at the MRCIAV5Z level, and the barrier height of TS1 is 0.133 eV, which is particularly consistent with the result at the MRCI(Q)/AV5dZ level (Gomes et al., 2022). Also, the attributes of TS1, LM, and TS4 showed good agreement with previous theoretical results, which are presented in detail in Table 3.
Figure 2d shows the contour plot for bond stretching of R1 and R2 at colinear configuration, including the OOP (upper left corner) and OPO (lower right corner) configurations. The notable features here are the OPO colinear transition state TS2 and POO colinear one TS3. The TS3 is predicted to locate at R1=2.475 a0, R2=2.917 a0, and R3=5.392 a0 and is connected with two second-order saddle points (SP1 and SP3). The configuration of the colinear TS2 is a0 and very close to GM. The potential energy of TS2 is 0.816 eV higher than that of GM, which is close to previous theoretical results of 1.05 and 0.93 eV at the CI/3-21G* level (Kabbadj and Liévin, 1989) and MP3/6-31G* level (Lohr, 1984), respectively. As shown in Table 3, the attributes of TS2 are similar to those of previous theoretical results (Kabbadj and Liévin, 1989; Lohr, 1984), except that the vibration frequencies are much less than those obtained at the SCF/3-21G* level (Kabbadj and Liévin, 1989).
Figure 3a is the contour plot for the P atom moving around the centre of mass of O2 with R1 fixed at 2.285 a0, which displays the smooth long-range behaviour of the CHIPR PES. There exist high barriers (SP1 and SP2) on the entrance channel of P(4S) + O2(X) when the P atom inserts along the mid-perpendicular or molecular axis of O2. When the Jacobi approaching angle is about 40–50∘, it is much easier for the P atom to cross the barrier (TS1) and reach the LM, followed by the subsequent reaction process. At relatively low collision energies, therefore, the approaching P atom will bond first with one of the two O atoms rather than with them at the same time. Figure 3b shows the contour plot for O moving around the centre of mass of PO with R2 fixed at 2.806 a0, exhibiting the exit channel of the P(4S) + O2(X) → O(3P) + PO(X2Π) reaction. As shown in Fig. 3b, both TS3 and TS4 can be reached from the LM, but the dissociation of the system is relatively difficult to occur at TS3 due to the high-barrier SP3 on the dissociation path. The two wells LM and GM represent the POO and OPO isomers, which are separated by the isomerization barrier TS4. The minimum exit channel is connected by LM, TS4, GM and TS2 in turn, and then the system dissociates into the products of O(3P) + PO(X2Π).
Figure 4 depicts the relaxed triangular contour plot (Varandas, 1987) for the CHIPR PES of PO2(X2A1) using the scaled hyperspherical coordinates ( and ), given by
The hidden coordinate Q (i.e. the sum of squares of the three bond distances) is allowed to relax to give the lowest potential energy, while β and γ define the shape of the triangle formed by the three atoms (see the work of Varandas, 1987, for details). It gives a better view of the major topographical features of the CHIPR PES, including the configurations and symmetries of all stationary points mentioned above. The MEP is connected by TS1, LM, TS4, GM and TS2 in turn. At high collision energies, the P atom is able to cross the C2v barrier SP2 and reach the GM directly, which will be confirmed in the following dynamics calculations. In this condition, the P atom approaches along the mid-perpendicular of O2 and the two PO bonds stretch symmetrically, accompanied by the progressively open OPO angle, as shown in Fig. 4. Thus, after the P atom crosses over the SP2, the system will reach the symmetric GM instead of the asymmetric TS1, LM, and TS4. Then, the system evolves through the linear transition state TS2 and finally dissociates into the products of O(3P) + PO(X2Π). There is also a collinear abstraction reaction path through TS3, which is difficult to occur due to the mutation of the molecular structure and the existence of collinear barriers (SP1 and SP3) on the entrance and exit channels. We should reiterate that the critical intermediates were carefully verified by the OPTG results, the relevant ab initio energy grids were constructed to be dense enough, and the CHIPR method reproduced them well. Hence, our CHIPR PES of PO2(X2A1) has reliable reaction channels and can be used to perform relevant dynamics calculations.
Based on our CHIPR PES of PO2(X2A1), the reaction probability, ICS, and rate constants of the P(4S) + O2(X) → O(3P) + PO(X2Π) reaction were calculated using the QCT and TDWP methods. For each QCT calculation, the sampled trajectories, initial distance of the reactants, and integration time step of classical equations of motion were 100 000, 15 Å, and 0.2 fs, respectively. The state-specified QCT ICS of P(4S) + O2(X; v, j) → O(3P) + PO(X2Π) was calculated by (Li et al., 2014):
where bmax is the maximum impact parameter, and N and Nr represent the total and reactive trajectories, respectively. The state-specified and thermal QCT rate constants, k(T), were obtained by (Li et al., 2014)
and
where is the reduced mass of the reactants, kB is the Boltzmann constant, Qvj(T) is the rotational–vibrational partition function for all the rotational–vibrational states of O2(X), Evj is the energy of the (v, j) state, and Etr is the translation energy. The rate constant was computed adiabatically for the ground-state PO2(X2A1) and the electronic degeneracy factor ge(T) assumed the following form (Graff and Wagner, 1990):
where gPO2(T)=2 is the degeneracy of the ground-state PO2(X2A1), qP(T)=4 is the electronic partition function accounting for the fine structure of P(4S), and qO2(T) takes into account two spin-orbit states for O2(X), given by
where , due to the doubly degenerate , and Δ=2.88 K (2 cm−1) is the spin-orbit splitting between and (Liu et al., 2014; Barrow and Yee, 1974).
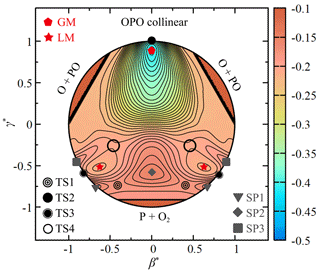
Figure 4The relaxed triangular contour plot for the ground-state PO2 in hyperspherical coordinates (see the definition in the text). Contours are equally spaced by 0.008 Eh, starting from −0.41 Eh.
Table 4Parameters used in the TDWP calculations. All parameters are given in atomic units, except for the numbers or quantities indicated otherwise.

During the TDWP calculations, the split-operator scheme was used to solve the Schrödinger equation. The Hamiltonian for the reactants (P and O2) in the PO2 system can be represented using the Jacobi coordinates:
where R is the distance of the P atom relative to the centre of mass of O2, r is the bond distance of O2, μR is the reduced mass between P and O2, μr is the reduced mass of O2, is the total angular momentum and is the rotational angular momentum of O2, V(R, r) is the Jacobi form of the CHIPR PES for PO2, and h(r) is the diatomic reference Hamiltonian, given by
where V(r) is the PEC of O2. For the TDWP calculations on the adiabatic PES of PO2(X2A1), the time-dependent wave function was expanded by the body-fixed (BF) translational–vibrational–rotational basis:
where M and K are the projection of J onto the z axis of the space-fixed and BF coordinates, respectively; , φv(r), and are the translational basis, reference vibration eigenfunction for O2, and total angular momentum eigenfunction, respectively; ε is the parity of the system; n is the label of the translational basis; and v0, j0, and K0 denote the initial rotational–vibrational state of O2.
The dynamics information is extracted from the final wave packet after a long propagation time. The reaction probability , total reaction cross section , and temperature-dependent rate constant can be calculated by
where k is the wavenumber of the initial state with the fixed collision energy E, and kB is the Boltzmann constant. Table 4 displays the parameters used in the TDWP calculations. The J-shifting method was used in the calculation, and the reaction probabilities of J=0 to 270 were obtained.
Figure 5 presents the CHIPR MEP for P(4S) + O2(X) → O(3P) + PO(X2Π) along with the potential energies of the corresponding intermediates relative to the P(4S) + O2(X) asymptote. This reaction is an exothermic reaction (−0.927 eV) with an intrinsic entrance barrier TS1 (0.133 eV) and two isomers (LM, GM) separated by the isomerization barrier TS4. Along the MEP, the P atom approaches O2 at the Jacobi angle of about 40–50∘ and bonds with one of the two O atoms to form an unstable transition state TS1, followed by a transitory POO isomer LM. The system then evolves through TS4, the OPO isomer GM, and the linear transition state TS2, accompanied by the progressively open OPO angle (i.e. 44.2∘ for TS4, 134.5∘ for GM, and 180∘ for TS2). Finally, the linear PO2 dissociates into the products of O(3P) + PO(X2Π). The structural diagrams of these intermediaries are also shown in Fig. 5, and the corresponding geometric parameters are given in Table 3.
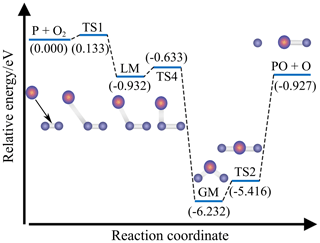
Figure 5The minimum energy path (MEP) and relative intermediates of P(4S) + O2(X) → O(3P) + PO(X2Π). Energies of intermediates relative to the P(4S) + O2(X) asymptote are given in brackets and in units of eV.
The TDWP reaction probability of P(4S) + O2(X; v=0, j=0) → O(3P) + PO(X2Π) at the total angular momentum values of J=0, 80, 160, and 240 are presented in Fig. 6. For J=0, the probability starts with a threshold and gradually rises to a peak. Subsequently, the probability decreases until the collision energy reaches 0.91 eV; then it climbs again and eventually stabilizes. The threshold is about 0.1 eV, resulting from the Cs barrier TS1 (0.133 eV) on the entrance channel. The secondary elevation after 0.91 eV is probably due to the opening of a new entrance channel, i.e. the P atom crosses the C2v barrier SP2 (0.936 eV relative to the P(4S) + O2(X) asymptote) along the mid-perpendicular of O2 and then reaches GM directly, as discussed in Sect. 4. Both the threshold and the starting point of the secondary elevation are slightly smaller than the corresponding entrance barrier heights because of the quantum tunnelling effects. The trend of probability divides into three stages, as marked in Fig. 6. The first and third stages are the two ascending ones in the probability, showing the most common tendency of reactions controlled by barriers (TS1 and SP2). The second stage is the descending one after the peak, which is dominated by the exothermicity of the reaction.
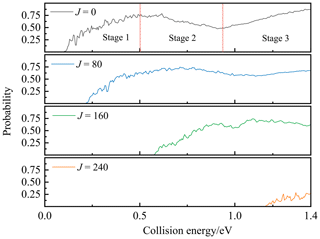
Figure 6The TDWP reaction probabilities for P(4S) + O2(X; v=0, j=0) → O(3P) + PO(X2Π) for J=0, 80, 160, and 240 as a function of the collision energy.
For rotational cases (J>0), the centrifugal effect appears, and the rotational (or centrifugal) energy is added to the potential energy to obtain an effective potential (Waage and Rabinovitch, 1970). Since the centrifugal energy is positively correlated with J, the centrifugal barrier gradually increases with the increment of J, resulting in the need for more translational energy to push the reactants over the barrier. Hence, the threshold shifts to larger collision energies with the increment of J, as shown in Fig. 6.
The reaction probabilities obtained by the TDWP method are also oscillatory in all three stages, which is the typical characteristic of quantum resonances. There are numerous bound and quasi-bound states which exist in the LM and GM potential wells, so the temporary reaction complexes are formed there under the bondage of the potential well, leading to resonances. As shown in Fig. 5, the potential energy of the exit channel is 5.305 eV higher than GM leading to a deep potential well, although this reaction is exothermic. Hence, the bondage of the potential well is strong at low collision energy, resulting in the long lifetimes of the collision complexes and plenty of sharp and violent resonances before the peak (stage 1). Higher collision energy can help the complex get rid of the bondage of the potential well and form a short-lived complex, which weakens the quantum resonance and makes the curves of probability smoother in stages 2 and 3.
Figure 7 displays the state-specified QCT (v=0, 1, and 2) and TDWP (v=0) ICSs for the P(4S) + O2(X; v, j=0) → O(3P) + PO(X2Π) reaction as a function of the collision energy. The TDWP ICSs of vibrational excitation were not calculated due to the extremely expensive cost for this reaction involving three heavy atoms and deep potential wells. As shown in Fig. 7, both QCT and TDWP ICSs rise rapidly from the threshold in stage 1 and gradually reach a plateau (stage 2); they then increase again and finally stabilize (stage 3). Also, the TDWP ICS at v=0 is larger than the QCT ICS at v=0 due to the quantum effects. The threshold is the minimum collision energy at which the reaction can occur (i.e. the point of intersection of ICS and the x axis); these thresholds are about 0.1 for TDWP ICS at v=0 and 0.133, 0.11, and 0.09 eV for QCT ICSs at v=0, v=1, and v=2, respectively. The threshold of QCT ICS at v=0 is consistent with the entrance barrier height, but the threshold of TDWP ICS at v=0 is less than it, because the TDWP method includes the tunnelling effect and the zero-point-energy (ZPE) correction.
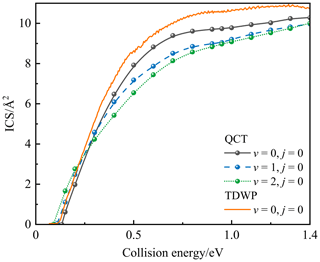
Figure 7The state-specified QCT (v=0, 1, and 2) and TDWP (v=0) integral cross sections for the P(4S) + O2(X; v, j=0) → O(3P) + PO(X2Π) reaction as a function of the collision energy.
Furthermore, the vibrational excitation of O2 has different effects on the reactivity for the three stages of this reaction. For stage 1, the reactivity increases with increasing vibrational excitation, because the increased vibrational energy facilitates the reaction through the path with a barrier, resulting in less collision energy required for high vibrational states. Also, the threshold tends to decrease for increasing vibrational excitations. For stage 2, where the exothermicity dominates, the vibrational excitations of the reactants suppress the reaction reactivity. For stage 3, both MEP and the new entrance channel are contributing to the reaction, in which the reaction through MEP is dominated by the exothermicity like stage 2, and the reaction through the new entrance channel is dominated by the entrance barrier (SP2) like stage 1. In other words, the reaction through the new entrance channel is promoted by the vibrational excitation, so the slopes of QCT ICSs at v=1 and v=2 are significantly greater than QCT ICS at v=0, as shown in Fig. 7. Moreover, the vibrational excitations of the reactants suppress the reactivity of the reaction through MEP, and the reaction mainly occurs in this channel. Hence, the combined effect of the vibrational excitation for the two channels in stage 3 is that the vibrational excitations of the reactants suppress the reaction reactivity.
Figure 8 presents the state-specified QCT and TDWP rate constants for P(4S) + O2(X; v=0, j=0) → O(3P) + PO(X2Π) versus temperature ranging below 5000 K. This reaction is exothermic and dominated by the entrance barrier TS1, so the rate constants show a significant Arrhenius linear behaviour at relatively low temperatures, as shown in Fig. 8b. At high temperatures, the rate constants deviate from the Arrhenius behaviour, because the effect of the barrier is weakened and the reaction activation energy becomes temperature-dependent. As expected, the TDWP rate constant is higher than the QCT rate constant due to the quantum effects, especially at low temperatures.
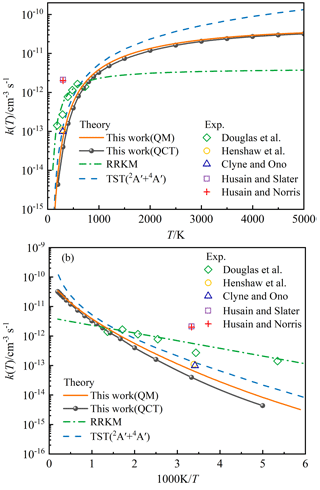
Figure 8(a) The state-specified rate constant k(T) for the P(4S) + O2(X; v=0, j=0) → O(3P) + PO(X2Π) reaction as a function of temperature. (b) The corresponding Arrhenius plot. The green dashed-dotted line corresponds to the theoretical k(T) () of P(4S) + O2 based on the RRKM theory (Douglas et al., 2019). The dashed blue line corresponds to the theoretical rate constant of P(4S) + O2(X) → O(3P) + PO(X2Π) based on the TST and carried out on MEPs of the 2A′ and 4A′ electronic states of PO2 (Gomes et al., 2022). Diamond symbols represent the experimental values using pulsed-laser photolysis and laser-induced fluorescence techniques (Douglas et al., 2019); circle symbols denote the experimental values using the discharge-flow method (Henshaw et al., 1987); triangle symbols represent the experimental values using resonance-fluorescence detection in a discharge-flow system (Clyne and Ono, 1982); quadrate symbols denote the experimental values using resonance fluorescence method (Husain and Slater, 1978); cross symbols represent the experimental values obtained from the attenuation of atomic resonance radiation in the vacuum ultraviolet (Husain and Norris, 1977).
Previous experimental rate constants are also given in Fig. 8 for comparison. Obviously, the rate constants at room temperature determined by various experiments differ by almost an order of magnitude. The earliest two experiments produced extremely large rate constants (Husain and Norris, 1977; Husain and Slater, 1978), and such large values were attributed to the large amounts of secondary dissociation products (Clyne and Ono, 1982). The subsequent experiments were carefully performed to minimize this possible effect and obtained relatively lower rate constants (Clyne and Ono, 1982; Henshaw et al., 1987; Douglas et al., 2019), in which the recent experiment presented the temperature-dependent rate constants (Douglas et al., 2019). As shown in the Arrhenius plot of Fig. 8b, however, the recent experimental rate constants do not exhibit a good linear behaviour, unless the values at maximum and minimum temperatures are excluded. Therefore, four experimental rate constants at about 300–600 K are expected to be more reliable. As shown in Fig. 8, the present QCT and TDWP rate constants are lower than the experimental values. It is partly because the experimental results may be suffering from secondary chemistry; that is, some O atoms and PO molecules could be produced from reactions of P(2P, 2D) + O2, albeit at extremely low quantities.
The theoretical rate constants based on the RRKM theory (Douglas et al., 2019) and TST (Gomes et al., 2022) are also shown in Fig. 8. The RRKM rate constant available for temperatures of 150–1400 K was optimized by the experimental data, and the TST rate constant was fitted from the calculated values at the temperatures below 1000 K. The rate constant obtained by TST includes the contribution of the doublet and quartet electronic states of PO2 corresponding to P(4S) + O2(X), in which the quartet state works mainly at temperatures above about 600 K (Gomes et al., 2022). We did not consider the contribution from the quartet state due to the extremely high computational cost; therefore, our rate constants at very high temperatures may be slightly underestimated. However, the entrance barrier height including ZPE correction for the quartet state (0.3 eV) is about 3 times above that of the doublet state (0.105 eV) (Gomes et al., 2022), so the effect of quartet state on the rate constant may be small. At low temperatures, the RRKM rate constant is much higher than the TST rate constant and our QCT and TDWP rate constant, which can be explained by the fact that the low-temperature reactivity of such barrier-dominated reaction like P(4S) + O2(X) → O(3P) + PO(X2Π) depends sensitively on the entrance barrier height. The entrance barrier height adopted when calculating the RRKM rate constant was obtained to be 0.032 eV at the B3LYP/AVQZ level (Douglas et al., 2019). This barrier height was also predicted to be 0.158, 0.142, and 0.137 eV at the MRCIAVXdZ (X=T, Q, 5) levels (Gomes et al., 2022), in which the MRCIAVTdZ result was modified to be 0.105 eV by including the ZPE correction, and then it was used in the TST study (Gomes et al., 2022). There is evidence that the B3LYP method is not good at predicting the barrier heights on the reaction path (Zhao and Truhlar, 2008; Peverati and Truhlar, 2012). Our CHIPR PES is fitted by the potential energies at the MRCIAV5Z level, and the entrance barrier height is 0.133 eV, which is particularly consistent with the result at the MRCIAV5dZ level (Gomes et al., 2022), so the CHIPR PES is accurate and reliable. The relatively small QCT rate constants at low temperatures are due to the ZPE problem in the QCT treatment. The TDWP rate constants consider the ZPE correction and the tunnelling through the entrance channel barrier, and the threshold of ICS is about 0.1 eV, agreeing with the modified barrier height (0.105 eV) used in the TST calculation. The difference in the barrier height (0.05 eV) may be due to the tunnelling effect.
At high temperatures, it is necessary to point out that the previous two theoretical Arrhenius formulas (Douglas et al., 2019; Gomes et al., 2022) were fitted without the backing of high-temperature rate constants. Since the rate constant will deviate from the Arrhenius behaviour at high temperatures, the RRKM and TST rate constants remains to be verified at high temperatures. Moreover, the rate constants obtained by RRKM theory are obviously lower than our QCT and TDWP rate constants at high temperatures, because the original Arrhenius formula () applied for the RRKM rate constants assumes that the reaction activation energy is temperature-independent, which is not applicable at high temperatures. Note that the population of the rotational–vibrational excited O2 increases at high temperatures, which could affect the reaction activity according to the analysis of ICS above. Figure 9 compares the state-specified (v=0, j=0) QCT and TDWP rate constants and thermal QCT rate constant for P(4S) + O2(X) → O(3P) + PO(X2Π) versus the temperature ranging from 2000 to 5000 K. The thermal TDWP rate constant was not calculated due to the extremely expensive cost. As shown in Fig. 9, the rotational–vibrational ground-state (v=0, j=0) O2 plays an absolutely dominant role at temperatures below 3000 K, while the rotational–vibrational excited O2 appears at temperatures above 3000 K and promotes the reactive activity. Hence, our TDWP rate constant is reliable at temperatures below 3000 K, while it probably underestimates the rate constant at temperatures above 3000 K due to the neglect of the rotational–vibrational excitation of O2.
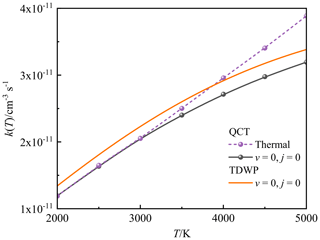
Figure 9The state-specified (v=0, j=0) QCT and TDWP rate constants and thermal QCT rate constant for the P(4S) + O2(X) → O(3P) + PO(X2Π) reaction as a function of temperature.
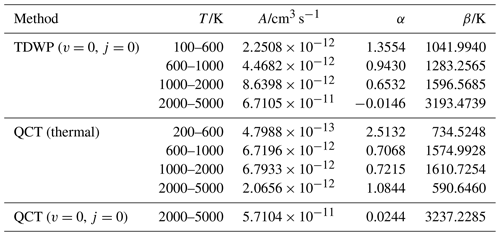
The rate constants of TDWP (v=0, j=0), QCT (v=0, j=0), and QCT (thermal) for the P(4S) + O2(X) → O(3P) + PO(X2Π) reaction can be approximated using the three-parameter Kooij function, given by (Laidler, 1996)
where A, α, and β are fitting parameters. The rate constant curves are divided into four temperature ranges, and the fitting parameters are summarized in Table 5. The fitted rate constants deviate less than 1 % from our calculated ones. These rate constants are calculated in the atom–diatom system and independent of pressure, which may be applicable to the ISM and upper planetary atmospheres.
The ablation of IDPs in the upper atmosphere (mainly at heights between 70 and 110 km) of terrestrial planets delivers about 6200 kg yr−1 of ablated phosphorus to the atmosphere (Carrillo-Sánchez et al., 2020), where the temperatures range from below 100 to over 2500 K (in ablation IDPs). Several reaction networks of meteor-ablated phosphorus in the Earth's upper atmosphere (Douglas et al., 2019, 2020; Plane et al., 2021) indicate that the initial oxidation of P will proceed through the successive oxidation by O2 to produce OPO (i.e. Reactions R1 and R2). The oxidation by O3 is not significant, because O2 is 105 times more abundant than O3 at this altitude. Also, OPO is likely dissociated into PO and P as a result of hyperthermal collisions with air molecules (Carrillo-Sánchez et al., 2020). Therefore, the P + O2 → O + PO reaction may occur throughout the upper mesosphere and thermosphere. Our rate constants are fitted by sufficient data below 5000 K, which is appropriate for most altitudes of the Earth's atmosphere and can be used to model its phosphorus chemistry.
A recent study developed a reaction network of phosphorus atmosphere chemistry (Plane et al., 2021), including the possible routes from P + O2 → O + PO to the stable reservoirs (H3PO3 and H3PO4). Subsequently, they incorporated the rate constants of the associated reactions into the Whole Atmosphere Community Climate Model from the US National Center for Atmospheric Research (Gettelman et al., 2019) and then explored the vertical profiles of the P-containing species and the global mean P deposition flux. Also, they estimated that the fraction of the ablated phosphorus forming bioavailable metal phosphites was 11 %.
One of our concerns is that the theoretical predicted rate constants of P + O2 → O + PO diverge from experimental result at 200 K, which is about the typical temperature of the upper mesosphere and lower thermosphere. For the reaction with entrance barrier, its rate constant usually has Arrhenius linear behaviour at relatively low temperatures. Our QCT and TDWP rate constants, as well as the TST rate constant (Gomes et al., 2022), exhibit highly consistent Arrhenius linear behaviour at relatively low temperatures, with slopes close to those of the experimental rate constants at about 300–600 K (Douglas et al., 2019), as shown in Fig. 8b. There is reason to believe that the experimental results of 300–600 K are very reliable, whereas the experimental rate constant at about 200 K diverges from this linear behaviour and seems to be slightly overestimated. Therefore, the lifetime of the P atoms in the atmosphere may be a little longer than previously thought (Carrillo-Sánchez et al., 2020). Further experiments for the rate constants at approximately 200 K of P + O2 → O + PO are encouraged in the future.
In this work, we have constructed a global CHIPR PES of the ground state PO2(X2A1) based on a total of 6471 ab initio energy points computed at the MRCIAV5Z level. The ab initio grids for the critical intermediates are constructed to be dense enough based on the OPTG results. The total RMSD of the CHIPR PES is 91.5 cm−1, and the RMSDs for the critical intermediates are lower than 25 cm−1. The PES presents complex topographical features with multiple potential wells and barriers. The long-range interactions, diatomic potentials, and dissociation energies of each asymptotic channel are reasonably reproduced. The attributes of the main intermediates agree well with available experimental and theoretical results as well as our OPTG results. The corresponding adiabatic MEP of P(4S) + O2(X) → O(3P) + PO(X2Π) features the barrier insertion of the P atom into the O2 bond at the Jacobi angle of about 40–50∘, and the reaction then evolves through LM, TS4, GM, and TS2 in turn. Based on the CHIPR PES, the state-specified reaction probability and ICSs for this reaction are calculated using QCT and TDWP methods. The results show three stages of reaction controlled by barrier TS1 (stage 1), exothermicity (stage 2), and barrier SP1 (stage 3) in turn. The vibrational excitation of O2 promotes the reaction in stages 1 and 3 but suppresses the reactivity in stage 2. Meanwhile, the state-specified and thermal rate constants are predicted for the temperatures ranging from 200 to 5000 K and then compared with available experimental and theoretical results. The rate constants show a significant Arrhenius linear behaviour at relatively low temperatures, but they deviate from the Arrhenius behaviour at high temperatures. The rotational–vibrational ground-state O2 plays an absolutely dominant role at temperatures below 3000 K, while the rotational–vibrational excitation of O2 promotes the reactive activity at temperatures above 3000 K.
The presented CHIPR PES of PO2(X2A1) can be used for molecular simulations of reactive or non-reactive collisions and photodissociation of the PO2 system in atmospheres and interstellar media. Moreover, this analytical PES of PO2 can provide reliable two-body fragments and three-body fragment for the construction of PO3 and HPO2 PESs using MBE form so as to carry out a dynamics study of Reactions (R2) and (R3), which are also important for generating H3PO3 in the Earth's atmosphere. The computed reaction probability, ICSs, and rate constants may help to explain the relevant thermochemical reactions in related atmospheric and interstellar media.
Additional relevant data and supporting information are given in the Supplement. All data used in this study are available upon request from the corresponding authors.
The ready-to-use Fortran code for the whole CHIPR PES of PO2(X2A1) is given in the Supplement, including the CHIPR function and all the coefficients of the O2(X) and PO(X2Π) PECs and three-body fragment. The supplement related to this article is available online at: https://doi.org/10.5194/acp-23-10643-2023-supplement.
ZQ and GC designed the concept of the study, carried out the calculations, interpreted the results, and prepared the paper. XL helped with data analysis. LL supervised the study and acquired the primary funding to support this research. All of the authors discussed the scientific findings and provided valuable feedback for manuscript editing.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Zhi Qin acknowledges the Young Scholars Program of Shandong University. The scientific calculations in this paper have been done on the HPC Cloud Platform of Shandong University.
This work is supported by the National Natural Science Foundation of China (grant no. 52106098) and the Natural Science Foundation of Shandong Province (grant no. ZR2021QE021). Zhi Qin also acknowledges the Postdoctoral Innovation Project of Shandong Province and the Postdoctoral Applied Research Project of Qingdao City.
This paper was edited by John Plane and reviewed by two anonymous referees.
Barrow, R. F. and Yee, K. K.: The X3Σ− ground states of the group VI–VI molecules, O2, SO … Te2, Acta. Phys. Hung., 35, 239–246, https://doi.org/10.1007/BF03159760, 1974.
Bauschlicher, C. W.: Heats of formation for POn and POnH (n=1–3), J. Phys. Chem. A, 103, 11126–11129, https://doi.org/10.1021/jp992409k, 1999.
Cai, Z., Hirsch, G., and Buenker, R. J.: Ab initio study of the electronic spectrum of the PO2 radical, Chem. Phys. Lett., 255, 350–356, https://doi.org/10.1016/0009-2614(96)00395-8, 1996.
Caridade, P. J. S. B., Horta, J.-Z. J., and Varandas, A. J. C.: Implications of the O + OH reaction in hydroxyl nightglow modeling, Atmos. Chem. Phys., 13, 1–13, https://doi.org/10.5194/acp-13-1-2013, 2013.
Carpenter, B. K.: Dynamic behavior of organic reactive intermediates, Angew. Chem. Int. Edit., 37, 3340–3350, https://doi.org/10.1002/(SICI)1521-3773(19981231)37:24<3340::AID-ANIE3340>3.0.CO;2-1, 1998.
Carrillo-Sánchez, J. D., Bones, D. L., Douglas, K. M., Flynn, G. J., Wirick, S., Fegley Jr, B., Araki, T., Kaulich, B., and Plane, J. M. C.: Injection of meteoric phosphorus into planetary atmospheres, Planet. Space Sci., 187, 104926, https://doi.org/10.1016/j.pss.2020.104926, 2020.
Chen, G., Qin, Z., Li, J., and Liu, L.: A global CHIPR potential energy surface of PH2(X2B1) via extrapolation to the complete basis set limit and the dynamics of P(2D) + H2(X1Σ + g) → PH(X3Σ−) + H(2S), Phys. Chem. Chem. Phys., 24, 19371–19381, https://doi.org/10.1039/D2CP02690B, 2022.
Clyne, M. A. A. and Ono, Y.: Kinetic studies of ground-state phosphorus atoms, J. Chem. Soc. Farad. T. 2, 78, 1149–1164, https://doi.org/10.1039/F29827801149, 1982.
Conway, E. K., Gordon, I. E., Tennyson, J., Polyansky, O. L., Yurchenko, S. N., and Chance, K.: A semi-empirical potential energy surface and line list for HO extending into the near-ultraviolet, Atmos. Chem. Phys., 20, 10015–10027, https://doi.org/10.5194/acp-20-10015-2020, 2020.
Cordes, H., and Witschel, W.: Einige aussagen zur oxydation des phosphors, Z. Phys. Chem., 46, 35-48, https://doi.org/10.1524/zpch.1965.46.1_2.035, 1965.
Davies, P. B. and Thrush, B. A.: The reactions of atomic oxygen with phosphorus and with phosphine, P. Roy. Soc. A, 302, 243–252, https://doi.org/10.1098/rspa.1968.0007, 1968.
De Beck, E., Kamiñski, T., Patel, N. A., Young, K. H., Gottlieb, C. A., Menten, K. M., and Decin, L.: PO and PN in the wind of the oxygen-rich AGB star IK Tauri, Astron. Astrophys., 558, A132, https://doi.org/10.1051/0004-6361/201321349, 2013.
Douglas, K. M., Blitz, M. A., Mangan, T. P., and Plane, J. M.: Experimental study of the removal of ground- and excited-state phosphorus atoms by atmospherically relevant species, J. Phys. Chem. A, 123, 9469–9478, https://doi.org/10.1021/acs.jpca.9b07855, 2019.
Douglas, K. M., Blitz, M. A., Mangan, T. P., Western, C. M., and Plane, J. M. C.: Kinetic study of the reactions PO + O2 and PO2 + O3 and spectroscopy of the PO radical, J. Phys. Chem. A, 124, 7911–7926, https://doi.org/10.1021/acs.jpca.0c06106, 2020.
Drowart, J., Myers, C. E., Szwarc, R., Vander Auwera-Mahieu, A., and Uy, O. M.: Determination by the mass spectrometric Knudsen cell method of the atomization energies of the molecules PO and PO2, J. Chem. Soc. Farad. T. 2, 68, 1749–1757, https://doi.org/10.1039/F29726801749, 1972.
Dunning, T. H., Peterson, K. A., and Wilson, A. K.: Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited, J. Chem. Phys., 114, 9244–9253, https://doi.org/10.1063/1.1367373, 2001.
Eckert, F., Pulay, P., and Werner, H. J.: Ab initio geometry optimization for large molecules, J. Comput. Chem., 18, 1473–1483, https://doi.org/10.1002/(SICI)1096-987X(199709)18:12<1473::AID-JCC5>3.0.CO;2-G, 1997.
Francisco, J. S.: Coupled cluster study of the energetic and spectroscopic properties of OPOx (x=O, +1, −1), J. Chem. Phys., 117, 3190–3195, https://doi.org/10.1063/1.1494063, 2002.
Gettelman, A., Mills, M. J., Kinnison, D. E., Garcia, R. R., Smith, A. K., Marsh, D. R., Tilmes, S., Vitt, F., Bardeen, C. G., McInerny, J., Liu, H.-L., Solomon, S. C., Polvani, L. M., Emmons, L. K., Lamarque, J.-F., Richter, J. H., Glanville, A. S., Bacmeister, J. T., Phillips, A. S., Neale, R. B., Simpson, I. R., DuVivier, A. K., Hodzic, A., and Randel, W. J.: The whole atmosphere community climate model version 6 (WACCM6). J. Geophys. Res.-Atmos., 124, 12380–12403, https://doi.org/10.1029/2019JD030943, 2019.
Gomes, A. C. R., Rocha, C. M. R., Jasper, A. W., and Galvão, B. R. L.: Formation of phosphorus monoxide through the P(4S) + O2(3Σ) → O(3P) + PO(2Π) reaction, J. Mol. Model., 28, 259, https://doi.org/10.1007/s00894-022-05242-4, 2022.
Graff, M. M. and Wagner, A. F.: Theoretical studies of fine-structure effects and long-range forces: Potential-energy surfaces and reactivity of O(3P) + OH(2Π), J. Chem. Phys., 92, 2423–2439, https://doi.org/10.1063/1.457986, 1990.
Hamilton, P. A.: The laser induced fluorescence spectrum and radiative lifetime of PO2, J. Chem. Phys., 86, 33–41, https://doi.org/10.1063/1.452624, 1987.
Henshaw, T. L., MacDonald, M. A., Stedman, D. H., and Coombe, R. D.: The P(4Su) + N3(2Πg) reaction: chemical generation of a new metastable state of PN, J. Phys. Chem., 91, 2838–2842, https://doi.org/10.1021/j100295a037, 1987.
Huber, K. P. and Herzberg, G.: Molecular spectra and molecular structure, IV. Constants of Diatomic Molecules, Springer, New York, ISBN 978-1-4757-0963-6, https://doi.org/10.1007/978-1-4757-0961-2, 1979.
Husain, D. and Norris, P. E.: Reactions of phosphorus atoms, P(34S), studied by attenuation of atomic resonance radiation in the vacuum ultraviolet, J. Chem. Soc. Farad. T. 2, 73, 1107–1115, https://doi.org/10.1039/F29777301107, 1977.
Husain, D. and Slater, N. K.: Time-resolved resonance fluorescence studies of ground state phosphorus atoms, P[3p3(4S], J. Chem. Soc. Farad. T. 2, 74, 1627–1643, https://doi.org/10.1039/F29787401627, 1978.
Jarrett-Sprague, S. A. and Hillier, I. H.: Ab initio calculations of the structure and infrared spectrum of As2O and As4O, Chem. Phys., 148, 325–332, https://doi.org/10.1016/0301-0104(90)89028-O, 1990.
Kabbadj, Y. and Liévin, J.: Ab initio study of the electronic structure of the PO2 radical, Phys. Scr., 40, 259–269, https://doi.org/10.1088/0031-8949/40/3/002, 1989.
Kawaguchi, K., Saito, S., Hirota, E., and Ohashi, N.: Far-infrared laser magnetic resonance detection and microwave spectroscopy of the PO2 radical, J. Chem. Phys., 82, 4893–4902, https://doi.org/10.1063/1.448661, 1985.
Knowles, P. J. and Werner, H.: An efficient second-order MC SCF method for long configuration expansions, Chem. Phys. Lett., 115, 259–267, https://doi.org/10.1016/0009-2614(85)80025-7, 1985.
Knowles, P. J. and Werner, H.: An efficient method for the evaluation of coupling coefficients in configuration interaction calculations, Chem. Phys. Lett., 145, 514–522, https://doi.org/10.1016/0009-2614(88)87412-8, 1988.
Laidler, K. J.: A glossary of terms used in chemical kinetics, including reaction dynamics (IUPAC Recommendations 1996), Pure Appl. Chem., 68, 149–192, https://doi.org/10.1351/pac199668010149, 1996.
Lawson, M. A., Hoffman, K. J., and Davies, P. B.: Infrared diode laser spectroscopy of the υ3 fundamental band of the PO2 free radical, J. Mol. Spectrosc., 269, 61–76, https://doi.org/10.1016/j.jms.2011.04.019, 2011.
Lefloch, B., Vastel, C., Viti, S., Jiménez-Serra, I., Codella, C., Podio, L., Ceccarelli, C., Mendoza, E., Lépine, J. R. D., and Bachiller, R.: Phosphorus-bearing molecules in solar-type star-forming regions: first PO detection, Mon. Not. Roy. Astron. Soc., 462, 3937–3944, https://doi.org/10.1093/mnras/stw1918, 2016.
Lei, J., Teslja, A., Nizamov, B., and Dagdigian, P. J.: Free-jet electronic spectroscopy of the PO2 radical, J. Phys. Chem. A, 105, 7828–7833, https://doi.org/10.1021/jp011778p, 2001.
Li, J., Caridade, P. J. S. B., and Varandas, A. J. C.: Quasiclassical trajectory study of the atmospheric reaction N(2D) + NO(X2Π) → O(1D) + N2(X1Σ + g), J. Phys. Chem. A, 118, 1277–1286, https://doi.org/10.1021/jp408487y, 2014.
Li, X., Qin, Z., Li, J., and Liu, L.: An accurate NH2(X2A′′) CHIPR potential energy surface via extrapolation to the complete basis set limit and dynamics of the N(2D) + H2(X1Σ + g) reaction, Phys. Chem. Chem. Phys., 24, 26564–26574, https://doi.org/10.1039/D2CP01961B, 2022.
Li, X., Qin, Z., Chen, G., and Liu, L.: Reaction dynamics of C(3P) + Si2(X3Σ−g) → Si(3P) + SiC(X3Π) on a global CHIPR potential energy surface of the ground state Si2C(X1A1), Mon. Not. Roy. Astron. Soc., 522, 3049–3057, https://doi.org/10.1093/mnras/stad1109, 2023.
Liang, J., Cui, F., Wang, R., Huang, W., and Cui, Z.: A general analytical expression for the three-dimensional Franck-Condon integral and simulation of the photodetachment spectrum of the PO anion, J. Mol. Spectrosc., 286, 12–20, https://doi.org/10.1016/j.jms.2013.02.009, 2013.
Liu, H., Shi, D., Sun, J., Zhu, Z., and Zhang, S.: Accurate calculations on the 22 electronic states and 54 spin-orbit states of the O2 molecule: Potential energy curves, spectroscopic parameters and spin-orbit coupling, Spectrochim. Acta A, 124, 216–229, https://doi.org/10.1016/j.saa.2014.01.003, 2014.
Liu, H., Shi, D., Sun, J., and Zhu, Z.: Accurate potential energy curves and spectroscopic properties of the 27 Λ−S states and 73 Ω states of the PO radical, Mol. Phys., 115, 714–730, https://doi.org/10.1080/00268976.2017.1280193, 2017.
Lodders, K.: Solar system abundances and condensation temperatures of the elements, Astrophys. J., 591, 1220, https://doi.org/10.1086/375492, 2003.
Lohr, L. L.: A theoretical study of the gaseous oxides PO2 and PO, their anions, and their role in the combustion of phosphorus and phosphine, J. Phys. Chem., 88, 5569–5574, https://doi.org/10.1021/j150667a022, 1984.
Maciá, E.: The role of phosphorus in chemical evolution, Chem. Soc. Rev., 34, 691–701, https://doi.org/10.1039/B416855K, 2005.
Maciá, E., Hernández, M. V., and Oro, J.: Primary sources of phosphorus and phosphates in chemical evolution, Origins Life Evol. B., 27, 459–480, https://doi.org/10.1023/A:1006523226472, 1997.
Martin, J. M. L. and Uzan, O.: Basis set convergence in second-row compounds. The importance of core polarization functions, Chem. Phys. Lett., 282, 16–24, https://doi.org/10.1016/S0009-2614(97)01128-7, 1998.
Murrell, J. N., Carter, S., Farantos, S., Huxley, P., and Varandas, A. J. C.: Molecular potential energy functions, John Wiley, New York, ISBN 9780471905400, 1984.
Pasek, M. A.: Rethinking early Earth phosphorus geochemistry, P. Natl. Acad. Sci. USA, 105, 853–858, https://doi.org/10.1073/pnas.0708205105, 2008.
Peslherbe, G. H., Wang, H., and Hase, W. L.: Monte Carlo sampling for classical trajectory simulations, John Wiley, New York, ISBN 9780470141649, ISBN 9780471196303, https://doi.org/10.1002/9780470141649.ch6, 1999.
Peverati, R. and Truhlar, D. G.: M11-L: A local density functional that provides improved accuracy for electronic structure calculations in chemistry and physics, J. Phys. Chem. Lett., 3, 117–124, https://doi.org/10.1021/jz201525m, 2012.
Plane, J. M. C., Flynn, G. J., Määttänen, A., Moores, J. E., Poppe, A. R., Carrillo-Sanchez, J. D., and Listowski, C.: Impacts of cosmic dust on planetary atmospheres and surfaces, Space Sci. Rev., 214, 23, https://doi.org/10.1007/s11214-017-0458-1, 2018.
Plane, J. M. C., Feng, W., and Douglas, K. M.: Phosphorus chemistry in the Earth's upper atmosphere, J. Geophys. Res.-Space, 126, e2021JA029881J, https://doi.org/10.1029/2021JA029881, 2021.
Prajapat, L., Jagoda, P., Lodi, L., Gorman, M. N., Yurchenko, S. N., and Tennyson, J.: ExoMol molecular line lists – XXIII. Spectra of PO and PS, Mon. Not. Roy. Astron. Soc., 472, 3648–3658, https://doi.org/10.1093/mnras/stx2229, 2017.
Qian, H., Davies, P. B., and Hamilton, P. A.: High-resolution spectroscopic study of the oxidation of white phosphorus, J. Chem. Soc. Faraday T., 91, 2993–2998, https://doi.org/10.1039/FT9959102993, 1995.
Rivilla, V. M., Drozdovskaya, M. N., Altwegg, K., Caselli, P., Beltrán, M. T., Fontani, F., Van Der Tak, F., Cesaroni, R., Vasyunin, A., Rubin, M., Lique, F., Marinakis, S., Testi, L., and the ROSINA team: ALMA and ROSINA detections of phosphorus-bearing molecules: the interstellar thread between star-forming regions and comets, Mon. Not. Roy. Astron. Soc., 492, 1180–1198, https://doi.org/10.1093/mnras/stz3336, 2020.
Rocha, C. M. R. and Varandas, A. J. C.: Accurate CHIPR potential energy surface for the lowest triplet state of C3, J. Phys. Chem. A, 123, 8154–8169, https://doi.org/10.1021/acs.jpca.9b03194, 2019a.
Rocha, C. M. R. and Varandas, A. J. C.: A global CHIPR potential energy surface for ground-state C3H and exploratory dynamics studies of reaction C2 + CH → C3 + H, Phys. Chem. Chem. Phys., 21, 24406–24418, https://doi.org/10.1039/C9CP04890A, 2019b.
Rocha, C. M. R. and Varandas, A. J. C.: A general code for fitting global potential energy surfaces via CHIPR method: Triatomic molecules, Comput. Phys. Commun., 247, 106913, https://doi.org/10.1016/j.cpc.2019.106913, 2020.
Rocha, C. M. R. and Varandas, A. J. C.: A general code for fitting global potential energy surfaces via CHIPR method: Direct-Fit Diatomic and tetratomic molecules, Comput. Phys. Commun., 258, 107556, https://doi.org/10.1016/j.cpc.2020.107556, 2021.
Rocha, C. M. R., Linnartz, H., and Varandas, A. J. C.: Reconciling spectroscopy with dynamics in global potential energy surfaces: The case of the astrophysically relevant SiC2, J. Chem. Phys., 157, 104301, https://doi.org/10.1063/5.0096364, 2022.
Schmidt, J. A., Johnson, M. S., Hattori, S., Yoshida, N., Nanbu, S., and Schinke, R.: OCS photolytic isotope effects from first principles: sulfur and carbon isotopes, temperature dependence and implications for the stratosphere, Atmos. Chem. Phys., 13, 1511–1520, https://doi.org/10.5194/acp-13-1511-2013, 2013.
Sordo, J. A.: Performance of CCSDT for first row AB/AB− diatomics: Dissociation energies and electron affinities, J. Chem. Phys., 114, 1974–1980, https://doi.org/10.1063/1.1335617, 2001.
Tenenbaum, E. D., Woolf, N. J., and Ziurys, L. M.: Identification of phosphorus monoxide (X2Πr) in VY Canis Majoris: Detection of the first PO bond in space, Astrophys. J., 666, L29, https://doi.org/10.1086/521361, 2007.
Thomas, J. B., Waas, J. R., Harmata, M., and Singleton, D. A.: Control elements in dynamically determined selectivity on a bifurcating surface, J. Am. Chem. Soc., 130, 14544–14555, https://doi.org/10.1021/ja802577v, 2008.
Todd, Z. R.: Sources of Nitrogen-, Sulfur-, and Phosphorus-containing feedstocks for prebiotic chemistry in the planetary environment, Life, 12, 1268, https://doi.org/10.3390/life12081268, 2022.
Varandas, A. J. C.: A useful triangular plot of triatomic potential energy surfaces, Chem. Phys. Lett., 138, 455–461, https://doi.org/10.1016/0009-2614(87)80540-7, 1987.
Varandas, A. J. C.: Combined-hyperbolic-inverse-power-representation of potential energy surfaces: A preliminary assessment for H3 and HO2, J. Chem. Phys., 138, 054120, https://doi.org/10.1063/1.4788912, 2013.
Varandas, A. J. C. and Murrell, J. N.: A many-body expansion of polyatomic potential energy surfaces: application to Hn systems, Faraday Discuss. Chem. Soc., 62, 92–109, https://doi.org/10.1039/DC9776200092, 1977.
Verma, R. D. and McCarthy, C. F.: A new spectrum of the PO2 radical, Can. J. Phys., 61, 1149–1159, https://doi.org/10.1139/p83-145, 1983.
Waage, E. V. and Rabinovitch, B. S.: Centrifugal effects in reaction rate theory, Chem. Rev., 70, 377–387, https://doi.org/10.1021/cr60265a004, 1970.
Werner, H. J. and Knowles, P. J.: An efficient internally contracted multiconfiguration–reference configuration interaction method, J. Chem. Phys., 89, 5803–5814, https://doi.org/10.1063/1.455556, 1988.
Werner, H. J., Knowles, P. J., Manby, F. R., Black, J. A., Doll, K., Heßelmann, A., Kats, D., Köhn, A., Korona, T., Kreplin, D. A., Ma, Q., Miller, T. F., Mitrushchenkov, A., Peterson, K. A., Polyak, L., Rauhut, G., and Sibaev, M.: The Molpro quantum chemistry package, J. Chem. Phys., 152, 144107, https://doi.org/10.1063/5.0005081, 2020.
Woon, D. E. and Dunning Jr., T. H.: Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 98, 1358–1371, https://doi.org/10.1063/1.464303, 1993.
Xianyi, Z., Jun, W., Fei, W., and Zhifeng, C.: Ab initio calculations and Franck-Condon analysis of photoelectron spectra of PO2, J. Mol. Struc.-Theochem., 851, 40–45, https://doi.org/10.1016/j.theochem.2007.10.030, 2008.
Xu, C., de Beer, E., and Neumark, D. M.: Photoelectron spectroscopy of PO, J. Chem. Phys., 104, 2749–2751, https://doi.org/10.1063/1.470983, 1996.
Zeng, H. and Zhao, J.: Theoretical study of the structure and analytic potential energy function for the ground state of the PO2 molecule, Chin. Phys. B, 21, 078202, https://doi.org/10.1088/1674-1056/21/7/078202, 2012.
Zhang, D. H. and Zhang, J. Z. H.: Photofragmentation of HF dimer: Quantum dynamics studies on ab initio potential energy surfaces, J. Chem. Phys., 99, 6624–6633, https://doi.org/10.1063/1.465854, 1993.
Zhang, D. H. and Zhang, J. Z. H.: Quantum reactive scattering with a deep well: Time-dependent calculation for H + O2 reaction and bound state characterization for HO2, J. Chem. Phys., 101, 3671–3678, https://doi.org/10.1063/1.467551, 1994.
Zhao, Y. and Truhlar, D. G.: Exploring the limit of accuracy of the global hybrid meta density functional for main-group thermochemistry, kinetics, and noncovalent interactions, J. Chem. Theory Comput., 4, 1849–1868, https://doi.org/10.1021/ct800246v, 2008.
Ziurys, L. M., Schmidt, D. R., and Bernal, J. J.: New circumstellar sources of PO and PN: The increasing role of phosphorus chemistry in oxygen-rich stars, Astrophys. J., 856, 169, https://doi.org/10.3847/1538-4357/aaafc6, 2018.
- Abstract
- Introduction
- Ab initio calculations
- The CHIPR potential energy surface
- Features of CHIPR PES
- Dynamics calculations
- Atmospheric implications
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Ab initio calculations
- The CHIPR potential energy surface
- Features of CHIPR PES
- Dynamics calculations
- Atmospheric implications
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement