the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
How can Brewer–Dobson circulation trends be estimated from changes in stratospheric water vapour and methane?
Liubov Poshyvailo-Strube
Rolf Müller
Stephan Fueglistaler
Michaela I. Hegglin
Johannes C. Laube
C. Michael Volk
Felix Ploeger
The stratospheric meridional overturning circulation, also referred to as the Brewer–Dobson circulation (BDC), controls the composition of the stratosphere, which, in turn, affects radiation and climate. As the BDC cannot be directly measured, one has to infer its strength and trends indirectly. For instance, trace gas measurements allow the calculation of average transit times.
Satellite measurements provide information on the distributions of trace gases for the entire stratosphere, with measurements of particularly long temporal and dense spatial coverage available for stratospheric water vapour (H2O). Although chemical processes and boundary conditions confound interpretation, the influence of methane (CH4) oxidation on H2O in the stratosphere is relatively straightforward, and thus H2O is an appealing tracer for transport analysis despite these caveats. In this work, we explore how mean age of air trends can be estimated from the combination of stratospheric H2O and CH4 data, by carrying out a proof of concept within the model environment of the Chemical Lagrangian Model of the Stratosphere (CLaMS). In particular, we assess the methodological uncertainties related to the two commonly used approximations of (i) instantaneous stratospheric entry mixing ratio propagation and (ii) constant correlation between mean age and the fractional release factor of CH4. Performing various sensitivity studies with CLaMS, we test different methods of the mean age of air trend estimation, and we aim to provide simple and practical advice on the adjustment of the used approximations for obtaining more reliable mean age of air trends from the measurements of H2O and CH4.
Our results show that the estimated mean age of air trends from the combination of stratospheric H2O and CH4 changes may be significantly affected by the assumed approximations. Depending on the investigated stratospheric region and the considered period, the error in estimated mean age of air trends can be large, especially in the lower stratosphere. For particular periods, the errors from the two approximations can lead to opposite effects, which may even cancel out. Finally, for a more reliable estimate of the mean age of air trends, we propose adjusting the approximation method by using an idealized age spectrum to propagate stratospheric entry mixing ratios. The findings of this work can be used for assessing the uncertainties in stratospheric BDC trend estimation from global satellite measurements.
- Article
(5611 KB) - Full-text XML
- BibTeX
- EndNote
The stratospheric Brewer–Dobson circulation (BDC) affects the atmospheric distributions of radiatively active trace gases and is an important element in the climate system. This global-scale circulation transports air masses upwards in the tropics, polewards, and downwards in middle and high latitudes (e.g. Holton et al., 1995). A particularly important greenhouse gas affected by the BDC is stratospheric water vapour (H2O), which induces cooling of the stratosphere and warming of the troposphere (e.g. Solomon et al., 2010; Maycock et al., 2011; Riese et al., 2012). The reliability of climate model predictions is significantly affected by the representation of the processes controlling the distribution of stratospheric H2O. Although the BDC is such a crucial factor influencing stratospheric H2O and Earth's climate, its long-term trends and associated effects on transport and dynamics are not well understood. In particular, climate models predict a strengthening BDC in a future climate with increasing greenhouse gas levels (e.g. Butchart, 2014), whereas trace gas observations show only insignificant changes (Engel et al., 2017; Fritsch et al., 2020).
Because of the slowness of BDC transport (global transit times on the order of years) and its zonal mean character, direct measurements of related circulation velocities are not possible, and the circulation must be inferred from temperature or trace gas observations. A commonly used diagnostic for BDC transport is the mean age of air (AoA), the average timescale for transport through the stratosphere. Garcia et al. (2011) pointed out that the AoA is difficult to estimate from sparse stratospheric observations. However, under some conditions, it is possible to infer AoA from trace gas concentrations (e.g. Hall and Plumb, 1994; Strunk et al., 2000; Engel et al., 2009). Suitable species are so-called “clock tracers” – trace gases with a linearly increasing source, which can provide the first moment of the age spectrum, namely AoA (Waugh and Hall, 2002; Schoeberl et al., 2005). Two examples of such tracers are SF6 or CO2, and these are frequently used to infer stratospheric AoA (e.g. Stiller et al., 2017; Engel et al., 2017). However, the availability of suitable observations with global coverage and extending over sufficiently long time periods necessary for estimating trends is very limited. Also, there are other complications; for instance SF6 has a strong mesospheric sink, and CO2 has a seasonal cycle, causing problems with inferring AoA. Hence, several recent and ongoing research activities focus on trace gas species other than SF6 and CO2, to infer stratospheric AoA and information on the BDC (e.g. Linz et al., 2017; Leedham Elvidge et al., 2018).
In particular, trace gas species with chemical sinks in the stratosphere provide information on the stratospheric circulation as the transport through the sink regions depends on the strength and depth of the circulation. For such long-lived species with stratospheric sinks, like N2O, CH4, or the chlorofluorocarbons (CFCs), the chemical loss can be described by a fractional release factor (FRF)
where χ is the observed mixing ratio in the stratosphere and χ[entry] the mixing ratio at the tropical tropopause where the air enters the stratosphere. Consequently, changes in the strength and pattern of the stratospheric circulation cause changes in α, and, in general, FRF highly correlates with AoA. On the one hand, it is more complicated for chemically active species to disentangle the effects of chemistry and transport. On the other hand, atmospheric measurements may be of higher quality, be more frequent, provide denser sampling, and cover longer time periods compared to the canonical species SF6 and CO2, which are the ones commonly used to investigate the BDC.
As many long-lived species are only sparsely measured, stratospheric H2O is particularly appealing as a tracer for estimating long-term trends, with a suite of measurements covering the past decades. The longest continuous in situ time series of stratospheric H2O (starting in 1980) comes from the frost point hygrometer observations in Boulder, Colorado, located at 40.0∘ N, 105.2∘ W. In addition, stratospheric H2O observations from different satellite platforms have existed since the mid-1980s, such as SAGE II (Satellite Aerosol and Gas Experiment, covering the period of 1984–2005; e.g. McCormick, 1987; Chu et al., 1993; Rind et al., 1993; Thomason et al., 1997), HALOE (Halogen Occultation Experiment, 1991–2005; e.g. Russell et al., 1993), MIPAS Envisat (Michelson Interferometer for Passive Atmospheric Sounding, 2002–2012; e.g. von Clarmann and Stiller, 2003; Raspollini et al., 2006; Fischer et al., 2008), ACE-FTS (Atmospheric Chemistry Experiment-Fourier Transform Spectrometer, 2004–2012; e.g. Bernath et al., 2005; Bernath, 2017), and Aura MLS (Microwave Limb Sounder, 2004–present; e.g. Waters et al., 1999, 2006). The different satellite observations are merged into homogeneous global datasets of high value for analysing stratospheric variability and trends (e.g. Hegglin et al., 2014; Davis et al., 2017). To this end, Hegglin et al. (2014) estimated trends of AoA from a novel merged satellite H2O data record, based on the conservation property of total water in the stratosphere (mainly the sum of H2O and 2 times CH4; for details see Sect. 2.3). Bönisch et al. (2011) and Hegglin et al. (2014) showed that a decrease in the H2O mixing ratios in the lower stratosphere, below about 10 hPa and an increase in the H2O mixing ratios above this level from the mid-1980s to 2010 are related to an accelerating shallow branch of the BDC (decreasing AoA below about 10 hPa) and to a decelerating deep branch of the BDC (increasing AoA above), as originally suggested by Engel et al. (2009). It is, however, not straightforward to accurately determine the AoA from stratospheric H2O distributions due to complex processes involved.
We consider that at a particular time and location of the stratosphere, H2O mixing ratios are determined by the value of the stratospheric entry mixing ratio, the propagation of this entry value into the stratosphere, and the chemical source of stratospheric H2O. This assumption does not hold in the lowermost stratosphere as convection and isentropic transport can cause multiple entry mixing ratios. The only significant source of H2O considered in this work is CH4 oxidation. The chemical source of stratospheric H2O from the oxidation of CH4 is done by O(1D), OH, and Cl radicals (e.g. Röckmann et al., 2004). The strength of the chemical source of H2O depends on transit path of air since entering the stratosphere and transit time, and is thus related to AoA, which in turn is a measure for only the transit time but not the transit pathway dependency. The full complexity of these processes is very challenging to represent in the analysis of stratospheric H2O; in particular, it remains an issue to disentangle the effects of changing transit time and changing transport pathways when diagnosing trends of the BDC from observations. Consequently, stratospheric H2O and CH4 are used in combination for AoA estimation, and the assumptions of (i) an instantaneous propagation of stratospheric entry mixing ratios and (ii) stationarity of the correlation between AoA and the fractional release factor of CH4 are frequently assumed approximations (e.g. Schoeberl et al., 2000, 2005; Hegglin et al., 2014). Hegglin et al. (2014) particularly point out that the assumption of stationarity is only valid due to the lack of a trend in tropospheric CH4 over the specific period they considered.
In this paper, we investigate the methodology to estimate AoA trends from stratospheric H2O and CH4. In particular, we address in detail the impact of the two frequently employed approximations described above of (i) instantaneous entry mixing ratio propagation and (ii) constant AoA–FRF correlation. For this purpose, we employ a closed model environment (the “model world”) in which the mean stratospheric AoA and its trend are known, which is not the case when atmospheric measurements are analysed. In this way, the effect of each approximation on the calculated AoA trend and the associated temporal development of H2O can be quantified (“proof of concept”). We aim for simple and practical advice on the approximate methods to estimate AoA trends from stratospheric measurements of H2O and CH4. Our results highlight the importance of assessing the robustness of observation-based methods against uncertainties in the underlying assumptions to test their validity and general applicability.
Section 2 introduces the methods, describing the Chemical Lagrangian Model of the Stratosphere (CLaMS, McKenna et al., 2002a; Pommrich et al., 2014), which is employed here as the model framework, as well as the methods for estimating AoA trends from H2O and CH4. Section 3 presents the main results on the impact of the used approximations on the resulting AoA trend, as well as introduces the adjustment to the approximations for an improved AoA trend estimation. Section 4 contains the discussion and Sect. 5 the overall conclusions.
2.1 CLaMS
This paper is based on a study performed within the model world using the Chemical Lagrangian Model of the Stratosphere, CLaMS (McKenna et al., 2002a, b). The model set-up is described in detail elsewhere (e.g. Poshyvailo et al., 2018). Briefly, CLaMS is a modular Lagrangian chemistry transport model based on 3D-forward trajectories with parameterization of small-scale mixing. CLaMS consists of several modules, such as Lagrangian advection (TRAJ), stratospheric mixing (MIX), sinks of H2O (CIRRUS), stratospheric chemistry, and several other modules responsible for simulation of various physical and chemical processes. The modules act successively at each time step of 24 h. The boundary conditions at the surface are prescribed based on ground-based measurements in the lowest model level (below ≈ 4 km). CH4 mixing ratios are taken from the zonally symmetric NOAA/ESRL dataset (e.g. Masarie et al., 1991) from 1990–2011 and from zonally resolved AIRS data (e.g. Xiong et al., 2008, 2013) for 2011–2017. The CH4 boundary condition was switched in 2011 to take advantage of the better sampling of AIRS data in comparison to NOAA, although accepting the apparent discontinuity. Because the results of CLaMS are internally consistent, the discontinuity has only negligible effects; see Fig. 1.
The CLaMS trajectory module TRAJ performs fully Lagrangian three-dimensional advection of an ensemble of approximately 2 million air parcels. The position of each air parcel is defined in hybrid isentropic coordinates (Pommrich et al., 2014) and longitude–latitude space. Horizontal resolution is about 100 km, while the vertical resolution is defined via a critical aspect ratio, of about 250 (Haynes and Anglade, 1997). The CLaMS simulations cover the atmosphere from the surface to the stratopause (2500 K or ≈ 60 km). The advection of forward trajectories in CLaMS is calculated using 6-hourly wind fields and total diabatic heating rates from meteorological ERA-Interim reanalysis (Dee et al., 2011). Wind fields are linearly interpolated from the adjacent grid points to the locations of the air parcels. The trajectory calculation advects air parcels to new positions within one model time step.
The parameterization of small-scale mixing in the CLaMS mixing module is based on the deformation rate in the large-scale flow: air parcels may be merged, or new air parcels may be inserted at each time step, depending on the critical distances between the air parcels (McKenna et al., 2002a; Konopka et al., 2004). Note that the mixing parameterization affects both horizontal (associated with deformation in the horizontal flow) and vertical (related to the vertical shear) diffusivity (Konopka et al., 2004, 2005).
Dehydration in CLaMS is performed with the CIRRUS module (e.g. Poshyvailo et al., 2018). The calculation includes freeze-drying in regions of cold temperatures, mainly occurring around the tropical tropopause and in the southern polar vortex. These cold temperatures cause formation and sedimentation of ice particles. If saturation along a CLaMS air parcel trajectory exceeds a critical saturation, then the H2O amount in excess is instantaneously transformed to the ice phase and sediments out. The parameterization of sedimentation is based on a mean ice particle radius, the characteristic sedimentation length, and the corresponding fall speed. The fall distance of the ice particles is calculated from the fall speed and the computation time step. After comparison of the fallen path with a characteristic sedimentation length of the vertical grid size, a respective fraction of ice is removed. If the parcel is sub-saturated and ice exists, the ice will be instantaneously evaporated to maintain saturation. CH4 oxidation is included in CLaMS as a source of H2O in the middle and upper stratosphere (for details see Pommrich et al., 2014). Note that due to the simple parameterization of ice microphysics and the omission of a parameterization of convective processes, the simulated H2O results are meaningful only above the tropopause.
2.2 Age spectrum calculated with CLaMS
In general, the mixing ratio of any long-lived trace gas χ(r,t) at a specific time and specific location in the stratosphere, with assumed absence of integrated loss, can be expressed as the following integral over all past times (Hall and Plumb, 1994; Waugh and Hall, 2002):
where t is the field time when the volume is sampled, t′ is the transit time, and is the boundary propagator or Green function of the transport operator. Here, G is interpreted as a transit time distribution (the “age spectrum”) and is the probability that the transit time of the air parcel travelling from the source r0 to the sample point r is in the range between t′ and . The first momentum of the age spectrum is the mean age of air (AoA). In this way, the stratospheric tracer distribution can be described through the contributions of the tropospheric evolution and transport.
In our study, the age spectrum is computed with CLaMS driven by the ERA-Interim reanalysis, using the “boundary impulse (time-)evolving” (BIER) method based on multiple tracer pulses (Ploeger and Birner, 2016). For the inert tracer χ with a pulse at the location r0, the field time t0, and the source time , the time evolution of the source can be described with a δ-distribution as . Thus, Eq. (2) can be transformed to
where is a transit time, and is the boundary impulse response at location r to a δ-boundary condition at the location r0 at source time . Having N different tracers χi with pulses at the source location r0 at times t0[i] provides the field time dependence of the propagator G. The age spectrum may be constructed at each field time t and location r as . Hence, the N different tracers provide N pieces of information for the age spectrum at the discrete transit times .
Here, N = 60 different boundary pulse tracers were used. These pulses were released directly at the tropical tropopause between 30∘ S–30∘ N. Precisely, the source region covers the potential temperature layer from 10 K below to 10 K above the WMO (lapse rate) tropopause. As a remark, this specific choice of the source region causes the uncertainty in our analyses as it does not exactly correspond to the region that determines the H2O and CH4 entry mixing ratios; the tropically controlled transition region bounds between approximately 380 and 450 K (Rosenlof et al., 1997; Li et al., 2012). However, this mismatch impacts the results only close to the tropopause, so the reconstruction of H2O and CH4 by the modelled age spectrum ensures the reliability of the method in most of the stratosphere. The particular tracer mixing ratio is set to 1 for each pulse for a period of 30 d at the location r0, and it is set to 0 in r0 at other times. Pulses are launched every month. Consequently, to build the age spectrum for January 1990, the most recent tracer pulse has source times in January 1990, the second tracer pulse in December 1989, and so on. In our study, the original length of each age spectrum is 10 years (threshold transit time). The tail of the age spectrum is approximated with an exponential function when transit time exceeds 10 years (e.g. Ploeger and Birner, 2016). We used the exponential correction for the tail back to January 1979 for each age spectrum.
2.3 Contributions to H2O changes
Changes in stratospheric H2O are determined by the stratospheric H2O entry mixing ratio through troposphere–stratosphere exchange (Fueglistaler and Haynes, 2005) and by chemical sources, mainly oxidation of CH4 and molecular hydrogen (H2) in the middle and high stratosphere (Dessler et al., 1994; Harries, 2015). H2O in the troposphere is continuously supplied from the Earth's surface. CH4 is largely emitted at the Earth's surface because of anaerobic reactions, and H2 originates from biomass burning and other natural sources; CH4 and H2 are transported from the troposphere into the stratosphere. Based on satellite and balloon observations, the sum of the principal components of the hydrogen budget (H2O, 2 × CH4, and H2) is constant with altitude over most of the stratosphere (e.g. Dessler et al., 1994).
In this paper, we investigate the methodology to estimate AoA trends within a closed model environment of CLaMS, in which the mean stratospheric H2O and CH4 and their trends are known. Trends in AoA can be calculated from trends in stratospheric H2O mixing ratios by using the conservation property of total hydrogen in the stratosphere and assuming that H2 production from CH4 oxidation is balanced by H2 oxidation, namely that the sum of H2O and 2 times CH4 mixing ratios is approximately constant (e.g. Le Texier et al., 1988; Dessler et al., 1994). This conservation property implies, for the H2O mixing ratio at a given location r and time t in the stratosphere,
where and are H2O and CH4 mixing ratios respectively at the specific location and time in the stratosphere, being transported from their entry location at the tropical tropopause without any chemical effects. Note that the usage of the simple parameterization (see Eq. 4) for the ratio between oxidized CH4 and produced H2O has its limitations; e.g. a ratio of 2 overestimates the production of H2O in the lower stratosphere and somewhat underestimates it in the upper stratosphere (Frank et al., 2018). It is questionable whether this parameterization can be used for future climate projections, when the BDC is expected to accelerate (e.g. Austin and Li, 2006; Li et al., 2008; Garcia and Randel, 2008), and, as a result, the transport of H2 molecules becomes an important factor for the vertical profile of the H2O in the stratosphere. We also note that an increase in tropospheric H2 might gain importance in a future hydrogen economy (e.g. Vogel et al., 2012).
The time series of CLaMS H2O and CH4 at the entry to the stratosphere, averaged over the tropics at 30∘ S–30∘ N and in the potential temperature layer 390–400 K (approximately 80 hPa), chosen just above the cold tropical tropopause region, are shown in Fig. 1. The H2O time series is highly variable (Fig. 1a), while the CH4 time series shows a clear positive trend (Fig. 1b). Besides freeze-drying at the tropical tropopause and in the Antarctic polar vortex, stratospheric H2O is controlled mainly by CH4 oxidation in the middle and high stratosphere (Fig. 1c, d). Consequently, CH4 mixing ratios generally decrease with increasing altitude, as it is gradually chemically transformed into H2O.
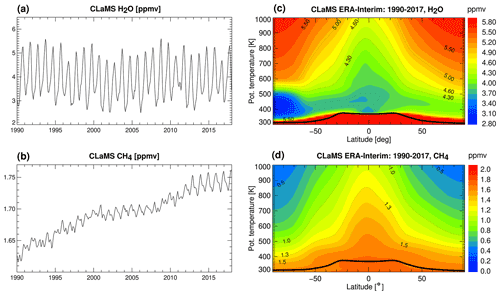
Figure 1Time series of CLaMS stratospheric entry H2O and CH4. Time series of H2O (a) and CH4 (b) mixing ratios (in ppmv) for 1990–2017 averaged over the tropics at 30∘ S–30∘ N and in the potential temperature layer 390–400 K. Annual zonal mean H2O distributions for H2O (c) and CH4 (d). Data shown are from the CLaMS simulation driven by ERA-Interim reanalysis.
The fractional release factor (FRF), α, describes the fraction of CH4 which has been dissociated in the stratosphere (Solomon and Albritton, 1992), and it is determined as
The FRF is strongly affected by the vertical transport of the BDC. Hence, information on circulation trends (in particular on AoA) can be deduced from trends in FRF (Hegglin et al., 2014). It should be noted that the change in FRF is due to transit time (age spectra) and circulation pathway (path spectra) changes, but AoA is a measure for only transit time and not the transit pathway dependency.
Assuming long-term trends as small perturbations to the basic state, Eq. (4) can be rewritten as an equation for the linear trend in stratospheric H2O over a given time period
Here, and are the trends in water vapour and methane transported from their stratospheric entry location at the tropical tropopause layer (neglecting chemistry), and Δα(r,t) is the trend in FRF. Note that and depend only on changes in transit times, while Δα(r,t) generally also depends on the changes in transport pathways. In addition, the sum of H2O and 2 times CH4 mixing ratios is not conserved around and below the tropopause and in the polar vortex, where dehydration causes loss of H2O. Hence, the presented analysis does not apply at the lowermost stratosphere, below the tropopause, and in the polar vortex or near its edges.
Using the above approach, it is possible to investigate the different contributions to stratospheric H2O changes related to changes in stratospheric H2O entry mixing ratio, changes in CH4 entry mixing ratio, and changes in the FRF, which are affected by stratospheric circulation changes and can be converted to AoA trend. In addition, the dependency of FRF changes on circulation pathways is implicitly taken into account by the AoA–FRF correlation functions in all used methods (Sect. 2.4).
2.4 Methods of assessing AoA trends from H2O changes
There are four methods of AoA trend calculation used in this study, depending on the assumed approximations of (i) an instantaneous propagation of stratospheric entry mixing ratios and (ii) stationarity of the correlation between AoA and the FRF. The summary of the different terms needed for AoA estimation with respect to the used method is shown in Table 1.
Table 1Specification of the terms (first column of the table) required for AoA trend estimation from H2O changes in different methods: full reconstruction (FULL), constant correlation (C-CORR), approximation (APPROX) and improved approximation (APPROX-improved) methods.
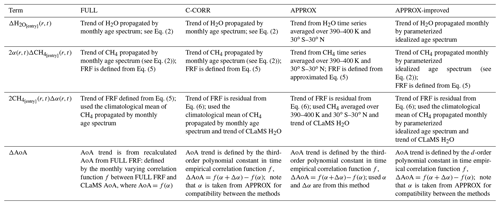
The full reconstruction method (FULL) includes the most detailed representation of the true atmospheric processes. In the FULL method, H2O and CH4 entry mixing ratios are propagated through the convolution of the tropical tropopause layer mixing ratios with the modelled age spectrum. The monthly varying AoA–FRF correlations are used for translating FRF into AoA changes, to include effects of the non-stationarity of the correlation. Neither of the approximations (i) or (ii) is used in the FULL method. Note that for estimating AoA trend with the FULL method, the propagated entry H2O mixing ratios are not needed; the AoA trend is deduced from the FRF, which requires only propagated entry CH4 mixing ratios.
The constant correlation method (C-CORR) includes the propagation of entry H2O and CH4 mixing ratios by the modelled age spectrum (same as for FULL), but the stationary relationship between FRF and modelled AoA is used (ii approximation). The difference between C-CORR and FULL is in the correlation between AoA–FRF and the method of calculating FRF and its trend.
The method based on both approximations (i) and (ii) is named “approximation method” in the following and is abbreviated APPROX. In fact, the APPROX method is used in the literature, and we evaluate it in this paper in detail. Finally, we introduce an improvement to the approximation method: instead of using approximation (i), stratospheric entry H2O and CH4 mixing ratios are propagated with the parameterized idealized age spectrum.
In the following we consider the consequences of the two major approximations (i) instantaneous propagation of stratospheric entry mixing ratios and (ii) constant correlation (stationary relationship) between FRF and AoA. We evaluate the effects of these approximations on the AoA trends inferred from H2O and CH4 changes through comparison of the “true” AoA trend (actual modelled with CLaMS) and the AoA trends estimated with the different methods. First, we consider the extended 1990–2017 period and thereafter 1990–2006. The results of this work provide an estimate of the reliability of the approximation method to deduce circulation trends from observed stratospheric H2O and CH4 mixing ratios.
3.1 Contributions to stratospheric H2O trend
AoA trends can be estimated from the separation of H2O changes into three different contributions (see Eq. 6). In a first step, we estimate here each term of Eq. (6) using the full reconstruction method FULL through propagation of H2O and CH4 entry mixing ratios by the modelled age spectrum (for details see Table 1).
We calculate the first term of Eq. (6) by the convolution of H2O mixing ratio at the tropical tropopause with the transport operator's Green function using Eq. (2). The Green function, or stratospheric age spectrum, has been simulated by CLaMS and is known over the considered period (for details see Sect. 2.2). Hence, the propagation of boundary mixing ratios to each grid point in the stratosphere provides the full reconstructed stratospheric tracer field. The analogous calculation is applied to derive CH4 mixing ratios in the stratosphere, transported without including chemical effects.
In our study, the entry time series of H2O and CH4 are taken from zonally averaged monthly mean data simulated with CLaMS driven by ERA-Interim reanalysis (see Fig. 1a, b). The location of entry to the stratosphere is approximated as the 390–400 K layer between 30∘ S–30∘ N, which is located just above the cold point tropopause to avoid complications related to H2O dehydration processes at the tropopause. The small difference between the age spectrum source region (tropopause ± 10 K) and the trace gas entry region has only a negligible impact on our results from above ≈420 K due to the small difference in the transit time between the two regions. The propagation procedure yields zonally averaged stratospheric entry H2O and CH4 distributions with a monthly resolution on the latitude–potential temperature grid.
For deducing FRF, the relation from Eq. (5) is used, where CH4(r,t) is monthly mean CH4 simulated with CLaMS driven by ERA-Interim reanalysis. The is calculated as described above, through the convolution of the tropical entry mixing ratio time series with the age spectrum. Consequently, the resulting FRF has a monthly resolution.
Thus, we can estimate each contribution to the stratospheric H2O mixing ratio. All trends are calculated through a linear regression, which minimizes the standard deviation at each latitude–potential temperature grid. The different contributions to the total stratospheric H2O change for 1990–2017 are shown in Fig. 2. Note that in this study we applied the propagation procedure to the period 1990–2017 because of the availability of the CLaMS data and the necessary age spectrum length. Figure 2a, b represent the first two terms of Eq. (6), related to the entry H2O and CH4 mixing ratio trends. Figure 2c shows the impact from circulation changes, in terms of the change in FRF. In general, the different contributions affect the stratospheric H2O changes differently in different regions, consistent with the findings of Hegglin et al. (2014). The strongest regional pattern is apparent in the contribution related to the stratospheric circulation change (Fig. 2c).
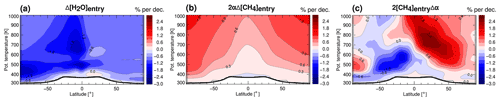
Figure 2Contributions to long-term changes in H2O 1990–2017 from the FULL method. Contributions to stratospheric H2O trends for 1990–2017 from (a) stratospheric H2O entry mixing ratio changes, (b) stratospheric CH4 entry mixing ratio changes, and (c) circulation changes. Stratospheric entry H2O and CH4 are derived through propagation of their stratospheric entry mixing ratios by convolution with the CLaMS modelled age spectrum. The data are from CLaMS simulations driven by ERA-Interim reanalysis and are presented in percentage per decade, with relation to the climatological 1990–2017 stratospheric H2O mixing ratios. The black line is the (lapse rate) tropopause calculated from ERA-Interim using the WMO definition (WMO, 1957). The white region below the tropopause denotes the region where the reconstruction method can not be applied.

Figure 3Contributions to H2O trends during 1990–2017. H2O trends during the 1990–2017 period and their reconstruction, shown in percentage per decade with respect to the 1990–2017 climatology. Panel (a) represents the reference (REF) true stratospheric H2O trend calculated from the CLaMS simulation driven by ERA-Interim reanalysis, (b) shows the reconstruction as the sum of the different contributions from Fig. 2, and (c) shows the absolute difference between (a) and (b). The black line is the tropopause calculated from ERA-Interim. Note that due to the simple parameterization of ice microphysics and the omission of a parameterization of convective processes in CLaMS, the simulated H2O shown in (a) is meaningful only above the tropopause.
For assessing the reliability of the method applied to estimate the different contributions, we compare the stratospheric H2O trend reconstructed as the sum of the calculated contributions (in Fig. 2) with the actual trend of CLaMS-simulated H2O. Figure 3a shows the true H2O trend from the CLaMS simulation, while Fig. 3b shows the sum of the three terms from Fig. 2. Figure 3c shows the absolute difference between the true and reconstructed trends, indicating clear quantitative differences. Particularly large differences occur in the Antarctic region. This is expected due to the strong local dehydration occurring in that region and the related failure of the total hydrogen conservation. Hence, the results of the reconstruction method should be interpreted with caution in the southern polar region. Further disagreement between Fig. 3a and b is partly related to inaccuracies in the modelled age spectrum (monthly pulsing, limited spectrum length) and to inaccuracies in the boundary time series (averaging in the layer of 390–400 K potential temperature and 30∘ S–30∘ N). Note that through the convolution of the age spectrum and the stratospheric entry time series it is possible to reconstruct mixing ratios only above the tropopause (or the level of the boundary time series, if chosen differently). Outside of the southern high-latitude regions and in the proximity of the extratropical tropopause (> 30∘ N/S), the overall differences shown in Fig. 3c are small, and the propagation procedure provides a good estimate of stratospheric H2O change and its contributions, at least regarding the large-scale patterns. Note that neither stratospheric entry H2O (Fig. 2a) nor CH4 changes (Fig. 2b) explain the pattern of the true H2O trend (Fig. 3a). Instead, the circulation change term (Fig. 2c) includes the regional characteristics of the actual stratospheric H2O trend.
3.2 AoA trend estimation using monthly AoA–FRF correlation in the full reconstruction method (FULL)
The changes in FRF can be translated into changes in AoA using the correlation between estimated FRF and known AoA, following the procedure described by Hegglin et al. (2014). In the full reconstruction method FULL (for details see Table 1), a monthly varying correlation between estimated FRF and CLaMS AoA is used, where AoA = f(α), and f is an empirically determined correlation function (Fig. 4).
In an example for January, April, and July of 1995 shown in Fig. 4a, the AoA–FRF correlation functions are unique for each month, because the differences in magnitude of the coefficients are greater than the standard error's range. Moreover, monthly AoA–FRF correlation functions have a very small difference for relatively young air (< 4 years) and low FRF (< 0.4), but there are visible differences towards older AoA.
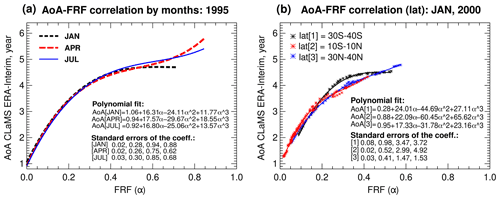
Figure 4Monthly relationship between FRF from the FULL method and CLaMS AoA. An example of the relationship between estimated FRF (with FULL method) and CLaMS AoA. In panel (a) are shown correlation functions for three months of 1995: January (black dashed line), April (red dashed line), and July (blue solid line); FRF and CLaMS AoA are taken at the whole range of latitudes (90∘ S–90∘ N). In panel (b) are shown the relationships between estimated FRF and CLaMS AoA for January 2000 for three intervals of latitudes: between 30 and 40∘ S (black line and black asterisks), 10∘ S–10∘ N (red line and red asterisks), and 30–40∘ N (blue line and blue asterisks). The estimated FRF and CLaMS AoA driven by ERA-Interim (zonally averaged) are taken between 450 and 1000 K, where FRF has positive values, in both panels. The AoA–FRF relationships are shown by monthly fitting a third-order polynomial function; in (a) the actual AoA–FRF distribution is not shown to avoid an overcrowded plot.
It is worth mentioning that the monthly AoA-FRF correlation functions are still a simplification and might introduce some bias in the reconstruction. In general, an accurate AoA-FRF correlation function depends not only on the considered time but also on longitude, latitude, and altitude. An example of the relationship between AoA and FRF with regard to different latitude ranges (30–40∘ S, 10∘ S–10∘ N, 30–40∘ N) is shown in Fig. 4b for January 2000. The AoA–FRF correlation functions are unique for each latitude range, because the differences in the magnitude of coefficients are out of the standard error's range. And, for instance, at the same FRF level of 0.3 air at the northern tropics (30–40∘ N) is younger than at the southern tropics (30–40∘ S) by almost half a year. It is likely due to stronger and deeper BDC in the Northern Hemisphere during boreal winter (e.g. Rosenlof, 1995; Butchart, 2014), causing air parcels of the same age to travel deeper pathways through the stratosphere and experience more chemical depletion compared to the Southern Hemisphere.
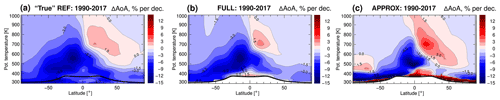
Figure 5Decadal changes of AoA during 1990–2017. Decadal changes of AoA during 1990–2017: (a) true AoA changes from the CLaMS simulation driven by ERA-Interim reanalysis, (b) using CH4 propagation by CLaMS age spectrum and monthly varying AoA–FRF correlation (FULL), and (c) AoA changes estimated with the approximation method (APPROX). The changes are presented in percentage per decade relative to the AoA 1990–2017 climatology in each used method of AoA calculation. The black line is the tropopause calculated from ERA-Interim.
AoA trend is calculated from the resulting AoA applying a linear fit (minimizing the standard deviation) at each latitude–potential temperature grid point. The reference true AoA trend calculated directly from CLaMS-simulated AoA is shown in Fig. 5a, whereas the resulting AoA trend calculated with the FULL method is shown in Fig. 5b. The estimated AoA trend with FULL is qualitatively and quantitatively highly reliable, when comparing to the reference CLaMS AoA trend. Note that for estimating AoA trends with the FULL method, the propagated entry H2O mixing ratios are not used; the AoA trend is deduced from the FRF, which requires only propagated entry CH4 mixing ratios. Visible differences between Fig. 4a and Fig. 4b are related to approximations in the AoA–FRF correlation: monthly AoA–FRF correlation functions are still a simplification and might introduce some bias in the reconstruction. The averaged (between 390–400 K potential temperature, from 30∘ S–30∘ N) CH4 boundary mixing ratios, which are used for the reconstruction, could induce biases as well.
3.3 AoA trend estimation in the approximation method (APPROX)
Accurate estimation of AoA from observed trace gas distributions is a complicated task. Even though it is desirable to have a complete age spectrum for AoA calculations, it is very difficult to obtain it from measurements. Consequently, different approximations are often applied when deriving AoA from trace gases observation with a non-linear increase, as well as assumptions about the age spectrum and its shape (e.g. Schoeberl et al., 2000, 2005; Ehhalt et al., 2007; Hegglin et al., 2014; Fritsch et al., 2020). In the following, we further investigate the method of AoA trend estimation from a combination of H2O and CH4 changes, applying the two major approximations introduced above: (i) instantaneous propagation of stratospheric entry mixing ratios and (ii) constant correlation (stationary relationship) between FRF and modelled AoA.
In the approximation method APPROX, each term of Eq. (6) is approximated. The actual trend of stratospheric H2O (left side of the Eq. 6) is assumed to be known beforehand. In our case it is the CLaMS-simulated H2O change over the considered period; if the method is applied to observations it would be the observed H2O change. The needed variables for the first and the second terms of Eq. (6) are obtained as a linear trend of the model entry mixing ratio time series, averaged over the 390–400 K potential temperature layer and 30∘ S–30∘ N, from the considered period (see Fig. 1). The FRF required for the second term is derived from Eq. (5). Therefore, following Hegglin et al. (2014) we use zonal mean CLaMS-simulated CH4(r,t) mixing ratios averaged over 2005–2006, and we calculate as a mean mixing ratio between 390–400 K potential temperatures and 30∘ S–30∘ N during 2002–2006. The third term is calculated as a residual between the actual CLaMS H2O trend over the considered period (left side of Eq. 6) and the other two terms. Dividing the third term by 2 yields the FRF changes.
In order to estimate the AoA trend induced by the changes in stratospheric H2O, we define the relationship between FRF from APPROX and CLaMS-modelled AoA (taken as 2005–2006 climatology in the APPROX method). The correlation function is derived by fitting a third-order polynomial, as suggested by Hegglin et al. (2014). In our study, the empirical relationship between APPROX FRF and CLaMS AoA is described by the function (see Appendix A). The approximation method assumes that the AoA–FRF relationship is stable in time (stationary). Note that by applying a constant AoA–FRF correlation function some atmospheric variability can be lost. Using the correlation function f(α) we obtain the AoA trends from previously estimated FRF and its changes, as . A summary of all terms defined within the APPROX method is provided in Table 1.
The resulting decadal AoA trend for 1990–2017 estimated with the approximation method is shown in Fig. 5c and can be compared to the true AoA trend from the reference CLaMS simulation, shown in Fig. 5a. There are visible quantitative differences between the true and the estimated trends of the AoA, especially in the Antarctic region. These differences are related to the dehydration processes occurring in that region. Also, the approximation method overestimates the AoA trend in the northern hemispheric subtropical middle stratosphere. In the extratropical lowermost stratosphere (below about 380 K), AoA trends calculated with the approximation method are even opposite compared to the true trends, likely related to significant transport into this region across the subtropical tropopause (e.g. Hauck et al., 2019), which is not represented in the APPROX. But overall, both APPROX and the true AoA trends show good agreement: decreasing AoA in the lower stratosphere and increasing AoA in the northern hemispheric middle stratosphere. Interestingly, for the 1990–2017 period the AoA trend shows clear differences between the Northern Hemisphere and Southern Hemisphere. The hemispheric differences might be related to the effect of mixing (e.g. Ploeger et al., 2015) and shifting stratospheric circulation patterns (Stiller et al., 2017), previously found in the long-term AoA trend derived from the observed stratospheric CH4 (Remsberg, 2015). Overall, APPROX provides a good estimate of the AoA trend for 1990–2017, corroborating the validity of the applicability of this method to H2O observations over similar time periods (e.g. Hegglin et al., 2014).
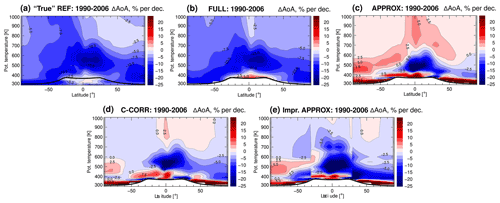
Figure 6Decadal changes of AoA during 1990–2006: true and full. Comparison of decadal AoA trends for the 1990–2006 period, estimated using different methods: (a) true AoA trend from CLaMS simulation driven by ERA-Interim reanalysis, (b) FULL, (c) APPROX, (d) C-CORR (stratospheric entry H2O and CH4 propagation by CLaMS age spectrum and a constant AoA–FRF correlation), and (e) improved approximation method (stratospheric entry H2O and CH4 propagation by the parameterized age spectrum and a constant AoA–FRF correlation). The AoA trends are presented in percentage per decade with respect to the 1990–2006 AoA climatology from the respective method. The black line is the climatological 1990–2006 tropopause calculated from ERA-Interim.
To assess the general applicability of the approximation method APPROX, we consider another period, 1990–2006. The true AoA trend for this period from the CLaMS simulation is presented in Fig. 6a, and the result from APPROX is shown in Fig. 6c. In this case, the APPROX AoA trend disagrees substantially when compared with the true CLaMS trend. Differences occur even in the sign of the AoA trend. Particularly clear differences occur in the strength of the AoA trend and its detailed pattern. Thus, the accuracy of the estimated AoA changes from APPROX largely depends on the considered period, which should be long enough to ensure that the effects of variability are small. In the following section, we further investigate the effects of the applied approximations and discuss their impact on the quality of the estimated AoA trend.
3.4 Effect of the approximations: entry mixing ratio propagation and constant AoA–FRF correlation
Firstly, we evaluate the effect of approximation (i) of the instantaneous entry mixing ratio propagation. For this purpose, we perform an additional sensitivity study, where the stationary relationship between FRF and modelled AoA is kept, but entry H2O and CH4 mixing ratios are propagated through the convolution of the CLaMS mixing ratios with the modelled age spectrum. This method is termed the constant correlation method, C-CORR, in the following (see Table 1 for details). Note that in both methods, C-CORR and APPROX, the same FRF distribution is used, but the changes in circulation (namely Δα) are different.
The estimated AoA trend from C-CORR for 1990–2006 is shown in Fig. 6d. The approximation of the instantaneous entry propagation largely affects the AoA trend, as evident from comparison of the resulting AoA trends from C-CORR, APPROX, and the CLaMS reference AoA trend (Fig. 6a, c, d). Including the entry H2O and CH4 propagation by the age spectrum in the method clearly improves the estimated AoA trend. When comparing C-CORR to APPROX the general trend patterns stay similar, but improvements are visible in the extratropical lower stratosphere and above about 600 K.
For evaluating the effect of the approximation (ii) of a constant correlation between FRF and AoA, we compare the resulting AoA trends from the C-CORR and FULL methods. The difference between the AoA trend results from the C-CORR and FULL methods stems from the differences in the AoA–FRF correlations used in each method and the explicit FRF trend calculation (see Table 1).
In C-CORR, the AoA trend is estimated from the residual circulation contribution (see Table 1). Consequently, the monthly varying AoA–FRF correlation improves the accuracy of the estimated AoA trend both qualitatively and quantitatively, when compared to the stationary AoA–FRF correlation (Fig. 6a, b, d). It was mentioned earlier in the paper that stratospheric H2O is a highly variable tracer and can lead to difficulties in estimating AoA trends. Hence, the good performance of the FULL method can be related to the fact that stratospheric entry H2O mixing ratios do not influence the calculation, provided that the polar regions are excluded (as explained in Sect. 3.1).
For a more precise assessment of the effects of the two approximations, the differences among AoA trends estimated with different methods (APPROX, C-CORR, FULL) and for two different periods (1990–2017 and 1990–2006) are analysed. The difference between AoA trends from APPROX and C-CORR gives an estimate of the effect of the approximation (i) assuming instantaneous entry mixing ratio propagation, whereas the difference between C-CORR and FULL gives an estimate of the effect of the approximation (ii) using a constant AoA–FRF correlation (Fig. 7).
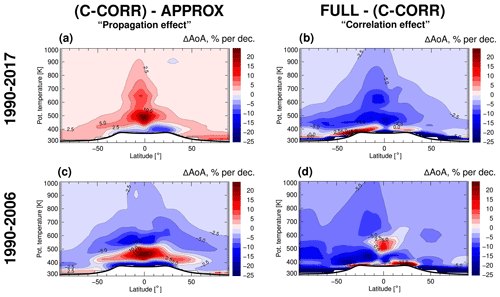
Figure 7Differences in AoA trends during 1990–2006. Differences in AoA trends estimated with three methods, APPROX, C-CORR, and FULL, for the periods of 1990–2017 (a, b) and 1990–2006 (c, d). The black line is the climatological tropopause calculated from ERA-Interim for the considered period.
Figure 7a, b show the differences in AoA trends for 1990–2017 between C-CORR and APPROX as well as FULL and C-CORR. The differences are less than 5 % per decade above 600 K. Below 600 K, the differences in AoA trends are higher, with the maximum at approximately 480 K. The larger differences in the lowest stratosphere directly above the tropopause should not be over-interpreted as the transit time resolution of used age spectra of 1 month is too coarse for a reliable reconstruction there. Interestingly, the effects of the first and second approximations are opposite in sign for 1990–2017 (Fig. 7a, b). Consequently, the effects from both approximations cancel out to some extent, such that the APPROX method yields results remarkably close to the CLaMS reverence AoA trend (see Fig. 5). However, in general such a cancellation can not be expected.
Figure 7c, d show the difference in AoA trends for 1990–2006. The difference above 600 K is around 5 % per decade or less. A more complex structure is found below 600 K. Generally, the instantaneous entry mixing ratio propagation causes an error in the estimated stratospheric entry H2O and CH4 contributions (see Sect. 4). This, in turn, causes an error in the derived residual circulation impact in C-CORR, which is further translated into the estimated AoA trend error.
The above analysis shows that the effects of both approximations (instantaneous propagation of stratospheric H2O and CH4 entry mixing ratios and a constant correlation between FRF and AoA) on the estimated AoA trend are comparable in magnitude; however they depend on the exact period considered. Interestingly, the effects of the approximations can be opposite in sign, cancelling each other out to some extent. Consequently, the approximation method can lead to a reliable estimation of AoA trends for certain periods, but this should not always be expected. A further improvement of the approximation method is proposed in the following Sect. 3.5.
3.5 Improved AoA trend estimation using parameterized age spectra
For estimating AoA trends from H2O and CH4 observations, the approximations (i) instantaneous entry mixing ratio propagation and (ii) constant AoA–FRF correlation are necessary. Nevertheless, the higher reliability of AoA trends can be achieved if the used approximations are adjusted. As a simple and practical improvement, we propose using an analytical, parameterized age spectrum for propagating stratospheric entry H2O and CH4 mixing ratios. Note that for a further improvement of AoA trend estimates, a non-stationary AoA–FRF relationship in principle would be needed as well. But due to the sparseness of available stratospheric CH4 measurements, deducing such a relationship from observations is challenging, and we refrain from including it in the methodological improvement.
In the following, we discuss the results of an additional sensitivity study with CLaMS stratospheric entry H2O and CH4 mixing ratios propagated by the parameterized idealized age spectrum and using a constant AoA–FRF correlation. This method is hereinafter referred to as the “improved approximation method” (see Table 1 for details). In this method we use an inverse Gaussian distribution (e.g. Newman et al., 2007; Bönisch et al., 2009; Hauck et al., 2019) as a parameterized age spectrum:
where Γ is the mean AoA and Δ is the width of the age spectrum. Here, we parameterize AoA in different zones or “regions” depending on the considered latitude, longitude, and height. The finer the separation into different regions, the less pronounced the discontinuities at the edges of the regions are. For a simple and practical method without assuming a priori knowledge of model age of air, we propose dividing the stratosphere into seven regions, prescribing one mean value of AoA for each region (see Appendix B). We apply the empirical relation between the age spectrum width and AoA proposed by Hall and Plumb (1994) and used in several other studies (e.g. Engel et al., 2002; Bönisch et al., 2009):
with the constant C=0.7 years, although we note that recent work of Hauck et al. (2019) suggests a larger value (2.0 years) for the lower stratosphere.
The resulting AoA trend estimated with the improved approximation method for 1990–2006 is shown in Fig. 6e. There is a clear improvement in the AoA trend estimation when compared to the pure approximation method APPROX (Fig. 6c). Note that in both methods the same FRF distribution is used, but the FRF changes are different depending on the propagation method of stratospheric entry H2O and CH4. The discrepancies in estimated AoA trends between APPROX and the improved approximation method stem from the residual calculation of the third term of Eq. (6), , with the major impact of the stratospheric entry H2O trend (see Sect. 4). The propagation of stratospheric entry H2O and CH4 by the proposed parameterized idealized age spectrum results in AoA trends close to those from the C-CORR method (Fig. 6d, e), which is the best estimate possible for the improved approximation method due to the usage of constant AoA–FRF correlation.
Hence, we encourage the usage of the improved approximation method when estimating AoA from the combination of H2O and CH4 observational data. Stratospheric entry mixing ratio time series for H2O and CH4 can be deduced from satellite measurements, such as ACE-FTS, HALOE, MIPAS, or SCIAMACHY (e.g. Bernath, 2017; Russell et al., 1993; Nassar et al., 2005; Raspollini et al., 2006; Scherer et al., 2008; Müller et al., 2016; Lossow et al., 2017; Noël et al., 2018). Due to the limited stratospheric CH4 observations, the stratospheric entry CH4 mixing ratio contribution can be kept as in APPROX (instantaneous propagation), because this term has only little effect on the resulting AoA trend (see Sect. 4). Our study shows that the usage of the parameterized idealized age spectrum clearly improves the representation of the stratospheric entry H2O term and hence the final AoA trend estimate.
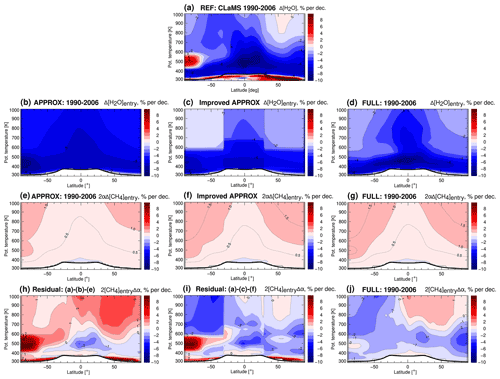
Figure 8Contributions to H2O trends during 1990–2006. The true stratospheric H2O 1990–2006 trend calculated from CLaMS simulations driven by ERA-Interim reanalysis is shown in (a). Further plots represent contributions to H2O trend calculated through different methods: APPROX (b, e, h), the improved approximation (c, f, i), and FULL (d, g, j). The contributions from circulation changes are calculated as the residual in APPROX and improved approximation methods (h, i) and as a linear trend in FULL (j). Note that all panels are presented in percentage per decade, with relation to the climatological mean 1990–2006 CLaMS stratospheric H2O mixing ratio. The black line is the tropopause calculated from ERA-Interim.
The contributions of stratospheric entry H2O mixing ratio trends ( in Eq. 6) calculated with APPROX, improved approximation, and FULL methods, as well as the true stratospheric H2O trend from CLaMS simulation, are shown in Fig. 8a–d. Note that the stratospheric entry H2O mixing ratio propagated by the CLaMS age spectrum is shown here only for comparison and is not used for AoA trend calculations in the FULL method. Comparison of Fig. 8b and d shows that APPROX overestimates the stratospheric entry H2O mixing ratio trend by approximately 3 % per decade, especially in the middle and upper stratosphere. The propagation of stratospheric entry H2O by the parameterized idealized age spectrum improves the representation of stratospheric entry H2O trend (see Fig. 8c, d) and thus leads to a more reliable AoA trend estimation.
The contributions from stratospheric entry CH4 mixing ratio trends ( in Eq. 6) are presented in Fig. 8e–g. The differences between the various stratospheric entry CH4 trends are below 0.5 % per decade. Although the pattern of the stratospheric entry CH4 mixing ratio trends is slightly improved when including propagation with the parameterized idealized age spectrum (Fig. 8f, g), overall, this term has a weak effect on the circulation contribution and the resulting AoA trend.
The circulation contributions ( in Eq. 6) in the APPROX and improved approximation methods are calculated as the residual between CLaMS H2O trend (see Fig. 8a) and the other two components. As FULL is the most exact method, the circulation terms from the approximate methods are evaluated against it. Figure 8h, j show that the error in the estimated circulation contribution in APPROX is large, and the sign of the circulation contributions is even opposite in particular regions. Propagating stratospheric entry H2O and CH4 by the parameterized idealized age spectrum (Fig. 8i) improves the representation of circulation change significantly. From the comparison of Fig. 8i, j, we conclude that calculating the circulation impact as a residual yields a reliable representation of the circulation contribution when an idealized parameterized age spectrum is used. Large discrepancies still occur in the Antarctic region where the reconstruction method is expected to fail because of local dehydration processes. The polar dehydration in the Antarctic region has a substantial drying effect, reaching 1 ppmv and even more below 600 K potential temperature in the Southern Hemisphere (Poshyvailo, 2020). This dehydration effect induces discrepancies in methods with the residual circulation term. Furthermore, the circulation contribution calculated as a residual also depends on the accuracy of the used stratospheric H2O trend, shown in Fig. 8a.
To summarize, the differences between the residual circulation components of APPROX and improved approximation methods are caused by the discrepancies in the stratospheric entry H2O and CH4 mixing ratio contributions, with the major impact from the stratospheric entry H2O trend. Consequently, the correct representation of the stratospheric entry H2O mixing ratio trend is crucial for a reliable estimate of the AoA trend.
We showed that biases in AoA trends estimated from stratospheric H2O can be large, questioning the usefulness of this approach. On the other hand, AoA estimates based on other trace gas species, like SF6 or CO2, show substantial uncertainties as well (e.g. Engel et al., 2009; Fritsch et al., 2020). An advantage of using H2O is the existence of several long and homogenized records of satellite measurements of comparatively high quality. Furthermore, the significant bias reduction in estimated AoA trends, related to the relatively simple methodological improvement by using a parameterized idealized age spectrum for entry mixing ratio propagation, seems very promising. Further improvements could be realized by including a chemistry-dependent propagator instead of the idealized age spectrum (see Ostermöller et al., 2017), or by using an inversion algorithm for fitting the parameterized age spectrum (e.g. Hauck et al., 2019).
We investigated the effects of two commonly used approximations, (i) instantaneous stratospheric entry mixing ratio propagation and (ii) stationary AoA–FRF correlation, to estimate long-term BDC changes from the combination of stratospheric H2O and CH4 by deducing AoA trend. We carried out different sensitivity experiments within the CLaMS model world: including both above-mentioned approximations (APPROX), only the constant correlation approximation but representing the correct entry mixing ratio propagation (C-CORR), and representing the non-stationarity of the correlation as well as the entry mixing ratio propagation (FULL). Estimated AoA trends were compared to the actual CLaMS AoA trend. We considered as case studies the 1990–2006 and 1990–2017 periods.
The results show that both approximations have an important effect on the calculated AoA trend, leading to noticeable differences in the derived mean AoA trend compared to the true CLaMS AoA trend. The discrepancies in the AoA trends are up to 5 % per decade above 600 K and more than 10 % below 600 K due to the applied approximations. Depending on the considered period, the effects from both approximations can also be opposite and may even cancel out to some extent, producing, incidentally, an estimation of AoA trend remarkably close to the true.
In order to increase the reliability of the derived AoA trend, we propose a simple and practical adjustment of the approximation (i) by propagating the stratospheric entry H2O and CH4 mixing ratios using a parameterized idealized age spectrum instead of instantaneous propagation. This refinement of the method considerably improves the reconstructed stratospheric entry H2O contribution, and, consequently, the derived AoA trend. The results of this article are of particular relevance for assessing the uncertainty in estimates of stratospheric circulation and BDC changes from global satellite measurements of stratospheric H2O.
In order to estimate the AoA trend induced by the changes in stratospheric H2O, we define a stationary relationship between zonally averaged FRF and AoA from CLaMS simulations driven by ERA-Interim reanalysis. We use CH4 mixing ratios averaged over 2005–2006 for FRF calculations (see Eq. 5), following Hegglin et al. (2014). This specific period is characterized by relatively constant tropospheric CH4 values. Accordingly, the dependence of stratospheric CH4 entry mixing ratios on transit time can be neglected, and CH4 can be assumed constant over these years. We assume that the stratospheric CH4 during 2005–2006 originated in the tropical tropopause layer during approximately 2002–2006. Thus, stratospheric entry CH4 can be approximated as the mean CH4 mixing ratio over 390–400 K and 30∘ S–30∘ N during the 2002–2006 period. Consequently, FRF is stable in time and does not depend on the chosen period.
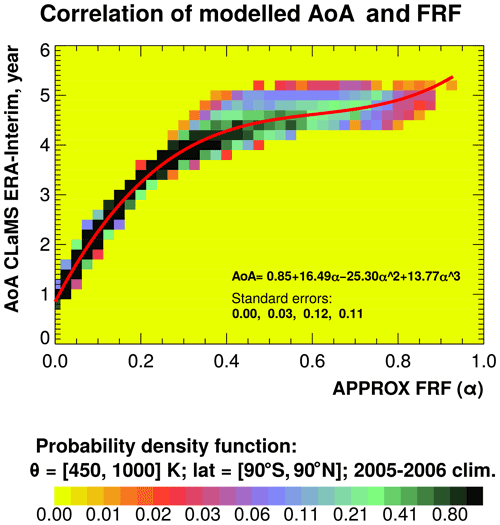
Figure A1Relationship between CLaMS AoA and FRF. Relationship between CLaMS FRF and AoA for the methods of AoA trend estimation using stationary approximation. FRF is defined from the climatological 2005–2006 CLaMS-simulated CH4, and AoA is the climatological 2005–2006 from CLaMS simulations. The considered correlated region is between 450–1000 K and 90∘ S–90∘ N. The colour bar represents the probability density function. The red line is a third-order polynomial fitting function.
The correlation function of the CLaMS-modelled AoA and estimated FRF function is presented in Fig. A1. It is derived by fitting a third-order polynomial to the AoA–FRF distribution, as suggested by Hegglin et al. (2014). The empirical relationship between the CLaMS AoA and the FRF is (see Fig. A1). The same relationship is applied for any investigated period, if the method implies a stationary AoA–FRF correlation function.
In the improved approximation method, we use parameterized idealized age spectrum to propagate stratospheric entry H2O and CH4 mixing ratios for the AoA trend estimation. The idealized age spectrum requires the width of the age spectrum that is defined from the empirical relation Eq. (8). Here, we make a simple parameterization of AoA (Γ) required for the idealized age spectrum. We separate the stratosphere (up to 1000 K or approximately 37 km) into seven zones; see Fig. B1. However, further improvement by other zone divisions is, in principle, possible. A better spatial resolution of propagated H2O, CH4 by idealized age spectrum, and consequently estimated AoA could be gained by using more zones or even by assigning different shape for zones (e.g. triangles).
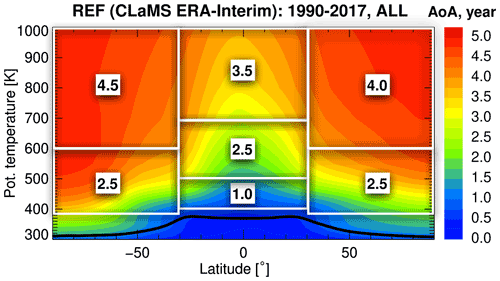
Figure B1AoA zonal mean. Zonal mean of AoA from CLaMS simulation driven by ERA-Interim reanalysis. Data shown are the climatology for 1990–2017. Regions defined with the white boxes are used for the idealized age spectrum calculations in the improved approximation method. Values denoted in each box are an approximate averaged AoA value of the region bounded by white box.
In the latitudinal directions, the middle zone between 30∘ S–30∘ N is associated with the tropical pipe region. In the height direction at the units of potential temperature, the lowest AoA value of 1 year is located just above the tropical tropopause layer between 400–500 K (or about 15–20 km). We assign an average AoA value equal to 2.5 years in three regions: in both hemispheres between 380–600 K (approx. 12–24 km) and at the tropics between 500–700 K (approx. 20–28 km). The averaged AoA value of 3.5 years is at the tropical middle stratosphere from 700–1000 K (approx. 28–37 km). The averaged AoA value is different for both hemispheres at the region between 600–1000 K (approx. 24–37 km): 4.5 years for the Southern Hemisphere and 4.0 years for the Northern Hemisphere. Such AoA asymmetry exists, since the deep branch of the circulation is stronger in the Northern Hemisphere and thus causes younger AoA (Butchart, 2014; Konopka et al., 2015).
The CLaMS code used in this article is available on the GitLab server: https://jugit.fz-juelich.de/clams/CLaMS (last access: 1 July 2021; e.g. McKenna et al., 2002a, b). ERA-Interim reanalysis data are available from the European Centre for Medium-Range Weather Forecasts (via https://apps.ecmwf.int/archive-catalogue/?class=ei, last access: 15 May 2021; Dee et al., 2011). The modelled data may be requested from the corresponding author (l.poshyvailo@fz-juelich.de).
The study was designed by FP and LPS with contributions by SF and RM. LPS and FP conducted the model runs and analysed the results. Partially, the work is based on the original concept from the study of MIH. LPS wrote the paper with further inputs from FP and RM. All co-authors contributed to the interpretation of the results, active discussions, and revision of the paper.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Chemistry and Physics. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Jens-Uwe Grooß, Paul Konopka, and Mengchu Tao for helpful discussions. We are also very grateful to the ECMWF for providing the reanalysis data (ERA-Interim). In addition, we acknowledge the computing time granted on the supercomputer JURECA at the Jülich Supercomputing Centre (JSC) under the VSR project ID JICG11. Liubov Poshyvailo-Strube is grateful to the Helmholtz Graduate School for Energy and Climate Research (HITEC) of Forschungszentrum Jülich for supporting her research stay at Princeton University. Finally, we thank three anonymous reviewers for the constructive comments that helped improve the paper.
This research has been supported by the German Ministry of Education and Research (ROMIC-TRIP, grant no. 01LG1222A) and by the Helmholtz Young Investigators Group A-SPECi (“Assessment of stratospheric processes and their effects on climate variability”, grant no. VH-NG-1128). Johannes C. Laube received funding from the ERC project EXC3ITE (grant no. EXC3ITE-678904-ERC-2015-STG).
The article processing charges for this open-access publication were covered by the Forschungszentrum Jülich.
This paper was edited by Gabriele Stiller and reviewed by three anonymous referees.
Austin, J. and Li, F.: On the relationship between the strength of the Brower-Dobson circulation and the age of stratospheric air, Geophys. Res. Lett., 33, L17807, https://doi.org/10.1029/2006GL026867, 2006. a
Bernath, P.: The Atmospheric Chemistry Experiment (ACE), J. Quant. Spectrosc. Ra., 186, 3–16, https://doi.org/10.1016/j.jqsrt.2016.04.006, 2017. a, b
Bernath, P. F., McElroy, C. T., Abrams, M. C., Boone, C. D., Butler, M., Camy-Peyret, C., Carleer, M., Clerbaux, C., Coheur, P.-F., Colin, R., DeCola, P., DeMazière, M., Drummond, J. R., Dufour, D., Evans, W. F. J., Fast, H., Fussen, D., Gilbert, K., Jennings, D. E., Llewellyn, E. J., Lowe, R. P., Mahieu, E., McConnell, J. C., McHugh, M., McLeod, S. D., Michaud, R., Midwinter, C., Nassar, R., Nichitiu, F., Nowlan, C., Rinsland, C. P., Rochon, Y. J., Rowlands, N., Semeniuk, K., Simon, P., Skelton, R., Sloan, J. J., Soucy, M.-A., Strong, K., Tremblay, P., Turnbull, D., Walker, K. A., Walkty, I., Wardle, D. A., Wehrle, V., Zander, R., and Zou, J.: Atmospheric Chemistry Experiment (ACE): Mission overview, Geophys. Res. Lett., 32, L15S01, https://doi.org/10.1029/2005GL022386, 2005. a
Bönisch, H., Engel, A., Curtius, J., Birner, T., and Hoor, P.: Quantifying transport into the lowermost stratosphere using simultaneous in-situ measurements of SF6 and CO2, Atmos. Chem. Phys., 9, 5905–5919, https://doi.org/10.5194/acp-9-5905-2009, 2009. a, b
Bönisch, H., Engel, A., Birner, T., Hoor, P., Tarasick, D. W., and Ray, E. A.: On the structural changes in the Brewer-Dobson circulation after 2000, Atmos. Chem. Phys., 11, 3937–3948, https://doi.org/10.5194/acp-11-3937-2011, 2011. a
Butchart, N.: The Brewer-Dobson circulation, Rev. Geophys., 52, 157–184, https://doi.org/10.1002/2013RG000448, 2014. a, b, c
Chu, W. P., Chiou, E. W., Larsen, J. C., Thomason, L. W., Rind, D., Buglia, J. J., Oltmans, S., McCormick, M. P., and McMaster, L. M.: Algorithms and sensitivity analyses for Stratospheric Aerosol and Gas Experiment II water vapor retrieval, J. Geophys. Res.-Atmos., 98, 4857–4866, https://doi.org/10.1029/92JD01628, 1993. a
Davis, S. M., Hegglin, M. I., Fujiwara, M., Dragani, R., Harada, Y., Kobayashi, C., Long, C., Manney, G. L., Nash, E. R., Potter, G. L., Tegtmeier, S., Wang, T., Wargan, K., and Wright, J. S.: Assessment of upper tropospheric and stratospheric water vapor and ozone in reanalyses as part of S-RIP, Atmos. Chem. Phys., 17, 12743–12778, https://doi.org/10.5194/acp-17-12743-2017, 2017. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kallberg, P., Koehler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. R. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011 (data available at: https://apps.ecmwf.int/archive-catalogue/?class=ei, last access: 15 May 2022). a
Dessler, A. E., Weinstock, E. M., Hintsa, E. J., Anderson, J. G., Webster, C. R., May, R. D., Elkins, J. W., and Dutton, G. S.: An examination of the total hydrogen budget of the lower stratosphere, Geophys. Res. Lett., 21, 2563–2566, https://doi.org/10.1029/94GL02283, 1994. a, b, c
Ehhalt, D. H., Rohrer, F., Blake, D. R., Kinnison, D. E., and Konopka, P.: On the use of nonmethane hydrocarbons for the determination of age spectra in the lower stratosphere, J. Geophys. Res., 112, D12208, https://doi.org/10.1029/2006JD007686, 2007. a
Engel, A., Strunk, M., Müller, M., Haase, H., Poss, C., Levin, I., and Schmidt, U.: Temporal development of total chlorine in the high-latitude stratosphere based on reference distributions of mean age derived from CO2 and SF6, J. Geophys. Res., 107, D12, https://doi.org/10.1029/2001JD000584, 2002. a
Engel, A., Möbius, T., Bönisch, H., Schmidt, U., Heinz, R., Levin, I., Atlas, E., Aoki, S., Nakazawa, T., Sugawara, S., Moore, F., Hurst, D., Elkins, J., Schauffler, S., Andrews, A., and Boering, K.: Age of stratospheric air unchanged within uncertainties over the past 30 years, Nat. Geosci., 2, 28–31, https://doi.org/10.1038/ngeo388, 2009. a, b, c
Engel, A., Bönisch, H., Ullrich, M., Sitals, R., Membrive, O., Danis, F., and Crevoisier, C.: Mean age of stratospheric air derived from AirCore observations, Atmos. Chem. Phys., 17, 6825–6838, https://doi.org/10.5194/acp-17-6825-2017, 2017. a, b
Fischer, H., Birk, M., Blom, C., Carli, B., Carlotti, M., von Clarmann, T., Delbouille, L., Dudhia, A., Ehhalt, D., Endemann, M., Flaud, J. M., Gessner, R., Kleinert, A., Koopman, R., Langen, J., López-Puertas, M., Mosner, P., Nett, H., Oelhaf, H., Perron, G., Remedios, J., Ridolfi, M., Stiller, G., and Zander, R.: MIPAS: an instrument for atmospheric and climate research, Atmos. Chem. Phys., 8, 2151–2188, https://doi.org/10.5194/acp-8-2151-2008, 2008. a
Frank, F., Jöckel, P., Gromov, S., and Dameris, M.: Investigating the yield of H2O and H2 from methane oxidation in the stratosphere, Atmos. Chem. Phys., 18, 9955–9973, https://doi.org/10.5194/acp-18-9955-2018, 2018. a
Fritsch, F., Garny, H., Engel, A., Bönisch, H., and Eichinger, R.: Sensitivity of age of air trends to the derivation method for non-linear increasing inert SF6, Atmos. Chem. Phys., 20, 8709–8725, https://doi.org/10.5194/acp-20-8709-2020, 2020. a, b, c
Fueglistaler, S. and Haynes, P. H.: Control of interannual and longer-term variability of stratospheric water vapor, J. Geophys. Res., 110, D24108, https://doi.org/10.1029/2005JD006019, 2005. a
Garcia, R. R. and Randel, W. J.: Acceleration of Brewer-Dobson circulation due to increase in greenhouse gases, J. Atmos. Sci., 65, 2731–2739, https://doi.org/10.1175/2008JAS2712.1, 2008. a
Garcia, R. R., Randel, W. J., and Kinnison, D. E.: On the Determination of Age of Air Trends from Atmospheric Trace Species, J. Atmos. Sci., 68, 139–154, https://doi.org/10.1175/2010JAS3527.1, 2011. a
Hall, T. M. and Plumb, R. A.: Age as a diagnostic of stratospheric transport, J. Geophys. Res., 99, 1059–1070, https://doi.org/10.1029/93JD03192, 1994. a, b, c
Harries, J.: Stratospheric chemistry topics, Hydrogen Budget, in: Encyclopedia of Atmospheric Sciences, edited by: North, G. R., Pyle, J., and Zhang, F., Academic Press, Oxford, 2nd Edn., 238–241, https://doi.org/10.1016/B978-0-12-382225-3.00388-1, 2015. a
Hauck, M., Fritsch, F., Garny, H., and Engel, A.: Deriving stratospheric age of air spectra using an idealized set of chemically active trace gases, Atmos. Chem. Phys., 19, 5269–5291, https://doi.org/10.5194/acp-19-5269-2019, 2019. a, b, c, d
Haynes, P. and Anglade, J.: The vertical scale cascade in atmospheric tracers due to large-scale differential advection, J. Atmos. Sci., 54, 1121–1136, https://doi.org/10.1175/1520-0469(1997)054<1121:TVSCIA>2.0.CO;2, 1997. a
Hegglin, M. I., Plummer, D. A., Shepherd, T. G., Scinocca, J. F., Anderson, J., Froidevaux, L., Funke, B., Hurst, D., Rozanov, A., Urban, J., von Clarmann, T., A.Walker, K., Wang, H. J., Tegtmeier, S., and Weigel, K.: Vertical structure of stratospheric water vapour trends derived from merged satellite data, Nat. Geosci., 7, 768–776, https://doi.org/10.1038/NGEO2236, 2014. a, b, c, d, e, f, g, h, i, j, k, l, m, n
Holton, J. R., Haynes, P., McIntyre, M. E., Douglass, A. R., Rood, R. B., and Pfister, L.: Stratosphere-troposphere exchange, Rev. Geophys., 33, 403–439, https://doi.org/10.1029/95RG02097, 1995. a
Konopka, P., Steinhorst, H.-M., Grooß, J.-U., Günther, G., Müller, R., Elkins, J. W., Jost, H.-J., Richard, E., Schmidt, U., Toon, G., and McKenna, D. S.: Mixing and Ozone Loss in the 1999–2000 Arctic Vortex: Simulations with the 3-dimensional Chemical Lagrangian Model of the Stratosphere (CLaMS), J. Geophys. Res., 109, D02315, https://doi.org/10.1029/2003JD003792, 2004. a, b
Konopka, P., Günther, G., McKenna, D. S., Müller, R., Offermann, D., Spang, R., and Riese, M.: How homogeneous and isotropic is stratospheric mixing? Comparison of CRISTA-1 observations with transport studies based on the Chemical Lagrangian Model of the Stratosphere (CLaMS), Q. J. R. Meteorol. Soc., 131, 565–579, https://doi.org/10.1256/qj.04.47, 2005. a
Konopka, P., Ploeger, F., Tao, M., Birner, T., and Riese, M.: Hemispheric asymmetries and seasonality of mean age of air in the lower stratosphere: Deep versus shallow branch of the Brewer-Dobson circulation, J. Geophys. Res., 120, 2053–2066, https://doi.org/10.1002/2014JD022429, 2015. a
Le Texier, H., Solomon, S., and Garcia, R. R.: The role of molecular hydrogen and methane oxidation in the water vapour budget of the stratosphere, Q. J. R. Meteorol. Soc., 114, 281–295, https://doi.org/10.1002/qj.49711448002, 1988. a
Leedham Elvidge, E., Bönisch, H., Brenninkmeijer, C. A. M., Engel, A., Fraser, P. J., Gallacher, E., Langenfelds, R., Mühle, J., Oram, D. E., Ray, E. A., Ridley, A. R., Röckmann, T., Sturges, W. T., Weiss, R. F., and Laube, J. C.: Evaluation of stratospheric age of air from CF4, C2F6, C3F8, CHF3, HFC-125, HFC-227ea and SF6; implications for the calculations of halocarbon lifetimes, fractional release factors and ozone depletion potentials, Atmo. Chem. Phys., 18, 3369–3385, https://doi.org/10.5194/acp-18-3369-2018, 2018. a
Li, F., Austin, J., and Wilson, J.: The Strength of the Brewer–Dobson Circulation in a Changing Climate: Coupled Chemistry–Climate Model Simulations, J. Clim., 21, 40–57, https://doi.org/10.1175/2007JCLI1663.1, 2008. a
Li, F., Waugh, D. W., Douglass, A. R., Newman, P. A., Pawson, S., Stolarski, R. S., Strahan, S. E., and Nielsen, J. E.: Seasonal variations in stratospheric age spectra in GEOSCCM, J. Geophys. Res., 117, D05134, https://doi.org/10.1029/2011JD016877, 2012. a
Linz, M., Plumb, R. A., Gerber, E. P., Haenel, F. J., Stiller, G., Kinnison, D., Ming, A., and Neu, J. L.: The strength of the meridional overturning circulation of the stratosphere, Nat. Geosci., 10, 663–667, https://doi.org/10.1038/ngeo3013, 2017. a
Lossow, S., Khosrawi, F., Nedoluha, G. E., Azam, F., Bramstedt, K., Burrows, Dinelli, B. M., Eriksson, P., Espy, P. J., García-Comas, M., Gille, J. C., Kiefer, M., Noël, S., Raspollini, P., Read, W. G., Rosenlof, K. H., Rozanov, A., Sioris, C. E., Stiller, G. P., Walker, K. A., and Weigel, K.: The SPARC water vapour assessment II: comparison of annual, semi-annual and quasi-biennial variations in stratospheric and lower mesospheric water vapour observed from satellites, Atmos. Meas. Tech., 10, 1111–1137, https://doi.org/10.5194/amt-10-1111-2017, 2017. a
Masarie, K. A., Steele, L. P., and Lang, P. M.: A rule-based expert system for evaluating the quality of long-term, in situ, gas chromatographic measurements of atmospheric methane, NOAA Tech. Memo. ERL CMDL-3, Climate Monitoring and Diagnostics Laboratory, Boulder, Colorado, https://repository.library.noaa.gov/view/noaa/21246, 1991. a
Maycock, A. C., Shine, K. P., and Joshi, M. M.: The temperature response to stratospheric water vapour changes, Q. J. R. Meteorol. Soc., 137, 1070–1082, https://doi.org/10.1002/qj.822, 2011. a
McCormick, M. P.: Sage II: An overview, Adv. Space Res., 7, 219–226, https://doi.org/10.1016/0273-1177(87)90151-7, 1987. a
McKenna, D. S., Konopka, P., Grooß, J.-U., Günther, G., Müller, R., Spang, R., Offermann, D., and Orsolini, Y.: A new Chemical Lagrangian Model of the Stratosphere (CLaMS): 1. Formulation of advection and mixing, J. Geophys. Res., 107, D16, https://doi.org/10.1029/2000JD000114, 2002a (data available at: https://jugit.fz-juelich.de/clams/CLaMS, last access: 1 July 2021). a, b, c
McKenna, D. S., Grooß, J.-U., Günther, G., Konopka, P., Müller, R., Carver, G., and Sasano, Y.: A new Chemical Lagrangian Model of the Stratosphere (CLaMS): 2. Formulation of chemistry scheme and initialization, J. Geophys. Res., 107, D15, https://doi.org/10.1029/2000JD000113, 2002b (data available at: https://jugit.fz-juelich.de/clams/CLaMS, last access: 1 July 2021). a
Müller, R., Kunz, A., Hurst, D. F., Rolf, C., Krämer, M., and Riese, M.: The need for accurate long-term water vapor measurements in the upper troposphere and lower stratosphere with global coverage, Earth's Future, 4, 25–32, https://doi.org/10.1002/2015EF000321, 2016. a
Nassar, R., Bernath, P. F., Boone, C. D., Manney, G. L., McLeod, S. D., Rinsland, C. P., Skelton, R., and Walker, K. A.: Stratospheric abundances of water and methane based on ACE-FTS measurements, Geophys. Res. Lett., 32, L15S04, https://doi.org/10.1029/2005GL022383, 2005. a
Newman, P. A., Daniel, J. S., Waugh, D. W., and Nash, E. R.: A new formulation of equivalent effective stratospheric chlorine (EESC), Atmos. Chem. Phys., 7, 4537–4552, https://doi.org/10.5194/acp-7-4537-2007, 2007. a
Noël, S., Weigel, K., Bramstedt, K., Rozanov, A., Weber, M., Bovensmann, H., and Burrows, J. P.: Water vapour and methane coupling in the stratosphere observed using SCIAMACHY solar occultation measurements, Atmos. Chem. Phys., 18, 4463–4476, https://doi.org/10.5194/acp-18-4463-2018, 2018. a
Ostermöller, J., Bönisch, H., Jöckel, P., and Engel, A.: A new time-independent formulation of fractional release, Atmos. Chem. Phys., 17, 3785–3797, https://doi.org/10.5194/acp-17-3785-2017, 2017. a
Ploeger, F. and Birner, T.: Seasonal and inter-annual variability of lower stratospheric age of air spectra, Atmos. Chem. Phys., 16, 10195–10213, https://doi.org/10.5194/acp-16-10195-2016, 2016. a, b
Ploeger, F., Abalos, M., Birner, T., Konopka, P., Legras, B., Müller, R., and Riese, M.: Quantifying the effects of mixing and residual circulation on trends of stratospheric mean age of air, Geophys. Res. Lett., 42, 2047–2054, https://doi.org/10.1002/2014GL062927, 2015. a
Pommrich, R., Müller, R., Grooß, J.-U., Konopka, P., Ploeger, F., Vogel, B., Tao, M., Hoppe, C. M., Günther, G., Spelten, N., Hoffmann, L., Pumphrey, H.-C., Viciani, S., D'Amato, F., Volk, C. M., Hoor, P., Schlager, H., and Riese, M.: Tropical troposphere to stratosphere transport of carbon monoxide and long-lived trace species in the Chemical Lagrangian Model of the Stratosphere (CLaMS), Geosci. Model Dev., 7, 2895–2916, https://doi.org/10.5194/gmd-7-2895-2014, 2014. a, b, c
Poshyvailo, L.: Lagrangian Simulation of Stratospheric Water Vapour: Impact of Large-Scale Circulation and Small-Scale Transport Processes, Vol. 503, Schriften des Forschungszentrums Jülich Reihe Energie & Umwelt/Energy & Environment, Forschungszentrum Jülich GmbH Zentralbibliothek, ISBN 978-3-95806-488-1, 2020. a
Poshyvailo, L., Müller, R., Konopka, P., Günther, G., Riese, M., Podglajen, A., and Ploeger, F.: Sensitivities of modelled water vapour in the lower stratosphere: temperature uncertainty, effects of horizontal transport and small-scale mixing, Atmos. Chem. Phys., 18, 8505–8527, https://doi.org/10.5194/acp-18-8505-2018, 2018. a, b
Raspollini, P., Belotti, C., Burgess, A., Carli, B., Carlotti, M., Ceccherini, S., Dinelli, B. M., Dudhia, A., Flaud, J.-M., Funke, B., Höpfner, M., López-Puertas, M., Payne, V., Piccolo, C., Remedios, J. J., Ridolfi, M., and Spang, R.: MIPAS level 2 operational analysis, Atmos. Chem. Phys., 6, 5605–5630, https://doi.org/10.5194/acp-6-5605-2006, 2006. a, b
Remsberg, E. E.: Methane as a diagnostic tracer of changes in the Brewer–Dobson circulation of the stratosphere, Atmos. Chem. Phys., 15, 3739–3754, https://doi.org/10.5194/acp-15-3739-2015, 2015. a
Riese, M., Ploeger, F., Rap, A., Vogel, B., Konopka, P., Dameris, M., and Forster, P.: Impact of uncertainties in atmospheric mixing on simulated UTLS composition and related radiative effects, J. Geophys. Res., 117, D16305, https://doi.org/10.1029/2012JD017751, 2012. a
Rind, D., Chiou, E.-W., Chu, W., Oltmans, S., Lerner, J., Larsen, J., McCormick, M. P., and McMaster, L.: Overview of the Stratospheric Aerosol and Gas Experiment II water vapor observations: Method, validation, and data characteristics, J. Geophys. Res.-Atmos., 98, 4835–4856, https://doi.org/10.1029/92JD01174, 1993. a
Röckmann, T., Grooß, J.-U., and Müller, R.: The impact of anthropogenic chlorine emissions, stratospheric ozone change and chemical feedbacks on stratospheric water, Atmos. Chem. Phys., 4, 693–699, https://doi.org/10.5194/acp-4-693-2004, 2004. a
Rosenlof, K. H.: Seasonal cycle of the residual mean meridional circulation in the stratosphere, J. Geophys. Res., 100, 5173–5191, https://doi.org/10.1029/94JD03122, 1995. a
Rosenlof, K. H., Tuck, A. F., Kelly, K. K., Russell III, J. M., and McCormick, M. P.: Hemispheric asymmetries in the water vapor and inferences about transport in the lower stratosphere, J. Geophys. Res., 102, 13213–13234, https://doi.org/10.1029/97JD00873, 1997. a
Russell III, J. M., Gordley, L. L., Park, J. H., Drayson, S. R., Hesketh, W. D., Cicerone, R. J., Tuck, A. F., Frederick, J. E., Harries, J. E., and Crutzen, P. J.: The Halogen Occultation Experiment, J. Geophys. Res., 98, 10777–10797, https://doi.org/10.1029/93JD00799, 1993. a, b
Scherer, M., Vömel, H., Fueglistaler, S., Oltmans, S. J., and Staehelin, J.: Trends and variability of midlatitude stratospheric water vapour deduced from the re-evaluated Boulder balloon series and HALOE, Atmos. Chem. Phys., 8, 1391–1402, https://doi.org/10.5194/acp-8-1391-2008, 2008. a
Schoeberl, M. R., Sparling, L. C., Jackman, C. H., and Fleming, E. L.: A Lagrangian view of stratospheric trace gas distributions, J. Geophys. Res., 105, 1537–1552, https://doi.org/10.1029/1999JD900787, 2000. a, b
Schoeberl, M. R., Douglass, A. R., Polansky, B., Boone, C., Walker, K. A., and Bernath, P.: Estimation of stratospheric age spectrum from chemical tracers, J. Geophys. Re.-Atmos., 110, D21303, https://doi.org/10.1029/2005JD006125, 2005. a, b, c
Solomon, S. and Albritton, D. L.: Time-dependent ozone depletion potentials for short- and long-term forecasts, Nature, 357, 33–37, https://doi.org/10.1038/357033a0, 1992. a
Solomon, S., Rosenlof, K., Portmann, R., Daniel, J., Davis, S., Sanford, T., and Plattner, G.-K.: Contributions of stratospheric water vapor to decadal changes in the rate of global warming, Science, 327, 1219–1223, https://doi.org/10.1126/science.1182488, 2010. a
Stiller, G. P., Fierli, F., Ploeger, F., Cagnazzo, C., Funke, B., Haenel, F. J., Reddmann, T., Riese, M., and von Clarmann, T.: Shift of subtropical transport barriers explains observed hemispheric asymmetry of decadal trends of age of air, Atmos. Chem. Phys., 17, 11177–11192, https://doi.org/10.5194/acp-17-11177-2017, 2017. a, b
Strunk, M., Engel, A., Schmidt, U., Volk, C. M., Wetter, T., Levin, I., and Glatzel-Mattheier, H.: CO2 and SF6 as sratospheric age tracers: consistency and the effect of mesospheric SF6 – loss, Geophys. Res. Lett., 27, 341–344, https://doi.org/10.1029/1999GL011044, 2000. a
Thomason, L. W., Poole, L. R., and Deshler, T.: A global climatoloy of stratospheric aerosol surface area density deduced from Stratospheric Aerosol and Gas Experiment II measurements: 1984–1994, J. Geophys. Res., 102, 8967–8976, https://doi.org/10.1029/96JD02962, 1997. a
Vogel, B., Feck, T., Grooß, J.-U., and Riese, M.: Impact of a possible future global hydrogen economy on Arctic stratospheric ozone loss, Energy Environ. Sci., 5, 6445–6452, https://doi.org/10.1039/C2EE03181G, minireview, 2012. a
von Clarmann, T. and Stiller, G.: Das Michelson Interferometer für Passive Atmosphärische Sondierung (MIPAS) auf dem Umweltforschungssarelliten ENVISAT, Nachrichten – Forschungszentrum Karlsruhe, 35, 41–45, https://publikationen.bibliothek.kit.edu/120054527, 2003. a
Waters, J. W., Read, W. G., Froidevaux, L., Jarnot, R. F., Cofield, R. E., Flower, D. A., Lau, G. K., Pickett, H. M., Santee, M. L., Wu, D. L., Boyles, M. A., Burke, J. R., Lay, R. R., Loo, M. S., Livesey, N. J., Lungu, T. A., Manney, G. L., Nakamura, L. L., Perun, V. S., Ridenoure, B. P., Shippony, Z., Siegel, P. H., Thurstans, R. P., Harwood, R. S., Pumphrey, H. C., and Filipiak, M. J.: The UARS and EOS Microwave Limb Sounder (MLS) Experiments, J. Atmos. Sci., 56, 194–218, https://doi.org/10.1175/1520-0469(1999)056<0194:TUAEML>2.0.CO;2, 1999. a
Waters, J. W., Froidevaux, L., Harwood, R. S., Jarnot, R. F., Pickett, H. M., Read, W. G., Siegel, P. H., Cofield, R. E., Filipiak, M. J., Flower, D. A., Holden, J. R., Lau, G. K., Livesey, N. J., Manney, G. L., Pumphrey, H. C., Santee, M. L., Wu, D. L., Cuddy, D. T., Lay, R. R., Loo, M. S., Perun, V. S., Schwartz, M. J., Stek, P. C., Thurstans, R. P., Boyles, M. A., Chandra, S., Chavez, M. C., Chen, G.-S., Chudasama, B. V., Dodge, R., Fuller, R. A., Girard, M. A., Jiang, J. H., Jiang, Y., Knosp, B. W., LaBelle, R. C., Lam, J. C., Lee, K. A., Miller, D., Oswald, J. E., Patel, N. C., Pukala, D. M., Quintero, O., Scaff, D. M., Snyder, W. V., Tope, M. C., Wagner, P. A., and Walch, M. J.: The Earth Observing System Microwave Limb Sounder (EOS MLS) on the Aura satellite, IEEE Trans. Geosci. Remote Sens., 44, 1075–1092, https://doi.org/10.1109/TGRS.2006.873771, 2006. a
Waugh, D. W. and Hall, T. M.: Age of stratospheric air: theory, observations, and models, Rev. Geophys., 40, 1–27, https://doi.org/10.1029/2000RG000101, 2002. a, b
WMO: Meteorology – a three-dimensional science, WMO Bull., VI, 134–138, https://library.wmo.int/doc_num.php?explnum_id=6960, 1957. a
Xiong, X., Barnet, C., Maddy, E., Sweeney, C., Liu, X., Zhou, L., and Goldberg, M.: Characterization and validation of methane products from the Atmospheric Infrared Sounder (AIRS), J. Geophys. Res.-Biogeo., 113, G00A01, https://doi.org/10.1029/2007JG000500, 2008. a
Xiong, X., Barnet, C., Maddy, E., Wofsy, S., Chen, L., Karion, A., and Sweeney, C.: Detection of methane depletion associated with stratospheric intrusion by atmospheric infrared sounder (AIRS), Geophys. Res. Lett., 40, 2455–2459, https://doi.org/10.1002/grl.50476, 2013. a
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Conclusions
- Appendix A: Stationary correlation function between FRF and modelled AoA
- Appendix B: Parameterization of AoA for idealized age spectrum calculations
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
model worlddifferent methods for estimating the mean age of air trends based on a combination of stratospheric water vapour and methane data. We also provide simple practical advice of a more reliable estimation of the mean age of air trends.
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Conclusions
- Appendix A: Stationary correlation function between FRF and modelled AoA
- Appendix B: Parameterization of AoA for idealized age spectrum calculations
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References





