A single-parameter hygroscopicity model for functionalized insoluble aerosol surfaces

The impact of molecular level surface chemistry for aerosol water-uptake and droplet growth is not well understood. In this work, spherical, nonporous, monodisperse polystyrene latex (PSL) particles treated with different surface functional groups are exploited to isolate the effects of aerosol surface chemistry for droplet activation. PSL is effectively water insoluble and changes in the particle surface may be considered a critical factor in the initial water uptake of water-insoluble material. The droplet growth of two surface modified types of PSL (PSL-NH₂ and PSL-COOH) along with plain PSL was measured in a supersaturated environment with a Cloud Condensation Nuclei Counter (CCNC). Three droplet growth models – traditional Köhler (TK), Flory–Huggins Köhler (FHK) and the Frenkel–Halsey–Hill adsorption theory (FHH-AT) were compared with experimental data. The experimentally determined single hygroscopicity parameter, κ, was found within the range from 0.002 to 0.04. The traditional Köhler prediction assumes Raoult's law solute dissolution and underestimates the water-uptake ability of the PSL particles. FHK can be applied to polymeric aerosol; however, FHK assumes that the polymer is soluble and hydrophilic. Thus, the FHK model generates a negative result for hydrophobic PSL and predicts non-activation behavior that disagrees with the experimental observation. The FHH-AT model assumes that a particle is water insoluble and can be fit with two empirical parameters (A_FHH and B_FHH). The FHH-AT prediction agrees with the experimental data and can differentiate the water uptake behavior of the particles owing to surface modification of PSL surface. PSL-NH₂ exhibits slightly higher hygroscopicity than the PSL-COOH, whereas plain PSL is the least hygroscopic among the three. This result is consistent with the polarity of surface functional groups and their affinity to water molecules. Thus, changes in A_FHH and B_FHH can be quantified when surface modification is isolated for the study of water-uptake. The fitted A_FHH for PSL-NH₂, PSL-COOH, and plain PSL is 0.23, 0.21, and 0.18 when B_FHH is unity. To simplify the use of FHH-AT for use in cloud activation models, we also present and test a new single parameter framework for insoluble compounds, κ_FHH. κ_FHH is within 5 % agreement of the experimental data and can be applied to describe a single-parameter hygroscopicity for water-insoluble aerosol with surface modified properties.

1 Introduction

Heterogeneous water-vapor condensation occurs for both soluble (Rose et al., 2008) and insoluble (Dalirian et al., 2018; Koehler et al., 2009; Kumar et al., 2009) particles. Traditionally, the cloud condensation nuclei (CCN) activation behavior has been described by Köhler theory (Köhler, 1936). In traditional Köhler (TK) theory, the droplet is assumed to be dilute, and the water activity follows Raoult's law; such that the water activity equals the water mole fraction, and the dilute droplet water activity coefficient is assumed to be unity. For water-soluble particles such as inorganic ammonium sulfate (Rose et al., 2008) and sucrose (Dawson et al., 2020; Gohil and Asa-Awuku, 2022), TK can predict their water uptake behavior. However, TK does not work as well for atmospherically relevant and abundant particles that are partially water soluble or water insoluble, less than a concentration of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$ (Kumar et al., 2009; Petters and Kreidenweis, 2008; Tang et al., 2016). Thus, alternative droplet growth models for the partial and insoluble particles are needed.

Flory–Huggins Köhler (FHK) (Petters et al., 2009) is one example of a droplet growth model specifically applied to the water-soluble polymers. FHK has been shown to work well for long-chained polymers such as gelatin, polyethylene glycol and polylactic acid (Mao et al., 2021; Petters et al., 2006, 2009). It uses a one fitting parameter that describes solvation and most recently was incorporated into a single-parameter hygroscopicity term that describes the water-uptake of water-soluble aerosol (Mao et al., 2021).

The droplet formation of water-insoluble particles has been previously described with adsorption activation models (Hatch et al., 2012; Kumar et al., 2009; Lintis et al., 2021; Malek et al., 2022; Navea et al., 2017; Pajunoja et al., 2015; Tang et al., 2016). Brunauer, Emmett, and Teller adsorption isotherm models are typically applied for multilayer adsorption analysis of water uptake on clays (Hatch et al., 2012) and fly ash (Navea et al., 2017). Lintis et al. (2021) applied the Dubinin–Serpinsky model for soot and concluded that nucleation occurred at oxidized and hydrophilic surface sites on the soot. Pajunoja et al. (2015) measured the TK hygroscopicity for SOA and demonstrated that the droplet growth of organic compounds with low O:C ratio was an adsorption-dominated process for both sub- and super-saturated water vapor conditions. Kumar et al. (2009) showed that the droplet activation of mineral dust could be described well using the Frenkel–Halsey–Hill adsorption theory (FHH-AT).

The FHH-AT determines droplet growth with the help of two empirical parameters defined as A_FHH and B_FHH (Sorjamaa and Laaksonen, 2007a). The parameter A_FHH is related to the interaction of the first layer of water and the particle surface, whereas the B_FHH represents the interaction between other layers of water molecules and the particles. Furthermore, it is postulated that A_FHH should range from 0.1 to 3.0, and B_FHH should be within the range 0.5 to 3.0 for mineral dust aerosols (Kumar et al., 2009). However, the reported and applied A_FHH and B_FHH parameters have varied significantly in the literature. For example, Karydis et al. (2017) used the FHH-AT model to simulate the aerosol indirect effect of insoluble mineral dust CCN with an A_FHH and B_FHH of 2.25±0.75, and 1.20±0.10 respectively. Furthermore, Karydis et al. (2017) concluded that the global CCN number would decrease 10 % for mineral dust with the use of those values. Hatch et al. (2014) measured montmorillonite dust and found that the A_FHH and B_FHH were 98±22 and 1.79±0.11 and the A_FHH and B_FHH were 75±17 and 1.77±0.11 for illite respectively. Particles of intermediate polarity and high porosity may lead to a higher CCN activity (Koehler et al., 2009) and Hatch et al. (2012) attributed the high value of A_FHH to the surface chemistry and the porosity of the clays.

Specifically, porosity leads to a higher perceived hygroscopicity because water molecules fill the microporous structure. Thus, it should be noted that in the aforementioned studies, the porosity of insoluble particles complicates the study of aerosol water-uptake and influences the role of aerosol chemistry that impacts the CCN activity. Moreover, the use of two parameters adds an additional degree of freedom that makes the direct comparison of different chemical species challenging; there may be multiple pairs of A_FHH and B_FHH solutions for a single compound with or without a porous structure. As a result, in the direct experimental measurement of the hygroscopicity of nonporous and spherical nuclei it is important to understand the adsorption water uptake ability of atmospheric aerosol.

To better understand the activation behavior of insoluble particles, we study the CCN activity of spherical, nonporous polystyrene latex (PSL) particles using the Cloud Condensational Nuclei Counter (CCNC) (Roberts and Nenes, 2005). PSL is a common material used for instrumentation calibration and model examination for aerosol optical properties (Miles et al., 2011; Pettersson et al., 2004; Singh et al., 2014). They are spherical, of uniform size, and do not dissolve in water. The surfaces of PSL particles are hydrophobic, but can be manufactured to have a high density of hydrophilic sites (Ottewill and Vincent, 1972). Different functional groups such as carboxyl (-COOH) or amine (-NH₂) groups can be added to the PSL surface to create hydrophilic adsorption sites. Previous studies have shown that surface chemistry of the insoluble particles affects ice nucleation (Cziczo et al., 2009; Koehler et al., 2009; Reitz et al., 2011; Sullivan et al., 2010). But little is known about the influence of surface chemistry for liquid cloud droplet activation.

To our knowledge, few studies have explored the effects of molecular level particle surface changes for CCN and droplet formation. Mainly, water-soluble aerosol that contributes solute to the solution and modifies droplet properties has been of great interest. Any changes at the surface of soluble aerosol are often overshadowed by the effects of solute dissolution if the solute is water soluble. Additionally, to understand the impacts of functionalized surfaces, the surface area or particle size of an aerosol must be well known. Given these constraints, spherical PSL aerosol with and without a functionalized surface provides an opportunity to advance the contributions of molecular surfaces to the discussion of water uptake.

In the following sections, we examine the impact of surface chemistry on the CCN activity in the TK, FHK, and the FHH-AT models. The first two models are generally applied to water-soluble compounds whereas the FHH-AT is for water-insoluble particles. Furthermore, FHK is specifically designed for high-molecular weight polymers such as PSL and therefore briefly considered. The following work also compares measurements with three hygroscopicity prediction models. Two single-parameter hygroscopicity representations have been previously derived using TK (Petters and Kreidenweis, 2007) and FHK (Mao et al., 2021) assumptions. Additionally, we derive a third theoretical hygroscopicity parameter using the FHH-AT model and analyze the role of surface chemistry in the adsorption-based hygroscopicity. Thus, the following data and analysis provide insight into the water-uptake of water-insoluble particles and the impact of surface modified functional groups for the perceived aerosol hygroscopicity and droplet formation.

2 Experimental procedure

2.1 Polystyrene latex composition and size

Four different particle sizes, ∼100, 200, 300, and 500 nm and three different PSL particles (plain, surface modified with amine functional group, -NH₂, and carboxyl functional group, -COOH), were purchased (Lab 261^®). The sizes provided by the manufacturer are determined with dynamic light scattering (DLS) techniques. In this study, we verify the size and report the electrical mobility measured particle size (D_d) of the PSL particles with a Differential Mobility Analyzer, DMA (TSI 3080) and Condensation Particle Sizer (TSI 3776) operated in size-scanning mode (Wang and Flagan, 1990). The measured geometric mean size was within ∼10 % difference of the manufacturer's reported particle sizes (Table 1).

Table 1 Important aerosol physical properties and parameters used to derive droplet growth.

It should be noted that the PSL solution from Lab 261^® contains Tween 20 surfactant; the surfactant is added to prevent coagulation. The atomized surfactant particles are much smaller than the PSL particles and form aerosol less than 100 nm. Thus, the majority of surfactant particles are excluded from the size-selected CCN measurement of the large PSL particles. The raw CCN data (Fig. S1 in the Supplement) shows only one sigmoid curve, indicating a uniform composition at the selected particle size. Moreover, the apparent hygroscopicity of surfactant particles, typically a hydrophilic polymer, is much larger than an insoluble polymer such as PSL. The measured TK hygroscopicity of Tween 20 is $\sim \mathrm{0.28}\pm \mathrm{0.05}$, whereas the measured TK hygroscopicity of the PSL particles varies from 0.002 to 0.02 (see Fig. 2) and thus the influence of the surfactant on the size-selected PSL aerosol is assumed negligible.

2.2 Aerosol generation

0.4 mL of the PSL particle solution was diluted in 50 mL ultra-purified water (Millipore^®, with conductivity <18.8 MΩ). Wet particles were then generated with a constant output atomizer (TSI, 3076). Wet droplets were then passed through two silica gel dryers and the relative humidity was 5 % after passing through the dryers. After drying, large particles were removed by a 0.71 cm impactor to prevent the multiple charging errors. Poly-disperse particles are charged and sampled by an electrostatic size classifier, specifically a Differential Mobility Analyzer (TSI, DMA 3080). The DMA was set to select the size of the PSL particles. The PSL particles are then passed through a Condensation Particle Counter (CPC, TSI 3776) with a flow rate of 0.3 L min⁻¹ and a CCNC. The particle density counted by the CPC is the condensation number concentration (CN) and is measured at a rate of 1 Hz. The sheath and sample flow ratio are 10:1 in both the CPC and the CCNC.

2.3 The critical supersaturation of PSL

The CCN activity for the selected particle size was measured with a continuous flow stream-wise thermal gradient Cloud Condensation Nuclei Counter (DMT CCN100) (Roberts and Nenes, 2005). A brief introduction is provided here and readers are directed to Roberts and Nenes (2005) for a more detailed discussion of the instrument. The CCNC is a column with a wet inner surface. Three thermal electrical controllers modify temperatures on the top, in the middle, and at the bottom of the CCNC column to establish a constant temperature gradient. A supersaturation is generated at the center of the column as air moves from the top to the bottom (Hoppel et al., 1979). The sampled particles in the CCNC column provide a surface for the occurrence of the heterogeneous condensation. An optical particle counter (OPC) at the bottom of the column counts the particles that form droplets greater than 0.75 µm and provides the CCN concentration every 1 Hz. Instrument supersaturations were achieved by modifying both inlet flowrate and the temperature gradient in the CCNC. Each supersaturation was calibrated using ammonium sulfate and Scanning Mobility CCN Analysis (SMCA) (Moore et al., 2010).

CCN activity is the ratio of the number of droplets to total aerosol ($\mathrm{CCN}/\mathrm{CN}$) measured at a given supersaturation and constant particle size (D_d). For each supersaturation, temperatures and flows are held constant for 10 min and CCN and CN data are measured every second. The CCN and CN concentration are then averaged in the 8th minute. The CCN activation for each sample is reported from 0.1 % to 1.4 % supersaturation. Critical supersaturation (s_c) for a given particle size (D_d) is defined at 50 % efficiency growth of the CCN (i.e., $\mathrm{CCN}/\mathrm{CN}=\mathrm{0.5}$). A smaller s_c for a constant D_d indicates that the particles are more hygroscopic. The s_c for all 12 PSL samples are listed in Table 1. The activation curves for all 12 PSL samples are provided in Fig. S1. The measured s_c and D_d values are used to compute and compare subsequent particle CCN activation and hygroscopicity.

3 Theory and analysis

The saturation ratio at the droplet surface can be generally described as follows:

$$\begin{array}{}\text{(1)}& S=a_{\mathrm{w}}\exp \left({\displaystyle \frac{A}{D}}\right);\text{and}A={\displaystyle \frac{\mathrm{4}{M}_{\mathrm{w}}{\mathit{\sigma }}_{\mathrm{w}}}{RT{\mathit{\rho }}_{\mathrm{w}}}},\end{array}$$

where S is the saturation ratio, a_w is the water activity of the solution, and D is the wet diameter of the droplet. The exponential term is known as the Kelvin term and describes the homogeneous nucleation of the droplet solvent. Thus, A is generally constant and is a function of the universal gas constant (R), the pure water droplet surface tension (σ_w), temperature (T), density (ρ_w), and molecular weight (M_w). Heterogeneous nucleation is considered in the water activity term. As aforementioned, for water-soluble inorganic salts and organics, e.g., ammonium sulfate and sucrose, the water activity is approximated with Raoult's law and the water mole fraction, x_w.

Petters and Kreidenweis (2007) employed Raoult's law to develop a single hygroscopicity parameter representation, κ, as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{1}}{a_{\mathrm{w}}}}=\mathrm{1}+\mathit{\kappa }{\displaystyle \frac{v_s}{v_{\mathrm{w}}}},\end{array}$$

where v_s is the total volume of the dry particle and v_w is the total volume of the water in a droplet. The κ in Eq. (2) is defined as the intrinsic hygroscopicity parameter of the compound, denoted by κ_int. If one assumes a dilute droplet, such that a_w=1, κ_int can be solved from known solute and solvent properties such that ${\mathit{\kappa }}_{\mathrm{int}}=v\frac{M_{\mathrm{w}}{\mathit{\rho }}_s}{M_s{\mathit{\rho }}_{\mathrm{w}}}$ (Sullivan et al., 2009), where M_w is the molecular weight of water, M_s is the molecular weight of the dry particle, ρ_w is the density of water, ρ_s is the density of the dry particle, v is the van't Hoff coefficient and is assumed to be one. If PSL is a polymer with ∼100 000 g mol⁻¹ molecular weight and a density of 1.06 g cm⁻³, κ_int∼0.0002, is a small number and approaches zero. One can also derive a hygroscopicity parameter based on TK, κ_TK, directly from measured experimental s_c and D_d data (Petters and Kreidenweis, 2007)

$$\begin{array}{}\text{(3)}& {\mathit{\kappa }}_{\mathrm{TK}}={\displaystyle \frac{\mathrm{4}{A}^{\mathrm{3}}}{\mathrm{27}{D}_{\mathrm{d}}^{\mathrm{3}}{\ln }^{\mathrm{2}}{s}_{\mathrm{c}}}},\end{array}$$

with ${\mathit{\kappa }}_{\mathrm{int}}={\mathit{\kappa }}_{\mathrm{TK}}=\mathrm{0.604}$ for ammonium sulfate (Rose et al., 2008). The intrinsic and experimentally derived values also agree well for water-soluble compounds and partially soluble organics (Dawson et al., 2020; Peng et al., 2021, 2022).

Traditional Köhler theory calculations from theory and measurement tend to disagree for high molecular weight organics, such as polymers (Petters et al., 2006, 2009). To calculate the water activity of high molecular weight compounds, Petters et al. (2006, 2009) combined the water activity of Flory–Huggins (Flory, 1942) with the Köhler theory for polymeric aerosols. Mao et al. (2021) derived a single-parameter-based hygroscopicity representation, κ_FHK as follows:

$$\begin{array}{}\text{(4)}& {\mathit{\kappa }}_{\mathrm{FHK}}={\displaystyle \frac{\mathrm{1}-\mathit{\phi }}{\mathit{\phi }}}\left[-\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{\left(\mathrm{1}-\mathit{\phi }\right)\exp \left[\left(\mathrm{1}-F\right)\mathit{\phi }+\mathit{\chi }{\mathit{\phi }}^{\mathrm{2}}\right]}}\right],\end{array}$$

where φ is the volume fraction of the polymer, F is the reciprocal of the chain segments of the polymer equal to the ratio of the molecular volume of water and the solute, and χ is the Flory–Huggins interaction parameter. Measured particle diameter, D_d, and s_c data are used to define empirical fits of χ and subsequently determine, κ_FHK.

Insoluble aerosol droplet activation is best described by an adsorption thermodynamic droplet growth model (Kumar et al., 2009). Sorjamaa and Laaksonen (2007a), suggested the FHH-AT to define the a_w using the isotherm as follows:

$$\begin{array}{}\text{(5)}& a_{\mathrm{w}}=\exp \left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)\text{and}\mathit{\theta }={\displaystyle \frac{D-D_{\mathrm{d}}}{\mathrm{2}{D}_{\mathrm{w}}}},\end{array}$$

where θ is the surface coverage, and describes the layers of water molecules adsorbed on to the dry particle surface (Sorjamaa and Laaksonen, 2007b). D_w is the diameter of a single water molecule and is equal to 0.275 nm. A_FHH and B_FHH are compound specific empirical parameters. The FHH-AT parameters can be estimated by fitting the FHH-AT with s_c and D_d CCN measurement data (Herich et al., 2009; Kumar et al., 2009).

To date, a single parameter hygroscopicity representation based on adsorption droplet growth does not exist in the current literature. In this work, we derive an experimental and theoretical adsorption hygroscopicity, κ_FHH,exp and κ_FHH,the respectively. If the critical wet droplet diameter, D_p,c, is known, κ_FHH,exp can then be expressed as a function of D_d and D_p,c as follows:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{\mathit{\kappa }}_{\mathrm{FHH},\exp }=& f\left(D_{\mathrm{d}},D_{p,\mathrm{c}}\right)\\ =& {\displaystyle \frac{\mathrm{6}\mathit{\theta }{D}_{\mathrm{w}}}{D_{\mathrm{d}}}}\left({\displaystyle \frac{\mathrm{1}}{\exp \left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)}}-\mathrm{1}\right).\end{array}\end{array}$$

Theoretically, droplet activation occurs when the derivative of the Köhler curve is equal to zero $\left(\frac{\mathrm{d}S}{\mathrm{d}{D}_{p,\mathrm{c}}}=\mathrm{0}\right)$. Hence, the relation between critical surface coverage and the dry particle size is constrained by the following equation:

$$\begin{array}{}\text{(7)}& \mathrm{1}-{\displaystyle \frac{\mathrm{2}{\mathit{\theta }}_{\mathrm{c}}{D}_{\mathrm{w}}}{D_{\mathrm{d}}}}={\left({\displaystyle \frac{\mathrm{2}A{D}_{\mathrm{w}}}{A_{\mathrm{FHH}}{B}_{\mathrm{FHH}}{D}_{\mathrm{d}}^{\mathrm{2}}}}\right)}^{\mathrm{1}/\mathrm{2}}{\mathit{\theta }}_{\mathrm{c}}^{\frac{B_{\mathrm{FHH}}+\mathrm{1}}{\mathrm{2}}}.\end{array}$$

The critical surface coverage, θ_c, is defined at the point where droplet activation occurs, and is obtained by solving Eq. (7). As a result, the theoretical hygroscopicity of the FHH-AT is derived:

$$\begin{array}{}\text{(8)}& {\mathit{\kappa }}_{\mathrm{FHH},\mathrm{the}}=f\left(D_{\mathrm{d}}\right)={\displaystyle \frac{\mathrm{6}{D}_{\mathrm{w}}}{D_{\mathrm{d}}}}{A}_{\mathrm{FHH}}{\mathit{\theta }}_{\mathrm{c}}^{-B_{\mathrm{FHH}}+\mathrm{1}}.\end{array}$$

Readers should refer to Appendix A for additional derivation details.

4 Results and discussion

4.1 The CCN activity for different types of PSL

Table 1 shows the mobility diameter of PSL and their corresponding critical supersaturation. Particle size matters most for water-uptake and thus larger particles (∼500 nm) exposed to a constant supersaturation activate earlier than smaller aerosol (∼100 nm) (Dusek et al., 2006). For example, PSL-NH₂ particles with diameters of 85 nm activate at 1.42 % supersaturation whereas particles with a diameter of 375 nm activate at 0.33 % supersaturation. PSL-COOH and the plain PSL show a similar trend as well. The data suggest that PSL particles are wettable and hygroscopic, more so than particles with κ=0. The parameters in Table 1 are used to predict CCN activation (s_c–D_d pairs) in Fig. 1a and b. The dashed red line in Fig. 1 shows the traditional Köhler prediction for ammonium sulfate (κ_int=0.604) for comparison purposes. All PSL particles are much less hygroscopic than ammonium sulfate (κ_int=0.604) with larger hygroscopicity than theoretical values derived from known solute properties (κ_int=0.0002). Traditional Köhler theory significantly underpredicts particle activation and droplet growth of PSL particles.

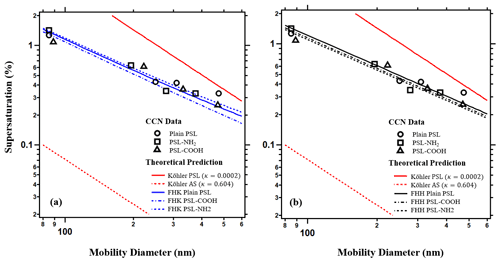
Figure 1 The s_c–D_d data for different types of PSL. The dashed red line is the tradition Köhler prediction for ammonium sulfate (κ=0.604). All types of PSL particles are more hygroscopic than the intrinsic hygroscopicity (κ_int=0.0002, solid red line). (a) Blue lines show the prediction from FHK. (b) Black lines show the prediction from FHH-AT model, with B_FHH=1.

Table 1 also shows the fitted parameters for the FHK and FHH-AT models required to subsequently calculate κ_FHK and κ_FHH,the. Both FHK and FHH-AT models have additional degrees of freedom compared with the traditional Köhler theory. In the FHK model, the molar volume becomes negligible and the water–polymer interaction parameter (χ), drives the droplet activation. χ describes the repulsive and attractive force between the solvent and the polymer. A χ smaller than 0.5 is an indication of miscibility and that water is a “good solvent” (Pethrick, 2003). χ is the only empirical free parameter in this study and when fitted to all three types of PSL, χ>0.5 and confirms the assumption that PSL particles are water insoluble. In Fig. 1a, the FHK model with only one free fitting parameter more closely agrees with experimental data than the TK theory (solid red lines).

Two empirical parameters (A_FHH and B_FHH) for the FHH-AT model are reported for each type of the PSL. The FHH-AT model with two degrees of freedom agrees with the experimental data better than the traditional Köhler theory model (Fig. 1b). However, multiple solutions of A_FHH and B_FHH may exist. The fit results for plain type PSL estimate A_FHH=0.17 and B_FHH=0.99; A_FHH is 0.3 and B_FHH is 1.08 for the carboxyl functional group modified PSL; A_FHH is 0.11 and B_FHH is 0.83 for the amine functional group modified PSL. Differences in the A_FHH and B_FHH values confirm that the FHH-AT model is sensitive to molecular level chemistry and can distinguish changes in surface chemistry. PSL-COOH shows a higher attraction to water molecules than the plain PSL. However, PSL-NH₂ is the most hygroscopic among the three types of PSL and the A_FHH=0.11 and the B_FHH=0.83 of PSL-NH₂ are the lowest values among all three types. If A_FHH represents the interaction between the first layer water molecules and the surface of the PSL particles, a higher A_FHH value implies higher attractive forces. Thus, the unconstrained FHH-AT parameter solutions must be reassessed.

The only chemical difference between the three types of PSL is due to surface modification. The attraction force between the particle core and the layers of the water molecules should be the same. Thus, a second constrained best-fit solution exists if we restrict B_FHH=1 (Table 1). The constrained and fitted A_FHH is 0.18 for plain PSL, 0.21 for PSL-COOH, and 0.23 for PSL-NH₂ (Table 1, Fig. 1b). With the constrained solution, the higher A_FHH is consistent with the most hygroscopic aerosol species. In Fig. 1b, the FHH-AT model prediction agrees well with the experimentally measured s_c–D_d data more than traditional Köhler Theory. This agreement with data is true for both the best-fit constrained (B_FHH=1, Fig. 1b) and unconstrained A_FHH and B_FHH values (not shown).

4.2 The impact of surface chemistry to hygroscopicity of PSL

The perceived single-parameter hygroscopicity, κ_TK, and the κ_FHH, can be derived from the traditional Köhler and FHH-AT models respectively (Fig. 2). In TK, the theoretical hygroscopicity is a constant value independent of the size of the particles. In Fig. 2a, the solid horizontal red line shows κ_int=0.0002. The red open symbols (circle, square, and triangle) are the hygroscopicity from measured data (Eq. 3) of the respective PSL particles. The experimental κ_TK values from traditional Köhler theory range from 0.002 to 0.04. Additionally, κ_TK of the PSL are size dependent and are larger than κ_int. Thus, TK should not be applied to predict the droplet growth and single-parameter hygroscopicity of insoluble PSL particles.

Figure 2 The single hygroscopicity parameter predicted from FHH-AT and traditional Köhler theory. Köhler theory from intrinsic properties (solid red line) predicts a constant hygroscopicity across particle sizes and hygroscopicity derived from experimental data (open symbols) shows size dependence. Hygroscopicity derived from the FHH-AT model from theory (solid black lines) and from experimental data (black symbols) are size dependent and agree well. Hygroscopicity derived from the FHH-AT model is also sensitive to functional surface chemistry.

In addition, FHK should not be used to predict droplet growth of PSL. Although the FHK model agrees well with s_c–D_d data (Fig. 1a), the derived hygroscopicity is problematic and nonsensical (and is therefore not shown). FHK assumes that the hydrophilic polymer swells in the water droplet and the interaction parameter represents the molecular force between water and polymer. χ values larger than 0.5 derived from PSL-NH₂, PSL-COOH and plain PSL subsequently estimate negative and implausible κ_FHK values. The experimental data indicate that the PSL does indeed grow into droplets and have a positive hygroscopicity. Thus, FHK should not be applied to water-insoluble polymers like PSL.

The hygroscopicity values derived from the FHH-AT model are plausible and show the best agreement between theory and experiment (Fig. 2). Both theoretical (κ_FHH,the) and experimental (κ_FHH,exp) hygroscopicity values from the FHH-AT model are less than the κ_TK (red open symbols), but higher than a constant κ_int value of 0.0002. κ_FHH,exp and κ_FHH,the for all 12 PSL samples are within 5 % of each other. The small deviation between κ_FHH,the and κ_FHH,exp demonstrates that the adsorption model is best for PSL. For insoluble particles, the experimental single-parameter hygroscopicity is size dependent and decreases with an increasing diameter (Fig. 2). This is because the core does not dissolve, and the total volume of the dry particle (Eq. 2) does not fully participate in the water uptake. The particle surface of an insoluble particle is proportional to the square of the size and dominates the adsorption-based water activation behavior. However, the single-parameter hygroscopicity is defined by the volume ratio of the solute and the solvent, which is proportional to the cube of the size. In adsorption-driven growth, the core inactive particle volume enlarges when the particle size increases and as a result the perceived size dependence in the experimental hygroscopicity is exhibited. The FHH-AT model accounts for the core volume contribution to the water activation in the B_FHH parameter. In the special case of PSL particles,B_FHH happens to be 1 (Table1), hence the κ_FHH,the is directly the reciprocal of the dry size (Eq. 8). κ_FHH,the accurately describes the inactive core volume behavior, demonstrating a decrease in hygroscopicity with an increasing particle size. Larger particles still activate earlier than smaller particles. For example, 500-nm particles activate earlier than 100-nm particles at 0.3 % supersaturation owing to a larger surface area, which provides more active sites for adsorption. Moreover, FHH-AT hygroscopicity is also sensitive to the small differences in surface chemistry. The theoretical prediction for the CCN activation of PSL-NH₂ particles (the dashed line) is larger than PSL–COOH (dashed-dotted line), whereas the plain PSL is the lowest (solid line).

5 Summary and implications

PSL particles are spherical, insoluble, nonporous, and mono-dispersed, and their surface can be modified to be hydrophilic or hydrophobic. The performance of the adsorption model is better than the traditional Köhler for PSL particles; experimentally derived κ_TK predicts a higher hygroscopicity and κ_int approaches zero. κ_FHK is negative for the insoluble particles and is inconsistent with the growing droplets. The single-parameter hygroscopicity of the FHH-AT model replicates the small differences of the functionalized surface. κ_FHH,exp and κ_FHH,the have only a 5 % difference. κ_FHH,the decreases with an increasing particle size, demonstrating the inactivity of the inner core of larger particles.

Using a droplet growth model with additional degrees of freedom improves the droplet growth prediction of PSL. The FHH-AT model is typically applied to effectively water-insoluble particles and the adsorption model agrees well with the experimental droplet growth data for hydrophobic and hydrophilic functionalized surfaces. This finding is consistent with the current body of work, which highlights the bulk aerosol composition as a critical factor in aerosol water uptake. However, the addition of polar functional groups to the surface of the water-insoluble particle exhibits discernible differences in activation and suggests that for atmospheric insoluble aerosol (e.g., soot, mineral dust) the modified surface chemistry should not be ignored.

We found from experiments that B_FHH was ≈1 for pure and coated PSL particles. This implied that for the samples studied in this work, B_FHH could be constrained to 1 to determine the A_FHH and postulate the contribution of surface chemistry to CCN activation. The method of constraining B_FHH can distinguish both the surface modification and potential coatings when the B_FHH of the core is known. If B_FHH of the pure core is known, only A_FHH needs to be measured and accounted for to estimate water uptake ability. Furthermore, it was found that if both A_FHH and B_FHH are left unconstrained, the values of A_FHH come out to be within 5 % of the A_FHH when B_FHH is constrained. It is also important to note from Eq. (A10) that the κ_FHH depends only on the surface properties of the compound (A_FHH) when B_FHH is constrained to unity. This can imply that the hygroscopic properties of the compound will only depend on the hydrophilic or hydrophobic properties of the functionalized surface regardless of the bulk properties if B_FHH is constrained to unity. In other words, extensions of this work could potentially apply A_FHH water-adsorption properties to similarly functionalized surfaces with different particle core compositions (i.e., varying B_FHH).

The findings presented here may be extended to atmospherically relevant insoluble particles that may be either coated or surface oxidized during different chemical processes. In ambient measurement, the composition of the surface and core is quite rarely simultaneously known; single-particle measurements are required to discern the individual composition and morphology. Thus, the singular κ_FHH value provides an important utility. Regardless of whether the FHH-AT model is constrained, κ_FHH reduces the degrees of freedom of the model and can discern changes in surface chemistry. It should be noted that the extent to which the adsorption-driven droplet growth can be applied to increasingly hydrophilic aerosol is uncertain but has been explored. Readers who are interested in the adsorption-driven water uptake ability of partially soluble compounds are referred to a companion paper by Gohil et al. (2022). In summary, water-insoluble aerosols can adsorb water and if their surfaces have been oxidized or functionalized with polar groups the aerosol can enhance their efficiency for water-uptake.

Appendix A

A typical droplet growth model is expressed as

$$\begin{array}{}\text{(A1)}& S=a_{\mathrm{w}}\cdot \exp \left({\displaystyle \frac{A}{D_p}}\right),\end{array}$$

where S is saturation, a_w is the water activity of the solution, and D_p is the diameter of the droplet. A is a coefficient related to pure water droplet properties, which is given as

$$\begin{array}{}\text{(A2)}& A={\displaystyle \frac{\mathrm{4}{M}_{\mathrm{w}}{\mathit{\sigma }}_{\mathrm{w}}}{RT{\mathit{\rho }}_{\mathrm{w}}}},\end{array}$$

where M_w is the molecular weight of water, R is the gas constant, T is the temperature and ρ_w is the density of water. σ_w is the surface tension of the droplet and is assumed to be the same as that of pure water.

If the solute is effectively insoluble, then the water activity term is expressed using the FHH-AT isotherm as

$$\begin{array}{}\text{(A3)}& a_{\mathrm{w}}=\exp \left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right),\end{array}$$

where θ is the surface coverage term and is related to a_w with the help of compound-specific empirical parameters (A_FHH,B_FHH). A simplified representation of θ is given as

$$\begin{array}{}\text{(A4)}& \mathit{\theta }={\displaystyle \frac{D_p-D_{\mathrm{d}}}{\mathrm{2}{D}_{\mathrm{w}}}},\end{array}$$

where D_p is the droplet size, D_d is the dry particle size, and D_w is the diameter of one water molecule. Equation (A3) can be equated with the a_w parameterization defined in terms of the single hygroscopicity parameter (κ), which is expressed as

$$\begin{array}{}\text{(A5)}& a_{\mathrm{w}}=\exp \left(-A_{\mathrm{FHH}}\cdot {\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)={\left[\mathrm{1}+\mathit{\kappa }\cdot {\displaystyle \frac{{\mathit{\nu }}_s}{{\mathit{\nu }}_{\mathrm{w}}}}\right]}^{-\mathrm{1}}.\end{array}$$

Rearranging Eq. (A5) provides the expression for κ_FHH as

$$\begin{array}{}\text{(A6)}& {\mathit{\kappa }}_{\mathrm{FHH}}={\displaystyle \frac{\mathrm{6}\mathit{\theta }{D}_{\mathrm{w}}}{D_{\mathrm{d}}}}\left({\displaystyle \frac{\mathrm{1}}{\exp \left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)}}-\mathrm{1}\right).\end{array}$$

Equation (A6) is the function of the measured D_d and D_p derived corresponding to the point of activation. Equation (A6) can be further simplified by making physically relevant mathematical assumptions for Eq. (A5). The right-hand side of Eq. (A5) can be simplified using the Taylor series expansion for an exponential function such that

$$\begin{array}{}\text{(A7)}& \begin{array}{rl}& \exp \left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)\\ & =\mathrm{1}+\left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)+{\left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)}^{\mathrm{2}}\\ & +{\left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)}^{\mathrm{3}}+\mathrm{\dots }.\end{array}\end{array}$$

As $-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\ll \mathrm{1}$, Eq. (A7) can be rewritten as

$$\begin{array}{}\text{(A8)}& \exp \left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)\approx \mathrm{1}+\left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right).\end{array}$$

The left-hand side of Eq. (A5) can be simplified under the assumption that v_w≫v_s such that

$$\begin{array}{}\text{(A9)}& {\left[\mathrm{1}+\mathit{\kappa }\cdot {\displaystyle \frac{v_s}{v_{\mathrm{w}}}}\right]}^{-\mathrm{1}}\approx \mathrm{1}-\mathit{\kappa }\cdot {\displaystyle \frac{v_s}{v_{\mathrm{w}}}}.\end{array}$$

Combining Eqs. (A8) and (A9) provides a reduced theoretical expression for κ_FHH:

$$\begin{array}{}\text{(A10)}& {\mathit{\kappa }}_{\mathrm{FHH},\mathrm{the}}={\displaystyle \frac{\mathrm{6}{D}_{\mathrm{w}}}{D_{\mathrm{d}}}}{A}_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}+\mathrm{1}}.\end{array}$$

Equation (A10) contains θ defined as the point of activation such that θ=θ_c. θ_c is determined by taking the first derivative of Eq. (A1) and equating it to 0 to represent the point of activation such that

$$\begin{array}{}\text{(A11)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}S}{\mathrm{d}{D}_p}}={\displaystyle \frac{\mathrm{d}}{\mathrm{d}{D}_p}}(& -A_{\mathrm{FHH}}\cdot {\left[{\displaystyle \frac{D_p-D_{\mathrm{d}}}{\mathrm{2}\cdot D_{\mathrm{w}}}}\right]}^{-B_{\mathrm{FHH}}}\\ & \cdot \exp \left({\displaystyle \frac{A}{D}}\right))=\mathrm{0},\end{array}\end{array}$$

$$\begin{array}{}\text{(A12)}& \mathrm{1}-{\displaystyle \frac{\mathrm{2}{\mathit{\theta }}_{\mathrm{c}}{D}_{\mathrm{w}}}{D_{\mathrm{d}}}}={\left({\displaystyle \frac{\mathrm{2}A{D}_{\mathrm{w}}}{A_{\mathrm{FHH}}{B}_{\mathrm{FHH}}{D}_{\mathrm{d}}^{\mathrm{2}}}}\right)}^{\mathrm{1}/\mathrm{2}}{\mathit{\theta }}_{\mathrm{c}}^{\frac{B_{\mathrm{FHH}}+\mathrm{1}}{\mathrm{2}}}.\end{array}$$