In situ and satellite-based estimates of cloud properties and aerosol–cloud interactions over the southeast Atlantic Ocean

In situ cloud probe data from the NASA ObseRvations of Aerosols above CLouds and their intEractionS (ORACLES) field campaign were used to estimate the effective radius (R_e), cloud optical thickness (τ), and cloud droplet concentration (N_c) for marine stratocumulus over the southeast Atlantic Ocean. The in situ R_e, τ, and N_c were compared with co-located Moderate Resolution Imaging Spectroradiometer (MODIS) retrievals of R_e and τ and MODIS-derived N_c. For 145 cloud profiles, a MODIS retrieval was co-located with in situ data with a time gap of less than 1 h. On average, the MODIS R_e and τ (11.3 µm and 11.7) were 1.6 µm and 2.3 higher than the in situ R_e and τ with Pearson's correlation coefficients (R) of 0.77 and 0.73, respectively. The average MODIS N_c (151.5 cm⁻³) was within 1 cm⁻³ of the average in situ N_c with an R of 0.90.

The 145 cloud profiles were classified into 67 contact profiles where an aerosol concentration (N_a) greater than 500 cm⁻³ was sampled within 100 m above cloud tops and 78 separated profiles where N_a less than 500 cm⁻³ was sampled up to 100 m above cloud tops. Contact profiles had a higher in situ N_c (by 88 cm⁻³), higher τ (by 2.5), and lower in situ R_e (by 2.2 µm) compared to separated profiles. These differences were associated with aerosol–cloud interactions (ACI), and MODIS estimates of the differences were within 5 cm⁻³, 0.5, and 0.2 µm of the in situ estimates when profiles with MODIS R_e>15 µm or MODIS τ>25 were removed. The agreement between MODIS and in situ estimates of changes in R_e, τ, and N_c associated with ACI was driven by small biases in MODIS retrievals of cloud properties relative to in situ measurements across different aerosol regimes. Thus, when combined with estimates of aerosol location and concentration, MODIS retrievals of marine stratocumulus cloud properties over the southeast Atlantic can be used to study ACI over larger domains and longer timescales than possible using in situ data.

1 Introduction

Uncertainties in the effective radiative forcing due to aerosol–cloud interactions (ACI) lead to variability in climate model estimates of the earth's energy budget in future climate scenarios (e.g., Boucher et al., 2013). The ACI for warm, low-level clouds are particularly important due to their dominating impact on the aerosol indirect forcing (Christensen et al., 2016). Further, the shortwave cloud radiative forcing of −17.1 W m⁻² (Loeb et al., 2009) is largely driven by the ubiquitous low-level clouds (Hartmann et al., 1992). Marine stratocumulus is the most common type of low-level cloud, with an annual mean coverage of 23 % of the earth's ocean surface (Wood, 2012). The radiative forcing due to well-mixed greenhouse gases (+2.83 W m⁻²) (Myhre et al., 2013) or the doubling of the CO₂ concentration (about +2.5 W m⁻²) could be offset by the radiative forcing from just a 15 % to 20 % reduction in droplet size for low clouds (Slingo, 1990). Low-level clouds are thus strong modulators of planetary albedo and global climate.

ACI lead to changes in the cloud radiative forcing through processes that impact cloud extinction (β) and optical thickness (τ), which are closely related to microphysical properties such as cloud droplet concentration (N_c), effective radius (R_e), and liquid water content (LWC). Cloud radiative forcing is a strong function of R_e, which represents the mean droplet size retrieved from radiative transfer calculations (Hansen and Travis, 1974). An increase in aerosol concentration (N_a) can increase the number of cloud condensation nuclei and lead to a higher N_c and lower R_e when LWC remains constant. These aerosol-induced changes in N_c and R_e lead to clouds with a higher reflectance or τ, which results in an indirect radiative forcing (Twomey, 1974, 1977). These changes in N_c and R_e can lead to adjustments in precipitation formation processes and an increase in cloud lifetime (Albrecht, 1989). An increase in τ and a decrease in precipitation rates associated with these ACI were observed for marine stratocumulus clouds over the southeast Atlantic Ocean (Gupta et al., 2021, hereafter “G21”; Gupta et al., 2022, hereafter “G22”).

However, ACI are often masked by meteorological conditions (Mauger and Norris, 2007), cloud adjustments to increasing N_a such as invigoration (Douglas and L'Ecuyer, 2021) or nonlinear liquid water path (LWP) responses to changes in N_c (Gryspeerdt et al., 2019), and the modulation of aerosol properties by clouds and precipitation (Wood et al., 2012). These confounding influences can be reduced by constraining meteorological variables that affect LWP and by comparing clouds with similar LWPs or low precipitation rates (e.g., McCoy et al., 2020; G22). Uncertainties in estimating the impact of ACI on cloud albedo are also driven by differences between process scales for ACI and the resolution of climate models or satellite retrievals (McComiskey and Feingold, 2012). The inconsistency in ACI estimates due to the scale differences is addressed by combining satellite retrievals with airborne observations for specific regimes such as marine stratocumulus clouds (Painemal and Zuidema, 2011, hereafter “PZ11”).

A regime of interest for ACI exists over the southeast Atlantic Ocean, where an extensive stratocumulus deck is overlaid by biomass burning aerosols from southern Africa (Haywood et al., 2004; Adebiyi and Zuidema, 2016). The biomass burning aerosols exert a direct radiative forcing by absorbing solar radiation (Cochrane et al., 2019), and heating due to the aerosol absorption can impact atmospheric stability (Cochrane et al., 2022). Changes in the thermodynamic profile can lead to changes in cloud properties and result in a semi-direct forcing (Johnson et al., 2004; McFarquhar and Wang, 2006; Wilcox, 2010). Climate models struggle to simulate these radiative effects and the altitude of the above-cloud aerosol layer over the southeast Atlantic, leading to biases in model estimates of low-cloud feedbacks and ACI (Das et al., 2020; Mallet et al., 2021).

Airborne campaigns have been conducted over the southeast Atlantic since 2016 to understand the ACI in this region and their impact on the global climate (Zuidema et al., 2016; Formenti et al., 2019; Haywood et al., 2021). During the NASA ObseRvations of Aerosols above CLouds and their intEractionS (ORACLES) field campaign (Redemann et al., 2021), in situ measurements of cloud droplet size distributions, from which N_c, R_e, and τ can be estimated, were collected over the southeast Atlantic at locations with contact or separation between the base of the aerosol layer and stratocumulus cloud tops. Variable vertical separation between the aerosol and cloud layers was associated with aerosol-induced changes in N_c, R_e, and τ (G21) and precipitation suppression (G22). Satellite retrievals of N_c, R_e, and τ and aerosol-induced changes in N_c, R_e, and τ could enable such investigations of ACI over larger domains and longer timescales than in situ measurements.

The Earth Observing System Terra and Aqua satellites provide global coverage of cloud microphysical properties using the Moderate Resolution Imaging Spectroradiometer (MODIS). MODIS acquires data for 36 atmospheric bands from 0.4 to 14.4 µm, including a non-absorbing band (0.86 µm over ocean) which provides information on τ and a water absorbing band (1.6, 2.1, or 3.7 µm) which provides information on R_e (Platnick et al., 2003). Reflectance pairs from these bands allow simultaneous retrievals of R_e and τ (Nakajima and King, 1990). In the absence of direct retrievals, MODIS N_c can be estimated assuming adiabatic LWC (Brenguier et al., 2000; Szczodrak et al., 2001). However, MODIS retrievals of cloud properties have biases relative to in situ N_c, R_e, and τ that depend on the cloud type and sampling strategy (Gryspeerdt et al., 2022; Fu et al., 2022), the occurrence of drizzle (Zinner et al., 2010), the width and shape of the droplet size distribution (Chang and Li, 2002; Brenguier et al., 2011), the vertical profile of R_e (McFarquhar and Heymsfield, 1998; Platnick, 2000), and cloud adiabaticity (Min et al., 2012; Merk et al., 2016; Braun et al., 2018). Results from comparisons of MODIS retrievals with in situ data also depend on the cloud probes used for in situ measurements (King et al., 2013; Witte et al., 2018) and the co-location of the MODIS and in situ datasets (PZ11).

A review of satellite-based estimates of N_c concluded that airborne datasets are underutilized for satellite retrieval evaluation (Grosvenor et al., 2018). This study compares in situ N_c, R_e, and τ from ORACLES with MODIS retrievals of R_e and τ (Platnick et al., 2017a) and the MODIS-derived N_c based on the assumption of adiabatic LWC. A number of studies have compared MODIS retrievals of marine stratocumulus cloud properties with in situ observations (e.g., PZ11; Min et al., 2012; Noble and Hudson, 2015; Braun et al., 2018; Witte et al., 2018). This study expands upon the existing literature by using a larger in situ dataset which provides cloud and aerosol measurements under conditions of variable vertical separation between the aerosol and cloud layers. Biases in MODIS retrievals of cloud properties are quantified as a function of the time gap between MODIS retrievals and in situ data. Biases in MODIS Aqua are compared with biases in MODIS Terra, and MODIS and in situ estimates of aerosol-induced changes in N_c, R_e, and τ are compared.

The paper is organized as follows. In situ observations and satellite retrievals used in the study are described in Sect. 2 along with the methodology for spatiotemporal co-location of the in situ and satellite datasets. In Sect. 3, the MODIS R_e, τ, and N_c are compared with in situ R_e, τ, and N_c, potential sources of biases are discussed, and uncertainties and errors are quantified. In Sect. 4, MODIS estimates of aerosol-induced changes in R_e, τ, and N_c over the southeast Atlantic are compared with in situ estimates. Implications for studies of ACI over the southeast Atlantic are discussed in Sect. 5. The conclusions are presented in Sect. 6.

2 Data and methodology

2.1 In situ observations

In situ observations of marine stratocumulus over the southeast Atlantic were collected during ORACLES using the NASA P-3B aircraft (Redemann et al., 2021). In situ cloud sampling was conducted during vertical profiles through the stratocumulus layer (hereafter “cloud profiles”) between 10^∘ W and 15^∘ E and between 5^∘ N and 20^∘ S in September 2016, August 2017, and October 2018 (G22). For each cloud profile, data from in situ cloud probes were used to derive the number distribution function (n(D)) for droplets with diameters (D) between 3 and 19 200 µm. The cloud probes used during ORACLES included a cloud and aerosol spectrometer (CAS) (Baumgardner et al., 2001), three cloud droplet probes (CDPs) (Lance et al., 2010), a two-dimensional stereo probe (2D-S) (Lawson et al., 2006), a phase Doppler interferometer (PDI) (Chuang et al., 2008), and a high volume precipitation sampler (HVPS-3) (Lawson et al., 1998). A King hot-wire probe (King et al., 1978) measured LWC (hereafter, King LWC). A passive cavity aerosol spectrometer probe (PCASP) (Cai et al., 2013) measured n(D) for accumulation-mode aerosols (0.1<D<3 µm).

The Airborne Data Processing and Analysis software package (Delene, 2011) was used to process the CAS, CDP, King hot-wire, and PCASP data. The University of Illinois/Oklahoma Optical Array Probe Processing Software (UIOOPS) (McFarquhar et al., 2018) was used to process the 2D-S and HVPS-3 data. A merged droplet size distribution was calculated using the CAS or CDP dataset for 3<D<50 µm, the 2D-S dataset for 50<D<1050 µm, and the HVPS-3 dataset for D>1050 µm. N_c was calculated by integrating droplet n(D) from the merged size distribution. Each 1 Hz data sample with N_c>10 cm⁻³ and King LWC >0.05 g m⁻³ was identified as in cloud. N_a was calculated by integrating the PCASP n(D) for out-of-cloud data samples.

Due to overlapping measurement ranges, the CAS, the CDPs, and the PDI provided at least two independent measurements of n(D) for 3<D<50 µm during each flight (G22). Data from one probe were chosen for inclusion in the merged size distribution based on the availability of valid measurements from the CAS, CDPs, or PDI and through comparisons of N_c and LWC between the CAS, CDP, and PDI datasets The CAS was used to represent droplets with 3<D<50 µm for research flights from ORACLES 2016 and the CDPs for research flights from ORACLES 2017 and 2018 (see G22 for justification and more details). The CAS n(D) for ORACLES 2016 was scaled using the King LWC for reference due to a potential sizing bias based on comparisons between the CAS LWC, CDP LWC, and King LWC (G22). The methodology for scaling the 2016 CAS n(D) is described in Appendix A, along with its impact on this study. The uncertainties associated with the in situ measurements of N_c, R_e, and τ are discussed in Appendix B.

For each individual vertical transect through marine stratocumulus, cloud top height (Z_T) and cloud base height (Z_B) were defined as the highest and the lowest altitude, respectively, with N_c and King LWC greater than 10 cm⁻³ and 0.05 g m⁻³, respectively (G21). Cloud thickness (H) was defined as the difference between Z_T and Z_B. During the ORACLES deployments, the average H was about 201 m (G22). R_e and the effective variance (V_e) for the merged size distribution were calculated following Hansen and Travis (1974) as

$$R_{\mathrm{e}}\left(h\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\int }_{\mathrm{3}}^{\mathrm{19}\mathrm{200}}{D}^{\mathrm{3}}n\left(D,h\right)\mathrm{d}D}{{\int }_{\mathrm{3}}^{\mathrm{19}\mathrm{200}}{D}^{\mathrm{2}}n\left(D,h\right)\mathrm{d}D}}$$

and

$$\begin{array}{}\text{(1)}& V_{\mathrm{e}}\left(h\right)={\displaystyle \frac{{\int }_{\mathrm{3}}^{\mathrm{19}\mathrm{200}}(D-\mathrm{2}{R}_{\mathrm{e}}(h){)}^{\mathrm{2}}{D}^{\mathrm{2}}n\left(D,h\right)\mathrm{d}D}{{\left(\mathrm{2}{R}_{\mathrm{e}}\left(h\right)\right)}^{\mathrm{2}}{\int }_{\mathrm{3}}^{\mathrm{19}\mathrm{200}}{D}^{\mathrm{2}}n\left(D,h\right)\mathrm{d}D}}.\end{array}$$

R_e can also be defined in terms of R_v (the mean volume radius) as

$$\begin{array}{}\text{(2)}& R_{\mathrm{e}}=k^{-\mathrm{1}/\mathrm{3}}{R}_{\mathrm{v}},k={\displaystyle \frac{{\left(\mathrm{1}+d^{\mathrm{2}}\right)}^{\mathrm{3}}}{{\left(a{d}^{\mathrm{3}}+\mathrm{1}+\mathrm{3}{d}^{\mathrm{2}}\right)}^{\mathrm{2}}}},\end{array}$$

where k is the droplet spectral width, which is a function of the skewness (a) and dispersion (d) of the droplet size distribution (Martin et al., 1994). K can vary depending on the aerosol conditions, occurrence of drizzle, cloud adiabaticity, and height in cloud (McFarquhar and Heymsfield, 2001; Brenguier et al., 2011). LWC was calculated as

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\mathrm{LWC}\left(h\right)& ={\displaystyle \frac{\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}}{\mathrm{6}}}{\int }_{\mathrm{3}}^{\mathrm{19}\mathrm{200}}{D}^{\mathrm{3}}n\left(D,h\right)\mathrm{d}D\\ & ={\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}{N}_{\mathrm{c}}\left(h\right)R_{\mathrm{v}}{\left(h\right)}^{\mathrm{3}},\end{array}\end{array}$$

where h is the height above Z_B and p_w is the liquid water density. At a height h in cloud, LWC is a function of the average N_c and R_v following Eq. (3). LWP and King LWP were calculated by integrating LWC and King LWC over h from Z_B to Z_T. τ was calculated as

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathit{\beta }}_{\mathrm{ext}}\left(h\right)& ={\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}{\int }_{\mathrm{3}}^{\mathrm{19}\mathrm{200}}{Q}_{\mathrm{ext}}{D}^{\mathrm{2}}n\left(D,h\right)\mathrm{d}D,\\ & \mathit{\tau }={\int }_{Z_{\mathrm{B}}}^{Z_{\mathrm{T}}}{\mathit{\beta }}_{\mathrm{ext}}\left(h\right)\mathrm{d}h,\end{array}\end{array}$$

where β_ext is the cloud extinction and the extinction efficiency (Q_ext) for cloud droplets is assumed to be 2 (Hansen and Travis, 1974) in the limit of geometric optics. The integrals in Eqs. (1), (3), and (4) were converted to discrete sums corresponding to the cloud probe size bins for D>3 µm with a maximum drop size limit of 19 200 µm.

2.2 Satellite retrievals

The MODIS instrument onboard Terra and Aqua acquires passive retrievals of radiance at non-absorbing and liquid water absorbing spectral bands (Platnick et al., 2003). R_e and τ are retrieved using the bispectral retrieval method with the 0.86 µm band paired with the 1.6, 2.1, or 3.7 µm band (Nakajima and King, 1990). R_e and τ from the MODIS Collection 6/6.1 Level 2 product (C6) (Platnick et al., 2017a) at 1 km resolution are used. Three retrievals were made for R_e (R_e16, R_e21, and R_e37) by pairing the 0.86 µm band with the 1.6, 2.1, and 3.7 µm band, respectively. Consistent with previous studies (e.g., PZ11), R_e21 was used as the primary retrieval, and MODIS R_e hereafter refers to R_e21. The wavelength dependence of MODIS τ is not examined, as τ is mainly determined by the reflectance from the non-absorbing band (King et al., 1998).

R_e16, R_e21, and R_e37 represent R_e at two to four optical depths below the cloud top, depending on liquid water absorption and a weighting function based on the vertical penetration of photons into cloud (McFarquhar and Heymsfield, 1998; Platnick, 2000). R_e37 corresponds to the level closest to the cloud top, followed by R_e21 and R_e16 in order of increasing distance from the cloud top. In an upgrade from the MODIS Collection 5.1 (C5) product, which reported R_e21, R_e21 minus R_e16, and R_e21 minus R_e37, the MODIS C6 product reported R_e16, R_e21, and R_e37 separately. Thus, biases in R_e16 and R_e37 associated with the condition of a successful R_e21 retrieval are removed (Platnick et al., 2017b) and R_e16, R_e21, and R_e37 can be compared (Sect. 3). Within the ORACLES sampling domain (10^∘ W to 15^∘ E and 5^∘ N to 20^∘ S; Fig. 1), R_e16, R_e21, and R_e37 from the C6 product can be up to 2 µm lower than the corresponding retrievals from the C5 product (Rausch et al., 2017).

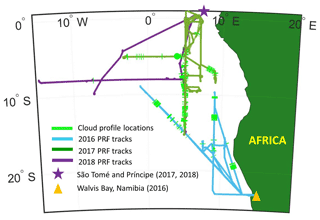
Figure 1 ORACLES flight tracks, bases of operations, and sampling locations for profiles with a MODIS retrieval co-located with in situ data for ΔT less than 3600 s.

The MODIS retrievals are integrated quantities which do not describe the vertical structure of the cloud. In the absence of in situ data, the vertical profiles of LWC and R_v can be approximated using the adiabatic model to parameterize N_c and LWP as functions of τ and R_e (Brenguier et al., 2000; Szczodrak et al., 2001). The adiabatic LWC was defined as

$$\begin{array}{}\text{(5)}& {\mathrm{LWC}}_{\mathrm{ad}}\left(h\right)=C_{\mathrm{w}}h={\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}{N}_{\mathrm{ad}}\left(h\right)R_{\mathrm{vad}}{\left(h\right)}^{\mathrm{3}},\end{array}$$

where C_w is the condensation rate and the subscript “ad” represents the adiabatic equivalent of a variable. Equations (1) to (4) were combined with Eq. (5) to determine τ_ad and LWP_ad following Brenguier et al. (2000) and Szczodrak et al. (2001), respectively, as

$${\mathit{\tau }}_{\mathrm{ad}}={\displaystyle \frac{\mathrm{3}}{\mathrm{5}}}\mathit{\pi }{Q}_{\mathrm{ext}}{\left({\displaystyle \frac{\mathrm{3}{C}_{\mathrm{w}}}{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}}}\right)}^{\mathrm{2}/\mathrm{3}}(k{N}_{\mathrm{c}}{)}^{\mathrm{1}/\mathrm{3}}{H}^{\mathrm{5}/\mathrm{3}}$$

and

$$\begin{array}{}\text{(6)}& {\mathrm{LWP}}_{\mathrm{ad}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{C}_{\mathrm{w}}{H}^{\mathrm{2}}={\displaystyle \frac{\mathrm{5}}{\mathrm{9}}}{\mathit{\rho }}_{\mathrm{w}}\mathit{\tau }{R}_{\mathrm{e}}.\end{array}$$

Using Eq. (5), N_c was parameterized in terms of τ and R_e following Szczodrak et al. (2001) as

$$\begin{array}{}\text{(7)}& N_{\mathrm{c}}={\displaystyle \frac{\sqrt{\mathrm{10}}}{\mathrm{4}\mathit{\pi }k}}{\left({\displaystyle \frac{\mathit{\alpha }{C}_{\mathrm{w}}\mathit{\tau }}{{\mathit{\rho }}_{\mathrm{w}}{R}_{\mathrm{e}}^{\mathrm{5}}}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}},\end{array}$$

where α is the adiabaticity, defined as LWP divided by LWP_ad. MODIS N_c was calculated using MODIS R_e and τ based on Eq. (7).

2.3 Data selection and co-location

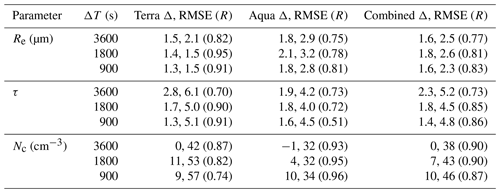
MODIS data with valid retrievals within the ORACLES sampling domain (10^∘ W to 15^∘ E and 5^∘ N to 20^∘ S; Fig. 1) were used. The Terra and Aqua satellites pass over the Equator at about 10:30 and 13:30 LT, respectively. Most cloud profiles from ORACLES were flown within 1 to 2 h of 12:00 UTC. The time range between the first and final cloud profiles during each flight is listed in Table 1. The time gap between the MODIS scan and the in situ sampling for a cloud profile was designated as ΔT. The analysis was limited to cloud profiles with a co-located MODIS retrieval with ΔT less than 3600 s. This assumes that the cloud layer did not undergo significant changes within 1 h. This assumption was tested by comparing MODIS retrievals against in situ measurements for different upper bounds of ΔT (Sect. 3).

Table 1 List of research flights analyzed and the time range, number, sampling duration (in parentheses), and cloud top height (Z_T) for profiles with a co-located MODIS retrieval with a time gap (ΔT) of less than 3600 s. Number and duration are listed for profiles classified by above-cloud aerosol location.

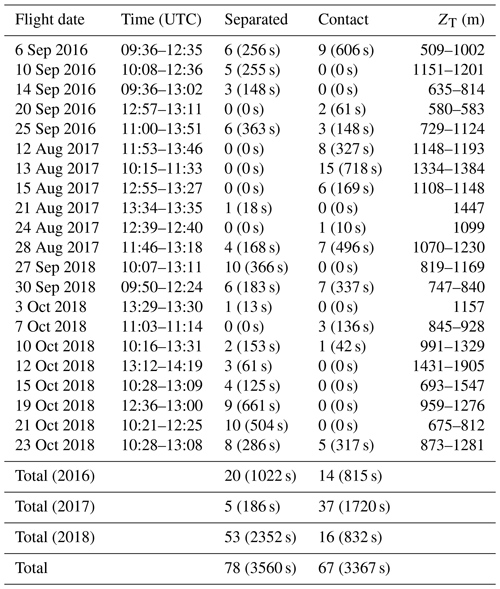
MODIS retrievals were co-located with in situ data following the criteria outlined by PZ11. The pixel closest to the cloud top latitude and longitude during a cloud profile was selected. The location of the selected pixel was adjusted to account for advection of the cloud field using the mean wind speed and direction during the profile from the Turbulent Air Motion Measurement System (Thornhill et al., 2003) on the NASA P-3 aircraft. The wind speed was between 5 to 10 m s⁻¹, which meant that the pixel location was adjusted by a distance of up to 18 to 36 km over an hour on average. The MODIS R_e and τ were averaged over a 5 × 5 pixel domain centered on the adjusted pixel to account for spatial inhomogeneity. The profile was rejected if, after adjusting for advection, the pixel was less than three pixels from the edge of the MODIS scan and if more than 10 % of the retrievals within the 5 × 5 pixel domain, i.e., at least three out of the 25 pixels, were invalid. Estimates of Z_T and cloud top temperature (T_T) from the MODIS C6 product were used to limit the analysis to warm, boundary-layer clouds. Four profiles were excluded from the analysis since the MODIS Z_T was greater than 2500 m or MODIS T_T was less than 273 K.

With the above criteria, at least one cloud profile from 21 research flights conducted during ORACLES had a co-located MODIS retrieval with ΔT<3600 s (Table 1). There were 74 cloud profiles with co-located MODIS Terra retrievals and 71 cloud profiles with co-located MODIS Aqua retrievals (Table 2). ΔT was evenly distributed, with 10 to 15 cloud profiles within every 300 s bin from 0 to 3600 s (except from 1200 to 1800 s) (Fig. 2a). For 97 out of the 145 cloud profiles, the distance between the cloud profile location and the MODIS pixel after adjusting for advection was below 12 km (Fig. 2b). The distance was greater than 36 km for five profiles.

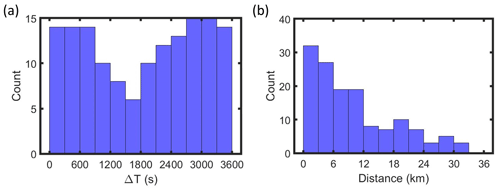
Figure 2 Histograms of (a) the time gap between a cloud profile and the co-located MODIS scan (ΔT) and (b) the distance between a cloud profile and the co-located MODIS pixel after adjusting for advection.

Table 2 Number of cloud profiles during ORACLES deployments with a co-located MODIS Terra or Aqua retrieval for ΔT less than 3600, 1800, or 900 s.

3 MODIS versus in situ

3.1 R_e comparisons

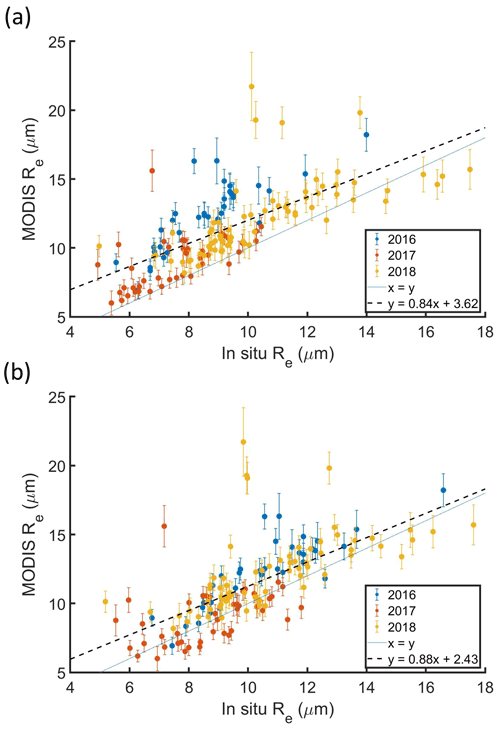
MODIS R_e was compared with the in situ R_e averaged over the top 10 % of the cloud layer sampled during cloud profiles with a co-located MODIS retrieval with ΔT<3600 s (Fig. 3a). The difference between the MODIS R_e and in situ R_e for a cloud profile was termed ΔR_e, with a positive ΔR_e indicating that the MODIS R_e was greater than the in situ R_e. The average MODIS R_e (11.3 µm) was greater than the average in situ R_e (9.7 µm), with Pearson's correlation coefficient (R) = 0.77 and the root mean square error (RMSE) = 2.5 µm. All but 12 cloud profiles had a positive ΔR_e. The average ΔR_e was 1.6 ± 1.8 µm, where the uncertainty estimate represents the sum of the average retrieval uncertainty for the MODIS R_e from the C6 product and the measurement uncertainty for the average in situ R_e (Appendix B). Previous comparisons between airborne measurements and MODIS retrievals of R_e for warm clouds have shown similar ΔR_e values. For example, the MODIS R_e and in situ R_e with ΔT<3600 s for marine stratocumulus over the southeast Pacific had an average ΔR_e of 2.1 µm (PZ11). The MODIS R_e and in situ R_e with ΔT<1500 s for liquid clouds over the North Atlantic had an average ΔR_e of 1.7 µm (Painemal et al., 2021).

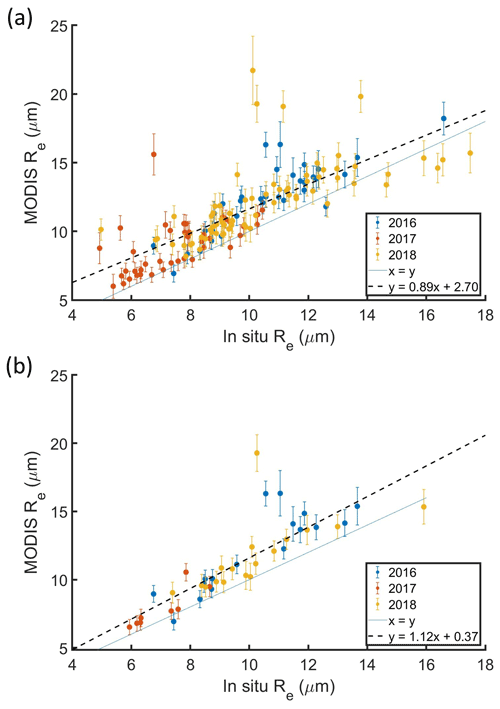
Figure 3 MODIS R_e versus in situ R_e for profiles with a MODIS retrieval co-located with in situ data for ΔT (a) less than 3600 s and (b) less than 900 s, colored by ORACLES deployment year. Each point represents a cloud profile with the in situ R_e averaged over the top 10 % of the cloud and the MODIS R_e averaged over a 5 × 5 pixel domain.

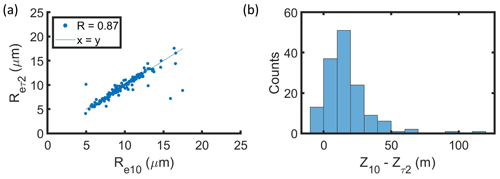
There were 104 profiles with ΔR_e less than ±2 µm, while eight profiles had ΔR_e>5 µm (Fig. 4a). ΔR_e was well correlated with MODIS R_e (R=0.62), and seven out of eight profiles with ΔR_e>5 µm had MODIS R_e>15 µm (Fig. 4a). The average ΔR_e and RMSE decreased from 1.6 to 1.4 and 2.5 to 1.8, respectively, when 13 profiles with MODIS R_e>15 µm were removed. The MODIS R_e retrieval uncertainty (5 % to 15 %) was poorly correlated with ΔR_e (Fig. 4b). For lower bounds of ΔT, the average ΔR_e and RMSE decreased and the correlation between MODIS R_e and in situ R_e increased (Table 3). Among the 42 cloud profiles with a co-located MODIS retrieval with ΔT<900 s, three of the profiles had ΔR_e>5 µm (Fig. 3b). All three of these profiles were associated with MODIS R_e>15 µm.

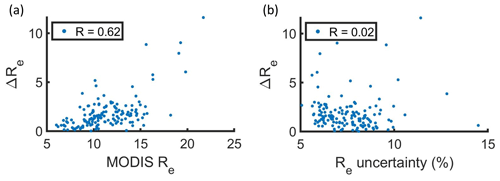
Figure 4 Magnitude of the difference between MODIS R_e and in situ R_e (ΔR_e) for profiles with a MODIS retrieval co-located with in situ data for ΔT less than 3600 s as functions of (a) MODIS R_e and (b) MODIS R_e uncertainty. Each point represents the average over a 5 × 5 pixel domain.

Table 3 Average bias (Δ), root mean square error (RMSE), and Pearson's correlation coefficient (R) for MODIS (Terra, Aqua, combined) retrievals relative to in situ R_e, τ, and N_c for different ΔT.

MODIS R_e was retrieved by MODIS Aqua for five out of the eight profiles with ΔR_e>5 µm. Consequently, retrievals from MODIS Aqua had a higher average ΔR_e and a lower correlation with in situ R_e compared to retrievals from MODIS Terra (Table 3). This was despite the lower average ΔT for retrievals from MODIS Aqua (1650 s) compared to retrievals from MODIS Terra (2020 s). The solar (μ_o) and sensor (μ) zenith angles for MODIS Aqua and MODIS Terra were obtained from the MODIS C6 product. There were minor differences between the average μ_o and μ for MODIS Terra (24.0 and 43.0^∘) and MODIS Aqua (29.7 and 40.0^∘) (Fig. 5). The MODIS R_e and ΔR_e had weak correlations with μ_o (R=0.18 and 0.16) and μ ($R=-\mathrm{0.05}$ and −0.09), which suggests that μ_o and μ had little impact on the performance of MODIS Terra relative to MODIS Aqua.

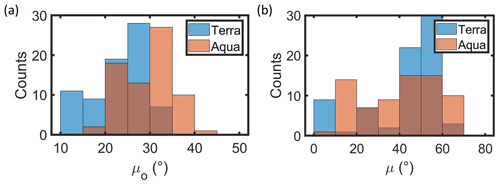
Figure 5 Histograms of (a) solar zenith angle (μ_o) and (b) sensor zenith angle (μ) for MODIS retrievals co-located with in situ data for ΔT less than 3600 s.

R_e16, R_e21, and R_e37 were compared (Fig. 6) to determine whether ΔR_e was dependent on the use of R_e21 as the primary retrieval. The average R_e16, R_e21, and R_e37 were 10.4, 11.3, and 11.7 µm, respectively. The average R_e16 and R_e21 had statistically significant differences, while the average R_e21 and R_e37 had statistically insignificant differences. The latter was consistent with global analyses that found that R_e37 minus R_e21 depends on cloud regime, with positive values (0 to 0.6 µm) for homogeneous marine stratocumulus (Zhang and Platnick, 2011; Fu et al., 2019). Differences between R_e16, R_e21, and R_e37 are associated with differences in the vertical penetration of photons into the cloud. The penetration depth decreases with increasing wavelength from 1.6 to 3.7 µm (Platnick, 2000). An increase in R_e with height in cloud (G22) resulted in R_e16<R_e21<R_e37. Although R_e21 minus R_e37 depends on μ_o, the average μ_o for ORACLES (26.8^∘) was lower than the range of μ_o (65 to 70^∘) for which R_e37 minus R_e21 exceeds 1 µm (Grosvenor and Wood, 2014). Consistent with Zhang and Platnick (2011), the correlation between R_e21 and R_e16 (or R_e37) decreased for values above 15 µm (Fig. 6). For values below 15 µm, R_e16, R_e21, and R_e37 had an average of 9.9, 10.8, and 11.1 µm, respectively, and there was high correlation between R_e16 and R_e21 (R=0.92) and R_e21 and R_e37 (R=0.95). Thus, MODIS R_e had a positive bias regardless of the retrieval wavelength. On average, R_e21 had lower retrieval uncertainty (0.8 µm) compared to R_e16 (1.9 µm) and R_e37 (1.1 µm), which suggests that R_e21 gives a robust estimate of the average ΔR_e.

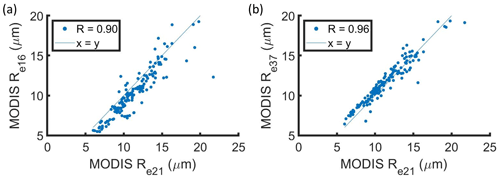
Figure 6 (a) R_e16 and (b) R_e37 as functions of R_e21 for MODIS retrievals co-located with in situ data for ΔT less than 3600 s. Each point represents average values over a 5 × 5 pixel domain.

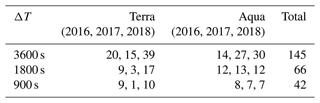
Since each MODIS R_e retrieval penetrates at least two optical depths into cloud, the altitude and in situ R_e at the level of two optical depths below the cloud top (Z_τ2 and R_eτ2) were compared with the altitude and in situ R_e averaged over the top 10 % of the cloud (R_e10 and Z₁₀). R_eτ2 and R_e10 were strongly correlated (R=0.87), with average values of 9.4 and 9.7 µm, respectively (Fig. 7a). R_eτ2 was less than R_e10 because the average Z_τ2 was 17 m lower than Z₁₀ (Fig. 7b) and R_e increased with height in cloud (G22). When five profiles with R_e>15 µm were removed, R_eτ2 and R_e10 had average values of 9.3 and 9.4 µm, respectively, with improved correlation (R=0.95). The average difference between R_eτ2 and R_e10 (0.3 µm) was lower than the average ΔR_e between MODIS R_e and R_e10 (1.7 µm). Thus, the choice of R_e10 did not have a large impact on the average ΔR_e.

Figure 7 (a) Scatter between R_e at two optical depths below the cloud top (R_eτ2) versus R_e averaged over the top 10 % of the cloud layer (R_e10) and (b) histogram of the difference between Z₁₀ and Z_τ2 for profiles with a MODIS retrieval co-located with in situ data for ΔT less than 3600 s.

3.2 τ comparisons

For profiles with a co-located MODIS retrieval with ΔT<3600 s, the average MODIS τ (11.7) was greater than the average in situ τ (9.4), with R=0.73 and RMSE = 5.2 (Fig. 8a). Δτ was defined as the difference between MODIS τ and in situ τ for a cloud profile, with positive values indicating that MODIS τ was higher. The average Δτ was 2.3 ± 3.4, where the uncertainty estimate represents the sum of the average retrieval uncertainty for MODIS τ from the C6 product and the measurement uncertainty for the average in situ τ (Appendix B). Nine profiles with MODIS τ>25 had an average Δτ of 8.1, with six of the profiles having Δτ>±10. When profiles with MODIS τ>25 were removed, the average Δτ and RMSE decreased from 2.3 to 2.0 and from 5.2 to 4.2, respectively. Retrievals from MODIS Terra had lower Δτ and better correlation with in situ τ compared to retrievals from MODIS Aqua (Table 3). The average Δτ decreased and the correlation between MODIS τ and in situ τ improved for profiles with lower ΔT (Table 3). This is consistent with the time-dependent improvement in correlations between MODIS τ and τ retrieved using the airborne Solar Spectral Flux Radiometer during ORACLES (Chang et al., 2021).

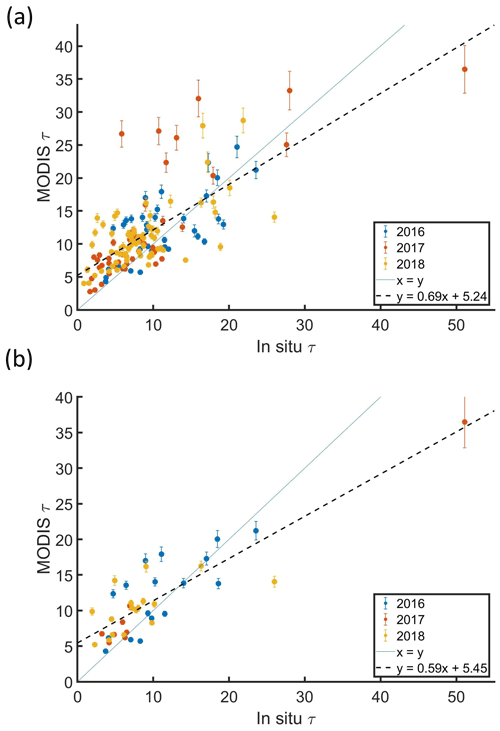
Figure 8 MODIS τ versus in situ τ for profiles with a MODIS retrieval co-located with in situ data for ΔT (a) less than 3600 s and (b) less than 900 s, colored by ORACLES deployment year. Each point represents a cloud profile with the MODIS τ averaged over a 5 × 5 pixel domain.

Profiles with a co-located MODIS retrieval with ΔT<900 s had Δτ=1.4, σ(τ)=2.2, and MODIS τ uncertainty = 0.6 on average. For 24 out of the 42 profiles with a co-located MODIS retrieval with ΔT<900 s, Δτ was greater than ±2 (Fig. 8b). A single profile with ΔT<900 s had MODIS τ>25, which was associated with a Δτ of −14.6. MODIS τ can have biases relative to in situ τ due to spatial heterogeneity of the cloud field or MODIS τ retrieval uncertainties. On average, MODIS τ had a standard deviation (σ(τ)) of 2.2 over the 25 pixel domain for each cloud profile, and σ(τ) was correlated with MODIS τ (R=0.72). The Δτ increased with MODIS τ (Fig. 9a) and the MODIS τ retrieval uncertainty increased with MODIS τ (Fig. 9b). The latter is expected, given a decrease in the sensitivity of τ to the non-absorbing reflectance as τ increases (King et al., 1998). However, the average retrieval uncertainty for MODIS τ (0.6) was less than the average Δτ (2.3).

Figure 9 MODIS τ versus (a) the magnitude of the difference between MODIS τ and in situ τ (Δ) and (b) the MODIS τ retrieval uncertainty for profiles with a MODIS retrieval co-located with in situ data for ΔT less than 3600 s. Each point represents the average value over a 5 × 5 pixel domain.

3.3 N_c comparisons

N_c calculated using MODIS R_e and τ in Eq. (7) (hereafter “MODIS N_c”) was compared with in situ N_c. Figure 10 shows cloud properties as a function of normalized height above cloud base (Z_N), where Z_N equals Z−Z_B divided by Z_T−Z_B. The in situ N_c was averaged over the top half of the cloud layer since entrainment mixing led to lower N_c over the top 10 % of the cloud height (Fig. 10a). Cloud-top entrainment did not affect R_e near the cloud top (Fig. 10b) and hence did not impact the comparisons between MODIS and in situ R_e. Eight profiles with MODIS τ<5 were removed from the N_c comparisons to avoid the impact of higher variability in MODIS retrievals for optically thin clouds (Zhang and Platnick, 2011). The exclusion of these profiles did not lead to significant changes in the R_e or τ comparisons.

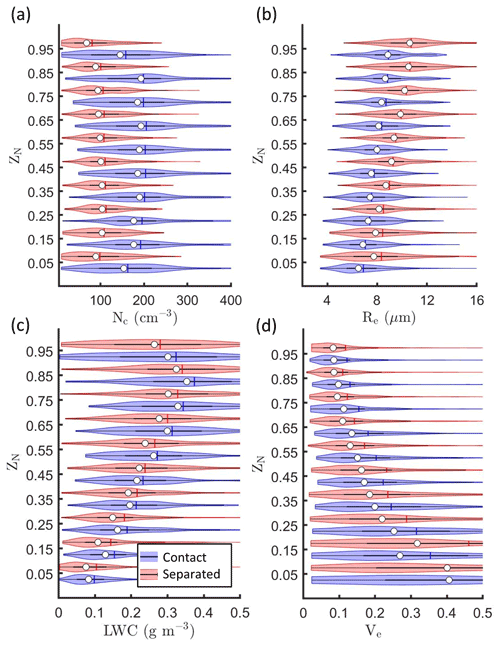
Figure 10 Kernel density estimates (indicated by the width of the shaded area) and boxplots showing the mean (vertical line) and median (white circle) for (a) N_c, (b) R_e, (c) LWC, and (d) V_e versus normalized height in cloud (Z_N) for profiles with a MODIS retrieval co-located with in situ data for ΔT less than 3600 s.

ΔN_c was defined as the difference between MODIS N_c and in situ N_c for a cloud profile, with a positive ΔN_c indicating that MODIS N_c was higher. For 137 profiles with a co-located MODIS retrieval with ΔT<3600 s and MODIS τ>5, the average MODIS N_c (151 cm⁻³) had good agreement with the average in situ N_c (151 cm⁻³), with R=0.90 and RMSE = 38 cm⁻³ (Fig. 11). The average ΔN_c was 0 ± 64 cm⁻³, where the uncertainty estimate represents the sum of the error in calculating the average MODIS N_c (Sect. 3.3.3) and the measurement uncertainty for the average in situ N_c (Appendix B). In comparison, stratocumulus over the southeast Pacific had an average ΔN_c of −4 cm⁻³ with R=0.94 (PZ11).

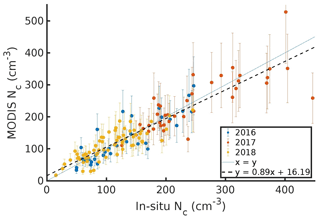
Figure 11 MODIS N_c versus in situ N_c for profiles with a MODIS retrieval co-located with in situ data for ΔT less than 3600 s, colored by ORACLES deployment year. Each point represents a cloud profile with the in situ N_c averaged over the top half of the cloud and MODIS N_c calculated using MODIS R_e and τ averaged over a 5 × 5 pixel domain.

Unlike the R_e or τ comparisons, lower ΔT was not associated with lower ΔN_c or better correlation between MODIS and in situ N_c. Further, MODIS Aqua N_c and MODIS Terra N_c had similar performance relative to in situ N_c (Table 3). There were 15 profiles with ΔN_c greater than ± 50 cm⁻³ (average ΔN_c=2 cm⁻³ and RMSE = 89 cm⁻³). These profiles were associated with higher variability in the in situ data, with an average standard deviation of 68 cm⁻³ for the in situ N_c. Similarly, the three profiles with ΔN_c>±100 cm⁻³ had an average standard deviation of 86 cm⁻³ for the in situ N_c. The correlation between MODIS N_c and in situ N_c increased to 0.93 and the RMSE decreased to 31 cm⁻³ when these three profiles were removed. For 50 % of the profiles, ΔN_c was below ±20 cm⁻³, which highlights the validity of the adiabatic assumption (Brenguier et al., 2000; Szczodrak et al., 2001) and the precision of the in situ estimates of k, C_w, and α (0.76, 2.94 g m⁻³ km⁻¹, and 0.74). The agreement between the average MODIS N_c and in situ N_c was driven by compensating uncertainties associated with the parameters used in Eq. (7), as has been reported previously (PZ11; Grosvenor and Wood, 2014). These uncertainties were examined along with their impact on the calculation of MODIS N_c.

3.3.1 Uncertainties associated with C_w, α, and k

MODIS does not retrieve the vertical profile of LWC. Parameters that represent the estimated rate of condensation with height in cloud (C_w) and the ratio of the vertical integrals of LWC and LWC_ad (α) can provide the largest sources of error in MODIS N_c (Janssen et al., 2011; Min et al., 2012). α had a negative correlation with H (Fig. 12) (Min et al., 2012; Braun et al., 2018) and C_w was a function of cloud base pressure and temperature (Brenguier et al., 2000). Based on the range of estimates in the existing literature, C_w and α contribute a factor ranging from 0.9 to 1.5 in Eq. (7) (Merk et al., 2016, and references therein). For 142 profiles with a co-located MODIS retrieval with ΔT<3600 s and LWP_ad>5 g m⁻², the average C_w and α were 2.94 ± 0.21 g m⁻³ km⁻¹ and 0.74 ± 0.26, respectively, where the uncertainty estimates represent one standard deviation. These values of C_w and α resulted in a factor of 1.47 in Eq. (7). In comparison, PZ11 assumed C_w=2 g m⁻³ km⁻¹ and α=1, with C_w and α contributing a factor of 1.41 in Eq. (7). Using C_w=2 and α=1 in Eq. (7) would decrease MODIS N_c, and the average ΔN_c would change to −6 cm⁻³ (from 0.1 cm⁻³ when C_w=2.94 and α=0.74 were used) while the RMSE remained unchanged.

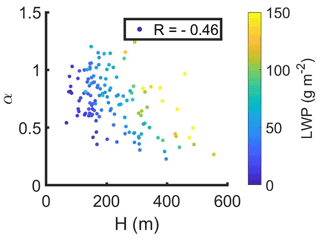
Figure 12 Cloud adiabaticity (α) versus cloud thickness (H) colored by liquid water path (LWP) for profiles with a MODIS retrieval co-located with in situ data for ΔT less than 3600 s.

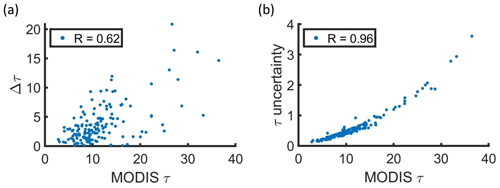
k represents the spectral width, which decreases when droplet size distributions get narrower. Consistent with PZ11, k averaged over the top 10 % of the cloud layer (0.76 ± 0.12) was higher than k averaged over the entire cloud layer (0.70 ± 0.15) (Fig. 13), where the uncertainty estimates represent one standard deviation. Since MODIS R_e corresponds to values near the cloud top, k=0.76 was used in Eq. (7). Using k=0.70 would increase MODIS N_c and the average ΔN_c and RMSE would change to 13 and 42 cm⁻³, respectively (from 0 and 38 cm⁻³ when k=0.76 was used). The value of the cloud top k (0.76) was consistent with the k calculated for marine clouds with entrainment mixing, where k decreased when α decreased (Brenguier et al., 2011). In comparison, a higher k (0.8) has been calculated for marine clouds without entrainment mixing (Martin et al., 1994). The decrease in N_c and LWC near the cloud top with increasing R_e was indicative of inhomogeneous mixing (Fig. 10), and spectral broadening due to entrainment or drizzle (Sinclair et al., 2021) would explain the higher values for k near the cloud top (Fig. 13).

Figure 13 Probability density function for k averaged over the entire cloud layer (blue) or the top 10 % of the cloud (red) for profiles with a MODIS retrieval co-located with in situ data for ΔT less than 3600 s.

3.3.2 Uncertainties associated with MODIS R_e and τ

The MODIS algorithm assumes a vertically homogeneous R_e and LWC (King et al., 1998), but R_e and LWC increased almost linearly with height (LWC decreased near the cloud top due to entrainment mixing) (Fig. 10b, c). The impact of this inconsistency was examined by quantifying ΔN_c for profiles with large MODIS biases in R_e or τ. The average ΔN_c for nine profiles with MODIS τ>25 (average Δτ=8.1) and 10 profiles with MODIS τ>5 and MODIS R_e>15 µm (average ΔR_e=4.4 µm) was −8 and −15 cm⁻³, respectively. The magnitude of ΔN_c was greater than 50 cm⁻³ for only two profiles with MODIS τ>25 and zero profiles with MODIS R_e>15 µm. This suggests that a large bias in MODIS R_e or τ did not necessarily result in a large bias in MODIS N_c.

The MODIS algorithm used a modified gamma distribution function to represent the droplet spectrum assuming V_e (Eq. 1) to be 10 % (Platnick et al., 2017b). For such size distributions, k is related to V_e as k= (1−V_e) × (1−2V_e) and V_e=10 % corresponds to k=0.72 (Grosvenor et al., 2018). For ORACLES, V_e decreased with height (Fig. 10d), with a median cloud top V_e of 8.4 %, corresponding to k=0.76. The a priori assumption of V_e=10 % could lead to biases of up to 1 µm for MODIS R_e (Chang and Li, 2002). Radiative transfer simulations to quantify the MODIS R_e bias associated with V_e were beyond the scope of this study. It is assumed the uncertainties associated with instrument error and atmospheric corrections were included in the retrieval uncertainty estimates in the MODIS C6 product.

The presence of drizzle could introduce biases into MODIS R_e or N_c due to the lower k associated with spectral broadening (Sinclair et al., 2021), higher V_e for a bimodal size distribution (Nakajima et al., 2010), or lower α due to cloud water removal through precipitation (Braun et al., 2018). However, the average rain rate for ORACLES was too low (0.06 mm h⁻¹) (G22) for drizzle to have a major impact on the R_e retrievals (Zinner et al., 2010; PZ11). This was supported by the positive values for R_e37 minus R_e21, which represent size distributions without a significant drizzle mode (Nakajima et al., 2010). The impact of cloud water removal through precipitation was included by using the in situ α (0.74) in Eq. (7).

3.3.3 MODIS N_c error analysis

The total error for MODIS N_c from Eq. (7) was quantified using the propagation of measurement uncertainties associated with k, C_w, and α and retrieval uncertainties associated with MODIS R_e and τ. Assuming that the covariances were normally distributed and random, the total error can be calculated using Gaussian error propagation as

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{\left({\displaystyle \frac{\mathit{\delta }{N}_{\mathrm{c}}}{N_{\mathrm{c}}}}\right)}^{\mathrm{2}}& ={\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathit{\delta }\mathit{\tau }}{\mathit{\tau }}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathrm{5}}{\mathrm{2}}}{\displaystyle \frac{\mathit{\delta }{R}_{\mathrm{e}}}{R_{\mathrm{e}}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathit{\delta }{C}_{\mathrm{w}}}{C_{\mathrm{w}}}}\right)}^{\mathrm{2}}\\ & +{\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathit{\delta }\mathit{\alpha }}{\mathit{\alpha }}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathit{\delta }k}{k}}\right)}^{\mathrm{2}},\end{array}\end{array}$$

where δ represents the error for each variable. For MODIS R_e and τ, the error was defined as the average of the retrieval uncertainty provided within the MODIS C6 product (7.5 % and 5 %, respectively). For k, C_w, and α, the error was defined as one standard deviation (16 %, 7.1 %, and 35 % of their averages).

Based on Eq. (8), MODIS N_c had an error of 30.5 %. This was smaller than previous estimates of 38 % (Janssen et al., 2011) and 78 % (Grosvenor et al., 2018). Consistent with Grosvenor et al. (2018), R_e was the parameter with the largest contribution to the total error in MODIS N_c, followed by α and k. Profiles with MODIS R_e>15 µm and an average ΔR_e of 4.4 µm had an average ΔN_c of −15 cm⁻³, highlighting the compensation of the R_e uncertainty in Eq. (7) by the other parameters. The MODIS N_c calculated using in situ estimates of k, C_w, and α from ORACLES was higher than the MODIS N_c determined using a priori assumptions for k, C_w, and α. For example, substituting C_w=2 g m⁻³ km⁻¹, α=1 (PZ11), and k=0.8 (Martin et al., 1994) into Eq. (7) would introduce a factor which was 9 % lower than using C_w=2.94 g m⁻³ km⁻¹, α=0.74, and k=0.76. The MODIS N_c calculated based on these a priori assumptions would have an average ΔN_c and RMSE of −14 and 39 cm⁻³, respectively (compared to 0 and 38 cm⁻³ using the in situ estimates).

4 Aerosol–cloud interactions

During the ORACLES research flights, variable vertical separation was observed between biomass burning aerosols from southern Africa and marine stratocumulus over the southeast Atlantic (Redemann et al., 2021). Cloud profiles were conducted at locations of both contact and separation between the base of the aerosol layer and the top of the cloud layer. Cloud profiles with an aerosol concentration (N_a) of greater than 500 cm⁻³ within 100 m above the cloud top were termed “contact profiles”, and cloud profiles with N_a<500 cm⁻³ up to 100 m above the cloud top were termed “separated profiles” (G21). Across the ORACLES campaigns, 173 contact profiles were conducted with higher in situ N_c (by 87 cm⁻³), lower in situ R_e (by 1.5 µm), and higher in situ τ (by 1.8) compared to 156 separated profiles (G22). These differences between in situ N_c, R_e, and τ for contact and separated profiles were statistically significant (p<0.02), based on a two-sample t-test. Given the statistically similar sea surface temperatures, lower tropospheric stabilities, and estimated inversion strengths at the locations of contact and separated profiles, the cloud microphysical differences were attributed to aerosol–cloud interactions (G22).

A co-located MODIS retrieval with ΔT less than 3600 s was available for 67 contact and 78 separated profiles (Table 1). When the in situ N_c and R_e were averaged over the top 50 % and top 10 % of the cloud, respectively, contact profiles had a higher in situ N_c (by 93 cm⁻³) and a lower in situ R_e (1.8 µm) compared to separated profiles. Differences between the in situ N_c, R_e, and τ and the MODIS N_c, R_e, and τ for contact and separated profiles were compared (Table 4). For simplicity, it is assumed that the MODIS and in situ uncertainties were consistent for contact and separated profiles. This assumption allows a direct comparison of MODIS estimates of the differences between cloud properties for contact and separated profiles with in situ estimates.

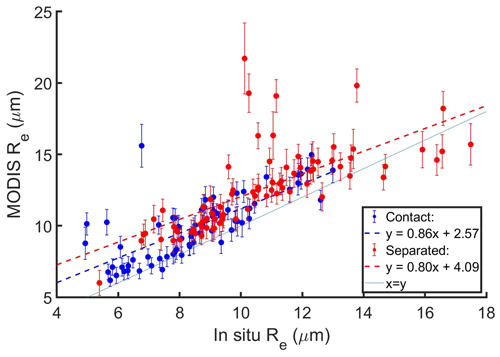
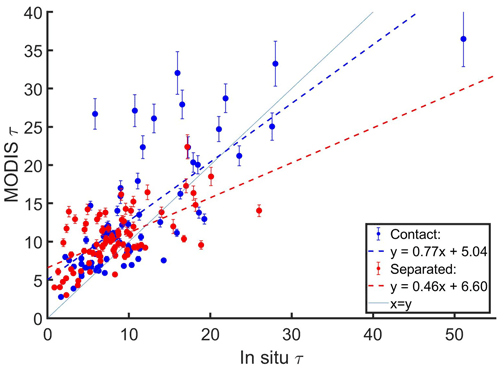
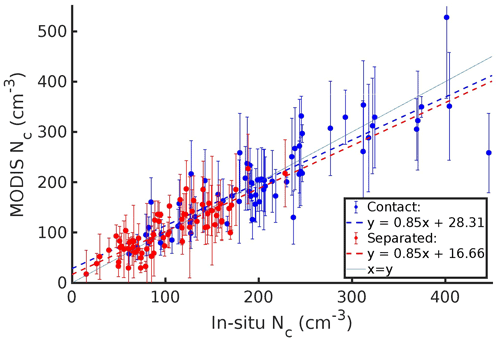
Table 4 Differences between the average R_e, τ, and N_c for contact and separated profiles based on MODIS retrievals (Terra, Aqua, and combined) and in situ measurements. Positive values indicate contact profiles had a higher value.

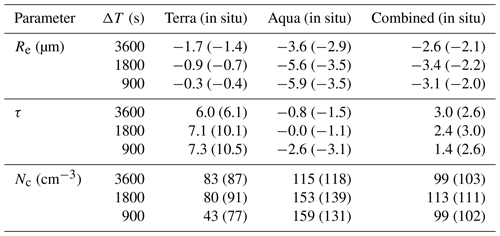
The average MODIS R_e was greater than the average in situ R_e for both contact and separated profiles (Fig. 14 and Table 5). Twelve out of the 13 profiles with MODIS R_e>15 µm and a high average ΔR_e (4.0 µm) (Fig. 4a) were classified as separated profiles, and the MODIS R_e estimate (2.6 µm) for the aerosol-induced increase in R_e was greater than the in situ R_e estimate (2.1 µm). MODIS R_e had a similar positive bias for contact and separated profiles with MODIS R_e<15 µm (1.3 and 1.5 µm, respectively). Thus, when profiles with MODIS R_e>15 µm were removed, the estimate of the R_e difference between contact and separated profiles using MODIS R_e and in situ R_e were closer (1.8 and 1.6 µm, respectively). Fewer profiles with R_e from MODIS Terra had MODIS R_e>15 µm compared to MODIS Aqua, and closer agreement was observed between the in situ R_e and MODIS R_e estimates of the aerosol-induced change in R_e for MODIS Terra compared to MODIS Aqua (Table 4).

Figure 14 Same as Fig. 3a but with cloud profiles colored based on regime classification.

Table 5 The average in situ and MODIS R_e, τ, and N_c for contact and separated profiles, along with R.

The average MODIS τ was greater than the average in situ τ for both contact and separated profiles (Fig. 15 and Table 5). The MODIS τ estimate (3.0) was greater than the in situ τ estimate (2.6) of the aerosol-induced increase in τ. The MODIS Terra τ underestimated the in situ τ increase from separated to contact profiles (Table 4) due to the profile with MODIS τ>25 and $\mathrm{\Delta }\mathit{\tau }=-\mathrm{14.6}$ (Fig. 15). When nine contact profiles with MODIS τ>25 and a high average Δτ (8.1) were removed, the average MODIS τ for contact profiles (10.8) was 1.6 optical depths greater than the in situ τ. Subsequently, the MODIS τ estimate (0.5) was less than the in situ τ estimate (1.0) of the aerosol-induced increase in τ from separated to contact profiles.

Figure 15 Same as Fig. 8a but with cloud profiles colored based on regime classification.

The average MODIS and in situ N_c were within 5 cm⁻³ for both contact and separated profiles (Fig. 16 and Table 5). This meant that the MODIS estimate for the aerosol-induced increase in N_c was within 5 cm⁻³ of the in situ estimate. When three profiles with ΔN_c>±100 cm⁻³ were removed, the MODIS and in situ estimates for the aerosol-induced increase in N_c were similar (95 and 94 cm⁻³, respectively). For MODIS Terra retrievals, the underestimation of the increase in in situ N_c from separated to contact profiles (Table 4) was driven by the profile with $\mathrm{\Delta }\mathit{\tau }=-\mathrm{14.6}$ and MODIS τ>25 (Fig. 15). The MODIS N_c calculated using a priori assumptions for k, C_w, and α underestimated the in situ N_c for contact profiles (by 20 cm⁻³) and separated profiles (by 8 cm⁻³). The a priori MODIS N_c estimate (91 cm⁻³) for the increase in N_c from separated to contact profiles was slightly lower than the in situ N_c estimate (103 cm⁻³).

Figure 16 Same as Fig. 11 but with cloud profiles colored based on regime classification.

5 Discussion

The positive biases in MODIS retrievals of cloud properties for marine stratocumulus over the southeast Atlantic were about 16 % for R_e, 30 % for τ, and negligible for N_c on average. However, the biases were within the overall uncertainty (in situ + MODIS) associated with the data. In comparison, previous studies have reported MODIS biases for R_e and τ of 15 to 20 % (PZ11), 17 to 24 % (Min et al., 2012), and 20 % to 40 % (Noble and Hudson, 2015), and negligible MODIS biases for N_c (PZ11, Braun et al., 2018; Gryspeerdt et al., 2022). Factors that frequently result in biases in MODIS retrievals of cloud properties include subpixel heterogeneity (Zhang and Platnick, 2011), solar and satellite viewing geometry (Grosvenor and Wood, 2014; Painemal et al., 2021), cloud thermodynamic phase (Ahn et al., 2018), and drizzle occurrence (Zinner et al., 2010; Sinclair et al., 2021). These factors had a limited impact on the MODIS retrievals used in this study due to the low latitude of the ORACLES domain and observations of homogeneous, warm, closed-cell marine stratocumulus over the southeast Atlantic with low precipitation rates (G21; G22). It is hypothesized that these biases could be reduced by addressing the in situ measurement uncertainty for k, the in situ derived uncertainty for α (e.g., Min et al., 2012; Merk et al., 2016; Braun et al., 2018; Witte et al., 2018), and the MODIS retrieval uncertainties associated with the bispectral retrieval technique (e.g., Fu et al., 2019, 2022).

Satellite estimates of the aerosol perturbation of N_c over the southeast Atlantic have biases of less than 10 % compared to the in situ estimates. The differences between the MODIS and in situ R_e or τ were reduced by screening data with MODIS R_e>15 µm or MODIS τ>25, respectively. This is consistent with the improvement in correlations between MODIS N_c and in situ N_c from multiple field campaigns when using a threshold of maximum R_e of around 15 µm (Gryspeerdt et al., 2022). The MODIS-based screening led to MODIS estimates of aerosol-induced changes in N_c, R_e, and τ that were within 5 cm⁻³, 0.5 µm, and 0.7 of the in situ estimates. The agreement between the MODIS and in situ estimates of aerosol-induced changes in N_c, R_e, and τ was associated with consistent biases in MODIS retrievals of cloud properties across different aerosol regimes. Such agreement suggests that cloud properties for horizontally homogeneous, warm, closed-cell marine stratocumulus can be estimated using MODIS retrievals in the absence of in situ datasets.

Differences between climate model and observational estimates of the effective radiative forcing due to ACI are largely driven by uncertainties in observational estimates of the radiative forcing due to aerosol effects on cloud albedo (RF_aci) (Gryspeerdt et al., 2020). Issues with satellite estimates of RF_aci persist due to biases in satellite retrievals of N_c (Grosvenor et al., 2018), above-cloud aerosol properties (Meyer et al., 2015; Painemal et al., 2020; Chang et al., 2021), and aerosol perturbations of N_c (Quaas et al., 2020). Better accuracy in remote sensing retrievals of the aerosol layer is needed to constrain the uncertainties in satellite estimates of RF_aci over the southeast Atlantic (Douglas and L'Ecuyer, 2020). In particular, biases in satellite estimates of the placement or optical and microphysical properties of the above-cloud aerosol layer need to be addressed (Rajapakshe et al., 2017; Painemal et al., 2020; Peers et al., 2021).

The High Spectral Resolution Lidar Generation 2 (HSRL-2) (Hair et al., 2008) was used to measure aerosol extinction and backscatter at 355, 532, and 1064 nm during all three ORACLES campaigns. Research using HSRL-2 data for estimating the vertical profile of cloud condensation nuclei is ongoing (Lenhardt, 2021). Accounting for the attenuation of upwelling solar radiation by above-cloud absorbing aerosols over the southeast Atlantic could increase the average MODIS τ and R_e by up to 9 % and 2 %, respectively (Meyer et al., 2015). The Research Scanning Polarimeter (RSP) (Cairns et al., 1999) was used during ORACLES to collect polarimetric retrievals of cloud properties (Alexandrov et al., 2012) which do not operate under the assumptions required for MODIS retrievals. RSP retrievals can help examine biases in MODIS retrievals of clouds with higher precipitation rates or bimodal size distributions (Sinclair et al., 2021; Fu et al., 2022) or a complicated solar and viewing geometry (e.g., Painemal et al., 2021). Future work will use RSP retrievals combined with other airborne datasets to evaluate MODIS retrievals while accounting for above-cloud aerosols (e.g., Chang et al., 2021).

6 Conclusions

In situ measurements of N_c, R_e, and τ for marine stratocumulus over the southeast Atlantic were collected during the NASA ORACLES field campaign. In situ data from 145 cloud profiles were co-located with MODIS retrievals from the Terra and Aqua satellites with ΔT less than 1 h. The average MODIS R_e and τ (11.3 µm and 11.7) were greater than the average in situ R_e and τ (9.7 µm and 9.4), with R=0.77 and 0.73, respectively. The average bias in MODIS R_e was 1.6 ± 1.8 µm and the average bias in MODIS τ was 2.3 ± 3.4, where the uncertainty represents the sum of the average MODIS retrieval uncertainty and the in situ measurement uncertainty. MODIS N_c (151 cm⁻³) had an estimated calculation error of 30.5 % and showed good agreement with in situ N_c (151 cm⁻³), with R=0.90 and an average bias of 0 ± 64 cm⁻³. The retrieval uncertainty for MODIS R_e provided the largest source of error in calculating MODIS N_c, but compensating uncertainties for τ, k, C_w, and α resulted in good agreement. Cloud profiles with an N_c bias greater than 50 cm⁻³ were associated with higher variability in the in situ N_c. The biases in MODIS R_e and τ were lower for lower bounds of ΔT and for retrievals from MODIS Terra compared to MODIS Aqua. Profiles with MODIS R_e>15 µm had larger biases in MODIS R_e (average bias = 4.5 µm) and profiles with MODIS τ>25 had larger biases in MODIS τ (average bias = 8.1).

Variability in the vertical profile of absorbing aerosols over the southeast Atlantic was associated with changes in N_c, R_e, and τ under similar meteorological conditions. There were 67 “contact” profiles where N_a>500 cm⁻³ was sampled within 100 m above cloud tops, while 78 “separated” profiles had N_a<500 cm⁻³ up to 100 m above cloud tops. Contact profiles had higher in situ N_c and τ (88 cm⁻³ and 2.5 higher) and lower in situ R_e (2.2 µm lower) compared to separated profiles. MODIS retrievals were able to estimate the signs of these aerosol-induced changes in N_c, R_e, and τ. The magnitude of the MODIS estimates of differences between contact and separated profiles was within 5 cm⁻³, 0.5, and 0.2 µm of the in situ estimates when profiles with MODIS R_e>15 µm or MODIS τ>25 were removed.

The agreement between MODIS and in situ estimates of aerosol-induced changes in cloud microphysical properties over the southeast Atlantic was associated with similar biases in MODIS retrievals across different aerosol conditions. This motivates the use of MODIS retrievals to study ACI for homogeneous marine stratocumulus over a larger domain of the southeast Atlantic and over longer timescales than is possible using in situ data. Future work will be aimed at improving lidar and polarimetric retrievals of the vertical profile and microphysical and optical properties of absorbing aerosols over the southeast Atlantic layers and the underlying cloud properties (Zeng et al., 2014; Rajapakshe et al., 2017; Painemal et al., 2020; Lenhardt, 2021).

Appendix A: Scaling the CAS/CDP n(D) based on the King LWC

For ORACLES 2016, CAS data were used in the analysis since CDP measurements were invalid due to an instrument misalignment issue. G22 showed there were statistically significant differences between the average CAS LWC of 0.15 ± 0.09 g m⁻³ (± one standard deviation) and the average King LWC of 0.28 ± 0.15 g m⁻³ (R=0.80). The LWC comparison provides an estimate of the uncertainties in the CAS data due to known issues such as coincidence of particles in the sample volume (Lance, 2012) and uncertainties in the collection geometry (e.g., Baumgardner et al., 2017). Comparisons between CAS and CDP N_c (when CDP data were available) indicate that the CAS may be affected by coincidence of particles within the sample volume. However, accounting for coincidence while processing the CAS data affected N_c by less than 2 %. Based on a recommendation by the manufacturers of CAS (Droplet Measurement Technologies, DMT), a sample area of 0.26 mm² was used to process CAS droplet counts to obtain N_c instead of using 0.13 mm² from the CAS manual.

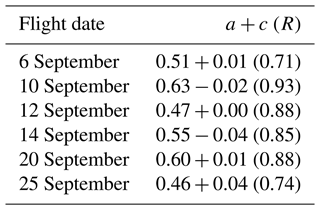
For the six flights selected for analysis, the King LWC and CAS LWC had a best-fit slope (a) between 0.46 and 0.63 and R=0.71 to 0.93 (Table A1). Therefore, an adjustment is used to increase the CAS LWC to match the King LWC. The simplest way to do this would be to increase the CAS sample area, which is a first-order adjustment that assumes the CAS is sizing the droplets correctly. However, based on the LWC differences, it is hypothesized the CAS was undersizing the droplets passing through the CAS sample volume. The methodology outlined by PZ11 was thus used to account for the sizing bias, wherein the CAS n(D) was scaled by adjusting the CAS size bins using the King LWC as a reference by setting

$$\begin{array}{}\text{(A1)}& \mathrm{CAS}\mathrm{LWC}=a\times \mathrm{King}\mathrm{LWC}.\end{array}$$

The scaled midpoint diameter for the ith CAS size bin ($D_i^{\ast }$) is determined as

$$\begin{array}{}\text{(A2)}& D_i^{\ast }=a^{-\mathrm{1}/\mathrm{3}}{D}_i,\end{array}$$

where D_i is the midpoint diameter for the ith CAS size bin. The D_i used to calculate the CAS R_e and LWC is replaced by $D_i^{\ast }$ to calculate the scaled CAS R_e and LWC. The CAS size bin midpoints were thus increased (by up to 30 %), since $D_i^{\ast }\mathit{>}{D}_i$ for a<1 and each flight had a<1. The average in situ R_e for the 34 profiles from ORACLES 2016 with a co-located MODIS retrieval (Table 2) increased from 8.6 µm for unscaled CAS n(D) to 10.6 µm for CAS n(D) scaled using Eqs. (A1) and (A2).

Table A1 ORACLES 2016 flight dates with the best-fit slope (a) and intercept (c) between the average CAS LWC and King LWC from the flight.

The average MODIS R_e (12.4 µm) overestimated the average in situ R_e from both the unscaled and the scaled CAS n(D). When the CAS n(D) was scaled, the number of profiles having in situ R_e> MODIS R_e increased from 0 to 2 and the average ΔR_e decreased from 3.8 µm (R=0.83) to 1.8 µm (R=0.86) relative to when the CAS n(D) was unscaled. These changes were consistent with the hypothesis of CAS undersizing the droplets passing through the CAS sample volume. Since the average ΔR_e for scaled CAS n(D) was consistent with previous studies (PZ11; Painemal et al., 2021), the scaled CAS n(D) was used in the analysis.

Valid CDP measurements were available for ORACLES 2017 and 2018. For the research flights from ORACLES 2017 and 2018, the average CDP LWC was 0.18 ± 0.16 and 0.21 ± 0.14 g m⁻³, the average King LWC was 0.21 ± 0.15 and 0.20 ± 0.12 g m⁻³, and the average CAS LWC was 0.09 ± 0.07 and 0.10 ± 0.07 g m⁻³, respectively (G22). The differences between the King LWC and the CDP LWC are within the typical uncertainties of these in situ cloud probes (Baumgardner et al., 2017). Nevertheless, the impact of scaling the CDP data was investigated using Eqs. (A1) and (A2) to determine if this would lead to qualitative changes in the results.

For 14 out of 18 flights from ORACLES 2017 and 2018, the King LWC and CDP LWC had 0.7<a<1.4 and the CDP size bin midpoints were adjusted by less than 13 % following Eq. (A2). When the CDP n(D) was scaled for the 42 profiles from ORACLES 2017, the average CDP R_e increased from 7.6 to 8.7 µm, the number of profiles having in situ R_e> MODIS R_e increased from 2 to 21, and the average ΔR_e decreased from 1.4 µm (R=0.57) to 0.3 µm (R=0.43) relative to when the CDP n(D) was unscaled. Scaling the CDP n(D) led to a decrease in the best-fit slope for MODIS R_e as a function of in situ R_e (0.73 to 0.50) along with an increase in the intercept (3.5 to 4.7 µm). These changes suggest the in situ R_e might be overestimated when the CDP n(D) is scaled, and the unscaled CDP n(D) was thus used in the study for ORACLES 2017. Given this and the closer agreement between CDP LWC and King LWC (compared to CAS LWC and King LWC), it is unlikely that the CDP had a sizing bias like the CAS, and thus the unscaled CDP n(D) was used in the analysis.

When the CDP n(D) was scaled for the 73 profiles from ORACLES 2018, the average CDP R_e increased from 10.5 to 10.8 µm, the number of profiles having in situ R_e> MODIS R_e increased from 9 to 15, and the average ΔR_e decreased from 1.9 µm (R=0.68) to 1.6 µm (R=0.62) relative when the CDP n(D) was unscaled. The use of the scaled CDP n(D) led to small changes in the best-fit slope for MODIS R_e as a function of in situ R_e (0.77 to 0.73) and the intercept (4.3 to 4.5 µm). Scaling the CDP n(D) for ORACLES 2018 did not have a major impact on the CDP dataset. To remain consistent with the use of unscaled CDP data for ORACLES 2017, unscaled CDP data were used in the study for ORACLES 2018 as well.

When MODIS R_e was compared with in situ R_e calculated using unscaled n(D) for all three campaigns, the average ΔR_e was 2.2 µm, with R=0.72 and a best-fit slope and intercept of 0.86 and 3.5 µm, respectively (Fig. A1a). In comparison, when MODIS R_e was compared with in situ R_e calculated using scaled n(D) for all three campaigns, the average ΔR_e was 1.3 µm, with R=0.70 and a best-fit slope and intercept of 0.90 and 2.4 µm, respectively (Fig. A1b). The use of either scaled or unscaled n(D) for all three campaigns did not lead to qualitative changes in the results presented in the study. MODIS R_e always had a positive bias greater than 1 µm relative to in situ R_e. It must be noted that the quantitative changes highlight the uncertainties associated with in situ data, which must be considered when validating satellite retrievals using airborne datasets (Witte et al., 2018).

Figure A1 Same as Fig. 3a but with in situ R_e calculated using (a) the unscaled CAS and CDP n(D) and (b) the CAS and CDP n(D) scaled based on the King LWC.

Appendix B: In situ measurement uncertainties

The error for in situ measurements of N_c, R_e, and τ depend on droplet sizing and concentration uncertainties associated with limitations of instrument measurement principles and data processing algorithms (Baumgardner et al., 2017; McFarquhar et al., 2017). Although sources of in situ measurement uncertainty are relatively well known, there is no established methodology for calculating sizing and concentration uncertainties or propagating uncertainties to the error for in situ N_c, R_e, or τ. A single probe is unable to characterize the entire spectrum of cloud droplets, and droplet size distributions are derived by combining number distribution functions from scattering and imaging probes (G22). This complicates uncertainty estimation and error propagation for in situ measurements. After accounting for instrument and data processing uncertainties, droplet sizing and concentration uncertainties can be ±20 % and ±50 % for imaging probes and ±50 % and ±20 % for scattering probes (Baumgardner et al., 2017).

Three approaches for estimating the error for in situ N_c, R_e, and τ are examined. First, sizing and concentration uncertainties of 10 % each are assumed throughout the size distribution (Baumgardner et al., 2017) to derive a minimum estimate of the error. Second, uncertainties are estimated based on intercomparisons between cloud probes with similar measurement size ranges. Third, the standard error of the mean, defined as the standard deviation divided by the square root of the sample size, is calculated. For each variable, the maximum estimate out of the three approaches is designated as the error estimate.

For the first approach, the droplet concentration (N_c) uncertainty is 10 %. Sizing and concentration uncertainties are not always independent, and Gaussian error propagation can underestimate the error. Thus, the error (δ) in R_e and τ is determined using the maximum and minimum concentrations and sizes as

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}\mathit{\delta }x& ={\displaystyle \frac{x\left(D+\mathit{\delta }D,N\left(D\right)+\mathit{\delta }N\left(D\right)\right)-x\left(D-\mathit{\delta }D,N\left(D\right)-\mathit{\delta }N\left(D\right)\right)}{\mathrm{2}}},\\ & x=\mathit{\{}\mathit{\tau },R_{\mathrm{e}}\mathit{\}},\end{array}\end{array}$$

where δD=0.1 D and δN(D)=0.1 N(D).

Following Eq. (B1), δτ equals 0.3 τ and δR_e equals 0.1 R_e. The fractional estimate for δτ is greater than the equivalent estimate from Gaussian error propagation (0.22 τ), while the estimate for δR_e is equivalent to the Gaussian error estimate. Following this approach, the average in situ N_c, R_e, and τ error estimates are 15 cm⁻³, 1.0 µm, and 2.8, respectively. For the second approach, average values of N_c, R_e, and τ from the scaled CAS datasets (Appendix A) are compared with the PDI dataset for ORACLES 2016 and with the CDP datasets for ORACLES 2017 and 2018 based on data availability (G22). Across deployments, the relative difference between N_c, R_e, and τ from the cloud probes was within 12.5 %, 10 %, and 21 %, respectively. Thus, the average in situ N_c, R_e, and τ error estimates are 19 cm⁻³, 1.0 µm, and 2.0, respectively. For the third approach, the standard deviation is divided by the square root of the sample size to determine the standard error of the mean. The N_c, R_e, and τ error estimates are 7.4 cm⁻³, 0.2 µm, and 0.5, respectively.

Using the highest error estimate out of the three approaches, the average in situ N_c, R_e, and τ along with the error estimates are 150 ± 19 cm⁻³, 9.7 ± 1.0 µm, and 9.4 ± 2.8, respectively. Uncertainty estimates for biases in MODIS retrievals relative to in situ measurements (Sect. 3) are defined as the sum of the retrieval uncertainty and the calculation error for MODIS N_c, R_e, and τ and the in situ measurement uncertainty. The average MODIS N_c was 150 ± 45 cm⁻³ and the bias in MODIS N_c was 0 ± 64 cm⁻³. The average MODIS R_e was 11.3 ± 0.8 µm and the bias in MODIS R_e was 1.6 ± 1.8 µm. The average MODIS τ was 11.7 ± 0.6 and the bias in MODIS τ was 2.3 ± 3.4. The average biases in MODIS retrievals relative to in situ measurements were within the MODIS retrieval and in situ measurement uncertainty for all three variables.