the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Hybrid water adsorption and solubility partitioning for aerosol hygroscopicity and droplet growth
Kanishk Gohil
Chun-Ning Mao
Dewansh Rastogi
Chao Peng
Mingjin Tang
In this work, we studied the cloud condensation nuclei (CCN) activity and subsaturated droplet growth of phthalic acid (PTA), isophthalic acid, (IPTA) and terephthalic acid (TPTA), significant benzene polycarboxylic acids and structural isomers found in the atmosphere. Köhler theory (KT) can be effectively applied for hygroscopicity analysis of PTA due to its higher aqueous solubility compared to IPTA and TPTA. As with other hygroscopicity studies of partially water-soluble and effectively water-insoluble species, the supersaturated and subsaturated hygroscopicity derived from KT principles do not agree. To address the disparities in the sub- and supersaturated droplet growth, we developed a new analytical framework called the Hybrid Activity Model (HAM). HAM incorporates the aqueous solubility of a solute within an adsorption-based activation framework. Frenkel–Halsey–Hill (FHH) adsorption theory (FHH-AT) was combined with the aqueous solubility of the compound to develop HAM. Analysis from HAM was validated using laboratory measurements of pure PTA, IPTA, TPTA and PTA–IPTA internal mixtures. Furthermore, the results generated using HAM were tested against traditional KT and FHH-AT to compare their water uptake predictive capabilities. A single hygroscopicity parameter was also developed based on the HAM framework. Results show that the HAM-based hygroscopicity parameter can successfully simulate the water uptake behavior of the pure and internally mixed samples. Results indicate that the HAM framework may be applied to atmospheric aerosols of varying chemical structures and aqueous solubility.
- Article
(4262 KB) - Full-text XML
-
Supplement
(1071 KB) - BibTeX
- EndNote
Aerosols can affect the global radiative balance and climate by either absorption and scattering of radiation (direct effect of aerosols) or by acting as cloud condensation nuclei (CCN), resulting in cloud formation (indirect effect of aerosols). While the direct effect is well studied and understood, the indirect effect is still the most significant source of uncertainties in climate forcing. This is primarily attributed to the poor understanding of the CCN activity and hygroscopic properties of organic aerosols (Talley et al., 2013). Organic aerosols are ubiquitous in the atmosphere. They contribute significantly to the atmospheric aerosol mass burden and account for 20 %–90 % of total tropospheric fine aerosol mass (Kanakidou et al., 2005). Furthermore, organic aerosols can mix with other organic and inorganic species in the atmosphere to modify their CCN activity and hygroscopic properties (for example, but not limited to, Schill et al., 2015; Vu et al., 2019; Sánchez Gácita et al., 2017; Su et al., 2010; Padró et al., 2012; Baustian et al., 2012; Fofie et al., 2018). Consequently, the CCN activity of organic aerosols needs to be well characterized to reduce uncertainties in the climate forcing due to the indirect effect of aerosols.
Much of the CCN-related research focuses on highly water-soluble and sparingly water-soluble compounds (for example, but not limited to, Jing et al., 2018; Samy et al., 2010; Asa-Awuku et al., 2010; Taylor et al., 2017). For such compounds, Köhler theory (KT) is traditionally applied to study their CCN activity and predict their hygroscopic properties. KT explains droplet growth by combining the water activity described using Raoult's law (solute effect) with the Kelvin effect (curvature effect) (Köhler, 1936). KT is applied under the assumptions of infinite and spontaneous water solubility of the solute and an infinitely dilute water droplet solution (Asa-Awuku et al., 2010; Hartz et al., 2006; Kreidenweis and Asa-Awuku, 2014; Barati et al., 2019; Dawson et al., 2020). That is, if the aerosol instantaneously disassociates in water, traditional KT aptly explains the droplet growth driven by molar volume and droplet surface tension (Köhler, 1936; Sullivan et al., 2009; Giordano et al., 2015). These assumptions work well for many aerosols that are highly soluble ( m3 solute m−3 water; Petters and Kreidenweis, 2007) that form thermodynamically ideal solutions in water. Moreover, the water uptake characteristics of such highly water-soluble compounds can be predicted with a single KT hygroscopicity parameter (κ) (Petters and Kreidenweis, 2007). The κ parameter derived in this way is defined as the “intrinsic κ” of the aerosol.
However, there is an abundance of partially and effectively water-insoluble organic compounds in the atmosphere. The CCN activity of such limited-water-solubility compounds has been predicted by incorporating the compound solubility in traditional KT (Hartz et al., 2006; Petters and Kreidenweis, 2008). Riipinen et al. (2015) prescribed a “solubility partitioning” framework using the traditional KT for CCN analysis of pure and internally mixed aerosols in a large range of aqueous solubility. Furthermore, a modified κ parameter accounting for the water solubility of the aerosols can also be derived based on this solubility-modified KT framework (Petters and Kreidenweis, 2008; Sullivan et al., 2009; Nakao, 2017). This modified hygroscopicity varies over the course of droplet growth and is dependent on the droplet size. Despite the modifications to traditional KT, differences have been observed between the experimental κ with either the intrinsic or solubility-modified κ of the aerosol (Sullivan et al., 2009; Kumar et al., 2009b). Specifically, aerosols with solubility m3 m−3 are “effectively insoluble” (Petters and Kreidenweis, 2008) and do not agree with the water uptake predictions using either traditional or solubility-modified KT.
Droplet growth can be explained for the effectively insoluble organic compounds using a water adsorption framework. CCN activity from adsorption can be modeled by combining the water activity from an adsorption isotherm with the Kelvin effect (for example, but not limited to, Kumar et al., 2009a, b, 2011a, b; Rahman and Al-Abadleh, 2018; Malek et al., 2022; Tang et al., 2016; Henson, 2007; Goodman et al., 2001; Hatch et al., 2012). One such mathematical formulation accounts for adsorption using the Frenkel–Halsey–Hill (FHH) isotherm (Sorjamaa and Laaksonen, 2007). The FHH isotherm consists of two empirical parameters denoted as AFHH and BFHH. AFHH explains the interaction of the first adsorbed water layer and the particle surface, while BFHH explains the interaction between subsequently adsorbed water layers and the particle. The FHH isotherm combined with the Kelvin effect provides the FHH adsorption theory (FHH-AT) for CCN activity analysis. Parameters specific to a given aerosol species can be experimentally determined by fitting FHH-AT through their CCN activity measurements. Studies have so far explored the application of the FHH-AT for CCN analysis of several water-insoluble compounds (for example, but not limited to, Kumar et al., 2009a; Kumar et al., 2009b; Kumar et al., 2011a; Kumar et al., 2011b; Hatch et al., 2014; Hatch et al., 2019; Dalirian et al., 2018; Laaksonen et al., 2016; Laaksonen et al., 2020). FHH-AT consists of two empirical parameters as opposed to a single κ parameter in traditional or modified KT. Additionally, an important assumption in FHH-AT and other similar adsorption models is that the aerosols are treated as completely water-insoluble. Only recently, in a companion paper (Mao et al., 2022), has FHH-AT been shown to work for insoluble particles with water-soluble and molecular-level functionalized surfaces. Thus, there now exists a transitional regime from a soluble to water-insoluble models to correctly describe droplet growth.
The following paper probes several aspects of water uptake to develop a comprehensive model to describe droplet formation of effectively water-insoluble to partially soluble organics. Specifically, a new CCN activity model is developed by combining the components of the solubility-modified KT with the FHH isotherm. This work is a companion and extension to the single-parameter framework developed in Mao et al. (2022). Throughout this paper, this model is referred to as the Hybrid Activity Model (HAM). Within the HAM framework, the aerosol particles are treated as completely water-insoluble at the start of the droplet growth process. The particle continues to fractionally dissolve into the aqueous phase as droplet growth progresses. While the dissolved fraction of the aerosol contributes to droplet growth via Raoult's law, the undissolved fraction contributes to droplet growth via adsorption of water on the surface. Furthermore, this work discusses the development of a single κ parameter based on HAM to represent the effect of aqueous solubility on droplet growth for a compound that would be otherwise treated as effectively water-insoluble.
The development and application of HAM is explained in this paper using the experimental droplet growth measurements of three low-water-solubility structural isomers of benzenedicarboxylic acid – phthalic acid (PTA), isophthalic acid (IPTA) and terephthalic acid (TPTA). PTA, IPTA and TPTA are among some of the significant benzene polycarboxylic acids detected in the atmosphere (Haque et al., 2019; Meng et al., 2018; Liu et al., 2019; Yassine et al., 2020; Fu et al., 2009; Kanellopoulos et al., 2021; Singh et al., 2017; Kunwar et al., 2019). PTA and its isomers are known to be tracers of benzanthracene, naphthalene-1 and methylnaphthalene-1, prominent emissions from combustion (Kleindienst et al., 2012; Al-Naiema et al., 2020; He et al., 2018). PTA is also a byproduct of pre-ozonation of fulvic acid, another significant marker of biomass burning emissions (Zhong et al., 2017b; Zhong et al., 2017a). IPTA and TPTA are also predominantly produced from biomass burning and emissions of automobile exhaust (Kawamura and Kaplan, 1987; Mkoma and Kawamura, 2013; Balla et al., 2018; Al-Naiema and Stone, 2017).
The hygroscopic properties of PTA, IPTA and TPTA have been studied in the past (for example, but not limited to, Petters and Kreidenweis, 2007; Hartz et al., 2006; Wang et al., 2021). However, a comprehensive comparison and discussion of the effects of structural isomers on the droplet growth of benzenedicarboxylic acids does not exist. Vapor sorption measurements of bulk PTA indicate hygroscopic growth at high ambient relative humidity (>90 % RH) (Wang et al., 2021). Hämeri et al. (2002) used tandem differential mobility analyzer (TDMA) technology and observed that PTA aerosol did not grow under subsaturated conditions. Other studies show that PTA internal mixtures with inorganics can deliquesce under subsaturated conditions (Jing et al., 2016; Jing et al., 2018). Furthermore, Hartz et al. (2006) showed that PTA could activate as CCN at 1 % supersaturation. The activation was consistent with KT, which assumed complete dissolution with no solubility considerations. Petters and Kreidenweis (2007) report the κ=0.059 and 0.051 for PTA under sub- and supersaturated conditions, respectively. To our knowledge only one other paper has measured droplet growth of IPTA. Hartz et al. (2006) found that IPTA behaves as an insoluble compound and does not obey traditional KT. Few studies have measured hygroscopic properties of TPTA, but not in the context of CCN (Diniz et al., 2017; Zhao et al., 2021). To our knowledge, the application of adsorption models has not been studied for CCN analysis of PTA, IPTA or TPTA.
Overall, HAM is used in this paper to extensively study the hygroscopic properties of PTA, IPTA and TPTA that are not yet cogently known. In addition to the aforementioned pure compounds, the internal mixtures of PTA and IPTA are also studied. The compounds and their mixtures considered in this work are useful and help us understand the efficacy of different CCN models to describe the droplet growth associated with different organic CCN with varying aqueous solubilities. The experimental CCN measurements provide an efficient means to validate the application of the newly developed HAM. In the following sections, we first describe the experimental setup used in this study to obtain droplet growth data for PTA, IPTA and TPTA and PTA–IPTA internal mixtures. We then describe the theory and formulation of HAM based on KT and FHH-AT, and how it was implemented for droplet growth analysis of aerosols. We subsequently explain the derivation of the single κ parameter using the HAM framework, followed by the discussion of results and conclusions of this study.
2.1 Compounds and aerosol generation
Phthalic acid (PTA; 1,2 – benzenedicarboxylic acid, >99.5 %, Sigma-Aldrich®), terephthalic acid (TPTA; 1,4 – benzenedicarboxylic acid, 98 %, Sigma-Aldrich®) and isophthalic acid (IPTA; 1,3 – benzenedicarboxylic acid, >99 %, Fisher Scientific®) were used as representative compounds for the aromatic acid aerosols (AAAs, hereafter). The physical properties of PTA, IPTA and TPTA are summarized in Table 1. Aqueous solutions of PTA, IPTA and TPTA were formed by mixing 30 mg of acid in 500 mL of ultrapure water (Milli-Q or Millipore®, 18.2 MΩ cm−1). Additionally, three internally mixed solutions of PTA and IPTA were also prepared by mixing 30 mg of dry acid mixture in 500 mL ultrapure water. The internally mixed solutions were prepared for three different mass fractions of PTA and IPTA (5:1, 1:1 and 1:5 wt/wt). To facilitate the dissolution of solute in aqueous solution, all the solutions were sonicated for 2 h in a warm water bath maintained at ∼ 40 ∘C to create a uniform suspension. The solution was subsequently cooled and maintained at 20 ∘C. Polydisperse aerosols were generated using a Collison nebulizer (TSI Atomizer 3076). The wet aerosol particles were then passed through a series of two silica gel diffusion dryers (TSI 3062) to remove moisture (to RH <10 %). The dry particles were then classified for supersaturated and subsaturated measurements.
2.2 CCNC experiments for supersaturated measurements and data analysis
A continuous flow streamwise thermal gradient cloud condensation nuclei counter (CCNC; Droplet Measurement Technologies, DMT; Roberts and Nenes, 2005; CCN 100) was used for the droplet activation measurements (for example, but not limited to, Engelhart et al., 2008; Moore et al., 2010; Tang et al., 2012; Barati et al., 2019; Vu et al., 2019) of AAAs under supersaturated conditions. Briefly described here, polydisperse aerosol was generated and dried as described in Sect. 2.1. The electrical mobility aerosol size from 8 to 352 nm was measured with an electrostatic classifier (TSI 3936, DMA 3081, and CPC 3776) every 2.25 min. The size-selected aerosols exiting the DMA were then split into two streams. A condensation particle counter (CPC; TSI 3776) samples the first stream at 0.3 L min−1 to measure total dry particle concentration (CCN), and the CCNC samples the second stream at 0.5 L min−1 and constant supersaturation to measure activated particle (droplet) counts (CCCN). A sheath flow rate of 8 L min−1 was applied to maintain a sheath-to-sample ratio of 10:1 across the experimental setup. The measurements were repeated 10 times for each supersaturation. Furthermore, the measurements were performed over supersaturations ranging between 0.6 % and 1.6 %. CCNC supersaturations were calibrated using ammonium sulfate ((NH4)2SO4, AS) aerosol (Sigma-Aldrich®, >99.9 %). AS data used for CCN calibration are provided in the Supplement (Sect. S1).
PyCAT 1.0 (Gohil and Asa-Awuku, 2022) was employed for data processing, analysis and visualization of the CCN measurements. CCN size-resolved activation curves were generated at a fixed supersaturation (S) as across a range of dry particle diameters (Ddry). The volume-equivalent diameters were used to represent particle sizes that were obtained by combining size-resolved particle dynamic shape factor (χ) with measured electrical mobility diameters (see Supplement Fig. S4). Multiple charging errors were removed from the size-resolved activation ratio following a combination of charge correction algorithms from Gunn (1956) and Wiedensohler (1988). Following this, a Boltzmann sigmoidal fit expressed as
was applied to the size-resolved activation ratio curve. In Eq. (1), y is the dependent variable ; A1 and A2 are the minimum and maximum of the sigmoid, respectively; dx is the slope of the sigmoid; x0 is the inflection point of the sigmoid (generally the midpoint of the sigmoid); and x is the independent variable (Ddry). The sigmoid fit is typically scaled over a range of 0.0 to 1.0, and so x0 corresponds to the critical dry diameter (Ddry,c) at the instrument supersaturation and is physically defined as the size at which 50 % of all particles are activated.
2.3 H-TDMA experiments for subsaturated measurements
A hygroscopicity tandem differential mobility analyzer (H-TDMA) measured droplet growth of AAAs in the subsaturated regime. The H-TDMA setup has been previously explained in detail (Rader and McMurry, 1986; Cruz and Pandis, 2000), and only a brief description is provided here. Dried polydisperse aerosol was first charged with a Kr-85 bipolar aerosol neutralizer (TSI 3081). Monodisperse charged particles with a dry diameter (Ddry) were size-selected using a differential mobility analyzer (DMA 1). The sample and the sheath flow rates were maintained at 0.3 and 3.0 L min−1, respectively (i.e., sheath-to-sample flow ratio ). The size-selected particles from DMA 1 were then exposed to 95±0.46 % RH using a Nafion humidification membrane (PermaPure M.H series). The humidified aerosol stream was then passed through the second DMA (DMA 2) that was equilibrated to a constant RH. DMA 2 was coupled with a condensation particle counter (CPC; TSI 3756) and operated in scanning mobility particle sizer (SMPS) mode. The median wet diameter (Dwet) of the size-resolved number concentration of the humidified aerosol stream from DMA 2 was reported. Dwet was used as the approximate final size to which the particles of size Ddry would grow under 95±0.46 % RH conditions. The hygroscopic growth factors (Gf) were obtained by taking the ratio of Dwet with respective Ddry,
The RH of the H-TDMA setup was calibrated using ammonium sulfate (see Fig. S1; Taylor et al., 2011). Calibration data are found in the Supplement.
2.4 VSA experiments for subsaturated measurements
A vapor sorption analyzer (VSA; TA Instruments New Castle, DE, USA) setup was used for the hygroscopicity measurements of bulk samples in the subsaturated regime. Mass change in AAAs as a function of RH (5 %–95 %) was measured at 25 ∘C. The instrument setup for the VSA has been described in detail in the literature (Gu et al., 2017), and thus, the experimental procedure is briefly explained here. During each experiment, bulk samples were first dried at <1 % RH, then the RH was incremented up to 90 % with a 10 % step, followed by a 5 % step from 90 % to 95 %. A high-precision balance was used in the VSA to measure the sample mass at different RHs with a stated sensitivity of <0.1 µg. For every RH, a ≤0.1 % change in the sample mass was considered to be the standard for stabilization. The initial dry mass of AAA samples used in this measurement was typically around 1.0 mg. For each sample, a minimum of three experiments were performed. At every RH, the sample mass (m) was normalized with respect to the initial mass of the dry sample (m0). Subsequently, the mass-based growth factor was calculated as .
3.1 Köhler theory (KT)
The equilibrium supersaturation (S) can be estimated over a droplet as a function of its size (Dp) as
where aw is the water activity term, is the droplet surface tension at the interface, Mw and ρw are respectively the molecular weight and density of water, R is the universal gas constant (8.314 J mol−1 K−1), and T is the temperature. The water activity is mathematically expressed as , where γw and xw are the activity coefficient and mole fraction of water in the droplet, respectively. In traditional Köhler theory (KT), the water activity is approximated as (Raoult's law), which assumes infinite dilution and complete dissolution of the solute. Furthermore, is the surface tension of a pure water droplet. The exponential quantity is the Kelvin term that describes the curvature effect. The solute effect and curvature effect are competing effects that describe droplet growth; the solute effect accounts for the water vapor pressure drop over the droplet due to the aerosol particle, and the curvature effect accounts for the water vapor rise over the droplet due to surface tension reduction.
3.2 Frenkel–Halsey–Hill (FHH) adsorption theory (FHH-AT)
Traditional KT, with or without the explicit treatment of aerosol solubility, can be effectively applied for highly soluble species. However, for partially or completely insoluble species Raoult's law is substituted with adsorption isotherms to model water uptake behavior. One such isotherm is the Frenkel–Halsey–Hill (FHH) adsorption isotherm that defines water activity through multilayer water adsorption as a function of relative surface coverage (θ, or the number of adsorbed water monomolecular layers). The FHH isotherm is expressed as (Sorjamaa and Laaksonen, 2007)
where AFHH and BFHH are FHH fit parameters that describe the intermolecular interactions responsible for the adsorption of water on particle surfaces. AFHH describes the interactions between the particle surface and first adsorbed water monolayer. BFHH describes the interactions between successively adsorbed monolayers. AFHH and BFHH regulate the amount of water adsorbed on the particle surface and the radial distance up to which attractive forces can contribute to adsorption of water, respectively. θ in Eq. (4) is expressed as , where Dp and Ddry have been previously defined, and Dw is the size of the water molecule. The mathematical representation for the FHH-AT is analogous to traditional KT and combines the FHH isotherm with the Kelvin term (Sorjamaa and Laaksonen, 2007; Kumar et al., 2009a) such that
The FHH parameters can be empirically determined for any aerosol species from their droplet growth measurements (Kumar et al., 2009a). For measurements in supersaturated environments, AFHH and BFHH are determined from least square minimization of the experimental data with the maxima of the FHH-AT equilibrium curves (Kumar et al., 2009a, b, 2011a, b). A higher value of AFHH implies a higher water adsorption, and a smaller value of BFHH implies stronger attractive forces over larger distances. It has been observed that BFHH has a larger influence on the shape of the adsorption isotherm and hence strongly drives CCN activation using FHH-AT (Kumar et al., 2009a; Hatch et al., 2019).
3.3 Hybrid Activity Model (HAM)
The assumptions of complete aqueous solubility or insolubility associated with KT and FHH-AT, respectively, represent two extreme possibilities of CCN activation and droplet growth. In this work, the two water activities were combined to develop a generalized “hybrid” water activity term. The droplet growth model thus obtained is called the Hybrid Activity Model, or HAM. Previous studies have discussed several other mathematical models built upon the traditional Köhler theory under different conditions. One such example is that of the solubility-partitioned Köhler theory (Petters et al., 2009, Riipinen et al., 2015), which explicitly includes the activity coefficient (γw) of the aerosol compounds to estimate the water activity. γw≃1 in the traditional Köhler theory only under the assumption of the infinite dilution of the aqueous phase of the droplet, which holds true for several highly soluble aerosol species. For limited-water-solubility compounds, γw is calculated by treating the aqueous solubility of the compound. However, even then the contribution of the undissolved fraction of the solute to the droplet growth is not treated. Another example of a modified Köhler model is the “core–shell” model (Kumar et al., 2011b), which combines the FHH isotherm and Raoult's law in a single framework to evaluate the contribution of the insoluble and soluble component of the mixture, respectively, on droplet growth. In the core–shell model, partial water solubility is not considered for any of the mixture components. HAM builds on the concepts delineated by Kumar et al. (2011b) and Riipinen et al. (2015) and considers all particles to be a “core–shell” morphology while also treating all the components as partially water-soluble. The general mathematical representation of HAM is as follows:
where , and the definitions of aw,KT and aw,FHH are provided in Sect. 3.1 and 3.2, respectively.
HAM sandwiches different phases of droplet growth for any given particle in three stages. In stage 1, HAM assumes that a particle suspended under humidified ambient conditions does not dissolve at the start of the activation process (time, t→0). That is, droplet growth at t→0 occurs entirely due to the adsorption of a water monolayer on the particle surface and can be explained using the FHH isotherm. In stage 1,
The FHH parameters (AFHH, BFHH) for any given species are determined by fitting the FHH-AT to the experimental data and can be subsequently used in the HAM framework.
Stage 2 begins as the droplet continues to grow, and more water accumulates in the aqueous phase. In this stage, the particle starts dissolving and enters the aqueous phase. The fraction of particle mass that dissolves or enters the aqueous phase depends on the solubility of the compound. Moreover, the dissolved fraction of the particle can be estimated at each step of droplet growth using the solubility partitioning concept introduced by Riipinen et al. (2015). Briefly described here, a droplet comprises a bulk dry (undissolved) phase and an aqueous (dissolved) phase. The bulk phase can be composed of one or more internally mixed species with varying water solubility. This causes the composition and core size of the bulk phase to vary dynamically during droplet growth. The amount of water in the aqueous phase increases as the droplet grows, thereby increasing the concentration of the compounds in the aqueous phase. There is a competition for dissolution between the compounds in the bulk phase which is dependent on their solubilities. Considering a dry particle consisting of n species with limited solubility, the undissolved mass fraction of a species i (χi) during droplet growth is expressed as (Riipinen et al., 2015)
where γi is the activity coefficient, ci (g H2 O−1) is the solubility of the pure species, mw is the mass of water in the droplet, mi,dry is the initial mass of the pure species in the dry particle, and Yi,dry is the initial mole fraction of the pure species in the dry particle. Equation (6a-1) implies that the dissolved mass fraction of the species i in the aqueous phase is given as 1−χi. A set of n coupled equations are simultaneously solved to obtain χi for all n species in the mixture. χi is then used to calculate the mole fraction of species i dissolved in the aqueous phase (xi) at any point during droplet growth. Subsequently, the KT water activity can be given as , where ns and nw are respectively the number of moles of solute and water in the aqueous phase. In stage 2, the contribution of the dissolved fraction of the compound in the aqueous phase (through Raoult's law) can be combined with the undissolved fraction in the solid phase (through the FHH isotherm) to generate the overall water activity term,
Equation (6b) highlights the main difference between the models presented by Kumar et al. (2009a) and Riipinen et al. (2015).
Stage 3 begins when the droplet is large enough to accommodate enough water in the aqueous phase and dissolve the particle mass entirely. This point onward, the droplet growth can be explained using traditional KT. In stage 3,
Equations (6a), (6b) and (6c) were combined to describe the water activity through the three stages of droplet growth in the HAM framework. Thus HAM can effectively estimate the droplet growth across a wide range of aqueous solubilities. The HAM sandwiches two extremes represented by fully soluble and fully insoluble behavior in a single framework. Indeed one can consider it to be (H)AMbidextrous and apply the concept to improve upon the single hygroscopicity parameterization (κ).
3.4 Hygroscopicity parameterization – single hygroscopicity parameter (κ)
Commonly, the CCN activity and water uptake tendencies of any given compound are expressed using a single hygroscopicity parameter (κ). A theoretical κ is derived using a simple parameterization of the solute water activity term in the droplet growth model. Additionally, critical dry particle sizes can be combined with their supersaturations to experimentally determine κ. In the following subsections, the κ parameter derived from different models is explained.
3.4.1 KT hygroscopicity
A single hygroscopicity parameter (κ) has been developed using the KT framework. κ can be defined through its effect on the water activity in the droplet as follows:
where Vs is the dry particulate (solute) volume, and Vw is the volume of water in the droplet. κ obtained from Eq. (7) is a parameterized quantity determined from the water activity based on Raoult's law. Using κ-based parameterization of aw, Eq. (3) can be modified for any Ddry as
For a given Ddry, the droplet size increases as the supersaturation above the droplet surface increases. Supersaturation increases until the point of activation, which is characterized using the critical wet droplet size (Dp,c). The supersaturation at the point of activation along with the corresponding Ddry and Dp,c depend on the κ of the compound. κ of any compound in an aqueous phase is difficult to measure, but it can be theoretically approximated using Raoult's law (κintrinsic). The κintrinsic of any species (denoted using a subscript i) can be expressed as follows:
where ν is the Van't Hoff factor of the compound and is related to its aqueous dissociation; Mi and Mw are the molecular weights of the solute i and water; and ρi and ρw are the density of the solute i and water, respectively. κintrinsic,i defined in Eq. (9) here is dependent only on solute composition and solvent (water) properties and is independent of size. κintrinsic of a mixture can be computed using a volume average mixing rule with the Zdanovskii–Stokes–Robinson (ZSR) approximation as follows (Petters and Kreidenweis, 2007):
where ϵi is the volume fraction of the ith component in the dry particle, and κintrinsic,i is the intrinsic hygroscopicity parameter of the ith component. ϵi in an internal mixture of n components is estimated as , where mi is the mass of the pure component i in the mixture. κ in Eq. (10) assumes complete aqueous solubility of the compound or mixture. Moreover, κ for a mixture in Eq. (10) can be applied to mixtures of soluble and insoluble compounds, where the κ of the insoluble species are considered to be 0. The hygroscopicity parameterization requires explicit treatment of aqueous solubility for compounds that are inherently insoluble or sparingly soluble but possess water uptake tendencies (Petters and Kreidenweis, 2008; Sullivan et al., 2009). In such cases, κ is mathematically expressed by modifying κintrinsic,i of the mixture components (κsolubility) as follows:
where Ci is the water solubility of the ith component of the dry particle (expressed as solute volume per volume of water), xi is the fraction of the ith component dissolved in water, and H(xi) is the distribution function of the fraction of the ith component dissolved in water. Equations (15a)–(12c) determine κ as a function of Dp. For unknown species with limited water solubility, some range of Dp corresponds to a volume of water which might not be sufficient to dissolve the volume of a dry particle. Therefore, experimental droplet growth data are required to determine particle hygroscopicity.
κ can also be determined if the supersaturation (S) and the critical dry diameter (Ddry,c) measured at S are experimentally known. The experimental κ derived using KT is denoted as κKT and expressed as follows:
Equation (12) also incorporates the same set of assumptions as Eqs. (7)–(15) – dilute solution and infinite and complete solubility of the compound.
3.4.2 FHH-AT hygroscopicity
For the FHH-AT, a similar κ parameterization as KT can be developed by combining the water activity with the FHH isotherm using Eq. (7) (Mao et al., 2022),
which can be expanded to derive the FHH single hygroscopicity parameter (κFHH). The κFHH thus determined depends on the experimental data. The measured S and the corresponding Ddry,c can be used to compute the Dp,c using Eq. (5) and subsequently used to estimate κFHH as follows:
The hygroscopicity obtained using the FHH framework explains water uptake and droplet growth through adsorption. At the point of activation, the FHH hygroscopicity explicitly depends on the dry particle size and the corresponding critical wet diameter. That is, at the point of activation. κFHH in Eq. (14) can be further simplified (κFHH,s) such that at the point of activation,
Equation (15) can be constrained using the critical surface coverage. At the point of activation, the critical surface coverage is determined as follows:
θc from Eq. (16) is substituted in Eq. (15) such that , which essentially represents the theoretical κFHH. It is important to note that κFHH,s is particle-size-dependent as opposed to κintrinsic (Eq. 9), which is not.
3.4.3 HAM hygroscopicity
Similar to KT or FHH-AT, a single hygroscopicity parameter was developed from the HAM framework (κHAM) using Eq. (7),
The inclusion of the Raoult term (xw) is the main difference between Eqs. (13) and (17). κHAM is also dependent on the experimental information (S or Dp,c along with the corresponding Ddry,c), and so Eq. (17) can be accordingly rearranged to obtain the HAM single hygroscopicity parameter as follows:
κHAM explains water uptake and droplet growth by combining the effects of aqueous solubility and water adsorption. At the point of activation, the HAM hygroscopicity depends on the dry particle size and the corresponding critical wet diameter. That is, θ→θc at the point of activation, where Dp,c can be computed using the generic Eq. (6) with the help of measured Ddry,c vs. S. In Eq. (6), xw is calculated using solubility partitioning as explained in Sect. 3.3. Equation (18) is the representation of experimental hygroscopicity of the particle based on the HAM framework. Equation (18) can be further simplified (κHAM,s) such that at the point of activation,
Equation (19) is the theoretical hygroscopicity based on the HAM framework, which is constrained using the surface coverage. The constraint at the point of activation is estimated from Eq. (6) as given by the following expression:
Equation (20) provides θc at the point of activation to substitute in Eq. (19), and hence . AFHH and BFHH are the empirically determined parameters from FHH-AT specific to the compound. Like κFHH and κFHH,s, κHAM and κHAM,s are also size-dependent. However, the size dependence of κHAM is variable and is controlled by the aqueous solubility of the compound. An extended derivation of κHAM is provided in the Supplement (Sect. S2).
4.1 Köhler theory application for pure and internally mixed AAAs
The critical dry diameters (Ddry,c) at supersaturations (S) in the range of 0.6 %–1.6 % were calculated using PyCAT 1.0. At any given supersaturation, the Ddry,c for each sample was calculated from the size-resolved activation ratio. The CCN measurements for pure AAAs over a range of supersaturations are shown in Fig. S2 (Sect. S3 in the Supplement). The activation diameters determined for every sample at applied supersaturations were corrected using their dynamic shape factor. The experimental setup for shape factor measurements and the shape factor dataset for AAAs and PTA–IPTA internal mixtures are shown in Sect. S4.1 and S4.2 (Supplement), respectively. The size-resolved shape factors were then used to transform the measured electrical mobility diameters to their respective volume-equivalent diameters (Tavakoli and Olfert, 2014; Yao et al., 2020; Gohil and Asa-Awuku, 2022). The volume-equivalent diameters along with their corresponding supersaturations were then used to estimate the experimental hygroscopicity based on traditional KT (κKT), for all the AAA samples.
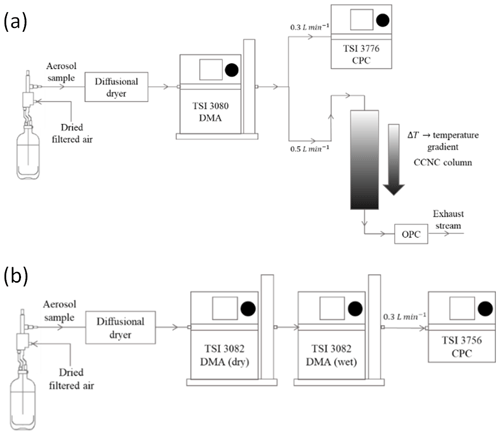
Figure 1(a) Schematic of a typical CCN measurement setup under supersaturated conditions. The DMA and the CPC collectively operate as an SMPS to obtain a distribution of dry particles. The CCNC is connected in parallel and provides the distribution of activated particles. (b) Schematic of a typical H-TDMA setup for subsaturated droplet growth measurements. The dry DMA (DMA 1) selects dry particles of a specified size. The classified particles are then humidified and passed through the wet DMA (DMA 2) and the CPC operating as an SMPS to generate the droplet distribution.
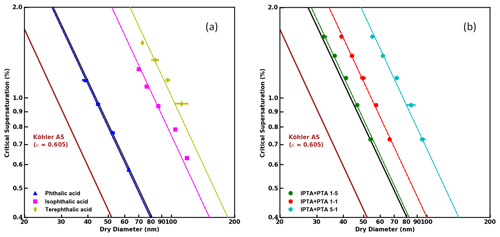
Figure 2(a) S vs. Ddry,c data obtained from supersaturated CCN measurements of pure phthalic acid (PTA), isophthalic acid (IPTA) and terephthalic acid (TPTA). (b) S vs. Ddry,c data obtained from supersaturated CCN measurements of internal mixtures of PTA and IPTA. The mixtures studied shown in this plot are 5:1, 1:1 and 1:5 by mass of PTA. The solid brown line in both subplots corresponds to ammonium sulfate and was used for CCNC calibration. The solid black lines were generated using the ideal Köhler theory (KT) for the respective samples, and the dashed colored lines are the KT fits obtained using the measured CCN data of each sample.
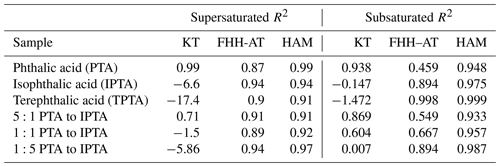
The activation properties of pure AAAs (PTA, IPTA and TPTA) along with their predicted κintrinsic and κKT are summarized in Table 2. The S values versus their corresponding Ddry,c for the samples are plotted in Fig. 2a. The experimental data are represented using individual markers. The solid and dashed lines represent the KT fits using the theoretical κintrinsic. The R2 scores are provided in Table 3. PTA is observed to have the best agreement with the KT prediction (R2≈0.99). IPTA and TPTA show poor agreement with traditional KT. The lack of agreement between measurements and traditional KT predictions for IPTA and TPTA can be attributed to their significantly low aqueous solubility compared to PTA (by an order of magnitude ∼102). In addition to the predicted and measured AAA data, (NH4)2SO4 is also shown in Fig. 2a.
Table 2Intrinsic and experimental hygroscopicity parameter and FHH empirical parameters used for FHH-AT and HAM analysis for pure and internally mixed AAA samples.
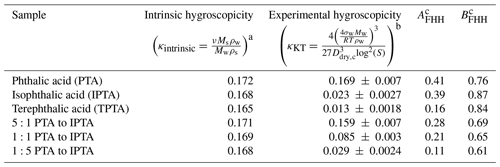
a Mw=18 g mol−1, ρw=1 g cm−3, ν=1 b σw = 0.072 J m−2, R=8.314 J mol−1 K−1, measured Ddry,c vs. S. Ddry,c: measured critical dry diameter. S: supersaturation. c Empirically determined FHH parameters from measured Ddry,c vs. S data for the given samples.
For compounds that are considered “sparingly soluble” or “effectively insoluble” (Petters and Kreidenweis, 2008; Fig. 3), an explicit treatment of the compound solubility can typically improve the agreement between predicted and measured activation properties. Based on this convention, PTA would also be considered “sparingly soluble”. However, our results suggest that an explicit treatment of PTA solubility is not required. Moreover, κintrinsic is a good representation of PTA hygroscopicity. Figure 2b shows the traditional and solubility-limited KT fits for internal mixtures of PTA and IPTA using their κintrinsic. The traditional KT predicts the CCN activity of the mixture containing excess PTA (5:1 mass ratio). This suggests that the mixture dominated by PTA must have an aqueous solubility closer to pure PTA and a κintrinsic≈κKT that can be obtained using the ZSR approximation. The agreement between traditional KT fits and experimental data reduces as the mass fraction of IPTA increases in the mixture.
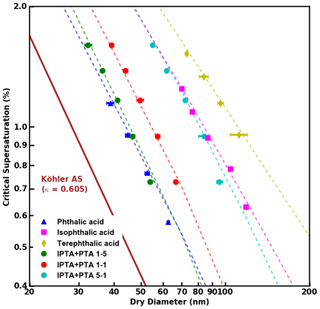
Figure 3S vs. Ddry,c data obtained from supersaturated CCN measurements of pure and internally mixed AAA samples. FHH-AT fits applied to the experimental data are shown as dashed lines.
The application of solubility-limited (modified) KT showed poor agreement with the pure AAAs and PTA–IPTA internal mixtures (Fig. S4 in the Supplement). Modified KT overpredicted the critical supersaturation for any given dry particle size for all 6 samples. Thus, the underprediction of AAAs' CCN activity is attributed to significantly low water solubility (in the range of 10−5–10−3 vol/vol water). Furthermore, a significant droplet growth is required to facilitate κsolubility=κintrinsic when solubility dependence is included in the hygroscopicity analysis (Fig. S5 in the Supplement). The AAA solubilities are 3 or more orders of magnitude smaller compared to highly soluble species such as ammonium sulfate (0.42 vol/vol water) or sucrose (1.26 vol/vol water). Quantitatively, the AAA droplets should grow to about 6.5, 23 and 45 times the dry particle size of PTA, IPTA and TPTA, respectively, when κsolubility=κintrinsic. The required droplet growth is significantly large compared to compounds like ammonium sulfate or sucrose, for which the droplet growth is 1.2 and 1.5 times the initial particle size, respectively, when κsolubility=κintrinsic (Fig. S6 in the Supplement). All of this implies that the hygroscopicity and CCN activity of AAAs and PTA–IPTA internal mixtures is more likely a consequence of water adsorption and not aqueous solubility.
4.2 FHH-AT application for pure and internally mixed AAAs
FHH adsorption theory (FHH-AT) was applied for the analysis of pure and internally mixed AAAs. Figure 3 shows the measured S vs. Ddry,c data for pure AAAs and PTA–IPTA internal mixtures. The dashed lines represent FHH-AT fits for their respective CCN activity datasets. It should be noted that agreement for the FHH-AT can be obtained for every set of CCN measurements since the FHH parameters are determined by applying power law fitting to the datasets. The empirically determined FHH parameters (AFHH,BFHH) for pure compounds and internal mixtures are summarized in Table 2.
The values of AFHH and BFHH can be used to qualitatively compare the water uptake properties of the pure and internally mixed species (Kumar et al., 2009b; Hatch et al., 2019). AFHH dictates the attractive forces between the particle surface and the first adsorbed monolayer of water. A larger AFHH implies a tendency to adsorb a higher amount of water on the particle surface. For the pure compounds, AFHH decreases in the order of PTA > IPTA > TPTA (Table 2). This suggests a declining tendency to adsorb water. Additionally, AFHH values for the pure PTA, IPTA and TPTA decrease like their aqueous solubilities (Table 1). For internal mixtures, AFHH decreases with a decreasing PTA mass fraction (). This also suggests a declining tendency to adsorb water with a decrease in PTA concentration.
BFHH controls the attractive forces between the particle surface and subsequently adsorbed monolayers of water. The smaller the value of BFHH, the stronger the attractive forces over a larger radial distance from the particle surface. For the pure compounds, BFHH varies in the order of IPTA > TPTA > PTA (Table 2). This suggests that the attractive force across the adsorbed monolayers is lowest in the case of the droplets formed on IPTA particles. For internal mixtures, BFHH follows a similar trend as AFHH and decreases with a decreasing PTA mass fraction (). This suggests that the attractive force across the adsorbed monolayers becomes stronger with a decrease in PTA concentration.
It can be inferred that AFHH follows the trends of solubility and is most likely controlled by functional groups, and BFHH drives overall droplet growth across different compositions and molar volumes. The results here are consistent with Mao et al. (2022), who showed that the AFHH values correlated with functionalized surfaces of aerosol with the same core (polystyrene latex, PSL). This suggests that the AFHH values may play a more important role with compounds of similar molar volume and highlights the importance of functionalized groups and isomeric structures in determining overall droplet growth.
4.3 Hybrid Activity Model (HAM) application for pure and internally mixed AAAs
One of the major factors affecting droplet growth studied in this work is the aqueous solubility of the compound. AAAs and their mixtures used in this work possess approximately equal molar mass and densities, and hence equal molar volumes. Nonetheless, they differ in terms of their water uptake. Analysis shows that the differences in their water uptake behavior could arise due to the significant variation between their aqueous solubilities. Results in the previous subsection show that either KT or an adsorption theory (FHH-AT) can be applied for the CCN analysis of moderate- and low-aqueous-solubility species, respectively. Alternatively, the Hybrid Activity Model (HAM) that sandwiches the FHH isotherm with Raoult's law through solubility partitioning may agree well with the experimental data.
Figure 4 shows the S vs. Ddry,c measurements for AAAs and PTA–IPTA internal mixtures plotted along with their HAM fits. The dot-dashed lines represent the HAM fits for the respective CCN dataset. The calculation of the water activity term for all the samples studied in this work was done following the method described in Sect. 3.3. It was observed that KT, FHH-AT and HAM provided similar fits for samples with aqueous solubility of the order of 10−3 m3 m−3. Thus similar fits for KT, FHH-AT and HAM were observed for the samples with higher PTA mass percentage (pure PTA and the 5:1 PTA–IPTA mixture). The comparison of the goodness of fit between KT, FHH-AT and HAM can be made using the R2 scores provided in Table 3. For pure PTA and 5:1 PTA–IPTA samples, all three models provided a goodness of fit. As the aqueous solubility of the sample was decreased (1:1 and 1:5 PTA–IPTA mixtures, pure IPTA, and pure TPTA, in that order), HAM still provided an improved CCN activity prediction for the samples (R2 scores of 0.92, 0.97, 0.94 and 0.91, respectively; Table 3). FHH-AT and HAM provided similar and improved R2 scores along the decline in the aqueous solubility of the species, whereas the R2 scores corresponding to KT fits were found to decline with decreasing aqueous solubility of the samples. Moreover, the R2 scores for HAM fittings were observed to be uniformly >0.9 and generally higher than those obtained for FHH-AT.
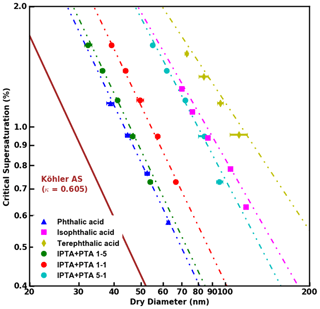
Figure 4S vs. Ddry,c data obtained from supersaturated CCN measurements of pure and internally mixed AAA samples. HAM fits applied to the experimental data are shown as dot-dashed lines.
4.4 Hygroscopicity parameterization for supersaturated conditions
The S vs. Ddry,c values of the AAA samples were transformed into a single hygroscopicity parameter (κ) based on KT, FHH-AT and HAM (Sect. 3.4). Figure 5 shows a closure plot between theoretical and experimental κ estimated for PTA, IPTA, TPTA and PTA–IPTA internal mixtures from KT, FHH-AT and HAM. The closure analysis provides a better understanding of the applicability of different CCN models. The shaded portion of the graph denotes a 95 % confidence interval across a 1–1 agreement line (dashed, black).
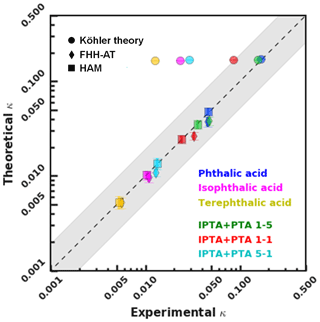
Figure 5Closure plot representing the experimental and theoretical single hygroscopicity parameters obtained using KT, FHH-AT and HAM CCN analysis frameworks. The goodness of fit was calculated for each compound and internal mixture.
The theoretical κ for KT has been represented using size-independent κintrinsic=0.172 calculated using Eqs. (4) and (5), respectively. κKT values computed using S vs. Ddry,c measurements are plotted for each compound. For KT (solid circles), the agreement between κKT and κintrinsic decreases with a decreasing aqueous solubility of the solute. Specifically, the experimental κ lies within 95 % confidence of the theoretical κ of pure PTA, 5:1 PTA–IPTA internal mixture and 1:1 PTA–IPTA internal mixture. TPTA is the sample with the lowest aqueous solubility and hence the lowest agreement between κKT and κintrinsic.
The theoretical adsorption-based parameterization (κFHH,s) and κFHH computed from the experimental data using the FHH-AT framework are shown using solid diamond markers in Fig. 5. The κFHH,s and κFHH were estimated using Eqs. (15) and (14), respectively. It was found that κFHH values had a generally good agreement with their respective κFHH,s (R2 in the range of 0.91 to 0.99). The lowest agreement between FHH-AT κ was observed for PTA and the 5:1 PTA–IPTA internal mixture, as both likely have the highest aqueous solubilities among the studied samples. Moreover, the κFHH and κFHH,s values of IPTA and TPTA are highly consistent with each other.
The theoretical and experimental κHAM values were computed using Eqs. (19) and (18), respectively. The data points for κHAM and κHAM,s are denoted using solid squares in Fig. 5. The most important feature of the HAM-based κ framework is that it explicitly accounts for the compound solubility within the hygroscopicity parameterization. Accounting for the contribution from the solid organic phase and dissolved aqueous phase to the overall hygroscopicity of the solute generates the best agreement between the κHAM and κHAM,s values. Consequently, the R2 scores observed between κHAM and κHAM,s of the six AAA samples are >0.97. It is also important to note that κ values for AAA samples obtained from FHH-AT and HAM frameworks are smaller than those obtained using KT.
4.5 Droplet growth under subsaturated conditions
All the measurements shown in Fig. 6 were performed at a 95 % RH. Figure 6a–c show the droplet sizes (Dwet) with respect to their initial dry sizes (Ddry) for pure PTA, IPTA and TPTA. Figure 6d–f show the Dwet with respect to the Ddry for PTA–IPTA internal mixtures. The Dwet predictions based on the KT–Raoult term, FHH isotherm and hybrid water activity were derived from the parameters provided in Table 2. The Raoult model estimates (dashed black lines) for the pure and internally mixed samples were generated using their average hygroscopic growth factor (Gf; Fig. 6, Eq. 7). The supersaturated average κ of 0.17 for the AAA samples was used to obtain the theoretical Dwet and Gf at given dry sizes. The R2 scores for the KT–Raoult model are summarized in Table 3. The KT–Raoult model agreed well for pure PTA and the 5:1 PTA–IPTA mixture.
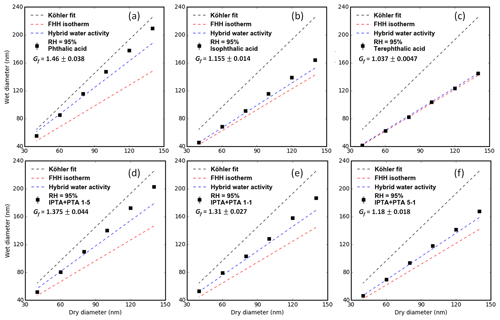
Figure 6Subsaturated measurements for pure AAA samples obtained using the H-TDMA setup are shown. Panels (a), (b) and (c) show the Dwet vs. Ddry data along with model fits for pure PTA, IPTA and TPTA. Panels (d), (e) and (f) show the Dwet vs. Ddry data along with model fits for PTA–IPTA internal mixtures. The KT–Raoult term, FHH isotherm and hybrid water activity fits are shown in black, red and blue, respectively, overlaid with the experimental data. The hygroscopic growth factors (Gf) for all AAA samples are shown in their legends.
The dashed red lines in Fig. 6 show the Dwet estimated using the FHH isotherm (Eq. 4). The empirical FHH parameters used here were determined by fitting the FHH-AT to the supersaturated CCNC measurements (Sect. 4.2, Table 2). FHH noticeably underpredicts the hygroscopic behavior of the AAAs except for IPTA and TPTA in the subsaturated regime (R2 estimates in Table 3). This implies that the insoluble behavior of IPTA and TPTA can be represented with high certainty in the subsaturated as well as the supersaturated regime, using the FHH theory. Moreover, the KT and FHH models (that agreed for soluble compounds, PTA and the 5:1 PTA–IPTA mixture) have different droplet growth predictions in the subsaturated regime.
The dashed blue lines in Fig. 6 show the Dwet estimated using the comprehensive hybrid water activity expressions described in Sect. 3.3 (Eq. 6). Again, the hybrid water activity requires the empirical FHH parameters obtained by fitting FHH-AT to the supersaturated CCNC measurements (Table 2) and the aqueous solubility of the compound to account for the dissolved fraction of solute (Table 1). The hybrid water activity replicated the subsaturated water uptake of all six of the AAAs with high certainty (R2 estimates in Table 3). This is due to the explicit consideration of both compound solubility and water adsorption to describe the droplet growth process. Notably, the hybrid water activity is similar to either the KT–Raoult or the FHH isotherm depending on the compound solubility. For sparingly soluble samples (e.g., pure PTA), the KT–Raoult and hybrid water activity generated similar fits (R2 of 0.938 and 0.948, respectively). For effectively insoluble samples (e.g., pure TPTA), the FHH isotherm and hybrid activity generated similar fits (R2 of 0.998 and 0.999, respectively).
The sub- and supersaturated analyses are consistent with the equilibrium curves for the pure and internally mixed AAA samples. Figure 7 shows droplet growth predicted using KT, FHH-AT and HAM corresponding to one of the experimentally determined Ddry,c. The predicted critical supersaturations (Sc) are also shown in the plots. KT-predicted Sc values deviate significantly (>10 %) from the experimental Sc, as the aqueous solubility of the solute decreases. This is because KT for the structural isomers assumes similar droplet growth (κintrinsic is ∼ 0.17). However, FHH-AT and HAM require higher supersaturations and are less CCN-active, and therefore the points of activation are shifted upwards and to the left. At a given relative humidity (RH) <100 %, the KT-derived Dwet is found to be larger than those predicted using either FHH-AT or HAM. This is consistent with the models and experimental data at 95 % RH shown in Fig. 6. KT-based Dwet was found to be close to the experimental Dwet for pure PTA and the 5:1 PTA–IPTA mixture, whereas Dwet values from FHH-AT and HAM were found close to the experimental Dwet for the remaining solutes. After critical activation, there may be a jump from a water-adsorption-driven droplet growth to one driven by complete dissolution of the solute (vertical jump in green line from blue to red). This is prominently seen in PTA but is not as evident in TPTA. Furthermore, multiple transitions are observed in internal mixtures.
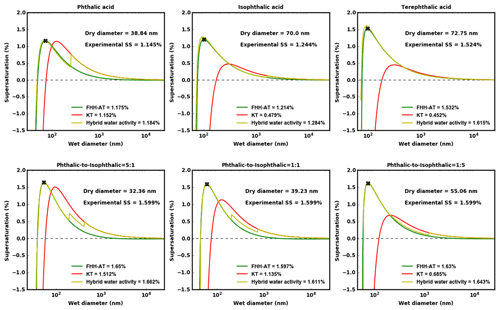
Figure 7Equilibrium droplet growth curves for PTA, IPTA, TPTA and PTA–IPTA internal mixtures are shown here. The figure header shows the solute for which the respective equilibrium curves are plotted. KT, FHH-AT and HAM lines are shown in red (solid), green (solid) and yellow (solid), respectively. An exemplarily measured activation point for the respective solute is denoted using a solid red cross. The Ddry,c and corresponding S used to generate these equilibrium curves are provided in Fig. 2.
VSA measured the water uptake of the three AAA compounds in the subsaturated regime. None of the AAAs showed significant water uptake (with mass growth factors smaller than <1 %) even at high RH (95 %) (Fig. 8). It should be noted that the VSA measurement uses materials in the range of micrometers to millimeters. Thus, the observed κHAM in Eq. (19) decreases with increasing diameter and eventually approaches zero. The results across different particle measurement platforms are consistent with the hygroscopicity parameterization that is particle-size-dependent.
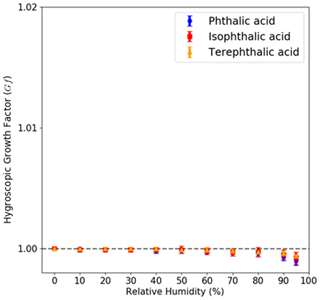
Figure 8Subsaturated measurements for pure AAA samples obtained using the VSA setup are shown. The mass hygroscopic growth factor is shown with respect to the relative humidity (RH). The measurements show that neither of PTA, IPTA or TPTA show any mass-based growth as the RH is increased from 5 % to 95 %.
It should be noted that in this work, we explicitly account for particle shape morphology (dynamic shape factor) and correct the electrical mobility diameters to volume-equivalent diameters as described in Gohil and Asa-Awuku (2022). Shape factors were measured and computed for all samples studied (Fig. S3). Over the mobility diameters of interest (from 50 to 150 nm), the dynamic shape factor values were found to range from 1.00 to 1.08 and were therefore within 10 % of 1.00. This suggests that the AAA samples studied in this work are composed mainly of spherical particles. The application of the dynamic shape factor of aerosols composed of fractals and agglomerates such as black carbon to the transition from soluble to sparingly soluble activation must be considered in future work.
This paper presents the droplet growth analysis of AAAs using a new Hybrid Activity Model (HAM). HAM estimates the thermodynamics of the droplet growth by combining the aqueous solubility of the compound in an adsorption activation framework. HAM accounts for the contributions from undissolved as well as the dissolved fractions of the particle mass to predict droplet growth. Thus, HAM is able to predict critical properties (e.g., Dwet,c, Sc, Gf) for droplet growth in both the supersaturated and subsaturated regimes.
HAM also predicts the droplet growth of internal mixtures. The three PTA–IPTA internal mixtures (5:1, 1:1 and 1:5 with respect to PTA) show a clear transition from sparingly water-soluble to effectively water-insoluble mixtures (Petters and Kreidenweis, 2008). For a mixture containing two or more components, the water activity based on Raoult's law is computed using solubility partitioning (Riipinen et al., 2015). Moreover, a solubility limit of vol/vol water (corresponding to a 3:1 internal mixture with respect to PTA) was determined using solubility partitioning. Below this limit, the discrepancies in CCN activity will likely be >10 % for traditional KT. It is therefore reasonable to assume that the effect of adsorption on droplet growth would be more dominant in determining the growth of the pure and internally mixed AAAs as their solubilities are decreased below vol/vol water. The current literature considers the two paradigms separately, and HAM provides a continuum to bridge and combine both mechanisms.
To do so, HAM requires three compound-specific parameters (Ci, AFHH and BFHH), and the use of the full HAM in cloud microphysical models may extend the computational burden to account for the aerosol chemistry. Therefore, a single hygroscopicity parameter was also developed and exhibited an improved hygroscopicity parameterization for all solutes studied in this work. Raoult's law generally overpredicts the hygroscopicity of effectively insoluble solutes. And the FHH isotherm generally underpredicts the hygroscopicity of sparingly soluble solutes. Combining the two droplet growth mechanisms in HAM provided a more robust approximation of the water uptake behavior in both subsaturated and supersaturated environments. Consequently, the experimental and simplified (theoretical) hygroscopicity estimates based on HAM (κHAM and κHAM,s) showed the best agreement and highest goodness of fits when applied to the experimental data.
Overall, HAM is a promising new droplet growth model that can be potentially used for the analysis of any type of atmospheric compound. HAM is effective because it combines the characteristic features of the traditional KT with solubility partitioning and FHH-AT. Additionally, HAM differs from previous analytical frameworks that are based on compound solubility in that for any species using HAM, the particles are treated as completely undissolved at the start of the activation process. This is vital because other solubility-limiting approaches begin with instantaneous dissolution and add the element of reduced solubility along the course of droplet growth. Indeed the approach is congruous to the concept of earlier works that explored the impact of slow dissolution (e.g., Shulman et al., 1996; Asa-Awuku and Nenes, 2007) and aligns with more current findings that describe the droplet growth of viscous, amorphous or glassy-like aerosols (e.g., Altaf et al., 2018; Tandon et al., 2019; Zobrist et al., 2008; Mikhailov et al., 2009; Peng et al., 2022).
In HAM, the contribution of the theorized undissolved fraction facilitates a surface until the particle fully dissolves, after which further droplet growth is controlled solely by the entire particle mass present in the aqueous phase. The HAM concept may have even more utility at lower temperatures and higher altitudes. In general the solubility of compounds in water will likely decrease at lower temperatures; thus the role of surface adsorption in the undissolved fraction will be important to droplet growth. Additionally, solute viscosity of atmospheric compounds has been shown to have more significant effects on droplet growth at lower temperatures in the subsaturated regime (Kasparoglu et al., 2021). Rather than considering complex morphological parameters (diffusivity, viscosity, rheology), HAM simplifies the concept by considering the presence (or lack thereof) of a surface. In addition to the factors considered in this work, surface tension can potentially play a role in both the water activity term and also in the solute partition and should therefore be treated explicitly in the droplet growth process. Incorporation of surface tension in the analysis was beyond the scope of this work, and well-designed experiments will be required to observe whether surface tension has any contribution to the water uptake of the AAAs studied in this paper. Furthermore, surface effects of a given species can be parameterized within the HAM framework and subsequently into the hygroscopicity to understand such effects for partially insoluble to effectively insoluble systems.
The next step is to evaluate the application of HAM for the CCN analysis of aerosol mixtures for a wider range of aerosol species and compositions. The shift from volume- to surface-based absorption principles may be more appropriate for significantly water-insoluble compounds. Specifically, the application of HAM can be examined for the hygroscopic growth and water uptake on black carbon agglomerates. Furthermore, HAM developed in this work may improve our predictions of a wide variety of atmospherically relevant aerosols. For example, many atmospheric organic aerosols may vary significantly from each other in terms of their chemical structures and aqueous solubilities (Petters and Kreidenweis, 2008; Sullivan et al., 2009). Therefore, HAM may potentially improve the representation of hygroscopicity of organic aerosols in large-scale global climate models (GCMs), hence reducing the uncertainties in the climate forcing due to the aerosol indirect effect.
The PyCAT code is available for public use through Zenodo (https://doi.org/10.5281/zenodo.6329787; Gohil, 2022). The measurement data can be provided by the authors on request.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-22-12769-2022-supplement.
KG and AAA designed the analysis for the supersaturated and subsaturated experimental data. KG and DR performed CCN and H-TDMA experiments to collect data. KG and CNM parameterized the FHH hygroscopicity. KG formulated HAM and parameterized the corresponding hygroscopicity. AAA conceived the idea for the study and designed and developed the experimental methodology. CP and MT collected VSA data and performed VSA analysis. All authors contributed to the writing and preparation of the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research has been supported by the National Science Foundation (grant nos. CHEM-1708337 and CHEM-2003927).
This paper was edited by Dantong Liu and reviewed by two anonymous referees.
Al-Naiema, I. M. and Stone, E. A.: Evaluation of anthropogenic secondary organic aerosol tracers from aromatic hydrocarbons, Atmos. Chem. Phys., 17, 2053–2065, https://doi.org/10.5194/acp-17-2053-2017, 2017. a
Al-Naiema, I. M., Offenberg, J. H., Madler, C. J., Lewandowski, M., Kettler, J., Fang, T., and Stone, E. A.: Secondary organic aerosols from aromatic hydrocarbons and their contribution to fine particulate matter in Atlanta, Georgia, Atmos. Environ., 223, 117227, https://doi.org/10.1016/j.atmosenv.2019.117227, 2020. a
Altaf, M. B., Dutcher, D. D., Raymond, T. M., and Freedman, M. A.: Effect of particle morphology on cloud condensation nuclei activity, ACS Earth Space Chem., 2, 634–639, 2018. a
Asa-Awuku, A. and Nenes, A.: Effect of solute dissolution kinetics on cloud droplet formation: Extended Köhler theory, J. Geophys. Res.-Atmos., 112, https://doi.org/10.1029/2005JD006934, 2007. a
Asa-Awuku, A., Nenes, A., Gao, S., Flagan, R. C., and Seinfeld, J. H.: Water-soluble SOA from Alkene ozonolysis: composition and droplet activation kinetics inferences from analysis of CCN activity, Atmos. Chem. Phys., 10, 1585–1597, https://doi.org/10.5194/acp-10-1585-2010, 2010. a, b
Balla, D., Voutsa, D., and Samara, C.: Study of polar organic compounds in airborne particulate matter of a coastal urban city, Environ. Sci. Pollut. Res., 25, 12191–12205, https://doi.org/10.1007/s11356-017-9993-2, 2018. a
Barati, F., Yao, Q., and Asa-Awuku, A. A.: Insight into the Role of Water-Soluble Organic Solvents for the Cloud Condensation Nuclei Activation of Cholesterol, ACS Earth Space Chem., 3, 1697–1705, 2019. a, b
Baustian, K. J., Cziczo, D. J., Wise, M. E., Pratt, K. A., Kulkarni, G., Hallar, A. G., and Tolbert, M. A.: Importance of aerosol composition, mixing state, and morphology for heterogeneous ice nucleation: A combined field and laboratory approach, J. Geophys. Res., 117, https://doi.org/10.1029/2011JD016784, 2012. a
Cruz, C. N. and Pandis, S. N.: Deliquescence and hygroscopic growth of mixed inorganic- organic atmospheric aerosol, Environ. Sci. Technol., 34, 4313–4319, 2000. a
Dalirian, M., Ylisirniö, A., Buchholz, A., Schlesinger, D., Ström, J., Virtanen, A., and Riipinen, I.: Cloud droplet activation of black carbon particles coated with organic compounds of varying solubility, Atmos. Chem. Phys., 18, 12477–12489, https://doi.org/10.5194/acp-18-12477-2018, 2018. a
Dawson, J. N., Malek, K. A., Razafindrambinina, P. N., Raymond, T. M., Dutcher, D. D., Asa-Awuku, A. A., and Freedman, M. A.: Direct Comparison of the Submicron Aerosol Hygroscopicity of Water-Soluble Sugars, ACS Earth Space Chem., 4, 2215–2226, https://doi.org/10.1021/acsearthspacechem.0c00159, 2020. a
Diniz, L. F., Carvalho, P. S., de Melo, C. C., and Ellena, J.: Reducing the Hygroscopicity of the Anti-Tuberculosis Drug (S, S)-Ethambutol Using Multicomponent Crystal Forms, Cryst. Growth Design, 17, 2622–2630, https://doi.org/10.1021/acs.cgd.7b00144, 2017. a
Engelhart, G. J., Asa-Awuku, A., Nenes, A., and Pandis, S. N.: CCN activity and droplet growth kinetics of fresh and aged monoterpene secondary organic aerosol, Atmos. Chem. Phys., 8, 3937–3949, https://doi.org/10.5194/acp-8-3937-2008, 2008. a
Fofie, E. A., Donahue, N. M., and Asa-Awuku, A.: Cloud condensation nuclei activity and droplet formation of primary and secondary organic aerosol mixtures, Aerosol Sci. Tech., 52, 242–251, https://doi.org/10.1080/02786826.2017.1392480, 2018. a
Fu, P., Kawamura, K., and Barrie, L. A.: Photochemical and Other Sources of Organic Compounds in the Canadian High Arctic Aerosol Pollution during Winter−Spring, Environ. Sci. Technol., 43, 286–292, https://doi.org/10.1021/es803046q, 2009. a
Giordano, M., Espinoza, C., and Asa-Awuku, A.: Experimentally measured morphology of biomass burning aerosol and its impacts on CCN ability, Atmos. Chem. Phys., 15, 1807–1821, https://doi.org/10.5194/acp-15-1807-2015, 2015. a
Gohil, K.: kgohil27/PyCAT: v1.0.1 (v1.1), Zenodo, https://doi.org/10.5281/zenodo.6329787, 2022. a
Gohil, K. and Asa-Awuku, A. A.: Cloud condensation nuclei (CCN) activity analysis of low-hygroscopicity aerosols using the aerodynamic aerosol classifier (AAC), Atmos. Meas. Tech., 15, 1007–1019, https://doi.org/10.5194/amt-15-1007-2022, 2022. a, b, c
Goodman, A. L., Bernard, E. T., and Grassian, V. H.: Spectroscopic Study of Nitric Acid and Water Adsorption on Oxide Particles: Enhanced Nitric Acid Uptake Kinetics in the Presence of Adsorbed Water, J. Phys. Chem. A, 105, 6443–6457, https://doi.org/10.1021/jp003722l, 2001. a
Gu, W., Li, Y., Zhu, J., Jia, X., Lin, Q., Zhang, G., Ding, X., Song, W., Bi, X., Wang, X., and Tang, M.: Investigation of water adsorption and hygroscopicity of atmospherically relevant particles using a commercial vapor sorption analyzer, Atmos. Meas. Tech., 10, 3821–3832, https://doi.org/10.5194/amt-10-3821-2017, 2017. a
Gunn, R.: The ratio of the positive and negative light ion conductivities within a neutral aerosol space, J. Colloid Sci., 11, 661–696, 1956. a
Hämeri, K., Charlson, R., and Hansson, H.-C.: Hygroscopic properties of mixed ammonium sulfate and carboxylic acids particles, AIChE J., 48, 1309–1316, https://doi.org/10.1002/aic.690480617, 2002. a
Haque, Md. M., Kawamura, K., Deshmukh, D. K., Fang, C., Song, W., Mengying, B., and Zhang, Y.-L.: Characterization of organic aerosols from a Chinese megacity during winter: predominance of fossil fuel combustion, Atmos. Chem. Phys., 19, 5147–5164, https://doi.org/10.5194/acp-19-5147-2019, 2019. a
Hartz, K. E. H., Tischuk, J. E., Chan, M. N., Chan, C. K., Donahue, N. M., and Pandis, S. N.: Cloud condensation nuclei activation of limited solubility organic aerosol, Atmos. Environ., 40, 605–617, https://doi.org/10.1016/j.atmosenv.2005.09.076, 2006. a, b, c, d, e
Hatch, C. D., Wiese, J. S., Crane, C. C., Harris, K. J., Kloss, H. G., and Baltrusaitis, J.: Water Adsorption on Clay Minerals As a Function of Relative Humidity: Application of BET and Freundlich Adsorption Models, Langmuir, 28, 1790–1803, https://doi.org/10.1021/la2042873, 2012. a
Hatch, C. D., Greenaway, A. L., Christie, M. J., and Baltrusaitis, J.: Water adsorption constrained Frenkel–Halsey–Hill adsorption activation theory: Montmorillonite and illite, Atmos. Environ., 87, 26–33, https://doi.org/10.1016/j.atmosenv.2013.12.040, 2014. a
Hatch, C. D., Tumminello, P. R., Cassingham, M. A., Greenaway, A. L., Meredith, R., and Christie, M. J.: Technical note: Frenkel, Halsey and Hill analysis of water on clay minerals: toward closure between cloud condensation nuclei activity and water adsorption, Atmos. Chem. Phys., 19, 13581–13589, https://doi.org/10.5194/acp-19-13581-2019, 2019. a, b
He, X., Huang, X. H. H., Chow, K. S., Wang, Q., Zhang, T., Wu, D., and Yu, J. Z.: Abundance and Sources of Phthalic Acids, Benzene-Tricarboxylic Acids, and Phenolic Acids in PM2.5 at Urban and Suburban Sites in Southern China, ACS Earth Space Chem., 2, 147–158, https://doi.org/10.1021/acsearthspacechem.7b00131, 2018. a
Henson, B. F.: An adsorption model of insoluble particle activation: Application to black carbon, J. Geophys. Res., 112, D24S16, https://doi.org/10.1029/2007JD008549, 2007. a
Jing, B., Tong, S., Liu, Q., Li, K., Wang, W., Zhang, Y., and Ge, M.: Hygroscopic behavior of multicomponent organic aerosols and their internal mixtures with ammonium sulfate, Atmos. Chem. Phys., 16, 4101–4118, https://doi.org/10.5194/acp-16-4101-2016, 2016. a
Jing, B., Wang, Z., Tan, F., Guo, Y., Tong, S., Wang, W., Zhang, Y., and Ge, M.: Hygroscopic behavior of atmospheric aerosols containing nitrate salts and water-soluble organic acids, Atmos. Chem. Phys., 18, 5115–5127, https://doi.org/10.5194/acp-18-5115-2018, 2018. a, b
Kanakidou, M., Seinfeld, J. H., Pandis, S. N., Barnes, I., Dentener, F. J., Facchini, M. C., Van Dingenen, R., Ervens, B., Nenes, A., Nielsen, C. J., Swietlicki, E., Putaud, J. P., Balkanski, Y., Fuzzi, S., Horth, J., Moortgat, G. K., Winterhalter, R., Myhre, C. E. L., Tsigaridis, K., Vignati, E., Stephanou, E. G., and Wilson, J.: Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 5, 1053–1123, https://doi.org/10.5194/acp-5-1053-2005, 2005. a
Kanellopoulos, P. G., Verouti, E., Chrysochou, E., Koukoulakis, K., and Bakeas, E.: Primary and secondary organic aerosol in an urban/industrial site: Sources, health implications and the role of plastic enriched waste burning, J. Environ. Sci., 99, 222–238, https://doi.org/10.1016/j.jes.2020.06.012, 2021. a
Kasparoglu, S., Li, Y., Shiraiwa, M., and Petters, M. D.: Toward closure between predicted and observed particle viscosity over a wide range of temperatures and relative humidity, Atmos. Chem. Phys., 21, 1127–1141, https://doi.org/10.5194/acp-21-1127-2021, 2021. a
Kawamura, K. and Kaplan, I. R.: Motor exhaust emissions as a primary source for dicarboxylic acids in Los Angeles ambient air, Environ. Sci. Technol., 21, 105–110, https://doi.org/10.1021/es00155a014, 1987. a
Kleindienst, T. E., Jaoui, M., Lewandowski, M., Offenberg, J. H., and Docherty, K. S.: The formation of SOA and chemical tracer compounds from the photooxidation of naphthalene and its methyl analogs in the presence and absence of nitrogen oxides, Atmos. Chem. Phys., 12, 8711–8726, https://doi.org/10.5194/acp-12-8711-2012, 2012. a
Kreidenweis, S. and Asa-Awuku, A.: Aerosol hygroscopicity: Particle water content and its role in atmospheric processes, Elsevier, 331–361, 2014. a
Kumar, P., Nenes, A., and Sokolik, I. N.: Importance of adsorption for CCN activity and hygroscopic properties of mineral dust aerosol, Geophys. Res. Lett., https://doi.org/10.1029/2009GL040827, 2009a. a, b, c, d, e, f, g
Kumar, P., Sokolik, I. N., and Nenes, A.: Parameterization of cloud droplet formation for global and regional models: including adsorption activation from insoluble CCN, Atmos. Chem. Phys., 9, 2517–2532, https://doi.org/10.5194/acp-9-2517-2009, 2009b. a, b, c, d
Kumar, P., Sokolik, I. N., and Nenes, A.: Cloud condensation nuclei activity and droplet activation kinetics of wet processed regional dust samples and minerals, Atmos. Chem. Phys., 11, 8661–8676, https://doi.org/10.5194/acp-11-8661-2011, 2011a. a, b, c
Kumar, P., Sokolik, I. N., and Nenes, A.: Measurements of cloud condensation nuclei activity and droplet activation kinetics of fresh unprocessed regional dust samples and minerals, Atmos. Chem. Phys., 11, 3527–3541, https://doi.org/10.5194/acp-11-3527-2011, 2011b. a, b, c, d, e
Kunwar, B., Kawamura, K., Fujiwara, S., Fu, P., Miyazaki, Y., and Pokhrel, A.: Dicarboxylic acids, oxocarboxylic acids and α-dicarbonyls in atmospheric aerosols from Mt. Fuji, Japan: Implication for primary emission versus secondary formation, Atmos. Res., 221, 58–71, https://doi.org/10.1016/j.atmosres.2019.01.021, 2019. a
Köhler, H.: The nucleus in and the growth of hygroscopic droplets, T. Faraday Soc., 32, 1152–1161, 1936. a, b
Laaksonen, A., Malila, J., Nenes, A., Hung, H.-M., and Chen, J.-P.: Surface fractal dimension, water adsorption efficiency and cloud nucleation activity of insoluble aerosol, Sci. Rep., 6, 25504, https://doi.org/10.1038/srep25504, 2016. a
Laaksonen, A., Malila, J., and Nenes, A.: Heterogeneous nucleation of water vapor on different types of black carbon particles, Atmos. Chem. Phys., 20, 13579–13589, https://doi.org/10.5194/acp-20-13579-2020, 2020. a
Liu, H., Kawamura, K., Kunwar, B., Cao, J., Zhang, J., Zhan, C., Zheng, J., Yao, R., Liu, T., and Xiao, W.: Dicarboxylic acids and related compounds in fine particulate matter aerosols in Huangshi, central China, J. Air Waste Manage. Assoc., 69, 513–526, https://doi.org/10.1080/10962247.2018.1557089, 2019. a
Malek, K. A., Gohil, K., Al-Abadleh, H. A., and Asa-Awuku, A. A.: Hygroscopicity of polycatechol and polyguaiacol secondary organic aerosol in sub- and supersaturated water vapor environments, Environ. Sci. Atmos., 2, 24–33, https://doi.org/10.1039/D1EA00063B, 2022. a
Mao, C.-N., Gohil, K., and Asa-Awuku, A.: A Single Parameter Hygroscopicity Model for Functionalized and Insoluble Aerosol Surfaces, Atmos. Chem. Phys. Discuss. [preprint], https://doi.org/10.5194/acp-2022-339, in review, 2022. a, b, c, d
Meng, J., Wang, G., Hou, Z., Liu, X., Wei, B., Wu, C., Cao, C., Wang, J., Li, J., Cao, J., Zhang, E., Dong, J., Liu, J., Ge, S., and Xie, Y.: Molecular distribution and stable carbon isotopic compositions of dicarboxylic acids and related SOA from biogenic sources in the summertime atmosphere of Mt. Tai in the North China Plain, Atmos. Chem. Phys., 18, 15069–15086, https://doi.org/10.5194/acp-18-15069-2018, 2018. a
Mikhailov, E., Vlasenko, S., Martin, S. T., Koop, T., and Pöschl, U.: Amorphous and crystalline aerosol particles interacting with water vapor: conceptual framework and experimental evidence for restructuring, phase transitions and kinetic limitations, Atmos. Chem. Phys., 9, 9491–9522, https://doi.org/10.5194/acp-9-9491-2009, 2009. a
Mkoma, S. L. and Kawamura, K.: Molecular composition of dicarboxylic acids, ketocarboxylic acids, α-dicarbonyls and fatty acids in atmospheric aerosols from Tanzania, East Africa during wet and dry seasons, Atmos. Chem. Phys., 13, 2235–2251, https://doi.org/10.5194/acp-13-2235-2013, 2013. a
Moore, R. H., Nenes, A., and Medina, J.: Scanning Mobility CCN Analysis—A Method for Fast Measurements of Size-Resolved CCN Distributions and Activation Kinetics, Aerosol Sci. Tech., 44, 861–871, 2010. a
Nakao, S.: Why would apparent κ linearly change with O/C? Assessing the role of volatility, solubility, and surface activity of organic aerosols, Aerosol Sci. Tech., 51, 1377–1388, https://doi.org/10.1080/02786826.2017.1352082, 2017. a
Padró, L. T., Moore, R. H., Zhang, X., Rastogi, N., Weber, R. J., and Nenes, A.: Mixing state and compositional effects on CCN activity and droplet growth kinetics of size-resolved CCN in an urban environment, Atmos. Chem. Phys., 12, 10239–10255, https://doi.org/10.5194/acp-12-10239-2012, 2012. a
Peng, C., Malek, K. A., Rastogi, D., Zhang, Y., Wang, W., Ding, X., Asa-Awuku, A. A., Wang, X., and Tang, M.: Hygroscopicity and cloud condensation nucleation activities of hydroxyalkylsulfonates, Sci. Total Enviro., 830, 154767, https://doi.org/10.1016/j.scitotenv.2022.154767, 2022. a
Petters, M. D., Wex, H., Carrico, C. M., Hallbauer, E., Massling, A., McMeeking, G. R., Poulain, L., Wu, Z., Kreidenweis, S. M., and Stratmann, F.: Towards closing the gap between hygroscopic growth and activation for secondary organic aerosol – Part 2: Theoretical approaches, Atmos. Chem. Phys., 9, 3999–4009, https://doi.org/10.5194/acp-9-3999-2009, 2009. a
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. a, b, c, d, e
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity – Part 2: Including solubility, Atmos. Chem. Phys., 8, 6273–6279, https://doi.org/10.5194/acp-8-6273-2008, 2008. a, b, c, d, e, f, g
Rader, D. and McMurry, P.: Application of the tandem differential mobility analyzer to studies of droplet growth or evaporation, J. Aerosol Sci., 17, 771–787, 1986. a
Rahman, M. A. and Al-Abadleh, H. A.: Surface Water Structure and Hygroscopic Properties of Light Absorbing Secondary Organic Polymers of Atmospheric Relevance, ACS Omega, 3, 15519–15529, https://doi.org/10.1021/acsomega.8b02066, 2018. a
Riipinen, I., Rastak, N., and Pandis, S. N.: Connecting the solubility and CCN activation of complex organic aerosols: a theoretical study using solubility distributions, Atmos. Chem. Phys., 15, 6305–6322, https://doi.org/10.5194/acp-15-6305-2015, 2015. a, b, c, d, e, f, g
Roberts, G. and Nenes, A.: A continuous-flow streamwise thermal-gradient CCN chamber for atmospheric measurements, Aerosol Sci. Tech., 39, 206–221, 2005. a
Samy, S., Mazzoleni, L. R., Mishra, S., Zielinska, B., and Hallar, A. G.: Water-soluble organic compounds at a mountain-top site in Colorado, USA, Atmos. Environ., 44, 1663–1671, https://doi.org/10.1016/j.atmosenv.2010.01.033, 2010. a
Sánchez Gácita, M., Longo, K. M., Freire, J. L. M., Freitas, S. R., and Martin, S. T.: Impact of mixing state and hygroscopicity on CCN activity of biomass burning aerosol in Amazonia, Atmos. Chem. Phys., 17, 2373–2392, https://doi.org/10.5194/acp-17-2373-2017, 2017. a
Schill, S. R., Collins, D. B., Lee, C., Morris, H. S., Novak, G. A., Prather, K. A., Quinn, P. K., Sultana, C. M., Tivanski, A. V., Zimmermann, K., and Cappa, C. D.: The Impact of Aerosol Particle Mixing State on the Hygroscopicity of Sea Spray Aerosol, ACS Cent. Sci., 1, 132–141, 2015. a
Shulman, M. L., Jacobson, M. C., Carlson, R. J., Synovec, R. E., and Young, T. E.: Dissolution behavior and surface tension effects of organic compounds in nucleating cloud droplets, Geophys. Res. Lett., 23, 277–280, 1996. a
Singh, D. K., Kawamura, K., Yanase, A., and Barrie, L. A.: Distributions of Polycyclic Aromatic Hydrocarbons, Aromatic Ketones, Carboxylic Acids, and Trace Metals in Arctic Aerosols: Long-Range Atmospheric Transport, Photochemical Degradation/Production at Polar Sunrise, Environ. Sci. Technol., 51, 8992–9004, https://doi.org/10.1021/acs.est.7b01644, 2017. a
Sorjamaa, R. and Laaksonen, A.: The effect of H2O adsorption on cloud drop activation of insoluble particles: a theoretical framework, Atmos. Chem. Phys., 7, 6175–6180, https://doi.org/10.5194/acp-7-6175-2007, 2007. a, b, c
Su, H., Rose, D., Cheng, Y. F., Gunthe, S. S., Massling, A., Stock, M., Wiedensohler, A., Andreae, M. O., and Pöschl, U.: Hygroscopicity distribution concept for measurement data analysis and modeling of aerosol particle mixing state with regard to hygroscopic growth and CCN activation, Atmos. Chem. Phys., 10, 7489–7503, https://doi.org/10.5194/acp-10-7489-2010, 2010. a
Sullivan, R. C., Moore, M. J. K., Petters, M. D., Kreidenweis, S. M., Roberts, G. C., and Prather, K. A.: Effect of chemical mixing state on the hygroscopicity and cloud nucleation properties of calcium mineral dust particles, Atmos. Chem. Phys., 9, 3303–3316, https://doi.org/10.5194/acp-9-3303-2009, 2009. a, b, c, d, e
Talley, L. D., Vaughan, D. G., Xie, S. P., Allen, M. R., Boucher, O., et al.: Climate Change 2013. The Physical Science Basis. Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change – Abstract for decision-makers, edited by: Stocker, T., 2013. a
Tandon, A., Rothfuss, N. E., and Petters, M. D.: The effect of hydrophobic glassy organic material on the cloud condensation nuclei activity of particles with different morphologies, Atmos. Chem. Phys., 19, 3325–3339, https://doi.org/10.5194/acp-19-3325-2019, 2019. a
Tang, M., Cziczo, D. J., and Grassian, V. H.: Interactions of Water with Mineral Dust Aerosol: Water Adsorption, Hygroscopicity, Cloud Condensation, and Ice Nucleation, Chem. Rev., 116, 4205–4259, https://doi.org/10.1021/acs.chemrev.5b00529, 2016. a
Tang, X., Cocker III, D. R., and Asa-Awuku, A.: Are sesquiterpenes a good source of secondary organic cloud condensation nuclei (CCN)? Revisiting β-caryophyllene CCN, Atmos. Chem. Phys., 12, 8377–8388, https://doi.org/10.5194/acp-12-8377-2012, 2012. a
Tavakoli, F. and Olfert, J. S.: Determination of particle mass, effective density, mass–mobility exponent, and dynamic shape factor using an aerodynamic aerosol classifier and a differential mobility analyzer in tandem, J. Aerosol Sci., 75, 35–42, 2014. a
Taylor, N. F., Collins, D. R., Spencer, C. W., Lowenthal, D. H., Zielinska, B., Samburova, V., and Kumar, N.: Measurement of ambient aerosol hydration state at Great Smoky Mountains National Park in the southeastern United States, Atmos. Chem. Phys., 11, 12085–12107, https://doi.org/10.5194/acp-11-12085-2011, 2011. a
Taylor, N. F., Collins, D. R., Lowenthal, D. H., McCubbin, I. B., Hallar, A. G., Samburova, V., Zielinska, B., Kumar, N., and Mazzoleni, L. R.: Hygroscopic growth of water soluble organic carbon isolated from atmospheric aerosol collected at US national parks and Storm Peak Laboratory, Atmos. Chem. Phys., 17, 2555–2571, https://doi.org/10.5194/acp-17-2555-2017, 2017. a
Vu, D., Gao, S., Berte, T., Kacarab, M., Yao, Q., Vafai, K., and Asa-Awuku, A.: External and internal cloud condensation nuclei (CCN) mixtures: controlled laboratory studies of varying mixing states, Atmos. Meas. Tech., 12, 4277–4289, https://doi.org/10.5194/amt-12-4277-2019, 2019. a, b
Wang, W., Lei, T., Zuend, A., Su, H., Cheng, Y., Shi, Y., Ge, M., and Liu, M.: Effect of mixing structure on the water uptake of mixtures of ammonium sulfate and phthalic acid particles, Atmos. Chem. Phys., 21, 2179–2190, https://doi.org/10.5194/acp-21-2179-2021, 2021. a, b
Wiedensohler, A.: An approximation of the bipolar charge distribution for particles in the submicron size range, J. Aerosol Sci., 19, 387–389, 1988. a
Yao, Q., Asa-Awuku, A., Zangmeister, C. D., and Radney, J. G.: Comparison of three essential sub-micrometer aerosol measurements: Mass, size and shape, Aerosol Sci. Technol., 54, 1197–1209, 2020. a
Yassine, M. M., Suski, M., and Dabek-Zlotorzynska, E.: Characterization of benzene polycarboxylic acids and polar nitroaromatic compounds in atmospheric aerosols using UPLC-MS/MS, J. Chromatogr. A, 1630, 461507, https://doi.org/10.1016/j.chroma.2020.461507, 2020. a
Zhao, H., Zhang, Z., Hou, H., and Zhang, J.: Hygroscopic salt-modulated UiO-66: Synthesis and its open adsorption performance, J. Solid State Chem., 301, 122304, https://doi.org/10.1016/j.jssc.2021.122304, 2021. a
Zhong, X., Cui, C., and Yu, S.: Exploring the pathways of aromatic carboxylic acids in ozone solutions, RSC Advances, 7, 34339–34347, https://doi.org/10.1039/C7RA03039H, 2017a. a
Zhong, X., Cui, C., and Yu, S.: The determination and fate of disinfection by-products from ozonation-chlorination of fulvic acid, Environ. Sci. Pollut. Res., 24, 6472–6480, https://doi.org/10.1007/s11356-016-8350-1, 2017b. a
Zobrist, B., Marcolli, C., Pedernera, D. A., and Koop, T.: Do atmospheric aerosols form glasses?, Atmos. Chem. Phys., 8, 5221–5244, https://doi.org/10.5194/acp-8-5221-2008, 2008. a