The effectiveness of the coagulation sink of 3–10 nm atmospheric particles

As a major source of ultrafine particles, new particle formation (NPF) occurs frequently in various environments. However, the survival of new particles and the frequent occurrence of NPF events in polluted environments have long been perplexing, since new particles are expected to be scavenged by high coagulation sinks. Towards solving these problems, we establish an experimental method and directly measure the effectiveness of the size-dependent coagulation sink of monodisperse 3–10 nm particles in well-controlled chamber experiments. Based on the chamber experiments and long-term atmospheric measurements from Beijing, we then discuss the survival of new particles in polluted environments. In the chamber experiments, the measured coagulation sink of 3–10 nm particles increases significantly with a decreasing particle size, whereas it is not sensitive to the compositions of test particles. Comparison between the measured coagulation coefficient with theoretical predictions shows that almost every coagulation leads to the scavenging of one particle, and the coagulation sink exceeds the hard-sphere kinetic limit due to van der Waals attractive force. For urban Beijing, the effectiveness of the coagulation sink and a moderate or high (e.g., > 3 nm h⁻¹) growth rate of new particles can explain the occurrence of measured NPF events; the moderate growth rate further implies that, in addition to gaseous sulfuric acid, other gaseous precursors also contribute to the growth of new particles.

1 Introduction

New particle formation (NPF), during which gaseous precursors form new particles via nucleation, is a major source of atmospheric aerosol number concentration (Kulmala et al., 2012a). A fraction of these new particles can grow up to the cloud condensation nucleus size (e.g., > 50 nm) and influence the climate (Kuang et al., 2009; Gordon et al., 2017). Some studies also report that new particles may contribute to haze formation (Guo et al., 2014; Kulmala et al., 2021). The influences of NPF are governed by the number of new particles formed via nucleation and their survival probabilities. In the past decade, instrument development (Jiang et al., 2011; Kulmala et al., 2013), atmospheric measurements (Chen et al., 2012; Bianchi et al., 2016; Sipilä et al., 2016; Yao et al., 2018; Lehtipalo et al., 2018), laboratory experiments (Kirkby et al., 2011; Kürten et al., 2014; Riccobono et al., 2014; He et al., 2021; Jen et al., 2014), and theoretical studies (Ortega et al., 2012; Yu et al., 2018) have led to significant advances in the understanding of nucleation. However, particle survival during the growth process is still poorly understood and under debate. Since the concentration of grown particles is more sensitive to survival probability than nucleation rate (Westervelt et al., 2014), understanding the growth process and accurately determining the survival probability are pivotal to assessing the influences of NPF on regional air quality and global climate.

One of the most confusing problems related to particle survival is the question of how, even after accounting for the high nucleation rate in polluted environments (Cai and Jiang, 2017; Yao et al., 2018; Cai et al., 2021c), new particles can survive and be frequently observed (Kulmala et al., 2017) at a high aerosol surface area concentration. One straightforward approach to address this problem is to retrieve particle survival probability from the evolution of particle size distributions (Weber et al., 1997; Kuang et al., 2009; Kulmala et al., 2017) and compare it to theoretical predictions. Such a comparison reduces the complexity of the problem, yet it does not provide the reasons why the retrieved and theoretical survival probabilities sometimes deviate from each other (Kulmala et al., 2017). Further, both the retrieved and theoretical survival probabilities may be very sensitive to measurement uncertainties and the non-homogeneity of the atmosphere, which presents a challenge to interpreting the comparison results.

Alternatively, one can examine the accuracy of the parameters determining the survival probability via direct measurements. According to theoretical derivations (Weber et al., 1997; Kerminen and Kulmala, 2002; McMurry et al., 2005), particle survival probability is determined by the ratio of their net growth rate (GR) to their loss rate, as characterized by the coagulation sink (CoagS), i.e., CoagS/GR. Hence, a bias in the theoretically predicted survival probability must be caused by biases in CoagS and/or GR. While the uncertainty range of GR retrieved from the measured particle size distributions could be estimated, the effectiveness of the theoretically calculated CoagS was questioned. For example, to explain the observed frequent NPF events in polluted megacities, Kulmala et al. (2017) hypothesized that the CoagS was overestimated due to unconsidered ineffective coagulation between new particles and large particles (i.e., scavengers).

Hence, although challenging, accurate determination of the coagulation coefficient between new particles and large particles using well-controlled experiments is fundamental to estimating particle survival probabilities and the influences of NPF. There have been studies measuring the coagulation coefficient. Okuyama et al. (1984) and Okuyama et al. (1986) measured the coagulation coefficients of NaCl, ZnCl₂, and Ag nanoparticles using a long metal pipe. They observed effective coagulation among these particles and reported significant contributions from van der Waals force to the coagulation coefficient. Similar findings for H₂SO₄–H₂O particles were reported in Chan and Mozurkewich (2001), in which study the coagulation coefficient of monodisperse particles was determined using a 5.2 L tank reactor. Ineffective coagulation was often reported for combustion-generated nascent soot particles (D'Alessio et al., 2005; Sirignano and D'Anna, 2013; Hou et al., 2020). These previous experiments were mainly focused on the coagulation between nanoparticles of similar size. The coagulation coefficients were estimated according to the change in the measured particle size distribution. For atmospheric NPF, however, CoagS is governed by the coagulation coefficients between small new particles and large (e.g., 100 nm) scavengers (Cai et al., 2017b). As a result, the effectiveness of the CoagS of new particles remains unknown, and its determination requires new methods and apparatus to minimize the change of particle size distribution due to self-coagulation between new particles.

In this study, we provide direct experimental evidence for the effectiveness of the CoagS of new particles. An experimental method is established to determine the size-dependent coagulation coefficient of monodisperse nanoparticles from their steady-state concentration and decay rate in chamber experiments. Using this method, we measure the coagulation coefficient of 3–10 nm particles composed of NH₄HSO₄, NaCl, and oxygenated organic molecules (OOMs). These test particles are used to represent new particles in the atmosphere formed by acid-base nucleation and organics nucleation. The sub-10 nm size range is selected because the scavenging of new particles is most significant in this range. The effectiveness of CoagS is then demonstrated by comparing the measured coagulation coefficients to theoretical values. Based on the measured effectiveness of CoagS, we further explore the potential reasons for frequent intensive NPF events using atmospheric data measured in urban Beijing.

2 Methods

2.1 Laboratory experiment

The size-dependent CoagS of 3–10 nm particles was experimentally determined using an environmental chamber. This chamber was made from Teflon, and its volume was 1 m³. The total flow rate through the chamber was 10 L min⁻¹; hence, the residence time was ∼ 100 min. A low-speed fan placed near the bottom center of the chamber was used to mix particles in the chamber; its mixing ability had been experimentally validated. Experiments were conducted at room temperature (∼ 20 ^∘C), and we note that the coagulation coefficient is not sensitive to temperature. Before each experiment, the chamber was flushed using filtered, compressed air to remove the remaining particles.

As shown in Fig. 1, 100 nm NH₄HSO₄ and NaCl particles were generated and injected into the chamber to provide the CoagS of sub-10 nm particles. The size of 100 nm was selected, because particles around this size contribute most to CoagS in urban environments (Cai et al., 2017b). Monodisperse sub-10 nm NH₄HSO₄, NaCl, and OOM particles were also injected into the chamber. The concentrations of 100 nm and sub-10 nm particles were controlled to be 10⁴–10⁵ cm⁻³, such that self-coagulation was negligible (< 0.5 × 3.3 × 10⁻⁹ cm³ s⁻¹ × 10⁵ cm${}^{-\mathrm{3}}=$ 1.7 × 10⁻⁴ s⁻¹) and the CoagS provided by the 100 nm particles were distinguishable against dilution and wall losses. Among the test particles, NH₄HSO₄ particles represent atmospheric new particles formed by acid-base nucleation (Chen et al., 2012; Yao et al., 2018); OOM particles represent new particles formed by nucleation with highly oxygenated organic molecules and particles coated by OOMs during their growth (Bianchi et al., 2016; Tröstl et al., 2016); and NaCl particles were used to keep consistency with previous studies (Okuyama et al., 1984, 1986) on the coagulation between nanoparticles with similar size. We generated these test particles outside the chamber instead of producing them within the chamber. In this way, we avoided the perturbation of significant vapor condensation on particle evolution during the experiments. NH₄HSO₄ and NaCl particles were generated in a tube furnace using the condensation–evaporation technique (Scheibel and Porstendörfer, 1983; Kangasluoma et al., 2013) (Fig. 1). They were charged, and then monodisperse particles with a certain size were classified using a Vienna-type differential mobility analyzer (DMA). The aerosol and sheath flow rates of the DMA were 3.5 and 10 L min⁻¹, respectively, to maximize the classified particle concentrations. A neutralizer (Ni-63, 90 MBq) was used to neutralize the classified charged particles before they entered the chamber via a Teflon tube, which removes the remaining sub-10 nm charged particles by electrostatic losses, since most (> 90 %) sub-10 nm particles are neutral at a steady-state charge distribution. An aerosol electrometer (Fernandez de la Mora et al., 2017) (SEADM S.L.) was used to monitor the classified particle concentration. Two mass flow controllers were used to control the classified particle concentration by adjusting the dilution ratio so that the particle concentration entering the chamber could be kept stable.

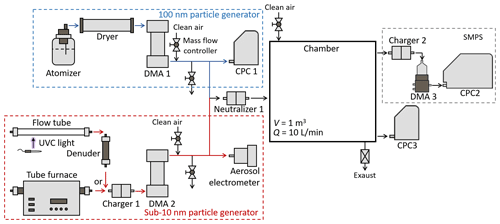
Figure 1 Schematic of the chamber experiment setup for measuring the size-dependent coagulation coefficient.

OOM particles were generated in a flow tube from ozone-initiated limonene oxidation products (Fig. 1). The inlet flow of the flow tube was made up of 2 L min⁻¹ dry zero air and 1 L min⁻¹ humidified zero air. A tiny amount of limonene was added to the inlet flow via diffusion from a syringe tip. By doing this, we minimized the amount of OOMs and hence the size of OOM particles. Ozone was generated in the flow tube using an ultraviolet-C lamp. The influence of OH radicals on OOMs generation was supposed to be minor, though it was not critical for this experiment. OOMs nucleated into particles in the flow tube, and the remaining gas-phase OOMs downstream of the flow tube were removed by a denuder containing activated carbon. In addition to the denuder, an open-loop DMA also contributed to separating particles from gas-phase OOMs, such that no new particles were formed in the chamber. The generated OOM particles were volatile, and they evaporated slowly in the vapor-free environment in the chamber. However, this slow evaporation did not affect particle number concentration, and the change of particle size was minor (< 20 %) during each experimental run.

Large NH₄HSO₄ and NaCl particles were generated using an atomizer. The generated particles were dried and then classified using a DMA with a centroid diameter of 100 nm. Classified particles were neutralized to reach a steady-state charge fraction, which is used to represent the charge fraction of atmospheric particles (Li et al., 2022). These neutralized particles were subsequently injected into the chamber. The concentration of 100 nm particles entering the chamber was monitored by a condensation particle counter (CPC; model 3750, TSI Inc.) and dynamically adjusted by two mass flow controllers so that the self-coagulation of 100 nm particles was negligible, whereas the CoagS of sub-10 nm particles contributed by these 100 nm particles could be well measured against wall loss and dilution.

Particle concentrations in the chamber were measured using a scanning mobility particle spectrometer (SMPS; model 3936, TSI Inc.) and a CPC (model 3772, TSI Inc.). The SMPS was mainly used to measure the size distributions of sub-10 nm particles, though it could also cover the distribution of 100 nm particles. When measuring the CoagS of small (e.g., 3–5 nm) particles, the scan range was focused on the sub-10 nm particle size to obtain good statistics. The CPC was used to measure total particle concentration in the chamber, which was approximately equal to 100 nm particle concentration because of the high wall loss of sub-10 nm particles.

The CoagS of sub-10 nm particles was determined using a steady-state concentration approach and a decay rate approach. For the steady-state concentration approach, we measured the pseudo-steady-state concentration of sub-10 nm particles as a function of 100 nm particle concentration. This approach benefited from a large number of data points for each experimental run, which overcame the uncertainties associated with measurements and fitting. For the decay rate approach, the CoagS was derived using the enhancement in the decay rates of sub-10 nm particles due to the CoagS contributed by a certain concentration of 100 nm particles. This approach has been used previously to measure the mass accommodation coefficient of volatile organic compounds (Krechmer et al., 2017). Here we used it for OOM particles whose concentration could not be kept stable for hours, as required by the steady-state concentration approach. For each experiment, we evaluated the CoagS of particles with a certain size. The size dependency of CoagS was obtained by repeating the experiment for different particle sizes.

2.2 Atmospheric measurements

Atmospheric NPF events used in this study were measured in Beijing from 16 January 2018 to 31 December 2019. The measurement site was located at the west campus of Beijing University of Chemical Technology (Scheibel and Porstendörfer, 1983). Size distributions of 1.5 nm–10 µm particles were measured using a homemade diethylene glycol SMPS (1.5–6 nm) (Cai et al., 2017a) and a particle size distribution system (3 nm–10 µm) (Liu et al., 2016). NPF days with intensive sub-3 nm particle formation and subsequent new particle growth were classified based on the measured size distributions (Deng et al., 2020). We use the occurrence of NPF events to characterize particle survival to avoid the potentially large uncertainties in the survival probability retrieved from particle size distributions. The gaseous sulfuric acid concentration was measured using a nitrate chemical ionization time-of-flight mass spectrometer (Aerodyne Inc.) (Lu et al., 2019). The condensation sink (CS) of sulfuric acid during NPF periods was calculated using the measured particle size distributions. Detailed information on the measurement site and the dataset can be found elsewhere (Deng et al., 2020, 2021).

2.3 Box model

A box model based on aerosol kinetics is used to simulate the evolution of particle concentration in the chamber. The governing population balance equation for sub-10 nm particle concentration is

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}{N}_{\mathrm{sub}\mathrm{10}}}{\mathrm{d}t}}=Q-\left[\mathit{\beta }\left(d_{\mathrm{p}}\right)N_{\mathrm{100}}+\mathrm{WL}\left(d_{\mathrm{p}}\right)+\mathrm{DL}\right]\cdot N_{\mathrm{sub}\mathrm{10}},\end{array}$$

where N_sub10 and N₁₀₀ are the concentrations (cm⁻³) of monodisperse sub-10 nm and 100 nm particles, respectively; t is time (s); Q is the source rate (cm⁻³ s⁻¹) of sub-10 nm particles resulting from particle injection into the chamber; β(d_p) is the coagulation coefficient (cm³ s⁻¹) between sub-10 nm and 100 nm particles; d_p is the diameter (nm) of sub-10 nm particles; WL(d_p) is the size-dependent wall loss rate (s⁻¹) of sub-10 nm particles; and DL is the dilution rate (s⁻¹). The size-dependent CoagS of sub-10 nm particles is equal to β(d_p)N₁₀₀.

Setting the dN_sub10 $/$ dt in Eq. (1) to zero yields the steady-state value of N_sub10 ($N_{\mathrm{sub}\mathrm{10}}^{\mathrm{ss}}$) as a function of d_p and N₁₀₀:

$$\begin{array}{}\text{(2)}& N_{\mathrm{sub}\mathrm{10}}^{\mathrm{ss}}\left(N_{\mathrm{100}}\right)={\displaystyle \frac{Q}{\mathit{\beta }\left(d_{\mathrm{p}}\right)N_{\mathrm{100}}+\mathrm{WL}\left(d_{\mathrm{p}}\right)+\mathrm{DL}}}.\end{array}$$

With a constant Q, the evolution of N_sub10 can be solved analytically. For the decay rate approach, Q is zero and its corresponding N_sub10 is

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{N}_{\mathrm{sub}\mathrm{10}}\left(t\right)& =N_{\mathrm{sub}\mathrm{10}}^{\mathrm{ini}}\\ & \cdot \exp \left\{-\left[\mathit{\beta }\left(d_{\mathrm{p}}\right)N_{\mathrm{100}}+\mathrm{WL}\left(d_{\mathrm{p}}\right)+\mathrm{DL}\right]\cdot t\right\},\end{array}\end{array}$$

where $N_{\mathrm{sub}\mathrm{10}}^{\mathrm{ini}}$ is the concentration at t= 0.

2.4 Coagulation coefficient

The measured coagulation coefficient was retrieved from the steady-state concentration or the decay rate of sub-10 nm particles using the box model. With a constant Q, N_sub10 as a function of a varying N₁₀₀ is

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{N_{\mathrm{sub}\mathrm{10}}^{\mathrm{ss}}\left(N_{\mathrm{100}}\right)}{N_{\mathrm{sub}\mathrm{10}}^{\mathrm{ss}}\left(\mathrm{0}\right)}}=\mathrm{1}-{\displaystyle \frac{N_{\mathrm{100}}}{N_{\mathrm{100}}+\frac{\mathrm{WL}\left(d_{\mathrm{p}}\right)+\mathrm{DL}}{\mathit{\beta }\left(d_{\mathrm{p}}\right)}}}.\end{array}$$

For the steady-state concentration approach, β(d_p) was retrieved by fitting Eq. (4) to the measured $N_{\mathrm{sub}\mathrm{10}}^{\mathrm{ss}}\left(N_{\mathrm{100}}\right)$. For the decay rate approach, β(d_p) was retrieved by fitting Eq. (3) to the measured N_sub10 as a function of t. Both approaches require predetermined values of WL(d_p)+ DL, which can be readily determined using the decay rate approach.

The theoretical Brownian coagulation coefficient was calculated using Eq. (5):

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\mathit{\beta }& \left(d_{\mathrm{1}},d_{\mathrm{2}},\mathit{\alpha },A\right)=\mathrm{2}\mathit{\pi }\left(d_{\mathrm{1}}+d_{\mathrm{1}}\right)\left(D_{\mathrm{1}}+D_{\mathrm{2}}\right)\\ & \cdot {\displaystyle \frac{\mathrm{1}+\mathit{Kn}}{\mathrm{1}+\mathrm{0.377}\mathit{Kn}+\frac{\mathrm{4}}{\mathrm{3}\mathit{\alpha }}\mathit{Kn}\left(\mathrm{1}+\mathit{Kn}\right)}}\cdot E\left({\displaystyle \frac{A}{kT}},\mathit{Kn}\right),\end{array}\end{array}$$

where βis the coagulation coefficient (cm³ s⁻¹) between two particles with the sizes (nm) of d₁ and d₂, D₁ and D₂ are particle diffusivities (m² s⁻¹); Kn is the Knudsen number (–) of particles determined by their sizes and mean free path (Fuchs and Sutugin, 1971); α is the mass accommodation coefficient characterizing the effectiveness of coagulation (–); A is the Hamaker constant (J); k is the Boltzmann constant (J K⁻¹); T is temperature (K); and E is a multiplicative factor characterizing the influence of the van der Waals attractive force on particle coagulation. The Kn term is used to correct for the transition and free molecular regimes, and Kn is herein defined as

$$\begin{array}{}\text{(6)}& {\displaystyle }\mathit{Kn}={\displaystyle \frac{\mathrm{2}\mathit{\lambda }}{d_{\mathrm{1}}+d_{\mathrm{2}}}}\text{(7)}& {\displaystyle }\mathit{\lambda }={\displaystyle \frac{\mathrm{3}\left(D_{\mathrm{1}}+D_{\mathrm{2}}\right)}{\sqrt{c_{\mathrm{1}}^{\mathrm{2}}+c_{\mathrm{2}}^{\mathrm{2}}}}},\end{array}$$

where λ is the mean free path (m) of particles and c is the thermal velocity (m s⁻¹) of particles.

The expression of β can be reduced to Eqs. (8) and (9) when Kn approaches zero and infinite, i.e.,

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathit{\beta }}_{\mathrm{C}}=\mathrm{2}\mathit{\pi }\left(d_{\mathrm{1}}+d_{\mathrm{1}}\right)\left(D_{\mathrm{1}}+D_{\mathrm{2}}\right)\cdot E\left({\displaystyle \frac{A}{kT}},\mathrm{0}\right),\text{(9)}& {\displaystyle }{\mathit{\beta }}_{\mathrm{FM}}={\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}\mathit{\alpha }{\left(d_{\mathrm{1}}+d_{\mathrm{1}}\right)}^{\mathrm{2}}\sqrt{c_{\mathrm{1}}^{\mathrm{2}}+c_{\mathrm{2}}^{\mathrm{2}}}\cdot E\left({\displaystyle \frac{A}{kT}},\mathrm{\infty }\right),\end{array}$$

where β_C and β_FM are the coagulation coefficients for the continuum limit and the free molecular limit, respectively.

For the coagulation between 3–10 and 100 nm particles, Kn ranges from 1.0 to 1.9. Consequently, coagulation occurred in the transition regime. To obtain the theoretical $E\left(A/kT,\mathit{Kn}\right)$, we first computed $E\left(A/kT,\mathrm{0}\right)$ and $E\left(A/kT,\mathrm{\infty }\right)$ using the formulae reported in Chan and Mozurkewich (2001), which were fitted to the numerical solution to the integral from Sceats (1989). The results were then extended to the transition regime using the interpolation formula in Alam (1987). We also compared $E\left(A/kT,\mathit{Kn}\right)$ to the results interpolated using the methods in Sceats (1989) and Ouyang et al. (2012), finding good consistencies among those methods. More details on the theoretical β and $E\left(A/kT,\mathrm{Kn}\right)$ can be found in the Supplement.

The value of the empirical Hamaker constant A was experimentally determined by fitting Eq. (5) to the measured coagulation coefficient as a function of particle size. With A= 0 J and correspondingly $E\left(A/kT,\mathit{Kn}\right)=$ 1, β is reduced to the hard-sphere coagulation coefficient. In Eq. (5), particles are assumed to be spherical, and their density is assumed to be equal to the bulk density. Therefore, the empirical E may also account for the influence of particle shape on the β of, for example, NaCl particles (Okuyama et al., 1984, 1986). Besides, the interaction between a charged particle and a neutral particle may influence the coagulation coefficient, which is also included in the experimentally determined E in this study. Besides the experimentally determined A from this study, we took the value of A from previous literature on NaCl particle coagulation (Okuyama et al., 1984) and H₂SO₄–NH₃ condensation (Stolzenburg et al., 2020) when computing the theoretical coagulation coefficient.

3 Results and discussion

3.1 Steady-state concentration approach

This approach was used to measure the CoagS of NH₄HSO₄ and NaCl particles. Figure 2 shows a typical experimental run using 4 nm particles. At the beginning of the experiment, monodisperse 4 nm particles were injected into the chamber, and their number concentration (N₄) at the chamber inlet was then maintained at a constant level until the end of the experiment. The N₄ in the chamber reached a plateau after ∼ 0.5 h, indicating that the 4 nm particle source was dynamically balanced with wall loss and dilution. After that, 100 nm particles were injected into the chamber, and their concentration increased slowly towards a high steady-state concentration. As shown in Fig. 2, N₄ in the chamber decreased significantly with an increasing N₁₀₀. Since the source (i.e., particle injection) and other sinks (i.e., wall loss and dilution) of 4 nm particles were kept constant, the decrease of N₄ must have been caused by the increasing CoagS. At t= ∼ 5.7 h, the inlet N₁₀₀ was set to zero. As a result, N₁₀₀ in the chamber decreased following an exponential decay curve (Eq. 3), and N₄ in the chamber increased correspondingly. The measured N_sub10 in the chamber during the increase and decrease of N₁₀₀ was approximated as the steady-state concentration. The validity of this approximation is guaranteed by the short residence time of sub-10 nm particles compared to that of 100 nm particles (e.g., 8.6 min seconds for 4 nm particles versus 65 min for 100 nm particles), which was verified using the box model. Data from when N₁₀₀ in the chamber changed quickly was excluded from the analysis for better accuracy.

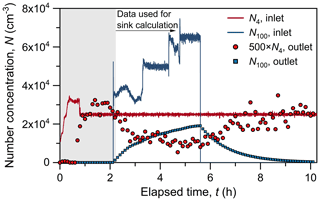
Figure 2 Time series of particle number concentrations measured at the inlets and outlets of the chamber during an experimental run. The inlet particle concentrations (N) were controlled using mass flow controllers. Assuming perfect mixing in the chamber, particle concentrations in the chamber are equal to the outlet concentrations. The subscript of N indicates particle size in nm. Due to the long residence time (∼ 1 h) of 100 nm particles, the outlet N₁₀₀ changed slowly towards its steady-state concentration when the inlet N₁₀₀ was kept stable.

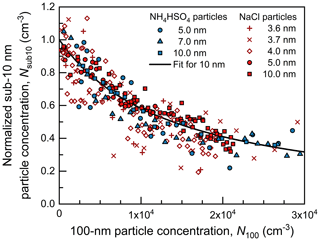
Using the box model in Eq. (4), we retrieved size-dependent (WL(d_p)+ DL) $/$ β(d_p) from the measured steady-state N_sub10 as a function of N₁₀₀. The parameters for every experiment are summarized in Table S1. As shown in Fig. 3, with the CoagS contributed by 1.2×10⁴ cm⁻³ 100 nm particles, the pseudo-steady-state N_sub10 decreased by half compared to the case with zero CoagS. The measured decreasing trend of N_sub10 with an increasing N₁₀₀ is very consistent with a curve fitted using Eq. (4), with (WL(d_p)+ DL) $/$ β(d_p) as the fit parameter. The value of β(d_p) is then obtained using a predetermined value of WL(d_p)+ DL, as depicted below.

Figure 3 The normalized pseudo-steady-state concentration of monodisperse sub-10 nm particles (N_sub10) as a function of 100 nm particle concentration (N₁₀₀). N_sub10 is normalized by dividing it by the value measured at N₁₀₀= 0. The curve is obtained by fitting Eq. (4) to the measured data.

3.2 Decay rate approach

This approach was used to measure the decay rate (i.e., total loss rate) of particles due to wall loss, dilution, and coagulation sink. As shown in Fig. 4, the exponential decay of monodisperse particle concentration in the chamber can be well characterized using the box model (Eq. 3). When measuring WL(d_p)+ DL, only sub-10 nm particles or 100 nm particles were injected into the chamber, and particle losses due to self-coagulation were negligible. Combining WL(d_p)+ DL and the (WL(d_p)+ DL) $/$ β(d_p) retrieved using the steady-state concentration approach, we obtained the size-dependent β(d_p) of NH₄HSO₄ and NaCl particles. Figure 4 also shows that WL(d_p)+ DL was strongly size dependent. For 100 nm particles whose decay was mainly driven by dilution, the measured decay rate was close to the theoretical dilution rate calculated using chamber volume and the total flow rate through the chamber. For sub-10 nm particles, wall loss governed the decay rate, and it increased quickly as d_p decreased. The size dependency of WL(d_p) is similar to that of β(d_p). For this reason, even though CoagS was expected to increase with a decreasing d_p, there was no obvious dependence in the relationship between N_sub10 and N₁₀₀ on d_p in Fig. 3.

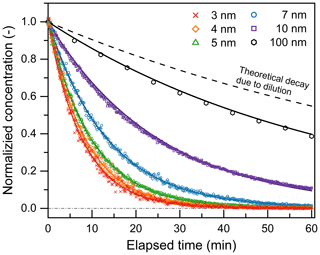
Figure 4 Decay of the concentration of NH₄HSO₄ and NaCl particles in the chamber due to wall loss and dilution. Particle concentration is normalized by dividing it by the value measured at t= 0. Curves are obtained by fitting Eq. (4) to the measured data.

The decay rate approach was also used to determine the CoagS of OOM particles. As shown in Fig. 5, with 2.6×10⁴ cm⁻³ 100 nm particles, N_sub10 decayed substantially faster than the rate contributed by only wall loss and dilution. According to the box model (Eq. 3), β(d_p) was calculated using the difference between the decay rates fitted to the experiments with and without 100 nm particles. When there were 100 nm particles in the chamber, N_sub10 could only be measured using the SMPS that focused on the sub-10 nm size range. Although the SMPS data demonstrated good consistency with the CPC data, the temporal resolution of SMPS was limited by its low overall detection efficiency. To reduce the statistical uncertainties of the decay rate approach, each experiment was performed at least three times, such that the measured difference between the decay rates was sufficient to provide a relatively accurate estimate of β(d_p).

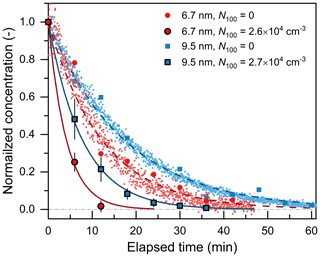
Figure 5 Decay of the concentration of sub-10 nm organic particles in the chamber due to wall loss, dilution, and coagulation sink. Sub-10 nm particle concentration is normalized by dividing it by the value measured at t= 0. N₁₀₀ is the concentration of 100 nm particles used to provide the coagulation sink. The small and large markers represent data measured by a CPC and an SMPS, respectively. The variation bar indicates the standard deviation of normalized sub-10 concentration in repeated experiments.

3.3 Coagulation coefficient

By comparing the measured coagulation coefficients to theoretical values, we demonstrate that the CoagS of the test 3–10 nm particles was effective, i.e., almost every collision between one 3–10 nm particle and one 100 nm particle contributed to CoagS, and the mass accommodation coefficient α for coagulation scavenging was near unity. As shown in Fig. 6, the measured coefficients were comparable to the theoretical coefficients calculated with α= 1.0. In contrast, the theoretical curve calculated with α= 0.1 was approximately 1 order of magnitude lower than the measured values. This large discrepancy was far beyond that which can be explained by measurement uncertainties. Hence, the measured coagulation sink must be effective.

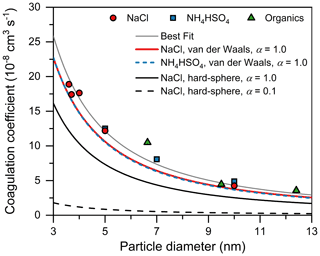
Figure 6 Measured and theoretical coagulation coefficients between sub-10 nm particles and 100 nm particles. The hard-sphere coagulation coefficient only accounts for particle diffusion. The van der Waals coagulation coefficient also accounts for the van der Waals attractive force. α is the mass accommodation coefficient characterizing the effectiveness of coagulation. The best fit is obtained by fitting the best empirical Hamaker constant to the measured size-dependent coagulation coefficient.

Further, we found that the CoagS of test particles are enhanced compared to the hard-sphere CoagS. This enhancement is likely due to the van der Waals force and potentially the interaction between a neutral sub-10 nm particle and a charged 100 nm particle. The contribution from the van der Waals force is usually accounted for in terms of the collision between vapors, clusters, and small particles, for which the multiplicative factor E in Eq. (5) typically ranges from 2 to 8 (Halonen et al., 2019; Stolzenburg et al., 2020; Okuyama et al., 1984). The empirical Hamaker constants for the condensation of H₂SO₄–NH₃ (Stolzenburg et al., 2020) vapors and the coagulation between NaCl particles (Okuyama et al., 1984, 1986) were estimated to be $\mathrm{4.6}\times {\mathrm{10}}^{-\mathrm{20}}$ and $\mathrm{8.9}\times {\mathrm{10}}^{-\mathrm{20}}$ J, respectively. Assuming these values are also valid for calculating the CoagS of sub-10 nm particles, the theoretically predicted E was ∼ 1.4 for particles in this size range, with a weak dependence on the particle size. As shown in Fig. 6, the van der Waals model could explain the measured coagulation coefficients better than the hard-sphere model, indicating the contribution of the van der Waals force to CoagS. We also estimated the value of empirical Hamaker constants by fitting a coagulation coefficient curve to experimental results (Fig. 6). The best-fit Hamaker constants for NH₄HSO₄, NaCl, and OOM particles were 1.6 × 10⁻¹⁹, 2.5 × 10⁻¹⁹, 9.0 × 10⁻²⁰ J, respectively. The differences between the coagulation coefficients calculated using the best-fit Hamaker constant (e.g., 2.5 × 10⁻¹⁹ J for NaCl) and the previously reported value (8.9 × 10⁻²⁰ J) (Okuyama et al., 1984, 1986) were minor (< 15 %).

No significant size dependence in the effectiveness of the CoagS was observed for the test sub-10 nm particles. With particle size being decreased from 10 to 3 nm, the value of the coagulation coefficient increased because of the increasing particle diffusivity (Fig. 6). However, the effectiveness of coagulation, as indicated by the ratio between the measured coagulation coefficients and theoretical predications, was relatively constant. In addition, we did not observe a significant size dependence in the effectiveness of particle wall loss to the Teflon surface, which provides circumstantial evidence for the effectiveness of CoagS contributed by scavenging particles.

Particle composition had only a minor influence on the CoagS of the test particles. As shown in Fig. 6, the measured coagulation coefficients of NH₄HSO₄, NaCl, and OOM particles were close to each other. More importantly, this closure implies that the effectiveness of CoagS was not affected by the composition of the test particles. The measured minor influence of particle composition is supported by the theoretical prediction that the coagulation coefficient is a weak function of composition-related properties such as particle density. For instance, there is a small (7 %) difference between the theoretical hard-sphere coagulation coefficients for NH₄HSO₄ and NaCl particles. Coincidentally, this small difference is further compensated by the different Hamaker constants for van der Waals coagulation coefficients.

3.4 Atmospheric implications

The measured effective CoagS of the test particles is strong evidence for the effectiveness of the CoagS of atmospheric new particles. In terms of particle composition, NH₄HSO₄ particles were used to represent atmospheric new particles formed by acid-base nucleation (Chen et al., 2012) and growth (McMurry et al., 2005), and OOM particles were used to represent organics nucleation and growth (Bianchi et al., 2016). Recent studies have shown that sulfuric acid (with stabilizing base and water) is a major contributor to new particle formation, and OOMs may also contribute to new particle growth in polluted urban environments (Yao et al., 2018; Cai et al., 2021c; Qiao et al., 2021). Hence, the test inorganic and organic particle compositions cover that of typical atmospheric new particles, though the latter is expected to be more complex. Further, the test OOM particles were unstable against evaporation in the chamber because the surrounding gaseous OOMs had been removed. Despite this, they were scavenged effectively by 100 nm particles as well as the Teflon chamber wall. Hence, it is unlikely that growing OOM particles surrounded by supersaturated gaseous OOMs in the atmosphere are not effectively scavenged by coagulation.

In terms of particle size, the chamber experiments provide evidence for the effective CoagS of 3–10 nm particles. Previous studies (Cai et al., 2021c; Deng et al., 2021) have reported the effectiveness of the CoagS of sub-1.5 nm acid-base clusters formed in NPF events. The 1.5–3 nm size range was not covered in this study, and the effectiveness of CoagS in this size range remains to be explored.

Concerning the effectiveness of CoagS, there are most likely to be other reasons for the frequent and intensive NPF events in polluted environments. To further investigate the reasons, we calculate the survival probability of new particles, which governs the occurrence of NPF events (McMurry et al., 2005; Cai et al., 2021b). The theoretical survival probability was predicted using Eq. (10) (Lehtinen et al., 2007):

$$\begin{array}{}\text{(10)}& \begin{array}{rl}P(d_{\mathrm{1}}\to d_{\mathrm{2}})& =\exp \left\{\right.-{\displaystyle \frac{\mathrm{1}}{m-\mathrm{1}}}\left[\mathrm{1}-{\left({\displaystyle \frac{d_{\mathrm{1}}}{d_{\mathrm{2}}}}\right)}^{m-\mathrm{1}}\right]\cdot d_{\mathrm{1}}\\ & \left.\cdot {\displaystyle \frac{\mathrm{CoagS}\left(d_{\mathrm{1}}\right)}{\mathrm{GR}}}\right\},\end{array}\end{array}$$

where P is the survival probability, d₁ is 3 nm, d₂ is 10 nm, and m is $-\mathrm{dlnCoagS}/\mathrm{dln}{d}_{\mathrm{p}}$. The value of m is determined as −1.7 according to the measured particle size distributions. Due to the strong size dependence of CoagS, new particles are mainly scavenged at small sizes; hence we focus on the survival of sub-10 nm particles in this study. When GR is size dependent, we calculate P by discretizing [d₁, d₂] into many size bins and then multiplying the survival probabilities for each bin. The CoagS was calculated using measured particle size distributions (Kulmala et al., 2012a). For the convenience of discussion, we use the condensation sink (CS) of sulfuric acid below to quantify the size-dependent CoagS, though it is worth being clarified that the effectiveness of the CS of condensable vapors (Krechmer et al., 2017; Tuovinen et al., 2020) is different from the effectiveness of CoagS.

The value of GR was retrieved from the measured particle size distributions using two methods. One is the mode-fitting method that tracks the temporal evolution of the peak diameter of the new particle mode (Kulmala et al., 2012a). The other is the appearance time method with coagulation correction that tracks the appearance of particles at different sizes (Cai et al., 2021a). Both methods have been used to estimate the GR in urban Beijing (Deng et al., 2020; Qiao et al., 2021), though there is a systematic difference in the GRs retrieved using these two methods. For instance, the GR of sub-5 nm particles estimated using the appearance time method was ∼ 3 times that of the GR estimated using the mode-fitting method for the same dataset. Due to measurement uncertainties, it was previously difficult to infer the accurateness of these two methods by comparing the retrieved GR and the theoretical GR contributed by gaseous precursors (Qiao et al., 2021). Using the CoagS and particle survival probability, we provide more information on the value of GR, as will be discussed in detail below. In addition to the retrieved GR, we also calculate the GR contributed by gaseous sulfuric acid.

The occurrence of NPF events in urban Beijing was significantly suppressed by the high CoagS. As shown in Fig. 7, the value of CS during NPF events in urban Beijing usually ranged from 0.003 to 0.03 s⁻¹, and a few NPF events were observed at a high CS up to 0.07 s⁻¹. Such a high CS is approximately 1 order of magnitude higher than the CS in relatively clean environments, such as Finnish boreal forests (Cai et al., 2017b). As a result, it substantially suppressed particle survival, as indicated by the low survival probability and the low NPF frequency at high CS (e.g., > 0.02 s⁻¹) in Fig. 7. Comparing the observed NPF events and the predicted survival probability indicates a moderate or high (e.g., > 3 nm h⁻¹) growth rate of new particles in urban Beijing. As shown in Fig. 7, most of the observed NPF events as well as the decreasing NPF frequency as a function of CS can be explained with a moderate median GR of 3 nm h⁻¹. The NPF events observed with CS > 0.03 s⁻¹ may be associated with high GRs and/or particle formation rates. In contrast, with a low GR of 1 nm h⁻¹, the theoretical survival probability is as low as 1 % at CS = 0.009 s⁻¹. Considering the typical new particle formation rate in urban Beijing (∼ 10 cm⁻³ s⁻¹ for 3 nm particles) (Kulmala et al., 2022), such a low survival probability cannot explain a majority of the observed NPF events.

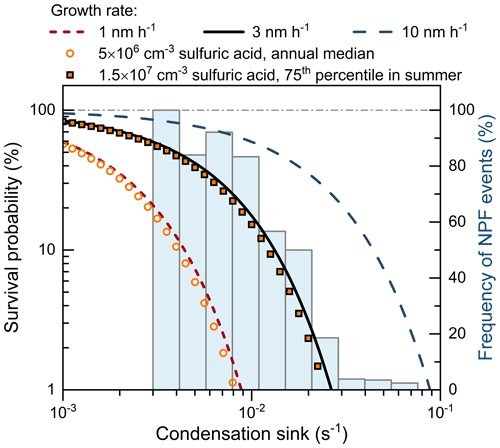
Figure 7 The theoretical survival probability of new particles and the measured frequency of new particle formation events in urban Beijing as a function of the condensation sink. The survival probability is calculated for 3–10 nm particles assuming an effective coagulation sink, i.e., the mass accommodation coefficient is equal to 1.0. The condensation sink characterizes the size-dependent coagulation sink during each new particle formation event. The NPF frequency is determined as the ratio of NPF days to all the measurement days within the given condensation sink range. This figure shows that a 1 nm h⁻¹ growth rate (or 5 × 10⁶ cm⁻³ sulfuric acid) is insufficient to explain the measured new particle formation in urban Beijing.

The moderate GR provides insights into new particle growth mechanisms. Sulfuric acid (with its stabilizing bases) is known to contribute to new particle growth for its low volatility (Stolzenburg et al., 2005, 2020). To provide a sufficient particle survival probability (equivalent to a 3 nm h⁻¹ GR), sulfuric acid concentration needs to be as high as ∼ 1.5 × 10⁷ cm⁻³ (Fig. 7). For urban Beijing, such a high concentration can only be occasionally observed in summer (Deng et al., 2020), in which season the sulfuric acid concentration is the highest due to the strongest solar radiation (Qiao et al., 2021). Hence, it can be implied that, although sulfuric acid is an important precursor for new particle growth, there should be other gaseous precursors (such as OOMs) contributing to the growth and survival of new particles.

Extending the above discussions from 3–10 nm to sub-3 nm provide hints for the growth mechanisms of sub-3 nm particles. The median GR of sub-3 nm particles in urban Beijing was previously reported to be ∼ 1 nm h⁻¹, which was consistent with the growth rate contributed by gaseous sulfuric acid with a median concentration of ∼ 5 × 10⁶ cm⁻³ (daily maximum value) (Deng et al., 2020). As a result of this consistency, sulfuric acid and its stabilizing bases were previously thought to govern the growth of sub-3 nm new particles in urban Beijing (Deng et al., 2020; Qiao et al., 2021). However, assuming an effective CoagS of sub-3 nm particles, it can be concluded that a moderate GR (e.g., 3 nm h⁻¹) of sub-3 nm particles is also needed to explain the observed NPF events (see Fig. S2), i.e., other undetected gaseous precursors or unrevealed mechanisms may also contribute majorly to sub-3 nm particle growth.

The moderate GR of sub-3 nm particles inferred from the survival probability is supported by the appearance time method, which reported a 3 nm h⁻¹ median GR for the same dataset (Qiao et al., 2021). We also find that the appearance time method tends to report a more accurate GR of sub-3 nm particles than the mode-fitting method, because the mode-fitting method may be influenced by the constantly forming new particles (see Figs. S3 and S4).

In addition to particle survival probabilities, the effectiveness of CoagS also solidifies the understanding of atmospheric new particles based on aerosol kinetics. For example, new particle formation rate is usually calculated using population balance equations (Kulmala et al., 2012b; Cai and Jiang, 2017), and the net coagulation sink term is the governing term for NPF in polluted environments (Deng et al., 2021; Cai and Jiang, 2017). If CoagS was overestimated by 1 order of magnitude, particle formation rate would be correspondingly overestimated by the same magnitude. By measuring the effectiveness of CoagS, we demonstrate the accuracy of the calculated particle formation rates. Another example is that, with a relatively accurate survival probability guaranteed by the effectiveness of CoagS, one can evaluate the influences of NPF on air quality by estimating the surface area and mass concentrations of grown new particles.

4 Conclusions

To investigate the survival of atmospheric new particles, especially in polluted environments with high coagulation sinks, we experimentally determine the effectiveness of the coagulation sink of 3–10 nm particles with chamber experiments. Monodisperse particles composed of ammonium bisulfate, sodium chloride, and oxygenated organic molecules were generated to represent typical new particles formed in the atmosphere. Their pseudo-steady-state concentration and decay rate were measured as a function of the concentration of 100 nm particles, which was used to scavenge the 3–10 nm particles. The coagulation coefficient between 3–10 nm particles and 100 nm particles was subsequently determined using a box model. We found that the measured coagulation coefficient increased sharply with a decreasing particle size, whereas it was not sensitive to the chemical composition of the test 3–10 nm particles. By comparing the measured coefficients with theoretical values, we demonstrated that the coagulation sink of the test 3–10 nm particles was effective, with a near-unity mass accommodation coefficient. Further, the measured coefficient suggests that van der Waals force contributes to the coagulation sink and results in a ∼ 40 % higher value than hard-sphere coagulation. These experiments indicate that the coagulation sink of atmospheric 3–10 nm new particles was unlikely to be substantially overestimated. Hence, the low theoretical survival probabilities of new particles contrasting to the new particle formation events observed at high coagulation sinks should be caused by underestimated growth rates. We show that a median growth rate of new particles at 3 nm h⁻¹ can explain most of the measured new particle formation events in urban Beijing. This 3 nm h⁻¹ growth rate is usually higher than the growth rate contributed by gaseous sulfuric acid. Hence, the measured effective coagulation sink indicates that, in addition to gaseous sulfuric acid, other gaseous precursors also contribute to the growth of new particles.