Stratospheric carbon isotope fractionation and tropospheric histories of CFC-11, CFC-12, and CFC-113 isotopologues

We present novel measurements of the carbon isotope composition of CFC-11 (CCl₃F), CFC-12 (CCl₂F₂), and CFC-113 (CF₂ClCFCl₂), three atmospheric trace gases that are important for both stratospheric ozone depletion and global warming. These measurements were carried out on air samples collected in the stratosphere – the main sink region for these gases – and on air extracted from deep polar firn snow. We quantify, for the first time, the apparent isotopic fractionation, ϵ_app(¹³C), for these gases as they are destroyed in the high- and mid-latitude stratosphere: ϵ_app(CFC-12, high-latitude) $=(-\mathrm{20.2}\pm \mathrm{4.4})$ ‰, and ϵ_app(CFC-113, high-latitude) $=(-\mathrm{9.4}\pm \mathrm{4.4})$ ‰, ϵ_app(CFC-12, mid-latitude) $=(-\mathrm{30.3}\pm \mathrm{10.7})$ ‰, and ϵ_app(CFC-113, mid-latitude) $=(-\mathrm{34.4}\pm \mathrm{9.8})$ ‰. Our CFC-11 measurements were not sufficient to calculate ϵ_app(CFC-11), so we instead used previously reported photolytic fractionation for CFC-11 and CFC-12 to scale our ϵ_app(CFC-12), resulting in ϵ_app(CFC-11, high-latitude) $=(-\mathrm{7.8}\pm \mathrm{1.7})$ ‰ and ϵ_app(CFC-11, mid-latitude) $=(-\mathrm{11.7}\pm \mathrm{4.2})$ ‰. Measurements of firn air were used to construct histories of the tropospheric isotopic composition, δ_T(¹³C), for CFC-11 (1950s to 2009), CFC-12 (1950s to 2009), and CFC-113 (1970s to 2009), with δ_T(¹³C) increasing for each gas. We used ϵ_app(high-latitude), which was derived from more data, and a constant isotopic composition of emissions, δ_E(¹³C), to model δ_T(¹³C, CFC-11), δ_T(¹³C, CFC-12), and δ_T(¹³C, CFC-113). For CFC-11 and CFC-12, modelled δ_T(¹³C) was consistent with measured δ_T(¹³C) for the entire period covered by the measurements, suggesting that no dramatic change in δ_E(¹³C, CFC-11) or δ_E(¹³C, CFC-12) has occurred since the 1950s. For CFC-113, our modelled δ_T(¹³C, CFC-113) did not agree with our measurements earlier than 1980. This discrepancy may be indicative of a change in δ_E(¹³C, CFC-113). However, this conclusion is based largely on a single sample and only just significant outside the 95 % confidence interval. Therefore more work is needed to independently verify this temporal trend in the global tropospheric ¹³C isotopic composition of CFC-113. Our modelling predicts increasing δ_T(¹³C, CFC-11), δ_T(¹³C, CFC-12), and δ_T(¹³C, CFC-113) into the future. We investigated the effect of recently reported new CFC-11 emissions on background δ_T(¹³C, CFC-11) by fixing model emissions after 2012 and comparing δ_T(¹³C, CFC-11) in this scenario to the model base case. The difference in δ_T(¹³C, CFC-11) between these scenarios was 1.4 ‰ in 2050. This difference is smaller than our model uncertainty envelope and would therefore require improved modelling and measurement precision as well as better quantified isotopic source compositions to detect.

1 Introduction

Chlorofluorocarbons (CFCs) have been produced since the 1940s for multiple uses, such as refrigerant gases, aerosol propellants, and in foam blowing. Since their role in ozone depletion was discovered (Molina and Rowland, 1974; Farman et al., 1985), there has been a global effort to phase out the production and use of CFCs, culminating in the essentially complete elimination of their production in 2015 under the Montreal Protocol. Long-term monitoring shows that the atmospheric mole fractions of the three most abundant CFCs (CFC-11, CFC-12, and CFC-113) have been declining as a result (Carpenter et al., 2014). However, recent studies highlight the need for continued, careful monitoring of CFCs. Montzka et al. (2018) found evidence for a recently emerged source of atmospheric CFC-11, with subsequent studies tracing these emissions largely to north-east China (Rigby et al., 2019; Adcock et al., 2020). In addition, Adcock et al. (2018) found increasing mole fractions of CFC-113a. Isotopic measurements could provide additional constraints when identifying sources and sinks of CFCs.

CFCs are released to the troposphere by industrial processes and emission from existing banks (Lickley et al., 2020). Once in the troposphere, CFCs are transported to the stratosphere, where they are subject to UV photolysis and reaction with O(¹D). Loss by photolysis is dominant, with loss by O(¹D) contributing around 2 %, 6 %, and 6 % for CFC-11, CFC-12, and CFC-113, respectively (Burkholder et al., 2013). The balance of these sources and sinks and the transport processes between them determine the atmospheric lifetime of a CFC and its tropospheric concentration.

These processes also influence the isotopic signature of CFCs. Breakdown in the stratosphere preferentially destroys light isotopologues, causing a fractionation that leaves the un-photolysed stratospheric CFC pool enriched in heavy isotopes – ¹³C and ³⁷Cl – relative to the troposphere. Such behaviour has been observed for δ(³⁷Cl, CFC-11), δ(³⁷Cl, CFC-12), and δ(³⁷Cl, CFC-113) (Allin et al., 2015; Laube et al., 2010a) and for other gases, such as N₂O (Griffith et al., 2000; Rahn and Wahlen, 1997; Röckmann et al., 2001; Kaiser et al., 2006; Toyoda et al., 2018), CH₄, and H₂ (Röckmann et al., 2003b; Rahn et al., 2003; Rhee et al., 2006; Röckmann et al., 2011). Heavy isotopologues of CFCs are enriched in the troposphere when this stratospheric pool mixes with the troposphere. There is a good conceptual understanding of isotopic budgets of CFCs, but significant uncertainties remain that hinder the use of isotopic methods to study CFC emissions, sources, and sinks.

One such uncertainty is the degree to which CFCs fractionate in the stratosphere. To date, few studies have been carried out to quantify the apparent isotopic fractionation, ϵ_app, in CFCs. ϵ_app relates the change in isotopic signature of a chemical to the degree of destruction observed in the atmosphere using a Rayleigh fractionation model. It is an empirical value that is affected by intrinsic photochemical fractionation, destruction by O(¹D), and transport and mixing (Kaiser et al., 2006). In the dominant stratospheric sink region, photochemical loss dominates loss from reaction with O(¹D) for CFC-11 and CFC-12 (Minschwaner et al., 2013). Laube et al. (2010b) measured vertical profiles of δ(³⁷Cl, CFC-12) in stratospheric air from tropical latitudes, calculating ϵ_app(³⁷Cl, CFC-12) $=(-\mathrm{12.1}\pm \mathrm{1.7})$ ‰. Using similar methodology, Allin et al. (2015) calculated ϵ_app(³⁷Cl, CFC-12) $=(-\mathrm{12.2}\pm \mathrm{1.6})$ ‰ at mid- and $(-\mathrm{6.8}\pm \mathrm{0.8})$ ‰ at high latitudes. This decrease in the magnitude of ϵ_app(³⁷Cl) with increasing latitude is qualitatively consistent with observations of δ(¹⁵N, N₂O) and δ(¹⁸O, N₂O) (Kaiser et al., 2006), though the decrease is larger for CFC-12. Allin et al. (2015) observed no latitude dependence for ϵ_app(³⁷Cl, CFC-11) (mid: $(-\mathrm{2.4}\pm \mathrm{0.5})$ ‰; high: $(-\mathrm{2.3}\pm \mathrm{0.4})$ ‰) and ϵ_app(³⁷Cl, CFC-113) (mid: $(-\mathrm{3.5}\pm \mathrm{1.5})$ ‰; high: $(-\mathrm{3.3}\pm \mathrm{1.2})$ ‰), though they speculated that some latitude dependence could be obscured by their uncertainties.

For CFCs, the only study of ϵ_app(¹³C) – from here, ϵ_app – under conditions representative of the stratosphere was the laboratory photolysis experiment of Zuiderweg et al. (2012). Laboratory experiments exclude the effects of atmospheric transport and mixing, which tend to dilute observed fractionations such that ϵ_app tends to be less-than-intrinsic photolytic fractionations, ϵ_p (Kaiser et al., 2006). Zuiderweg et al. (2012) reported ϵ_p under stratospherically relevant conditions for CFC-11 ($(-\mathrm{23.8}\pm \mathrm{0.9})$ ‰ at 203 K to $(-\mathrm{23.0}\pm \mathrm{1.1})$ ‰ at 233 K) and CFC-12 ($(-\mathrm{66.2}\pm \mathrm{3.1})$ ‰ at 203 K to $(-\mathrm{55.3}\pm \mathrm{3.0})$ ‰ at 233 K). These values imply greater levels of fractionation for δ(¹³C) than for δ(³⁷Cl) in the stratosphere.

Another uncertainty in our understanding of CFC isotopologues is the isotopic signature of their sources. Allin et al. (2015) used their measured ϵ_app for CFC-11, CFC-12, and CFC-113 to model a tropospheric history of δ(³⁷Cl) in these chemicals following the approach of Röckmann et al. (2003a). Allin et al. (2015) constructed a tropospheric history of the isotopic composition of these chemicals from measurements of tropospheric and firn air — deep, compacted snow containing an archive of tropospheric air going back decades (e.g. Buizert et al., 2012). When a constant isotopic source signature was assumed, the model agreed well with measurements of δ(³⁷Cl) representative of tropospheric air from around 1970 onwards. Five pre-1970 air samples had δ(³⁷Cl) values that were inconsistent with the model. However, no clear trend was observable for these five samples, and, in addition, the disagreement was not significant to 2σ. The authors concluded that a constant source signature is likely consistent with measured δ(³⁷Cl) since 1970 and that, with current measurement precisions, it is premature to assign a source change to CFC-11, CFC-12, and CFC-113 in the period before this.

In contrast, Zuiderweg et al. (2013) presented evidence for a past change in δ(¹³C, CFC-12). Large depletions, around −40 ‰ relative to the present-day troposphere, were measured in one deep firn air sample that corresponded to a mean age of around 1965. A significant change in the source signature of CFC-12 is required to explain this observation, and Zuiderweg et al. (2013) suggest that a change in feedstock during CFC production is the most promising explanation. But the results of Zuiderweg et al. (2013) rely heavily on one firn air sample that was potentially biased due to interference from a nearby chromatographic peak (see below and Appendix C). The tropospheric history of δ(¹³C, CFC-12) remains uncertain.

We remeasured the firn profile analysed by Zuiderweg et al. (2013) using a method similar to Allin et al. (2015) and Laube et al. (2010a) to better constrain and independently assess the history of δ(¹³C, CFC-12). Together with δ(¹³C, CFC-12), we also measured δ(¹³C, CFC-11) and δ(¹³C, CFC-113) in firn and stratospheric air samples. For the first time, stratospheric measurements were used to calculate ϵ_app(¹³C) for CFC-11, CFC-12, and CFC-113. We then used these ϵ_app values to quantify the isotope effect associated with the stratospheric removal in a two-box model, using a constant isotopic source signature, and calculated the temporal evolution of tropospheric δ(¹³C) for these chemicals since 1937 (CFC-12), 1946 (CFC-11), and 1962 (CFC-113). Model results were compared to the firn measurements to investigate whether changes in isotopic source composition are required to explain the δ(¹³C) history of these chemicals.

2 Methodology

2.1 Sample collection

We present new data from two stratospheric and two tropospheric data sets (Table 1). One stratospheric data set, which we call “Kiruna”, was collected at high latitudes from high-altitude Geophysica flights out of Kiruna, Sweden, using the BONBON-I, BONBON-II, and CLAIRE cryogenic whole-air samplers (Laube et al., 2010b). The other, which we call “Gap”, was collected at mid-latitudes from balloons launched from Gap, France, using the whole-air sampler of the then Max Planck Institute for Aeronomy (Kaiser et al., 2006). The firn air samples were collected at North Greenland Eemian Ice Drilling (NEEM) in northern Greenland during field campaigns in 2008 and 2009. Shallow ice cores were drilled, stopping every few metres for air sampling, with the borehole sealed off from ambient air using a bladder (Allin et al., 2015; Schwander et al., 1993).

Table 1 Samples analysed in this study.

^a 62 to 72^∘ N, 2^∘ W to 24^∘ E; 9–19 km; Laube et al. (2010b). ^b 44.4 to 44.8^∘ N, 3.1 to 6.3^∘ E; 8–34 km; Kaiser et al. (2006). ^c 77.45^∘ N, 51.06^∘ W; Buizert et al. (2012). ^d 77.45^∘ N, 51.06^∘ W; Zuiderweg et al. (2013). ^e Mean ages of the age distributions of the firn air samples.

2.2 Sample preparation and analysis

All of the samples were analysed using an established gas chromatography (GC)–mass spectrometry (MS) method that has produced robust and consistent results for chlorine isotope ratios in natural abundances of CFC-11, CFC-12, and CFC-113 (Laube et al., 2010b; Allin et al., 2015). In short, an Agilent 6890 GC was coupled to a VG/Waters tri-sector mass spectrometer. Air samples were dried by passing them through magnesium perchlorate granules before being concentrated onto a Hayesep D 80/100 mesh held at −78 ^∘C in a sample loop using a dry-ice–ethanol mixture. Desorption from the Hayesep D was achieved by heating the sample loop to around 95 ^∘C using hot water. A high-purity helium stream transferred the sample to a 0.32 mm internal diameter GS-GasPro (30 m) or KCl-passivated CP-PLOT Al₂O₃ (50 m) column held at −10 ^∘C. The column was heated at 10 ^∘C min⁻¹ to 200 ^∘C to release the chemicals of interest, separated by their retention strength, and pass them to the MS. Every fourth injection was a standard. While the above method was used for every sample analysed, different volumes were trapped for the stratospheric samples (200 mL at 20 ^∘C and 1 bar, method A) and the NEEM 2008/09 firn samples (600 mL at 20 ^∘C and 1 bar, method B). Also, method A used similar instrument settings to Allin et al. (2015). Method B uses the same MS and chromatography, but we increased the detector voltage (from 375 to 400 V), reduced the number of mass fragments measured at any given time, and optimised our source and collector slit parameters for maximum signal. Measurements of δ(³⁷Cl, CFC-11), δ(³⁷Cl, CFC-12), and δ(³⁷Cl, CFC-113) in firn and stratospheric air samples using method A were presented previously by Allin et al. (2015). In this study, we use method A (Allin et al., 2015) and method B, which differers from method A by slight changes to the instrument settings and by looking at different ion fragments (Sect. 2.3). We further validate our method in Appendix B, where we show that our method produces δ(¹³C, CFC-12) that is consistent with a gas chromatography–isotope ratio mass spectrometry (GC–IRMS) system over a wide range of δ(¹³C, CFC-12).

Our method allows measurements of δ(³⁷Cl) (Allin et al., 2015) and δ(¹³C) (this study) for CFCs with main isotopologues in the pmol mol⁻¹ range. A key advantage of our method is that we can make these measurements using only a few hundred millilitres of air, which is important when measuring typical stratospheric and firn air samples where sample volumes are restricted.

2.3 Data processing

δ(¹³C) was calculated using

$$\begin{array}{}\text{(1)}& \mathit{\delta }{(}^{\mathrm{13}}\text{C})={\displaystyle \frac{R_{\text{samp}}(\mathrm{102}/\mathrm{101})}{R_{\text{std}}(\mathrm{102}/\mathrm{101})}}-\mathrm{1},\end{array}$$

where $R_{\text{samp}}(\mathrm{102}/\mathrm{101})$ and $R_{\text{std}}(\mathrm{102}/\mathrm{101})$ are the ratios of the ¹³C³⁵Cl₂F⁺ ($m/z=\mathrm{101.9}\approx \mathrm{102}$) to ¹²C³⁵Cl₂F⁺ ($m/z=\mathrm{100.9}\approx \mathrm{101}$) ion fragments for the sample and the reference gas, respectively. R_std was taken to be the weighted mean ratio of two preceding and subsequent reference gases. Measured δ(¹³C, CFC-11) and δ(¹³C, CFC-12) reflect the total fractionation of each gas, whereas δ(¹³C, CFC-113) only reflects the fractionation on the CCl₂F fragment, neglecting fractionation on the CClF₂ fragment. The reference used for all measurements was 2005 Northern Hemisphere background air, AAL-071170 – from here referred to as “AAL”. For the stratospheric samples (method A), $R(\mathrm{102}/\mathrm{101})$ was calculated by regressing separate raw intensities for each ion fragment against each other (Laube et al., 2010a; Allin et al., 2015). For the firn samples (method B, using a larger air volume) the intensity of the $m/z$ 101 fragment saturated the detector, and we instead used the ¹²C³⁷Cl₂F⁺ ($m/z=\mathrm{104.9}\approx \mathrm{105}$) fragment to calculate $R(\mathrm{102}/\mathrm{105})$, again by the regression of the separate raw intensities for each fragment. To recover $R(\mathrm{102}/\mathrm{101})$, we applied a correction to the measured $R(\mathrm{102}/\mathrm{105})$ based on the expected $R(\mathrm{105}/\mathrm{101})$ using the relation

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{R_{\text{samp}}(\mathrm{102}/\mathrm{101})}{R_{\text{std}}(\mathrm{102}/\mathrm{101})}}={\displaystyle \frac{R_{\text{samp}}(\mathrm{102}/\mathrm{105})}{R_{\text{std}}(\mathrm{102}/\mathrm{105})}}\cdot {\displaystyle \frac{R_{\text{samp}}(\mathrm{105}/\mathrm{101})}{R_{\text{std}}(\mathrm{105}/\mathrm{101})}}.\end{array}$$

The expected $R(\mathrm{105}/\mathrm{101})$ values correspond to ${}^{\mathrm{12}}{\mathrm{C}}^{\mathrm{37}}{\mathrm{Cl}}_{\mathrm{2}}{\mathrm{F}}_{\mathrm{2}}{/}^{\mathrm{12}}{\mathrm{C}}^{\mathrm{35}}{\mathrm{Cl}}_{\mathrm{2}}{\mathrm{F}}_{\mathrm{2}}$ isotopologue ratios (relative mass difference of 4) and were calculated based on the modelling of diffusive and gravitational fractionation in firn (Sect. 2.4), assuming a constant isotopic source composition. In this case, $\frac{R_{\text{samp}}(\mathrm{105}/\mathrm{101})}{R_{\text{std}}(\mathrm{105}/\mathrm{101})}=\mathrm{1}+\mathrm{4}c$, with c being the correction for a relative mass difference of 1. Substituting Eq. (2) into (1) allows us to recover δ values from measurements of $R(\mathrm{102}/\mathrm{105})$. With this treatment we use ¹²C³⁷Cl₂F₂ as a standard, assuming that δ_T(^37,37Cl) for CFC-11, CFC-12, and CFC-113 is determined dominantly by diffusive and gravitational fractionation in the firn. As a check on our correction, we plot depth profiles of 2c and δ(³⁷Cl) measurements of the NEEM 2009 firn profile presented in Allin et al. (2015) (Fig. 1); 2c is similar to δ(³⁷Cl), within the precision of the data, as expected considering Allin et al. (2015) did not observe temporal signals in δ(³⁷Cl). Given the lack of temporal signals in δ(³⁷Cl), we do not expect large temporal changes in tropospheric δ(^37,37Cl). The median magnitude of the effect of this correction on our δ(¹³C) is 0.8 ‰ (CFC-11), 0.7 ‰ (CFC-12), and 0.5 ‰ (CFC-113). The impact of the correction on δ(¹³C) increases with depth in the firn, reaching maximum magnitudes of 4.2 ‰ (CFC-11), 4.3 ‰ (CFC-12), and 0.9 ‰ (CFC-113).

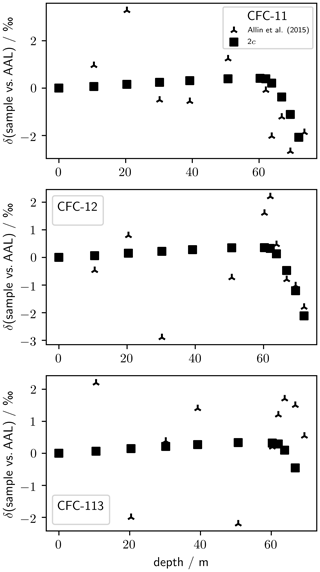
Figure 1 δ(³⁷Cl) as measured by Allin et al. (2015) against depth in NEEM 2009 firn air samples. Also shown is the correction factor, c, used in this work to convert $R(\mathrm{102}/\mathrm{105})$ to $R(\mathrm{102}/\mathrm{101})$ (Eq. 2), multiplied by 2; c gives the fractionation for a relative mass difference of 1 and, assuming no change in δ(³⁷Cl), which has a relative mass difference of 2, 2c should be consistent with δ(³⁷Cl).

To ascertain the linearity of the response of our analytical system, we performed dilution series for both methods, as described in Appendix A and shown in Fig. A1. For method A, the dilution series showed that below a certain threshold (minimum peak area) there are systematic deviations in our measurement methods. Based on these results, a number of stratospheric samples, for which the peak area fell blow this threshold, were excluded. From a total of 38 measurements of each CFC, we rejected 22 (CFC-11), 9 (CFC-12), and 12 (CFC-113) measurements because they fell outside of the linearity limit of our method. For method B, we did not reject any of the 56 measurements performed based on the dilution series. We did, however, exclude the 69.4 and 71.9 m NEEM 2009 samples (10 measurements) for CFC-113 because, for the corresponding mean ages, there was too little CFC-113 in the atmosphere (Adcock et al., 2018) to reliably determine δ(¹³C) values. These 10 measurements are shown in Fig. A1 but did not contribute to our analysis.

2.4 Modelling firn air transport

Differing masses and diffusivities cause gases and isotopologues of a given gas to move through firn at different rates. Here, a model of gas transport in firn air (Witrant et al., 2012) was used to predict both the age distribution for CFC-11, CFC-12, and CFC-113 at each firn sampling depth and the gravitational and diffusive fractionation of each of these CFCs using a constant isotopic source composition. The gravitational and diffusive corrections for a relative mass difference of 1 (c in Sect. 2.3 and Fig. 1) range from −1.0 ‰ to 0.2 ‰ (CFC-11), −1.1 ‰ to 0.2 ‰ (CFC-12), and −0.2 ‰ to 0.2 ‰ (CFC-113). In the upper firn, enrichment due to gravitational fractionation gives positive c, while in the deeper firn, c is negative as diffusive fractionation overwhelms the gravitational fractionation. Once measurements of firn air are corrected for this fractionation, any change in δ(¹³C) is indicative of changes in the tropospheric isotopic composition, δ_T(¹³C).

2.5 Modelling the tropospheric isotopic composition

We modelled δ_T(¹³C, CFC-11), δ_T(¹³C, CFC-12), and δ_T(¹³C, CFC-113) from 1937 to 2050 using a two-box model. The model was used by Röckmann et al. (2003a), Bernard et al. (2006), and Prokopiou et al. (2017) for N₂O isotopologue budget calculations and was adopted by Allin et al. (2015) to model the evolution of chlorine isotopes in CFC-11, CFC-12, and CFC-113. This model is detailed in Allin et al. (2015), so we only present a brief overview. The model boxes represent the troposphere and stratosphere. CFCs are emitted to the tropospheric box with a constant isotopic composition, δ_E(¹³C). Some portion of the tropospheric CFC load is transported to the stratospheric box, where CFCs are destroyed and fractionated according to ϵ_app. As these fractionated CFCs are exchanged with the troposphere, they alter the tropospheric isotopic composition – our desired variable. Troposphere–stratosphere exchange is parameterised according to Holton (1990) and Appenzeller et al. (1996). The dominant uncertainties in the model are the uncertainty in ϵ_app and the magnitude of the bulk air troposphere–stratosphere exchange flux, both of which are accounted for in the model uncertainty envelope. We offset modelled δ_T(¹³C) such that it is 0 ‰ in 2005. This treatment ensures that the modelled δ_T(¹³C) is relative to the tropospheric composition in 2005, consistent with our data, which are referenced to a 2005 air standard (AAL). We also shift the uncertainty envelope such that it is 0 ‰ in 2005 and increases backwards and forwards in time, reflecting the fact that in 2005 δ_T(¹³C)=0 ‰ by definition. Our only change to the modelling of Allin et al. (2015) is to the value of ϵ_app such that it reflects ¹³C rather than ³⁷Cl fractionation.

3 Results

3.1 Measurements of δ(¹³C) in firn air

Measurements of firn air from NEEM 2008/09, plotted against mean age of air, are shown in Fig. 2. In the absence of a calibration of our AAL standard against the international standard Vienna Pee Dee Belemnite (VPDB), we present δ(¹³C, CFC-11) and δ(¹³C, CFC-113) relative to our 2005 background air reference gas (AAL). For CFC-12, there were measurements of the same samples on the VPDB scale (Zuiderweg et al., 2013), allowing us to rescale our measurements. Taking the mean of the NEEM 2009 samples from 50.7 to 10.5 m gave δ(¹³C, sample vs. VPDB) $=(-\mathrm{42.4}\pm \mathrm{1.4})$ ‰ and δ(¹³C, sample vs. AAL) $=(\mathrm{0.6}\pm \mathrm{1.9})$ ‰, resulting in

$$\begin{array}{}\text{(3)}& \begin{array}{r}\mathit{\delta }({}^{\mathrm{13}}\mathrm{C},\text{AAL vs. VPDB})=\\ \frac{\mathit{\delta }({}^{\mathrm{13}}\mathrm{C},\text{sample vs. AAL})-\mathit{\delta }{(}^{\mathrm{13}}\text{C},\text{sample vs. VPDB})}{\mathrm{1}+\mathit{\delta }({}^{\mathrm{13}}\mathrm{C},\text{sample vs. AAL})}=\\ (\mathrm{43.0}\pm \mathrm{2.3})\mathrm{‰},\end{array}\end{array}$$

which we used to rescale our δ(¹³C, CFC-12, sample vs. AAL) measurements to VPDB. A smooth δ(¹³C) trend and uncertainty envelope was calculated using the non-parametric LOESS (locally weighted scatter plot smoothing) technique. Uncertainty in the trend derives from measurement uncertainty and the width of the age distribution at each depth. To account for the age uncertainty, we sub-sampled the relevant probability-weighted age distribution 200 times for each measurement and calculated the LOESS using the resulting measurement pairs. All further details are supplied in the Supplement. The mean standard error in the LOESS was 1.0 ‰ (CFC-11), 1.3 ‰ (CFC-12), and 1.6 ‰ (CFC-113).

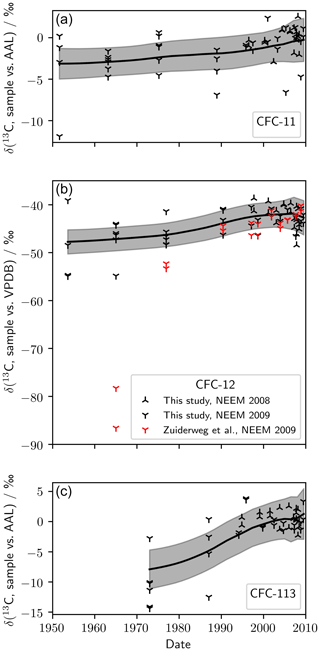
Figure 2 (a) Measured δ(¹³C, CFC-11), (b) δ(¹³C, CFC-12), and (c) δ(¹³C, CFC-113) in NEEM 2008 and 2009 firn air. Also shown is δ(¹³C, CFC-12) as measured by Zuiderweg et al. (2013) in the same NEEM 2009 firn air samples. The smoothed trend (black line) and 95 % confidence bounds (grey shading) were generated using a LOESS regression.

We calculated trends in δ(¹³C) using the LOESS. For each CFC we saw an increase in δ(¹³C) from the oldest to the youngest air: δ(¹³C, CFC-11) increased by (2.9±1.6) ‰ between 1952 and 2009, δ(¹³C, CFC-12) increased by (5.3±2.2) ‰ between 1954 and 2009, and δ(¹³C, CFC-113) increased by (9.3±2.7) ‰ between 1973 and 2009 (standard error and mean age). The observed trends had large relative uncertainty and were similar in magnitude to our $m/z$ 105-to-$m/z$ 101 correction.

For CFC-12, there was general agreement between our measured firn profile and the measurements of Zuiderweg et al. (2013) after around 1990. However, in the oldest two samples measured by Zuiderweg et al. (2013) – corresponding to mean ages of 1965 and 1977 – there was a significant difference between our measurements of the NEEM 2009 profile and those presented by Zuiderweg et al. (2013). For the 1965 sample, the measurements of Zuiderweg et al. (2013) were around 40 ‰ outside of our 95 % confidence intervals, an order of magnitude larger than our $m/z$ 105-to-$m/z$ 101 correction.

3.2 Calculating ϵ_app from stratospheric measurements

Our stratospheric measurements are presented as Rayleigh plots in Fig. 3, where f is the fractional release factor quantifying the degree of stratospheric destruction (Leedham Elvidge et al., 2018). Destruction of CFC-12 and CFC-113 (corresponding to an increase in fractional release factor and decreasing ln (1−f)) was concurrent with an increase in δ(¹³C) for the remaining stratospheric pool (Fig. 3). The gradient of the linear regression of ln (1+δ(¹³C)) with ln (1−f) gives ϵ_app, which was negative for CFC-12 and CFC-113 in both latitude regions. CFC-11 is omitted from Fig. 3 because we do not take ϵ_app(CFC-11) forward for our modelling or analysis. We present stratospheric CFC-11 data and justify their omission from our analysis in Appendix D.

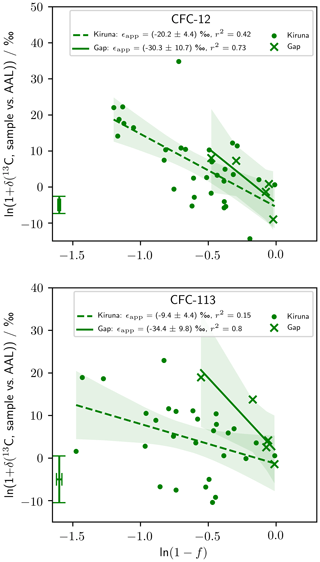
Figure 3 Rayleigh plots of our stratospheric measurements. The linear regression (lines) and 95 % confidence bounds on the regression (shading) are shown for the high-latitude (Kiruna) and mid-latitude (Gap) data sets. The gradients of these regressions, corresponding to ϵ_app, are given in the legend with 1 standard error. The error bar in the bottom left corner of each graph shows the median repeatability of the reference gas measurements over the measurement days and the median error deriving from the fractional release factor. CFC-11 data are presented in Appendix D.

From our stratospheric measurements, we derived ϵ_app(CFC-12, high-latitude) $=(-\mathrm{20.2}\pm \mathrm{4.4})$ ‰ (p<0.01), ϵ_app(CFC-12, mid-latitude) $=(-\mathrm{30.3}\pm \mathrm{10.7})$ ‰ (p=0.07), ϵ_app(CFC-113, high-latitude) $=(-\mathrm{9.4}\pm \mathrm{4.4})$ ‰ (p=0.04), and ϵ_app(CFC-113, mid-latitude) $=(-\mathrm{34.4}\pm \mathrm{9.8})$ ‰ (p=0.04) (Table 2). Of these, ϵ_app(CFC-12, mid-latitude) is significant at 90 % confidence, with the others significant at 95 %.

Table 2 The apparent isotopic fractionation, ϵ_app, derived from our stratospheric measurements and the photolytic isotopic fractionation, ϵ_p, measured by Zuiderweg et al. (2012). All uncertainties are 1 standard error.

^* Calculated using Eq. (4). Taking the mean of the 203 and 233 K measurements gives $\frac{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-11}\right)}{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-12}\right)}=\mathrm{0.39}\pm \mathrm{0.02}$.

We derived ϵ_app(CFC-11) by scaling our measured ϵ_app(CFC-12) based on previous laboratory measurements of photolytic carbon isotope fractionation, ϵ_p (Zuiderweg et al., 2012). ϵ_app is less than ϵ_p because atmospheric mixing dilutes the isotopic effect of photolytic fractionation (Kaiser et al., 2006). Atmospheric mixing affects CFC-11 and CFC-12 similarly, so we expect

$$\begin{array}{}\text{(4)}& {\mathit{ϵ}}_{\text{app}}\left(\text{CFC-11}\right)\approx {\mathit{ϵ}}_{\text{app}}\left(\text{CFC-12}\right){\displaystyle \frac{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-11}\right)}{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-12}\right)}}.\end{array}$$

Taking the mean of ϵ_p measured at stratospherically relevant temperatures (203 and 233 K) gives ϵ_p(¹³C, CFC-11) $=(-\mathrm{23.4}\pm \mathrm{0.7})$ ‰ and ϵ_p(¹³C, CFC-12) $=(-\mathrm{60.8}\pm \mathrm{2.2})$ ‰, such that $\frac{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-11}\right)}{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-12}\right)}=\mathrm{0.39}\pm \mathrm{0.02}$. Scaling our measured ϵ_app(CFC-12) by this factor gives ϵ_app(¹³C, CFC-11, high-latitude) $=(-\mathrm{7.8}\pm \mathrm{1.7})$ ‰ and ϵ_app(¹³C, CFC-11, mid-latitude) $=(-\mathrm{11.7}\pm \mathrm{4.2})$ ‰. These are the best estimates of ϵ_app(¹³C, CFC-11) possible using our measurements. For each CFC, ϵ_app was more negative at mid-latitudes. High-latitude ϵ_app was derived from more data than the mid-latitude ϵ_app. Of the three CFCs, ϵ_app(CFC-11) was least negative at both latitudes, while ϵ_app(CFC-12) was most negative at high latitudes, and ϵ_app(CFC-113) was most negative at mid-latitudes. We took ϵ_app(high-latitude) forward for our modelling because these were derived from more data, and we have more confidence in them.

3.3 Reconstructed tropospheric isotopic composition

We now turn to our measured and modelled δ_T(¹³C) (Fig. 4). Our firn measurements have been corrected for gravitational and diffusive fractionation. The smoothed trend and 95 % confidence interval were, similar to the firn profiles, based on LOESS regression on these corrected data. The standard error in the δ_T(¹³C) reconstruction was equal to that of the firn profile to within 0.1 ‰ for each CFC. Modelled δ_T(¹³C) is presented with 95 % confidence intervals. The model was forced with our derived ϵ_app(high-latitude), prescribed CFC emissions, and a constant isotopic composition of emissions. For CFC-12, we also show the polynomial presented by Zuiderweg et al. (2013) representing the tropospheric trend that best captured their firn measurements.

As with the firn profile, we calculated trends in measured δ_T(¹³C) using a LOESS. For each CFC, measured δ_T(¹³C) increased through time: δ_T(¹³C, CFC-11) increased by (2.1±1.6) ‰ between 1952 and 2009, δ_T(¹³C, CFC-12) increased by (4.8±2.2) ‰ between 1956 and 2009, and δ_T(¹³C, CFC-113) increased by (9.0±2.7) ‰ between 1975 and 2009 (standard error and mean age). These trends are similar to and slightly smaller than the trends in the firn because of the gravitational and diffusive correction. The polynomial of Zuiderweg et al. (2013) only agreed with our reconstructed δ_T(¹³C, CFC-12) after around 1995. Our measurements are compared to previously published δ_T(¹³C, CFC-11), δ_T(¹³C, CFC-12), and δ_T(¹³C, CFC-113) in Table 3. Our δ_T(¹³C, CFC-12) measurements were rescaled to Zuiderweg et al. (2013) using 50.7 m and shallower samples representative of mean ages of around 2000 to 2009. In this period, our measured δ_T(¹³C, CFC-12) is therefore consistent with Zuiderweg et al. (2013) by definition. These measurements were consistent with Bahlmann et al. (2011) ($-\mathrm{41.2}\pm \mathrm{0.2}$) ‰ and with Redeker et al. (2007) ($-\mathrm{40.3}\pm \mathrm{2.6}$) ‰ to within 1 standard deviation. For each CFC, our δ_T(¹³C, sample vs. AAL) for this period was consistent with 0 ‰, as expected given that our AAL reference was collected in 2005. For CFC-11 and CFC-113, a quantitative comparison of our data to previous measurements (Thompson et al., 2002; Redeker et al., 2007; Bahlmann et al., 2011) was not possible due to our data being on a different scale.

Thompson et al. (2002)Redeker et al. (2007)Bahlmann et al. (2011)Zuiderweg et al. (2013)

Table 3 Comparison of δ_T(¹³C) measurements for CFC-11, CFC-12, and CFC-113 from various studies. Only measurements from background, rural, or coastal sites are included as these are most representative of the remote firn measurements presented here. The uncertainties are 1 standard deviation, and the number in brackets gives the number of observations.

^a Thompson et al. (2002), sampled July 1999 to March 2001 background Northern (Alert, Canada (82.5^∘ N, 62.3^∘ W)) and Southern Hemisphere (Baring Head, New Zealand (41.4^∘ S, 174.9^∘ E)) air. ^b Redeker et al. (2007), sampled August to November 2004, Crossgar (54.40^∘ N, 5.76^∘ W), Hillsborough (54.46^∘ N, −6.08^∘ W), and Mace Head (53.20^∘ N, 9.54^∘ W). ^c Bahlmann et al. (2011), marine-influenced air, Wadden Sea Station in List on Sylt (55.02^∘ N, 8.44^∘ E), August to September 2010. ^d Zuiderweg et al. (2013), firn air samples representing depths 50.7 m and shallower, representing 2002 to 2009; NEEM 2009 campaign. ^e This study, firn air samples corrected for gravitational and diffusive fractionation, depths 50.7 m and shallower, representing 2001 to 2009 (CFC-11), 2002 to 2009 (CFC-12), 2000 to 2009 (CFC-113); NEEM 2008/09 campaigns.

We take the mean of the δ_T(¹³C) as predicted using the Appenzeller et al. (1996) and Holton (1990) stratosphere–troposphere exchange parameterisations for a given emissions scenario and ϵ_app to be one model scenario. Hence, four model scenarios are shown in Fig. 4: one for each CFC using Velders and Daniel (2014) emissions (three scenarios, labelled V&D) plus an additional scenario for CFC-11 that differs from V&D by fixing emissions after 2012 (one scenario, labelled M18). The model uncertainty for a scenario is taken to be the full δ_T(¹³C) envelope as predicted using the two stratosphere–troposphere exchange parameterisations. The dominant uncertainty was from ϵ_app, as shown by the strong overlap between the uncertainty envelopes of the two stratosphere–troposphere exchange parameterisations. Each model run predicted an increase in δ_T(¹³C) through time. This behaviour is qualitatively consistent with our measurements for each CFC. There was quantitative agreement between our measurements and modelling for CFC-11 and CFC-12 for the entire period covered by the measurements. For CFC-113, the model is consistent with the measurements after around 1980 but predicts too little fractionation to capture the observed δ_T(¹³C) depletion measured in the sample with a mean age of 1975.

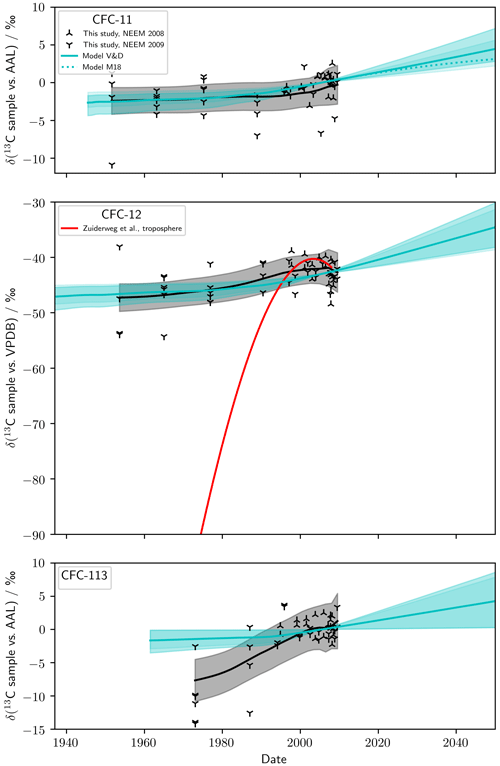
Figure 4 Measured and modelled δ_T(¹³C, CFC-11), δ_T(¹³C, CFC-12), and δ_T(¹³C, CFC-113). The smoothed trend and 95 % confidence intervals for measured δ_T(¹³C) are shown by the solid black line and grey shading, respectively. The solid blue line shows the mean modelled δ_T(¹³C) for the Velders and Daniel (2014) scenario (V&D) and the two stratosphere–troposphere exchange parameterisations (Holton, 1990; Appenzeller et al., 1996). ϵ_app(high-latitude) was used for each CFC. Blue shading shows the 95 % uncertainty envelope for the Holton (1990) and Appenzeller et al. (1996) parameterisations. For CFC-11 only, the dotted blue line shows the mean modelled δ_T(¹³C) for the M18 scenario, with the uncertainty envelope omitted for clarity. For CFC-12, the red line shows δ_T(¹³C) as predicted by Zuiderweg et al. (2013) (amending a typo in the coefficients presented by Zuiderweg et al. (2013), δ_T(¹³C, CFC-12) $=-\mathrm{265.4280}+\mathrm{4.8315}x+(\mathrm{7.8555}\times {\mathrm{10}}^{-\mathrm{5}})x^{\mathrm{2}}-(\mathrm{3.3070}\times {\mathrm{10}}^{-\mathrm{4}})x^{\mathrm{3}}$, where $x=t-\mathrm{1933.5}$, and t gives the date).

Our model returned a value for the isotopic composition of emissions, δ_E(¹³C), such that modelled δ_T(¹³C)=0 ‰ in 2005 (Table 4). Hence, more negative ϵ_app, which drives greater fractionation up to 2005, produces more negative δ_E(¹³C). We take δ_E(¹³C) as the mean of the predictions using the Appenzeller et al. (1996) and Holton (1990) stratosphere–troposphere exchange parameterisations. For each CFC, δ_E(¹³C) was negative and significantly different from 0 ‰, and it was relatively depleted in ¹³C compared to 2005 tropospheric air. For CFC-12, we can perform a quantitative comparison with previously reported δ(¹³C, sample vs. VPDB) values of CFC-12 gas that was purchased from manufacturers, which range from −33 ‰ (Ertl, 1997) to ($-\mathrm{46.8}\pm \mathrm{0.2}$) ‰ (Archbold et al., 2012) (Table 4). We modelled δ_E(¹³C, CFC-12) $=(-\mathrm{47.1}\pm \mathrm{1.3})$ ‰ (2 standard errors), within the range of previously reported δ_E(¹³C, CFC-12).

4 Discussion

Our measurements provide the first observational constraints on ϵ_app(¹³C) for CFC-12 and CFC-113. Our derived ϵ_app(¹³C, CFC-12) is consistent with previously reported ϵ_p(¹³C, CFC-12) (Zuiderweg et al., 2012), being a factor of 2 to 3 lower than ϵ_p(¹³C, CFC-12), as expected given the effect of mixing and diffusion in the atmosphere (Kaiser et al., 2006). Kaiser et al. (2006) also discuss in detail the effects of mixing and transport on the apparent isotope fractionations for N₂O (which we know with much better precision). While mixing and transport are certainly relevant and reduce the observed apparent stratospheric isotope fraction compared with the intrinsic photochemical isotope effects, the variations in these mixing and transport effects are negligible for the precision that we report for CFCs, as can be inferred from the more precise observations for N₂O. The meridional differences observed in ϵ_app(CFC-12) are qualitatively consistent with previously reported isotopic fractionation patterns of other elements in long-lived trace gases, such as δ(³⁷Cl, CFC-12) (Allin et al., 2015; Laube et al., 2010b) and N₂O isotopologues (Kaiser et al., 2006). For CFC-113, we have only measured the δ(¹³C) of the CCl₂F fragment, and our results do not provide information on the CClF₂ fragment or for the molecule as a whole. Our derived ϵ_app(CFC-113) is internally consistent with our firn air measurements, with both data sets being measured on the same fragment. Allin et al. (2015) do not observe meridional differences for ϵ_app(³⁷Cl, CFC-113) – as we observe for ϵ_app(¹³C, CFC-113) – but speculate that differences could be masked by their uncertainties. Given our best understanding of compact tracer–tracer correlations in the lower stratosphere, we do not expect significant meridional differences in ϵ_app for the range of observed fractional releases $\left(\ln \right(\mathrm{1}-f)>-\mathrm{0.6})$ (Volk et al., 1997). The lack of a latitude dependence for lower-stratospheric Rayleigh fractionation is supported by stratospheric observations of other long-lived trace gases, in particular carbon and hydrogen isotope fractionation in CH₄ (Röckmann et al., 2011) and nitrogen and oxygen isotope fractionation in N₂O (Kaiser et al., 2006), which are constrained by a much wider range of observations, with lower measurement uncertainties, than currently available for CFCs. CH₄ and N₂O have global atmospheric mean lifetimes of 10 years and 123 years, respectively, which covers the range of lifetimes of CFC-11 (52 years), CFC-113 (93 years), and CFC-12 (102 years). The three CFCs also have the same chemical sinks as N₂O – photolysis and oxidation by O(¹D), in similar proportions as N₂O. We therefore do not expect these CFCs to behave any differently than CH₄ and N₂O. The observed meridional differences could be statistical artefacts deriving from our poorly constrained ϵ_app(mid-latitude).

Ertl (1997)Thompson et al. (2002)Archbold et al. (2005)Horst et al. (2015)Phillips et al. (2019)

Table 4 δ_E(¹³C) as predicted by our modelling and as reported in previous studies for CFC-11, CFC-12, and CFC-113. With the exception of Ertl (1997), all uncertainties are 2 standard errors.

We derived ϵ_app(CFC-11) by scaling our measured ϵ_app(CFC-12) to previously reported $\frac{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-11}\right)}{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-12}\right)}$ (Zuiderweg et al., 2012). While our presented ϵ_app(CFC-11) values are our best estimates, they are dependent on our ϵ_app(CFC-12) estimates, ϵ_p(CFC-11), and ϵ_p(CFC-12). Our rescaled ϵ_app(CFC-11) also omits the effect of fractionation by O(¹D), though given the around 2 % contribution of O(¹D) to stratospheric CFC-11 loss (Burkholder et al., 2013), we expect this omission to have little effect. Appendix D gives technical details on why we do not use our CFC-11 measurements in our analysis and modelling. For all three CFCs, our ϵ_app(high-latitude) was derived from more data than our ϵ_app(mid-latitude), so we have more confidence in our ϵ_app(high-latitude). For each CFC, ϵ_app(¹³C) is larger than previously reported ϵ_app(³⁷Cl) (Allin et al., 2015), causing more negative fractionation during stratospheric destruction.

Our tropospheric reconstructions and modelling (Fig. 4) allow us to investigate changes in δ_E(¹³C). Our model was run using a constant δ_E(¹³C), and agreement between our reconstructed and modelled δ_T(¹³C) is therefore evidence that no large change in δ_E(¹³C) has occurred over the time period spanned by the measurements. For CFC-12, there was agreement between our reconstructed δ_T(¹³C) and comparable previous measurements (Table 3). This agreement reflects the calibration of Zuiderweg et al. (2013), to which our measurements were rescaled, but is still a check on the quality of our reconstruction. Our modelled and measured δ_T(¹³C, CFC-12) was in agreement for the entire period covered by the measurements (Fig. 4). Our results are therefore consistent with a constant δ_E(¹³C, CFC-12). Furthermore, δ_E(¹³C, CFC-12) as predicted by our model was within the range of previously reported isotopic source compositions for CFC-12 (Table 4). While some variation in δ_E(¹³C, CFC-12) is possible within our uncertainties, these confluent lines of evidence suggest that no dramatic change in δ_E(¹³C, CFC-12), as proposed by Zuiderweg et al. (2013), has occurred since around 1956. The cause of this discrepancy was likely an analytical artefact in Zuiderweg et al. (2013), discussed further in Appendix C. Our measurements and modelling of δ_T(¹³C, CFC-11) are in agreement for the entire period covered by measurements and are therefore consistent with a constant δ_E(¹³C, CFC-11) since at least 1952. For CFC-113, our modelling did not agree with our measurements earlier than around 1980. This discrepancy may be indicative of a change in δ_E(¹³C, CFC-113) though, given that our measurements do not provide a complete picture of the fractionation in CFC-113, and given that this discrepancy is caused by one measurement depth, these results do not confirm a change in δ_E(¹³C, CFC-113). Multiple industrial processes use CFC-113 as a feedstock or produce CFC-113 as an intermediate (Adcock et al., 2018), so a change in δ_E(¹³C, CFC-113) is plausible. The discrepancy between the modelled and reconstructed confidence bounds is at most −1.9 ‰. The range of published δ_E(CFC-113) is ($-\mathrm{31.3}\pm \mathrm{0.5}$) ‰ to ($-\mathrm{26.5}\pm \mathrm{0.8}$) ‰ (Table 4), around 5 ‰. The discrepancy seen for measured and modelled δ_T(CFC-113) can be accounted for by the range of published δ_E(CFC-113).

Our modelling predicts increasing δ_T(¹³C) for CFC-11, CFC-12, and CFC-113 as lighter isotopologues are preferentially destroyed in the stratosphere, and the remaining stratospheric CFC pool, enriched in ¹³C, is mixed with tropospheric air. An acceleration in the rate of increase in δ_T(¹³C) was modelled for each CFC, starting in around 1990. This acceleration is caused by reduced emissions, with relatively depleted δ_E(¹³C) as emissions mitigate stratospheric ¹³C enrichment. Therefore, the new CFC-11 emissions identified by Montzka et al. (2018) have the potential to decrease the rate of increase in δ_T(¹³C, CFC-11). We estimated the potential effect of these new emissions by comparing the V&D and M18 scenarios. As expected, in M18, δ_T(¹³C, CFC-11) was lower than V&D after 2012. Using ϵ_app(CFC-11, high-latitude), the difference was 1.4 ‰ in 2050 – well within our uncertainty envelope. Improved modelling precision and more precise knowledge of δ_E(¹³C, CFC-11) would be needed if δ_T(¹³C, CFC-11) measurements were to be used as a tool for monitoring global CFC-11 emissions, though the isotopic signal from emissions may be more pronounced on regional scales.

5 Conclusions

We presented a new data set of the δ(¹³C) of CFC-11, CFC-12, and CFC-113 for stratospheric air samples and derived values for the apparent isotopic fractionation, ϵ_app, at high latitudes and mid-latitudes of ϵ_app(CFC-11, high-latitude) $=(-\mathrm{7.8}\pm \mathrm{1.7})$ ‰, ϵ_app(CFC-11, mid-latitude) $=(-\mathrm{11.7}\pm \mathrm{4.2})$ ‰, ϵ_app(CFC-12, high-latitude) $=(-\mathrm{20.2}\pm \mathrm{4.4})$ ‰, ϵ_app(CFC-12, mid-latitude) $=(-\mathrm{30.3}\pm \mathrm{10.7})$ ‰, ϵ_app(CFC-113, high-latitude) $=(-\mathrm{9.4}\pm \mathrm{4.4})$ ‰, and ϵ_app(CFC-113, mid-latitude) $=(-\mathrm{34.4}\pm \mathrm{9.8})$ ‰. While for CFC-12 and CFC-113 these estimates are independent, the ϵ_app(CFC-11) estimates are not, having been derived by scaling our ϵ_app(CFC-12) measurements. Further measurements of δ(¹³C, CFC-11) in the stratosphere are required to estimate ϵ_app(CFC-11) independent of CFC-12. For CFC-113, these ϵ_app values are only applicable to the CCl₂F fragment of the molecule. When used to model the tropospheric isotopic composition, δ_T(¹³C), our derived ϵ_app(high-latitude) drives strong fractionation from the mid 1900s through to 2050. Our stratospheric data complement previous, similar measurements of δ(³⁷Cl) for CFC-11, CFC-12, and CFC-113 (Allin et al., 2015; Laube et al., 2010a).

We also reconstructed δ_T(¹³C) from firn air measurements. Comparing these with the model shows that the histories of δ_T(¹³C, CFC-11) and δ_T(¹³C, CFC-12) are consistent with a constant isotopic source composition, δ_E(¹³C), and with stratospheric processing as the sole sink of these chemicals. Our results contradict previous reports of extreme depletion for δ_T(¹³C, CFC-12) and δ_E(¹³CFC-12). Such extreme depletions could have challenged the history of CFC-12 industrial processes and feedstocks, the current understanding of their atmospheric cycling, and/or raised questions about their inertness in the biogeosphere. The discrepancy between reconstructed and modelled δ_T(¹³C, CFC-113) suggests a change in δ_E(¹³C, CFC-113). Changes in industrial processes that produce CFC-113 – as an end product or by-product – could explain such a discrepancy, and the range of reported δ_E(¹³C, CFC-113) would be sufficient to cause such a discrepancy. We caution, however, that this discrepancy derives from only one sample and takes into account the fractionation of only one CFC-113 fragment. Further work would be needed to definitively assign a change in δ_E(¹³C, CFC-113). The modelled increase in δ_T(¹³C) from 2009 through 2050 is sensitive to new emissions. We compared future δ_T(¹³C, CFC-11) trends in scenarios with and without new CFC-11 emissions. The difference between scenarios was within uncertainty bounds; showing better modelling precision and precise quantification of the isotopic composition of emissions would be needed to detect the isotopic signature of recently reported new CFC-11 emissions in background air.

Appendix A: Dilution series and quality control

We measured two dilution series to account for any errors or biases that may be introduced by the low concentrations of CFCs in some samples (Fig. A1). The first dilution series was produced using method A and is therefore applicable to measurements of the Kiruna and Gap samples. The second dilution series was produced using method B and is therefore applicable to measurements of the NEEM 2008/09 firn samples. Each dilution series included repeat measurements of a reference gas (unpolluted tropospheric air collected in 2009; SX-0706077) at five concentrations ranging from (2.9±0.02) to (245.1±3.6) pmol mol⁻¹ (CFC-11), (6.6±0.1) to (540.0±3.4) pmol mol⁻¹ (CFC-12), and (0.9±0.01) to (78.1±0.2) pmol mol⁻¹ (CFC-113). Measurements of this dilution series were previously reported by Allin et al. (2015, SI). The $m/z$ 102 peak area was used as an indicator of the level of dilution in the sample. Noting that the true δ(¹³C, sample vs. SX-0706077) value of each measurement is 0 ‰, we assessed the performance of our method by plotting peak area against measured δ(¹³C, sample vs. SX-0706077) for each sample.

For method A, the measured δ(¹³C) was negative for the samples with the lowest $m/z$ 102 peak area. We have therefore taken the lowest-dilution series $m/z$ 102 peak area where we do not see this behaviour to be the lower $m/z$ 102 peak area limit for method A, above which we have reliable data. This limit was 39 000 (CFC-11), 57 000 (CFC-12), and 44 000 (CFC-113) and is shown in Fig. A1 by the dotted red line. Kiruna and Gap measurements with $m/z$ 102 peak areas below this threshold were excluded from our results but are provided in the Supplement. For method B, the measured δ(¹³C) showed no bias for lower peak areas, and we therefore retained all data. We have excluded the 69.4 and 71.9 m NEEM 2009 samples for CFC-113 because, for the corresponding mean ages, there was too little CFC-113 in the atmosphere (Adcock et al., 2018) to reliably determine δ(¹³C).

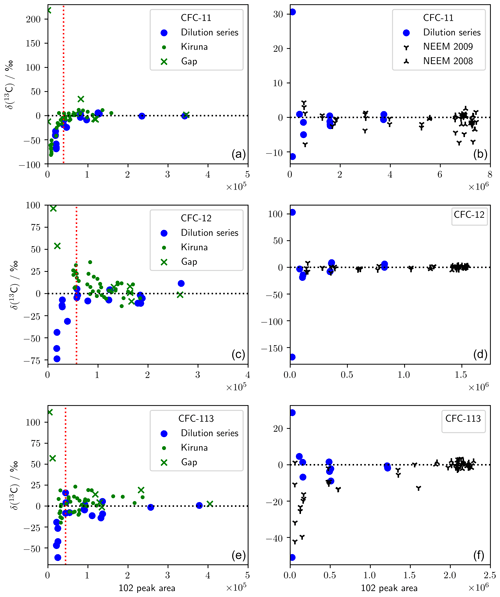
Figure A1 Dilution series for the analytical methodologies used in this work. (a, c, e) Method A, which was used to measure stratospheric samples. The dotted red line shows the lower limit of $m/z$ 102 peak areas that were retained. (b, d, f) Method B, which was used to measure firn air. Dilution series measurements are relative to SX-0706077 (2009 air), and stratospheric and firn air measurements are relative to AAL (2005 air).

Appendix B: Comparison of GC–MS with GC–IRMS measurements

Single-detector GC–MS has been used previously to measure carbon isotope ratios (Eiler et al., 2017; Hauri et al., 2002; Schutten et al., 1957; Nier, 1940), and our single-detector GC–MS analytical system has been used previously to measure chlorine isotopes in stratospheric and firn air samples (Allin et al., 2015; Laube et al., 2010a). As a check on the quality of our method, we have compared measurements made of a suite of photolysis samples using GC–IRMS (Zuiderweg et al., 2011) as presented in Zuiderweg et al. (2012) to our own measurements – using GC–MS – of those samples (Fig. B1). These samples were not subject to the CH₃Cl chromatographic interference seen in Zuiderweg et al. (2013). The samples were diluted by a factor of 1000 before measurement on our system to accommodate the higher sensitivity of our GC–MS method.

The agreement between the methods is good (Fig. B1). Linear regression gives a high regression coefficient (r²=0.92) and a gradient consistent with unity (1.0±0.1). This agreement holds over a range of δ spanning almost 60 ‰. The intercept is (46.3±2.7) ‰. This intercept results in a δ value for CFC-12 in AAL-071170 on the VPDB scale of ($-\mathrm{44.2}\pm \mathrm{2.5}$) ‰ – consistent with the (43.0±2.3) ‰ derived using Eq. (3).

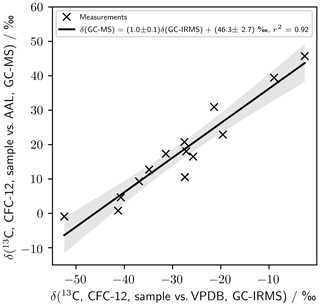
Figure B1 Comparison of measurements presented by Zuiderweg et al. (2012) using GC–IRMS (Zuiderweg et al., 2011) to our own measurements of those same samples.

Appendix C: Reason for NEEM 2009 discrepancy

We measured δ(¹³C, CFC-12) in the same NEEM 2009 flask samples as Zuiderweg et al. (2013) and linked our measurements to the VPDB calibration scale used by Zuiderweg et al. (2013). The measurements in these two studies were consistent, except for the samples at 66.8 and 69.4 m, corresponding to mean ages of 1977 and 1965, respectively (Fig. 2). For the sample corresponding to a mean age of 1965, the discrepancy between data sets is around 40 ‰, an order of magnitude larger than our 95 % confidence intervals and any corrections made to our measurements. The discrepancy is larger when δ_T(¹³C, CFC-12) is considered, with the tropospheric scenario presented by Zuiderweg et al. (2013) predicting δ_T(¹³C) $=-\mathrm{123}$ ‰ in 1965, whereas our measured δ_T(¹³C, CFC-12) $=(-\mathrm{46.8}\pm \mathrm{2.4})$ ‰ (2 standard errors). Assuming sample integrity was preserved between studies, at most one data set can be accurate.

The cause of this discrepancy was likely a measurement artefact in Zuiderweg et al. (2013). In the method of Zuiderweg et al. (2013), methyl chloride elutes before CFC-12. Zuiderweg et al. (2013) model the methyl chloride tail using an exponentially decaying function and subtract this signal from their CFC-12 peak before integration. Zuiderweg et al. (2013) performed a dilution series to evaluate their method, including their treatment of the methyl chloride peak. However, in their dilution series the proportion of methyl chloride to CFC-12 was constant because methyl chloride and CFC-12 were diluted concurrently. In the NEEM 2009 firn air samples, the proportion of methyl chloride to CFC-12 increased in the deeper samples (see Fig. 2 in Zuiderweg et al., 2013). This increase reflects the changing ratio of the CFC-12 mole fraction, γ(CFC-12), to the CH₃Cl mole fraction, γ(CH₃Cl), since the early 1900s (Fig. C1). The methyl chloride baseline correction was therefore performed, on the sample at 69.4 m and, to a lesser extent, on the sample at 66.8 m, on a methyl chloride peak that was larger than that evaluated in the dilution series for a given CFC-12 peak area. Indeed, the trend in δ(¹³C) depletion in the NEEM 2009 profile was qualitatively similar to the trend in tropospheric $\mathit{\gamma }\left(\text{CFC-12}\right)/\mathit{\gamma }\left({\mathrm{CH}}_{\mathrm{3}}\mathrm{Cl}\right)$ over that time period, with lower $\mathit{\gamma }\left(\text{CFC-12}\right)/\mathit{\gamma }\left({\mathrm{CH}}_{\mathrm{3}}\mathrm{Cl}\right)$ for the depleted δ(¹³C) measurements and relatively constant $\mathit{\gamma }\left(\text{CFC-12}\right)/\mathit{\gamma }\left({\mathrm{CH}}_{\mathrm{3}}\mathrm{Cl}\right)$ in the period of little change in δ(¹³C). The dilution series performed by Zuiderweg et al. (2013) therefore did not adequately assess variations in $\mathit{\gamma }\left(\text{CFC-12}\right)/\mathit{\gamma }\left({\mathrm{CH}}_{\mathrm{3}}\mathrm{Cl}\right)$.

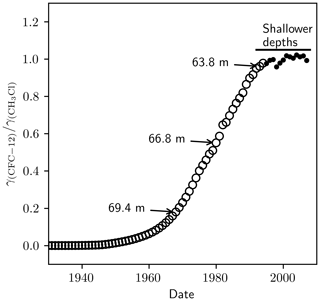
Figure C1 The ratio of the tropospheric mole fraction of CFC-12 to CH₃Cl. Circles were taken from Butler et al. (1999). The dots were calculated using data from the National Oceanic and Atmospheric Administration – Halocarbons & other Atmospheric Trace Species (NOAA-HATS). The annotations indicate the points on the curve that correspond to different depth samples in the NEEM 2009 firn profile.

Appendix D: Stratospheric CFC-11

We presented ϵ_app(CFC-11) based on scaling of our measured ϵ_app(CFC-12) (Table 2, Eq. 4). These best-estimate values were used in our analysis and modelling. We took this approach because the ϵ_app(CFC-11) derived from our stratospheric measurements was inadequate. Figure 3 shows stratospheric Rayleigh plots for our CFC-11 data, from which we derived ϵ_app(CFC-11, high-latitude) $=(-\mathrm{3.8}\pm \mathrm{4.9})$ ‰ and ϵ_app(CFC-11, mid-latitude) $=(-\mathrm{26.5}\pm \mathrm{4.0})$ ‰ (1 standard error). ϵ_app(CFC-11, high-latitude) is not significantly different from 0 ‰ and therefore, when used to force our model, gives confidence intervals that, while consistent with our observations, span 0 ‰. ϵ_app(CFC-11, high-latitude) derived from our stratospheric CFC-11 measurements is consistent with our presented best estimate, ϵ_app(CFC-11, high-latitude) $=(-\mathrm{7.8}\pm \mathrm{1.7})$ ‰. We do not reject our ϵ_app(CFC-11, high-latitude) derived directly from our CFC-11 observations as it is reasonable and derived from relatively many data. We used a different estimate in our analysis simply to achieve the best possible model precision. In contrast, we do not believe our derived ϵ_app(CFC-11, mid-latitude) $=(-\mathrm{26.5}\pm \mathrm{4.0})$ ‰ is correct based on consideration of previously reported ϵ_p (Zuiderweg et al., 2012, Table 2). Our ϵ_app(CFC-11, mid-latitude) derived from our stratospheric CFC-11 measurements is greater than previously reported ϵ_p(CFC-11), which is inconsistent with our best understanding of atmospheric mixing (Kaiser et al., 2006). Also, our derived $\frac{{\mathit{ϵ}}_{\text{app}}(\text{CFC-11},\text{mid-latitude})}{{\mathit{ϵ}}_{\text{app}}(\text{CFC-12},\text{mid-latitude})}=\mathrm{0.87}\pm \mathrm{0.33}$, inconsistent with $\frac{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-11}\right)}{{\mathit{ϵ}}_{\text{p}}\left(\text{CFC-12}\right)}=\mathrm{0.39}\pm \mathrm{0.02}$. Our mid-latitude stratospheric CFC-11 regressions were derived from few data (n=5) and are heavily influenced by one data point with $\ln (\mathrm{1}-f)=-\mathrm{1.49}$. We believe, with additional measurements, ϵ_app(CFC-11) would likely decrease in magnitude.

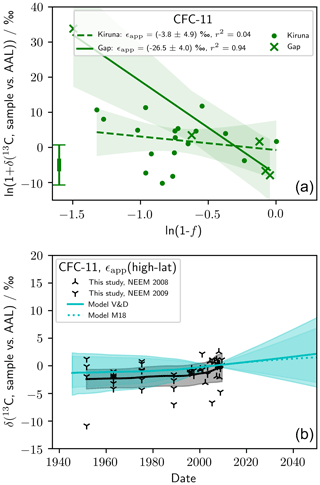
Figure D1 (a) Rayleigh plot showing observations of δ¹³(C, CFC-11) and derived ϵ_app(CFC-11, high-latitude) and ϵ_app(CFC-11, mid-latitude). (b) Also shown is measured and modelled δ_T(CFC-11) (see Fig. 4 and Sect. 2.5 for a description of the model). The model was forced with ϵ_app(CFC-11, high-latitude). The error bar in the bottom left corner of (a) shows the median repeatability of the reference gas measurements over the measurement days and the median error deriving from the fractional release factor.