Impact of organic molecular structure on the estimation of atmospherically relevant physicochemical parameters

Many methods are currently available for estimating physicochemical properties of atmospherically relevant compounds. Though a substantial body of literature has focused on the development and intercomparison of methods based on molecular structure, there has been an increasing focus on methods based only on molecular formula. However, prior work has not quantified the extent to which isomers of the same formula may differ in their properties or, relatedly, the extent to which lacking or ignoring molecular structure degrades estimates of parameters. Such an evaluation is complicated by the fact that structure-based methods bear significant uncertainty and are typically not well constrained for atmospherically relevant molecules. Using species produced in the modeled atmospheric oxidation of three representative atmospheric hydrocarbons, we demonstrate here that estimated differences between isomers are greater than differences between three widely used estimation methods. Specifically, isomers tend to differ in their estimated vapor pressures and Henry's law constants by a half to a full order of magnitude greater than differences between estimation methods, and they differ in their rate constant for reaction with OH radicals (k_OH) by a factor of 2. Formula-based estimation of these parameters, using certain methods, is shown to agree with structure-based estimates with little bias and approximately normally distributed error. Specifically, vapor pressure can be estimated using a combination of two existing methods, Henry's law constants can be estimated based on vapor pressure, and k_OH can be approximated as a constant for all formulas containing a given set of elements. Formula-based estimation is, therefore, reasonable when applied to a mixture of isomers but creates uncertainty commensurate with the lack of structural information.

1 Introduction

The fate of an organic compound in the atmosphere is dictated by a number of physicochemical properties. Its volatility controls whether it partitions to suspended particulate mass or remains in the gas phase, its reactivity controls its lifetime against degradation by ever-present oxidants, and its solubility may control its uptake to particles or its deposition to surfaces (Heald et al., 2020; Jimenez et al., 2009; Knote et al., 2015; Krieger et al., 2012; Ziemann and Atkinson, 2012). The parameters that describe these properties (e.g., vapor pressure) are consequently a critical term in models describing the physical and chemical transformations of atmospheric constituents. In some cases, an exact estimation of these parameters may not be important; for instance, a compound will almost certainly condense when given the opportunity, whether its vapor pressure is extremely low or merely very low. However, many compounds exist in transition regimes in environments typical of atmospheric conditions in which they can partition between phases and may vary in their fates, such as the following: semivolatile compounds that partition between the gas and particle phase (Donahue et al., 2006); compounds with moderate reactivity that may last hours or days, depending on oxidant concentrations (Price et al., 2019); or compounds with sufficient solubility to partition to particles with an aqueous phase but not dry particles (Wania et al., 2015). For these atmospheric components (which likely account for at least tens of percent of atmospheric organic carbon; Hunter et al., 2017), an accurate estimate of their physicochemical parameters is critical.

Unfortunately, physicochemical parameters for atmospherically relevant compounds are poorly constrained by experimental data. Vapor pressures and Henry's law constants (HLCs) are known primarily for higher volatility compounds, typically with few (one to three) functional groups (Compernolle et al., 2011; Raventos-Duran et al., 2010). Little observational data exists for, e.g., compounds with vapor pressures sufficiently low to partition under typical atmospheric conditions. In contrast, the atmosphere contains thousands or tens of thousands of compounds across ∼15 orders of magnitude in vapor pressure (Jimenez et al., 2009), wide ranges of oxygenation, volatility and solubility (e.g., Donahue et al., 2011; Hodzic et al., 2014; Lannuque et al., 2018), and several orders of magnitude in reactivities (Lee et al., 2006), with many multifunctional components (e.g., Aumont et al., 2005; Saunders et al., 2003). Most observational databases are consequently of little direct use, though there have been some recent efforts to develop data sets relevant to the ranges of properties observed in the atmosphere (Dang et al., 2019; Krieger et al., 2018). In order to estimate these parameters beyond the range of observational constraints, several methods have been developed that relate physicochemical parameters to structure through structure–activity relationships (SARs). These typically take the form of a group contribution, in which a molecular structure is parsed into component groups (carbonyls, esters, carbon–carbon double bonds, etc.), with each group assigned an empirically determined impact on a parameter of interest. Various methods exist to estimate volatility (e.g., Barley and McFiggans, 2010; Camredon and Aumont, 2006; Compernolle et al., 2011), HLC (e.g., Meylan and Howard, 1991; Raventos-Duran et al., 2010), and gas-phase reaction rates (e.g., Vereecken et al., 2018). Though these SARs are frequently used to estimate physicochemical parameters of atmospheric constituents, their application to atmospheric oxidation products often requires extrapolation far beyond the chemical space (i.e., volatility and chemical functionality) used in their development. Furthermore, many of the molecules present in the atmosphere contain multiple functional groups, and the substituent groups within a complex molecule may not obviously “map” to the groups used to define an SAR or may interact with neighboring groups in ways not captured by an SAR. This need to extrapolate the volatility and functionality domain of SARs for atmospheric applications leads to higher uncertainty, and previous work has demonstrated that SARs' estimates of vapor pressures, HLC, and gas-phase reaction rates for atmospheric species tend to diverge with increasing numbers of organic functional groups on the carbon backbone (Raventos-Duran et al., 2010; Valorso et al., 2011).

Earlier work on vapor pressure implemented a two-step estimation method in which boiling point is estimated using an SAR, and vapor pressure is estimated from this boiling point using a separate SAR. Widely used boiling point estimation methods include Stein and Brown (1994), Nannoolal et al. (2004), and Joback (1984) and Reid et al. (1987), while widely used vapor pressure estimation methods include Nannoolal et al. (2008) and Myrdal and Yalkowsky (1997). Comparison by Barley and McFiggans (2010) of these eight possible combinations (and a few less widely used methods) suggest that the estimation of boiling point, using the Nannoolal et al. (2004) method, yields the best agreement with experimental data, in particular when using the Nannoolal et al. (2008) vapor pressure estimation method; this combination was similarly found to have the lowest bias in a later comparison by O'Meara et al. (2014). Other vapor pressure estimations also perform well when using the Nannoolal et al. (2004) boiling point estimation, most notably the Lee–Kesler method (Reid et al., 1987), which exhibits a similarly low bias method (Barley and McFiggans, 2010; O'Meara et al., 2014). More recently, vapor pressure estimation methods have been developed that use SARs to directly estimate vapor pressure, specifically SIMPOL (Pankow and Asher, 2008) and EVAPORATION (Compernolle et al., 2011). These two methods have been previously shown to agree well with those estimated by the Nannoolal et al. (2004) method (Compernolle et al., 2011). Prior work, therefore, suggests that at least three methods (i.e., SIMPOL, EVAPORATION, and Nannoolal) comparably estimate vapor pressures, and one of these methods (Nannoolal) is in reasonable agreement with the experimental data. However, these experimental data are mostly limited to vapor pressures greater than 10⁻⁸ atm (saturation concentration; $c^{*}>\sim {\mathrm{10}}^{\mathrm{1.5}}$ µg m⁻³), which is at the lower limit of vapor pressures expected to partition to the particle phase under typical atmospheric conditions (Donahue et al., 2006). These three methods consequently represent some of the current best SARs for estimating vapor pressure, but they remain highly uncertain. None of these methods was found to be accurate to better than approximately half an order of magnitude for their best constrained regions, and methods tend to diverge at lower vapor pressures (Barley and McFiggans, 2010; Compernolle et al., 2011; Valorso et al., 2011). Even relatively accurate estimates can introduce large errors in transition regimes. An error of half an order of magnitude in vapor pressure for a compound with an estimated saturation concentration near ambient particulate matter concentrations may “move” a compound from mostly in the gas phase to mostly in the particle phase (Compernolle et al., 2011). Furthermore, uncertainty estimates of half an order of magnitude may be optimistic as recent work has found orders-of-magnitude discrepancies between measured vapor pressures of low-volatility compounds and those estimated by the Nannoolal et al. (2008) method (Dang et al., 2019), but data are still limited.

For most volatile organic compounds (VOCs), the atmospheric oxidation is mainly driven by the reaction with OH radical. Various methods, based on SARs, are available in the literature to estimate VOC and OH gas-phase rate constants, k_OH (Vereecken et al., 2018). A very commonly used SAR was developed by Kwok and Atkinson (1995), for which a few revised and extended versions are now available (e.g., Jenkin et al., 2018a, b).

A few methods are available for the estimation of HLC, which parameterizes the partitioning of gases into a liquid (typically dilute aqueous) phase. For atmospheric chemistry applications, most commonly used SARs are HWINb (US Environment Protection Agency, 2019) and the more recently developed GROMHE (GROup contribution Method for Henry's law Estimate; Raventos-Duran et al., 2010), the latter of which has been shown to be somewhat more accurate. There are, consequently, fewer alternatives around the selection of a method to estimate these parameters, but there can nevertheless be large errors in their estimation (e.g., orders of magnitude in HLC estimates).

To avoid the need to extrapolate SARs and the concomitant uncertainty that arises from this approach, a new generation of tools allows physicochemical properties to be directly estimated using quantum-chemistry-based calculations. These tools include commercial products that can directly calculate physicochemical properties (e.g., vapor pressure) or can calculate solvation parameters to estimate partitioning between phases, for instance, COSMOtherm (available from Dassault Systèmes, based on COSMO-RS; Klamt, 1995; Klamt and Eckert, 2000) and SPARC (SPARC Performs Automated Reasoning in Chemistry; available from ARChem, LP; based on Hilal et al., 2004). In a related approach, a calibrated fit to experimental partitioning data can be developed based on solvation parameters (a poly-parameter linear free energy relationship or ppLFER), which can, in turn, be calculated using commercial products like Absolv (ACD/Labs; Arp et al., 2008a, b; Wania et al., 2014). By calculating parameters directly from molecular structure, these methods do not suffer the same degree of uncertainty caused by extrapolation beyond the empirically constrained regions of SARs and have been shown to handle multifunctional compounds with no bias and modest increases in uncertainty (Wang et al., 2017). These methods have also been shown to agree well in their estimations of partitioning between vapor and condensed phase organics (related to vapor pressure) but still exhibit large differences in estimations of partitioning of organics into water (related to HLC; Wang et al., 2017). Quantum-chemistry-based calculations may therefore represent a new approach for estimating partitioning in atmospheric systems (e.g., Wania et al., 2015), but they have not yet seen widespread adoption in the atmospheric science community, and so the work presented here focuses on the more commonly used SAR-based approach.

In addition to these methods for the estimation of physicochemical parameters based on molecular structure, there has been a recent focus on developing approaches that rely only on molecular formula. This is largely driven by the rapid increase in the use of direct mass spectrometry, in particular direct chemical ionization mass spectrometry (CIMS), which samples at atmospheric pressure and can, therefore, detect nearly all gas- and particle-phase atmospheric constituents with minimal pretreatment (Aljawhary et al., 2013; Huey et al., 1995; Hunter et al., 2017; Isaacman-Vanwertz et al., 2018). By allowing direct measurement of chemically and/or thermally labile atmospheric constituents, these instruments have profoundly increased understanding of atmospheric chemistry (e.g., Ehn et al., 2014; Lee et al., 2016; Nguyen et al., 2015). However, direct mass spectrometry generally lacks any mechanism for the resolution of isomers, yielding data only on the molecular formula of detected analytes, with little structural information. Some approaches to CIMS are limited to specific compound classes (e.g., acids), thus providing some information, but provide no resolution of isomers within these classes (Thompson et al., 2016). In order to situate measurements by CIMS and other direct mass spectrometers in a chemical space useful for modeling or understanding the atmosphere (e.g., Isaacman-VanWertz et al., 2017; Mohr et al., 2019), methods have been developed and applied for estimating physicochemical parameters from formulas alone. These methods are primarily limited to estimation of vapor pressure (Daumit et al., 2013; Donahue et al., 2011; Li et al., 2016) and k_OH (Donahue et al., 2013); no formula-based methods for estimation of HLC have been published.

Formula-based estimation of physicochemical parameters is necessarily less exact than structure-based estimation, as it has less information available as an input (i.e., lack of structure). To some extent, isomers are known to differ in their physicochemical properties. Different functional groups containing the same atoms vary in their SAR group contributions (e.g., carboxylic acid vs. ester), and prior work has demonstrated that even positional isomers may differ in their vapor pressures (Dang et al., 2019). However, the extent to which a lack of structural information degrades parameter estimation has not been previously shown. If, for example, the uncertainty in parameter estimation is significantly larger than differences caused by structure, there would be no significant loss in accuracy caused by not knowing the structure. It is, therefore, an important, but unanswered, question to determine to what extent isomers differ in their parameters and how this compares to precision in parameter estimation. Addressing this issue would provide an understanding of the degree to which it is relevant to know the structure of a molecule when estimating a given parameter. It is important to note that application of SARs frequently includes extrapolation beyond well-constrained laboratory data, which may decrease their accuracy. Formula-based estimations are typically built off these existing SARs, inherently including their limitations and biases. It is consequently less informative to discuss the accuracy of a formula-based estimation, which is largely driven by the underlying SAR(s) and for which experimental data are limited, so we rather discuss the precision of such a method, i.e., the ability to recreate a structure-based estimate using only its molecular formula.

Given the large number of available methods, selection of a method for the estimation of a physicochemical parameter is nontrivial, and researchers are left navigating a complex issue without obvious best practices. Selection of one method over another is frequently an issue of convenience or familiarity, often with little consideration of the accuracy of a method, which may itself be poorly constrained due to a lack of experimental data for atmospherically relevant compounds. The range of choices is further complicated by the fact that many methods have multiple publicly available implementations (e.g., online interfaces), which, we show in this work, may disagree for a significant fraction of compounds. In an effort to understand the current landscape, we examine here some widely used methods for the estimation of three critical physicochemical parameters, namely vapor pressure, Henry's law constant (HLC), and k_OH. We combine widely used methods for estimation of these parameters to answer the following questions:

1. How different are the various methods available for both structure-based and formula-based estimations of vapor pressure, Henry's law constants, and gas-phase OH reaction rates?

2. Does knowing the structure of a molecule improve the estimation of its physicochemical parameters? That is, are differences in physicochemical parameters between isomers sufficiently large to outweigh uncertainty in their estimation?

3. How much additional uncertainty is introduced in parameter estimation when structural information is unavailable?

2 Methods

To answer the questions posed above, physicochemical parameters were estimated for approximately 38 000 atmospherically relevant species representing approximately 1200 formulas. Parameters were estimated using a large number of methods currently in widespread use by the atmospheric chemistry scientific community. Differences between structure-based estimation methods for an individual compound were compared to differences between isomers of a formula for a given method. These were further compared to parameters estimated using formula-based methods. Details of species generation and parameter estimation are provided below. A critical issue to consider throughout this work is that extending results beyond the training data may significantly increase uncertainty. The results herein are most reasonably applied to products of gas-phase atmospheric oxidation, with heavy representation by compounds that are highly oxygenated, are multi-functional, and/or contain nitrate groups.

Throughout the paper, the notation used to describe derived quantities about a property, x, estimated by a structure-based estimation method (i.e., SAR), m, include the following:

• Δx is the difference in x between two isomers;

• 〈Δx〉_formula is the average difference in x between all isomer pairs for a given formula;

• Δm_x is the difference in x for a given species as estimated by two different SARs;

• 〈Δm_x〉 is the average difference in x between all SAR pairs for a given species;

• $\stackrel{\mathrm{‾}}{x}$ is the average x of a species, estimated using all SARs; and

• ${\stackrel{\mathrm{‾}}{x}}_{\text{formula}}$ is the average x of a formula, estimated using all SARs for all isomers.

Properties studied include the following: pure component subcooled liquid vapor pressure, p, in units of log(atm); Henry's law constant, HLC or H, in units of log(M atm⁻¹); and gas-phase OH reaction rate constant, k_OH or k, in units of ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$.

2.1 Generation of atmospherically relevant molecular structures

Atmospherically relevant species were generated using the simulated oxidation of precursor hydrocarbons. A total of three hydrocarbons – α-pinene, decane, and toluene – were selected to represent different chemical classes common in the atmosphere (cyclic alkene, saturated alkane, and aromatic, respectively) and different expected emissions sources. The gas-phase oxidation mechanism for these hydrocarbons was generated using the Generator of Explicit Chemistry and Kinetics of Organics in the Atmosphere (GECKO-A). GECKO-A is a computer program designed to automatically generate the complete mechanism involved in the oxidation of a broad range of atmospherically important hydrocarbons. The tool generates chemical mechanisms according to a prescribed protocol, providing reaction rates based on experimental and theoretical data and SARs. The protocol implemented in GECKO-A is described by Aumont et al. (2005), with chemistry updates given in Lannuque et al. (2018). With the purpose of the study being to explore the properties of isomer distributions, oxidation was explicitly considered up to the fifth generation, and no lumping was performed using surrogate species during the generation process. To limit the size of the mechanism, gas-phase chemistry for species having a vapor pressure below 10⁻¹³ atm was not generated, as those species are expected to partition almost exclusively to the condensed phase under typical atmospheric conditions (e.g., Valorso et al., 2011). The numbers of species generated are 2.0×10⁵, 5.5×10⁵, and 7.5×10⁵ for the decane, toluene, and α-pinene mechanisms, respectively. Nonradical species are considered in both the gas and particle phase. Condensed phase reactions are not considered in this model configuration.

Simulations are performed in a box model using conditions roughly representative of average continental atmospheric conditions (Lannuque et al., 2018). In these runs, temperature is fixed at 298 K, photolysis frequencies are computed for midlatitude and for a solar zenith angle of 45^∘ using the Tropospheric Ultraviolet and Visible (TUV) model (Madronich and Flocke, 1999), and the relative humidity is set to 70 %. Mixing ratios are prescribed for methane (1750 ppb – parts per billion), CO (120 ppb), HCHO (2 ppb), NO_x (500 ppt – parts per trillion), O₃ (40 ppb). Furthermore, a proxy species is introduced to include the influence of nonmethane volatile organic compound oxidation on the HO_x and NO_x cycles. A first-order loss rate of OH, with respect to that proxy, is set to 6 s⁻¹ and leads to the formation of a surrogate peroxy radical, with a chemistry assumed to be similar to CH₃O₂. To allow gas and/or particle partitioning, a preexisting mass concentration of organic particle is assumed and set to 10 µg m⁻³. This condensed phase is assumed to behave as a well-mixed ideal organic phase made of nonvolatile organic matter. Finally, the parent hydrocarbon initial mixing ratio is set to an arbitrary value of 10 ppt carbon, a value low enough to not substantially modify the prescribed buffered conditions. Time integration of the mechanisms is performed for 5 d. These simulations served primarily to generate various species representative of the molecular structures expected in typical ambient atmospheres under both high- and low-NO_x conditions. The analysis performed in this study is not sensitive to the exact oxidation conditions, as described below.

The number of species considered in the GECKO-A mechanisms is excessively large, and a threshold was set in this work to perform the analysis. The species representing the (approximately) 200 most abundant molecular formulas in each the gas and particle phase were analyzed for each oxidation system. “Abundance” is considered here as the summed concentration across the modeled period. Separately considering the abundance of gas- and particle-phase compounds ensures a data set spanning the atmospherically relevant range of properties. Some of the same formulas may be abundant in both the gas- and particle-phase components of a given oxidation system, but a given formula may be comprised of a different set of isomers or the same isomers in different proportions. A total of 1193 formulas, comprised of roughly 182 000 unique compounds, were consequently included in this analysis, roughly evenly split between the three oxidation systems and between gas- and particle-phase components. Roughly two-thirds of these formulas contain nitrogen, in most cases in the form of organonitrates.

For each formula, isomers were included in this analysis if they accounted for at least 0.1 % of the abundance of each formula. This threshold was selected to maximize statistical robustness by providing a large data set, while minimizing the impact of species expected to be produced at negligibly small concentrations. Selection of higher thresholds (e.g. 1 %, 10 %) were investigated but not observed to significantly change the results of this work. In order to prevent this analysis from being too strongly impacted by the specific chemistry of the model, isomers were not weighted by their abundance in any of the analyses below; instead, isomers were included with equal weight as long as they exceeded the 0.1 % threshold. A total of 38 594 species exceeded the 0.1 % threshold in at least one oxidation system and phase. Each formula may include a variable number of isomers, so compounds are not equally distributed between oxidation systems, i.e., 5 % α-pinene gas-phase components, 6 % decane gas, 10 % toluene gas, 20 % α-pinene particle, 16 % decane particle, and 43 % toluene particle. From this distribution, it is apparent that, in general, the model predicts particle-phase formulas to contain 3 to 4 times as many isomers as gas-phase formulas, and toluene oxidation produces twice as many isomers per formulas as the other two systems studied. Due to these differences, the six data sets are discussed separately, where relevant, throughout this work. Furthermore, species that have both a gas- and particle-phase component exceeding the 0.1 % threshold (N is equal to 3241 species) are included in both systems when gas- and particle-phase compounds are analyzed or discussed separately.

Each compound is described by a SMILES string from which the physicochemical properties could be estimated computationally. Most structure-based estimation methods involve a two-step process in which the SMILES notation is parsed into the chemical functional groups relevant to the method, and then the impact of each group is combined. All structure-based estimation in this work was executed through publicly available online tools that performed both the parsing of the SMILES string and the computation of the properties, as described below. SMILES strings and estimated parameters are provided in the Supplement for all compounds used in this work (all ∼182 000 compounds provided, with the most relevant 38 594 denoted).

2.2 Structure-based estimation of vapor pressure

2.2.1 SIMPOL

SIMPOL is a structure–activity relationship in which the subcooled liquid vapor pressure contributions of individual chemical functional groups are summed to generate a subcooled pure liquid vapor pressure (Pankow and Asher, 2008). No second-order interaction terms are included to account for neighboring functional groups. There are two implementations of SIMPOL publicly available, namely the GECKO-A online interface (http://geckoa.lisa.u-pec.fr/, last access: 20 April 2021) and the Python package APRL Substructure Search Program, developed and made publicly available by Satoshi Takahama (Ruggeri and Takahama, 2016). At the time of publication, the GECKO-A online interface does not accept standard SMILES strings, requiring instead a modified notation that uses explicit hydrogens and a few other differences, making its widespread use somewhat more difficult. Both implementations of SIMPOL were compared as part of this work. While small differences are expected due to uncertainty in parsing SMILES notation and ambiguity in chemical functional group assignment, vapor pressures estimated by SIMPOL should ideally be nearly identical between implementations. In the case of decane and α-pinene oxidation products, these implementations were in excellent agreement (Fig. S1 in the Supplement). However, significant differences were observed in their estimations of toluene oxidation products with complex molecular structures. To understand the differences observed for toluene oxidation products, SIMPOL was implemented manually for a random set of compounds that were observed to not agree, with results shown in Table S1 in the Supplement. While some differences may be attributable to real errors in implementations, a larger uncertainty appears to be associated with needing to extrapolate beyond the functional groups identified within the SIMPOL SAR. For example, SIMPOL does not include the α-carbonyl peroxide (-C(=O)-O-O-R) functional group; while a peroxide group is included, carbonyls are included only as ketones and aldehydes, neither of which is an accurate description of this case. APRL treats this group as a peroxide, with no contribution from the carbonyl group, while GECKO-A treats this group as an ester ether; little or no data exist to determine which approach is more accurate. This example points to a systematic limitation of SARs, and the inherent potential differences between implementations for complex atmospheric oxidation products.

In the case of SIMPOL, manual investigation suggests that most differences between implementations could be traced to differences in the interpretation or extrapolation of the SAR for functional groups outside the prescribed bounds. Neither implementation was found to be clearly more suitable or faithful to the published SAR. The GECKO-A implementation of SIMPOL was used in this work because the online interface of GECKO-A provides a logistical benefit by implementing this method alongside multiple other structure-based parameter estimations. Results in this work are found to be relatively insensitive to the choice of implementation as they are nearly identical for decane and α-pinene oxidation products.

2.2.2 EVAPORATION

EVAPORATION is a structure–activity relationship for the estimation of subcooled liquid vapor pressure that includes vapor pressure contributions of individual chemical functional groups and terms to account for interactions between neighboring groups (Compernolle et al., 2011). Currently, this method lacks terms to describe several less abundant but nevertheless atmospherically relevant functional groups, including -NO₂ and -C(=O)ONO₂. For the purpose of this analysis, these groups were replaced by -ONO₂ and -C(=O)OONO₂ respectively, which are predicted to have similar impacts on vapor pressure based on SIMPOL (Sect. 2.2.1) and the Estimation Programs Interface (EPI) Suite (Sect. 2.2.5). EVAPORATION currently also lacks a treatment of aromaticity, but this limitation has little impact on this data set. Though toluene is aromatic, oxidation quickly breaks its aromaticity, and fewer than 200 oxidation products contained aromatic carbon; aromatic carbons were replaced with aliphatic carbons for these compounds, which is expected to introduce bias of approximately half an order of magnitude for this small subset of compounds.

At the time of publication, two implementations of the EVAPORATION method are publicly available as online resources. A direct online interface is available through the Royal Belgian Institute for Space Aeronomy (hereafter referred to as IASB; https://tropo.aeronomie.be, last access: 20 April 2021), the institution at which the SAR was developed. A separate implementation is available as part of the UManSysProp package for the estimation of a wide range of physicochemical and system parameters, developed and published by researchers at the University of Manchester (Topping et al., 2016). UManSysProp is available both as a stand-alone Python package and an online interface at http://umansysprop.seaes.manchester.ac.uk (last access: 20 April 2021).

Both the IASB and UManSysProp implementations of EVAPORATION were compared as part of this work in order to ensure that inclusion of this estimation method in this work is as faithful as possible to the published SAR. Though the comparison of these implementations, shown in Fig. S2, fell generally along a one-to-one line as expected, some significant differences were observed. Vapor pressures estimated for decane oxidation products were almost always nearly identical, but oxidation products of α-pinene differed by approximately an order of magnitude for a large fraction of the tested compounds, and toluene oxidation products differed significantly and variably for a substantial majority of compounds. To assess these differences, the EVAPORATION SAR was tested manually for a small set of compounds that differed between implementations. Values manually computed were found, in most cases, to be in reasonable agreement with the IASB implementation but frequently differed from the UManSysProp implementation (Table S2). Not all differences in methods could be obviously explained by extrapolation beyond prescribed functional groups, but these differences nevertheless highlight the difficulties encountered in implementing a given SAR for a highly diverse and complex molecular structure. This work relies on the IASB implementation for the estimation of vapor pressures by the EVAPORATION method, based on its agreement with manual implementation and the fact that this implementation is provided by the institution at which the SAR was developed. We note that the open-source nature of the UManSysProp package allows a user to understand and/or modify its source code, so future updates may impact these comparisons, but no attempt was made in this work to reconcile the two methods.

2.2.3 Nannoolal

Nannoolal and co-workers (2008) developed a group contribution method for the prediction of vapor pressure, given the structure and boiling point of a molecule. This method includes a substantially larger number of groups than either SIMPOL or EVAPORATION, encompassing a broader range of compounds including inorganic groups, and includes second-order terms to account for interactions between neighboring groups. Boiling point can, in turn, be estimated from molecular structure using a group contribution method developed by Nannoolal and co-workers (2004). “Nannoolal” in this work refers to the estimation method using both the vapor pressure and boiling point group contribution methods developed by Nannoolal et al. (2004, 2008). There are two implementations of Nannoolal available through online interfaces, specifically using the GECKO-A interface and the UManSysProp package. Some differences were observed between these implementations (Fig. S3), similar in scope and scale to the EVAPORATION comparison above. It is clear from the comparisons of Nannoolal and EVAPORATION implementations that the estimation of vapor pressures for toluene oxidation products poses unique complexities. Due to the general similarity between implementations for the nonaromatic precursors and the use of the Nannoolal SAR as the default estimation method in the GECKO-A model itself, no further examination of the implementation in the two tools was undertaken. In this work, Nannoolal refers to the GECKO-A implementation of this method.

2.2.4 Myrdal and Yalkowsky

The vapor pressure estimation method developed by Myrdal and Yalkowsky consists of a group contribution correction to a previous semiempirical estimation method that relied only on boiling and melting points and on estimations of the entropy of boiling, entropy of melting, and heat capacity change upon boiling (Myrdal and Yalkowsky, 1997). In this modification, a small number of groups (fewer than a dozen) and molecular properties (e.g., rotational symmetry) are considered for their impacts to these three estimated physicochemical properties. For calculation of subcooled liquid vapor pressures, the terms considering temperatures and entropies of melting can be ignored. Consequently, vapor pressure estimation by the Myrdal and Yalkowsky method for this work depends only on molecular structure and boiling points.

This work relies on the UManSysProp implementation of the Myrdal and Yalkowsky method, which allows estimation of the boiling point by any one of several methods. Where the Myrdal and Yalkowsky method are considered in this work, boiling points were estimated using the Nannoolal estimation technique (Nannoolal et al., 2004). Another implementation is available through the GECKO-A interface using the Joback and Reid boiling point group contribution estimation technique (Joback, 1984; Reid et al., 1987), with some modifications as described by Camredon and Aumont (2006). The Myrdal and Yalkowsky SAR has been shown previously to be comparable to, but somewhat less accurate and more biased than, the Nannoolal SAR when the Nannoolal boiling point estimation technique (Nannoolal et al., 2004) is used and to be substantially biased when Joback and Reid is used (Barley and McFiggans, 2010; O'Meara et al., 2014). The Myrdal and Yalkowsky method is, therefore, not included in most of the analyses in this work, and the GECKO-A and UManSysProp implementations of this SAR are, consequently, not compared in detailed.

2.2.5 EPI

The U.S. Environmental Protection Agency makes the EPI Suite^™ available for the estimation of environmentally relevant parameters (US Environment Protection Agency, 2019), which include a module (MPBPVP) for the estimation of vapor pressures and subcooled liquid vapor pressures, using SMILES strings as inputs. This module uses the modified Grain method, which estimates vapor pressure based on a near-unity structural factor and an estimated boiling point. Boiling point is, in turn, estimated using the Stein and Brown (1994) group contribution method, an extension of the Joback and Reid method (Joback, 1984; Reid et al., 1987). This approach includes group contributions for a wide variety of molecular structures, including a wide range of inorganic components. Estimation of vapor pressures by the EPI Suite is perhaps most common for estimating small numbers of vapor pressures due to its readily available implementation, though it has higher error than some other methods (e.g., Nannoolal) when compared against experimental data (Barley and McFiggans, 2010, wherein the method referred to as SB/BK closely approximates the EPI method).

2.3 Structure-based estimation of Henry's law constant

A total of two structure-based methods were considered in this work for the estimation of Henry's law constants (HLCs). The first method used here is HWINb, the bond contribution method implemented by the HENRYWIN module of the EPI Suite (US Environment Protection Agency, 2019). This method is similar to a group contribution method, but instead of using groups, individual bonds are considered with correction factors for different chemical classes (Hine and Mookerjee, 1975; Meylan and Howard, 1991). The second method used here is GROMHE, a group contribution method that also includes a group contribution term for the effect of hydration of carbonyls (Raventos-Duran et al., 2010). GROMHE is the HLC estimation method used by GECKO-A, which is the implementation used in this work. Previous work has suggested GROMHE to be more accurate than HWINb, but this conclusion was based on a relatively small amount of experimental data (<500 compounds) with relatively low HLCs (Raventos-Duran et al., 2010). We, consequently, do not assume the accuracy of one method over another and, instead, assume that the variability between methods is due to uncertainty in the structure-based estimation of HLC.

2.4 Structure-based estimation of k_OH

A total of two structure-based methods were considered in this work for the estimation of k_OH. Perhaps the most common method is that developed by Kwok and Atkinson (1995), a group contribution method that includes additive terms for hydrogen abstraction from or radical addition to individual atoms or bonds. An additional second-order term accounts for substituent effects on each atom. The implementation of this method is the AOPWIN module of the EPI Suite (Meylan and Howard, 1993; US Environment Protection Agency, 2019). The other method used here is the group contribution method of Jenkin et al., which functions similarly to the Kwok and Atkinson (1995) approach but with updated and extended coefficients (Jenkin et al., 2018). Jenkin et al. (2018) is the k_OH estimation method used by GECKO-A, which is the implementation used in this work and which is available through the GECKO-A online interface.

2.5 Formula-based estimation of vapor pressure

2.5.1 Daumit et al. (2013)

Daumit and co-workers (2013) use a basic set of assumptions about the structures of atmospheric components to apply the SIMPOL estimation method in the absence of molecular structure. Essentially, all oxygen atoms in a molecule are apportioned between hydroxyl and carbonyl groups based on the degree of unsaturation calculated from the $\mathrm{H}/\mathrm{C}$ and $\mathrm{O}/\mathrm{C}$ ratios. To accurately calculate degrees of unsaturation, an assumption must be made about the number of rings present in the molecule. We assume there are no rings, as this is consistent with the majority of compounds in this data set, but the need to make this assumption represents a general source of uncertainty in the Daumit et al. (2013) method. While Daumit et al. (2013) do not explicitly treat nitrogen, they note that the nitrate group is expected, in SIMPOL, to have a similar impact to the hydroxyl group. The carbonylperoxynitrate group, another major form of organic nitrogen in the atmosphere (e.g., peroxyacetyl nitrate – PAN), similarly has an impact comparable as its hydroxyl analog, the carbonyl peroxyacid group. To explicitly extend this method to nitrogen, we make the assumption that nitrogen is predominantly present as nitrate groups, and each nitrate group is treated as being equivalent to a hydroxyl group; this assumption is reasonable for a system dominated by products of gas-phase oxidation, in which R-ONO₂ compounds and peroxynitrates are the dominant source of organic nitrogen (Beaver et al., 2012; Lee et al., 2016), but it should be applied only cautiously to other systems. For every three oxygen atoms present in the formula, two oxygen atoms and one nitrogen atom is removed until all nitrogen has been removed. The resulting formula, in which all possible NO₃ groups have been formulaically converted to OH, are treated as per Daumit et al. (2013). As an example, the formula C₈H₁₅O₆N, interpreted as containing one nitrate group, one carbonyl, and two hydroxyl groups would be treated as C₈H₁₆O₄, interpreted as containing one carbonyl, and three hydroxyl groups. In environments in which nitrogen is present in forms other than nitrate, Daumit et al. (2013) lack an explicit mechanism for considering nitrogen. An additional limitation of this approach is that while certain groups can be approximated as a combination of carbonyl and hydroxyl oxygens, others may be poorly described in this way. For example, the vapor pressure contribution of a carboxylic acid is estimated to be similar to that of a ketone or an aldehyde plus a hydroxyl group, but a hydroperoxide has a substantially lower impact than that of two hydroxyl groups.

2.5.2 Modified Li et al. (2016; molecular corridors)

The formula-based approach for the estimation of vapor pressures developed by Li et al. (2016) as part of their work on “molecular corridors” uses empirical coefficients to quantify the impact of each atom on vapor pressure, with a minor term for interactions between carbon and oxygen (Li et al., 2016; Shiraiwa et al., 2014). Formulas are first categorized by their component elements, with a separate set of coefficients for, e.g., CHO formulas vs. CHON formulas. This method was developed by multilinear regressions against a training set of vapor pressures estimated by the EPI Suite. As with any empirical method, it is, to some extent, limited to the compound classes on which it was trained and can only be as accurate as the SAR estimation method with which it was developed (EPI). Most notably, despite the relative prevalence of organic nitrates (R-ONO₂) in the atmosphere (Lee et al., 2016), few such compounds exist in the CHON training set used by Li et al. (2016). Of the 13 628 CHON compounds used to build the relationship, only nine (0.07 %) are organic nitrates and 750 (5.5 %) are organic nitro compounds, which have a similar impact on vapor pressure; all other included compounds represent amines, amides, amino acids, and other groups that contain C−N bonds, which are expected to have a very different impact on vapor pressure. Consequently, application of the Li et al. (2016) formula-based estimation technique to compounds containing nitrates is expected to be significantly biased. We test this hypothesis here in order to apply this method more accurately to the data set.

Comparison of vapor pressures estimated by Li et al. (2016) to vapor pressures estimated for the same compound using structure-based methods (Fig. S4) demonstrates significant biases that increase with the number of nitrogen atoms, which, in this data set, are almost wholly contained in nitrate, nitro, and peroxynitrate groups. To address this bias, we propose two similar possible approaches based on the observation that a nitrate group (NO₃) has a similar impact on vapor pressure to a hydroxyl group (OH), and thus, each nitrogen has the effect of canceling the effect of two oxygen atoms. Either the nitrogen coefficient for CHON formulas can be forced to equal to twice the negative of the oxygen atom ($b_{\mathrm{N}}=-\mathrm{2}\times b_{\mathrm{O}}$), or the formula used to estimate vapor pressure can be amended to convert all potential nitrate groups into hydroxyl groups, as described in the implementation of Daumit et al. (2013). Both approaches are shown in Fig. S4 to similarly remove the nitrogen-dependent bias and are generally equivalent in this data set. In mixed environments in which functionalized amines and organonitrates may coexist, formulaically converting nitrate groups to hydroxyl groups may be preferred in order to more accurately treat nitrogen in excess of potential nitrate groups (i.e., in cases where the number of nitrogen is greater than the number of sets of three oxygens). However, given the nitrate-dominated nature of this data set, for simplicity we use a modified Li et al. (2016) method in which $b_{\mathrm{N}}=-\mathrm{2}\times b_{\mathrm{O}}$.

2.5.3 Donahue et al. (2011)

A relatively simple, formula-based estimation method is provided by Donahue et al. (2011) that relies only on carbon and oxygen number. This method represents a general relationship based on average expected trends in the structures of atmospheric components. It cannot be easily extended to nitrogen-containing formulas, so they are excluded from analyses using this approach in the present work.

2.6 Formula-based estimation of Henry's law constant

To the best of our knowledge, no explicit method for a formula-based estimation of Henry's law constant (HLC) has been published. However, explicit modeling of gas-phase oxidation has previously shown a relationship between HLC and vapor pressure for organic species of atmospheric interest (Hodzic et al., 2014; Lannuque et al., 2018). Given the previously demonstrated feasibility of formula-based estimation of vapor pressure, this suggests that a formula-based estimation of HLC is possible, at least for compounds with shared characteristics (e.g., multifunctional atmospheric oxidation products).

2.7 Formula-based estimation of k_OH

In a separate work from their formula-based vapor pressure estimation, Donahue and co-workers (2013) have developed a formula-based approach for the estimation of gas-phase OH reaction rates (k_OH). The equation they provide is roughly based on the observations that as carbon number increases, available hydrogens for OH abstraction also increase, and as oxygen number increases, hydrogens become easier to abstract, but there is a decrease in the number of abstractable hydrogens. Donahue et al.(2013) recognize it only as a rough approximation and not a particularly robust estimation method, a conclusion consistent with results in this work.

2.8 Summary

Given the large number of methods employed in this work, we summarize them below alongside the notation used hereafter in this work.

2.8.1 Structure-based estimation of vapor pressure

• SIMPOL – calculated from SIMPOL as implemented by GECKO-A;

• EVAPORATION – calculated from EVAPORATION as implemented by the Royal Belgian Institute for Space Aeronomy (IASB);

• Nannoolal – calculated based on Nannoolal et al. (2008) using boiling points estimated by Nannoolal et al. (2004), as implemented by GECKO-A;

• Myrdal and Yalkowsky – calculated based on Myrdal and Yalkowsky (1997) using boiling points estimated by Nannoolal et al. (2004), as implemented by the UManSysProp Python package;

• EPI – calculated by the EPI Suite, an implementation of the modified Grain method using boiling points estimated by Stein and Brown (1994).

2.8.2 Structure-based estimation of Henry's law constant

• HWINb – calculated by the EPI Suite, using the bond contribution method of the HENRYWIN module;

• GROMHE – calculated with the GROMHE group contribution method, as implemented by GECKO-A.

2.8.3 Structure-based estimation of k_OH

• Kwok and Atkinson – calculated based on Kwok and Atkinson (1995) method, as implemented by the AOPWIN module of the EPI suite;

• Jenkin – calculated based on Jenkin et al. (2018a, b), as implemented by GECKO-A.

2.8.4 Formula-based estimation of vapor pressure

• Daumit – calculated based on Daumit et al. (2013), with consideration for nitrates;

• Modified Li – calculated based on Li et al. (2016), with modified nitrogen coefficient;

• Donahue – calculated based on Donahue et al. (2011), not used for nitrogen-containing formulas.

2.8.5 Formula-based estimation of Henry's law constant

• None previously published.

2.8.6 Formula-based estimation of k_OH

• Donahue – calculated based on Donahue et al. (2013), not used for nitrogen-containing formulas.

3 Results

3.1 Isomer differences for vapor pressures

A primary objective of this work is to understand typical differences in estimated vapor pressures between isomers. We evaluate these differences here by calculating the average difference in the vapor pressure of any two isomers of a given formula estimated by a given structure-based method. For each formula containing n isomers, ($n\times (n-\mathrm{1})/\mathrm{2}$) distinct pairs of isomers can be counted. For each possible pair of isomers i and j, the absolute difference in the estimated log vapor pressure is computed as $\mathrm{\Delta }p=\left|\log \right(p_i)-\log (p_j\left)\right|$. The average difference in vapor pressure among isomers of a given formula (hereafter denoted as 〈Δp〉_formula) is then computed as the average of the Δp obtained for all pairs of a given formula. For all five structure-based vapor pressure estimation methods included in this work, 〈Δp〉_formula is relatively evenly distributed between 0 and 2 log units (Fig. 1a). The overall average of 〈Δp〉_formula is between 0.8 and 1.0 log units across all five estimation methods, indicating that the central tendency is for two isomers to differ by approximately 1 log unit in vapor pressure. The distribution of 〈Δp〉_formula depends on the oxidation system studied, as is clear from the breakdown of distributions by precursor and phase shown for Nannoolal in Fig. 1b; the trends observed for Nannoolal are generally representative of the other four methods, shown in Figs. S6 and S7. Estimated vapor pressures of isomers are more similar for decane oxidation products (〈Δp〉_formula≈0.5 log units) and less similar for toluene oxidation products (〈Δp〉_formula∼1.5 log unit), with α-pinene oxidation products in between (〈Δp〉_formula≈1 log unit). Phase of the compound also has some impact, with somewhat higher 〈Δp〉_formula for formulas abundant in the particle phase. Note that the components are distinguished as gas- and particle-phase based on their abundance in either phase – a minor fraction of species is represented in both data sets. This phase dependence in the estimated differences in isomer vapor pressures is likely influenced by the following two complementary issues in applying SARs to this data set: (a) phase serves as a proxy for volatility and, (b) given that all compounds are products of the same precursors, volatility is decreased primarily by the addition of functional groups and is a proxy for increased functionality. Consequently, the increased variability in estimated vapor pressures of particle-phase isomers may be due in part to the need to extrapolate the SARs toward lower volatility and higher functionality, which is farther from their well-constrained domains.

The 〈Δp〉_formula metric obscures some of the larger individual differences between isomer pairs. The complete cumulative frequency distribution of Δp is shown in Fig. 1c for all isomer pairs. While 50 % of Δp values differ by less than 1 log unit, a long tail indicates that, in many cases, isomers may differ by up to around 3 log units (or, rarely, 4 or 5 log units) in their estimated vapor pressures. These trends are relatively robust, exhibited across all five tested estimation methods. The various oxidation systems (Fig. 1d) vary in their Δp cumulative frequency distribution in qualitatively similar ways to their distributions of 〈Δp〉_formula; toluene oxidation isomers differ substantially more in their vapor pressures than the isomers in other systems, and gas-phase isomers are slightly less variable in their estimated vapor pressures than particle-phase isomers.

It is, consequently, difficult to provide a single number to characterize the typical 〈Δp〉_formula values due to the wide distribution, variabilities between systems, and differences between methods. However, it is a reasonable overall summary that vapor pressures of isomers estimated by most structure-based methods differ by between 0.5 and 3 log units, with a central tendency of ∼1 log unit. Estimation methods typically agree about the range of 〈Δp〉_formula, but it is sensitive to the oxidation system being studied. Similar to phase dependence, system dependence may be due in part to varying degrees of extrapolating each SAR to functional groups or intramolecular interactions not captured in their development.

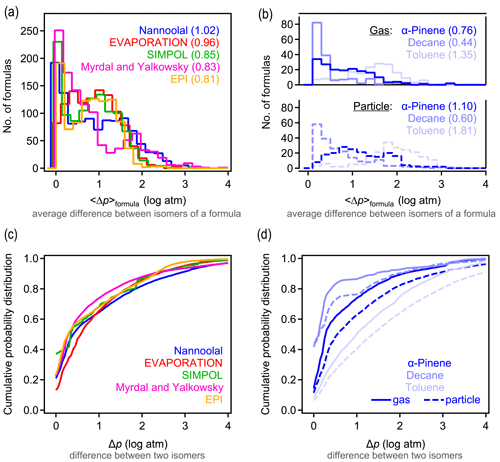
Figure 1 Differences in vapor pressure between isomers. (a) Distribution of 〈Δp〉_formula, the average difference between vapor pressures of isomers of a given formula for the five structure-based estimation methods examined, with (b) the same distribution broken out by oxidation system for the Nannoolal method. Average values of each distribution are provided in parentheses. (c) Cumulative probability distribution of Δp, the difference between any two isomers of a given formula for the five structure-based estimation methods examined, with (d) the same distribution broken out by the oxidation system for the Nannoolal method. The other four methods are shown in Figs. S6–S7.

Though 1 log unit (a factor of 10), is a substantial difference in vapor pressures, it must be placed in the context of our ability to estimate the parameter. In other words, if estimation methods differ by more than this for a given species, details of the molecular structure are less important than which estimation method is used, so knowing the molecular structure would not substantively improve the estimate. In the Supplement, compare EPI, Myrdal and Yalkowsky, SIMPOL, and EVAPORATION vs. Nannoolal estimation methods, both as scatterplots (Fig. S8) and histograms of the difference between two methods (Fig. S9). The Myrdal and Yalkowsky (using the Nannoolal boiling point estimation) and EPI methods estimate substantially higher vapor pressures for low-volatility oxidation products than the other three methods, consistent with previous work (Compernolle et al., 2011). This trend is in agreement with previous work that has shown overestimation of vapor pressures, particularly at lower vapor pressures, by the Myrdal and Yalkowsky method and the Stein and Brown method upon which EPI is based (Barley and McFiggans, 2010). In turn, Nannoolal estimates somewhat lower vapor pressures than SIMPOL and EVAPORATION for low-volatility compounds but to a lesser extent. Similar trends between SIMPOL, Nannoolal, EVAPORATION, and Myrdal and Yalkowsky have been previously shown for the oxidation products of α-pinene (Compernolle et al., 2011; Valorso et al., 2011). There is no sufficiently large database of known vapor pressures to know which of these methods is most accurate in these regions. We instead assume that the best available estimate for the vapor pressure of a compound is the average of the SIMPOL, Nannoolal, and EVAPORATION estimates. This assumption is largely based on previous work demonstrating agreement between Nannoolal and experimental data (Barley and McFiggans, 2010; O'Meara et al., 2014), and the similarity of the other two methods (SIMPOL and EVAPORATION) to Nannoolal. The EPI and Myrdal and Yalkowsky methods are treated as outliers based on their bias relative to experimental data (shown by Barley and McFiggans, 2010, and O'Meara et al., 2014). By averaging the vapor pressures estimated for each compound with the Nannoolal, SIMPOL, and EVAPORATION methods, we mitigate any biases present in any one method. The average of these three methods provides an average structure-based estimate for a given species, denoted here as $\stackrel{\mathrm{‾}}{p}$. The methods treated here are, of course, not exhaustive, but these three methods represent several of the most widely used methods in the field, perform well in comparison to experimental data, and rely on completely independent parameterizations. Other methods that performed well in prior reviews (Barley and McFiggans, 2010; O'Meara et al., 2014), such as the Lee–Kesler method, are not included here either because they are not widely used within the atmospheric field and/or they use the Nannoolal boiling point estimation method (2004) and, consequently, do not represent a truly independent source of bias or error.

To understand precision in a structure-based estimation, we quantify the differences between methods in the predicted property of a given species. For each compound, the vapor pressure is estimated using the three selected methods above. We denote Δm_p as the absolute difference in estimated vapor pressure of a given species between any two methods q and r $(\mathrm{\Delta }{m}_p=|\log \left(m_{p,q}\right)-\log \left(m_{p,r}\right)\left|\right)$ and 〈Δm_p〉 as the average value for the three possible combinations. The 〈Δm_p〉 frequency distribution is shown in Fig. 2a–b; it is important to note that these distributions are strongly sensitive to the set of methods that are included and/or excluded. For gas-phase components, Δm_p for the three test methods is within 1 log unit, with 〈Δm_p〉 around 0.5 log units. This is in reasonable agreement with reported uncertainties for each individual method. Estimation methods appear to have somewhat less skill for particle-phase atmospheric oxidation products, as expected due to their farther extrapolation from experimental constraints. For lower-volatility compounds, 〈Δm_p〉 is around 1 log unit, with most compounds within 2 log units in estimated vapor pressure. Note that, for both gas- and particle-phase compounds, toluene oxidation products again tend to differ more in their estimated vapor pressures. In other words, while isomers for this system have higher vapor pressure differences, models are also less reliable at estimating this property; these facts may be related (high uncertainty in estimation may contribute to larger differences between isomers) and may point to a lack of experimental constraints on group contributions of the functionalities formed from oxidation of an aromatic compound.

The difference in the variability between estimates for gas- vs. particle-phase components is primarily a function of differences in volatility. This issue is qualitatively observed in the direct comparison between methods shown in Fig. S8, in which methods diverge at lower vapor pressure, but we examine this issue more explicitly here. Figure 2c shows 〈Δm_p〉 as a function of average vapor pressure, $\stackrel{\mathrm{‾}}{p}$, for all species and methods considered here; averages (and standard deviations) of 10 bins of equal points each (deciles) are shown to make trends clear. At higher vapor pressures, differences between methods remain under 1 log unit, while this increases substantially at the lowest vapor pressures (and oxidation products decane and α-pinene always have lower 〈Δm_p〉 than those from toluene). As discussed above in the case of isomer variability, this increasing 〈Δm_p〉 at low volatility is likely an indication of increased uncertainty for compounds that are well below the volatility range with which these SARs were constrained, and volatility in this data set acts, in part, as a proxy for functionality. The decrease in vapor pressure caused by each functional group is, of course, uncertain, so methods diverge as the number of functional groups increases and volatility decreases (Valorso et al., 2011).

As in our discussion of vapor pressure differences between isomers, it is difficult to provide a single number to characterize the skill of these methods in estimating vapor pressure from a molecular structure. It is a reasonable overall summary that higher vapor pressures can be estimated within 1 log unit, with a central tendency of ∼0.5 log unit. This 〈Δm_p〉 range is somewhat smaller than the typical differences between isomers, 〈Δp〉_formula. We estimate that the effect of isomers is 0.5–1.5 log units greater than the variability between estimation methods for high-to-moderate vapor pressures. At lower vapor pressures, however, 〈Δp〉_formula is not substantially larger than 〈Δm_p〉, so the impact of structure is less than the variability in estimation methods. Both conclusions are likely insensitive to the specific assumptions about which methods to include in this comparison, as the uncertainty in most estimation methods is generally the lowest for high-volatility compounds and high for low-volatility compounds. However, the transition vapor pressure below which differences between isomers are lost in the uncertainty of these methods is sensitive to the methods included in the comparison. For the three methods included in this comparison, the transition can reasonably be considered to be in the range of 10⁻¹⁰ to 10⁻¹² atm ($c^{*}\approx {\mathrm{10}}^{-\mathrm{2.5}}$ to 10^−0.5 µg cm⁻³), where the average difference between methods, 〈Δm_p〉, is approximately equal to the average difference between isomers, 〈Δp〉_formula (∼1 log unit). This suggests that the difference in vapor pressures between isomers is likely relevant for estimating vapor pressures of semivolatile oxidation products – those that can partition back and forth between the gas and particle phases under typical atmospheric conditions (roughly $c^{*}\approx {\mathrm{10}}^{-\mathrm{0.5}}$ to 10^2.5 µg cm⁻³ as per Donahue et al., 2009, 2011).

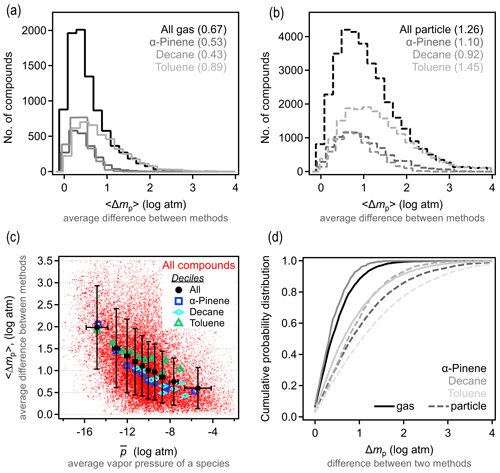
Figure 2 Differences in vapor pressures between the Nannoolal, SIMPOL, and EVAPORATION estimation methods. (a) Distribution of 〈Δm_p〉, the average difference between vapor pressures estimated for a given compound in the (a) gas and (b) particle phase, with each oxidation system shown in a different shade. Average values of each distribution are provided in parentheses. (c) Distribution of 〈Δm_p〉 as a function of vapor pressure (as the average vapor pressure of a species, $\stackrel{\mathrm{‾}}{p}$), broken out by oxidation system. Red dots are individual species; larger markers and error bars are the average and standard deviation of deciles. (d) Cumulative probability distribution of Δm_p, which is the difference between any two methods for given species.

3.2 Estimation of vapor pressure by formulas

The above analysis indicates that isomers are sufficiently different between their estimated vapor pressures so that structure should be taken into account when estimating this parameter. However, due to the increasing use of mass spectrometric instruments that measure atmospheric constituents by their formulas with no accompanying structural information, there is an increasing need to estimate vapor pressure and other parameters by formula only. Formula-based estimation will necessarily be more uncertain as it relies on less information (i.e., lacks molecular structure). A goal of this work is to assess the precision of current formula-based estimation approaches. For each formula, an average estimated vapor pressure of a formula (denoted ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$) is computed as the average, $\stackrel{\mathrm{‾}}{p}$, of all isomers of that formula. ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$ therefore represent a composite structure-based estimate of the vapor pressure using the three structure-based methods (i.e. SIMPOL, Nannoolal, and EVAPORATION) and all isomers. Including all isomers and all methods in the average of each formula provides the most direct possible comparison between a formula- and structure-based estimation, mitigating bias introduced by any one structure-based estimation method or uncertainties driven by any one isomer. The standard deviation of this average, σ_p, also provides an estimate of the range of the vapor pressures that species of a given formula may be estimated to have. This range represents the variability in estimated vapor pressure driven by differences in molecular structure, accounting for both differences between isomers and between SARs, and thus provides an estimate of the maximum precision of an estimation method that ignores structure. Assuming an approximately normal distribution, ∼68 % of isomers of a formula are expected to have a vapor pressure within the range of [${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}-{\mathit{\sigma }}_p$, ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}+{\mathit{\sigma }}_p$], and ∼95 % of estimates fall within 2 standard deviations. The precision of the three formula-based estimation methods (Daumit, modified Li, and Donahue) is assessed by comparing their estimated vapor pressure with ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$ (Fig. 3). An unbiased, formula-based estimation would be expected to fall along a 1:1 line, with two-thirds of estimates falling within the expected range of [${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}-{\mathit{\sigma }}_p$, ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}+{\mathit{\sigma }}_p$].

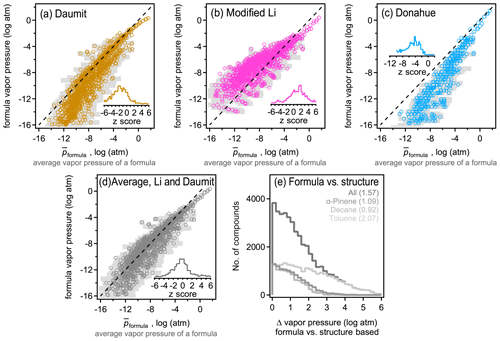
Figure 3 Comparison between average vapor pressure of a formula ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$ (average of all methods and all isomers; see the text) and the formula-based estimate using the (a) Daumit method, (b) Li method, modified to remove its bias for nitrates, (c) Donahue method, and the (d) average of the Daumit and modified Li methods. Each formula is represented as an open circle at ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$, with light gray bars representing a standard deviation of the average, σ_p, to indicate the approximate range. Insets are distributions of z scores for each method, calculated as the difference between the formula-based method and ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$, relative to the standard deviation of ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$. (e) Distribution of error from applying the average Daumit–Li method to any given compound, with each oxidation system shown in a different shade (gas and particle phases combined). Average values of each distribution are provided in parentheses.

Biases and uncertainty in the three formula-based estimation techniques can be understood in the context of their development. All three methods demonstrate a relatively high skill at predicting the estimated vapor pressures for more volatile components, where isomer differences are lower and structure-based estimation methods tend to agree due to better constraints. The formula-based methods diverge from each other and from the composite structure-based estimate at lower vapor pressures. The Daumit method (Fig. 3a) tends to estimate lower vapor pressures than expected, which is predictable upon closer inspection of this method. Daumit treats all oxygen as a combination of hydroxyl and carbonyl groups, which is reasonable in some cases (e.g., carboxyl acids). In cases where this approximation does not hold, it is generally true that the decrease in vapor pressure caused by a functional group is less than sum of its component oxygens. For example, peroxides have relatively little impact on vapor pressure but will be treated as two hydroxyl groups as discussed in Sect. 2.5.1. As the number of groups increases, vapor pressure decreases faster than it should, leading to a low bias in the Daumit method. Conversely, the Li method (implemented here with a modified nitrogen coefficient) is based on vapor pressures calculated by the EPI method, which tends to estimate higher vapor pressures for low-volatility species (Fig. S8). Consequently, the Li method follows the same trend, estimating higher than expected vapor pressures at low vapor pressures (Fig. 3b). The Donahue method (Fig. 3c) roughly follows but exceeds the biases of the Daumit method as it is based on simpler assumptions about molecular structure (and cannot treat nitrogen-containing components). In general, the formula-based estimations from all three methods fall well outside the range of ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$. Distributions of z scores are shown as insets, calculated as the difference between the formula-based estimate and ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$, relative to the standard deviation of ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$, i.e., z score $=(p-{\stackrel{\mathrm{‾}}{p}}_{\text{formula}})/{\mathit{\sigma }}_p$. Observed z scores are usually greater than 1 and frequently approach 4 (see the distribution in Fig. 3), indicating that the vapor pressures estimated from formula-based method is several standard deviations away from the structure-based ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$.

An interesting (though likely coincidental) conclusion from this analysis is that the Daumit and modified Li methods are biased, from the composite structure-based estimate, by roughly equal but opposite amounts. Consequently, an average of these two methods (Fig. 3d) provides a relatively accurate estimate of the vapor pressure of a formula. An ideal formula-based approach cannot be more accurate than the actual variability in ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$, so should produce a normal distribution of error. The combined Daumit–Li method exhibits little to no bias, with 57 % of estimates within 1 standard deviation, 80 % within 2 standard deviations. This distribution is only a little broader than ideal (i.e., longer tails of high error), so this formula-based estimation method can reproduce the structure-based estimate almost as precisely as possible. With other it approaches may be possible to achieve these results (e.g., refitting coefficients for the Li method), but no such effort is attempted here as they are unlikely to substantially improve on the precision of this formula-based method and are no less empirical than combining existing empirical methods.

These results demonstrate that formula-based parameter estimation can provide a representative estimate of vapor pressure for a given formula, i.e., typical of a large mixture of isomers. However, the error in this approach increases if used to estimate the vapor pressure of an individual compound. The difference between the formula-based and structure-based estimate of vapor pressure for a given molecule is frequently several orders of magnitude (Fig. 3e), even if using the lowest error method (the average of the Daumit and Modified Li methods). This error is significantly higher in the case of toluene oxidation products, further supporting the conclusion that estimating vapor pressure for these compounds is particularly challenging. The error in estimating the vapor pressure of an individual molecule using only its formula is approximately the same as 〈Δp〉_formula, which is the difference in vapor pressures between isomers (i.e., Fig. 1a compared to Fig. 3e). This level of error is expected for an optimal, formula-based method as the lack of structural information as an input means the formula-based method does not distinguish between isomers, so it cannot be more precise than differences between them. Considering the average and distribution of error, the combined Daumit–Li method (modified to consider nitrates) appears to represent a nearly optimal approach to estimating vapor pressure from a molecular formula.

3.3 Isomer differences for Henry's law constant

Like vapor pressure, the estimation of HLC can be critical for estimating the partitioning of an atmospheric organic species between vapor and condensed phases. We, consequently, seek to address the same issue here of whether differences in the estimated HLC of isomers are larger than the differences between SARs.

Similar to Δp and 〈Δp〉_formula above, ΔHLC and 〈ΔHLC〉_formula here denote the absolute difference in estimated HLC of any isomer pair and the average value of all possible pairs of a given formula, respectively. Isomers are observed to substantially differ in their estimated HLC. Using HWINb, 〈ΔHLC〉_formula is less than 3 orders of magnitude, with an overall average of approximately 1.5 log units (Fig. 4a). This is slightly lower than the estimate from GROMHE, for which 〈ΔHLC〉_formula is less than 4 orders of magnitude, with an overall average of approximately 2 log units. Average variability again obscures the more extreme cases observed across all isomer pairs. The distribution of ΔHLC for all possible isomer pairs is shown in Fig. 4b. ΔHLC sometimes reaches up to 4 or 5 log units (Fig. 4b). These estimates suggest that 〈ΔHLC〉_formula is typically ∼1 log unit larger than 〈Δp〉_formula and up to several log units more in extreme cases. This may be due, in part, to the relatively high uncertainty in estimating HLC relative to estimating vapor pressure (Hodzic et al., 2014; Wang et al., 2017), as the high uncertainty may contribute to larger variability between estimates for isomers.

For a given species, HLC estimated with GROMHE and HWINb frequently differ by several orders of magnitude (Fig. 4c–d; additional comparisons in Fig. S10). We denote the difference between HLC estimation methods for a given species as 〈Δm_H〉. As observed for 〈Δm_p〉, the differences in vapor pressure estimation methods, 〈Δm_H〉 is largest for particle-phase components, especially for the toluene oxidation system; similarly, this is due, in part, to the uncertainty inherent in extrapolating these SARs to high HLC and multiple functional groups. Based on 〈Δm_H〉, it is a reasonable summary of these data that estimates of HLC agree between methods to within 2 log units, with a central tendency of ∼1 log unit. Overall, 〈ΔHLC〉_formula is generally ∼1 log unit higher than the variability between estimation methods, similar to the case of vapor pressure.

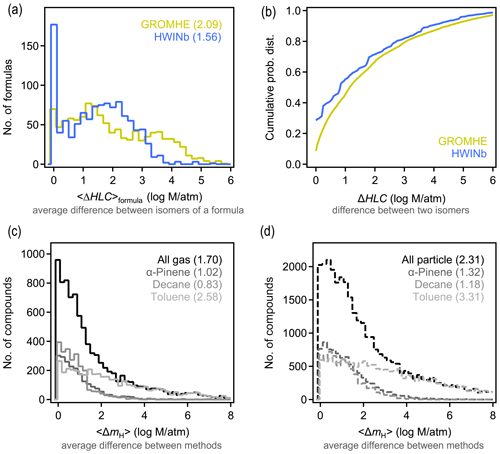
Figure 4 Differences in Henry's law constant (HLC) between isomers and methods. (a) Distribution of 〈ΔHLC〉_formula, which is the average difference between HLC of isomers of a given formula for the two structure-based estimation methods examined. (b) Cumulative probability distribution of ΔHLC, which is the difference between any two isomers of a given formula for the two methods examined. (c–d) Distribution of absolute differences between structure-based estimates of HLC for a given compound in the (c) gas and (d) particle phase, with each oxidation system shown in a different shade. Average values of each distribution are provided in parentheses.

3.4 Estimation of Henry's law constants by formulas

Similar to ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$ above, a composite structure-based estimate, ${\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}$, was computed for each formula as the average value of HLC estimated with both GROMHE and HWINb and for all isomers with that formula. Given the relationship (in log space) observed between vapor pressure and HLC in previous studies (Hodzic et al., 2014; Lannuque et al., 2018), a formula-based estimation of HLC is expected to be achievable. We apply that concept here through a simple linear regression (Fig. 5a) between ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$ and ${\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}$ (i.e., estimated parameter for a formula calculated as the average for all isomers using all structure-based estimation methods). These parameters are observed to have a linear relationship (R²=0.75) of the form $\log \left({\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}\right)=-\mathrm{1.15}\log \left({\stackrel{\mathrm{‾}}{p}}_{\text{formula}}\right)-\mathrm{0.78}$, where ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$ is in units of standard atmosphere and ${\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}$ is in units of molarity per standard atmosphere. This equation (shown as a purple line in Fig. 5b) also effectively describes the relationship between ${\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}$ and its vapor pressure estimated using the average of the modified Li and Daumit methods. Estimation of HLC in the absence of any structural information (i.e., from formulas alone) is consequently in good agreement with the average estimated HLC of a formula, which exhibits little bias within 1 standard deviation of ${\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}$ 57 % of the time and 2 standard deviations 80 % of the time (Fig. 5c). As in the case of vapor pressure, estimating HLC of a single species using its formula is less reliable, with errors up to 6 orders of magnitude (Fig. 5d). The relationship between estimated HLC and estimated vapor pressure is again approximately as precise as possible for a formula-based method for the estimation of HLC (as in the case of vapor pressure estimation, there is a longer tail of high error than expected for an ideal normal distribution). Formula-based estimation of HLC therefore appears to reasonably precisely capture the estimated HLC of a typical mixture of isomers. However, the average relationship described by this linear fit is necessarily a function of the data with which it was generated, and previous work found the slope to vary depending on the oxidized precursor (Hodzic et al., 2014). Consequently, while the relationship shown in Fig. 5 represents a reasonable, formula-based approach to estimating HLC for a complex mixture of atmospheric oxidation products (moderate to low volatility, with multiple functional groups), it should not be extended to other systems (e.g., large, nonpolar compounds) without further investigation.

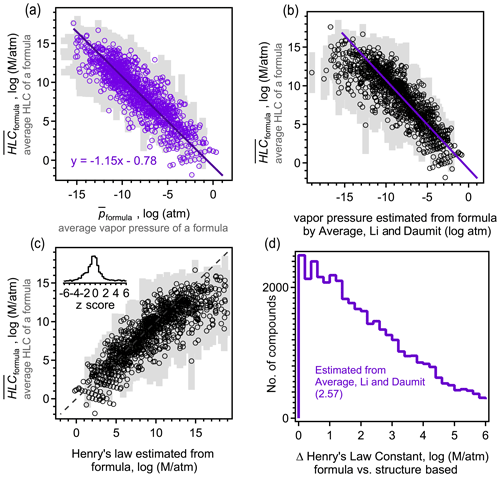
Figure 5 Comparison between ${\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}$ (average HLC of all methods and all isomers) and (a) ${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$, the average vapor pressure of a formula with best fit line shown, and (b) the estimated vapor pressure using the formula-based average Daumit–Li method estimate, with same fit line shown in purple. (c) Comparison between ${\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}$ and the HLC estimated from vapor pressure calculated from the Daumit–Li method using the best-fit equation shown in (a). Each formula is represented as an open circle at ${\stackrel{\mathrm{‾}}{\text{HLC}}}_{\text{formula}}$, with light gray bars representing a standard deviation of the average, σ_p, to indicate the approximate range. (d) Distribution of error from applying this method to any given compound, with all oxidation system combined and the average value provided in parentheses.

3.5 Estimation of k_OH

The last physicochemical parameter we examine in this work is the rate constant for the reaction between a gas-phase organic compound and the OH radical, k_OH. The variability in rate constants is also substantially lower for k_OH than for other parameters, with nearly all molecules having a rate constant between 10⁻¹² and 10⁻¹⁰ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ (as opposed to many orders of magnitude for vapor pressure and HLC). As opposed to the absolute differences in log terms used for the other parameters, comparisons are consequently more reasonably quantified in terms of relative difference, i.e., $\mathrm{\Delta }k=|k_{\mathrm{OH},i}-k_{\mathrm{OH},j}|/k_{\mathrm{OH},i}$, where i in this work refers to Jenkin and j refers to Kwok and Atkinson. Both methods selected here for structure-based estimation of this parameter (Jenkin; Kwok and Atkinson) agree that the average difference between isomers, 〈Δk〉_formula, is approximately a factor of 2 to 3 (100 %–200 % relative difference; Fig. 6a). In contrast, the two methods tend to differ by only 25 %–50 % (Fig. S11; 75 % for toluene products). Differences in the estimated k_OH of isomers are therefore significantly larger than the apparent variability in their estimation. Similar to vapor pressure and HLC, for each formula, we compute a composite structure-based average ${\stackrel{\mathrm{‾}}{k}}_{\text{formula}}$ as the average of both methods for all isomers of a given formula. Due to the relatively narrow range of possible k_OH, and the significant variability between isomers, ${\stackrel{\mathrm{‾}}{k}}_{\text{formula}}$ is not particularly variable across formulas. Most formulas containing only carbon, hydrogen, and oxygen have estimated rate constants in the range of 2–$\mathrm{4}\times {\mathrm{10}}^{-\mathrm{11}}$ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$, with an overall average of $\mathrm{2.8}\times {\mathrm{10}}^{-\mathrm{11}}$ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ (Fig. 6b). Formulas also containing nitrogen (roughly two-thirds of formulas; primarily nitrates and peroxynitrates in this data set) have an estimated OH reaction rate constant of approximately half this, with a tight distribution centered around an average of $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{11}}$ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$. These distributions indicate that, for any given formula, assuming a constant k_OH within a formula class is almost always accurate to within a factor of 2. It is important to note that, given the data set used in this work to calculate these distributions and averages, these results apply only to atmospheric oxidation products and are not directly applicable to directly emitted compounds or other atmospheric constituents.

In contrast to the low variability observed for ${\stackrel{\mathrm{‾}}{k}}_{\text{formula}}$, the formula-based estimation method developed by Donahue spans a larger range and typically overestimates k_OH (Fig. 6c). No correlation is observed between reactivity, ${\stackrel{\mathrm{‾}}{k}}_{\text{formula}}$, and vapor pressure,${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$ (Fig. 6d; R² is equal to 0.15 within a formula class; R² is equal to 0.02 in the combined data set), consistent with results reported by Lannuque et al. (2018), also showing no clear trend between k_OH and p. This is in contrast with the Donahue method, which predicts a strong correlation between these properties (Fig. S5; R² is equal to 0.80). However, Fig. 6d demonstrates some trends that are in rough agreement with the broad conclusions Donahue et al. (2011) put forth in the paper developing their method, i.e., higher volatility compounds react somewhat slower, moderate volatility compounds have rate constants around $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{11}}$ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$, and lower volatility compounds have slightly higher reaction rates but are likely to partition to the particle phase and, therefore, not react quickly with OH.

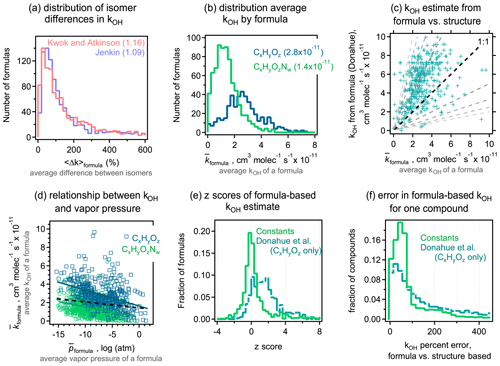
Figure 6 (a) Differences in k_OH between isomers for the two structure-based estimation methods examined. (b) Distribution of ${\stackrel{\mathrm{‾}}{k}}_{\text{formula}}$, which is the average k_OH for a given formula calculated as the average of both methods for all isomers, shown separately for formulas with and without nitrogen, with the average value provided in parentheses. (c) Comparison of formula-based Donahue estimate to ${\stackrel{\mathrm{‾}}{k}}_{\text{formula}}$; dashed lines are 1:1, 1:2, 1:3, etc. (d) Comparison of average k_OH ($\stackrel{\mathrm{‾}}{k}$) to average vapor pressure (${\stackrel{\mathrm{‾}}{p}}_{\text{formula}}$) for a given formula, separated into formulas with and without nitrogen. Trend lines (R² is equal to 0.15) are shown in the same colors, with the trend line for the combined set (R² is equal to 0.02) shown as a dashed black line. (e) Z scores of each formula-based method are calculated as described in Fig. 3 and the main text. (f) Distribution of error from applying this method to any given compound, with all oxidation system combined. In contrast to other figures, this shown in relative terms, as the number of compounds that do not contain nitrogen is a minority subset of the full data set and is thus obscured when shown with an absolute y axis.

The general overestimation of the Donahue method, coupled with the observation that variability in the k_OH of a formula is quite low, suggests an improved method of estimating k_OH for a given formula is to simply assume it to have the average value of its formula class (i.e., $\mathrm{2.8}\times {\mathrm{10}}^{-\mathrm{11}}$ and $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{11}}$ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ for CHO and CHON, respectively). The distribution of z scores in Fig. 6e indicates that the composite structure-based average k_OH for a given compound is usually (71 % of the time) within 1 standard deviation of this average value and within 2 standard deviations 86 % of the time. This is, once again, approximately as precise as a formula-based method can be. In contrast, the Donahue method frequently overestimates k_OH of a formula by several standard deviations. As in the case of vapor pressure and HLC, the formula-based estimation of k_OH of an individual molecule yields errors similar to the average differences between isomers (Fig. 6f). However, due to the relatively low variability of these values, this approach is still typically within a factor of 2 (100 % error) of the average values for each formula class. These data consequently suggest that approaches to actually estimate the OH reactivity of a gas-phase formula (including the Donahue approach) are likely to introduce more errors than simply a rough assumption of a few $\times {\mathrm{10}}^{-\mathrm{11}}$ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$.

4 Discussion

In general, structure-based estimation methods tested in this work agree to within approximately half an order of magnitude for vapor pressure, 1 order of magnitude for HLC, and <50 % for k_OH. The estimated vapor pressures and Henry's law constants of two isomers typically tend to differ by a half to a full order of magnitude more than the variability in their estimation (i.e., differences between SARs), and isomers differ in their k_OH by several times the variability in their estimation. Estimation of a physicochemical parameter from a formula can approximate the average of all relevant isomers within that formula with reasonable precision and low bias, but application of formula-based methods to an individual molecule from only its formula introduces higher error. These results support the following three important conclusions:

1. differences in the physicochemical parameters in isomers tend to be larger than the differences between estimation methods,

2. inclusion of the molecular structure, when it is available, in the estimation of physicochemical parameters improves the precision of the estimate, and

3. estimation of parameters based only on formula is feasible, but it is more meaningful if considered as a representative value for a typical mixture of isomers rather than any species in particular.

We base these conclusions on the methods used in this work to estimate the properties of a formulas in this work, i.e., vapor pressure as the average of EVAPORATION, SIMPOL, and Nannoolal methods; Henry's law constant as the average of GROMHE and HWINb; and k_OH as the average of the Jenkin and Kwok and Atkinson methods. These approaches were selected based on the accuracy of each SAR, as published in previous work, and their publicly available implementations.

An outcome of this work that is of critical importance to the broader atmospheric chemistry community is the demonstration that different publicly available implementations of a given published structure-based vapor pressure estimation method (e.g., EVAPORATION) may not all produce the same estimates for a given species. While five structure-based methods were considered in this work, three of them have two known publicly available implementations, and in all three cases, these two implementations disagree, often by at least an order of magnitude for a large fraction of the species tested. This implies that, while five methods might be nominally used in the literature, there may be up to eight de facto methods used (not including manual implementations). Some differences could simply be due to errors in implementing complex parameterizations, but of more fundamental interest is the observation that many differences may be unavoidable outcomes of extrapolating SARs beyond the chemical ranges in which they are well constrained. In other words, the complexity of atmospheric species is not always easily described in clear-cut way by the functional groups included in an SAR, and each implementation may parse a structure differently. When possible, estimating a parameter as the average of multiple methods would help to minimize the impacts of potential uncertainties in the implementations of each method, in addition to mitigating potential biases or uncertainties of any one method.

Similarly, this work demonstrates the issue that the development of empirical techniques, such as formula-based estimation methods, can be biased by the data used in their development. In particular, the Li et al. (2016) method for estimating vapor pressure from formulas (sometimes known as the molecular corridors method) contained few nitrates in its training data, and subsequently, it exhibits significant bias in the nitrate-heavy systems studied here. We propose a modification to this method to address this limitation, specifically with respect to the treatment of each NO₃ unit in a formula as an OH unit.

By combining existing methods and new approaches in this work, we also provide new methods for the estimation of vapor pressure, HLC, and k_OH for a given molecular formula. The methods below agree with composite structure-based estimates for the formula (i.e., average of all structure-based methods for all major isomers) with approximately normally distributed errors (with a somewhat longer tail), suggesting they are nearly as precise as possible. The application of the recommended formula-based methods to an individual molecule introduces an error comparable to the difference between isomers, which further supports the conclusions that these methods are approximately as precise as such a method can be. Consequently, while the estimation of parameters for a formula can be reasonably accomplished, it nevertheless suffers from higher uncertainty due to the lack of structural information. It should be noted that the accuracy of formula-based methods is limited by the accuracy of the SARs upon which they are built. This work therefore seeks only to understand the precision, not the accuracy, of formula-based methods in estimating the average SAR-estimated properties of a mixture of isomers of a given formula. These conclusions are also necessarily limited to the types of compounds analyzed in this data set, namely oxidation products from the gas-phase oxidation of a few representative compound classes. These results can, therefore, reasonably be extended to oxygenated compounds in complex atmospheric mixtures, particularly with multiple functional groups in which organic nitrogen is in the form of nitrates. Extending the conclusions and methods of this work to broader systems will necessarily increase the uncertainty.

Formula-based estimation methods that are found to estimate the average properties of a formula with, approximately, as high a precision as possible are as follows:

• Vapor pressure – average of the Daumit method and the Li method, after modifying the latter to address its bias for nitrates. The error is roughly 1–2 orders of magnitude.

• Henry's law constant – estimated from the above vapor pressure, using the linear relationship $\log \left(\text{HLC}\right)=-\mathrm{1.15}\log \left(p^{\mathrm{0}}\right)-\mathrm{0.78}$ (see Fig. 5a). The error is roughly 2–3 orders of magnitude.

• k_OH – constant, depending on whether the formula contains only carbon, hydrogen, or oxygen ($k_{\mathrm{OH}}=\mathrm{2.8}\times {\mathrm{10}}^{-\mathrm{11}}$ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$) or if it also contains nitrogen ($k_{\mathrm{OH}}=\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{11}}$ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$). The error is roughly a factor of 2.

The error is estimated as the ability of the formula-based method to recreate the structure-based estimated property of a formula and is not based on the accuracy of the existing SARs on which they are built. The error in vapor pressure and HLC is estimated as a range due, in part, to its dependence on volatility (more uncertainty at lower volatility) and oxidation system (more errors in the aromatic system studied). We reiterate that these formula-based estimation methods are empirical and, consequently, subject to biases as with other formula-based approaches. We attempt to minimize this issue by developing these methods using the types of atmospherically relevant compounds to which these methods are often applied (oxygenated oxidation products of common precursors) but stress that no empirical method can be fully free of development bias.

To facilitate the adoption of these formula-based approaches, we are including, as part of this paper, the Parameter Estimation for Atmospheric Chemistry (PEACh) package, written in the Igor Pro programming environment (WaveMetrics, Inc.) that is widely used by the atmospheric chemistry community. PEACh v.1 is included in the Supplement and will be updated and maintained as a GitHub repository (https://github.com/gabrielivw/PEACh, last access: 20 April 2021). This package implements formula-based estimation by the methods described above. For structure-based estimation, we encourage the practice of averaging multiple SARs for structure-based estimates of properties and point the reader toward the publicly available implementations used in this work.