the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The temperature dependence of ice-nucleating particle concentrations affects the radiative properties of tropical convective cloud systems
Rachel E. Hawker
Annette K. Miltenberger
Jonathan M. Wilkinson
Adrian A. Hill
Ben J. Shipway
Zhiqiang Cui
Richard J. Cotton
Ken S. Carslaw
Paul R. Field
Benjamin J. Murray
Convective cloud systems in the maritime tropics play a critical role in global climate, but accurately representing aerosol interactions within these clouds persists as a major challenge for weather and climate modelling. We quantify the effect of ice-nucleating particles (INPs) on the radiative properties of a complex tropical Atlantic deep convective cloud field using a regional model with an advanced double-moment microphysics scheme. Our results show that the domain-mean daylight outgoing radiation varies by up to 18 W m−2 depending on the chosen INP parameterisation. The key distinction between different INP parameterisations is the temperature dependence of ice formation, which alters the vertical distribution of cloud microphysical processes. The controlling effect of the INP temperature dependence is substantial even in the presence of Hallett–Mossop secondary ice production, and the effects of secondary ice formation depend strongly on the chosen INP parameterisation. Our results have implications for climate model simulations of tropical clouds and radiation, which currently do not consider a link between INP particle type and ice water content. The results also provide a challenge to the INP measurement community, as we demonstrate that INP concentration measurements are required over the full mixed-phase temperature regime, which covers around 10 orders of magnitude.
- Article
(8817 KB) - Full-text XML
- BibTeX
- EndNote
Deep convective clouds are important drivers of local, regional and global climate and weather (Arakawa, 2004; Lohmann et al., 2016). They produce substantial precipitation (Arakawa, 2004), and the associated phase changes release latent heat that helps to drive global atmospheric circulation (Fan et al., 2012). Convective clouds have a direct impact on climate through interactions with incoming shortwave and outgoing longwave radiation (Lohmann et al., 2016) – for example, by producing radiatively important long-lived cirrus clouds (Luo and Rossow, 2004). The clouds extend from the warmer lower levels of the atmosphere where only liquid exists to the top of the troposphere where only ice exists (Lohmann et al., 2016). Between these levels is the mixed-phase region where both liquid and ice coexist and interact (Seinfeld and Spyros, 2006). Within the mixed-phase region, primary ice particles can form heterogeneously through the freezing of cloud droplets by ice-nucleating particles (INPs). The importance and relative contribution of heterogeneous freezing to ice crystal number concentrations (ICNCs) and resultant cloud properties, such as cloud reflectivity, is very uncertain (Cantrell and Heymsfield, 2005; Kanji et al., 2017). This uncertainty stems from the difficulty of predicting INP number concentrations (Kanji et al., 2017; Lacher et al., 2018) as well as the difficulty of quantifying complex interactions between heterogeneous freezing and other ice production mechanisms (Crawford et al., 2012; Huang et al., 2017; Phillips et al., 2005).
Understanding the effects of INPs on convective clouds presents substantial challenges. Measurements indicate that INP number concentrations can vary by as much as 6 orders of magnitude at any one temperature due to variations in factors such as the aerosol source, chemical or biological composition, and surface morphology (DeMott et al., 2010; Kanji et al., 2017). Large variability even exists in measurements of individual regions or aerosol populations (Boose et al., 2016b; Kanji et al., 2017; Lacher et al., 2018). For example, there are variations of 4 orders of magnitude in summertime measurements of INP number concentrations in the Saharan Air Layer at −33 ∘C (Boose et al., 2016b). Even for particles of similar and known mineralogy, measurements of ice-nucleation efficiency can span several orders of magnitude: the spread in laboratory measurements of ice nucleation active site densities (ns) for different types of feldspar spans 7 orders of magnitude at −15 ∘C (Atkinson et al., 2013; Harrison et al., 2016, 2019; Peckhaus et al., 2016). Our ability to understand and quantify such variability in INP concentrations has improved as more measurements have been made. Although INP concentrations do not simply correlate with meteorological variables such as pressure and temperature (Boose et al., 2016a; Lacher et al., 2018; Price et al., 2018), aerosol surface area (Lacher et al., 2018) and diameter (DeMott et al., 2015) provide some predictability, and global models based on known INP-active materials show reasonable skill in simulating global INP concentrations (Shi and Liu, 2019; Vergara-Temprado et al., 2017).
It is known from model simulations that changes in INP number concentration affect the microphysical properties and behaviour of deep convective clouds (Deng et al., 2018; Fan et al., 2010a, b; Gibbons et al., 2018; Takeishi and Storelvmo, 2018). However, in these model studies perturbations to INP number concentrations have predominantly involved uniform increases in aerosol or INP concentrations with all simulations using the same INP parameterisation (Carrió et al., 2007; Connolly et al., 2006; Deng et al., 2018; Ekman et al., 2007; Fan et al., 2010a; Gibbons et al., 2018; van den Heever et al., 2006; Phillips et al., 2005), i.e. the temperature dependence of INP number concentrations was not altered. When different INP parameterisations have been used (Eidhammer et al., 2009; Fan et al., 2010b; Liu et al., 2018; Takeishi and Storelvmo, 2018), the results have in most cases been interpreted in terms of the overall increase in INP number concentration (Fan et al., 2010b; Liu et al., 2018; Takeishi and Storelvmo, 2018). However, there are important structural differences between different INP parameterisations that have not yet been explored in detail. For example, currently available and regularly used parameterisations of INPs vary substantially with respect to the dependence of INP activity on temperature. We hypothesise that the difference between parameterisations will be particularly important for deep convective clouds because heterogeneous ice formation occurs over a very wide temperature range from just below 0 to around −38 ∘C in the mixed-phase region of these clouds. For the same dust particle concentration, predicted INP concentrations can increase by up to 3 orders of magnitude from −15 to −20 ∘C (corresponding to an approximate 1 km altitude change) using an INP parameterisation with a steep temperature dependence (lower INP concentrations at high temperatures and higher INP concentrations at low temperatures) (Atkinson et al., 2013), but by less than 1 order of magnitude using an INP parameterisation with a shallower dependence (DeMott et al., 2010; Meyers et al., 1992). We hypothesise that such large differences in ice production rates between INP parameterisations are likely to affect cloud properties. In simulations of deep convective clouds over North America (Takeishi and Storelvmo, 2018), there were differences in the magnitude and altitude of droplet depletion depending on the INP parameterisation choice (Bigg, 1953; DeMott et al., 2010, 2015).
Uncertainty in mixed-phase cloud properties is compounded further by a lack of quantification of the interaction of heterogeneous freezing with other ice production mechanisms. Ice crystals in the mixed-phase region can also be formed by secondary ice production (SIP) from existing hydrometeors (Field et al., 2017), and droplets can freeze homogeneously below around −33 ∘C (Herbert et al., 2015). In observations of convective clouds with relatively warm cloud-top temperatures (Fridlind et al., 2007; Heymsfield and Willis, 2014; Ladino et al., 2017; Lasher-Trapp et al., 2016; Lawson et al., 2015), the ICNC has frequently exceeded INP number concentrations by several orders of magnitude, suggesting that secondary ice production is the dominant small-ice formation mechanism in mixed-phase regions (Ladino et al., 2017). The importance of heterogeneous ice production relative to secondary and homogeneous freezing has, therefore, been questioned (Ladino et al., 2017; Phillips et al., 2007), and it has been proposed that INP concentrations may only be relevant up to a threshold needed to initiate SIP (Ladino et al., 2017; Phillips et al., 2007), a value that may be as low as 0.01 L−1 (Crawford et al., 2012; Huang et al., 2017) for the Hallett–Mossop process (Hallett and Mossop, 1974). If this is the case, in clouds where SIP may also be initiated by the primary freezing of a few large (∼ 1 mm) droplets in a rising parcel (Field et al., 2017), INP number concentrations may be largely irrelevant to cloud ice properties. The effect of INPs and INP parameterisation on convective cloud properties must therefore be examined taking the presence of, and interactions with, SIP into account.
Here, we explore how the choice of INP parameterisation affects the properties of a large and realistic cloud field containing clouds at all levels as well as deep convective systems in the eastern tropical Atlantic with a focus on the top-of-atmosphere (TOA) outgoing radiation. The eastern tropical Atlantic is an ideal location in which to examine the role of INP concentrations in convective cloud systems because, owing to its position at the interface between the Saharan Air Layer and the Intertropical Convergence Zone, it is subject to both high levels of convective activity and high loadings of desert dust, which is a relatively well-defined INP type (DeMott et al., 2003; Niemand et al., 2012; Price et al., 2018). First, we determine how the presence of INPs alters the radiative properties of the cloud field. We then examine how the properties of the simulated cloud field, including cloud shortwave reflectivity, cloud fraction and anvil extent, depend on the choice of INP parameterisation. In particular, we examine the importance of the dependence of INP number concentration on temperature, referred to as INP parameterisation slope herein, as a major factor that determines cloud properties. We also examine the effect of the inclusion of SIP due to the Hallett–Mossop process on cloud properties.
2.1 Model set-up
2.1.1 Regional domain and initial conditions
The simulations described in this article were performed using the Unified Model (UM) version 10.8 (GA6 configuration) (Walters et al., 2017). The UM is a numerical weather prediction model developed by the UK Met Office. We use a regional nest within the global model simulation (Fig. 1a), which has a grid spacing of 1 km (900∗700 grid points) and 70 vertical levels. Meteorology of the driving global model is based on operational analysis data. Within the nested domain, the Cloud–AeroSol Interacting Microphysics scheme (CASIM) is employed to handle cloud microphysical properties. A global model simulation (UM vn 8.5, GA6 configuration, N512 resolution; Walters et al., 2017) is used to initialise the nested simulation at 00:00 UTC on 21 August 2015 and is used throughout the simulation for the boundary conditions.
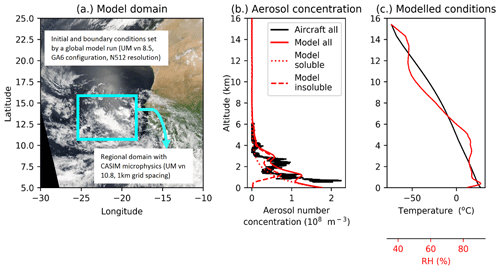
Figure 1Modelled domain location and resolution details (a), observed (black line) and modelled (red lines) aerosol concentrations (b), and mean modelled domain-mean temperature and relative humidity profiles (c). The observed aerosol profile shown in panel (b) was measured using the passive cavity aerosol spectrometer probe (PCASP) which captures aerosols between 0.1 and 3 µm in size. The insoluble aerosol profile shown in panel (b) is extracted from a regional UM vn 10.3 simulation (8 km grid spacing, CLASSIC dust scheme). The modelled aerosol profiles are applied throughout the regional domain shown in panel (a) at the start of the simulation (00:00, 21 August 2015) and at the boundaries throughout. INP concentrations in the D10, N12 and A13 simulations are linked to the insoluble aerosol profile shown in panel (b). The image shown in panel (a) is Moderate Resolution Imaging Spectroradiometer (MODIS) Corrected Reflectance imagery produced using the MODIS Level 1B data and downloaded from the NASA Worldview website.
The 21 August 2015 was chosen for simulation to coincide with flight B933 of the Ice in Clouds Experiment – Dust (ICE-D) July–August 2015 field campaign that targeted convective clouds extending to and beyond the freezing level. The aerosol profile measured during flight B933 (Fig. 1b) was used to derive the aerosol profiles prescribed over the nested domain at the beginning of the simulation and are constantly applied at the boundaries. Model profiles were calculated as follows: the UM vn 10.3 was used to simulate a domain comprising the entire tropical Atlantic and West Africa. This simulation was initiated on 18 August 2015 with a grid spacing of 8 km using the UM operational one-moment microphysics (i.e. not CASIM) and the CLASSIC aerosol scheme with a six-bin dust model (Johnson et al., 2015a). On the day of the B933 flight (21 August 2015), a dust layer was present between 2 and 3 km altitude. Comparison to MODIS AOD (aerosol optical depth) data indicates agreement between the model and observations (not shown). This UM vn 10.3 simulation was used to calculate the average dust profile (mass and number concentration) over the CASIM domain on 21 August 2015, and these dust profiles are applied in the nested domain as the insoluble aerosol profiles (Fig. 1b). The approximate difference between the dust aerosol profile provided by the UM regional simulation and the observed aerosol profile measured during flight B933 (comprising both insoluble and soluble particles) is used as the soluble aerosol profile (Fig. 1b). The simulations are 24 h in length.
2.1.2 CASIM microphysics
CASIM is a multi-moment bulk scheme, which is configured to be two-moment in this work. Both number concentration and mass concentration for each of the five hydrometeor classes, cloud droplets, rain droplets, ice crystals (or cloud ice), graupel and snow, are prognostic variables. The model set-up is very similar to that used in Miltenberger et al. (2018) including the parameter choices within CASIM. CASIM has been used and tested previously in simulations of coastal mixed-phase convective clouds (Miltenberger et al., 2018), South-East Pacific stratocumulus clouds (Grosvenor et al., 2017), Southern Ocean supercooled shallow cumulus (Vergara-Temprado et al., 2018), midlatitude cyclones (McCoy et al., 2018) and cloud-condensation-nuclei-limited Arctic clouds (Stevens et al., 2018). The parameters used in the representation of the size distribution, density and terminal fall speed velocities of each of the five hydrometeor classes represented by CASIM are shown in Table 2 of Miltenberger et al. (2018).
Cloud droplet activation is parameterised according to (Abdul-Razzak and Ghan, 2000). The soluble accumulation-mode aerosol profile shown in Fig. 1b is used for cloud droplet activation and a simplistic cloud condensation nuclei (CCN) activation parameterisation is included for the insoluble aerosol mode (Abdul-Razzak and Ghan, 2000) that assumes a 5 % soluble fraction on dust. Scavenging of CCN or INP is not represented. Collision–coalescence, riming of ice crystals to graupel and aggregation of ice crystals to snow is represented. Rain drop freezing is described using the parameterisation of Bigg (1953). For reference, the modelled domain-mean out-of-cloud temperature and relative humidity are shown in Fig. 1c. The model time step is 5 s.
Heterogeneous ice nucleation is represented using five different parameterisations: Cooper (1986), C86; Meyers et al. (1992), M92; DeMott et al. (2010), D10; Niemand et al. (2012), N12; and Atkinson et al. (2013), A13 (Fig. 2). C86 and M92 calculate a freezing rate based on temperature and are independent of the aerosol concentration. D10 calculates an INP concentration from temperature and the concentration of insoluble dust aerosol with a diameter greater than 0.5 µm. N12 and A13 calculate an INP concentration from the temperature-dependent active surface site density and the surface area of insoluble dust aerosol (ns). For A13, a potassium-feldspar fraction of 0.25 is assumed. This is the upper recommended fraction (Atkinson et al., 2013) which was deemed appropriate because of the study region's exposure to Saharan dust outflow. M92 is described as a deposition and condensation freezing parameterisation (Meyers et al., 1992) and is often used alongside an immersion freezing parameterisation in modelling studies (Deng et al., 2018; Fan et al., 2010b, a; Gibbons et al., 2018). However, the M92 parameterisation is based on aircraft continuous flow diffusion chamber measurements, and those measurements should capture all relevant nucleation mechanisms (see Vali et al., 2015). To represent nucleation at conditions relevant for clouds with liquid water present, we have set the saturation term in the M92 parameterisation to water saturation. One simulation is conducted with no active heterogeneous ice nucleation representation (NoINP). The INP parameterisations inspect the conditions (temperature, cloud droplet number, ICNC) and aerosol concentrations within a grid box and use that information to predict an ice production rate via heterogeneous freezing. The supercooled droplets are depleted by the freezing parameterisation, but scavenging of INPs is not represented. Homogeneous freezing of cloud droplets is parameterised according to Jeffery and Austin (1997).
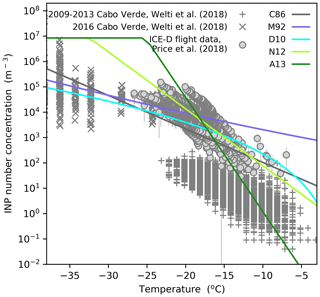
Figure 2Dependence of the INP number concentration on temperature (d[INP]dT) for the five heterogeneous freezing parameterisations simulated in this study (C86, M92, D10, N12 and A13) compared to INP number concentrations measured in the eastern tropical Atlantic (Price et al., 2018; Welti et al., 2018). Parameterisations are shown for the aerosol concentrations at approximately the first freezing level in our simulations (∼ 8 cm−3). D10, N12 and A13 are dependent on the aerosol concentrations, whereas C86 and M92 are not dependent on the aerosol concentration. N12 and A13 are calculated assuming a mean dust particle radius of 0.7 µm. In D10, all particles are assumed to be larger than 0.5 µm. Note that the Welti et al. (2018) dataset is from surface INP measurements at Cabo Verde, whereas the Price et al. (2018) dataset is measured from an aircraft flown from Cabo Verde.
The INP parameterisations tested in this study represent only immersion freezing. Heterogeneous ice nucleation by deposition and contact nucleation are not represented. Other mechanisms of heterogeneous ice formation should be tested and included in future studies, but this was beyond the scope of this work. However, immersion freezing is expected to be the dominant mechanism of heterogeneous ice formation in convective clouds (Ansmann et al., 2008; De Boer et al., 2011; Kanji et al., 2017); therefore, the simulations presented here should capture the majority of heterogeneous ice nucleation relevant for cloud properties. Immersion and homogeneous freezing of haze droplets are not represented, but it is unlikely that they contribute significantly to ice crystal number concentration in the main anvil cloud derived from mixed-phase cloud regions. However, the importance of these mechanisms on anvil cloud properties should be investigated in future work. Secondary ice production (SIP) is represented using an approximation of the Hallett–Mossop process which occurs between −2.5 and −7.5 ∘C. The efficiency of the Hallett–Mossop process increases from −2.5 and −7.5 ∘C to 100 % at −5 ∘C. The rate of splinter production per rimed mass is prescribed with 350 new ice splinters produced per milligram of rime at −5 ∘C. Splinters are produced from rime mass of snow and graupel. The ice splinters produced by the representation of the Hallett–Mossop process are the smallest allowable size of ice in the model (i.e. 10−18 kg, volume radius ∼ 0.11 µm). The rate of splinter production by the Hallett–Mossop process is based on the best available estimate of the efficacy of the mechanism (Connolly et al., 2006; Hallett and Mossop, 1974; Mossop, 1985). In situ cloud observations have frequently observed ICNCs that could be explained by the Hallett–Mossop process, but the mechanism underlying the Hallett–Mossop process as well as the ice particle production rate remain uncertain and not well quantified (Field et al., 2017). A maximum splinter production rate of 350 per milligram of rimed material has been measured in a number of laboratory studies (Hallett and Mossop, 1974; Mossop, 1985) and has been applied as the best estimate here and in previous modelling studies (Connolly et al., 2006), although other rates have also been measured (Heymsfield and Mossop, 1984; Saunders and Hosseini, 2001). Uncertainties regarding the rate of splinter production by Hallett–Mossop are an important consideration that will be investigated in future work; this study explores the structural uncertainty of the presence/absence of the Hallett–Mossop process as currently understood. Other mechanisms of SIP such as collision fragmentation, droplet shattering and sublimation fragmentation have been proposed (Field et al., 2017), but they are not represented in these simulations, in part because they are very poorly defined and it is not clear how important they are. Other studies have attempted to model some of these additional SIP processes (Phillips et al., 2018; Sullivan et al., 2018), but it was beyond the scope of this study.
2.1.3 Cloud radiation
The radiative processes are represented by the Suite of Community RAdiative Transfer codes based on Edwards and Slingo (SOCRATES) (Edwards and Slingo, 1996; Manners et al., 2017), which considers cloud droplet number and mass, as well as ice crystal and snow water paths for the calculation of cloud radiative properties. It does not explicitly consider changes in ice crystal or snow number concentration or size (although changes in number and size will affect mass concentrations which are considered), and it does not consider any changes to rain or graupel species. The cloud droplet single-scattering properties are calculated from the cloud droplet mass and effective radius in each grid box using the equations detailed in Edwards and Slingo (1996). Snow and ice are combined to form one ice category for the purposes of the radiation calculations. The single-scattering properties of this snow and ice category are calculated from their combined mass and the ambient temperature. The parameterisation of bulk optical properties of snow and ice used in the model is detailed in Baran et al. (2014).
The radiative properties (shortwave, longwave and total radiation) are calculated for daylight hours only (i.e. 10:00–17:00 UTC). For all other modelled properties presented, except when plotted against a corresponding radiative property, values are calculated for the last 14 h of the simulation (i.e. from 10:00–24:00). The sensitivity of the outgoing longwave radiation and the cloud fraction to time period selection was tested and found to have little impact. The overall outgoing radiation (shortwave and longwave) will be sensitive to the time period selection owing to the absence of outgoing shortwave radiation at night-time. We focus on the radiation during daylight hours only because our simulation is only 24 h in length owing to computational restrictions; therefore, when the spin-up period is excluded from the analysis, less than 24 h of simulation data remains with many of the night-time hours removed with the spin-up period.
Changes to outgoing radiation from cloudy regions and changes in the cloud fraction both contribute to the total overall change in outgoing radiation between two simulations. The contributions from changes in outgoing radiation from cloudy regions and cloud fraction to the overall radiative differences between simulations were calculated separately as described below. The cloudy regions contribution (ΔRadREFL), i.e. the difference in outgoing radiation between two cloudy regions due to changes in cloud albedo or thickness ignoring any changes in cloud fraction, to a domain radiative difference between a sensitivity simulation (s) and a reference simulation (r) (s−r) is calculated using Eq. (1):
where cfr is the cloud fraction of simulation r, and ΔRadcl is the change in outgoing radiation from cloudy areas only between simulations (s−r). The reference run (r) in Sect. 3.1–3.4 refers to the NoINP simulation, whereas the sensitivity run (s) refers to simulations that include an INP parameterisation. In Sect. 3.5, the reference run (r) refers to a simulation that has no representation of SIP, and the sensitivity run (s) refers to a simulation that includes SIP due to the Hallett–Mossop process. The contribution of cloud fraction changes, i.e. the change in radiation that can be attributed to an area of clear sky in simulation s becoming cloudy in simulation r or vice versa, to the total change in domain outgoing radiation (ΔRadCF) is calculated using Eq. (2):
where Radr,cl is the mean outgoing radiation from cloudy regions in simulation r, Radr,cs is the mean outgoing radiation from clear-sky regions in simulation r, and Δcf is the difference in domain cloud fraction between simulations s and r (s−r). There is interaction between the outgoing radiation from cloudy regions and cloud fraction changes (ΔRadINT) which is calculated in Eq. (3).
The contribution of changes in the outgoing radiation from clear-sky areas (ΔRadCSKY) can be calculated as shown in Eq. (4):
where ΔRadcs is the change in mean outgoing radiation from clear-sky areas between simulations s and r, and cfs is the cloud fraction of simulation s.
Thus, the total outgoing radiation difference between simulations s and r (ΔRads−r) is as shown in Eq. (5).
The interaction term (ΔRadINT) and the clear-sky term (ΔRadCSKY) were found to be negligible and are, therefore, ignored for the purposes of this paper.
2.1.4 Model simulations
The conducted simulations are as follows:
-
Five simulations with different heterogeneous ice nucleation parameterisations (C86, M92, D10, N12 and A13) with a representation of the Hallett–Mossop process (SIP_active).
-
One simulation with no heterogeneous ice nucleation (NoINP) but with a representation of the Hallett–Mossop process (SIP_active).
-
Five simulations with different heterogeneous ice nucleation parameterisations (C86, M92, D10, N12 and A13) without a representation of the Hallett–Mossop process (SIP_inactive).
The INP number concentration ([INP]) predicted by the five INP parameterisations (C86, M92, D10, N12 and A13) are compared with the available measurements from the study region (Price et al., 2018; Welti et al., 2018) in Fig. 2, including those taken during the ICE-D field campaign (Price et al., 2018). All parameterisations are in reasonable agreement with the measurements (and with each other) at around −17 ∘C, but they deviate strongly at higher and lower temperatures. It should be noted that all parameterisations tested in this work were developed between specific temperature ranges and extrapolation beyond these temperatures adds uncertainty. However, for the purposes of this paper and to allow a direct comparison between parameterisations, all parameterisations have been applied between 0 and −37 ∘C. Importantly, the INP parameterisation slopes of the chosen parameterisations span the range used within regional models, from a shallow dlog10[INP]d in M92 (Meyers et al., 1992) to a steep dlog10[INP]d in A13 (Atkinson et al., 2013).
When analysing the simulation output, cloudy grid boxes were classed as those containing more than 10−5 kg kg−1 condensed water from cloud droplets, ice crystals, graupel and snow. Rain was not included to ensure that the analysis did not include areas below the cloud base. Other cloud thresholds were tested and found to have no notable effect on the results. For cloud categorisation into low, mid and high clouds, model vertical columns containing cloudy grid boxes were categorised by cloud altitude: low cloud occurs below 4 km, mid cloud occurs between 4 and 9 km, and high cloud occurs above 9 km. Columns with cloudy grid boxes in two or more cloud categories were classified as mixed-category columns according to the vertical placement of the cloudy grid boxes, e.g. low and high for columns containing cloud below 4 km and above 9 km respectively. Levels of 4 and 9 km were chosen as the respective low–mid and mid–high division points because they are just below two well-defined peaks in cloud base heights (not shown) and roughly correspond to the beginning of the heterogeneous and homogeneous freezing regions respectively. For the correlation analysis where model outputs were plotted against parameterisation slope (dlog10[INP]dT), a straight line was fitted to the D10 parameterisation between −3 and −37 ∘C to obtain an approximate INP parameterisation slope. Other temperature ranges were tested and were found to have no notable effect on the results.
2.2 The observed case
MODIS visible images of 21 August 2015 are shown in Fig. 3a and b alongside snapshots of the TOA outgoing longwave radiation in one of our simulations (Fig. 3c, d). The simulated cloud field has more cloud-free areas than the satellite images but generally produces clouds similar to those shown in the satellite image and in approximately the correct location. Overall, the simulations produce a complex and realistic cloud field. Snapshots of the simulated model TOA outgoing shortwave radiation are shown in Fig. A1.
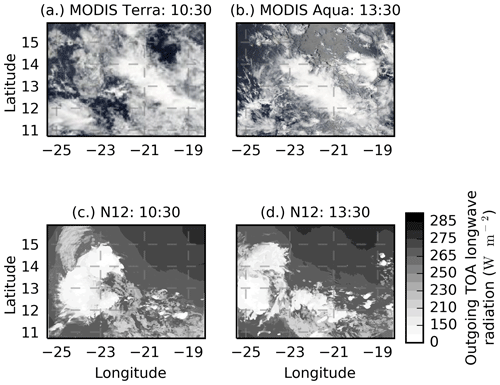
Figure 3Cloud field evolution. MODIS Terra (a) and Aqua (b) Corrected Reflectance images of the modelled domain for 21 August 2015 and the corresponding simulated top-of-atmosphere outgoing longwave radiation for the N12 simulation (c, d). Note that the colour bar relates to panels (c) and (d) only. Images shown in panels (a) and (b) are Moderate Resolution Imaging Spectroradiometer (MODIS) Corrected Reflectance imagery produced using the MODIS Level 1B data and downloaded from the NASA Worldview website.
In situ measurements of cloud and aerosol properties were made using the UK FAAM BAe 146 research aircraft, which was flown from Praia, Cabo Verde. An extensive suite of in situ aerosol and cloud particle instruments were operated onboard the aircraft and are described in detail in Lloyd et al. (2020). The aircraft penetrated the growing convective clouds at a range of altitudes from just below the freezing level up to −20 ∘C. In order to show that the model reproduces the observed conditions, the observational data were compared to the conditions in modelled clouds of a similar size to those that the aircraft flew in (10–150 km2) where a comparison was thought to be appropriate. Comparisons of a selection of simulated cloud properties with aircraft data are shown in Fig. A2. In-cloud measurements from the aircraft were selected using the same total water content threshold as for the model data (10−5 kg kg−1). Note that observational data only sample clouds along the 1D flight path, whereas model results include all grid points inside the selected clouds.
The vertical wind and cloud droplet and ice number concentrations are shown Fig. A2. The vertical wind speeds from the model and aircraft measurements agree well (Fig. A2a). The aircraft data exhibit fewer measurements of vertical wind speeds above 10 m s−1; however, this is expected as the aircraft was purposefully not flown in very high updraught speeds. The aircraft cloud droplet number concentration (CDNC), measured using a Droplet Measurement Technologies (DMT) cloud droplet probe (which allows measurement of the cloud droplet size distribution for particles with diameters between 3 and 50 µm; Lloyd et al., 2020), falls predominantly in the regions of parameter space most highly populated by model data when plotted against vertical wind speed (Fig. A2b). Note that the simulated points in Fig. A1b represent values of the CDNC and updraught speed in all cloudy grid boxes, not just those at cloud base. The updraught speed is co-located with the CDNC and, therefore, does not necessarily represent the updraught speed at which the cloud droplets were activated. The higher CDNC values exhibited in the model data may be due to the higher updraught speeds which were not measured by the aircraft. The observed ICNC was derived from measurements using the DMT cloud imaging probes (CIP-15 and CIP-100, photodetector widths of 15 and 100 µm respectively, both with 64 detector elements) and the SPEC stereoscopic optical array probe covering a size range from 10 to 6200 µm using the SODA2 (System for OAP (optical array probe) Data Analysis) processing code (McFarquhar et al., 2017) to reconstruct ice particle images that are fully contained within the probe sample volume. Because of uncertainties in the optical array probe sample volume for very small images, only ice particle images greater than 100 µm were included. The aircraft ICNCs fall almost entirely within the range of the model values (Fig. A2c).
3.1 Effect of INPs and INP parameterisation on outgoing radiation
We first examine the effect of INP parameterisation on the TOA outgoing daytime (10:00–17:00 UTC) radiation relative to the simulation where the only source of primary ice production was through homogeneous freezing (NoINP). Ice crystals formed via homogeneous freezing and sedimented to lower levels can initiate ice production via the Hallett–Mossop process once converted to snow or graupel. When contrasting the effect of different INP parameterisations in Sect. 3.1–3.4, the Hallett–Mossop process was always active, including in the NoINP simulation. As stated in Sect. 2.1.3, the radiation code is represented by the Suite Of Community RAdiative Transfer codes based on Edwards and Slingo (SOCRATES) (Edwards and Slingo, 1996; Manners et al., 2017) and responds to changes in cloud droplet number and cloud droplet, ice crystal and snow mass. The results detailed below relate to either the domain-wide properties or all in-cloud regions within the domain. This means that the results describe the direct and indirect changes (e.g. changes to the Hallett–Mossop ice production) occurring due to the presence of INP across all cloud present in the domain, including low-level liquid clouds, mixed-phase clouds without a convective anvil and very deep convective clouds with an anvil. The effects of INP parameterisation and SIP on convective anvils are discussed in Sect. 3.4.
Domain-mean TOA outgoing radiation (daylight hours; shortwave and longwave) is enhanced by the inclusion of INP in all cases (Fig. 4a). The enhancement of outgoing radiation varies between 2.6 W m−2 for D10 and 20.8 W m−2 for A13 relative to the NoINP simulation. There is a variation of up to 18.2 W m−2 depending on the chosen representation of heterogeneous ice nucleation, which shows that the INP parameterisation can affect outgoing radiation as much as excluding or including heterogeneous freezing altogether. The difference in radiation between the NoINP and the simulations where INP are present are caused mainly by changes to outgoing shortwave radiation. The inclusion of INP enhances outgoing shortwave radiation by between 5.3 W m−2 for D10 and 26.6 W m−2 for A13 (Fig. A3a). Differences in outgoing longwave radiation are comparatively small (−2.7 W m−2 for D10 to −5.8 W m−2 for A13; Fig. A3b) due to similar cloud-top heights between simulations of these thermodynamically limited clouds. Bear in mind that SIP was active (SIP_active) in the simulations summarised in Fig. 4a, including in the NoINP simulation in which the Hallett–Mossop process can be initiated by settling ice-phase hydrometeors (either by settling homogeneously frozen ice crystals subsequently converted to snow or graupel or by settling snow or graupel formed from homogeneously frozen ice crystals at upper cloud levels), indicating that these cloud systems are sensitive to INP even in the presence of SIP. This is consistent with a comparatively small change in TOA radiation when SIP is active relative to when it is inactive (Fig. 4b); we discuss the role of SIP in more detail in Sect. 3.5.
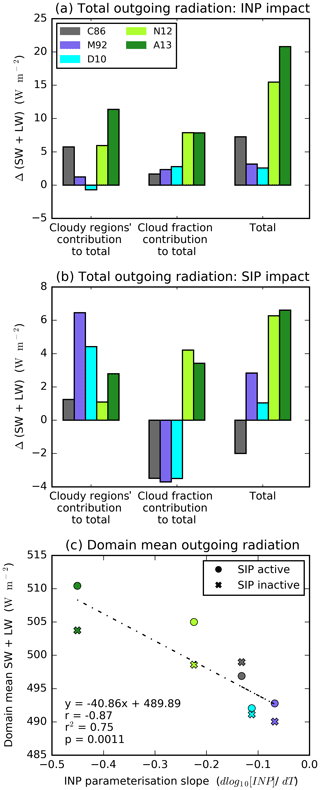
Figure 4Effect of INP and secondary production on top-of-atmosphere (TOA) daytime (10:00–17:00 UTC) outgoing radiation. The effect of INP parameterisation (a) and SIP (a representation of the Hallett–Mossop process) (b) on domain-mean daytime TOA outgoing radiation and total domain-mean daytime TOA outgoing radiation plotted against INP parameterisation slope (c). In panel (a), the change from the NoINP simulation is shown (INP – NoINP) with SIP active. In panel (b), the change from SIP_active to SIP_inactive is shown (SIP_active – SIP_inactive). A positive value indicates more outgoing radiation when INPs or SIP is active. In panels (a) and (b), the relative contributions of changes in outgoing radiation from cloudy regions (left; i.e. ΔRadREFL from Eq. 1) and the cloud fraction (middle; i.e. ΔRadCF from Eq. 2) to the total radiative forcing (right; i.e. ΔRads−r from Eq. 5, with simulation s referring to simulations with INP active in panel a and to the SIP_active simulations in panel b and simulation r referring to the NoINP simulation in panel a and to the SIP_inactive simulations in panel b) are shown (calculation described in Sect. 2.1.3). In addition to the simulated values, a regression line (n=10) is shown in panel (c) along with its associated statistical descriptors.
The slope of the INP parameterisation (i.e. the dependence of the INP number concentration on temperature) is a key determinant of the outgoing radiation. There is a statistically significant correlation between the INP parameterisation slope and the total TOA outgoing radiation (r2=0.75, p<0.01, n=10; Fig. 4c). Changes in outgoing radiation due to the presence of INPs are caused by a combination of changes in the outgoing radiation from cloudy regions, which is caused by changes in cloud structure and microphysical properties, and changes in the domain cloud fraction, whose contributions to the total radiative difference are shown in Fig. 4a (left and centre). In order to appreciate the reasons for these trends, we will now take a closer look at the effect of INPs on outgoing radiation from cloudy regions only, the domain cloud fraction and the cloud type.
3.2 Effect of INPs and INP parameterisation on outgoing radiation from cloudy regions
Here, we discuss the changes in daytime outgoing radiation from cloudy regions only due to the INP parameterisation choice. Daytime outgoing radiation from cloudy regions increases due to INPs for all but one INP parameterisation (Fig. 5a). The absolute change in outgoing radiation from cloudy regions is between −0.8 W m−2 (D10) and +28.1 W m−2 (A13), and the larger values are a result of large increases in reflected shortwave radiation (up to +37.2 W m−2) and relatively moderate decreases in outgoing longwave radiation (up to −11.1 W m−2) from cloudy regions. The above absolute changes in outgoing radiation from cloudy regions contribute between −0.7 and +11.4 W m−2 to the domain-mean change in outgoing radiation due to the presence of INPs (Fig. 4a; cloudy regions' contribution).
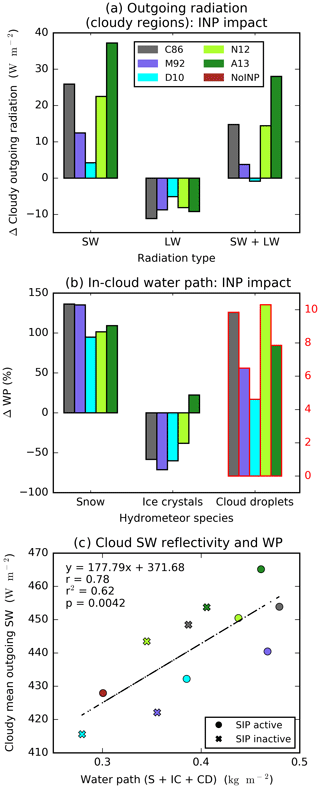
Figure 5INPs and TOA outgoing daytime (10:00–17:00 UTC) radiation from cloudy regions. Absolute change in outgoing shortwave, longwave and total radiation from cloudy regions relative to the NoINP simulation (i.e. ΔRadcl used in Eq. 1) (a); the percentage change in water path (WP) associated with snow (S), ice crystals (IC) and cloud droplets (CD) relative to the NoINP simulation (b); and mean daytime outgoing shortwave radiation from cloudy regions plotted against the sum of S, IC and CD water paths (c). Note the different scale for CD water path in panel (b). In addition to the simulated values, a regression line (n=11) is shown in panel (c) along with its associated statistical descriptors.
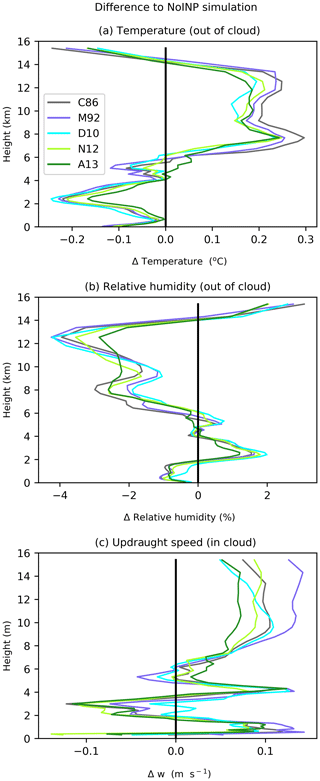
The enhancement of outgoing radiation from cloudy regions due to INPs is caused primarily by increases in cloud condensate relative to the NoINP simulation (Fig. 5b). When INPs are included in a simulation, the snow and cloud droplet water paths are enhanced, causing increases in total cloud condensate, despite decreases (in all except A13) in the ice crystal water path due to a reduction in ice crystal number and mass concentrations caused by a reduction in the availability of cloud droplets for homogeneous freezing. Snow, cloud droplets and ice crystals are the hydrometeors that affect outgoing radiation in CASIM, and the combined water path of these three species is significantly positively correlated with cloud shortwave reflectivity (r2=0.62, p<0.01, n=11; Fig. 5c). The mechanism for this INP-induced increase in cloud condensate and, consequently, cloud shortwave reflectivity is as follows: when heterogeneous ice nucleation is active, liquid is consumed in the warmer regions of mixed-phase clouds because of increased heterogeneous ice nucleation (Fig. 2) and SIP (Fig. A4a). The resultant additional ice crystals in mixed-phase regions facilitate riming, which causes increases in snow and graupel (Fig. A4c, d) and, in turn, increases the snow water path and reflectivity in mixed-phase and ice clouds. At the same time, the enhanced production of relatively heavy snow and graupel increases precipitation which, upon melting to form rain below the freezing level and subsequent evaporation below 4 km, reduces out-of-cloud temperature and increases relative humidity (Fig. A5a, b). This leads to increases in the water path in low-level liquid clouds and, thus, an enhancement in their shortwave reflectivity.
However, increases in total cloud condensate alone cannot account for the differences in outgoing radiation from cloudy regions between simulations using different INP parameterisations, which are caused by a combination of cloud microphysical responses. We find that outgoing radiation from cloudy regions is significantly negatively correlated with the INP parameterisation slope (r2=0.63, p<0.01, n=10; Fig. 6a), i.e. simulations using a steep INP parameterisation have a higher outgoing radiation from cloudy regions. This result makes sense when we consider the relationships between the INP parameterisation slope and a multitude of cloud microphysical properties affecting cloud radiative properties. In particular, a steep INP parameterisation results in a mixed-phase cloud region characterised by a higher ice crystal water path aloft (r2=0.80, p<0.01, n=10; Fig. 6b) and higher cloud droplet number concentrations at the bottom of the mixed-phase region (r2=0.89, p<0.01, n=10; Fig. 6c) when compared to shallower parameterisations. A steeper INP parameterisation slope allows increased transport of liquid to upper cloud levels due to lower rates of heterogeneous freezing at the mid-bottom region of the mixed-phase cloud (lower supercooling; Fig. 2) and SIP at high temperatures (Fig. A4a). This, combined with higher INP concentrations at low temperatures (Fig. 2), increases the ICNC at upper mixed-phase altitudes as well as enhancing the lifetime of liquid cloud droplets at lower altitudes in the mixed-phase region when compared with shallower INP parameterisations.
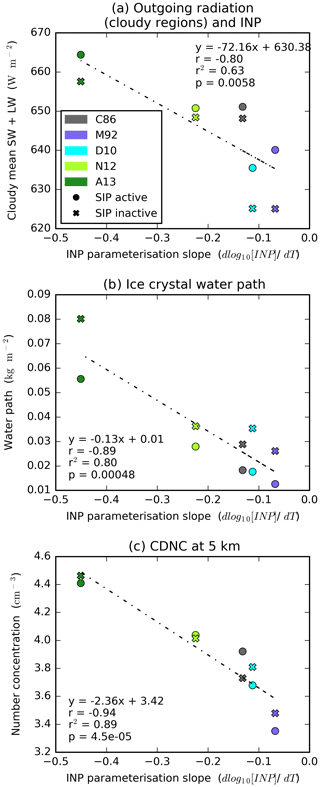
Figure 6Outgoing daytime (10:00–17:00 UTC) radiation from cloudy regions and the INP parameterisation slope. Scatter plots of the INP parameterisation slope and total daytime outgoing radiation from cloudy regions (a), the in-cloud mean ice crystal (cloud ice only) water path (b) and the in-cloud cloud droplet number concentrations at the start of the mixed-phase region (5 km) (c). Also shown are the respective regression lines (n=10) and associated statistical descriptors.
3.3 Effect of INPs and INP parameterisation on the cloud fraction
Overall the cloud fraction is increased by INPs for all INP parameterisations, and these increases in the cloud fraction contribute about as much to changes in domain-mean daytime radiation as the changes in outgoing radiation from cloudy regions (Fig. 4a; cloud fraction contribution). Increases in the domain cloud fraction due to INPs are driven by cloud cover increases in the warm and mixed-phase regions of the cloud (∼ 4–6 km), offset somewhat by decreases in the cloud fraction due to reduced homogeneous freezing in the ∼ 10–14 km regime (Fig. 7a). Cloud fraction increases at mid-levels occur because heterogeneous ice nucleation induces an increase in precipitation-sized particles (snow and graupel) which sediment to lower levels and moisten the atmosphere by evaporation (Fig. A5a, b). This increases new cloud formation and may prolong the lifetime of existing cloud cells. Additionally, increased droplet freezing and riming in the mixed-phase cloud region releases latent heat and invigorates cloud development with increases in updraught speed just above 4 km (Fig. A5c). The increased cloud fraction at mid-levels due to INPs are partially offset by a reduced cloud fraction above 10 km (Fig. 7a) which is caused by an INP-induced enhancement in freezing and riming in the mixed-phase region reducing moisture transport to the homogeneous freezing regime. The ability of heterogeneous freezing to reduce the availability of moisture for homogeneous freezing has been previously observed (e.g. Gasparini et al., 2020; van den Heever et al., 2006; Kärcher and Lohmann, 2003; Lohmann and Gasparini, 2017; Phillips et al., 2005, 2007; Storelvmo et al., 2013).
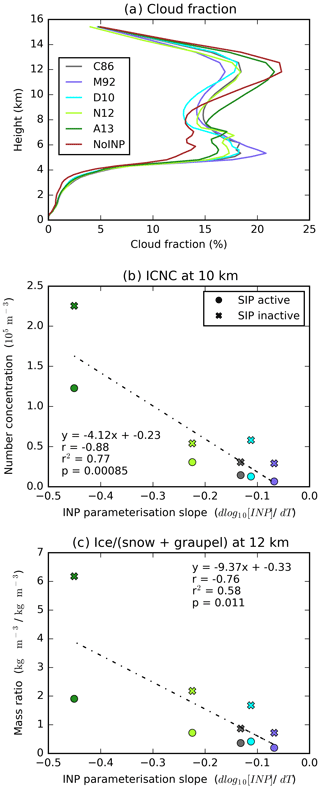
Figure 7Cloud fraction and INP parameterisation slope. Domain-mean cloud fraction profile (a), INP parameterisation slope plotted against the ice crystal number concentration at 10 km (b), and mass ratio of ice crystals to snow and graupel at 12 km (c). Also shown in panels (b) and (c) are the respective regression lines (n=10) and associated statistical descriptors.
The effects of INPs on the altitude profile of the cloud fraction are strongest for shallow INP parameterisation slopes, which have a freezing profile most different to that of the NoINP simulation (Fig. 7a). At 5 km, the shallowest parameterisation (M92) causes the largest increase in cloud fraction, whereas the steepest parameterisation (A13) causes the smallest (r2=0.83, p<0.05, n=5). At 12 km, the order is reversed, and steep parameterisations exhibit the highest cloud fraction (r2=0.94, p<0.01, n=5). The largest cloud-fraction-induced increases in outgoing radiation relative to the NoINP simulation (Fig. 4a) are seen in simulations using steeper INP parameterisations because these simulations exhibit higher cloud fractions at high altitudes (∼ 12 km), translating into a higher total cloud fraction. These slope-dependent changes in the cloud fraction are explained by a relationship between the cloud fraction and several microphysical properties affecting the cloud fraction. For example, steeper INP parameterisations produce higher ICNCs at the top of the mixed-phase region (10 km) as well as higher ratios of ice crystal mass to snow and graupel mass within the homogeneous freezing region (12 km) (Fig. 7b, c). A higher number and mass of ice crystals relative to those of larger precipitation-sized hydrometeors with the steepest parameterisations results in lower frozen hydrometeor sedimentation, a longer cloud lifetime and a higher cloud fraction.
3.4 Effect of INPs and INP parameterisation on cirrus anvils
Our results show that the INP parameterisation affects the properties and spatial extent of cirrus anvils. We define cirrus anvils to be regions where cloud is present above 9 km only (further details available in Sect. 2.1.4). The 2D aerial images of cloud categorisation (Fig. 8a–f) show well-defined regions of anvil cloud (light blue – H) surrounding a large convective system containing clouds at a range of altitudes from <4 to >9 km. There are clearly differences in the extent and position of cloud categories between simulations (Fig. 8a–f).
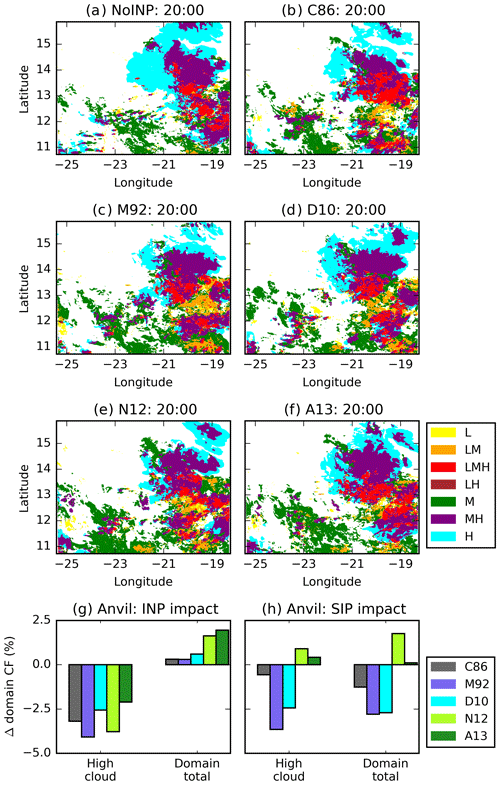
Figure 8Vertical composition of cloud. The 2D distribution of cloud type at 20:00 for all six SIP_active simulations (a–f) as well as anvil and domain cloud fraction change (10:00–24:00 UTC) due to INP (g) and due to SIP (h). Clouds are categorised according to their altitude into low (L, <4 km), mid (M, 4–9 km) and high (H, >9 km) levels and mixed-category columns if cloud (containing more than 10−5 kg kg−1 condensed water from cloud droplets, ice crystals, snow and graupel) was present in more than one of these levels (a more detailed description can be found in Sect. 2.1.4). A positive value in panel (g) or (h) indicates higher values when INPs (g) or SIP (h) are active.
The presence of INPs reduces the convective anvil extent by between 2.1 % and 4.1 % of the domain area depending on the choice of INP parameterisation (Fig. 8g), corresponding to a decrease in anvil cloud of between 22 % and 53 % relative to the NoINP simulation (not shown). The reduction in anvil extent in the presence of INPs is caused by increased liquid consumption at all mixed-phase levels, due to heterogeneous freezing, enhanced SIP, and increased graupel and snow production, reducing the availability of cloud droplets for homogeneous freezing (Fig. A4b), decreasing the ICNC at the cloud top and reducing the cloud anvil extent (Fig. 8g), in agreement with previous studies (e.g. Gasparini et al., 2020; van den Heever et al., 2006; Kärcher and Lohmann, 2003; Lohmann and Gasparini, 2017; Phillips et al., 2005, 2007; Storelvmo et al., 2013).
Reductions in the anvil extent caused by INPs are somewhat offset by the overall increases in the cloud fraction across the domain (Fig. 8g). However, it is possible that the effect of INPs and the INP parameterisation choice on the anvil cloud fraction, as well as the contribution of anvil cloud to overall cloud fraction and radiative changes, would become larger with a longer analysis period. This is because detrained convective anvils can persist longer in the atmosphere than the convective core that creates them (Luo and Rossow, 2004; Mace et al., 2006), but this is beyond the scope of the current study.
3.5 Importance of secondary ice production
It has been argued that the observed (or derived) primary ice particle production rate is unimportant for convective cloud properties when secondary ice production (SIP) is active (Fridlind et al., 2007; Heymsfield and Willis, 2014; Ladino et al., 2017; Lawson et al., 2015), as primary ice crystal concentrations are often overwhelmed by ice crystals formed via SIP (Field et al., 2017). However, the results shown in Fig. 4a (in which the simulations included SIP) do not support this argument. We find that the microphysical and radiative properties of the cloud field depend strongly on the properties of the INPs, even when SIP due to the Hallett–Mossop process occurs. Furthermore, the effect of including SIP on daylight domain-mean outgoing radiation varies between −2.0 and +6.6 W m−2 (Fig. 4b), showing that the presence of the Hallett–Mossop process has a smaller effect than the INP parameterisation and that the sign and magnitude of this effect depend on the INP parameterisation. The mean effect of including INPs on daylight domain-mean outgoing radiation is +9.8 W m−2, whereas the mean effect of including SIP via the Hallett–Mossop process is +2.9 W m−2. Therefore, rather than primary ice being simply overwhelmed by SIP, it actually determines how SIP affects cloud microphysics. Other mechanisms of SIP have been proposed (Field et al., 2017; Korolev and Leisner, 2020; Lauber et al., 2018), and the impact of INPs on cloud properties in the presence of these mechanisms, particularly those present at temperatures below 10 ∘C such as droplet shattering (Lauber et al., 2018), should be tested in future; however, this was beyond the scope of the present study.
The effect of SIP on the radiative properties of the cloud field is dependent on the INP parameterisation choice, both in magnitude and sign of change (Fig. 4b). SIP makes the clouds more reflective independent of the chosen parameterisation (Fig. 4b; cloudy regions contribution) due to increases in the snow and cloud droplet water path. N12 and A13 have the largest overall radiative response to SIP because changes in the radiative forcing from cloudy regions and cloud fraction contributions act to increase outgoing radiation (Fig. 4b). However, the cloud fraction response to SIP is the opposite for C86, M92 and D10, meaning that the cloudy regions and cloud fraction contributions act in opposite directions, reducing the total radiative forcing.
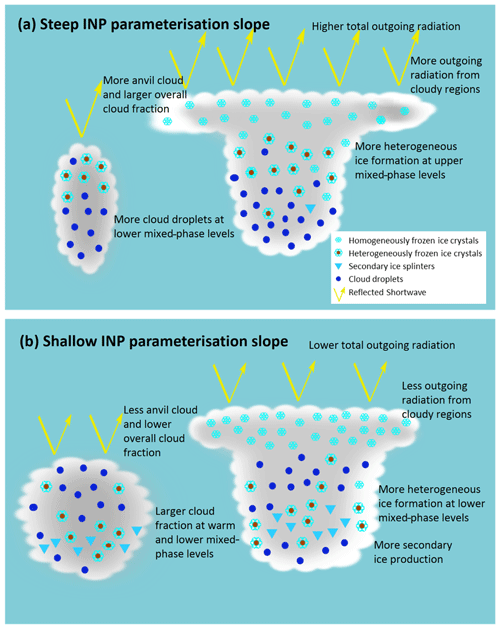
The different response of the domain cloud fraction to the presence of SIP is caused by substantial variation between simulations in the anvil cloud extent (Fig. 8h), from an increase of 10 % (+0.9 % of the domain area) in N12 to a decrease of 40 % (−3.6 % of the domain area) in M92 (Fig. 8h). These non-uniform changes in the cloud fraction and outgoing radiation can be explained by differences in the response of cloud freezing profiles to SIP due to variations in the INP parameterisation slope. For all INP parameterisations, SIP reduces the availability of liquid at higher altitudes. For shallower parameterisations such as M92, this causes a reduction in the amount of cloud droplets reaching the homogeneous freezing regime, thereby reducing the ICNC and cloud anvil spatial extent. However, in simulations using a steep parameterisation, almost all available droplets are frozen heterogeneously before they reach the homogeneous regime (see reduced homogeneous ice production rates in N12 and A13 in Fig. A4b). Therefore, in simulations using a steeper parameterisation, such as N12, a reduction in liquid availability due to SIP occurs at the top of the heterogeneous freezing regime, reducing the availability of liquid for riming and causing a reduction in the frozen hydrometeor size at high altitudes, a decrease in hydrometeor sedimentation and an increase in anvil extent. The effects of the INP parameterisation slope and the Hallett–Mossop process on the simulated cloud field properties are summarised in Fig. 9. Overall, our simulations show that the INP parameterisation choice and slope is an important determinant of cloud field micro- and macrophysical properties, even when SIP is active, and that the choice of INP parameterisation affects the cloud field response to SIP.
The lack of consideration of the ice and snow particle number by the SOCRATES radiation scheme is an important limitation of the results presented here. Changes to the ICNC, without a co-occurring change in the ice crystal mass concentrations, will not be reflected in modelled radiative fluxes. However, our results are still very relevant for climate model simulations, as climate models do not typically account for ICNCs in their radiation calculations and have frequently been shown to poorly represent ice crystal mass concentrations (Baran et al., 2014; Waliser et al., 2009). The SOCRATES representation of radiation with a dependence on ice mass is a more accurate and realistic representation of radiation than is seen in many climate models, which often derive bulk optical properties using empirically derived deterministic relationships between ice particle size and environmental temperature and/or ice water content (Baran et al., 2014; Edwards et al., 2007; Fu et al., 1999; Gu et al., 2011). However, the effect of INP parameterisation on deep convective clouds' radiative properties using a radiation code that considers ice particle number should be explored in future studies. The sensitivity of the cloud field to the chosen INP parameterisation and SIP indicates the importance of accurately representing ice water content in climate models and linking this ice water content to the ice-nucleating particle type.
Another limitation of the SOCRATES radiation code is its lack of consideration of rain and graupel particles. The effects of these hydrometeors are expected to be less than that of ice, snow and cloud droplets as they precipitate faster and, therefore, have a shorter lifetime. Furthermore, the effect of graupel on the tropical longwave radiative effect has been found to be negligible and dwarfed by that of snow (Chen et al., 2018). The global radiative effect of rain has also been found to be small in the vast majority of cases even at high temporal and spatial resolution (Hill et al., 2018). The effect of the incorporation of these hydrometeors into radiative transfer parameterisations should however be tested in future studies.
The use of both aerosol-dependent (D10, N12 and A13) and solely temperature-dependent (C86 and M92) parameterisations in this study means that we have examined the radiative sensitivity of a complex cloud field to a larger variety of INP parameterisations used in weather and climate models than if we had exclusively used parameterisations that consider the aerosol concentration. However, this experimental design has limitations. For example, due to the lack of aerosol dependence of the C86 and M92 schemes, a “presumed” dust concentration is implicitly present in these two cases and remains uniform throughout the simulation period. The effect of the INP parameterisation choice on convective cloud field properties should also be examined with the inclusion of aerosol scavenging, but this was beyond the scope of this study. Aerosol scavenging would allow the aerosol number concentration to be reduced by cloud droplet activation and the number of dust particles within cloud droplets to be tracked and depleted when frozen heterogeneously. In the simulations presented here, the heterogeneous freezing rate is calculated using the interstitial aerosol number concentration and the ICNC of the grid box in question, meaning that ice crystals advected into the grid box will reduce the heterogeneous nucleation rate even if they were frozen elsewhere in the domain.
Furthermore, while many cloud macro- and microphysical properties were correlated with the INP parameterisation slope, the slope of the parameterisation at low temperatures for the A13 and N12 parameterisations can be flat because the parameterisations plateau once they reach the number concentration of dust represented in the model grid box in question. This means that at high dust concentrations, the slope of the INP parameterisation correlates with the INP concentration at temperatures between −25 and −35 ∘C (Fig. 2). Thus, the absolute number concentration of aerosols capable of nucleating ice is not decoupled from the INP parameterisation slope in some INP parameterisations, and some cloud responses attributed to changes in the INP parameterisation slope may have in fact been caused by the absolute INP number concentration at cold temperatures. The relative importance of the INP parameterisation slope and the absolute number concentration of aerosols capable of nucleating ice will be investigated in future work. However, whether the INP number concentration plateaus at cold temperatures is determined in part by the INP parameterisation slope, and correlations with the INP parameterisation slope are evident at both warm and cold cloud altitudes, indicating the importance of the INP parameterisation slope.
This study utilised our best estimate of ice production by the Hallett–Mossop process (Connolly et al., 2006; Hallett and Mossop, 1974; Mossop, 1985), the most well-studied SIP mechanism, to try and understand the effect of the process, as currently understood, on deep convective cloud properties. The work indicates that INP concentrations at all mixed-phase temperatures can be important for cloud properties even in the presence of the Hallett–Mossop process, and that the impact of the Hallett–Mossop process depends on the INP number concentrations. The dependence of the rate of ice production by the Hallett–Mossop process on INP number concentrations (Fig. A4a) in particular highlights that the role of SIP in clouds may be dependent on INP. However, the rate of ice production by the Hallett–Mossop process is very uncertain, and other mechanisms of SIP have also been proposed (Field et al., 2017). We recommend that similar studies examining the effect of INPs should be conducted with the inclusion of other proposed SIP mechanisms, particularly those that may be present at temperatures below −10 ∘C, such as droplet shattering (Lauber et al., 2018). However, this was beyond the scope of the present study due in part to the lack of quantification and parameterisations for these other mechanisms (Field et al., 2017). Future work will attempt to overcome the above-mentioned caveats by using statistical emulation (Johnson et al., 2015b) to examine the interacting effects of the dust number concentration, INP parameterisation slope and SIP in an idealised deep convective cloud.
We quantified the effect of the INP parameterisation choice on the radiative properties of a deep convective cloud field using a regional model with advanced double-moment capabilities. The simulated domain exceeds 600 000 km2 and, therefore, captures the effects of INPs and INP parameterisation on a typical large, complex and heterogeneous convective cloud field. The presence of INPs increases domain-mean daylight TOA outgoing radiation by between 2.6 and 20.8 W m−2, and the choice of INP parameterisation can have as large an effect on cloud field properties as the inclusion or exclusion of INPs. These effects are evident even in the presence of SIP due to the Hallett–Mossop process, refuting the hypothesis that INPs are irrelevant beyond a minimum concentration needed to initiate the Hallett–Mossop process (Crawford et al., 2012; Ladino et al., 2017; Phillips et al., 2007). An important caveat of this result is that other SIP mechanisms, such as droplet shattering (Ladino et al., 2017; Lauber et al., 2018), are not represented in our model simulations. Furthermore, the effects of SIP on the cloud field properties are strongly dependent on the INP parameterisation choice. Both the magnitude and direction of change in the cloud fraction and total outgoing radiation due to SIP vary according to the INP parameterisation choice. Microphysical alterations to cloud properties are important contributors to radiative differences between simulations, in agreement with previous studies documenting the effect of aerosol–cloud interactions to the radiative forcing by deep convective clouds (Fan et al., 2013). For example, increasing cloud condensation nuclei concentrations, with no perturbations to INPs, was shown to increase cloud albedo and cloud fraction, deepen clouds and increase TOA outgoing radiation by 2–4 W m−2 (Fan et al., 2013). Here, we find that even for the same aerosol and CCN concentrations, just altering the relationship between aerosol concentration and ice-nucleating ability can cause changes in daylight TOA outgoing radiation of up to 18.2 W m−2 in our domain.
Our results indicate that the slope of the INP parameterisation with respect to temperature (dlog[INP]dT) is particularly important: outgoing total radiation, along with many cloud field and microphysical properties affecting radiation, was significantly correlated with the INP parameterisation slope. Best practise for accurately representing INP number concentrations based on current knowledge is to utilise parameterisations that link aerosol number and particle size to INP number concentration (e.g. D10, N12 and A13) but that is not enough without also using a parameterisation in which the temperature dependence of the INP number concentrations matches reality; the largest differences in domain outgoing radiation existed in this study between simulations using aerosol-dependent parameterisations (D10 and A13). These large variations in outgoing radiation between simulations using different aerosol-dependent INP parameterisations justify investment in observational campaigns to more effectively constrain the range of expected INP concentrations and parameterisation slopes in the Saharan dust outflow region and other regions dominated by maritime deep convective activity.
The significance of the slope of the INP parameterisation indicates the potential importance of accounting for differences in aerosol composition in modelling studies. For example, INPs derived from marine organics (Wilson et al., 2015) have a shallower slope than mineral dust INPs (Atkinson et al., 2013; Niemand et al., 2012). Furthermore, real-world INP concentrations are known to have complex temperature dependencies with biological INPs, such as soil-borne fungus and plant-related bacteria, making significant contributions at the warmest temperatures and mineral components being more important at lower temperatures (O'Sullivan et al., 2018). The work here suggests that the presence of biological INPs might reduce liquid water transport to the upper levels of the cloud, reducing cirrus anvil extent, but also increase the low cloud fraction. Nevertheless, measurements in the eastern tropical Atlantic indicate that biological INPs in the Saharan dust plumes are at most a minor contribution and that the parameterisations with a shallow slope in Fig. 2 produce too much glaciation at warm temperatures.
The results presented here also present a new framework for understanding the effect of SIP by identifying a potential relationship between the effect of the Hallett–Mossop process and the INP parameterisation slope. The significance of the INP parameterisation slope also highlights the importance of characterising the INP concentration across the entirety of the mixed-phase temperature range rather than just at one temperature or in a narrow temperature range, as is common in many field campaigns. For example, in the ICE-D field campaign, INP concentrations at temperatures above −7 and below −27 ∘C were not measurable due to experimental and sampling constraints (Price et al., 2018). Measuring INPs over the entire mixed-phase temperature range, throughout which deep convective clouds extend, conceivably covering around 10 orders of magnitude in INP number concentration, represents a major experimental challenge. This issue is compounded by the fact that INP spectra cannot reliably be extrapolated to higher or lower temperatures as our underpinning physical understanding of what makes an effective nucleation site is lacking (Coluzza et al., 2017; Holden et al., 2019; Kanji et al., 2017). This work demonstrates the importance of solving these problems and measuring the INP number concentrations across the entirety of the mixed-phase temperature spectrum, as has been demonstrated in previous work (e.g. Liu et al., 2018; Takeishi and Storelvmo, 2018).
Figure A1The cloud field. Simulated top-of-atmosphere outgoing shortwave radiation for the N12 simulation at 10:30 (a) and 13:30 (b).
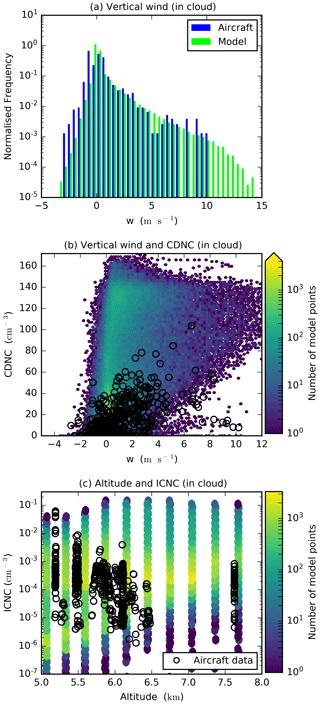
Figure A2Comparison of observed conditions from the B933 ICED field campaign flight on 21 August 2015 and the modelled conditions. Vertical wind speed from the model and aircraft data (a), a 2D histogram of modelled vertical wind against cloud droplet number concentration (CDNC) (b) and altitude plotted against ice crystal number concentration (ICNC) (c) with the aircraft data overlaid. Modelled values are selected from clouds between 10 and 150 km2 in size from the N12 simulation.
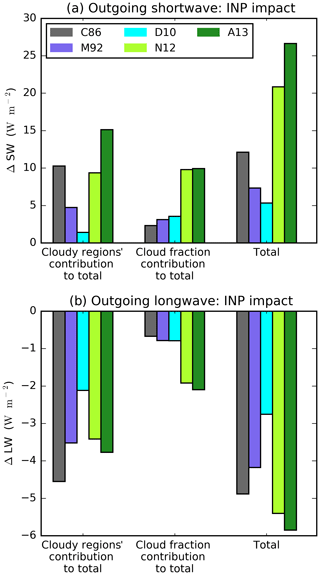
Figure A3Effect of INPs on domain-mean TOA outgoing daytime (10:00–17:00 UTC) shortwave and longwave radiation. The change from the NoINP simulation is shown (INP – NoINP). A positive value indicates more outgoing radiation when INPs are present. The contributions of changes in outgoing radiation from cloudy regions (left; i.e. ΔRadREFL from Eq. 1) and the cloud fraction (middle; i.e. ΔRadCF from Eq. 2) to the total radiative forcing (right; i.e. ΔRads−r from Eq. 5 with simulation s referring to the simulations with INP active and simulation r referring to the NoINP simulation) are also shown (calculation described in Sect. 2.1.3).
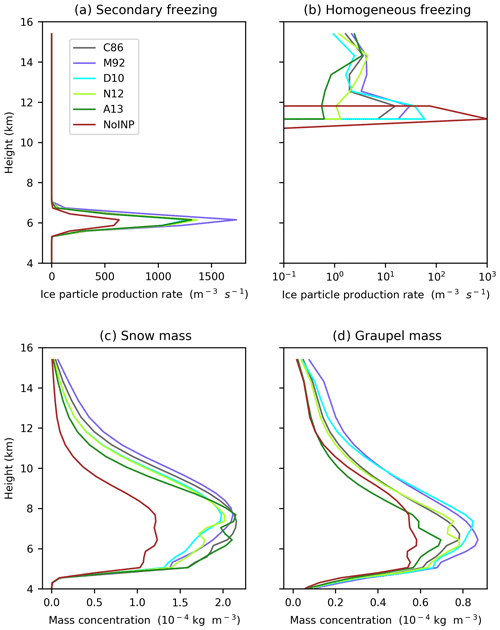
Figure A4Profiles of some microphysical properties of the simulated clouds. Mean in-cloud ice particle production rates from secondary (a) and homogeneous (b) freezing, snow mass concentration (c) and graupel mass concentration (d).
The datasets generated and analysed in this study are available from the corresponding author upon reasonable request.
REH, AKM, KSC, PRF and BJM contributed to the design, development and direction of the study. REH and AKM set up and ran the UM-CASIM simulations presented in the paper. REH processed and analysed the UM-CASIM datasets. JMW, AAH and BJS built and maintained the Met-Office CASIM model used to run the simulations. ZC and RJC provided processed aircraft data from the ICE-D B933 flight and helped with the comparison of model data with aircraft measurements. REH, AKM, JMW, AAH, ZC, RJC, KSC, PRF and BJM edited the paper.
Ken Carslaw is an ACP executive editor.
We acknowledge the use of Monsoon, a collaborative high-performance computing facility funded by the Met Office and NERC. We acknowledge the use of JASMIN, the UK collaborative data analysis facility. We obtained Moderate Resolution Imaging Spectroradiometer (MODIS) Corrected Reflectance images from the NASA Worldview website (https://worldview.earthdata.nasa.gov/, last access: 2 April 2021). Airborne measurements were obtained from the ICE-D field campaign, specifically the B933 flight on 21 August 2015. The ICE-D campaign used the BAe 146-301 Atmospheric Research Aircraft, which is operated by Directflight Ltd (now Airtask) and managed by the Facility for Airborne Atmospheric Measurements (FAAM). At the time of the measurements, FAAM was a joint entity of NERC and the UK Met Office. We thank all of the people involved in the ICE-D campaign.
This research has been supported by the European Research Council (ERC; grant 648661 MarineIce) and the Natural Environment Research Council (NERC; grant NE/M00340X/1).
This paper was edited by Martina Krämer and reviewed by Xiaohong Liu and three anonymous referees.
Abdul-Razzak, H. and Ghan, S. J.: A parameterization of aerosol activation: 2. Multiple aerosol types, J. Geophys. Res., 105, 6837–6844, https://doi.org/10.1029/1999JD901161, 2000.
Ansmann, A., Tesche, M., Althausen, D., Müller, D., Seifert, P., Freudenthaler, V., Heese, B., Wiegner, M., Pisani, G., Knippertz, P., and Dubovik, O.: Influence of Saharan dust on cloud glaciation in southern Morocco during the Saharan Mineral Dust Experiment, J. Geophys. Res., 113, D04210, https://doi.org/10.1029/2007JD008785, 2008.
Arakawa, A.: The cumulus parameterization problem: Past, present, and future, J. Climate, 17, 2493–2525, https://doi.org/10.1175/1520-0442(2004)017<2493:RATCPP>2.0.CO;2, 2004.
Atkinson, J. D., Murray, B. J., Woodhouse, M. T., Whale, T. F., Baustian, K. J., Carslaw, K. S., Dobbie, S., O'Sullivan, D., and Malkin, T. L.: The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds, Nature, 498, 355–358, https://doi.org/10.1038/nature12278, 2013.
Baran, A. J., Hill, P., Furtado, K., Field, P., and Manners, J.: A Coupled Cloud Physics–Radiation Parameterization of the Bulk Optical Properties of Cirrus and Its Impact on the Met Office Unified Model Global Atmosphere 5.0 Configuration, J. Climate, 27, 7725–7752, https://doi.org/10.1175/JCLI-D-13-00700.1, 2014.
Bigg, E. K.: The formation of atmospheric ice crystals by the freezing of droplets, Q. J. Roy. Meteor. Soc., 79, 510–519, https://doi.org/10.1002/qj.49707934207, 1953.
Boose, Y., Kanji, Z. A., Kohn, M., Sierau, B., Zipori, A., Crawford, I., Lloyd, G., Bukowiecki, N., Herrmann, E., Kupiszewski, P., Steinbacher, M., and Lohmann, U.: Ice nucleating particle measurements at 241K during winter months at 3580m MSL in the swiss alps, J. Atmos. Sci., 73, 2203–2228, https://doi.org/10.1175/JAS-D-15-0236.1, 2016a.
Boose, Y., Sierau, B., García, M. I., Rodríguez, S., Alastuey, A., Linke, C., Schnaiter, M., Kupiszewski, P., Kanji, Z. A., and Lohmann, U.: Ice nucleating particles in the Saharan Air Layer, Atmos. Chem. Phys., 16, 9067–9087, https://doi.org/10.5194/acp-16-9067-2016, 2016b.
Cantrell, W. and Heymsfield, A.: Production of ice in tropospheric clouds: a review, B. Am. Meteorol. Soc., 86, 795–808, https://doi.org/10.1175/BAMS-86-6-795, 2005.
Carrió, G. G., van den Heever, S. C., and Cotton, W. R.: Impacts of nucleating aerosol on anvil-cirrus clouds: A modeling study, Atmos. Res., 84, 111–131, https://doi.org/10.1016/j.atmosres.2006.06.002, 2007.
Chen, Y., Seiki, T., Kodama, C., Satoh, M., and Noda, A. T.: Impact of Precipitating Ice Hydrometeors on Longwave Radiative Effect Estimated by a Global Cloud-System Resolving Model, J. Adv. Model. Earth Sy., 10, 284–296, https://doi.org/10.1002/2017MS001180, 2018.
Coluzza, I., Creamean, J., Rossi, M., Wex, H., Alpert, P., Bianco, V., Boose, Y., Dellago, C., Felgitsch, L., Fröhlich-Nowoisky, J., Herrmann, H., Jungblut, S., Kanji, Z., Menzl, G., Moffett, B., Moritz, C., Mutzel, A., Pöschl, U., Schauperl, M., Scheel, J., Stopelli, E., Stratmann, F., Grothe, H., and Schmale, D.: Perspectives on the Future of Ice Nucleation Research: Research Needs and Unanswered Questions Identified from Two International Workshops, Atmosphere-Basel, 8, 138, https://doi.org/10.3390/atmos8080138, 2017.
Connolly, P. J., Choularton, T. W., Gallagher, M. W., Bower, K. N., Flynn, M. J., and Whiteway, J. A.: Cloud-resolving simulations of intense tropical Hector thunderstorms: Implications for aerosol-cloud interactions, Q. J. Roy. Meteor. Soc, 132, 3079–3106, https://doi.org/10.1256/qj.05.86, 2006.
Cooper, W. A.: Ice initiation in natural clouds, in: Precipitation enhancement–A scientific challenge, American Meteorological Society, Boston, MA, 29–32, 1986.
Crawford, I., Bower, K. N., Choularton, T. W., Dearden, C., Crosier, J., Westbrook, C., Capes, G., Coe, H., Connolly, P. J., Dorsey, J. R., Gallagher, M. W., Williams, P., Trembath, J., Cui, Z., and Blyth, A.: Ice formation and development in aged, wintertime cumulus over the UK: observations and modelling, Atmos. Chem. Phys., 12, 4963–4985, https://doi.org/10.5194/acp-12-4963-2012, 2012.
De Boer, G., Morrison, H., Shupe, M. D., and Hildner, R.: Evidence of liquid dependent ice nucleation in high-latitude stratiform clouds from surface remote sensors, Geophys. Res. Lett., 38, L01803, https://doi.org/10.1029/2010GL046016, 2011.
DeMott, P. J., Sassen, K., Poellot, M. R., Baumgardner, D., Rogers, D. C., Brooks, S. D., Prenni, A. J., and Kreidenweis, S. M.: African dust aerosols as atmospheric ice nuclei, Geophys. Res. Lett., 30, 1732–1726, https://doi.org/10.1029/2003GL017410, 2003.
DeMott, P. J., Prenni, A. J., Liu, X., Kreidenweis, S. M., Petters, M. D., Twohy, C. H., Richardson, M. S., Eidhammer, T., and Rogers, D. C.: Predicting global atmospheric ice nuclei distributions and their impacts on climate, P. Natl. Acad. Sci. USA, 107, 11217–11222, https://doi.org/10.1073/pnas.0910818107, 2010.
DeMott, P. J., Prenni, A. J., McMeeking, G. R., Sullivan, R. C., Petters, M. D., Tobo, Y., Niemand, M., Möhler, O., Snider, J. R., Wang, Z., and Kreidenweis, S. M.: Integrating laboratory and field data to quantify the immersion freezing ice nucleation activity of mineral dust particles, Atmos. Chem. Phys., 15, 393–409, https://doi.org/10.5194/acp-15-393-2015, 2015.
Deng, X., Xue, H., and Meng, Z.: The effect of ice nuclei on a deep convective cloud in South China, Atmos. Res., 206, 1–12, https://doi.org/10.1016/J.ATMOSRES.2018.02.013, 2018.
Edwards, J. M. and Slingo, A.: Studies with a flexible new radiation code. I: Choosing a configuration for a large-scale model, Q. J. Roy. Meteor. Soc., 122, 689–719, https://doi.org/10.1002/qj.49712253107, 1996.
Edwards, J. M., Havemann, S., Thelen, J. C., and Baran, A. J.: A new parametrization for the radiative properties of ice crystals: Comparison with existing schemes and impact in a GCM, Atmos. Res., 83, 19–35, https://doi.org/10.1016/j.atmosres.2006.03.002, 2007.
Eidhammer, T., Demott, P. J., and Kreidenweis, S. M.: A comparison of heterogeneous ice nucleation parameterizations using a parcel model framework, J. Geophys. Res.-Atmos., 114, D06202, https://doi.org/10.1029/2008JD011095, 2009.
Ekman, A. M. L., Engström, A., and Wang, C.: The effect of aerosol composition and concentration on the development and anvil properties of a continental deep convective cloud, Q. J. Roy. Meteor. Soc., 133, 1439–1452, https://doi.org/10.1002/qj.108, 2007.
Fan, J., Comstock, J. M., and Ovchinnikov, M.: The cloud condensation nuclei and ice nuclei effects on tropical anvil characteristics and water vapor of the tropical tropopause layer, Environ. Res. Lett., 5, 044005, https://doi.org/10.1088/1748-9326/5/4/044005, 2010a.
Fan, J., Comstock, J. M., Ovchinnikov, M., McFarlane, S. A., McFarquhar, G., and Allen, G.: Tropical anvil characteristics and water vapor of the tropical tropopause layer: Impact of heterogeneous and homogeneous freezing parameterizations, J. Geophys. Res., 115, D12201, https://doi.org/10.1029/2009JD012696, 2010b.
Fan, J., Rosenfeld, D., Ding, Y., Leung, L. R., and Li, Z.: Potential aerosol indirect effects on atmospheric circulation and radiative forcing through deep convection, Geophys. Res. Lett., 39, L09806, https://doi.org/10.1029/2012GL051851, 2012.
Fan, J., Leung, L. R., Rosenfeld, D., Chen, Q., Li, Z., Zhang, J., and Yan, H.: Microphysical effects determine macrophysical response for aerosol impacts on deep convective clouds., P. Natl. Acad. Sci. USA, 110, E4581–E4590, https://doi.org/10.1073/pnas.1316830110, 2013.
Field, P. R., Lawson, R. P., Brown, P. R. A., Lloyd, G., Westbrook, C., Moisseev, D., Miltenberger, A., Nenes, A., Blyth, A., Choularton, T., Connolly, P., Buehl, J., Crosier, J., Cui, Z., Dearden, C., DeMott, P., Flossmann, A., Heymsfield, A., Huang, Y., Kalesse, H., Kanji, Z. A., Korolev, A., Kirchgaessner, A., Lasher-Trapp, S., Leisner, T., McFarquhar, G., Phillips, V., Stith, J., and Sullivan, S.: Chapter 7. Secondary ice production – current state of the science and recommendations for the future, Meteorol. Monogr., American Meteorological Society, Washington, DC, 7.1–7.20, https://doi.org/10.1175/AMSMONOGRAPHS-D-16-0014.1, 2017.
Fridlind, A. M., Ackerman, A. S., McFarquhar, G., Zhang, G., Poellot, M. R., DeMott, P. J., Prenni, A. J., and Heymsfield, A. J.: Ice properties of single-layer stratocumulus during the Mixed-Phase Arctic Cloud Experiment: 2. Model results, J. Geophys. Res., 112, D24202, https://doi.org/10.1029/2007JD008646, 2007.
Fu, Q., Sun, W. B., Yang, P., Fu, Q., Sun, W. B., and Yang, P.: Modeling of Scattering and Absorption by Nonspherical Cirrus Ice Particles at Thermal Infrared Wavelengths, J. Atmos. Sci., 56, 2937–2947, https://doi.org/10.1175/1520-0469(1999)056<2937:MOSAAB>2.0.CO;2, 1999.
Gasparini, B., McGraw, Z., Storelvmo, T., and Lohmann, U.: To what extent can cirrus cloud seeding counteract global warming?, Environ. Res. Lett., 15, 054002, https://doi.org/10.1088/1748-9326/ab71a3, 2020.
Gibbons, M., Min, Q., and Fan, J.: Investigating the impacts of Saharan dust on tropical deep convection using spectral bin microphysics, Atmos. Chem. Phys., 18, 12161–12184, https://doi.org/10.5194/acp-18-12161-2018, 2018.
Grosvenor, D. P., Field, P. R., Hill, A. A., and Shipway, B. J.: The relative importance of macrophysical and cloud albedo changes for aerosol-induced radiative effects in closed-cell stratocumulus: insight from the modelling of a case study, Atmos. Chem. Phys., 17, 5155–5183, https://doi.org/10.5194/acp-17-5155-2017, 2017.
Gu, Y., Liou, K. N., Ou, S. C., and Fovell, R.: Cirrus cloud simulations using WRF with improved radiation parameterization and increased vertical resolution, J. Geophys. Res., 116, D06119, https://doi.org/10.1029/2010JD014574, 2011.
Hallett, J. and Mossop, S. C.: Production of secondary ice particles during the riming process, Nature, 249, 26–28, https://doi.org/10.1038/249026a0, 1974.
Harrison, A. D., Whale, T. F., Carpenter, M. A., Holden, M. A., Neve, L., O'Sullivan, D., Vergara Temprado, J., and Murray, B. J.: Not all feldspars are equal: a survey of ice nucleating properties across the feldspar group of minerals, Atmos. Chem. Phys., 16, 10927–10940, https://doi.org/10.5194/acp-16-10927-2016, 2016.
Harrison, A. D., Lever, K., Sanchez-Marroquin, A., Holden, M. A., Whale, T. F., Tarn, M. D., McQuaid, J. B., and Murray, B. J.: The ice-nucleating ability of quartz immersed in water and its atmospheric importance compared to K-feldspar, Atmos. Chem. Phys., 19, 11343–11361, https://doi.org/10.5194/acp-19-11343-2019, 2019.
Herbert, R. J., Murray, B. J., Dobbie, S. J., and Koop, T.: Sensitivity of liquid clouds to homogenous freezing parameterizations, Geophys. Res. Lett., 42, 1599–1605, https://doi.org/10.1002/2014GL062729, 2015.
Heymsfield, A. and Willis, P.: Cloud conditions favoring secondary ice particle production in tropical maritime convection, J. Atmos. Sci., 71, 4500–4526, https://doi.org/10.1175/JAS-D-14-0093.1, 2014.
Heymsfield, A. J. and Mossop, S. C.: Temperature dependence of secondary ice crystal production during soft hail growth by riming, Q. J. Roy. Meteor. Soc., 110, 765–770, https://doi.org/10.1002/qj.49711046512, 1984.
Hill, P. G., Chiu, J. C., Allan, R. P., and Chern, J. -D.: Characterizing the Radiative Effect of Rain Using a Global Ensemble of Cloud Resolving Simulations, J. Adv. Model. Earth Sy., 10, 2453–2470, https://doi.org/10.1029/2018MS001415, 2018.
Holden, M. A., Whale, T. F., Tarn, M. D., O'Sullivan, D., Walshaw, R. D., Murray, B. J., Meldrum, F. C., and Christenson, H. K.: High-speed imaging of ice nucleation in water proves the existence of active sites, Sci. Adv., 5, eaav4316, https://doi.org/10.1126/sciadv.aav4316, 2019.
Huang, Y., Blyth, A. M., Brown, P. R. A., Choularton, T. W., and Cui, Z.: Factors controlling secondary ice production in cumulus clouds, Q. J. Roy. Meteor. Soc., 143, 1021–1031, https://doi.org/10.1002/qj.2987, 2017.
Jeffery, C. A. and Austin, P. H.: Homogeneous nucleation of supercooled water: Results from a new equation of state, J. Geophys. Res.-Atmos., 102, 25269–25279, https://doi.org/10.1029/97jd02243, 1997.
Johnson, C. E., Bellouin, N., Davison, P. S., Jones, A., Rae, J. G. L., Roberts, D. L., Woodage, M. J., Woodward, S., Or Õ Nez, C., and Savage, N. H.: CLASSIC Aerosol Scheme, Unified Model Doc. Pap. (Vn 10.3), available at: https://code.metoffice.gov.uk/doc/um/vn10.3/papers/umdp_020.pdf (last access: 9 March 2017), 2015a.
Johnson, J. S., Cui, Z., Lee, L. A., Gosling, J. P., Blyth, A. M., and Carslaw, K. S.: Evaluating uncertainty in convective cloud microphysics using statistical emulation, J. Adv. Model. Earth Sy., 7, 162–187, https://doi.org/10.1002/2014MS000383, 2015b.
Kanji, Z. A., Ladino, L. A., Wex, H., Boose, Y., Burkert-Kohn, M., Cziczo, D. J., Krämer, M., Kanji, Z. A., Ladino, L. A., Wex, H., Boose, Y., Burkert-Kohn, M., Cziczo, D. J., and Krämer, M.: Overview of Ice Nucleating Particles, Meteorol. Monogr., 58, 1.1–1.33, https://doi.org/10.1175/AMSMONOGRAPHS-D-16-0006.1, 2017.
Kärcher, B. and Lohmann, U.: A parameterization of cirrus cloud formation: Heterogeneous freezing, J. Geophys. Res., 108, 4402, https://doi.org/10.1029/2002JD003220, 2003.
Korolev, A. and Leisner, T.: Review of experimental studies of secondary ice production, Atmos. Chem. Phys., 20, 11767–11797, https://doi.org/10.5194/acp-20-11767-2020, 2020.
Lacher, L., Steinbacher, M., Bukowiecki, N., Herrmann, E., Zipori, A., and Kanji, Z. A.: Impact of air mass conditions and aerosol properties on ice nucleating particle concentrations at the High Altitude Research Station Jungfraujoch, Atmosphere-Basel, 9, 363, https://doi.org/10.3390/atmos9090363, 2018.
Ladino, L. A., Korolev, A., Heckman, I., Wolde, M., Fridlind, A. M., and Ackerman, A. S.: On the role of ice-nucleating aerosol in the formation of ice particles in tropical mesoscale convective systems, Geophys. Res. Lett., 44, 1574–1582, https://doi.org/10.1002/2016GL072455, 2017.
Lasher-Trapp, S., Leon, D. C., DeMott, P. J., Villanueva-Birriel, C. M., Johnson, A. V., Moser, D. H., Tully, C. S., and Wu, W.: A Multisensor Investigation of Rime Splintering in Tropical Maritime Cumuli, J. Atmos. Sci., 73, 2547–2564, https://doi.org/10.1175/JAS-D-15-0285.1, 2016.
Lauber, A., Kiselev, A., Pander, T., Handmann, P., Leisner, T., Lauber, A., Kiselev, A., Pander, T., Handmann, P., and Leisner, T.: Secondary Ice Formation during Freezing of Levitated Droplets, J. Atmos. Sci., 75, 2815–2826, https://doi.org/10.1175/JAS-D-18-0052.1, 2018.
Lawson, R. P., Woods, S., Morrison, H., Lawson, R. P., Woods, S., and Morrison, H.: The Microphysics of Ice and Precipitation Development in Tropical Cumulus Clouds, J. Atmos. Sci., 72, 2429–2445, https://doi.org/10.1175/JAS-D-14-0274.1, 2015.
Liu, X., Fu, Y., Cao, Z., and Jin, S.: Influence of ice nuclei parameterization schemes on the hail process, Adv. Meteorol., 2018, 4204137 https://doi.org/10.1155/2018/4204137, 2018.
Lloyd, G., Choularton, T., Bower, K., Crosier, J., Gallagher, M., Flynn, M., Dorsey, J., Liu, D., Taylor, J. W., Schlenczek, O., Fugal, J., Borrmann, S., Cotton, R., Field, P., and Blyth, A.: Small ice particles at slightly supercooled temperatures in tropical maritime convection, Atmos. Chem. Phys., 20, 3895–3904, https://doi.org/10.5194/acp-20-3895-2020, 2020.
Lohmann, U. and Gasparini, B.: A cirrus cloud climate dial, Science, 357, 248–249, 2017.
Lohmann, U., Lüönd, F., and Mahrt, F.: An introduction to clouds: From the microscale to climate, Cambridge University Press, Cambridge CB2 8BS, United Kingdom, 2016.
Luo, Z. and Rossow, W. B.: Characterizing tropical cirrus life cycle, evolution, and interaction with upper-tropospheric water vapor using lagrangian trajectory analysis of satellite observations, J. Climate, 17, 4541–4563, https://doi.org/10.1175/3222.1, 2004.
Mace, G. G., Deng, M., Soden, B., and Zipser, E.: Association of tropical cirrus in the 10–15-km layer with deep convective sources: An observational study combining millimeter radar sata and satellite-derived trajectories, J. Atmos. Sci., 63, 480–503, https://doi.org/10.1175/JAS3627.1, 2006.
Manners, J., Edwards, J. M., Hill, P., and Thelen, J.-C.: SOCRATES technical guide Suite Of Community RAdiative Transfer codes based on Edwards and Slingo, Tech. Rep., pp. 1–87, Met Office, FitzRoy Rd, Exeter EX1 3PB, United Kingdom, 2017.
McCoy, D. T., Field, P. R., Schmidt, A., Grosvenor, D. P., Bender, F. A.-M., Shipway, B. J., Hill, A. A., Wilkinson, J. M., and Elsaesser, G. S.: Aerosol midlatitude cyclone indirect effects in observations and high-resolution simulations, Atmos. Chem. Phys., 18, 5821–5846, https://doi.org/10.5194/acp-18-5821-2018, 2018.
McFarquhar, G. M., Baumgardner, D., Bansemer, A., Abel, S. J., Crosier, J., French, J., Rosenberg, P., Korolev, A., Schwarzoenboeck, A., Leroy, D., Um, J., Wu, W., Heymsfield, A. J., and Dong, J.: Processing of Ice Cloud In Situ Data Collected by Bulk Water, Scattering, and Imaging Probes: Fundamentals, Uncertainties, and Efforts toward Consistency, Meteorol. Monogr., 58, 11.1–11.31, 2017.
Meyers, M. P., DeMott, P. J., Cotton, W. R., Meyers, M. P., DeMott, P. J., and Cotton, W. R.: New primary ice-nucleation parameterizations in an explicit cloud model, J. Appl. Meteorol., 31, 708–721, https://doi.org/10.1175/1520-0450(1992)031<0708:NPINPI>2.0.CO;2, 1992.
Miltenberger, A. K., Field, P. R., Hill, A. A., Rosenberg, P., Shipway, B. J., Wilkinson, J. M., Scovell, R., and Blyth, A. M.: Aerosol–cloud interactions in mixed-phase convective clouds – Part 1: Aerosol perturbations, Atmos. Chem. Phys., 18, 3119–3145, https://doi.org/10.5194/acp-18-3119-2018, 2018.
Mossop, S. C.: Secondary ice particle production during rime growth: The effect of drop size distribution and rimer velocity, Q. J. Roy. Meteor. Soc., 111, 1113–1124, https://doi.org/10.1002/qj.49711147012, 1985.
Niemand, M., Möhler, O., Vogel, B., Vogel, H., Hoose, C., Connolly, P., Klein, H., Bingemer, H., DeMott, P., Skrotzki, J., Leisner, T., Niemand, M., Möhler, O., Vogel, B., Vogel, H., Hoose, C., Connolly, P., Klein, H., Bingemer, H., DeMott, P., Skrotzki, J., and Leisner, T.: A particle-surface-area-based parameterization of immersion freezing on desert dust particles, J. Atmos. Sci., 69, 3077–3092, https://doi.org/10.1175/JAS-D-11-0249.1, 2012.
O'Sullivan, D., Adams, M. P., Tarn, M. D., Harrison, A. D., Vergara-Temprado, J., Porter, G. C. E., Holden, M. A., Sanchez-Marroquin, A., Carotenuto, F., Whale, T. F., McQuaid, J. B., Walshaw, R., Hedges, D. H. P., Burke, I. T., Cui, Z., and Murray, B. J.: Contributions of biogenic material to the atmospheric ice-nucleating particle population in North Western Europe, Sci. Rep.-UK, 8, 13821, https://doi.org/10.1038/s41598-018-31981-7, 2018.
Peckhaus, A., Kiselev, A., Hiron, T., Ebert, M., and Leisner, T.: A comparative study of K-rich and Na/Ca-rich feldspar ice-nucleating particles in a nanoliter droplet freezing assay, Atmos. Chem. Phys., 16, 11477–11496, https://doi.org/10.5194/acp-16-11477-2016, 2016.
Phillips, V. T. J., Andronache, C., Sherwood, S. C., Bansemer, A., Conant, W. C., Demott, P. J., Flagan, R. C., Heymsfield, A., Jonsson, H., Poellot, M., Rissman, T. A., Seinfeld, J. H., Vanreken, T., Varutbangkul, V., and Wilson, J. C.: Anvil glaciation in a deep cumulus updraught over Florida simulated with the Explicit Microphysics Model. I: Impact of various nucleation processes, Q. J. Roy. Meteor. Soc., 131, 2019–2046, https://doi.org/10.1256/qj.04.85, 2005.
Phillips, V. T. J., Donner, L. J., Garner, S. T., Phillips, V. T. J., Donner, L. J., and Garner, S. T.: Nucleation processes in deep convection simulated by a cloud-system-resolving model with double-moment bulk microphysics, J. Atmos. Sci., 64, 738–761, https://doi.org/10.1175/JAS3869.1, 2007.
Phillips, V. T. J., Patade, S., Gutierrez, J., and Bansemer, A.: Secondary Ice Production by Fragmentation of Freezing Drops: Formulation and Theory, J. Atmos. Sci., 75, 3031–3070, https://doi.org/10.1175/JAS-D-17-0190.1, 2018.
Price, H. C., Baustian, K. J., McQuaid, J. B., Blyth, A., Bower, K. N., Choularton, T., Cotton, R. J., Cui, Z., Field, P. R., Gallagher, M., Hawker, R., Merrington, A., Miltenberger, A., Neely III, R. R., Parker, S. T., Rosenberg, P. D., Taylor, J. W., Trembath, J., Vergara-Temprado, J., Whale, T. F., Wilson, T. W., Young, G., and Murray, B. J.: Atmospheric ice-nucleating particles in the dusty tropical Atlantic, J. Geophys. Res.-Atmos., 123, 2175–2193, https://doi.org/10.1002/2017JD027560, 2018.
Saunders, C. P. and Hosseini, A.: A laboratory study of the effect of velocity on Hallett–Mossop ice crystal multiplication, Atmos. Res., 59–60, 3–14, https://doi.org/10.1016/S0169-8095(01)00106-5, 2001.
Seinfeld, J. H. and Spyros, N. P.: Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 3rd edn., Wiley, New York, USA, 2006.
Shi, Y. and Liu, X.: Dust Radiative Effects on Climate by Glaciating Mixed-Phase Clouds, Geophys. Res. Lett., 46, 6128–6137, https://doi.org/10.1029/2019GL082504, 2019.
Stevens, R. G., Loewe, K., Dearden, C., Dimitrelos, A., Possner, A., Eirund, G. K., Raatikainen, T., Hill, A. A., Shipway, B. J., Wilkinson, J., Romakkaniemi, S., Tonttila, J., Laaksonen, A., Korhonen, H., Connolly, P., Lohmann, U., Hoose, C., Ekman, A. M. L., Carslaw, K. S., and Field, P. R.: A model intercomparison of CCN-limited tenuous clouds in the high Arctic, Atmos. Chem. Phys., 18, 11041–11071, https://doi.org/10.5194/acp-18-11041-2018, 2018.
Storelvmo, T., Kristjansson, J. E., Muri, H., Pfeffer, M., Barahona, D., and Nenes, A.: Cirrus cloud seeding has potential to cool climate, Geophys. Res. Lett., 40, 178–182, https://doi.org/10.1029/2012GL054201, 2013.
Sullivan, S. C., Hoose, C., Kiselev, A., Leisner, T., and Nenes, A.: Initiation of secondary ice production in clouds, Atmos. Chem. Phys., 18, 1593–1610, https://doi.org/10.5194/acp-18-1593-2018, 2018.
Takeishi, A. and Storelvmo, T.: A study of enhanced heterogeneous ice nucleation in simulated deep convective clouds observed during DC3, J. Geophys. Res.-Atmos., 123, 13396–13420, https://doi.org/10.1029/2018JD028889, 2018.
Vali, G., DeMott, P. J., Möhler, O., and Whale, T. F.: Technical Note: A proposal for ice nucleation terminology, Atmos. Chem. Phys., 15, 10263–10270, https://doi.org/10.5194/acp-15-10263-2015, 2015.
van den Heever, S. C., Carrió, G. G., Cotton, W. R., DeMott, P. J., and Prenni, A. J.: Impacts of nucleating aerosol on Florida storms. Part I: Mesoscale simulations, J. Atmos. Sci., 63, 1752–1775, https://doi.org/10.1175/JAS3713.1, 2006.
Vergara-Temprado, J., Murray, B. J., Wilson, T. W., O'Sullivan, D., Browse, J., Pringle, K. J., Ardon-Dryer, K., Bertram, A. K., Burrows, S. M., Ceburnis, D., DeMott, P. J., Mason, R. H., O'Dowd, C. D., Rinaldi, M., and Carslaw, K. S.: Contribution of feldspar and marine organic aerosols to global ice nucleating particle concentrations, Atmos. Chem. Phys., 17, 3637–3658, https://doi.org/10.5194/acp-17-3637-2017, 2017.
Vergara-Temprado, J., Miltenberger, A. K., Furtado, K., Grosvenor, D. P., Shipway, B. J., Hill, A. A., Wilkinson, J. M., Field, P. R., Murray, B. J., and Carslaw, K. S.: Strong control of Southern Ocean cloud reflectivity by ice-nucleating particles., P. Natl. Acad. Sci. USA., 115, 2687–2692, https://doi.org/10.1073/pnas.1721627115, 2018.
Waliser, D. E., Li, J. L. F., Woods, C. P., Austin, R. T., Bacmeister, J., Chern, J., Del Genio, A., Jiang, J. H., Kuang, Z., Meng, H., Minnis, P., Platnick, S., Rossow, W. B., Stephens, G. L., Sun-Mack, S., Tao, W. K., Tompkins, A. M., Vane, D. G., Walker, C., and Wu, D.: Cloud ice: A climate model challenge with signs and expectations of progress, J. Geophys. Res.-Atmos., 114, D00A21, https://doi.org/10.1029/2008JD010015, 2009.
Walters, D., Boutle, I., Brooks, M., Melvin, T., Stratton, R., Vosper, S., Wells, H., Williams, K., Wood, N., Allen, T., Bushell, A., Copsey, D., Earnshaw, P., Edwards, J., Gross, M., Hardiman, S., Harris, C., Heming, J., Klingaman, N., Levine, R., Manners, J., Martin, G., Milton, S., Mittermaier, M., Morcrette, C., Riddick, T., Roberts, M., Sanchez, C., Selwood, P., Stirling, A., Smith, C., Suri, D., Tennant, W., Vidale, P. L., Wilkinson, J., Willett, M., Woolnough, S., and Xavier, P.: The Met Office Unified Model Global Atmosphere 6.0/6.1 and JULES Global Land 6.0/6.1 configurations, Geosci. Model Dev., 10, 1487–1520, https://doi.org/10.5194/gmd-10-1487-2017, 2017.
Welti, A., Müller, K., Fleming, Z. L., and Stratmann, F.: Concentration and variability of ice nuclei in the subtropical maritime boundary layer, Atmos. Chem. Phys., 18, 5307–5320, https://doi.org/10.5194/acp-18-5307-2018, 2018.
Wilson, T. W., Ladino, L. A., Alpert, P. A., Breckels, M. N., Brooks, I. M., Browse, J., Burrows, S. M., Carslaw, K. S., Huffman, J. A., Judd, C., Kilthau, W. P., Mason, R. H., McFiggans, G., Miller, L. A., Nájera, J. J., Polishchuk, E., Rae, S., Schiller, C. L., Si, M., Temprado, J. V., Whale, T. F., Wong, J. P. S., Wurl, O., Yakobi-Hancock, J. D., Abbatt, J. P. D., Aller, J. Y., Bertram, A. K., Knopf, D. A., and Murray, B. J.: A marine biogenic source of atmospheric ice-nucleating particles, Nature, 525, 234–238, https://doi.org/10.1038/nature14986, 2015.