Biodegradation by bacteria in clouds: an underestimated sink for some organics in the atmospheric multiphase system

Water-soluble organic compounds represent a significant fraction of total atmospheric carbon. The main oxidants towards them in the gas and aqueous phases are OH and NO₃ radicals. In addition to chemical solutes, a great variety of microorganisms (e.g., bacteria, viruses, fungi) have been identified in cloud water. Previous lab studies suggested that for some organics, biodegradation by bacteria in water is comparable to their loss by chemical processes. We perform model sensitivity studies over large ranges of biological and chemical process parameters using a box model with a detailed atmospheric multiphase chemical mechanism and biodegradation processes to explore the importance of biodegradation of organics in the aqueous phase. Accounting for the fact that only a small number fraction of cloud droplets (∼0.0001–0.001) contains active bacterial cells, we consider only a few bacteria-containing droplets in the model cloud. We demonstrate that biodegradation might be most efficient for water-soluble organic gases with intermediate solubility ($\sim {\mathrm{10}}^{\mathrm{4}}\le K_{\mathrm{H}\left(\mathrm{eff}\right)}$ [M atm⁻¹] ≤10⁶, e.g., formic and acetic acids). This can be explained by the transport limitation due to evaporation of organics from bacteria-free droplets to the gas phase, followed by the dissolution into bacteria-containing droplets. For cloud condensation nuclei (CCN)-derived compounds, such as dicarboxylic acids, the upper limit of organic loss by biodegradation can be approximated by the amount of organics dissolved in the bacteria-containing droplets (<0.1 %). We compare results from our detailed drop-resolved model to simplified model approaches, in which (i) either all cloud droplets are assumed to contain the same cell concentration (0.0001–0.001 cell per droplet), or (ii) only droplets with intact bacterial cells are considered in the cloud (liquid water content $\sim {\mathrm{10}}^{-\mathrm{11}}$ vol $/$ vol). Conclusions based on these approaches generally overestimate the role of biodegradation, particularly for highly water-soluble organic gases. Our model sensitivity studies suggest that current atmospheric multiphase chemistry models are incomplete for organics with intermediate solubility and high bacterial activity.

1 Introduction

Clouds provide a medium for multiphase chemical reactions, in which chemical species from the aqueous, solid, and gas phases are transformed and can affect significantly the transport and distribution of chemical species in the atmosphere (Lelieveld and Crutzen, 1991). The chemical composition of cloud water is a complex mixture containing a multitude of organic and inorganic species with a range of chemical and physical properties (e.g., reactivity, solubility, volatility). The organic fraction includes water-soluble organic gases and water-soluble cloud condensation nuclei (CCN)-derived components, such as aldehydes, mono- and dicarboxylic acids, and organonitrogen and organosulfur compounds. Water-soluble organic gases are dissolved from the gas phase to the aqueous phase; CCN-derived compounds enter the aqueous phase via nucleation scavenging of condensation nuclei (CCN) (Ervens, 2015; Löflund et al., 2002). Water-soluble organic carbon (WSOC) constitutes a significant portion of the total atmospheric organic carbon mass, ranging from ∼14 % to ∼64 % depending on the sampling location (Decesari et al., 2000; Gao et al., 2016; Varga et al., 2001).

In addition to chemical solutes, cloud water contains microorganisms such as bacteria, yeast, and fungi (Delort et al., 2010; Hu et al., 2018). Typical concentrations of bacterial cells are on the order of 10⁶ to 10⁸ cells L⁻¹; fungi and yeast cell concentrations are usually lower (∼10⁵ to ∼10⁷ cells L⁻¹) (Amato et al., 2007b; Sattler et al., 2001). The atmosphere is a stressful environment for microorganisms (low temperature, UV exposure, acidic pH, quick hydration–drying cycles, and the presence of oxidants such as OH and H₂O₂) (Sattler et al., 2001), which might limit the survival time of cells in the atmosphere.

Several studies have shown that bacteria can grow and be metabolically active in cloud droplets. Marker compounds such as adenosine 5^′-triphosphate (ATP) (Amato et al., 2007c), rRNA (Krumins et al., 2014a), or mRNA (Amato et al., 2019) have been used to demonstrate metabolic activity in the atmosphere. The ADP $/$ ATP ratio (where ADP is adenosine diphosphate), monitored during lab experiments with real cloud water, showed that even after exposure to oxidants over several hours, biodegradation rates were not significantly affected (Vaïtilingom et al., 2013). Metabolic activity and cell generation of bacteria is likely restricted to the time cells spend in clouds due to the abundance of liquid water (Ervens and Amato, 2020; Haddrell and Thomas, 2017); bacteria have been found to be dormant at lower relative humidity than in clouds (Kaprelyants and Kell, 1993).

The metabolic activity of bacterial strains identified in cloud water (e.g., Pseudomonas, Sphingomonas) has been investigated in lab studies, and it was shown that they can biodegrade organics (e.g., malonate, succinate, adipate, pimelate, formaldehyde, methanol, acetate, formate, phenol, and catechol) (Amato et al., 2007a; Ariya et al., 2002; Delort et al., 2010; Fankhauser et al., 2019; Husárová et al., 2011; Jaber et al., 2020; Vaïtilingom et al., 2010, 2011, 2013). Based on comparisons of experimentally derived biodegradation rates to chemical rates of oxidation reactions by radicals (e.g., OH, NO₃) in the aqueous phase, it was concluded that they might be similar under some conditions and that, depending on the abundance and metabolic activity of bacteria strains, oxidation and biodegradation processes of organics may compete in clouds. The biodegradation rate likely depends on the availability of the substrate in the aqueous phase. In the case of soluble substrates, it can be expected that uptake of soluble substrates from the gas phase leads to a continuous replenishment of the organics.

There are several estimates of WSOC loss by bacteria on a global scale: Sattler et al. (2001) estimated a sink of 1–10 Tg yr⁻¹, smaller than the estimate by Vaïtilingom et al. (2013) (10–50 Tg yr⁻¹). However, the latter is likely an overestimate as complete respiration was implied, i.e., total conversion of organics into CO₂. More conservatively, Ervens and Amato (2020) suggested a global WSOC loss of 8–11 Tg yr⁻¹, being comparable to that by chemical processes (8–20 Tg yr⁻¹). Similarly, Fankhauser et al. (2019) postulated that the role of biodegradation is likely small, but they did not quantify the loss of different organics by bacteria.

Current atmospheric multiphase chemistry models include chemical mechanisms of different complexity with up to thousands of chemical reactions describing the transformation of inorganic and organic compounds, e.g., (Ervens et al., 2003a; Mouchel-Vallon et al., 2017; Tilgner et al., 2013; Woo and McNeill, 2015). However, they do not include the biodegradation of organics by bacteria despite the available data sets discussed above.

Cloud chemistry models often assume initially identical composition of all cloud droplets. While this might be a reasonable assumption for the chemical droplet composition due to internally mixed CCN and the phase transfer from the gas phase into all droplets, it is not appropriate for the distribution of bacteria. Due to their small number fraction of the total CCN concentration (0.001 %–0.1 %, e.g., Zhang et al., 2020), the fraction of cloud droplets that contain bacterial cells is small (<0.001). Thus, to explore biodegradation of organics in the atmospheric multiphase system, a realistic distribution within cloud droplet population needs to be assumed.

The aim of our study is to identify conditions under which biodegradation in clouds is significant in the atmosphere. Using a cloud multiphase box model, we explore the biological and chemical degradation of organic compounds over large parameter ranges of biodegradation activities, chemical rate constants, and Henry's law constants. We compare (1) the biodegradation rates in the aqueous phase to the chemical rates in both phases and (2) the fraction of organics consumed by biodegradation to that by chemical processes. The results of our sensitivity studies elucidate the organics for which biodegradation competes with chemical processes. Our study will give guidance for future experimental and modeling studies to further complete atmospheric models in order to more comprehensively describe organic degradation in the atmosphere.

2 Methods

2.1 Description of the multiphase box model

We use a multiphase box model with detailed gas- and aqueous-phase chemistry (75 species, 44 gas-phase reactions, 31 aqueous reactions) (Ervens et al., 2008).

The chemical aqueous-phase mechanism with rate constants is listed in Table S1 in the Supplement. The chemical gas-phase mechanism is based on the NCAR Master Mechanism (Aumont et al., 2000; Madronich and Calvert, 1989).

The two phases are coupled by 26 phase transfer processes which are described kinetically based on the resistance model by Schwartz (1986). The parameters describing the phase transfer of the soluble species are presented in Table S2. In addition, the initial mixing ratios of gas-phase species are included in Table S3. The equations for the mass transfer coefficient k_mt and the differential equations for the aqueous- and gas-phase concentrations can be found in the Supplement (Eq. S1–S3; Section “Description of phase transfer”) (Seinfeld and Pandis, 1998). In addition to the base chemical mechanism, we define one organic species “Org” that undergoes chemical radical reactions in the gas and aqueous phases and biodegradation by bacteria only in the aqueous phase in a small subset of the droplets as shown in Fig. 1. We consider a polydisperse droplet population of 263 droplets cm⁻³ in 11 size classes with drop diameters of $\mathrm{5}\mathrm{\mu }\mathrm{m}\le D_{\mathrm{droplet}}\le \mathrm{30}\mathrm{\mu }\mathrm{m}$ and a total liquid water content of $\text{LWC}=\mathrm{6.8}\times {\mathrm{10}}^{-\mathrm{7}}$ vol $/$ vol. Only one droplet size class includes bacterial cells (D_droplet=20 µm; N_droplet= cell concentration =0.01 cm(gas)⁻³). Thus, the cell concentration in the cloud water ($C_{\mathrm{cell},\mathrm{aq}}=\mathrm{1.5}\times {\mathrm{10}}^{\mathrm{7}}$ cell L⁻¹) is similar to that found in ambient clouds and as used in lab experiments (Vaïtilingom et al., 2013). The model simulations are performed for 600 s, which corresponds approximately to the droplet lifetime during one cloud cycle (Ervens et al., 2004).

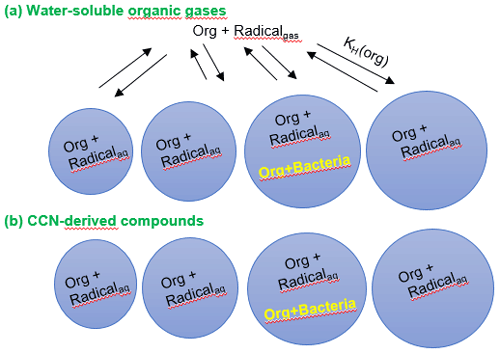
Figure 1 Schematic of the multiphase box model including chemical radical reactions in the gas and aqueous phases. Chemical reactions occur in both phases and in all droplets, whereas biodegradation processes only occur in the aqueous phase in a small fraction of droplets, depending on the assumed bacterial cell concentration in clouds. (a) Water-soluble organic gases that partition between the two phases; (b) CCN-derived compounds that only get processed in the aqueous phase.

We categorize four various compound groups based on their solubility in water and their Henry's law constant, and we distinguish the following:

1. Low-solubility species with K_H<10³ M atm⁻¹. Their dissolved fraction is <1 % for the liquid water content (LWC) of 0.68 g m⁻³ in our model.

2. Intermediate-solubility species with ${\mathrm{10}}^{\mathrm{3}}\mathrm{M}{\mathrm{atm}}^{-\mathrm{1}}<K_{\mathrm{H}}<{\mathrm{10}}^{\mathrm{6}}$ M atm⁻¹ with dissolved fractions of ∼1 %–95 % (LWC=0.68 g m⁻³).

3. High-solubility species with K_H>10⁶ M atm⁻¹ for which the dissolved fraction exceeds 95 % (LWC=0.68 g m⁻³).

4. Water-soluble CCN components which are dissolved in the aqueous phase upon dissolution of the condensation nucleus on which the cloud droplet grew. While these compounds have usually low volatility or are semivolatile, they also need to be water soluble to be available for aqueous-phase processes.

2.2 Kinetic data in the gas and aqueous phases

2.2.1 Chemical rates and Henry's law constants

Table 1 includes chemical rate constants for radical (OH, NO₃) reactions in the aqueous and gas phases for organic compounds, for which lab data on their biodegradation rates are available (Sect. 2.2.2). These data cover ranges of 10³≤k_chemaq [M⁻¹ s⁻¹] ≤10¹⁰ and ${\mathrm{10}}^{-\mathrm{17}}\le k_{\mathrm{chemgas}}$ [cm³ s⁻¹ ] $\le {\mathrm{10}}^{-\mathrm{10}}$, respectively, over which the model sensitivity studies in the following are performed.

Table 1 Literature data on chemical rate constants in the aqueous (k_OH,aq; $k_{{\mathrm{NO}}_{\mathrm{3}},\mathrm{aq}}$) and gas phases (k_OH,gas; $k_{{\mathrm{NO}}_{\mathrm{3}},\mathrm{gas}}$) and physical Henry's law constants (K_H) and effective Henry's law constants (K_H(eff)) for acids at pH=3 and pH=6, respectively.

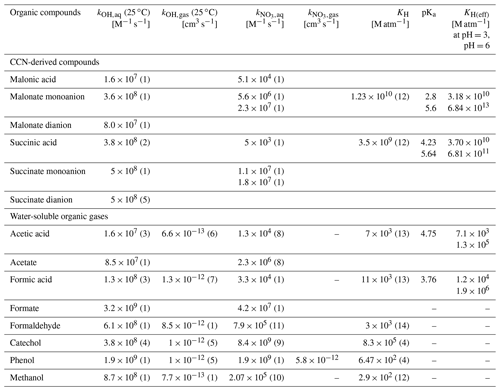
1: Herrmann (2003), 2: Cabelli et al. (1985), 3: Vaïtilingom et al. (2010), 4: Pillar et al. (2014), 5: Ervens et al. (2003c), 6: Butkovskaya et al. (2004), 7: Anglada (2004), 8: Exner et al. (1994), 9: Hoffmann et al. (2018), 10: Mezyk et al. (2017), 11: Gaillard De Sémainville et al. (2007), 12: Sander (2015), 13: Johnson et al. (1996), 14: Allou et al. (2011). “–” means no rate constant available.

In order to generalize our results for different radical concentrations, we present them in terms of chemical rates R_chem [s⁻¹], i.e., as the products of the rate constants k_chemaq and k_chemgas and radical concentrations:

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}& R_{\mathrm{chemaq}}\left[{\mathrm{s}}^{-\mathrm{1}}\right]={\displaystyle \frac{-\mathrm{d}(\text{Org}{)}_{\mathrm{radical}}}{\mathrm{d}t}}\\ & =k_{\mathrm{chemaq}}\left[\mathrm{L}{\mathrm{mol}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}\right]\times [\mathrm{radical}{]}_{\mathrm{aq}}\left[\mathrm{mol}{\mathrm{L}}^{-\mathrm{1}}\right],\end{array}\text{(2)}& {\displaystyle }\begin{array}{rl}& R_{\mathrm{chemgas}}\left[{\mathrm{s}}^{-\mathrm{1}}\right]={\displaystyle \frac{-\mathrm{d}(\text{Org}{)}_{\mathrm{radical}}}{\mathrm{d}t}}\\ & =k_{\mathrm{chemgas}}\left[{\mathrm{cm}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}\right]\times [\mathrm{radical}{]}_{\mathrm{gas}}\left[{\mathrm{cm}}^{-\mathrm{3}}\right].\end{array}\end{array}$$

Typical radical concentrations are on the order of 10⁻¹⁵ mol L⁻¹ for OH and NO₃ radicals in the aqueous phase of clouds (Arakaki et al., 2013; Herrmann, 2003) and 10⁶ and 10⁷–10⁸ cm⁻³ in the gas phase, respectively (Cantrell et al., 1997; Khan et al., 2008). The Henry's law constants for the same organic compounds are also listed in Table 1. They cover a range of 10²≤K_H [M atm⁻¹] ≤10⁹. For carboxylic acids, we also report effective Henry's law constants at pH=3 and pH=6 as being typical for cloud water.

2.2.2 Biodegradation rates

In the literature, experimental rates for metabolic processes are usually reported in units of [mol cell⁻¹ s⁻¹] (Table 2). We converted these rates into first-order loss rates $k_{\mathrm{bact}}^{\mathrm{1}\mathrm{st}}$ [s⁻¹] by dividing them by the ratio of the concentration of the organic compound [mol L⁻¹] to C_cell,aq [cell L⁻¹] used in the respective experiments. To obtain a value with units corresponding to chemical rate constants, this rate is divided by the constant model cell concentration ($C_{\mathrm{cell},\mathrm{aq}}=\mathrm{1.5}\times {\mathrm{10}}^{\mathrm{7}}$ cell L⁻¹) resulting in a range of ${\mathrm{10}}^{-\mathrm{18}}\le k_{\mathrm{bact}}$ [L cell⁻¹ s⁻¹] $\le {\mathrm{10}}^{-\mathrm{11}}$. This cell concentration is on the same order of magnitude as found in many clouds (Amato et al., 2007c).

Table 2 Summary of biodegradation rates from the literature and calculated rate constants (k_bact) for the consumption of small organic species by bacteria isolated from cloud water.

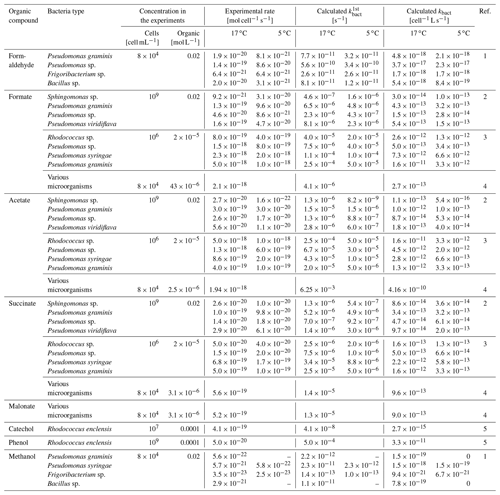
1: Husárová et al. (2011), 2: Vaïtilingom et al. (2010), 3: Vaïtilingom et al. (2011), 4: Vaïtilingom et al. (2013), 5: Jaber et al. (2020). Several experiments showed that temperature only had a small influence on the biodegradation rates that differed at most by a factor of 2 in experiments at 5 or 17 ^∘C (Husárová et al., 2011; Vaïtilingom et al., 2010, 2011).

Experiments with 17 different cloud bacteria in artificial cloud water with pH=5.0 and pH=6.5 also showed nearly identical results (Vaïtilingom et al., 2011). Similar results were shown by Razika et al. (2010), who demonstrated that biodegradation rates of phenol by Pseudomonas aeruginosa were very similar when incubated at pH=5.8, 7.0, and 8.0. When exposed to very broad ranges of external pH values, bacteria can control their intracellular pH (∼6.5–7) by internal buffering (Delort et al., 2017). As biodegradation occurs inside the cell, it takes place at these (nearly) neutral conditions. The efficiency of buffering decreases at extreme conditions, e.g., pH<2 or pH>10 (Guan and Liu, 2020). However, such a pH range is not representative for cloud water where more moderate pH values (∼3–6) are typically found (Deguillaume et al., 2014). Therefore, we do not consider a potential pH dependency of biodegradation rates in our model studies.

Similar to the chemical processes (Eqs. 1 and 2), we express the biological activity in terms of a rate:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{R}_{\mathrm{bact}}\left[{\mathrm{s}}^{-\mathrm{1}}\right]& ={\displaystyle \frac{-\mathrm{d}(\text{Org}{)}_{\mathrm{bact}}}{\mathrm{d}t}}=k_{\mathrm{bact}}\left[\mathrm{L}{\mathrm{cell}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}\right]\\ & \times C_{\mathrm{cell},\mathrm{aq}}\left[\mathrm{cell}{\mathrm{L}}^{-\mathrm{1}}\right],\end{array}\end{array}$$

where k_bact is the bacterial rate constant [L cell⁻¹ s⁻¹], and C_cell,aq is the concentration of bacteria in cloud water [cell L⁻¹].

2.3 Definition of model output parameters

2.3.1 Relative contributions to biodegradation and chemical loss rates

Several previous studies compared biodegradation and chemical rates in order to conclude on the potential importance of biological processes in clouds (Ariya et al., 2002; Husárová et al., 2011; Jaber et al., 2020; Vaïtilingom et al., 2011, 2013). Similarly, we define the relative contributions of the bacterial and the chemical processes in the two phases to the total loss rate of an organic compound.

$$\begin{array}{}\text{(4)}& {\displaystyle }R{{}^{\prime }}_{\mathrm{bact}}\left[\mathrm{mol}{\mathrm{L}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}\right]=R_{\mathrm{bact}}\left[{\mathrm{s}}^{-\mathrm{1}}\right]\times C_{\mathrm{org},\mathrm{aq}}\left[\mathrm{mol}{\mathrm{L}}^{-\mathrm{1}}\right],\text{(5)}& {\displaystyle }R{{}^{\prime }}_{\mathrm{chemaq}}\left[\mathrm{mol}{\mathrm{L}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}\right]=R_{\mathrm{chemaq}}\left[{\mathrm{s}}^{-\mathrm{1}}\right]\times C_{\mathrm{org},\mathrm{aq}}\left[\mathrm{mol}{\mathrm{L}}^{-\mathrm{1}}\right],\text{(6)}& {\displaystyle }R{{}^{\prime }}_{\mathrm{chemgas}}\left[{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}\right]=R_{\mathrm{chemgas}}\left[{\mathrm{s}}^{-\mathrm{1}}\right]\times C_{\mathrm{org},\mathrm{gas}}\left[{\mathrm{cm}}^{-\mathrm{3}}\right],\end{array}$$

where C_org,aq and C_org,gas are the concentration of water-soluble organic gases in the aqueous [mol L⁻¹] and gas phases [cm⁻³], respectively. Their relative contributions are then expressed as

$$\begin{array}{}\text{(7)}& {\displaystyle }{\text{fr}}_{\mathrm{bact}}\left[\mathit{\%}\right]={\displaystyle \frac{R{{}^{\prime }}_{\mathrm{bact}}}{R{{}^{\prime }}_{\mathrm{bact}}+R{{}^{\prime }}_{\mathrm{chemaq}}+R{{}^{\prime }}_{\mathrm{chemgas}}}}\times \mathrm{100},\text{(8)}& {\displaystyle }{\text{fr}}_{\mathrm{chemaq}}\left[\mathit{\%}\right]={\displaystyle \frac{R{{}^{\prime }}_{\mathrm{chemaq}}}{R{{}^{\prime }}_{\mathrm{bact}}+R{{}^{\prime }}_{\mathrm{chemaq}}+R{{}^{\prime }}_{\mathrm{chemgas}}}}\times \mathrm{100},\text{(9)}& {\displaystyle }{\text{fr}}_{\mathrm{chemgas}}\left[\mathit{\%}\right]={\displaystyle \frac{R{{}^{\prime }}_{\mathrm{chemgas}}}{R{{}^{\prime }}_{\mathrm{bact}}+R{{}^{\prime }}_{\mathrm{chemaq}}+R{{}^{\prime }}_{\mathrm{chemgas}}}}\times \mathrm{100},\end{array}$$

where these fractions always add up to 100 %. As CCN-derived compounds are only in the aqueous phase, ${\text{fr}}_{\mathrm{chemgas},\mathrm{CCN}\text{-}\mathrm{derived}}=\mathrm{0}$.

2.3.2 Contributions to total loss of organics by bacterial and chemical processes

While fr_bact, fr_chemaq, and fr_chemgas define the relative importance of the bacterial and chemical loss rates, they do not give quantitative information on the total loss of the organics. To define this sink strength, we introduce the parameter L_t [%] as

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{L}_{\mathrm{t}}\left[\mathit{\%}\right]& =\mathrm{100}-\left[{\displaystyle \frac{{\left[\text{Org}\right]}_{\mathrm{t}}}{{\left[\text{Org}\right]}_{\mathrm{0}}}}\times \mathrm{100}\right]\\ & =L_{\mathrm{bact}}+L_{\mathrm{chemaq}}+L_{\mathrm{chemgas}},\end{array}\end{array}$$

where [Org]₀ is the initial organic concentration (1 ppb) and [Org]_t is the organic concentration at time t (for most simulations: t=600 s). Accordingly, L_bact, L_chemaq and L_chemgas are the fractions [%] of organics consumed by bacteria and radicals in the aqueous and gas phases, respectively.

$$\begin{array}{}\text{(11)}& {\displaystyle }{L}_{\mathrm{bact}}\left[\mathit{\%}\right]={\text{fr}}_{\mathrm{bact}}\left[\mathit{\%}\right]\times L_{\mathrm{t}}\left[\mathit{\%}\right]÷\mathrm{100}\mathit{\%},\text{(12)}& {\displaystyle }{L}_{\mathrm{chemaq}}\left[\mathit{\%}\right]={\text{fr}}_{\mathrm{chemaq}}\left[\mathit{\%}\right]\times L_{\mathrm{t}}\left[\mathit{\%}\right]÷\mathrm{100}\mathit{\%},\text{(13)}& {\displaystyle }{L}_{\mathrm{chemgas}}\left[\mathit{\%}\right]={\text{fr}}_{\mathrm{chemgas}}\left[\mathit{\%}\right]\times L_{\mathrm{t}}\left[\mathit{\%}\right]÷\mathrm{100}\mathit{\%}.\end{array}$$

As both the fractions “fr” and L are expressed in percent, we divided by 100 % in Eqs. (11)–(13). Unlike the sum of fr_bact, fr_chemaq, and fr_chemgas that always yields 100 % (Eqs. 7–9), by definition L_t does not have to reach 100 %. As we only consider one cloud cycle in our simulations (t=600 s), the values of L_t, L_bact, L_chemgas, and L_chemaq are rather small (a few percent at most); however, it should be kept in mind that particles likely undergo multiple cloud cycles during their residence time in the atmosphere. Thus, the contribution of chemical and biological processes to the total loss for a specific organic species can be extrapolated for longer timescales based on our results. However, as one of the main goals of our study is to compare biodegradation to the better constrained chemical losses, our conclusions will be independent of the timescales.

3 Results and discussion

3.1 Relative loss rate of organics by biological processes (fr_bact)

3.1.1 fr_bact of water-soluble organic gases

We first compare the contributions of biodegradation and chemical losses to the total loss rate for water-soluble organic gases. In order to cover a representative parameter range of the physicochemical properties of the organic compound, we performed five simulations in which the full ranges of K_H and of R_chemaq over 8 orders of magnitude were explored (Sect. 2.2). The simulations differ by the assumptions of R_chemgas and R_bact that are kept constant in the individual model runs. For the results shown in Fig. 2a, b, and c, we applied $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{8}}$, 10⁻⁶, and 10⁻⁴ s⁻¹ and $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, respectively. For the three sets of simulations shown in Fig. 2b, d, and e, $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ and R_chemgas equal to 10⁻⁶, 10⁻⁵, and 10⁻⁴ s⁻¹ were assumed. Thus, in total three values each for R_chemgas and R_bact are discussed in the following.

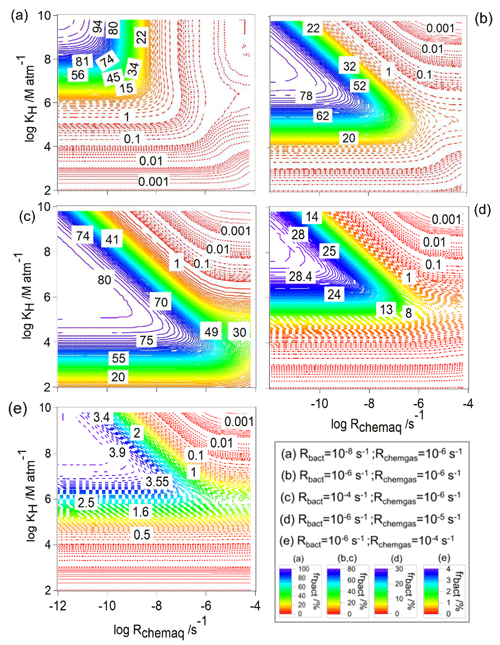
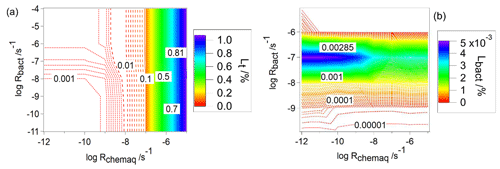
Figure 2 Relative contribution of bacteria to the total loss rate of organics (fr_bact, Eq. 7) as a function of R_chemaq and K_H. All figure panels have the same scales on the ordinates and abscissas. The simulations were performed for constant values of R_bact and R_chemgas; their values are indicated in the box at the bottom right.

In general, for all combinations of R_chemgas and R_bact, the highest fr_bact is predicted for organics with the highest solubility (K_H [M atm⁻¹] ≥10⁸) and lowest chemical reaction rate in the aqueous phase (R_chemaq [s⁻¹] $\le {\mathrm{10}}^{-\mathrm{11}}$). For the lowest biological activity ($R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{8}}$ s⁻¹, Fig. 2a), fr_bact reaches a maximum value of ∼100 %. For higher biological activity ($R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ and 10⁻⁴ s⁻¹), fr_bact is always smaller and only reaches at most ∼80 % (Fig. 2b and c). This trend seems counterintuitive as for the highest R_bact the highest importance of biodegradation may be expected. We will explore the reasons for this further in Sect. 3.1.2 where we compare loss rates in individual droplets as a function of time.

The comparison of Fig. 2b and c shows that the parameter ranges, for which fr_bact has the maximum value, are broader for higher R_bact: when $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ (Fig. 2b), fr_bact is ∼80 % within the ranges of $\sim {\mathrm{10}}^{\mathrm{7}}\le K_{\mathrm{H}}$ [M atm⁻¹] $\le \sim {\mathrm{10}}^{\mathrm{9}}$ and ${\mathrm{10}}^{-\mathrm{12}}\le R_{\mathrm{chemaq}}$ [s⁻¹] $\le {\mathrm{10}}^{-\mathrm{10}}$; i.e., both R_chemaq and K_H span about 2 orders of magnitude. For $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹ (Fig. 2c), these ranges are $\sim {\mathrm{10}}^{\mathrm{5}}\le K_{\mathrm{H}}$ [M atm⁻¹] $\le \sim {\mathrm{10}}^{\mathrm{9}}$ and ${\mathrm{10}}^{-\mathrm{12}}\le R_{\mathrm{chemaq}}$ s⁻¹] $\le {\mathrm{10}}^{-\mathrm{9}}$, i.e., wider by about 2 and 1 orders of magnitude, respectively.

This widening of the parameter space can be explained by the contributions of the chemical processes to the total organic loss rate, i.e., fr_chemaq and fr_chemgas (Figs. S1 and S2 in the Supplement); for the two values of R_bact, fr_chemaq is highest (>80 %) for a combination of (i) $\sim {\mathrm{10}}^{\mathrm{5}}\le K_{\mathrm{H}}$ [M atm⁻¹] ≤10⁹ and $\sim {\mathrm{10}}^{-\mathrm{9}}\le R_{\mathrm{chemaq}}$ [s⁻¹] $\le {\mathrm{10}}^{-\mathrm{5}}$, or of (ii) low or intermediate solubility ($\sim {\mathrm{10}}^{\mathrm{3}}\le K_{\mathrm{H}}$ [M atm⁻¹] $\le \sim {\mathrm{10}}^{\mathrm{5}}$) and high chemical aqueous-phase reactivity (${\mathrm{10}}^{-\mathrm{6}}\le R_{\mathrm{chemaq}}$ [s⁻¹] $\le {\mathrm{10}}^{-\mathrm{5}}$). These trends are due to the predominant partitioning of highly soluble organics to the aqueous phase (>90 % for K_H≥10⁶ M atm⁻¹). If R_chemaq is low, the organics do not undergo efficient chemical processes in the aqueous phase. Therefore, fr_bact is highest for this parameter combination. The comparison of the results for $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ and three values of R_chemgas (Fig. 2b, d, e) shows a decrease in the maximum value of fr_bact from 80 % (Fig. 2b) to 4 % (Fig. 2e) for similar ranges of K_H and R_chemaq because of the dependence of fr_bact on fr_chemgas: for compounds with highest R_chemgas, the dominant loss is the gas-phase reaction, leading to a high fr_chemgas and consequently to a lower fr_bact (Fig. 2e). Therefore, the parameter ranges of K_H and R_chemaq, where fr_bact is maximum, do not change for different R_chemgas but decrease when the gas-phase chemistry dominates the loss of the organic species.

Overall, the variation in fr_bact as a response to changes in R_chemaq, R_chemgas, and K_H shows different sensitivities: for example, for organics with K_H=10⁶ M atm⁻¹, $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{9}}$ s⁻¹, and $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, fr_bact is ∼8 % when $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{8}}$ s⁻¹ (red area in Fig. 2a). This fraction increases to fr_bact∼73 %, i.e., by a factor of ∼9, when $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ (blue area in Fig. 2b) and approaches ∼80 % when $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹ (purple area in Fig. 2c). Similarly, for organics with K_H∼10⁶ M atm⁻¹, $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{9}}$ s⁻¹, and $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, an increase in R_chemgas from 10⁻⁶ s⁻¹ (Fig. 2b) to 10⁻⁵ s⁻¹ (Fig. 2d) and 10⁻⁴ s⁻¹ (Fig. 2e) decreases fr_bact from 73 % to 23 % and 3 %, respectively. Based on these nonlinear trends, one can hypothesize that (i) a change in R_bact and/or R_chemgas translates into a less than proportional change in fr_bact, and (ii) an increase in R_bact might translate into a larger change in fr_bact than an increase in R_chemgas by the same factor. Therefore, fr_bact is more sensitive to a change in R_bact than in R_chemgas. Given that R_chemgas only differs by about 2 orders of magnitude for most organics relevant in the atmospheric multiphase system (Table 1), we conclude that fr_bact may be largely independent of the gas-phase chemical reactivity. Additional sensitivity studies (not shown) reveal that using combinations of R_bact and R_chemgas other than those in Fig. 2 result in slightly different locations of the maximum of fr_bact but in similar shapes and widths of parameter spaces, for which fr_bact is maximum. Therefore, our conclusions on the sensitivities seem robust for wide parameter ranges and combinations.

3.1.2 fr_bact of CCN-derived compounds and comparison to water-soluble organic gases

For CCN-derived compounds, the analysis of fr_bact is limited to exploring the ranges of R_bact and R_chemaq (Fig. 1). Similar to the findings based on Fig. 2a, b, and c for water-soluble organic gases, highest values of fr_bact are predicted for intermediate values of ${\mathrm{10}}^{-\mathrm{10}}\le R_{\mathrm{bact}}$ [s⁻¹] $\le {\mathrm{10}}^{-\mathrm{7}}$ and R_chemaq [s⁻¹] $\le {\mathrm{10}}^{-\mathrm{10}}$; for the highest biological activity ($R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹), fr_bact is nearly zero (Fig. 3). In order to understand the reasons for these trends, we explore in the following the variables determining fr_bact (Eq. 7).

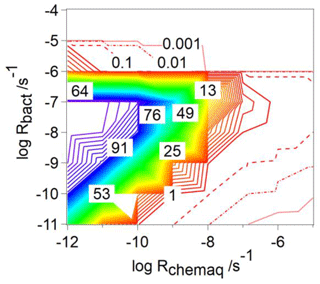
Figure 3 Relative contribution of bacteria to the total loss rate of CCN-derived organics (fr_bact, Eq. 7) as a function of R_bact [s⁻¹] and R_chemaq [s⁻¹].

As shown in Fig. 1, only one drop size class in the model contains bacteria; in all other droplets, the bacterial activity is zero, and only chemical processes occur. In Fig. 4a, we show the evolution of the organic concentration of CCN-derived compounds in the bacteria-containing droplets ([Org]_bact) over 600 s, $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{11}}$ s⁻¹, and $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, i.e., for relatively low chemical reactivity in both phases. It is obvious that for the highest R_bact (10⁻⁴ s⁻¹), the organics are immediately depleted, whereas for lower biological activity ($R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹), [Org]_bact decreases more slowly or even stays constant ($R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{8}}$ s⁻¹). As for the highest R_bact, the concentration approaches zero after ∼10 s, $R{{}^{\prime }}_{\mathrm{bact}}$ (Eq. 4) becomes negligible and fr_bact approaches 0 % (Eq. 7, Fig. 4c). In Fig. 4b, we show the equivalent to Fig. 4a but for water-soluble organic gases and for three K_H values (10², 10⁵, and 10⁹ M atm⁻¹). For the lowest R_bact and all K_H values, [Org]_bact stays also nearly constant at the initial value as the organics are not efficiently consumed in any droplet. For the intermediate and highest R_bact (10⁻⁶ and 10⁻⁴ s⁻¹) and K_H=10⁹ M atm⁻¹, [Org]_bact remains higher than for the CCN-derived compounds and levels off at t∼300 s. For these two, R_bact, [Org]_bact significantly drops by several orders of magnitude. However, unlike for the CCN-derived compounds, fr_bact does not drop to ∼0 % but levels off at ∼70 % for K_H=10⁹ M atm⁻¹ (Fig. 4d). For these two R_bact and K_H=10⁵ M atm⁻¹, [Org]_bact stays also nearly constant over the whole simulation time (600 s) and is higher for lowest R_bact=10⁻⁶ s⁻¹ (Fig. 4b). However, fr_bact is higher for the highest $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹ (Fig. 4d). Fig. S3a and b show the ratio of the organic concentrations in bacteria-containing and bacteria-free droplets of the same diameter (20 µm). For these conditions of low R_chemgas and R_chemaq, the concentration ratio is near unity for both CCN-derived compounds and water-soluble organic gases (K_H=10⁵ and 10⁹ M atm⁻¹) when $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{8}}$ s⁻¹. For higher $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ and K_H=10⁵ and 10⁹ M atm⁻¹, the concentration ratio for the water-soluble organic gases is near unity and 10⁻³, respectively, and for the CCN-derived compounds it is much lower ($\sim {\mathrm{10}}^{-\mathrm{6}}$). For $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, this ratio is also higher for K_H=10⁵ M atm⁻¹ than for K_H=10⁹ M atm⁻¹ ($\sim {\mathrm{10}}^{-\mathrm{1}}$ and 10⁻⁵, respectively) and $\ll {\mathrm{10}}^{-\mathrm{11}}$ for CCN-derived compounds. It can be summarized that (1) for water-soluble organic gases the concentration in bacteria-containing droplets is higher for compounds with intermediate solubility (K_H∼10⁵ M atm⁻¹) than for highly soluble ones (K_H=10⁹ M atm⁻¹), and (2) the concentration in bacteria-containing droplets is predicted to be always smaller for the CCN-derived compounds than for the water-soluble organic gases with at least intermediate solubility.

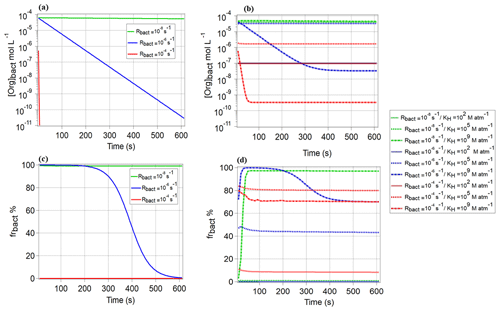
Figure 4 Comparison of the organic concentration in the bacteria-containing droplets [Org]_bact [mol L⁻¹] for (a) CCN-derived compounds, (b) water-soluble organic gases (K_H=10², 10⁵ and 10⁹ M atm⁻¹), and (c, d) the resulting fr_bact for these compounds. Results are shown for $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{8}}$, 10⁻⁶, and 10⁻⁴ s⁻¹; $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹; and $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{11}}$ s⁻¹.

This difference between water-soluble organic gases and CCN-derived compounds can be explained by the schematic in Fig. 5: the insets in the droplets schematically depict the temporal evolution of the organic concentrations as shown in Fig. 4. The efficient consumption of organics by bacteria in the bacteria-containing droplets (I) leads to a significant decrease in the organic concentration in these droplets. For water-soluble organic gases, this results in a strong deviation from thermodynamic equilibrium of the gas- and aqueous-phase concentrations, as defined by Henry's law (II). As a consequence, organics diffuse from the gas phase into the bacteria-containing droplets (III). As this diffusion leads to a decrease in the gas-phase concentration, thermodynamic equilibrium between the gas phase and the bacteria-free droplets is not fulfilled anymore (IV), resulting in a concentration gradient between these droplets and the gas phase. Finally, organics from the bacteria-free droplets evaporate to replenish the gas-phase concentration (V) and eventually the organic concentration in the bacteria-containing droplets. These coupled equilibria between the gas phase and droplets lead to a continuous replenishment of water-soluble organic gases in the bacteria-containing droplets. However, since all processes are associated with different timescales (evaporation, gas-phase diffusion, transport through the gas $/$ water interface, loss by chemical and biological processes in the aqueous phase; Schwartz, 1986), thermodynamic equilibrium is not instantaneously established. For organics with low K_H (∼10² M atm⁻¹), the fraction of dissolved material is very small; therefore, organics are mostly consumed in the gas phase and only a small fraction partitions to the droplets. For intermediate K_H(∼10⁵ M atm⁻¹), the consumption of the organics in the bacteria-containing droplets is fast, leading to large concentration gradients between the phases. Consequently, the evaporation and diffusion rates are high; thus, the replenishment of the bacteria-containing droplets by the organics is most efficient. Extremely highly soluble organics (K_H∼10⁹ M atm⁻¹) are nearly completely dissolved in the aqueous phase; thus, only a small fraction will be consumed by the bacteria, leading to relatively smaller concentration gradients between gas and bacteria-containing droplets (process I and Fig. 4b) and therefore to less efficient replenishment and longer timescales to establish thermodynamic equilibrium. Thus for such organics, the organic consumption by bacteria is relatively less efficient. For CCN-derived compounds, only process I occurs as there is no coupling to the gas phase; thus, only the amount of organics that is initially dissolved in the bacteria-containing droplets can be consumed.

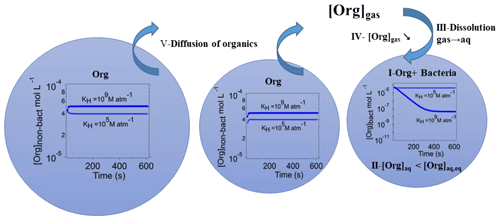
Figure 5 Schematic of the partitioning of water-soluble organic gases between the bacteria-containing and bacteria-free droplets and the gas phase: the inset figures show the temporal evolution of the organic concentration in the bacteria-containing droplets ([Org]_bact) and bacteria-free droplets ([Org]_non−bact) for water-soluble organic gases with K_H=10⁵ and 10⁹ M atm⁻¹.

3.2 Total loss of the organic compound (L_t) and sinks of organics by bacteria (L_bact)

3.2.1 L_t for water-soluble organic gases

While the analysis of fr_bact in Sect. 3.1 quantifies the relative importance of the biological and chemical processes for the organic loss, we explore in the following the absolute loss of these processes (L_t, Eq. 10).

Unlike the sum of fr_bact, fr_chemaq, and fr_chemgas that always yields 100 %, the ranges of L_t that will be discussed in the following are rather small, i.e., ${\mathrm{10}}^{-\mathrm{4}}\le L_{\mathrm{t}}$ [%] ≤12, given that we only simulate approximately one cloud cycle (600 s). Figure 6 shows L_t for the same parameters (R_chemgas, R_bact) as in Fig. 2. For all combinations of R_bact and R_chemgas, the highest values of L_t are predicted for organics with highest K_H and R_chemaq. Generally, all panels show the highest values for L_t for the highest R_chemaq, but in all panels there is a small maximum for low-to-intermediate K_H and nearly independent of R_chemaq. This feature becomes more prominent with increasing R_chemgas (10⁻⁶, 10⁻⁵, 10⁻⁴ s⁻¹, Fig. 6c–e), with the overall highest L_t (∼12 %) for the highest R_chemgas and lowest K_H. Comparing Fig. 6a, b, and c, for which the model conditions only differ in R_bact, a small increase in L_t from 1.2 % to 1.6 % at intermediate K_H values can be seen. We focus on these trends in Sect. 3.2.2 where L_bact, i.e., the contribution of the bacterial process to L_t, will be explored. Comparing the contours of the three panels shows that L_t is additive as with increasing R_bact, L_t reaches a maximum (1.6 %) at K_H of ∼10⁴ M atm⁻¹, and R_chemaq is $\sim {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹ (Fig. 6c). Similar to our findings for fr_bact (Sect. 3.1.1), we also see in the trends of L_t that a change of several orders of magnitude in R_bact or R_chemgas translates into a smaller change in L_t. Thus, one can conclude that L_t has a similarly low sensitivity to the various parameters as fr_bact.

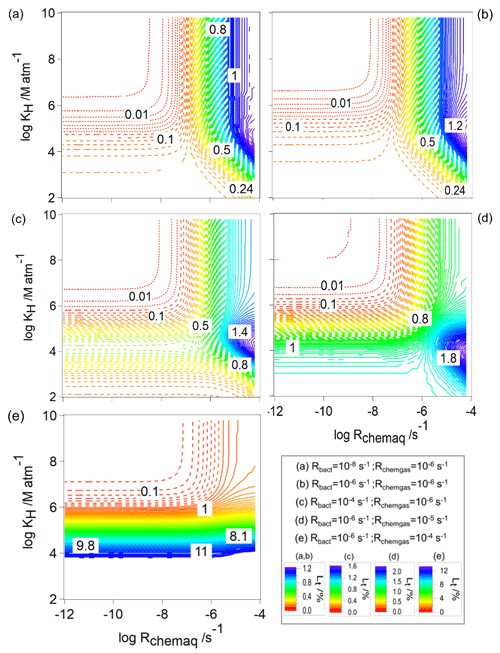
Figure 6 The total loss of water-soluble organic gases (L_t, Eq. 10) as a function of R_chemaq and K_H. All figure panels have the same scales on the ordinates and abscissas. The simulations were performed for constant values of R_bact and R_chemgas; their values are indicated in the box at the bottom right.

3.2.2 L_bact for water-soluble organic gases

To understand the contribution of bacteria (L_bact) in the total consumption of the organics (L_t), we explore L_bact for the same values of R_bact and R_chemgas as in Figs. 2 and 6 (Fig. 7). As suggested in the comparison of Fig. 6a–c, the contribution of the organic loss by bacteria increases with increasing R_bact (Fig. 7a–c); i.e., L_bact increases from 0.025 % to 0.45 %.

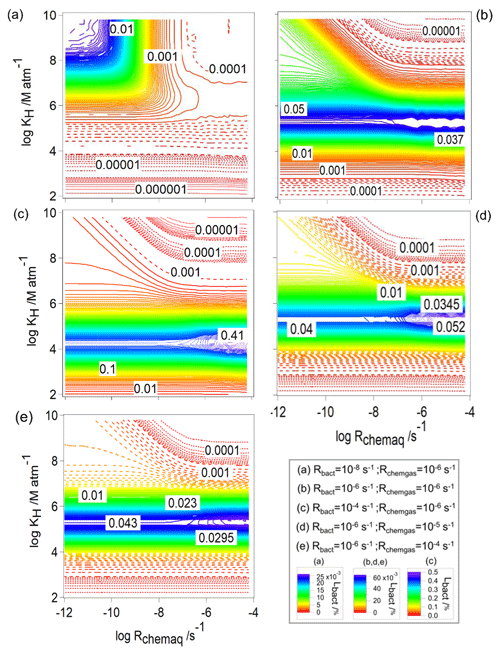
Figure 7 The loss of water-soluble organic gases by bacteria (L_bact, Eq. 11) as a function of R_chemaq and K_H. All figure panels have the same scales on the ordinates and abscissas. The simulations were performed for constant values of R_bact and R_chemgas; their values are indicated in the box at the bottom right.

For all conditions, there is a contribution of L_bact∼0.025 % for the lowest R_chemaq and highest K_H, i.e., when chemical activity in the aqueous phase is lowest and solubility is highest. However, when $R_{\mathrm{bact}}\ge {\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, the maximum value of L_bact is predicted for a narrow range of $\sim {\mathrm{10}}^{\mathrm{4}}\le K_{\mathrm{H}}$ [M atm⁻¹] ≤10⁶, nearly independent of R_chemaq. The highest value of L_bact (0.4 %) is observed for highest R_bact ($R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹; Fig. 7c). This corresponds to nearly a quarter of the total loss (L_t≤1.4 %; Fig. 6c). To further explore why L_bact has a maximum for these intermediate values of K_H, we compare L_bact for K_H=10², 10⁵, and 10⁹ M atm⁻¹ for $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, and $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{11}}$ s⁻¹, i.e., for the same conditions as the examples in Fig. 4b and d. When K_H is low (10² M atm⁻¹), a very small fraction (0.16 %) of the organics is dissolved; thus, L_bact is lowest. For K_H=10⁹ M atm⁻¹ (Fig. 4b, blue line), [Org]_aq is low because – as mentioned before – it is consumed quickly and the transport from the gas phase is not fast enough, resulting in a low L_bact. For K_H∼10⁵ M atm⁻¹ (Fig. 4b, blue line), [Org]_aq is relatively high, because the thermodynamic equilibrium can be more quickly established and thus L_bact is high.

For each set of conditions, i.e., in the various panels of Fig. 7, the maximum value L_bact is independent of R_chemaq and does not greatly vary for the same R_bact ($L_{\mathrm{bact},\max }\sim \mathrm{0.05}$ %) (Fig. 7b, d, e). This is unlike the trends of fr_bact (Fig. 2) that show a decrease with increasing R_chemaq. By definition (Eq. 7), fr_bact and fr_chemaq are coupled; thus, an increase in one value causes a decrease in the other. Contrary, L_bact is independent of the chemical contributions as it describes the absolute consumption rate related to the initial organic concentration. Comparing the trends in Figs. 2 and 7, it is evident that the maximum of L_bact (intermediate K_H, independent of R_chemaq) does not coincide with the parameter ranges for which fr_bact is maximum (highest K_H, lowest R_chemaq). This finding highlights that previous estimates on the importance of biodegradation that were solely based on comparing rates (e.g., Jaber et al., 2020) are misleading. In these studies, it was concluded that biodegradation for highly soluble compounds is likely most important.

3.2.3 L_t and L_bact for CCN-derived compounds

For CCN-derived compounds, the analysis of trends in L_t is simpler as it is the sum of L_bact and L_chemaq only. L_t increases with increasing R_chemaq, nearly independently of R_bact up to a maximum value of ∼1.1 % (Fig. 8a). Comparison of L_t to L_bact (Fig. 8b) shows that the consumption by bacteria is smaller by several orders of magnitude ($L_{\mathrm{bact},\max }=\mathrm{0.005}$ %); thus, it is not a major contribution to the total loss. Figures 3 and 8b exhibit similar contours; i.e., after 600 s simulation time, the highest relative and absolute contributions are predicted for CCN-derived compounds with intermediate bacterial and low aqueous-phase chemical activity. The trend in Fig. 8b can also be explained by the findings in Fig. 4: after 600 s, the CCN-derived compounds in the bacteria-containing droplets are completely depleted for high R_bact; thus, both fr_bact and L_bact approach zero. Since there is no exchange with the gas phase or other replenishment of CCN-derived compounds into bacteria-containing droplets, L_bact,maximum of these compounds can be estimated: if one assumes in a first approximation that the mass fraction of CCN-derived compounds in the initial CCN population scales with the liquid water content associated with the resulting droplets, one can conclude that at most 0.0065 % (= LWC(bacteria-containing droplets $/$ total LWC) can be consumed.

Figure 8 Predicted loss of CCN-derived species as a function of R_chemaq and R_bact, (a) total loss (L_t), (b) loss by biodegradation (L_bact).

3.3 Comparison of our model approach to simplified assumptions

3.3.1 Simplified model approaches

The results in Fig. 4 demonstrate that the coupled equilibria between the gas phase and the droplets with and without bacteria need to be considered, in order to correctly predict the organic sink strength by bacterial processes in the multiphase system. Previous estimates of the role of biodegradation in the multiphase system have been performed assuming simplified assumptions. (i) For the bulk model, biodegradation and chemical rates were compared in a bulk aqueous phase (Vaïtilingom et al., 2013) or in a population of droplets with identical composition (Jaber et al., 2020). However, since the bacterial cell concentration (∼0.01 cells cm⁻³) in clouds is much smaller than the droplet number concentration (=263 droplets cm⁻³, in our model), this results in a ratio of $\sim \mathrm{4}\times {\mathrm{10}}^{-\mathrm{5}}$ bacterial cells per droplet. (ii) For the low-LWC model, the multiphase system is considered with only droplets that contain an intact bacterial cell, resulting in a liquid water content of $\sim {\mathrm{10}}^{-\mathrm{11}}$ vol $/$ vol, similar to Fankhauser et al. (2019). In Fig. 9, we schematically contrast these approaches. While it is clear that none of the two approaches reflect the conditions as encountered in real clouds, we will analyze in the following the extent to which these simplified model approaches lead to similar results as predicted in our detailed model discussed so far (Fig. 1).

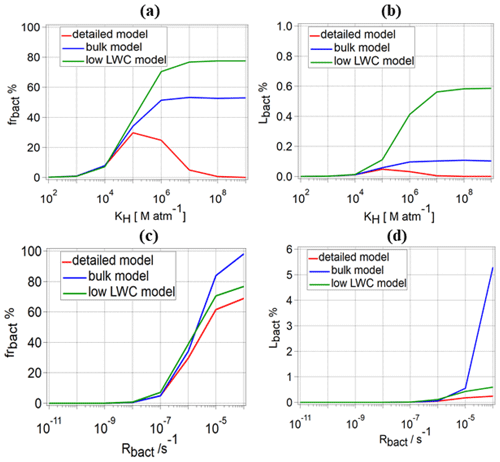
Figure 9 Comparison of (a) fr_bact and (b) L_bact for water-soluble organic gases for three different model approaches: detailed model (red line), bulk approach (blue line), and low-LWC model (green line) for different values of K_H, $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{7}}$ s⁻¹, $R_{\mathrm{bact}.}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, and $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹; (c) fr_bact and (d) L_bact for water-soluble organic gases for the same approaches for different R_bact, one value for K_H=10⁵ M atm⁻¹, two values for R_chemaq (10⁻⁷ s⁻¹, 10⁻¹¹ s⁻¹), and $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹.

3.3.2 Comparison of fr_bact, L_t, and L_bact using simplified model approaches

For water-soluble organic gases, we compare fr_bact and L_bact for the three model approaches for the full range of K_H values, $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{7}}$ s⁻¹, and $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ (Fig. 9a, b). For 10²≤K_H [M atm⁻¹] ≤10⁴, only a small difference in fr_bact and L_bact is predicted for a given R_bact because of the low organic fraction in the aqueous phase. For all K_H values, fr_bact is the highest for the low-LWC model approach, because it only considers bacteria-containing droplets and thus neglects the aqueous-phase chemistry in a majority of droplets; therefore, fr_chemaq is significantly underestimated. Consequently, the competition between biodegradation and chemical degradation takes place only in the bacteria-containing droplets, and fr_bact is the highest.

For 10⁵≤K_H [M atm⁻¹] ≤10⁷, L_bact values based on the bulk and low-LWC models are higher than for the detailed model. For example, for K_H=10⁶ M atm⁻¹, L_bact values in the low-LWC model are 4.3 and 12.7 times higher than in the bulk and our detailed models, respectively. For the highest K_H (10⁷≤K_H [M atm⁻¹] ≤10⁹), the comparison of L_bact for $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ shows that both simplified model approaches overestimate L_bact by up to several orders of magnitude (Fig. 9b) for K_H=10⁸ M atm⁻¹ ($L_{\mathrm{bact},\mathrm{lowLWC}}=\mathrm{5.8}\times {\mathrm{10}}^{-\mathrm{1}}$ %; $L_{\mathrm{bact},\mathrm{bulk}}=\mathrm{1.07}\times {\mathrm{10}}^{-\mathrm{1}}$ %; $L_{\mathrm{bact},\mathrm{detailed}}=\mathrm{6.12}\times {\mathrm{10}}^{-\mathrm{4}}$ %). For organics with intermediate or low solubility, the differences between the three models are smaller. Given that we identified biodegradation to be most important for organics with intermediate solubility (Sect. 3.2.2), we compare fr_bact and L_bact for K_H=10⁵ M atm⁻¹, $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, and $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{7}}$ s⁻¹ as a function of R_bact (Fig. 9c, d). Similar to the results from the detailed model (Sect. 3.1.2), the low-LWC approach leads to fr_bact<100 % at t=600 s, because organics are efficiently consumed in the bacteria-containing droplets. However, for the bulk model, fr_bact is ∼100 % for the highest R_bact, even after 600 s, because bacterial processes take place in all droplets with a reduced efficiency as compared to the processes in the single droplet in the detailed model. Consequently, the concentration of organics in all droplets remains relatively high for extended timescales, even for the highest R_bact. Figure 9d shows the dependence of L_bact between the three models on R_bact: for $R_{\mathrm{bact}}\le {\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, L_bact is similar for the detailed and the bulk models ($\sim \mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$ %), whereas it is twice as high for the low-LWC model ($\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$ %). However, for the highest R_bact (10⁻⁴ s⁻¹), the highest L_bact is predicted by the bulk approach (∼5 %) which is more than 2 orders of magnitude higher than predicted from the detailed model (∼0.2 %). The similarity of L_bact between the detailed and the bulk models for $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ is due to the efficient replenishment of organics with intermediate K_H (Fig. 5); i.e., the amounts of organics available to bacteria are similar. However, for the highest R_bact, L_bact is much higher for the bulk model, because the consumption of the organics occurs without any kinetic limitations of the various transport processes that are only presented by the detailed model.

For the CCN-derived compounds, we compare fr_bact and L_bact for different R_bact and two R_chemaq (10⁻¹¹ and 10⁻⁷ s⁻¹) (Fig. S4a, b). For $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{8}}$ s⁻¹ and $R_{\mathrm{chemaq}}={\mathrm{10}}^{-\mathrm{11}}$ s⁻¹, fr_bact is about 99 % for all three approaches, which is not the case for highest R_chemaq (10⁻⁷ s⁻¹) (Fig. S4a). However, for $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, fr_bact is ∼0 % (at t=600 s) in the detailed model for both R_chemaq values for the reasons explained in Sect. 3.1.2, whereas fr_bact∼99 % for the bulk model because of continuous bacterial activity in all droplets. Moreover, fr_bact and L_bact are always 100 % for the low-LWC model. The role of aqueous-phase chemistry in the multiphase system is predicted to be negligible by the low-LWC approach as it is equally reduced as the LWC, leading to the dominance of the bacterial processes. If we compare L_bact for the bulk (blue line in Fig. S4b) and the detailed models (red line), one finds an increasing discrepancy between the model results: for the lowest R_bact considered here (10⁻⁸ s⁻¹) and the two R_chemaq values : 10⁻¹¹ s⁻¹ and 10⁻⁷ s⁻¹, respectively, L_bact for the bulk model is predicted to be ∼9.3 and 11.6 times higher than for the detailed model. For $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ and the two R_chemaq values, this factor increases to 2.5×10⁴ and 1.3×10⁶. For the highest $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, L_bact between the bulk and our detailed model after 600 s of simulation cannot be reasonably compared as in the detailed model after <100 s. The CCN-derived compounds in the bacteria-containing droplets are completely depleted for high R_bact; thus, no further consumption occurs (L_bact∼0 %) (Sect. 3.2.3). In the bulk model, the organic consumption by bacteria is predicted to occur continuously as the bacteria could, in theory, consume all organics on “infinite” timescales.

Our model comparison shows that for water-soluble organic gases and CCN-derived compounds, both the bulk and low-LWC models overestimate the importance of biodegradation, i.e., both fr_bact and L_bact. The biases are highest in the bulk approach for high R_bact and high K_H. Also, the comparison shows that the bulk approach leads to wrong conclusions in terms of the importance of biodegradation as a function of the solubility of organics. Our model analysis emphasizes that a detailed model is needed in order to correctly represent the partitioning of water-soluble organic gases between the gas phase and the droplets with and without bacteria.

4 Atmospheric implications: how important is biodegradation for organic compounds identified in cloud water?

4.1 L_bact of organic cloud water constituents

Based on our model sensitivity studies discussed in the previous sections and the literature data for cloud water organics summarized in Tables 1 and 2, we assess the importance of biodegradation of these compounds. The contour plots representations in Fig. 10 are the same as in Fig. 7a–c (water-soluble organic gases) and Fig. 8b (CCN-derived compounds). The added symbols correspond to L_bact of the compounds in Table 1 for a single R_bact in each figure panel. Given that R_chemgas only differs by about 2 orders of magnitude for the organics in Table 1, we present the results with $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹. The reasoning for the assumed single R_bact is further discussed in Sect. 4.2.

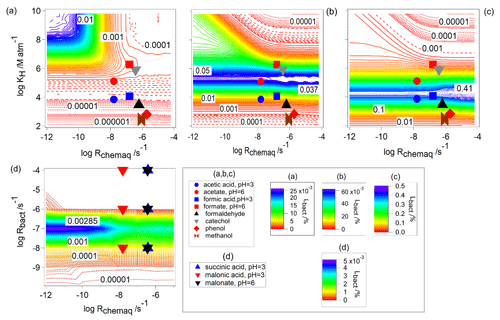
Figure 10 (a–c) L_bact for water-soluble organic gases. The contour plots are identical to Fig. 7a–c. Symbols show combinations of R_chemaq and K_H for specific compounds (Table 1). For all simulations, $R_{\mathrm{chemgas}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹; (a) $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{8}}$ s⁻¹, (b) $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, (c) $R_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, and (d) L_bact for CCN-derived organics (Table 1). The contour plot is identical to Fig. 8b. Note that R_chemaq and R_bact for succinate (pH=6) are nearly identical to the values for succinic acid (pH=3) and were therefore omitted from the figure.

For the carboxylic acids, two values are shown, i.e., K_H(eff) and R_chemaq at pH=3 and 6 (Table 3). R_chemaq at the two pH values are calculated based on the rate constants k_chemaq as a function of the proportion of the acidic and anionic forms depending on pH and pK_a and the rate constants of the OH reactions for the acid and anion. Similarly, rate constants for other (e.g., NO₃) reactions could be derived using data summarized in Table 1.

Table 3 k_bact [cell L⁻¹] calculated from literature data, theoretical C_cell [cell L⁻¹] based on Eq. (14), and the ratio $L_{\mathrm{bact}}/L_{\mathrm{t}}$ for three R_bact values (10⁻⁸, 10⁻⁶ and 10⁻⁴ s⁻¹) for water-soluble organic gases and CCN-derived compounds. Values with ^* show bacterial concentrations that are realistic for cloud water.

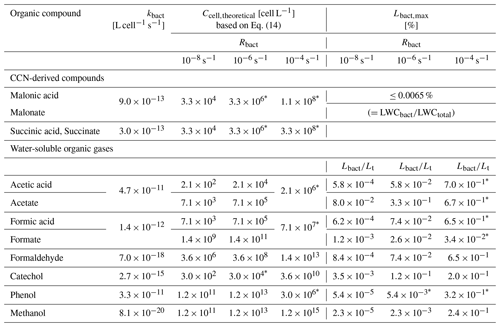
As discussed in Sect. 2.2.2 and by Vaïtilingom et al. (2013), the bacterial activity does not show any systematic difference in this pH range; therefore, we only show one R_bact value for each acid. For the lowest R_bact (10⁻⁸ s⁻¹), the physicochemical properties (K_H(eff), R_chemaq) of the water-soluble organic gases (acetic acid $/$ acetate, formic acid $/$ formate, formaldehyde, catechol, phenol and methanol) are in the range where L_bact has its minimum values of $\sim {\mathrm{10}}^{-\mathrm{6}}\le L_{\mathrm{bact}}$ [%] $\le {\mathrm{10}}^{-\mathrm{3}}$ (Fig. 10a).

For higher R_bact (10⁻⁶ s⁻¹, Fig. 10b), which implies higher cell concentration in the cloud, highly soluble compounds, such as acetate and catechol, are in the range where L_bact shows a maximum ($\sim \mathrm{0.04}\le L_{\mathrm{bact}}$ [%] ≤0.06) and less soluble compounds such as formic acid, formate, and formaldehyde (10⁴<K_H(eff) [M atm⁻¹] <10⁶) are in the area where $\sim \mathrm{0.02}\le L_{\mathrm{bact}}$ [%] ≤0.04. Less soluble compounds (K_H(eff)<10³ M atm⁻¹), such as acetic acid, phenol, and methanol are in the area of much lower L_bact ($\sim {\mathrm{10}}^{-\mathrm{5}}\le L_{\mathrm{bact}}$ [%] $\le {\mathrm{10}}^{-\mathrm{3}}$). As discussed in Sect. 3.2, the maximum value of L_bact increases with higher R_bact and is predicted for compounds with moderate K_H(eff) (Fig. 5). Therefore, at the highest assumed R_bact (10⁻⁴ s⁻¹), the less soluble compounds formic acid, formaldehyde, and acetic acid are in the range where L_bact has its maximum values (0.3<L_bact [%] <0.4; Fig. 10c).

Figure 10d repeats the full parameter ranges of R_bact and R_chemaq. We discuss L_bact for the CCN-derived compounds (malonic acid, malonate, succinic acid, succinate) for the same R_bact as in Fig. 10a–c: the maximum consumption of CCN-derived compounds by bacteria corresponds to the fraction of the organics present in bacteria-containing droplets (∼0.0065 % in our simulations). Therefore, the predicted L_bact [%] values are very similar for all compounds considered here (malonate $/$ malonic acid and succinate $/$ succinic acid) and do not differ, independently of R_bact.

4.2 Dependence of L_bact on bacterial cell concentration in cloud water

According to Eq. (3), R_bact is the product of the biodegradation rate constant k_bact [cell L⁻¹] (Table 2) and the cell concentration C_cell [cell L⁻¹]. Based on the three R_bact values and the k_bact data for the various organics, we calculate C_{cell,theoretical} that would be needed to reach these R_bact:

$$\begin{array}{}\text{(14)}& C_{\mathrm{cell},\mathrm{theoretical}}\left[\mathrm{cell}{\mathrm{L}}^{-\mathrm{1}}\right]={\displaystyle \frac{R_{\mathrm{bact}}\left[{\mathrm{s}}^{-\mathrm{1}}\right]}{k_{\mathrm{bact}}\left[\mathrm{L}{\mathrm{cell}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}\right]}}.\end{array}$$

The resulting C_{cell,theoretical} [cell L⁻¹] values are listed in Table 3, together with k_bact [cell L⁻¹]. Among the water-soluble organic gases, C_{cell,theoretical} is predicted to be $\sim {\mathrm{10}}^{\mathrm{2}}\le C_{\mathrm{cell},\mathrm{theoretical}}$ [cell L⁻¹] ≤10⁷ for acetic acid, formic acid, and phenol, while it is much higher ($\sim {\mathrm{10}}^{\mathrm{7}}\le C_{\mathrm{cell},\mathrm{theoretical}}$ [cell L⁻¹] ≤10¹⁵) for catechol, formaldehyde, and methanol that have much lower k_bact than the former compounds. Typical bacterial cell concentrations in cloud water are in the range of 10⁶–10⁸ cell L⁻¹ (Amato et al., 2007b). Comparing this range to C_{cell,theoretical} reveals that for several compounds C_{cell,theoretical} falls into a realistic range (values with ^* in Table 3); for ambient cell concentrations in cloud water, malonic acid $/$ malonate, succinic acid $/$ succinate, acetic acid $/$ acetate, formic acid $/$ formate, cathecol, and phenol might fall into a range where the maximum consumption of organics by biodegradation can be expected, while for formaldehyde and methanol C_{cell,theoretical} is unrealistic (≥10⁹ cells L⁻¹) based on the available studies of bacterial cell concentrations in cloud water.

4.3 For which organics is biodegradation an efficient sink in the atmosphere?

The maximum value of L_bact is ∼0.7 % in all our simulations, but one should keep in mind that also the predicted L_t is not higher than a few percent (Fig. 6a–c) as we restrict our simulations to the timescale of approximate one cloud cycle. However, in a relative sense, our results allow us to compare the importance of biodegradation to chemical loss for the compounds shown in Fig. 10. To quantify the contribution of bacteria to the total consumption (L_t), we list the ratio $L_{\mathrm{bact}}/L_{\mathrm{t}}$ in Table 3. Our results clearly show that biodegradation might add significantly to the loss of formic acid $/$ formate ($L_{\mathrm{bact}}/L_{\mathrm{t}}=\mathrm{0.65}$) and acetic acid $/$ acetate ($L_{\mathrm{bact}}/L_{\mathrm{t}}=\mathrm{0.70}$) at cell concentrations of $\sim \mathrm{7}\times {\mathrm{10}}^{\mathrm{7}}$ and 2×10⁶ cells L⁻¹, respectively. These acids contribute on average ∼68 % to the total dissolved carbon in cloud and fog water (Herckes et al., 2013). Their removal by dry and wet deposition is considered the major loss process in the atmosphere (Khare et al., 1999). However, several studies also suggested that the oxidation of formic acid $/$ formate in cloud water may be a net sink (Jacob, 1986). Measurements during different seasons in the Amazon showed that indeed formic and acetic acids have stronger sinks during the wet season (Herlihy et al., 1987). While wet deposition was described to contribute, to a large extent, to the observed removal; chemical and possibly bacterial processes were suggested to act as additional sinks. While the latter was regarded as being inefficient due to long incubation time as observed in lab experiments, more recent experiments suggest that such incubation times are likely not occurring in the atmosphere where bacterial cells are continuously exposed to water and substrates (Amato et al., 2007a; Vaïtilingom et al., 2010, 2013). We conclude that biodegradation of these major cloud water organics may be a significant sink under ambient conditions, possibly even comparable to the loss by chemical reactions. While phenol is not a major contributor to the WSOC content in cloud water (5–95 nM) (Jaber et al., 2020) as compared to 10 µM (Ervens et al., 2003b; Löflund et al., 2002; Sun et al., 2016) for formic and acetic acids, respectively, its degradation processes in the atmosphere might be of interest due to its toxic properties. Overall, our results are in agreement with previous findings that neither chemical processes nor biodegradation are major WSOC losses as compared to deposition (Ervens and Amato, 2020; Fankhauser et al., 2019). However, in order to comprehensively describe the loss processes and timescales of organic degradation and residence timescales in the atmosphere, both chemical and biological processes should be considered. Hence, we suggest that biological processes of organics with properties similar to those of formic and acetic acids and phenol ($\sim {\mathrm{10}}^{\mathrm{3}}<K_{\mathrm{H}\left(\mathrm{eff}\right)}$ [M atm⁻¹] $<\sim {\mathrm{10}}^{\mathrm{6}}$, $k_{\mathrm{bact}}={\mathrm{10}}^{-\mathrm{11}}$ s⁻¹) should be included in atmospheric multiphase models.

The importance of biodegradation of CCN-derived compounds is limited by the number fraction of cloud droplets that contain bacteria. Malonate $/$ malonic acid and succinate $/$ succinic acid contribute on average to <5 % to the total organic aerosol mass in ambient particles, e.g., Fu et al. (2013) and Kawamura and Ikushima (1993). Their loss by chemical and biological processes will not affect the total carbon budget to a large extent nor the budget of the individual compounds. These conclusions can be generalized for other CCN-derived aerosol constituents, for which biodegradation has been suggested to occur in the atmosphere. Our assumption of static cloud droplets in the box model is certainly a simplified representation of cloud microphysics. Droplets might experience collision $/$ coalescence in clouds, leading to mixing of the cloud water constituents in the resulting larger droplets. However, such processes are unlikely to add significantly to the loss of CCN-derived compounds by bacteria due to (i) the number small fraction of bacteria-containing droplets (0.001–0.0001) and (ii) the limited atmospheric residence time of large droplets which are efficiently removed by precipitation as a function of drop size (Beard and Ochs, 1984).

5 Summary and conclusions

Our model sensitivity study is the first comprehensive analysis of the importance of biodegradation of organics by bacteria in the atmospheric multiphase system in comparison to chemical loss for wide ranges of chemical and biodegradation kinetic data. We use a box model with drop-size-resolved aqueous-phase chemistry and additional biological processes that only occur in a small number of cloud droplets, in agreement with ambient ratios of cell and droplet concentrations. We neglect the fact that bacterial cells may form agglomerates in the atmosphere; consequently, there might be more than one cell per droplet. This effect could be included in our model by multiplying the biological activity in the respective droplets with the number of cells.

We compare the predicted loss rates of chemical processes in both phases to those of biological processes in the aqueous phase only. In addition to presenting the relative loss rates (fr_bact, fr_chem) as in previous studies (Jaber et al., 2020; Vaïtilingom et al., 2010), we discuss the relative amounts of organics (L_t) consumed by chemical (L_chem) and biological processes (L_bact). We find that the relative loss rate of organics by biological processes (fr_bact) is generally higher for water-soluble organic gases than for CCN-derived compounds. However, the total loss of the organics (L_t) is predicted to not reach any value higher than ∼12 %, because our simulations were restricted to a period of 600 s (approximately the drop lifetime within one cloud cycle); it would be higher if the total particle processing time during multiple cloud cycles in the atmosphere were considered. The contribution of bacteria (L_bact) to the total loss is predicted to be highest for water-soluble organic gases with intermediate solubility ($\sim {\mathrm{10}}^{\mathrm{4}}\le K_{\mathrm{H}}$ [M atm⁻¹] $\le \sim {\mathrm{10}}^{\mathrm{6}}$). This can be explained by the replenishment of these compounds in the bacteria-containing droplets upon uptake from the gas phase and evaporation from the bacteria-free droplets, in which less efficient consumption of the organics occurs. Less soluble organics (K_H<10⁴ M atm⁻¹) that partition to a smaller extent (<1 %) to the aqueous phase are mostly consumed by chemical processes in the gas phase; more soluble compounds (K_H>10⁶ M atm⁻¹) are predominately partitioned to the aqueous phase. Thus, the evaporation to the gas phase and consequently the redistribution from the bacteria-free to the bacteria-containing droplets is kinetically more limited and less efficient. The ratio of the consumption of water-soluble organic gases by bacteria to the total loss ($L_{\mathrm{bact}}/L_{\mathrm{t}}$) might be as high as 0.7 for high biological activity and cell concentrations (∼10⁸ cells L⁻¹). These values suggest that biological processes might add significantly (>70 %) to the loss processes in the atmospheric multiphase system for organics with intermediate solubility such as formic acid $/$ formate, acetic acid $/$ acetate, or phenol. For CCN-derived compounds, the amount of organics consumed by bacteria is restricted to the fraction of the organic species dissolved in bacteria-containing droplets (∼0.001 %) as no efficient replenishment from the gas phase or from the other droplets occurs. Thus, biodegradation of CCN-derived compounds does not significantly affect their atmospheric budget. Recent experiments of airborne bacteria suggested that metabolic rates are a function of substrate availability in oligotrophic media such as cloud droplets (Krumins et al., 2014b). In the case of CCN-derived organics or those that are inefficiently replenished by uptake from the gas phase, substrate limitation might result in lower biodegradation rates. Currently, no data are available on the absolute changes in k_bact at different levels of substrate availability and/or on the timescales during which k_bact might adjust to such conditions. In addition, the biodegradation rates may be affected under highly acidic conditions. Some studies demonstrated that some bacteria can develop an acid resistance to survive under acidic conditions (Lu et al., 2013). However, these strategies do not necessarily imply that the bacteria maintain the same biodegradation activities at high acidity, but they allow for survival of the cells in the atmosphere. It can be expected that internal buffering of bacterial cells allows them to maintain their metabolic activity over wide pH ranges (∼3 to 6) as found in cloud water. Therefore, we do not consider a potential pH dependency of biodegradation rates in our model studies.

In addition to our detailed model with a realistic bacterial cell distribution within a cloud droplet population, we apply simpler model approaches: (i) similar to many chemical model studies, bacterial cells are distributed equally in all droplets (“bulk approach”), resulting in cell concentrations of 10⁻⁵ cells per droplet, which is clearly an unphysical assumption for intact bacterial cells. (ii) A multiphase system with only cloud droplets which contain bacteria resulting in a liquid water content of $\sim {\mathrm{10}}^{-\mathrm{11}}$ vol $/$ vol as compared to $\sim {\mathrm{10}}^{-\mathrm{7}}$ vol $/$ vol in clouds (“low-LWC approach”) is applied. Comparing L_bact predicted from these approaches to results of our detailed model shows that all approaches agree in predicting L_bact for organics of low solubility (K_H(eff)<10⁴ M atm⁻¹). However, for such species the importance of biodegradation is low due to their inefficient partitioning to the aqueous phase. The bulk approach increasingly overestimates L_bact of organics with higher K_H; the greatest discrepancy is predicted for highly soluble compounds (K_H(eff)>10⁶ M atm⁻¹) as the bulk approach does not take into account the kinetic limitation due to the organic species redistribution between the bacteria-free and bacteria-containing droplets. As the bulk approach implies organics in all droplets, it does not allow for limiting the organic species consumption by biodegradation. Predictions of the relative role of biodegradation as compared to chemical processes by the low-LWC approach are biased high, because the loss due to aqueous-phase processes is only considered in an unrealistically small fraction of droplets.

The current data sets for microbial rates of organic compounds are limited to very few compounds. Our model sensitivity study shows that biodegradation by bacteria in clouds is most efficient for compounds with intermediate (effective) Henry's law constants (∼10⁴ M atm⁻¹ $<K_{\mathrm{H}\left(\mathrm{eff}\right)}<{\mathrm{10}}^{\mathrm{6}}$ M atm⁻¹) as found for common cloud water constituents such as formic acid $/$ formate and acetic acid $/$ acetate but also for less abundant species such as phenol, largely independent of their chemical reactivity. Our framework allows us to estimate the potential importance of biodegradation of organics in comparison to chemical processes. It also gives guidance to future lab and model studies to further explore the role of biodegradation of specific organics in the multiphase system.