Self-consistent global transport of metallic ions with WACCM-X

The NCAR Whole Atmosphere Community Climate Model with thermosphere and ionosphere eXtension (WACCM-X) v2.1 has been extended to include the neutral and ion–molecule chemistry and dynamics of three metals (Mg, Na, and Fe), which are injected into the upper mesosphere–lower thermosphere by meteoric ablation. Here we focus on the self-consistent electrodynamical transport of metallic ions in both the E and F regions. The model with full ion transport significantly improves the simulation of global distribution and seasonal variations of Mg⁺, although the peak density is slightly lower (about 35 % lower in peak density) compared with the SCIAMACHY measurements. Near the magnetic equator, the diurnal variation in upward and downward transport of Mg⁺ is generally consistent with the “ionosphere fountain effect”. The thermospheric distribution of Fe is shown to be closely coupled to the transport of Fe⁺. The effect of ion mass on ion transport is also examined: the lighter ions (Mg⁺ and Na⁺) are transported above 150 km more easily than the heavy Fe⁺. We also examine the impact of the transport of major molecular ions, NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$, on the distribution of metallic ions.

1 Introduction

The presence of layers of meteor-ablated metal atoms between 80 and 105 km has been known for decades (Plane et al., 2015). More recently, there have been a growing number of observations of the thermospheric metal layers up to 200 km. For example, Chu et al. (2011) reported neutral Fe layer observations up to 155 km at McMurdo, Antarctica (77.8^∘ S, 166.7^∘ E); Gao et al. (2015) found that several observations of Na layers reached up to 170 km, using a large-aperture astronomical telescope at Lijiang, China (26.7^∘ N, 100.0^∘ E); and Friedman et al. (2013) investigated a descending thermospheric K layer from altitudes above 155 km at Arecibo, Puerto Rico (18.35^∘ N, 66.75^∘ W). These high-altitude thermospheric neutral metal layers are challenging to explain, since ablation occurs predominantly below these altitudes, which raises interesting questions regarding their formation mechanisms. Neutral metal atoms and their corresponding atomic ions are tightly coupled through ionization (via photo-ionization or charge transfer with ambient ions, e.g. NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$) and neutralization (via dielectronic recombination with electrons, or dissociative electron recombination if they have formed a molecular ion) (Plane et al., 2015). Thus, the vertical and horizontal transport of metallic ions is a key process for controlling the behaviour of neutral atoms in the thermosphere (E and F regions). Interestingly, the reported occurrence of thermospheric metal layers appears to show great geographical variability, underlining the importance of global ion transport. In addition, metallic ions play a central role in the formation of thin, concentrated layers of ions in the E region (sporadic E layers, or Es), which affect radio transmission (e.g. Narcisi, 1968; Layzer, 1972; Plane et al., 2015; Yu et al., 2021).

Thus far, a number of modelling studies have attempted to simulate the transport of metal ions in the thermosphere and, more recently, the role of metallic ions in the formation of the thermospheric metal layers. For example, Carter and Forbes (1999) developed a two-dimensional (2-D) model to examine both global and local transport of Fe⁺ ions; Chu and Yu (2017) used a thermosphere–ionosphere $\mathrm{Fe}/{\mathrm{Fe}}^{+}$ model to investigate the formation of thermospheric Fe layers observed by lidar at McMurdo, Antarctica; and Cai et al. (2019) conducted a 2-D simulation of $\mathrm{Na}/{\mathrm{Na}}^{+}$ in the E and F regions to explore the formation of thermospheric sodium layers observed at the Andes Lidar Observatory (30.25^∘ S, 70.74^∘ W). Recently, Huba et al. (2019) have included the global transport of metallic ions (Mg⁺ and Fe⁺) in the SAMI3 model of the E and F regions and concluded from a 2 d model run that ions are redistributed by the combined effects of the neutral wind and electric field. However, no previous studies appear to have examined the full transport of metal ions in a self-consistent global chemical-dynamical model, incorporating the full life cycle of the thermospheric metal atom and metal ion chemistry and the injection of these metals from meteoric ablation.

This paper describes the development of a new global model of three metal species (magnesium, iron, and sodium) in the E and F regions, to gain a detailed understanding of the effects of multi-scale atmospheric motions from the lower atmosphere and solar activity on the thermospheric metal layers. The main contribution reported here is to incorporate a self-consistent solution of full global transport of Mg⁺, Fe⁺, and Na⁺ in both the E and F regions, within the chemistry–climate WACCM-X 2.1 model (NCAR Whole Atmosphere Community Climate Model with thermosphere and ionosphere eXtension v2.1), in addition to a detailed description of the neutral and ion–molecule chemistry of these metals and the meteoric ablation source required to model the metal atom layers around 90 km. This is described in Sect. 2. Section 3 presents the findings of the model simulation, focusing on the seasonal and the diurnal variation of ions and the effects of ion electrodynamical transport. The final section includes a brief summary and a discussion of future directions with the model.

2 Model description and ion transport

2.1 Model description

WACCM-X is extended in the present study to include the full life cycle of meteoric metals combined with interactive chemistry, dynamics, deposition, and ion transport in the ionosphere. WACCM-X is an atmospheric component of the Community Earth System Model (CESM, version 2.1.3; Hurrell et al., 2013) developed by the National Center for Atmospheric Research. The key chemistry and dynamical features are based on CAM4 and WACCM4 and are described in detail in Marsh et al. (2013b) and Neale et al. (2013). Validated metal chemistry modules for magnesium (Langowski et al., 2015), sodium (Marsh et al., 2013a), and iron (Feng et al., 2013) with updated rate coefficients from Plane et al. (2015), Bones et al. (2016), and Viehl et al. (2016) are added. The meteoric input functions (MIFs) were estimated from the Leeds Chemical ABLation MODel (CABMOD-3) combined with an astronomical model (Carrillo-Sánchez et al., 2020). The transport of the neutral and ionized metallic species by eddy/molecular diffusion and winds is treated in the same way as the transport of most active chemical species (for example, O₃ and CO₂).

A detailed description of WACCM-X 2.0 is provided by Liu et al. (2018a), and a brief summary is given here. The model has some key features and improvements compared to WACCM-X 1.0 (Liu et al., 2010), including a self-consistent electrodynamics module, F-region O⁺ transport, a solver for electron and ion temperatures, and reduction in the damping coefficient of atmospheric tides (Liu et al., 2018b). The model top is set at $\mathrm{4.1}\times {\mathrm{10}}^{-\mathrm{10}}$ hPa (∼500 to ∼700 km, depending on solar activity), with a vertical resolution of a quarter of a scale height in the mesosphere and thermosphere. The horizontal resolution is 1.9^∘ in latitude and 2.5^∘ in longitude, and all model results used in the paper are from 1-year free-running simulations (perpetual year 2000 AD) under solar medium conditions (constant F10.7 = 130 sfu (solar flux units) and Kp = 1) with an output frequency of 1 h. The O⁺ transport method is described in detail by Liu et al. (2018a).

2.2 Ion transport equation

Since meteoric ablation, deposition, transport by the neutral winds, eddy and molecular diffusion, chemical production, and loss are already contained in the metal chemistry modules, the metal ion transport is calculated separately, in a similar way to the treatment of O⁺ transport described by Liu et al. (2018a). The continuity equation of metal ion transport can be simplified as

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle \frac{\partial n_{\mathrm{i}}}{\partial t}}=-\mathrm{\nabla }\cdot \left(n_{\mathrm{i}}{\mathit{V}}_{\mathrm{i}}\right),\end{array}$$

where n_i represents the number density of metal ions, and V_i is the ion transport velocity. The ion transport velocity is adapted from the derivation described by Carter and Forbes (1999) and Chu and Yu (2017), extended to a 3-D global model:

$$\begin{array}{ll}{\displaystyle }{\mathit{V}}_{\mathrm{i}}=& {\displaystyle }{\displaystyle \frac{\mathit{\xi }}{\mathrm{1}+{\mathit{\xi }}^{\mathrm{2}}}}{\displaystyle \frac{{\mathit{V}}_{\mathrm{n}}\times \mathit{B}}{B}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+{\mathit{\xi }}^{\mathrm{2}}}}{\displaystyle \frac{\left({\mathit{V}}_{\mathrm{n}}\cdot \mathit{B}\right)\mathit{B}}{B^{\mathrm{2}}}}\\ \text{(2)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathit{\xi }}{\mathrm{1}+{\mathit{\xi }}^{\mathrm{2}}}}{\displaystyle \frac{\mathit{E}}{B}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+{\mathit{\xi }}^{\mathrm{2}}}}{\displaystyle \frac{\mathit{E}\times \mathit{B}}{B^{\mathrm{2}}}}+{\mathit{V}}_{\text{ambi}},\end{array}$$

where E and B are the electric field and the Earth's magnetic field, respectively. V_n is the neutral wind, and $\mathit{\xi }=\frac{{\mathit{\nu }}_{\text{i\hspace{0.17em}n}}}{{\mathit{\omega }}_{\mathrm{i}}}$ is the ratio of ion-neutral collision frequency (in the laboratory frame of reference (Banks and Kockarts, 1973) to the ion gyro-frequency. V_ambi is the ion velocity due to ambipolar diffusion, derived from Schunk and Nagy (2000, Eqs. 5.54 and 5.70), where we treat the metallic ions as minor ions and the ion with higher density in NO⁺ and O⁺ as a major ion species. Note that the term corresponding to transport is omitted from Eq. (2) because advection by the neutral wind is already included in the dynamical core of WACCM-X. The first two terms are related to contributions by the neutral winds, with the first term being the V×B drift, i.e. the Lorenz force. The third and fourth terms are due to the electric field. A flux-corrected transport (FCT) algorithm (Boris et al., 1993) is applied to compute the vertical transport velocity; this algorithm is designed for solving steep density gradients.

As mentioned above, charge transfer from molecular ions such as NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ to metal atoms provides a major source of metallic ions. However, due to the short lifetime of these two molecular ions (∼5 min in the daytime), they were assumed to be in chemical equilibrium in WACCM-X 2.0. In this study, the transport of molecular ions NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ is now considered along with the metal ions. Simulation results with and without the molecular ion transport are compared to determine the impact on the metal ion distribution.

3 Results and discussion

Na⁺, Fe⁺, and Mg⁺ undergo similar transport forces in the E and F regions, apart from the effect of their mass differences. Because Mg⁺ is the only one of these ions for which near-global observations are available (Langowski et al., 2015), we focus here on the results for Mg⁺. However, we also explore $\mathrm{Fe}/{\mathrm{Fe}}^{+}$ ion-neutral coupling in the formation of thermospheric metal layers, since Fe is the most abundant and widely studied thermospheric metal species. In addition, the ${\mathrm{Mg}}^{+}/{\mathrm{Fe}}^{+}$ and ${\mathrm{Mg}}^{+}/{\mathrm{Na}}^{+}$ ratios are employed to examine the effect of metal ion mass difference because Fe⁺ is more than twice as heavy as Mg⁺ (56 versus 24 amu), while the masses of Na⁺ and Mg⁺ are very similar (23 versus 24 amu).

3.1 Seasonal variation of Mg⁺ simulated by WACCM-X

Figure 1 shows the monthly mean density of Mg⁺ as a function of latitude and altitude, where the monthly mean data are zonally averaged. An obvious seasonal signal is exhibited with clear latitudinal dependence, which is generally consistent with the SCIAMACHY measurements (Fig. 6 in Langowski et al., 2015). Nevertheless, WACCM-X Mg⁺ density is slightly underestimated relative to SCIAMACHY observations (by ∼35 %), which is likely related to the MIF used in the simulation. The peak altitude of Mg⁺ in the summer hemisphere at middle latitudes ($\sim \mathrm{40}{}^{\circ }\pm \mathrm{10}{}^{\circ }$) is ∼10 km higher than at other latitudes, in accord with observations (Langowski et al., 2015). This appears to be caused by the vertical ion velocity due to the neutral wind (first and second terms in Eq. 2), with the monthly mean drift velocities shown in Fig. 1. Since the metallic ions are the main reservoir for neutral metal atoms in the lower thermosphere (Plane et al., 2015), this is in good agreement with the summer peak occurrence of lower thermospheric neutral Na layers observed by mid-latitude lidars (Wang et al., 2012; Dou et al., 2013; Yuan et al., 2014; Xun et al., 2020).

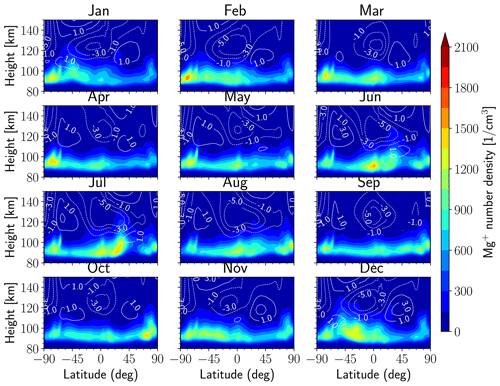
Figure 1 Monthly and zonal mean of the Mg⁺ number density (coloured contours) and the drift velocity (in m s⁻¹) due to the neutral wind (line contours) as a function of latitude and altitude in different months.

In contrast to the SCIAMACHY measurements, which show a minimum at the equator, the WACCM-X simulation shows a maximum in peak altitude and number density at the equator. Note that the SCIAMACHY observations are made at a particular local time of around 10:00 LT, whereas the WACCM-X data in Fig. 1 are a diurnal and zonal average. To address this, we also present the simulation results at the same local time (10:00 LT) in Fig. 2, and they are in better agreement with SCIAMACHY observations. Another noteworthy feature is that this simulation shows the pronounced maximum in peak altitude and density at ∼45^∘ (N$/$S) at 10:00 LT, in accord with the SCIAMACHY observations, which is absent in WACCM-Mg in Langowski et al. (2015). However, the number densities at 10:00 LT are even lower, and the peak altitude is about 5 km lower than the daily averaged simulation (Fig. 1). The pronounced discrepancy between Fig. 2 and SCIAMACHY measurements is probably due to the diurnal variation of ion electrodynamical transport, which should be further investigated in the future.

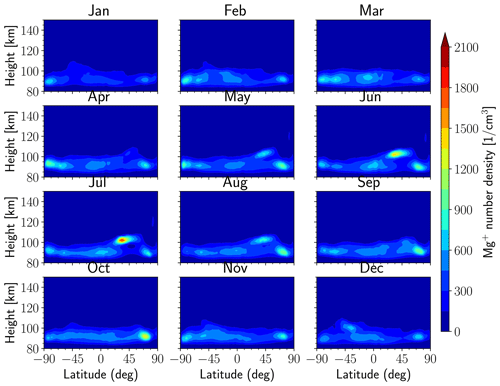
Figure 2 Monthly mean Mg⁺ number density obtained by averaging data at 10:00 LT for all longitudes as a function of latitude and altitude in different months.

Figure 3a–d present the global geographical distribution of Mg⁺ column densities at the equinoxes and solstices and at 00:00 UTC. The dashed white line depicts the dip equator. Despite the high accumulation of column density at the poles, the Mg⁺ column density exhibits relatively high values at lower and middle latitudes in the summer hemisphere (Fig. 3b and d). This is in good agreement with the conclusion of a summertime maximum shown in Fig. 1. Interestingly, the geographic distributions in all four seasons show stronger convergences along the magnetic equator, which might be related to the modulation of the “equatorial fountain effect”.

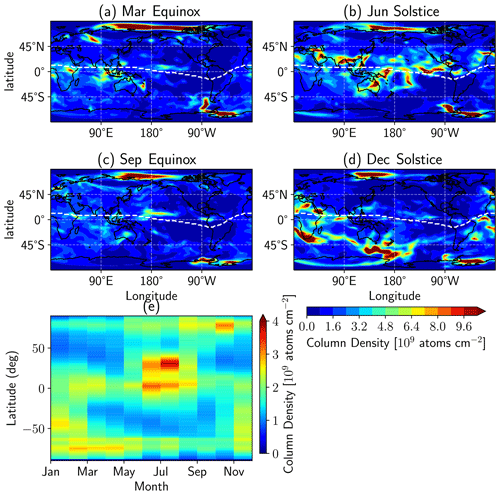
Figure 3 (a–d) Global geographical distribution of the Mg⁺ column density during the equinoxes and solstices, at 00:00 UTC. (e) Seasonal variation of the zonal mean Mg⁺ column density as a function of month and latitude. The dashed white lines indicates the position of the dip equator.

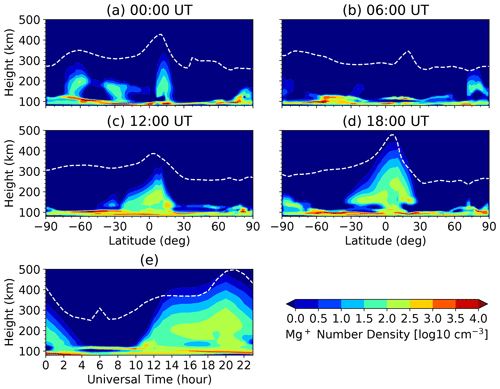
Figure 4 (a–d) Mg⁺ density as a function of latitude and altitude at the December solstice and longitude 0^∘, at four universal times (local times): 00:00, 06:00, 12:00, and 18:00 UT. (e) Mg⁺ density over (12^∘ N, 0^∘) as a function of universal time and altitude. The dashed white lines denote hmF₂.

In Fig. 3e we show the seasonal variation of zonal-averaged Mg⁺ column density at different latitudes. The modelled Mg⁺ column exhibits a maximum in the summer hemisphere at middle and high latitudes, which is in general agreement with the results derived from the SCIAMACHY measurements and WACCM-Mg model results (Figs. 9 and 16 in Langowski et al., 2015) and the SBUV nadir measurements (Fig. 9 in Joiner and Aikin, 1996). The partial column density above 110 km still shows a similar seasonal variation, which is probably due to thermospheric ion transport (not shown).

3.2 Diurnal variations of Mg⁺ simulated by WACCM-X

To investigate the diurnal variation of metallic ions in the model, we present the Mg⁺ number density (on a log scale) as a function of latitude and altitude at the December solstice and 0^∘ longitude; the panels show universal times (i.e. local times) of 00:00, 06:00, 12:00, and 18:00 UT (Fig. 4a–d). The dotted white line denotes the F₂-layer height of the peak electron density (hmF₂). This shows that the strongest diurnal variations are found in equatorial and high latitudes. Here we focus on the fountain effect on ion transport, where the equatorial ions are first lofted to higher altitudes via E×B motion and then drift down along the magnetic field lines (Kelley, 2009). Mg⁺ is expected to be lofted to high altitudes (∼400 km) by the E×B drift above the magnetic equator during the day because of the daytime eastward electric fields (Huba et al., 2019). Figure 4e shows the diurnal variation of Mg⁺ number density near the dip equator (12^∘ N, 0^∘) as a function of local time; the upward drift of Mg⁺ peaks at around 20:00 LT, and the Mg⁺ then drifts down towards the main layer at midnight (∼02:00 LT). Note that the reduction of Mg⁺ at the equator at 06:00 LT confirms that the ion density at the equator is largely dependent on local time (Fig. 4b and e). The phase of Mg⁺ diurnal variation shows a high correlation with variations in the electron density (the change of hmF₂). Instead of being redistributed along the magnetic field lines to the subtropical region by the “classical” fountain effect (e.g. Pi et al., 2009), the Mg⁺ shows a more complex downward trajectory; i.e. the ions are not transported symmetrically to both sides of the geomagnetic equator, which is closer to the scenario proposed by Cai et al. (2019).

3.3 Fe and Fe⁺ vertical profile comparison

In order to demonstrate the effect of electrodynamical transport on the metals, a standard simulation without metal ion transport was performed (termed the control run). Figure 5 shows the Fe⁺ and Fe vertical profiles for the ion transport run (solid lines) and control run (dotted/dashed lines) at the equinoxes and solstices. Three geographic latitudes at a longitude of 180^∘ are chosen for comparison: 0^∘ for the magnetic equator, 20^∘ S for the subtropical region corresponding to the fountain effect downward drift, and 45^∘ S for the middle latitudes corresponding to the summertime peak altitude. Without the ion transport (the control run), both Fe and Fe⁺ exhibit roughly Gaussian-shaped layers, with peak heights between 90 and 100 km (dotted/dashed lines). When ion transport is turned on, the vertical profiles of Fe⁺ vary depending on latitude and season. For instance, Fe⁺ near the equator is always transported to a higher altitude (blue lines), consistent with the fountain effect in the dip equator region. However, ions at subtropical (20^∘ S) (orange lines) and middle (45^∘ S) latitudes (green lines) exhibit quite different transport motions. At the December solstice at midnight, Fe⁺ is transported to a high level (∼1 cm⁻³ at 200–300 km) at middle and subtropical latitudes, which is related to the dominant upward drift velocity due to neutral wind (not shown). In other seasons, these ions can be transported both upward and downward, depending on the vertical ion velocity.

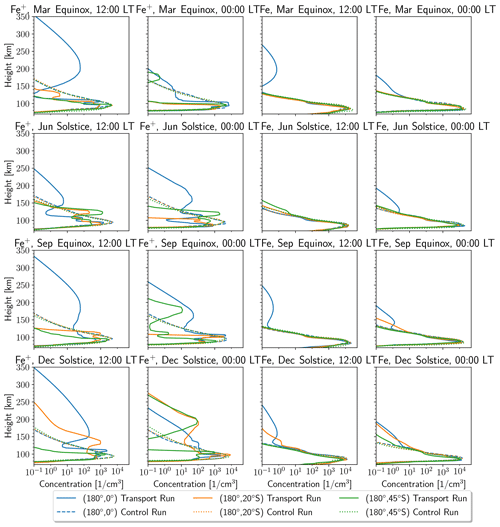
Figure 5 Comparison of the vertical profiles of the Fe⁺ (left two panels) and Fe (right two panels) number densities, for the control run (dotted/dashed lines) and the run with ion transport (solid lines) over selected geographic latitudes, at the equinoxes and solstices and midday (12:00 LT) and midnight (00:00 LT).

Since the neutral atoms are not directly transported by the electromagnetic field, they are influenced by ions through the recombination between ions and electrons. The last two panels in Fig. 5 illustrate the Fe atom distributions. In general, changes in Fe (at densities >1 cm⁻³) do not appear to be synchronized with the upward transport of Fe⁺, so that the vertical distribution of Fe in the transport run is similar to that in the control run. However, there is an obvious increase in high-altitude Fe (i.e. above ∼140 km) in the equatorial region (blue line), corresponding to the upward transport of ions; and at the December solstice around midnight, the Fe number density above 150 km is much higher than that in the control run at all southern latitudes.

3.4 Effect of metal ion mass on transport

Figure 6 compares the ${\mathrm{Mg}}^{+}/{\mathrm{Fe}}^{+}$ ratio (left panels) and the ${\mathrm{Mg}}^{+}/{\mathrm{Na}}^{+}$ ratio (right panels) as a function of height and latitude at the equinoxes and solstices. Note that changes in the ratios below 100 km are due to differences in the ion–molecule chemistries of the metals (Plane et al., 2015), which is not the focus here. There are several advantages in choosing these three metallic ions. First, Fe⁺ is more than twice as heavy as Mg⁺. Second, Fe⁺ is much heavier and Mg⁺ is slightly lighter than the mean mass of air molecules in the E region. Third, Na⁺ has a comparable mass with Mg⁺. As expected, the lighter ions are transported above 150 km more easily than the heavy Fe⁺, so that the ${\mathrm{Mg}}^{+}/{\mathrm{Fe}}^{+}$ ratio increases from ∼1 at 120 km to >2 above 150 km and to >30 above 300 km. By the same token, the ${\mathrm{Mg}}^{+}/{\mathrm{Na}}^{+}$ ratio shows very little change above 120 km.

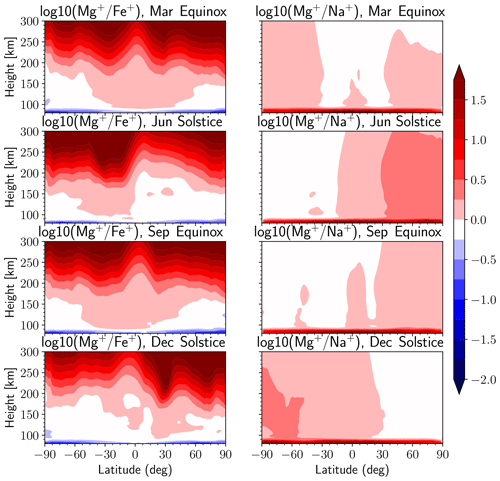
Figure 6 The zonally averaged ${\mathrm{Mg}}^{+}/{\mathrm{Fe}}^{+}$ ratio (left panels) and ${\mathrm{Mg}}^{+}/{\mathrm{Na}}^{+}$ ratio (right panels) versus height and latitude at the equinoxes and solstices.

The zonally averaged ${\mathrm{Fe}}^{+}/{\mathrm{Mg}}^{+}$ ratio below 200 km simulated by WACCM-X also accords with the limited available observations (Dymond et al., 2003; Kumar and Hanson, 1980), which showed that the average ${\mathrm{Fe}}^{+}/{\mathrm{Mg}}^{+}$ ratio is around 1.5:1. The present study also simulates the extreme variability of the ${\mathrm{Fe}}^{+}/{\mathrm{Mg}}^{+}$ ratio above 300 km (as low as 1:50 in Kumar and Hanson, 1980). However, the unexpectedly large ${\mathrm{Fe}}^{+}/{\mathrm{Mg}}^{+}$ ratio (∼10–50) reported by Dymond et al. (2003) is only captured at a few points about 150 km in our model (not shown). Interestingly, the striking differences between distinct thermosphere–ionosphere Fe and diffuse thermosphere–ionosphere Na reported by Chu et al. (2020) are thought to be related to mass separation. There is no question that more observations are needed to confirm and validate these findings.

Figure 6 shows that whereas the ${\mathrm{Mg}}^{+}/{\mathrm{Fe}}^{+}$ ratios (left panels) show relatively little latitudinal variation compared with the variation with altitude (mostly caused by the mass difference of the ions), the ${\mathrm{Mg}}^{+}/{\mathrm{Na}}^{+}$ ratios (right panels) show marked interhemispheric differences at the solstice periods. The reason for this is the difference in the ion–molecule chemistry of Na⁺, compared with Mg⁺ (and Fe⁺). The Na⁺ ion has a closed electronic shell (it is isoelectronic with the inert gas Ne) and so does not react with O₃, in contrast to Mg⁺ and Fe⁺ (Plane et al., 2015). Formation of MgO⁺ by the fast reaction with O₃ is the main route to neutralization of Mg⁺ above 90 km (Whalley et al., 2011). During summer at mid-latitudes to high latitudes ($>\mathrm{30}{}^{\circ }$), O₃ above 90 km is heavily depleted through a combination of longer diurnal photolysis and reaction with the elevated levels of H produced from H₂O which upwells over the summer pole (Plane et al., 2015). In contrast, the O₃ density in the lower thermosphere is more than an order of magnitude higher in the winter polar vortex. The result is that lower thermospheric Mg⁺ ions at latitudes higher than ∼30^∘ are relatively long-lived in summer and can be transported vertically throughout the thermosphere. This leads to the higher ${\mathrm{Mg}}^{+}/{\mathrm{Na}}^{+}$ ratios in the summer hemisphere, as shown in Fig. 6. The converse operates at latitudes higher than 30^∘ in the winter hemisphere, where the relatively high O₃ tends to neutralize lower thermospheric Mg⁺. Because Na⁺ and Mg⁺ have very similar masses, their ratios above 100 km are fairly constant with height.

3.5 Effect of NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ transport

Figures 7 and 8 compare the distribution of metal ions from two simulations, one with the transport of all ions (hereafter TA) and the other with NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ in chemical equilibrium (hereafter CE). Note that the simulation results presented herein investigate the potential impacts of the transport of two major molecular ions on the distribution of metallic ions and do not provide a comprehensive review of all possible effects.

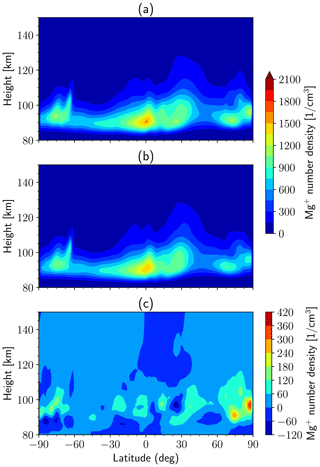
Figure 7 The monthly and zonal mean of the Mg⁺ number density in June from (a) the TA simulation and (b) the CE simulation. (c) The difference between the TA and CE simulations.

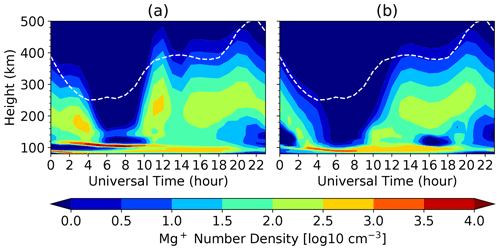
Figure 8 Mg⁺ density over (12^∘ N, 0^∘, near the dip equator) as a function of universal time and altitude at June solstice. The dashed lines denote hmF2. (a) for the TA simulation and (b) for the CE simulation.

Figure 7 shows the monthly mean density of Mg⁺ as a function of latitude and altitude in June for the TA (Fig. 7a) and CE (Fig. 7b) simulations, along with their difference (Fig. 7c), where the monthly mean data are zonally averaged. In general, there is a good correspondence between the two simulations in terms of the latitude–altitudinal distribution of the monthly mean Mg⁺ density. As seen in Fig. 7c, the peak density in CE simulation is generally a little higher than that in the TA simulation, especially in the high latitudes of the Southern Hemisphere. Figure 8 compares the diurnal variation of Mg⁺ in the two simulations. Both cases simulate the significant fountain effect, which was discussed in Sect. 3.2. With the transport of major molecular ions, the peak height of the metal layer after midnight is higher. As discussed by Plane et al. (2015), the charge transfer of neutral metal atoms with NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ is the major sources of metallic ions in the E region. Due to the very short lifetimes of NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ during daytime, the transport of these molecular ions between model grid boxes has little effect on the metallic ions. In contrast, the reduced densities of the molecular ions (and electrons) at night mean that their increased lifetimes become comparable to transport time step. Additional metallic ions are therefore produced via charge transfer with the downward transport of NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ at night in the TA simulation.

4 Conclusions

The WACCM-X high-altitude chemistry–climate model has been extended to incorporate the full life cycle of multiple meteoric metal ions and atoms (Mg, Na, and Fe, currently). A major advantage of WACCM-X is the self-consistent treatment of dynamics and electrodynamics, allowing us to quantitatively investigate the global distribution of metal ions and the formation mechanisms of thermospheric metal layers. The present study explores, for the first time, the seasonal variations of thermospheric metal ions by including global metal ion transport in the E and F regions.

There are a number of interesting findings: (1) a clear seasonal cycle is found in the monthly averaged global distributions of Mg⁺, in good agreement with the SCIAMACHY measurements (Langowski et al., 2015), although the peak height and peak density are about 5 km and 35 % lower than the observations, respectively. (2) Uplift of metal ions in the summer hemisphere at mid-latitudes ($\sim \mathrm{40}{}^{\circ }\pm \mathrm{10}{}^{\circ }$), driven by the vertical ion velocity due to the neutral wind, appears to explain the summer peak occurrence of lower thermospheric neutral Na layers observed by mid-latitude lidars (Wang et al., 2012; Dou et al., 2013; Yuan et al., 2014; Xun et al., 2020). (3) Upward transport of metallic ions by E×B forcing is generally consistent with the fountain effect. (4) The formation of thermospheric neutral metal layers is strongly influenced by the upward transport of ions, since metallic atoms and ions are coupled by relatively fast reactions in the lower thermosphere (Plane et al., 2015). (5) A pronounced mass separation of Fe⁺ with the two lighter ions, Mg⁺ and Na⁺, is demonstrated above 150 km, with the ratio between the lighter ions (Mg⁺ and Na⁺) and heavier ions (Fe⁺) increasing with height by more than a factor of 2 above 150 km. More satellite observations of the ${\mathrm{Mg}}^{+}/{\mathrm{Fe}}^{+}$ ratio are needed to test this prediction. (6) The role of NO⁺ and ${\mathrm{O}}_{\mathrm{2}}^{+}$ transport in the distribution of metal ions in the model is examined by comparing the two simulation results. It is found that they have little effect on the monthly means of metal ions but affect the peak heights of metallic ions in the descending phase of the fountain effect.

Previous research has established that thermospheric neutral metal layers are modulated by dynamics (e.g. gravity waves, atmospheric tides) (e.g. Chu et al., 2011; Xue et al., 2013; Liu et al., 2016; Cai et al., 2017; Qiu et al., 2016; Chu et al., 2020). In the future, this new version of WACCM-X can be used to better investigate the effect of lower atmospheric dynamical processes on the formation of thermospheric neutral metal layers using the “specified dynamics” version of the model (SD-WACCM-X).