Impact of pyruvic acid photolysis on acetaldehyde and peroxy radical formation in the boreal forest: theoretical calculations and model results

Based on the first measurements of gas-phase pyruvic acid (CH₃C(O)C(O)OH) in the boreal forest, we derive effective emission rates of pyruvic acid and compare them with monoterpene emission rates over the diel cycle. Using a data-constrained box model, we determine the impact of pyruvic acid photolysis on the formation of acetaldehyde (CH₃CHO) and the peroxy radicals CH₃C(O)O₂ and HO₂ during an autumn campaign in the boreal forest.

The results are dependent on the quantum yield (φ) and mechanism of the photodissociation of pyruvic acid and the fate of a likely major product, methylhydroxy carbene (CH₃COH). With the box model, we investigate two different scenarios in which we follow the present IUPAC (IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation, 2021) recommendations with φ = 0.2 (at 1 bar of air), and the main photolysis products (60 %) are acetaldehyde + CO₂ with 35 % C–C bond fission to form HOCO and CH₃CO (scenario A). In the second scenario (B), the formation of vibrationally hot CH₃COH (and CO₂) represents the main dissociation pathway at longer wavelengths (∼ 75 %) with a ∼ 25 % contribution from C–C bond fission to form HOCO and CH₃CO (at shorter wavelengths). In scenario 2 we vary φ between 0.2 and 1 and, based on the results of our theoretical calculations, allow the thermalized CH₃COH to react with O₂ (forming peroxy radicals) and to undergo acid-catalysed isomerization to CH₃CHO.

When constraining the pyruvic acid to measured mixing ratios and independent of the model scenario, we find that the photolysis of pyruvic acid is the dominant source of CH₃CHO with a contribution between ∼ 70 % and 90 % to the total production rate. We find that the photolysis of pyruvic acid is also a major source of the acetylperoxy radical, with contributions varying between ∼ 20 % and 60 % dependent on the choice of φ and the products formed. HO₂ production rates are also enhanced, mainly via the formation of CH₃O₂. The elevated production rates of CH₃C(O)O₂ and HO₂ and concentration of CH₃CHO result in significant increases in the modelled mixing ratios of CH₃C(O)OOH, CH₃OOH, HCHO, and H₂O₂.

1 Introduction

Organic acids play a crucial role in tropospheric chemistry, impacting secondary organic aerosol formation, air quality, and climate (Kanakidou et al., 2005; Hallquist et al., 2009). Pyruvic acid (CH₃C(O)C(O)OH), an organic acid that is central in plant metabolism as part of the Krebs cycle (Walker, 1962), is found in tropospheric air in the gas phase as well as in the aerosol phase, especially in the boundary layer over vegetated regions. Gas-phase mixing ratios ranging from a few to several hundred parts per trillion (pptv) have been reported in various locations around the world, including the tropical rainforest, boreal forest, rural areas with temperate forest, and regions influenced by urban outflow. A recent overview of existing measurements of gas-phase pyruvic acid is given by Eger et al. (2020).

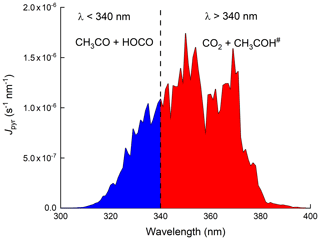
Figure 1 Wavelength-resolved photolysis rates (J_pyr) for 13 September 2016 at solar noon. J_pyr was calculated using a photolysis quantum yield of 1 and the absorption cross sections at 298 K preferred by IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation (2021).

A known source of pyruvic acid is the photo-oxidation of isoprene, via the ozonolysis of methyl vinyl ketone and subsequent hydrolysis of the Criegee intermediates (Jacob and Wofsy, 1988; Grosjean et al., 1993; Paulot et al., 2009). Further potential sources are the photolysis of methylglyoxal (Raber and Moortgat, 1995), the gas-phase photo-oxidation of aromatics in the presence of NO_x (Grosjean, 1984; Praplan et al., 2014), the aqueous-phase oxidation of methylglyoxal (Stefan and Bolton, 1999), and reactions taking place within biomass burning plumes (Andreae et al., 1987; Helas et al., 1992). In addition, pyruvic acid has been reported to be directly emitted from vegetation (Talbot et al., 1990; Jardine et al., 2010a, b; Eger et al., 2020). Compared to acetic acid, the presence of a second (non-acidic) carbonyl group imparts on pyruvic acid an absorption spectrum that extends from ultraviolet to visible wavelengths (see Fig. 1), and photolysis is a major sink of pyruvic acid in the boundary layer, with deposition and heterogeneous uptake to the aerosol phase also contributing to its removal. Photolysis of pyruvic acid in air results in a number of different radical and stable products; the major ones are expected to be acetaldehyde, HO₂, and CH₃C(O)O₂ (more details are presented in Sect. 1.1). These products can have a significant impact on tropospheric chemistry, e.g. via the formation of peroxyacetyl nitrate (PAN), peracetic acid, and formaldehyde (HCHO).

Global models have recently revealed discrepancies between simulated and measured acetaldehyde concentrations (Millet et al., 2010; Wang et al., 2019; Wang et al., 2020). Wang et al. (2020) reported CH₃CHO mixing ratios that were up to a factor of 10 higher than predicted by a global chemistry-transport model (EMAC) in the marine boundary layer around the Arabian Peninsula, implying missing sources of CH₃CHO in remote and polluted regions. Wang et al. (2019) also found that models systematically underestimate CH₃CHO compared to observations, implying a missing source of acetaldehyde in the remote troposphere. This finding was supported by the simultaneous measurement of peracetic acid (which is formed, for example, via the degradation of acetaldehyde in remote environments) with the organic aerosol source of CH₃CHO also being insufficient to explain the results. Instead, Wang et al. (2019) suggested that CH₃CHO arises from the degradation of gas-phase organic compounds. Pyruvic acid, among other organic acids in the gas and aerosol phase, might be one of the compounds that can be converted to acetaldehyde in the remote troposphere, and its integration into global models might contribute to resolve discrepancies, especially in forested regions.

Generally, field measurements as well as modelling and laboratory-based kinetic studies on pyruvic acid are limited, and its impact on atmospheric chemistry is still poorly understood. In this study we highlight the potential role of pyruvic acid in the boreal forest, one of the largest terrestrial biomes on Earth. For this, we use data from a measurement campaign in 2016 (IBAIRN, Influence of Biosphere–Atmosphere Interactions on the Reactive Nitrogen budget).

The photolysis of pyruvic acid: quantum yields and products

Because its reaction with OH is slow (k_{OH+pyruvic acid} = 1.2 × 10⁻¹³ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molecule}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ at 298 K; Mellouki and Mu, 2003), photolysis and dry deposition are the dominant loss terms for gas-phase pyruvic acid. Heterogeneous uptake to atmospheric aerosols is also calculated to be inefficient during the IBAIRN campaign in the boreal forest (see below), where particle surface area densities were of the order of 2 × 10⁻⁷ cm² cm⁻³, and the particles contained a large organic fraction (Liebmann et al., 2019) that is likely to reduce the uptake coefficient compared to that measured for pure aqueous particles (γ = 0.06; Eugene et al. 2018).

The photodissociation of pyruvic acid at actinic wavelengths is not well understood. According to the most recent IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation (2021) evaluation, which considers experimental data until 2017, the three thermodynamically accessible photolysis channels are

$$\begin{array}{}\text{(R1)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}& {\displaystyle }+h\mathit{\nu }\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{CHO}+{\mathrm{CO}}_{\mathrm{2}}\text{(R2)}& {\displaystyle }& {\displaystyle }\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}+\mathrm{CO}\text{(R3)}& {\displaystyle }& {\displaystyle }\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{CO}+\mathrm{HOCO}.\end{array}$$

IUPAC recommends a photodissociation quantum yield (φ) of 0.2 at 1 bar pressure (i.e. for boundary layer conditions), with branching ratios of 0.6, 0.05, and 0.35 for Reactions (R1), (R2), and (R3), respectively, which implicitly assumes that the initially formed carbene (CH₃COH) immediately isomerizes to acetaldehyde. The radical products of Reaction (R3) (CH₃CO and HOCO) react rapidly in air to form peroxy radicals (Reactions R4 and R5).

$$\begin{array}{}\text{(R4)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{CO}+{\mathrm{O}}_{\mathrm{2}}+M\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right){\mathrm{O}}_{\mathrm{2}}+M\text{(R5)}& {\displaystyle }& {\displaystyle }\mathrm{HOCO}+{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{HO}}_{\mathrm{2}}+{\mathrm{CO}}_{\mathrm{2}}\end{array}$$

The formation of methylhydroxy carbene (CH₃COH) as an intermediate in pyruvic acid photolysis has been postulated for many years (Vesley and Leermakers, 1964; Yamamoto and Back, 1985). Schreiner et al. (2011) observed isomerization of singlet CH₃COH to acetaldehyde in an Ar matrix at 11 K; their high-level theoretical analysis revealed high barriers for isomerization, where H-atom tunnelling through the energy barrier led to a lifetime of about 1 h at 11 K, which favoured the formation of acetaldehyde over that of vinyl alcohol. Only very recently has CH₃COH been detected experimentally as a product of pyruvic acid photolysis in the gas-phase (Samanta et al., 2021) and its unimolecular isomerization to both CH₃CHO and CH₂=CHOH confirmed to be efficient at the experimental pressure of a few millibars (mbar) of helium. Indeed, Samanta et al. (2021) show that, at a photolysis wavelength of 351 nm (close to the maximum cross-section of pyruvic acid) formation of an energy-rich carbene (CH₃COH^#) and CO₂ (Reaction R6) is essentially the only product channel operating. CH₃CHO and CH₂=CHOH were formed subsequently (at ∼ 2:1 ratio favouring CH₃CHO) in the unimolecular isomerization of CH₃COH^# (Reactions R7 and R8).

$$\begin{array}{}\text{(R6)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}+& {\displaystyle }h\mathit{\nu }\to {\mathrm{CH}}_{\mathrm{3}}{\mathrm{COH}}^{\mathrm{\#}}+{\mathrm{CO}}_{\mathrm{2}}\text{(R7)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}{\mathrm{COH}}^{\mathrm{\#}}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{CHO}\text{(R8)}& {\displaystyle }& {\displaystyle }\to {\mathrm{CH}}_{\mathrm{2}}=\mathrm{CHOH}\end{array}$$

Samanta et al. (2021) suggest that, at ambient pressures, a significant fraction of the energized, nascent carbene will be deactivated by collisions with air (Reaction R9) and the thermalized carbene (CH₃COH), which can no longer rapidly overcome the barriers to isomerization, may react with oxygen or water vapour (Reed Harris et al., 2016, 2017b; Eger et al., 2020; Samanta et al., 2021) (Reactions R10 and R11).

$$\begin{array}{}\text{(R9)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}{\mathrm{COH}}^{\mathrm{\#}}+M\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{COH}+M\text{(R10)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{COH}+{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)+{\mathrm{HO}}_{\mathrm{2}}\text{(R11)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{COH}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{CH}(\mathrm{OH}{)}_{\mathrm{2}}\end{array}$$

As summarized by IUPAC, there have been many experimental studies deriving primary photodissociation quantum yields and product yields following the photolysis of pyruvic acid. The studies which were carried out at atmospherically relevant wavelengths (i.e. within the ∼ 300–400 nm absorption band) are listed in Table S1 in the Supplement. The experiments were carried out at different pressures of various bath gases and at different wavelengths and at different concentrations of pyruvic acid, all of which appear to play a role in determining the products formed. Table S1 shows that CO₂ is formed at a yield of close to 100 %, whereas the yield of CH₃CHO is highly variable. CH₂=CHOH has been detected both at a few torr of helium (Samanta et al., 2021) and at 1 bar of air (Calvert et al., 2011). Other end products observed during the photolysis of pyruvic acid in 1 bar of air include acetic acid (Calvert et al., 2011; Reed Harris et al., 2016, 2017b) and PAN (Grosjean, 1983; Berges and Warneck, 1992) when NO₂ was present, which together provide evidence for the formation of the acetyl peroxy radical (CH₃C(O)O₂) and thus CH₃CO, for example, in Reactions (R3) and (R4) when sunlight or solar-simulating light sources are used. Secondary products (resulting, for example, from the further reactions of CH₃CHO) such as HCHO and CH₃OH have also been observed at pressures close to 1 bar (Grosjean, 1983; Calvert et al., 2011; Reed Harris et al., 2016; Reed Harris et al., 2017a). While the Norrish type 1 process (C–C bond fission) forming CH₃CO and HOCO appears to be unimportant at 351 nm (Samanta et al., 2021), it may be favoured at wavelengths < 340 nm (Chang et al., 2014). This is illustrated in Fig. 1 where we present the wavelength-resolved photolysis rate constants across the UV absorption spectrum of pyruvic acid (assuming an overall photolysis quantum yield of 1, and absorption cross-sections recommended by IUPAC). The wavelength-resolved actinic flux was calculated for the IBAIRN measurement site on the 13 September 2016 using the Tropospheric Ultraviolet and Visible Radiation model (TUV; https://www.acom.ucar.edu/Models/TUV/Interactive_TUV/, last access: 1 September 2020). Integration of the J values at wavelengths < 340 nm indicates that (at local noon) ≈ 25 % of pyruvic acid dissociation occurs at these shorter wavelengths.

2 Methods

The goal of this study is to evaluate the impact of pyruvic acid on acetaldehyde and radical formation rates in the boreal forest using a data-constrained, chemical box model. For this purpose we make use of experimental data from a field study, which was performed in the Finnish boreal forest at the Station for Measuring Ecosystem-Atmosphere Relations II (SMEAR II) in Hyytiälä (61.846^∘ N, 24.295^∘ E; 180 m above sea level; see Hari and Kulmala, 2005), an area that is characterized by large emission rates of biogenics (mainly monoterpenes) and low-NO_x concentrations (Rinne et al., 2000; Williams et al., 2011; Aalto et al., 2015; Fischer et al., 2021).

The variability in the reported photodissociation quantum yield and product distributions (see discussion above) suggests that pyruvic acid photodissociation is not yet fully understood, In addition, the fate of the potentially dominant carbene product (Samanta et al., 2021) is unknown. Therefore, in order to better constrain the fate of CH₃COH in the atmosphere, quantum chemical calculations were undertaken to characterize its likely atmospheric reactions, for which experimental data do not exist.

2.1 The IBAIRN campaign

The IBAIRN campaign took place in September 2016, during the summer–autumn transition, and was characterized by frequent temperature inversions near ground level during night-time (Liebmann et al., 2018a), which led to the accumulation of nocturnally emitted trace gases from vegetation. A detailed description of the campaign and the instruments deployed can be found elsewhere (Liebmann et al., 2018a; Eger et al., 2020). A summary (with details of detection limit, etc.) is provided in Table S2. Briefly, pyruvic acid was measured by a chemical ionization quadrupole mass spectrometer (Eger et al., 2020), the sum of monoterpenes (henceforth referred to as MT) was measured by a PTR-ToF-MS, and single MTs were monitored by a GC-AED (Liebmann et al., 2018a). Despite some discrepancies related to instrument location and inhomogeneity in terpene emissions within the forest, both instruments were in reasonably good agreement throughout the campaign. Since a high temporal resolution is preferable for our simulation, we have used the PTR-ToF-MS dataset. NO and NO₂ were measured by a chemiluminescence detector and a cavity ring-down spectrometer (Sobanski et al., 2016; Liebmann et al., 2018b), ozone was measured by optical absorption, and CO was measured by quantum-cascade-laser absorption spectroscopy (Eger et al., 2020). Formic and acetic acid as well as methyl ethyl ketone (MEK) and methyl vinyl ketone (MVK) were taken from the continuous PTR-MS measurements at the site at heights between 42 and 336 m. Photolysis rate coefficients were derived using actinic flux measurements from a spectral radiometer (METCON GmbH) (METCON GmbH) and evaluated cross sections and quantum yields (Burkholder et al., 2015). Mixing layer (MXL) heights were derived by combining in situ measurements made by a scanning Doppler lidar (Hellén et al., 2018) with results from the ECMWF ERA-Interim reanalysis (Dee et al., 2011), with a spatial resolution of ∼ 80 km. Since the lidar was unable to resolve MXL heights < 60 m (as regularly experienced during nocturnal inversions), all values below this threshold have been set to 60 m, representing an upper limit.

2.2 Theoretical analysis of the fate of singlet methylhydroxy carbene, CH₃COH

We investigated the reactions of CH₃COH theoretically under atmospheric conditions, examining its unimolecular reactions and bimolecular reactions with O₂, H₂O, and HC(O)OH, where the latter is representative of carboxylic acids. The reaction with pyruvic acid itself is also briefly explored. The rovibrational characteristics and energetics of all critical points on the potential energy surface were characterized at the CCSD(T)/aug-cc-pVTZ//M06-2X-D3/aug-cc-pVTZ level of theory with a wavenumber scaling factor of 0.971 (Zhao and Truhlar, 2008; Dunning, 1989; Purvis and Bartlett, 1982; Grimme et al., 2011; Database of Frequency Scale Factors for Electronic Model Chemistries (Version 4); Alecu et al., 2010). This method compares favourably with the more rigorous focal point analysis of Schreiner et al. (2011), with energy differences in the singlet state unimolecular chemistry of less than 0.7 kcal mol⁻¹, indicating that the method is reliable for kinetic predictions under atmospheric temperatures. Where necessary, broken-symmetry SCF (self-consistent field) calculations were used to describe singlet biradicals (Noodleman, 1981), and IRC (intrinsic reaction coordinate) calculations were used to verify the pathways. For reactants, products, and transition states, we exhaustively characterized all conformers; for complexes we only characterized those directly connecting to a transition state. All quantum chemical calculations were performed using the Gaussian-16 program suite (Frisch et al., 2016).

The quantum chemical data were then used to calculate high-pressure rate coefficients for reactions over a saddle point using multi-conformer transition state theory (MC-TST) calculations (Vereecken and Peeters, 2003), under a rigid rotor harmonic oscillator approximation. Tunnelling corrections are performed assuming an asymmetric Eckart barrier (Eckart, 1930; Johnston and Heicklen, 1962). Most reactions have high energy barriers, and the presence of pre- and post-reaction complexes has a negligible influence on the reaction rate. For barrierless reactions, typically complexation reactions, we assume the reaction rate is close to the collision limit unless indicated otherwise.

2.3 Box model

We have used the CAABA/MECCA atmospheric chemistry box model to numerically simulate the impact of pyruvic acid photolysis on the formation of radicals and CH₃CHO over the diel cycle during the IBAIRN campaign. Our study is based on model version 4.4.2, with updated reactions related to pyruvic acid in which two different scenarios were investigated (see Sect. 3.3) in order to examine the sensitivity of the model output to, for example, photolysis quantum yields and products.

The chemical mechanism used in this study contains > 600 gas-phase species and ∼ 2000 gas-phase reactions and photolysis steps. In addition to the basic ozone, HO_x and NO_x chemistry, the mechanism contains the detailed “Mainz Organic Mechanism” (MOM) for non-methane hydrocarbons (NMHC), isoprene, terpenes, and aromatics. MOM is derived from a reduced version of the Master Chemical Mechanism (MCM). Full details about CAABA/MECCA and MOM are available in Sander et al. (2019). Photolysis reactions are calculated for a latitude of 62^∘ N. A complete reaction scheme and source of rate coefficients can be found in the data archive (see Data availability section).

Several parameters (temperature, pressure, relative humidity) and trace-gas concentrations (pyruvic acid, O₃, NO, NO₂, PAN, CO, MTs, formic and acetic acid, methyl ethyl ketone (MEK), and methyl vinyl ketone, MVK) as well as the photolysis rate constants of various trace gases were constrained to values measured during the IBAIRN campaign.

Based on the GC-AED measurements, the MTs were split into α-pinene (49 %), β-pinene (13 %), Δ-carene (27 %), and camphene (8 %). Limonene is not included in the standard chemical mechanism of CAABA/MECCA, but as its contribution to the MTs during IBAIRN was only 3 % it was treated as Δ-carene (increasing the Δ-carene contribution to 30 %).

The atmospheric methane mixing ratio was set to a constant value of 1.8 ppmv. Non-methane alkanes, the degradation of which represents ∼ 30 %–45 % of the acetaldehyde source globally (Millet et al., 2010), were constrained to 1000 pptv of ethane, 250 pptv of propane, and 150 pptv of n-butane, as found in similar environments in Finland (Hakola et al., 2006; Hellén et al., 2015). The mixing ratio of PAN, which is generally the most abundant of the peroxy acetyl nitrates (PNs), was calculated from a measurement of the sum of peroxy nitrates, whereby [PAN] = 0.9 × Σ[PNs] (estimation based on observations by, for example, Shepson et al., 1992b; Roberts et al., 2004; Roiger et al., 2011). The model-generated, averaged OH concentration through the diel cycle was in good agreement (within ∼ 20 %) with that calculated from the correlation of ground-level OH measurements with UVB radiation intensity at the Hyytiälä site (with [OH] = 5.62 × 10⁵ [UVB]^0.62 molecule cm⁻³ when UVB is in units of W m⁻²; Petäjä et al., 2009; Hellén et al., 2018) but showed more variability resulting from changes in NO mixing ratios and the conversion of HO₂ to OH.

3 Results and discussion

In the following, we analyse in situ measurements of pyruvic acid to derive emission rates, present the results of the theoretical calculations of the fate of CH₃OH, and discuss the box-model output for the IBAIRN campaign with a focus on pyruvic acid emission rates and its impact on acetaldehyde and radical chemistry in the boundary layer of the boreal forest.

3.1 Pyruvic acid emission rate relative to monoterpenes during IBAIRN

In order to derive the pyruvic acid emission rate (E_pyr) during IBAIRN, we assume that only photolysis and dry deposition contribute significantly to its overall loss rate and that pyruvic acid is in steady state. The latter assumption is reasonable as its mean lifetime was (2 ± 0.5) h. Due to a homogeneous fetch at the measurement site, we can neglect transport processes, and E_pyr is defined by Eq. (1), where [pyr]_ss is the measured mixing ratio, J_pyr is the photolysis rate constant of pyruvic acid, k_dep is the first-order loss rate constant for its dry deposition, and h_MXL is the well-mixed boundary layer height.

$$\begin{array}{}\text{(1)}& E_{\text{pyr}}=[\mathrm{pyr}{]}_{\mathrm{ss}}(J_{\text{pyr}}+k_{\text{dep}})h_{\text{MXL}}\end{array}$$

E_pyr is effectively an emission rate normalized to the MXL height (h_MXL). As the photolysis is a substantial fraction of the overall losses of CH₃C(O)C(O)OH, the choice of quantum yield φ directly impacts the calculated emission rate.

The deposition rate of pyruvic acid was calculated from k_dep = $v_{\text{dep}}{h}_{\text{MXL}}^{-\mathrm{1}}$ during the day and k_dep = $\mathrm{2}{v}_{\text{dep}}{h}_{\text{MXL}}^{-\mathrm{1}}$ during the night (Shepson et al., 1992a), with the transition following the diel variation in the mixing layer height h_MXL (see Fig. S1 in the Supplement). Further, as pyruvic acid and H₂O₂ have similar solubilities, we assumed that their deposition velocities are equal, so that v_dep = 8.4 cm s⁻¹ during the day and v_dep = 0.8 cm s⁻¹ during the night, as derived by Crowley et al. (2018) for the same site. This resulted in a minimum dry-deposition loss rate constant of k_dep = 0.9 × 10⁻⁴ s⁻¹ during the day and a maximum of k_dep = 1.8 × 10⁻⁴ s⁻¹ during the night.

The same calculation is performed for the MTs (E_MT) over the same period (and thus for the same MXL height). We note that h_MXL controls not only the value of k_dep, but also directly affects the mixing ratios of both MTs and pyruvic acid for a given emission rate. The relative emission rate ($E_{\text{pyr}}/E_{\text{MT}}$) can be calculated from Eq. (2), where terms in square brackets are concentrations.

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{E_{\text{pyr}}}{E_{\text{MT}}}}={\displaystyle \frac{[\mathrm{pyr}{]}_{\mathrm{ss}}(J_{\text{pyr}}+k_{\text{dep}})}{[\mathrm{MT}{]}_{\mathrm{ss}}\left(k_{\mathrm{OH}}\left[\mathrm{OH}\right]+k_{{\mathrm{NO}}_{\mathrm{3}}}\left[{\mathrm{NO}}_{\mathrm{3}}\right]+k_{{\mathrm{O}}_{\mathrm{3}}}\left[{\mathrm{O}}_{\mathrm{3}}\right]\right)}}\end{array}$$

In the denominator, k_OH, $k_{{\mathrm{NO}}_{\mathrm{3}}}$, and $k_{{\mathrm{O}}_{\mathrm{3}}}$ are rate coefficients for reaction of MTs with OH, NO₃, and O₃, respectively. As we do not have GC data at high time resolution, an effective rate coefficient for loss of the monoterpenes was derived from the mean MT composition as measured by GC-AED (49 % α-pinene, 13 % β-pinene, 27 % carene (sum of 2-carene and 3-carene), 3 % d-limonene, and 8 % camphene) and the corresponding rate coefficients (Perring et al., 2013; Gaona-Colman et al., 2017; IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation, 2021). This will introduce significant uncertainty (factor of ∼ 2) into the calculation of the MT emission rates. Further uncertainty arises from the measurement of pyruvic acid, ΣMT, OH, O₃, NO₃, h_MXL, and J_pyr. In particular, the results are very sensitive to the deposition velocity (v_dep) of pyruvic acid, which is an estimate based on the deposition velocity of H₂O₂, which itself has an uncertainty of ∼ 90 % (Fischer et al., 2019). Further, our calculations are based on the assumption that the sources of pyruvic acid and MT are evenly distributed, and measurements made at ∼ 8.5 m above the ground are representative of the entire boundary layer (i.e. that the boundary layer is well-mixed, including the very shallow boundary layer at night). A gradient in pyruvic acid mixing ratios at night cannot be ruled out, which would impact on our results. We estimate that the emission ratio ($E_{\text{pyr}}/E_{\text{MT}}$) in Eq. (2) is associated with an overall uncertainty of a factor of ∼ 3 notwithstanding the use of different quantum yields (and thus J values) for pyruvic acid photolysis.

A time series of pyruvic acid and MT mixing ratios along with the MXL height (h_MXL) derived from a lidar measurement and from the ERA-Interim reanalysis is shown in Fig. S2. Whereas both MXL height datasets agree very well during the night when the MXL is shallow (usually < 100 m), the lidar data are on average a factor of ∼ 2 lower during the day and characterized by a much higher variability. For the derivation of the diel profile of h_MXL (Fig. S1), we took an average of both datasets. The diel variation displayed in Fig. S2, with the highest MT mixing ratios at night, is characteristic of this boreal forest site and has been observed in earlier studies (Hellén et al., 2018).

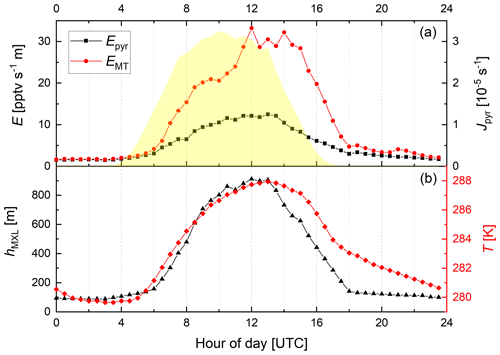
Figure 2 Diel variation of the (MXL height-corrected) emission rates of pyruvic acid (E_pyr, scenario B) and monoterpenes (E_MT) along with J_pyr (yellow shaded), T, and h_MXL for the IBAIRN campaign.

In the following, we focus on the mean, diel profiles of E_pyr, E_MT, J_pyr, T, and h_MXL for the IBAIRN campaign, which are presented in Fig. 2. A plot showing the variability of the MT and pyruvic acid mixing ratios over the same period was previously reported (see Fig. 3 of Eger et al., 2020).

During September, the emission rate of pyruvic acid (E_pyr) reaches its maximum a few hours after solar noon when the temperature peaks, similar to E_MT. However, the amplitude of the day-to-night difference in E_pyr is a factor of ∼ 3 smaller than observed for E_MT. This could indicate that pyruvic acid emissions are less temperature-dependent than MT emissions (see below) and that other environmental factors might additionally play a role at this time of year.

The emission rates of the MTs derived as described above show a large day–night variation with values a factor of ∼ 20 larger around noontime compared to midnight. This is significantly larger than the expected variation (factor of 2–3) based on the average noon-to-midnight temperature difference of 10 K and the parameterization of Guenther et al. (1993), whereby $E_{\text{MT}}\propto \exp \left(\mathit{\beta }\right(T-\mathrm{297}\mathrm{K}\left)\right)$ with β = 0.1 K⁻¹ (which is in line in with the empirical value of β = 0.12 K⁻¹ that was derived for this site in September by Hellén et al., 2018). One potential reason for this discrepancy may be emissions in autumn from fresh leaf litter that significantly contribute to the observed mixing ratios (Hellén et al., 2018) although the assumption of evenly distributed sources and a well-mixed boundary layer is not necessarily valid during the night, especially during strong temperature inversions.

Figure S3 shows that the daytime emission of pyruvic acid relative to MT ($E_{\text{pyr}}/E_{\text{MT}}$) varies by a factor of ∼ 2, depending on the chosen scenario, whereas the nighttime emission ratio is only dependent on the deposition velocity of pyruvic acid. For further analysis we adopt a quantum yield of 0.2, as presently preferred by IUPAC. On average, ($E_{\text{pyr}}/E_{\text{MT}}$) ∼ 0.6, with a minimum value of ∼ 0.3 in the evening and a maximum value of ∼ 1 in the early morning, indicating elevated pyruvic acid emissions relative to MT at night. To derive a T-dependent expression from the diurnal profile of the emission factor, we fit an exponential function to the plot of temperature versus $E_{\text{pyr}}/E_{\text{MT}}$ (Fig. S4), yielding

$$\begin{array}{}\text{(3)}& E_{\text{pyr}}=\left[\mathrm{0.28}+\mathrm{3.17}\cdot \exp \left({\displaystyle \frac{\mathrm{273}-T}{\mathrm{4.24}}}\right)\right]\cdot \text{EMT}.\end{array}$$

We note that (like the values of E_pyr) the temperature dependence derived is strongly influenced by the diel variation of the MXL height and thus carries significant uncertainty and may not be transferable to other locations or even times of the year.

As our measurements of pyruvic acid are the first to have been made in the boreal forest, we cannot compare our relative emission ratio ($E_{\text{pyr}}/E_{\text{MT}}$) with previous measurements in a similar environment. Instead, where possible, we derive the emission ratio from measurements of MTs, isoprene, and pyruvic acid in warmer climates.

Table 1 Emission rate of pyruvic acid (E_pyr) relative to isoprene (E_iso) and MT (E_MT).

Jardine et al. (2010b) performed measurements in an enclosed (glass dome) tropical forest biome at Biosphere 2 in Arizona, US, where they found maximum mixing ratios of 120 ppbv isoprene, 6 ppbv MTs, and 15 ppbv pyruvic acid. As the glass dome absorbed actinic wavelengths and prevented active photochemistry, the chemical loss processes for pyruvic acid, isoprene, and MT (including photolysis and reactions with OH, O₃, and NO₃) are negligible. Initially disregarding the deposition of isoprene and MT, we derive lower limits of ($E_{\text{pyr}}/E_{\text{iso}}$) ∼ 0.17 and ($E_{\text{pyr}}/E_{\text{MT}}$) ∼ 4 (see Table 1). However, due to the presence of large concentrations of isoprene-consuming microbes in the soil of Biosphere 2, the isoprene loss rate via deposition may be enhanced, which will decrease the effective emission ratio ($E_{\text{pyr}}/E_{\text{iso}}$). In addition, branch enclosure studies were performed on a Mangifera indica (mango) tree within Biosphere 2, yielding mean fluxes (in $\mathrm{nmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) of 3.2 for isoprene, 0.09 for MT, and 0.15 for pyruvic acid. Pyruvic acid emissions peaked during the day when temperature and photosynthetically active radiation (PAR) were highest and correlated very well with isoprene emissions and (to a certain extent) with MT emissions. Assuming that a mango tree is representative of the tropical vegetation, we derive an emission ratio of ($E_{\text{pyr}}/E_{\text{iso}}$ ∼ 0.05 and ($E_{\text{pyr}}/E_{\text{MT}}$) ∼ 1.7 (see Table 1), which is consistent with our estimations for the IBAIRN campaign. However, given that Talbot et al. (1990) observed great variability in pyruvic acid emission fluxes among five different tree species during measurements in the tropical Ducke Forest Reserve close to Manaus, Brazil, this agreement may, to some extent, be coincidental. Talbot et al. (1990) also reported a mean emission flux (derived from enclosure experiments) relative to isoprene of ($E_{\text{pyr}}/E_{\text{iso}}$) ∼ 0.003, which is about 1 order of magnitude smaller than in the study of Jardine et al. (2010b). In a further branch enclosure study by Jardine et al. (2010a) emissions from a creosote bush (Larrea divaricata), which is typically found in US drylands, were investigated. Average noontime branch emission rates (in $\mathrm{\mu }\mathrm{g}\mathrm{C}{\mathrm{gdw}}^{-\mathrm{1}}{\mathrm{h}}^{-\mathrm{1}}$) of 7.5, 10.4, and 0.2 for isoprene, MT, and pyruvic acid resulted in relative emission ratios of ($E_{\text{pyr}}/E_{\text{iso}}$) ∼ 0.05 and ($E_{\text{pyr}}/E_{\text{MT}}$) ∼ 0.07 for this mixed isoprene–MT-emitting species.

The comparison with the few datasets available in the literature indicates that the variability of the emission factors ($E_{\text{pyr}}/E_{\text{MT}}$) and ($E_{\text{pyr}}/E_{\text{iso}}$) among different plant species and different environments is large. In addition, a lack of pyruvic acid measurements over different seasons in the boreal forest means that we cannot exclude that the value we derive is biased by emissions (e.g. from ground-level, decaying plant litter in September) that are particular to this season and environment. The emission rates we derive are therefore relevant for the autumnal boreal forest but require validation before being extended to other regions and seasons with confidence.

3.2 Theoretical calculations on the fate of CH₃COH

Singlet methylhydroxy carbene, CH₃COH, is best characterized as having an sp²-hybridized central carbon, bearing an in-plane lone pair in an sp² orbital and an empty p orbital perpendicular to the CCO plane. The lone pairs of the hydroxy O atom back-donate into the empty p orbital, such that the most favourable geometry has the hydroxy–H atom in the CCO plane. The orientation of the terminal OH group has a large impact on the energy, with 3 kcal mol⁻¹ energy difference between the syn- and anti-conformers. Due to the interaction between the hydroxy O atom and the carbene functionality, internal rotation of the OH group has a very high barrier, 24 kcal mol⁻¹. Concomitantly, syn/anti-interconversion is very slow, with predicted rate coefficients at 300 K of less than 10⁻² s⁻¹. Under atmospheric conditions, thermalized syn- and anti-CH₃COH are thus best considered as separate species, with possibly distinct chemistry. No information is available on the relative yield of these conformers from pyruvic acid photolysis.

Table 2 Theory-predicted high-pressure rate coefficients for reaction of singlet CH₃COH.

Calculations were performed at the CCSD(T)//M06-2X-D3 with MC-TST level of theory. Rate coefficients are given at 298 K (s⁻¹ or ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molecule}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$). Temperature-dependent rate coefficients can be calculated using the parameters of a Kooij expression k(200-450 K) = $A\cdot (T/K{)}^n\cdot \exp (-E_{\mathrm{a}}/T)$ with A given per second (s⁻¹) or cubic centimetres per molecule per second (${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molecule}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$) and E_a in kelvin (K).

3.2.1 Unimolecular reactions of CH₃COH

Both syn- and anti-CH₃COH can isomerize to vinyl alcohol over high barriers ≥ 24 kcal mol⁻¹ (see Fig. 3). Anti-CH₃COH has an additional pathway for isomerization to acetaldehyde, with a barrier of 23 kcal mol⁻¹. Due to these high barriers, the thermal rate of isomerization is comparatively slow, with a 300 K rate coefficient of ≤ 4 × 10⁻⁴ s⁻¹ (see Table 2). As already discussed by Schreiner et al. (2011), formation of CH₃CHO from anti-CH₃COH is most favourable at low temperatures, owing to a thinner energy barrier and hence faster tunnelling. At temperatures above 260 K, we find that formation of CH₂=CHOH from anti-CH₃COH becomes dominant, with a ∼ 3.5:1 ratio of CH₂=CHOH to CH₃CHO at room temperature.

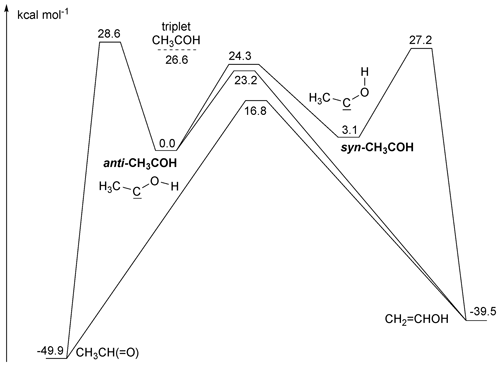
Figure 3 Zero point energy (ZPE)-corrected potential energy surface for unimolecular reactions of singlet CH₃COH at the CCSD(T)//M06-2X-D3 level of theory.

Given the low predicted thermal rate coefficients, it seems unlikely that the experimentally observed acetaldehyde and vinyl alcohol in pyruvic acid photolysis are formed from isomerization of thermalized CH₃COH. The energy distribution of energized, nascent carbenes would be rather broad as the available energy upon pyruvic acid photodissociation is distributed over all fragments and their relative motion, and the isomerization yield would then be pressure-dependent. The CH₃CHO and CH₂=CH₂OH isomers formed would have enough energy to undergo keto-enol tautomerization, but given the high barrier exceeding 55 kcal mol⁻¹, it is more probable they will instead be stabilized by collisional energy loss.

Figure 4 ZPE-corrected potential energy surface for reaction of singlet CH₃COH with O₂ at the CCSD(T)//M06-2X-D3 level of theory.

3.2.2 Reaction of CH₃COH with O₂

Under atmospheric conditions, the reaction with O₂ is potentially an important loss process for CH₃COH (Reed Harris et al., 2016, 2017a; Eger et al., 2020). The potential energy surface is shown in Fig. 4. Contrary to radicals, which react with O₂ by (near-)barrierless radical recombination, the singlet CH₃COH carbene does not have an unpaired electron and the reaction proceeds mostly by association of its out-of-plane empty p orbital with a lone electron pair in O₂, requiring orbital rearrangement to a triplet C^•OO^• moiety with a sp³-hybridized central carbon. This unfavourable process has high barriers, > 9 kcal mol⁻¹, and concomitantly low rate coefficients, k(298 K) ∼ 10⁻²⁰ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molecule}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ (see Table 2). The rate coefficient is however highly uncertain, owing to an uncertainty (∼ 1 to 2 kcal mol⁻¹) on the barrier height.

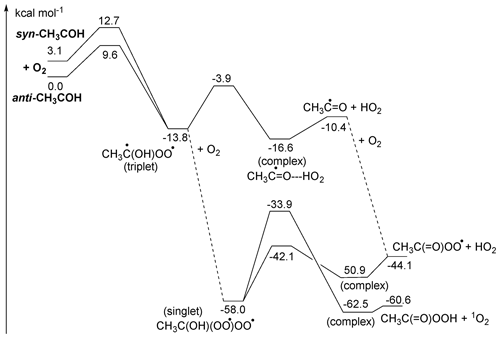
The decomposition of the CH₃C^•(OH)OO^• triplet diradical intermediate, forming CH₃C^•=O + HO₂, is reminiscent of the chemistry of α-OH alkyl radicals with unpaired electrons and should occur rapidly owing to the sufficiently high energy content of the peroxyl-alkyl diradical (Hermans et al., 2005, 2004; Dillon et al., 2012; Olivella et al., 2001; Dibble, 2002). Note that this chemistry is very distinct from that of the singlet CH₃C(OH)OO Criegee intermediate. The acyl radical product is expected to recombine rapidly with a second O₂ molecule, forming acylperoxy radicals, CH₃C(=O)OO^•. Alternatively, the triplet CH₃C^•(OH)OO^• intermediate can react with a second O₂ molecule by a barrierless recombination reaction (Fig. 4), forming the diperoxy singlet diradical CH₃C(OH)(OO^•)OO^•, which in turn can eliminate HO₂, similar to other α-OH peroxy radicals, forming the acylperoxy radicals directly. This second O₂ addition is sufficiently exothermic to allow for formation of peracetic acid with a singlet O₂ molecule, but this process has a rather large barrier of ∼ 24 kcal mol⁻¹ and is expected to be a minor contributor, leaving CH₃C(O)O₂ + HO₂ as the likely dominant products of the overall reaction of CH₃COH with oxygen molecules.

3.2.3 Reactions of CH₃COH with carboxylic acids

Samanta et al. (2021) observed loss of CH₃COH via reaction with pyruvic acid, which may indicate that its fate in the atmosphere may also be (partially) controlled by similar reactions. To theoretically investigate the reaction of CH₃COH with carboxylic acids, we used formic acid in the calculations. Not only is formic acid an abundant organic acid in the atmospheric boundary layer, but also its reactivity is related to the properties of the –C(=O)OH moiety, and the results are transferable to other oxoacids, including pyruvic acid, which was present in high concentrations in most laboratory investigations.

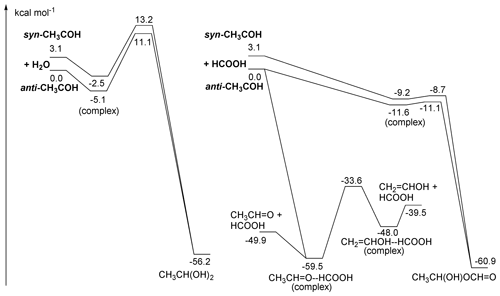
Figure 5 ZPE-corrected potential energy surface for reactions of singlet CH₃COH with H₂O (left) and HCOOH (right) at the CCSD(T)//M06-2X-D3 level of theory.

As shown in Fig. 5, CH₃COH forms strong complexes with HC(O)OH, with 11 kcal mol⁻¹ stability. From this complex, an addition process occurs that is best described as the transfer of the acidic H⁺ atom to the carbene lone pair on the CH₃COH central carbon, with simultaneous association of one of the negatively charged lone electron pair of the carbonyl oxygen to the carbene vacant p orbital, forming a 1-hydroxyethyl ester (CH₃CH(OH)OC(O)H). Due to the concerted association of the two carbene orbitals with suitable partners in the carboxylic moiety, this process has a very low barrier (≤ 1 kcal mol⁻¹). This mechanism is feasible due to the size of the –C(O)OH group and the possibility of shifting the double bond to the other oxygen atom upon H-atom loss. For the anti-CH₃COH carbene, we also found that an in-plane approach of the carboxylic acid towards the COH moiety in methylhydroxy carbene can simultaneously transfer the acidic H atom to the carbene carbon while the carbene hydroxy H atom is transferred to the carbonyl oxygen in the acid, reforming the HC(O)OH co-reactant. This catalysis reaction converts anti-CH₃COH to acetaldehyde, CH₃CHO, without an energy barrier. Both adduct formation and the catalysis reaction should proceed with rate coefficients near the collision limit.

Carboxylic acids can also catalyse keto-enol tautomerization, possibly helping the isomerization between CH₃CHO and CH₂=CH₂OH by reducing the effective barrier by over 50 kcal mol⁻¹ though the thermal reaction remains slow (see Table 2). The only reaction of CH₃COH that has been investigated experimentally to date is that with pyruvic acid (Samanta et al., 2021), which we also examine theoretically in the Supplement. Note that the large rate coefficient for CH₃COH with organic acids calculated here would imply that reaction of thermalized CH₃COH with pyruvic acid would overwhelm any other bimolecular CH₃COH reaction in their work and most of the experiments listed in Table S1.

3.2.4 Reactions of CH₃COH with H₂O

Based on the reactivity of small carbenes towards closed-shell molecules, Samanta et al. (2021) suggested that reaction with H₂O might be an important loss process of the CH₃COH carbene intermediate. We have characterized the insertion reaction of CH₃COH in the H₂O molecule and found very high barriers, ≥ 11 kcal mol⁻¹, with very low rate coefficients ∼ 10⁻²⁰ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molecule}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ (see Fig. 5 and Table 2). The reaction is significantly slower than with carboxylic acid as the smaller H₂O molecule is unable to simultaneously reach both carbene orbitals in a favourable geometry. The reaction of H₂O with CH₃COH is best described as a shift of an H⁺ atom to the carbene lone pair orbital, followed by migration of the water HO⁻ moiety to the vacant carbene orbital to form a bond with a lone electron pair. The reaction is further hindered by the back-donation of the CH₃COH oxygen atom into the vacant carbene orbital, partially filling the vacant carbene orbital and reducing the reactivity of the carbene functionality. We therefore propose that CH₃COH will be significantly less reactive towards closed shell species than the ²CH and ¹CH₂ carbenes which are known to exhibit very fast insertion and cyclo-addition reactions (Vereecken et al., 1998; Goulay et al., 2009; Douglas et al., 2019; Jasper et al., 2007; Gannon et al., 2010).

3.2.5 Summary of theoretical calculations: the fate of thermalized CH₃COH in 1 bar of air

The theoretical analysis of the fate of CH₃COH carbene intermediates formed in PA photolysis indicates that the acetaldehyde formation observed in many experiments could be the result of a fast catalysis reaction of CH₃COH with pyruvic acid, which under typical experimental conditions dominates over competing reactions, such as with O₂, by several orders of magnitude. This conclusion is consistent with the experimental observations of Reed Harris et al. (2017a), who report a reduction in the acetaldehyde yield when low pyruvic acid concentrations are used and an increase in the formation of acetic acid (which can be formed in the reaction of CH₃C(O)O₂ radicals with HO₂). In the atmospheric boundary layer atmosphere, where the concentrations of organic acids may lie between 10¹⁰ and 10¹¹ molecule cm⁻³ (Millet et al., 2015) and that of O₂ is close to 5 × 10¹⁸ molecule cm⁻³, the reactions of CH₃COH with organic acids and O₂ are competitive, whereas reaction of CH₃COH with water is minor. Table 2 lists the predicted rate coefficients for these reactions.

3.3 Box-model results: contribution of pyruvic acid to acetaldehyde and radical formation

To account for the large variability in photodissociation quantum yields and product yields reported in the literature (see above), we modelled two scenarios, A and B:

• Scenario A. In this scenario we used pyruvic acid cross sections, quantum yields, and product yields according to the IUPAC recommendations with a photodissociation quantum yield (φ) of 0.2 at 1 bar pressure and branching ratios of 0.6, 0.05, and 0.35 for Reactions (R1), (R2), and (R3) as listed in Sect. 1.1.

• Scenario B. Here we use the same absorption cross-sections as scenario A but build on the recent observations of (Samanta et al., 2021) and the theoretical work presented in Sect. 3.2, which considers the formation and fate of an excited CH₃COH molecule (+ CO₂). In scenario B, we consider the effects of using photodissociation quantum yields of 0.2, 0.5, and 1 (scenarios B_0.2, B_0.5, and B₁, respectively). Photolysis at wavelengths < 340 nm was considered to generate CH₃CO + HOCO, whereas photolysis at wavelengths > 340 nm was assumed to form CO₂ + energy rich CH₃COH^#, which undergoes the reactions outlined in Sect. 1. Assuming a quantum yield that is independent of wavelength results in 25 % of pyruvic acid photolysis at noon taking place at wavelengths < 340 nm and 75 % at wavelengths > 340 nm. In the model, we assume that this ratio does not change (i.e. we neglect wavelength-dependent variations in the relative actinic flux through the diel cycle). The values of 25 % and 75 % listed above roughly correspond to the relative importance of peroxy radical formation (via Reactions R3, R4, and R5) at the shorter wavelengths compared to CH₃COH + CO₂ formation (Reaction R6) at the longer wavelengths. Some experimental data indicate that addition of O₂ can reduce the CH₃CHO yield in favour of formation of, for example, acetic acid. For this reason we use a rate coefficient for reaction of CH₃COH with O₂ that is competitive with the reaction between CH₃COH and organic acids. This is a factor of ∼ 10 larger than the value obtained theoretically, but we consider this value still within the uncertainty (∼ 1 to 2 kcal mol⁻¹ on the barrier height) of our current theoretical results as the peculiar wavefunction of CH₃COH may require even higher levels of theory to be described accurately.

In the box model, in addition to reaction with O₂, the thermalized carbene also reacts with formic and acetic acids to form acetaldehyde:

$$\begin{array}{}\text{(R12)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{COH}+\mathrm{HCOOH}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{CHO}+\mathrm{HCOOH}\text{(R13)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{COH}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{CHO}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}\end{array}$$

with a rate coefficient of 5 × 10⁻¹¹ ${\mathrm{cm}}^{\mathrm{3}}{\mathrm{molecule}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$.

We assumed that (at 1 bar) 70 % of CH₃COH^# was quenched to CH₃COH, 20 % isomerized to CH₃CHO, and 10 % isomerized to CH₂=CHOH in order to reproduce the CH₃CHO-to-CH₂=CHOH ratio reported by Samanta et al. (2021). A summary reaction scheme for the photodissociation of pyruvic acid and the fate of the initial products is given in the SI.

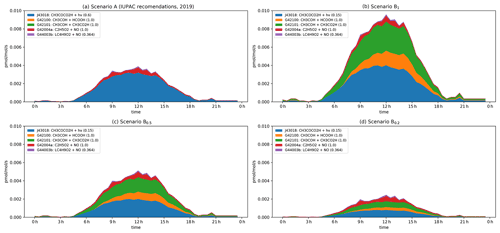
Figure 6 Modelled rates of CH₃CHO formation (in pptv s⁻¹) through the diel cycle from photolysis of pyruvic acid (blue, orange, and green) and other reactions during IBAIRN. (a) Scenario A (IUPAC). (b) Scenario B₁. (c) Scenario B_0.5. (d) Scenario B_0.2. In the legend, the first term is the equation tag used by CAABA/MECCA for the reaction. LC4H9O2 is the peroxy radical formed in the reaction of OH with butane. A full listing of the reactions can be downloaded (see Data availability section).

3.3.1 CH₃CHO formation

The modelled formation of CH₃CHO from pyruvic acid photolysis through the diel cycle when considering scenario A is displayed as a stacked plot of contributing reactions in Fig. 6. Immediately apparent from this figure is the dominance of pyruvic acid photolysis compared to all other processes. Under scenario A, even with the low quantum yield (φ = 0.2) recommended by IUPAC, pyruvic acid photolysis contributes > 80 % to the overall CH₃CHO production term, with a maximum of ∼ 15 % (at noon) arising from reactions of the ethylperoxy radical, formed in the reaction of OH with ethane (7.5 %) and butane (3.75 %) and in the photolysis of CH₃C(O)C₂H₅ (3.75 %).

Under scenario B, pyruvic acid photolysis still dominates the formation of CH₃CHO, with a noontime contribution of 91 %, 86 %, and 71 % when quantum yields of 1, 0.5, and 0.2 are considered. Of the pyruvic acid contribution, 45 % of the CH₃CHO arises via isomerization of the initially formed, energized carbene (blue), while the remaining 55 % results from reactions of the thermalized carbene with formic (orange) and acetic (green) acids, the concentrations of which were constrained by observations. The modelled, noontime mixing ratio of CH₃CHO varies from 400 pptv (scenario B₁) to 160 pptv (scenario B_0.2) when pyruvic acid photolysis is included and is reduced to ∼ 100 pptv when the quantum yield is set to zero. Unfortunately, reliable measurements of the CH₃CHO mixing ratios with which to compare the model simulations were not available for the IBAIRN campaign as the in situ PTR-MS data set ($m/z$45) varied from −400 to + 400 pptv over the diel cycle. The modelled, maximum mixing ratio of CH₃CHO increases from ∼ 100 pptv when pyruvic acid photolysis is neglected to > 400 pptv under scenario B₁ (see Fig. S6).

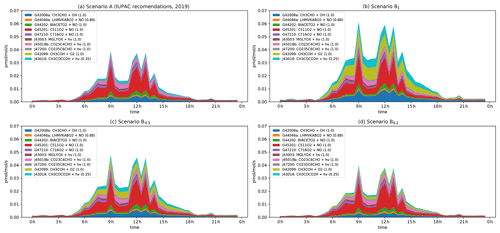
Figure 7 Modelled rates of CH₃CO formation (in pptv s⁻¹) through the diel cycle from photolysis of pyruvic acid (blue, orange, and green) and other photochemical processes during IBAIRN. (a) Scenario A (IUPAC). (b) Scenario B₁. (c) Scenario B_0.5. (c) Scenario B_0.2. In the legend, the first term is the equation tag used by CAABA/MECCA for the reaction. A full listing of the reactions can be downloaded (see Data availability section).

3.3.2 CH₃C(O)O₂ formation

The CH₃C(O)O₂ radical is formed in a termolecular reaction between the CH₃CO radical and O₂. Figure 7 displays the main photochemical reactions that lead to the formation of CH₃CO in our model. The spikes in the simulated production rates are connected to spikes in the diel average NO mixing ratio at the site. In analysing the data, we therefore consider not only the contributions at noon (when NO mixing ratios were large), but also at 10:30 when NO mixing ratios were comparably low.

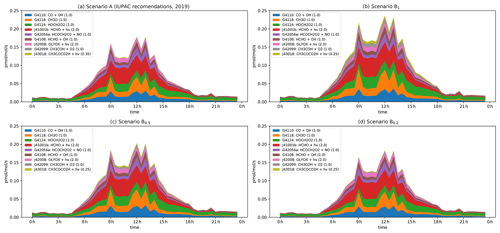
Figure 8 Modelled rates of HO₂ formation (in pptv s⁻¹) through the diel cycle from photolysis of pyruvic acid (blue, orange, and green) and other photochemical processes during IBAIRN. (a) Scenario A (IUPAC). (b) Scenario B₁. (c) Scenario B_0.5. (d) Scenario B_0.2. In the legend, the first term is the MCM designation for the reaction. A full listing of the reactions can be downloaded (see Data availability section).

Under scenario A, where φ = 0.2 and the yield of the CH₃CO radical is 0.35, the contribution of pyruvic acid photolysis to the overall production rate at 12:00 and 10:30 is about 23 % and 16 %, respectively, roughly equally divided into a direct contribution (J43018) and an indirect contribution (G42008a) arising via enhanced CH₃CHO levels. The main contributors to the formation of CH₃CO are reactions initiated by the degradation of isoprene and MTs (in the legend of Fig. 7: BIACETO2, C511O2, C716O2, CO23C4CHO, CO235C6CHO), which involve reactions of peroxy radicals with NO.

Under scenario B₁, the photolysis of pyruvic acid becomes significantly more important, contributing a total of 63 % of the total production rate for CH₃CO at 10:30 and 42 % at 12:00. When considering scenarios B_0.5 and B_0.2 the contributions of pyruvic acid photolysis are reduced to 46 % (29 %) and 29 % (17 %), respectively, where the numbers in parentheses are for the “high-NO_x” situation. Generally, the reaction of the thermalized carbene with O₂ (G42099), the direct photolysis at wavelengths < 340 nm (J43018), and the indirect enhancement in CH₃CO formation via the enhanced levels of CH₃CHO (G42008a) contribute roughly equally to the formation of CH₃CO resulting from pyruvic acid photolysis. The modelled mixing ratio of the CH₃C(O)O₂ radical at noon increases by a factor of ∼ 1.5 when comparing scenario B₁ with the quantum yields for pyruvic acid photodissociation set to zero.

3.3.3 HO₂ formation

In Fig. 8, we plot the nine most important model pathways to HO₂ production through the diel cycle. The dominant modelled production terms for HO₂ involve HCHO (photolysis HCHO and reaction with OH, G4108, J41001b), the reaction of methoxy radicals (G4118, whereby CH₃O is generated mainly in the reaction of CH₃O₂ radicals with NO), and the reaction of OH with CO. The direct contribution of pyruvic acid photolysis to HO₂ formation (via its photolysis (J43018) and through the reaction of CH₃COH with O₂, G42099) is ∼ 10 % under scenario B₁ under low-NO_x conditions (i.e. at 10:30). Under all other scenarios it is lower, with values (in percent) of < 1 (scenario A at both 10:30 and 02:00), ∼ 6 (scenario B₁ at 12:00), ∼ 5 and ∼ 3.5 (scenario B_0.5 at 10:30 and 12:00, respectively), and ∼ 1.5 and < 1 (scenario B_0.2 at 10:30 and 12:00, respectively). However, although the direct impact of pyruvic acid photolysis is weak, it has a significant indirect effect via the enhanced formation of CH₃C(O)O₂ radicals (directly via Reactions R3 + R4 and R10 and indirectly via CH₃CHO formation), which, in the presence of O₂, reacts with NO to form CH₃O₂. Enhanced production rates of CH₃O₂ result in enhanced production rates of CH₃O and HCHO and thus HO₂.

$$\begin{array}{}\text{(R14)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right){\mathrm{O}}_{\mathrm{2}}+\mathrm{NO}(+{\mathrm{O}}_{\mathrm{2}})\to {\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{NO}}_{\mathrm{2}}+{\mathrm{CO}}_{\mathrm{2}}\text{(R15)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{NO}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{NO}}_{\mathrm{2}}\text{(R16)}& {\displaystyle }& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}\to \mathrm{HCHO}+{\mathrm{HO}}_{\mathrm{2}}\text{(R17)}& {\displaystyle }& {\displaystyle }\mathrm{HCHO}+h\mathit{\nu }(+\mathrm{2}{\mathrm{O}}_{\mathrm{2}})\to \mathrm{2}{\mathrm{HO}}_{\mathrm{2}}+\mathrm{CO}\end{array}$$

The model simulations have shown that the photolysis of pyruvic acid at the levels observed during the IBAIRN campaign has a potentially significant effect on both CH₃CHO mixing ratios and production rates of HO₂ and CH₃C(O)O₂ radicals, the latter being especially enhanced under low-NO_x conditions. The enhanced production rates and concentrations of CH₃C(O)O₂ and HO₂ also result in significant increases in the modelled mixing ratios of several trace gases that are formed from these radicals. Comparing scenario B₁ to the case in which the pyruvic acid photodissociation quantum yield (φ) is set to zero results in an increase by factors of 2.2, 2.0, and 1.6 for CH₃C(O)OOH, CH₃OOH, and H₂O₂, respectively (see Fig. S6). HCHO mixing ratios are enhanced by a factor of 1.2. Vinyl alcohol mixing ratios of up to 40 pptv were generated in scenario B₁. Clearly, the photolysis of pyruvic acid can potentially impact strongly on the concentrations of, for example, C1 and C2 carbonyl compounds and peroxides in the boreal environment.

4 Conclusions

We have combined measurements of pyruvic acid in an autumn campaign in the boreal forest (IBAIRN) with theoretical calculations designed to characterize the fate of the methylhydroxy carbene radical (CH₃COH, the major product of pyruvic acid photodissociation) with a box-modelling study. We investigated the impact of pyruvic acid photolysis on the rates of production of acetaldehyde (CH₃CHO) and the peroxy radicals CH₃C(O)O₂ and HO₂. The theoretical study revealed unexpected features of CH₃COH chemistry, including slow reactions of thermalized carbene with H₂O but an efficient acid-catalysed conversion to CH₃CHO in the presence of organic acids such as HC(O)OH. The reaction of CH₃COH with O₂ is slow but will contribute to its fate (and thus the formation of CH₃C(O)O₂ and HO₂) in the lower atmosphere where O₂ concentrations are high if the rate constant used (elevated by an order of magnitude compared to the theoretical value) is correct.

In our box model, the photolysis of pyruvic acid was parameterized as presently recommended by IUPAC (whereby the main products are CH₃CHO and CO₂) and also using a more detailed mechanism in which the formation and fate of CH₃COH was considered and in which the quantum yield was varied. In all scenarios, we find that the photolysis of pyruvic acid was the dominant source of CH₃CHO during IBAIRN and that its instantaneous contribution to the daytime formation of CH₃C(O)O₂ varied between 16 % and 63 %, dependent on the assumed scenario and also on the NO concentration. Pyruvic acid photodissociation results in a significant increase in the mixing ratios of several carbonyl compounds and peroxides in the boreal environment.

The results of our modelling study are strongly dependent on the chosen quantum yields and photodissociation mechanism. To reduce the uncertainty in the role of pyruvic acid photolysis, there is an urgent need for further experimental and theoretical work on the photochemistry of pyruvic acid and on the fate of methylhydroxy carbene under atmospheric conditions. In addition, further measurements of pyruvic acid mixing ratios and of its deposition velocity in different environments are required to better constrain its abundance and lifetime and thus the impact of its photolysis. Enclosure studies would be helpful to investigate the dependence of pyruvic acid emission rates on different plant types and environmental conditions.