Optical properties of coated black carbon aggregates: numerical simulations, radiative forcing estimates, and size-resolved parameterization scheme

The formation of black carbon fractal aggregates (BCFAs) from combustion and subsequent ageing involves several stages resulting in modifications of particle size, morphology, and composition over time. To understand and quantify how each of these modifications influences the BC radiative forcing, the optical properties of BCFAs are modelled. Owing to the high computational time involved in numerical modelling, there are some gaps in terms of data coverage and knowledge regarding how optical properties of coated BCFAs vary over the range of different factors (size, shape, and composition). This investigation bridged those gaps by following a state-of-the-art description scheme of BCFAs based on morphology, composition, and wavelength. The BCFA optical properties were investigated as a function of the radius of the primary particle (a_o), fractal dimension (D_f), fraction of organics (f_organics), wavelength (λ), and mobility diameter (D_mob). The optical properties are calculated using the multiple-sphere T-matrix (MSTM) method. For the first time, the modelled optical properties of BC are expressed in terms of mobility diameter (D_mob), making the results more relevant and relatable for ambient and laboratory BC studies. Amongst size, morphology, and composition, all the optical properties showed the highest variability with changing size. The cross sections varied from 0.0001 to 0.1 µm² for BCFA D_mob ranging from 24 to 810 nm. It has been shown that MAC_BC and single-scattering albedo (SSA) are sensitive to morphology, especially for larger particles with D_mob > 100 nm. Therefore, while using the simplified core–shell representation of BC in global models, the influence of morphology on radiative forcing estimations might not be adequately considered. The Ångström absorption exponent (AAE) varied from 1.06 up to 3.6 and increased with the fraction of organics (f_organics). Measurement results of AAE ≫ 1 are often misinterpreted as biomass burning aerosol, it was observed that the AAE of purely black carbon particles can be ≫ 1 in the case of larger BC particles. The values of the absorption enhancement factor (E_λ) via coating were found to be between 1.01 and 3.28 in the visible spectrum. The E_λ was derived from Mie calculations for coated volume equivalent spheres and from MSTM for coated BCFAs. Mie-calculated enhancement factors were found to be larger by a factor of 1.1 to 1.5 than their corresponding values calculated from the MSTM method. It is shown that radiative forcings are highly sensitive to modifications in morphology and composition. The black carbon radiative forcing ΔF_TOA (W m⁻²) decreases up to 61 % as the BCFA becomes more compact, indicating that global model calculations should account for changes in morphology. A decrease of more than 50 % in ΔF_TOA was observed as the organic content of the particle increased up to 90 %. The changes in the ageing factors (composition and morphology) in tandem result in an overall decrease in the ΔF_TOA. A parameterization scheme for optical properties of BC fractal aggregates was developed, which is applicable for modelling, ambient, and laboratory-based BC studies. The parameterization scheme for the cross sections (extinction, absorption, and scattering), single-scattering albedo (SSA), and asymmetry parameter (g) of pure and coated BCFAs as a function of D_mob were derived from tabulated results of the MSTM method. Spanning an extensive parameter space, the developed parameterization scheme showed promisingly high accuracy up to 98 % for the cross sections, 97 % for single-scattering albedos (SSAs), and 82 % for the asymmetry parameter (g).

1 Introduction

Black carbon (BC), also called light-absorbing carbon (LAC), is produced from incomplete combustion of fossil fuels, biomass, and biofuels and is reported to be the second-largest contributor to global warming after CO₂, with the global forcing estimates ranging between 0.4 and 1.2 W m⁻² (Ramanathan and Carmichael, 2008). It has been found that annual anthropogenic BC emissions increased from 6.6 to 7.2 Tg during 2000–2010 (Klimont et al., 2017). Moreover, due to rapid urbanization in many developing regions like China, South Asia, and Southeast Asia, the total aerosol mass constitutes a significantly large portion of BC (Kumar et al., 2018; Bond et al., 2007; Wiedensohler et al., 2018; Madueño et al., 2019, 2020). In addition to the warming effect, BC also decreases snow albedo (Doherty et al., 2010), causes adverse health effects (Janssen et al., 2011), and lowers visibility (Wang et al., 2020).

Optical properties of BC are of scientific interest because they allow conclusions to be drawn on the nature of the particles and investigations of their radiative impacts (Liu et al., 2015; Safai et al., 2014). After emission into the atmosphere, BC particles undergo various changes in shape, size, and composition (Fierce et al., 2015). In the early stages of formation, BC particles consist of loosely bound agglomerates made of numerous small spherules, which collide to form strongly bound chain-like aggregates (Michelsen, 2017). Depending upon the atmospheric conditions after emission, irregularly shaped primary spherules provide active sites for the deposition of water vapour, which causes changes in the hygroscopicity of the particles (Petzold et al., 2005; Peng et al., 2017). In addition to this, different by-products of combustion like organic vapours are deposited around the particles (Siegmann et al., 2002; Rudich et al., 2007). These processes lead to the formation of coatings on BC cores (Bond and Bergstrom, 2006) and reshaping of the BC particles into more spherical structures (Abel et al., 2003). With the BC particles becoming more compact, an increase in the extinction cross section is observed (Liu et al., 2012). It was theoretically shown in clusters of absorbing spherules that the change in the optical cross sections with an increasing number of spherules (aggregation) is strongly dependent on the morphology (Berry and Percival, 1986). Laboratory and ambient studies also show changes in the optical properties of BC with an increasing volume of organic coating (Shiraiwa et al., 2010; Cheng et al., 2009). Even though the organic coating is less absorbing by nature, an increase in the absorption cross section is observed due to the lensing effect (Zhang et al., 2018; Zanatta et al., 2016; Saleh et al., 2015). Additionally, there is a class of organic carbon (OC) with light-absorbing properties known as brown carbon that strongly absorbs solar radiation in the blue and near-ultraviolet spectrum (Fleming et al., 2020; Feng et al., 2013; Chakrabarty et al., 2010; Chen and Bond, 2010). Numerical modelling has been proven to be helpful in better understanding the effect of the changes that BC particles undergo on their optical properties (Scarnato et al., 2013; Kahnert, 2010b; Smith and Grainger, 2014). The advantage of modelling studies is the ability and flexibility they offer to simulate BC particles of desired size, shape, and composition, hence improving our understanding of BCFAs at the microphysical level.

The representation of simulated BC particles plays an essential role in their numerically derived optical properties. The assumption of BC particles as spheres is widely used by atmospheric scientists, especially in the field of climate modelling (Stier et al., 2005; Ma et al., 2011; Düsing et al., 2018). In the case of aged BC, a spherical BC core is commonly considered to be encapsulated inside another sphere representing the coating. This morphology is used in the core–shell Mie theory (Bohren and Huffman, 1998) for obtaining the optical properties of such particles. Even though this method is simple, it might result in larger discrepancies when compared to actual measurements (Wu et al., 2018). Mie theory also overestimates absorption for the core–shell configuration of BC particles in the visible range of light (Adachi et al., 2010). It was shown that the ratio of non-BC to BC components plays an important role in determining the performance of different methods used for simulating the BC optical properties (Liu et al., 2017). Electron microscopy results of samples from laboratory and ambient measurements of BC (Ouf et al., 2016; Dong et al., 2018) showed that BC particles consist of agglomerates made up of numerous primary particles. It has been observed that these particles show self-similarity when viewed over a range of scales, which is an important characteristic of fractals (Forrest and Witten, 1979). This makes BC particles suitable to be termed black carbon fractal aggregates (BCFAs), which is used as such throughout this study.

Discrepancies due to Mie theory have caused increasing interest in the simulation of BC optical properties assuming a more realistic fractal morphology. A size-dependent empirical formula for the optical properties of BCFAs was derived for the wavelength range from 200 nm up to 12.2 µm (Kahnert, 2010a). The optical properties of pure BCFAs, i.e. without any coating, were investigated by Smith and Grainger (2014), further developing a parameterization for optical properties of pure BCFAs with respect to the number of primary particles (N_s). A method to estimate the optical properties of BCFAs was proposed using the machine-learning model “support vector machine” (Luo et al., 2018a). Empirical equations on the BC Ångström absorption exponent (AAE) were derived for different BC morphologies (Liu et al., 2018). A database containing optical data was developed that includes the aggregation structure, refractive index, and particle size of BCFAs (Liu et al., 2019).

Various ambient and laboratory studies have emphasized the role of organic external coating in influencing BC absorption and scattering properties (Zhang et al., 2008; Ouf et al., 2016; Dong et al., 2018; Shiraiwa et al., 2010). However, previous modelling-based studies were not able to take into account information about the coating of the BCFAs. The reason for this could be that time-consuming simulations make the computational load for such a task substantially large. It was also pointed out that improved size-resolved datasets and models for light-absorbing carbon (LAC) are required that include observables like optical properties, OC $/$ BC ratio, burning phase, and fuel types (Liu et al., 2020). Therefore, a size-resolved parameterization scheme for optical properties of BCFAs including the external coating parameter is very important.

This investigation involved computationally intensive modelling aimed at understanding and quantifying the changes that BCFAs and their optical properties undergo by simulating various cases of BCFAs under an elaborated systematic approach that is designed to span a wide parameter space. The coating parameter is quantified through the fraction of organics (f_organics). The BCFA cases are classified according to various f_organics, morphologies, and wavelengths. This approach of categorization involving f_organics of BCFAs aims to bridge the gaps that are present in modelled optical data from previous studies. The optical properties were calculated using the T-matrix code (Mackowski, 2013), and the findings are presented and discussed with respect to the equivalent mobility diameter (D_mob), making them more relevant and comparable for laboratory and ambient studies in which mobility spectrometers are often used for size classification.

The study highlights how modifications in the morphology and f_organics of BCFAs can further influence the BC radiative forcing. Finally, the parameterization scheme for optical properties (extinction, scattering, and absorption) of coated BCFAs was developed as a function of size for different morphologies, f_organics, and wavelengths.

2 Methods

2.1 Morphology of BCFAs

The formation of BCFAs from combustion is a process involving several stages. Along with BC, complex mixtures of gas-phase organic compounds with a spectrum of molecular structures are co-emitted during incomplete combustion (Siegmann et al., 2002; Gentner et al., 2017). Depending upon the source of burning, different types of polycyclic aromatic hydrocarbons (PAHs) are considered to be the direct precursors of BCFAs (Bockhorn, 2009). Small PAHs such as acetylene (C₂H₂) are attached to larger precursor PAHs, resulting in the growth of these elementary structures. It is postulated that the nucleation of two large PAHs leads to the formation of small three-dimensional particles with diameters ranging from 1–2 nm (Calcote, 1981).

Processes like surface growth and coagulation of gaseous-phase molecules or PAHs leads to further growth of these particles. High-resolution transmission electron microscopy (TEM) images revealed these particles to be spherules up to the diameter of 10–30 nm specific to the flame (Homann, 1967). These primary particles show a randomly ordered microstructure of graphite layers (Hess et al., 1969). Following the processes of nucleation and coagulation, the primary particles form larger BCFAs, which subsequently grow by aggregation (Sorensen, 2001). Following this concept of fractal morphology, a mathematical description of fractal aggregates was formulated (Mishchenko et al., 2002):

$$\begin{array}{}\text{(1)}& N_{\mathrm{s}}=k_{\mathrm{f}}{\left({\displaystyle \frac{R_{\mathrm{g}}}{a_{\mathrm{o}}}}\right)}^{D_{\mathrm{f}}},\end{array}$$

where a_o is the radius of primary particles, N_s is the number of primary particles, D_f is the fractal dimension, and k_f is a fractal prefactor. R_g is the radius of gyration, which characterizes the spatial size of the aggregate. It is defined as the root mean square (rms) distance of the aggregate from its geometrical centre by

$$\begin{array}{}\text{(2)}& R_{\mathrm{g}}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{N_{\mathrm{s}}}}\sum _{i=\mathrm{1}}^{N_{\mathrm{s}}}{\left(r_i-r_{\mathrm{o}}\right)}^{\mathrm{2}},\end{array}$$

where r_i is the position vector of the ith primary particle, and r_o is the position vector of the centre of mass of an aggregate with radius of gyration R_g.

The size of a BCFA is determined by two parameters, the radius of the primary particle (a_o) and number of primary particles (N_s). Both are sensitive to the emission source. BCFAs originating from the combustion of biomass have a radius of the primary particle varying between 15 and 25 nm (Chakrabarty et al., 2006). On the other hand, emissions from aircraft turbines comprise primary particles with a radius of 5 nm (Liati et al., 2014). Aggregates emitted from diesel engines have a radius of the primary particle varying between 10 and 12 nm (Guarieiro et al., 2017). Some experimental studies indicate that in the atmosphere, the radius of the primary particle is polydisperse in nature, varying from 10–100 nm (Bescond et al., 2014). Following these studies, Liu et al. (2015) reported differences in the optical properties of BCFAs due to the monodisperse and polydisperse distribution of the radii of the primary particles. Contrarily, Berry and Percival (1986) showed that light absorption measurements are insensitive to the radii of the primary particles. Additionally, Kahnert (2010b) pointed out that insensitivity is present when the radii of the primary particle fall in the range of 10–25 nm. For the sake of simplicity, aggregates of monodisperse primary particle size were used in this study.

Further, the reshaping of BCFAs into collapsed, sphere-like structures while ageing can be described by the fractal dimension (D_f) (Sorensen, 2001). The value of D_f increases as an aggregate reshapes into a more spherical particle. A D_f value of 3 is the value for a sphere, whereas D_f of 1 represents an open-chain-like aggregate. In the early stages of their formation, BCFAs have a fractal dimension (D_f) between 1.5 and 1.9 (China et al., 2013; Wentzel et al., 2003). However, as a consequence of atmospheric ageing, the aggregates transform from being bare to partly coated, embedded in coatings. In this case, the fractal dimension can go up to 2.2 (Wang et al., 2017). Exposure to humidity and coatings can collapse the BCFA into a structure having even a larger fractal dimension up to 2.6. (Zhang et al., 2008; Bambha et al., 2013). Hence, studying BC particles under the assumption of aggregate morphology provides a wider range of parameter space (particle size, primary particle size, and morphology). This is limited to only particle size in the case of spherical assumptions.

Aggregates are formed from the random motion of a cluster meeting a cluster (Sorensen, 2001). If the probability of sticking is considered 1, the process of formation is called diffusion-limited cluster aggregation (Witten and Sander, 1983). Following this principle, diffusion-limited algorithms (DLAs) have been developed, which include cluster–cluster aggregation (CCA) (Thouy and Julien, 1994) and particle–cluster aggregation (PCA) methods (Hentschel, 1984). In this study, the tunable diffusion-limited aggregation (DLA) software developed by Woźniak (2012) was used, which iteratively adds the primary particles one by one, preserving the fractal parameters at each step.

2.2 Description scheme of the simulated BCFAs

Previous modelling studies (Kahnert, 2010a; Smith and Grainger, 2014) investigated the optical properties of pure BCFAs, i.e. without any coating. From the simulated optical properties, parameterizations for pure BCFAs with respect to the number of primary particles at various fractal dimensions and wavelengths were given (Smith and Grainger, 2014). Ouf et al. (2016) conducted near-edge X-ray absorption fine structure (NEXAFS) analysis on BC produced from a diffusion flame-based mini-CAST burner and found that organics (by-products of combustion) get attached to the edge of graphite crystallites without changing the inner structure of the core. This laboratory result can be simulated for coated BC in radiative modelling studies by assuming a spherical coating around each individual primary particle of a BC aggregate (Luo et al., 2018b). It must be noted that the focus of our study is on BCFAs with coatings consisting of non-absorbing organics. If a brown carbon coating was to be included in the study, information and extra computational time regarding refractive indices would be needed. Unfortunately, due to the time-consuming nature of simulations, the generated database could not include BCFAs with brown carbon coating.

For the sake of simplicity and computational limitations, this representation of coated BC shown in Fig. 2 (bottom panel) was chosen for the entire study. In order to simulate such BC aggregates with individually coated primary particles, the inner radius of the primary particle (a_i) is fixed to 15 nm, whereas the outer radius of the primary particle (a_o) consisting of the organics is varied from 15.1 to 30 nm with the fraction of organics (f_organics) changing from 1 % to 90 %, respectively. The relationship between the outer radius of the primary particle (a_o), the inner radius of the primary particle (a_i), and the fraction of organics (f_organics) is shown below:

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathit{\pi }{a}_{\mathrm{i}}^{\mathrm{3}}=\left(\mathrm{1}-f_{\mathrm{organics}}\right){\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathit{\pi }{a}_{\mathrm{o}}^{\mathrm{3}}.\end{array}$$

It must be noted that when the fraction of organics (f_organics) is larger than 80 % and the morphology of the aggregate becomes compact, using this coated BC representation results in a practically unrealistic particle (randomly immersed BC primary particles in a spherical coating structure). Therefore, both the composition and morphology of the aggregate play a role when choosing the representation for coated BC. Keeping the above facts in mind, we have limited the use of this coating model only to coated BCFAs with a fractal dimension D_f below 2.2. In such cases, in which the BC aggregate does not have a completely compact structure, the results are expected to be reliable (Luo et al., 2018b). Moreover, Kahnert (2017) compared the coating model (closed-cell model) used in this study to a realistic model, which showed good comparability.

Figure 1 The description scheme of black carbon fractal aggregates (BCFAs) adopted in this study.

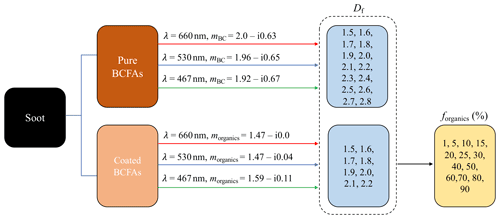
Luo et al. (2018b) kept the overall size of aggregates constant to study the sensitivity of optical properties at various numbers of primary particles (N_s) and vice versa. In our study, the size of the BC aggregates is increased gradually to study the subsequent changes in the optical properties. The optical properties of BC aggregates were calculated for various cases following a well-designed description scheme summarized in Fig. 1. All the optical properties are calculated at three wavelengths in the visible range, i.e. 467, 530, and 660 nm. The values are chosen following the availability of the refractive index at these specific wavelengths from Kim et al. (2015). For pure BC aggregates, the optical properties were calculated for 1.5 $\le D_{\mathrm{f}}\le$ 2.8 in steps of 0.1. In the case of coated BC aggregates, the optical properties are calculated at the above-mentioned wavelengths for 1.5 $\le D_{\mathrm{f}}\le$ 2.2 in steps of 0.1 and for 1 % $\le f_{\mathrm{organics}}\le$ 90 % in increments of 5 %. The approach of assuming a spherical coating around each individual BC primary particle results in an unlikely structure for coated BCFAs with D_f > 2.2; hence, those cases were omitted in this study. Figure 2 shows a few of the aggregates from the classification at a fixed D_f andf_organics. The large dataset obtained from the classification helped in further developing the comprehensive parameterization scheme.

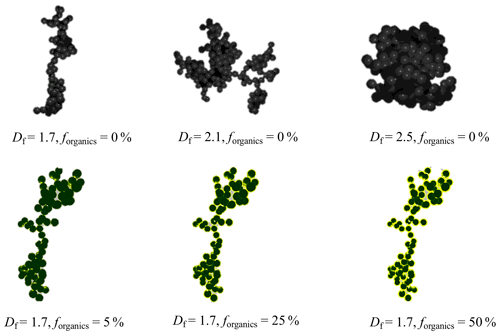
Figure 2 Examples of black carbon fractal aggregates (BCFAs) with 200 primary particles and varying D_f and f_organics.

In each case of the mentioned classification, the size of the BCFA is changed by incrementing N_s with 5 % and rounded to an integer value, starting from 1 up to 1000. It must be noted that in the results, the size of the BCFA is expressed in terms of mobility diameter (D_mob) instead of the number of primary particles (N_s) using the simple conversion developed by Sorensen (2001) given below:

$$\begin{array}{}\text{(4)}& D_{\mathrm{mob}}=\mathrm{2}{a}_{\mathrm{o}}\left({\mathrm{10}}^{-\mathrm{2}x+\mathrm{0.92}}\right)N_{\mathrm{s}}^x,\end{array}$$

where x is the mobility mass scaling exponent given by x=0.51Kn^0.043, with 0.46 < x < 0.56 having an estimated error of ±0.02 (Sorensen, 2001). Kn is the Knudsen number, which is the ratio of the molecular free path to the agglomerate mobility radius.

The conversion formula given in Eq. (4) is well founded over the entire range, spanning from the continuum to the free molecular regime. Using pre-calculated values of x, the mobility diameter (D_mob) is derived for the entire dataset. The relationship between the derived mobility diameter (D_mob), number of primary particles (N_s), and volume equivalent diameter (D_equ) for a case of pure BCFA with a_o=15 nm is shown in Fig. 3.

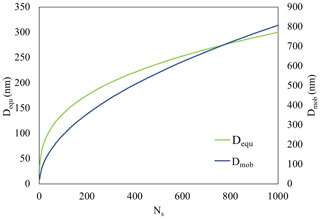
Figure 3 Relationship between mobility diameter (D_mob), number of primary particles (N_s), and volume equivalent diameter (D_equ) for pure BCFAs with a_o = 15 nm.

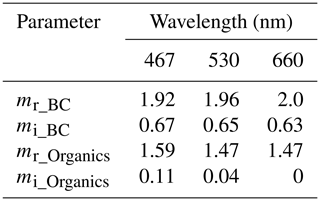
BC has a refractive index that is fairly wavelength-independent in the visible and near-visible spectrum range (Bond and Bergstrom, 2006). There are modelling studies which assume a wavelength-independent refractive index of $m=\mathrm{1.95}+\mathrm{0.79}i$ for BC over the visible spectrum range (Smith and Grainger, 2014; Luo et al., 2018a). For organic carbon, the imaginary part of the refractive index (m_i) is highly wavelength-dependent at the shorter wavelengths in the visible and ultraviolet (UV) wavelengths (Moosmüller et al., 2009; Alexander at al., 2008). Contrary to other studies, Kim et al. (2015) concluded that BC shows a fair amount of wavelength dependency and provided refractive indices for BC and organics in the visible spectrum. Following their study, the real (m_r) and imaginary (m_i) part of the refractive indices used for BC and organics at different wavelengths in this study are summarized in Table 1.

Table 1 Refractive indices (m_r and m_i) of BC and organics at various wavelengths in the visible range (Kim et al., 2015) used in this study.

2.3 Optical properties from the multi-sphere T-matrix (MSTM) method

The multi-sphere T-matrix (MSTM) method consists of an algorithm for calculating the time-harmonic electromagnetic properties of a set of arbitrary spheres (Mishchenko et al., 2004; Mackowski and Mishchenko, 2011). MSTM version 3.0 (Mackowski, 2013) calculates the optical properties for fixed and random orientations, the latter being used in this study. MSTM code can calculate the optical properties of coated BCFAs involving nested spheres with the condition that there should be no intersecting surfaces of individual primary particles. Radius and position vectors of the inner and outer primary particle of the BCFA are obtained from the tunable DLA software (Woźniak, 2012), which is coupled to the MSTM code.

The optical properties of the aggregates were modelled at three wavelengths, i.e. 467, 530, and 660 nm. At the wavelengths of 660 and 530 nm, the optical properties from MSTM code are obtained for 1 $\le N_{\mathrm{s}}\le$ 1000. Because of the increasing processing time of the MSTM code at lower wavelengths, the calculations are limited to 1 $\le N_{\mathrm{s}}\le$ 500 for a wavelength of 467 nm.

For reference purposes, the optical properties were also calculated using the Mie theory and the absorption cross section from Rayleigh–Debye–Gans (RDG) theory. For the Mie theory calculations, spheres with volume equivalent radius of aggregates were taken. In the case of the coated aggregates, a concentric core–shell configuration was used (He at al., 2015). The RDG theory considers the primary particles in the aggregate to be individual Rayleigh scatters, while ignoring the inter-particle scattering (Sorensen, 2001). Therefore, in the RDG theory, the total absorption cross section of the aggregate $\left(C_{\mathrm{abs}}^{\mathrm{agg}}\right)$ is the summation of the absorption cross sections $\left(C_{\mathrm{abs}}^{\mathrm{pp}}\right)$ of individual primary particles (N_s). For a monodisperse distribution, the absorption cross section from the RDG theory is given as

$$\begin{array}{}\text{(5)}& C_{\mathrm{abs}}^{\mathrm{agg}}=N_{\mathrm{s}}{C}_{\mathrm{abs}}^{\mathrm{pp}}.\end{array}$$

2.4 Optical properties and simplified radiative forcing model

The radiative parameters calculated from the model are briefly presented below. The MSTM code provides the extinction, absorption, and scattering efficiency (Q), and the asymmetry parameter (g) of BCFAs. The extinction, absorption and scattering cross sections ($C_{\mathrm{ext}/\mathrm{abs}/\mathrm{sca}}$) are further obtained as the product of efficiency (Q) and geometric cross section (C_geo) by

$$\begin{array}{}\text{(6)}& C_{\mathrm{ext}/\mathrm{abs}/\mathrm{sca}}=\left(Q_{\mathrm{ext}/\mathrm{abs}/\mathrm{sca}}\right)\times C_{\mathrm{geo}}.\end{array}$$

In spherical objects with radii (R), the geometric cross section (C_geo) is related to the radius by

$$\begin{array}{}\text{(7)}& C_{\mathrm{geo}}=\mathit{\pi }{R}^{\mathrm{2}}.\end{array}$$

Therefore, for a BCFA, the cross sections ($C_{\mathrm{ext}/\mathrm{abs}/\mathrm{sca}}$) with volume equivalent radius (R_v) are defined as follows:

$$\begin{array}{}\text{(8)}& C_{\mathrm{ext}/\mathrm{abs}/\mathrm{sca}}=Q_{\mathrm{ext}/\mathrm{abs}/\mathrm{sca}}\mathit{\pi }{R}_{\mathrm{v}}^{\mathrm{2}}.\end{array}$$

The volume equivalent radius (R_v) is calculated by

$$\begin{array}{}\text{(9)}& R_{\mathrm{v}}=a_{\mathrm{o}}{N}_{\mathrm{s}}^{\frac{\mathrm{1}}{\mathrm{3}}}.\end{array}$$

The single-scattering albedo (SSA) is the ratio of scattering efficiency (Q_sca) and extinction efficiency (Q_ext), where Q_ext is the sum of absorption and scattering efficiency as shown below:

$$\begin{array}{}\text{(10)}& \mathrm{SSA}={\displaystyle \frac{Q_{\mathrm{sca}}}{Q_{\mathrm{ext}}}}={\displaystyle \frac{Q_{\mathrm{sca}}}{Q_{\mathrm{sca}}+Q_{\mathrm{abs}}}}.\end{array}$$

Values of ω vary from 0 for a purely absorbing particle to 1 for a completely scattering particle.

The mass absorption cross section (MAC) is calculated from the ratio of absorption cross section (C_abs) and BC mass (m_BC) as

$$\begin{array}{}\text{(11)}& \mathrm{MAC}={\displaystyle \frac{C_{\mathrm{abs}}}{m_{\mathrm{BC}}}}={\displaystyle \frac{C_{\mathrm{abs}}}{\frac{\mathrm{4}}{\mathrm{3}}\mathit{\pi }{R}_{\mathrm{v}}^{\mathrm{3}}{\mathit{\rho }}_{\mathrm{BC}}}},\end{array}$$

where ρ_BC is the density of BC fixed to 1.8 g cm⁻³ (Bond and Bergstrom, 2006).

The wavelength dependence of light absorption, represented by the Ångström absorption exponent (AAE), is calculated using the absorption cross section (C_abs) at the three wavelengths (λ) of 467, 530, and 660 nm. The AAE value is obtained by

$$\begin{array}{}\text{(12)}& C_{\mathrm{abs}}\left(\mathit{\lambda }=\mathrm{467},\mathrm{530},\mathrm{660}\right)=b{\mathit{\lambda }}^{-\mathrm{AAE}},\end{array}$$

where b is a constant.

The absorption enhancement factor (E_λ) is defined by the ratio of absorption cross section of coated BCFA ($C_{\mathrm{abs}}^{\mathrm{coated}}$) and pure BCFA ($C_{\mathrm{abs}}^{\mathrm{pure}}$) as shown below:

$$\begin{array}{}\text{(13)}& E_{\mathit{\lambda }}={\displaystyle \frac{C_{\mathrm{abs}}^{\mathrm{coated}}}{C_{\mathrm{abs}}^{\mathrm{pure}}}}.\end{array}$$

This implies that the enhancement is given for particles of different total mass but the same BC mass.

To understand the atmospheric implications, the radiative forcing is estimated using a model for absorbing aerosols given by Chylek and Wong (1995). The black carbon radiative forcing at the top of the atmosphere is calculated as

$$\begin{array}{}\text{(14)}& \begin{array}{rl}\mathrm{\Delta }{F}_{\mathrm{TOA}}& =-{\displaystyle \frac{S_{\mathrm{o}}}{\mathrm{4}}}\left(\mathrm{1}-N_{\mathrm{cloud}}\right)T^{\mathrm{2}}\mathrm{2}\mathit{\tau }\\ & \times \left[(\mathrm{1}-a{)}^{\mathrm{2}}\mathit{\beta }\mathit{\omega }-\mathrm{2}a(\mathrm{1}-\mathit{\omega })\right],\end{array}\end{array}$$

where S_o is the solar constant, N_cloud is the cloud fraction, T is the transmittance of the sky above the layer of aerosols, τ is the aerosol optical depth, β is the upward scattering function, a is the surface albedo, and ω is the single-scattering albedo. From Sagan and Pollack (1967), the upward scattering function β is calculated from the asymmetry parameter g by

$$\begin{array}{}\text{(15)}& \mathit{\beta }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}-g).\end{array}$$

The model given by Chylek and Wong (1995) for the calculation of top-of-atmosphere (TOA) forcing is a simplified version of the multiple reflection model (Haywood and Shine, 1995; Sheridan and Ogren, 1999) with some implicit approximations. It is important to note that this is an analytical model which can be useful to understand the sensitivities of radiative forcing to various parameters (Chylek and Wong, 1995; Lesins et al., 2002). The simplified version was used in this study to highlight the sensitivity of the TOA forcing towards the morphology and composition of BC. However, the model cannot be used to replace accurate direct radiative forcing calculations.

3 Results and discussion

3.1 Variability in optical properties due to randomized particle generation

In the tunable DLA programme, the user-specified values of the number of spheres (N_s), radius of the primary particle (a_o), and fractal dimension (D_f) are used to generate the fractal aggregate. This gives rise to a possibility of more than one representation of a fractal aggregate satisfying the same fractal dimension (D_f), i.e. randomized particle generation. The difference between the various representations is only the different positions of the primary particles constituting the aggregate. This further results in an uncertainty in the radiative results. Depending on the complexity, some studies averaged the radiative results over 5–10 representations (Wu et al., 2016; Luo et al., 2018b), whereas others consider only a single representation (Smith and Grainger, 2014).

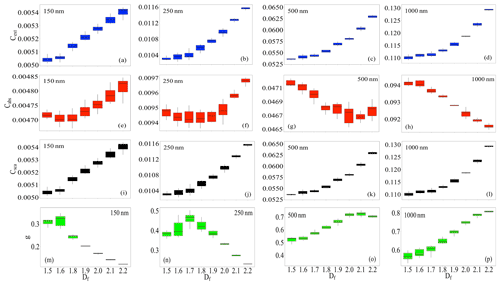
Figure 4 The variability in the optical properties at λ = 660 nm for 30 representations of pure BCFAs with D_mob increasing (left to right). The panels show the extinction cross section C_ext (first row), absorption cross section C_abs (second row), scattering cross section C_sca (third row), and asymmetry parameter g (fourth row). The box plots show the interquartile range between the 75th and 25th percentile, with the centre bar in the box indicating the median. The whiskers on the top and bottom of the box plot mark the largest and smallest value within 1.5 times the interquartile range.

Considering the large dataset in this study, the option of taking an average of the multiple representations would be time-consuming. Therefore, the general uncertainty in optical properties for 30 representations of the pure BCFAs is discussed. This is done for various cases of size (D_mob) and morphology (D_f). Figure 4 shows the variability in the extinction cross section C_ext (first row), absorption cross section C_abs (second row), scattering cross section C_sca (third row), and asymmetry parameter g (fourth row) as a function of D_f. The results were calculated at a wavelength of 660 nm for pure BCFAs with D_mob values 150, 250, 500, and 1000 nm increasing from left to right in Fig. 4.

The uncertainty in the optical properties was studied for 30 representations of BCFAs with the same value of the fractal dimension. The amount of variability in the optical property at each fractal dimension (x axis) must be seen from the whiskers of the box plot in Fig. 4. The sensitivity of the optical properties with respect to various fractal dimensions can be figured out from the amount of overlap of the y-axis values between adjacent box plots.

For extinction and scattering cross sections (first and third row), the uncertainty is more pronounced at D_f < 1.7. This is because of the overlap of extinction and scattering cross sections values at D_f < 1.7. The absorption cross section (C_abs) shows the highest uncertainty towards various representations of a BCFA, which can be seen from higher heights of box plots in panels (e), (f), and (g) in Fig. 4. Additionally, at 150 and 250 nm, C_abs is seen to be less sensitive to D_f, ranging between 1.5 and 2, whereas for box plots in panel (g) representing a 500 nm BCFA, the C_abs values overlap for D_f > 1.8. It may be noted that the C_abs increases with D_f for smaller BCFA (panels e and f), whereas the opposite is true for larger BCFA (panels g and h) as also reported by Luo et al. (2018b). This is further explained in detail in Sect. 3.3. The asymmetry parameter (g) shows a similar uncertainty trend as that of the extinction and scattering cross sections, i.e. lower variability but some overlap at certain D_f seen in the fourth row. In general, it is observed that the uncertainty of optical properties at larger sizes (D_mob=1000 nm; last column) is comparatively low. The standard deviation in the optical properties is averaged over size and summarized for various cases of D_f in Table 2.

Table 2 Summary of the variability (%) in the optical properties of pure BCFAs. The variability of the extinction cross section C_ext, absorption cross section C_abs, scattering cross section C_sca, asymmetry parameter g, and single-scattering albedo (SSA) is shown for a fractal dimension (D_f) between 1.5 and 2.2. For each case, the resultant variability is an average of the sizes of 100, 250, 500, and 1000 nm.

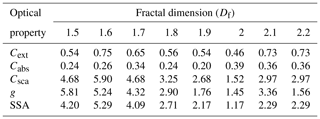
3.2 Optical properties of BCFAs at different radius of the primary particle

The absorption cross section (C_abs) and BC mass absorption cross section (MAC_BC) have been reported to be insensitive to the radius of the primary particle (a_o) for a fixed particle volume (Kahnert, 2010b). Figure 5 shows the optical properties of pure BCFAs with the radius of primary particle (a_o) varying between 15nm and 30 nm as a function of D_mob. The results were calculated for a wavelength of 660 nm for pure BCFAs with D_f=1.7. The absorption cross section C_abs shown in panel (b) increases by a factor of almost 10 from a_o of 15 to 30 nm. Since our results here are represented against D_mob instead of volume equivalent radius (R_equ), they are not expected to follow the findings of Kahnert (2010b). The results with respect to R_equ are provided in Fig. S1 of the Supplement, which follows the findings of Kahnert (2010b). The asymmetry parameter shows the least dependency on a_o as can be seen in panel (d). The single-scattering albedo (SSA) and the BC mass absorption cross section (MAC_BC) shown in panels (e) and (d) in Fig. 5 show a larger increase at a_o > 20 nm for the same D_mob. Acknowledging the effect of changing a_o on the optical properties, for the sake of simplicity, in this study the inner radius of the primary particle (a_i) was fixed to 15 nm, and the outer radii of the primary particle (a_o) were increased with f_organics.

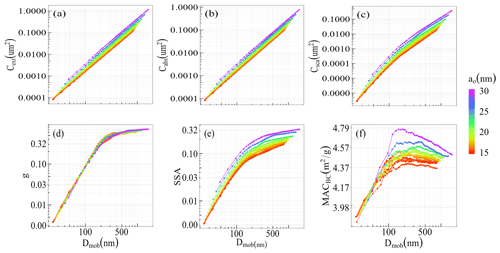
Figure 5 Optical properties of pure BCFAs at various radii of the primary particle (a_o) with respect to mobility diameter (D_mob): (a) extinction cross section C_ext, (b) absorption cross section C_abs, (c) scattering cross section C_sca, (d) asymmetry parameter g, (e) single-scattering albedo (SSA), and (f) black carbon mass absorption cross section MAC_BC at λ = 660 nm.

3.3 Dependency of BCFA optical properties on the morphology

Different optical properties as a function of changing D_mob and D_f are shown in Fig. 6. The results were calculated for pure BCFAs (f_organics=0) at a wavelength of 660 nm. The cross sections (panels a, b, and c) show an increase with D_mob. The cross sections vary from 0.0001 to 0.1 µm² for BCFA D_mob ranging from 24 to 810 nm. The extinction and scattering cross sections are larger for higher D_f, suggesting an increasing coherent scattering for compact morphologies, as also reported by Smith and Grainger (2014). The dependency of the optical cross section on the fractal dimension (D_f) was pointed out by Berry and Percival (1986); the change in the cross sections depends on whether the fractal dimension (D_f) is less than 2 or greater than 2. The results from Mie calculations for a spherical particle (D_f=3) follow the trend of the MSTM results, as seen in Fig. 6.

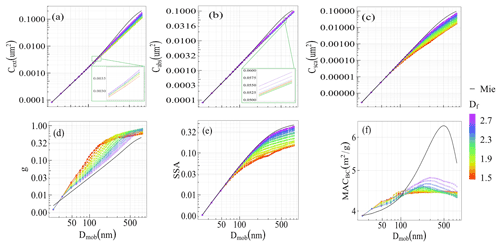
Figure 6 Optical properties of pure BCFAs as a function of D_mob at various fractal dimensions (D_f): (a) extinction cross section C_ext, (b) absorption cross section C_abs, (c) scattering cross section C_sca, (d) asymmetry parameter g, (e) single-scattering albedo (SSA), and (f) black carbon mass absorption cross section MAC_BC at λ = 660 nm. Radiative results from the Mie calculations are shown by the black line (panels a–f). The C_abs from the Rayleigh–Debye–Gans (RDG) theory is represented by a dashed line (panel b).

For smaller BCFAs, the absorption cross section shows negligible dependence on D_f. With increasing size, the absorption cross section decreases with D_f. This decrease can be interpreted as a shielding effect due to the primary particles on the surface of the aggregate. Further, with D_f > 2.5, the absorption cross section increases with D_f, showing the highest value for a spherical particle (D_f=3). This may be caused by Mie resonances in larger BCFAs. Earlier studies have also reported higher values for the sphere equivalent (D_f=3) calculations of BCFA (Liu et al., 2018; Li et al., 2016).

The single-scattering albedo (SSA $=C_{\mathrm{sca}}/C_{\mathrm{ext}}$) shown in panel (e) of Fig. 6 has values up to 0.42. The SSA also increases with D_mob and D_f; the latter is explained by the decreasing scattering in loosely packed BCFAs. This is due to compact aggregates following a Rayleigh-like polarization curve (Gustafson and Kolokolova, 1999). The asymmetry parameter (g) (panel d) shows a range of values between 0 and 1 for D_mob values between 24 and 810 nm. The asymmetry parameter is higher for chain-like BCFAs with lower D_f, indicating larger forward scattering in asymmetrical structures, as also reported by Luo et al. (2018b). When the BCFAs grow larger, the rate of increase in g with size gradually decreases for lower D_f because of the scattering tending to the Rayleigh scattering regime.

Black carbon mass absorption cross section (MAC_BC) values shown in panel (f) fall within the range of findings reported in the literature (Bond and Bergstrom, 2006). The MAC_BC increases with D_mob, showing a peak at D_mob∼ 250 nm. The dependency of MAC_BC on D_f is similar to that of the absorption cross section; i.e. Mie resonances contribute to the increase at higher D_f, explaining the large discrepancy between MSTM and Mie results for MAC_BC. The above results with respect to R_equ are provided in Fig. S2.

3.4 Dependency of BCFA optical properties on f_organics

Figure 7 shows how the optical properties of BCFAs are influenced by the increasing content of organics. The calculations were done for a BCFA of chain-like morphology with D_f = 1.7 at a wavelength of 660 nm. The results are shown as a function of D_mob at various fractions of organics (f_organics). The extinction and absorbing cross sections (Fig. 7a and b) decrease steadily with increasing f_organics for constant mobility diameters because of the increasing less-absorbing volume fraction in the aggregate. The dependence of the asymmetry parameter g (Fig. 7d) on f_organics is very small, meaning that g is more sensitive to morphology than composition. The single-scattering albedo (SSA) increases with f_organics, and this is again because of the increasing fraction of less-absorbing material. From the results of black carbon mass absorption cross section (MAC_BC) values shown in Fig. 7f, a dominating dependence of BCFA on composition is seen in comparison to size and morphology. Similar results for a compact BCFA of D_f = 2.2 at a wavelength of 660 nm can be found in Fig. S4 in the Supplement.

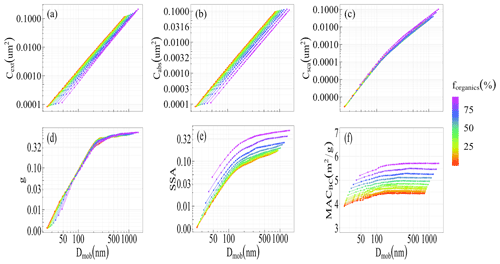
Figure 7 Optical properties of BCFAs (D_f = 1.7) as a function of D_mob at various fractions of organics (f_organics): (a) extinction cross section C_ext, (b) absorption cross section C_abs, (c) scattering cross section C_sca, (d) asymmetry parameter g, (e) single-scattering albedo (SSA), and (f) black carbon mass absorption cross section MAC_BC at λ = 660nm.

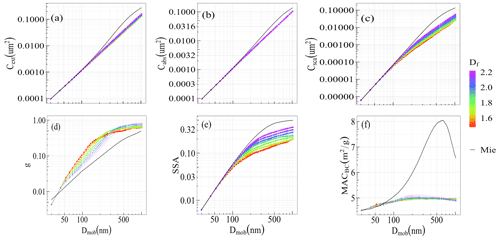
Figure 8 Optical properties of coated BCFAs (f_organics = 50 %) as a function of D_mob at various fractal dimensions (D_f): (a) extinction cross section C_ext, (b) absorption cross section C_abs, (c) scattering cross section C_sca, (d) asymmetry parameter g, (e) single-scattering albedo (SSA), and (f) black carbon mass absorption cross section MAC_BC at λ = 660 nm.

Figure 8 is similar to Fig. 6 but shows the dependency of optical properties on the fractal dimension (D_f) for organic-coated BCFAs with f_organics of 50 % at the wavelength of 660 nm. The cross sections and asymmetry parameter show similar behaviour as that of the pure BCFAs. The SSA has an upper limit of 0.35 at D_f= 2.2. The black carbon mass absorption cross section (MAC_BC) is rather independent of D_f but values increase with coating by a factor of 1.2 for coated BCFAs with f_organics of 50 % as shown in Fig. 7.

The gradually decreasing impact of the fractal morphology on the optical properties of coated BC particles was shown by Liu et al. (2017). In this study, it is seen that in the case of a non-coated BC particle (Fig. 6c), C_sca is more sensitive to D_f, whereas when the BC particles are coated (Figs. 7c, 8c), C_sca is less sensitive to D_f and f_organics. It is observed that the C_sca and SSA (Fig. 8c, e) become more sensitive to D_f when the BCFA grows in size; therefore, the impact of the fractal morphology on the optical properties is also a function of particle size. Moreover, it must be noted that even though there is a decreasing impact of the fractal morphology on optical properties, parameters like C_abs, MAC_BC, and g showed significant variability towards changes in f_organics (Fig. 7a, b, e, and f).

Global models use Mie theory for calculations of BC optical properties (Bond et al., 2013). The Mie theory considers BC to be homogeneously mixed spheres or a core–shell configuration. The results of SSA, g, and MAC_BC in both Figs. 6 and 8 clearly demonstrate a significant influence of morphology. This is clearly seen from the difference between the coloured lines representing various morphologies of BC as aggregates and the black solid line representing the result when BC is assumed as a core–shell. Therefore, the factor of changing morphology is not adequately considered when using the Mie theory for BC optical properties in global models.

3.5 Dependency of BCFA optical properties on wavelength

In the sections before, the dependency of BCFA optical properties on size, morphology, and composition was discussed. In this section, besides showing the spectral dependency of BCFA optical properties, it is also demonstrated how this dependency changes with morphology and composition in the visible wavelength range.

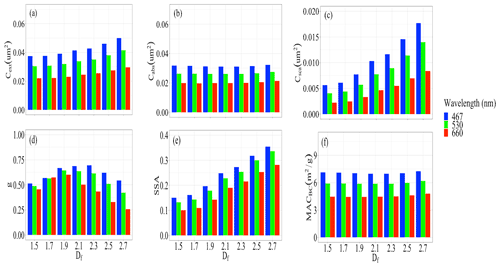
Figure 9 Spectral dependency of the pure BCFA optical properties (D_mob = 330 nm) on fractal dimension (D_f): (a) extinction cross section C_ext, (b) absorption cross section C_abs, (c) scattering cross section C_sca, (d) asymmetry parameter g, (e) single-scattering albedo (SSA), and (f) black carbon mass absorption cross section MAC_BC. For the variability (%) in different cases of D_f refer to Table 2.

Figure 9 shows the changes in the pure BCFA optical properties with wavelength (λ) at various morphologies represented by D_f. Pure BCFAs with fixed D_mob equal to 330 nm were taken for this case to demonstrate the effect of morphology. All the optical properties show a decrease with λ in the visible range. Furthermore, whether the rate of decrease might vary for various morphologies was studied. Figure 9 shows that the spectral dependency is insensitive to morphology for the absorption cross section C_abs (panel b) and black carbon mass absorption cross section MAC_BC (panel f). The spectral dependence of scattering cross section C_sca (panel c) is seen to be somewhat sensitive to changes in morphology. The highest sensitivity of spectral dependence to morphology was seen for the asymmetry parameter (g), which is dominant at higher D_f, i.e. for compact aggregates.

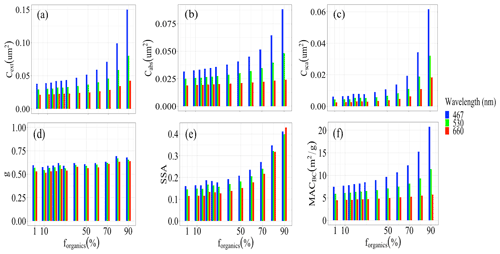
Figure 10 Spectral dependency of coated BCFA optical properties (N_s = 200, D_f = 1.7) on fraction of organics (f_organics): (a) extinction cross section C_ext, (b) absorption cross section C_abs, (c) scattering cross section C_sca, (d) asymmetry parameter g, (e) single-scattering albedo (SSA), and (f) black carbon mass absorption cross section MAC_BC. For the variability (%) refer to the case D_f = 1.7 in Table 2.

Figure 10 is provided to illustrate how the spectral dependency of BCFAs changes with composition, i.e. fraction of organics (f_organics). For this case, BCFAs are considered with N_s and D_f equal to 200 and 1.7, respectively. It must be noted that the size of the BCFAs is also increasing with f_organics. Contrary to the results from Fig. 9, all the cross sections (panels a, b, and c) and black carbon mass absorption cross section MAC_BC (panel f) show a significant increase in the spectral dependency with f_organics. The spectral dependency of single-scattering albedo (SSA; panel d) shows a comparatively lower sensitivity to f_organics, whereas it is nearly negligible for the asymmetry parameter (g) seen in panel (e). Additionally, the change in the spectral dependency on size is also shown in Fig. S5 of the Supplement.

3.6 Ångström absorption exponent (AAE) and enhancement factors (E_λ)

Figure 11 shows the Ångström absorption exponent (AAE) of a chain-like BCFA (D_f=1.7) as a function of mobility diameter (D_mob) and increasing fraction of organics (f_organics). The AAE is derived from the slope of C_abs vs. λ at 467, 530, and 660 nm as shown in Eq. (12). As expected, the AAE shows a straightforward dependency on the fraction of organics (f_organics). In this case, the values of AAE vary from 1.4 up to 3.6 with an increase in f_organics from 1 % until 90 %. The variability in the modelled values of AAE may be attributed to the selection of the refractive indices and wavelengths (Liu et al., 2018). A similar result for the Ångström absorption exponent (AAE) of a more compact BCFA (D_f = 2.2) is provided in Fig. S6. Additionally, the impact of morphology or fractal dimension (D_f) on the AAE for pure BCFAs is shown in Fig. 12 with values ranging from 1.06 to 1.47. It can be observed that for smaller BCFAs, the AAE increases as the BCFA becomes more compact, whereas for larger BCFA an opposite effect is seen. Figures 11 and 12 could be interpreted as the ageing process of BC in the atmosphere focusing on changing composition and shape, respectively.

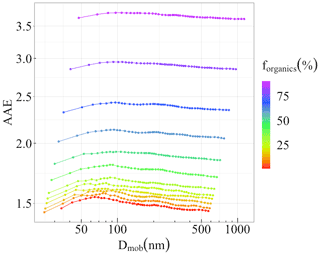
Figure 11 Ångström absorption exponent (AAE) of coated BCFAs (D_f = 1.7) with changing fraction of organics (f_organics) and mobility diameter (D_mob).

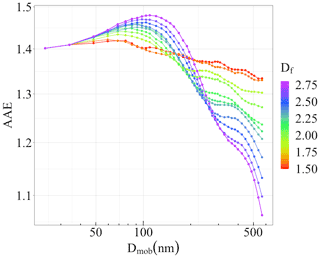
Figure 12 Ångström absorption exponent (AAE) of pure BCFAs (f_coating = 0 %) with changing fractal dimension (D_f) and mobility diameter (D_mob).

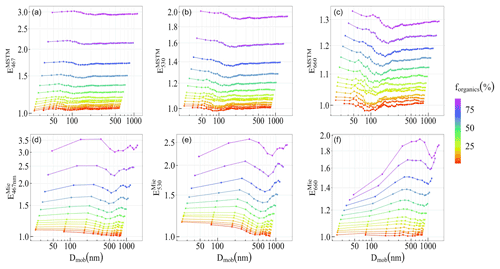
Figure 13 Absorption enhancement factor (E_λ) in BCFAs with D_f = 1.7, changing fraction of organics (f_organics), and mobility diameter (D_mob). Panels (a)–(c) show the E_λ derived from the MSTM method, whereas the ones derived from Mie code are shown in panels (d)–(f). The enhancement factors are shown for wavelengths equal to 660, 530, and 467 nm (right to left).

Figure 13 shows the trend in absorption enhancement factors (E_λ) as a function of mobility diameter (D_mob) and increasing fraction of organics (f_organics) for a BCFA with D_f = 1.7. The top row shows the absorption enhancement factors calculated from the results of the MSTM code $\left(E_{\mathrm{MSTM}}^{\mathit{\lambda }}\right)$, whereas the ones derived from the Mie calculations $\left(E_{\mathrm{Mie}}^{\mathit{\lambda }}\right)$ are displayed in the bottom row. In general, the Mie-derived absorption enhancement factors are larger by a factor of 1.1 to 1.5. The enhancement results from both MSTM and Mie calculations are shown for three wavelengths, i.e. 660, 530, and 467 nm (right to left). There is an expected increase in the absorption enhancement factors as the wavelength decreases. The values of the modelled absorption enhancement factors follow the results from various ambient studies which measured enhancement factors ranging from 1.0 to 2.25 at wavelengths between 532 and 678 nm (Cappa et al., 2012; Cui et al., 2016; Wu et al., 2018).

Liu et al. (2017) emphasized the role of the mass ratio of non-BC to BC on the performance of various methods used for simulating the scattering cross section and enhancement factors of BC particles. In this study, it is shown that the Ångström absorption exponent (AAE) calculated from just the MSTM method can show variability of up to a factor of 2 with an increasing non-BC mass fraction larger than 90 %. Similarly, it can be seen that the difference in the enhancement factors calculated from the core–shell theory and fractal assuming MSTM method can be between 1.1 and 1.5.

3.7 Implications of morphology and composition for black carbon radiative forcing

In this section, the dependence of the black carbon radiative forcing on modifying composition and morphology of BCFAs is discussed. The relative changes in the top-of-the-atmosphere radiative forcing (ΔF_TOA) are quantified as a function of fractal dimension (D_f) and fraction of organics (f_organics). It is a sensitivity analysis applicable mostly to scenarios with an urban pollution and a high mass fraction of combustion aerosols. The black carbon radiative forcing at the top of the atmosphere (ΔF_TOA) is estimated using Eq. (14) with fixed values of S_o = 1368 W m⁻², N_cloud= 0.6, T= 0.79, τ= 0.03, and a= 0.1 (Chylek and Wong, 1995; Lesins et al., 2002). To focus primarily on radiative effects of BC, the optical depth τ is taken as 0.03 for smoke aerosol (Penner et al., 1992). The values of β and ω change with fractal dimension (D_f) and fraction of organics (f_organics), and they are obtained from the MSTM bulk optical properties. The bulk optical properties are calculated at a wavelength of 530 nm over a lognormal polydisperse size distribution with the geometric mean radius (r_o) and standard deviation (σ) fixed to 0.12 µm and 1.5, respectively. Details about the bulk optical properties can be found in the Supplement of this work.

Table 3 shows how the values of black carbon radiative forcing change for various morphologies represented by the fractal dimension (D_f) for pure black carbon. This can be further understood by the relative change C defined by

$$\begin{array}{}\text{(16)}& C={\displaystyle \frac{\mathrm{\Delta }{F}_{\mathrm{TOA}}-\mathrm{\Delta }{F}_{\mathrm{TOA}}^{\mathrm{Ref}}}{\mathrm{\Delta }{F}_{\mathrm{TOA}}^{\mathrm{Ref}}}}\times \mathrm{100},\end{array}$$

where $\mathrm{\Delta }{F}_{\mathrm{TOA}}^{\mathrm{Ref}}$ is the top-of-the-atmosphere radiative forcing for a reference case in which the fractal dimension (D_f) is 1.7, i.e. a freshly emitted black carbon particle.

Table 3 Black carbon radiative forcing ΔF_TOA (W m⁻²) calculated for various fractal dimensions (D_f) and relative change (C) with respect to a reference case with D_f = 1.7.

Similarly, the values of black carbon radiative forcing for various compositions represented by fraction of organics (f_organics) in a case in which the fractal dimension (D_f) is fixed to 2.2 are shown in Table 4. The values of relative change (C) are calculated using Eq. (16) with respect to $\mathrm{\Delta }{F}_{\mathrm{TOA}}^{\mathrm{Ref}}$ as a reference case of zero fraction of organics (f_organics), i.e. pure black carbon particle.

Table 4 Black carbon radiative forcing ΔF_TOA (W m⁻²) calculated for various fractions of organics (f_organics) and relative change (C) with respect to a reference case with f_organics = 0 %.

Global models use the simplified core–shell representation for BC (Bond et al., 2013), which is morphologically close to a coated BCFA of D_f 2.8. In the case of coated BCFA, there is a relative change (C) of 20 % when D_f increases from 1.5 to 2.2. Following the results in Table 4 the relative change (C) in ΔF_TOA of coated BCFA is also expected to increase as D_f approaches 2.8. Therefore, the influence of morphology on ΔF_TOA is adequately considered when using the simplified core–shell representation of BC.

It can be seen from Table 4 that the top-of-the-atmosphere forcing ΔF_TOA decreases by up to 55 % as the organic content of the particles increases to 90 %. This result is in agreement with the findings of Zeng et al. (2019), wherein the increasing hygroscopicity of the BC particle results in negative top-of-the-atmosphere forcing. However, it must be noted that in the study of Zeng et al. (2019), the focus was on aged BC particles with 90 %–99 % coating fraction, and the Santa Barbara DISORT Atmospheric Radiative Transfer (SBDART) model was used for estimating the radiative forcing.

Even though the simplified radiative model for absorbing aerosols is used, the results of relative change (C) in Tables 3 and 4 can provide insight about the implications of BC ageing for radiative forcing estimates. It is demonstrated that the radiative forcing results are highly sensitive towards modifications in morphology and composition when using the aggregate representation. It must be noted that these results are of high relevance in BC hotspot regions of Asia: for example, Manilla in the Philippines, where the BC emission shared up to 70 % of calculated PM₁ (particulate matter with diameter < 1 µm) mass emission factors (Madueño et al., 2019).

3.8 Parameterization scheme for coated BCFAs

In this section, the optimal fits for the results of the optical properties obtained from the MSTM code are discussed. For the extinction and absorption cross sections, a first-order polynomial on logarithmic scales was found to be the best fit.

$$\begin{array}{}\text{(17)}& {\displaystyle }\ln C_{\mathrm{ext}}=c_{\mathrm{0}}+c_{\mathrm{1}}\ln D_{\mathrm{mob}}\text{(18)}& {\displaystyle }\ln C_{\mathrm{abs}}=g_{\mathrm{0}}+g_{\mathrm{1}}\ln D_{\mathrm{mob}}\end{array}$$

For the fittings of scattering cross section (C_sca) and SSA, an equation of the following form was found to fit best. The asymmetry parameter (g) is well captured by a cubic polynomial in a logarithm space of D_mob.

$$\begin{array}{}\text{(19)}& {\displaystyle }\ln C_{\mathrm{sca}}=H_{\mathrm{0}}+H_{\mathrm{1}}\ln D_{\mathrm{mob}}+H_{\mathrm{2}}\ln \left(\ln D_{\mathrm{mob}}\right)\text{(20)}& {\displaystyle }\ln \mathrm{SSA}=k_{\mathrm{0}}+k_{\mathrm{1}}\ln D_{\mathrm{mob}}+k_{\mathrm{2}}\ln \left(\ln D_{\mathrm{mob}}\right)\text{(21)}& {\displaystyle }\ln g=\sum _{n=\mathrm{0}}^{\mathrm{3}}{s}_n\ln D_{\mathrm{mob}}^n\end{array}$$

Since the nature of the curve for the mass absorption cross section (MAC_BC) changes for various D_f, it was not possible to find an optimal function representative for the entire dataset. For all the fits, a limitation was found: the smaller particles are not well represented by the above-mentioned functions. Therefore, in order to find an overall good fit, the data are taken for points with D_mob larger than 50 nm. Previous studies have also attempted to fit the optical properties of pure BCFAs with respect to the number of primary particles (N_s) (Smith and Grainger, 2014; Kahnert, 2010b).

In this study, a parameterization scheme is developed for five BC optical properties: the extinction cross section C_ext, absorption cross section C_abs, scattering cross section C_sca, single-scattering albedo (SSA), and asymmetry parameter g with respect to BC size. In total, the fit coefficients for the five BC optical properties are provided for 192 cases comprising various combinations of wavelengths (λ), fractal dimensions (D_f), and fraction of organics (f_organics) shown in Fig. 1. For each case, linear regression models were applied individually to the MSTM-modelled optical properties for BC sizes ranging from 10 to 1000 nm. The fit coefficients for the five optical properties in each case are provided in tabular form in the Supplement to this work.

The resultant parameterization scheme provides the user an option to estimate the five optical properties at desired BC size for any of the 192 combinations of λ, D_f, and f_organics. It must be noted that the MSTM-modelled optical properties were calculated for fixed values of the refractive index because of limited computational resources. Therefore, the parameterization scheme provided in this study is not able to account for variable refractive indices.

Error analysis of the parameterization scheme

In this scheme, the parameterization for optical properties of BCFAs is provided for each point of the classification given in Fig. 1. In the case of pure BCFAs, the parameterization is provided for all combinations of $\mathit{\lambda }\left(\mathrm{nm}\right)=\mathit{\{}\mathrm{467},\mathrm{530},\mathrm{660}\mathit{\}}$ and $D_{\mathrm{f}}=\mathit{\{}\mathrm{1.5},\mathrm{1.6},\mathrm{1.7},\mathrm{1.8},\mathrm{1.9},\mathrm{2.2},\mathrm{2.1},\mathrm{2.3},\mathrm{2.4},\mathrm{2.5},\mathrm{2.6},\mathrm{2.7},\mathrm{2.8}\mathit{\}}$. In the coated BCFAs the parameterization scheme is available for combinations of $\mathit{\lambda }\left(\mathrm{nm}\right)=\mathit{\{}\mathrm{467},\mathrm{530},\mathrm{660}\mathit{\}}$, $D_{\mathrm{f}}=\mathit{\{}\mathrm{1.5},\mathrm{1.6},\mathrm{1.7},\mathrm{1.8},\mathrm{1.9},\mathrm{2.2}\mathit{\}}$, and $f_{\mathrm{organics}}\left(\mathit{\%}\right)=\mathit{\{}\mathrm{1},\mathrm{5},\mathrm{10},\mathrm{15},\mathrm{20},\mathrm{25},\mathrm{30},\mathrm{40},\mathrm{50},\mathrm{60},\mathrm{70},\mathrm{80},\mathrm{90}\mathit{\}}$. This scheme is named P_I and allows the user the advantage of selecting among various cases suitable for their purpose.

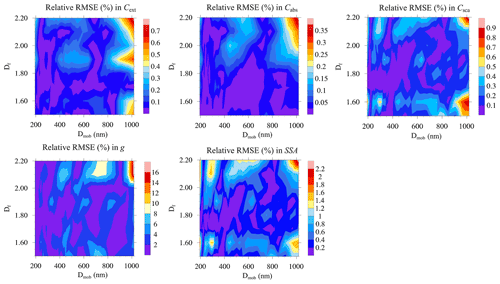
Figure 14 The relative RMSE between MSTM-modelled and parameterized values of C_ext, C_abs, C_sca, g, and SSA for various cases of fractal dimension (D_f) at λ = 660 nm. In this case, the fraction of organics (f_organics) amounts to 50 %.

In order to examine and test the P_I scheme, the relative root mean square errors (RMSEs) between the MSTM-modelled and fitted values of optical properties were measured. Figure 14 shows the values of relative RMSEs over a range of D_mob for the cases of λ(nm)={660}, f_organics(%)={50}, and $D_{\mathrm{f}}=\mathit{\{}\mathrm{1.5},\mathrm{1.6},\mathrm{1.7},\mathrm{1.8},\mathrm{1.9},\mathrm{2.2}\mathit{\}}$. For the entire range of D_mob and D_f, the errors in cross sections are less than 1 %. The relative RMSE is < 2.5 % for SSA and up to 16 % for g.

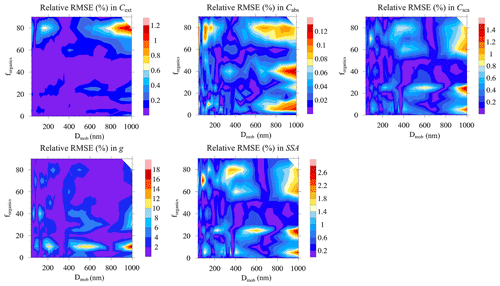
Figure 15 The relative RMSE between MSTM-modelled and parameterized values of C_ext, C_abs, C_sca, g, and SSA for various cases of fraction of organics (f_organics) at λ = 660 nm. The fractal dimension (D_f) is fixed to 1.7.

Similarly, relative RMSE values for the entire range of f_organics can be seen in Fig. 15. For the results shown in Fig. 15, the cases with values of λ(nm)={660}, D_f={1.7}, and $f_{\mathrm{organics}}\left(\mathit{\%}\right)=\mathit{\{}\mathrm{1},\mathrm{5},\mathrm{10},\mathrm{15},\mathrm{20},\mathrm{25},\mathrm{30},\mathrm{40},\mathrm{50},\mathrm{60},\mathrm{70},\mathrm{80},\mathrm{90}\mathit{\}}$ were used. The errors in the cross sections are comparable to Fig. 11, being < 1.5 % in all cases. Similarly, the relative RMSE for SSA is < 3 %. The error in g peaks to 18 % at f_organics < 20 % for larger sizes.

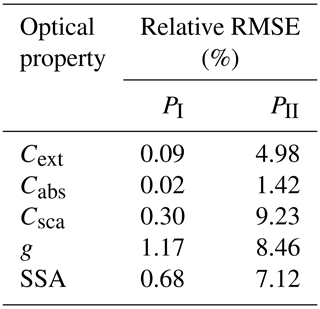
It is expected that a dataset of BCFA optical properties with higher resolution for the individual parameters gives better results. To demonstrate this, the P_I scheme is compared to another scheme P_II with a reduced dataset. In the P_II scheme, the same fits were applied, but optical properties were averaged for D_f in the range from 1.5 to 1.7 and f_organics in the range from 60 %–90 % to obtain the “averaged” fit coefficients. The errors from this parameterization scheme P_II were compared to the errors from their corresponding cases (D_f = 1.7 and f_organics = 60 %) within the parameterization scheme P_I. The results are summarized in Table 5. The relative RMSEs for P_II are evidently larger than for P_I and give evidence that the dataset with higher resolution minimizes errors when deriving parameterization schemes.

Table 5 Comparison between the relative RMSEs of parameterization schemes over a single case of BCFA (D_f = 1.7, f_organics = 60 %, and λ= 660 nm). The errors on the left (P_I) are for the original scheme developed in this study, whereas the errors on right show the errors resulting from P_II, which is the condensed form of P_I, i.e. D_f = 1.5–1.7, and f_organics = 60 %–90 %.

4 Conclusions

Optical properties of pure and coated black carbon fractal aggregates (BCFAs) were systematically investigated as a function of particle size (D_mob), primary particle size (a_o), morphology (D_f), composition (f_organics), and wavelength (λ), developing a parameterization scheme for BCFA optical properties.

Modelled optical properties of BCFAs were found to be sensitive to changes in the radius of the primary particle (a_o) at a fixed D_mob. The highest sensitivity was seen for cross sections (C_ext, C_abs, and C_sca), increasing by a factor of almost 10 when a_o is changed from 15 to 30 nm, at a fixed D_mob. When the volume equivalent radius R_equ of a BCFA is fixed, the values of C_ext and C_abs with changing a_o were constant, as also shown by the study of Kahnert (2010b).

In addition to the dependency of BCFA cross sections on size, a size dependency of the optical parameters SSA, g, and MAC_BC was also seen. All the BCFA optical properties showed dependencies on morphology and composition, with the nature of these dependencies being specific to each optical property and size-dependent. In terms of morphology, C_sca, SSA, and g showed the highest sensitivity to D_f, which is more pronounced as the BCFA grows in size. In contrast to the results of C_sca, SSA, and the asymmetry parameter, C_ext, C_abs, and MAC_BC were more sensitive with respect to changing composition of BCFAs. The values of MAC_BC increased by a factor of 1.5 with an increasing amount of f_organics up to 90 % at λ=660 nm. The optical properties SSA, g, and MAC_BC are needed to simulate the BC radiative forcing in global models. Therefore, the simplified core–shell representation of BC in global models does not adequately consider the above-discussed impacts of morphology on the BC optical properties.

In the visible range, the decrease in the optical properties C_ext, C_abs, C_sca, and MAC_BC with λ was large, whereas a smaller decrease in SSA and g with λ was shown. The nature of the spectral dependencies with respect to changing morphology and composition varied for various optical properties. While the other optical properties had a less significant spectral dependence on morphology, the asymmetry parameter (g) showed the highest sensitivity that was dominant at a higher D_f, i.e. for compact aggregates. The ratio of g at λ=467 nm and λ= 660 nm changed from 1.1 to 2.6 when going from lower to higher values of D_f. All the cross sections and the black carbon mass absorption cross section MAC_BC showed a significant increase in the spectral dependency with an increasing fraction of organics f_organics. The spectral dependency of MAC_BC increased from a factor of 1.97 at a 1 % fraction of organics to a factor of 4 at a 90 % fraction of organics. It was shown that the MAC_BC for a BCFA can be very high for cases with high organic content, such as 20 m² g⁻¹ for a 90 % fraction of organics at λ= 467 nm.

The dependencies of the Ångström absorption exponent (AAE) on morphology and composition were investigated. The values of AAE changed from 1.06 up to 3.6 depending on the fraction of organics (f_organics), fractal dimension (D_f), and size (D_mob). It is evident from the results that the AAE of a black carbon particle without organic coating can significantly differ to values of about unity, contradicting the interpretation of AAE in some studies. The interpretation of the measurement values of AAE ≫ 1 as biomass burning aerosol might be misleading in the Sandradewi model (Sandradewi et al., 2008). The values of the absorption enhancement factor (E_λ) via coating calculated from the MSTM model varied from 1.0 to 3.0 as a function of wavelength (λ) and size (D_mob), whereas the Mie-theory-derived E_λ varied from 1.0 to 3.5. The ratio between the MSTM and Mie-derived E_λ changed from 1.1 to 1.5 as a function wavelength (λ). The largest discrepancies between the MSTM and Mie-derived E_λ were seen at the red wavelength (λ= 660 nm) due to the presence of Mie resonances in larger particles.

The key message of this study is that the sensitivity of various optical properties, especially SSA, g, and MAC_BC, to changing morphology and composition can be significant. Further, to understand the atmospheric and climate implications of our findings, a sensitivity study of black carbon radiative forcing ΔF_TOA was conducted. It was shown that black carbon radiative forcing ΔF_TOA (W m⁻²) can decrease up to 61 % as the BCFA becomes more compact in morphology, i.e. a higher fractal dimension (D_f). Therefore, the influence of morphology on the top-of-the-atmosphere radiative forcing is neglected when using the simplified core–shell representation of BC in global model simulations. With respect to changing composition, a decrease of more than 50 % in ΔF_TOA was seen as the organic content of a particle increases. These findings are particularly relevant for modelling polluted urban environments. It is generally assumed that the impact of a BC particle becoming more compact and the increase in organic content are linked. It was shown that the changes in these two ageing factors in tandem result in an overall decrease in the ΔF_TOA. Therefore, these factors must be kept under consideration when modelling absorption of BC-containing particles and for assessing radiative impacts using global models.

The parameterization scheme provides the user an option to estimate the BC optical properties (extinction cross section – C_ext, absorption cross section – C_abs, scattering cross section – C_sca, single-scattering albedo – SSA, and asymmetry parameter – g) at the desired BC size for various combinations of λ, D_f, and f_organics. Even though simple linear regression models were used in this study, the parameterization scheme showed low differences between the parameterized and tabulated MSTM-modelled values of optical properties. For the entire parameterization scheme, the relative root mean square errors (RMSEs) in C_ext, C_abs, and C_sca were less than 1 %. Similarly, the relative RMSE for SSA was less than 3 %. The largest error of about 18 % was found in g at f_organics less than 20 % for larger sizes. It must be noted that the proposed parameterization scheme is able to accurately predict the BC optical properties above D_mob of 50 nm under various scenarios not including uncertainties due to a fixed primary particle size and refractive index.

It is acknowledged that the results from the parameterization scheme might vary compared to the results from laboratory and ambient measurements. To understand the nature of discrepancy in modelled optical properties, we encourage users to compare results of this study to results from laboratory or ambient measurements if applicable. It is important to mention that parameterization schemes and databases based on a realistic representation of BC, like the one developed in this study, represent a successful step forward towards a more accurate characterization of BC-containing particles and radiative forcing in climate models. Therefore, further studies should be conducted to develop more comprehensive databases that include more information on primary particle size and composition, physical variables like hygroscopicity, and optical parameters like refractive indices.