the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Impact of high- and low-vorticity turbulence on cloud–environment mixing and cloud microphysics processes
Rahul Ranjan
Man-Kong Yau
Sudarsan Bera
Suryachandra A. Rao
Turbulent mixing of dry air affects the evolution of the cloud droplet size spectrum via various mechanisms. In a turbulent cloud, high- and low-vorticity regions coexist, and inertial clustering of cloud droplets can occur in low-vorticity regions. The nonuniformity in the spatial distribution of the size and in the number of droplets, variable vertical velocity in vortical turbulent structures, and dilution by entrainment/mixing may result in spatial supersaturation variability, which affects the evolution of the cloud droplet size spectrum via condensation and evaporation processes. To untangle the processes involved in mixing phenomena, a 3D direct numerical simulation of turbulent mixing followed by droplet evaporation/condensation in a submeter-sized cubed domain consisting of a large number of droplets was performed in this study. The analysis focused on the thermodynamic and microphysical characteristics of the droplets and the flow in high- and low-vorticity regions. The impact of vorticity generation in turbulent flows on mixing and cloud microphysics is illustrated.
- Article
(3649 KB) - Full-text XML
- BibTeX
- EndNote
-
Regions of high vorticity are prone to homogeneous mixing due to faster mixing by air circulation.
-
The microphysical droplet size distribution is wider or narrower in high- or low-vorticity volumes, respectively.
-
Drier environmental air mixing initially leads to a higher spectral width.
-
The k-means clustering algorithm (an unsupervised machine learning technique) is used to identify regions of high vorticity in the computational domain.
Clouds are a visible manifestation of tiny water droplets or ice crystals in the Earth's atmosphere. They play multiple roles in atmospheric processes, ranging from the radiation budget to the hydrological cycle (Bengtsson, 2010; Grabowski and Petch, 2009; Harrison et al., 1990; Randall and Tjemkes, 1991). The size of clouds may extend from a few meters to several kilometers. However, the suspended droplets that constitute a cloud are much smaller – with a typical radius of 1–20 µm. The journey from a cloud droplet to a raindrop (∼103 µm) is a complicated process. Condensation and collision–coalescence, the two key processes involved in the growth of a droplet, are prominent at different stages of cloud development (Rogers and Yau, 1996). For example, up to a size of 15 µm, diffusional-condensation growth dominates, whereas collision–coalescence is effective when the droplet radius reaches approximately 40 µm (Pruppacher and Klett, 1997). The rapid growth of droplets in the size range between 15 and 40 µm – for which neither condensational growth nor collision–coalescence is effective – is poorly understood. This size range has been termed the “condensation–coalescence bottleneck” or the “size gap” (Grabowski and Wang, 2013). The rapid growth of droplets in the size gap is regarded as one of the important unresolved problems in cloud physics. To explain the rapid growth, several mechanisms like entrainment, turbulent supersaturation fluctuations, enhanced collision rates due to turbulence, and the role of giant aerosols have been proposed. This study focuses on the interaction between droplets and turbulence to explore how this interaction modifies the droplet characteristics.
1.1 Role of turbulence in cloud microphysics
Understanding the impact of turbulence on the dynamics and microphysics of clouds is a long-standing problem (Devenish et al., 2012; Grabowski and Wang, 2013; Khain et al., 2007; Shaw, 2003; Vaillancourt and Yau, 2000) and has been an active area of research using in situ observations and numerical models. The position and movement of droplets are controlled by turbulent eddies of varying sizes. Simultaneously, evaporation or condensation of droplets incurs changes in the local environment (∼ scale of droplet itself) through latent heat exchange. Additionally, buoyancy generated by phase change (when a bunch of droplets evaporate or condense instead of a few) may impact cloud-scale motions. The inertial response time “τp” is a quantity that determines how quickly droplets respond to changes in the surrounding fluid motion (Clift et al., 1978). Some droplets are tiny and precisely follow the flow trajectory, whereas larger droplets can modify the flow. Thus, droplet–turbulence interaction is a multiscale process and is nonlocal in nature.
There are several macrophysical and microphysical implications of droplet–turbulence interactions. Droplets in the decaying part of a cloud may be transported by turbulence to the more active regions to undergo further growth (Baker and Latham, 1979; Jonas, 1991). The inhomogeneous mixing model used by Cooper et al. (1986) and Cooper (1989) shows that when a parcel of air undergoes successive entrainment events, each of which reduces the droplet concentration, it can lead to enhanced droplet growth. However, Jonas (1996) argues that ascent leading to droplet growth may activate some entrained nuclei to limit the maximum supersaturation achieved which, in turn, limits the droplet growth rate. Vaillancourt et al. (1997) gives further insight into the nature of turbulent entrainment at the cloud edges. They argue that the interaction between the ambient and the cloudy air is not the same everywhere. There are some prominent regions of entrainment with vortex circulations.
The study of microphysical droplet–turbulence interaction has gained momentum in recent years due to advances in computational capabilities. Several possibilities such as turbulence-induced supersaturation fluctuation and enhanced collision rates have been investigated. Some studies (Chen et al., 2016; Franklin et al., 2005; Pinsky et al., 2000; Riemer and Wexler, 2005; Shaw, 2003; Vaillancourt and Yau, 2000) indicate an enhanced collision rate in a turbulent environment. Shaw et al. (1998) performed a model simulation with a Rankine vortex and found that the preferential clustering of droplets in the low-vorticity regions increases the spatially varying supersaturation. On the other hand, droplets in the high-vorticity regions experience enhanced supersaturation and grow faster. This work laid the foundation for droplet clustering in clouds and its effect on the droplet size distribution. However, Grabowski and Vaillancourt (1999) commented on the limitations of applying the results of Shaw et al. (1998) to atmospheric clouds due to the absence of droplet sedimentation, the assumption of the high volume fraction of vortex tubes (50 %), and the strong dependence on the vortex lifetime.
There is no clear theory regarding vorticity characteristics in 3D homogeneous turbulent flows, despite increasing research on turbulence. Vorticity has a profound impact on the spatial distribution of droplets. Due to preferential clustering, relatively fewer droplets are left in high-vorticity regions (Karpińska et al., 2019). The difference in the spatial distribution of droplets induces supersaturation fluctuations. The low number of droplets competing for the available vapor field in high-vorticity regions should experience enhanced growth. However, for this to happen, droplets should stay in these regions for a duration long enough for the supersaturation field to act. In general, little is known about the spatial scale and lifetime of high-vorticity regions (Grabowski and Wang, 2013). Due to these limitations, the effect of preferential clustering on the diffusional growth of droplets is poorly understood.
In this study, we examine the diffusional growth and evaporation of cloud droplets in an entrainment and mixing scenario using direct numerical simulation (DNS). We compare the droplet characteristics, such as spectral width, volume mean radius, number concentration, probability density function (PDF) of droplet radii, and supersaturation, in high- and low-vorticity regions. As reported by Vaillancourt et al. (1997), the main entrainment sites and mixing zones were located in the vortex circulation areas. Accordingly, using DNS, we aim to look for locations with vortex circulations in the main entrainment sites and mixing zones. In summary, the main purpose of this study is to seek answers to the questions regarding the volume fraction of high-intensity vortices in a turbulent domain and the dominant locations of mixing in the high- and low-vorticity regions. Thus, the specific scientific considerations in this work are (i) variations in droplet spectral properties in high- and low-vorticity regions, (ii) quantification of the degree of mixing in these regions, and (iii) the impact of relative humidity on the evolution of the droplet size spectra.
The organization of the paper is as follows: Sect. 2 provides details of the methods and data used; results and discussions are provided in Sect. 3, with further four subsections containing the discussion of the flow and the droplet characteristics in low- and high-vorticity regions; and we concluded our findings in Sect. 4.
We carried out a DNS following the setup of Kumar et al. (2014, 2018) to simulate the entrainment and mixing mechanisms at cloud edges. This DNS code uses the Euler–Lagrangian framework, solves the flow equations at each grid point, and tracks each droplet inside a grid by integrating the equations for its position, velocities, and growth rate. The simulation produces the output in two formats: one is from the Eulerian framework in NetCDF format developed by UCAR/Unidata, and the other is the droplet dynamics output saved in SION format (SIONLib, 2020). The simulation domain was chosen (51.2 cm)3 with a 1 mm grid resolution and, thus, contained a total of (512)3 grid points in the domain. An initial setup of the computational domain is detailed in Sect. 3.
Two simulation setups are considered in this study. In particular, there are two relative humidity (RH) cases (85 % and 22 %) initialized with a polydisperse droplet size distribution. We also attempted two simulations (two RH cases) initialized by a monodisperse droplet size (20 µm). However, our discussion is focused only on the results from the polydisperse case as the monodisperse case does not provide any additional results. The polydisperse setup contains the droplet size distribution (size range 2–18 µm) from cloud observations (Cloud Aerosol Interaction and Precipitation Enhancement Experiment – CAIPEEX: https://www.tropmet.res.in/~caipeex/, last access: 11 August 2021) used in Kumar et al. (2017) with a mean radius of 9.3 µm. The two humidity levels, corresponding to dry (RH = 22 %) and moist air (RH = 85 %), were taken from observations of the monsoon environment (Bera et al., 2016). A supersaturated cloudy slab in the DNS domain is specified to simulate the mixing processes.
This study aims to investigate droplet characteristics in high- and low-vorticity regions in cloud turbulence. Therefore, the vorticity magnitudes were first calculated using the Eulerian data at each grid point containing the velocity components in the x, y and z directions. The next step is to find the high- and low-vorticity regions in the DNS computational domain. This requires calculating and visualizing the actual vortices generated by the turbulent flow. As the grid size is 1 mm, it is not feasible to obtain a vortex inside a single grid box; instead, a volume containing the vortex must be sought, encompassing multiple grid boxes. It is a challenging task to locate a small box to cover a minimal portion of the low-vorticity region. We used an unsupervised machine learning (ML) algorithm (mentioned in the next subsection) to address this problem.
2.1 Locating high-vorticity regions
To locate high-vorticity regions in the domain, we used the k-means clustering algorithm from the “scikit-learn” Python package (Pedregosa, 2011). k-means clustering (Bock, 2007) is one of the most popular and the simplest unsupervised machine learning algorithms. It makes “k” groups or clusters from a dataset based on the Euclidean distance between individual data points. However, k-means clustering cannot guess the optimum number of clusters for a particular dataset; instead, the user has to assign it. Therefore, selecting the number of groups or clusters in which a dataset has to be grouped or clustered is crucial. This algorithm was used to locate high-vorticity regions from the vorticity data.
The absolute vorticity ω related to the velocity components is calculated as follows (see Sect. 4.2 in Holton and Hakim, 2013):
where
The values of ω range from 0 to 200 s−1 in our DNS data, as seen in Fig. 1a. Vaillancourt and Yau (2000) mentioned that only a small fraction of the cloud core is occupied by high-vorticity regions, and no preferential concentration of cloud droplet was observed there. We also found that less than 2 % of the grids (by volume) have a vorticity with a magnitude greater than 60 s−1. For larger vorticity magnitudes, even fewer grids (an almost negligible number) were located. Based on these findings a threshold value of vorticity magnitude of 60 s−1 was chosen as the high-vorticity criterion in this work. We also investigated the droplets' characteristics with a threshold of 50 s−1, but the trends showed no difference. We also mention that using 30 s−1 as a threshold for high vorticity, which is less than one-fifth of the maximum vorticity magnitude (200 s−1), does not seem to be justified. Figure 1b depicts the fraction of grid points for different threshold values of vorticity magnitude.
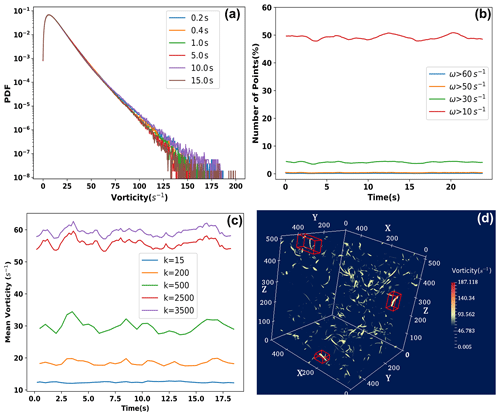
Figure 1Panel (a) displays the probability density function (PDF) of vorticity at different times. The fraction of high-vorticity points (based on threshold values) are depicted in panel (b). Panel (c) represents vorticity values for different values of k. Panel (d) shows high-vorticity regions (enclosed by a rectangular cuboid) obtained for k=500.
Once the threshold value for vorticity magnitude is decided, the next step is to locate 3D boxes enclosing the high-vorticity regions. We look for these regions at every time step. To locate the boxes with high vorticity, we applied a machine learning algorithm, namely, k-means clustering. When using this algorithm, two input variables have to be assigned a value: (i) the number of clusters (“k”) and (ii) the maximum number of iterations. As vortices have tubular or sheet-like structures, it is possible that a 3D box may contain many low-vorticity points for a typical value of k. Hence, an optimal value of k is required to select small enough 3D boxes to avoid the low-magnitude vorticity points.
We identified the value of k to be used in the algorithm by conducting several experiments and selected the optimal value k=3500 based on the chosen threshold value for high vorticity. At k=3500, the average vorticity in the boxes reaches close to the selected threshold (60 s−1), as shown in Fig. 1c. This figure provides the vorticity values for different values of k and confirms the appropriate choice of k=3500. The value of k also affects the size of the cluster. With an increasing value of k, the size of the clusters decreases. Consequently, some clusters may become so small that they might only include as many as approximately two or three high-vorticity points, which are all in the same plane. These points in the same plane will not be useful, as they cannot form a cuboid. Therefore, the k=3500 value was found to be optimal. For a higher value of k, we may get many zero volume boxes. That is the reason why increasing the value of k indefinitely is not advisable. Similarly, the optimal numbers of iterations were chosen as 200 to keep the computational cost moderate. A typical visualization of finding a volume enclosing a high-vorticity region is shown in Fig. 1d, where a cuboid is shown to surround the high-vorticity region. It was noted that high-vorticity regions occupy only a tiny fraction (0.1 %–0.2 %) of the total domain.
Shaw et al. (1998)Table 1A comparison of this study with the previous study of Shaw et al. (1998) that laid the foundation for droplet clustering and its impact on the droplet size distribution. Kolmogorov timescales in natural clouds are in the range of 0.01–0.1 s. The Kolmogorov timescale for DNS is 0.0674 s, which lies in the above mentioned range.

This finding of a tiny fraction for high-vorticity regions in a cloud core is in agreement with the DNS study of Jimenez et al. (1993) and Vaillancourt and Yau (2000) but disagrees with the assumed high volume fraction (≈ 50 %) from Squires and Eaton (1991) and later from Shaw et al. (1998). There are important differences between this study and the study of Shaw et al. (1998), who laid the foundation of inertial clustering of cloud droplets and motivated us to conduct the present study. Shaw et al. (1998) hypothesized that the preferential concentration (inertial clustering) occurs at small spatial scales and that a low (high) particle concentration corresponds to high (low) vorticity regions using a Rankine vortex in their model. They assumed a high fraction (50 %) of vortex structure and that the preferential concentration of droplets was severalfold higher than the mean droplet concentration. In contrast, the high-vorticity region in the present simulation is very small (≈ 0.2 % volume fraction) with a droplet concentration that is about 1.5-fold higher than in the low-vorticity region.
A comparison of the methods in this work and the study of Shaw et al. (1998) is provided in Table 1. For calculating the volume fraction of a high-vorticity region, Shaw et al. (1998) considered two zones of vortices (high and low vorticity) in their parcel model with a Rankine vortex and considered the same volume fraction (i.e., 50 %) for the two vorticity zones.
In this section, we discuss the various analyses from the two humidity simulations initialized with a polydisperse droplet size spectrum.
3.1 Initial simulation setup
The interface between cloud volume and the subsaturated air is distinguishable during the early evolution of the flow. To see if any features of the flow exhibit distinct properties at the edges, three separate volumes from the entire domain have been selected. The cloudy slab area lies between 142 and 372 mm along the x axis, with the rest of the domain occupied by the subsaturated air. Of the two interface volumes, one is on the left side (between x=70 and 140 mm), and the other is on the right side (between x=364 and 434 mm). The volume lying between x=182 and 322 mm is in the core region, as depicted in Fig. 2.
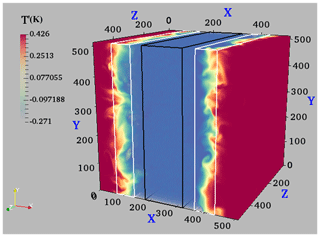
Figure 2A snapshot of the DNS domain at a time of 0.2 s, which can be considered as the initial state of the simulation. The figure also shows two boxes at the edges (left and right white boxes) and the initial cloud slab (central black box). The legend represents the fluctuation from the mean temperature.
3.2 Turbulence characteristics at the edges and core of cloud
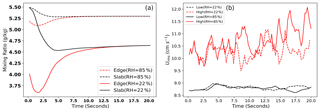
The cloudy volume properties initially see sharp changes, which were confirmed by analyzing the variations in kinetic energy (KE), vorticity and mixing ratio. The edges are the most turbulent part of the clouds during early evolution, and considerable robust fluctuations in KE are experienced there, as depicted in Fig. 3a. The availability of more kinetic energy at the cloud edges makes them the hot spots for vorticity generation. Initially, a higher mean vorticity value is observed at the edges in both humidity cases, which is evident in Fig. 3b. Near the edges, strong gradients of mixing ratio and temperature exist, leading to the generation of instabilities and, consequently, turbulent mixing. Turbulent kinetic energy (TKE) is initially associated with the vortical motions at the interface; however, additional TKE is also generated due to negative buoyancy production by droplet evaporation. This energy is transported to the cloud slab as time progresses by the vortices (“eddies”) that propagate inward. However, there are periodic changes in the TKE variations between the interface and the cloud slab that are possibly due to the periodic boundary condition of the DNS setup. A notable feature between the two RH simulations (22 % and 85 %) is the larger difference in vorticity between the interface and the cloud slab in the drier case (RH = 22 %) due to the strongest evaporation.
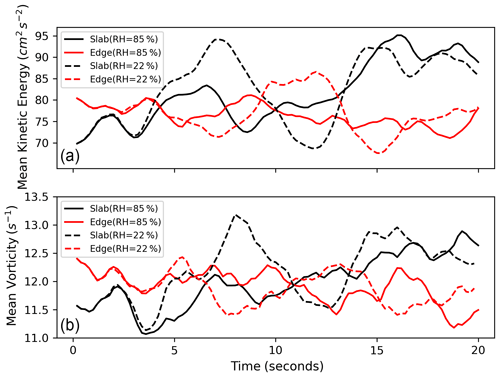
Figure 3Panel (a) shows the variation in kinetic energy (KE) for both the drier and humid cases in the cloudy slab and edges. Mean vorticity variations at the edges and within the cloudy slab (for both cases) are shown in panel (b). The KE was averaged over the cloudy slab and both drier edges. The vorticity average was taken in each box enclosing them.
3.3 Flow characteristics in high- and low-vorticity regions
The previous subsection presented the variation in flow characteristics at the cloud core and the edges. Another part of this study is to investigate these characteristics in the high-vorticity (HV) regions of the turbulent flow, with a vorticity magnitude greater than 60 s−1. Similarly, points with vorticity less than 30 s−1 were classified as regions of low vorticity (LV).
We also investigated the evolution of the vapor mixing ratio (qv) in both the drier (RH = 22 %) and the more humid cases (RH = 85 %). The incursion of drier air results in a lower mixing ratio at the edges, as evident from Fig. 4a. In both the HV and LV regions, we further determined the root mean square velocity Urms. For the dry and humid cases, Urms is found to be higher in HV regions as depicted in Fig. 4a.
3.4 Droplet characteristics
One of the main aims of this study is to examine various droplet characteristics, such as number concentration, volume mean radius, spectral width, and the mixing process in HV and LV regions. This subsection focuses on all of these characteristics.
3.4.1 Number concentration and mean volume radius
There have been many kinds of research on the distribution of droplets in a turbulent flow field. Several laboratory studies (Lian et al., 2013) and model simulations (Shaw et al., 1998; Ayala et al., 2008) reported on the process of preferential clustering of cloud droplets in low-vorticity regions. The preferential clustering means that droplets prefer to cluster in some specific flow regions rather than randomly distributed everywhere. A high amount of rotation characterizes the highly vortical part of a fluid. When a droplet enters this region, it is flung out due to its inertia and accumulates in a low-vorticity region.
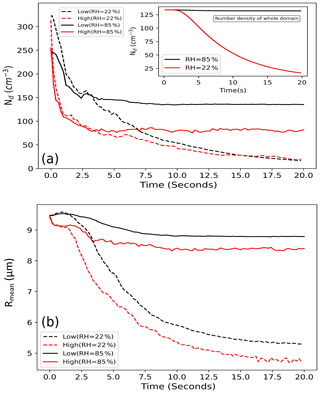
Figure 5The evolution of the number concentration (Nd) in the whole domain is shown in the inset of panel (a). In both RH cases, initial number densities (in the entire domain) were close to 130 cm−3. However, as seen in panel (a), the evolution of Nd in high- and low-vorticity regions has different magnitudes: it is always greater in the low-vorticity regions. Panel (b) shows the volume mean radius, which is always smaller in the high-vorticity regions.
This process leads to a heterogeneous droplet concentration in space – an important aspect that affects the droplet growth rate and the size distribution. In a polydisperse size distribution, the larger droplets are more prone to be affected by the vorticity compared with smaller droplets that may follow the flow streamline due to their low inertia. For this reason, larger droplets accumulate in low-vorticity regions and result in a larger mean volume radius.
In Fig. 5a, both humidity cases show almost the same trend (i.e., a higher number concentration in the low-vorticity region due to inertial clustering). Figure 5b shows the variation in the mean volume radius in high- and low-vorticity regions. The arid-like conditions in the case with RH = 22 % leads to fast evaporation of droplets, as indicated by the rapid decay in the droplet number concentration and the mean volume radius. Consequently, the number concentration curves almost merge after 7.5 s. Due to preferential clustering, the high-vorticity regions have a relatively small number of droplets. It is to be noted that the low-vorticity region always has a larger mean volume radius during the simulations, as shown in Fig. 5b.
There may be two possible reasons for the smaller value of the mean radius in high-vorticity regions: (i) droplets experience a drier environment and evaporate faster during the early stage of mixing when high vorticity forms at the cloud edge, and (ii) larger droplets are more likely to be flung out of the high-vorticity region as a consequence of a greater inertia effect, leaving behind only the smaller droplets (i.e., preferential clustering is more prominent for larger droplets). The second possibility is more valid during the later part of the simulation (approx. after 5 s) when high vorticity forms inside the cloud slab. To clarify whether preferential clustering alone determines the volume mean radius distribution or whether the other mechanisms are responsible, we investigated the droplet spectra, the trends of the mean supersaturations and the evolution of the droplet size distribution.
3.4.2 Evolution of droplet size spectra
The variation in the spectral width is presented in Fig. 6a, showing an entirely different picture of the evolution of droplet spectra in the two cases. Figure 6b illustrates the dispersion of the droplet size distribution (DSD).
During the initial mixing of the cloud slab with the environmental dry air in the RH = 22 % case, the spectral width of the DSD increases rapidly until the 5–7 s mark and then decreases thereafter, whereas in the RH = 85 % case, a gradual increase can be seen for the initial 10 s and remains almost constant after that. One of the most important results of this study is that the spectral width of the DSD is different in high- and low-vorticity regions, as depicted in Fig. 6. The droplet size dispersion also confirms that the broadening is always stronger in the high-vorticity regions. For the RH = 22 % case, the spectral width is wider for droplets situated in a high-vorticity region during the initial 5 s of mixing when the spectral width increases rapidly. However, the opposite scenario occurs after 7.5 s (i.e., narrower spectral width in high-vorticity regions). Nevertheless, the spectral width is always wider in the high-vorticity regions in the RH = 85 % case.
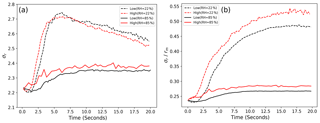
Figure 6The variation in the spectral width in high- and low-vorticity regions is shown in panel (a). The spectral width is always greater in the high-vorticity region in the RH = 85 % case, whereas it is only greater for the initial 5 s in the RH = 22 % case. Panel (b) depicts the variation in the dispersion of the droplet size distribution with time.
The initial growth and later decay of the spectral width during mixing for the RH = 22 % case is associated with the modification of the spectral shape by droplet evaporation and the number concentration dilution (see Bera, 2021). In this case, evaporation is very significant due to the mixing of the much drier environmental air. When evaporation starts, the smaller droplets of the DSD evaporate faster than the larger droplets in accordance with the inverse relation of growth rate with droplet size (Rogers and Yau, 1996). As a result, the spectra shift towards the smaller size tail, as shown in Fig. 7. This is the reason for the increasing spectral width for the initial 5 s in RH = 22 % and during the entire 20 s of RH = 85 %. However, when evaporation is such that the smaller size tail of the spectra is evaporated completely and only larger droplets remain, the spectra start to shrink and the spectral width decreases, as shown in Fig. 7c (see Luo et al., 2020). This is the situation for RH = 22 % with mixing after 7.5 s but does not occur for RH = 85 % case where the evaporation is much slower due to moist air mixing (as shown in Fig. 7d).
The difference in the spectral width in the HV and LV regions can be identified by the higher droplet evaporation in high-vorticity regions. Initially, high vorticity forms at the cloud edges where dry air mixing occurs, leading to faster evaporation of droplets. A second possibility is that high-vorticity regions are pockets of rotating air motions that can easily transport the vapor mass (produced by droplet evaporation) out of the region to facilitate enhanced evaporation. These two plausible reasons result in higher evaporation rate in regions of high vorticity and, consequently, impact of the droplet spectral width.
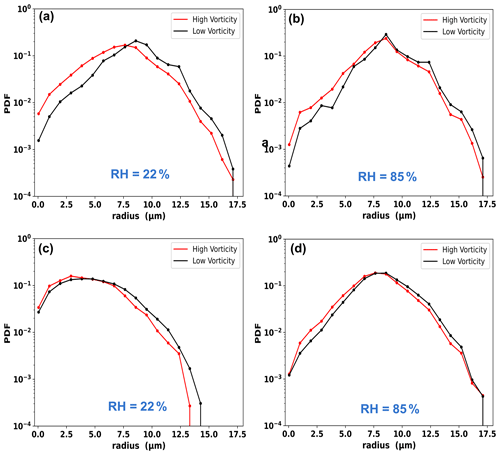
Figure 7The probability density function (PDF) of the droplet radii for RH = 22 % (a, c) and RH = 85 % (b, d). Panels (a) and (c) depict the plots for 3 s, and panels (b) and (d) depict the plots for 17.8 s.
The differences in the PDFs of HV and LV regions are very noticeable at 3 and 17.8 s. During this time, a greater spectral width exists in the high-vorticity region (refer to Fig. 6) for both humidity cases (i.e., RH = 22 % and RH = 85 %). The PDFs confirm that high- and low-vorticity regions contain almost the same maximum and minimum drop sizes, but the difference comes from the distribution. The following possibilities can explain the characteristics of the PDF depicted:
-
saturation ratio is lower in high-vorticity regions, which triggers enhanced evaporation;
-
due to enhanced evaporation, there are smaller droplets in the vortices, as depicted by the size distribution;
-
bigger droplets are more vulnerable to be thrown out of the vortices, leaving only the smaller ones.
For further understanding, we also analyzed the trend of the droplet supersaturation, as outlined in the following.
3.4.3 Mean saturation ratio
Figure 8 depicts the mean and standard deviation of supersaturation variation in HV and LV vorticity regions for the RH = 22 % and RH = 85 % cases. The droplets in high-vorticity regions experience a comparatively lower saturation ratio until around 6 s, after which the difference tends to vanish. Hence, during the entrainment of drier air into the cloudy volume, droplets encounter a more subsaturated environment in the highly vortical regions, and it is the lower saturation ratio values that produce a larger standard deviation. In the RH = 22 % case, the saturation ratio drops to −15 %, whereas in the RH = 85 % case, although a similar pattern exists, the saturation ratio only drops to −3 %. In summary, the high-vorticity regions can be identified as zones of entrainment.
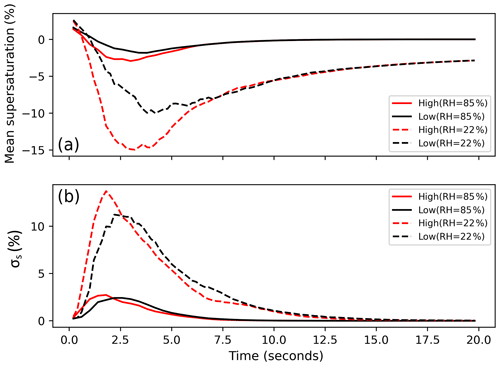
Figure 8Panel (a) shows the evolution of the mean saturation ratio in the high- and low-vorticity regions. The saturation ratio is lower in the high-vorticity regions during the initial 5–7 s; its value reaches a minimum of −15 % in the RH = 22 % case, whereas it only drops to −3 % in the RH = 85 % case. The evolution of the standard deviation of the saturation ratio in high- and low-vorticity regions is shown in panel (b). The standard deviation sees a steeper increase and decrease in high-vorticity regions. It has a large variation (0–14) in the RH = 22 % case, whereas the variation is small (0–2.8) in the RH = 85 % case.
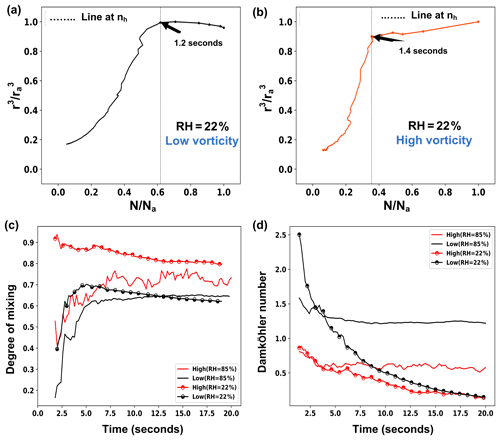
Figure 9Panels (a) and (b) represent the mixing diagrams for the respective low- and high-vorticity regions for the RH = 22 % case. nh represents the homogeneous number concentration used in Eq. (3). Degrees of homogeneous mixing for all four cases are compared in panel (c). A comparison of the Damköhler number for all the cases is shown in panel (d).
3.4.4 Degree of mixing
One of the best metrics to investigate the entrainment and mixing process is the degree of mixing, which depends on the mixing diagram and has a wider application in numerical models (Lehmann et al., 2009; Kumar et al., 2017, 2018). In the mixing diagram, the volume mean radius cube (r3) is plotted against the number concentration (Nd). Sometimes, a normalized version is plotted, in which the radius and number concentration are normalized by the respective adiabatic values (Gerber et al., 2008; Kumar et al., 2014). In a similar manner, we performed the mixing diagram calculation, and we depict the values in Fig. 9a and b. Here, we have considered the initial values (t=0 s) as adiabatic in the mixing diagram.
An analysis of the mixing diagrams in the high- and low-vorticity regions for both the moist and dry cases were performed. Variations in mixing diagrams in high- and low-vorticity regions for the RH = 22 % case are depicted in Fig. 9a and b, respectively. The mixing diagrams, for both RH cases, show a clear picture of mixing types. In the low-vorticity case, the mixing is inactive up to 1.2 s, whereas for HV case, it remains inactive up to 1.4 s. During this time, entrained air just dilutes the number concentration (nh) without acting on droplet evaporation (because the cloudy slab expands during this time and droplets scatter into the entire domain). Afterward, physical mixing occurs, the mixing line takes a turn toward the homogenous mixing line (vertical line representing constant number concentration), and both the number density and the mean volume radius decrease rapidly, indicating an intermediate or transient-type mixing scenario.
One can summarize that the mixing in HV regions remains more homogeneous compared with LV regions, as can be seen by the more rapid droplet evaporation (decrease in r) than the decrease in number density.
The degree of mixing was calculated using the following formula from Lu et al. (2012), which is based on a “β” parameter:
β is normalized by to obtain a mixing degree that varies between [0,1]. In this equation, r is the mean volume radius; ra stands for the adiabatic volume mean radius; and n, nh and na are the number concentration, homogeneous number concentration and adiabatic number concentration, respectively.
The degree of mixing is presented in Fig. 9c. It is calculated using Eq. (3) (Lu et al. , 2012). The values of the degree are in the range [0,1]. The value 1 represents homogeneous mixing, and extreme inhomogeneous mixing has a 0 value. We observed a higher mixing degree in the HV regions in both RH cases. The moist case shows relatively inhomogeneous mixing initially for both LV and HV regions and gradually shifts towards homogeneous mixing, although the HV region always remains at the higher side of homogeneous mixing.
A comparison of Damköhler numbers for all four cases is presented in Fig. 9d. The Damköhler number also measures the degree of mixing as a quantity related to two timescales, namely the fluid timescale () and the phase relaxation timescale ( (Kumar et al., 2012), where Urms is the root mean square of the turbulent velocity fluctuation, L is a characteristic length (energy injection) scale of the flow, nd is the droplet number density, D is the modified diffusivity and r denotes volume mean radius of the droplets.
The Damköhler number, , represents an estimation of the mixing scenario. Da≫1 indicates an inhomogeneous process, whereas Da≪1 represents a homogeneous process (Latham and Reed, 1997). In Fig. 9d, the evolution of the Damköhler number has been shown. Low-vorticity regions always have a bigger Da than high-vorticity regions. A value closer to zero indicates a higher degree of homogeneous mixing. Like the mixing diagrams, the Damköhler number also suggests a greater homogeneous mixing in the high-vorticity regions. High vorticity (i.e., circulations of fluid) indeed helps to promote faster mixing and produce a well-mixed homogeneous cloud volume.
Droplet characteristics in high-vorticity (HV) and low-vorticity (LV) regions in a 3D DNS of cloud–environment mixing in cumulus clouds have been studied. We have taken initial (polydisperse) drop size distributions, from the CAIPEEX observations (Bera et al., 2016) . Entrainment simulations were performed with two initial relative humidity values, namely 22 % and 85 %, for the ambient air that mixes with a cloud slab.
A DNS model setup similar to Kumar et al. (2014) has been considered. This setup has a cloudy volume and surrounding subsaturated air, which are allowed to mix as the entrainment simulation kicks in. During the entrainment and mixing process, the flow in the domain develops spatially varying characteristics. The magnitude of turbulence (decaying with time) is not the same everywhere. Some regions are highly turbulent and possess a high value of vorticity. The vortices may influence the distribution and growth of cloud droplets. To study the dependency of droplet characteristics on vorticity, we located HV regions in the computational domain. Finding HV regions is challenging because the shape, size and position of the vortices change within a fraction of a second. We have applied an unsupervised machine learning algorithm, k-means clustering, to categorize the high- and low-vorticity clusters. To our knowledge, it is the first time that the machine learning algorithm for investigating cloud turbulence properties has been applied. We answered the following scientific questions in this study:
- i.
How much of the volume fraction does intense vorticity occupy in the domain?
- ii.
Where is the cloud–clear-air interaction most prominent – in highly turbulent regions or weakly turbulent regions?
- iii.
Is preferential clustering the same for all droplet sizes?
- iv.
How do the spectral properties of droplets vary in high- and low-vorticity regions?
- v.
Does the relative humidity of the ambient air have any impact on the evolution of the droplet size spectra?
- vi.
What are the mixing characteristics in high- and low-vorticity regions?
Entrainment and mixing is a turbulent process, and during the initial few seconds, the cloud edges, where a large water vapor field gradient exists, are the most turbulent. More robust KE fluctuations were found at cloud edges, making them hot spots for vorticity generation. A distinct difference in the KE fluctuations was noted between two RH simulations (22 % and 85 %): a bigger difference was observed in the drier (RH = 22 %) case. Turbulent velocity fluctuations (Urms) were found to be higher in HV regions for both simulation cases.
Droplets tend to cluster in the LV region, although smaller droplets show a lower tendency to do so, which may lead to a heterogeneous number concentration in space and time, consequently affecting the droplet size distribution. Clustering of larger droplets in the LV region resulted in a higher mean volume radii in that area. The most important result from this study is the different spectral widths (σr) in the HV and LV regions. In the drier case, a higher value of σ occurred in the HV region during the first 5 s; after that, the opposite scenario was observed. This opposite behavior can be connected to droplet evaporation and dilution of the number concentration in the HV region. More air circulation in the HV region leads to more incoming drier ambient air as well as more outgoing moist air (as a result of droplet evaporation) from the region to promote much faster droplet evaporation. The spectral width always remains higher in the HV area for the moist case (RH = 85 %); this may be due to higher droplet evaporation which is influenced by the presence of rotating air pockets, helping to transport the vapor mass out of the HV region.
The intrusion of subsaturated air is most prominent in the high-vorticity regions which reflects in the evolution of the droplet supersaturation. Enhanced evaporation produces a wider droplet and supersaturation spectra. The time series of the droplet number concentration and the volume mean radius can be used to obtain mixing diagrams of high- and low-vorticity regions. The degree of mixing calculated based on the mixing diagram shows more mixing homogeneity in the HV regions. The Damköhler number, which depends upon fluid and phase timescales, also indicates a higher degree of homogeneous mixing in HV regions. We emphasize that our findings are strongly affected by entrainment and mixing of drier air at the cloud edges. The results may differ in adiabatic cloud cores where entrainment and mixing are absent.
The DNS output data used in this study are archived on the Aaditya HPC system at IITM Pune and can be made available upon request.
BK and MKY formulated the concept of this work. BK prepared the paper. RR ran the simulation and produced the results. SB carried out analysis and contributed to the paper preparation. SAR contributed to the paper preparation.
The authors declare that they have no conflict of interest.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The IITM Pune is funded by the Ministry of Earth Science (MoES), Government of India. The simulations were carried out on “Aaditya” HPC system (http://aadityahpc.tropmet.res.in/Aaditya/index.html, last access: 11 August 2021) provided by MoES. This research is partially supported by a NSERC/Hydro-Quebec Industrial Research Chair program grant to Man Kong Yau. The authors would like to thank Manmeet Singh, CCCR, IITM, for a productive discussion on machine learning algorithms that greatly aided this work.
This research has been supported by the Ministry of Earth Science (MoES), Government of India, and has been partially supported by a NSERC/Hydro-Quebec Industrial Research Chair program grant to Man Kong Yau.
This paper was edited by Corinna Hoose and reviewed by Emmanuel Olutayo Akinlabi and one anonymous referee.
Ayala, O., Rosa, B., Wang L. P., and Grabowski, W. W.: Effects of turbulence on the geometric collision rate of sedimenting droplets, Part 1: Results from direct numerical simulation, New J. Phys., 10, 075015, https://doi.org/10.1088/1367-2630/10/7/075015, 2008. a
Baker, M. B. and Latham, J.: The Evolution of Droplet Spectra and the Rate of Production of Embryonic Raindrops in Small Cumulus Clouds, J. Atmos. Sci., 36, 1612–1615, 1979. a
Bengtsson, L.: The global atmospheric water cycle, IOP Publishing Ltd, Environ. Res. Lett., 5, 025202, https://doi.org/10.1088/1748-9326/5/2/025202, 2010. a
Bera, S.: Droplet spectral dispersion by lateral mixing process in continental deep cumulus clouds, J. Atmos. Sol.-Terr. Phys., 214, 105550, https://doi.org/10.1016/j.jastp.2021.105550, 2021. a
Bera, S., Prabha, T. V., and Grabowski, W. W.: Observations of monsoon convective cloud microphysics over India and role of entrainment-mixing, J. Geophys. Res.-Atmos., 121, 9767–9788, https://doi.org/10.1002/2016JD025133, 2016. a, b
Bock, H. H.: Clustering Methods: A History of K-Means Algorithms, in: Selected Contributions in Data Analysis and Classification, edited by: Brito, P., Cucumel, G., Bertand, P., and de Carvalho, F., Berlin, Heidelberg, Springer Berlin Heidelberg, 161–172, https://doi.org/10.1007/978-3-540-73560-1_15, 2007. a
Brenguier, J. and Chaumat, L.: Droplet Spectra Broadening in Cumulus Clouds, Part I: Broadening in Adiabatic Cores, J. Atmos. Sci., 58, 628–641, 2001.
Chen, S., Bartello, P., Yau, M. K., Vaillancourt, P. A., and Zwijsen, K.: Cloud Droplet Collisions in Turbulent Environment: Collision Statistics and Parameterization, J. Atmos. Sci., 73, 621–636, https://doi.org/10.1175/JAS-D-15-0203.1, 2016. a
Clift, R., Grace, J. R., and Weber, M. E.: Bubbles, Drops, and Particles, Dover Publications, Incorporated, 1978. a
Cooper, W. A.: Effects of Variable Droplet Growth Histories on Droplet Size Distributions, Part I: Theory, J. Atmos. Sci., 46, 1301–1311, https://doi.org/10.1175/1520-0469(1989)046<1301:EOVDGH>2.0.CO;2, 1989. a
Cooper, W. A., Baumgardner, D., and Dye, J. E.: Evolution of the droplet spectra in Hawaiian orographic clouds, in: Preprints AMS Conf. Cloud Phys., Snowmass, 52–55, 1986. a
Devenish, B. J., Bartello, P. Brenguier, J. L., Collins, L. R., Grabowski, W. W., IJzermans, R. H. A., Malinowski, S. P., Reeks, M. W., Vassilicos, J. C., Wang, L. P., and Warhaft, Z.: Droplet growth in warm turbulent clouds, Q. J. Roy. Meteor. Soc., 138, 1401–1429, https://doi.org/10.1002/qj.1897, 2012. a
Franklin, C. N., Vaillancourt, P. A., Yau, M. K., and Bartello, P.: Collision Rates of Cloud Droplets in Turbulent Flow, J. Atmos. Sci., 62, 2451–2466, https://doi.org/10.1175/JAS3493.1, 2005. a
Gerber, H. E., Frick, G. M., Jensen, J. G., and Hudson, J. G.: Entrainment, Mixing, and Microphysics in Trade-Wind Cumulus, J. Meteorol. Soc. Jpn. Ser. II, 86, 87–106, 2008. a
Grabowski, W. W. and Petch, J. C.: Clouds in the Perturbed Climate System: Their Relationship to Energy Balance, Atmospheric Dynamics, and Precipitation, Struengmann Forum Report, in: DEEP CONVECTIVE CLOUDS. NCAR, USA, Opensky, available at: https://opensky.ucar.edu/islandora/object/books:211 (last access: 11 August 2021), 2009. a
Grabowski, W. W. and Vaillancourt, P.: Comments on Preferential concentration of cloud droplets by turbulence: Effects on the early evolution of cumulus cloud droplet spectra, J. Atmos. Sci., 56, 1433–1436, 1999. a
Grabowski, W. W. and Wang, L. P.: Growth of Cloud Droplets in a Turbulent Environment, Ann. Rev. Fluid Mech., 45, 293–324, https://doi.org/10.1146/annurev-fluid-011212-140750, 2013. a, b, c
Harrison, E. F., Minnis P., Barkstrom, B. R., Ramanathan V., Cess, R. D., and Gibson, G. G.: Seasonal variation of cloud radiative forcing derived from the Earth Radiation Budget Experiment, J. Geophys. Res.-Atmos., 95, 18687–18703, https://doi.org/10.1029/JD095iD11p18687, 1990. a
Holton, J. R. and Hakim, G. J.: An Introduction to Dynamic Meteorology (Fifth Edition), Academic Press, ISBN 9780123848666, https://doi.org/10.1016/B978-0-12-384866-6.00039-8, 2013. a
Jimenez, J., Wray, A. A., Saffman, P. G., and Rogallo, R. S.: The structure of intense vorticity in isotropic turbulence, J. Fluid Mech., 255, 65–90, 1993. a
Jonas, P.: Growth of droplets in cloud edge downdraughts, Q. J. Roy. Meteor. Soc., 117, 243–255, https://doi.org/10.1002/qj.49711749711, 1991. a
Jonas, P. R.: Turbulence and Cloud Microphysics, Elsevier, 40, 283–306, https://doi.org/10.1016/0169-8095(95)00035-6, 1996. a
Karpińska, K., Bodenschatz, J. F. E., Malinowski, S. P., Nowak, J. L., Risius, S., Schmeissner, T., Shaw, R. A., Siebert, H., Xi, H., Xu, H., and Bodenschatz, E.: Turbulence-induced cloud voids: observation and interpretation, Atmos. Chem. Phys., 19, 4991–5003, https://doi.org/10.5194/acp-19-4991-2019, 2019. a
Khain, A. M., Pinsky, T., Elperin, N., Kleeorin, I., Rogachevskii, A., and Kostinski, A.: Critical comments to results of investigations of drop collisions in turbulent clouds, Atmos. Res., 86, 1–20, https://doi.org/10.1016/j.atmosres.2007.05.003, 2007. a
Kumar, B., Schumacher, J., and Shaw, R. A.: Lagrangian Mixing Dynamics at the Cloudy-Clear Air Interface, J. Atmos. Sci., 71, 2564–2580, https://doi.org/10.1175/JAS-D-13-0294.1, 2014. a, b
Kumar, B., Janetzko, F., Schumacher, J., and Shaw, R. A.: Extreme responses of a coupled scalar–particle system during turbulent mixing, New J. Phys., 14, 115020, https://doi.org/10.1088/1367-2630/14/11/115020, 2012. a
Kumar, B., Bera, S., Prabha, T. V., and Grabowski, W. W.: Cloud-edge mixing: Direct numerical simulation and observations in Indian Monsoon clouds, J. Adv. Model. Earth Sy., 9, 332–353, https://doi.org/10.1002/2016MS000731, 2017. a, b
Kumar, B., Götzfried, P., Suresh, N., Schumacher, J., and Shaw R. A.: Scale Dependence of Cloud Microphysical Response to Turbulent Entrainment and Mixing, J. Adv. Model. Earth Sy., 10, 2777–2785, https://doi.org/10.1029/2018MS001487, 2018. a
Latham, J. and Reed, R. L.: Laboratory studies of the effects of mixing on the evolution of cloud droplet spectra, Q. J. Roy. Meteor. Soc., 103, 297–306, https://doi.org/10.1002/qj.49710343607, 1997. a
Lehmann, K., Siebert, H., and Shaw, R. A.: Homogeneous and Inhomogeneous Mixing in Cumulus Clouds: Dependence on Local Turbulence Structure, J. Atmos. Sci., 66, 3641–3659, https://doi.org/10.1175/2009JAS3012.1, 2009. a
Lian, H., Charalampous, G., and Hardalupas, Y.: Preferential concentration of poly-dispersed droplets in stationary isotropic turbulence, Exper. Fluids, 54, 1525, https://doi.org/10.1007/s00348-013-1525-3, 2013. a
Lu, C., Liu, Y., Niu, S., Krueger, S., and Wagner, T.: Exploring parameterization for turbulent entrainment‐mixing processes in clouds, J. Geophys. Res.-Atmos., 118, 185–194, https://doi.org/10.1029/2012JD018464, 2013. a, b
Luo, S., Lu, C., Liu, Y., Bian, J., Gao, W., Li, J., Xu, X., Gao, S., Yang, S., and Guo, X.: Parameterizations of entrainment‐mixing mechanisms and their effects on cloud droplet spectral width based on numerical simulations, J. Geophys. Res.-Atmos., 125, e2020JD032972, https://doi.org/10.1029/2020JD032972, 2020. a
Pedregosa, F.: Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res.h, 12, 2825–2830, 2011. a
Pinsky, M., Khain, A., and Shapiro, M.,: Stochastic effects of cloud droplet hydrodynamic interaction in a turbulent flow, Atmos. Res., 53, 131–169, https://doi.org/10.1016/S0169-8095(99)00048-4, 2000. a
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation, Springer, 1997. a
Randall, D. A. and Tjemkes, S. : Clouds, the earth’s radiation budget, and the hydrologic cycle, Glob. Planet. Change, 4, 3–9, https://doi.org/10.1016/0921-8181(91)90063-3, 1991. a
Riemer, N. and Wexler, A. S.: Droplets to Drops by Turbulent Coagulation, J. Atmos. Sci., 62, 1962–1975, https://doi.org/10.1175/JAS3431.1, 2005. a
Rogers, R. R. and Yau, M. K.: A Short Course in Cloud Physics, Elsevier, Oxford, United Kingdom, 1996. a, b
Shaw, R. A.: Particle-turbulence interactions in atmospheric clouds, Annu. Rev. Fluid Mech., 35, 183–227, https://doi.org/10.1146/annurev.fluid.35.101101.161125, 2003. a, b
Shaw, R. A., Reade, W. C., Collins, L. R., and Verlinde, J.: Preferential Concentration of Cloud Droplets by Turbulence: Effects on the Early Evolution of Cumulus Cloud Droplet Spectra, J. Atmos. Sci., 55, 1965–1976, https://doi.org/10.1175/1520-0469(1998)055<1965:PCOCDB>2.0.CO;2, 1998. a, b, c, d, e, f, g, h, i, j
SIONLib: Scalable library for parallel access to task-local files. Germany: Forschungszentrum Jülich, available at: https://www.fz-juelich.de/ias/jsc/EN/Expertise/Support/Software/SIONlib/_node.html (last access: 11 August 2021), 2020. a
Squires, K. D. and Eaton, J. K.: Measurements of particle dispersion obtained from direct numerical simulations of isotropic turbulence, J. Fluid Mech., 226, 1–35, 1991. a
Vaillancourt, P. A. and Yau, M. K.: Review of Particle-Turbulence Interactions and Consequences for Cloud Physic, B. Am. Meteorol. Soc., 81, 285–298, https://doi.org/10.1175/1520-0477(2000)081<0285:ROPIAC>2.3.CO;2, 2000. a, b, c, d
Vaillancourt, P. A., Yau, M. K., and Grabowski, W. W.: Upshear and Downshear Evolution of Cloud Structure and Spectral Properties, J. Atmos. Sci., 54, 1203–1217, https://doi.org/10.1175/1520-0469(1997)054<1203:UADEOC>2.0.CO;2, 1997. a, b
Vaillancourt, P. A., Yau, M. K., Bartello, P., and Grabowski, W. W.: Microscopic Approach to Cloud Droplet Growth by Condensation, Part II: Turbulence, Clustering, and Condensational Growth, J. Atmos. Sci., 59, 3421–3435, https://doi.org/10.1175/1520-0469(2002)059<3421:MATCDG>2.0.CO;2, 2002.