the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Coupled and decoupled stratocumulus-topped boundary layers: turbulence properties
Holger Siebert
Kai-Erik Szodry
Szymon P. Malinowski
We compare turbulence properties in coupled and decoupled marine stratocumulus-topped boundary layers (STBLs) using high-resolution in situ measurements performed by the helicopter-borne Airborne Cloud Turbulence Observation System (ACTOS) platform in the region of the eastern North Atlantic.
The thermodynamically well-mixed coupled STBL was characterized by a comparable latent heat flux at the surface and in the cloud-top region, and substantially smaller sensible heat flux in the entire depth. Turbulence kinetic energy (TKE) was efficiently generated by buoyancy in the cloud and at the surface, and dissipated with comparable rate across the entire depth. Structure functions and power spectra of velocity fluctuations in the inertial range were reasonably consistent with the predictions of Kolmogorov theory. The turbulence was close to isotropic.
In the decoupled STBL, decoupling was most obvious in humidity profiles. Heat fluxes and buoyant TKE production at the surface were similar to the coupled case. Around the transition level, latent heat flux decreased to zero and TKE was consumed by weak stability. In the cloud-top region, heat fluxes almost vanished and buoyancy production was significantly smaller than for the coupled case. The TKE dissipation rate inside the decoupled STBL varied between its sublayers. Structure functions and power spectra in the inertial range deviated from Kolmogorov scaling. This was more pronounced in the cloud and subcloud layer in comparison to the surface mixed layer. The turbulence was more anisotropic than in the coupled STBL, with horizontal fluctuations dominating. The degree of anisotropy was largest in the cloud and subcloud layer of the decoupled STBL.
Integral length scales, of the order of 100 m in both cases, indicate turbulent eddies smaller than the depth of the coupled STBL or of the sublayers of the decoupled STBL. We hypothesize that turbulence produced in the cloud or close to the surface is redistributed across the entire coupled STBL but rather only inside the sublayers where it was generated in the case of the decoupled STBL. Scattered cumulus convection, developed below the stratocumulus base, may play a role in transport between those sublayers.
- Article
(8172 KB) - Full-text XML
- BibTeX
- EndNote
Low-level stratocumulus clouds cover around 20 % of the Earth's surface in annual mean, more than any other cloud type. They occupy the upper few hundred meters of the planetary boundary layer, preferentially in the conditions of large-scale subsidence, strong lower-tropospheric stability and moisture supply from the surface (Wood, 2012). Those are usually present in the regions of subtropical and midlatitude oceans with upwelling of cold deep water. Widespread presence, persistence and high albedo makes marine stratocumulus important for the energy balance of the planet (Hartmann et al., 1992). Minor variations in coverage and optical thickness impact the radiation budget and therefore also model-based climate predictions (Boucher et al., 2013; Schneider et al., 2019).
The primary mechanism driving the circulation inside the stratocumulus-topped boundary layer (STBL) is longwave radiative cooling at the cloud top which produces convective instability. An additional source of turbulence is provided by surface buoyancy, wind shear, latent heat release in updrafts, evaporation in downdrafts or evaporative cooling associated with entrainment of dry, warm air from the free troposphere (Lilly, 1968; Stevens, 2002; Gerber et al., 2016; Mellado, 2017). Properties of the STBL are dependent on the level to which stratocumulus cloud is coupled with sea surface fluxes, in particular of latent and sensible heat (Bretherton and Wyant, 1997; Xiao et al., 2011; Zheng et al., 2018a).
Moderately shallow STBLs are often well mixed (Stull, 1988; Markowski and Richardson, 2010). Their typical vertical structure features an adiabatic lapse rate (dry below cloud, moist inside), a strong capping inversion at the top, near-constant concentration of moist-conserved variables (such as total water mass fraction and liquid water potential temperature) from the surface up to the inversion. However, when the circulation ceases to mix the air over entire depth, the STBL becomes decoupled; i.e., the cloud is separated from the moisture supply from the surface (Nicholls, 1984; Turton and Nicholls, 1987; Wood, 2012). The radiatively driven stratocumulus layer (SCL) and the subcloud layer (SBL) in the upper part might be still mixed by negatively buoyant eddies generated at cloud top, while the surface mixed layer (SML) at the bottom might be mixed by positive buoyancy or shear. A stable or conditionally unstable intermediate transition layer (TSL) emerges in between. Conditional instability allows for the cumulus updrafts to penetrate through and intermittently restore the coupling (Bretherton and Wyant, 1997; De Roode and Duynkerke, 1997).
Decoupling can be caused either by reducing the intensity of radiatively driven circulation in relation to STBL depth or by stabilizing the subcloud layer (Zheng et al., 2018b). The first possibility might be realized with daytime shortwave radiative heating which offsets longwave cooling (Nicholls, 1984; Turton and Nicholls, 1987) or by extensive entrainment of warm and dry free-tropospheric air which deepens the STBL to such an extent that the turbulence is no longer sufficient to sustain the mixing (Bretherton and Wyant, 1997). The second possibility involves stratification of the lower part by cooling, for instance, due to precipitation evaporation (Caldwell et al., 2005; Dodson and Small Griswold, 2021) or advection over colder sea surface (Stevens et al., 1998).
STBL decoupling is the factor which strongly influences further evolution of cloud pattern and boundary layer structure. It constitutes an intermediate stage of transition from overcast stratocumulus into shallow cumulus convection over subtropical oceans as the air masses are advected by the trade winds towards the Equator (Albrecht et al., 1995; Bretherton and Wyant, 1997; De Roode et al., 2016; Zheng et al., 2020). Successful representation and prediction of such transition between the two STBL regimes poses a challenge for atmospheric general circulation models (Xiao et al., 2012), in large part due to limited understanding of the interaction of various processes involved.
Previous observational studies have documented the structure of the coupled and decoupled STBLs in terms of thermodynamic and radiative features (Wood and Bretherton, 2004; Jones et al., 2011; Ghate et al., 2015; Zheng and Li, 2019) as well as aerosol and cloud properties (Dong et al., 2015; Wang et al., 2016; Goren et al., 2018; Zheng et al., 2018b). On the other hand, modeling efforts provided insightful conceptual explanations of the mechanisms leading to a switch between coupled and decoupled regimes (Turton and Nicholls, 1987; Bretherton and Wyant, 1997; Stevens, 2000; Xiao et al., 2011).
Although the concept of circulation and turbulence being insufficiently strong in order to maintain the mixing throughout the entire depth plays a central role in the conventional rationale of decoupling, few works attempted to quantitatively characterize small-scale (integral length scales and below) turbulence (e.g., Lambert and Durand, 1999; Dodson and Small Griswold, 2021). The major reason is the technical difficulty in measuring turbulent fluctuations of wind velocity, temperature or humidity with adequate spatial resolution and accuracy. Within the present study, we compare the properties of turbulence derived from unique helicopter-borne observations performed in coupled and decoupled STBLs in the region of the eastern North Atlantic. Particular attention is given to small-scale features and deviations from the assumption of stationary homogeneous isotropic turbulence.
The paper is structured as follows. Section 2 introduces the measurements, including instrumentation, sampling strategy and general synoptic conditions. The selection of the two cases, coupled and decoupled STBLs, is explained. Section 3 describes the stratification of the STBL in terms of thermodynamics and stability. The division into sublayers is delineated and the degree of coupling is expressed quantitatively according to literature criteria. Section 4 provides relevant details concerning derivation of turbulence parameters. Section 5 compares properties of turbulence: turbulence kinetic energy, its production and dissipation rates, fluxes of sensible and latent heat, anisotropy of turbulent motions and typical length scales. Finally, the results of the comparison are summarized and discussed in the last section.
2.1 Location and synoptic conditions
Observations were collected in July 2017 during the ACORES (Azores stratoCumulus measurements Of Radiation, turbulEnce and aeroSols) campaign in the eastern North Atlantic around the island of Graciosa in the Azores archipelago. A comprehensive description of the project, including weather conditions, instrumentation, sampling strategy and selected research highlights is provided by Siebert et al. (2021).
The area of the experiment is considered to be influenced by a wide range of synoptic-scale meteorological conditions. Graciosa is located near the boundary of subtropics and midlatitudes. Therefore, the impacts of both a subtropical trade wind system and midlatitude cyclones are relevant. The climatology of the marine boundary layer was inferred by Rémillard et al. (2012) based on the long-term ground-based measurements of the CAP-MBL (Clouds, Aerosol, and Precipitation in the Marine Boundary Layer) project (Wood et al., 2015) utilizing the Atmospheric Radiation Measurement (ARM) facility established right next to the Graciosa airport. They reported that boundary layer decoupling and multiple cloud types (for instance, cumulus under stratocumulus) are very frequent at the site throughout the year. Indeed, the range of weather conditions was observed during the ACORES, related to the location and strength of Azores High, as well as occasional front passages (Siebert et al., 2021).
2.2 Instrumentation
Measurements were performed with the Airborne Cloud Turbulence Observation System (ACTOS, Siebert et al., 2006a) and the Spectral Modular Airborne Radiation measurement sysTem – HELIcopter-borne ObservationS (SMART-HELIOS, Werner et al., 2013, 2014). Both instrumental payloads were carried by the BO-105 helicopter as two separate external cargos on one long tether: SMART-HELIOS mounted 20 m below the helicopter and ACTOS another 150 m underneath. Typical true air speed of 20 m s−1 and a high sampling rate of individual instruments provided spatial resolution much higher than for a typical research aircraft.
For the complete instrumentation of the helicopter payloads, see Tables 1 and 2 in Siebert et al. (2021). In the current study, we used the following ACTOS data: three-dimensional wind vector in the Earth-fixed system and longitudinal–vertical wind components (u,w) in platform-fixed system (derivation explained in Sect. 4) provided by the combination of the ultrasonic anemometer–thermometer (Gill Solent HS, Siebert and Teichmann, 2000) and a high-accuracy motion package (inertial navigation system and GPS); virtual temperature Tv derived from the speed of sound measured with the same ultrasonic anemometer–thermometer (Siebert and Muschinski, 2001); temperature T and its small-scale fluctuations measured by the Ultrafast Thermometer (UFT, Haman et al., 1997; Nowak et al., 2018) combined with the precise calibrated PT100; specific humidity qv from the open-path infrared absorption hygrometer (LI-COR LI-7500, Lampert et al., 2018); liquid water mass fraction ql determined with the Particle Volume Meter (PVM-100A, Gerber et al., 1994; Wendisch et al., 2002).
The standard deviations due to uncorrelated noise for sonic measurements are 0.02 m s−1 for wind and 0.02 K for virtual temperature (Siebert and Muschinski, 2001). The PT100 was calibrated prior to the campaign in a thermostated water tank using the Greisinger GMH 3750 reference thermometer which provides accuracy better than 0.05 K. The UFT was calibrated for each flight separately against the PT100. For the UFT records, the standard deviation due to uncorrelated noise is 4 mK (Siebert et al., 2003). The hygrometer provides qv with a noise floor of about 0.005 g kg−1. This instrument was verified to agree well with a few hygrometers of different types and operate satisfactorily on the helicopter-towed Helipod system by Lampert et al. (2018). The PVM-100A measures ql with the accuracy of 5 %, and its noise floor was estimated by Siebert et al. (2003) to be about 0.001 g kg−1. The exact sensitivity depends to some extent on droplet size distribution; see Wendisch et al. (2002) for details. For a more general discussion of the instrumentation on the ACTOS platform, see Siebert et al. (2006a).
2.3 Data overview
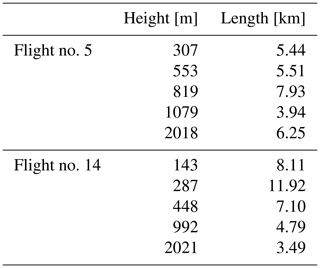
Helicopter flights during ACORES were typically performed over the ocean inside the 10 by 10 km square adjacent to the northern coast of Graciosa. Specific flight path and maneuvers depended on the local cloud situation. Within the flight time of 2 h, the usual strategy involved the following: vertical profile up to roughly 2000 m (a.s.l.), a few 10 km long horizontal legs at selected levels and several steep porpoise dives around stratocumulus top. Two flights were selected for our comparative study: flight no. 5 on 8 July 2017 and flight no. 14 on 18 July 2017. The choice was dictated by stratocumulus presence, STBL stratification (considerably well mixed in flight no. 5, considerably decoupled in flight no. 14) and a flight pattern involving substantial sampling time below SC.
Segments of two types were selected from the measurement records: profiles (PROFs) and horizontal legs (LEGs). For convenience, for each flight PROFs are ordered chronologically according to their time of execution and referred to as PROF1–PROF5, while LEGs are ordered according to their mean altitude (meters above sea level). The segmentation was done manually so that the influence of sharp turns and pendulum-like motion of the payload is avoided. This resulted in the reduced length of the LEGs, between 3.5 and 12 km. LEGs were flown with a true air speed of 15–20 m s−1 and some minor displacements in vertical are unavoidable for the payload on a 170 m long rope. The mean altitudes and exact lengths are listed in Table 1.
PROFs are in fact slanted with an ascent or descent rate of about 3–5 m s−1, which results in an aspect ratio of 0.15–0.25. The horizontal component of motion is necessary to avoid the downwash of the helicopter affecting wind and turbulence measurements on ACTOS. More details about measuring turbulence below a helicopter can be found in Siebert et al. (2006a) and Muschinski et al. (2001).
Flight no. 5 was performed in the afternoon (14:28–16:26 UTC1) on 8 July 2017. Stratocumulus clouds emerged behind the cold front which had passed the island the day before. The cloud field was moderately thick and quite heterogeneous in structure, with some visible clearings. The satellite image from MODIS on Aqua (Fig. 1) confirms this observation, showing dispersed cloud patches in the vicinity of Graciosa.
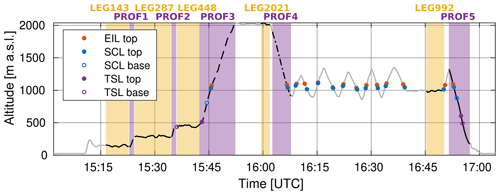
The flight pattern (Fig. 2) involved the following: deep PROF from minimum flight level (60 m) into the free troposphere (FT), two LEGs in the FT with one close to the stratocumulus top and three LEGs in the STBL with one inside stratocumulus cloud, close to its top. Specific PROFs are indicated in the figure with different line styles which are used hereafter in the vertical profiles of various derived parameters. Altitude ranges corresponding to PROF2–PROF5 of this flight do not overlap; hence, we marked them all with dashed lines.
Flight no. 14 was performed in the afternoon (15:01–17:04 UTC) on 18 July 2017, shortly after weak precipitation had been noted at the site. The sky was overcast with stratocumulus cloud of homogeneous structure. Many little cumulus clouds, probably at the initial state of formation, were reported over the ocean below the stratocumulus deck. However, they were not observed to reach the stratocumulus base. A MODIS Aqua image (Fig. 3) shows a large solid patch of stratocumulus clouds with signatures of closed-cell convection regime. The flight pattern (Fig. 4) involved the following: four LEGs in the STBL with one inside the stratocumulus cloud, close to its top, one LEG in the FT and a number of PROFs connecting LEG levels. In this figure and hereafter, PROF1–PROF3 are all marked with dashed lines because their altitude ranges do not overlap.

Figure 1Satellite True Color image (250×250 km) taken on 8 July 2017 at 15:45 UTC (i.e., during flight no. 5; the time given corresponds to the left swath covering most of the image) by the MODIS instrument on Aqua overpassing Azores, centered on Graciosa airport (blue circle), with the overlaid helicopter operation area (red box). The image was acquired from NASA Worldview Snapshots.
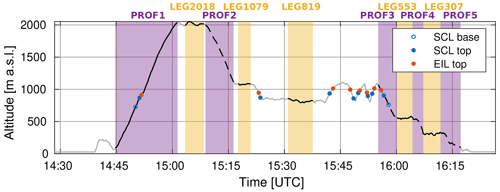
Figure 2ACTOS altitude in flight no. 5 with marked selected profiles and horizontal legs. PROFs are ordered chronologically; LEGs are ordered according to their altitude. Line styles of the PROFs are consistent with the figures in the following sections. Altitude ranges corresponding to PROF2–PROF5 of this flight do not overlap and are all marked with dashed lines. Dots indicate the penetrations of the boundaries of the specific sublayers described in Sect. 3.

Figure 3As in Fig. 1 but taken on 18 July 2017 at 14:43 UTC (shortly before flight no. 14). The image was acquired from NASA Worldview Snapshots.
3.1 Derivation of meteorological and stability parameters
Meteorological conditions and stability parameters derived from PROFs are shown in Figs. 5 and 6 for flight no. 5 and no. 14, respectively. Liquid water potential temperature θl was calculated following the approximation by Betts (1973):
where θ denotes potential temperature, Lv latent heat of vaporization for water and cp specific heat of dry air at constant pressure. Horizontal wind speed U and direction dd result from appropriate transformation of measured flow velocity (Edson et al., 1998). Because helicopter climb rate was not exactly constant in time and individual instruments differ in sampling rate, data points were grouped and averaged in 10 m high altitude bins (yet separately for each PROF). To reduce the effect of random eddy penetration and improve clarity, wind profiles were additionally smoothed with a five-point moving average.
Lifting condensation level (LCL) was then derived for each height according to Bolton (1980). Such a result is sensitive to gradients of thermodynamic properties in subcloud layer, signalling the degree of boundary layer coupling. To characterize static stability, the Brunt–Vaisala frequency Nb was used:
where θv is virtual potential temperature derived from speed of sound (provided by an ultrasonic anemometer–thermometer), g gravitational acceleration and z height above sea level. Shear rate Sh quantifies the vertical gradient of horizontal wind:
where ue is the eastward and ve the northward wind component. The derivatives were evaluated as the tangent of linear least-squares fit of 10 m binned variable versus z performed inside symmetric five-point windows.
3.2 Quantitative judgment of the degree of coupling
In order to objectively confirm the fact of coupling or decoupling of STBL, we employed several methods from the literature (Jones et al., 2011; Wood and Bretherton, 2004; Yin and Albrecht, 2000).
The first criterion of Jones et al. (2011) involves the differences of θl and total water mixing ratio between the uppermost and the lowermost quarters of the boundary layer (instead of the latter quantity, we used our total water mass fraction , which does not influence the conclusions because those two measures are approximately equal). The sounding is classified as coupled when 0.5 K and 0.5 g kg−1, and decoupled otherwise. The second criterion of Jones et al. (2011) involves the difference between the observed cloud base height CB and the LCL corresponding to the conditions at the bottom of the boundary layer. It is classified as coupled when 150 m, and decoupled otherwise. Here, we used mean conditions of the lowest leg (LEG307 for flight no. 5, LEG143 for flight no. 14) to estimate LCLbot and ql in PROFs to estimate the cloud base height.
Wood and Bretherton (2004) proposed two decoupling parameters:
where superscripts +, −, 0 denote the values just above the inversion, just below the inversion and in the surface mixed layer, respectively. Wood and Bretherton (2004) calculated αθ and αq over the subtropical eastern Pacific at around 0 to 0.4; however, no exact critical value for decoupling was determined. The higher those parameters, the more a decoupled boundary layer is considered. Here, instead of first finding the SML, we apply mean values in the lower quarter of the boundary layer ( and ).
Yin and Albrecht (2000) introduced a stability parameter to identify transitions in boundary layer soundings:
where depends on the ratio of gas constants for water vapor Rv and dry air Rd, while rv is the water vapor mixing ratio. Their procedure detects transition in the subcloud zone anytime the value of μ exceeds the average between 980 and 900 hPa by a factor of 1.3. Here, instead of using pressure levels, we specify as the boundary layer mean.
The above parameters were estimated using PROF1 of flight no. 5 and PROF5 of flight no. 14. According to the criteria of Jones et al. (2011), it is evident that flight no. 5 ( 0.51 ∘C, Δqt= 0.13 g kg−1, 72 m) was performed in a coupled STBL, while flight no. 14 (Δθl= 1.19 ∘C, Δqt= 0.90 g kg−1, Δz= 216 m) was done in a decoupled STBL. Negative values of Δθl and Δz suggest instability but it might be also attributed to horizontal inhomogeneities of stratocumulus structure (Sect. 2.3) in combination with a slanted flight path. Consistently, the parameters of Wood and Bretherton (2004) are smaller for flight no. 5 (0.12, αq= 0.04) than for flight no. 14 (αθ= 0.26, αq= 0.26). The parameter μ is plotted in panel (d) of Figs. 5 and 6. It varies significantly with height, and the critical value is occasionally exceeded in both flights. This method was probably optimized for radiosoundings in different climate regimes and does not seem robust in the case of our data.
Following previous studies looking for differences of cloud-top entrainment instability between coupled and decoupled clouds (e.g., Xiao et al., 2011), we calculated the Randall–Deardorff parameter (Randall, 1980; Deardorff, 1980):
In both our cases (κ= 0.71 for flight no. 5 and κ= 0.34 for no. 14), it exceeds the critical value of about 0.23, indicating the possibility of buoyancy reversal resulting from mixing and evaporative cooling at cloud top.
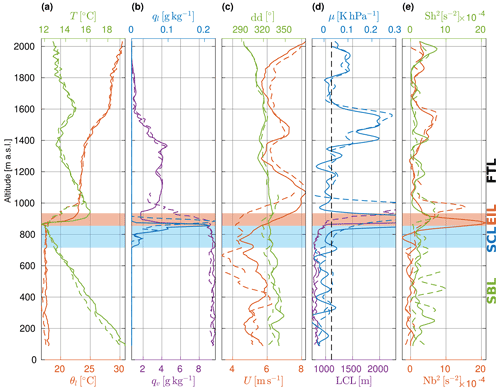
Figure 5Vertical structure of the coupled STBL (flight no. 5): (a) temperature T and liquid water potential temperature θl, (b) liquid water mass fraction ql and specific humidity qv, (c) wind speed U and direction dd, (d) LCL and stability parameter μ of Yin and Albrecht (2000) with its critical level for the detection of transitions (dashed black line), (e) squared Brunt–Vaisala frequency Nb2 and wind shear rate Sh2. Line styles correspond to specific profiles – consistently with Fig. 2. Color shadings denote the sublayers: entrainment interface layer (red) and stratocumulus layer (blue).
3.3 Structure of the coupled STBL
The profiles in flight no. 5 exhibit a well-mixed STBL (Fig. 5). Temperature falls with height with a near-constant lapse rate ΓT inside the boundary layer, followed by a sharp inversion at the top. Liquid water potential temperature is almost constant from close to the surface up to the stratocumulus top, where it features an increase of ∼ 5 K. Total water mass fraction behaves analogously, with a decrease of ∼ 7 g kg−1 above the cloud top. Interestingly, very dry air is located at the top of the temperature inversion. It is further capped by a layer of considerably higher qv; however, it is much lower than inside the boundary layer. Liquid water mass fraction in the cloud is moderate and suggests non-trivial cloud structure. There were cloud clearings penetrated as ACTOS moved along the slanted path, visible in the high rate records of ql (not shown here). Wind velocity fluctuates in the boundary layer within ±1 m s−1 around the mean ∼ 5 m s−1. Wind shear across the cloud top and the inversion can be noticed. Wind direction is from the NNW throughout the sampled height.
Significant differences can be observed between the PROFs in wind speed and the position of inversion. Subsequent PROFs were not performed at the same time and location, so certain variability is expected. Airborne sampling features inevitable randomness due to probing specific structures (eddies, updrafts, cloud holes, etc.); thus, slanted profiles do not represent mean conditions accurately.
LCL stays roughly equal from the lowest level up to the cloud base. Interestingly, it is slightly higher than the actual cloud base, which might be again related to horizontal inhomogeneities in cloud structure. Brunt–Vaisala frequency indicates weak static instability in the boundary layer, stronger inside the cloud than below, and very strong stability at the capping inversion. Wind shear is more variable, which can be attributed to sampling various eddies.
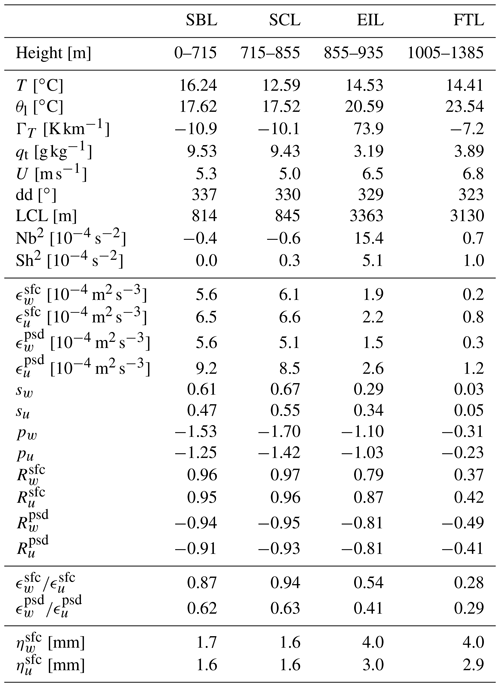
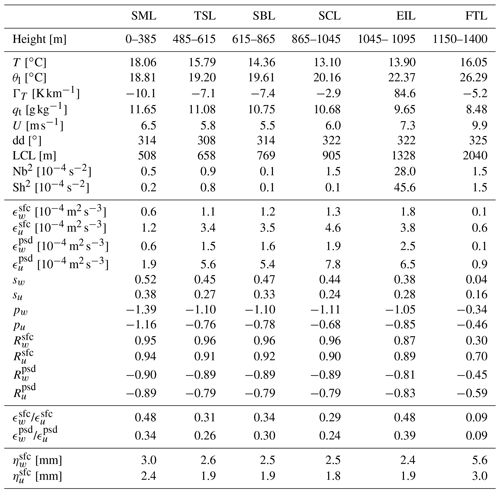
Based on θl, ql and qv, we manually distinguished the following sublayers: the entrainment interface layer (EIL) including the temperature inversion and the very top of the cloud, the stratocumulus layer (SCL) containing the cloud, the subcloud layer (SBL) ranging from cloud base down to the surface and the free tropospheric sublayer (FTL) representing the typical conditions in the lower FT (not necessarily adjacent to the EIL top). For reference, the EIL and SCL are marked with red and blue shading in Fig. 5 and in the figures in Sect. 5. The heights and average properties inside the sublayers are listed in Table A1 in the Appendix. The deepest profile (PROF1, solid line) was used for sublayer distinction because the specific heights may vary between the PROFs. The individual penetrations of the sublayer boundaries during other segments (PROFs and dolphin porpoises) are indicated in Fig. 2.
3.4 Structure of the decoupled STBL
The profiles in flight no. 14 exhibit a decoupled STBL (Fig. 6). Liquid water potential temperature gradually rises with height, whereas specific humidity decreases stepwise. Despite the distinct qv gradient in the middle of the boundary layer, its value in the lowest part and in the subcloud section is relatively stable. This suggests that both the upper and the lower STBL portions are internally mixed. The FT is quite humid, with values of qv larger than for flight no. 5. The difference in θl at the stratocumulus top is ∼ 5 K, while in qt it is only ∼ 3 g kg−1. The stratocumulus is thicker and more abundant in liquid water than in the previous case. Wind velocity varies ±1 m s−1 around the mean ∼ 6 m s−1. Wind direction is predominantly NW. There is significant wind shear across the inversion, with difference in U reaching ∼ 4 m s−1. LCL replicates the gradients of qv in the middle of the boundary layer. It corresponds to the cloud base height only in the section right below the cloud, which is a signature of decoupling. The Brunt–Vaisala frequency indicates weak static stability throughout most of the profile, including the cloud. Its peak in the inversion layer coincides well with the maximum of Sh2.
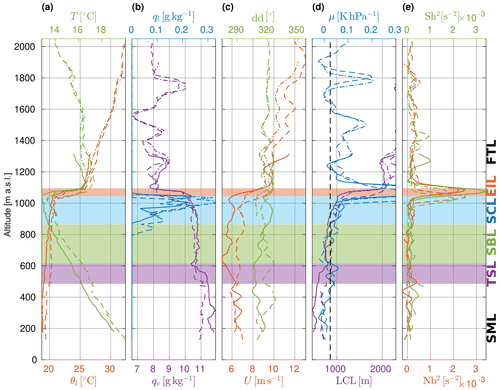
Similarly to flight no. 5, we distinguished the sublayers: the FTL, the EIL, the SCL and the SBL extending from cloud base down to the level where LCL is no longer in agreement with the observed cloud base height. In addition, two more sublayers typical for decoupled conditions were introduced: the transition layer (TSL) containing the major gradients in specific humidity and wind speed, and the surface mixed layer (SML) extending from the surface up to the bend in θl profile (where it begins to rise with height, see Fig. 6a). A somewhat arbitrary boundary of 385 m was chosen to represent the section directly influenced by surface processes. For reference, the EIL, SCL, SBL and TSL are marked with red, blue, green and purple shading, respectively, in Fig. 6 and the figures in Sect. 5. The heights and average properties inside the sublayers are listed in Table A2. PROF5 was used for sublayer identification because it covers most of the STBL depth. The individual penetrations of the sublayer boundaries during other segments are indicated in Fig. 4.
Parameters of turbulence were derived using high-resolution measurements of wind velocity, temperature and humidity. Depending on the quantity, the results were obtained for PROFs or LEGs specified in Sect. 2.3. In the case of PROFs, our procedure resembles the approach of Tjernstrom (1993). After time series of a parameter had been computed, appropriate segments were extracted and data were averaged in 10 m altitude bins (as in Sect. 3.1). For LEGs, the full segment was used to calculate a desired parameter. Next, each LEG was divided into seven subsegments of equal length, overlapping by half of the length, and the very same method was applied to calculate respective quantity in each subsegment. Standard deviation among subsegments is regarded as parameter variability and shown with error bars in plots.
The lateral channel of the ultrasonic anemometer was affected by a substantial level of artificial fluctuations (up to 1 m s−1 in amplitude) due to instrumental issues. The origin of this problem is under investigation. It seems to appear for true air speed above about 12 m s−1, which makes it relevant for most of the flight time. Therefore, we applied simplified geometrical transformation to the measured velocity vector, so that high-resolution retrieval of wind velocity is possible. In comparison with the standard transformation (Lenschow, 1986), we included pitch rotation but neglected roll and yaw rotations to prevent the lateral channel from coupling with the others. The resulting vector can be interpreted as wind velocity in horizontal longitudinal, horizontal lateral and vertical directions, respectively, as long as the platform is not tilted left or right (roll angle is small). This condition was satisfied throughout most of the flight time, except for major turns. For calculating turbulence properties, we selected segments with the roll angle < 0.1 rad. The lateral wind v cannot be used for turbulence analysis, but longitudinal u and vertical w are free of the disturbances. The modification described is not necessary to obtain mean wind profiles (U, dd) because averaging and smoothing is applied anyway (see Sect. 3.1).
Reynolds decomposition of the signals (cf. Stull, 1988),
into large-scale slowly varying X(t) and small-scale fluctuations x′(t) was realized with a simple symmetric running mean. Fluctuations x′(t) were obtained by subtracting that mean from the original signal. Unless specified otherwise, the chosen window was 50 s which corresponds to the distance of ∼ 1 km. Such length is enough to penetrate at least a few large turbulent eddies typical for the atmospheric boundary layer (Malinowski et al., 2013).
4.1 Turbulence kinetic energy and variances
Variances of turbulent fluctuations , , , and the third moment of vertical velocity fluctuations were obtained by taking the average along LEG, denoted as 〈 〉. Because lateral wind fluctuations were not available, we assumed horizontal isotropy to approximate missing with in turbulence kinetic energy (TKE) calculation:
It is worth remembering that variances and TKE usually represent mostly large scales because larger eddies in turbulence cascade are more energetic than smaller ones.
The accuracy of the results is severely limited by the length of the LEGs. Based on the methods of Lenschow et al. (1994), in the boundary layer, the variances are subject to the systematic sampling error of about 5 % and the random sampling error of about 20 %. In the case of , those errors are accordingly larger (order of 10 % and 100 %, respectively, unless is not very close to zero). Importantly, in the plots, we provide the variability among subsegments which was found to be of the same order as the total sampling error and in most cases larger than it.
4.2 TKE production and heat fluxes
Turbulence kinetic energy can be generated by buoyancy and wind shear (ignoring advection and turbulent transport). We estimated two respective terms of the TKE budget equation (Stull, 1988), buoyancy production/consumption B and shear production S, employing eddy correlation:
Here, we could provide only the longitudinal component of shear production because lateral wind fluctuations were not available. Correlations were computed along the LEGs. Derivatives were estimated from the PROFs covering the relevant altitude range. Inevitably, such an approach introduces some inaccuracy, as the exact place and time of derivative estimation are different from those for the correlation estimation. To quantify vertical transport of heat and moisture, we estimated sensible and latent heat fluxes according to
where ρ is air density.
The range of scales represented in the correlations is limited by the lowest spatial resolution of the two multiplied signals. The anemometer (u, w, θv) resolves scales down to ∼ 0.5 m (where this limit stems from the path length and spectral transfer properties (Kaimal et al., 1968)), the thermometer (θ) down to ∼ 2 cm and the hygrometer (qv) down to ∼ 1 m. As a result, , and are resolved down to ∼ 0.5 m, while is resolved down to ∼ 1 m. Those three instruments work satisfactorily also inside clouds of moderate liquid water and droplet concentration, as our stratocumulus (Cruette et al., 2000; Siebert and Teichmann, 2000). In comparison with some other studies, the buoyancy estimation in the cloud does not include the contributions of liquid water flux and droplet sedimentation, which are expected to be relatively small (considering moderate ql) and of opposite sign, and therefore partly compensate.
Similarly to variances, the accuracy of the fluxes obtained with the method of eddy correlation is limited by the length of the LEGs. In the boundary layer, the systematic sampling error was estimated for about 5 %–10 %, while the random sampling error was estimated for about 50 % (Lenschow et al., 1994), unless the flux does not vanish. The subsegment variability (marked with error bars in the plots) is in most cases larger than the total sampling error.
Additionally, B, Qs and ql at the surface were estimated with the Coupled Ocean–Atmosphere Response Experiment bulk algorithm in version 3.0 (COARE 3.0) described in Fairall et al. (2003). Sea surface temperature was taken from the satellite multi-mission product provided by the Group for High Resolution Sea Surface Temperature (JPL MUR MEaSUREs Project, 2015), while all the other inputs were our measurements from the lowest point of the PROFs.
4.3 TKE dissipation rate
TKE dissipation rate ϵ was calculated by invoking common assumption of homogeneous, isotropic and stationary turbulence which leads to the specific form of power spectra and structure functions (Kolmogorov, 1941). Nevertheless, theoretical assumptions are often hardly satisfied in the atmosphere, e.g., considering complex stratification, and therefore ϵ estimation from moderate-resolution (not directly resolving dissipative scales) measurements is challenging (Siebert et al., 2006b; Jen-La Plante et al., 2016; Wacławczyk et al., 2017, 2020). To account for possible anisotropy, ϵ was derived separately for longitudinal and vertical velocity fluctuations, following the methods of Siebert et al. (2006b). We also characterized the quality of estimations with additional parameters describing the deviation of experimental data from theoretical dependencies.
4.3.1 Structure function method
Second-order structure function (SFC) was calculated for measured u′ and w′ according to the same equation:
where r is distance between data points (given by true air speed) and the average is taken over positions x along the flight path. SFC was then resampled, i.e., averaged inside logarithmically equidistant bins covering the assumed inertial range m, with eight bins per decade (see Fig. 7). The resampling was applied in order to account for the density of data points increasing with scale in logarithmic coordinates.
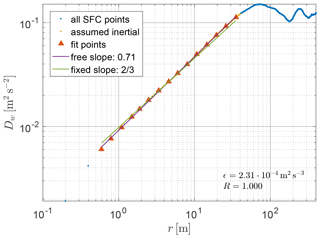
Figure 7Example of ϵ derivation with structure function method (flight no. 5, LEG307, vertical component). Computed SFC (Eq. 11, blue) is resampled in the assumed inertial range (yellow) to obtain logarithmically spaced points (triangles) which are used for least-squares fits: one with free slope (Eq. 13, purple), one with fixed theoretical slope (Eq. 12, green).
Theory predicts that in the inertial range SFC has the form (Pope, 2000)
where C is a constant, experimentally determined to Cu≈2.0 for longitudinal and Cw≈2.6 for vertical velocity components. We calculated ϵsfc by least-squares fit of this relationship to the resampled SFC. The second fit was performed according to
with two fitted parameters: prefactor C* and exponent s corresponding to the slope in a log–log plot. The exponent is used as a benchmark of the agreement of the SFC form with theory. Additionally, the Pearson correlation coefficient Rsfc was computed for the resampled points. It quantifies the linearity of the experimental SFC in log–log coordinates. Consequently, s and Rsfc assess to some extent the reliability of derived ϵ.
4.3.2 Power spectrum method
Power spectral density (PSD) of u′ and w′ was calculated with the Welch algorithm. The window was chosen as half the length of the segment. The windows overlap by half of their length, so in turn there are three individual PSDs averaged in the Welch scheme. PSD was resampled in the assumed inertial range, analogously to SFC (see Fig. 8).
Theory predicts the following PSD form in the inertial range (Pope, 2000):
where f is frequency and C′ is a constant ( for longitudinal and for vertical components). We derived ϵpsd by fitting this relationship to the resampled PSD. The second fit was performed according to
where the fitted PSD exponent p corresponds to the slope in the log–log plot. Together with Pearson correlation coefficient for the resampled points Rpsd, it measures the agreement of PSD form with theory and reliability of derived ϵ.
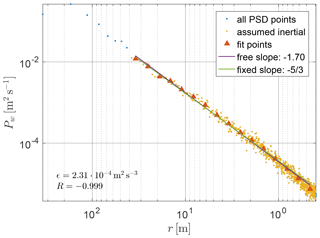
Figure 8Example of ϵ derivation with power spectrum method (flight no. 5, LEG307, vertical component). Computed PSD (blue) is resampled in the assumed inertial range (yellow) to obtain logarithmically spaced points (triangles) which are used for least-squares fits: one with free slope (Eq. 15, purple), one with fixed theoretical slope (Eq. 14, green).
4.3.3 Application of the methods
For PROFs, the moving window of 2 s was applied to the time series u′ and w′. In each window, ϵ was derived separately with the two methods, together with s, Rsfc, p and Rpsd. Such a solution was verified to provide sufficiently good fits and constitutes the compromise between high final spatial resolution (short window desired) and adequate representation of SFC or PSD (long window desired). Our approach follows earlier studies which determined the instantaneous dissipation rate utilizing the same type of data as ours (Siebert et al., 2006b; Katzwinkel et al., 2012). Siebert et al. (2006b) have chosen the window of 1 s based on their sensitivity tests and the arguments provided by Frehlich et al. (2004) and Muschinski et al. (2004). Because we derive not only ϵ but also the slopes and correlations, we increased the window to 2 s so that the linear fit covers considerable portion of the inertial range and the sufficient number of logarithmically equidistant resampled points (see Sect. 4.3.1).
In the case of LEGs, both methods were applied to the whole segment. Then, SFC and PSD were in practice averaged over relatively long horizontal distance. This approach provides an estimate of mean dissipation in contrast to local values computed in short windows which might differ from the mean (Kolmogorov, 1962). Also, SFC and PSD derived on long horizontal segments are expected to follow the theoretical form more accurately, which is indeed the case.
Our results (Sect. 5.3) demonstrate a good agreement between the methods as long as relative variations with height are concerned. In terms of absolute values, ϵpsd is usually higher than ϵsfc (around a factor of 2). In general, derived SFC resembles its theoretical form better than PSD, which is indicated by the fitted exponents and correlation coefficients. This agrees with Siebert et al. (2006b), who found the SFC method to be more robust for ϵ estimation from airborne platforms.
In order to estimate the uncertainties of the results, we used the random errors of the fitted parameters (computed with a standard method from least-squares fit residuals). The random error of “instantaneous” (calculated in 2 s windows and serving for the derivation of the profiles) dissipation rate is equal to ∼ 50 % in the boundary layer and ∼ 150 % in the FT. The error of the LEG-derived ϵ is ∼ 30 % for longitudinal component and ∼ 15 % for vertical component in the boundary layer, while it is ∼ 150 % for both components in the FT. The random error of the fitted slopes is ∼ 0.04 for s and ∼ 0.16 for p corresponding to the “instantaneous” estimations, while it is ∼ 0.02 in the case of both LEG-derived slopes. Notwithstanding, the given values represent the uncertainties due to the random errors of the fit only. The reliability of the derived dissipation rates can be also assessed by comparing the results of the two derivation methods, by comparing the fitted SFC and PSD slopes with their theoretical values or using the deviation of the computed correlation coefficients from unity.
4.4 Anisotropy
The assumption of isotropy might be violated in many specific situations in the atmospheric boundary layer, e.g., under strong buoyancy and wind shear at stratocumulus top (Malinowski et al., 2013; Jen-La Plante et al., 2016; Akinlabi et al., 2019). To investigate deviations from isotropy, we use anisotropy ratios A of two types, bulk and spectral, relating w-derived parameters to u-derived ones.
We define the following bulk anisotropy ratios:
The first relates mostly to larger eddies which have dominant contribution to total variance. Isotropy is indicated by the values close to 1, while 1 and 1 indicate anisotropic turbulence dominated by horizontal and vertical fluctuations, respectively. On the other hand, and regard mostly the inertial range eddies because ϵ derivation exploits SFC or PSD scaling in the inertial range. Analogously, values close to unity indicate isotropy.
The spectral anisotropy is the scale-dependent ratio of PSDs for vertical and longitudinal velocity:
where true air speed is utilized to convert frequency into distance. A similar approach was exercised by Pedersen et al. (2018), who compared modeled and measured anisotropy in the region of stratocumulus top. In the inertial range, Kolmogorov theory predicts . Such a value of the experimentally derived AP(r) should then indicate isotropy at the particular scale r, as in the analysis of Siebert and Muschinski (2001). We applied the same resampling procedure as in Sect. 4.3.2 to the LEG-derived PSDs but across the whole available range of scales (not only the inertial), and the ratio was then calculated point by point.
4.5 Length scales
Turbulence energy cascade is often characterized by several length scales: integral scale L, Taylor microscale λ and Kolmogorov scale η. The integral length scale corresponds to the energy-containing eddies which are involved in TKE generation. In the energy cascade, it marks the beginning of the inertial subrange where turbulent flow is considerably isotropic despite the anisotropy of large-scale factors. The indefinite integral of the autocorrelation function involved in the formal definition of L cannot be evaluated experimentally due to the limited length available. We estimated the distance where the autocorrelation,
declines by a factor of e. This method is robust enough to provide reasonable results in all our cases. The very same procedure was applied to longitudinal as well as vertical velocity to provide Lu and Lw, respectively. According to Pope (2000), under isotropic conditions, . Such a proportion can then indicate isotropy in the relevant large eddy scale.
At the Taylor microscale, viscosity starts to substantially affect the dynamics of turbulent eddies. Under the assumption of isotropy, it can be related to velocity variance and dissipation rate. We estimated two Taylor scales, longitudinal and vertical:
where ν is air viscosity for which we accounted for temperature and pressure dependence (Sutherland, 1893). In homogeneous isotropic turbulence, (Pope, 2000).
The Kolmogorov scale corresponds to the smallest eddies where TKE is dissipated into heat by viscosity. Following dimensional arguments of the famous similarity hypothesis, it equals
It was calculated separately for longitudinal (ηu) and vertical (ηw) directions with the same formula. Provided local small-scale isotropy, they should be equal. For convenience, in λ and η derivation, we used only ϵsfc and neglected ϵpsd because SFC proved to resemble its theoretical form better (see Sect. 5.3).
Turbulence properties in coupled and decoupled STBLs are documented in a series of plots. Mean PROF-derived values inside the sublayers are listed in Tables A1 and A2.
5.1 Turbulence kinetic energy and variances
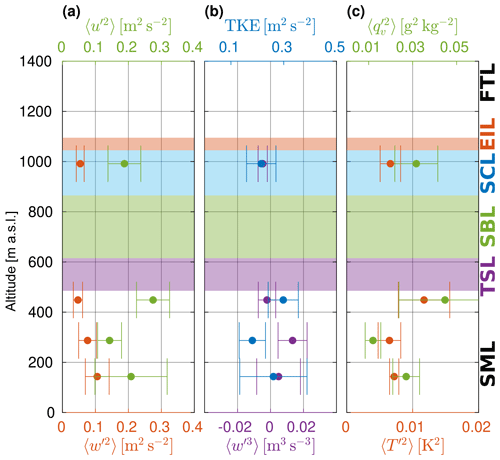
Figures 9 and 10 present variances of vertical and longitudinal velocity fluctuations, TKE, third moments of vertical velocity, variances of temperature and specific humidity in the LEGs of flight no. 5 and no. 14, respectively. Generally, the TKE inside the coupled STBL decreases with height from the middle of the SBL up to the cloud top. Despite slightly unstable stratification, the contribution from horizontal velocity variance is dominant over the vertical one. The latter reaches a minimum value below the cloud, where the buoyancy production is close to zero (compare Fig. 11 in the next section).
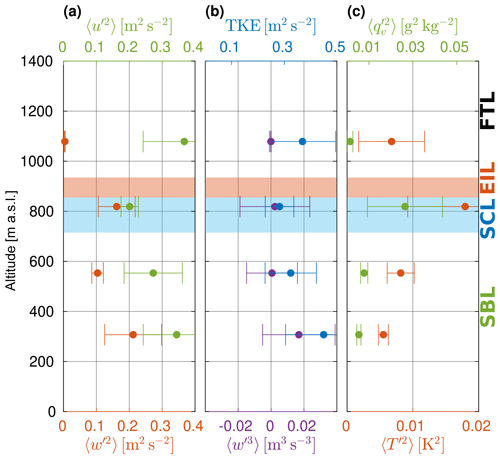
Figure 9Statistics of turbulent fluctuations in the coupled STBL (flight no. 5): (a) variance of horizontal and vertical velocity , (b) turbulence kinetic energy TKE and third moment of vertical velocity , (c) variance of temperature and specific humidity .
Estimated values of the TKE are also large in the FT above the temperature inversion. This is rather an artifact due to the presence of gravity waves favored under stable conditions (the power spectra of w, u, qv, θv and the cospectra of wu, wqv and wθv indicate the dominant contribution of the wavelength of about 450 m). Recall that LEG1079 was flown very close to the EIL and the cloud top which often features undulated interface.
The third moment of vertical velocity is positive in the lowest LEG307, suggesting strong but localized updrafts and weak but widespread downdrafts. Higher up, it is close to zero. These results ought to be interpreted with caution because the estimation of can be subject to errors due to insufficient statistics related to the small chance of penetrating infrequent but intense events (Lenschow et al., 1994; Kopec et al., 2016).
Fluctuations of temperature and humidity can be significant wherever there are spatial gradients of those quantities or in the presence of sources or sinks of heat and moisture. Such conditions occur close to the cloud top, where radiative cooling is the sink of heat and mixing between the air volumes of considerably contrasting properties occurs. Indeed, measured variances are highest in the cloud segment and decrease downward into the boundary layer where T and qv are locally more uniform.
In the decoupled STBL, TKE level is in general lower than in the coupled case. The profiles of velocity variances across the SML resemble a typical mixed layer with shear, i.e., high TKE at the bottom and the top which is realized mostly by the contribution of horizontal velocity variance (e.g., Stull, 1988, chap. 4). The prevalence of horizontal in comparison to vertical is particularly visible for LEG448, close to the transition, where the vertical velocity variance reaches its minimum. Similarly to TKE, humidity and temperature variances exhibit a maximum at this level. T and qv can be considered passive scalars which undergo mixing. The increased variances are caused by gradient production (term IV in the variance budget equations in the formulation of Stull, 1988, his Eqs. 4.3.2 and 4.3.3) rather than by any diabatic sources.
Skewness of vertical velocity is slightly positive in the SML with the maximum in LEG287. At the transition and in the cloud, it is close to zero with a tendency towards negative values. This suggests the dominant role of updrafts in the SML and downdrafts in the SCL. Altogether, the results can be interpreted as a signature of decoupling between the circulations in the lower and upper parts of the boundary layer, as downdrafts originated at cloud top and updrafts originated at the surface slow down and diverge horizontally at the transition level.
5.2 TKE production and turbulent fluxes
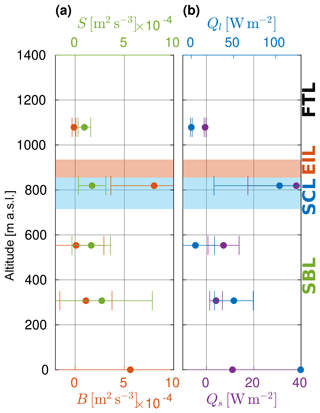
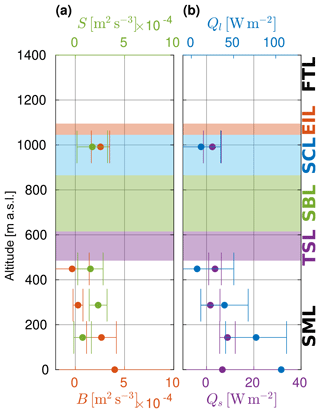
Buoyant production of TKE is expected to be significant inside the cloud and close to the surface, while the shear production is expected to be significant at the bottom and at the top of the boundary layer (Markowski and Richardson, 2010). Such a picture is in general agreement with our results for flight no. 5. In the coupled STBL observed there (Fig. 11), B is maximum in the LEG flown inside the cloud ( m2 s−3), drops to nearly zero below the cloud and increases towards the surface, reaching m2 s−3 (estimated with the COARE algorithm). S is more uniform in the boundary layer, yet subject to substantial variability among subsegments.
Sensible heat flux reaches maximum of almost 40 W m−2 close to the cloud top, stays small and positive in the middle of the boundary layer with the surface value of around Qs= 11 W m−2 (according to COARE parameterization). Latent heat flux follows near linear decrease from Ql= 130 W m−2 at the ocean surface, which is the source of moisture due to evaporation, to roughly zero below the cloud. At low levels in the atmosphere (at the surface and in LEG307), the contribution of moisture transport to buoyancy is of the same order as the contribution of heat transport (not shown). In the cloud-top region, Ql exceeds 100 W m−2 (subject to very large variability). It is not clear what are the contributions of radiative and evaporative cooling towards the observed heat fluxes there. LEG819 was performed close to the cloud top but neither exactly at the interface nor inside the EIL. Although cloud-top entrainment instability parameter κ significantly exceeds the critical value (see Sect. 3.2), which suggests the importance of evaporation, radiative cooling might still be dominant as in the study of Gerber et al. (2016).
In the decoupled STBL observed in flight no. 14 (Fig. 12), production terms are of the same order as in the coupled case. The COARE algorithm provides B= m2 s−3, Qs= 6.7 W m−2 and Ql= 107 W m−2 at the surface. B decreases with height turning into weak buoyancy consumption at the transition. This can be considered an important signature of decoupling. Above, in the cloud, B is again positive, yet significantly smaller ( m2 s−3) than at a similar location in the coupled STBL. Shear production is present in the SML and at the transition as well as in the cloud-top region.
Sensible heat flux in the decoupled boundary layer is relatively small reaching maximum of ∼ 10 W m−2 at ∼ 140 m. Latent heat flux features near-linear decrease with height from the maximum of ∼ 100 W m−2 at the surface to roughly zero at the transition. In the lower part of the STBL (at the surface, in LEG143 and LEG287), the contribution of moisture transport to buoyancy is of the same order as the contribution of heat transport (not shown). Both sensible and latent heat fluxes observed in the cloud (LEG992) are small, in contrast to the coupled case. Together with rather moderate B in the cloud, this suggests that the drivers of convection, i.e., radiative and evaporative cooling, are not as efficient in this situation which might have been one of the reasons why decoupling occurred. The cloud-top entrainment instability parameter κ (Sect. 3.2) is indeed smaller in the decoupled cloud in comparison to the coupled one which implies less efficient evaporative cooling. However, the comparison of radiative cooling effects between the cases requires further investigation. Another observation is that the moisture delivery from the ocean surface to the cloud ought to be more difficult in the decoupled STBL as Ql vanishes at much lower height in relation to the cloud base than in the coupled case.
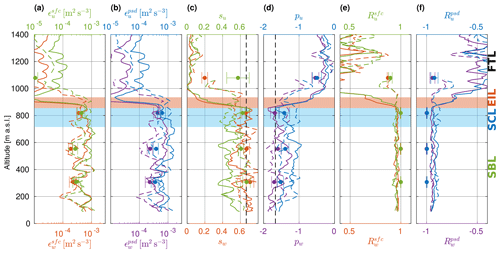
Figure 13TKE dissipation rate and inertial range scaling in the coupled STBL (flight no. 5): (a, b) dissipation rate ϵ, (c, d) fitted exponents s and p, (e, f) correlation coefficient R. Superscripts sfc and psd denote the structure function and power spectrum methods, respectively. Subscripts u and w denote horizontal and vertical velocity components, respectively. Dissipation rates for LEG1079 which are not visible in panels (a), (b) are smaller than 10−5 m2 s−3.
5.3 TKE dissipation rate
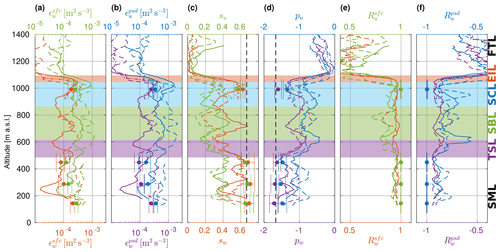
Measurements in the coupled STBL during flight no. 5 (Fig. 13) indicate relatively small variability of TKE dissipation rate throughout the boundary layer depth and substantial decrease right above the cloud top. The values fluctuate by roughly 1 order of magnitude, between 10−4 and 10−3 m2 s−3. Importantly, those variations do not correlate between the PROFs; hence, they are the manifestation of some intermittency and random effects involved in airborne sampling rather than any systematic stratification. Among the LEGs, the highest dissipation rate was observed in the one close to the cloud top, where also substantial buoyant production of TKE was revealed (see Sect. 5.2). On the other hand, continuous profiles of ϵ derived from PROFs do not show significant difference between the cloud and the subcloud part. It suggests that even though the TKE might be produced at specific places, it is probably redistributed well by the circulation across the STBL before being dissipated by viscosity (cf. transport analysis by Kopec et al., 2016).
Inside the STBL, the exponents of structure function s (Sect. 4.3.1) and of power spectra p (Sect. 4.3.2) are close to their theoretical values ( and , respectively), in striking contrast to the FT. Individual deviations occasionally reach 40 % in the STBL. On average, the deviations are a bit smaller inside the SCL than in the SBL (see Table A1). Typically, SFCs and PSDs seem to be flatter than the theory predicts (absolute values of s and p smaller than theoretical). Such behavior might be attributed to the non-homogeneity and non-stationarity of turbulence and different stages of its development, e.g., decay (Vassilicos, 2015). When different velocity components are concerned, SFCs and PSDs of vertical fluctuations follow Kolmogorov theory closer than the longitudinal ones, signalling some anisotropy in turbulence energy cascade.
Correlation coefficients Rsfc and Rpsd (Sect. 4.3) are close to unity in the coupled STBL. This implies both the SFC and the PSD can be considered linear in log–log coordinates in the assumed inertial range of scales. The correlation is higher for LEGs than for PROFs due to better averaging. It sharply decreases across the EIL, suggesting that in the FT the assumptions involved in the derivation of ϵ are not satisfied. Therefore, ϵ estimates above the boundary layer cannot be considered credible (Akinlabi et al., 2019). On the other hand, inside the STBL, the observed forms of SFC and PSD are reasonably consistent with theoretical predictions.
Measurements in the decoupled STBL during flight no. 14 (Fig. 14) present lower values of ϵ and more variability with respect to height. PROF-derived results averaged across the sublayers increase from the SML up to the SCL (see Table A2). Such a trend is consistent for all derivation methods and velocity components, despite differences in the absolute values among them. The LEG-derived ϵ decreases with height, from the surface up to the transition.
Vertical profiles of the fitted exponents s and p reveal internal layering of the STBL. In contrast to the coupled case, all PROF-derived exponents deviate significantly from theoretical values. The deviations are appreciably smaller in the SML than in the SBL and the SCL, clearly demonstrating that turbulence in the upper part of decoupled STBL is further from Kolmogorov's concepts than in the lower part. The parameters inside the SCL and the SBL are comparable, suggesting there is an efficient circulation and mixing across them. Those facts were expected, taking into account our analysis of stratification (Sect. 3.4) and TKE production (Sect. 5.2). Most probably, turbulence generated in the cloud-top region is redistributed by the large eddies and the transport terms of the TKE balance equation (Stull, 1988) across the SCL and the SBL. However, the properties of such turbulence are remarkably far from the Kolmogorov theory assuming homogeneity, isotropy and stationarity. In the light of this observation, the dissipation rates obtained with the methods based on the theoretical inertial range scalings can become questionable. The assumptions are better resembled by the conditions in the lowermost part of the atmosphere, albeit they are still distant from being exactly fulfilled. The profiles of Rsfc and Rpsd are in agreement with the above hypothesis suggesting different character and origin of turbulence in the upper and lower parts of the STBL. The absolute values are smaller than in the coupled case. In the SBL and the SCL, the correlation is even quite poor at some particular heights.
In contrast to the PROFs, the LEG-derived exponents stay mostly close to or , accordingly, while the correlations are close to 1. We suppose that the observed discrepancy results from the combination of horizontal inhomogeneity and intermittency of turbulence. PROF-derived and LEG-derived parameters should not be directly compared because they represent small and large fluid volumes, respectively. Unfortunately, none of the horizontal segments was performed in the SBL.
5.4 Anisotropy
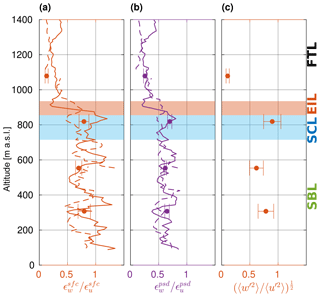
The coupled STBL sampled in flight no. 5 features bulk anisotropy ratios predominantly in the range between 0.5 and 1.0 (Fig. 15). The variance anisotropy ratio is the largest (0.9) for the horizontal segment inside the cloud, close to its top where the turbulence is efficiently generated by buoyancy (Sect. 5.2). In the SBL, the values are a bit smaller. Despite substantial local fluctuations observed in and , their average level can be considered constant across the boundary layer. There is very little difference between the SBL and the SCL. The SFC-derived anisotropy ratio is relatively close to unity, suggesting near-isotropic conditions. However, the PSD-derived ratio, typically around 0.6, seems to indicate the dominant role of horizontal fluctuations. The reason for such a discrepancy between the methods is not clear. It can be related to the bias in the estimation of dissipation rates between them (cf. Wacławczyk et al., 2020). Nevertheless, both anisotropy measures indicate no internal layering inside the STBL. In the FT, under static stability and weak turbulence production, horizontal motions dominate.
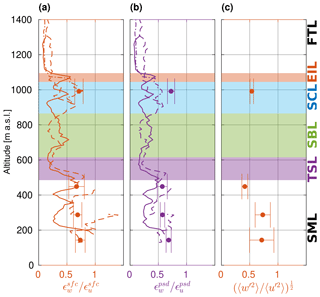
In the decoupled STBL investigated in flight no. 14, bulk anisotropy ratios are on average smaller than in the previous case (Fig. 16), signalling prevalence of horizontal fluctuations over vertical ones. is the largest in the surface layer (reaching 0.72), smaller in the cloud (0.54) and close to the transition (0.41) between the two circulation systems, cloud driven and surface driven. Dissipation-derived anisotropy ratios imply the separation of the STBL into two parts with the border in the TSL. In the upper part, covering the SCL and the SBL, and are visibly smaller than in the SML. Again, the PSD-derived rate is systematically lower than the SFC-derived, but the discrepancy is not as pronounced as in the case of flight no. 5. Importantly, the change at ∼ 500 m correlates well with the change in the fitted SFC and PSD exponents (see Sect. 5.3) as well as with the gradient of specific humidity (see Sect. 3.4). This fact confirms the hypothesis involving two major circulation circuits dividing the STBL into two parts which are internally relatively well mixed but feature turbulence of different character. In the SML, turbulence seems to be more vigorous and isotropic than in the SCL and the SBL.
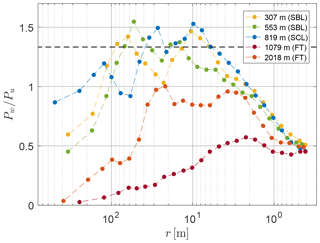
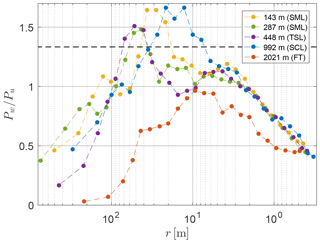
Spectral anisotropy ratios in the coupled STBL presented in Fig. 17 are of similar form for all three LEGs inside the boundary layer, contrasting with those performed in the FT. Inside the STBL, AP matches approximately the theoretical value of in the range of 5–100 m, indicating isotropic properties of turbulence in the inertial subrange of the energy cascade. The anisotropy ratios gradually decreases for larger scales which are of the order of the integral length scale (see Sect. 5.5). The scales of the size of a few hundred meters, which is close to the boundary layer depth (about 850 m), might be additionally influenced by the proximity of the bottom and top interfaces limiting their vertical extent. On the opposite side of the spectrum (small scales), AP can be affected by the differences in the spectral transfer functions of the sonic anemometer for different velocity components (Kaimal et al., 1968). A similar effect was briefly described by Siebert et al. (2006b). In the FT, AP hardly reaches 1.0 because vertical excursions are damped by stability. In the case of LEG1079, it is particularly small, probably because that level was very close to the strongly stable temperature inversion.
In the decoupled STBL sampled in flight no. 14 (Fig. 18), AP follows similar pattern to that observed in flight no. 5. Nonetheless, maximum values are higher, reaching up to 1.7 at the scale of 20–40 m in LEG143 and LEG992, which are the lowest and highest segments inside STBL. One may speculate those scales, featuring prevalence of vertical fluctuations, are related to the typical size of surface layer plumes and to the typical size of cloud-top downdrafts manifested as cloud holes (Gerber et al., 2005). The range of scales where AP indicates conditions close to local isotropy is narrower than in the coupled STBL. On the side of large scales, AP falls below the theoretical already at around 70 m for the two central LEGs and at around 50 m for the two peripheral LEGs (regarding the perspective of the STBL). This observation can be related to the integral length scales which are smaller than in flight no. 5 for the most part (see Sect. 5.5). What is more, the depths of the two sections of the boundary layer corresponding to the supposed circulation circuits (∼ 500 m) are also smaller than the total depth of the coupled STBL (∼ 850 m).
5.5 Length scales
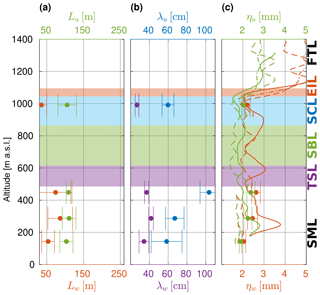
In the coupled STBL, the estimated integral scales vary around 100–150 m (Fig. 19). The longitudinal scale Lu increases, whereas the vertical Lw decreases with height. The ratio decreases from about 1.3 in the lowest LEG to about 0.5 (as expected for isotropic turbulence) close to the cloud top. The variability of integral scales among the subsegments of the LEGs is extensive, reflecting poor averaging on relatively short distances which prevents accurate calculation of decorrelation length.
Estimated Taylor microscales fit into the range of 30–80 cm and decline with height from the middle to the top of the STBL. As predicted, the longitudinal λu values are larger than the vertical λw. Their ratio equals (corresponding to isotropy of small-scale turbulence) only in the cloud LEG and is larger below. We may speculate that the turbulence is close to isotropic at the time and location of generation but such isotropy is broken in the process of transport. The Kolmogorov microscale is almost constant across the STBL (∼ 2 mm), which can be expected as it depends practically only on the dissipation rate (the viscosity changes only by a minor part in the lower atmosphere). There is also no major difference between the horizontal and vertical directions.
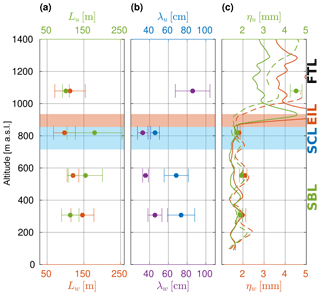
Figure 19Turbulent length scales in the coupled STBL (flight no. 5): (a) integral scale L, (b) Taylor microscale λ, (c) Kolmogorov scale η. Subscripts u and w denote horizontal and vertical velocity components, respectively. Some of the results for LEG1079 in the FT are out of the range presented.
In the decoupled STBL, integral scales are significantly smaller in comparison to the previous case, hardly exceeding 100 m (Fig. 20). The longitudinal Lu dominates over the vertical Lw, probably due to the separation of the circulation into two circuits and weak static stability, both of which limit the vertical extent of eddies and promote horizontal elongation. In contrast to the coupled case, the ratio is equal to about one-half in the lowest LEG close to the surface which is, however, again the location of intensive TKE production.
The Taylor microscale is mostly of the same order as in the former case. In the transition zone and in the cloud, a substantial detachment between the longitudinal and the vertical can be observed. is significantly larger than expected for isotropic turbulence. This effect is most pronounced in LEG448 close to the transition. We may speculate it might be the consequence of decaying turbulence – far from the production in the cloud and at the surface, the TKE is here dissipated and consumed by weak buoyant stability (Sect. 5.2). The Kolmogorov scale visibly fluctuates but on average stays close to constant across the STBL. In contrast to the coupled case, there is some difference between ηu and ηw, which directly relates to discussed in Sect. 5.4.
Two cases of marine stratocumulus-topped boundary layer, coupled (C) and decoupled (D), have been compared in terms of stratification and turbulence properties. The observations were performed in summer in the region of the eastern North Atlantic with the use of the helicopter-borne ACTOS platform. Its moderate true air speed in combination with closely collocated fast-response instruments provides high-spatial-resolution measurements of turbulent fluctuations of wind velocity, temperature and humidity. Similarities and differences between the two cases can be summarized as follows.
-
Stratification
- C:
Conserved variables, θl and qt, feature nearly constant profiles up to the capping inversion at ∼ 850 m. LCL can be considered consistent with cloud base height.
- D:
Above the relatively well-mixed SML, θl slowly increases with height up to the capping inversion at ∼ 1050 m, indicating weak stability. There is a significant gradient of qt in the TSL. LCL is close to the observed CB in the SBL only. Decoupling of the STBL was detected according to simple thermodynamic criteria.
In both cases, winds are moderate and appreciable wind shear is observed across the cloud top and the EIL.
- C:
-
TKE production
- C:
TKE is efficiently generated by buoyancy with simultaneous importance of in-cloud and surface processes. Buoyancy production follows typical STBL profile: decreases with height from the surface upwards, vanishes or turns slightly negative below cloud base, to be again substantial inside the cloud due to latent heat release and diabatic cooling.
- D:
TKE is generated by buoyancy at the surface and B decreases with height to zero at the SML top, turning into buoyancy consumption in the TSL. In the cloud B is weaker than at the surface, about 3 times smaller than for the coupled case. Buoyancy effects can be also deduced from spectral anisotropy in the uppermost and lowermost boundary layer LEGs, which suggests dominance of vertical motions in scales of 10–40 m.
The contribution of shear to TKE production is not negligible in both cases. This result can be partly artifact because only the longitudinal term could be evaluated and due to inaccurate estimation of horizontal wind gradient involved in shear term.
- C:
-
Heat fluxes
In both cases, latent heat flux qualitatively resembles the profile of B, which is consistent with the considerable contribution of moisture transport to buoyancy in the lower part of the STBL. Ql is large at the ocean surface and decreases to zero at a similar level to the minimum of B. Sensible heat flux is positive throughout observed layers but mostly smaller than Ql.
- C:
Ql and Qs are positive and of significant magnitude close to the cloud top, which can be attributed to diabatic cooling (radiative and/or evaporative).
- D:
Ql and Qs are small close to the cloud top, about an order of magnitude weaker than for the coupled STBL. Additionally, Ql vanishes at a level much lower in relation to the cloud base, which might disturb moisture delivery from the ocean to the stratocumulus cloud.
- C:
-
Turbulent fluctuations
In both cases, TKE is dominated by the contribution of horizontal velocity fluctuations. Variances of temperature and humidity are significant in the regions where mixing between air volumes of different properties occurs – due to local gradients or sources/sinks, i.e., at the cloud top, at the surface and at the transition in the decoupled STBL.
- C:
Maximum TKE is found in the middle of the SBL which together with positive at this level point out the role of surface-related factors in generating convection. The vertical velocity variance suggests a profile somewhat different than the convective similarity scaling. In cloud, and are almost equal implying isotropic conditions.
- D:
The SML follows the structure of a typical mixed layer with shear (cf. Stull, 1988). Updrafts are stronger than downdrafts. TKE, and are largest close to the transition. In the cloud, fluctuations are relatively weak, in particular , in concordance with limited B and small heat fluxes.
- C:
-
TKE dissipation
- C:
Derived ϵ varies weakly throughout the height; i.e., despite accidental variations, no systematic layering can be observed. Although TKE is efficiently produced by buoyancy in the cloud and at the surface, it is probably redistributed well across the depth before being dissipated by viscosity. The form of SFCs and PSDs is reasonably consistent with theoretical predictions for inertial range scaling in homogeneous, isotropic, stationary turbulence (Kolmogorov, 1941). However, less steep scaling (smaller absolute values of s and p) can be found at some places in the SBL.
- D:
Derived ϵ is smaller than in the coupled case and features differences between the sublayers. Despite relatively high B at the surface, similar to the coupled case, the average ϵ in the SML is smaller than in the SCL. Importantly, SFC and PSD scaling in the inertial range considerably deviates from the theoretical. Such behavior is characteristic of decaying turbulence (less energy than expected in large scales). These deviations are more pronounced and more variable in the SCL and SBL in comparison with the SML, underlining different character of turbulence in the upper and lower parts of the decoupled STBL. Probably, TKE generated in the surface region and in the cloud, respectively, is redistributed in the two circulation zones separately, without major transport through the transition.
Discrepancies between PROF-derived and LEG-derived quantities result from the contrast between local and mean turbulence characteristics. The observed relative tendencies are consistent among derivation methods and velocity components, in spite of discrepancies in the absolute values.
- C:
-
Anisotropy of turbulence
- C:
Derived anisotropy ratios indicate that turbulence is relatively close to isotropy. This condition is met best in the cloud where significant TKE production occurs.
- D:
The degree of anisotropy varies between the sublayers. In the uppermost part (SCL and SBL), horizontal small-scale velocity fluctuations dominate over the vertical. This effect is less pronounced in the SML. The change in anisotropy ratios in the TSL coincides with the difference in s and p right below the strong qv gradient.
- C:
-
Length scales of turbulence
Integral length scales of the order of 100 m show that turbulent eddies are substantially smaller than the depths of STBL or decoupled sublayers. Thus, they can be considered small enough to be transported by larger circulations.
- C:
In the middle SBL, w′ is correlated on longer distances than u′, while the opposite holds in the SCL. This agrees with the supposed form of circulation in the boundary layer, i.e., downdrafts originated at cloud top and updrafts originated at the surface pair in the middle and diverge horizontally in the vicinity of top and bottom boundaries.
- D:
Integral length scales are smaller than in the coupled case. In accordance with anisotropy ratios, Lu is larger than Lw. The same holds for Taylor microscales. The difference between λu and λw is particularly pronounced close to the transition. It seems that even smaller turbulent eddies there are elongated in horizontal.
Interestingly, implied by isotropy assumption holds only in the regions of intensive buoyant TKE production: in the cloud for the coupled STBL and close to the surface for the decoupled STBL. The Kolmogorov scale is ∼ 2 mm in both cases.
- C:
Most of our results concerning the coupled case are consistent with previous studies of stratocumulus dynamics (e.g., Nicholls and Turton, 1986; Duynkerke et al., 1995; Stevens et al., 2005; Kopec et al., 2016; Dodson and Small Griswold, 2021). In particular, the B profiles show that convection is driven both by cloud-top cooling and by surface thermal instability. However, our results suggest the profile of being somewhat different from the convective similarity scaling (Lenschow et al., 1980) but rather having maximum in the cloud and minimum below it, with following the same behavior, similarly to Dodson and Small Griswold (2021). Together with high TKE and positive in the middle SBL, this highlights the importance of surface process. It might be related to small cloud depth (relative to STBL depth) and net cooling at cloud top reduced during daytime in comparison to often considered nocturnal stratocumulus. In contrast to the works listed above, we do not clearly observe the maximum of ϵ at the top and at the bottom of the STBL, but it is rather because others applied considerable horizontal averaging in comparison to local variability captured in our PROFs.
Our observations in the decoupled STBL summarized in points 1–4 fit well into the range of conditions reported in the literature, in particular the properties of the SML. Buoyant TKE production is positive in the cloud, while there is a region of negative B around the transition (Nicholls, 1984; Nicholls and Turton, 1986; Turton and Nicholls, 1987; Durand and Bourcy, 2001). Moreover, Ql decreases from the surface to zero at the transition and it is substantially larger than Qs in the SML (Nicholls, 1984; Tjernström and Rogers, 1996; De Roode and Duynkerke, 1997; Lambert and Durand, 1999; Durand and Bourcy, 2001). However, Lambert and Durand (1999) dispute the nearly linear character of this decrease, suggesting a rather sharp gradient right at the SML top. Comparable to Nicholls (1984), our variances , are significant close to the surface and have a local minimum in the middle SML where in turn is relatively large. As in De Roode and Duynkerke (1997), is positive in the SML and nearly zero in the SCL, although the LEGs were rather too short to ensure statistical significance of those results. On the other hand, we did not collect enough data in the SCL and SBL to judge whether they together exhibit upside-down convective scaling as in Nicholls and Turton (1986), Tjernström and Rogers (1996) and De Roode and Duynkerke (1997).
The results of our comparison between coupled and decoupled STBL are in agreement with the common concept of the dominant mixing patterns in such boundary layers (e.g., Wood, 2012). Decoupling occurs when the thermally driven circulation weakens to the level that it cannot mix air throughout entire depth. Then, STBL separates into two parts: cloud driven and surface driven. Explaining the particular mechanism of decoupling operating in our case is beyond the scope of this study and would require more complete data on air mass history. Nevertheless, the “deepening-warming” mechanism (Bretherton and Wyant, 1997) seems plausible. Such a conclusion was reached by Kazemirad and Miller (2020), who modeled the Lagrangian evolution of STBL on a synoptic scale in the period including our measurements. The deepening-warming mechanism is typical for the region of the eastern North Atlantic where air masses are advected over progressively warmer waters. The most important driver for this process is the increasing ratio of surface latent heat flux to net radiative cooling in the cloud. The former was indeed relatively large; the latter was probably reduced by daytime solar heating. In addition, some precipitation was reported shortly before the flight, and evaporative cooling could have contributed to stabilizing the lower STBL. Finally, decoupling occurs more readily for large entrainment efficiency. Derived B is weak in the cloud, much smaller than in the coupled one, which might be the result of enhanced entrainment warming offsetting radiative cooling (cf. De Roode and Duynkerke, 1997).
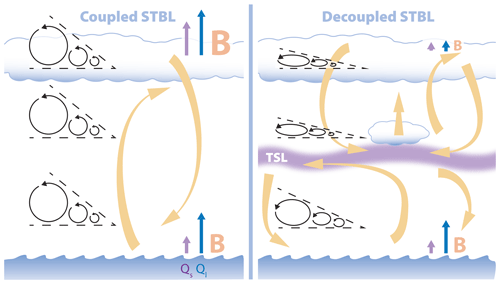
Figure 21Schematic of main processes in the coupled (left) and decoupled (right) STBLs: primary circulation (yellow arrows), turbulence eddy cascade (circular arrows confined in an angle with extent proportional to inertial range scaling exponent p), TKE buoyancy production (red B letter of size proportional to strength), sensible and latent heat fluxes (purple and blue arrows, respectively, of length proportional to strength) at the surface and in the cloud-top region.

Figure 22Cumulus clouds under stratocumulus in the decoupled STBL. Photograph was taken during PROF5 of flight no. 14 by the camera mounted on the bottom of ACTOS.
The important novelty of our work is the results on small-scale turbulence (points 5–7 of the summary). As far as we know, local ϵ profile, inertial range scaling exponents and anisotropy ratios were not addressed in the context of STBL coupling before. Based on the observations, we hypothesize that turbulence is redistributed across the depth of the coupled STBL but in the case of the decoupled STBL primarily in the sublayer where it was generated. Therefore, specific microscopic properties – TKE dissipation rate, inertial range scaling and anisotropy – can differ between the parts of the decoupled STBL.
We consider it important to emphasize often omitted distinction between circulation and turbulence. By circulation, we understand motions responsible for mixing across relatively deep layers of vertical scales comparable to the boundary layer depth. They usually originate from thermally driven plumes, sinking from the cloud top or rising from the surface. Circulation might take the form of organized structures of downdrafts and updrafts (resembling Rayleigh–Bénard convection cells). Those correspond to the peak in vertical velocity spectra, typically at ∼ 1 km in STBL (Lambert et al., 1999). Turbulence features cascade of eddies with universal scaling properties (Kolmogorov, 1941), spanning from the integral length scale (∼ 100 m in STBL) down to the Kolmogorov scale (∼ 1 mm), where TKE is dissipated by viscosity. Such turbulence can be generated by flow instabilities at specific locations (here typically close to the surface and cloud top) and distributed by circulation within STBL, alongside other constituents. Importantly, the variances and fluxes estimated in our study include contributions of both phenomena. Circulation is only partly resolved as we applied the cutoff of ∼ 1 km in Reynolds decomposition due to limited length of LEGs. A similar issue was also raised by De Roode and Duynkerke (1997). The advantage of our work is a good representation of turbulence because we resolve a significant portion of the inertial range. The main processes operating in the coupled and decoupled STBLs, including circulation and turbulence, are schematically illustrated in Fig. 21.
Both turbulence and circulation can contribute to vertical transport of heat and moisture, which is crucial for maintaining stratocumulus cloud. In the decoupled STBL, transport by turbulence through the transition is rather limited. However, we speculate it can be efficiently realized by a small number of updrafts which are strong and moist enough to penetrate the conditionally unstable TSL (measured ΓT= −7.1 K km−1, moist adiabatic ΓT= −4.7 K km−1), reach their LCL and form cumulus clouds. The image of those cumuli was captured by a camera onboard ACTOS (Fig. 22). Based on the series of images from PROF5, we estimated the cloud base height ∼ 660 m (equal to mean LCL in the TSL) and cloud depth ∼ 100 m. None of those cumuli were penetrated by ACTOS, so it is not possible to distinguish dynamic effects responsible for their formation. Detailed analysis of vertical transport calls for high-resolution numerical simulations to be set up with the help of our results.
The onset of cumulus convection depends on the properties of the TSL which is then important for overall STBL dynamics. However, it is a challenge to conduct relevant systematic climatological analysis of TSL existence and properties due to a limited number of observations. The reason is often insufficient resolution of routine radiosoundings. For instance, the layer of the strongest gradient in qv (550–600 m) penetrated in PROF5 features the differences of Δθ= 0.4 K, Δqv= 1 g kg−1 (equivalent to ΔRH= 8 %) and ΔLCL= 160 m. With the ascent rate of ∼ 5 m s−1 and sampling interval of ∼ 2 s, a hygrometer with the time constant of a second and the accuracy of a single percent in RH would be desired. Moreover, TSL is not exactly flat but rather undulated as suggested by our data of LEG448. Therefore, even aircraft measurements may fail to properly capture local conditions. This was pointed out already by Turton and Nicholls (1987, p. 997) who underlined the role of good observation strategy: “While cloud layer decoupling is predicted to occur quite often, the consequential modification of the horizontally averaged vertical thermodynamic structure remains fairly small. (…) Data averaged in this way will appear “nearly well-mixed” whether separation has occurred or not. A more detailed analysis of individual profiles and turbulence data is necessary to determine whether decoupling has taken place”.
Average meteorological parameters and turbulence properties inside the sublayers of the atmosphere are summarized in Tables A1 and A2 for the coupled (flight no. 5) and decoupled (flight no. 14) cases, respectively. The selection of the sublayers is explained in Sect. 3. The average values were obtained from the data of the same PROF which served for sublayer selection, i.e., PROF1 in the coupled case, PROF5 in decoupled case. ΓT, Nb2 and Sh2 were calculated by estimating derivatives over sublayer depth. Other parameters were simply averaged in the relevant altitude range.
The whole dataset collected within the ACORES field project is planned to be archived on the PANGAEA server for public access. The data used in the present study are also available from the authors upon request.
All the authors participated in the instrument preparation, measurements and data postprocessing within the ACORES project, where HS was the principal investigator. JLN designed the presented analysis with advice from SPM and HS. The analysis was performed by JLN with contributions from KES and with the guidance of HS and SPM. JLN wrote the manuscript with contributions from SPM and HS.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Jakub L. Nowak acknowledges the 1-year grant awarded by the German Academic Exchange Service (DAAD) for his research visit to Leibniz Institute for Tropospheric Research. We acknowledge the use of imagery from the Worldview Snapshots application (https://wvs.earthdata.nasa.gov, last access: 15 September 2020), part of the Earth Observing System Data and Information System (EOSDIS). The authors are also grateful to Marta Waclawczyk for discussions on the manuscript and to Katarzyna Nurowska for drawing the sketch in Fig. 21.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant nos. SI 1543/4-1, WE 1900/33-1, WE 2757/2-1 and HE 6770/2-1) and the Narodowe Centrum Nauki (grant no. 2013/08/A/ST10/00291).
This paper was edited by Markus Petters and reviewed by Ian Brooks and three anonymous referees.
Akinlabi, E. O., Wacławczyk, M., Mellado, J. P., and Malinowski, S. P.: Estimating turbulence kinetic energy dissipation rates in the numerically simulated stratocumulus cloud-top mixing layer: Evaluation of different methods, J. Atmos. Sci., 76, 1471–1488, https://doi.org/10.1175/JAS-D-18-0146.1, 2019. a, b
Albrecht, B. A., Bretherton, C. S., Johnson, D., Schubert, W. H., and Frisch, A. S.: The Atlantic Stratocumulus Transition Experiment – ASTEX, B. Am. Meteorol. Soc., 76, 889–904, https://doi.org/10.1175/1520-0477(1995)076<0889:TASTE>2.0.CO;2, 1995. a
Betts, A. K.: Non-precipitating cumulus convection and its parameterization, Q. J. Roy. Meteor. Soc., 99, 178–196, https://doi.org/10.1002/qj.49709941915, 1973. a
Bolton, D.: The computation of equivalent potential temperature, Mon Weather Rev., 108, 1046–1053, https://doi.org/10.1175/1520-0493(1980)108<1046:TCOEPT>2.0.CO;2, 1980. a
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V.-M., Kondo, Y., Liao, H., Lohmann, U., Rasch, P., Satheesh, S., Sherwood, S., Stevens, B., and Zhang, X.-Y.: Clouds and Aerosols, in: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9781107415324.016, 2013. a
Bretherton, C. S. and Wyant, M. C.: Moisture transport, lower-tropospheric stability, and decoupling of cloud-topped boundary layers, J. Atmos. Sci., 54, 148–167, https://doi.org/10.1175/1520-0469(1997)054<0148:MTLTSA>2.0.CO;2, 1997. a, b, c, d, e, f
Caldwell, P., Bretherton, C. S., and Wood, R.: Mixed-layer budget analysis of the diurnal cycle of entrainment in southeast Pacific stratocumulus, J. Atmos. Sci., 62, 3775–3791, https://doi.org/10.1175/JAS3561.1, 2005. a
Cruette, D., Marillier, A., Dufresne, J. L., Grandpeix, J. Y., Nacass, P., and Bellec, H.: Fast temperature and true airspeed measurements with the airborne ultrasonic anemometer-thermometer (AUSAT), J. Atmos. Ocean. Tech., 17, 1020–1039, https://doi.org/10.1175/1520-0426(2000)017<1020:FTATAM>2.0.CO;2, 2000. a
De Roode, S. R. and Duynkerke, P. G.: Observed lagrangian transition of stratocumulus into cumulus during ASTEX: Mean state and turbulence structure, J. Atmos. Sci., 54, 2157–2173, https://doi.org/10.1175/1520-0469(1997)054<2157:OLTOSI>2.0.CO;2, 1997. a, b, c, d, e, f
De Roode, S. R., Sandu, I., van der Dussen, J. J., Ackerman, A. S., Blossey, P., Jarecka, D., Lock, A., Siebesma, A. P., and Stevens, B.: Large-eddy simulations of EUCLIPSE-GASS lagrangian stratocumulus-to-cumulus transitions: Mean state, turbulence, and decoupling, J. Atmos. Sci., 73, 2485–2508, https://doi.org/10.1175/JAS-D-15-0215.1, 2016. a
Deardorff, J. W.: Cloud top entrainment instability, J. Atmos. Sci., 37, 131–147, https://doi.org/10.1175/1520-0469(1980)037<0131:CTEI>2.0.CO;2, 1980. a
Dodson, D. S. and Small Griswold, J. D.: Turbulent and boundary layer characteristics during VOCALS-REx, Atmos. Chem. Phys., 21, 1937–1961, https://doi.org/10.5194/acp-21-1937-2021, 2021. a, b, c, d
Dong, X., Schwantes, A. C., Xi, B., and Wu, P.: Investigation of the marine boundary layer cloud and CCN properties under coupled and decoupled conditions over the Azores, J. Geophys. Res.-Atmos., 120, 6179–6191, https://doi.org/10.1002/2014JD022939, 2015. a
Durand, P. and Bourcy, T.: Observations of the turbulence structure within two stratocumulus-topped, marine boundary layers, Bound.-Lay. Meteorol., 99, 105–125, https://doi.org/10.1023/A:1018999221303, 2001. a, b
Duynkerke, P. G., Heqing Zhang, and Jonker, P. J.: Microphysical and turbulent structure of nocturnal stratocumulus as observed during ASTEX, J. Atmos. Sci., 52, 2763–2777, https://doi.org/10.1175/1520-0469(1995)052<2763:MATSON>2.0.CO;2, 1995. a
Edson, J. B., Hinton, A. A., Prada, K. E., Hare, J. E., and Fairall, C. W.: Direct covariance flux estimates from mobile platforms at sea, J. Atmos. Ocean. Tech., 15, 547–562, https://doi.org/10.1175/1520-0426(1998)015<0547:DCFEFM>2.0.CO;2, 1998. a
Fairall, C. W., Bradley, E. F., Hare, J. E., Grachev, A. A., and Edson, J. B.: Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm, J. Climate, 16, 571–591, https://doi.org/10.1175/1520-0442(2003)016<0571:BPOASF>2.0.CO;2, 2003. a
Frehlich, R., Meillier, Y., Jensen, M. L., and Balsley, B.: A statistical description of small-scale turbulence in the low-level nocturnal jet, J. Atmos. Sci., 61, 1079–1085, https://doi.org/10.1175/1520-0469(2004)061<1079:ASDOST>2.0.CO;2, 2004. a
Gerber, H., Arends, B. G., and Ackerman, A. S.: New microphysics sensor for aircraft use, Atmos. Res., 31, 235–252, https://doi.org/10.1016/0169-8095(94)90001-9, 1994. a
Gerber, H., Frick, G., Malinowski, S. P., Brenguier, J. L., and Burnet, F.: Holes and entrainment in stratocumulus, J. Atmos. Sci., 62, 443–459, https://doi.org/10.1175/JAS-3399.1, 2005. a
Gerber, H., Malinowski, S. P., and Jonsson, H.: Evaporative and Radiative Cooling in POST Stratocumulus, J. Atmos. Sci., 73, 3877–3884, https://doi.org/10.1175/JAS-D-16-0023.1, 2016. a, b
Ghate, V. P., Miller, M. A., Albrecht, B. A., and Fairall, C. W.: Thermodynamic and radiative structure of stratocumulus-topped boundary layers, J. Atmos. Sci., 72, 430–451, https://doi.org/10.1175/JAS-D-13-0313.1, 2015. a
Goren, T., Rosenfeld, D., Sourdeval, O., and Quaas, J.: Satellite Observations of Precipitating Marine Stratocumulus Show Greater Cloud Fraction for Decoupled Clouds in Comparison to Coupled Clouds, Geophys. Res. Lett., 45, 5126–5134, https://doi.org/10.1029/2018GL078122, 2018. a
Haman, K. E., Makulski, A., Malinowski, S. P., and Busen, R.: A new ultrafast thermometer for airborne measurements in clouds, J. Atmos. Ocean. Tech., 14, 217–227, https://doi.org/10.1175/1520-0426(1997)014<0217:ANUTFA>2.0.CO;2, 1997. a
Hartmann, D. L., Ockert-Bell, M. E., and Michelsen, M. L.: The Effect of Cloud Type on Earth's Energy Balance: Global Analysis, J. Climate, 5, 1281–1304, https://doi.org/10.1175/1520-0442(1992)005<1281:teocto>2.0.co;2, 1992. a
Jen-La Plante, I., Ma, Y., Nurowska, K., Gerber, H., Khelif, D., Karpinska, K., Kopec, M. K., Kumala, W., and Malinowski, S. P.: Physics of Stratocumulus Top (POST): turbulence characteristics, Atmos. Chem. Phys., 16, 9711–9725, https://doi.org/10.5194/acp-16-9711-2016, 2016. a, b
Jones, C. R., Bretherton, C. S., and Leon, D.: Coupled vs. decoupled boundary layers in VOCALS-REx, Atmos. Chem. Phys., 11, 7143–7153, https://doi.org/10.5194/acp-11-7143-2011, 2011. a, b, c, d, e
JPL MUR MEaSUREs Project: GHRSST Level 4 MUR Global Foundation Sea Surface Temperature Analysis. Ver. 4.1. PO.DAAC, JPL NASA, https://doi.org/10.5067/GHGMR-4FJ04, 2015. a
Kaimal, J. C., Wyngaard, J. C., and Haugen, D. A.: Deriving Power Spectra from a Three-Component Sonic Anemometer, J. Appl. Meteorol., 7, 827–837, https://doi.org/10.1175/1520-0450(1968)007<0827:dpsfat>2.0.co;2, 1968. a, b
Katzwinkel, J., Siebert, H., and Shaw, R. A.: Observation of a Self-Limiting, Shear-Induced Turbulent Inversion Layer Above Marine Stratocumulus, Bound.-Lay. Meteorol., 145, 131–143, https://doi.org/10.1007/s10546-011-9683-4, 2012. a
Kazemirad, M. and Miller, M. A.: Summertime post-cold-frontal marine stratocumulus transition processes over the eastern north atlantic, J. Atmos. Sci., 77, 2011–2037, https://doi.org/10.1175/JAS-D-19-0167.1, 2020. a
Kolmogorov, A. N.: The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers, Dokl. Akad. Nauk SSSR, 30, 301–304, https://doi.org/10.1098/rspa.1991.0075, 1941. a, b, c
Kolmogorov, A. N.: A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number, J. Fluid Mech., 13, 82–85, https://doi.org/10.1017/S0022112062000518, 1962. a
Kopec, M. K., Malinowski, S. P., and Piotrowski, Z. P.: Effects of wind shear and radiative cooling on the stratocumulus-topped boundary layer, Q. J. Roy. Meteor. Soc., 142, 3222–3233, https://doi.org/10.1002/qj.2903, 2016. a, b, c
Lambert, D. and Durand, P.: The marine atmospheric boundary layer during semaphore. I: Mean vertical structure and non-axisymmetry of turbulence, Q. J. Roy. Meteor. Soc., 125, 495–512, https://doi.org/10.1002/qj.49712555407, 1999. a, b, c
Lambert, D., Durand, P., Thoumieux, F., Bénech, B., and Druilhet, A.: The marine atmospheric boundary layer during semaphore. II: Turbulence profiles in the mixed layer, Q. J. Roy. Meteor. Soc., 125, 513–528, https://doi.org/10.1002/qj.49712555408, 1999. a
Lampert, A., Hartmann, J., Pätzold, F., Lobitz, L., Hecker, P., Kohnert, K., Larmanou, E., Serafimovich, A., and Sachs, T.: Comparison of Lyman-alpha and LI-COR infrared hygrometers for airborne measurement of turbulent fluctuations of water vapour, Atmos. Meas. Tech., 11, 2523–2536, https://doi.org/10.5194/amt-11-2523-2018, 2018. a, b
Lenschow, D. H.: Aircraft Measurements in the Boundary Layer, in: Probing the Atmospheric Boundary Layer, American Meteorological Society, 39–55, https://doi.org/10.1007/978-1-944970-14-7_5, 1986. a
Lenschow, D. H., Wyngaard, J. C., and Pennell, W. T.: Mean-field and second-moment budgets in a baroclinic, convective boundary layer, J. Atmos. Sci., 37, 1313–1326, https://doi.org/10.1175/1520-0469(1980)037<1313:MFASMB>2.0.CO;2, 1980. a
Lenschow, D. H., Mann, J., and Kristensen, L.: How long is long enough when measuring fluxes and other turbulence statistics?, J. Atmos. Ocean. Tech., 11, 661–673, https://doi.org/10.1175/1520-0426(1994)011<0661:HLILEW>2.0.CO;2, 1994. a, b, c
Lilly, D. K.: Models of cloud-topped mixed layers under a strong inversion, Q. J. Roy. Meteor. Soc., 94, 292–309, https://doi.org/10.1002/qj.49709440106, 1968. a
Malinowski, S. P., Gerber, H., Jen-La Plante, I., Kopec, M. K., Kumala, W., Nurowska, K., Chuang, P. Y., Khelif, D., and Haman, K. E.: Physics of Stratocumulus Top (POST): turbulent mixing across capping inversion, Atmos. Chem. Phys., 13, 12171–12186, https://doi.org/10.5194/acp-13-12171-2013, 2013. a, b
Markowski, P. and Richardson, Y.: Mesoscale Meteorology in Midlatitudes, John Wiley and Sons, Ltd, Chichester, UK, https://doi.org/10.1002/9780470682104, 2010. a, b
Mellado, J. P.: Cloud-Top Entrainment in Stratocumulus Clouds, Annu. Rev. Fluid Mech., 49, 145–169, https://doi.org/10.1146/annurev-fluid-010816-060231, 2017. a
Muschinski, A., Frehlich, R., Jensen, M., Hugo, R., Hoff, A., Eaton, F., and Balsley, B.: Fine-scale measurements of turbulence in the lower troposphere: An intercomparison between a kit-and balloon-borne, and a helicopter-borne measurement system, Bound.-Lay. Meteorol., 98, 219–250, https://doi.org/10.1023/A:1026520618624, 2001. a
Muschinski, A., Frehlich, R. G., and Balsley, B. B.: Small-scale and large-scale intermittency in the nocturnal boundary layer and the residual layer, J. Fluid Mech., 515, 319–351, https://doi.org/10.1017/S0022112004000412, 2004. a
Nicholls, S.: The dynamics of stratocumulus: Aircraft observations and comparisons with a mixed layer model, Q. J. Roy. Meteor. Soc., 110, 783–820, https://doi.org/10.1002/qj.49711046603, 1984. a, b, c, d, e
Nicholls, S. and Turton, J. D.: An observational study of the structure of stratiform cloud sheets: Part II. Entrainment, Q. J. Roy. Meteor. Soc., 112, 461–480, https://doi.org/10.1002/qj.49711247210, 1986. a, b, c
Nowak, J. L., Kumala, W., Kwiatkowski, J., Kwiatkowski, K., Czyzewska, D., Karpinska, K., and Malinowski, S. P.: UltraFast Thermometer 2.0-new temperature sensor for airborne applications and its performance during ACORES 2017, Geophys. Res. Abstr., 20, p. 12492, 2018. a
Pedersen, J. G., Ma, Y., Grabowski, W. W., and Malinowski, S. P.: Anisotropy of Observed and Simulated Turbulence in Marine Stratocumulus, J. Adv. Model. Earth Sy., 10, 500–515, https://doi.org/10.1002/2017MS001140, 2018. a
Pope, S. B.: Turbulent flows, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9780511840531, 2000. a, b, c, d
Randall, D. A.: Conditional instability of the first kind up-side down., J. Atmos. Sci., 37, 125–130, https://doi.org/10.1175/1520-0469(1980)037<0125:CIOTFK>2.0.CO;2, 1980. a
Rémillard, J., Kollias, P., Luke, E., and Wood, R.: Marine boundary layer cloud observations in the Azores, J. Climate, 25, 7381–7398, https://doi.org/10.1175/JCLI-D-11-00610.1, 2012. a
Schneider, T., Kaul, C. M., and Pressel, K. G.: Possible climate transitions from breakup of stratocumulus decks under greenhouse warming, Nat. Geosci., 12, 164–168, https://doi.org/10.1038/s41561-019-0310-1, 2019. a
Siebert, H. and Muschinski, A.: Relevance of a tuning-fork effect for temperature measurements with the Gill solent HS ultrasonic anemometer-thermometer, J. Atmos. Ocean. Tech., 18, 1367–1376, https://doi.org/10.1175/1520-0426(2001)018<1367:ROATFE>2.0.CO;2, 2001. a, b, c
Siebert, H. and Teichmann, U.: Behaviour of an ultrasonic anemometer under cloudy conditions, Bound.-Lay. Meteorol., 94, 165–169, https://doi.org/10.1023/A:1002446723575, 2000. a, b
Siebert, H., Wendisch, M., Conrath, T., Teichmann, U., and Heintzenberg, J.: A new tethered balloon-borne payload for fine-scale observations in the cloudy boundary layer, Bound.-Lay. Meteorol., 106, 461–482, https://doi.org/10.1023/A:1021242305810, 2003. a, b
Siebert, H., Franke, H., Lehmann, K., Maser, R., Saw, E. W., Schell, D., Shaw, R. A., and Wendisch, M.: Probing finescale dynamics and microphysics of clouds with helicopter-borne measurements, B. Am. Meteorol. Soc., 87, 1727–1738, https://doi.org/10.1175/BAMS-87-12-1727, 2006a. a, b, c
Siebert, H., Lehmann, K., and Wendisch, M.: Observations of small-scale turbulence and energy dissipation rates in the cloudy boundary layer, J. Atmos. Sci., 63, 1451–1466, https://doi.org/10.1175/JAS3687.1, 2006b. a, b, c, d, e, f
Siebert, H., Szodry, K.-E., Egerer, U., Wehner, B., Henning, S., Chevalier, K., Lückerath, J., Welz, O., Weinhold, K., Lauermann, F., Gottschalk, M., Ehrlich, A., Wendisch, M., Fialho, P., Roberts, G., Allwayin, N., Schum, S., Shaw, R. A., Mazzoleni, C., Mazzoleni, L., Nowak, J. L., Malinowski, S. P., Karpinska, K., Kumala, W., Czyzewska, D., Luke, E. P., Kollias, P., Wood, R., and Mellado, J. P.: Observations of Aerosol, Cloud, Turbulence, and Radiation Properties at the Top of the Marine Boundary Layer over the Eastern North Atlantic Ocean: The ACORES Campaign, B. Am. Meteorol. Soc., 102, E123–E147, https://doi.org/10.1175/bams-d-19-0191.1, 2021. a, b, c
Stevens, B.: Cloud transitions and decoupling in shear-free stratocumulus-topped boundary layers, Geophys. Res. Lett., 27, 2557–2560, https://doi.org/10.1029/1999GL011257, 2000. a
Stevens, B.: Entrainment in stratocumulus-topped mixed layers, Q. J. Roy. Meteor. Soc., 128, 2663–2690, https://doi.org/10.1256/qj.01.202, 2002. a
Stevens, B., Cotton, W. R., Feingold, G., and Moeng, C. H.: Large-eddy simulations of strongly precipitating, shallow, stratocumulus-topped boundary layers, J. Atmos. Sci., 55, 3616–3638, https://doi.org/10.1175/1520-0469(1998)055<3616:LESOSP>2.0.CO;2, 1998. a
Stevens, B., Moeng, C. H., Ackerman, A. S., Bretherton, C. S., Chlond, A., de Roode, S., Edwards, J., Golaz, J. C., Jiang, H., Khairoutdinov, M., Kirkpatrick, M. P., Lewellen, D. C., Lock, A., Müller, F., Stevens, D. E., Whelan, E., and Zhu, P.: Evaluation of large-eddy simulations via observations of nocturnal marine stratocumulus, Mon. Weather Rev., 133, 1443–1462, https://doi.org/10.1175/MWR2930.1, 2005. a
Stull, R. B.: An Introduction to Boundary Layer Meteorology, Springer Netherlands, Dordrecht, https://doi.org/10.1007/978-94-009-3027-8, 1988. a, b, c, d, e, f, g
Sutherland, W.: The viscosity of gases and molecular force, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 36, 507–531, https://doi.org/10.1080/14786449308620508, 1893. a
Tjernstrom, M.: Turbulence length scales in stably stratified free shear flow analyzed from slant aircraft profiles, J. Appl. Meteorol., 32, 948–963, https://doi.org/10.1175/1520-0450(1993)032<0948:TLSISS>2.0.CO;2, 1993. a
Tjernström, M. and Rogers, D. P.: Turbulence structure in decoupled marine stratocumulus: A case study from the ASTEX field experiment, J. Atmos. Sci., 53, 598–619, https://doi.org/10.1175/1520-0469(1996)053<0598:TSIDMS>2.0.CO;2, 1996. a, b
Turton, J. D. and Nicholls, S.: A Study of the Diurnal Variation of Stratocumulus Using A Multiple Mixed Layer Model, Q. J. Roy. Meteor. Soc., 113, 969–1009, https://doi.org/10.1002/qj.49711347712, 1987. a, b, c, d, e
Vassilicos, J. C.: Dissipation in Turbulent Flows, Annu. Rev. Fluid Mech., 47, 95–114, https://doi.org/10.1146/annurev-fluid-010814-014637, 2015. a
Wacławczyk, M., Ma, Y.-F., Kopeć, J. M., and Malinowski, S. P.: Novel approaches to estimating the turbulent kinetic energy dissipation rate from low- and moderate-resolution velocity fluctuation time series, Atmos. Meas. Tech., 10, 4573–4585, https://doi.org/10.5194/amt-10-4573-2017, 2017. a
Wacławczyk, M., Gozingan, A. S., Nzotungishaka, J., Mohammadi, M., and P. Malinowski, S.: Comparison of Different Techniques to Calculate Properties of Atmospheric Turbulence from Low-Resolution Data, Atmosphere, 11, 199, https://doi.org/10.3390/atmos11020199, 2020. a, b
Wang, Z., Mora Ramirez, M., Dadashazar, H., MacDonald, A. B., Crosbie, E., Bates, K. H., Coggon, M. M., Craven, J. S., Lynch, P., Campbell, J. R., Azadi Aghdam, M., Woods, R. K., Jonsson, H., Flagan, R. C., Seinfeld, J. H., and Sorooshian, A.: Contrasting cloud composition between coupled and decoupled marine boundary layer clouds, J. Geophys. Res.-Atmos., 121, 11679–11691, https://doi.org/10.1002/2016JD025695, 2016. a
Wendisch, M., Garrett, T. J., and Strapp, J. W.: Wind tunnel tests of the airborne PVM-100A response to large droplets, J. Atmos. Ocean. Tech., 19, 1577–1584, https://doi.org/10.1175/1520-0426(2002)019<1577:WTTOTA>2.0.CO;2, 2002. a, b
Werner, F., Siebert, H., Pilewskie, P., Schmeissner, T., Shaw, R. A., and Wendisch, M.: New airborne retrieval approach for trade wind cumulus properties under overlying cirrus, J. Geophys. Res.-Atmos., 118, 3634–3649, https://doi.org/10.1002/jgrd.50334, 2013. a
Werner, F., Ditas, F., Siebert, H., Simmel, M., Wehner, B., Pilewskie, P., Schmeissner, T., Shaw, R. A., Hartmann, S., Wex, H., Roberts, G. C., and Wendisch, M.: Twomey effect observed from collocated microphysical and remote sensing measurements over shallow cumulus, J. Geophys. Res.-Atmos., 119, 1534–1545, https://doi.org/10.1002/2013JD020131, 2014. a
Wood, R.: Stratocumulus Clouds, Mon. Weather Rev., 140, 2373–2423, https://doi.org/10.1175/MWR-D-11-00121.1, 2012. a, b, c
Wood, R. and Bretherton, C. S.: Boundary layer depth, entrainment, and decoupling in the cloud-capped subtropical and tropical marine boundary layer, J. Climate, 17, 3576–3588, https://doi.org/10.1175/1520-0442(2004)017<3576:BLDEAD>2.0.CO;2, 2004. a, b, c, d, e
Wood, R., Wyant, M., Bretherton, C. S., Rémillard, J., Kollias, P., Fletcher, J., Stemmler, J., De Szoeke, S., Yuter, S., Miller, M., Mechem, D., Tselioudis, G., Chiu, J. C., Mann, J. A., O'Connor, E. J., Hogan, R. J., Dong, X., Miller, M., Ghate, V., Jefferson, A., Min, Q., Minnis, P., Palikonda, R., Albrecht, B., Luke, E., Hannay, C., and Lin, Y.: Clouds, aerosols, and precipitation in the marine boundary layer: An arm mobile facility deployment, B. Am. Meteorol. Soc., 96, 419–439, https://doi.org/10.1175/BAMS-D-13-00180.1, 2015. a
Xiao, H., Wu, C. M., and Mechoso, C. R.: Buoyancy reversal, decoupling and the transition from stratocumulus to shallow cumulus topped marine boundary layers, Clim. Dynam., 37, 971–984, https://doi.org/10.1007/s00382-010-0882-3, 2011. a, b, c
Xiao, H., Wu, C. M., Mechoso, C. R., and Ma, H. Y.: A treatment for the stratocumulus-to-cumulus transition in GCMs, Clim. Dynam., 39, 3075–3089, https://doi.org/10.1007/s00382-012-1342-z, 2012. a
Yin, B. and Albrecht, B. A.: Spatial variability of atmospheric boundary layer structure over the eastern equatorial Pacific, J. Climate, 13, 1574–1592, https://doi.org/10.1175/1520-0442(2000)013<1574:SVOABL>2.0.CO;2, 2000. a, b, c
Zheng, Y. and Li, Z.: Episodes of Warm-Air Advection Causing Cloud-Surface Decoupling During the MARCUS, J. Geophys. Res.-Atmos., 124, 12227–12243, https://doi.org/10.1029/2019JD030835, 2019. a
Zheng, Y., Rosenfeld, D., and Li, Z.: The Relationships Between Cloud Top Radiative Cooling Rates, Surface Latent Heat Fluxes, and Cloud-Base Heights in Marine Stratocumulus, J. Geophys. Res.-Atmos., 123, 11678–11690, https://doi.org/10.1029/2018JD028579, 2018a. a
Zheng, Y., Rosenfeld, D., and Li, Z.: Estimating the Decoupling Degree of Subtropical Marine Stratocumulus Decks From Satellite, Geophys. Res. Lett., 45, 12560–12568, https://doi.org/10.1029/2018GL078382, 2018b. a, b
Zheng, Y., Rosenfeld, D., and Li, Z.: A More General Paradigm for Understanding the Decoupling of Stratocumulus-Topped Boundary Layers: The Importance of Horizontal Temperature Advection, Geophys. Res. Lett., 47, e2020GL087697, https://doi.org/10.1029/2020GL087697, 2020. a
In Azores, the local time in summer is equivalent to UTC.