the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantifying the nitrogen isotope effects during photochemical equilibrium between NO and NO2: implications for δ15N in tropospheric reactive nitrogen
Xuan Zhang
John Orlando
Geoffrey Tyndall
Greg Michalski
Nitrogen isotope fractionations between nitrogen oxides (NO and NO2) play a significant role in determining the nitrogen isotopic compositions (δ15N) of atmospheric reactive nitrogen. Both the equilibrium isotopic exchange between NO and NO2 molecules and the isotope effects occurring during the NOx photochemical cycle are important, but both are not well constrained. The nighttime and daytime isotopic fractionations between NO and NO2 in an atmospheric simulation chamber at atmospherically relevant NOx levels were measured. Then, the impact of NOx level and NO2 photolysis rate on the combined isotopic fractionation (equilibrium isotopic exchange and photochemical cycle) between NO and NO2 was calculated. It was found that the isotope effects occurring during the NOx photochemical cycle can be described using a single fractionation factor, designated the Leighton cycle isotope effect (LCIE). The results showed that at room temperature, the fractionation factor of nitrogen isotopic exchange is 1.0289±0.0019, and the fractionation factor of LCIE (when O3 solely controls the oxidation from NO to NO2) is 0.990±0.005. The measured LCIE factor showed good agreement with previous field measurements, suggesting that it could be applied in an ambient environment, although future work is needed to assess the isotopic fractionation factors of . The results were used to model the NO–NO2 isotopic fractionations under several NOx conditions. The model suggested that isotopic exchange was the dominant factor when NOx>20 nmol mol−1, while LCIE was more important at low NOx concentrations (<1 nmol mol−1) and high rates of NO2 photolysis. These findings provided a useful tool to quantify the isotopic fractionations between tropospheric NO and NO2, which can be applied in future field observations and atmospheric chemistry models.
- Article
(1724 KB) - Full-text XML
- BibTeX
- EndNote
The nitrogen isotopic composition (δ15N) of reactive nitrogen compounds in the atmosphere is an important tool in understanding the sources and chemistry of atmospheric NOx (NO+NO2). It has been suggested that the δ15N value of atmospheric nitrate (HNO3, nitrate aerosols and nitrate ions in precipitation and snow) imprints the δ15N value of NOx sources (Elliott et al., 2009; Kendall et al., 2007); thus many studies have used the δ15N values of atmospheric nitrate to investigate NOx sources (Chang et al., 2018; Felix et al., 2012; Felix and Elliott, 2014; Gobel et al., 2013; Hastings et al., 2004, 2009; Morin et al., 2009; Park et al., 2018; Walters et al., 2015, 2018). However, there remain questions about how isotopic fractionations that may occur during photochemical cycling of NOx could alter the δ15N values as it partitions into NOy (NOy = atmospheric nitrate, NO3, N2O5, HONO, etc.; Chang et al., 2018; Freyer, 1991; Hastings et al., 2004; Jarvis et al., 2008; Michalski et al., 2005; Morin et al., 2009; Zong et al., 2017). Similarly, other complex reactive nitrogen chemistry, such as nitrate photolysis and redeposition in ice and snow (Frey et al., 2009), may impact the δ15N of NOy and atmospheric nitrate. The fractionation between NO and NO2 via isotope exchange has been suggested to be the dominant factor in determining the δ15N of NO2 and ultimately atmospheric nitrate (Freyer, 1991; Freyer et al., 1993; Savarino et al., 2013; Walters et al., 2016). However, isotopic fractionations occur in most, if not all, NOx and NOy reactions, while most of these are still unknown or, if calculated (Walters and Michalski, 2015), unverified by experiments. Since the atmospheric chemistry of NOy varies significantly in different environments (e.g., polluted vs. pristine, night vs. day), the isotopic fractionations associated with NOy chemistry are also likely to vary in different environments. These unknowns could potentially bias conclusions about NOx source apportionment reached when using nitrogen isotopes. Therefore, understanding the isotopic fractionations between NO and NO2 during photochemical cycling could improve our understanding of the relative role of sources versus chemistry for controlling the δ15N variations in atmospheric NO2 and nitrate.
In general, there are three types of isotopic fractionation effects associated with NOx chemistry (Fig. 1a). The first type is the equilibrium isotopic effect (EIE), i.e., isotope exchange between two compounds without forming new molecules (Urey, 1947; Bigeleisen and Mayer, 1947), which for nitrogen isotopes in the NOx system is the exchange reaction (Begun and Melton, 1956; Walters et al., 2016). The second type is the kinetic isotopic effect (KIE) associated with difference in isotopologue rate coefficients during unidirectional reactions (Bigeleisen and Wolfsberg, 1957). In the NOx system this KIE would manifest in the oxidation of NO into NO2 by . The third type is the photochemical isotope fractionation effect (PHIFE; Miller and Yung, 2000), which for NOx is the isotopic fractionation associated with NO2 photolysis. All three fractionations could impact the δ15N value of NO2 and consequently atmospheric nitrate, but the relative importance of each may vary.
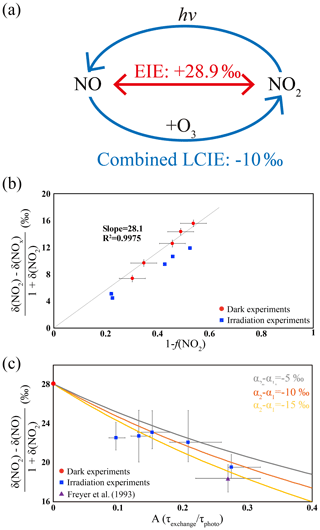
Figure 1(a) A sketch of the isotopic fractionation processes between NO and NO2; both fractionation factors are determined in this work. (b) Results from five dark experiments (red circles) yielded a line with slope of 28.1 ‰ and an α(NO2–NO) value of 1.0289, while the results from five UV irradiation experiments (blue squares) showed a smaller slope. (c) Results from five UV irradiation experiments (blue squares) and a previous field study (purple triangle), comparing to the dark experiments (red circle). The three lines represent different (α2−α1) values: the (α2−α1) ‰ line showed the lowest RMSE to our experimental data as well as the previous field observations. The error bars in panels (b) and (c) represented the combined uncertainties of NOx concentration measurements and isotopic analysis.
The limited number of studies on the EIE in the NOx cycle have significant uncertainties. Discrepancies in the EIE for have been noted in several studies. Theoretical calculations predicted isotope fractionation factors (α) ranging from 1.035 to 1.042 at room temperature (Begun and Fletcher, 1960; Monse et al., 1969; Walters and Michalski, 2015) due to the different approximations used to calculate harmonic frequencies in each study. Likewise, two separate experiments measured different room temperature fractionation factors of 1.028±0.002 (Begun and Melton, 1956) and 1.0356±0.0015 (Walters et al., 2016). A concern in both experiments is that they were conducted in small chambers with high NOx concentrations (hundreds of micromoles per mole), significantly higher than typical ambient atmospheric NOx levels (usually less than 0.1 µmol mol−1). Whether the isotopic fractionation factors determined by these experiments are applicable in the ambient environment is uncertain because of possible wall effects and formation of higher oxides, notably N2O4 and N2O3 at these high NOx concentrations.
Even less research has examined the KIE and PHIFE occurring during NOx cycling. The KIE of NO+O3 has been theoretically calculated (Walters and Michalski, 2016) but has not been experimentally verified. The NO2 PHIFE has not been experimentally determined or theoretically calculated. As a result, field observation studies often overlook the effects of PHIFE and KIE. Freyer et al. (1993) measured NOx concentrations and the δ15N values of NO2 over a 1-year period at Julich, Germany, and inferred a combined NOx isotope fractionation factor (EIE+KIE+PHIFE) of 1.018±0.001. Freyer et al. (1993) suggested that the NOx photochemical cycle (KIE and PHIFE) tends to diminish the equilibrium isotopic fractionation (EIE) between NO and NO2. Even if this approach were valid, applying this single fractionation factor elsewhere, where NOx and O3 concentrations and actinic fluxes are different, would be tenuous given that these factors may influence the relative importance of EIE, KIE and PHIFE (Hastings et al., 2004; Walters et al., 2016). Therefore, to quantify the overall isotopic fractionations between NO and NO2 at various tropospheric conditions, it is crucial to know (1) isotopic fractionation factors of EIE, KIE and PHIFE individually and (2) the relative importance of each factor under various conditions.
In this work, we aim to quantify the nitrogen isotope fractionation factors between NO and NO2 at photochemical equilibrium. First, we measure the N isotope fractionations between NO and NO2 in an atmospheric simulation chamber at atmospherically relevant NOx levels. Then, we provide mathematical solutions to assess the impact of NOx level and NO2 photolysis rate (j(NO2)) on the relative importance of EIE, KIE and PHIFE. Subsequently we use the solutions and chamber measurements to calculate the isotopic fractionation factors of EIE, KIE and PHIFE. Lastly, using the calculated fractionation factors and the equations, we model the NO–NO2 isotopic fractionations at several sites to illustrate the behavior of δ15N values of NOx in the ambient environment.
The experiments were conducted using a 10 m3 atmospheric simulation chamber at the National Center for Atmospheric Research (see descriptions in Appendix A and Zhang et al., 2018). A set of mass flow controllers was used to inject NO and O3 into the chamber. NO was injected at 1 L min−1 from an in-house NO∕N2 cylinder (133.16 µmol mol−1 NO in ultrapure N2), and O3 was generated by flowing zero air through a flow tube equipped with a UV Pen-Ray lamp (UVP LLC., CA) into the chamber at 5 L min−1. NO and NO2 concentrations were monitored in real time by chemiluminescence with a detection limit of 0.5 nmol mol−1 (model CLD 88Y, Eco Physics, MI) as were O3 concentrations using a UV absorption spectroscopy with a detection limit of 0.5 nmol mol−1 (model 49, Thermo Scientific, CO). In each experiment, the actual amounts of NO and O3 injected were calculated using measured NOx and O3 concentrations after a steady state was reached (usually within 1 h). The wall loss rate of NO2 was tested by monitoring O3 (29 nmol mol−1) and NOx (62 nmol mol−1) over a 4 h period. After the NO and NO2 concentrations reached a steady state, no decrease in NO2 concentrations was observed, showing that chamber wall loss was negligible.
Three experiments were conducted to measure the δ15N value of the tank NO (i.e., the δ15N value of total NOx). In each of these experiments, a certain amount of O3 was first injected into the chamber, then approximately the same amount of NO was injected into the chamber to ensure 100 % of the NOx was in the form of NO2 with little O3 (<15 nmol mol−1) remaining in the chamber such that the O3+NO2 reaction was negligible. The NO2 in the chamber was then collected and its δ15N value measured, which equates to the δ15N value of the tank NO.
Two sets of experiments were conducted to separately investigate the EIE, KIE and PHIFE. The first set of experiments was conducted in the dark. In each of these dark experiments, a range of NO and O3 ([O3] < [NO]) was injected into the chamber to produce NO–NO2 mixtures with [NO]∕[NO2] ratios ranging from 0.43 to 1.17. The N isotopes of these mixtures were used to investigate the EIE between NO and NO2. The second set of experiments was conducted under irradiation of UV lights (300–500 nm; see Appendix A for irradiation spectrum). Under such conditions, NO, NO2 and O3 reached a photochemically steady state, which combined the isotopic effects of EIE, KIE and PHIFE.
In all experiments, the concentrations of NO, NO2 and O3 were allowed to reach a steady state, and the product NO2 was collected from the chamber using a honeycomb denuder tube. After the NO, NO2 and O3 concentrations reached a steady state, well-mixed chamber air was drawn out through a 40 cm long Norprene thermoplastic tubing at 10 L min−1 and passed through a honeycomb denuder system (Chemcomb 3500, Thermo Scientific). Based on flow rate, the NO2 residence time in the tubing was less than 0.5 s; thus in the light-on experiments where NO and O3 coexisted, the NO2 produced inside the transfer tube through NO+O3 reactions should be <0.03 nmol mol−1 (using the upper limit of NO and O3 concentrations in our experiments). The honeycomb denuder system consisted of two honeycomb denuder tubes connected in series. Each honeycomb denuder tube is a glass cylinder 38 mm long and 47 mm in diameter and consists of 212 hexagonal tubes with inner diameters of 2 mm. Before collecting samples, each denuder tube was coated with a solution of 10 % KOH and 25 % guaiacol in methanol and then dried by flowing N2 gas through the denuder tube for 15 s (Williams and Grosjean, 1990; Walters et al., 2016). The NO2 reacted with the guaiacol coating and was converted into that was retained on the denuder tube wall (Williams and Grosjean, 1990). NO was inert to the denuder tube coating: a control experiment sampled pure NO using the denuder tubes, which did not show any measurable . The NO2 collection efficiency of a single honeycomb denuder tube was tested in another control experiment: air containing 66 nmol mol−1 of NO2 was drawn out of the chamber through a denuder tube, and the NO2 concentration at the exit of the tube holder was measured and found to be below the detection limit (<1 nmol mol−1), suggesting that the collection efficiency was nearly 100 % when [NO2] <66 nmol mol−1. Furthermore, when the denuder system consisted of two denuder tubes in series, in the second denuder was below the detection limit, indicating trivial NO2 breakthrough. Each NO2 collection lasted for 0.5–3 h in order to collect enough for isotopic analysis (at least 300 nmol). After collection, the was leached from each denuder tube by rinsing thoroughly with 10 mL deionized water into a clean polypropylene container and stored frozen until isotopic analysis. Isotopic analysis was conducted at the Purdue Stable Isotope Laboratory. For each sample, approximately 50 nmol of the extract was mixed with 2 M sodium azide solution in an acetic acid buffer in an airtight glass vial, then shaken overnight to completely reduce all the to N2O(g) (Casciotti and McIlvin, 2007; McIlvin and Altabet, 2005). The product N2O was directed into a Thermo Scientific GasBench equipped with a cryotrap, then the δ15N of the N2O was measured using a Delta-V isotope ratio mass spectrometer (IRMS). Six coated denuder tubes that did not get exposed to NO2 were also analyzed using the same chemical procedure, which did not show any measurable signal on the IRMS, suggesting that the blank from both the sampling process and the chemical conversion process was negligible. The overall analytical uncertainty for δ15N analysis was 0.5 ‰ (1σ) based on replicate analysis of in-house standards.
3.1 Equilibrium isotopic fractionation between NO and NO2
The equilibrium isotope fractionation factor, α(NO2–NO), is the 15N enrichment in NO2 relative to NO and is expressed as the ratio of rate constants k2∕k1 of two reactions:
where k1 is the rate constant of the isotopic exchange, which was previously determined to be cm3 s−1 (Sharma et al., 1970). The reaction time required for NO–NO2 to reach isotopic equilibrium was estimated using the exchange rate constants in a simple kinetics box model (BOXMOX; Knote et al., 2015). The model predicts that at typical NOx concentrations used during the chamber experiments (7.7–62.4 nmol mol−1), isotopic equilibrium would be reached within 15 min (see Appendix B). Since the sample collection usually started 1 h after NOx was well mixed in the chamber, there was sufficient time to reach full isotope equilibrium. The isotope equilibrium fractionation factor (α(NO2–NO)) is then calculated to be
where R(NO,NO2) are the 15N∕14N ratios of NO and NO2. By definition, the δ15N(NO) is ‰, and δ15N(NO2) is ‰, but hereafter, the δ15N values of NO, NO2 and NOx are referred to as δ(NO), δ(NO2) and δ(NOx), respectively. Equation (1) leads to
Using Eq. (2) and applying NOx isotopic mass balance (, ) yields
Here, δ(NOx) equals the δ15N value of the cylinder NO, and f(NO2) is the molar fraction of NO2 with respect to total NOx. Three experiments (Table 1) that measured δ(NOx) showed consistent δ(NOx) values of ‰ (n=3), indicating that δ(NOx) remained unchanged throughout the experiments (as expected for isotope mass balance). Thus, the δ(NOx) can be treated as a constant in Eq. (3), and the linear regression of versus 1−f(NO2) should have an intercept of 0 and a slope of .
Table 1Experimental conditions; concentrations of NO, NO2 and O3 at a steady state; and measured δ(NO2) values.
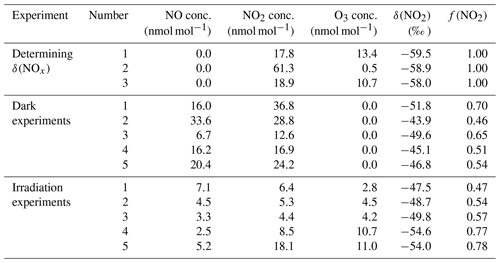
The plot of as a function of 1−f(NO2) values from five experiments yields an α(NO2–NO) value of 1.0289±0.0019 at room temperature (Fig. 1b and Table 1). This fractionation factor is comparable to previously measured values but with some differences. Our result agrees well with the α(NO2–NO) value of 1.028±0.002 obtained by Begun and Melton (1956) at room temperature. However, Walters et al. (2016) determined the α(NO2–NO) values of NO–NO2 exchange in a 1 L reaction vessel, which showed a slightly higher α(NO2–NO) value of 1.035. This discrepancy might originate from rapid heterogeneous reactions on the wall of the reaction vessel at high NOx concentrations and the small chamber size used by Walters et al. (2016). They used a reaction vessel made of Pyrex, which is known to absorb water (Do Remus et al., 1983; Takei et al., 1997) and can react with NO2, forming HONO, HNO3 and other N compounds. Additionally, previous studies have suggested that Pyrex walls enhance the formation rate of N2O4 by over an order of magnitude (Barney and Finlayson-Pitts, 2000; Saliba et al., 2001), which at isotopic equilibrium is enriched in 15N compared to NO and NO2 (Walters and Michalski, 2015). Therefore, their measured α(NO2–NO) might be slightly higher than the actual α(NO2–NO) value. In this work, the 10 m3 chamber has a much smaller surface-to-volume ratio relative to Walters et al. (2016), which minimizes wall effects, and the walls were made of Teflon, which minimizes NO2 surface reactivity, as evidenced by the NO2 wall loss control experiment. Furthermore, the low NOx mixing ratios in our experiments minimized N2O4 and N2O3 formation. At NO and NO2 concentrations of 50 nmol mol−1, the steady-state concentrations of N2O4 and N2O3 were calculated to be 0.014 and 0.001 pmol mol−1, respectively (Atkinson et al., 2004). Therefore, we suggest that our measured α(NO2–NO) value (1.0289±0.0019) may better reflect the room temperature (298 K) NO–NO2 EIE in the ambient environment.
Unfortunately, the chamber temperature could not be controlled, so we were not able to investigate the temperature dependence of the EIE. Hence, we speculate that the α(NO2–NO) follows a similar temperature dependence pattern calculated in Walters et al. (2016). Walters et al. (2016) suggested that the α(NO2–NO) value would be 0.0047 higher at 273 K and 0.002 lower at 310 K relative to room temperature (298 K). Using this pattern and our experimentally determined data, we suggest that the α(NO2–NO) values at 273, 298 and 310 K are 1.0336±0.0019, 1.0289±0.0019 and 1.0269±0.0019, respectively. This 0.0067 variation at least partially contributes to the daily and seasonal variations in δ15N values of NO2 and nitrate in some areas (e.g., polar regions with strong seasonal temperature variation). Thus, future investigations should be conducted to verify the EIE temperature dependence.
3.2 Kinetic isotopic fractionation of Leighton cycle
The photochemical reactions of NOx will compete with the isotope exchange fractionations between NO and NO2. The NO–NO2 photochemical cycle in the chamber was controlled by the Leighton cycle: NO2 photolysis and the NO+O3 reaction. This is because there were no volatile organic compounds (VOCs) in the chamber, so no RO2 was produced, which excludes the NO+RO2 reaction. Likewise, the low water vapor content (relative humidity <10 %) and the minor flux of photons (<310 nm) results in minimal OH production and hence little HO2 formation, and subsequently a trivial amount of NO2 would be formed by NO+HO2. Applying these limiting assumptions, the EIE between NO and NO2 (Reactions R1–R2) is only competing with the KIE (Reactions R3–R4) and the PHIFE in Reactions (R5)–(R6):
in which j(NO2) is the NO2 photolysis rate ( s−1 in these experiments), k5 is the rate constant for the NO+O3 reaction ( cm3 s−1; Atkinson et al., 2004), and α1,2 are isotopic fractionation factors for the two reactions. Previous studies (Freyer et al., 1993; Walters et al., 2016) have attempted to assess the competition between EIE (Reactions R1–R2), KIE and PHIFE (Reactions R3–R6), but none of them quantified the relative importance of the two processes, nor were α1 or α2 values experimentally determined. Here we provide the mathematical solution of EIE, KIE and PHIFE to illustrate how Reactions (R1)–(R6) affect the isotopic fractionations between NO and NO2.
First, the NO2 lifetime with respect to isotopic exchange with NO (τexchange) and photolysis (τphoto) was determined:
We then define an A factor:
Using Reactions (R1)–(R6) and Eqs. (1)–(6), we solved steady-state δ(NO2) and δ(NO) values (see calculations in Appendix C). Our calculations show that the δ(NO2)–δ(NO) and δ(NO2)–δ(NOx) values at a steady state can be expressed as functions of α1, α2, α(NO2–NO) and A:
Equation (7) shows the isotopic fractionation between NO and NO2; δ(NO2)–δ(NO) is mainly determined by A; the EIE factor (α(NO2–NO)−1) and the (α2−α1) factor assuming 1+δ(NO2) is close to 1. This (α2−α1) represents a combination of KIE and PHIFE, suggesting that they act together as one factor; therefore, we name the (α2−α1) factor the Leighton cycle isotopic effect (LCIE). Using measured δ(NO2) and δ(NOx) values, A values (Table 1), and the previously determined α(NO2–NO) value, we plot against the A value and use Eqs. (7) and (8) to estimate the (α2−α1) value (Fig. 1c). The plot shows that the best fit for the LCIE factor is () ‰ (root mean square error, RMSE, was lowest when ‰). The uncertainties in the LCIE factor are relatively higher than that of the EIE factor, mainly because of the accumulated analytical uncertainties at low NOx and O3 concentrations and low A values (0.10–0.28) due to the relatively low j(NO2) value ( s−1) under the chamber irradiation conditions.
This LCIE factor determined in our experiments is in good agreement with theoretical calculations. Walters and Michalski (2016) previously used an ab initio approach to determine an α2 value of 0.9933 at room temperature, 0.9943 at 237 K and 0.9929 at 310 K. The total variation in α2 values from 273 to 310 K is only 1.4 ‰, significantly smaller than our experimental uncertainty (±5 ‰). The α1 value was calculated using a zero-point energy (ZPE) shift model (Miller and Yung, 2000) to calculate the isotopic fractionation of NO2 by photolysis. Briefly, this model assumes both isotopologues have the same quantum yield function, and the PHIFE was only caused by the differences in the 15NO2 and 14NO2 absorption cross section as a function of wavelength; thus α1 values do not vary by temperature. The 15NO2 absorption cross section was calculated by shifting the 14NO2 absorption cross section by the 15NO2 zero-point energy (Michalski et al., 2004). When the ZPE shift model was used with the irradiation spectrum of the chamber lights, the resulting α1 value was 1.0023. Therefore, the theoretically predicted α2−α1 value should be −0.0090, i.e., ‰ when the temperature ranges from 273 to 310 K. This result shows excellent agreement with our experimentally determined room temperature α2−α1 value of ‰ .
This model was then used to evaluate the variations in α1 under different lighting conditions. The tropospheric ultraviolet and visible (TUV) radiation model (TUV5.3.2; Madronich and Flocke, 1999) was used to calculate the solar wavelength spectrum at three different conditions: early morning or late afternoon (solar zenith angle =85∘), midmorning or afternoon (solar zenith angle =45∘), and 12:00 local time (LT; solar zenith angle =0∘). These spectra were used in the ZPE shift model to calculate the α1 values, which are 1.0025, 1.0028 and 1.0029 at solar zenith angles of 85, 45 and 0∘, respectively. These values, along with the predicted α1 value in the chamber, showed a total span of 0.6 ‰ (1.0026±0.0003), which is again significantly smaller than our measured uncertainty. Therefore, we suggest that our experimentally determined LCIE factor ( ‰) can be used in most tropospheric solar irradiation spectra.
The equations can also be applied in tropospheric environments to calculate the combined isotopic fractionations of EIE and LCIE for NO and NO2. First, the NO2 sink reactions (mainly NO2+OH in the daytime) are at least 2–3 orders of magnitude slower than the Leighton cycle and the NO–NO2 isotope exchange reactions (Walters et al., 2016); therefore their effects on the δ(NO2) should be minor. Second, although the conversion of NO into NO2 in the ambient environment is also controlled by NO+RO2 and HO2 in addition to NO+O3 (e.g., King et al., 2001), Eq. (7) still showed good agreement with field observations in previous studies. Freyer et al. (1993) determined the annual average daytime δ(NO2)–δ(NO) at Julich, Germany, along with average daytime NO concentration (9 nmol mol−1, similar to our experimental conditions) to be ‰. Using Eq. (7), assuming the daytime average j(NO2) value throughout the year was , and a calculated A value from measured NOx concentration ranged from 0.22 to 0.33, the average NO–NO2 fractionation factor was calculated to be ‰ (Fig. 1c), in excellent agreement with the measurements in the present study. This agreement suggests that the reactions might have similar fractionation factors as NO+O3. Therefore, we suggest that Eqs. (7) and (8) can be used to estimate the isotopic fractionations between NO and NO2 in the troposphere.
3.3 Calculating nitrogen isotopic fractionations of NO–NO2
First, Eq. (7) was used to calculate the Δ(NO2–NO)=δ(NO2)–δ(NO) at a wide range of NOx concentrations and f(NO2) and j(NO2) values (Fig. 2a–d), assuming . j(NO2) values of 0 s−1 (Fig. 2a), s−1 (Fig. 2b), s−1 (Fig. 2c) and s−1 (Fig. 2d) were selected to represent nighttime, dawn (as well as the laboratory conditions of our experiments), daytime average and 12:00 LT, respectively. Each panel represented a fixed j(NO2) value, and the Δ(NO2–NO) values were calculated as a function of the A value, which was derived from NOx concentration and f(NO2). The A values have a large span, from 0 to 500, depending on the j(NO2) value and the NO concentration. When A=0 (j(NO2)=0) and f(NO2)<1 (meaning NO and NO2 coexist and [O3] = 0), Eqs. (7) and (8) become Eqs. (2) and (3), showing that the EIE was the sole factor; the Δ(NO2–NO) values were solely controlled by EIE, which has a constant value of +28.9 ‰ at 298 K (Fig. 2a). When j(NO2)>0, the calculated Δ(NO2–NO) values showed a wide range from −10.0 ‰ (controlled by LCIE factor: ‰) to +28.9 ‰ (controlled by EIE factor: ‰). Figure 2b–d display the transition from an LCIE-dominated regime to an EIE-dominated regime. The LCIE-dominated regime is characterized by low [NOx] (<50 pmol mol−1), representing remote ocean areas and polar regions (Beine et al., 2002; Custard et al., 2015). At this range the A value can be greater than 200; thus Eq. (7) can be simplified as , suggesting that the LCIE almost exclusively controls the NO–NO2 isotopic fractionation. The Δ(NO2–NO) values of these regions are predicted to be <0 ‰ during most times of the day and ‰ at 12:00 LT. On the other hand, the EIE-dominated regime was characterized by high [NOx] (>20 nmol mol−1) and low f(NO2) (<0.6), representative of regions with intensive NO emissions, e.g., near roadside or stack plumes (Clapp and Jenkin, 2001; Kimbrough et al., 2017). In this case, the τexchange are relatively short (10–50 s) compared to the τphoto (approximately 100 s at 12:00 LT and 1000 s at dawn); therefore the A values are small (0.01–0.5). The EIE factor in this regime thus is much more important than the LCIE factor, resulting in high Δ(NO2–NO) values (>20 ‰). Between the two regimes, both EIE and LCIE are competitive, and therefore it is necessary to use Eq. (7) to quantify the Δ(NO2–NO) values.
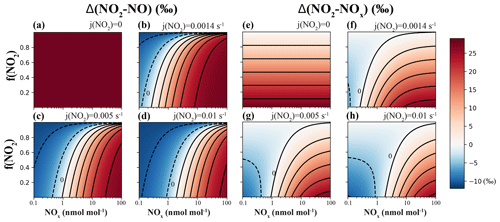
Figure 2Calculating isotopic fractionation values between NO–NO2 (Δ(NO2–NO); a–d) and NOx–NO2 (Δ(NO2–NOx); e–h) at various j(NO2), NOx level and f(NO2) using Eqs. (7) and (8). Each panel represents a fixed j(NO2) value (on the upper-right side of each panel), and the fractionation values are shown by color. Lines are contours with the same fractionation values at an interval of 5 ‰; the contour line representing 0 ‰ was marked in each panel except for panels (a) and (e).
Figure 2 also implies that changes in the j(NO2) value can cause the diurnal variations in Δ(NO2–NO) values. Changing j(NO2) would affect the value of A and consequently the NO–NO2 isotopic fractionations in two ways: (1) changes in the j(NO2) value would change the photolysis intensity and therefore the τphoto value; (2) in addition, changes in the j(NO2) value would also alter the steady-state NO concentration, therefore changing the τexchange (Fig. 2c). The combined effect of these two factors on the A value varies along with the atmospheric conditions and thus needs to be carefully calculated using NOx concentration data and atmospheric chemistry models.
We then calculated the differences in δ15N values between NO2 and total NOx, e.g., Δ(NO2–NOx)=δ(NO2)–δ(NOx) in Fig. 2e–h. Since Δ(NO2–NOx) are connected through the observed δ15N of NO2 (or nitrate) to the δ15N of NOx sources, this term might be useful in field studies (e.g., Chang et al., 2018; Zong et al., 2017). The calculated Δ(NO2–NOx) values (Fig. 2e–h) also showed an LCIE-dominated regime at low [NOx] and an EIE-dominated regime at high [NOx]. The Δ(NO2–NOx) values were dampened by the 1−f(NO2) factor comparing to Δ(NO2–NO), as shown in Eqs. (3) and (8): Δ(NO2–NOx)=Δ(NO2–NO) (1−f(NO2)). At high f(NO2) values (>0.8), the differences between δ(NO2) and δ(NOx) were less than 5 ‰; thus the measured δ(NO2) values were similar to δ(NOx), although the isotopic fractionation between NO and NO2 could be noteworthy. Some ambient environments with significant NO emissions or high NO2 photolysis rates usually have f(NO2) values between 0.4 and 0.8 (Mazzeo et al., 2005; Vicars et al., 2013). In this scenario, the Δ(NO2–NOx) values in Fig. 2f–h showed wide ranges of −4.8 ‰ to +15.6 ‰, −6.0 ‰ to +15.0 ‰ and −6.3 ‰ to +14.2 ‰ at , and s−1, respectively. These significant differences again highlighted the importance of both LCIE and EIE (Eqs. 7 and 8) in calculating the Δ(NO2–NOx). In the following discussion, we assume that (1) the α1 value remains constant (see discussion above), (2) the reactions have the same fractionation factors (α2) as NO+O3, and (3) both EIE and LCIE do not display significant temperature dependence. We then use Eqs. (7) and (8) and this laboratory-determined LCIE factor (−10 ‰) to calculate the nitrogen isotopic fractionation between NO and NO2 at various tropospheric atmospheric conditions.
The daily variations in Δ(NO2–NOx) values at two roadside NOx monitoring sites were predicted to demonstrate the effects of NOx concentrations to the NO–NO2 isotopic fractionations. Hourly NO and NO2 concentrations were acquired from a roadside site at Anaheim, CA (https://www.arb.ca.gov, last access: 9 August 2019), and an urban site at Evansville, IN (http://idem.tx.sutron.com, last access: 9 August 2019), on 25 July 2018. The hourly j(NO2) values output from the TUV model (Madronich and Flocke, 1999) at these locations were used to calculate the daily variations in Δ(NO2–NOx) values (Fig. 3a, b) by applying Eq. (8) and assuming . Hourly NOx concentrations were 12–51 nmol mol−1 at Anaheim and 9–38 nmol mol−1 at Evansville, and the f(NO2) values at both sites did not show significant daily variations (0.45±0.07 at Anaheim and 0.65±0.08 at Evansville), likely because the NOx concentrations were controlled by the high NO emissions from the road (Gao, 2007). The calculated Δ(NO2–NOx) values using Eq. (8) showed significant diurnal variations. During the nighttime, the isotopic fractionations were solely controlled by the EIE; the predicted Δ(NO2–NOx) values were ‰ and ‰ at Anaheim and Evansville, respectively. During the daytime, the existence of LCIE lowered the predicted Δ(NO2–NOx) values to ‰ at Anaheim and ‰ at Evansville, while the f(NO2) values at both sites remained similar. The lowest Δ(NO2–NOx) values for both sites (+7.0 ‰ and +1.7 ‰) occurred around 12:00 LT, when the NOx photolysis was the most intense. In contrast, if one neglects the LCIE factor in the daytime, the Δ(NO2–NOx) values would be ‰ and ‰, respectively, an overestimation of 3.1 ‰ and 6.9 ‰. These discrepancies suggested that the LCIE played an important role in the NO–NO2 isotopic fractionations, and neglecting it could bias the NOx source apportionment using δ15N of NO2 or nitrate.
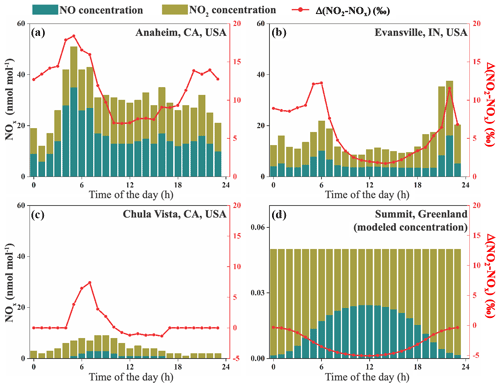
Figure 3NOx concentrations and calculated Δ(NO2–NOx) values at four sites. Stacked bars show the NO and NO2 concentrations extracted from monitoring sites (a–c) or calculated using a 0-D box model (d); the red lines are Δ(NO2–NOx) values at each site. Note that the NOx concentration (left y axis in panel d) is different from the rest.
The role of LCIE was more important in less polluted sites. The Δ(NO2–NOx) values were calculated for a suburban site near San Diego, CA, USA, again using the hourly NOx concentrations (https://www.arb.ca.gov; Fig. 3c) and j(NO2) values calculated from the TUV model. NOx concentrations at this site varied from 1 to 9 nmol mol−1, assuming . During the nighttime, NOx was in the form of NO2 (f(NO2=1) because O3 concentrations were higher than NOx; thus the δ(NO2) values should be identical to δ(NOx) (Δ(NO2–NOx)=0). In the daytime a certain amount of NO was produced by direct NO emission and NO2 photolysis, but the f(NO2) was still high (0.73±0.08). Our calculation suggested that the daytime Δ(NO2–NOx) values should be only ‰, with a lowest value of −1.3 ‰. These Δ(NO2–NOx) values were similar to the observed and modeled summer daytime δ(NO2) values in West Lafayette, IN (Walters et al., 2018), which suggest that the average daytime Δ(NO2–NOx) values at nmol mol−1 should range from +0.1 ‰ to +2.4 ‰. In this regime, we suggest that the Δ(NO2–NOx) values were generally small due to the significant contribution of LCIE and high f(NO2).
The LCIE should be the dominant factor controlling the NO–NO2 isotopic fractionation in remote regions, resulting in a completely different diurnal pattern of Δ(NO2–NOx) compared with the urban–suburban area. Direct hourly measurements of NOx at remote sites are rare; thus we used a total NOx concentration of 50 pmol mol−1 and a daily O3 concentration of 20 nmol mol−1 at Summit, Greenland (Dibb et al., 2002; Hastings et al., 2004; Honrath et al., 1999; Yang et al., 2002) and assumed and that the conversion of NO to NO2 was completely controlled by O3 to calculate the NO∕NO2 ratios. Here the isotopes of NOx were almost exclusively controlled by the LCIE due to the high A values (>110). The Δ(NO2–NOx) values displayed a clear diurnal pattern (Fig. 3d), with a maximum value of −0.3 ‰ in the “nighttime” (solar zenith angle >85∘) and a minimum value of −5.0 ‰ during midday. This suggests that the isotopic fractionations between NO and NO2 were almost completely controlled by LCIE in remote regions when NOx concentrations were <0.1 nmol mol−1. However, since the isotopic fractionation factors of nitrate formation reactions (NO2+OH, NO3+HC, N2O5+H2O) are still unknown, more studies are needed to fully explain the daily and seasonal variations in δ() in remote regions.
Nevertheless, our results have a few limitations. First, currently there are very few field observations that can be used to evaluate our model; therefore, future field observations that measure the δ15N values of ambient NO and NO2 should be carried out to test our model. Second, more work, including theoretical and experimental studies, is needed to investigate the isotope fractionation factors occurring during the conversion from NOx to NOy and nitrate: in the NOy cycle, EIE (isotopic exchange between NO2, NO3 and N2O5), KIE (formation of NO3, N2O5 and nitrate) and PHIFE (photolysis of NO3, N2O5, HONO and sometimes nitrate) may also exist and be relevant for the δ15N of HNO3 and HONO. In particular, the N isotope fractionation occurring during the reaction needs investigation. Such studies could help us to model the isotopic fractionation between NOx emission and nitrate and eventually enable us to analyze the δ15N value of NOx emission by measuring the δ15N values of nitrate aerosols and nitrate in wet depositions. Third, our discussion only focuses on the reactive nitrogen chemistry in the troposphere; however, the nitrogen chemistry in the stratosphere is drastically different from the tropospheric chemistry; thus future studies are also needed to investigate the isotopic fractionations in the stratospheric nitrogen chemistry. Last, the temperature dependence of both EIE and LCIE needs to be carefully investigated because of the wide range of temperature in both the troposphere and stratosphere. Changes in temperature could alter the isotopic fractionation factors of both EIE and LCIE as well as contribute to the seasonality of isotopic fractionations between NOx and NOy molecules.
The effect of NOx photochemistry on the nitrogen isotopic fractionations between NO and NO2 was investigated. We first measured the isotopic fractionations between NO and NO2 and provided mathematical solutions to assess the impact of NOx level and NO2 photolysis rate (j(NO2)) on the relative importance of EIE and LCIE. The EIE and LCIE isotope fractionation factors at room temperature were determined to be 1.0289±0.0019 and 0.990±0.005, respectively. These calculations and measurements can be used to determine the steady-state Δ(NO2–NO) and Δ(NO2–NOx) values at room temperature. Subsequently we applied our equations to polluted, clean and remote sites to model the daily variations in Δ(NO2–NOx) values. We found that the Δ(NO2–NOx) values could vary from over +20 ‰ to less than −5 ‰ depending on the environment: in general, the role of LCIE becomes more important at low NOx concentrations, which tend to decrease the Δ(NO2–NOx) values. Our work provided a mathematical approach to quantify the nitrogen isotopic fractionations between NO and NO2 that can be applied to many tropospheric environments, which could help interpret the measured δ15N values of NO2 and nitrate in field observation studies.
The chamber is a 10 m3 Teflon bag equipped with several standard instruments including a temperature and humidity probe, NOx monitor and O3 monitor. A total of 128 wall-mounted blacklight tubes surrounded the chamber to mimic tropospheric photochemistry, and the photolysis rate of NO2 (j(NO2)) when all lights are on has been previously determined to be s−1, similar to a j(NO2) coefficient at an 81∘ solar zenith angle. The irradiation spectrum of the black lights is shown in Fig. A1. The chamber was kept at room temperature and 1 atm. Before each experiment, the chamber was flushed with zero air at 40 L min−1 for at least 12 h to ensure the background NOx, O3 and other trace gases were below the detection limit.
The time needed to reach NO–NO2 isotopic equilibrium during light-off experiments was assessed using a 0-D box model. This box model contains only two reactions:
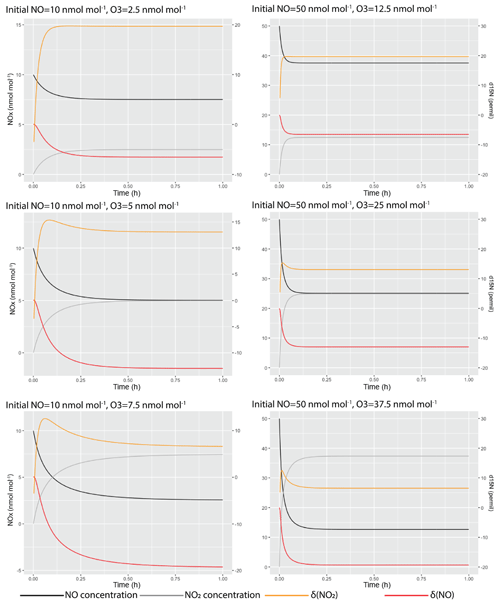
where k and k′ are rate constants of the reactions. The differences in rate constants were calculated by assuming an α(NO2–NO) value of 1.0289. Six simulations were conducted at various initial NO (with δ15N=0 ‰) and O3 levels that were similar to our experiment. Then the δ15N values of NO and NO2 during the simulation were calculated from the model and are shown in Fig. B1, suggesting that in our experimental condition, all systems should reach isotopic equilibrium within 1 h.
When the system (Reactions R1–R6) reaches a steady state, we have
Therefore, using Reactions (R1)–(R6)
From here we refer to 14NO2 and 14NO as NO2 and NO for convenience. Rearranging the above equation, we get
Meanwhile, since the Leighton cycle reaction still holds for the majority of isotopes (NO and NO2), we have
Thus,
From the text, when , we defined . Using the above equations, we know
Next, to calculate δ(NO2)–δ(NO), we use the definition of delta notation:
Divide both sides by k1[NO][NO2]:
Rearrange and substitute and with A:
Thus,
Then, using mass balance
we can derive Eq. (8):
Data acquired from this study were deposited at Open Sciences Framework (Li, 2019; https://doi.org/10.17605/OSF.IO/JW8HU).
JL and GM designed the experiments, XZ and JL conducted the experiments. XZ, GM, JO and GT helped JL in interpreting the results. The manuscript was written by JL, and all the authors have contributed during the revision of the manuscript.
The authors declare that they have no conflict of interest.
We thank the NCAR's Advanced Study Program for providing support to Jianghanyang Li. The National Center for Atmospheric Research is operated by the University Corporation for Atmospheric Research under the sponsorship of the National Science Foundation.
This research has been supported by the National Science Foundation.
This paper was edited by Jan Kaiser and reviewed by Matthew Johnson and one anonymous referee.
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume I – gas phase reactions of Ox, HOx, NOx and SOx species, Atmos. Chem. Phys., 4, 1461–1738, https://doi.org/10.5194/acp-4-1461-2004, 2004.
Barney, W. S. and Finlayson-Pitts, B. J.: Enhancement of N2O4 on porous glass at room temperature: A key intermediate in the heterogeneous hydrolysis of NO2?, J. Phys. Chem. A, 104, 171–175, https://doi.org/10.1021/jp993169b, 2000.
Begun, G. M. and Fletcher, W. H.: Partition function ratios for molecules containing nitrogen isotopes, J. Chem. Phys., 33, 1083–1085, https://doi.org/10.1063/1.1731338, 1960.
Begun, G. M. and Melton, C. E.: Nitrogen isotopic fractionation between NO and NO2 and mass discrimination in mass analysis of NO2, J. Chem. Phys., 25, 1292–1293, https://doi.org/10.1063/1.1743215, 1956.
Beine, H. J., Honrath, R. E., Dominé, F., Simpson, W. R., and Fuentes, J. D.: NOx during background and ozone depletion periods at Alert:Fluxes above the snow surface, J. Geophys. Res.-Atmos., 107, ACH-7, https://doi.org/10.1029/2002JD002082, 2002.
Bigeleisen, J. and Mayer, M. G.: Calculation of equilibrium constants for isotopic exchange reactions, J. Chem. Phys., 15, 261–267, https://doi.org/10.1063/1.1746492, 1947.
Bigeleisen, J. and Wolfsberg, M.: Theoretical and experimental aspects of isotope effects in chemical kinetics, Adv. Chem. Phys., 1, 15–76, https://doi.org/10.1002/9780470143476.ch2, 1957.
Casciotti, K. L. and McIlvin, M. R.: Isotopic analyses of nitrate and nitrite from reference mixtures and application to Eastern Tropical North Pacific waters, Mar. Chem., 107, 184–201, https://doi.org/10.1016/j.marchem.2007.06.021, 2007.
Chang, Y., Zhang, Y., Tian, C., Zhang, S., Ma, X., Cao, F., Liu, X., Zhang, W., Kuhn, T., and Lehmann, M. F.: Nitrogen isotope fractionation during gas-to-particle conversion of NOx to in the atmosphere – implications for isotope-based NOx source apportionment, Atmos. Chem. Phys., 18, 11647–11661, https://doi.org/10.5194/acp-18-11647-2018, 2018.
Clapp, L. J. and Jenkin, M. E.: Analysis of the relationship between ambient levels of O3, NO2 and NO as a function of NOx in the UK, Atmos. Environ., 35, 6391–6405, https://doi.org/10.1016/S1352-2310(01)00378-8, 2001.
Custard, K. D., Thompson, C. R., Pratt, K. A., Shepson, P. B., Liao, J., Huey, L. G., Orlando, J. J., Weinheimer, A. J., Apel, E., Hall, S. R., Flocke, F., Mauldin, L., Hornbrook, R. S., Pöhler, D., General, S., Zielcke, J., Simpson, W. R., Platt, U., Fried, A., Weibring, P., Sive, B. C., Ullmann, K., Cantrell, C., Knapp, D. J., and Montzka, D. D.: The NOx dependence of bromine chemistry in the Arctic atmospheric boundary layer, Atmos. Chem. Phys., 15, 10799–10809, https://doi.org/10.5194/acp-15-10799-2015, 2015.
Dibb, J. E., Arsenault, M., Peterson, M. C., and Honrath, R. E.: Fast nitrogen oxide photochemistry in Summit, Greenland snow, Atmos. Environ., 36, 2501–2511, https://doi.org/10.1016/S1352-2310(02)00130-9, 2002.
Do Remus, R. H., Mehrotra, Y., Lanford, W. A., and Burman, C.: Reaction of water with glass: influence of a transformed surface layer, J. Mater. Sci., 18, 612–622, https://doi.org/10.1007/BF00560651, 1983.
Elliott, E. M., Kendall, C., Boyer, E. W., Burns, D. A., Lear, G. G., Golden, H. E., Harlin, K., Bytnerowicz, A., Butler, T. J., and Glatz, R.: Dual nitrate isotopes in dry deposition: Utility for partitioning NOx source contributions to landscape nitrogen deposition, J. Geophys. Res.-Biogeo., 114, G04020, https://doi.org/10.1029/2008JG000889, 2009.
Felix, J. D. and Elliott, E. M.: Isotopic composition of passively collected nitrogen dioxide emissions: Vehicle, soil and livestock source signatures, Atmos. Environ., 92, 359–366, https://doi.org/10.1016/j.atmosenv.2014.04.005, 2014.
Felix, J. D., Elliott, E. M., and Shaw, S. L.: Nitrogen isotopic composition of coal-fired power plant NOx: influence of emission controls and implications for global emission inventories, Environ. Sci. Technol., 46, 3528–3535, https://doi.org/10.1021/es203355v, 2012.
Frey, M. M., Savarino, J., Morin, S., Erbland, J., and Martins, J. M. F.: Photolysis imprint in the nitrate stable isotope signal in snow and atmosphere of East Antarctica and implications for reactive nitrogen cycling, Atmos. Chem. Phys., 9, 8681–8696, https://doi.org/10.5194/acp-9-8681-2009, 2009.
Freyer, H. D.: Seasonal variation of 15N∕14N ratios in atmospheric nitrate species, Tellus B, 43, 30–44, https://doi.org/10.1034/j.1600-0889.1991.00003.x, 1991.
Freyer, H. D., Kley, D., Volz-Thomas, A., and Kobel, K.: On the interaction of isotopic exchange processes with photochemical reactions in atmospheric oxides of nitrogen, J. Geophys. Res.-Atmos., 98, 14791–14796, https://doi.org/10.1029/93JD00874, 1993.
Gao, H. O.: Day of week effects on diurnal ozone∕NOx cycles and transportation emissions in Southern California, Transport. Res. D-Tr. E., 12, 292–305, https://doi.org/10.1016/j.trd.2007.03.004, 2007.
Gobel, A. R., Altieri, K. E., Peters, A. J., Hastings, M. G., and Sigman, D. M.: Insights into anthropogenic nitrogen deposition to the North Atlantic investigated using the isotopic composition of aerosol and rainwater nitrate, Geophys. Res. Lett., 40, 5977–5982, https://doi.org/10.1002/2013GL058167, 2013.
Hastings, M. G., Steig, E. J., and Sigman, D. M.: Seasonal variations in N and O isotopes of nitrate in snow at Summit, Greenland: Implications for the study of nitrate in snow and ice cores, J. Geophys. Res.-Atmos., 109, D20306, https://doi.org/10.1029/2004JD004991, 2004.
Hastings, M. G., Jarvis, J. C., and Steig, E. J.: Anthropogenic impacts on nitrogen isotopes of ice-core nitrate, Science, 324, 1288,https://doi.org/10.1126/science.1170510, 2009.
Honrath, R. E., Peterson, M. C., Guo, S., Dibb, J. E., Shepson, P. B., and Campbell, B.: Evidence of NOx production within or upon ice particles in the Greenland snowpack, Geophys. Res. Lett., 26, 695–698, https://doi.org/10.1029/1999GL900077, 1999.
Jarvis, J. C., Steig, E. J., Hastings, M. G., and Kunasek, S. A.: Influence of local photochemistry on isotopes of nitrate in Greenland snow, Geophys. Res. Lett., 35, L21804, https://doi.org/10.1029/2008GL035551, 2008.
Kendall, C., Elliott, E. M., and Wankel, S. D.: Tracing anthropogenic inputs of nitrogen to ecosystems, Stable Isotopes in Ecology and Environmental Science, 2, 375–449, https://doi.org/10.1002/9780470691854.ch12, 2007.
Kimbrough, S., Owen, R. C., Snyder, M., and Richmond-Bryant, J.: NO to NO2 conversion rate analysis and implications for dispersion model chemistry methods using Las Vegas, Nevada near-road field measurements, Atmos. Environ., 165, 23–34, https://doi.org/10.1016/j.atmosenv.2017.06.027, 2017.
King, M. D., Canosa-Mas, C. E. and Wayne R. P.: Gas-phase reactions between RO2 and NO, HO2 or CH3O2: correlations between rate constants and the SOMO energy of the peroxy (RO2) radical, Atmos. Environ., 35.12, 2081–2088, https://doi.org/10.1016/S1352-2310(00)00501-X, 2001.
Knote, C., Tuccella, P., Curci, G., Emmons, L., Orlando, J. J. Madronich, S., Baró, R., Jiménez-Guerrero, P., Luecken, D., Hogrefe, C., Forkel, R., Werhahn, J., Hirtl, M., Pérez, J. L., San José, R., Giordano, L., Brunner, D., Yahya, K., and Zhang, Y.: Influence of the choice of gas-phase mechanism on predictions of key gaseous pollutants during the AQMEII phase-2 intercomparison, Atmos. Environ., 115, 553–568, https://doi.org/10.1016/j.atmosenv.2014.11.066, 2015.
Li, J.: Quantifying the nitrogen equilibrium and photochemistry-induced kinetic isotopic effects between NO and NO2, OSF, https://doi.org/10.17605/OSF.IO/JW8HU, 2019.
Madronich, S. and Flocke, S.: The role of solar radiation in atmospheric chemistry. In Environmental photochemistry, in: The Handbook of Environmental Chemistry (Reactions and Processes), vol. 2/2L, Springer, Berlin, Heidelberg, 1–26, https://doi.org/10.1007/978-3-540-69044-3_1, 1999.
Mazzeo, N. A., Venegas, L. E., and Choren, H.: Analysis of NO, NO2, O3 and NOx concentrations measured at a green area of Buenos Aires City during wintertime, Atmos. Environ., 39, 3055–3068, https://doi.org/10.1016/j.atmosenv.2005.01.029, 2005.
McIlvin, M. R. and Altabet, M. A.: Chemical conversion of nitrate and nitrite to nitrous oxide for nitrogen and oxygen isotopic analysis in freshwater and seawater, Anal. Chem., 77, 5589–5595, https://doi.org/10.1021/ac050528s, 2005.
Michalski, G., Jost, R., Sugny, D., Joyeux, M., and Thiemens, M.: Dissociation energies of six NO2 isotopologues by laser induced fluorescence spectroscopy and zero-point energy of some triatomic molecules, J. Chem. Phys., 121, 7153–7161, https://doi.org/10.1063/1.1792233, 2004.
Michalski, G., Bockheim, J. G., Kendall, C., and Thiemens, M.: Isotopic composition of Antarctic Dry Valley nitrate: Implications for NOy sources and cycling in Antarctica, Geophys. Res. Lett., 32, L13817, https://doi.org/10.1029/2004GL022121, 2005.
Miller, C. E. and Yung, Y. L.: Photo-induced isotopic fractionation, J. Geophys. Res.-Atmos., 105, 29039–29051, https://doi.org/10.1029/2000JD900388, 2000.
Monse, E. U., Spindel, W., and Stern, M. J.: Analysis of isotope-effect calculations illustrated with exchange equilibria among oxynitrogen compounds, Rutgers-The State Univ., Newark, NJ, https://doi.org/10.1021/ba-1969-0089.ch009, 1969.
Morin, S., Savarino, J., Frey, M. M., Domine, F., Jacobi, H.-W., Kaleschke, L., and Martins, J. M. F.: Comprehensive isotopic composition of atmospheric nitrate in the Atlantic Ocean boundary layer from 65∘ S to 79∘ N, J. Geophys. Res., 114, D05303, https://doi.org/10.1029/2008JD010696, 2009.
Park, Y.-M., Park, K.-S., Kim, H., Yu, S.-M., Noh, S., Kim, M.-S., Kim, J.-Y., Ahn, J.-Y., Lee, M.-D., Seok, K.-S., and Kin, Y.-H.: Characterizing isotopic compositions of TC-C, -N, and -N in PM2.5 in South Korea: Impact of China's winter heating, Environ. Pollut., 233, 735–744, https://doi.org/10.1016/j.envpol.2017.10.072, 2018.
Saliba, N. A., Yang, H., and Finlayson-Pitts, B. J.: Reaction of gaseous nitric oxide with nitric acid on silica surfaces in the presence of water at room temperature, J. Phys. Chem. A, 105, 10339–10346, https://doi.org/10.1021/jp012330r, 2001.
Savarino, J., Morin, S., Erbland, J., Grannec, F., Patey, M. D., Vicars, W., Alexander, B., and Achterberg, E. P.: Isotopic composition of atmospheric nitrate in a tropical marine boundary layer, P. Natl. Acad. Sci. USA, 110, 17668–17673, https://doi.org/10.1073/pnas.1216639110, 2013.
Sharma, H. D., Jervis, R. E., and Wong, K. Y.: Isotopic exchange reactions in nitrogen oxides, J. Phys. Chem., 74, 923–933, https://doi.org/10.1021/j100699a044, 1970.
Takei, T., Yamazaki, A., Watanabe, T., and Chikazawa, M.: Water adsorption properties on porous silica glass surface modified by trimethylsilyl groups, J. Colloid Interf. Sci., 188, 409–414, https://doi.org/10.1006/jcis.1997.4777, 1997.
Urey, H. C.: The thermodynamic properties of isotopic substances, J. Chem. Soc., 0, 562–581, https://doi.org/10.1039/JR9470000562, 1947.
Vicars, W. C., Morin, S., Savarino, J., Wagner, N. L., Erbland, J., Vince, E., Martins, J. M. F., Lerner, B. M., Quinn, P. K., Coffman, D. J., Williams, E. J., and Brown, S. S.: Spatial and diurnal variability in reactive nitrogen oxide chemistry as reflected in the isotopic composition of atmospheric nitrate: Results from the CalNex 2010 field study, J. Geophys. Res.-Atmos., 118, 10567–10588, https://doi.org/10.1002/jgrd.50680, 2013.
Walters, W. W. and Michalski, G.: Theoretical calculation of nitrogen isotope equilibrium exchange fractionation factors for various NOy molecules, Geochim. Cosmochim. Ac., 164, 284–297, https://doi.org/10.1016/j.gca.2015.05.029, 2015.
Walters, W. W. and Michalski, G.: Ab initio study of nitrogen and position-specific oxygen kinetic isotope effects in the NO+O3 reaction, J. Chem. Phys., 145, 224311, https://doi.org/10.1063/1.4968562, 2016.
Walters, W. W., Goodwin, S. R., and Michalski, G.: Nitrogen stable isotope composition (δ15N) of vehicle-emitted NOx, Environ. Sci. Technol., 49, 2278–2285, https://doi.org/10.1021/es505580v, 2015.
Walters, W. W., Simonini, D. S., and Michalski, G.: Nitrogen isotope exchange between NO and NO2 and its implications for δ15N variations in tropospheric NOx and atmospheric nitrate, Geophys. Res. Lett., 43, 440–448, https://doi.org/10.1002/2015GL066438, 2016.
Walters, W. W., Fang, H., and Michalski, G.: Summertime diurnal variations in the isotopic composition of atmospheric nitrogen dioxide at a small midwestern United States city, Atmos. Environ., 179, 1–11, https://doi.org/10.1016/j.atmosenv.2018.01.047, 2018.
Williams, E. L. and Grosjean, D.: Removal of atmospheric oxidants with annular denuders, Environ. Sci. Technol., 24, 811–814, https://doi.org/10.1021/es00076a002, 1990.
Yang, J., Honrath, R. E., Peterson, M. C., Dibb, J. E., Sumner, A. L., Shepson, P. B., Frey, M., Jacobi, H.-W., Swanson, A., and Blake, N.,: Impacts of snowpack emissions on deduced levels of OH and peroxy radicals at Summit, Greenland, Atmos. Environ., 3.6, 2523–2534, https://doi.org/10.1016/S1352-2310(02)00128-0, 2002.
Zhang, X., Ortega, J., Huang, Y., Shertz, S., Tyndall, G. S., and Orlando, J. J.: A steady-state continuous flow chamber for the study of daytime and nighttime chemistry under atmospherically relevant NO levels, Atmos. Meas. Tech., 11, 2537–2551, https://doi.org/10.5194/amt-11-2537-2018, 2018.
Zong, Z., Wang, X., Tian, C., Chen, Y., Fang, Y., Zhang, F., Li, C., Sun, J., Li, J., and Zhang, G.: First assessment of NOx sources at a regional background site in North China using isotopic analysis linked with modeling, Environ. Sci. Technol., 51, 5923–5931, https://doi.org/10.1021/acs.est.6b06316, 2017.
- Abstract
- Introduction
- Methods
- Results and discussions
- Implications
- Conclusions
- Appendix A: Chamber descriptions
- Appendix B: Box model assessing the time needed for NO–NO2 to reach isotopic equilibrium
- Appendix C: Deriving Eqs. (7) and (8)
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Methods
- Results and discussions
- Implications
- Conclusions
- Appendix A: Chamber descriptions
- Appendix B: Box model assessing the time needed for NO–NO2 to reach isotopic equilibrium
- Appendix C: Deriving Eqs. (7) and (8)
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References