Combining atmospheric and snow radiative transfer models to assess the solar radiative effects of black carbon in the Arctic

The magnitude of solar radiative effects (cooling or warming) of black carbon (BC) particles embedded in the Arctic atmosphere and surface snow layer was explored on the basis of case studies. For this purpose, combined atmospheric and snow radiative transfer simulations were performed for cloudless and cloudy conditions on the basis of BC mass concentrations measured in pristine early summer and more polluted early spring conditions. The area of interest is the remote sea-ice-covered Arctic Ocean in the vicinity of Spitsbergen, northern Greenland, and northern Alaska typically not affected by local pollution. To account for the radiative interactions between the black-carbon-containing snow surface layer and the atmosphere, an atmospheric and snow radiative transfer model were coupled iteratively. For pristine summer conditions (no atmospheric BC, minimum solar zenith angles of 55^∘) and a representative BC particle mass concentration of 5 ng g⁻¹ in the surface snow layer, a positive daily mean solar radiative forcing of +0.2 W m⁻² was calculated for the surface radiative budget. A higher load of atmospheric BC representing early springtime conditions results in a slightly negative mean radiative forcing at the surface of about −0.05 W m⁻², even when the low BC mass concentration measured in the pristine early summer conditions was embedded in the surface snow layer. The total net surface radiative forcing combining the effects of BC embedded in the atmosphere and in the snow layer strongly depends on the snow optical properties (snow specific surface area and snow density). For the conditions over the Arctic Ocean analyzed in the simulations, it was found that the atmospheric heating rate by water vapor or clouds is 1 to 2 orders of magnitude larger than that by atmospheric BC. Similarly, the daily mean total heating rate (6 K d⁻¹) within a snowpack due to absorption by the ice was more than 1 order of magnitude larger than that of atmospheric BC (0.2 K d⁻¹). Also, it was shown that the cooling by atmospheric BC of the near-surface air and the warming effect by BC embedded in snow are reduced in the presence of clouds.

1 Introduction

Black carbon (BC) aerosol particles, which mostly originate from incomplete combustion of organic material (Bond et al., 2013; Petzold et al., 2013), absorb and scatter solar radiation in the visible wavelength range and, therefore, influence the atmospheric solar radiative energy budget. The manifold sources of BC particles and their atmospheric transport paths have been studied extensively (Law et al., 2014). However, the source strengths of the emissions are hard to quantify, which makes it challenging to quantify the transport of BC particles into the Arctic by simulations (Stohl et al., 2013; Arnold et al., 2016; Schacht et al., 2019). Major sources of BC particles are forest fires, industrial activities, and traffic-related emissions, which are the main factors in lower latitudes: northern parts of Europe, America, and Siberia. The BC particles emitted at the surface of the midlatitudes are lifted and transported into the Arctic, where they can stay for several days and longer (Liu et al., 2011). Contrarily, particles produced locally in the Arctic through ship traffic emissions, flaring from the oil industry, or other ground-based activities settle down quickly on the surface and may alter the radiation budget within the snowpack (Bond et al., 2013). Today, local sources are only a minor component. In the future, a strong intensification of the ship traffic in the Arctic Ocean and further polluting human activities are expected (Corbett et al., 2010). Still, the direct radiative impact by these future additional BC particle emissions is assumed to be of minor importance (Gilgen et al., 2018).

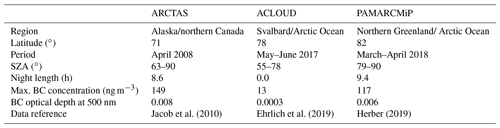
The BC magnitude of the atmospheric particle mass concentrations (in units of nanograms per cubic meter) depends on the season and general meteorological conditions. In the case of BC particle plumes reaching the Arctic by long-range transport, atmospheric concentrations of up to 150 ng m⁻³ were observed (Schulz et al., 2019). Sharma et al. (2013) compared atmospheric BC particle mass concentrations measured during different Arctic campaigns. They identified large differences depending on region and season. Measurements in spring 2008 covering Alaska and northern Canada showed values above 200 ng m⁻³ in higher altitudes, while in spring 2009 more pristine air masses were encountered, showing BC particle mass concentrations of less than 100 ng m⁻³ integrated over the entire vertical column.

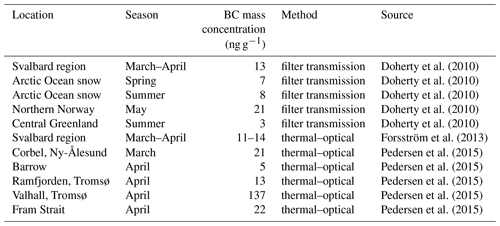
To quantify the amount of BC in a snowpack volume, the BC mass concentration (nanograms of BC in 1 g of snow) is used commonly. Typical values observed in Greenland range between 1 and 10 ng g⁻¹ and in the Canadian Arctic between 5 and 20 ng g⁻¹, and in the northern parts of Russia values may reach 100 ng g⁻¹. Table 1 summarizes observational data of measured BC mass concentrations in snow for different Arctic regions, as reported by Doherty et al. (2010), Forsström et al. (2013), and Pedersen et al. (2015). The numbers given in Table 1 were derived from different measurement methods. More precisely, thermal–optical techniques were applied in Forsström et al. (2013) and Pedersen et al. (2015) and provide the elemental carbon (EC) mass concentration, while filter transmission methods result in BC concentrations (Doherty et al., 2010). As a consequence of the different measurement methods, the ratio of the BC to EC concentration in snow can reach values of 1.3 as reported by Dou et al. (2017). A full discussion of the EC ∕ BC terminology can be found in Petzold et al. (2013).

Due to the absorption of solar radiation, BC particles may contribute to the currently ongoing drastic Arctic climate changes (called arctic amplification; e.g., Wendisch et al., 2017). The absorption effect can add to the warming of the atmosphere or the snowpack, when the BC particles are suspended either in the air or embedded in the snow. Furthermore, the BC particles may lead to a reduction of the snow surface albedo if the BC sediments on or into the snowpack (Sand et al., 2013). Warren (2013) estimated a decrease of 2 % in snow albedo in the visible spectral range for a snowpack with a BC mass concentration of 34 ng g⁻¹, which corresponds to the maximum value observed on the Greenland ice sheet (Doherty et al., 2010). More typical BC mass concentrations in Arctic snow range between 5 and 20 ng g⁻¹ (Table 1), which would lead to a reduction of the snow surface albedo of around 1 %. For typical Arctic summer conditions with a downward irradiance of 400 W m⁻² at the surface, a snow surface albedo reduction by 1 % would cause an additional absorption of solar radiative energy of 4 W m⁻² (Flanner et al., 2007). As a further consequence, the absorption by BC particles supports the melting of snow and increases the snow grain size due to an enhanced snow metamorphism, leading to further reduction of the surface albedo. The increase in the snow grain size also feeds back to the absorption by BC particles, which is more efficient for larger snow grain sizes (Warren and Wiscombe, 1980).

BC particles suspended in the atmosphere influence the absorption and scattering of the incoming solar radiation. If atmospheric BC particles are located in high altitudes, enhanced backscattering and absorption of incoming solar radiation by the BC layer lead to a reduction of the solar radiation reaching the surface. At the same time, the absorbed radiation warms the atmospheric BC layer. In extreme cases, the absorption due to atmospheric BC particles can affect the thermodynamic stability of the BC-containing atmospheric layer (Wendisch et al., 2008). The radiative heating of the lofted BC layers and the local cooling of the surface may enhance the thermodynamic stability of the Arctic boundary layer over the snow- and ice-covered areas (Flanner, 2013).

Several regional and global climate models account for the opposite radiative effects of atmospheric BC particles and snow-embedded BC particles (Samset et al., 2014). However, estimates of the total net forcing rely on the accuracy of the distribution of the BC particles assumed in the particular model. Samset et al. (2014) compared 13 aerosol models from the AeroCom Phase II; all of them included BC. They found that modeled atmospheric BC particle mass concentrations often show a spread over more than 1 order of magnitude. In remote regions, dominated by long-range transport, these models tend to overestimate the atmospheric BC concentrations compared to airborne observations. On the other hand, an underestimation of deposition rates induces a lower BC mass concentration in snow (Namazi et al., 2015). While this may introduce significant local and temporal uncertainties of the BC concentration and related radiative effects, long-term trends and mean multi-model results are representative for Arctic-wide observations (Sand et al., 2017).

Doherty et al. (2010)Doherty et al. (2010)Doherty et al. (2010)Doherty et al. (2010)Doherty et al. (2010)Forsström et al. (2013)Pedersen et al. (2015)Pedersen et al. (2015)Pedersen et al. (2015)Pedersen et al. (2015)Pedersen et al. (2015)

Table 1 Values of the black carbon mass concentration in snowpack observed in different regions and seasons in the Arctic. Note that Pedersen et al. (2015) and Forsström et al. (2013) derived the mass concentration of elemental carbon applying a thermal–optical measurement method.

Most previous studies quantifying the radiative impact of BC particles focused either on estimates of cooling or warming effects in the atmosphere (e.g., Wendling et al., 1985; Samset et al., 2013) or on radiative effects of BC in the snow surface layer (Dou and Cun-De, 2016). In contrast, this paper combines both effects by iteratively coupling radiative transfer simulations in both compartments, the atmosphere and the snowpack. On the basis of measured Arctic BC particle mass concentrations for spring and summer months, the instantaneous radiative forcing of BC particles embedded in the snow surface layer and in the atmosphere was quantified for specific cases. Here, the instantaneous radiative forcing refers to the change of the surface radiation budget caused by the presence of BC particles. With the help of the coupled model, the interaction of radiative effects in the atmosphere and the snowpack was considered. In particular, the role of clouds in the cooling or warming effect caused by BC particles was examined. Due to the fact that clouds enhance the atmospheric multi-scattering between surface and cloud layer, but also enhance the surface albedo (Choudhury and Chang, 1981), it is expected that clouds also alter the radiative impact by BC particles. To our knowledge, this interaction was not explicitly discussed in previous publications.

The radiative transfer simulations used in this study were based on airborne observations of atmospheric BC concentration in the Arctic, which were taken during three field campaigns in the European and Canadian Arctic. The applied models and observations are introduced in Sect. 2. Section 3 discusses the radiative forcing of BC particles on the surface solar radiative budget. Vertical profiles of heating rates in the atmosphere and in the snowpack are presented for clean and polluted conditions. To estimate the impact of BC particles, effective heating rates are calculated by separating the BC radiative effect from the total heating rates.

2 Configuration of radiative transfer simulations and iterative model coupling

2.1 BC profiles from aircraft campaigns

The input for the radiative transfer simulations was adapted to campaign-specific conditions. The atmospheric BC particle mass concentrations were derived from airborne measurements with the Single Particle Soot Photometer (SP2; Moteki and Kondo, 2007). Measured profiles of the atmospheric BC were used from three aircraft campaigns representing typical cases with higher BC concentrations (polluted case) in early spring with low Sun and lower BC concentration (pristine conditions) in early summer during the polar day. The Arctic Research of the Composition of the Troposphere from Aircraft and Satellites (ARCTAS) spring campaign was performed in April 2008 (Jacob et al., 2010; Matsui et al., 2011). The aircraft operation of ARCTAS mainly took place in northern Alaska and the Arctic Ocean. Similar SP2 measurements were performed during the Polar Airborne Measurements and Arctic Regional Climate Model Simulation Project (PAMARCMiP) campaigns (Herber et al., 2012; Stone et al., 2010). In this paper, measurements from the PAMARCMiP 2018 observations conducted from 10 March to 8 April 2018 were analyzed. The research flights, starting from Station Nord, Greenland, were performed above the sea ice in the Arctic Ocean north of Station Nord and the Fram Strait. In contrast to both spring campaigns, the Arctic CLoud Observations Using airborne measurements during polar Day (ACLOUD) campaign was conducted in early summer 2017 characterizing the atmosphere over the Arctic Ocean north and west of Svalbard (Wendisch et al., 2019; Ehrlich et al., 2019). ACLOUD was coordinated with the Physical Feedbacks of Arctic Boundary Layer, Sea Ice, Cloud and Aerosol (PASCAL) cruise of the research vessel Polarstern which provided a ground-based characterization of snow properties (Wendisch et al., 2019).

Mean vertical profiles of the measured atmospheric BC particle mass concentrations averaged for each of the three campaigns (ACLOUD, ARCTAS, and PAMARCMiP), are shown in Fig. 1a. The conditions between the individual flights were highly variable (see the standard deviation of each layer in Fig. 1). ACLOUD shows rather low mean BC concentrations, which do not exceed 30 ng m⁻³. During PAMARCMiP, the background concentrations were similarly low, with the exception of measurements at about 5 km altitude, where more than 100 ng m⁻³ was recorded. For ARCTAS observations, conducted at lower latitudes, significantly higher BC concentrations of up to 150 ng m⁻³ were observed. Similar to PAMARCMiP, the maximum concentrations were observed at about 5 km altitude, indicating that the BC particles were linked to long-range transport (Nakoudi et al., 2020). Besides the differences in atmospheric BC concentrations, the range of the daily solar zenith angle (SZA) and, thus, the available incoming solar radiation varied significantly for the three campaign periods. When analyzing the radiative impact of BC on the basis of daily averages, the magnitude of the incident solar radiation and the length of the day play a major role. While the early summer conditions of ACLOUD were characterized by the polar day and SZA between 55 and 78^∘, during ARCTAS the available incoming solar radiation was lower due to lower values of the SZA (minimum at noon of 62.5^∘). PAMARCMiP was conducted in the most northern region and earlier in the year, such that the Sun was about 9.5 h below the horizon and the minimum SZA was 79^∘ at noon. Table 2 summarizes the key characteristics of the three analyzed data sets.

Jacob et al. (2010)Ehrlich et al. (2019)Herber (2019)

Table 2 Region, period, solar zenith angle range, and maximum BC particle mass concentration and mean optical depth of BC at the 500 nm wavelength characterizing the three data sets obtained within ARCTAS, ACLOUD, and PAMARCMiP.

Therefore, the constructed profiles of PAMARCMiP and ACLOUD are assumed to be representative for Arctic early spring and early summer conditions, respectively.

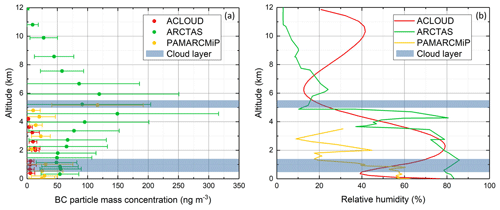
Figure 1 Mean profiles of atmospheric BC particle mass concentration (a) and relative humidity (b) averaged for each of the three campaigns (ACLOUD, ARCTAS, and PAMARCMiP) as used for the radiative transfer simulations. Horizontal bars indicate the standard deviation. The positions of the two implemented cloud layers (blue shaded area) are marked.

2.2 Atmospheric radiative transfer model

To simulate vertical profiles of the spectral upward and downward irradiance, the library for radiative transfer routines and programs (libRadtran, Emde et al., 2016; Mayer and Kylling, 2005) was used (http://www.libradtran.org/doku.php, last access: 10 June 2020). The model also provides the ratio of the direct to global irradiance f_dir∕glo, which is required as a boundary condition of the snowpack radiative transfer model. As a solver for the radiative transfer equation, the Discrete Ordinate Radiative Transfer solver (DISORT) 2 (Stamnes et al., 2000) routine running with 16 streams was chosen.

For the calculations, a plane-parallel atmosphere was assumed, which is justified for the Arctic conditions during the three campaigns. Using a pseudo-spherical geometry in libRadtran would change the broadband downward irradiance by less than 0.1 % (0.7 %) for a calculation with a SZA of 60^∘ (75^∘). The vertical resolution of the simulated irradiances was adjusted to the measured BC profiles, ranging between 100 m and 1 km. The spectral resolution of the simulations was set to 1 nm covering a wavelength range between 350 and 2400 nm. The extraterrestrial spectrum was taken from Gueymard (2004). The BC optical properties including the refractive index, density, extinction coefficient, single-scattering albedo, and scattering phase function from the OPAC aerosol database were applied (Hess et al., 1998). Corresponding to the campaign average BC profiles, the range of the SZA values was set to values representing the campaign conditions (see Table 2).

The meteorological input for the model was based on standard profiles of trace gases, temperature, humidity, and pressure from Anderson et al. (1986). Sub-Arctic summer conditions were chosen for the early summer case (ACLOUD) and subarctic winter conditions for the winter and spring cases (ARCTAS, PAMARCMiP). The standard profiles were adapted to observations from radio soundings near the airborne observations or dropsondes released during the flights and represent the middle of the individual campaign periods. Figure 1b shows the profiles of relative humidity used for the simulations. PAMARCMiP was characterized by rather dry air. Only in the boundary layer was an average humidity up to 60 % often observed linked to boundary layer clouds. ACLOUD and ARCTAS showed a higher relative humidity at a higher altitude of up to 6 km, which indicates the influence of higher-level clouds.

To test the sensitivity of the BC radiative effects with respect to cloud occurrence, two cloud layers were synthetically included in the atmospheric profiles as illustrated in Fig. 1. The cloud layer properties were based on observations by Bierwirth et al. (2013), Leaitch et al. (2016), and Blanchard et al. (2017) to represent typical Arctic cloud conditions. A low-level liquid water cloud was placed between 500 m and 1.4 km representing the humid boundary layer observed during PAMARCMiP. The liquid water content increases from 0.1 g m⁻³ at cloud base to 0.3 g m⁻³ at cloud top; the cloud particle effective radius increased from 6 to 12 µm. The second cloud layer represents a thin ice water cloud and was positioned between 5 and 5.5 km representing the higher-level clouds observed during ACLOUD and ARCTAS. This thin cloud was assumed to be homogeneous with an ice water content of 0.006 g m⁻³ and an effective cloud particle radius of 40 µm, according to airborne measurements reported by Wyser (1998) and Luebke et al. (2013). Optical properties of the liquid cloud droplets were calculated from Mie theory, while the ice crystal optical properties are based on Fu (2007). The assumed cloud properties correspond to a cloud optical thickness of 15 for the water cloud and 0.2 for the thin ice cloud.

2.3 Snowpack radiative transfer model

The Two-streAm Radiative TransfEr in Snow model (TARTES, https://github.com/ghislainp/tartes, last access: 6 February 2020) was used to simulate the radiative transfer through the snowpack (Libois et al., 2013, 2014). In TARTES, the snow profile is constructed of a predefined number of horizontally homogeneous snow layers, which allows us to account for the stratification of the snowpack. To consider the single-scattering properties of each layer, the method described by Kokhanovsky and Zege (2004) is applied in TARTES. To solve the radiative transfer equation, the delta-Eddington approximation (Joseph et al., 1977) is used. As a result, TARTES computes the spectral surface albedo and the profile of the irradiance within the snowpack. As the boundary condition, the SZA and f_dir∕glo have to be predefined. For each of the snow layers, the optical and microphysical properties have to be given, such as the snow density (ρ_ice), the specific surface area (SSA), and the snow grain shape parameters, which represents a mixture of different grains as suggested by Libois et al. (2013). Furthermore, the specific values of the so-called absorption enhancement parameter B=1.6 and the geometric asymmetry factor g^G=0.85 were applied. The specific surface area can be translated into the optical snow grain size r_opt by

$$\begin{array}{}\text{(1)}& r_{\mathrm{opt}}={\displaystyle \frac{\mathrm{3}}{{\mathit{\rho }}_{\mathrm{ice}}\cdot \mathrm{SSA}}}.\end{array}$$

TARTES allows us to consider impurities in each snow layer, which are characterized by the impurity type and mass concentration. The impurities are externally mixed and assumed to interact by Rayleigh scattering. To simulate a BC-containing snow layer, the complex refractive index and the density of BC particles given by Bond et al. (2013) are applied.

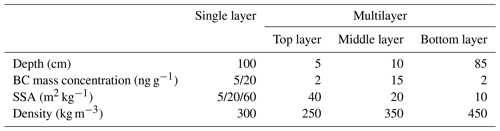
The input parameters of the snowpack model are summarized in Table 3. For the bottom layer, a soil albedo of 0.3 was assumed representing the reflection properties below the snowpack. The impact of the soil albedo on the albedo of the snow surface depends on the depth of the overlying snowpack. Sensitivity studies have shown that for snow depths of more than 20 cm the albedo of a snow surface is independent of the choice of the soil albedo below. In this study the snowpack depth was set to 1 m thickness. Reference simulations assuming a pristine homogeneous snow layer were performed. Simulations including BC impurities were based on BC particle mass concentrations summarized in Table 1 (Doherty et al., 2010; Forsström et al., 2013; Pedersen et al., 2015) and observations during PASCAL and PAMARCMiP. For the simulations of a single homogeneous snow layer, typical BC particle mass concentrations of 5 and 20 ng g⁻¹ were chosen. The default values of snow density and SSA were based on measurements during PASCAL and PAMARCMiP and were set to 300 kg m⁻³ and 20 m² kg⁻¹, respectively. To analyze the sensitivity of the snow surface albedo with respect to the snow grain size, SSA values of 5 and 60 m² kg⁻¹ were used. The vertical model resolution was set to 1 cm.

In addition to the simulations of a homogeneously mixed snow layer, a second model setup was used to consider a multilayer snowpack. Pit measurements in Greenland (Doherty et al., 2010) identified typical multilayer structures, where BC accumulated in a melting layer approximately 10 cm below the surface. Referring to these measurements, the snowpack of the second model setup consists of three snow layers. The top layer is 5 cm and the BC-containing middle layer is 10 cm thick. The bottom layer below continues to 1 m depth. For this multilayer approach, BC was included in the middle layer, representing an aged melting layer in which impurities had accumulated (SSA = 20 m² kg⁻¹, snow density of 350 kg m⁻³, and a BC mass concentration of 15 ng g⁻¹). The top layer was assumed to be of fresh and clean snow with SSA = 40 m² kg⁻¹, a snow density of 250 kg m⁻³, and a BC mass concentration of 2 ng g⁻¹, representing measurements from the PASCAL campaign. The aged snow layer at the bottom was characterized by an enhanced snow grain size and density of SSA = 10 m² kg⁻¹ and ρ_ice=450 kg m⁻³, respectively, and a BC mass concentration of 2 ng g⁻¹.

Table 3 Snowpack model setups for the single-layer and multilayer cases. The default SSA for the single-layer case is 20 m² kg⁻¹.

2.4 Iterative coupling

The surface albedo is an important boundary condition to simulate the radiative transfer in the atmosphere. It depends on the illumination conditions defined by the solar zenith angle, the spectral distribution of downward irradiance, and the ratio of direct-to-global irradiance (e.g., Wiscombe and Warren, 1980; Gardner and Sharp, 2010; Stapf et al., 2019). The transition from cloudy to cloudless atmospheric conditions increases the direct-to-global ratio (f_dir∕glo) and the contribution of short wavelengths to the broadband downward irradiance (Warren, 1982). Therefore, a cloud cover typically increases the broadband surface albedo. For example, simulations with TARTES assuming cloudless and cloudy conditions changed the broadband snow surface albedo from about 0.8 to 0.9 for a SZA of 60^∘ and a snowpack (no impurities) characterized by SSA =20 m² kg⁻¹. As clouds absorb solar radiation mostly at wavelengths larger than 1000 nm, the shorter wavelengths, where BC particles strongly absorb solar radiation, become more relevant. Because of the significant surface–cloud interactions, the atmospheric and snowpack radiative transfer models need to be coupled, interactively. Therefore, an iterative method coupling libRadtran and TARTES via their boundary conditions, surface albedo, and direct-to-global ratio (f_dir∕glo) of the incident radiation, was applied. Both parameters were transferred between the models as schematically illustrated in Fig. 2.

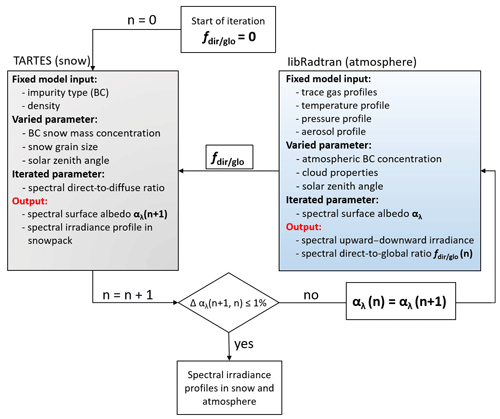
Figure 2 Schematics of the coupling of TARTES (gray box) and libRadtran (blue box) by exchanging the spectral surface albedo and the direct-to-global ratio. The list of varied parameters addresses the variables which were changed between the different realizations. Only the iterated parameters f_dir∕glo and α_λ were adjusted within an individual iteration cycle.

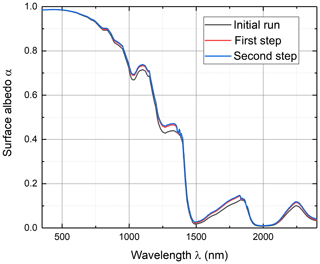
In the first iteration step, only diffuse radiation was assumed ($f_{\mathrm{dir}/\mathrm{glo}}=\mathrm{0}$) to calculate the snow surface albedo by TARTES, which subsequently serves as input for the libRadtran simulations. Then a new spectral direct-to-global ratio representing the atmospheric conditions was calculated by libRadtran, which is in turn used to readjust TARTES, starting a revised iteration (n+1) to calculate a new spectral surface albedo α_λ(n+1). This procedure was repeated until the deviation of the surface albedo calculated in the previous step (n) and calculated in the revised step (n+1) decreases below 1 %. Exemplarily, Fig. 3 illustrates the change of the spectral surface albedo for a cloudless case without atmospheric BC and a SZA of 60^∘. The BC mass concentration in snow was set to 5 ng g⁻¹. Two iteration steps were necessary in this particular example to match the 1 % termination criterion, which is a typical number for all studied cases. Starting with purely diffuse conditions allows faster calculations in cloudy cases. This quick convergence of the iteration enables the consideration of different cloud properties and atmospheric conditions and facilitates the calculation of the radiative effects of BC particles in the atmosphere and within the snowpack simultaneously. The assumption of a pure diffuse illumination in the initial run caused no significant difference of the calculated visible snow albedo to the first and second iteration step. In contrast, the iterated direct-to-global ratio adjusts the snow albedo in the near infrared because the direct fraction is quickly approaching unity in this spectral range.

Figure 3 Change of the spectral snow albedo for cloudless conditions with a SZA of 60^∘ due to the iterative adjustment by the coupled atmosphere and snow radiative transfer models. The initial run assumes a direct-to-global ratio of zero.

2.5 Quantities used to characterize the impact of BC particles

In the following, the surface radiative forcing of BC particles and profiles of heating rates are analyzed. The total radiative forcing at the surface ΔF_tot is separated into the forcing of BC particles suspended in the atmosphere ΔF_atm and the forcing of BC particles deposited in the snowpack ΔF_snow. ΔF_snow is defined by the difference of the net irradiance (downward minus upward solar irradiance) if BC is considered in the snow layer (F_net,BC) and a clean reference case without BC in the snow layer (F_net,clean). Similarly, ΔF_atm is defined as the difference between the net irradiances derived for BC in snow and the atmosphere and the atmospheric BC-free reference case:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{F}_i=F_{\mathrm{net},\mathrm{BC}}-F_{\mathrm{net},\mathrm{clean}},\end{array}$$

with index “i” standing for “tot”, “atm”, or “snow”. For the separated forcings, F_net,clean refers to either a clean atmosphere or a clean snow layer, while the other part does consider BC particles. The default case of a clean atmosphere used a BC mass concentration in the snow layer of 5 ng g⁻¹. Vice versa, the default case of a clean snow layer assumed the atmospheric BC profile of the ACLOUD campaign. For ΔF_tot, the clean reference assumed both a pristine atmosphere and pristine snow layer.

The calculation of atmospheric and snow heating rate profiles HR(z) (K d⁻¹) was based on the net irradiances at the top (t) and bottom (b) of selected atmospheric or snow layer z, the layer density ρ(z), the specific heat capacity under constant pressure c_p, and the layer thickness (z_t−z_b):

$$\begin{array}{}\text{(3)}& \mathrm{HR}\left(z\right)={\displaystyle \frac{\mathrm{\Delta }T}{\mathrm{\Delta }t}}\left(z\right)={\displaystyle \frac{F_{\mathrm{net}}\left(z_{\mathrm{t}}\right)-F_{\mathrm{net}}\left(z_{\mathrm{b}}\right)}{\mathit{\rho }\left(z\right)\cdot c_{\mathrm{p}}\cdot \left(z_{\mathrm{t}}-z_{\mathrm{b}}\right)}}.\end{array}$$

For atmospheric profiles, the vertical resolution from the BC profiles was used. Similarly, the heating rate profiles within the snowpack were calculated applying Eq. (3) by accounting for the snow density (set to 300 kg m⁻³) and the specific heat capacity of ice $c_{\mathrm{p},\mathrm{snow}}=\mathrm{2060}$ J kg⁻¹ K⁻¹ at a temperature of 0 ^∘C. The layer thickness within TARTES and therefore the resolution of the heating rate profiles is 1 cm.

To separate the contribution of BC particles to the total heating rate, the effective BC heating rate HR_BC(z) was calculated as the difference between the total heating rate HR_tot(z) and the heating rate of the clean reference case HR_clean(z):

$$\begin{array}{}\text{(4)}& {\mathrm{HR}}_{\mathrm{BC}}\left(z\right)={\mathrm{HR}}_{\mathrm{tot}}\left(z\right)-{\mathrm{HR}}_{\mathrm{clean}}\left(z\right).\end{array}$$

If not indicated differently, radiative effects reported in this study refer to daily means accounting for the change of the SZA and the nighttime. Therefore, simulations were performed for a full diurnal cycle with a temporal resolution of 5 min. The simulated upward and downward irradiance were averaged. Then these daily mean irradiances were applied to calculate mean values of ΔF_tot, ΔF_atm, ΔF_snow, HR_tot(z), and HR_BC(z).

3 Results

3.1 Radiative impact of BC at surface level

3.1.1 Effect on surface albedo

The reduction of the snow surface albedo by BC impurities depends on the snow grain size. Here, changes of the snow surface albedo due to the combination of BC impurities and snow grain size variations were evaluated for Arctic conditions. The single-layer snowpack setup, as defined in Sect. 2, was used together with atmospheric properties representing the ACLOUD conditions. The SZA was set to a constant value of 60^∘. Figure 4 shows the spectral snow albedo for variable BC particle mass concentrations (0, 5, and 20 ng g⁻¹) as calculated with TARTES. The selected SSA values represent different snow types, as freshly fallen snow with small snow grains (SSA =60 m² kg⁻¹), aged snow which has undergone snow metamorphism (SSA =5 m² kg⁻¹) when surface temperature approaches 0 ^∘C, and moderately aged snow without melting (SSA =20 m² kg⁻¹), which was considered the default case. As expected, the highest values of surface albedo were obtained for the case with clean and fresh snow. Adding BC particles caused a decrease in the spectral surface albedo, in particular in the visible spectral range up to 700 nm, shown in the enlargement of Fig. 4. In contrast, the near-infrared spectral range was dominated by ice absorption, which is affected by the SSA (grain size).

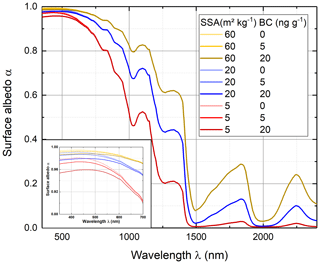
Figure 4 Spectral surface albedo of snow for cloudless conditions and a SZA of 60^∘ for different SSA and BC particle mass concentrations. The inlay shows an enlargement of the spectral albedo between 350 and 700 nm.

From the simulations shown in Fig. 4 it becomes apparent that the decrease in surface albedo with increasing BC mass concentration is stronger for aged snow than for fresh snow. Fresh snow with smaller grains leads to an enhanced backscattering of the incident radiation, while larger grains allow for a deeper penetration of the incident radiation into the snowpack. Since the penetration depth for aged snow is deeper, the probability is higher that the radiation gets absorbed by the BC particles, leading to a decrease in the spectral surface albedo.

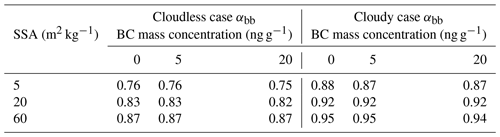
In the same way, the radiative forcing of BC particles embedded in the snow layer was calculated for overcast cloudy conditions (predefined low-level liquid water cloud case) to assess the relevance of changes of the BC mass concentration compared to variations in SSA and the illumination conditions. To estimate the relevance for the surface energy budget, the solar broadband forcing was analyzed by calculating the broadband albedo α_bb. Therefore, the spectral albedo simulated by TARTES and the spectral downward irradiance $F_{\mathit{\lambda }}^{\downarrow }\left(\mathit{\lambda }\right)$ simulated by libRadtran were used:

$$\begin{array}{}\text{(5)}& {\mathit{\alpha }}_{\mathrm{bb}}={\displaystyle \frac{\int \mathit{\alpha }\left(\mathit{\lambda }\right)\cdot F_{\mathit{\lambda }}^{\downarrow }\left(\mathit{\lambda }\right)\mathrm{d}\mathit{\lambda }}{\int F_{\mathit{\lambda }}^{\downarrow }\left(\mathit{\lambda }\right)\mathrm{d}\mathit{\lambda }}}.\end{array}$$

The calculated broadband surface albedo values are summarized in Table 4 for the cloudy and cloudless cases, respectively. For both cases, even the most extreme BC mass concentration reduced the surface albedo by less than 1 %. Contrarily, the snow grain size and the presence of clouds cause significant changes of the snow albedo. The difference of the broadband surface albedo between fresh and aged snow ranges up to 0.12 and 0.08 for cloudless and cloudy conditions, respectively, which is of the same order of magnitude as the effect of clouds (0.12 for fresh snow and 0.07 for aged snow). Therefore, for Arctic conditions, the impact of BC impurities on the broadband snow albedo is of minor importance, compared to the impact of modifying the snow grain size. Also, Warren and Wiscombe (1980) and Warren (2013) found only a small reduction of the broadband albedo between 0 % and 1 % for fresh snow and 0 %–3 % for aged snow when adding BC with a mass concentration of 34 ng g⁻¹ to the clean snow.

Table 4 Broadband surface albedo (α_bb) of fresh (SSA =60 m² kg⁻¹) and aged snow (SSA =5 and 20 m² kg⁻¹) depending on the BC particle mass concentration and illumination condition.

3.1.2 Surface radiative forcing

The decrease in the snow surface albedo due to an increase in BC particle mass concentration or snow grain size directly alters the surface radiative forcing ΔF_snow. To quantify these radiative effects, ΔF_snow was first calculated for a fixed solar zenith angle of 60^∘. A typical Arctic range of BC particle mass concentrations in snow and SSA values assuming the ACLOUD atmospheric conditions was applied. Figure 5 shows a contour plot of ΔF_snow for combinations of SSA and BC particle mass concentrations. For a BC particle mass concentration of 5 ng g⁻¹ in snow representing clean conditions and a SSA larger than 20 m²kg⁻¹, ΔF_snow ranges between 0.4 and 0.7 W m⁻². Higher BC particle mass concentrations increase ΔF_snow depending on the snow grain size or SSA. The strongest increase in the solar radiative warming was calculated for small SSA values, corresponding to larger snow grain sizes. With the larger penetration depth for a smaller SSA, more radiation can be absorbed by the BC particles.

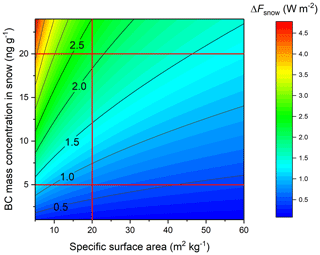
Figure 5 Solar surface radiative forcing of BC impurities in snow ΔF_snow calculated for different SSA values and BC particle mass concentrations. The atmospheric conditions correspond to the ACLOUD case with a fixed SZA of 60^∘. Horizontal red lines indicate typical Arctic conditions with rather clean and more polluted snow; the vertical line represents the most typical SSA.

To compare the radiative forcing at the surface of atmospheric BC particle profiles observed during the three aircraft campaigns ACLOUD, PAMARCMiP, and ARCTAS, the daily averaged surface radiative forcing was then analyzed. To limit the degree of freedom, the SSA was set to a default value of SSA = 20 m² kg⁻¹ representative for snow-covered Arctic sea ice. To estimate the relevance of the atmospheric BC particles, their separated radiative forcing ΔF_atm was calculated. Additionally, the total radiative forcing ΔF_tot combining the atmospheric and snow BC was analyzed. Figure 6 summarizes the daily averaged ΔF_snow (panel a), ΔF_atm (panel b), and ΔF_tot (panel c) for different BC particle mass concentrations in snow (0, 5, 20 ng g⁻¹) on cloudless and cloudy conditions.

The BC particles embedded in snow lead to warming effects of up to 0.7 W m⁻² for high BC mass concentrations of 20 ng g⁻¹ and ACLOUD conditions. For ARCTAS ΔF_snow was slightly lower and for PAMARCMiP reduced by a factor of about 3. This difference is caused by the lower maximum Sun elevation during PAMARCMiP (location in higher latitude) resulting in a lower amount of available incoming solar irradiance compared to ACLOUD and ARCTAS (see range of SZA in Table 2).

Atmospheric BC particles reduce the incident solar radiation at the surface due to extinction, such that the atmospheric radiative forcing ΔF_atm is negative in all scenarios (Figure 6b). This cooling at the surface is strongest with values up to −0.2 W m⁻² in cloudless conditions for the ARCTAS case, where the largest atmospheric BC particle concentrations were observed. Despite having a BC optical depth of similar magnitude, the PAMARCMiP case (AOD_BC=0.006) shows a weaker radiative cooling compared to the ARCTAS case (AOD_BC=0.008) caused by the higher solar zenith angles in PAMARCMiP. Minor cooling of less than −0.02 W m⁻² was observed for the ACLOUD case, where the atmosphere was rather clear with significant reduced atmospheric BC particle concentrations (factor of 10 lower than during ARCTAS). Comparing the simulations with different BC mass concentrations in snow showed only few effects of the surface properties on the radiative forcing of atmospheric BC. A slight decrease in ΔF_atm with increasing BC mass concentrations was observed for the ARCTAS case, indicating that a lower surface albedo enhances the radiative forcing of atmospheric BC particles.

The cooling effect of atmospheric BC counteracts the warming effect of BC particles in snow and can lead to a positive and negative total radiative forcing. Figure 6c shows the total radiative forcing ΔF_tot for all cases. For BC mass concentration of 20 ng g⁻¹, all cases showed a total warming effect when the warming of BC in the snowpack exceeds the cooling by atmospheric BC. The strongest warming effect of up to 0.7 W m⁻² was found for the ACLOUD case which is characterized by the pristine atmospheric conditions in the Arctic summertime. For less polluted snow (5 ng g⁻¹), warming and cooling scenarios can occur depending on the concentration of atmospheric BC (ARCTAS shows a slight cooling) and the solar zenith angle (ACLOUD shows a significant warming effect). ΔF_tot calculated for ACLOUD even exceeds the warming effect of PAMARCMiP for the higher BC mass concentration in the snow layer. This clearly demonstrates that the competition between the individual BC radiative forcings ΔF_atm and ΔF_snow is strongly driven by solar zenith angle and the available solar radiation and is less affected by the BC concentrations itself.

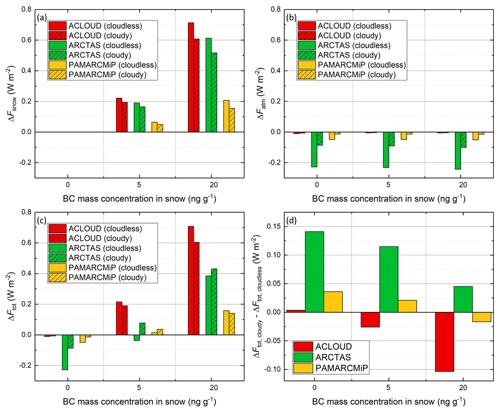
Figure 6 Daily mean of the solar surface radiative forcing simulated for the conditions of the three campaigns ACLOUD, PAMARCMiP, and ARCTAS assuming a fixed SSA of 20 m² kg⁻¹. The separated forcings by BC embedded in snow (ΔF_snow, panel a), atmospheric BC (ΔF_atm, panel b), and the total forcing (ΔF_tot, panel c) are shown. The daily mean solar radiative forcing of BC in cloudy conditions is displayed by shaded bars. The difference of ΔF_tot between simulations with and without clouds is given in (d).

The available solar irradiance is strongly affected by the presence of clouds. Therefore, the impact of clouds on the BC radiative forcing was analyzed. Two cloud layers as defined in Sect. 2.2 were implemented in the simulations and considered in the calculation of $\mathrm{\Delta }{F}_{\mathrm{tot}/\mathrm{atm}/\mathrm{snow}}$ (clean cloudy and polluted cloudy case in Eq. 2) to extract the pure BC radiative forcing. In Fig. 6 the BC radiative forcing of the cloudy scenarios are shown by the shaded bars. The magnitudes of ΔF_snow (panel a) and ΔF_atm (panel b) are always reduced by the presence of clouds. ΔF_snow drops by about 15 % in all cases (0.1 W m⁻² for ACLOUD and ARCTAS and high BC mass concentration in snow), while ΔF_atm increases by more than 50 %, which amounts for ARCTAS to an absolute increase of 0.14 W m⁻². Clouds reduce ΔF_snow because less radiation reaches the surface and can be absorbed by BC particles in the snowpack. The shift from a mostly direct illumination of the snow surface by the Sun to a diffuse illumination below the clouds is less significant as demonstrated in Table 4.

These different cloud effects counterbalance in the total radiative forcing ΔF_atm (Fig. 6c). To illustrate the total effect by clouds, Fig. 6d shows the difference between cloudy and cloudless simulations. In all scenarios, still slight differences between cloudy and cloudless conditions were observed, but with different directions. For the ACLOUD case, the clouds reduce the warming effect of BC particles mainly due to a reduction of radiation that reaches the surface. As almost no atmospheric BC was present, only ΔF_snow is affected.

For the ARCTAS cases, the clouds always increased ΔF_tot. For a BC mass concentration of 5 ng g⁻¹ even the sign shifts from a total cooling to a total warming effect of BC. For ARCTAS, with high atmospheric BC concentrations, the presence of clouds mainly reduce the cooling effect of the atmospheric BC, ΔF_atm. As the atmospheric BC layer was located mostly above the cloud, the radiative effect of the clouds, which is typically much stronger than the absorption by the atmospheric BC, reduces the significance of the atmospheric BC forcing. For higher BC mass concentrations in the snow, the increase in ΔF_tot by adding a cloud becomes weaker because ΔF_snow simultaneously slightly decreases in cloudy conditions.

The PAMARCMiP case, characterized by the low Sun elevation, in general, showed a reduced effect by clouds. Here, the reduction of the cooling effect of atmospheric BC, ΔF_atm, and the increase in the BC snow forcing, ΔF_snow, compete with each other and result in different total cloud radiative effects. Model runs with and without the upper ice cloud layer did not show any significant difference in $\mathrm{\Delta }{F}_{\mathrm{tot}/\mathrm{atm}/\mathrm{snow}}$, which allows the conclusion that mainly the presence of the low liquid water clouds affects the radiative forcing of BC particles.

In summary, the comparison of the radiative forcing by BC particles in snow and the atmosphere with typical concentrations and mass concentrations observed in Arctic spring and summer is rather small compared to other parameters (SZA, grain size) which contribute to solar cooling or heating at the surface level. The highest radiative cooling of BC particles was in the range of 1 W m⁻² and is estimated for low SZA, high BC particle mass concentrations, and large grains.

3.2 Vertical radiative impact of BC particles in the atmosphere and snow

3.2.1 Heating rate profiles in the atmosphere

To quantify the absorption of solar radiation by Arctic atmospheric BC particles and consequent local warming effects, profiles of the heating rates were simulated for the three cases ACLOUD, ARCTAS, and PAMARCMiP. Based on simulations with and without atmospheric BC, the total heating rate HR_tot(z) and the effective heating rate of BC particles HR_BC(z) were calculated (see Eqs. 3 and 4). Figure 7 shows daily averaged profiles of HR_tot(z) and HR_BC(z) calculated for the three BC profiles. Solid lines represent the cloudless scenarios while dotted lines show simulations where the two predefined cloud layers were added. The location of the clouds is indicated by the gray shaded area. The highest total heating rates in cloudless conditions were found for the ACLOUD case, with maximum values of more than 1.2 K d⁻¹ at about 2–4 km altitude. This altitude range was characterized by enhanced humidity leading to a stronger absorption of solar radiation by the water vapor. The spring campaigns ARCTAS and PAMARCMiP were characterized by lower water vapor concentrations (factor of 4 and 10 lower than for ACLOUD, respectively) and reduced incident solar radiation due to the time of year and latitude of the observations. This leads to significant lower values of HR_tot(z) compared to the ACLOUD case. While ARCTAS showed a similar vertical pattern with maximum HR_tot(z) of 0.5 K d⁻¹ in the lower troposphere below 5 km altitude, the conditions during PAMARCMiP lead to a maximum of HR_tot(z) of about 0.25 K d⁻¹ located at 5–6 km altitude. This corresponds to the rather dry lower troposphere observed in springtime in the central Arctic. By adding clouds in the simulations, the highest HR_tot(z) values were observed within the liquid water cloud layer, where solar radiation is absorbed by the cloud particles. Similar to the cloudless scenarios, the ACLOUD case showed the highest values of HR_tot(z) with up to 4.1 K d⁻¹ at cloud top of the lower liquid cloud layer. The absorption in the ice cloud is less pronounced, and the increase in HR_tot(z) is significantly lower.

The profiles of the effective BC heating rate HR_BC(z) (Fig. 7b) show a completely different pattern compared to HR_tot(z). In general, HR_BC(z) was about 1 order of magnitude lower than HR_tot(z) for all three cases. Significant BC heating rates were observed only for the ARCTAS and PAMARCMiP cases with values up to 0.1 K d⁻¹. The profiles of HR_BC(z) are strongly correlated with the vertical distribution of BC particles in the measured profiles. Maximum HR_BC(z) values were located in the pollution layers. The pollution layer observed during PAMARCMiP at 5 km and the BC layers of ARCTAS above 5 km altitude showed the largest relative impact of BC particles where nearly one-fifth and one-third, respectively, of the total solar heating is attributed to BC absorption. In lower altitudes of the ARCTAS case, the enhanced absorption by water vapor reduced the relative importance of BC particles. For the summer case of ACLOUD, HR_BC(z) was rather small at all altitudes and contributed to the total radiative heating by only 10 %. However, in low altitudes, the absolute values of HR_BC(z) were of the same order for both ACLOUD and the PAMARCMiP. This illustrates that the effect of a higher BC particle concentration during PAMARCMiP was compensated for by the dependence of HR_BC(z) on the amount of the available incoming solar radiation and the atmospheric water vapor concentration.

Adding clouds in the simulations affected HR_BC(z) of the three cases differently. While the clean atmosphere layer of ACLOUD and the PAMARCMiP cases shows almost no differences to cloudless conditions, a minor cloud effect was observed for the ARCTAS case and the polluted layer of PAMARCMiP. In both cases, the ice cloud led to a slight increase in HR_BC(z) by about 5 % within and above the cloud layer. This was caused by the enhanced reflection of the incoming radiation which led to additional absorption of the reflected radiation by the atmospheric BC particles. At altitudes between the ice and liquid water clouds no significant effect by the clouds was observed. Within and below the liquid water cloud HR_BC(z) was significantly reduced by almost 0.01 K d⁻¹ for the ARCTAS case. This cloud effect was caused by the strong reflection of radiation at the cloud top leading to a reduction of radiation reaching into and below the cloud layer.

Comparing all simulations, it can be concluded that the absolute radiative effects of atmospheric BC particles are potentially strongest in early spring when incoming solar radiation starts to increase and BC particle concentration is still high enough. Furthermore, the surface conditions in spring were dominated by snow and ice coverage, which causes an increase in the amount of upward radiation contributing to the atmospheric heating rate. In late spring and summer, the BC particle concentration decreased rapidly, while the absorption by water vapor became more and more dominant with increasing temperatures.

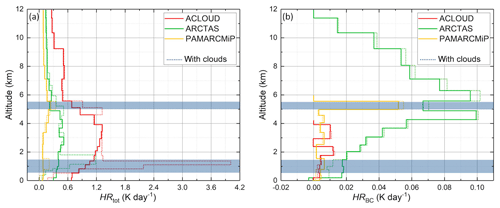
Figure 7 Daily averaged profiles of the total radiative heating rate HR_tot(z) (a) and the effective BC heating rate HR_BC(z) (b) calculated for the three cases ACLOUD, ARCTAS, and PAMARCMiP. Both cloudless simulations (solid lines) and cloudy scenarios (dotted lines) are shown. The gray shaded areas indicate the location of the cloud layers.

Figure 8 (a) Transmissivity profiles of solar radiation within the snowpack for three single layers and one multilayer case assuming ACLOUD conditions. (b) Corresponding daily mean total heating rate profiles within a snowpack HR_tot(z). (c) Corresponding effective BC heating rate profiles HR_BC(z).

3.2.2 Heating rate profiles in the snowpack

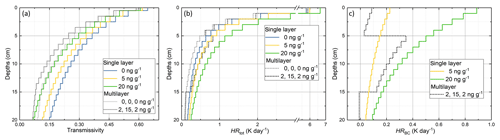
Not only the snow albedo but also the transmission of radiation through the snowpack is affected by BC particles. For the atmospheric boundary conditions of the ACLOUD case, the radiative transfer in the snowpack was simulated and analyzed for different single-layer and multilayer scenarios as introduced in Table 3. The transmissivity was calculated from the ratio of the downward irradiance in the snow layer to the downward irradiance at the top of the snow layer. Figure 8a shows the transmissivity profiles of solar radiation within the snowpack. The homogeneous single-layer reference case without BC particles (SSA =20 m² kg⁻¹) illustrates the general decrease in transmissivity, which is reduced to 0.3 in 20 cm snow depth. Adding a typical Arctic BC concentration of 5 ng g⁻¹ reduces the transmissivity to almost 0.2. This obviously may have an impact on the radiative processes below the snowpack, in and below the sea ice as discussed by, e.g., Tuzet et al. (2019) and Marks and King (2014). The inhomogeneous multilayer case shows in general lower transmissivities due to the enhanced reflection of the smaller snow grains at the top of the layer (SSA =60 m² kg⁻¹ down to 5 cm depth) but also indicates a significant dimming effect of the BC particles.

To assess, in which layers of the snowpack the strongest absorption of solar radiation and, therefore, a potential enhancement of the snow metamorphism is located, profiles of the heating rates within the snowpack HR_tot(z) were calculated. To quantify how BC particles deposited in snow may change these heating profiles, the effective BC heating rates HR_BC(z) were derived in a second step. Figure 8 shows HR_tot(z) (panel a) and HR_BC(z) (panel b) for all cases in the first 20 cm of the snowpack. For all cases, the total heating rate rapidly decreases by 1 order of magnitude within the first 10 cm of depth. The simulation for the single-layer (solid lines) snowpack shows the maximum values of HR_tot(z) which were located in the topmost layers and reach values up to 6.6 K d⁻¹ (note the scale break in Fig. 8a).

Assuming different BC mass concentrations in the single-layer case slightly increases HR_tot(z) in the entire column. In the multilayer case, this increase is limited to the upper part of the profile. This contribution of BC particles to the total radiative heating was quantified by HR_BC(z) and shown in Fig. 8b. The largest HR_BC(z) values were observed for the most polluted single-layer case with a BC mass concentration of 20 ng g⁻¹. For this case, the contribution by BC particles amounts to almost 0.9 K d⁻¹ in the topmost layer, dropping down to a value of less than 0.1 K d⁻¹ at 20 cm snow depth. Compared to the total radiative effect, HR_BC(z) contributes about 15 % to the heating rate at the top snow layer and 40 % to the heating in the base layer. For the typical Arctic BC mass concentration of 5 ng g⁻¹, this contribution of BC particles is significantly lower, ranging between 3 % and 20 %.

The multilayer cases are characterized by smaller snow grains in the top layer (SSA =40 m² kg⁻¹) compared to the single-layer cases (SSA =20 m² kg⁻¹) and, therefore, shows reduced values of HR_tot(z). According to the structure of the snowpack, HR_BC(z) is largest in the layer of the highest BC mass concentration. Beneath this layer (z<15 cm) the heating rates for the pristine and polluted cases are almost similar (HR_BC(z)≈0 K d⁻¹). In this base layer, the largest snow grains are assumed (lowest SSA), which increases the absorption of radiation by the snow ice water.

Based on these results, it becomes evident that the absorption of solar radiation by the ice water of the snow grains dominates the total heating rate in the snowpack, especially at the top layer, where most radiation is absorbed. Therefore, in Arctic conditions the snow grain size typically plays a larger role than the concentration of BC particles embedded in snow. To estimate if BC particles can accelerate the snow metamorphism, coupled snow physical models need to be applied (e.g., Tuzet et al., 2017). However, compared to the results reported by Tuzet et al. (2017), who studied alpine snow with at least a magnitude higher BC mass concentrations, for Arctic conditions it is likely that the self-amplification of the snow metamorphism is dominated by the reduction of the surface albedo.

Simulations in cloudy conditions (not shown here) resulted in a reduced HR_tot(z) and HR_BC(z) because the clouds reduce the incoming solar radiation. Similarly, a change of the solar zenith angle affects the results by changing the available solar radiation. Therefore, the ACLOUD case used in the simulations presented in this section represents the maximum radiative effects compared to ARCTAS and PAMARCMiP conditions. In general, it can be concluded that the solar heating by BC particles embedded in the snowpack is most effective for low SZA (spring and summer conditions with high amount of available incoming radiation), decreasing SSA (aged snow in conditions near melting temperature), and increasing BC particle mass concentrations (accumulated BC particles caused by melting). Such conditions are mostly linked to late spring and summer, when the Sun is high, snow is close to melting, and BC has accumulated. This suggests that the maximum heating rates due to atmospheric BC and BC embedded in the snowpack typically occur in different periods of the year, early spring and early summer, respectively.

4 Summary and conclusions

This study analyzed the instantaneous solar radiative effect at the surface of Arctic BC particles (suspended in the atmosphere and embedded in the snowpack) over the sea-ice-covered Arctic Ocean. The difference of the BC effects in cloudless and cloudy conditions was compared. For this purpose, an atmospheric and a snow radiative transfer model were iteratively coupled to account for the radiative interactions between both compartments (atmosphere and snow layer). Typical atmospheric BC vertical profiles and BC particle mass concentrations in the snowpack, derived from three field campaigns in the North American and the North Atlantic Arctic, ACLOUD, ARCTAS, and PAMARCMiP, were used in the simulations. These locations typically are not affected by local pollution, but by long-range transport of BC particles. The BC radiative effects were quantified by the surface radiative forcing and profiles of heating rates in the atmosphere and the snow, which were presented on the basis of daily averages. For the surface radiative forcing, the contributions by atmospheric and snow BC particles were separated. For the heating rate profiles, the effective contribution of BC particles to the total heating rates was derived and compared to further atmospheric and snow parameters also leading to a warming or cooling (e.g., water vapor, clouds, snow grain size).

The magnitude of the atmospheric BC radiative forcing at the surface derived in this study (up to −0.2 W m⁻²) agrees quite well with findings from Wendling et al. (1985). They reported a BC-induced solar cooling in the range of 0.0 to −0.5 W m⁻² for spring measurements in the Svalbard area. Further, the solar surface radiative forcing due to BC embedded in snow showed solar warming between 0.05 and 0.7 W m⁻² depending on the BC mass concentration and incident solar irradiance. For comparison, Dou and Cun-De (2016) deduced an averaged solar warming over Svalbard in spring of 0.54 W m⁻² based on a BC mass concentration of 5 ng g⁻¹ in snow.

The simulations suggest that for the specific Arctic cases investigated in our study, the radiative forcing of BC is small compared to the radiative impact of other parameters (water vapor, clouds, snow grain size). The significance of the BC radiative effects shows a strong seasonal dependence. In cloudless conditions, the absorption by atmospheric water vapor shows a much stronger contribution to the atmospheric heating rates than the radiative effect of BC particles. In summer (ACLOUD) and in lower latitudes (ARCTAS), the Arctic shows the most humid conditions, where absorption of water vapor dominates over the BC radiative effects. Similarly, the available incident solar radiation limits the magnitude of the BC radiative effects. Despite the more polluted atmosphere, the low solar zenith angle of the cases of PAMARCMiP (high latitude) and ARCTAS (early spring season) did show lower BC radiative effects than the ACLOUD case. Thus, over the sea-ice-covered Arctic Ocean, the BC radiative effect is about an order of magnitude lower than observed in lower and tropical latitudes, where the pollution level is also typically higher. For example, studies investigating strong pollution conditions in northern India or China reported BC heating rates in the atmosphere larger than 2 K d⁻¹, which may significantly influence the lapse rate and the atmospheric stability (Tripathi et al., 2007; Wendisch et al., 2008). For the rather pristine Arctic, this study showed significantly lower daily mean BC heating rates of maximum 0.1 K d⁻¹, which do not have the potential to significantly modify the atmospheric stability. However, in other Arctic regions characterized by higher atmospheric BC particle concentrations due to local fires, e.g., northern Siberia, a stronger impact can be expected.

Similarly, the mass concentration of BC particles embedded in the Arctic snowpack is far lower than observed in alpine snow in lower latitudes. Accordingly, the absorption of radiation by the snow water itself dominates the radiative warming in the snowpack. For typical conditions of the central Arctic, the absorption due to BC particles contributes only 3 % to the total heating rate in the uppermost snow layer. These results indicate that the microphysical properties of the snowpack (mainly snow grain sizes) are more important drivers for the degree and strength of the snow metamorphism. It needs to be considered that this picture might change if the accumulation of BC particles is more efficient than it is over the snow-covered Arctic sea ice, where the sea ice and snowpack do not last more than 1 to 3 years. Accumulation of BC on the Greenlandic glaciers will amplify the radiative forcing on a local scale. Furthermore, BC particles are not the only light-absorbing impurities which are transported into the Arctic. The relevance of dust particles and microorganisms is currently the subject of the scientific discussion and may exceed the effect of BC particles (Kylling et al., 2018; Skiles et al., 2018).

However, the changing relevance of the BC radiative effects suggests that the maximum heating rates due to atmospheric BC and BC embedded in the snowpack typically occur in different periods of the year. While atmospheric BC particles reveal the largest radiative effects in early spring (high concentration of atmospheric BC, medium–high Sun, low water vapor), the BC particles embedded in snow warm more effectively in early summer (accumulation of BC particles in snow, high Sun, large snow grain size). To estimate the role of clouds in the surface warming or cooling by BC particles and the BC heating rates, radiative transfer simulations assuming cloudless and cloudy conditions were compared. Clouds reflect the incident solar radiation and, therefore, reduce the available radiation reaching the surface. This reduces the potential of the warming effect by BC particles embedded in the snow. Similarly, the cooling effect by atmospheric BC on the surface radiative budget is weakened in the presence of clouds. The competition of these two cloud effects depends on the BC concentrations in the snow and atmosphere and is affected by the increased broadband surface albedo and the multiple scattering in the presence of a cloud layer. The profiles of the effective BC heating rates are mainly affected by the ice cloud at higher altitude. Within and above the cloud, the radiation reflected by the cloud enhances the local radiative heating by BC. Contrarily, a low liquid water cloud reduces the available incoming radiation, such that the effective BC radiative effect is lower for the cloudy case compared to the cloudless case. For the same reason, the presence of clouds reduces the radiative heating rates within the snowpack.

For the sea-ice-covered Arctic Ocean, we conclude that (i) the warming effect of BC embedded in the snow overcompensates for the atmospheric BC cooling effect at the surface, (ii) the impact of clouds reduces both the surface cooling by atmospheric BC particles and the warming by BC particles embedded in snow, and (iii) the BC radiative effect is of minor importance compared to other absorbers. However, for the expected increase in BC particle mass concentrations in the future, the relative importance of BC particles might need to be re-evaluated. Additionally, ongoing research, e.g., triggered by the current MOSAiC (Multidisciplinary drifting Observatory for the Study of Arctic Climate) experiment, will enable the quantification of the radiative effects of BC in the eastern and central Arctic also using the methods proposed here.