Radiative forcing of anthropogenic aerosols on cirrus clouds using a hybrid ice nucleation scheme

Anthropogenic aerosols impact cirrus clouds through ice nucleation, thereby changing the Earth's radiation budget. However, the magnitude and sign of anthropogenic forcing in cirrus clouds is still very uncertain depending on the treatments for ice-nucleating particles (INPs), the treatments for haze particle freezing, and the ice nucleation scheme. In this study, a new ice nucleation scheme (hereafter the HYBRID scheme) is developed to combine the best features of two previous ice nucleation schemes, so that global models are able to calculate the ice number concentration in both updrafts and downdrafts associated with gravity waves, and it has a robust sensitivity to the change of aerosol number. The scheme is applied in a box model, and the ice number concentrations (9.52±2.08 L⁻¹) are somewhat overestimated but are in reasonable agreement with those from an adiabatic parcel model (9.40±2.31 L⁻¹). Then, the forcing and cloud changes associated with changes in aircraft soot, sulfur emission, and all anthropogenic emissions between the preindustrial (PI) period and the present day (PD) are examined using the CESM/IMPACT global model with the HYBRID scheme. Aircraft soot emissions decrease the global average ice number concentration (N_i) by $-\mathrm{1.0}\pm \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{7}}$ m⁻² (−1 %) (over the entire column) due to the inhibition of homogeneous nucleation and lead to a radiative forcing of $-\mathrm{0.14}\pm \mathrm{0.07}$ W m⁻², while the increase in sulfur emissions increases the global average N_i by $\mathrm{7.3}\pm \mathrm{2.9}\times {\mathrm{10}}^{\mathrm{7}}$ m⁻² (5 %) due to the increase in homogeneous nucleation and leads to a radiative forcing of $-\mathrm{0.02}\pm \mathrm{0.06}$ W m⁻². The possible effects of aerosol and cloud feedbacks to the meteorological state in remote regions partly contribute to reduce the forcing and the change in N_i due to anthropogenic emissions. The radiative forcing due to all increased anthropogenic emissions from PI to PD is estimated to be $-\mathrm{0.20}\pm \mathrm{0.05}$ W m⁻². If newly formed secondary organic aerosols (SOAs) act as INPs and inhibit homogeneous nucleation, the N_i formed from heterogeneous nucleation is increased. As a result, the inclusion of INPs from SOA increases the change in N_i to $\mathrm{12.0}\pm \mathrm{2.3}\times {\mathrm{10}}^{\mathrm{7}}$ m⁻² (9 %) and increases (makes less negative) the anthropogenic forcing on cirrus clouds to $-\mathrm{0.04}\pm \mathrm{0.08}$ W m⁻² from PI to PD.

1 Introduction

Atmospheric aerosol loading has increased significantly since the preindustrial (PI) period, mainly due to anthropogenic emissions associated with the burning of fossil fuels and biomass. Most studies to date have focused on how the increase in anthropogenic aerosols impacts climate via warm clouds, thereby exerting a net cooling effect (Wang and Penner, 2009; Zhu et al., 2019; Gordon et al., 2016; IPCC, 2013). Compared to warm clouds, there has been much less attention paid to anthropogenic forcing as a result of changes to cirrus clouds, which is one of the least understood processes in the climate system (Fan et al., 2016). Cirrus clouds cover about 30 % of the Earth's area (Wang et al., 1996) and play an important role in the Earth's radiation budget and also influence global precipitation and the hydrologic cycle (Waliser et al., 2009; Hong et al., 2016; Matus and L'Ecuyer 2017). Ice particles in cirrus clouds are nucleated on aerosol particles, so that changes to the aerosol composition and loading may alter cirrus clouds by altering cloud microphysics, resulting in a cirrus cloud radiative forcing.

There are major uncertainties in calculating the radiative forcing of cirrus clouds using global climate models, in terms of both its magnitude (since PI) and its sign (Storelvmo, 2017). The ice particles in the cirrus clouds can form either by homogeneous freezing of solution droplets (or haze particles) (Koop et al., 2000) or by heterogeneous nucleation of ice-nucleating particles (INPs; Cantrell and Heymsfield, 2005). Supercooled aqueous solutions such as sulfate haze particles can form ice through homogeneous nucleation when the relative humidity with respect to ice (RH_i) is high (of the order of 150 %), which may be the dominant mechanism for the ice formation in cirrus clouds (Hendricks et al., 2011; Kuebbeler et al., 2014; Penner et al., 2018). However, heterogeneous ice nucleation of INPs formed from dust, soot, and other insoluble aerosols requires much lower RH_i, so that heterogeneous nucleation is able to occur in advance of homogeneous nucleation in a rising air parcel (Hoose and Möhler, 2012). As a result, heterogeneous and homogeneous ice formation compete for the available water vapor. Heterogeneous nucleation can lead to a significant reduction of the number of ice particles that form compared to homogeneous freezing because the number of INPs is much smaller than the number of haze particles. However, if additional INPs are added to a region where heterogeneous nucleation already dominates, an increase in ice crystal number is expected. Therefore, the radiative effect of aerosols on cirrus clouds could differ in both magnitude and sign depending on the competition between these two ice nucleation processes. Ice nucleation by INPs vs. haze freezing is determined by both the number of homogeneous and heterogeneous ice-nucleating particles and the updraft velocity or cooling rate.

Despite the relatively low level of understanding of ice nucleation, a few physically based parameterizations that treat the competition between homogeneous and heterogeneous nucleation have been developed in order to study the effect of ice nucleation in global climate models (Liu and Penner, 2005; Kärcher et al., 2006; Barahona and Nenes, 2008). The Liu and Penner (2005) parameterization (hereafter LP) is derived from fitting the simulation results of an adiabatically rising cloud parcel (Liu and Penner, 2005). The LP parameterization is only able to treat cases for which the updraft velocity is positive, so the evaporation of drops during downdrafts is neglected. The parameterization developed by Barahona and Nenes (2008) (hereafter BN) is derived from an analytical solution of the cloud parcel equations (Barahona and Nenes, 2008). The LP and BN parameterizations always show a similar trend when there is an increase in either the haze aerosol number concentrations or INPs (Shi and Liu, 2018), and they result in very similar ice number concentrations when the water vapor accommodation coefficient is set to 0.1 (Zhou et al., 2016). The Kärcher et al. (2006) parameterization (hereafter KL) explicitly calculates the evolution of ice supersaturation in a rising cloud parcel when different aerosol types freeze (Kärcher et al., 2006). The KL parameterization was used in previous studies on the effect of aerosol particles on cirrus clouds because it includes an explicit representation of the relevant physics (Penner et al., 2009, 2018), and Penner et al. (2018) added the capability to represent evaporation of water in downdrafts. However, in the KL parameterization, aerosol particles in different size bins will freeze chronologically from the largest size bin until the rate at which RH_i decreases by water vapor deposition equals the rate at which RH_i increases as a result of temperature decreases. Under this assumption, competition among different aerosol size bins for water deposition is not allowed. As a result, the homogeneous freezing of some particles in small size bins is underestimated in the KL parametrization (Liu and Shi, 2018). The KL parametrization results in a smaller sensitivity to increases in sulfate aerosol number than the LP and BN parametrizations except at very low sulfate number concentrations, while the three parameterizations have similar sensitivity to the number concentration of INPs (Shi and Liu, 2018).

Global numerical simulation experiments of aerosol effects on cirrus cloud formation have been carried out in a limited number of studies with different ice nucleation parameterizations and updraft treatments. Penner et al. (2009) used the KL and LP parameterizations to estimate the radiative forcing of aerosols on cirrus clouds using an offline ice nucleation and radiative transfer model. They found a negligible forcing from sulfate but a significant cooling (ranging from −0.38 to −0.56 W m⁻²) from surface-based and aircraft emissions of soot with the assumption that 100 % of soot particles are efficient INPs (Penner et al., 2009). As a result, the radiative forcing of all anthropogenic aerosols was estimated to be −0.53 to −0.67 W m⁻² using the LP and KL parameterizations. However, observations later indicated that only 0.01 % to 0.1 % of the less-hygroscopic soot from fossil fuels and biomass fires acts as good INPs at supersaturations near 140 % RH_i and low temperatures (Koehler et al., 2009; Pratt et al., 2011; Prenni et al., 2012). Gettelman et al. (2012) used the LP and BN parameterizations and calculated that the radiative forcing associated with aerosol effects on cirrus clouds is 0.27±0.10 W m⁻² (the uncertainty is the standard deviation of the interannual variations hereafter) as a consequence of increasing anthropogenic sulfur emissions (with no effect from soot) (Gettelman et al., 2012).

In addition to assumptions of the extent to which soot might act as an INP, a second source of uncertainty in the calculation of aerosol forcing in cirrus clouds is the treatment of the sub-grid-scale updraft velocity used in the nucleation scheme (Zhou et al., 2016). Penner et al. (2009) used a normal probability distribution with a standard deviation of 0.33 m s⁻¹ (Penner et al., 2009) while Wang and Penner (2010) used a single updraft velocity based on the standard deviation of mesoscale temperature fluctuations associated with gravity waves (Wang and Penner, 2010). Other models chose a sub-grid-scale updraft velocity associated with the predicted turbulent kinetic energy (Liu et al., 2012; Kärcher and Lohmann, 2002; Lohmann, 2002; Lohmann et al., 1999). Joos et al. (2008) added the effect of the contribution of orographic waves to the vertical velocity. Penner et al. (2018) first used a wave spectrum (instead of a constant updraft velocity) together with the KL parameterization to treat the formation of ice crystals. They used the equatorial spectrum of observed gravity waves presented by Podglajen et al. (2016) together with the seasonal and latitudinal variations determined by Gary (2006, 2008). They also varied the standard deviation from Podglajen et al. (2016) based on the vertical stratification of atmospheric stability, atmospheric density, and topography. However, the radiative forcing of sulfate as well as all anthropogenic aerosols were not explored due to the deficiencies in the KL parameterization (Liu and Shi, 2018).

Secondary organic aerosols (SOAs) have been shown to have a highly viscous semisolid or even glassy state at low temperatures and low RH_i in many experiments (Koop et al., 2011; Pajunoja et al., 2014; Renbaum-Wolff et al., 2013; Saukko et al., 2012). Observations also found SOA acting as INPs and in the ice crystal residues of cirrus clouds (Ignatius et al., 2016; Wagner et al., 2017; DeMott et al., 2003; Cziczo et al., 2013; Wilson et al., 2012). A peak in the number concentration of ultrafine particles was observed near 12 km in the Amazon and identified as primarily organic. Furthermore, a marker molecule indicated that a substantial fraction of the organics in aerosol-rich layers in the upper troposphere were associated with the oxidation of isoprene (Andreae et al., 2018). A modeling study that included the nucleation of new particles through organic nucleation predicted that there are a large number of accumulation mode SOA particles existing in the upper tropical troposphere which may be important for the ice nucleation (Zhu and Penner, 2019). SOA particles have a strong potential to act as INPs to form ice particles via heterogeneous freezing under the conditions conducive to ice formation in the upper troposphere (Knopf et al., 2018). However, the influence of SOA on cirrus clouds is not yet fully studied (but see Penner et al., 2018).

In this study, we combined the best features of the LP and KL parameterizations to develop a hybrid ice nucleation scheme that accounts for the changes in ice number concentrations in both the updrafts and downdrafts associated with a spectrum of gravity waves. Using a global climate model coupled with the new ice nucleation scheme, the radiative forcing of aircraft soot and sulfate was examined. Furthermore, the radiative forcing of anthropogenic aerosols on cirrus clouds since the PI time period was estimated both including and excluding the effect of changes in SOA. A global average negative anthropogenic forcing of $-\mathrm{0.20}\pm \mathrm{0.05}$ W m⁻² without SOA as a result of aerosol effects in cirrus clouds is suggested. The forcing is reduced to $-\mathrm{0.04}\pm \mathrm{0.08}$ W m⁻² when SOA is included.

Table 1 Summary of assumptions for aerosols to be effective INPs in the model.

2 Methodology

2.1 Model

We used the Community Earth System Model (CESM) version 1.2.2 (refer to http://www.cesm.ucar.edu/models/cesm1.2/, last access: 14 November 2019, for details) coupled to the University of Michigan IMPACT aerosol model (Liu et al., 2005, with updates as described herein) with a resolution of 1.9^∘ (longitude) $\times \mathrm{2.5}{}^{\circ }$ (latitude) and 30 vertical layers to simulate aerosols and their effects on cirrus clouds. This version of the IMPACT model simulates the number and mass of pure sulfate in three modes (i.e., nucleation, < 5 nm; Aitken, 5–50 nm; and accumulation, > 50 nm) and their interaction with the following 14 other aerosol species/types. Sulfate is the only aerosol participating in homogeneous ice nucleation in the model. Soot from fossil fuel and biofuel burning (fSoot) is simulated in three modes with different hygroscopicities according to the number of monolayers of sulfate on its surface (Yun et al., 2013) while soot from biomass burning (bSoot) is simulated in one mode. a total of 0.05 % of fSoot with fewer than one monolayer of sulfate and 0.1 % of fSoot coated with one to three monolayers of sulfate as well as 0.1 % of bSoot are assumed to be effective INPs. The hygroscopicity of fSoot and bSoot is determined by volume averaging the hygroscopicity of the underlying particles and the number of sulfate monolayers on the particles. Aircraft soot is simulated in two modes. The first mode has acted as an ice nuclei within contrails that subsequently evaporated (cSoot). The second mode, which was not an ice nuclei within contrails, is not considered to act as an INP in the model. The soot that has already been included in contrail ice is pre-activated. We assume the pre-activated aircraft soot coated with fewer than three monolayers of sulfate to be an INP similar to the treatment in Zhou and Penner (2014) (see also Mahrt et al., 2019). Dust and sea salt are each carried in four separate bins with varying radii. Dust with fewer than three monolayers of sulfate coating is used to form heterogeneous INPs in the model. This treatment is consistent with the results of field studies by DeMott et al. (2003), Cziczo et al. (2004), and Richardson et al. (2007). The assumptions for aerosols to be effective INPs in the model are summarized in Table 1. The aerosols simulated by the IMPACT model are only able to nucleate the initial ice crystal number concentration in cirrus clouds in the CESM model. Thereafter, the growth and sedimentation as well as evaporation of ice crystals follow the treatment in the CESM. In addition, the changes to cirrus clouds have feedbacks as a result of changes to the radiation budget, temperature, and formation of warm clouds, as simulated in the CESM model.

2.2 Ice nucleation parameterization

The LP parameterization is only able to calculate the ice nucleation in a rising parcel, but it is not able to predict the changes in the supersaturation or simulate the evaporation of ice in downdrafts. As a result, the scheme used by Penner et al. (2018) to treat gravity waves cannot be used with the LP parameterization as it was originally formulated. The KL scheme calculates the changes in the sub-grid-scale variation in RH_i in a cloud parcel as a result of updrafts or downdrafts and the growth or decay of ice particles. Unlike some schemes (e.g., Shi et al., 2015) which consider that the initial nucleation in an updraft takes place in the presence of ice from the previous time step, we assume the first parcel updraft within a general circulation model (GCM) time step does not carry any preexisting ice. Thereafter if ice forms it may either grow and decrease the supersaturation or evaporate, adding water vapor to the parcel. However, aerosols freeze in the order of size bins and this neglects the competition among different aerosol size bins, which results in an underestimation of the ice formed from aerosols in small size bins and a low sensitivity to the change of aerosol number (Liu and Shi, 2018). In this study, we combined the LP and KL parameterizations to develop a new ice nucleation scheme (hereafter HYBRID) to make use of their strengths and avoid their defects.

In the HYBRID scheme, the supersaturation (S_i) in the cloud parcel is calculated explicitly using the KL scheme so that ice particles are able to grow or decay throughout the time variations in the updrafts and downdrafts associated with gravity waves. S_i is calculated as a function of the updraft and aerosol concentrations at each grid. S_i is updated every second using

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}{S}_i}{\mathrm{d}t}}=a_{\mathrm{1}}{S}_{i}w-\left(a_{\mathrm{2}}+a_{\mathrm{3}}{S}_i\right){\int }_{\mathrm{0}}^{\mathrm{\infty }}\mathrm{d}{r}_{\mathrm{0}}{\displaystyle \frac{\mathrm{d}n}{\mathrm{d}{r}_{\mathrm{0}}}}{R}_{\mathrm{im}}\left(r_{\mathrm{0}}\right),\end{array}$$

where the parameter a₁ is given by $a_{\mathrm{1}}=\left(L_{\mathrm{s}}{M}_{\mathrm{w}}g\right)/\left(c_{\mathrm{p}}R{T}^{\mathrm{2}}\right)-Mg/\left(RT\right)$, with the molar mass of air M and water M_w, latent heat of sublimation L_s, constant of gravity g, heat capacity at constant pressure c_p, universal gas constant R, and air temperature T. w is the vertical velocity. $a_{\mathrm{2}}=\mathrm{1}/n_{\mathrm{sat}}$ with the water vapor number density at ice saturation n_sat. $a_{\mathrm{3}}=L_{\mathrm{s}}^{\mathrm{2}}{M}_{\mathrm{w}}{m}_{\mathrm{w}}/\left(c_{\mathrm{p}}pTM\right)$, with the mass of a water molecule m_w and the air pressure p. R_im is the monodisperse freezing–growth integral,

$$\begin{array}{}\text{(2)}& R_{\mathrm{im}}={\displaystyle \frac{\mathrm{4}\mathit{\pi }}{v}}{\int }_{-\mathrm{\infty }}^t\mathrm{d}{t}_{\mathrm{0}}{\dot{n}}_{\mathrm{i}}\left(t_{\mathrm{0}}\right)r_i^{\mathrm{2}}\left(t_{\mathrm{0}},t\right){\displaystyle \frac{\mathrm{d}{r}_i}{\mathrm{d}t}}\left(t_{\mathrm{0}},t\right),\end{array}$$

where v is the specific volume of a water molecule. $\mathrm{d}{t}_{\mathrm{0}}{\dot{n}}_{\mathrm{i}}\left(t_{\mathrm{0}}\right)$ is the number density of aerosol particles that nucleate ice and freeze within the time interval between t₀ and t₀+dt₀, r_i(t₀,t) is the radius of the spherical ice particle at time t that froze and commenced to grow at time t<t₀, and dr_i∕dt is the radial growth rate of that ice particle. In the HYBRID scheme, ${\dot{n}}_{\mathrm{i}}\left(t_{\mathrm{0}}\right)$ is determined using the LP parameterization.

A series of updraft velocities at each grid point were generated based on a fitted wave spectrum to the observed equatorial gravity waves from Podglajen et al. (2016). The standard deviation of this wave spectrum was extended to other latitudes and seasons by using the parameterization proposed by Gary (2006, 2008). It was extended vertically based on the static stability, atmospheric density, and topography. This parameterization of the wave spectrum associated with gravity waves is described in Penner et al. (2018).

When the updraft velocity is positive, the LP parameterization is used to calculate the increase in the ice number from homogeneous and/or heterogeneous freezing, so that the HYBRID scheme avoids the lack of sensitivity to changes in aerosol number in the KL parameterization when calculating the number of new ice particles. The LP parameterization is derived by fitting the results of a large set of parcel model simulations covering different conditions in the upper troposphere (Liu and Penner, 2005). Two separate regimes are identified by the sign of $T-\mathrm{6.07}\ln w+\mathrm{55.0}$ (where T is the temperature and w is the updraft velocity) to calculate the change of N_i due to homogeneous nucleation. When the sign is positive, the solution is in a fast-growth regime which is associated with higher T and lower w. The number concentration of new ice crystals (N_i or ${\dot{n}}_{\mathrm{i}}\left(t_{\mathrm{0}}\right)$ as in the above) is then calculated with the following equation:

$$\begin{array}{}\text{(3)}& N_{\mathrm{i}}=min\left\{\exp \left(a_{\mathrm{2}}\right)N_{\mathrm{a}}^{a_{\mathrm{1}}}\exp \left(bT\right)w^c,N_{\mathrm{a}}\right\},\end{array}$$

where $b=b_{\mathrm{1}}\ln N_{\mathrm{a}}+b_{\mathrm{2}}$, and $c=c_{\mathrm{1}}\ln N_{\mathrm{a}}+c_{\mathrm{2}}$. N_a is the number concentration of sulfate in the Aitken and accumulation modes. The coefficients a₁, a₂, b₁, b₂, b₃, c₁, and c₂ are constant and can be found in Table 1 of Liu and Penner (2005). For lower T and higher w (the slow-growth regime), the following equation is applied to calculate N_i:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{N}_{\mathrm{i}}& =min\left\{\exp \left[a_{\mathrm{2}}+\left(b_{\mathrm{2}}+b_{\mathrm{3}}\ln w\right)T+c_{\mathrm{2}}\ln w\right]\right.\\ & \left.N_{\mathrm{a}}^{a_{\mathrm{1}}+b_{\mathrm{1}}T+c_{\mathrm{1}}\ln w},N_{\mathrm{a}}\right\},\end{array}\end{array}$$

where the coefficients a₁, a₂, a₃, b₁, b₂, b₃, c₁, and c₂ are again listed in Table 1 of Liu and Penner (2005) and are different from those in the fast-growth regime. The number concentration of N_i from INPs in the heterogeneous nucleation regime is given as

$$\begin{array}{}\text{(5)}& N_{\mathrm{i}}=min\left\{\exp \left(a_{\mathrm{22}}\right)N_{\mathrm{INP}}^{b_{\mathrm{22}}}\exp \left(bT\right)w^c,N_{\mathrm{INP}}\right\},\end{array}$$

where $b=\left(a_{\mathrm{11}}+b_{\mathrm{11}}\ln N_{\mathrm{INP}}\right)\ln w+\left(a_{\mathrm{12}}+b_{\mathrm{12}}\ln N_{\mathrm{INP}}\right)$ and $c=a_{\mathrm{21}}+b_{\mathrm{21}}\ln N_{\mathrm{INP}}$. N_INP is the number concentration of total INPs. The coefficients a₁₁, a₁₂, a₂₁, a₂₂, b₁₁, b₁₂, b₂₁, and b₂₂ can be found in Sect. 4.2 of Liu and Penner (2005). When the updraft velocity is low and temperature is high, heterogeneous ice nucleation takes place initially and depletes the water vapor in the parcel so that homogeneous ice freezing never occurs. The threshold temperature T_c for heterogeneous nucleation only is given by

$$\begin{array}{}\text{(6)}& T_c>a\ln \left(w\right)+b,\end{array}$$

where $a=-\mathrm{1.4938}\ln \left(N_{\mathrm{INP}}\right)+\mathrm{12.884}$; $b=-\mathrm{10.41}\ln \left(N_{\mathrm{INP}}\right)-\mathrm{67.69}$. When the regime is in a transition from heterogeneous-dominated to homogeneous-dominated regimes, the total ice number concentration from nucleation can be higher than the ice concentration from only heterogeneous nucleation but lower than that from the pure homogeneous nucleation case. Then, N_i is interpolated from

$$\begin{array}{}\text{(7)}& N_{\mathrm{i}}=N_{\mathrm{Het}}{\left({\displaystyle \frac{N_{\mathrm{Het}}}{N_{\mathrm{Hom}}}}\right)}^{\frac{N_{\mathrm{INP}}-N_{\mathrm{c}}}{\mathrm{0.9}{N}_{\mathrm{c}}}},\end{array}$$

where N_Het is the ice number from pure heterogeneous nucleation, N_Hom is the ice number from pure homogeneous nucleation, N_INP is the number concentration of INPs, and N_c is the critical number concentration of INPs for the heterogeneous nucleation-only regime.

Based on the method outlined above, the HYBRID scheme calculates the increase in N_i using LP parameterization. The new ice crystals from nucleation either grow or decay with consumption or evaporation of water vapor and therefore change S_i, which is determined using the KL parameterization. The changes in S_i then influence which particles are able to nucleate, forming ice crystals.

We define cirrus clouds for which the effects of aerosols are defined or calculated as all large-scale clouds formed at temperatures < −35^∘. Cirrus clouds at these temperatures include anvil cirrus that are formed by the outflow from deep convection as well as large-scale cirrus formed by in situ gravity waves. The detrained ice crystal number concentration in anvils is calculated from the detrained ice mass by assuming a spherical particle with a constant volume-mean radius, which is approximated as $\mathrm{3}{\mathit{\rho }}_{\mathrm{0}}Q/(\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{i}}{r}_{\mathrm{iv}}^{\mathrm{3}}$) following Lohmann (2002). ρ_i is the ice crystal density, ρ₀ is the air density, r_iv is the volume mean radius determined from a temperature-dependent lookup table (Kristjánsson et al., 2000; Boville et al., 2006), and Q is the detrainment rate of cloud water mass diagnosed from the convection parameterization. The new clouds generated by convective detrainment are assumed to be at saturation with respect to ice. In doing this, anvil clouds and in situ cirrus compete for the available water vapor within a grid box. When anvil clouds are formed due to convective detrainment, it reduces the saturation ratio in the clear-sky portion of a grid and can potentially reduce the frequency of in situ large-scale cirrus formation (Wang and Penner, 2010; Wang et al., 2014). We only calculate N_i as a result of the nucleation of aerosol in large-scale cirrus, so that when anvils occur in a grid box, we average the concentrations to determine the total ice number concentration in cirrus clouds. Anthropogenic emissions contribute to the change in the number concentration of ice crystals in large-scale cirrus cloud, but these are then averaged with the crystals in anvils.

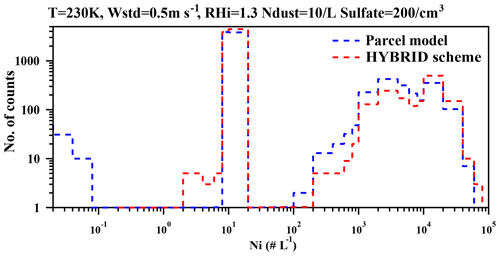
Figure 1 Histogram of predicted ice number concentration for 10 000 simulations using an adiabatic parcel model (blue dashed line) and a box model using the HYBRID scheme (red dashed line). Wstd is the standard deviation of the assumed pdf of updraft velocities, while Ndust and Sulfate are the assumed dust and sulfate number concentrations.

Evaluation of the HYBRID scheme

In order to examine the ability of the HYBRID ice nucleation scheme to simulate ice number concentration, the results from a box model using the HYBRID scheme are compared with those from an adiabatic parcel model under the same simulation conditions. The adiabatic parcel model was that used to generate the LP parameterization and was introduced in Liu and Penner (2005). The two models are run for 30 min for each simulation, which is the time step used in the CESM. During the 30 min, the updraft velocity is updated every 2.2 min as recommended by Podglajen et al. (2016). The ice number concentrations after the 30 min simulation from the two models are compared. We ran both the adiabatic parcel model and the HYBRID box model using a constant updraft velocity for each 2.2 min interval. When the velocity is positive ice crystals form and grow in the HYBRID box model as described above. For downdrafts, if the supersaturation is below 100 %, the two models use the same method to simulate the evaporation of any existing ice particles, which is also the same method used in the global model as suggested in Kärcher et al. (2006). The scheme used here for the HYBRID box model is the same as the HYBRID scheme used in the global model. Note that the final interval within each 30 min simulation is shortened in order to match the treatment used in the CESM/IMPACT model which uses a 30 min time step. When run within the CESM model, this final ice number concentration is then passed back to the CESM model after this 30 min interval.

The updraft- and downdraft-associated gravity waves are determined from a Laplace distribution as suggested by the fit to the observed gravity waves by Podglajen et al. (2016). We conducted 10 000 simulations using a random selection of the updrafts and downdrafts for each model. Both models use the same selection of updrafts and downdrafts in each simulation. We set up an initial condition with a temperature of 230 K, the standard deviation for the updraft velocities was 0.5 m s⁻¹, and the initial RH_i was 130 %. The sulfate number concentration was set to 0.2 L⁻¹ while the dust concentration was 10 L⁻¹. These particles then participate in either homogeneous nucleation or heterogeneous immersion nucleation.

Figure 1 shows a histogram of the predicted ice number concentration (N_i) for 10 000 simulations of the adiabatic parcel model and the box model using the HYBRID scheme. Two populations of N_i are shown in Fig. 1. The lower population (with concentrations of the order of 10 L⁻¹ or less) represents primarily heterogeneous nucleation on dust particles, while the higher population (with concentrations of the order of 10² L⁻¹ or more) represents primarily homogeneous nucleation on sulfate aerosols. The results in the simulations dominated by heterogeneous nucleation are mostly similar for the two models, although the HYBRID scheme overestimates the N_i between 1 and 10 L⁻¹ when the results from the adiabatic parcel model are less than 10⁻¹ L⁻¹ for some of these same simulations. The average N_i from heterogeneous nucleation over 10 000 simulations from the adiabatic parcel model is 9.40±2.31 L⁻¹, while that from the HYBRID scheme is 9.52±2.08 L⁻¹.

The box model using the HYBRID scheme predicts larger N_i from homogeneous nucleation than the parcel model in the 88 % of simulations where homogeneous nucleation occurs. There are more simulations using the HYBRID scheme that predict larger N_i from homogeneous nucleation than the parcel model as indicated by a larger number of counts of large N_i (10⁴ L⁻¹ or more) in Fig. 1. The HYBRID scheme uses the LP parameterization for every small time step of 2.2 min. Since the LP parameterization was built using the largest N_i in an ascending parcel after 30 min, there is a tendency for the HYBRID scheme to overpredict N_i. The average N_i from homogeneous nucleation over the 10 000 simulations in the two models is 1.41±4.23 L⁻¹ from the parcel model, while it is 1.52±4.83 L⁻¹ from the HYBRID model. The HYBRID scheme overestimates the N_i from homogeneous nucleation by 7.4 %, which dominates the difference in total N_i between two models. Overall, the average total N_i over the 10 000 simulations is 1.53±4.83 L⁻¹ using the HYBRID scheme, which is 7.3 % larger than the result from the parcel model (1.42±4.23 L⁻¹). We also examined the difference between the above case when sulfate was 200 cm⁻³ compared to when sulfate was 20 cm⁻³, and the difference was within 7.2 % of that using the full parcel model. Although the HYBRID scheme predicts a somewhat larger number of nucleated ice particles, on average, the results are reasonable compared to the results from the parcel model.

Table 2 Description of cases.

Note: SOA: secondary organic aerosol; INP: ice-nucleating particle.

2.3 Experiments with the global model

We performed a series of model experiments in which different emissions of aerosols and aerosol precursors are used. Table 2 provides a summary of these experiments. The base case (PD_Base) uses emissions for the present day (PD, for the year 2000) for anthropogenic sulfur and soot from fossil fuel adopted from the Community Emission Data System (CEDS) (Hoesly et al., 2018). Emissions from van Marle et al. (2017) are adopted for biomass burning emissions. These emissions are the same as the emissions data sets used for the CMIP6 simulations. The year 2000 emissions are used for all years of our simulation. We included soot from aircraft for 2006 based on the Aviation Environment Design Tool (AEDT) data set (Barrett et al., 2010). The AEDT data are presumed to be more accurate than the CMIP6 aircraft emissions since they were developed based on the original flight tracks of each of 31 million commercial flights worldwide (Wilkerson et al., 2010). The dimethylsulfide (DMS) emissions from the ocean are assumed constant in the PD and PI periods (Tilmes et al., 2016). The emission of dust uses the scheme from Zender et al. (2003). In a sensitivity experiment (PI_cSoot), the emission of cSoot is removed from PD_Base to examine its impact on ice number concentration and radiative forcing. We also set a case (PI_SO4) with the emission of anthropogenic sulfur changed to PI (≈1750) to calculate the radiative forcing of sulfur. The case PI_ALL set all emissions to those of the PI period (≈1750) to examine the radiative forcing of all anthropogenic aerosols on cirrus cloud. Additionally, we set up two experiments to examine the effect of SOA as an INP on anthropogenic forcing in cirrus clouds. The cases PD_SOA and PI_SOA add newly nucleated SOA particles that have grown to the accumulation mode as additional INPs to the cases of PD_Base and PI_ALL. The cases including SOA in the PD and PI read in the explicit number concentration of newly formed SOA in the accumulation mode nucleated from highly oxygenated organic molecules (HOMs) that form from the oxidation of α-pinene. The nucleated SOA particles grow by deposition and coagulation of sulfuric acid as well as the oxidation products of isoprene, α-pinene, limonene, and aromatics, which are in the aerosol phase. This SOA was simulated using the version of the CESM/IMPACT model outlined in Zhu et al. (2017, 2019) and Zhu and Penner (2019, 2020). The SOA that meets the requirements of the glass transition temperature and RH_i calculated using the equations in Wang et al. (2012) acts as an effective heterogeneous INP.

The changes in aerosol emissions only influence the number concentration of ice nuclei in the CESM and thereby give the indirect radiative effect in cirrus clouds. The direct radiative effect caused by the change of aerosols is not included. Clear-sky radiative forcing in this study is not associated with direct aerosol radiative forcing but is rather mainly due to changes in water vapor which leads to changes in the clear-sky longwave radiation (Wang and Penner, 2010). All cases were run with prescribed sea surface temperatures for the present day, and winds were nudged towards ECMWF reanalysis data for the years 2005–2011 using a nudging time of 6 h (Zhang et al., 2014). The data for the last 6 years were used for analysis in this study.

3 Results from the global model

3.1 Ice number concentrations

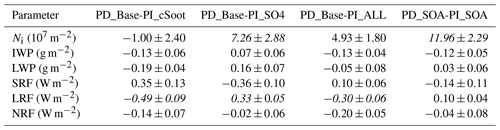
The predicted N_i in the PD_Base case is compared with the observed N_i reported by Krämer et al. (2009, 2020) in Fig. S1 in the Supplement. Data from the model have been selected to have ice water mixing ratios > 10⁻⁸ kg kg⁻¹ to match values seen in the in situ observations (Krämer et al., 2016). The global model using the HYBRID scheme is able to do a reasonable job in predicting N_i with the difference in the median value between the simulation and observation less than 50 % for all temperatures except for the high concentrations seen between 197 and 213 K. The model predicts ∼3 times higher N_i on average compared to the observations between 197 and 213 K. Although the comparison of ice number concentration between our model and observation has not improved significantly compared to that shown by Penner et al. (2018), the new nucleation scheme improves the ability of nucleation to occur on small-sized particles, since it avoids the calculation of ice nucleation chronologically from large sizes to small sizes used in the KL scheme, which results in an underestimation of ice crystals formed from small-sized particles.

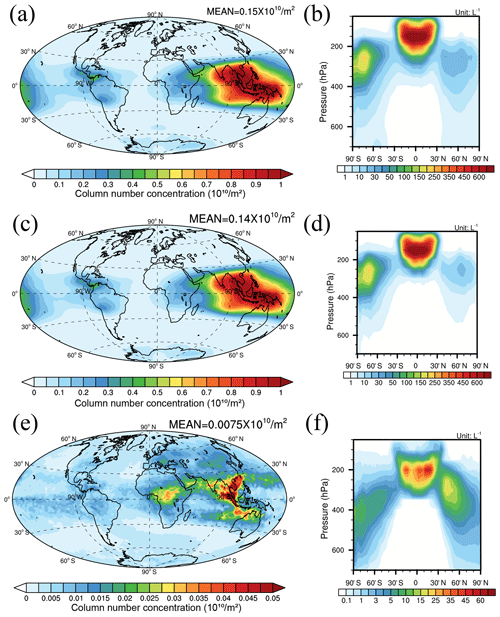
Figure 2 The vertically integrated total N_i in the PD_Base case (a), N_i from homogeneous nucleation (c), and N_i from heterogeneous nucleation (e). The zonal average plots of N_i in the PD_Base case (b), N_i from homogeneous nucleation (d), and N_i from heterogeneous nucleation (f). Note: the vertical axes in (b), (d), and (f) are in hybrid pressure levels.

The global average N_i in the PD_Base is 0.15×10¹⁰ m⁻² with the largest N_i in the tropics of the eastern hemisphere (Fig. 2a). Most ice particles nucleate in the upper troposphere (150–200 hPa) in the tropics, while some ice nucleation occurs in the lower troposphere (around 300 hPa) in the polar regions (Fig. 2b). The ice particles formed from homogeneous nucleation dominate the total N_i in most regions over the world (Fig. S2a) and are responsible for ∼95 % of global average N_i (Fig. 2c). The large number concentration of sulfate in the Aitken and accumulation modes in the upper troposphere over the west Pacific Ocean and north Indian Ocean contributes to the remarkably large N_i in the tropical eastern hemisphere. Heterogeneous nucleation dominates the N_i in the northern middle–high latitudes where anthropogenic soot emission is high (Fig. S2a), although the N_i from heterogeneous nucleation is high in the tropics (Fig. 2e). Homogeneous nucleation mostly occurs in the upper troposphere (around 200 hPa in the tropics and around 300 hPa in the extratropical regions), while heterogeneous nucleation is an important contributor to N_i in the middle and lower troposphere (Fig. S2b). Although the N_i from homogeneous nucleation is high, the occurrence frequency of homogeneous nucleation (calculated as the ratio of the time steps when homogeneous nucleation occurs to all time steps with nucleation occurring) is up to ∼20 % in the tropics and < 5 % in most other regions (Fig. S2c). Due to the lack of the effect of orographic waves on ice nucleation, the observed increases in ice number over orography, particularly over the Andes, Rockies, Antarctic mountains, and Greenland, are not shown in Fig. 2.

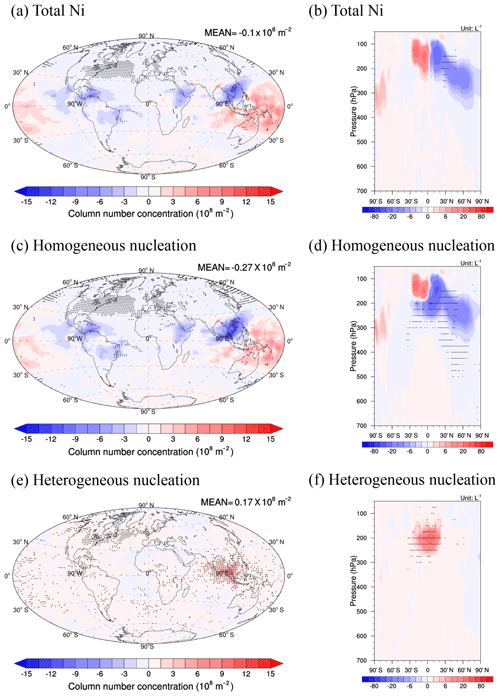
Figure 3 The annual average change in column number concentration (a, c, e) and zonal average number concentration (b, d, f) of total ice (a, b), ice from homogeneous nucleation (c, d), and ice from heterogeneous nucleation (e, f) for the difference between the PD_Base and PI_cSoot cases. Differences significant at the 90 % level according to a Student's t test are depicted by points.

The competition between the heterogeneous INPs and homogeneous haze particles determines the change in N_i between the PD and PI periods. We set up three sensitivity cases to separately examine the effects of the emission of cSoot for aircraft, anthropogenic sulfur, and all anthropogenic emissions on N_i. INPs always nucleate prior to homogeneous nucleation in a rising air parcel, so they consume the available water vapor and inhibit homogeneous freezing when added to regions dominated by homogeneous nucleation. The N_i formed from heterogeneous nucleation increases significantly around 200 hPa over the world due to the inclusion of INPs from cSoot, especially near Southeast Asia (Fig. 3e, f). Simultaneously, homogeneous nucleation is inhibited significantly around 200 hPa in Southeast Asia and other tropical regions (Fig. 3c, d). The emissions of aircraft soot that form contrails peak near 200 hPa with the spatial distribution shown in Fig. 1a in Zhou and Penner (2014). Although the emissions of aircraft soot are large in the midlatitudes, the effect of inhibiting homogeneous nucleation as a result of adding the heterogeneous nucleation is large in the tropics (Fig. 3c). That is because of the largest number concentration of ice nuclei from homogeneous nucleation in the tropics as shown in Fig. 2c. Due to the much larger decrease in N_i from homogeneous nucleation than the increase in N_i from heterogeneous nucleation, the global average N_i is decreased by 0.1×10⁸ m⁻² (1 %) when including the emission of aircraft soot (Fig. 3a). The change in N_i due to cSoot is small with a significant change only over the North Atlantic Ocean and east coastal regions in North America (Fig. 3a).

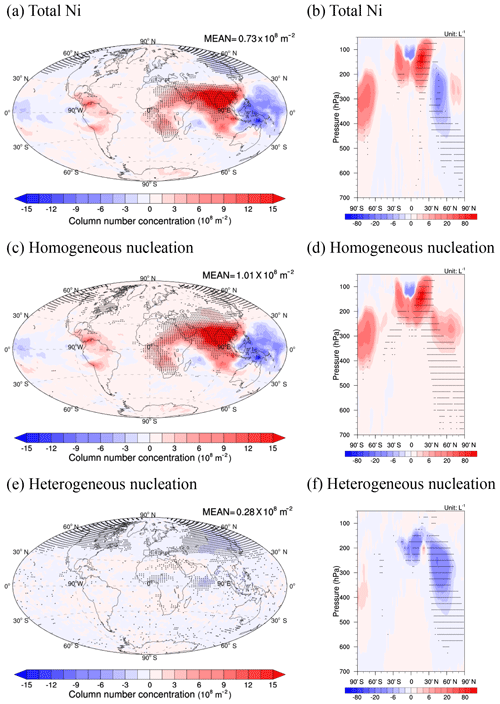
Figure 4 As in Fig. 3 but for the difference between the PD_Base and PI_SO4 cases. Differences significant at the 90 % level according to a Student's t test are depicted by points.

In contrast to the case of aircraft soot, the increase in the sulfur emissions from PI to PD leads to a large increase in N_i from homogeneous nucleation in most regions, which causes an increase of 1.01×10⁸ m⁻² in the global average N_i (Fig. 4c). The increase in N_i from homogeneous nucleation contributes to the significant increase in N_i near 150 hPa over South Asia, Africa, and the north Indian Ocean (Fig. 4a). The decrease in N_i from heterogeneous nucleation offsets some of the increase in N_i from homogeneous nucleation and leads to a significant decrease in N_i near 300 hPa over the North Pacific Ocean (Fig. 4a). In total, the global average N_i is increased by 0.73×10⁸ m⁻² (5 %) due to the increase in sulfur emissions.

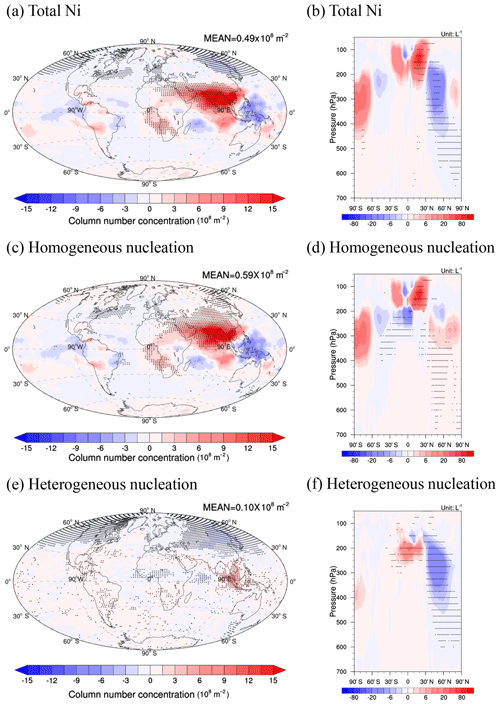
Figure 5 As in Fig. 3 but for the difference between the PD_Base and PI_ALL cases. Differences significant at the 90 % level according to a Student's t test are depicted by points.

The change in N_i from PI to PD due to all anthropogenic emissions is a balance among the effects of increasing INPs from surface emissions and aircraft soot as well as the increase in haze particles. The effect of all anthropogenic emissions on N_i is mostly dominated by the increase in N_i from homogeneous nucleation caused by the increase in sulfur emissions, but homogeneous nucleation is inhibited somewhat by increased INPs from soot (compare Figs. 5c and 4c). As a result, the global average increase in N_i from homogeneous nucleation between PD_Base and PI_ALL is only 58 % of that between PD_Base and PI_SO4. The change in N_i from heterogeneous nucleation is decreased in the midlatitudes to high latitudes of the Northern Hemisphere (NH) from PD_Base to PI_ALL similar to the decrease from PD_Base to PI_SO4 (Fig. 5e, f). However, the increase in INPs from soot near Southeast Asia leads to a small increase in N_i from heterogeneous nucleation there (Fig. 5e). In total, the increase in all anthropogenic emissions causes a significant increase in N_i in South Asia and the north Indian Ocean while a significant decrease in N_i is found in midlatitude regions and some Arctic regions, resulting in 0.49×10⁸ m⁻² (3 %) more N_i from PI to PD for the global average.

It is conspicuous that sulfur and aircraft soot emissions have effects with different signs for the change in N_i (Figs. 3a, 4a). Generally, INPs from aircraft soot decrease N_i due to the suppression of homogeneous nucleation in the regions dominated by homogeneous nucleation, while the increase in sulfur emissions increases N_i in these same regions due to the enhancement of homogeneous nucleation. However, the changes to N_i have opposite signs in the west Pacific Ocean off the coast of Southeast Asia, where the homogeneous nucleation is most active (Fig. 2c). We attribute this to the possible effect of aerosol and cloud feedbacks to the meteorological state. When including aircraft soot, the temperature is decreased (Fig. S3b) and the RH_i is increased (Fig. S3a) around 150 hPa over the west Pacific Ocean, where N_i from homogeneous nucleation increases a lot (Fig. 3c). The decrease in temperature is beneficial to homogeneous nucleation. Meanwhile, the emission of aircraft soot is very low in the west Pacific Ocean due to the lack of flight routes there (refer to Fig. 1a in Zhou and Penner, 2014), so that the effect of aircraft soot on the suppression of homogeneous nucleation is weak in that region (Fig. 3e). As a result, the N_i from homogeneous nucleation is increased, which determines the increase in the N_i near 150 hPa over the west Pacific Ocean due to the emission of aircraft soot (Fig. 3a). Similarly, when the sulfur emissions are increased from PI to PD, the change in cirrus clouds influences the meteorological state. A large decrease in RH_i at 150 hPa is found in the west Pacific Ocean (Fig. S4a), so that the occurrence frequency of homogeneous nucleation decreases when sulfur emissions increase (Fig. S4d). Additionally, the temperature at 150 hPa increases over the world (Fig. S4b), which also contributes partly to the decrease in the occurrence frequency of homogeneous nucleation. Although global sulfur emissions increase sharply from PI (2.2 Tg S yr⁻¹) to PD (55 Tg S yr⁻¹), the anthropogenic emissions mainly occur on the mainland with much smaller emissions over the ocean even though the sulfur emissions from shipping increase by 6.4 Tg S yr⁻¹. The column number concentration of sulfate having the potential to freeze homogeneously does not increase significantly over most ocean regions (Fig. S4c), so that the decrease in the occurrence frequency of homogeneous nucleation leads to a decrease in N_i from homogeneous nucleation over the west Pacific Ocean (Fig. 4c). The increase in the temperature in the upper troposphere over the world (Fig. S4b) also partly explains the decrease in N_i from heterogeneous nucleation when only sulfur emissions increase (Fig. 4e). The feedbacks to the meteorological state in remote regions always have an opposite effect on the changes in N_i compared to the effect in regions with large anthropogenic emissions. These meteorological feedbacks partly reduce the changes in global average N_i due to anthropogenic emissions. Although these opposite changes in N_i due to meteorological feedbacks are not statistically significant (Figs. 3a, 4a, 5a), our conjecture based on the model results indicates that the meteorological feedbacks caused by the radiative effects of aerosols might contribute to the change in N_i in remote regions. These important feedback processes need to be investigated further.

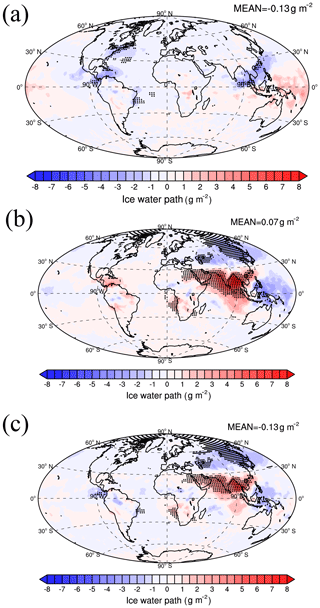
Figure 6 Annual mean plots of the change in vertically integrated averaged ice water path for the difference between the PD_Base and PI_cSoot cases (a), PD_Base and PI_SO4 cases (b), and PD_Base and PI_ALL cases (c). Differences significant at the 90 % level according to a Student's t test are depicted by points.

Table 3 Forcing and cloud changes associated with changes in aircraft soot, sulfur, and all anthropogenic aerosols.

Note: Differences significant at the 90 % level according to a Student's t test are italic.

3.2 Radiative forcing

The decrease in N_i in the upper troposphere usually leads to an increase in the size of ice particles, which promotes the gravitational removal and formation of snow, causing a decrease in the ice water path (IWP) and vice versa. As a result, the change in IWP is mainly determined by the change in N_i and has a similar geographic pattern. The global average IWP in the model is 14.6 g m⁻² for the PD_Base case, which is lower than that observed in different CloudSat and CALIPSO analyses (21–28 g m⁻²) (Li et al., 2012). We used a cutoff diameter of 250 µm to move cloud ice to snow. A cutoff diameter of 400 µm in the model almost doubles the IWP in our model (compare IWP of dbfc_mg10 and dbfc in Table 3 in Penner et al., 2018). The emission of aircraft soot leads to a significant decrease in IWP in Southeast Asia and the east coast of North America, caused by the inhibition of homogeneous nucleation (Fig. 6a). As shown in Fig. 6b, the increase in the sulfur emissions leads to a significant increase in IWP in the north Indian Ocean due to the changes in N_i from homogeneous nucleation. The decrease in IWP in East Asia and the Arctic is attributed to the decrease in N_i from heterogeneous nucleation (Fig. 6b). The geographic pattern of changes in IWP due to the change in all anthropogenic emissions from PI to PD is dominated by the changes in IWP caused by the changes in sulfur emissions (compare Fig. 6b and c). However, the increase in IWP in tropical regions is smaller, and the decrease in IWP in the middle and high latitudes of the NH is more negative in the PD_Base-PI_ALL case compared to the PD_Base-PI_SO4 case because of the inhibition of homogeneous nucleation caused by the increase in the emission of surface and aircraft soot. As a result, although the geographical pattern of the changes in IWP is similar for the PD_Base-PI_ALL and PD_ Base-PI_SO4 cases, the magnitude of changes in the global average IWP switches from positive (0.07 g m⁻² for PD_Base-PI_SO4, Fig. 6b) to negative (−0.13 g m⁻² for PD_Base-PI_ALL, Fig. 6c).

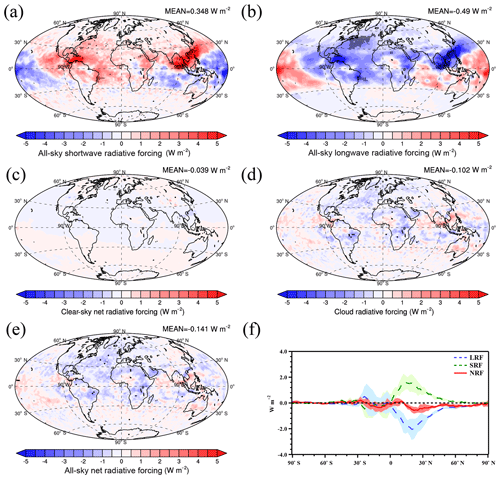
Figure 7 Annual mean plots of all-sky shortwave radiative forcing (a), all-sky longwave radiative forcing (b), clear-sky net radiative forcing (c), cloud radiative forcing (d), and all-sky net radiative forcing (e) as well as all-sky longwave radiative forcing (f, LRF, blue dashed line), all-sky shortwave radiative forcing (f, SRF, green dashed line), and all-sky net radiative forcing (f, NRF, red solid line) versus latitude for the difference between the PD_Base and PI_cSoot cases. Differences significant at the 90 % level according to a Student's t test are depicted by points. The shading in (f) represents 1 standard deviation of the interannual variation over 6 years.

The changes in N_i and IWP lead to a change in the cirrus cloud fraction and also feedback to produce a change in the lapse rate of temperature, which has an effect on the delivery of water vapor and the strength of convection, and these changes influence the formation and lifetime of liquid water clouds. The liquid water path (LWP) changes due to these complex dynamical feedbacks are shown in Fig. S5. The changes in global average LWP are all less than 0.5 % with only a small number of grids with a significant change. The changes in the shortwave and longwave radiative fluxes are determined by the changes in LWP and IWP (as well as the change in N_i), although they are dominated by the change in IWP. The changes in aerosol only have a direct effect on the cirrus clouds in our model, while the changes in warm clouds are caused by feedbacks due to the change in cirrus clouds. The changes in the all-sky shortwave radiative forcing (SRF) and longwave radiative forcing (LRF) at the top of the atmosphere (TOA) generally follow the changes in IWP but have the opposite sign (Figs. 7, 8, and 9). The changes in LWP could either enhance or offset the effect of changes in IWP on the radiative fluxes depending on whether the sign of the changes in IWP and LWP reinforces or not. The emission of cSoot leads to a positive global average SRF due to the significant increase in shortwave radiative fluxes off the coast of East Asia and over the north Indian Ocean, while the significant decrease in the longwave radiative fluxes over East Asia, the north Indian Ocean, and North Atlantic Ocean contribute to a negative global average LRF mostly due to the decrease in the global average IWP (Fig. 7). On the other hand, the increase in sulfur emissions causes a negative global average SRF largely due to the significant decrease over South Asia, North Africa, and the north Indian Ocean (Fig. 8a). Simultaneously, the increase in the IWP in these regions leads to a significant increase in longwave radiative fluxes resulting in a positive global average LRF, although the LRF is significantly negative in the middle to high latitudes over the east coast of Asia (Fig. 8b). The changes in the SRF and LRF due to the increase in all anthropogenic emissions have a similar geographic pattern to those caused by the increase in sulfur emissions but the global average forcings have opposite signs (compare Figs. 8c, d and 9c, d). This is due to the decrease in the global average IWP caused by the inhibition of homogeneous nucleation as a result of the increased emissions of soot.

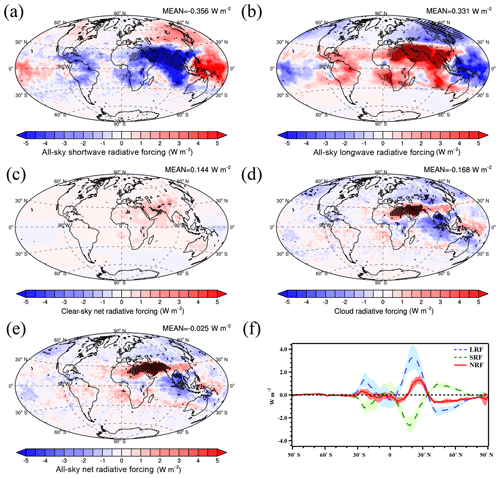
Figure 8 As in Fig. 7 but for the difference between the PD_Base and PI_SO4 cases. Differences significant at the 90 % level according to a Student's t test are depicted by points. The shading in (f) represents 1 standard deviation of the interannual variation over 6 years.

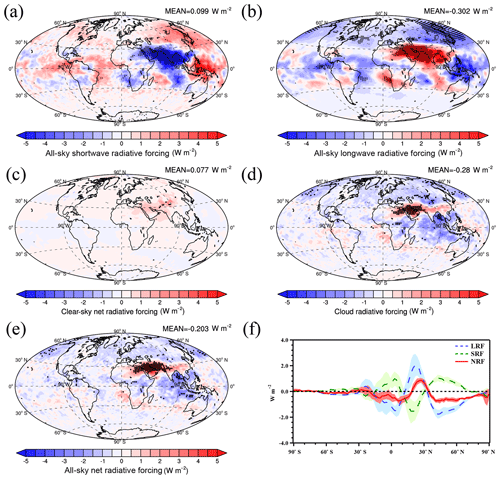
Figure 9 As in Fig. 7 but for the difference between the PD_Base and PI_ALL cases. Differences significant at the 90 % level according to a Student's t test are depicted by points. The shading in (f) represents 1 standard deviation of the interannual variation over 6 years.

The total all-sky net forcing (NRF) is determined by the balance between SRF and LRF. The radiative effects in cirrus clouds are dominated by longwave radiative effects. However, it is still possible that the radiative forcing due to changes in N_i in cirrus clouds in some regions is dominated by SRF due to the combined effects on shortwave forcing from the changes in cirrus clouds together with changes to warm clouds caused by feedbacks. The emission of cSoot has a negative global average NRF of $-\mathrm{0.14}\pm \mathrm{0.07}$ W m⁻² in cirrus clouds with only a few significant grids, although the SRF and LRF due to cSoot are significant in some coastal regions off of East and South Asia (Fig. 7). The NRF due to cSoot is most negative around 30^∘ N where the emission of aircraft soot is high, while there is a small positive forcing around 10^∘ N dominated by SRF (Fig. 7f). The NRF is the sum of the clear-sky net radiative forcing (NRFC) and the cloud radiative forcing (CRF) caused by changes in cSoot. The global average CRF is $-\mathrm{0.10}\pm \mathrm{0.07}$ W m⁻², which dominates over the NRFC and explains 72 % of the NRF of cSoot (Fig. 7c, d).

Although the increase in sulfur emissions from PI to PD leads to an increase in the global average N_i and IWP, the global average NRF due to sulfur emissions is near zero, $-\mathrm{0.02}\pm \mathrm{0.06}$ W m⁻². The NRF due to sulfur emissions is significant and positive (up to 7.1 W m⁻²) around 30^∘ N in South Asia and North Africa (Fig. 8e). The NRF is negative over most middle to high latitudes of the NH, which is attributed to the decrease in LRF associated with the feedback to the decrease in N_i from heterogeneous nucleation there. However, the significant negative NRF in the north Indian Ocean and positive NRF in the west Pacific Ocean are dominated by the change in SRF (Fig. 8a, e). The LWP increases in the north Indian Ocean as a result of dynamic feedbacks from the changes in the cirrus clouds, leading to the significant SRF together with the changes in IWP and cirrus clouds. The negative NRF in the north Indian Ocean and middle to high latitudes of the NH offset the positive NRF around 30^∘ N (Fig. 8e). The significant negative NRF over the north Indian Ocean is dominated by the CRF, while the significant positive NRF over South Asia and North Africa is the combined effect of CRF and NRFC. The global average CRF is $-\mathrm{0.17}\pm \mathrm{0.06}$ W m⁻² and determines the sign of the global average NRF. However, the global average NRFC is 0.14±0.02 W m⁻² with a wide area of positive values over the NH, which offsets most of CRF.

Compared to the NRF due to the increased sulfur emissions, the NRF is less positive in South Asia and more negative over the middle to high latitudes of the NH and the north Indian Ocean when including the increased emissions of surface and aircraft soot as well as sulfur together (Fig. 9e). In the middle to high latitudes of the Southern Hemisphere (SH), SRF and LRF always cancel each other so that NRF is negligible. As a result, the global average NRF due to all the increased anthropogenic emissions from PI to PD is $-\mathrm{0.20}\pm \mathrm{0.05}$ W m⁻², which is mainly dominated by the changes in LRF (Fig. 9e, f). Both the CRF and NRFC due to all anthropogenic emissions are largely explained by the CRF and NRFC caused by change in emission of sulfur (compare Figs. 9c, d and 8c, d). The global average CRF is $-\mathrm{0.28}\pm \mathrm{0.04}$ W m⁻² due to the changes in all anthropogenic emissions, while the NRFC is slightly positive (0.08±0.02 W m⁻²).

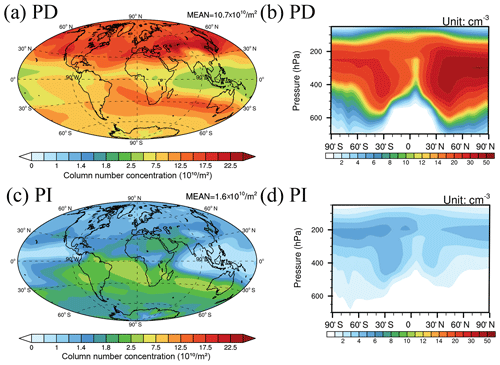
Figure 10 The vertically integrated number of INPs (a, c) and zonal average plots of INPs (b, d) from SOA in the PD_SOA (a, b) and PI_SOA (c, d) cases.

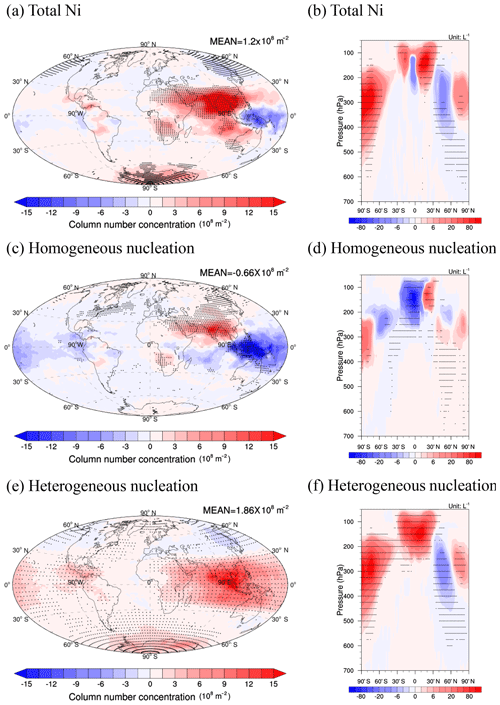
Figure 11 The annual average change in column number concentration (a, c, e) and zonal average number concentration (b, d, f) of total ice (a, b), ice from homogeneous nucleation (c, d), and ice from heterogeneous nucleation (e, f) for the difference between the PD_SOA and PI_SOA cases. Differences significant at the 90 % level according to a Student's t test are depicted by points.

3.3 The influence of SOA on anthropogenic forcing

SOA particles have a strong potential to act as INPs and therefore influence the formation of cirrus clouds. We examined the radiative forcing of all anthropogenic aerosols on cirrus clouds when including the INPs from newly nucleated SOA particles. Figure 10 shows the column number concentration of INPs and zonal average of INPs from SOA in the PD and PI atmosphere. Changes in natural SOA precursors between the PI and PD atmospheres (i.e., isoprene, α-pinene, and limonene emissions) are caused by changes in temperature as well as by changes in land use, while changes in aromatic emissions are associated with anthropogenic emission growth. In addition, newly formed SOA particles grow to accumulation mode size as a result of coagulation of particles (sulfate and other newly formed SOA particles), deposition of gaseous sulfate, and incorporation of other SOA compounds (e.g., through partitioning or kinetic uptake). Thus, the number concentration of INPs from SOA is much higher in the PD than that in the PI due to the much higher concentration of SOA in the accumulation mode in the PD (Zhu et al., 2019). The INPs from SOA are highest in the middle latitudes of the NH in the PD, while the INPs from SOA are higher in the SH than those in the NH in the PI atmosphere (Fig. 10a, b). The INPs from SOA in the PD are spread between 600 and 150 hPa with a peak around 300 hPa, so there is a possible influence on the formation of cirrus clouds (Fig. 10b). The INPs from SOA in the PI have a peak concentration that is a little higher than those in the PD (Fig. 10d). The global average N_i from heterogeneous nucleation increases by 1.86×10⁸ m⁻² from PI to PD when including the INPs from SOA (Fig. 11e), which is in contrast to the decrease in the global average N_i from heterogeneous nucleation in the case without SOA (Fig. 5e). The INPs from SOA increase the N_i from heterogeneous nucleation in both the PD and PI cases when compared to the PD_Base and PI_ALL cases (Figs. S6e, S7e). However, the increase in N_i from heterogeneous nucleation in the PD is much larger than that in the PI because of the larger number concentration of INPs from SOA in the PD. As a result, the large increase in INPs from SOA between the PD and the PI enhances heterogeneous nucleation, resulting in an increase in N_i from heterogeneous nucleation, especially in the tropics around 150 hPa and in the Antarctic from 400 to 200 hPa (Fig. 11f). The increase in the heterogeneous nucleation when including SOA widely inhibits homogeneous nucleation in both the PD and PI (Figs. S6c, S7c). In the PD, the increase in N_i from heterogeneous nucleation even outweighs the decrease in N_i from homogeneous nucleation, leading to an increase of 0.4×10⁸ m⁻² in the global average N_i due to SOA compared to the PD_Base case (Fig. S6a). In contrast, the INPs from SOA in the PI case make a larger contribution to the decrease in N_i from homogeneous nucleation than the increase in N_i from heterogeneous nucleation, resulting in a decrease in total N_i of $-\mathrm{0.31}\times {\mathrm{10}}^{\mathrm{8}}$ m⁻² compared to the PI_ALL case (Fig. S7a). The inclusion of INPs from SOA decreases N_i in the tropics but increases N_i in the middle to high latitudes in both the NH and SH (Figs. S6b, S7b). The global average N_i in the PD increases while the global average N_i in the PI is decreased. Both changes are caused by additional INPs from SOA (Figs. S6a, S7a) resulting in a larger increase in the global average N_i from the PI to PD compared to the case without SOA (compare Figs. 5a and 11a). When including INPs from SOA, N_i increases to a large extent over South Asia, and the north Indian Ocean N_i decreases over the middle to high latitudes of East Asia and the North Pacific Ocean (compare Figs. 11a and 5a).

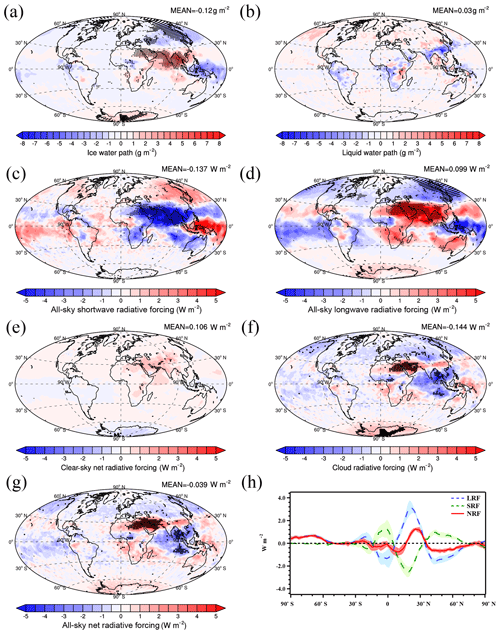
Figure 12 Annual mean plots of the changes in ice water path (a), liquid water path (b), all-sky shortwave radiative forcing (c), all-sky longwave radiative forcing (d), clear-sky net radiative forcing (e), cloud radiative forcing (f), and all-sky net radiative forcing (g) as well as longwave radiative forcing (h, LRF, blue dashed line), shortwave radiative forcing (h, SRF, green dashed line), and all-sky net radiative forcing (h, NRF, red solid line) versus latitude for the difference between the PD_SOA and PI_SOA cases. Differences significant at the 90 % level according to a Student's t test are depicted by points. The shading in (h) represents 1 standard deviation of the interannual variation over 6 years.

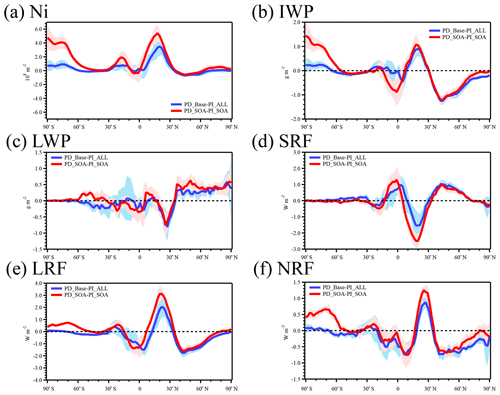
Figure 13 Change in vertically integrated ice number concentration (a), ice water path (b), liquid water path (c), and shortwave radiative forcing (d), longwave radiative forcing (e), and all-sky net radiative forcing (f) for the difference between the PD_SOA and PI_SOA cases (red line) as well as the PD_Base and PI_ALL cases (blue line). The shading represents 1 standard deviation of the interannual variation over 6 years.

The increased N_i leads to a significant increase in the IWP in South Asia, the north Indian Ocean, and Antarctica due to the reduction of gravitational removal, while the IWP decreases significantly in the middle to high latitudes of East Asia, which is caused by the decrease in N_i (Fig. 11a). Compared with the case without SOA (PD_Base-PI_ALL), the inclusion of SOA increases the difference in the IWP between the PD and PI in Antarctica significantly because of the increase in N_i from heterogeneous nucleation of INPs from SOA there (Fig. 12a). The change in the LWP due to dynamic feedbacks in the case with SOA is significant in only a few grids, which is similar to the case without SOA (Fig. 12c). The larger increases in N_i and IWP over South Asia and the north Indian Ocean lead to the larger changes in both SRF and LRF when including SOA compared to the case without SOA, while the significant decrease in N_i in the middle to high latitudes over East Asia leads to a significant decrease in the LRF. The increase in N_i and IWP in Antarctica only increases the LRF but does not change the SRF because of the very low shortwave flux in polar regions (Fig. 12c, d). The larger decrease in the SRF offsets the increase in the LRF in the tropics when including SOA, resulting in a similar value for NRF in the tropics for the cases with and without SOA (Fig. 13f). However, the more positive changes in the LRF from PI to PD in Antarctica and the Arctic when including SOA explain the more positive NRF there compared to the case without SOA (Fig. 13f). In addition, the NRF in South Asia and North Africa around 30^∘ N, where NRF is most positive in the case without SOA, becomes even more positive when including SOA due to the larger increases in N_i. As a result, the significant and larger positive NRF over Antarctica as well as South Asia and North Africa around 30^∘ N causes an increase in the global average NRF due to all anthropogenic aerosol to $-\mathrm{0.04}\pm \mathrm{0.08}$ W m⁻² when including SOA compared to the value of $-\mathrm{0.20}\pm \mathrm{0.05}$ W m⁻² in the case without SOA. The NRF when including SOA is up to 6.6 W m⁻² in the Arabian Peninsula while it is as low as −4.8 W m⁻² in the north Indian Ocean (Fig. 12g). Compared to the case without SOA, the global average CRF is less negative ($-\mathrm{0.14}\pm \mathrm{0.07}$ W m⁻² compared to −0.28 W m⁻²) largely due to the significant positive CRF over Antarctica (Fig. 12f). Simultaneously, the NRFC is more positive in the case with SOA than the case without SOA, which offset 73 % of the CRF (Fig. 12e).

4 Conclusion and discussion

This work develops a new ice nucleation parameterization, HYBRID, which is a combination of the LP and KL parameterizations. The global model using this new scheme is able to simulate the growth and decay of ice particles in the updrafts and downdrafts associated with gravity waves as in the modified KL scheme (Penner et al., 2018) and is able to treat the changes in aerosol number concentration from freezing haze particles with fidelity in the sign of the change as in the LP scheme. The HYBRID scheme overcomes some of the deficiencies in previous ice nucleation schemes. We evaluated the HYBRID ice nucleation scheme by comparing the scheme with the Liu and Penner (2005) adiabatic parcel model and by comparing its global predictions using observed N_i. We used 10 000 parcel model simulations to show that the HYBRID box model predicts 7.3 % larger N_i than the LP adiabatic parcel model with 21.5 % larger N_i from homogeneous nucleation. The global model using the HYBRID scheme overestimates N_i between 195 and 215 K somewhat compared to observations, as do earlier simulations with only the KL scheme (Penner et al., 2018). The results of N_i from the HYBRID scheme are in reasonable agreement with observations and thus were used in the CESM/IMPACT global model to estimate the radiative forcing of aerosols in large-scale cirrus clouds. The predicted N_i depends on the competition between homogeneous and heterogeneous nucleation. These two ice nucleation processes dominate the formation of N_i in different regions and altitudes. The global average N_i is dominated by homogeneous nucleation in the PD atmosphere.

We performed a series of model experiments using the HYBRID ice nucleation scheme to explore the forcing and cloud changes associated with changes in aircraft soot, sulfur emissions and all anthropogenic emissions from the PI to PD. Results are summarized in Table 3. The INPs from aircraft soot usually decrease N_i by the inhibition of homogeneous nucleation in spite of some areas with small increases in N_i. In contrast, the increase in sulfur emissions from PI to PD enhances homogeneous nucleation in most regions and leads to a small decrease in the N_i formed as a result of heterogeneous nucleation. We found that the effect of aerosols in cirrus clouds could feed back to the meteorological state as determined by temperature and RH_i, which could have an opposite effect on the changes in N_i due to either aircraft soot or sulfur emissions in the remote regions like the west Pacific Ocean. These meteorological feedbacks partly reduce the changes in the global average N_i due to anthropogenic emissions. The changes in N_i from PI to PD caused by all anthropogenic emissions are dominated by the changes due to the sulfur emissions, but the changes in surface and aircraft soot emission have some effects on the inhibition of homogeneous nucleation.

The changes in N_i due to anthropogenic aerosols lead to changes in IWP as well as LWP due to dynamical feedbacks. The changes in SRF and LRF are always determined by the changes in the IWP (and N_i), but the changes in LWP could either enhance or offset the effects of IWP on the radiative fluxes. Emissions of aircraft soot lead to a positive change in the global average SRF while the global average LRF is negative. The changes in sulfur emissions from the PI to PD atmosphere lead to opposite changes in the global average SRF and LRF compared to aircraft soot because of the different signs of changes in N_i. The total net forcing in cirrus clouds is usually dominated by LRF but it is dominated by SRF when the changes in warm clouds cause a feedback that reinforces the effect of cirrus clouds on shortwave fluxes. As a result, the emission of aircraft soot has a negative global average NRF of $-\mathrm{0.14}\pm \mathrm{0.07}$ W m⁻² in large-scale cirrus clouds, while the changes in the sulfur emissions from the PI to the PD lead to a small negative global average NRF of $-\mathrm{0.02}\pm \mathrm{0.06}$ W m⁻². The global average NRF due to all anthropogenic emissions from PI to PD, which is estimated to be $-\mathrm{0.20}\pm \mathrm{0.05}$ W m⁻², is dominated by the NRF caused by increased sulfur emissions but is more negative than the forcing by sulfur emissions alone due to changes in the emissions of soot.

The influence of SOA on the anthropogenic forcing of aerosols in large-scale cirrus clouds was examined. The additional INPs from SOA increase the N_i from heterogeneous nucleation and decrease N_i from homogeneous nucleation, but the sign of the changes in the total N_i depends on the balance of these two effects. The high number concentration of INPs from SOA in the PD atmosphere causes an increase in N_i compared to not including INPs from SOA while the low number concentration in the PI atmosphere causes a decrease. As a result, the changes in N_i due to the changes in anthropogenic emissions from PI to PD are larger when including INPs from SOA than the case without SOA. The inclusion of SOA mainly increases the changes in the NRF in the polar regions and the regions around 30^∘ N, resulting in a less negative NRF of $-\mathrm{0.04}\pm \mathrm{0.07}$ W m⁻² associated with the change in all anthropogenic emissions.

The radiative forcing of anthropogenic aerosols' effect on cirrus clouds estimated in this study is less negative than the result indicated in Penner et al. (2009) (−0.38 to −0.56 W m⁻²) and has a different sign compared with the result shown in Gettelman et al. (2012) (0.27±0.10 W m⁻²). This is mostly caused by the different treatments for updraft velocity, the concentration of haze particles, and INPs as well as the application of a different ice nucleation scheme. Current models show that homogeneous nucleation dominates the formation of new ice particles in most regions over the world with the largest contribution to cirrus cloud formation in the tropical upper troposphere (Zhou et al., 2016; Shi and Liu, 2018; Shi et al., 2015). However, some observations indicated the importance and high occurrence frequency of heterogeneous nucleation in the tropical tropopause region (Jensen et al., 2013). Although the inclusion of INPs from newly formed SOA in this study inhibits homogeneous nucleation in the tropics, homogeneous nucleation is still responsible for 75 % of total N_i in the PD atmosphere. Laboratory measurements have supported other species acting as INPs and enhancing heterogeneous nucleation such as solid ammonium sulfate (Abbatt et al., 2006), which has not been considered in current global climate models. Additional INPs from anthropogenic ammonium sulfate can be expected to increase the anthropogenic forcing in cirrus clouds to be less negative and possibly even positive. The HYBRID ice nucleation scheme somewhat overestimates the ice number concentration produced from homogeneous nucleation compared to a full parcel model. An explicit representation of the ice nucleation process used in the global climate model may be helpful to predict the ice number and therefore radiation budget more correctly in the future. The ability of SOA to act as an INP probably varies depending on the property of different SOA compounds as well as their particle size and mixing state (Baustian et al., 2013; Berkemeier et al., 2014; Charnawskas et al., 2017; Shiraiwa et al., 2017). A global climate model coupled online with the formation mechanism of SOA together with an increased understanding of the ability of SOA to act as an INP would help in estimating the contribution of SOA to ice particle formation more accurately.