A revisiting of the parametrization of downward longwave radiation in summer over the Tibetan Plateau based on high-temporal-resolution measurements

The Tibetan Plateau (TP) is one of the research hot spots in the climate change research due to its unique geographical location and high altitude. Downward longwave radiation (DLR), as a key component in the surface energy budget, has practical implications for radiation budget and climate change. A couple of attempts have been made to parametrize DLR over the TP based on hourly or daily measurements and crude clear-sky discrimination methods. This study uses 1 min shortwave and longwave radiation measurements at three stations over the TP to parametrize DLR during summer months. Three independent methods are used to discriminate clear sky from clouds based on 1 min radiation and lidar measurements. This guarantees the strict selection of clear-sky samples that is fundamental for the parametrization of clear-sky DLR. A total of 11 clear-sky and 4 cloudy DLR parametrizations are examined and locally calibrated. Compared to previous studies, DLR parametrizations here are shown to be characterized by smaller root-mean-square errors (RMSEs) and higher coefficients of determination (R²). Clear-sky DLR can be estimated from the best parametrization with a RMSE of 3.8 W m⁻² and R²>0.98. Systematic overestimation of clear-sky DLR by the locally calibrated parametrization in one previous study is found to be approximately 25 W m⁻² (10 %), which is very likely due to potential residual cloud contamination on previous clear-sky DLR parametrization. The cloud base height under overcast conditions is shown to play an important role in cloudy DLR parametrization, which is considered in the locally calibrated parametrization over the TP for the first time. Further studies on DLR parametrization during nighttime and in seasons except summer are required for our better understanding of the role of DLR in climate change.

1 Introduction

The downward longwave radiation (DLR) at the Earth's surface is the largest component of the surface energy budget, being nearly double the downward shortwave radiation (DSR; Kiehl and Trenberth, 1997). DLR has shown a remarkable increase during the process of global warming (Stephens et al., 2012). This is closely related to the fact that both a warming and a moistening of the atmosphere (especially in the lower atmosphere associated with the water vapor feedback) positively contribute to this change. Understanding of the complex spatiotemporal variation in DLR and its implications is necessary for improving weather prediction and climate simulation as well as water-cycling modeling. Unfortunately, errors in DLR are considered substantially larger than errors in any of the other components of surface energy balance, which is most likely related to the lack of DLR measurements of high quality (Stephens et al., 2012). The 2σ uncertainty in DLR measurement by using a well-calibrated and well-maintained pyrgeometer is estimated to be 2.5 % or 4 W m⁻² (Stoffel, 2005). However, global-wide surface observations are very limited, especially in some remote regions. On the other hand, it has been known for almost 1 century that clear-sky DLR is determined by the bulk emissivity and effective temperature of the overlying atmosphere (Ångström, 1915). Since these two quantities are not easily observed for a vertical column of the atmosphere, clear-sky DLR is widely parametrized as a function of surface air temperature and water vapor density, assuming that the clear sky radiates toward the surface like a grey body at screen-level temperature. Dozens of parametrization formulas of DLR have been developed in which clear-sky effective emissivity (ε_c) is a function of the screen-level temperature (T) and water vapor pressure (e; T and e have the same meaning and unit in the following equations if not specified) or simply in which localized coefficients with given functions are used. Two formulas, i.e., an exponential function (Idso, 1981) and a power law function (Brunt, 1932; Swinbank, 1963), have been widely used to depict the relationship of ε_c to T and e. The coefficients of these functions are derived by a regression analysis of collocated measurements of T, e and DLR. Most of these proposed parametrizations are empirical in nature and only specific for definite atmospheric conditions. An exception is that Brutsaert (1975) developed a model based on the analytic solution of the Schwarzschild equation for standard atmospheric lapse rates of T and e. Prata (1996) found that the precipitable water content (w) was much better able to represent the effective emissivity of the atmosphere than e, which was loosely based on radiative-transfer simulations. Dilley and O'Brien (1998) adopted this scheme but empirically tuned their parametrization using an accurate radiative-transfer model. Since DLR is to some extent impacted by water vapor and temperature profile (especially in cases of the existence of an inversion layer) and diurnal variation in T, a new model with two more coefficients considering these effects was developed (Dupont et al., 2008).

In the presence of clouds, total effective emissivity of the sky is remarkably modulated by clouds. The existing clear-sky parametrization should be modified according to the cloud fraction (CF) and other cloud parameters such as cloud base height (CBH). CF is generally used to represent a fairly simple cloud modification under cloudy conditions. Dozens of equations with cloudiness correction have been developed and evaluated by DLR measurements across the world (Crawford and Duchon, 1999; Niemelä et al., 2001). CF can be obtained by trained human observers (Iziomon et al., 2003) or derived from DSR (Crawford and Duchon, 1999) and DLR measurements (Dürr and Philipona, 2004). A high temporal resolution of DSR or DLR measurements (for example, 1 min) can also provide cloud type information (Duchon and O'Malley, 1999) and thereby allow for the consideration of potential effects of cloud types on DLR (Orsini et al., 2002).

With an average altitude exceeding 4 km above sea level (a.s.l.), the Tibetan Plateau (TP) exerts a huge influence on regional and global climate through mechanical and thermal forcing because of it being the highest and most extensive highland in the world (Duan and Wu, 2006). The TP, compared to other high-altitude regions and the poles, has been relatively more sensitive to climate change. The most rapid warming rate over the TP occurred in the latter half of the 20th century, likely associated with a relatively large increase in DLR. Duan and Wu (2006) indicated that an increase in low-level nocturnal cloud amount and thereby DLR could partly explain the increase in the minimum temperature, despite a decrease in total cloud amount during the same period. By using the observed sensitivity of DLR to changes in specific humidity in the Alps, Rangwala et al. (2009) suggested that an increase in water vapor appeared to be partly responsible for the large warming over the TP. Since the coefficients of certain empirical parametrizations and their performances showed spatiotemporal variations, the establishment of localized DLR parametrizations over the TP is of high significance. Further studies on DLR, including its spatiotemporal variability and its parametrization as well as its sensitivity to changes in atmospheric variables, would be expected to improve our understanding of climate change over the TP (Wang and Dickinson, 2013).

DLR measurements from high-quality radiometers with high temporal resolutions over the TP are quite scarce. To the best of our knowledge, there are very few publications on DLR and its parametrization over the TP. Wang and Liang (2009) evaluated clear-sky DLR parametrizations of Brunt (1932) and Brutsaert (1975) at 36 globally distributed sites, in which DLR data at two TP stations were used. Yang et al. (2012) used hourly DLR data at six stations to study major characteristics of DLR and to assess the all-sky parametrization of Crawford and Duchon (1998). Zhu et al. (2017) evaluated 13 clear-sky and 10 all-sky DLR models based on hourly DLR measurements at five automatic meteorological stations. The Kipp & Zonen CNR1 is composed of a CM3 pyranometer and CG3 pyrgeometer that are used to measure DLR and DSR, respectively. The CG3 is a second-class radiometer according to the International Organization for Standardization (ISO) classification. The root-mean-square error of hourly DLR is less than 5 W m⁻² after field recalibration and window-heating correction (Michel et al., 2008). Note that human observations of cloud every 3–6 h or hourly DLR and DSR data were used to determine clear sky and cloud cover, respectively, in these previous studies.

In order to further our understanding of DLR and DSR over the TP, measurements of 1 min DSR and DLR at three stations over the TP using state-of-the-art instruments have been performed in summer months since 2011. These data provide us with the opportunity to evaluate clear-sky DLR models and quantitatively assess cloud impacts on DLR. This study makes progress in the following aspects as compared to previous studies: (1) clear-sky discrimination and CF estimation are based on 1 min DSR and DLR measurements that are objective in nature; (2) misclassification of cloudiness as cloud-free skies is minimized by adopting strict cloud-screening procedures based on 1 min DSR, DLR and lidar measurements; (3) potential effects of CBH on DLR are also investigated. Localized parametrizations of clear-sky and all-sky DLRs are ultimately achieved, which can be expected to improve DLR estimations over the TP.

2 Site, instrument and data

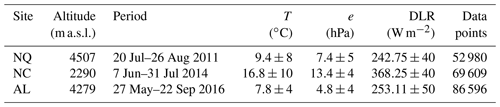
Measurements of DLR and DSR conducted over 1–4 months over the TP at three stations (Table 1), including Nagqu (NQ; 31.29^∘ N, 92.04^∘ E; 4507 m a.s.l.), Nyingchi (NC; 29.4^∘ N, 94.2^∘ E; 2290 m a.s.l.) and Ali (AL; 32.5^∘ N, 80^∘ E; 4287 m a.s.l.) are used for the DLR parametrization. DLR and DSR were measured by CG4 and CM21 radiometers, respectively (Kipp & Zonen, Delft, the Netherlands). The sampling frequency was 1 Hz, and the averages of the samples over 1 min intervals were logged on a Campbell Scientific CR23X data logger. Simultaneous 1 min averages of T and e were taken from the automatic meteorological stations. With the aid of its specific material and unique construction, the CG4 is designed for DLR measurement with high reliability and accuracy. Window heating due to absorption of solar radiation in the window material, the major error source of DLR measurement, is strongly suppressed by the CG4's unique construction conducting away the absorbed heat very effectively. The CM21 is a high-performance research grade pyranometer. The introduction of individually optimized temperature compensation for the CM21 makes it have a much smaller thermal offset than the CM3. The installation of the CG4 and CM21 on the Kipp & Zonen CV2 ventilation unit prevents dew deposition on the window of the CG4 and the quartz dome of the CM21. The radiometers are calibrated before and after field measurements to the standards held by the China National Centre for Meteorological Metrology.

Table 1 Description of stations and measurements (magnitude and variability) at three stations in the Tibetan Plateau.

A micropulse lidar (MPL-4B, Sigma Space Corporation, United States) was installed side by side the radiometers. The Nd:YLF laser of the MPL produces an output power of 12 µJ at 532 nm. The repletion rate is 2500 Hz. The vertical resolution of the MPL data is 30 m, and the integration time of the measurements is 30 s. The MPL backscattering profiles are used to identify the cloud boundaries and derive the CBHs (He et al., 2013). The dataset used in this article contains about 700 h of coincident DLR, DSR, lidar and meteorological measurements.

DLR and DSR were also measured at Lhasa (29.9^∘ N, 91.1^∘ E; 3649 m a.s.l.) during summer in 2012 using the same instruments as those in other stations. Lhasa data are mainly used for independent validation because of no lidar data there.

3 Methods

3.1 Clear-sky discrimination

Clear skies and cloudy conditions should be discriminated between before performing DLR parametrization, which is achieved by the synthetical analysis of DSR, DLR and CBH from the MPL.

Following the method initiated by Crawford and Duchon (1999), we calculate two quantities reflecting DSR magnitude and variability based on 1 min observed DSR (DSR_obs) and calculated clear-sky DSR (DSR_cal) values. DSR_cal is calculated by the C model of Iqbal (1983), in which direct and diffuse DSR are parametrized separately. Direct DSR (DSR_dir) is calculated as follows.

$$\begin{array}{}\text{(1)}& {\mathrm{DSR}}_{\mathrm{dir}}=S_{\mathrm{0}}{\mathit{\tau }}_{\mathrm{r}}{\mathit{\tau }}_{\mathrm{w}}{\mathit{\tau }}_{\mathrm{o}}{\mathit{\tau }}_{\mathrm{a}}{\mathit{\tau }}_{\mathrm{g}},\end{array}$$

where S₀ is solar constant and τ_r, τ_w, τ_o, τ_a and τ_g are transmittances due to Rayleigh scattering, water vapor absorption, ozone absorption, aerosol extinction, and absorption by uniformly mixed gases O₂ and CO₂, respectively. Diffuse radiation is estimated as the sum of Rayleigh and aerosol scattering as well as multiple reflectance. Total ozone column (DU) is provided by a Brewer spectrophotometer. Values of w (cm) are from Vaisala RS92 radiosonde profiles in AL and Global Positioning System measurements in NC and NQ. They are used to create linear regression relationships to collocated ground level e (hPa) measurements, which are then used to estimate w from 1 min measurements of e. The Ångström wavelength exponent and Ångström turbidity are from CE318 sun photometer observations in NC and AL, while in NQ we adopt the same value as that in AL because the altitudes of the two sites are similar. The climatic value of single-scattering albedo retrieved from long-period CE318 observation in Lhasa is 0.90 (Che et al., 2019), which is used in three stations. This is reasonable because of high altitude and extremely low aerosol loading over the TP. Surface albedo is 0.25 and 0.22 in Al and NQ according to in situ measurements (Liang et al., 2012). In NC, it is 0.183 (Zhao et al., 2011).

DSR_cal values are first scaled to a constant value of 1400 W m⁻² for each minute of each day. We adopt this value according to Duchon and O'Malley (1999) and Long and Ackerman (2000). Afterwards, DSR_obs values are scaled by multiplying the same set of scale factors. Finally, the mean and standard deviation of the scaled DSR in a 21 min moving window (±10 min centered on the time of interest) are used for cloud screening. The selection of the width of 21 min is empirical but a consequence of having a reasonable time span for estimating the mean and variance (Duchon and O'Malley, 1999). Clear-sky DSR should satisfy three requirements: (1) the ratio of DSR_obs to DSR_cal is within 0.95 to 1.05; (2) the difference between scaled DSR_obs and DSR_cal is less than 20 W m⁻²; (3) standard deviation (δ) of scaled DSR_obs in a 21 min moving window is less than 20 W m⁻².

Temporal variability in DLR is also used for cloud screening according to Marty and Philipona (2000) and Sutter et al. (2004). Here, δ of scaled DLR (scaled to 500 W m⁻²) in a 21 min moving window is used for this purpose. A cloud-free sample is determined if δ is less than 5 W m⁻².

Since both DSR and DLR experience difficulties in detecting clouds in the portion of the sky far away from the sun (Duchon and O'Malley, 1999) or high-altitude cirrus clouds (Dupont et al., 2008), coincident MPL backscatter measurements are used to strictly select clear-sky samples. There should be a cloud element somewhere in the sky when the MPL identifies cloud; it is thus required that no clouds are detected by the MPL in a 21 min moving window, otherwise it is defined as cloudy.

Given the fact that these methods are complementary to each other to some extent (Orsini et al., 2002), we use the following strategy to guarantee a proper selection of clear-sky samples. If DSR, DLR and MPL measurements at the time of interest synchronously satisfy these specified clear-sky conditions, the sample is thought to be taken under unambiguously cloud-free conditions; on the contrary, the measurements are made under unambiguously cloudy conditions if any method suggests cloudy conditions. Our following clear-sky and cloudy DLR parametrizations are based on measurements under unambiguously cloud-free (8195 min) and cloudy conditions (69 318 min), respectively.

Figure 1 shows an example of clear-sky discrimination results based on our method. DSR_obs presents a smooth temporal variation from sunrise to about 14:00 (LT), being consistent with DSR_clr. Similarly, DLR also varies very smoothly during the same period when 21 min standard deviations of DLR are <5 W m⁻². Both facts suggest sunny and cloudless skies. This inference is supported by the MPL that suggests no cloud is detected overhead. Contrarily, abrupt changes of 1 min DSR_obs and DLR are evident during 14:00–17:00 LT, and we can see DSR_obs occasionally exceeds the expected DSR_clr, indicating the frequent occurrence of fair-weather cumulus clouds. The MPL detects a persistent thin cloud layer at 4 km aboveground, which agrees with DSR and DLR measurements very well.

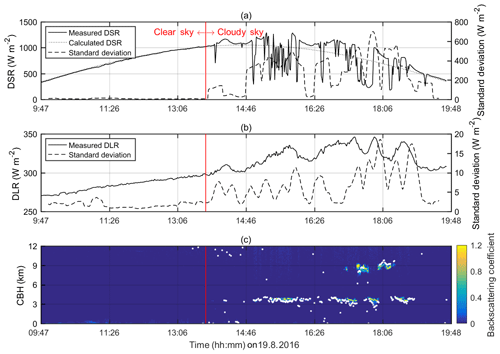
Figure 1 Time series of data sample on 19 August 2016 (time given is local time) transiting from clear sky to cloudy sky: (a) measured (black line) and calculated (dotted black line) downward shortwave radiation and its 21 min standard deviation (grey line), (b) measured downward longwave radiation and 21 min standard deviation, and (c) MPL backscattering coefficient and the cloud base height.

3.2 Cloud fraction estimation

Given synoptic cloud observations are very limited and temporally sparse, various parametrizations using DSR or DLR data have been developed to estimate CF (e.g., Deardorff, 1978; Marty and Philipona, 2000; Dürr and Philipona, 2004; Long et al., 2006; Long and Turner, 2008). Because of good agreement between clear-sky DSR_obs and DSR_cal calculated by the Iqbal C calculations (Iqbal, 1983; Gubler et al., 2012), with a mean bias of 1.7 W m⁻² and root-mean-square error (RMSE) of 10.7 W m⁻² (not shown), we use the Deardorff (1978) method to calculate CF from DSR_obs and DSR_cal. The method is based on a fairly simple cloud modification to DSR as follows.

$$\begin{array}{}\text{(2)}& \mathrm{CF}=\mathrm{1}-{\displaystyle \frac{{\mathrm{DSR}}_{\mathrm{obs}}}{{\mathrm{DSR}}_{\mathrm{cal}}}}\end{array}$$

CF (no unit) has values ranging from 0 to 1. To avoid the error caused by abrupt DSR variation, the 21 min mean DSR value rather than its instantaneous measurements are used here.

4 Results

4.1 Clear-sky DLR parametrization evaluation and localization

A total of 11 clear-sky DLR (DLR_clr) parametrizations (Table 2) are evaluated based on 1 min DLR measurements under unambiguously cloud-free conditions. To compare the performance of these 11 models, the RMSE and the coefficient of determination (R²) are shown by a Taylor diagram in Fig. 2a. Relatively smaller RMSEs (generally <15 W m⁻²) and larger R² values (>0.95) are derived for the Brutsaert (1975), Konzelmann et al. (1994), Dilley and O'Brien (1998), and Prata (1996) models. This is likely because these parametrizations were developed in cool and dry areas, for example, in England (Brutsaert, 1975), Greenland (Konzelmann et al., 1994) and dry desert region in Australia (Prata, 1996). The climate in those areas is likely similar to that over the TP to some extent, so those parametrizations are expected to perform well. The higher RMSE (>37 W m⁻²) and the lower R² (∼0.7) are derived for the Swinbank (1963) and Idso and Jackson (1969) models. This can be partly explained by the fact that only Tis used in these two methods. Previous studies suggest substantial uncertainty (RMSE >37.5 W m⁻² and R²<0.75) if the water vapor effect on DLR_clr is not accounted for (Duarte et al., 2006). Since w is very low over the TP and thereby DLR is highly sensitive to variation in w in that case, much more attention should be paid to the water vapor effect on the parametrization of DLR_clr.

Table 2 Details of 11 clear-sky DLR parametrizations and their specific conditions.

^* Alt. is the altitude above sea level (m a.s.l.); e is screen-level water vapor pressure in hPa, and T represents surface temperature in K.

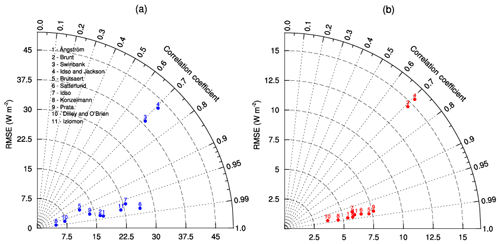
Figure 2 RMSE and R² for the clear-sky DLR parametrizations using original (a) and locally calibrated (b) coefficients.

The coefficients in 11 parametrizations (Table 2) were originally calibrated and determined in different geographical locations; therefore, they may not be the optimal values for the TP. Thus we make use of 1 min clear-sky DLR samples to locally calibrate the parameters of these parametrizations. We use the 10-fold cross-validation method to determine the parameters. This is a widely used method to estimate the skill of a regression model on unseen data. It is expected to result in a less biased or less optimistic estimate of the model skill than other methods, such as a simple train–test split (James et al., 2013). All the data are randomly divided into 10 groups of approximately equal size; the coefficients are computed by using nine groups as a training set, and the remaining group is used as validation. This procedure is repeated 10 times to get the representational value of coefficients (with the lowest test error).

The coefficient values derived from the nonlinear least-squares fitting of the DLR_clr parametrizations (Table 2) over the TP are presented in Table 3. For each fitted parametrization, we calculated the RMSE and R², and the results are shown in Fig. 2b. When using the parametrizations with the locally fitted parameters, the accuracy of the parametrization relative to the published values is obviously improved. Most RMSEs are <10 W m⁻² except the parametrization proposed by Swinbank (1963) and Idso and Jackson (1969) that still produce the worst results (with R² of 0.71 and RMSE of 15 W m⁻²) even after the parameters are locally calibrated. This is probably because e is not considered in these two methods.

Table 3 Locally fitted clear-sky DLR parametrizations over the TP.

The Dilley and O'Brien (1998) parametrization, which is initially developed by considering the adaptation of climatological diversities, is expected to be able to fit the measurements in tropical, midlatitude and polar regions. This expectation is verified by its wide deployment in DLR_clr estimations in different climate regimes and altitude levels, for example, in tropical lowland (eastern Pará state, Brazil) and mild mountainous area (Boulder, United States; Marthews et al., 2012; Li et al., 2017). The present study confirms that the Dilley and O'Brien (1998) parametrization is the best clear-sky parametrization over the TP. The locally calibrated equation is as follows.

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\mathrm{DLR}}_{\mathrm{clr}}=& -\mathrm{2.53}+\mathrm{158.10}\times {\left({\displaystyle \frac{T}{\mathrm{273.16}}}\right)}^{\mathrm{6}}\\ & +\mathrm{106.40}\times {\left({\displaystyle \frac{\mathrm{46.50}\times \frac{e}{T}}{\mathrm{2.50}}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\end{array}\end{array}$$

The RMSE and R² of Eq. (3) are ∼3.8 W m⁻² and >0.98, respectively, which are substantially lower than those in previous studies over the TP; for example, the RMSE was 9.5 W m⁻² (Zhu et al., 2017). The Dilley and O'Brien (1998) parametrization was suggested to give the most reliable estimates of DLR_clr over the TP (Zhu et al., 2017). Note that the parameters here differ quite a lot from their values (Zhu et al., 2017), as shown in Eq. (4).

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathrm{DLR}}_{\mathrm{clr}}=& \mathrm{30.00}+\mathrm{157.00}\times {\left({\displaystyle \frac{T}{\mathrm{273.16}}}\right)}^{\mathrm{6}}\\ & +\mathrm{97.93}\times {\left({\displaystyle \frac{\mathrm{46.50}\times \frac{e}{T}}{\mathrm{2.50}}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\end{array}\end{array}$$

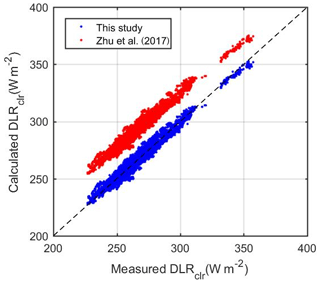
Figure 3 compares instantaneous clear-sky DLR data from measurements with calculations by Eq. (3) of this study and by Eq. (4) from Zhu et al. (2017). The former performs very well as shown by an overwhelmingly large number of data points falling along or overlapping the 1:1 line. By contrast, the latter overestimates DLR by 25 W m⁻² (10 %). This difference is not very likely due to different DLR measurements used to produce Eqs. (3) and (4) giving the following considerations. First, this systematic overestimation is much larger than the expected uncertainty in DLR measurements (2.5 % or 4 W m⁻²; Stoffel, 2005). More important, comparison of cloudy DLR parametrizations between this study and Zhu et al. (2017) showed good agreement (not shown). Note that only 1 h CG3 DLR observations are used for clear-sky discrimination in Zhu et al. (2017). This method was shown to be very likely contaminated by the thin high cloud (Sutter et al., 2004). This certainly would produce an overestimation of clear-sky DLR parametrization since larger DLRs are associated with potential residual clouds relative to real clear-sky DLRs.

Figure 3 Scatterplots of measured clear-sky DLR data and calculated clear-sky DLR as a function of calculations by Eq. (3) of this study (blue dots) and Eq. (4) by Zhu et al. (2017) (red dots). The dashed black line is the 1:1 line.

4.2 Parametrization of cloudy-sky DLR

Parametrizations of cloudy-sky DLR (DLR_cld) are based on estimated DLR_clr coupled with the effect of cloudiness or cloud emissivity, which depends primarily on CF as well as other cloud parameters, like CBH and cloud type (Arking, 1990; Viúdez-Mora et al., 2015). Four parametrizations (Table 4), which modify the bulk emissivity depending on CF, are assessed and locally calibrated in this section.

DLR_clr is estimated according to Eq. (3). The fitted values of the coefficients (using 10-fold cross validation) of the four cloudy parametrizations are presented in Table 4. The RMSEs and R² values of original and locally fitted parametrizations over the TP are presented in Fig. 4.

Table 4 4 Ordinary and locally fitted cloudy-sky DLR parametrizations.

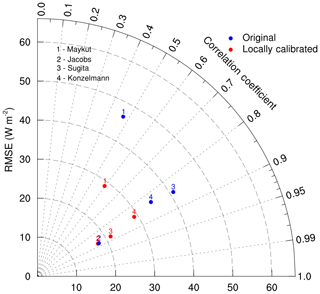
Figure 4 RMSE and R² for the cloudy-sky DLR (DLR_cld) parametrizations using the original (blue) and locally calibrated (red) coefficient.

Relative to clear-sky conditions, cloudy parametrizations using the given parameters have higher RMSEs (generally exceeding 35 W m⁻²) except the one developed by Jacobs (1978) (RMSE of 18 W m⁻²). R² was generally smaller than 0.9. RMSE values decrease significantly in Maykut and Church (1973) and Sugita and Brutsaert (1993) as locally calibrated parameters are used. Relatively smaller and almost no RMSE improvements are found for the methods developed by Konzelmann et al. (1994) and Jacobs (1978), respectively.

Equation (5) shows the best cloudy-sky parametrization over the TP by combining the clear-sky parametrization of Dilley and O'Brien (1998) with the cloud modulation correction scheme of Jacobs (1978).

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\mathrm{DLR}}_{\mathrm{cld}}=& \left(\mathrm{1}+\mathrm{0.23}\times \mathrm{CF}\right)\times \left(\mathrm{59.38}+\mathrm{113.70}\right.\\ & \left.\times {\left({\displaystyle \frac{T}{\mathrm{273.16}}}\right)}^{\mathrm{6}}+\mathrm{96.96}\times {\left({\displaystyle \frac{\mathrm{46.50}\times \frac{e}{T}}{\mathrm{2.50}}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\right)\end{array}\end{array}$$

The RMSE and R² are ∼18 W m⁻² and ∼0.89, respectively. The RMSE here is close to the 15 W m⁻² obtained in different-altitude areas in Switzerland (Gubler et al., 2012) and slightly lower than the 23 W m⁻² obtained in mountainous area in Germany (Iziomon et al., 2003). Compared to previous studies over the TP (RMSE of 22 W m⁻² in Zhu et al., 2017), our cloudy model produces better results.

In order to validate the newly developed DLR parametrizations, clear-sky and cloudy-sky DLR parametrizations are validated against DLR measurements at Lhasa. The results are shown in Fig. 5. Compared to the existing parametrizations, Eqs. (3) and (5) produce the smallest bias (both less than 2 W m⁻²) and RMSE (Eq. 3 bias is less than 5 W m⁻², and Eq. 5 bias is less than 25 W m⁻²). This independently demonstrates that the improved DLR parametrizations can be used in other stations over the TP.

Figure 5 Bias and RMSE for the DLR parametrizations using (a) the published clear-sky parametrizations and Eq. (3) and (b) cloudy-sky parametrizations and Eq. (5).

4.3 Effect of CBH on DLR under overcast conditions

Since clouds behave approximately as a blackbody, the most relevant cloud parameter (besides CF) to DLR under overcast skies (DLR_ovc) is CBH (Kato et al., 2011; Viúdez-Mora et al., 2015). Firstly, CBH defines the temperature of the lowest cloud boundary, which through the Stefan–Boltzmann law drives the cloud emittance; secondly, DLR emitted by the atmospheric layers above a cloud is totally absorbed by the cloud itself (clouds are thick enough). Radiative-transfer-model simulation has suggested that CBH under overcast conditions is an important modulator for DLR. The cloud radiation effect (CRE), the difference between DLR_obs and DLR_clr, decreases with increasing CBH at a rate of 4–12 W m⁻² that depends on climate profiles (Viúdez-Mora et al., 2015). This indicates that overcast DLR parametrization would be improved if CBH were considered.

A close relationship between CRE and CBH under overcast conditions over the TP is presented in Fig. 6. Compared to Viúdez-Mora (2015) results derived in Girona, Spain, a midlatitude site with low altitude, CRE over the TP is generally lower by 5–10 W m⁻². This is likely because clouds over the TP with the same CBH as that at Girona have relatively lower temperature, thereby producing lower radiative effect on DLR. CRE generally decreases as CBH increases. The result agrees with the expectation since CBH influence on DLR should decrease as CBH increases as a result of increasing water vapor effects on DLR. According to Fig. 6, CRE is about 70 W m⁻² for clouds <1 km and decreases to ∼40 W m⁻² for clouds at 3–4 km over the TP. The decreasing rate of CRE with CBH is estimated to be −9.8 W m⁻² km⁻¹ over the TP, which agrees with model simulations (Viúdez-Mora et al., 2015).

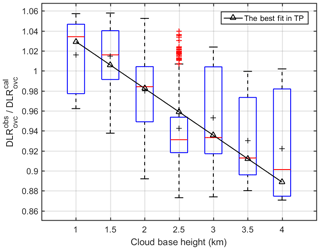
Figure 6 Distributions of the ratio of observed DLR and calculated DLR by Eq. (5) under overcast conditions against measured cloud base height are represented by box plot (the blue boxes indicate the 25th and 75th percentiles; the whiskers indicate the 5th and 95th percentiles; the middle red line is the median; the black plus sign is the mean). The black triangle line is the fitting line.

Since the CBH effect on overcast DLR is apparent, we introduced a modified parametrization to consider the CBH effect on DLR under overcast conditions. A linear correlation is firstly established based on the measured CBH and the ratio of observed DLR (${\mathrm{DLR}}_{\mathrm{ovc}}^{\mathrm{obs}}$) and calculated DLR by Eq. (5) (${\mathrm{DLR}}_{\mathrm{ovc}}^{\mathrm{cal}}$) under overcast conditions in Fig. 6. Since we can see that ${\mathrm{DLR}}_{\mathrm{ovc}}^{\mathrm{cal}}$ is equal to DLR_clr times 1.23 (because CF is equal to 1 in Eq. 5), we derived a CBH-corrected DLR_ovc parametrization as follows.

$$\begin{array}{}\text{(6)}& {\mathrm{DLR}}_{\mathrm{ovc}}=\mathrm{1.23}\times {\mathrm{DLR}}_{\mathrm{clr}}\times (\mathrm{1.0746}\times \mathrm{CBH}),\end{array}$$

where CBH is given in kilometers. The bias and RMSE of Eq. (6) between measurements and calculations are −2.15 and 19.79 W m⁻², respectively, which are significantly lower than those of Eq. (5) (10.3 and 21.4 W m⁻²) in overcast conditions. The result indicates a remarkable improvement in the estimation of DLR under overcast conditions by introducing CBH to the DLR parametrization; therefore, the introduction of such instruments as ceilometers to measure CBH is highly significant for studying clouds' impacts on DLR.

5 Discussion and conclusions

The parametrization of clear-sky DLR requires a well-defined distinction between clear-sky and cloudy-sky situations that commonly depends on human cloud observations 4–6 times each day. Human observation is subjective in nature, and its low temporal resolution cannot resolve dramatic high-resolution variation in clouds. Furthermore, synoptic cloud observations by humans show a tendency to give stronger weight to the horizon where DLR is not highly sensitive (Marty and Philipona, 2000). Clear-sky discrimination based on hourly DSR or DLR measurements also tends to be very suspect of residual clouds due to their low temporal resolution. Parametrization of clear-sky DLR based on these two methods is hence very likely biased as a consequence of the selection of cloud-contaminated clear-sky measurements. This would result in biased estimation of cloud DLR effect since it is the difference between clear-sky and measured all-sky DLRs (Dupont et al., 2008).

Using 1 min DSR and DLR measurements at three stations over the TP, DLR parametrizations are evaluated and localized parametrizations are developed based on a comprehensive cloud-screening method. We test the fitted parametrizations based on independent DLR measurements at Lhasa. The potential CBH effect on overcast DLR is experimentally determined. Our major conclusions are as follows.

Among 11 clear-sky DLR parametrizations tested in this study, two methods using only atmospheric temperature largely deviate from other parametrizations. The best method suitable for the TP is the parametrization developed by Dilley and O'Brien (1998). DLR estimation can be improved by the localization of these parametrizations. Locally calibrated parametrization can produce clear-sky DLR with a RMSE of 3.8 W m⁻².

Overcast DLR is highly sensitive to CBH. The parametrization can be substantially improved by consideration of the CBH effect. The bias between empirically parametrized calculations and measurements decreases from 10.3 to 1.3 W m⁻².

The focus of this study is on daytime DLR parametrization over the TP since DSR is used in the cloud-screening method. Given the significant role played by DLR in the surface energy budget during nighttime, it is highly desirable to perform further study on the nighttime DLR parametrization. These results are based on summer DLR measurements, so the conclusions here need to be further tested in other seasons, especially in winter when an increasing tendency in DLR has been observed (Rangwala et al., 2009). Further investigations on these issues are expected to shed new light on how and why DLR has changed over the TP. Our results clearly showed a substantial CBH effect on overcast DLR, which should be considered in the future when ceilometers are widely used to measure CBH.