Scattering matrices of mineral dust aerosols: a refinement of the refractive index impact

Mineral dust, as one of the most important aerosols, plays a crucial role in the atmosphere by directly interacting with radiation, while there are significant uncertainties in determining dust optical properties to quantify radiative effects and to retrieve their properties. Laboratory and in situ measurements of the refractive indices (RIs) of dust differ, and different RIs have been applied in numerical studies used for model developments, aerosol retrievals, and radiative forcing simulations. This study reveals the importance of the dust RI for the development of a model of dust optical properties. The Koch-fractal polyhedron is used as the modeled geometry, and the pseudospectral time domain method and improved geometric-optics method are combined for optical property simulations over the complete size range. We find that the scattering matrix elements of different kinds of dust particles are reasonably reproduced by choosing appropriate RIs, even when using a fixed particle geometry. The uncertainty of the RI would greatly affect the determination of the geometric model, as a change in the RI, even in the widely accepted RI range, strongly affects the shape parameters used to reproduce the measured dust scattering matrix elements. A further comparison shows that the RI influences the scattering matrix elements in a different way than geometric factors, and, more specifically, the P₁₁, P₁₂, and P₂₂ elements seem more sensitive to the RI of dust. In summary, more efforts should be devoted to account for the uncertainties on the dust RI in modeling its optical properties, and the development of corresponding optical models can potentially be simplified by considering only variations over different RIs. Considerably more research, especially from direct measurements, should be carried out to better constrain the uncertainties related to the dust aerosol RIs.

1 Introduction

Atmospheric aerosols play an important role in the global radiation balance directly by scattering and absorbing incident solar radiation and indirectly by influencing cloud formation as cloud condensation nuclei (CCN) or ice nuclei (IN) (Chýlek et al., 1978; Sokolik et al., 2001; Yi et al., 2011). According to the IPCC Fifth Assessment Report (IPCC, 2014), aerosols are still one of the largest sources of uncertainty in the total estimate of radiative forcing. As a major type of aerosol, mineral dust is widely distributed around the world, especially in arid regions. Mineral dust single-scattering properties are fundamental for quantifying radiative effects, and for developing satellite retrieval algorithms from optical observations (Kahn et al., 2005; Huang et al., 2014; Xu et al., 2017a).

Several aerosol optical property databases, e.g., the Global Aerosol Data Set (GADS; Koepke et al., 1997) and the Optical Properties of Aerosols and Clouds (OPAC; Hess et al., 1998), have been built to meet the needs of aerosol remote sensing and radiation studies for all aerosols as well as for particular kinds of aerosols (Meng et al., 2010; Bi et al., 2018b; Liu et al., 2019). However, for simplification, the optical properties of atmospheric aerosols are often investigated by assuming a relatively simple model, e.g., using spheres and spheroids, which has resulted in obvious errors (Mishchenko et al., 1997; Feng et al., 2009). For example, the measured phase functions of dust particles are clearly different from the phase functions of spherical particles at sideward and backward scattering angles (Koepke and Hess, 1988; Dubovik et al., 2002; Nousiainen, 2009). Databases with more accurate dust optical properties can contribute to applications such as radiative forcing calculation and remote sensing.

Several efforts have been devoted to studying the optical properties of dust aerosols (Bi et al., 2010; Meng et al., 2010; Ishimoto et al., 2010; Liu et al., 2013; Jin et al., 2016; Xu et al., 2017b). Although it is difficult but possible to mathematically define the exact shape of an actual dust particle in numerical studies (Kahnert et al., 2014; Lindqvist et al., 2014), the use of a simplified but optically equivalent model is more convenient and easier to process (Nousiainen and Kandler, 2015; Liu et al., 2013). By using the measured particle size information and the assumed refractive index (RI), most studies treat the geometry as an unknown variable and look for geometric parameters that result in simulated optical properties that are consistent with measurements (Bi et al., 2010; Dubovik et al., 2006; Liu et al., 2013; Lin et al., 2018; Mishchenko et al., 1997; Osborne et al., 2011). Different nonspherical shapes have been developed and applied, such as spheroids (Mishchenko et al., 1997; Dubovik et al., 2002; Ge et al., 2011; Merikallio et al., 2011), ellipsoids (Bi et al., 2009; Meng et al., 2010; Kemppinen et al., 2015), and superellipsoids (Bi et al., 2018a). Additionally, more complex and irregular particles have also been considered, e.g., spatial Poisson–Voronoi tessellation (Ishimoto et al., 2010), Gaussian random field (GRF) particles (Grynko et al., 2013), Koch-fractal particles (Liu et al., 2013; Jin et al., 2016), and nonsymmetric hexahedra (Bi et al., 2010; Liu et al., 2014). These “irregular” geometries as well as spheroids can achieve close agreement with measurements by using appropriate shape parameters or combining the results from multiple shapes, which indicates that certain geometries may be optically similar or equivalent with respect to scattering light. Nousiainen and Kandler (2015) found that the scattering properties of a cube-like dust particle can be mimicked by those of spheroids with a suitable shape distribution. Liu et al. (2014) found that the surface roughness and irregularity also share an optical equivalence. Lin et al. (2018) revealed that the scattering matrix elements of different types of dust particles can be achieved by changing only two parameters to specify the geometry of the superspheroids. Such “optical equivalences” are important for practical applications using dust optical properties because we can use those from a relatively simple numerical model, instead those based on the exact and actual dust particles, for downstream remote sensing and radiative transfer applications.

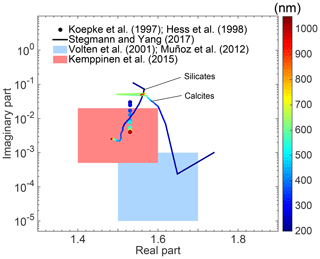
Figure 1 Refractive index from different sources. The color bar indicates the wavelengths at which the corresponding refractive indices are given (for the two lines and dots).

In addition to the particle geometry, there are also significant uncertainties related to the dust RI, which is often considered an inherent characteristic (Kahnert and Nousiainen, 2006; Stegmann and Yang, 2017), to which much less attention has been devoted during the model development. Previous studies often assumed a fixed RI during simulations of the corresponding optical properties at the incident wavelength of interest. The real part (Re) of dust RI is normally set to approximately 1.5, and, excluding hematite and magnetite, the imaginary part (Im) is normally set between 0.001 and 0.01 at visible wavelengths (Sokolik and Toon, 1999; Volten et al., 2001; Kandler et al., 2007; Meng et al., 2010). Previous studies using both measurements and numerical investigations reveal that a relatively large variation in the RI of dust materials in different regions or with different components does exist (Meng et al., 2010; Bi et al., 2011; Stegmann and Yang, 2017). Kemppinen et al. (2015) revealed that the retrieved dust RIs based on the comparisons of scattering matrices between simulations and laboratory measurements deviate from the true dust RIs.

Figure 1 shows some examples of the RIs around the visual wavelengths, and we illustrate values from various studies, including those from two well-accepted optical properties databases, i.e., the Global Aerosol Data Set (GADS; Koepke et al., 1997) and the Optical Properties of Aerosols and Clouds (OPAC; Hess et al., 1998), and the RI spectra of silicates and calcites (important components of mineral dust) based on measurement studies (Stegmann and Yang, 2017) with the incident wavelengths from 200 to 1000 nm. The shaded areas indicate the estimated values given by the Amsterdam–Granada Light Scattering Database (AGLSD, Muñoz et al., 2012; Volten et al., 2001) at wavelengths of 442 and 633 nm, and the assumed values from a study by Kemppinen et al. (2015) on the optical properties of mineral dust at a wavelength of 550 nm are presented as an example. The Re values are mainly between 1.4 and 1.7, and the range of Im values covers a few orders of magnitude from 0.00001i to 0.1i. The uncertainty of the RI is obvious, and a better understanding of the RI is an important prerequisite for studying the optical properties of dust and its further application.

This study uses the measured dust scattering properties from the AGLSD as the reference to “evaluate” the modeled results. However, we will not pay too much attention to the effect or performance of different geometric factors, as this topic has been covered in several previous studies. Considering the obvious uncertainties and less attention related to the particle RI, this study introduces the important roles of the dust RI in developing corresponding models for the numerical simulation of their optical properties. Section 2 introduces the models considered and the computational methods applied in this study. Section 3 investigates the impacts of the RI on the reproduction of the optical properties of several types of mineral dust particles. The effects of the RI on model development are revealed in Sect. 4, and the impacts of RI and geometry on the optical properties of dust are compared. Section 5 concludes the work.

2 Methodology

This study focuses on the effects of the RI on modeling the dust scattering matrix elements. The Koch-fractal particle is used as the presumed geometry (Macke et al., 1996; Falconer, 2004; Liu et al., 2013; Jin et al., 2016). The Koch-fractal particle geometry has been used to produce concave polyhedra based on tetrahedron elements of different generations and is flexible in representing both the particle overall geometries and their detailed surface structures. Macke et al. (1996) used second-generation Koch-fractal particles with different irregularities to explore the scattering properties of complex ice crystals using a geometric-optics method. Liu et al. (2013) extended the applications of Koch-fractal particle geometries to mineral dust particles and found that the corresponding optical properties represent those from measurements.

Figure 2 shows three examples of third-generation Koch-fractal particle geometries. The sequential number of the Koch-fractal generation indicates the complexity of the surface structure, and an irregular ratio (IR), which specifies particle irregularity, is a real number within the range [0, 0.5] used to constrain the random movement of the positions of successor-generation tetrahedra apexes to generate irregular particles. A larger IR makes the Koch-fractal geometry surfaces more irregular and asymmetrical. Liu et al. (2013) introduced the aspect ratio (AR, the ratio of height to width) to generate prolate or oblate particles. Macke et al. (1996) and Liu et al. (2013) include more details on the definition of Koch-fractal particles. In Fig. 2, the Koch-fractal particle on the left is a regular particle with an AR of 1.0 and an IR of 0. The middle particle has an IR of 0 but an AR of 2.5, and the particle on the right, which is the most irregular particle, has an AR of 2.5 and an IR of 0.3. Previous studies indicate that geometries with proper irregularity have better potential to characterize the geometric features of several types of actual dust particles. To constrain the geometric variations considered, all particles considered in this study will be third-generation Koch-fractal particles with an IR of 0.3, and we will only consider different ARs. If not particularly mentioned, the two values (for IR and AR) will be used as our default particle geometry.

Figure 2 Third-generation Koch-fractal particles with different geometric parameters. The aspect ratios of the particles from left to right are 1.0, 2.5, and 2.5, and the irregular ratios are 0, 0, and 0.3, respectively.

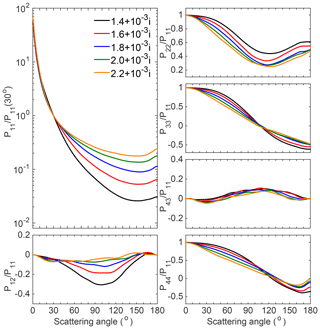
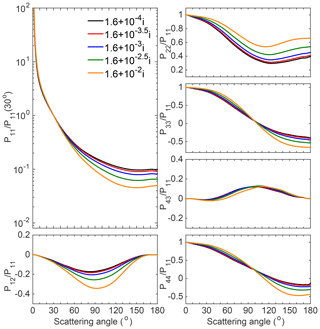
Figure 3 Simulated scattering matrix elements for Koch-fractal particles with different refractive indices. Here, the imaginary part is fixed at 0.001i, and the real part is changed from 1.4 to 2.2 with a step of 0.2. The particles are assumed to have the size distribution of feldspar, and the optical properties are simulated by considering an incident wavelength of 633 nm.

To account for irregular geometries, multiple numerical models are available for calculating the single-scattering properties of nonspherical particles (Yang and Liou, 1996a; Mishchenko et al., 1997; Yurkin and Hoekstra, 2011; Bi et al., 2013). Following Liu et al. (2013), this study uses a combination of the pseudospectral time domain (PSTD) method (Liu, 1997; Liu et al., 2012) and the improved geometric-optics method (IGOM; Yang and Liou, 1996b; Yang and Liou, 1998; Bi et al., 2014) to cover the required range of dust size parameters at visible incident wavelengths. For the irregular fractal particles, we use r, i.e., the radius of a volume-equivalent sphere, to define their sizes, so the size parameter x is defined as $x=\mathrm{2}\mathit{\pi }r/\mathit{\lambda }$ (with λ being the wavelength). Simultaneous size measurements by the AGLSD have sample sizes ranging from 0.076 to 105 µm (Volten et al., 2006; Muñoz et al., 2012); therefore, we perform numerical simulations within the same range. The PSTD is applied to handle the optical properties of geometries with size parameters up to 30, and those with size parameters over 30 are calculated by the IGOM (Liu et al., 2013). For the computations of the PSTD, the optical properties of randomly oriented particles are averaged over those from 128 different orientations, resulting in relatively smooth scattering matrix elements. After integration of the optical properties over the simultaneously measured dust size distributions given by the AGLSD, the resulting bulk scattering matrix elements of certain RIs and particle geometries can be compared with the AGLSD measurements, and the agreements between the measurements and simulations are used to specify the potentials of the corresponding methods.

The squared values of the relative differences between the simulated and measured P₁₁ are used to quantify the differences between the simulations and observations (Kemppinen et al., 2015), and the difference d is defined as Eq. (1):

$$\begin{array}{}\text{(1)}& d=\sum _{\mathit{\theta }={\mathrm{5}}^{\circ }}^{\mathrm{173}{}^{\circ }}{\left({\displaystyle \frac{P_{\mathrm{11}}^{\text{mea}}\left(\mathit{\theta }\right)-P_{\mathrm{11}}^{\text{simu}}\left(\mathit{\theta }\right)}{P_{\mathrm{11}}^{\text{mea}}\left(\mathit{\theta }\right)}}\right)}^{\mathrm{2}},\end{array}$$

where $P_{\mathrm{11}}^{\text{mea}}\left(\mathit{\theta }\right)$ is the measured P₁₁ element at scattering angle θ and $P_{\mathrm{11}}^{\text{simu}}\left(\mathit{\theta }\right)$ is that for the simulated value. Note that the AGLSD provides the scattering matrix elements with scattering angles between 5^∘ and 173^∘. The numerical model that results in the smallest value of d will be defined as our optimal model for each dust sample. Actually, we also compared the differences among other scattering matrix elements, and the optimal case is mostly consistent with the one considering only P₁₁. As a result, we try to keep the evaluation simple and use only d as a criterion.

The scattering matrices of feldspar, quartz, loess, Lokon volcanic ash, and red clay from the AGLSD are considered references, and again this study emphasizes the role of the RI of dust. These actual dust particles have different compositions, shapes, and size distributions, which cause their unique optical properties. Therefore, by considering multiple kinds of dust particles, we attempt to demonstrate that the effects of the RI generally hold. Furthermore, the influences of particle geometries can hardly be isolated or avoided during the study, so the roles of the RI and geometry will be compared. Note that the phase functions will be presented by normalizing P₁₁ (30^∘) to 1, i.e., showing $P_{\mathrm{11}}\left(\mathit{\theta }\right)/P_{\mathrm{11}}\left(\mathrm{30}{}^{\circ }\right)$, and the other nonzero scattering matrix elements are normalized with respect to P₁₁.

Figure 4 Similar to Fig. 3, except that the real part is fixed at 1.6, the imaginary part is changed from 10⁻⁴ to 10⁻² with a step of 10^0.5, and the particles are assumed to have the size distribution of Lokon volcanic ash.

3 The impact of the refractive index

As discussed in Sect. 1, large variations in the RIs at visible wavelengths do exist for dust particles in different regions due to the differences in their components. To take advantage of the numerical investigation, we consider relatively larger ranges of RIs. The Re ranges from 1.4 to 2.2 in steps of 0.1 (nine values), and values from 10⁻⁴ to 10⁻² in steps of 10^−0.5 (in logarithmical scale, i.e., five values) are used for the Im. We mostly focus on the optical properties at an incident wavelength of 633 nm, and the spectral consistency will be briefly discussed at the end of Sect. 3.

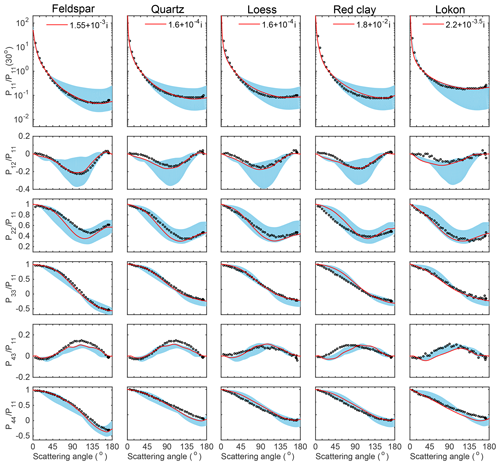
Figure 5 Comparison of the scattering matrix elements of feldspar, quartz, loess, red clay, and Lokon volcanic ash particles with different refractive indices between laboratory measurements (hallow dots) and computed results (shaded areas) at a wavelength of 633 nm. The optimal cases are also shown as the red curves.

Figure 3 illustrates the bulk scattering matrices of simulated Koch-fractal particles with different Re values. Third-generation Koch-fractal particles with the AR of 2.5 and the IR of 0.3 are applied. Figure 3 clearly shows that different scattering matrix elements have distinct sensitivities to the changes in the Re. The effects of Re on the normalized phase function $P_{\mathrm{11}}/P_{\mathrm{11}}\left(\mathrm{30}{}^{\circ }\right)$ mainly appear in the sideward and backward directions, and scattering at scattering angles larger than 30^∘ becomes stronger as Re increases. With an increase in Re, P₁₂∕P₁₁ becomes closer to zero, and P₂₂/P₁₁ becomes further from 1. The differences for the other three elements, i.e., P₃₃/P₁₁, P₄₃/P₁₁, and P₄₄/P₁₁, are less significant. Another noteworthy phenomenon is that the differences between the computed scattering matrix elements with Re between 1.4 and 1.6 are more obvious than those with Re values of 2.0 and 2.2, illustrating that the scattering matrix elements are more sensitive to the changes in Re when the value of Re is relatively small (e.g., 1.4).

Figure 4 is similar to Fig. 3 but for results with different Im values. Im directly affects particle absorption, but its impact on particle scattering properties cannot be ignored. We consider a dust sample with relatively larger sizes to better demonstrate the effect of the Im. The bulk scattering matrix elements are obtained based on the size distribution of Lokon volcanic ash samples, which have an effective radius of 7.1 µm. Again, different scattering matrix elements have different sensitivities to the change in the Im, and the P₁₁, P₁₂, and P₂₂ elements are more sensitive to the Im. With increasing Im, P₁₁/P₁₁(30^∘) decreases at scattering angles from 30^∘ to 180^∘, indicating weaker side and backward scattering. P₂₂/P₁₁ increases as the Im increases. P₃₃/P₁₁, P₄₃/P₁₁, and P₄₄/P₁₁ show less variation for different Im values. The scattering matrix elements show similar variation as Re increases or Im decreases. Generally, the scattering matrix elements change in the same directions as the Re increases or the Im decreases.

Figures 3 and 4 clearly show the impacts of the RIs on the modeling particle scattering matrix elements. With the size distribution measured simultaneously, the RI and geometry both remain variables for the numerical studies. In contrast to previous studies with a fixed RI and variable particle shapes (Merikallio et al., 2011, 2013; Ishimoto et al., 2010; Tang and Lin, 2013; Bi et al., 2010; Nousiainen and Kandler, 2015), this study tests whether the scattering matrix elements of different dust aerosols can be reproduced by models with a fixed particle shape but different RIs.

Table 1 The estimated refractive index (RI) values given by the Amsterdam–Granada Light Scattering Database (AGLSD) and the RIs corresponding to our optimal numerical results.

^∗The optimal RI values were based on the Koch-fractal particle geometry and the 50 different RI values considered in this study.

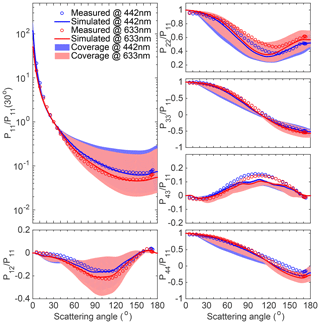
Figure 6 Comparisons of the scattering matrix elements between the measured and computed results for feldspar at wavelengths of 442 and 633 nm. The hallow dots indicate the measurement, the thick lines indicate the optimal computed results, and the shaded areas indicate the variety range by different RIs. The optimal RI at both wavelengths is $\mathrm{1.55}+{\mathrm{10}}^{-\mathrm{3}}i$.

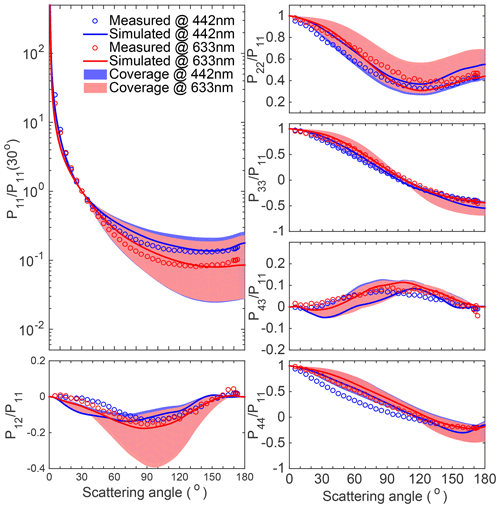
Figure 7 Similar to Fig. 6, but for the loess sample. The optimal RI is $\mathrm{2.2}+{\mathrm{10}}^{-\mathrm{2}}i$ at the wavelength of 442 nm and $\mathrm{1.6}+{\mathrm{10}}^{-\mathrm{4}}i$ at the wavelength of 633 nm.

Figure 5 compares the simulated scattering matrices of five dust species (i.e., feldspar, quartz, loess, red clay, and Lokon volcanic ash, from left to right), with measured values. For the modeling results, the default geometry, i.e., the third-generation Koch-fractal particle with the AR of 2.5 and the IR of 0.3, is used for all simulations. Most previous numerical and observational studies suggest that the Re values lie between 1.5 and 1.6, and the scattering matrix elements are more sensitive to the Re change when the Re values are relatively small. Therefore, we include an additional Re of 1.55 in this study, which results in a total of 50 complex RIs (10 Re and 5 Im values). The blue shaded regions in Fig. 5 indicate the variations in the simulated scattering matrix elements with the 50 RIs, and the red curves correspond to the optimal cases that give the minimum d among the 50 cases. Even with a fixed geometry, the simulated results of the five dust samples can achieve reasonable agreement with the measurements, especially for P₁₁/P₁₁ (30^∘), P₁₂/P₁₁, and P₃₃/P₁₁. For the feldspar sample, P₁₁/P₁₁ (30^∘), P₁₂/P₁₁, P₃₃/P₁₁, and P₄₄/P₁₁ of the optimal case agree closely with the measurements. Differences are noticed only for P₂₂/P₁₁ at scattering angles from 60^∘ to 150^∘ and P₄₃/P₁₁ from 75^∘ to 150^∘. Similar results are obtained for quartz and loess samples. The optimal results for the red clay sample are less consistent with the measurements than the results for the three samples above. Certain deviations between the computed and measured results appear at the forward direction for every nonzero matrix element of red clay except P₁₁/P₁₁ (30^∘). Furthermore, the RI of the optimal case for the red clay sample is also obviously different from those discussed above, i.e., 1.8 for the Re and 10⁻² for the Im. The computed results for Lokon volcanic ash particles are relatively consistent with the measurements with an Re that is much larger than expected values, i.e., 2.2. However, the reproductions of the forward directions of P₁₂/P₁₁ and P₄₃/P₁₁ are not satisfactory. Most of the RIs obtained for the optimal cases have a real part of 1.5–1.6 and an imaginary part between 10⁻⁴ and 10⁻³, consistent with generally accepted values and those suggested by the AGLSD. Table 1 lists the estimated RIs of five types of dust given by the AGLSD and the corresponding optimal RIs based on the particular geometry. Both the simulated and measured results of P₁₂/P₁₁ show considerable variations, and the simulated results match the measurements by mainly changing the real part of the RI. However, the computed and measured results of P₂₂/P₁₁ show obvious differences. Both the simulated and measured results of P₃₃/P₁₁ show less variation, indicating that P₃₃/P₁₁ is less sensitive to the changes in the RI, and the simulated results with almost any RI satisfactorily agree with the measurements. P₄₄/P₁₁ has features similar to those of P₃₃/P₁₁, but the consistencies between the numerical results and the measurements are slightly worse than those of the P₃₃/P₁₁. Generally, the scattering matrices of different dust samples can be reproduced by applying proper RIs with a fixed geometry, although the differences between the simulated and measured quantities of some particular elements (e.g., P₂₂/P₁₁) are noticeable, as also occurs with models that consider geometric variations.

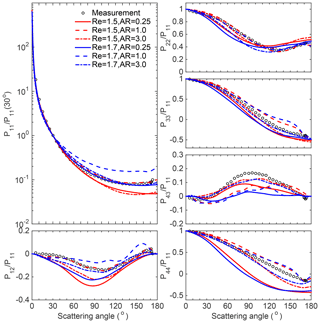
Figure 8 Comparison of the scattering matrix elements between the simulations and measurements for quartz samples with three different particle ARs at two different RIs: $\mathrm{1.5}+{\mathrm{10}}^{-\mathrm{3}}i$ and $\mathrm{1.7}+{\mathrm{10}}^{-\mathrm{3}}i$. The incident wavelength is 633 nm.

Figure 6 compares the computed and measured scattering matrices of feldspar at two different incident wavelengths, where blue and red represent the results at incident wavelengths of 633 and 442 nm, respectively. Again, the numerical results are based on the fixed Koch-fractal geometry and 50 different RIs, as mentioned above. The optimal numerical results show similar agreement with the measurements at the two wavelengths, as discussed above, i.e., close agreement for P₁₁/P₁₁ (30^∘), P₁₂/P₁₁, P₃₃/P₁₁, and P₄₄/P₁₁ while relatively larger differences for P₂₂/P₁₁ and P₄₃/P₁₁. Furthermore, the spectral differences regarding the measured results for P₂₂/P₁₁ are not shown by the simulated results, while other elements show only slight spectral differences or agree with the simulations. The optimal cases for both wavelengths correspond to the same RI of $\mathrm{1.55}+{\mathrm{10}}^{-\mathrm{3}}i$, which indicates relatively small wavelength dependence of feldspar RI. In other words, the Koch-fractal particle has a clear spectral consistency for modeling dust optical properties at multiple wavelengths, which can hardly be achieved by spheroid models (Merikallio et al., 2011; Dubovik et al., 2006; Lin et al., 2018). We also compare the spectral performance for the red clay and quartz scattering matrices, and similar results (the same optimal RI at the two incident wavelengths) are obtained.

However, the results for loess and Lokon volcanic ash are slightly different. Figure 7 illustrates the results for the loess sample as an example. The optimal results at wavelengths of 442 and 633 nm correspond to RIs of $\mathrm{2.2}+{\mathrm{10}}^{-\mathrm{2}}i$ and $\mathrm{1.6}+{\mathrm{10}}^{-\mathrm{4}}i$, respectively. Additionally, the consistencies of the computed and measured results at the wavelength of 633 nm are slightly better than those at the wavelength of 442 nm, especially for the forward directions of P₁₂/P₁₁ and P₄₃/P₁₁. For Lokon volcanic ash, the same real part of RI (Re = 2.2) is obtained at the two wavelengths, while the imaginary parts are slightly different (10⁻³i at 442 nm and 10^−3.5i at 633 nm). Thus, loess and Lokon volcanic ash may have stronger spectral differences with respect to their optical properties, which have to be considered for downstream radiative studies and remote sensing applications.

4 Refractive index vs. geometry

The importance of particle geometry in modeling dust optical properties has been well studied (Bi et al., 2010; Osborne et al., 2011; Lin et al., 2018), and Sect. 3 indicates the clear role of the RI. Thus, with particle size relatively well constrained, it becomes interesting to investigate whether the geometry or RI plays the same or different roles in modeling the dust optical properties for remote sensing and radiative forcing studies.

We first test whether different presumed RIs influence the determination of particle geometries for developing dust optical models. Figure 8 gives the measured and simulated scattering matrix elements of quartz, and the simulated results of Koch-fractal particles with three different geometries (different ARs only) and two different RIs are illustrated. The particles with ARs of 0.25, 1.0, and 3.0 and the RIs of $\mathrm{1.5}+{\mathrm{10}}^{-\mathrm{3}}i$ (the red curves) and $\mathrm{1.7}+{\mathrm{10}}^{-\mathrm{3}}i$ (the blue curves) are used. If the quartz RI is assumed to be $\mathrm{1.5}+{\mathrm{10}}^{-\mathrm{3}}i$ for the numerical simulations, the modeled results based on the Koch-fractal particles with the AR of 1.0 agree most closely with the measurements (for almost all six elements), and those with larger (3.0) or smaller (0.25) ARs both depart from the measurements. However, if the RI is assumed to be $\mathrm{1.7}+{\mathrm{10}}^{-\mathrm{3}}i$, then the results based on the particles with ARs of 0.25 and 3.0 agree more closely with the measurements, except for P₂₂/P₁₁. Clearly, Fig. 8 indicates that if different RIs are assumed, then different geometries must be applied to represent the scattering properties of actual aerosols. Similar results are obtained for the loess and red clay samples as well (not shown here). These comparisons illustrate that the RI can significantly influence the determination of appropriate geometries in modeling studies of dust optical properties.

Furthermore, we directly compare the roles of the RI and geometry in reproducing dust scattering matrices. To assess the effects of the geometry, third-generation Koch-fractal geometries with different ARs and the fixed IR of 0.3 are tested. Because the AR shows the most significant influences on the scattering properties for our Koch-fractal particles, 10 different ARs (0.25, 0.5, 0.75, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, and 4.0) are considered in the tests. The RI is fixed at $\mathrm{1.6}\pm {\mathrm{10}}^{-\mathrm{3.5}}i$ (close to the RIs of feldspar, quartz, loess, and red clay obtained for Fig. 5). For comparison, the effects of different RIs will be illustrated by considering particles with the fixed geometries used above.

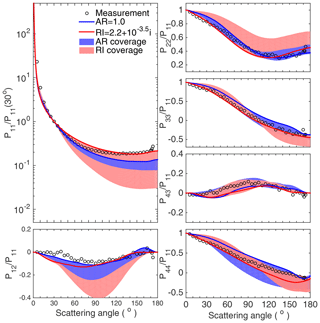
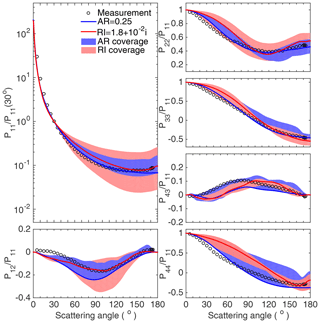
Figure 9 Comparison between the simulated results of the scattering matrix elements of the Lokon volcanic ash samples with different variable parameters, including coverage with the AR as the variable (shaded blue area), coverage with the RI as the variable (shaded red area), optimal case for the two variable parameters (blue and red lines), and the measurement given by the AGLSD (black hallow dots).

Figure 9 illustrates the scattering matrices of Lokon volcanic ash and the simulated results for particles with different ARs and RIs. The blue curves indicate the optimal case (AR = 1.0) among those with different ARs and the same RI, and the red curves are for the optimal case with an RI of $\mathrm{2.2}+{\mathrm{10}}^{-\mathrm{3.5}}i$ among those with different RIs. First, we discuss the results for P₁₁. The results for particles with different geometries, i.e., ARs, but a fixed RI are illustrated by the blue areas. If the RI close to the suggested values is considered (i.e., $\text{RI}=\mathrm{1.6}+{\mathrm{10}}^{-\mathrm{3.5}}i$), the results based on any geometry differ from the measurements, especially for the values with scattering angles larger than 90^∘. However, the red areas can cover the measurements at the edge and indicate that simulated results with an extreme RI can better reproduce the scattering matrix of Lokon volcanic ash. For other elements, the optimal results, i.e., the red and blue curves, agree with the measurements, especially for P₃₃/P₁₁, P₄₃/P₁₁, and P₄₄/P₁₁. Overall, for the Lokon volcanic ash measurements, a more reasonable RI has to be used to reproduce their optical properties, and this may be the reason why few results on modeled Lokon volcanic ash samples have been previously published. The other features illustrated by Fig. 9 are the coverage differences among the red and blue regions, which indicate the sensitivities of the particle geometry and RI. For P₁₁, P₁₂/P₁₁, and P₂₂/P₁₁, the red areas clearly cover the blue ones, indicating that particles with different RIs result in larger variations in the corresponding elements than those with different geometries. P₃₃/P₁₁ and P₄₃/P₁₁ for particles with either different geometries or different RIs show similar coverages, while the particle geometry may lead to larger variations in P₄₄/P₁₁. These differences may become useful during the development of numerical dust optical models based on observed results such as the AGLSD.

Figure 10 Similar to Fig. 9 but for the red clay sample.

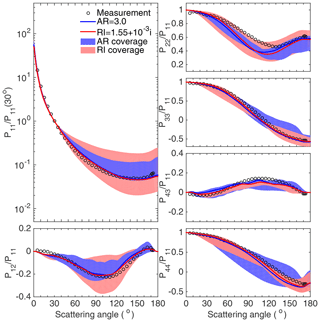
Figure 10 is similar to Fig. 9, except for the red clay particles. The blue curves correspond to results with the AR of 0.25, and the red curves correspond to those with the RI of $\mathrm{1.8}+{\mathrm{10}}^{-\mathrm{2}}i$. Comparing the two optimal cases with the different ARs and RIs, the optimal results among particles with different ARs achieve a better consistency with the measurement for P₁₁, P₂₂/P₁₁, P₃₃/P₁₁, and P₄₄/P₁₁, whereas the P₁₂/P₁₁ results from the RI optimal case are slightly better. P₄₃/P₁₁ from both cases differs from the measurements. For this case, the agreement between the modeled and measured results is clearly improved by changing the particle geometry. Similar to Fig. 9, Fig. 10 also illustrates that the changes in the geometry and RI can provide the simulations for different scattering matrix elements with different degrees of variation.

Figure 11 Similar to Figs. 9 and 10 but for the feldspar sample.

For the results of the feldspar particles in Fig. 11, the most notable feature is that the two optimal cases with different variables are highly consistent; the reproductions of the matrix elements (excluding P₂₂) are quite successful, and the simulated results of P₂₂/P₁₁ for the two optimal cases both deviate from the measurement with scattering angles between 60^∘ and 140^∘. For feldspar, i.e., the most extensively studied dust sample in the AGLSD (Bi et al., 2009; Dubovik et al., 2006; Liu et al., 2013; Lin et al., 2018; Merikallio et al., 2011; Volten et al., 2001), multiple models with appropriate combinations of the particle RI and geometry all result in close agreement with measurements. Reasonable results can be obtained by merely changing the RI even if the geometry is relatively different from reality and vice versa.

Obviously, both RI and geometry significantly affect mineral dust optical properties; however, they do so quite differently. Furthermore, even without consideration of the influence of particle size, an accurate RI has to be determined to develop an appropriate dust geometric model, and vice versa. However, if only an optically equivalent model at a single wavelength or a limited number of wavelengths is required, our results indicate that either RI or geometry can be treated as a variable while fixing the other. Thus, instead of constructing a dust model by building different geometries (e.g., Mishchenko et al., 1997; Bi et al., 2010; Liu et al., 2012; Lin et al., 2018), it is potentially possible to consider only the results from a fixed particle geometry but with various RIs. Fixing a geometry and changing only RI may be more convenient, because the RI can be defined more quantitatively.

5 Conclusions

This study investigates the role of the RI in modeling dust scattering matrix elements. Instead of reproducing the dust scattering properties by building one or a group of nonspherical geometries at a fixed RI, which may or may not be accurate, we emphasize the sensitivities of the scattering matrix on the particle RI. By simply changing the RI during numerical modeling, it is possible to characterize the optical properties of different dust particles, even if the model geometry is fixed. As a result, it becomes possible to simplify the model developments for different mineral dust particles. To be more specific, instead of constructing and testing various geometric models, using results from particles with different RIs but a fixed geometry can also be a solution for calculating the scattering properties of dust particles at different wavelengths, which would be more flexible and computationally efficient.

As expected, if different RIs are considered for dust optical property simulations, the appropriate geometry that leads to the best agreement to the observation will change accordingly. By comparing the sensitivities of the dust scattering matrix elements, it is noticed that the reproductions of the scattering matrix elements of different dust particles respond differently to changes in the RI and geometry. With a known particle size distribution, the scattering matrix of some kinds of dust (e.g., feldspar, quartz, and loess) can be well reproduced by adjusting either the RI or the geometry with the other parameters fixed, but those of other dust particles (e.g., red clay and Lokon volcanic ash) can only be reproduced by applying an extreme and fixed geometry or RI. As a result, more efforts should also be devoted to better constraining the particle RI during the development of aerosol optical properties for remote sensing and radiative transfer applications. Finally, to better constrain either particle RI or geometry for dust optical property studies, more observations on dust microphysical and optical properties should be considered.