the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical note: Estimating aqueous solubilities and activity coefficients of mono- and α,ω-dicarboxylic acids using COSMOtherm
Reyhaneh Heshmatnezhad
Jonas Elm
Theo Kurtén
We have used the COSMOtherm program to estimate activity coefficients and solubilities of mono- and α,ω-dicarboxylic acids and water in binary acid–water systems. The deviation from ideality was found to be larger in the systems containing larger acids than in the systems containing smaller acids. COnductor-like Screening MOdel for Real Solvents (COSMO-RS) underestimates experimental monocarboxylic acid activity coefficients by less than a factor of 2, but experimental water activity coefficients are underestimated more especially at high acid mole fractions. We found a better agreement between COSMOtherm-estimated and experimental activity coefficients of monocarboxylic acids when the water clustering with a carboxylic acid and itself was taken into account using the dimerization, aggregation, and reaction extension (COSMO-RS-DARE) of COSMOtherm. COSMO-RS-DARE is not fully predictive, but fit parameters found here for water–water and acid–water clustering interactions can be used to estimate thermodynamic properties of monocarboxylic acids in other aqueous solvents, such as salt solutions. For the dicarboxylic acids, COSMO-RS is sufficient for predicting aqueous solubility and activity coefficients, and no fitting to experimental values is needed. This is highly beneficial for applications to atmospheric systems, as these data are typically not available for a wide range of mixing states realized in the atmosphere, due to a lack of either feasibility of the experiments or sample availability. Based on effective equilibrium constants of different clustering reactions in the binary solutions, acid dimer formation is more dominant in systems containing larger dicarboxylic acids (C5–C8), while for monocarboxylic acids (C1–C6) and smaller dicarboxylic acids (C2–C4), hydrate formation is more favorable, especially in dilute solutions.
- Article
(3101 KB) - Full-text XML
-
Supplement
(341 KB) - BibTeX
- EndNote
Mono- and dicarboxylic acids (which are CH3(CH2)n−2COOH and COOH(CH2)m−2COOH, respectively) are common atmospheric compounds that have been detected in both the gas (Kawamura et al., 2000; Fisseha et al., 2006) and aerosol phases (Fisseha et al., 2006; Verma et al., 2017; Guo et al., 2015; Hyder et al., 2012). Carboxylic acids have been detected in high abundance in various environments, such as urban (Zhao et al., 2018; Kawamura et al., 2000; Fisseha et al., 2006; Jung et al., 2010; Guo et al., 2015), semiurban (Verma et al., 2017), marine (Kawamura and Sakaguchi, 1999; Mochida et al., 2003), and Antarctic (Kawamura et al., 1996) measurement sites. In general, small carboxylic acids (n≤3 and m≤4) are more abundant than large acids (n>3 and m>4) (Jung et al., 2010; Fisseha et al., 2006; Tsai and Kuo, 2013; Zhao et al., 2018; Guo et al., 2015; Kawamura et al., 2000). For example, Tsai and Kuo (2013) found that 77.2 % of all carboxylic acids in fine particulate matter (PM2.5) were small carboxylic acids (formic, acetic, and oxalic acids) in a broadleaved forest in central Taiwan.
An accurate description of the different aerosol phases is important for determining parameters used in aerosol modeling, such as gas-to-particle partitioning (in particular water uptake) and chemical reactivity. A large number of reactions in the aqueous aerosol phase are strongly pH dependent (Pye et al., 2020; Weber et al., 2016), but accurate predictions of aerosol acidity are highly challenging. One element to resolve is the nature and amount of acidic material dissolved in the aqueous aerosol phase. The aqueous bulk solubility of mono- and dicarboxylic acids have been measured in multiple studies (Saxena and Hildemann, 1996; Apelblat and Manzurola, 1987, 1989, 1990; Cornils and Lappe, 2000; Song et al., 2012; Romero and Suárez, 2009; Omar and Ulrich, 2006; Brooks et al., 2002). However, acid activity data of carboxylic acid–water systems are much scarcer. Jones and Bury (1927) derived the activity coefficients of formic (n= 1), acetic (n= 2), propanoic (n= 3), and butanoic (n= 4) acids in aqueous solutions at the freezing points of the binary solutions using freezing-point depression measurements. Using freezing-point depression measurements, activity coefficients are calculated using Lewis and Randall's equation for non-electrolytes. Hansen et al. (1955) derived activity coefficients of acetic, propanoic, and butanoic acids in water and the activity coefficients of water in acetic, propanoic, butanoic, pentanoic (n= 5), and hexanoic (n= 6) acids, at 298.15 K, using partial pressure measurements. In addition, Hansen et al. (1955) represented the experimental points using self-consistent activity coefficient functions. Activity coefficients of malonic, succinic, and glutaric acids (m= 3, 4, and 5) have been measured by Davies and Thomas (1956) and Soonsin et al. (2010) in bulk and particle experiments, respectively.
Group contribution methods, such as UNIFAC (Fredenslund et al., 1975) and AIOMFAC (Zuend et al., 2008), are often used to estimate activity coefficients of atmospherically relevant compounds. More recently, a quantum-chemistry-based COnductor-like Screening MOdel for Real Solvents (COSMO-RS; Klamt, 1995; Klamt et al., 1998; Eckert and Klamt, 2002) has been used to predict thermodynamic properties of multifunctional compounds. Solubilities and activity coefficients of carboxylic acids have also been estimated using the COSMO-RS theory implemented in the COSMOtherm program (COSMOtherm, 2019). For instance, Schröder et al. (2010) estimated the aqueous solubilities of various polycarboxylic acids using the BP_TZVP_C21_0025 parametrization of COSMOtherm and found that COSMOtherm was able to predict the temperature dependence of the solubilities of dicarboxylic acids (m= 2–8) well, while the absolute solubility estimates were not in good agreement with experiments. Additionally, Michailoudi et al. (2020) estimated the activity coefficients of monocarboxylic acids with even numbers of carbon atoms (n= 2, 4, 6, 8, 10, 12) at infinite dilution. In addition, they estimated the solubility of the same acids in pure water and different aqueous electrolyte solutions. They found a good agreement between experimental and estimated aqueous solubilities of the acids with the exception of butanoic acid, which in experiments has been seen to be fully soluble (Saxena and Hildemann, 1996), while COSMOtherm predicted a finite solubility.
Recent work has shown that the absolute COSMOtherm solubility and activity coefficient estimates can be improved by excluding conformers containing intramolecular hydrogen bonds from the COSMOtherm calculation (Hyttinen and Prisle, 2020). However, based on the hydrogen bonding definition of COSMOtherm, monocarboxylic acids are not able to form intramolecular hydrogen bonds. Therefore, other methods are needed to improve COSMOtherm estimates of monocarboxylic acids. On the other hand, carboxylic acids are able to form hydrogen-bonded dimers where two molecules are bound by two simultaneous intermolecular hydrogen bonds. These concerted multiple contacts, such as is seen in carboxylic acid dimer formation, are not captured by COSMO-RS. A dimerization, aggregation, and reaction extension to the COSMO-RS theory (COSMO-RS-DARE) was developed to account for these interactions (Sachsenhauser et al., 2014). For example, Cysewski (2019) was able to improve the agreement between experimental and estimated solubilities of ethenzamide in various organic solvents using COSMO-RS-DARE.
Most atmospherically relevant multifunctional compounds are not readily available for experimental determination of thermodynamic properties. Accurate theoretical estimates are therefore essential for advancing current aerosol process modeling to include more complex compounds and mixtures. Here, we demonstrate the applicability of COSMO-RS theory in calculating condensed-phase properties of atmospherically relevant organic compounds. Carboxylic acids are among the most abundant and well-characterized organic compounds in the troposphere and are, therefore, a good compound class to use to validate the use of COSMO-RS in atmospheric research. We use the newly developed COSMO-RS-DARE, as well as COSMO-RS, to estimate activity coefficients of monocarboxylic acids (n= 1–6) and α,ω-dicarboxylic acids (m= 2–8) with water in binary acid–water mixtures. In addition, we estimate aqueous solubilities and effective equilibrium constants of cluster formation of the acids.
We use the COSMOtherm software (release 19 and parametrization BP_TZVPD_FINE_19) (COSMOtherm, 2019) to estimate the solubilities and activity coefficient of linear mono- and dicarboxylic acids in binary aqueous solutions. In addition, we compute the effective equilibrium constants of water and acid dimerization (formation of a hydrogen-bonded cluster containing two water molecules or two acid molecules, respectively) and acid hydration (formation of a hydrogen-bonded cluster containing one acid and one water molecule).
2.1 Activity coefficients
COSMOtherm calculates the activity coefficient (γ) of compound i with mole fraction xi using the pseudo-chemical potentials at composition {xi} () and at the reference state (). By default, the reference state used in COSMOtherm is the pure compound (labeled as convention I; Levine, 2009):
at P=105 Pa reference pressure. T is the temperature (K), and R is the gas constant (, when μ* is given in kJ mol−1).
Pseudo-chemical potential (Ben-Naim, 1987) is an auxiliary quantity defined using the chemical potential at the reference state μ∘:
Pseudo-chemical potential has recently been used in molecular level solvation thermodynamics instead of chemical potential (Sordo, 2015). The benefit of pseudo-chemical potential is that it is valid for any concentration and fluid mixture, while the conventional chemical potential cannot necessarily be used to describe infinite dilution (xi→0) (Ben-Naim, 1978). By definition, the activity coefficient of a compound at the reference state is unity (), which leads to equal chemical and pseudo-chemical potential at the reference state. At other states (xi<1), the relation between chemical and pseudo-chemical potentials (μ and μ*, respectively) can be expressed as
Unless otherwise mentioned, the mole fractions xi correspond to mole fractions of undissociated acid or neutral non-protonated water.
2.2 Solubility
Solubilities are calculated by finding the liquid–liquid equilibrium (LLE) or the solid–liquid equilibrium (SLE) of the binary liquid–water or solid–water systems, respectively. In LLE, the chemical potential (μ) of a compound is equal in both of the liquid phases (α and β):
Combining Eqs. (2) and (3) gives the relation between chemical potential and pseudo-chemical potential at the reference state:
Equation (5) can be substituted for chemical potential in Eq. (4), giving
where and are the activities (a=xγ) of compound i in phases α and β, respectively. The liquid–liquid equilibrium condition between the solvent-rich phase (α) and the solute-rich phase (β) becomes
The SLE is solved from the solid–liquid equilibrium condition (Eckert and Klamt, 2019):
where xSOL,i is the mole fraction solubility (SOL) of compound i in the solvent. The free energy of fusion of the solute (ΔGfus(T)) is calculated from the experimentally determined heat of fusion (ΔHfus) and melting point (Tmelt) using the Schröder–van Laar equation (Prigogine and Defay, 1954):
Here the heat capacity of fusion (ΔCp,fus) is estimated from the melting point and the heat of fusion:
Table 1 shows experimental melting points and heats of fusion of the dicarboxylic acids of this study. Melting points and heats of fusion of the monocarboxylic acids are not used, since all of the monocarboxylic acids studied here are in liquid phase at 298.15 K.
Table 1List of the studied α,ω-dicarboxylic acids and their experimentally determined melting points and heats of fusion. The values were measured using anhydrous acids (crystalline at 298.15 K). The melting point of oxalic acid reported by Booth et al. (2010) (370 K) is likely the temperature of the phase transition from dihydrate to anhydrous crystal polymorph. Similar transition was seen by Omar and Ulrich (2006) at 378.35 K in their differential scanning calorimetry experiment.
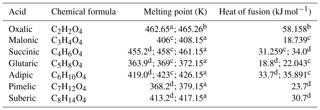
a Cornils and Lappe (2000). b Omar and Ulrich (2006). c Booth et al. (2010). d Roux et al. (2005).
2.3 Effective equilibrium constants
COSMOtherm estimates effective equilibrium constants of condensed-phase reactions from the free energy of the reaction ():
The reaction free energy is calculated from the free energies of the pure reactants () and products ():
The free energy of compound i is the sum of the energy of the solvated compound (ECOSMO), the averaged correction for the dielectric energy (dE; Klamt et al., 1998), and the pseudo-chemical potential of the pure compound:
2.4 Concentration-dependent reactions (COSMO-RS-DARE)
In COSMO-RS, the surface of a molecule is divided into surface segments that represent the surface charges of the molecule. The surface is considered an interface between a virtual conductor around the molecule and the cavity formed by the molecule (Klamt and Schüürmann, 1993). Each surface segment has an area (Å−2) and a screening charge density (σ, given in units of eÅ−2, where e represents the charge on an electron). Interactions between molecules are described through the interaction between surface segments of the different molecules. Examples of σ surfaces used in COSMOtherm calculations are shown in Fig. 1. The red color of a σ surface signifies a positive screening charge density (negative partial charge) and the blue color a negative screening charge density (positive partial charge).
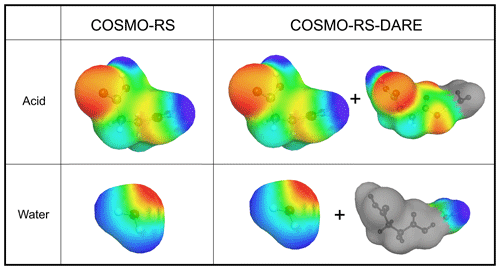
Figure 1The σ surfaces of succinic acid and water conformers used in COSMO-RS and COSMO-RS-DARE calculations. The conformer distributions in COSMO-RS-DARE include parts of cluster σ surfaces (in this example a hydrate cluster). Color coding of σ surfaces: red is negative partial charge, blue is positive partial charge, green is neutral partial charge, and grey is omitted σ surface.
Concerted multiple contacts, such as carboxylic acid dimer formation, are not captured by COSMO-RS. COSMOtherm is able to consider these hydrogen-bonded clusters using the dimerization, aggregation, and reaction extension (COSMO-RS-DARE; Sachsenhauser et al., 2014). We use the COSMO-RS-DARE method in our activity coefficient and solubility calculations. In our equilibrium constant calculations, the clusters in the system are included as the product of the clustering reactions. The method is described below and the full COSMO-RS-DARE derivation can be found in Sachsenhauser et al. (2014).
A clustering reaction between molecules A and B can be described by the equilibrium:
In acid–water systems, A and B can be either a carboxylic acid or a water molecule. In COSMO-RS-DARE, the product clusters are included in COSMOtherm calculations by using the σ surfaces of molecule A in the cluster and omitting the part of the σ surface that is assigned to the molecule clustered with A (i.e., molecule B). Similarly, the clustering product of molecule B is included in the calculation by omitting the σ surface assigned to molecule A from the σ surface of A⋅B. Examples of these partial σ surfaces are shown on the right-hand side of Fig. 1.
The formation of hydrogen bonds (in hydrates or dimers) is taken into account using the interaction energy of the two reacting compounds. The formation free energy of the cluster (G(A,A⋅B)) is calculated using fit parameters cH and cS (enthalpic and entropic contributions, respectively) to describe the interaction between the monomers A and B in the cluster (A⋅B):
The fit parameters are used because COSMOtherm is unable to calculate the energy of a monomer in a cluster. Instead, the energy of a monomer in a cluster is assumed to be equal to the energy of the lowest-energy conformer of the same compound, and the favorability of the cluster formation is estimated using the fit parameters. Without temperature-dependent experimental data, it is not possible to fit both fit parameters. We therefore consider the enthalpic parameter cH as the total formation free energy parameter at 298.15 K, setting the entropic parameter cS to zero.
COSMO-RS-DARE was originally developed for systems containing carboxylic acids in nonpolar solvents (Sachsenhauser et al., 2014). In a carboxylic acid–water system, both the carboxylic acid and water are able to form strongly bound clusters. In addition, hydrated acids can be formed. We are thus including the interactions of the clustering reactions for both A and B, even when A = B.
2.5 Input file generation
The “.cosmo” files of water and the monocarboxylic acids with a low number of conformers (< 10) are taken from the COSMObase (COSMObase, 2011) database. For the dicarboxylic acids, acid and water dimers, and the hydrates of pimelic (m= 7) and suberic (m= 8) acids, we use the following systematic conformer search approach detailed by Kurtén et al. (2018) as it has been shown to give more consistent results than other conformer sampling approaches. The conformers are found using the systematic conformer search in the Spartan program (Wavefunction Inc., 2014, 2016). The conformer set is then used as input to the COSMOconf program (COSMOconf, 2013) (using the TURBOMOLE program; TURBOMOLE, 2010), which runs initial single-point COSMO calculations at the BP/def-SV(P) level of theory to compare the pseudo-chemical potentials of the conformers and remove similar structures. Initial geometry optimizations are calculated at the BP/def-SV(P) level of theory, and duplicate structures are removed by comparing the new geometries and pseudo-chemical potentials. Final geometries are optimized at the BP/def-TZVP level of theory, and after a second duplicate removal step, final single-point energies are calculated at the BP/def2-TZVPD-FINE level of theory.
For acid dimers, we use the lowest gas-phase energy structures found by Elm et al. (2019) as a starting structure for systematic conformer search. For hydrated monocarboxylic acids and smaller dicarboxylic acids (m≤ 6), the clusters are built by adding a water molecule to each conformer of the free acids. For monocarboxylic acids, the water molecule is placed on the carboxylic acid group forming two intermolecular hydrogen bonds between the molecules. For dicarboxylic acids, a water molecule is added to either end of the acid, forming two hydrate conformers from a single acid conformer. For the dicarboxylic acid conformers with the two acid groups close to each other, additional conformers are created for cases where the water molecule is interacting with both acid groups. Figure 2 illustrates the formation of two different adipic acid hydrate conformers from a single monomer conformer. A cluster conformer where the water molecule is attached to one carboxylic acid group is shown on the top right corner, and in the bottom right corner conformer, the water molecule is bound to both acid groups. Due to the large number of conformers of nonhydrated pimelic (m= 7) and suberic (m= 8) acids (75 and 132, respectively), the monohydrate conformers of those two acids are sampled separately using Spartan.
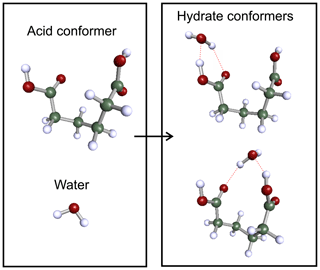
Figure 2The formation of dicarboxylic acid hydrate conformers. Color coding: green is C, white is H, and red is O.
We use only clusters of two molecules in our calculations. In carboxylic acid dimers, the hydrogen bond donors and acceptors are saturated, which means that carboxylic acids are unlikely to form larger clusters than dimers (Vawdrey et al., 2004; Elm et al., 2014, 2019). Computational studies (Aloisio et al., 2002; Weber et al., 2012; Kildgaard et al., 2018) have shown that, in the gas phase, the energetically most favorable dihydrate is formed by two water molecules attaching to the same carboxylic acid group. Therefore, adding a second water molecule to the cluster does not significantly change the probability distribution of the screening charge density (σ profile) of the acid in the cluster compared to the acid in a monohydrate or dimer.
Conformers containing no intramolecular hydrogen bonds (Kurtén et al., 2018; Hyttinen and Prisle, 2020) are used in the COSMO-RS solubility and activity coefficient calculations. Due to the intermolecular hydrogen bonding in the hydrate and dimer clusters, all conformers (up to 40 conformers) of monomers and clusters are used in the effective equilibrium constant calculations. In COSMO-RS-DARE calculations, we use all conformers of the monomers and only the lowest solvated energy conformers of the clusters.
3.1 Effective equilibrium constants of clustering reactions
We estimated the effective equilibrium constants of the different clustering reactions (i.e., hydration and dimerization) of the binary acid–water systems. A comparison between the hydration and acid dimerization equilibrium constants in the aqueous phase is given in Fig. 3 and Table 2. The equilibrium constants for both the dimerization and hydration reactions are similar between all of the monocarboxylic acids (not labeled in Fig. 3). For the dicarboxylic acid, we can see larger variation in both the hydration and dimerization reactions. Note that the COSMO-RS-DARE method is not used in the effective equilibrium constant calculations, because the clusters are already included in the calculation as products.
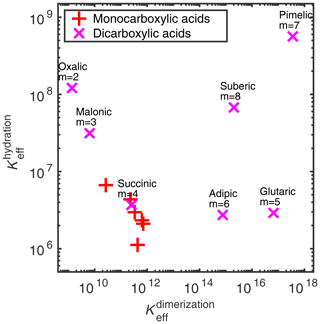
Figure 3Dimensionless effective equilibrium constants of acid dimer and hydrate formation ( and , respectively) in condensed phase, at 298.15 K. See Table 2 for the values.
Table 2Dimensionless effective equilibrium constants (Keff) of cluster formation in condensed phase at 298.15 K.
For all of the acids, the effective equilibrium constant of dimerization is higher than that of the hydrate formation of the corresponding acid, meaning that acid dimer formation is energetically more favorable than hydrate formation. However, in dilute conditions, water is more abundant, shifting the equilibrium from acid dimerization to hydration. The dimerization-to-hydration ratio is the lowest for oxalic (m= 2) and malonic (m= 3) acids, while monocarboxylic acids and succinic acid (m= 4) have similar (intermediate) ratios, and the larger dicarboxylic acids (m= 5–8) have higher ratios. This means that, in dilute solutions, oxalic, malonic, and succinic acids will most likely interact with water instead of other acid molecules.
Vawdrey et al. (2004) calculated the dimerization enthalpies (at the B3LYP/6-31++G(2d,p) level of theory) of monocarboxylic acids (n= 2–6) and found a notable even–odd variation (dimerization of the acids with odd numbers of carbon atoms is more favorable than of acids with even numbers of carbon atoms). The same is seen here in the condensed phase, where the effective equilibrium constants of butanoic and hexanoic acids are lower than of propanoic and pentanoic acids, respectively. Otherwise, there is a slightly increasing trend in the effective equilibrium constants with increasing number of carbon atoms in the monocarboxylic acids. For larger dicarboxylic acids (m≥4), Elm et al. (2019) found an even–odd alternation in the dimer-to-monomer ratio in the gas phase, calculated at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory. We observe a similar increase in the effective equilibrium constants with the increasing carbon chain length in the smaller dicarboxylic acids (m= 2–5) and an even–odd alternation in the larger dicarboxylic acids (m= 4–8) in any condensed phase.
3.2 Activity coefficients
3.2.1 Monocarboxylic acids
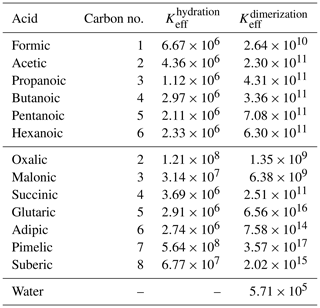
We calculated the activity coefficient of the monocarboxylic acids and water in the binary acid–water mixtures using the COSMO-RS-DARE method. Hansen et al. (1955) derived the activity coefficients of acetic (n= 2), propanoic (n= 3), and butanoic (n= 4) acids in mixtures with water from partial pressure measurements. In addition, they determined activity coefficients of water in aqueous acetic, propanoic, butanoic, pentanoic (n= 5), and hexanoic (n= 6) acid mixtures. We used these experimental activity coefficients to fit the enthalpic parameters (cH) for each of the acids in the COSMO-RS-DARE calculations. Figure 4 shows a comparison between the estimated and experimentally determined activity coefficients of these monocarboxylic acids, and formic acid (n= 1), for which no experimental activity coefficient data are available.
The reactions included in the calculations are water dimer (H2O⋅H2O) and acid hydrate (RCOOH⋅H2O) formation. A comparison between COSMO-RS-estimated activity coefficients and COSMO-RS-DARE-estimated activity coefficients, with different clusters included in the calculation, is shown for acetic acid in Fig. S1 of the Supplement. For acetic acid, we found the best fit between experimental and estimated activity coefficients using cH=0 kJ mol−1 for both the water dimerization and acid hydration reactions. Decreasing the cH of either clustering reaction leads to stronger deviation from ideality, which in our case leads to a worse fit for water activity coefficient, and positive parameter values cannot be used to lower the interaction enthalpy. The effective equilibrium constant for water dimer formation (5.71×105) is below that of acetic acid hydration (4.36×106), which explains why the fit parameter of the water dimer hydration should be higher (or equal, since positive values are not possible) than the parameter for acid hydrate formation. Additionally, we calculated UNIFAC predictions of acid and water activity coefficients using AIOMFAC-web (AIOMFAC-web, 2020; Zuend et al., 2008, 2011). These calculations (without inorganic ions) correspond to modified UNIFAC calculations by Peng et al. (2001). From Fig. S1 we see that, for acetic acid, the UNIFAC model underestimates the experimental activity coefficients more than even the COSMO-RS estimate. Similar to COSMO-RS, UNIFAC is not able to predict the increasing trend of water activity coefficients with the increasing acid mole fraction.
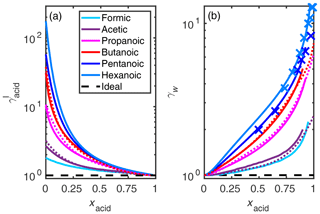
Figure 4Activity coefficients (γI) of (a) monocarboxylic acids and (b) water in all mixing states of the binary aqueous solutions, at 298.15 K. The solid lines represent activity coefficient estimates using COSMO-RS-DARE, dotted lines are calculated from the equations fitted to experiments by Hansen et al. (1955), and the markers are the experimental points from the same study. For the studied acids with finite aqueous solubilities at 298.15 K (pentanoic and hexanoic acid), water activity coefficients were measured using acid-rich solutions (Hansen et al., 1955). The water activity coefficients at high xacid are not shown in the figure, because COSMO-RS-DARE overpredicts the experiments by several orders of magnitude. All activity coefficient values are given in Tables S3 and S4 of the Supplement.
For the other monocarboxylic acids studied here, we used the same cH value for water dimerization that was found for the acetic acid–water system, and we fitted the cH of acid hydrate formation to the experimental activity coefficients of water and the acids in the corresponding acid–water systems (Hansen et al., 1955). The enthalpic parameter values of acid hydration used to estimate the activity coefficients shown in Fig. 4 are 0.0, 0.0, −10.5, −14.6, −9.2, and −8.4 kJ mol−1 for formic (n= 1), acetic (n= 2), propanoic (n= 3), butanoic (n= 4), pentanoic (n= 5), and hexanoic (n= 6) acid, respectively. For formic acid, we used the same cH parameter as for acetic acid due to lack of experimental activity coefficients. If the enthalpic parameters in COSMO-RS-DARE calculations are not fitted to experimental activity coefficients and instead are set to zero, the activity coefficients of both acid and water underestimate the experimental activity coefficients of Hansen et al. (1955) (see Fig. S2 of the Supplement). If no experimental activity coefficients are available for fitting the COSMO-RS-DARE parameters, COSMO-RS estimates agree with experiments and are overall better than COSMO-RS-DARE or UNIFAC. COSMO-RS-estimated acid activity coefficients are close to the measured values in all mixing states, and for water activity coefficients, the agreement between COSMO-RS and experiments is good in mixing states with xacid<0.75.
Sachsenhauser et al. (2014) used the COSMO-RS-DARE method for binary systems containing either acetic (n= 2) or propanoic (n= 3) acid and a nonpolar organic solvent. Their calculations show that the dimerization parameter (equivalent to cH in our calculations) is higher for propanoic acid than for acetic acid. This is opposite to what we observed for the hydration parameters, where cH was found to be higher for acetic acid than for propanoic acid. This indicates that the fit parameters of one clustering reaction cannot be used to estimate the corresponding fit parameters of another clustering reactions of the same compound.
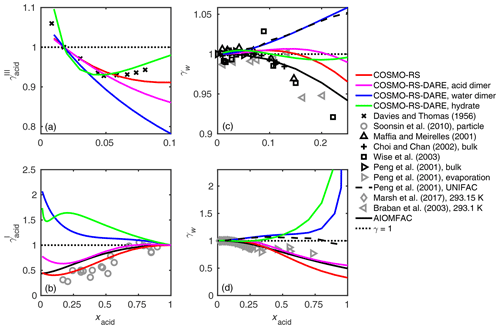
Figure 5Activity coefficients of (a, b) malonic acid and (c, d) water in the binary mixtures at 298.15 K calculated using different clustering reactions in the COSMO-RS-DARE calculation. As a comparison are activity coefficients of malonic acid by Davies and Thomas (1956) (at 298.15 K given in convention III) and Soonsin et al. (2010) (particle measurements at various temperatures given in convention I) and of water by Maffia and Meirelles (2001), Choi and Chan (2002), Wise et al. (2003), Peng et al. (2001), Marsh et al. (2017), Braban et al. (2003), and AIOMFAC-web (2020).
While COSMO-RS is fully predictive, COSMO-RS-DARE requires parameter fitting using experimental data. Fitted COSMO-RS-DARE parameters from one system can be used in other systems where the same clustering reactions are relevant. For instance, Sachsenhauser et al. (2014) found that the same interaction parameters of acid dimers can be used in systems containing other similar (nonpolar) solvents. This indicates that our interaction enthalpies can be applied to other aqueous systems, e.g., ternary systems containing an inorganic salt, in addition to the carboxylic acid and water. This would allow for extending the findings of this study to atmospherically relevant aerosol solutions.
The increasing length of the acid carbon backbone leads to larger deviation from ideality (γ=1) for both the acid and water. In convention I, this means the acid and water activity coefficient values are higher in mixtures containing the longer acids than the shorter acids. We observe that COSMO-RS-DARE estimated activity coefficients agree well with the experiments once the cH parameter is fitted. However, when the hydrate and water dimer reactions are included, COSMO-RS-DARE is not able to predict realistic activity coefficients for water at high mole fractions (xacid>0.9) of the acids. This is likely due to the low concentration of water in the binary solution, leading to errors in the description of the interactions between water molecules. Still, COSMO-RS-DARE estimates agree well with the experiments at least up to 0.9 mole fraction of the monocarboxylic acids. This is an improvement compared to the UNIFAC model, which fails to reproduce experimental water activity coefficients already at acid mole fractions above 0.25. At very high acid mole fractions (xacid>0.95), COSMO-RS-DARE predicts several orders of magnitude higher activity coefficients than what was seen in experiments.
3.2.2 Dicarboxylic acids
We tested the effect of including different clusters in the activity coefficient calculation of malonic acid (m= 3). A comparison between the experimental, UNIFAC-modeled, and COSMOtherm-estimated activity coefficients is shown in Fig. 5. The malonic acid activity coefficients are compared in convention III (Fig. 5a) and in convention I (Fig. 5b). In convention III, acid activity coefficients are given with respect to a 1 mol kg−1 solution reference state (see the Supplement for more information). The COSMOtherm-estimated water activity coefficients are compared with experimental bulk (Fig. 5c) and particle (Fig. 5d) phase activity coefficients and UNIFAC-estimated activity coefficients.
For malonic acid (and other studied dicarboxylic acids; see Figs. S3–S5 of the Supplement), COSMO-RS-DARE is not able to improve the agreement between experiments and COSMOtherm estimates; the best overall fit is found using COSMO-RS. The water activity coefficients estimated using COSMO-RS are close to ones estimated using the UNIFAC model (modified UNIFAC; Peng et al., 2001). Similarly to what has been seen with the UNIFAC model, COSMO-RS is able to predict water activity coefficients obtained from bulk and evaporation (supersaturated) measurements.
Figure S4 of the Supplement shows comparisons between experimental and COSMOtherm-estimated water activity coefficients in oxalic, adipic, and pimelic acids. For these three acids, only water activities have been determined experimentally (Braban et al., 2003; Maffia and Meirelles, 2001; Marsh et al., 2017; Peng et al., 2001). In addition, water activities in adipic and pimelic acid solutions were only measured in particle solutions (Marsh et al., 2017). We found a good agreement between the particle measurements and COSMO-RS-estimated water activity coefficients, with COSMO-RS slightly overestimating the experiments. This result is in line with previous comparisons of hydroxy carboxylic acids (Hyttinen and Prisle, 2020).
The COSMO-RS-estimated activity coefficients of the studied dicarboxylic acids are shown in Fig. 6. We can see that, using convention I, the activity coefficients of the smaller dicarboxylic acids are lower than of the larger dicarboxylic acids. Comparing COSMO-RS (solid lines) and UNIFAC estimates (dotted lines), there is less variation between the UNIFAC-estimated activity coefficients for the different acids studied than between the COSMO-RS estimates. This indicates that, in COSMO-RS, the number of carbon atoms has a larger effect on activity coefficients than estimated by UNIFAC.
Additionally, we computed activity coefficients with consideration of the first dissociation step for oxalic acid (the most acidic dicarboxylic acid of this study) with dissociation of oxalic acid included in the COSMO-RS calculation. In this case, the system contains neutral oxalic acid (H2A) and water (H2O), as well as singly or doubly deprotonated oxalic acid (HA− or A2−, respectively) and hydronium ion (H3O+) according to the dissociation equilibrium.
While both acid groups of oxalic acid can dissociate, here we consider only the first deprotonation, because the second dissociation constant of oxalic acid in water is higher (3.81; Rumble, 2018) than the first one (1.25; Rumble, 2018) and has a smaller effect on the equilibrium. Figure S6 of the Supplement shows the difference between activity coefficients in a system where dissociation of oxalic acid is included and the binary system containing only neutral compounds. The calculation procedure is explained in more detail in the Supplement. There is no large difference in water activity coefficients when the ions are added to the system. A small change is seen in the acid activity coefficients, especially in the concentrated solutions where the estimated mole fraction of dissociated acid and hydronium ion is high. For the other carboxylic acids studied here, the effect of including dissociation is likely to be smaller than for oxalic acid, due to the lower mole fractions of ions present in solutions of less acidic compounds.
Figure 6COSMO-RS- (solid lines) and UNIFAC-estimated (dotted lines; AIOMFAC-web, 2020) activity coefficients (γI) of (a) dicarboxylic acids and (b) water in the binary acid–water mixtures at 298.15 K. All COSMOtherm-estimated activity coefficient values are given in Tables S5 and S6 of the Supplement.
3.3 Aqueous solubility
We estimated the aqueous solubility of the monocarboxylic acids (n= 1–6) using the COSMO-RS-DARE method. Since activity coefficients are used in the equilibrium conditions of the LLE calculations, we used the same cH parameters that were fitted in the activity coefficient calculations to determine whether the same parameter value can be used in LLE calculations. As a comparison, we computed the same solubilities using COSMO-RS. Based on previous COSMOtherm calculations, Michailoudi et al. (2020) found a good agreement with experimental aqueous solubilities of fatty acids with even numbers of carbon atoms (n= 2, 4, 6, … , 12). A comparison between experimentally determined aqueous solubilities and the COSMOtherm estimates of monocarboxylic acids are shown in Fig. 7.
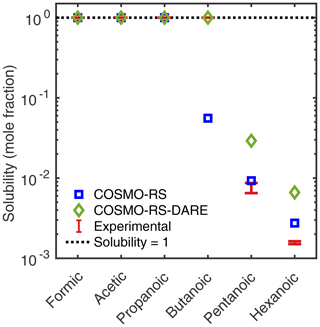
Figure 7COSMOtherm-estimated aqueous solubility of monocarboxylic acids calculated using COSMO-RS and COSMO-RS-DARE, at 298.15 K. Experimental solubilities by Saxena and Hildemann (1996) (n= 1–6) and Romero and Suárez (2009) (n= 5–6).
We see that when using COSMO-RS-DARE, COSMOtherm is able to predict the miscibility of the smaller monocarboxylic acids (n= 1–4), but the experimental solubilities of pentanoic (n= 5) and hexanoic (n= 6) acids are overestimated to a greater degree than when using COSMO-RS. On the other hand, COSMO-RS underestimates the experimental solubility of butanoic acid by a factor of 18, while COSMO-RS-DARE overestimates the experimental solubilities (upper limit) of pentanoic and hexanoic acids only by factors of 3.4 and 4.1, respectively.
For dicarboxylic acids, we estimated aqueous solubilities using COSMO-RS. The COSMOtherm-estimated and experimental solubilities are shown in Fig. 8. Different experimental heat of fusion and melting point values have been reported for some of the studied dicarboxylic acids. We calculated the lower and upper limit free energies of fusion by combining the different experimental values, and the aqueous solubilities were estimated using the two different free energy of fusion values. The higher ΔGfus estimate gives a lower aqueous solubility. The variability in the COSMOtherm-estimated solubilities is smaller than in the experimental solubilities.
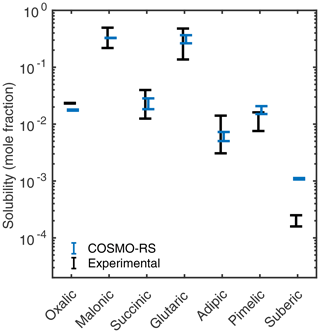
Figure 8Estimated solubilities of the dicarboxylic acids compared to their experimental solubilities by Apelblat and Manzurola (1987) (m= 2–4, 6), Apelblat and Manzurola (1989) (m= 5), Apelblat and Manzurola (1990) (m= 7–8), Saxena and Hildemann (1996) (m= 2–6), Omar and Ulrich (2006) (m= 2), Zhang et al. (2013) (m= 2–8), Brooks et al. (2002) (m= 4), Song et al. (2012) (m= 5), and O'Neil (2013) (m= 5), at 298.15 K. The lower and upper limit solubility estimates are obtained using the highest and lowest free energies of fusion (estimated from experimental melting point and heat of fusion values in Table 1), respectively.
The COSMO-RS solubility estimates of most of the dicarboxylic acids (m= 3–7) are within the range of experimentally determined solubilities. Using all lowest-energy conformers (up to 40 conformers), instead of only conformers containing no intramolecular hydrogen bonds, lowers the solubility estimates of all acids by a factor of 1.2 on average. The same effect of including conformers containing intramolecular hydrogen bonds has been previously seen in aqueous solubilities of citric, tartaric, malic, and maleic acids, as well as multifunctional organosulfates (Hyttinen and Prisle, 2020).
We compared COSMOtherm-estimated activity coefficients and aqueous solubilities of simple carboxylic acids with experimental values and a commonly used UNIFAC model, and we generally found a good agreement between experiments and COSMO-RS estimates. Using COSMO-RS-DARE, we were able to further improve the agreement between estimated and experimental water activity coefficients in binary monocarboxylic acid–water systems significantly compared to using COSMO-RS or UNIFAC. The COSMO-RS estimates of monocarboxylic acid activity coefficient in aqueous solutions agree with the experiments quite well, and they were further improved by COSMO-RS-DARE when the enthalpic fitting parameters were fitted using experimental activity coefficients. We were also able to estimate activity coefficients of pentanoic and hexanoic acids using only experimental water activity coefficients in the fitting of the COSMO-RS-DARE enthalpic parameters. In addition, COSMO-RS-DARE was able to predict the miscibility of butanoic acid in water (using the fitting parameters of activity coefficient calculations), while COSMO-RS predicted a finite solubility. However, in aqueous solubility calculations of pentanoic and hexanoic acids, COSMO-RS led to a better agreement between the experiments and estimates compared to COSMO-RS-DARE.
For dicarboxylic acid–water systems, COSMO-RS produced better agreement with experiments than COSMO-RS-DARE. The experimental water activity coefficients from different sources have large variations and COSMO-RS-estimated water activity coefficients fit within the range of experimental water activity coefficients obtained from bulk and evaporation measurements. We also found a good agreement between COSMO-RS-estimated coefficients and experimental acid activity coefficients at all acid mole fractions.
COSMO-RS was able to reproduce the same even–odd behavior of the dicarboxylic acid properties that has previously been seen experimentally in vapor pressures (Bilde et al., 2003) and solubilities (Zhang et al., 2013), as well as computationally in gas-phase dimer formation (Elm et al., 2019). The calculated even–odd behavior observed here in aqueous solubilities is likely partially due to the even–odd variation of the melting points and heats of fusion. There is also no visible even–odd behavior in the COSMO-RS-estimated activity coefficients of the dicarboxylic acids. However, even–odd variation is seen in the effective equilibrium constants of dimerization of the larger dicarboxylic acids (m≥4), which do not rely on experimental properties.
Mono- and dicarboxylic acids are very common in the atmosphere and often used as model compounds for oxygenated functionalities in a range of applications from vapor pressure, condensation–evaporation, cloud condensation nuclei activity, and hygroscopicity but also aerosol-phase and heterogeneous reactivity (Prenni et al., 2001; McNeill et al., 2008; Schwier et al., 2012; Rossignol et al., 2016). Solubilities and activity coefficients of these secondary organic aerosol (SOA) constituents are needed to accurately predict their activities and to determine central properties such as composition, phase state, and chemical reactivity. Accurate computational tools are critical to provide this information for systems where experimental data are not readily accessible in literature or by experimental design. We showed that COSMOtherm provides a good solution to estimating thermodynamic properties of atmospherically relevant organic compounds that are not commercially available for measurements. In addition to simple binary systems studied here, COSMOtherm can be used to predict liquid-phase properties, such as activity coefficients, in complex, atmospherically relevant systems.
The research data have been deposited in a reliable public data repository (the CERN Zenodo service) and can be accessed at https://doi.org/10.5281/zenodo.3842593 (Hyttinen et al., 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-20-13131-2020-supplement.
NH performed the COSMOtherm calculations. NH, RH, and JE generated input files for the COSMOtherm calculations. NH and NLP analyzed the results with contributions from all co-authors. NH wrote the first version of the manuscript and the response to reviewers with contributions from all co-authors. NLP conceived, planned, supervised, and secured funding for the project.
The authors declare that they have no conflict of interest.
We thank CSC IT Center for Science, Finland, for computational resources.
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program, project SURFACE (grant agreement no. 717022); the Academy of Finland (grant nos. 308238, 314175, 315600 and 335649); the Swedish Research Council Formas (project no. 2018-01745-COBACCA); and the Independent Research Fund Denmark (grant no. 9064-00001B).
Open access funding provided by Helsinki University Library.
This paper was edited by Barbara Ervens and reviewed by two anonymous referees.
AIOMFAC-web: version 2.32, available at: http://www.aiomfac.caltech.edu, last access: 11 August 2020. a, b, c
Aloisio, S., Hintze, P. E., and Vaida, V.: The hydration of formic acid, J. Phys. Chem. A, 106, 363–370, https://doi.org/10.1021/jp012190l, 2002. a
Apelblat, A. and Manzurola, E.: Solubility of oxalic, malonic, succinic, adipic, maleic, malic, citric, and tartaric acids in water from 278.15 to 338.15 K, J. Chem. Thermodyn., 19, 317–320, https://doi.org/10.1016/0021-9614(87)90139-X, 1987. a, b
Apelblat, A. and Manzurola, E.: Solubility of ascorbic, 2-furancarboxylic, glutaric, pimelic, salicylic, and o-phthalic acids in water from 279.15 to 342.15 K, and apparent molar volumes of ascorbic, glutaric, and pimelic acids in water at 298.15 K, J. Chem. Thermodyn., 21, 1005–1008, https://doi.org/10.1016/0021-9614(89)90161-4, 1989. a, b
Apelblat, A. and Manzurola, E.: Solubility of suberic, azelaic, levulinic, glycolic, and diglycolic acids in water from 278.25 K to 361.35 K, J. Chem. Thermodyn., 22, 289–292, https://doi.org/10.1016/0021-9614(90)90201-Z, 1990. a, b
Ben-Naim, A.: Standard thermodynamics of transfer. Uses and misuses, J. Phys. Chem., 82, 792–803, https://doi.org/10.1021/j100496a008, 1978. a
Ben-Naim, A.: Solvation Thermodynamics, Plenum Press, New York, London, 1987. a
Bilde, M., Svenningsson, B., Mønster, J., and Rosenørn, T.: Even-odd alternation of evaporation rates and vapor pressures of C3-C9 dicarboxylic acid aerosols, Environ. Sci. Technol., 37, 1371–1378, https://doi.org/10.1021/es0201810, 2003. a
Booth, A. M., Barley, M. H., Topping, D. O., McFiggans, G., Garforth, A., and Percival, C. J.: Solid state and sub-cooled liquid vapour pressures of substituted dicarboxylic acids using Knudsen Effusion Mass Spectrometry (KEMS) and Differential Scanning Calorimetry, Atmos. Chem. Phys., 10, 4879–4892, https://doi.org/10.5194/acp-10-4879-2010, 2010. a, b
Braban, C. F., Carroll, M. F., Styler, S. A., and Abbatt, J. P. D.: Phase transitions of malonic and oxalic acid aerosols, J. Phys. Chem. A, 107, 6594–6602, https://doi.org/10.1021/jp034483f, 2003. a, b
Brooks, S. D., Wise, M. E., Cushing, M., and Tolbert, M. A.: Deliquescence behavior of organic/ammonium sulfate aerosol, Geophys. Res. Lett., 29, 1917, https://doi.org/10.1029/2002GL014733, 2002. a, b
Choi, M. Y. and Chan, C. K.: Continuous measurements of the water activities of aqueous droplets of water-soluble organic compounds, J. Phys. Chem. A, 106, 4566–4572, https://doi.org/10.1021/jp013875o, 2002. a
Cornils, B. and Lappe, P.: Dicarboxylic acids, aliphatic, Ullmann's Encyclopedia of Industrial Chemistry, 1–18, 2000. a, b
COSMObase: version 17.01, COSMOlogic GmbH & Co. KG., Leverkusen, Germany, 2011. a
COSMOconf: version 4.3, COSMOlogic GmbH & Co. KG., Leverkusen, Germany, 2013. a
COSMOtherm: version C3.0, Release 19, COSMOlogic GmbH & Co. KG., Leverkusen, Germany, 2019. a, b
Cysewski, P.: Prediction of ethenzamide solubility in organic solvents by explicit inclusions of intermolecular interactions within the framework of COSMO-RS-DARE, J. Mol. Liq., 290, 111163, https://doi.org/10.1016/j.molliq.2019.111163, 2019. a
Davies, M. and Thomas, D. K.: Isopiestic Studies of Aqueous Dicarboxylic Acid Solutions, J. Phys. Chem., 60, 41–44, https://doi.org/10.1021/j150535a011, 1956. a, b
Eckert, F. and Klamt, A.: Fast solvent screening via quantum chemistry: COSMO-RS approach, AIChE J., 48, 369–385, https://doi.org/10.1002/aic.690480220, 2002. a
Eckert, F. and Klamt, A.: COSMOtherm Reference Manual, version C30, Release 19, COSMOlogic GmbH & Co, KG., Leverkusen, Germany, 2019. a
Elm, J., Kurtén, T., Bilde, M., and Mikkelsen, K. V.: Molecular interaction of pinic acid with sulfuric acid: Exploring the thermodynamic landscape of cluster growth, J. Phys. Chem. A, 118, 7892–7900, https://doi.org/10.1021/jp503736s, 2014. a
Elm, J., Hyttinen, N., Lin, J. J., Kurtén, T., and Prisle, N. L.: Strong Even/Odd Pattern in the Computed Gas-Phase Stability of Dicarboxylic Acid Dimers: Implications for Condensation Thermodynamics, J. Phys. Chem. A, 123, 9594–9599, https://doi.org/10.1021/acs.jpca.9b08020, 2019. a, b, c, d
Fisseha, R., Dommen, J., Gaeggeler, K., Weingartner, E., Samburova, V., Kalberer, M., and Baltensperger, U.: Online gas and aerosol measurement of water soluble carboxylic acids in Zurich, J. Geophys. Res.-Atmos., 111, D12316, https://doi.org/10.1029/2005JD006782, 2006. a, b, c, d
Fredenslund, A., Jones, R. L., and Prausnitz, J. M.: Group-contribution estimation of activity coefficients in nonideal liquid mixtures, AIChE J., 21, 1086–1099, https://doi.org/10.1002/aic.690210607, 1975. a
Guo, H., Zhou, J., Wang, L., Zhou, Y., Yuan, J., and Zhao, R.: Seasonal variations and sources of carboxylic acids in PM2.5 in Wuhan, China, Aerosol Air Qual. Res., 15, 517–528, https://doi.org/10.4209/aaqr.2014.02.0040, 2015. a, b, c
Hansen, R. S., Miller, F. A., and Christian, S. D.: Activity Coefficients of Components in the Systems Water–Acetic Acid, Water–Propionic Acid and Water–n-Butyric Acid at 25∘, J. Phys. Chem., 59, 391–395, https://doi.org/10.1021/j150527a003, 1955. a, b, c, d, e, f, g
Hyder, M., Genberg, J., Sandahl, M., Swietlicki, E., and Jönsson, J. Å.: Yearly trend of dicarboxylic acids in organic aerosols from south of Sweden and source attribution, Atmos. Environ., 57, 197–204, https://doi.org/10.1016/j.atmosenv.2012.04.027, 2012. a
Hyttinen, N. and Prisle, N. L.: Improving solubility and activity estimates of multifunctional atmospheric organics by selecting conformers in COSMOtherm, J. Phys. Chem. A, 124, 4801–4812, https://doi.org/10.1021/acs.jpca.0c04285, 2020. a, b, c, d
Hyttinen, N., Heshmatnezhad, R., Elm, J., Kurtén, T., and Prisle, N. L.: Supplementary data for the manuscript ”Technical note: Estimating aqueous solubilities and activity coefficients of mono- and α,ω-dicarboxylic acids using COSMO-RS-DARE” (Version 1), Data set, Zenodo, https://doi.org/10.5281/zenodo.3842593, 2020. a
Jones, E. R. and Bury, C. R.: LXXVII. The freezing-points of concentrated solutions – Part II. Solutions of formic, acetic, propionic, and butyric acids, London, Edinburgh Dublin Philos. Mag. J. Sci., 4, 841–848, https://doi.org/10.1080/14786441008564388, 1927. a
Jung, J., Tsatsral, B., Kim, Y. J., and Kawamura, K.: Organic and inorganic aerosol compositions in Ulaanbaatar, Mongolia, during the cold winter of 2007 to 2008: dicarboxylic acids, ketocarboxylic acids, and α-dicarbonyls, J. Geophys. Res.-Atmos., 115, D22203, https://doi.org/10.1029/2010JD014339, 2010. a, b
Kawamura, K. and Sakaguchi, F.: Molecular distributions of water soluble dicarboxylic acids in marine aerosols over the Pacific Ocean including tropics, J. Geophys. Res.-Atmos., 104, 3501–3509, https://doi.org/10.1029/1998JD100041, 1999. a
Kawamura, K., Seméré, R., Imai, Y., Fujii, Y., and Hayashi, M.: Water soluble dicarboxylic acids and related compounds in Antarctic aerosols, J. Geophys. Res.-Atmos., 101, 18721–18728, https://doi.org/10.1029/96JD01541, 1996. a
Kawamura, K., Steinberg, S., and Kaplan, I. R.: Homologous series of C1–C10 monocarboxylic acids and C1–C6 carbonyls in Los Angeles air and motor vehicle exhausts, Atmos. Environ., 34, 4175–4191, https://doi.org/10.1016/S1352-2310(00)00212-0, 2000. a, b, c
Kildgaard, J. V., Mikkelsen, K. V., Bilde, M., and Elm, J.: Hydration of Atmospheric Molecular Clusters II: Organic Acid–Water Clusters, J. Phys. Chem. A, 122, 8549–8556, https://doi.org/10.1021/acs.jpca.8b07713, 2018. a
Klamt, A.: Conductor-like screening model for real solvents: a new approach to the quantitative calculation of solvation phenomena, J. Phys. Chem., 99, 2224–2235, https://doi.org/10.1021/j100007a062, 1995. a
Klamt, A. and Schüürmann, G.: COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc. Perkin Trans., 2, 799–805, https://doi.org/10.1039/P29930000799, 1993. a
Klamt, A., Jonas, V., Bürger, T., and Lohrenz, J. C. W.: Refinement and parametrization of COSMO-RS, J. Phys. Chem. A, 102, 5074–5085, https://doi.org/10.1021/jp980017s, 1998. a, b
Kurtén, T., Hyttinen, N., D'Ambro, E. L., Thornton, J., and Prisle, N. L.: Estimating the saturation vapor pressures of isoprene oxidation products C5H12O6 and C5H10O6 using COSMO-RS, Atmos. Chem. Phys., 18, 17589–17600, https://doi.org/10.5194/acp-18-17589-2018, 2018. a, b
Levine, I. N.: Physical Chemistry, McGraw-Hill, New York, USA, 6th edn., 2009. a
Maffia, M. C. and Meirelles, A. J. A.: Water activity and pH in aqueous polycarboxylic acid systems, J. Chem. Eng. Data, 46, 582–587, https://doi.org/10.1021/je0002890, 2001. a, b
Marsh, A., Miles, R. E. H., Rovelli, G., Cowling, A. G., Nandy, L., Dutcher, C. S., and Reid, J. P.: Influence of organic compound functionality on aerosol hygroscopicity: dicarboxylic acids, alkyl-substituents, sugars and amino acids, Atmos. Chem. Phys., 17, 5583–5599, https://doi.org/10.5194/acp-17-5583-2017, 2017. a, b, c
McNeill, V. F., Yatavelli, R. L. N., Thornton, J. A., Stipe, C. B., and Landgrebe, O.: Heterogeneous OH oxidation of palmitic acid in single component and internally mixed aerosol particles: vaporization and the role of particle phase, Atmos. Chem. Phys., 8, 5465–5476, https://doi.org/10.5194/acp-8-5465-2008, 2008. a
Michailoudi, G., Hyttinen, N., Kurtén, T., and Prisle, N. L.: Solubility and Activity Coefficients of Atmospheric Surfactants in Aqueous Solution Evaluated using COSMOtherm, J. Phys. Chem. A, 124, 430–443, https://doi.org/10.1021/acs.jpca.9b09780, 2020. a, b
Mochida, M., Kawamura, K., Umemoto, N., Kobayashi, M., Matsunaga, S., Lim, H.-J., Turpin, B. J., Bates, T. S., and Simoneit, B. R.: Spatial distributions of oxygenated organic compounds (dicarboxylic acids, fatty acids, and levoglucosan) in marine aerosols over the western Pacific and off the coast of East Asia: Continental outflow of organic aerosols during the ACE-Asia campaign, J. Geophys. Res.-Atmos., 108, 8638, https://doi.org/10.1029/2002JD003249, 2003. a
Omar, W. and Ulrich, J.: Solid liquid equilibrium, metastable zone, and nucleation parameters of the oxalic acid- water system, Cryst. Growth Des., 6, 1927–1930, https://doi.org/10.1021/cg060112n, 2006. a, b, c, d
O'Neil, M. J.: The Merck index: an encyclopedia of chemicals, drugs, and biologicals, RSC Publishing, 2013. a
Peng, C., Chan, M. N., and Chan, C. K.: The hygroscopic properties of dicarboxylic and multifunctional acids: Measurements and UNIFAC predictions, Environ. Sci. Technol., 35, 4495–4501, https://doi.org/10.1021/es0107531, 2001. a, b, c, d
Prenni, A. J., DeMott, P. J., Kreidenweis, S. M., Sherman, D. E., Russell, L. M., and Ming, Y.: The effects of low molecular weight dicarboxylic acids on cloud formation, J. Phys. Chem. A, 105, 11240–11248, https://doi.org/10.1021/jp012427d, 2001. a
Prigogine, I. and Defay, R.: Chemical Thermodynamics, Longmans Green, 1st edn., 1954. a
Pye, H. O. T., Nenes, A., Alexander, B., Ault, A. P., Barth, M. C., Clegg, S. L., Collett Jr., J. L., Fahey, K. M., Hennigan, C. J., Herrmann, H., Kanakidou, M., Kelly, J. T., Ku, I.-T., McNeill, V. F., Riemer, N., Schaefer, T., Shi, G., Tilgner, A., Walker, J. T., Wang, T., Weber, R., Xing, J., Zaveri, R. A., and Zuend, A.: The acidity of atmospheric particles and clouds, Atmos. Chem. Phys., 20, 4809–4888, https://doi.org/10.5194/acp-20-4809-2020, 2020. a
Romero, C. M. and Suárez, F.: Effect of temperature on the solubility of short-chain carboxylic acids in water, J. Solution Chem., 38, 315–320, https://doi.org/10.1007/s10953-009-9375-6, 2009. a, b
Rossignol, S., Tinel, L., Bianco, A., Passananti, M., Brigante, M., Donaldson, D. J., and George, C.: Atmospheric photochemistry at a fatty acid–coated air-water interface, Science, 353, 699–702, https://doi.org/10.1126/science.aaf3617, 2016. a
Roux, M. V., Temprado, M., and Chickos, J. S.: Vaporization, fusion and sublimation enthalpies of the dicarboxylic acids from C4 to C14 and C16, J. Chem. Thermodyn., 37, 941–953, https://doi.org/10.1016/j.jct.2004.12.011, 2005. a
Rumble, J. R. (Ed.): CRC Handbook of Chemistry and Physics, CRC Press/Taylor & Francis, Boca Raton, FL, 101st edn., Internet Version 2020, 2018. a, b
Sachsenhauser, T., Rehfeldt, S., Klamt, A., Eckert, F., and Klein, H.: Consideration of dimerization for property prediction with COSMO-RS-DARE, Fluid Phase Equilib., 382, 89–99, https://doi.org/10.1016/j.fluid.2014.08.030, 2014. a, b, c, d, e, f
Saxena, P. and Hildemann, L. M.: Water-soluble organics in atmospheric particles: A critical review of the literature and application of thermodynamics to identify candidate compounds, J. Atmos. Chem., 24, 57–109, https://doi.org/10.1007/BF00053823, 1996. a, b, c, d
Schröder, B., Santos, L. M. N. B. F., Marrucho, I. M., and Coutinho, J. A. P.: Prediction of aqueous solubilities of solid carboxylic acids with COSMO-RS, Fluid Phase Equilib., 289, 140–147, https://doi.org/10.1016/j.fluid.2009.11.018, 2010. a
Schwier, A., Mitroo, D., and McNeill, V. F.: Surface tension depression by low-solubility organic material in aqueous aerosol mimics, Atmos. Environ., 54, 490–495, https://doi.org/10.1016/j.atmosenv.2012.02.032, 2012. a
Song, M., Marcolli, C., Krieger, U. K., Zuend, A., and Peter, T.: Liquid-liquid phase separation and morphology of internally mixed dicarboxylic acids/ammonium sulfate/water particles, Atmos. Chem. Phys., 12, 2691–2712, https://doi.org/10.5194/acp-12-2691-2012, 2012. a, b
Soonsin, V., Zardini, A. A., Marcolli, C., Zuend, A., and Krieger, U. K.: The vapor pressures and activities of dicarboxylic acids reconsidered: the impact of the physical state of the aerosol, Atmos. Chem. Phys., 10, 11753–11767, https://doi.org/10.5194/acp-10-11753-2010, 2010. a, b
Sordo, J. Á.: Solvation thermodynamics: two formulations and some misunderstandings, RSC Adv., 5, 96105–96116, https://doi.org/10.1039/c5ra17305a, 2015. a
Tsai, Y. I. and Kuo, S.-C.: Contributions of low molecular weight carboxylic acids to aerosols and wet deposition in a natural subtropical broad-leaved forest environment, Atmos. Environ., 81, 270–279, https://doi.org/10.1016/j.atmosenv.2013.08.061, 2013. a, b
TURBOMOLE: Version 7.11, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, TURBOMOLE GmbH, 2010. a
Vawdrey, A. C., Oscarson, J. L., Rowley, R. L., and Wilding, W. V.: Vapor-phase association of n-aliphatic carboxylic acids, Fluid Phase Equilib., 222, 239–245, https://doi.org/10.1016/j.fluid.2004.06.043, 2004. a, b
Verma, N., Satsangi, A., Lakhani, A., and Kumari, K. M.: Low molecular weight monocarboxylic acids in PM2.5 and PM10: Quantification, seasonal variation and source apportionment, Aerosol Air Qual. Res., 17, 485–498, https://doi.org/10.4209/aaqr.2016.05.0183, 2017. a, b
Wavefunction Inc.: Spartan'14, Irvine, CA, 2014. a
Wavefunction Inc.: Spartan'16, Irvine, CA, 2016. a
Weber, K. H., Morales, F. J., and Tao, F.-M.: Theoretical study on the structure and stabilities of molecular clusters of oxalic acid with water, J. Phys. Chem. A, 116, 11601–11617, https://doi.org/10.1021/jp308499f, 2012. a
Weber, R. J., Guo, H., Russell, A. G., and Nenes, A.: High aerosol acidity despite declining atmospheric sulfate concentrations over the past 15 years, Nat. Geosci., 9, 282–285, https://doi.org/10.1038/ngeo2665, 2016. a
Wise, M. E., Surratt, J. D., Curtis, D. B., Shilling, J. E., and Tolbert, M. A.: Hygroscopic growth of ammonium sulfate/dicarboxylic acids, J. Geophys. Res.-Atmos., 108, 4638–4642, https://doi.org/10.1029/2003JD003775, 2003. a
Zhang, H., Xie, C., Liu, Z., Gong, J., Bao, Y., Zhang, M., Hao, H., Hou, B., and Yin, Q.-x.: Identification and molecular understanding of the odd–even effect of dicarboxylic acids aqueous solubility, Ind. Eng. Chem. Res., 52, 18458–18465, https://doi.org/10.1021/ie4030837, 2013. a, b
Zhao, W., Kawamura, K., Yue, S., Wei, L., Ren, H., Yan, Y., Kang, M., Li, L., Ren, L., Lai, S., Li, J., Sun, Y., Wang, Z., and Fu, P.: Molecular distribution and compound-specific stable carbon isotopic composition of dicarboxylic acids, oxocarboxylic acids and α-dicarbonyls in PM2.5 from Beijing, China, Atmos. Chem. Phys., 18, 2749–2767, https://doi.org/10.5194/acp-18-2749-2018, 2018. a, b
Zuend, A., Marcolli, C., Luo, B. P., and Peter, T.: A thermodynamic model of mixed organic-inorganic aerosols to predict activity coefficients, Atmos. Chem. Phys., 8, 4559–4593, https://doi.org/10.5194/acp-8-4559-2008, 2008. a, b
Zuend, A., Marcolli, C., Booth, A. M., Lienhard, D. M., Soonsin, V., Krieger, U. K., Topping, D. O., McFiggans, G., Peter, T., and Seinfeld, J. H.: New and extended parameterization of the thermodynamic model AIOMFAC: calculation of activity coefficients for organic-inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups, Atmos. Chem. Phys., 11, 9155–9206, https://doi.org/10.5194/acp-11-9155-2011, 2011. a





