the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Impact of aerosols and turbulence on cloud droplet growth: an in-cloud seeding case study using a parcel–DNS (direct numerical simulation) approach
Lulin Xue
Man-Kong Yau
This paper investigates the relative importance of turbulence and aerosol effects on the broadening of the droplet size distribution (DSD) during the early stage of cloud and raindrop formation. A parcel–DNS (direct numerical simulation) hybrid approach is developed to seamlessly simulate the evolution of cloud droplets in an ascending cloud parcel. The results show that turbulence and cloud condensation nuclei (CCN) hygroscopicity are key to the efficient formation of large droplets. The ultragiant aerosols can quickly form embryonic drizzle drops and thus determine the onset time of autoconversion. However, due to their scarcity in natural clouds, their contribution to the total mass of drizzle drops is insignificant. In the meantime, turbulence sustains the formation of large droplets by effectively accelerating the collisions of small droplets. The DSD broadening through turbulent collisions is significant and therefore yields a higher autoconversion rate compared to that in a nonturbulent case. It is argued that the level of autoconversion is heavily determined by turbulence intensity. This paper also presents an in-cloud seeding scenario designed to scrutinize the effect of aerosols in terms of number concentration and size. It is found that seeding more aerosols leads to higher competition for water vapor, reduces the mean droplet radius, and therefore slows down the autoconversion rate. On the other hand, increasing the seeding particle size can buffer such a negative feedback. Despite the fact that the autoconversion rate is prominently altered by turbulence and seeding, bulk variables such as liquid water content (LWC) stays nearly identical among all cases. Additionally, the lowest autoconversion rate is not co-located with the smallest mean droplet radius. The finding indicates that the traditional Kessler-type or Sundqvist-type autoconversion parameterizations, which depend on the LWC or mean radius, cannot capture the drizzle formation process very well. Properties related to the width or the shape of the DSD are also needed, suggesting that the scheme of Berry and Reinhardt (1974) is conceptually better. It is also suggested that a turbulence-dependent relative-dispersion parameter should be considered.
- Article
(2955 KB) - Full-text XML
- BibTeX
- EndNote
Aerosol–cloud–precipitation interactions represent one of the major uncertainties in weather and climate prediction (Fan et al., 2016). Current atmospheric models cannot resolve the microphysical processes and thus rely on parameterizations to represent those interactions. Studies show that model results of the location and intensity of precipitation are sensitive to microphysics schemes (Xue et al., 2017; White et al., 2017; Grabowski et al., 2019). For example, White et al. (2017) showed that the autoconversion scheme is the dominant factor to account for the difference in rain production, and the uncertainty due to the choice of microphysical parameterizations exceeds the effects of aerosols. No benchmark “truth” from either measurements or modeling exists to gauge the performance of various microphysics schemes. On the one hand, in situ measurements cannot directly obtain the process rates, such as the rate of autoconversion and accretion, which prevents such microphysical processes from being accurately modeled (Morrison et al., 2020). The community has to rely on laboratory experiments, indirect observations, or theoretical models to develop and validate microphysical schemes (e.g., Stoelinga et al., 2003; Wood et al., 2002; Wang et al., 2005). On the other hand, it is difficult to create laboratory facilities, such as cloud chambers, with environments that are scalable to real clouds. Furthermore, the effects of chamber walls, such as the heat and moisture fluxes fed into the solid wall and the droplet loss due to their contact with the wall, are challenging to quantify with considerable uncertainties in the measurements (e.g., Thomas et al., 2019).
In this study, we implement the idea of in-cloud seeding, i.e., seeding hygroscopic particles near the cloud base, to investigate the effects of aerosols in droplet growth and rain formation. Hygroscopic cloud seeding, owing to its potential effect of increasing rainfall, has been conducted in research and operational contexts globally to address the shortage of water resources in arid environments (e.g., Silverman and Sukarnjanaset, 2000; Terblanche et al., 2000). The general concept of hygroscopic cloud seeding for rain enhancement is that the introduction of artificial cloud condensation nuclei (seeding particles) into warm clouds can, on the one hand, suppress the activation of small natural aerosols, and on the other hand, generate large initial particles that accelerate or enhance the collision–coalescence process (Cooper et al., 1997). Regardless of its existence in operational weather modification for decades, the direct effect of seeding is still inconclusive (partly due to the chaotic nature of the convective cloud system), making it impossible to conduct controllable seeding experiments because of the limitation in detecting and assessing the seeding results with current instrumentation (Silverman, 2003; Flossmann et al., 2019). Nevertheless, the progress made in cloud seeding does advance our understanding of cloud–aerosol–precipitation interactions. A leading idea of this study is to make use of the concept of cloud seeding experiments to separate the influence of aerosols on rain initiation from the effects of natural cloud processes such as turbulence and aerosol hygroscopicity, as well as to shed light on the long-existing question of whether cloud seeding could enhance precipitation.
Currently, direct numerical simulation (DNS) is believed to be the only numerical approach capable of simulating the growth of individual cloud particles in turbulent flows (Grabowski et al., 2019). Only a few DNS studies to date investigated the evolution of the droplet size distribution (DSD) in an updraft environment (e.g., Chen et al., 2018b; Gotoh et al., 2016; Saito and Gotoh, 2018). However, the solute effect (aerosol hygroscopicity) and curvature effect were excluded in those works for simplicity. Parcel model studies on droplet condensation in a lifted parcel show that the curvature term and the solute term can lead to condensational broadening on the droplet size spectrum. Srivastava (1991) demonstrated that the curvature effect is essential for DSD broadening in an ascending parcel. Korolev (1995) found that the curvature effect and the solute effect lead to irreversible broadening when supersaturation fluctuations are present. It is also found that aerosols of different sizes and different hygroscopicity can cause spectral broadening without supersaturation fluctuations (Çelik and Marwitz, 1999; Jensen and Nugent, 2017). Therefore, it is crucial to examine whether these effects are important in spectral broadening when they dynamically couple with droplet collisional growth in a turbulent environment.
It is recognized that DNS is computationally expensive. To achieve an accurate representation of cloud microphysics while maintaining a feasible computational load, a hybrid modeling framework that combines a parcel model and a DNS model is proposed in this study. The parcel model provides the mean state of the air parcel and can be used when the effect of turbulence is less prominent. The DNS model explicitly resolves all small-scale turbulent eddies which are key to cloud particle interactions. The Lagrangian particle-by-particle method is employed in the DNS to track the evolution of individual cloud particles coupling with the turbulent flow. This hybrid parcel–DNS approach allows for a close examination of the growth history of cloud particles from aerosol activation to drizzle formation. By comparing simulations with different aerosol and turbulent conditions, we are able to evaluate the contribution of each microphysical component to warm rain initiation. The ultimate goal is to provide a numerical benchmarking tool to better understand aerosol–cloud–precipitation interaction at fine scales and improve the subgrid-scale representation of clouds and precipitation in numerical weather and climate prediction.
Chen et al. (2018b) found that the evolution of DSD in turbulence is different depending on whether droplets grow by condensation-only, collision-only, or condensation–collision (Fig. 1 in their paper). This reveals that droplet condensation and collisions, when interacting with turbulence, cannot be treated as the linear addition of the two processes. Many past DNS studies focused on either the condensation-only process or the collision-only process, which might yield biased results. It should be pointed out that autoconversion defined as the mass transfer from small droplets to embryonic drizzle drops via collision–coalescence should not exclude the impact of condensational growth, as the two processes dynamically interact with each other.
This paper presents a sequel to the study of Chen et al. (2018b) by addressing several caveats mentioned in their paper. Firstly, Chen et al. (2018b) treated only pure-water droplets as is commonly assumed in most DNS studies (e.g., Sardina et al., 2015; Vaillancourt et al., 2001, 2002; Paoli and Shariff, 2009). This simplification may underestimate the rate of droplet growth by condensation. Jensen and Nugent (2017) found that cloud condensation nuclei (CCN) strongly enhance the particle growth, and droplets with giant CCN can even grow in regions of subsaturated downdrafts. In our new hybrid approach, we use an accurate droplet diffusional growth equation including both curvature effect and solute effect. Secondly, the initial DSD in Chen et al. (2018b) obtained from flight observations was a result of averages over a long time period and along a long sampling path (including both core regions and cloud edges). The average might mask the local property of an adiabatic core that the DNS aims to simulate. The adiabatic cores are regions free of entrainment of dry air. This region has a higher liquid water content (LWC) than the rest of the cloud and is argued to favor the formation of raindrops (Khain et al., 2013). To represent the DSD evolution at the core region, we prescribe here a dry aerosol size distribution in the subcloud region, and the aerosol activation process is explicitly simulated by a parcel model to provide a more physically based initial DSD for the DNS.
The main purpose of the present study is to investigate the relative importance of turbulence, CCN hygroscopicity, and aerosols (size and number concentration) on the DSD broadening in cumulus clouds. The paper is organized as follows. Section 2.1–2.2 introduce the hybrid model of a parcel–DNS framework. In Sect. 2.3, the configuration of the 12 numerical simulations are described to compare the microphysical responses to turbulence (turbulent vs. nonturbulent), hygroscopicity (pure-water droplets vs. solute-containing droplets), aerosol size and number concentration (with or without seeding particles), and droplet growth mechanisms (condensation-only vs. condensation–collision). Results are presented in Sect. 3, showing that turbulence and CCN hygroscopicity are key to the formation of big droplets, and seeding slows down the broadening and lowers the autoconversion rate. The summary and outlook for future work are in Sect. 4.
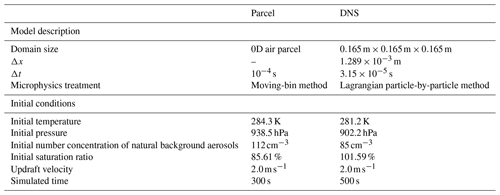
A hybrid model is used in this paper for simulating the droplet growth inside an ascending cloud parcel. The ascent is divided into two phases based on the distinct dominant microphysical processes. A parcel model and a DNS model are combined to seamlessly simulate the two phases, as illustrated in the schematic diagram in Fig. 1. The first phase starts from the unsaturated subcloud region (≈300 m below cloud base) to the level where the supersaturation reaches a maximum (≈43 m above cloud base; see Fig. 2a). During this phase, supersaturation increases with height, and the microphysical process is dominated by aerosol activation. Cloud particles remain small and collisional growth is negligible. A nonturbulent parcel model is employed to calculate the droplet growth by condensation in this phase. The second phase starts from the level of maximum supersaturation (=1.59 %) to 1 km above, which takes 500 s in simulated time (Table 1). At this stage, no new activation occurs as the supersaturation starts to decrease with height. This phase is dominated by cloud droplet growth. The DNS model is employed to calculate individual droplet growth by condensation and collision, and these droplets are affected by their immediate local turbulent environment. The parcel model state at the height with maximum supersaturation is fed into the DNS model as initial conditions. Because unactivated aerosols have little influence on the subsequent droplet growth or on the water vapor field, only the activated aerosols from the parcel model are carried over to the DNS model as the initial background aerosol condition to decrease the computational load. The CCN size distribution and droplet size distribution are displayed in Fig. 2c. This parcel–DNS hybrid model provides an economical approach, and is the first step towards a fully DNS-resolved simulation of the entire ascending process.
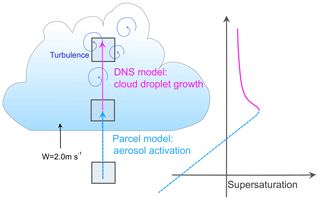
Figure 1Schematic diagram of the parcel–DNS hybrid model along with the unscaled bulk supersaturation with height. The parcel model simulates the ascending process below the height of maximum supersaturation (dashed blue line), and the DNS simulates the subsequent ascending process (solid violet line).
Figure 2(a) Supersaturation and (b) radius of droplets with different initial wet sizes varying with the height from cloud base (H−HCB). Only bins of activated particles are illustrated in (b). (c) The background natural CCN (dry particle) size distribution in the parcel model (light dotted blue histogram) and in the DNS model (darker solid blue histogram), as well as the droplet size distribution at maximum supersaturation (Smax=1.59 %) in the parcel model (light dotted violet histogram) and in the DNS model (darker solid violet histogram). The vertical axis denotes the number concentration of the assigned particle size in the model.
2.1 Parcel model
The parcel model is adopted from Jensen and Nugent (2017) with two main modifications. (1) The droplet collision–coalescence is excluded for simplicity, because most particles in this phase are smaller than 10 µm. These droplets have very low collision rates even in strong turbulence (Chen et al., 2016, 2018a), and the growth is dominated by condensation. (2) The hygroscopicity parameter, κ, proposed by Petters and Kreidenweis (2007, their Eq. 6) is employed in the droplet diffusional growth equation:
where R is droplet radius, Rd is the radius of CCN, is surface tension of water against air, is individual gas constant for water vapor, ρw and ρa are the density of water and air, respectively, T is air temperature, and es is the saturated water vapor pressure. D′ and K′ are, respectively, the water vapor diffusivity and thermal conductivity that include kinetic effects (see Eq. 11a–b in Grabowski et al., 2011), and is the latent heat of vaporization. S is supersaturation ratio defined as , where qv and qvs are water vapor mixing ratios at the current conditions and at saturated conditions, respectively. fv is the ventilation coefficient, which takes into account the distortion in water vapor field around the droplet surface when the droplet moves relative to the flow. Studies show that the effect is negligible when droplets are smaller than 10 µm in radius (Rogers and Yau, 1989, p. 116). Therefore, the ventilation effect is excluded in this phase (i.e., fv=1). In DNS, we apply the empirical formulas of fv from Beard and Pruppacher (1971), which depend on the droplet Reynolds number and Schmidt number (see also Eqs. B2–B3 in Chen et al., 2018b).
There are two advantages to using the hygroscopicity parameter. (1) The chemical information of the aerosol (i.e., molecular weight, van 't Hoff factor, density, etc.) is simplified into a single parameter in the solute term; (2) the hygroscopicity parameter of mixed solute due to collision–coalescence can be simply calculated by a weighted average of the volume fractions of each component in the mixture (Petters and Kreidenweis, 2007).
The initial environmental conditions are taken from the cumulus cloud case of Jensen and Nugent (2017, Table 2). The parcel ascends from H=600 m (≈284 m below cloud base) with a constant updraft velocity of 2.0 m s−1, resembling a fair-weather cumulus cloud condition. The detailed information is listed in Table 1. The CCN (dry aerosol) size distribution fits a lognormal distribution, taken from the pristine case by Xue et al. (2010) (light blue histogram in Fig. 2c). The distribution consists of three lognormal modes in which the geometric mean dry radii in the three modes are , the geometric standard deviations are , and the total number concentrations of the whole size range are . The initial size is discretized into 39 bins on a log scale with the bin width set by doubling the mass or with a multiplication factor in radius of 2.0. In this way, the resolution is higher at small particle sizes and lower at large particle sizes. The bin size ranges from 0.006 and 49 µm, which gives a total number concentration of . To examine the variation in the activation fraction of the aerosols due to bin width resolution, we performed a sensitivity test with the number of bins spanning from 32 to 253, corresponding to a multiplication factor from 2.2 to 1.1. The result shows that the variation caused by changing the bin resolution has a decreasing trend with increasing resolution, with a maximum variation of 2.3 % of the total aerosol number concentration in the 32-bin case. In particular, the 39-bin case has only 0.6 cm−3 more aerosols activated than in the 253-bin case.
It is worth noting that the number concentration of CCN larger than 10 µm is below , corresponding to less than one particle in the DNS domain (L=16.5 cm). The hygroscopicity parameter of all aerosols is assumed to be κ=0.47. The moving-bin method or moving-size-grid method (see discussion in Yang et al., 2018) is applied to calculate the evolution of the DSD. For aerosols with dry radius Rd≤1 µm, the initial wet radius is set to the size when the droplet is in equilibrium at the given ambient humidity: (Jensen and Nugent, 2017). For giant aerosols with Rd>1 µm, the initial wet size is assumed to be twice the dry volume (i.e., ). As illustrated in Fig. 2b, the droplets with initial radius below 1 µm grow quickly by condensation between 20–40 m above the cloud base before the maximum supersaturation is reached, and droplets larger than 1 µm grow slower, creating a narrow DSD near the cloud base.
2.2 DNS model
All DNS simulations are initialized with an identical mean state listed in Table 1. A constant mean updraft speed of 2 m s−1 is prescribed to lift the air parcel. The initial mean-state variables for DNS are obtained from the parcel model output at maximum supersaturation (S=1.59 %). Above this altitude, no further activation is expected in the parcel due to the decreasing supersaturation. The inactivated aerosols, corresponding to the first two bins of the light blue histogram in Fig. 2c, do not influence the subsequent evolution of the DSD. Therefore, only the activated aerosols from the parcel model are carried over to the DNS, reducing the particle number concentration to . This treatment avoids the computation of tracking the inactivated particles. In the parcel model, the droplet size is calculated by using the moving-bin method. The dry radius of each bin remains constant, and the wet radius grows by condensation. To assign the initial droplet size and its dry radius in the DNS, we regrouped the activated droplet bins into 15 droplet size groups (R=2–16 µm) with an interval of 1 µm. Their CCN sizes remain at the original values. Due to the parallelization setup in the model, the initial number of each droplet size group has to be an exact multiple of the number of processors in the simulation (64 processors are used in the present simulations). Therefore, a small difference in the resulting DSD between the two models is expected, as shown in Fig. 2c.
The DNS model in the present study was initially developed by Vaillancourt et al. (2001) and has undergone a few modifications since then (Franklin et al., 2005; Chen et al., 2016, 2018a, b). The model employs two sets of equations: (1) the macroscopic equations to calculate the base-state (bulk) variables and (2) the microscopic equations to calculate the fluctuation of the variables affected by the small-scale turbulence and the local droplet condensation. A detailed description of the DNS model can be found in Chen et al. (2018b, Sect. 2 and Appendix B of that paper).
Two modifications are made in the present study. First, we use Eq. (1) to replace the simplified version of the droplet growth equation in Chen et al. (2018b, Eq. B1 of that paper) where the curvature term and the solute term are excluded. Second, droplets with R<5 µm are treated as non-inertial particles due to their small Stokes number, i.e., their velocity is equal to the flow velocity. The length of a time step is constrained by the inertial response time of the smallest inertial particle (see discussion in Chen et al., 2018a, on the length of the time step). The treatment above avoids using too small a time step when small droplets are present. For droplets between 5 and 40 µm, their motion is determined by both the Stokes drag force and gravity; for droplets over 40 µm, nonlinear drag force is considered (see full description below Eq. B10 in Chen et al., 2018b). Droplets over 50 µm is size are treated as fallout and are removed from the simulation.
2.3 DNS experimental design
Two sets of experiments are performed. Each set consists of 6 cases, which gives 12 simulations in total. The first set of the experiments includes both condensational and collisional growth of droplets and will be referred to as the “condensation–collision” set. The second set excludes the droplet collision and will be referred to as the “condensation-only” set. The model setup for the two sets is the same other than the difference mentioned above. The configuration of the six cases is listed in Table 2. We focus on the condensation–collision set in the Results section unless explicitly specified, and the condensation-only set is for the purpose of comparison to evaluate the influence by condensation and collision–coalescence.
Table 2Model configuration of the six cases in each set of the experiment. Two sets of experiments are performed: set one includes both collision and condensation in the droplet growth and is referred to as the condensation–collision set; set two only considers droplet condensation and is referred to as the condensation-only set. This gives 12 cases in total. The natural DSD is taken from the parcel model output at S=1.59 %. Monodisperse seeding is considered in seeded cases with CCN size (Rd) and initial droplet size (R) listed in the table.
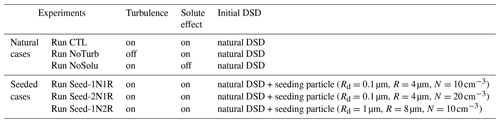
Run CTL is the control run. Only one condition is changed in each of the other five cases. Run CTL, Run NoTurb, and Run NoSolu use the same initial DSD from the parcel model and are referred to as the “natural” cases. Turbulence and solute effects are switched off in Run NoTurb and Run NoSolu, respectively, to gauge the effects of turbulence and CCN hygroscopicity on the DSD. When turbulence is switched off, the background velocity fluctuation is set to 0 m s−1. Therefore, particle motion is only affected by the mean updraft and gravitational settling, and the supersaturation fluctuation is only induced by droplet condensation and evaporation. When the solute term is switched off (i.e., κ=0), droplets consist of only pure water. Run Seed-1N1R, Run Seed-2N1R, and Run Seed-1N2R are referred to as “seeded” cases, because an extra number of monodisperse aerosols are introduced near the cloud base (at the beginning of DNS). Two seeding sizes and two number concentrations are considered, as described in Table 2. Unlike traditional cloud seeding, the same hygroscopicity of κ=0.47 is assumed for both the natural aerosols and the seeding particles. In Run Seed-1N1R, we introduce seeding particles of dry radius Rd=0.1 µm, wet radius R=4 µm, and number concentration . We double the seeding particle number concentration in Run Seed-2N1R. In Run Seed-1N2R, the dry size of the seeding particles increased 10-fold and the wet size doubled relative to Run Seed-1N1R (see Table 2). It should be pointed out that the dissipation rate in cumulus clouds tends to increase with height (Seifert et al., 2010). For simplicity, the eddy dissipation rate (ϵ) for all the turbulent cases is set to be statistically stationary (). The advantage of this idealized, simplified treatment is that the effect of turbulence can be easily separated from aerosol effects. A dissipation rate of 500 cm2 s−3 represents a strongly turbulent environment in cumulus clouds to examine the upper bound of turbulent effects on the DSD evolution.
3.1 Natural cases
We first compare the results of the natural cases (Run CTL, Run NoTurb, and Run NoSolu) to examine the effect of turbulence and hygroscopicity (solute) on the droplet evolution. Figure 3 shows that including solute and turbulence effectively broadens the DSD at different times. With droplets containing no solute in Run NoSolu, the DSD broadening is suppressed within the first 6 min. However, the tail evolution quickly catches up and converges to that in Run CTL afterwards. Meanwhile, switching off turbulence in Run NoTurb suppresses the DSD broadening at a later time (Fig. 3). The tail of the spectrum in Run CTL (and Run NoTurb) stays similar in the first 2 min and starts to differ by a large amount afterwards.
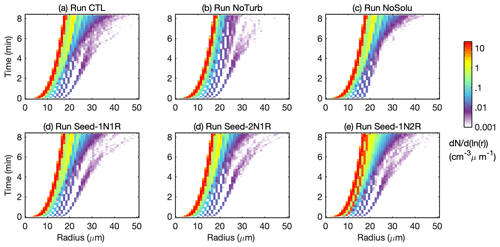
Figure 3Time evolution of the droplet size distribution in the condensation–collision set of experiments. The droplet number concentration (cm−3) is indicated by colors with its value shown in the color bar. The configuration of each experiment is listed in Table 2.
Turbulence effects on the DSD broadening are minor before T=6 min (Fig. 4a–b). Both Run CTL and Run NoTurb produce a similar number of droplets over 25 µm in size at T=6 min. The majority of this size group is grown from the ultragiant aerosol with initial dry and wet sizes of Rd=4.9 µm and R=16 µm, respectively. They grow rapidly to 25 µm by condensation within the first 2 min in Run CTL and Run NoTurb. However, droplets can hardly reach beyond 30 µm solely by condensation (Fig. 4d–e). The tail over 30 µm is mainly formed by the subsequent collision–coalescence process. Once droplets are over 25 µm, gravitational collection becomes effective, leading to a similar DSD tail with or without turbulence. However, gravitational collection of droplets below 25 µm in Run NoTurb is ineffective to sustain the formation of large droplets. After T=6 min, the tail of DSD in Run NoTurb becomes quasistationary for droplets over 20 µm in size (red and blue histograms in Fig. 4b) due to negligible gravitational collisions. This can be illustrated by a negligible collision frequency in Run NoTurb in Fig. 6e. In contrast, a substantial number of droplets >20 µm are constantly formed in Run CTL after T=2 min through rapid turbulent collisions. Comparing to collision frequency in Run NoTurb (Fig. 5b), turbulence substantially enhances the collisional growth of droplets of R<20 µm. The total collisions in turbulent cases increase by a factor of 20. It is also found that the turbulent enhancement of collisions is strongest among droplet pairs of similar sizes, i.e., with a radius ratio of . Similar-sized collisions increase by nearly a factor of 50 in turbulent cases, contributing to over 80 % of the total collisions as opposed to 34 % in Run NoTurb. This is because a nonturbulent environment does not favor similar-sized collisions due to a similar droplet settling speed. Turbulence, on the one hand, increases the relative motion between droplets and on the other hand, induces a stronger clustering of similar-sized droplets. The two effects jointly strengthen the similar-sized collisions. The turbulent enhancement on similar-sized collisions is then amplified by the condensational process. Chen et al. (2018b) also demonstrated that as the condensation process reduces the DSD width and generates more similar-sized droplets, turbulence enhances the similar-sized collision and thus broadens the DSD.
Even though turbulence intensifies the collisional growth, the modulation on the droplet condensation is found insignificant. The DSDs in Run CTL and NoTurb in the condensation-only set are nearly identical (Fig. 4d–e). This is because the supersaturation fluctuations are weak in an adiabatic core region. Vaillancourt et al. (2002) found that in a quasiadiabatic environment both particle sedimentation and short-lived turbulent coherent structure reduce the supersaturation fluctuation and decrease the time that droplets are exposed to these fluctuations. We expect that the turbulent-induced condensational broadening is more significant at the cloud edge, where entrainment mixing induces a large variation in supersaturation fluctuations.
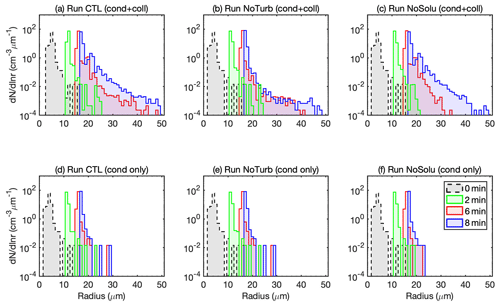
Figure 4Droplet size distributions (DSDs) at T=0 min (grey), (green), T=6 min (red), and T=8 min (blue) of the natural cases (Run CTL, Run NoTurb, and Run NoSolu). The upper panels (a–c) are the DSD in the condensation–collision set of experiments, and the lower panels (d–f) are the DSD in the condensation-only set of experiments.
When the solute effect is absent in Run NoSolu, droplets can hardly reach beyond 30 µm before T=6 min (Fig. 4c) because of a lack of ultragiant aerosols (Rd>4 µm). Embryonic drizzle drops at the early stage (T<6 min) are formed from the fast growth of the ultragiant aerosols as seen in both Run CTL and Run NoTurb. No significant change is found to be in the mean droplet radius or the relative dispersion between Run CTL and Run NoSolu (Fig. 7d). Only a slightly lower collision frequency in the droplet size group of R>20 µm results from a lack of ultragiant aerosols (see the green histograms in Fig. 5). This implies that the solute effect on droplet condensation in DSD broadening is small for aerosols below Rd<4 µm. The ultragiant aerosols (Rd=4.9 µm in this study), due to their scarcity, have a negligible contribution in shifting the mean radius and relative dispersion (Fig. 7). As shown in Fig. 3c, an efficient broadening is triggered at T=6 min, resulting in a similar DSD as in Run CTL at the end of the simulation. It is shown that droplets between 20 and 30 µm are produced through turbulent collisions by the end of T=6 min (Fig. 4c), causing a boost in collisions of droplets over 20 µm in size (Fig. 6d).
The time evolution of collision frequency in Fig. 6 shows that all five turbulent cases show a similar trend in total collisional frequency, even though the trend at the four size groups varies. The nonturbulent gravitational collection process is very weak with the collision frequency lowered by at least 1 order of magnitude in Run NoTurb. Still, a slightly higher droplet number concentration at R>40 µm is observed in Run CTL and Run NoTurb than in Run NoSolu because of the presence of ultragiant aerosols. At the same time, the collision frequency of the four size groups in Run CTL and Run NoSolu are almost identical. Even though the ultragiant aerosols are important in forming early drizzle embryos, due to a low number concentration, they do not sustain an efficient collection process.
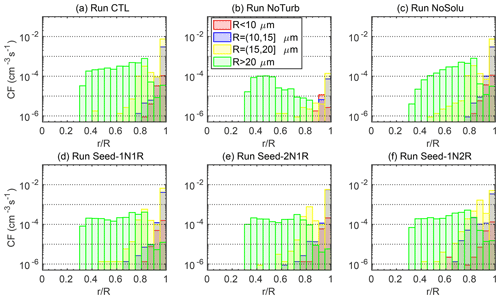
Figure 5Collision frequency (CF) varying with r∕R in the condensation–collision set of experiments. r∕R is the radius ratio between the small droplet and the large droplet of collided droplet pairs. The droplet pairs are divided into four size groups by the big droplet radius, R, shown in the legend.
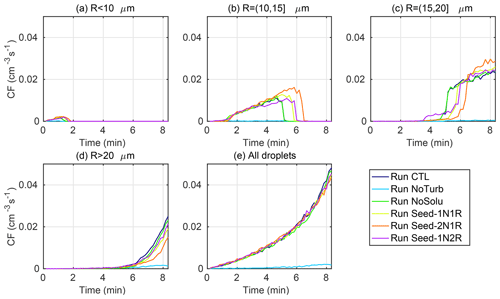
Figure 6(a–d) Time evolution of collision frequency for droplet pairs of four different size groups mentioned in Fig. 5. (e) Time evolution of collision frequency for all droplet pairs.
The relative dispersion, defined as the ratio between the standard deviation of the DSD and the mean droplet radius, is an indicator of the width of the DSD. The values among the six cases at the end of the simulation range from 0.01 to 0.1, which is highly consistent with the theoretical study by Liu et al. (2006b, Fig. 1) for an aerosol number concentration close to 100 cm−3. The dashed lines in Fig. 7c demonstrate that condensational growth narrows the DSD and decreases the relative dispersion throughout the simulation in the condensation-only set. Droplet growth in the first 2 min is prevailed by condensation, as the relative dispersions in the condensation–collision set of experiments well overlaps with that in the condensation-only set. After T=2 min the relative dispersion in the condensation–collision set and the condensation-only set start to deviate from one another. This is mainly due to two factors: (1) the condensation narrowing slows down as droplets get larger and supersaturation gets lower; (2) the collision rate increases with the increasing droplet mean radius and thus leads to a higher collision rate to strengthen the DSD broadening. In Run NoTurb, the collision rate stays the lowest of all cases throughout the simulation (Fig. 6e), leading to the smallest relative dispersion of all six cases.
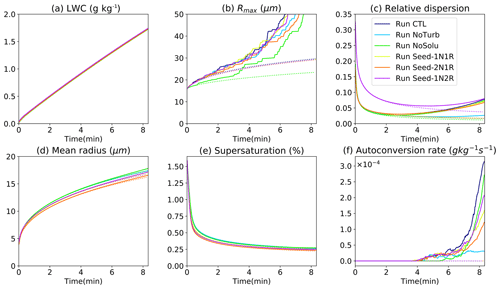
Figure 7The temporal variation of bulk (a) liquid water content (LWC), (b) maximum droplet radius (Rmax), (c) relative dispersion, (d) droplet mean radius, (e) supersaturation ratio, and (f) autoconversion rate in the condensation–collision set of experiments (solid lines) and in the condensation-only set of experiments (dotted lines). The relative dispersion is defined as the standard deviation of the droplet radius divided by the mean radius. The autoconversion rate here is defined as the mass transfer rate from droplets smaller than R=30 µm to droplets larger than 30 µm. The droplets over 50 µm in size are treated as fallouts and removed from the domain. Thus (b) only shows a maximum droplet size at 50 µm.
Despite the fact that DSDs differ among the six cases, the modulation of the bulk condensation by both turbulence and aerosol is negligible, as supported by an almost identical LWC of the six cases (Fig. 7a). This is because the fallout mass of drizzle drops of R>50 µm before T=500 s is negligible, and the bulk LWC of the six cases is approximately adiabatic. Turbulence and aerosols redistribute water mass among different droplet sizes by modifying the condensational and collisional growth of individual droplets, thus shifting the droplet statistics such as the mean radius and relative dispersion, and eventually alter the autoconversion rate (Fig. 7f). The autoconversion rate here is defined as the mass transfer rate from droplets smaller than R=30 µm to droplets larger than 30 µm. It is also found that even though Run NoTurb produces the second largest mean radius, the autoconversion rate stays the lowest, which is accompanied by the smallest relative dispersion. Therefore, properties such as the shape of the DSD and relative dispersion are more relevant to autoconversion than the LWC. The traditional autoconversion parameterizations such as the Kessler-type parameterization (Kessler, 1969; Liu and Daum, 2004) and the Sundqvist-type parameterizations (Sundqvist, 1978; Liu et al., 2006a) customarily use a threshold function based on the mean radius and/or the LWC. It is suggested that autoconversion rate is also influenced by various other parameters (see Noh et al., 2018, and references therein). The present study demonstrates that both parameters, in particular the LWC, cannot properly capture the trend of the autoconversion. The autoconversion rate by Berry and Reinhardt (1974), and its modified versions which include both the mean droplet size and dispersion parameter, is conceptually better than the Kessler-type schemes. Our results thus agree with Gilmore and Straka (2008), who found that the scheme of Berry and Reinhardt (1974) is more sophisticated and requires less tuning to match the observed onset of rain and proportions of cloud and rain. They also found that the growth rate of rain mass and number concentration are highly sensitive to the shape and dispersion parameters. Additionally, it is worth noting that turbulence modifies the collision rate and thus shifts the DSD shape and relative dispersion. Therefore, a turbulence-dependent relative-dispersion parameter is needed in developing the autoconversion scheme.
3.2 Seeded cases
Seeding reduces the mean droplet radius due to higher competition for water vapor among individual droplets (Fig. 7d). Therefore, seeding slows down the autoconversion process. Nevertheless, the LWC is not affected by seeding (Fig. 7a), which again indicates that the LWC is not a well-related quantity to autoconversion in this case.
When investigating the relative importance of aerosol and turbulence to droplet growth, it is found that the modulation of droplet mean radius by seeding particles is larger than the modulation by collision–coalescence. In Fig. 7d, the difference between seeded and unseeded cases exceeds the difference between the condensation-only set (dotted lines) and condensation–collision set (solid lines) of each case. Regardless, turbulent collision–coalescence yields large droplets over 30 µm and increases the width of the DSD. The total collision rate is heavily determined by the turbulence level and mildly affected by seeding or CCN hygroscopicity (Fig. 6e). Besides, the change in Rmax and relative dispersion due to collisions exceeds that from changing the aerosol condition. As condensational growth can hardly produce droplets over 30 µm, turbulent enhancement of collision is determinant in the mass conversion from small droplets to drizzle embryos. Meanwhile, seeding increases the competition for water vapor among droplets and reduces the mean droplet size, leading to more collisions of small droplets and fewer collisions of large droplets (Fig. 6a–d). Specifically, by doubling the seeding particle number in Run Seed-2N1R, the condensational growth of small droplets is further inhibited due to a higher competition of water vapor, resulting in more small droplets. Increasing the size of seeding particles in Run Seed-1N2R buffers the abovementioned inhibition effect caused by increasing aerosol number concentration. The resulting autoconversion rate ordering is Run CTL > Run Seed-1N2R > Run Seed-1N1R > Run Seed-2N1R.
Finally, aerosol hygroscopicity is key to the onset time of autoconversion. All five solute-containing cases see a similar onset time around T=4 min. Removing the solute (hygroscopic material) in Run NoSolu delays the onset of autoconversion by about 1.5 min (green line Fig. 7f). Nevertheless, after T=6–7 min, the autoconversion rate in Run NoSolu exceeds all seeded cases. First, solute (CCN hygroscopicity) has a negligible effect on the growth of small aerosols, as the size distribution of small droplets in Run CTL and Run NoSolu remain almost identical. This is substantiated by the almost identical collision frequency of droplets below 20 µm of the two cases (Fig. 6a–c). Second, seeding reduces the mean radius of the droplets. This leads to a reduction in collisions for droplets over 20 µm (Fig. 6d) and subsequently decelerates the autoconversion process. The above findings imply that increasing the aerosol size (ultragiant aerosol) shortens the lifetime of the clouds through a fast onset of rain. And increasing the number of aerosols decelerates the rain process.
This paper investigates the effects of turbulence and aerosol properties (hygroscopicity, number concentration, and size) on the microphysics during early cloud and rain development. A parcel–DNS hybrid modeling framework is developed. The parcel model is used to generate the initial size distribution of activated aerosols, and the DNS model calculates the subsequent growth of those activated aerosols affected by both the microscopic (turbulent fluctuation) and the macroscopic (bulk) environment. By using this economical modeling framework, continuous particle growth from subcloud aerosols to cloud droplets is accurately represented.
Overall, ultragiant aerosols in the natural cases quickly form the drizzle embryo and thus determine the onset time of autoconversion. However, they only form a few big raindrops due to their scarcity, which has little impact on the level of autoconversion. Turbulence enhances the collision frequency by more than 1 order of magnitude and determines the level of autoconversion. Specifically, turbulence enhances the collisions among similar-sized droplets that are less likely to happen in a nonturbulent environment, effectively broadening the DSD. Therefore, the autoconversion in a turbulent environment is significantly greater than in a nonturbulent environment. It is also found that seeding (increasing aerosol number and size) modifies the level of autoconversion. On the one hand, increasing the aerosol number reduces the mean radius due to stronger competition for water vapor, and therefore slows down the autoconversion. On the other hand, increasing the seeding size can buffer such a negative feedback. However, the seeding of particles in this study only covers a limited range of dry radius (R=0.1, 1 µm) and number concentration (N=10, 20 cm−3, corresponding to a 10 %–20 % increase in the total number concentration). Conditions with more ultragiant aerosols (R≫1 µm), lower aerosol concentrations (), or highly polluted environment () will be of interest to further assess the relative importance of aerosols and turbulence. It is argued that predicting the rain onset time requires accurate information and representation of ultragiant aerosols. And an accurate autoconversion scheme requires a well-quantified turbulent collisions kernel.
Even though the autoconversion rate differs among the six cases, it is found that the bulk variables such as LWC, mean radius, and supersaturation are not sensitive to turbulence level and aerosol conditions. In this case the LWC and mean droplet radius, which are key parameters in Kessler-type or Sundqvist-type autoconversion parameterizations, are not well-related quantities to autoconversion rate, and information on turbulence intensity and aerosols is essential to determine the autoconversion rate. It is argued that these bulk variables are mainly affected by the updraft speed, which is held the same among the six cases. Sensitivity studies are needed in the future to investigate the effect of the LWC on the autoconversion rate due to a change in the updraft.
Cloud models are sensitive to microphysics schemes, and the autoconversion parameterization is one of the main sources of uncertainty in the representation of warm clouds and rain with few observations to verify against. The large uncertainty may be ascribed to the decoupling of microphysics from subgrid-scale turbulence and a lack of aerosol information in the parameterization. Therefore, the aerosol effect evaluated by the models should be cautiously interpreted. The hybrid parcel–DNS model can be used for verifying the autoconversion rate affected by turbulence and aerosols at the subgrid scale of large-eddy simulation (LES).
Despite a good number of improvements made, the current modeling framework still presents the following shortcomings. For simplicity, the same hygroscopic parameter (κ=0.47) is assumed among the natural aerosols and the seeding particles. Besides, seeding is initialized 40 m above the cloud base, while traditional hygroscopic seeding introduces particles around 100–300 m below the cloud base. This treatment might affect the model results as seeding below the cloud base influences the activation and growth of the background aerosols and thus modifies the DSD at the cloud base (Cooper et al., 1997).
Our idealized simulations focus on the cloud adiabatic core region and therefore exclude entrainment mixing, which is highly active near the cloud edge. Activation of laterally entrained aerosols might occur in cumulus clouds outside the adiabatic core (Hoffmann et al., 2015; Slawinska et al., 2012). The newly activated aerosols might lead to a further broadening of the DSD (e.g., Lasher-Trapp et al., 2005). In addition, the in-cloud mixing at a much larger scale than the DNS domain transports and mixes both the air and droplets from different parts of the cloud, including the cloud edge, leading to a highly perturbed Lagrangian history of supersaturation experienced by droplets (Grabowski and Abade, 2017, “eddy hopping effect”). On the other hand, larger turbulent eddies can generate higher supersaturation fluctuations due to a higher variation in a vertical motion and thus may both affect the aerosol activation and broaden the DSD. Traditional DNS, which is confined to a relatively small domain size (<1 m), and the impact of supersaturation fluctuations are significantly restricted. Methods such as an upscaled DNS with superdroplets (e.g., Thomas et al., 2020) or representing large-scale mixing with an external forcing on the thermodynamic fields (Paoli and Shariff, 2009) can be used for studying the impact of turbulent scales on the supersaturation fluctuations and thus on the condensational broadening of DSD. In conclusion, the relative importance of entrainment, eddy hopping effect, small-scale turbulence, and aerosols requires further investigation.
This study proposes the first DNS model framework for scrutinizing the microphysical impact of cloud seeding and presents the first results of such a model. Full DNS modeling from below the cloud base will be the next step to include the effect of turbulence on aerosol activation. Additionally, more realistic scenarios resembling actual hygroscopic seeding conditions – such as utilizing multi-dispersive size distributions, different hygroscopicity parameters, and seeding below the cloud base – will be designed in the future development and deployment of this framework.
The data produced by the direct numerical simulation (DNS) model and parcel model can be accessed in the Harvard Dataverse repository (Chen et al., 2019, https://doi.org/10.7910/DVN/HBIKKV). The parcel model and DNS model used to produce the dataset are available upon request.
This study was co-designed by SC, LX, and MKY. SC conducted the model simulation, did the data analysis, and wrote the article. LX and MKY provided advice and discussions on the model results and revised the article.
The authors declare that they have no conflict of interest.
The work is original and has not been formally published before. It is also not under consideration for publication elsewhere.
We thank the two anonymous reviewers for their invaluable comments. We would like to acknowledge high-performance computing (HPC) support from Cheyenne, Graham, and Cedar. HPC resources at Cheyenne (https://doi.org/10.5065/D6RX99HX) are provided by NCAR's Computational and Information Systems Laboratory and sponsored by the US National Science Foundation. HPC resources at Graham and Cedar are provided by Compute Canada (http://www.computecanada.ca, last access: 6 April 2020).
This research has been supported by the Advanced Study Program at National Center for Atmospheric Research, sponsored by the US National Science Foundation (grant no. 1852977). Part of this work has been supported by the National Center of Meteorology, Abu Dhabi, UAE (UAE Research Program for Rain Enhancement Science).
This paper was edited by Corinna Hoose and reviewed by two anonymous referees.
Beard, K. V. and Pruppacher, H. R.: A Wind Tunnel Investigation of the Rate of Evaporation of Small Water Drops Falling at Terminal Velocity in Air, J. Atmos. Sci., 28, 1455–1464, https://doi.org/10.1175/1520-0469(1971)028<1455:awtiot>2.0.co;2, 1971. a
Berry, E. X. and Reinhardt, R. L.: An Analysis of Cloud Drop Growth by Collection Part II. Single Initial Distributions, J. Atmos. Sci., 31, 1825–1831, https://doi.org/10.1175/1520-0469(1974)031<1825:aaocdg>2.0.co;2, 1974. a, b, c
Çelik, F. and Marwitz, J. D.: Droplet Spectra Broadening by Ripening Process. Part I: Roles of Curvature and Salinity of Cloud Droplets, J. Atmos. Sci., 56, 3091–3105, https://doi.org/10.1175/1520-0469(1999)056<3091:dsbbrp>2.0.co;2, 1999. a
Chen, S., Bartello, P., Yau, M. K., Vaillancourt, P. A., and Zwijsen, K.: Cloud Droplet Collisions in Turbulent Environment: Collision Statistics and Parameterization, J. Atmos. Sci., 73, 621–636, https://doi.org/10.1175/JAS-D-15-0203.1, 2016. a, b
Chen, S., Yau, M. K., and Bartello, P.: Turbulence Effects of Collision Efficiency and Broadening of Droplet Size Distribution in Cumulus Clouds, J. Atmos. Sci., 75, 203–217, https://doi.org/10.1175/JAS-D-17-0123.1, 2018a. a, b, c
Chen, S., Yau, M.-K., Bartello, P., and Xue, L.: Bridging the condensation–collision size gap: a direct numerical simulation of continuous droplet growth in turbulent clouds, Atmos. Chem. Phys., 18, 7251–7262, https://doi.org/10.5194/acp-18-7251-2018, 2018b. a, b, c, d, e, f, g, h, i, j, k
Chen, S., Xue, L., and Yau, M.: Data support for “Impact of CCN hygroscopicity and turbulence on cloud droplet growth: An in-cloud seeding case study using parcel-DNS approach”, Harvard Dataverse, https://doi.org/10.7910/DVN/HBIKKV, 2019. a
Cooper, W. A., Bruintjes, R. T., and Mather, G. K.: Calculations Pertaining to Hygroscopic Seeding with Flares, J. Appl. Meteorol., 36, 1449–1469, https://doi.org/10.1175/1520-0450(1997)036<1449:cpthsw>2.0.co;2, 1997. a, b
Fan, J., Wang, Y., Rosenfeld, D., and Liu, X.: Review of Aerosol–Cloud Interactions: Mechanisms, Significance, and Challenges, J. Atmos. Sci., 73, 4221–4252, https://doi.org/10.1175/JAS-D-16-0037.1, 2016. a
Flossmann, A. I., Manton, M., Abshaev, A., Bruintjes, R., Murakami, M., Prabhakaran, T., and Yao, Z.: Review of Advances in Precipitation Enhancement Research, B. Am. Meteorol. Soc., 100, 1465–1480, https://doi.org/10.1175/bams-d-18-0160.1, 2019. a
Franklin, C. N., Vaillancourt, P. A., Yau, M. K., and Bartello, P.: Collision Rates of Cloud Droplets in Turbulent Flow, J. Atmos. Sci., 62, 2451–2466, https://doi.org/10.1175/jas3493.1, 2005. a
Gilmore, M. S. and Straka, J. M.: The Berry and Reinhardt Autoconversion Parameterization: A Digest, J. Appl. Meteorol. Clim., 47, 375–396, https://doi.org/10.1175/2007jamc1573.1, 2008. a
Gotoh, T., Suehiro, T., and Saito, I.: Continuous growth of cloud droplets in cumulus cloud, New J. Phys., 18, 043042, https://doi.org/10.1088/1367-2630/18/4/043042, 2016. a
Grabowski, W. W. and Abade, G. C.: Broadening of Cloud Droplet Spectra through Eddy Hopping: Turbulent Adiabatic Parcel Simulations, J. Atmos. Sci., 74, 1485–1493, https://doi.org/10.1175/jas-d-17-0043.1, 2017. a
Grabowski, W. W., Andrejczuk, M., and Wang, L.-P.: Droplet growth in a bin warm-rain scheme with Twomey CCN activation, Atmos. Res., 99, 290–301, https://doi.org/10.1016/j.atmosres.2010.10.020, 2011. a
Grabowski, W. W., Morrison, H., Shima, S.-I., Abade, G. C., Dziekan, P., and Pawlowska, H.: Modeling of Cloud Microphysics: Can We Do Better?, B. Am. Meteorol. Soc., 100, 655–672, https://doi.org/10.1175/BAMS-D-18-0005.1, 2019. a, b
Hoffmann, F., Raasch, S., and Noh, Y.: Entrainment of aerosols and their activation in a shallow cumulus cloud studied with a coupled LCM–LES approach, Atmos. Res., 156, 43–57, https://doi.org/10.1016/j.atmosres.2014.12.008, 2015. a
Jensen, J. B. and Nugent, A. D.: Condensational Growth of Drops Formed on Giant Sea-Salt Aerosol Particles, J. Atmos. Sci., 74, 679–697, https://doi.org/10.1175/jas-d-15-0370.1, 2017. a, b, c, d, e
Kessler, E.: On the Distribution and Continuity of Water Substance in Atmospheric Circulations, in: On the Distribution and Continuity of Water Substance in Atmospheric Circulations, American Meteorological Society, 1–84, https://doi.org/10.1007/978-1-935704-36-2_1, 1969. a
Khain, A., Prabha, T. V., Benmoshe, N., Pandithurai, G., and Ovchinnikov, M.: The mechanism of first raindrops formation in deep convective clouds, J. Geophys. Res.-Atmos., 118, 9123–9140, https://doi.org/10.1002/jgrd.50641, 2013. a
Korolev, A. V.: The Influence of Supersaturation Fluctuations on Droplet Size Spectra Formation, J. Atmos. Sci., 52, 3620–3634, https://doi.org/10.1175/1520-0469(1995)052<3620:tiosfo>2.0.co;2, 1995. a
Lasher-Trapp, S. G., Cooper, W. A., and Blyth, A. M.: Broadening of droplet size distributions from entrainment and mixing in a cumulus cloud, Q. J. Roy. Meteor. Soc., 131, 195–220, https://doi.org/10.1256/qj.03.199, 2005. a
Liu, Y. and Daum, P. H.: Parameterization of the Autoconversion Process.Part I: Analytical Formulation of the Kessler-Type Parameterizations, J. Atmos. Sci., 61, 1539–1548, https://doi.org/10.1175/1520-0469(2004)061<1539:potapi>2.0.co;2, 2004. a
Liu, Y., Daum, P. H., McGraw, R., and Wood, R.: Parameterization of the Autoconversion Process. Part II: Generalization of Sundqvist-Type Parameterizations, J. Atmos. Sci., 63, 1103–1109, https://doi.org/10.1175/jas3675.1, 2006a. a
Liu, Y., Daum, P. H., and Yum, S. S.: Analytical expression for the relative dispersion of the cloud droplet size distribution, Geophys. Res. Lett., 33, L02810, https://doi.org/10.1029/2005gl024052, 2006b. a
Morrison, H., Lier-Walqui, M., Fridlind, A. M., Grabowski, W. W., Harrington, J. Y., Hoose, C., Korolev, A., Kumjian, M. R., Milbrandt, J. A., Pawlowska, H., Posselt, D. J., Prat, O. P., Reimel, K. J., Shima, S.-I., Diedenhoven, B., and Xue, L.: Confronting the challenge of modeling cloud and precipitation microphysics, J. Adv. Model. Earth Sy., 12, L02810, https://doi.org/10.1029/2019ms001689, 2020. a
Noh, Y., Oh, D., Hoffmann, F., and Raasch, S.: A Cloud Microphysics Parameterization for Shallow Cumulus Clouds Based on Lagrangian Cloud Model Simulations, J. Atmos. Sci., 75, 4031–4047, https://doi.org/10.1175/jas-d-18-0080.1, 2018. a
Paoli, R. and Shariff, K.: Turbulent Condensation of Droplets: Direct Simulation and a Stochastic Model, J. Atmos. Sci., 66, 723–740, https://doi.org/10.1175/2008JAS2734.1, 2009. a, b
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. a, b
Rogers, R. R. and Yau, M. K.: A Short Course in Cloud Physics, 3rd edn., Butterworth-Heinemann, Oxford, United Kingdom, 1989. a
Saito, I. and Gotoh, T.: Turbulence and cloud droplets in cumulus clouds, New J. Phys., 20, 023001, https://doi.org/10.1088/1367-2630/aaa229, 2018. a
Sardina, G., Picano, F., Brandt, L., and Caballero, R.: Continuous Growth of Droplet Size Variance due to Condensation in Turbulent Clouds, Phys. Rev. Lett., 115, 184501, https://doi.org/10.1103/PhysRevLett.115.184501, 2015. a
Seifert, A., Nuijens, L., and Stevens, B.: Turbulence effects on warm-rain autoconversion in precipitating shallow convection, Q. J. Roy. Meteor. Soc., 136, 1753–1762, https://doi.org/10.1002/qj.684, 2010. a
Silverman, B. A.: A Critical Assessment of Hygroscopic Seeding of Convective Clouds for Rainfall Enhancement, B. Am. Meteor. Soc., 84, 1219–1230, https://doi.org/10.1175/bams-84-9-1219, 2003. a
Silverman, B. A. and Sukarnjanaset, W.: Results of the Thailand Warm-Cloud Hygroscopic Particle Seeding Experiment, J. Appl. Meteorol., 39, 1160–1175, https://doi.org/10.1175/1520-0450(2000)039<1160:rottwc>2.0.co;2, 2000. a
Slawinska, J., Grabowski, W. W., Pawlowska, H., and Morrison, H.: Droplet Activation and Mixing in Large-Eddy Simulation of a Shallow Cumulus Field, J. Atmos. Sci., 69, 444–462, https://doi.org/10.1175/jas-d-11-054.1, 2012. a
Srivastava, R. C.: Growth of Cloud Drops by Condensation: Effect of Surface Tension on the Dispersion of Drop Sizes, J. Atmos. Sci., 48, 1596–1599, https://doi.org/10.1175/1520-0469(1991)048<1596:gocdbc>2.0.co;2, 1991. a
Stoelinga, M. T., Hobbs, P. V., Mass, C. F., Locatelli, J. D., Colle, B. A., Houze, R. A., Rangno, A. L., Bond, N. A., Smull, B. F., Rasmussen, R. M., Thompson, G., and Colman, B. R.: Improvement of Microphysical Parameterization through Observational Verification Experiment, B. Am. Meteorol. Soc., 84, 1807–1826, https://doi.org/10.1175/BAMS-84-12-1807, 2003. a
Sundqvist, H.: A parameterization scheme for non-convective condensation including prediction of cloud water content, Q. J. Roy. Meteor. Soc., 104, 677–690, https://doi.org/10.1002/qj.49710444110, 1978. a
Terblanche, D. E., Steffens, F. E., Fletcher, L., Mittermaier, M. P., and Parsons, R. C.: Toward the Operational Application of Hygroscopic Flares for Rainfall Enhancement in South Africa, J. Appl. Meteorol., 39, 1811–1821, https://doi.org/10.1175/1520-0450(2001)039<1811:ttoaoh>2.0.co;2, 2000. a
Thomas, L., Grabowski, W. W., and Kumar, B.: Diffusional growth of cloud droplets in homogeneous isotropic turbulence: DNS, scaled-up DNS, and stochastic model, Atmos. Chem. Phys., 20, 9087–9100, https://doi.org/10.5194/acp-20-9087-2020, 2020. a
Thomas, S., Ovchinnikov, M., Yang, F., Voort, D., Cantrell, W., Krueger, S. K., and Shaw, R. A.: Scaling of an Atmospheric Model to Simulate Turbulence and Cloud Microphysics in the Pi Chamber, J. Adv. Model. Earth Sy., 11, 1981–1994, https://doi.org/10.1029/2019ms001670, 2019. a
Vaillancourt, P. A., Yau, M. K., and Grabowski, W. W.: Microscopic Approach to Cloud Droplet Growth by Condensation. Part I: Model Description and Results without Turbulence, J. Atmos. Sci., 58, 1945–1964, https://doi.org/10.1175/1520-0469(2001)058<1945:MATCDG>2.0.CO;2, 2001. a, b
Vaillancourt, P. A., Yau, M. K., Bartello, P., and Grabowski, W. W.: Microscopic Approach to Cloud Droplet Growth by Condensation. Part II: Turbulence, Clustering, and Condensational Growth, J. Atmos. Sci., 59, 3421–3435, https://doi.org/10.1175/1520-0469(2002)059<3421:MATCDG>2.0.CO;2, 2002. a, b
Wang, L.-P., Ayala, O., Kasprzak, S. E., and Grabowski, W. W.: Theoretical Formulation of Collision Rate and Collision Efficiency of Hydrodynamically Interacting Cloud Droplets in Turbulent Atmosphere, J. Atmos. Sci., 62, 2433–2450, https://doi.org/10.1175/JAS3492.1, 2005. a
White, B., Gryspeerdt, E., Stier, P., Morrison, H., Thompson, G., and Kipling, Z.: Uncertainty from the choice of microphysics scheme in convection-permitting models significantly exceeds aerosol effects, Atmos. Chem. Phys., 17, 12145–12175, https://doi.org/10.5194/acp-17-12145-2017, 2017. a, b
Wood, R., Field, P., and Cotton, W.: Autoconversion rate bias in stratiform boundary layer cloud parameterizations, Atmos. Res., 65, 109–128, https://doi.org/10.1016/s0169-8095(02)00071-6, 2002. a
Xue, L., Teller, A., Rasmussen, R., Geresdi, I., and Pan, Z.: Effects of Aerosol Solubility and Regeneration on Warm-Phase Orographic Clouds and Precipitation Simulated by a Detailed Bin Microphysical Scheme, J. Atmos. Sci., 67, 3336–3354, https://doi.org/10.1175/2010jas3511.1, 2010. a
Xue, L., Fan, J., Lebo, Z. J., Wu, W., Morrison, H., Grabowski, W. W., Chu, X., Geresdi, I., North, K., Stenz, R., Gao, Y., Lou, X., Bansemer, A., Heymsfield, A. J., McFarquhar, G. M., and Rasmussen, R. M.: Idealized Simulations of a Squall Line from the MC3E Field Campaign Applying Three Bin Microphysics Schemes: Dynamic and Thermodynamic Structure, Mon. Weather Rev., 145, 4789–4812, https://doi.org/10.1175/MWR-D-16-0385.1, 2017. a
Yang, F., Kollias, P., Shaw, R. A., and Vogelmann, A. M.: Cloud droplet size distribution broadening during diffusional growth: ripening amplified by deactivation and reactivation, Atmos. Chem. Phys., 18, 7313–7328, https://doi.org/10.5194/acp-18-7313-2018, 2018. a