The impact of solar radiation on polar mesospheric ice particle formation

Mean temperatures in the polar summer mesopause can drop to 130 K. The low temperatures in combination with water vapor mixing ratios of a few parts per million give rise to the formation of ice particles. These ice particles may be observed as polar mesospheric clouds. Mesospheric ice cloud formation is believed to initiate heterogeneously on small aerosol particles (r<2 nm) composed of recondensed meteoric material, so-called meteoric smoke particles (MSPs). Recently, we investigated the ice activation and growth behavior of MSP analogues under realistic mesopause conditions. Based on these measurements we presented a new activation model which largely reduced the uncertainties in describing ice particle formation. However, this activation model neglected the possibility that MSPs heat up in the low-density mesopause due to absorption of solar and terrestrial irradiation. Radiative heating of the particles may severely reduce their ice formation ability. In this study we expose MSP analogues (Fe₂O₃ and Fe_xSi_1−xO₃) to realistic mesopause temperatures and water vapor concentrations and investigate particle warming under the influence of variable intensities of visible light (405, 488, and 660 nm). We show that Mie theory calculations using refractive indices of bulk material from the literature combined with an equilibrium temperature model presented in this work predict the particle warming very well. Additionally, we confirm that the absorption efficiency increases with the iron content of the MSP material. We apply our findings to mesopause conditions and conclude that the impact of solar and terrestrial radiation on ice particle formation is significantly lower than previously assumed.

1 Introduction

The lowest temperatures in the terrestrial atmosphere are encountered in the polar summer mesopause, where mean daily temperatures at high latitudes can fall to below 130 K (e.g., Lübken, 1999; Lübken et al., 2009). These low temperatures in combination with H₂O concentrations of a few parts per million (Hervig et al., 2009; Seele and Hartogh, 1999) lead to highly supersaturated conditions which allow for the formation of ice particles (e.g., Lübken et al., 2009; Rapp and Thomas, 2006). When the ice particle radii reach about 30 nm and their concentration is of the order of 100 cm⁻³ they become optically visible and may be observed as polar mesospheric clouds (PMCs) (e.g., Rapp and Thomas, 2006). When observed from the ground, these clouds are often referred to as noctilucent clouds (NLCs). Because of their particular wavy appearance and their high elevation of about 83 km, PMCs have received much attention since their first reported observation in 1885 (Leslie, 1885). The current scientific interest in these extraordinary clouds is substantiated in their potential role as tracer for the dynamical structure of the summer mesopause (e.g., Demissie et al., 2014; Kaifler et al., 2013; Rong et al., 2015; Witt, 1962) or for long-term trends of temperature and H₂O concentration caused by anthropogenic emissions of CO₂ and CH₄ (e.g., Hervig et al., 2016; Thomas and Olivero, 2001; Thomas et al., 1989). However, in order to use observation of PMCs as a tracer, an in-depth understanding of the processes involved in PMC formation is necessary.

Wilms et al. (2016) found that in addition to dynamical processes the description of the initial formation of the ice particles significantly affects modeled PMC properties. Ice particle formation is believed to initiate heterogeneously on nanometer-sized recondensed meteoric material, so-called meteoric smoke particles (MSPs) (e.g., Gumbel and Megner, 2009; Keesee, 1989; Rapp and Thomas, 2006; Turco et al., 1982). This conjecture is strongly supported by satellite and rocket-borne observations showing that MSPs are included in PMC ice particles (Antonsen et al., 2017; Havnes et al., 2014; Hervig et al., 2012). The initial ice particle formation has been described in two different ways. Either activation-barrier-free growth is assumed to set in for saturations in excess of the equilibrium saturation over the curved particle surface (e.g., Berger and Lübken, 2015; Schmidt et al., 2018) or ice particle formation is described using classical nucleation theory (e.g., Asmus et al., 2014; Bardeen et al., 2010; Rapp and Thomas, 2006; Wilms et al., 2016). Both approaches assume the formation of hexagonal ice and the latter typically requires much higher critical saturations to initiate ice particle growth. In order to reduce the large uncertainties in describing the initial formation of PMC ice particles, we designed a laboratory experiment to study ice particle formation under realistic mesopause conditions (Duft et al., 2015). Recently, we investigated the ice activation and growth behavior on SiO₂, Fe₂O₃, and mixed iron silicate nanoparticles which serve as analogues for MSPs. We found that the primary ice phase forming on the MSP analogues under the conditions of the summer mesopause is amorphous solid water (ASW) (Nachbar et al., 2018b, c). Additionally, we showed that MSPs adsorb up to several layers of water until ice growth activates as soon as the saturation exceeds the saturation vapor pressure of ASW including the Kelvin effect for the ice-covered or “wet” particle radius and considering the collision radius of water molecules (Duft et al., 2019).

Asmus et al. (2014) pointed out that MSPs may heat up in the low-density atmosphere of the mesopause by absorbing solar and terrestrial irradiation. The extent of this effect depends on the MSP composition and has been proposed to increase with increasing iron content. Interestingly, satellite and rocket-borne investigations indicate that MSPs are most likely composed of iron-rich materials such as magnetite (Fe₃O₄), wüstite (FeO), magnesiowüstite (Mg_xFe_1−xO, x=0–0.6), and iron-rich olivine (Mg_2xFe_2−2xSiO₄, x=0.4–0.5) (Hervig et al., 2017; Rapp et al., 2012). Using nucleation theory, Asmus et al. (2014) concluded that the warming for such MSP materials significantly impacts the ice-forming ability of the particles, thus rendering them ineffective nuclei. However, up until now this conclusion has not been confirmed experimentally. To this end, we extended our experimental setup with a laser system, which allows MSP analogues to be exposed to a known intensity of visible light at three wavelengths (405, 488, and 660 nm). We studied the number of adsorbed H₂O molecules on Fe₂O₃ and Fe_xSi_1−xO₃ nanoparticles under the influence of the laser light at controlled gas-phase H₂O concentration and background pressure. In this way, we could determine the offset of the particle temperature from the ambient temperature. The experimental method is described in more detail in Sect. 2. From the experimentally determined temperature offsets we then deduce absorption efficiencies using a light absorption model, which is introduced in Sect. 3. In Sect. 4, we present our results on the absorption efficiencies and compare them to Mie theory calculations using literature values of the refractive indices. We estimate the maximum temperature offset for MSPs in the summer mesopause and discuss the consequences on ice particle formation. Finally, we summarize our main conclusions in Sect. 5.

2 Experimental method

We produce spherical, singly charged Fe₂O₃, SiO₂, or Fe_xSi_1−xO₃ particles with radii smaller than 4 nm in a nonthermal low-pressure microwave plasma particle source (Nachbar et al., 2018a). The particles are transferred online into the vacuum system of the experiment (illustrated in Fig. 1), which has been described in detail elsewhere (Duft et al., 2015; Meinen et al., 2010; Nachbar et al., 2016, 2018b). In brief, singly charged nanometer-sized particles enter the vacuum chamber through an aerodynamic lens and a skimmer. After the skimmer, the particles enter an rf octupole serving as an ion guide. The particles are mass selected ($\mathrm{\Delta }m/m\le \mathrm{7}\mathit{\%}$) with an electrostatic quadrupole deflector (DF₁) and subsequently enter into the molecular flow ice cell (MICE). MICE is a modified quadrupole ion trap. A temperature-controlled He environment at a pressure of $\left(\mathrm{1}-\mathrm{5}\right)\times {\mathrm{10}}^{-\mathrm{3}}$ mbar thermalizes the particles under molecular flow conditions. The helium pressure is adjusted with a leak valve attached to a helium cylinder (99.999 % purity) and the pressure is measured and corrected (Yasumoto, 1980) using a pressure sensor (Ionivac ITR 90). In MICE, the particles also interact with a well-calibrated (Nachbar et al., 2018b) concentration of gas-phase H₂O molecules, which is maintained by temperature-controlled sublimation of water vapor from ice-covered surfaces (Duft et al., 2015). For a typical experiment, MICE is filled with 10⁷ particles in about 1 s, followed by storing of the particles for up to several hours. Depending on the conditions applied in MICE, H₂O molecules adsorb on the particles until an equilibrium state is reached or ice growth initiates on the particles. These processes are monitored by periodically extracting a small portion of the trapped particle population from MICE. After extraction, the particles are accelerated orthogonally into a time-of-flight (TOF) spectrometer for mass measurement.

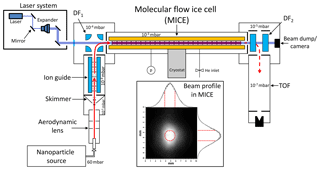
Figure 1 Illustration of the experimental setup. The insert shows a camera image of the laser beam profile (λ=488 nm) taken at the exit of MICE. Vertical and horizontal cross sections of the laser beam profile are shown above and right of the image, overlaid with fitted Gaussian curves. The red dashed lines indicate the radial extent of the levitated nanoparticle cloud. See the text for more details.

The setup has been extended with a laser system equipped with three lasers of different wavelengths, λ=405 nm (Obis LX 405), λ=488 nm (Obis LX 488), and λ=660 nm (Obis LX 660). A combination of a laser beam expander (Edmund Optics 10X VIS broadband beam expander), mirrors, and a quartz glass window guides the expanded laser beam horizontally through the center of MICE pointing onto a beam dump. The light intensity in MICE was calibrated by measuring the power and the beam profile in MICE with a power-meter (Coherent PM USB PS19Q) and a CCD camera (Thorlabs 4070M-GE-TE). A typical beam profile of the expanded 488 nm laser beam is shown in the insert of Fig. 1. The red dashed lines indicate the maximum ion cloud diameter d=2 mm calculated for the combinations of particle mass ($\mathrm{2}\times {\mathrm{10}}^{\mathrm{4}}\mathrm{Da}-\mathrm{50}\times {\mathrm{10}}^{\mathrm{4}}$ Da; 1 Da ≜1 atomic mass unit $=\mathrm{1.6605}\times {\mathrm{10}}^{-\mathrm{27}}$ kg), radio frequency (30–1000 kHz), and amplitude (200–1000 V) applied in the present study (Majima et al., 2012). Allowing for a misalignment of the laser beam of up to 0.5 mm from the ion trap center, we conclude that the particles are located within a diameter of 3 mm from the center of the expanded laser beam. We use the mean of the intensity values at d=3 mm and the center of the laser beam to describe the light intensity irradiating from the particles. The uncertainty is defined by the difference between the intensity value at the center of the laser beam and the mean value.

In this work, we apply conditions with saturations below the threshold for ice growth, i.e., where only adsorption occurs. Each experiment begins by filling MICE with a fresh charge of nanoparticles. The initially dry nanoparticles adsorb H₂O molecules until an equilibrium state between adsorbing H₂O flux and desorbing flux is reached. The process of reaching the equilibrium state is illustrated in Fig. 2a, which shows the time evolution of the particle mass for Fe₂O₃ particles with a dry particle radius $r_{\mathrm{dry}}={\left(\mathrm{3}{m}_{\mathrm{0}}/\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{p}}\right)}^{\mathrm{1}/\mathrm{3}}=\mathrm{2.9}$ nm (ρ_p=5.2 g cm⁻³), a H₂O gas-phase concentration $n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{1.1}\times {\mathrm{10}}^{\mathrm{16}}$ m⁻³, and a temperature of the environment surrounding the particles T_env=148.8 K. The black squares show the adsorption curve without light irradiation for which T_env equals the particle temperature T_p. If the particles are heated by light irradiation (T_p>T_env), the water molecule flux desorbing from a particle increases, which causes a reduction in the number of adsorbed H₂O molecules in equilibrium. This effect is shown by the colored data for illumination with the 488 nm laser at various mean light intensities. Figure 2b shows the corresponding particle temperature offsets ΔT, which were determined by analyzing the steady-state mass of adsorbed water molecules. The method for deriving ΔT is presented below.

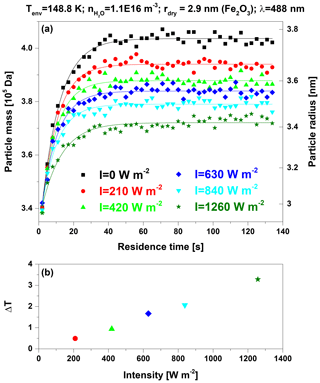
Figure 2 (a) Mean particle mass as a function of residence time in MICE for six different mean light intensities (λ=488 nm, r_dry=2.9 nm (Fe₂O₃), T_env=148.8 K, $n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{1.1}\times {\mathrm{10}}^{\mathrm{16}}$ m⁻³). The solid curves represent fits of Eq. (2) to the data. (b) Particle temperature offsets ΔT (Eq. 4) as a function of the mean light intensities.

We analyze the adsorption data with a parameterization which was originally used to describe the equilibrium concentration of adsorbed water molecules $c_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ on a planar surface with sub-monolayer coverage (Pruppacher and Klett, 2010). In our previous work we have modified this parameterization to account for the curvature of the nanometer-sized particles and have proven its functionality for coverages of more than one monolayer (Duft et al., 2019). The parameterization is derived from the assumption that each water molecule which collides with a particle adsorbs on it. In equilibrium, the flux density of water molecules colliding with a particle j_ads must equal the flux density desorbing from the particle j_des :

$$\begin{array}{}\text{(1)}& \underset{j_{\mathrm{ads}}}{\underbrace{{\displaystyle \frac{n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\cdot v_{\mathrm{th}}}{\mathrm{4}}}}}=\underset{j_{\mathrm{des}}}{\underbrace{c_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\cdot f\cdot \exp \left(-{\displaystyle \frac{E_{\mathrm{des}}^{\mathrm{0}}}{R{T}_{\mathrm{p}}}}+{\displaystyle \frac{\mathrm{2}\mathit{\sigma }v}{R{T}_{\mathrm{p}}{r}_{\mathrm{dry}}}}\right)}}.\end{array}$$

The flux density in the molecular flow regime (left-hand side of Eq. 1) depends on gas-phase properties, namely the concentration $n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and the mean thermal velocity $v_{\mathrm{th}}=\sqrt{\mathrm{8}k{T}_{\mathrm{env}}/\mathit{\pi }{m}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}$ of gas-phase H₂O molecules. The desorbing flux density (right-hand side of Eq. 1), however, depends on properties of the particle. The desorbing flux density is the product of the concentration of adsorbed water molecules in equilibrium $c_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, the vibrational frequency of a water molecule on the particle surface f = 10¹³ Hz, and an exponential function which describes the probability that an adsorbed molecule desorbs. This probability depends on the ideal gas constant R, the particle temperature T_p, and the mean desorption energy of a H₂O molecule for a planar surface of the particle material $E_{\mathrm{des}}^{\mathrm{0}}$. The second term in the exponential function of Eq. (1) describes the curvature dependence of the desorption energy, which can be calculated using the properties of amorphous solid water (ASW) (Duft et al., 2019). Here, $v=\mathrm{6.022}\times {\mathrm{10}}^{\mathrm{23}}\cdot m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}/{\mathit{\rho }}_{\mathrm{ice}}$ is the volume of 1 mol of H₂O molecules in ASW. The densities of ASW and crystalline ice are very similar at the temperatures under investigation (Brown et al., 1996; Loerting et al., 2011). We use the parameterization ${\mathit{\rho }}_{\mathrm{ice}}\left[{\mathrm{g}\mathrm{cm}}^{-\mathrm{3}}\right]=\mathrm{0.9167}-\mathrm{1.75}\times {\mathrm{10}}^{-\mathrm{4}}\cdot T_{\mathrm{p}}\left[{}^{\circ }\mathrm{C}\right]-\mathrm{5}\times {\mathrm{10}}^{-\mathrm{7}}\cdot {\left(T_{\mathrm{p}}\left[{}^{\circ }\mathrm{C}\right]\right)}^{\mathrm{2}}$ for crystalline ice (Pruppacher and Klett, 2010). For the surface tension of ASW we use $\mathit{\sigma }\left[{\mathrm{mN}\mathrm{m}}^{-\mathrm{1}}\right]=\left(\mathrm{114.81}-\mathrm{0.144}\cdot T\left[K\right]\right)$, which is based on an extrapolation of experimental data for supercooled water (Nachbar et al., 2018c). The equilibrium concentration of adsorbed water molecules $c_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is the adsorbed mass of H₂O molecules in equilibrium m_ads divided by the surface area of a dry nanoparticle $A_{\mathrm{p}}=\mathrm{4}\mathit{\pi }{r}_{\mathrm{dry}}^{\mathrm{2}}$ and the mass of a water molecule $m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ ($c_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=m_{\mathrm{ads}}/A_{\mathrm{p}}/m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$). We derive the adsorbed mass of H₂O molecules in equilibrium m_ads from the experimental data with an exponential fit (represented by the solid curves in Fig. 2a) of the following form:

$$\begin{array}{}\text{(2)}& m\left(t\right)=m_{\mathrm{0}}+m_{\mathrm{ads}}\cdot \left(\mathrm{1}-\exp \left({\displaystyle \frac{-t_{\mathrm{res}}}{\mathit{\tau }}}\right)\right).\end{array}$$

The radius of the wet particle is indicated by the right ordinate in Fig. 2a and follows from the measured particle mass according to

$$\begin{array}{}\text{(3)}& r_{\mathrm{wet}}={\left(r_{\mathrm{dry}}^{\mathrm{3}}+{\displaystyle \frac{\mathrm{3}}{\mathrm{4}\mathit{\pi }}}{\displaystyle \frac{m_{\mathrm{ads}}}{{\mathit{\rho }}_{\mathrm{ice}}}}\right)}^{\mathrm{1}/\mathrm{3}}.\end{array}$$

The particle temperature offset ΔT is determined by a set of two measurement runs, one without and one with light illumination. The mean desorption energy for a H₂O molecule is determined from the measurement without light illumination (T_p=T_env) by solving Eq. (1) for $E_{\mathrm{des}}^{\mathrm{0}}$. For the data shown in Fig. 2, this procedure results in $E_{\mathrm{des}}^{\mathrm{0}}=\mathrm{42.52}$ kJ mol⁻¹. We only analyze data with coverages above 1 monolayer for which the desorption energy is expected to depend only weakly on H₂O coverage (Mazeina and Navrotsky, 2007; Navrotsky et al., 2008; Sneh et al., 1996). For such coverages we did not observe any significant influence of the H₂O coverage or the particle temperature on the values of $E_{\mathrm{des}}^{\mathrm{0}}$ determined in our previous study (Duft et al., 2019). Therefore, we can determine the particle temperature under light illumination assuming a constant $E_{\mathrm{des}}^{\mathrm{0}}$ value. Rearranging Eq. (1) yields

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{T}_{\mathrm{p}}=T_{\mathrm{env}}+\mathrm{\Delta }T=\left(E_{\mathrm{des}}^{\mathrm{0}}-{\displaystyle \frac{\mathrm{2}\mathit{\sigma }v}{r_{\mathrm{dry}}}}\right)\\ \text{(4)}& {\displaystyle }& {\displaystyle }/\left(R\cdot \ln \left({\displaystyle \frac{m_{\mathrm{ads}}\left(T_{\mathrm{p}}\right)\cdot f}{m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\mathit{\pi }{n}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{v}_{\mathrm{th}}{r}_{\mathrm{dry}}^{\mathrm{2}}}}\right)\right).\end{array}$$

Since σ and ρ_ice are dependent on the particle temperature, Eq. (4) should be solved numerically. However, a sensitivity analysis has shown that calculating ΔT analytically using constant σ(T_env) and ρ_ice(T_env) deviates less than 1 % from the numerical solution. We therefore analyzed our data using σ(T_env) and ρ_ice(T_env). The determined temperature offset ΔT can be used with an equilibrium temperature model to calculate the light absorption efficiency of the particles Q_abs. The equilibrium temperature model is introduced in the next section.

3 Equilibrium temperature model

The equilibrium temperature of particles levitated in MICE is described by a balance between power sources and sinks. Sources are absorption of laser light $P_{\mathit{\lambda }}^{\mathrm{a}}$ and of infrared radiation emitted by the environment $P_{\mathrm{env}}^{\mathrm{a}}$. Sinks are cooling due to collisions with the He background gas P_col and blackbody radiation of the particle in the infrared $P_{\mathrm{rad}}^{\mathrm{e}}$. Note that in equilibrium, the heat from sublimation and condensation cancels. The balance equation is

$$\begin{array}{}\text{(5)}& P_{\mathit{\lambda }}^{\mathrm{a}}+P_{\mathrm{env}}^{\mathrm{a}}=P_{\mathrm{rad}}^{\mathrm{e}}+P_{\mathrm{col}}.\end{array}$$

The absorption of laser light with intensity I depends on the material and wavelength-dependent absorption efficiency of the particles Q_abs. The absorption efficiency is defined as the absorption cross section divided by the geometrical cross section $A_{\mathrm{geo}}=\mathit{\pi }{r}_{\mathrm{dry}}^{\mathrm{2}}$. We assume the layer of adsorbed water molecules to be entirely transparent to visible light so that $P_{\mathit{\lambda }}^{\mathrm{a}}$ is the power absorbed by the MSP alone:

$$\begin{array}{}\text{(6)}& P_{\mathit{\lambda }}^{\mathrm{a}}=I\cdot Q_{\mathrm{abs}}\left(\mathit{\lambda },r_{\mathrm{dry}}\right)\cdot A_{\mathrm{geo}}.\end{array}$$

For the cooling due to collisions with the He gas we use the description presented in Asmus et al. (2014):

$$\begin{array}{}\text{(7)}& P_{\mathrm{col}}=A_{\mathrm{col}}\cdot {\displaystyle \frac{\mathit{\alpha }\cdot p}{\mathrm{4}k{T}_{\mathrm{env}}}}{v}_{\mathrm{th}}\cdot k{\displaystyle \frac{\mathit{\gamma }+\mathrm{1}}{\mathrm{2}\left(\mathit{\gamma }-\mathrm{1}\right)}}\cdot \mathrm{\Delta }T.\end{array}$$

For particles in the nanometer regime, the collision surface area A_col must include the radius of the colliding He atom (r_He=0.14 nm, Bondi, 1964), so that $A_{\mathrm{col}}=\mathrm{4}\mathit{\pi }{\left(r_{\mathrm{wet}}+r_{\mathrm{He}}\right)}^{\mathrm{2}}$. The helium pressure in MICE is represented by p, $v_{\mathrm{th}}=\sqrt{\mathrm{8}k{T}_{\mathrm{env}}/\mathit{\pi }{m}_{\mathrm{He}}}$ is the mean thermal velocity of He atoms, γ is the heat capacity ratio, $\mathrm{\Delta }T=T_{\mathrm{p}}-T_{\mathrm{env}}$ is the temperature difference between the particle and the environment, and α is the thermal accommodation coefficient. The particles investigated in this work are water-covered metal oxides. The thermal accommodation coefficient of He on comparable surfaces has been measured to be 0.525±0.125 (Fung and Tang, 1988; Ganta et al., 2011). Note that when applying the equilibrium temperature model to the summer mesopause in Sect. 4.2 we use the thermal accommodation coefficient of air α_air=1 (Fung and Tang, 1988; Ganta et al., 2011).

For the conditions applied in MICE, $P_{\mathrm{rad}}^{\mathrm{e}}$ and $P_{\mathrm{env}}^{\mathrm{a}}$ are several orders of magnitude smaller than $P_{\mathit{\lambda }}^{\mathrm{a}}$ andP_col and can be neglected in the analysis of the experimental results. For mesospheric conditions, these two terms may be calculated as presented in Asmus et al. (2014). Substituting Eqs. (6) and (7) in Eq. (5) and solving for the absorption efficiency Q_abs(λ,r_dry) yields

$$\begin{array}{}\text{(8)}& Q_{\mathrm{abs}}\left(\mathit{\lambda },r_{\mathrm{dry}}\right)={\displaystyle \frac{A_{\mathrm{col}}}{I\cdot A_{\mathrm{geo}}}}\mathit{\alpha }p{v}_{\mathrm{th}}{\displaystyle \frac{\left(\mathit{\gamma }+\mathrm{1}\right)}{\mathrm{8}{T}_{\mathrm{env}}\left(\mathit{\gamma }-\mathrm{1}\right)}}\mathrm{\Delta }T.\end{array}$$

4 Results and discussion

4.1 Absorption efficiencies

H₂O adsorption measurements similar to those presented in Fig. 2 were recorded for Fe₂O₃ particles with dry particle radii between 1.3 and 3.2 nm. Particle temperature offsets ΔT were determined from the equilibrium adsorption measurements according to Eq. (4) and converted to absorption efficiencies for each light intensity according to Eq. (8). The absorption efficiencies for each set of experiments with the same dry particle radius were averaged. The results are shown in Fig. 3 as a function of dry particle radius on a double logarithmic scale. The main measurement uncertainties originate from the inhomogeneous intensity profile of the expanded laser beam and the uncertainty of the thermal accommodation coefficient α, which are systematic error sources. The error bars shown for the particle radius represent the width of the particle size distribution. In order to compare our data to Q_abs values derived from literature data of the complex refractive index $m=n+i\cdot k$, Q_abs was calculated from the extinction efficiency Q_ext and from the scattering efficiency Q_scat using Mie theory (Bohren and Huffmann, 2007) according to

$$\begin{array}{}\text{(9)}& Q_{\mathrm{abs}}\left(\mathit{\lambda },r_{\mathrm{dry}},m\right)=Q_{\mathrm{ext}}\left(\mathit{\lambda },r_{\mathrm{dry}},m\right)-Q_{\mathrm{scat}}\left(\mathit{\lambda },r_{\mathrm{dry}},m\right).\end{array}$$

Note that the size parameter $x=\mathrm{2}\mathit{\pi }{r}_{\mathrm{dry}}/\mathit{\lambda }$ is much smaller than 1 (Rayleigh regime) for all particle sizes investigated in the present study and that the absorption cross section for such size parameters is proportional to the volume of the particle and thus Q_abs is proportional to r_dry.

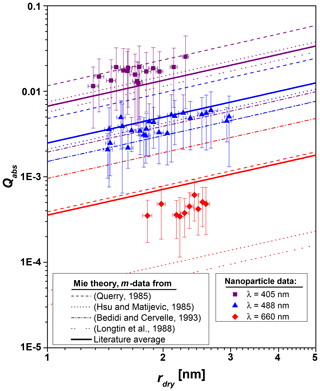
Figure 3 Absorption efficiencies as a function of dry particle radius for Fe₂O₃ nanoparticles at λ=405, λ=488, and λ=660 nm. The dotted and dashed curves represent Mie theory calculations using refractive indices from literature with the colors indicating the wavelength.

Large differences exist throughout the literature for the imaginary part of the refractive index for hematite (Fe₂O₃) in the visible and near-infrared ranges (Zhang et al., 2015). These differences increase with increasing wavelength and reach a factor of 40 at λ=660 nm. In order to compare our results with literature data, we collated all works which determined the real part n and the imaginary part k of the refractive index for Fe₂O₃ between 400 and 700 nm (Bedidi and Cervelle, 1993; Hsu and Matijević, 1985; Longtin et al., 1988; Querry, 1985). Note that the data reported in Longtin et al. (1988) are based on measurements from Kerker et al. (1979). We calculated the absorption efficiencies for all sets of refractive indices as a function of the particle radius. The results are shown by the dashed and dotted curves in Fig. 3 with the colors indicating the wavelength. The solid lines are mean values of the absorption efficiencies calculated from literature data. Note that the data obtained with the refractive indices from Bedidi and Cervelle (1993) and Longtin et al. (1988) are identical at 488 nm. Our data at λ=405 nm agree well with the Mie theory calculations using the literature refractive indices, except for Bedidi and Cervelle (1993). Our data for 488 nm are also in good agreement with literature, except for the calculations using the refractive indices from Querry (1985). At 660 nm our experimental results lie within the large scatter of the literature values. The absorption efficiencies deduced from the refractive indices of Hsu and Matijević (1985) and Longtin et al. (1988) are smaller than our results, whereas the values deduced from Querry (1985) and Bedidi and Cervelle (1993) are larger. The latter is supported by the work of Meland et al. (2011), who concluded from angle-resolved light scattering experiments using hematite particles that the values of the imaginary part k of the refractive index of Querry (1985) and Bedidi and Cervelle (1993) are too high.

Overall, the experimentally determined absorption efficiencies show a linear trend with particle radius (compare to Mie theory calculations) and are within the spread of Mie theory calculations using the literature refractive indices. We therefore conclude that our method of determining Q_abs from the equilibrium temperature of nanoparticles via the amount of adsorbed water is validated. Furthermore, we conclude that the equilibrium temperature model presented in this work can be used with literature values of bulk refractive indices of potential MSP materials to estimate the equilibrium temperature of MSPs in the mesopause.

Asmus et al. (2014) proposed that the temperature increase in MSPs due to absorption of solar irradiation increases linearly with increasing iron content of the particle material. In order to experimentally test this hypothesis, we measured the absorption efficiency at λ=488 nm (the laser wavelength closest to the maximum of the solar irradiation) for Fe₂O₃ and iron silicate particles Fe_xSi_1−xO₃ (0<x<1) (r_dry=2 nm) of varying iron content. The results are shown in Fig. 4 together with Mie theory calculations using the refractive indices for Mg_xFe_1−xSiO₃ (Dorschner et al., 1995), FeO (Henning et al., 1995), FeOOH (Bedidi and Cervelle, 1993), and the mean value for Fe₂O₃ from Fig. 3. The data support the assumption that Q_abs depends linearly on the iron content. Consequently, the potential MSP material which would heat up the most is FeO with a stoichiometric iron content of 0.5.

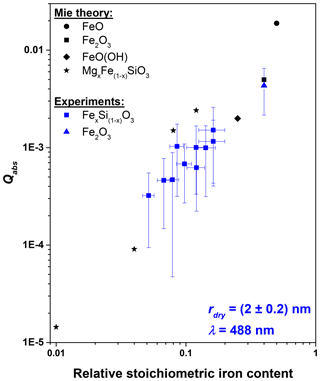
Figure 4 Absorption efficiencies for r_dry=2 nm particles at λ=488 nm of various particle materials as a function of the relative stoichiometric iron content. Blue squares and the triangle represent experimental results for Fe_xSi_1−xO₃ (0<x<1) and Fe₂O₃ particles, respectively. The black circle, square, diamond, and stars represent Mie theory calculations for FeO, Fe₂O₃, FeO(OH), and Mg_xFe_1−xSiO₃ particles using refractive indices from literature (see text).

4.2 The impact of solar radiation on ice particle formation

In this section we discuss the impact of solar radiation on the critical temperature of the environment T_cr,env needed to activate ice growth. To this end we combine our previously presented ice growth activation model (Duft et al., 2019) with the equilibrium temperature model of this work. A description of the method can be found in Appendices A and B. In order to estimate the maximum impact of solar radiation, we assume that the particles are composed of FeO, the potential MSP material with the highest iron content and which is therefore expected to heat up the most. To calculate the water coverage on FeO particles we use an energy of desorption $E_{\mathrm{des}}^{\mathrm{0}}=\mathrm{42.7}$ kJ mol⁻¹, which was previously determined for Fe₂O₃ particles (Duft et al., 2019). For the incoming solar irradiation we use the maximum solar zenith angle of 45.6^∘ (21 June, noon) at 69^∘ N, a typical latitude of MSP observations. In Fig. 5a we compare calculated critical temperatures as a function of the MSP radius with and without particle heating by solar irradiation for an altitude of 87 km (0.27 Pa). Here, we assume a constant H₂O mixing ratio of 3 ppm which is typical for the polar summer mesopause (Hervig et al., 2009).

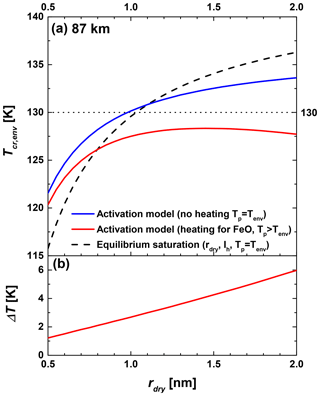
Figure 5 Critical temperature (a) and particle temperature offset (b) at 87 km in altitude for FeO particles as a function of dry particle radius. The blue curve represents critical temperatures calculated with the activation model neglecting solar irradiation, and the red curves consider solar irradiation. For comparison, we show the equilibrium saturation calculated using the Kelvin equation for hexagonal ice with the dry particle radius represented by the dashed black curve.

The solid blue curve in Fig. 5a shows results obtained when neglecting solar heating of the particles (T_p=T_env), i.e., representing non-absorbing particles. For comparison, the dashed black curve shows calculated critical temperatures using the Kelvin effect of hexagonal ice at the dry particle radius, which represent the highest activation temperatures currently assumed in mesospheric models (e.g., Berger and Lübken, 2015; Schmidt et al., 2018). For r_dry<1.1 nm, the size range of most MSPs in the polar summer mesopause (Bardeen et al., 2010; Megner et al., 2008a, b; Plane et al., 2014), the new activation model excluding solar irradiation predicts ice particle formation at higher temperatures than currently assumed in models. This is explained by the uptake of water molecules by the MSPs, which increases the particle size and therefore causes a reduction of the Kelvin effect. This effect outweighs the vapor pressure difference between ASW and hexagonal ice for particle radii smaller than 1.1 nm. The horizontal dotted line at T=130 K indicates the measured mean temperatures at 87 km and 69^∘ N during June and July (Lübken, 1999). This line intersects with the calculations for non-absorbing particles at a dry particle radius of about 1 nm, which means that at the mean temperature of 130 K particles larger than r_dry=1 nm will activate ice growth. The solid red curve in Fig. 5a shows results obtained when including solar heating of the particles (T_p > T_env), yielding lower T_cr,env values. With solar heating no particles will activate at the mean particle temperature of 130 K. However, typical temperature variations in the summer mesopause are on the order of 10 K (Rapp et al., 2002), which leads us to conclude that the atmospheric temperature of the summer mesopause frequently falls below the critical temperature of non-absorbing as well as of absorbing MSPs for particle radii above 0.5 nm.

Figure 5b shows the offset of the particle temperature from the ambient temperature ΔT at critical conditions for particles with the highest absorption efficiency (FeO). These values are almost identical to the difference in critical temperatures between the activation model without and with solar heating. We find that below r_dry=1.5 nm even the most absorbing particles warm by less than 4 K at 87 km in altitude. The particle heating will be much less for other MSP materials and at lower altitudes due to the higher collisional cooling rate at higher pressures. In general, the particle temperature offset reported here is about 5 times less than previous estimates (Asmus et al., 2014) for two main reasons: (1) the uptake of water molecules increases the particle surface area and therefore the collisional cooling rate, and (2) the thermal accommodation coefficient of α=0.5 used in previous calculations (see also Espy and Jutt, 2002, and Grams and Fiocco, 1977) is very likely an underestimation. We use a value of 1 based on recent results of laboratory experiments, which increases the collisional cooling rate by a factor of 2 (see Appendix B for more details).

5 Summary and conclusions

We have presented H₂O adsorption measurements on MSP analogues (Fe₂O₃ and Fe_xSi_1−xO₃ nanoparticles) exposed to variable intensities of visible light at 405, 488, and 660 nm. The experiments were performed at particle temperatures and H₂O concentrations representative for the polar summer mesopause, and the visible light covers the maximum in the solar irradiance. The reduction in the number of adsorbed water molecules under irradiation allows direct determination of the particle temperature increase caused by light absorption. We used the measured temperature increase in an equilibrium temperature model to determine the absorption efficiency of the particles. The results show that the equilibrium temperature model is applicable and it can be used with literature values of bulk refractive indices to calculate the temperature increase in MSPs in the polar summer mesopause. Additionally, we confirmed that the absorption efficiency increases with increasing iron content of potential MSP materials (Asmus et al., 2014).

We find that the impact of solar radiation on polar mesospheric ice particle formation is lower than previously assumed. Critical temperatures for ice growth activation at 69^∘ N decrease at most by 4 K for typical MSP particle sizes. However, for assessing the significance of solar heating of MSPs on PMC properties, the whole life cycle of mesospheric ice particles has to be considered. Therefore, we propose that the updated ice activation model (Appendix A and B) is used in future model studies with and without solar irradiation for various potential MSP materials in order to evaluate if absorption of solar irradiation alters properties of polar mesospheric clouds.

Appendix A: Critical temperatures under the influence of solar radiation

At the conditions of the polar summer mesopause, ice particle formation proceeds via deposition of compact amorphous solid water (ASW) on MSPs (Duft et al., 2019; Nachbar et al., 2018c). Ice growth is activated if the saturation S(T_p) is larger than the critical saturation S_cr(T_p). In the following, we present a method for calculating the temperature at which this condition is fulfilled, the so-called critical temperature.

For a given water vapor mixing ratio MR and atmospheric pressure p_atm, the saturation is determined by

$$\begin{array}{}\text{(A1)}& {\displaystyle }S\left(T_{\mathrm{p}}\right)={\displaystyle \frac{MR\cdot p_{\mathrm{atm}}}{p_{\mathrm{s},\mathrm{a}}\left(T_{\mathrm{p}}\right)}}\cdot \sqrt{{\displaystyle \frac{T_{\mathrm{env}}}{T_{\mathrm{p}}}}},\end{array}$$

with the saturation vapor pressure of ASW described by (Nachbar et al., 2018c)

$$\begin{array}{}\text{(A2)}& {\displaystyle }{p}_{\mathrm{s},\mathrm{a}}=p_{\mathrm{s},\mathrm{h}}\cdot \exp \left({\displaystyle \frac{\mathrm{2312}\left[\mathrm{J}{\mathrm{mol}}^{-\mathrm{1}}\right]-\mathrm{1.6}\left[\mathrm{J}{\mathrm{mol}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}\right]\cdot T}{RT}}\right).\end{array}$$

p_s,h represents the saturation vapor pressure of hexagonal ice (Murphy and Koop, 2005). The critical saturation S_cr needed to activate ice growth depends on the Kelvin effect calculated at the particle radius r_wet (including the number of adsorbed H₂O molecules) and considering the collision radius of a water molecule ($r_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.15}$ nm, Bickes et al., 1975) (Duft et al., 2019):

$$\begin{array}{}\text{(A3)}& {\displaystyle }{S}_{\mathrm{cr}}\left(T_{\mathrm{p}}\right)={\left({\displaystyle \frac{r_{\mathrm{wet}}}{r_{\mathrm{wet}}+r_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}\right)}^{\mathrm{2}}\cdot \exp \left({\displaystyle \frac{\mathrm{2}v\mathit{\sigma }}{R{T}_{\mathrm{p}}{r}_{\mathrm{wet}}}}\right).\end{array}$$

To determine the critical temperature at which ice growth is activated, the environmental temperature T_env is decreased until S(T_p) ≥S_cr(T_p). A reasonable starting point for T_env is the temperature at which the saturation over a flat surface is 1 (solve for $p_{\mathrm{s},\mathrm{a}}\left(T_{\mathrm{env}}\right)=MR\cdot p_{\mathrm{atm}}$). The coupled calculation of T_p and r_wet is described in Appendix B and has to be repeated every time T_env is decreased. The environmental temperature fulfilling S(T_p)=S_cr(T_p) is the critical temperature needed to activate ice growth and $\mathrm{\Delta }T=T_{\mathrm{p}}-T_{\mathrm{env}}$ is the increase in the particle temperature at conditions of ice particle formation.

Appendix B: Equilibrium particle temperature and wet particle radius

Substituting Eqs. (6) and (7) in Eq. (5) and solving for the increase in the particle temperature ΔT considering the dependency of the solar spectrum and of Q_abs on λ yields

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\Delta }T=T_{\mathrm{p}}-T_{\mathrm{env}}=(A_{\mathrm{geo}}\cdot {\int }_{\mathrm{0}}^{\mathrm{\infty }}I\left(\mathit{\lambda }\right)\cdot Q_{\mathrm{abs}}\left(\mathit{\lambda },r_{\mathrm{dry}}\right)\mathrm{d}\mathit{\lambda }\\ \text{(B1)}& {\displaystyle }& {\displaystyle }+P_{\mathrm{env}}^{\mathrm{a}}-P_{\mathrm{rad}}^{\mathrm{e}})/\left(A_{\mathrm{col}}\mathit{\alpha }\mathrm{p}{v}_{\mathrm{th}}{\displaystyle \frac{(\mathit{\gamma }+\mathrm{1})}{\mathrm{8}T(\mathit{\gamma }-\mathrm{1})}}\right).\end{array}$$

Here, I(λ) (blackbody radiation assuming T=5780 K), $P_{\mathrm{env}}^{\mathrm{a}}$, and $P_{\mathrm{rad}}^{\mathrm{e}}$ were calculated as presented in Asmus et al. (2014). The thermal accommodation coefficient α, which is typically used in literature to describe the heating of MSPs or NLC particles, is 0.5 (e.g., Asmus et al., 2014; Espy and Jutt, 2002). This value seems to originate from the work of Grams and Fiocco (1977) and was chosen due to a lack of relevant measurements determining α at realistic mesopause conditions. More recently, measurements of α for N₂ on water droplets and for air on fused silica which show that α is close to unity have become available (Fung and Tang, 1988; Ganta et al., 2011). We therefore used α=1. The collision surface area of a particle $A_{\mathrm{col}}=\mathrm{4}\mathit{\pi }{\left(r_{\mathrm{wet}}+r_{{\mathrm{N}}_{\mathrm{2}}}\right)}^{\mathrm{2}}$ is described by the collision radius of a nitrogen molecule $r_{{\mathrm{N}}_{\mathrm{2}}}=\mathrm{0.19}$ nm (Hirschfelder et al., 1966) and the wet particle radius r_wet (Eq. 3). The wet particle radius can be calculated with the mass of adsorbed water in equilibrium m_ads, which can be obtained by rearranging Eq. (1):

$$\begin{array}{}\text{(B2)}& {\displaystyle }{m}_{\mathrm{ads}}=A_{\mathrm{p}}\cdot m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\cdot {\displaystyle \frac{n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\cdot v_{\mathrm{th}}}{\mathrm{4}f}}\cdot \exp \left({\displaystyle \frac{E_{\mathrm{des}}^{\mathrm{0}}}{R{T}_{\mathrm{p}}}}-{\displaystyle \frac{\mathrm{2}\mathit{\sigma }v}{R{T}_{\mathrm{p}}{r}_{\mathrm{dry}}}}\right).\end{array}$$

Note that m_ads and $P_{\mathrm{rad}}^{\mathrm{e}}$ depend on the particle temperature. Consequently, ΔT (Eq. B1) has to be solved numerically. In our approach we alternatingly calculate T_p and m_ads until the relative change in ΔT is less than 0.01 %.