Technical note: The role of evolving surface tension in the formation of cloud droplets

The role of surface tension (σ) in cloud droplet activation has long been ambiguous. Recent studies have reported observations attributed to the effects of an evolving surface tension in the activation process. However, the adoption of a surface-mediated activation mechanism has been slow and many studies continue to neglect the composition dependence of aerosol–droplet surface tension, using instead a value equal to the surface tension of pure water (σ_w). In this technical note, we clearly describe the fundamental role of surface tension in the activation of multicomponent aerosol particles into cloud droplets. It is demonstrated that the effects of surface tension in the activation process depend primarily on the evolution of surface tension with droplet size, typically varying in the range 0.5σ_w≲σ≤σ_w due to the partitioning of organic species with a high surface affinity. We go on to report some recent laboratory observations that exhibit behavior that may be associated with surface tension effects and propose a measurement coordinate that will allow surface tension effects to be better identified using standard atmospheric measurement techniques. Unfortunately, interpreting observations using theory based on surface film and liquid–liquid phase separation models remains a challenge. Our findings highlight the need for experimental measurements that better reveal the role of composition-dependent surface tensions, critical for advancing predictive theories and parameterizations of cloud droplet activation.

1 Introduction

The formation of a cloud involves a complex series of steps as nanometer-sized aerosol particles, termed cloud condensation nuclei (CCN), grow by condensation of water vapor to become supermicron-sized cloud droplets in a process known as CCN activation. Activation depends on the physicochemical properties of the aerosol, such as hygroscopicity and surface tension, as well as atmospheric conditions, such as temperature and humidity. To accurately predict cloud formation and properties, these factors must be included in modeling schemes. However, due to computational limitations, approximations and simplifications are needed, which often obscures the underlying physics and may limit the accuracy of predictions. A key challenge is in the development of a simple model that captures the basic processes involved in CCN activation, while allowing complicating factors such as surface tension variability, solubility, and phase separation to be included in a physically representative manner. In this note, we focus on the role of surface tension and discuss the limitations of current approximations in light of recently published works that reveal how it is primarily the evolution of surface tension that impacts the activation process.

In recent publications, the role of surface tension in the activation of aerosol particles to cloud droplets has been reexamined (Forestieri et al., 2018; Ovadnevaite et al., 2017; Ruehl et al., 2016). These studies show that the evolution of surface tension can have a large effect during the activation process compared to when surface tension is assumed to be a static parameter. It is well established that surface tension is a factor in activation and that dissolved species can suppress surface tension (Li et al., 1998). Traditionally, however, surface tension has been reduced to a fixed term in the Köhler equation (Abdul-Razzak and Ghan, 2000; Facchini et al., 2000; Petters and Kreidenweis, 2007) and is usually given a temperature-independent value equal to that of pure water at 25 ^∘C. This is because for any decrease in surface tension due to bulk–surface partitioning and surface adsorption, it is assumed that there is an increase in the solution water activity because adsorbed material, previously acting as a hygroscopic solute, is removed from the droplet (bulk) solution (Fuentes et al., 2011; Prisle et al., 2008; Sorjamaa et al., 2004). Thus, the effects approximately cancel out in the calculation of a droplet's equilibrium saturation ratio via the Köhler equation and so are often neglected. Furthermore, it has been shown in some cases that there is insufficient material in a droplet at the sizes approaching activation to sustain a surface tension depression (Asa-Awuku et al., 2009; Prisle et al., 2010). The lack of experimental evidence to the contrary has led to the adoption of these assumptions in popular single-parameter models, such as κ-Köhler theory, that reduce the complexity of the activation process (Petters and Kreidenweis, 2007). These parameterizations provide a compact and useful means of relating key observables, such as the critical supersaturation and activation diameter, to hygroscopicity and allow for a general comparison between systems with arbitrary compositions. The κ-Köhler framework has also been adapted to account for surface tension effects (Petters and Kreidenweis, 2013). However, a single-parameter implementation cannot account for the full effects of an evolving surface tension and, by omitting the microphysical processes associated with bulk–surface partitioning, the presence and magnitudes of any surface effects are often difficult to ascertain.

In the works of Ruehl and coworkers (Ruehl et al., 2016; Ruehl and Wilson, 2014), Forestieri and coworkers (Forestieri et al., 2018), and Ovadnevaite and coworkers (Ovadnevaite et al., 2017), laboratory and observation-based measurements, respectively, combined with a partitioning model have revealed key signatures of surface tension lowering in the activation process due to non-surfactant organic compounds. Notably, a modification of the Köhler curve can result in lower critical supersaturations and vastly different droplet sizes at activation compared to the expectation when assuming a constant surface tension. Dynamic factors may also play a role, as discussed by Nozière and coworkers (Nozière et al., 2014), who have shown that surface tension can vary over time due to slow changes in the bulk–surface partitioning of material, leading to a time dependence in the role of surface tension. This may be especially important for droplets that initially contain micelles or oligomers that exhibit slow breakdown kinetics and diffusion. Furthermore, surface partitioning may be influenced by non-surface active components in the system, such as the presence of inorganic material and co-solutes (Asa-Awuku et al., 2008; Boyer et al., 2016; Boyer and Dutcher, 2017; Frosch et al., 2011; Petters and Petters, 2016; Prisle et al., 2011; Svenningsson et al., 2006; Wang et al., 2014). Other factors that have been shown to influence the shape of Köhler curves are (1) solute dissolution, encompassing both water solubility and solubility kinetics (Asa-Awuku and Nenes, 2007; Bilde and Svenningsson, 2017; McFiggans et al., 2006; Petters and Kreidenweis, 2008; Shulman et al., 1996), (2) liquid–liquid phase separation (i.e., limited liquid–liquid solubility) (Rastak et al., 2017; Renbaum-Wolff et al., 2016), and (3) the dynamic condensation (or gas–particle partitioning) of organic vapors (Topping et al., 2013; Topping and McFiggans, 2012). While measured cloud droplet number concentrations in the atmosphere have been explained in several cases with simple parameterizations that neglect dynamic surface effects (Nguyen et al., 2017; Petters et al., 2016), there are many observations that are not fully explained in such simple terms and in those cases a substantial population of CCN may exhibit behavior characteristic of surface effects (Collins et al., 2016; Good et al., 2010; Ovadnevaite et al., 2011; Yakobi-Hancock et al., 2014). In order to gain a robust and predictive understanding of CCN activation, a molecular-level theory must be developed and adopted by the atmospheric chemistry community.

In this technical note, we offer a perspective on the role of surface tension in the activation process, drawing on recent studies and interpretations of cloud droplet activation measurements (e.g., Forestieri et al., 2018; Ovadnevaite et al., 2017; Ruehl et al., 2016; Ruehl and Wilson, 2014). We go on to discuss how surface tension may be considered in the activation process and finally present some new data highlighting potential indicators of surface tension effects in measurements of critical supersaturation. Our aim is to provide a platform for discussion and help foster a molecular-based interpretation of the role of organic material in the activation of aerosol to cloud droplets.

2 Clarifying how surface tension alters cloud droplet activation

On a fundamental level, the influence of surface tension on droplet activation is straightforward and was discussed in the late 1990s for aerosol particles containing surfactants (Li et al., 1998). Unfortunately, the simplicity of the role of surface tension in CCN activation has been lost in the complex descriptions of surface and phase partitioning models, limiting the broader application of the insights gained from recent experimental results. For context, we begin our discussion with Köhler theory (Köhler, 1936), which describes the thermodynamic conditions required for CCN activation based on two contributions that control the equilibrium (saturation) vapor pressure of water above a liquid surface. The classic Köhler equation is often written as (Petters and Kreidenweis, 2007)

$$\begin{array}{}\text{(1)}& S_{\mathrm{d}}={\displaystyle \frac{p_{\mathrm{w},\mathrm{d}}\left(D\right)}{p_{\mathrm{w}}^{\mathrm{0}}}}=a_{\mathrm{w}}\exp \left[{\displaystyle \frac{\mathrm{4}{M}_{\mathrm{w}}\mathit{\sigma }}{RT{\mathit{\rho }}_{\mathrm{w}}D}}\right]\end{array}$$

where S_d is the equilibrium saturation ratio of water in the vapor phase surrounding a droplet surface, p_w,d(D) is the equilibrium partial pressure of water vapor above a droplet (subscript d) of diameter D and a certain chemical composition, $p_{\mathrm{w}}^{\mathrm{0}}$ is the pressure of water above a flat, macroscopic surface of pure liquid water at temperature T, a_w is the mole-fraction-based water activity of the droplet solution, M_w is the molecular mass of water, σ is the surface tension of the particle (at the air–liquid interface), R is the ideal gas constant, and ρ_w is the density of liquid water at T. The water activity contribution, known as the solute or Raoult effect, describes a lowering of the equilibrium water vapor pressure above a liquid surface due to the presence of dissolved (hygroscopic) species that reduce the water activity to a value below 1. The second contribution, known as the Kelvin effect, describes an increase in the equilibrium water vapor pressure above a microscopic curved surface and is dependent upon the surface-area-to-volume ratio of the droplet (a size effect) and the surface tension, i.e., the gas–liquid interfacial energy per unit area of surface. The latter term arises from the energy associated with creating and maintaining a certain surface area and is thus reduced when the surface tension is lowered or when the droplet size increases, leading to a smaller surface-to-volume ratio. The magnitude of the Kelvin effect scales with the inverse of the droplet radius and is sometimes referred to as the “curvature effect”. The combined contributions from the Raoult and Kelvin effects in Köhler theory define a thermodynamic barrier to droplet growth. It is important to note that the Köhler equation describes the specific saturation ratio S_d in thermodynamic equilibrium with a certain solution droplet of interest; however, the value of S_d may differ from that of the environmental saturation ratio, S_env, present in the air parcel containing the droplet, since S_env is established by an interplay of moist thermodynamic processes. The environmental saturation ratio is defined by $S_{\mathrm{env}}=\frac{p_{\mathrm{w}}}{p_{\mathrm{w}}^{\mathrm{0}}}$, where p_w is the partial pressure of water in air at a specific location and time, irrespective of the presence or absence of aerosols and cloud droplets. The global maximum in a Köhler curve marks the point of activation for a certain CCN, as shown in Fig. 1a. For conditions of S_d≤S_env, e.g., in a rising, adiabatically expanding air parcel, aqueous CCN equilibrate relatively quickly to their environmental conditions such that S_d=S_env is maintained (stable growth and evaporation). However, when S_env exceeds the global maximum in S_d for a certain CCN, such an equilibration becomes unattainable and net condensation of water prevails, leading to so-called unstable condensational growth for as long as S_env>S_d holds (while S_d varies according to the pertaining Köhler curve).

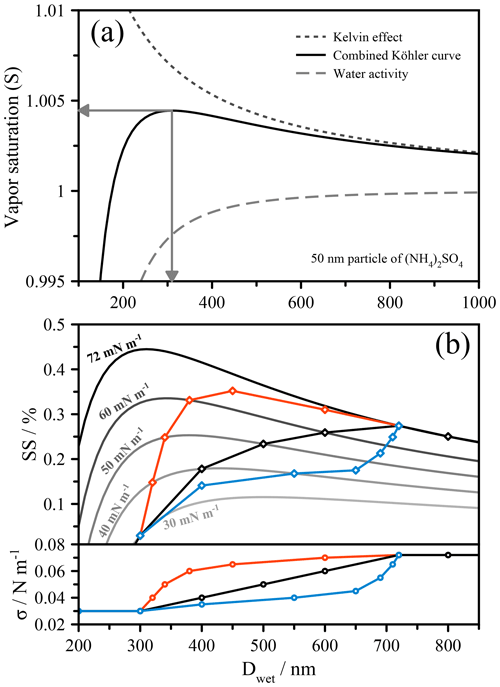
Figure 1 (a) Köhler curve construction from the combination of the water activity term and the Kelvin effect, shown here for 50 nm particles of ammonium sulfate. The arrows indicate the critical supersaturation (SS_crit) and the critical wet activation diameter (D_crit). (b) Köhler curves (NB. $\mathrm{SS}=(S-\mathrm{1})\times \mathrm{100}$ %) of varying fixed surface tension values for 50 nm (dry diameter) particles with water activity treated as an ammonium sulfate solution. A schematic linear dependence of surface tension on droplet diameter is shown in black, and the Köhler curve construction that takes into account the change in surface tension is shown in bold and with diamond symbols. Additional surface tension dependencies are shown in red, which exhibits activation at σ<σ_w, and in blue, which shows a dramatic increase in the critical wet diameter.

A Köhler curve shows the relationship between the droplet's equilibrium water vapor saturation ratio and the wet droplet size. The wet droplet size, or more specifically the chemical composition (solute concentration), solubility, and nonideal mixing determines the water activity, while the size and surface tension determine the Kelvin effect. Since the solute concentration changes with the droplet size, e.g., during net growth conditions when the environmental saturation ratio in an air parcel increases and water vapor condenses, the water activity term varies accordingly, typically in a nonlinear manner. The Kelvin term should also change with droplet size due to both the changing surface-to-volume ratio of the droplet and changes in surface tension as a result of changes in solute concentration and related surface composition. In most scenarios, only the diameter change is accounted for, while the surface tension is assumed to remain constant, usually with the value for pure water ($\mathit{\sigma }={\mathit{\sigma }}_{\mathrm{w}}\approx \mathrm{72}$ mN m⁻¹ at 298 K). This oversimplifies the problem, especially when organic solutes are present that adsorb at the surface of the growing droplet. In experimental studies in which only the critical supersaturation or critical dry diameter are measured, this assumption can lead to errors, as the complexity of the system may not allow for such simplified treatments to yield sufficiently accurate representations of a real-world problem. In such cases, one must consider how the changing size of the droplet (or, again, more specifically the solution composition) results in changes in bulk–surface partitioning and ultimately surface tension.

Recent work has shown that a rigorous account of bulk–surface partitioning leads to complex Köhler curves whose shapes are often difficult to interpret (Ruehl et al., 2016). These shapes can be more easily understood by considering a very simple example, shown in Fig. 1b. Here, a series of fixed surface tension (iso-σ) Köhler curves with values ranging from 72 to 30 mN m⁻¹ are shown, using the same 50 nm particle (of ammonium sulfate) from Fig. 1a. Distinct schematic dependences of the surface tension on the droplet size, representative of the types of dependence that might be encountered in real aerosol, are imposed for the purpose of illustration, shown in the lower panel of Fig. 1b. At each point along these dependences, the saturation ratio will be determined by the position on the Köhler curve corresponding to that specific surface tension. This means that instead of following a single trajectory along an iso-σ curve, the system is better envisioned as traversing across these curves, producing a very different final shape to the Köhler curve than would normally be expected. In the case of a linear dependence of σ on D (black curve), the Köhler curve cuts across the iso-σ lines until σ reaches the value of pure water. In this case, this coincides with reaching the maximum in the droplet's saturation ratio and thus reflects the activation point. In the case shown in red, activation occurs prior to the surface tension returning to the value of pure water. In the case shown in green, activation follows a pseudo two-step process, whereby initially a large increase in size occurs for a small increase in supersaturation, and thus the droplet may appear to be activated, while in this case true activation occurs at the point corresponding to the intersection with the Köhler curve of σ=σ_w. It is important to note that it is not necessarily the magnitude of the suppression of surface tension that drives unusual activation behavior, but the dependence of the surface tension on concentration, which is dictated by the droplet size and the thermodynamics of the system.

It is apparent from these examples that an evolving surface tension may introduce abrupt changes in the activation curve that arise due to the phase behavior of monolayer systems. The most obvious change is where the surface tension returns to the value of pure water. Following this point, the system will follow the iso-σ curve corresponding to pure-water surface tension (under continued and sufficient supersaturation conditions). Depending on the exact relationship of surface tension and droplet size, this point can mark the activation barrier of the system, as is the case in Fig. 1b for the black and green curves. This also seemingly supports previous assertions, as discussed in Sect. 1, that surface tension does not impact activation, since it is generally argued that at the point of activation the droplet is sufficiently dilute and essentially exhibits a surface tension like pure water (Fuentes et al., 2011; Prisle et al., 2008; Sorjamaa et al., 2004). While that is the case in this example, the trajectory of the activation process is significantly altered by the surface tension history of the droplet. In other words, for the systems described by the black or green curves in Fig. 1b, the surface tension at the point of CCN activation is that of pure water, yet if one assumed the surface tension of the droplet to be constantly that of pure water at any size prior to activation, the critical supersaturation, SS_crit, would be significantly higher and the critical (wet) activation diameter, D_crit, substantially smaller (see the Köhler curve for σ=σ_w). Clearly, an evolving surface tension prior to activation can matter in such systems and, consequently, knowing the surface tension only at the point of activation is in a general case insufficient for determining the critical properties at activation (absent any droplet size measurement) because the position of the maximum in the Köhler curve, and thus the droplet size at activation, will depend on the trajectory of surface tension evolution. Moreover, knowing the surface tension at the activation point only may not allow for an accurate prediction of whether a droplet of given dry diameter will activate at a given environmental supersaturation (compare the green curve with the iso-σ curve of 72 mN m⁻¹ in Fig. 1b, both having the same surface tension at their points of CCN activation, yet different critical supersaturations and wet diameters). Similar conclusions have been drawn previously (e.g., Prisle et al., 2008), although the results of Ruehl et al. (2016) were the first to verify this experimentally.

3 Surface tension evolution during activation

A major consequence of an evolving surface tension is that the droplet size at activation is larger, and the actual critical supersaturation depends on how surface tension varies in the droplet as it grows. These effects were directly measured using a thermal gradient chamber (TGC) (Roberts and Nenes, 2010; Ruehl et al., 2016). In the 2016 work, mixed ammonium sulfate and organic aerosols were introduced into the TGC at various supersaturations (up to and including the activation supersaturation). The size of the aerosol particles was measured under these conditions, allowing for a direct measurement of the stable equilibrium branch of the Köhler curve (i.e., the size up to the point of activation). It was shown that for highly soluble and surface inactive solutes such as ammonium sulfate and sucrose, the data exhibit the behavior expected when assuming an iso-σ Köhler curve. However, for the case when organic acids, spanning a range of water solubilities, were coated on ammonium sulfate particles of specific dry sizes, the measurements clearly show modifications to the Köhler curve in comparison to an iso-σ Köhler curve, which were explained by changes in surface tension corresponding to bulk–surface partitioning as predicted by a compressed film model. Without these observations, assuming σ=σ_w, one could attribute the critical supersaturation to a single, apparent κ value that describes the hygroscopic effect of the mixture of solutes in the absence of any surface tension constraints (Petters and Kreidenweis, 2007). Low-solubility and low-hygroscopicity species should exhibit very small κ values. However, in the case of suberic acid, for example, the CCN activation data of Ruehl et al. would require a κ value of approximately 0.5 for the organic component, assuming a fixed surface tension equal to that of water. This κ value is unphysically large considering that the molar volume ratio suggests a value of ∼0.13 for suberic acid when assuming full solubility, the surface tension of pure water, and ideal mixing with water. A different prediction, accounting for limited solubility and assuming a constant surface tension using the value of the saturated aqueous solution, estimates its value as κ≈0.003 (Kuwata et al., 2013). Moreover, the apparent κ value derived from CCN activation data of pure suberic acid particles indicates a value of ∼0.001 (Kuwata et al., 2013). Invoking a surface tension model here is the only way to make physical sense of these observations, allowing even low-solubility and nonhygroscopic solutes to contribute significantly to the activation efficiency in mixed droplets. The modeling approaches of Ruehl and coworkers (Ruehl et al., 2016) and Ovadnevaite and coworkers (Ovadnevaite et al., 2017) use Köhler theory with either a bulk–surface partitioning model (compressed film model) or an equilibrium gas–particle partitioning and liquid–liquid phase separation (LLPS) model with variable surface tension. Both studies also employed simplified organic film models, in which the assumption is made that all organic material resides in a water-free surface film, as options for comparison with the more sophisticated approaches.

A bulk–surface partitioning model is comprised of two components: a two-dimensional equation of state that relates the surface tension to the surface concentration and a corresponding isotherm that relates the surface and bulk solution concentrations. In the work of Ruehl et al., the compressed film (Jura and Harkins, 1946) and Szyszkowski–Langmuir equations of state were compared. The latter has been used in several studies exploring bulk–surface partitioning in organic aerosol (Prisle et al., 2010; Sorjamaa et al., 2004; Topping et al., 2007). The compressed film model reproduced the experimental observations, capturing the complex shapes of the measured Köhler curves. The Szyszkowski–Langmuir method was unable to explain several of the observations, attributed partly to the lack of a two-dimensional phase transition between a film state and a non-film state, which is a unique feature of the compressed film model. Earlier work by Ruehl and coworkers successfully used a van der Waals equation of state to model the behavior of organic and inorganic mixed droplets at high relative humidity (Ruehl and Wilson, 2014), demonstrating the effect of surface tension following the onset of film formation once sufficient organic material was present. While we know the factors that contribute to the equation of state and isotherm for well-controlled systems, the enormous complexity of atmospheric aerosol presents a significant challenge in developing and utilizing a predictive general model or theoretical framework.

The equilibrium gas–particle partitioning and liquid–liquid phase separation model is based on the Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients (AIOMFAC) model (Zuend et al., 2008, 2011), coupled to a relatively simple phase-composition- and morphology-specific surface tension model. A detailed description of this AIOMFAC-based model, its variants, and sensitivities to model parameters and assumptions is given in the Supplement of Ovadnevaite et al. (2017). Briefly, the equilibrium gas–particle and liquid–liquid partitioning model is used to predict the phases and their compositions for a bulk mixture “particle”, here of known dry composition, at given RH and temperature. For other applications with given total gas + particle input concentrations, the equilibrium condensed-phase concentrations can be computed as a function of RH (accounting for the partitioning of semivolatiles). Assuming spherical particles of a certain dry diameter with a core–shell morphology of liquid phases in the case of LLPS, density information from all constituents is used to compute volume contributions and the size of the particle at elevated RH. In addition, the surface tension of each individual liquid phase is computed as a volume-fraction-weighted mean of the pure-component surface tension values. In the case of LLPS, the surface coverage of the (organic-rich) shell phase is evaluated by considering that it must be greater than or equal to a minimum film thickness (monolayer as a lower limit); this determines whether complete or partial surface coverage applies for a certain wet diameter. The effective surface tension of the whole particle is then computed as the surface-area-weighted mean of the surface tensions of contributing phases. This way the surface tension evolves in a physically reasonable manner as a droplet grows, including the possibility for abrupt transitions from a low surface tension, established due to full organic droplet coverage under LLPS, to partial organic film coverage after monolayer film breakup, and further to the complete dissolution of organics in the aqueous inorganic-rich phase (single aqueous phase). This equilibrium model is referred to here as AIOMFAC-EQUIL. We also employed two AIOMFAC-CLLPS model variants, in which the organic constituents are assumed to reside constantly in a separate phase from ammonium sulfate (complete LLPS, an organic film) either with or without water present in that phase, as discussed in Sect. 4. This approach, introduced by Ovadnevaite and coworkers (Ovadnevaite et al., 2017), shows promise due to its ability to predict the existence of a surface tension activation effect consistent with CCN observations taken in marine air containing a nascent ultrafine aerosol size mode. In that study, enhanced CCN activity of ultrafine particles was observed for aerosols consisting of organic material mixed with inorganic salts and acids in North Atlantic marine air masses, which could not be explained when accounting for hygroscopicity or solubility alone (when assuming the surface tension of water). While the LLPS-based model and the compressed film model of Ruehl et al. (2016) employ different principles and descriptions to account for the surface composition, both agree that gradual surface tension changes dominate the CCN activation process for these systems. Interestingly, while the observations of Ruehl et al.. (2016) showed activation occurring when the surface tension returns to its maximum value (i.e., that of pure water), the phase separation model predicted activation prior to the surface tension returning to its maximum (for ultrafine particles). As discussed by Ovadnevaite et al. (2017), this difference in the surface tension value reached at the point of CCN activation depends in some cases on the size range of the (dry) particles considered (for the same dry composition). Ovadnevaite et al.. (2017) show that for particles of larger dry diameters (e.g., 175 nm for the case of their aerosol model system), CCN activation is predicted to occur at a point at which the particle's surface tension has reached the value of pure water (see the Supplement to that study). Hence, both observations are consistent with the picture developed in Fig. 1b and the details depend on the particle size range and functional form describing the change in surface tension of the system considered. Moreover, it is important to recognize that – regardless of whether the surface tension is equivalent to or lower than that of pure water at the CCN activation point – a CCN exhibiting an evolving, lowered surface tension while approaching the activation point during hygroscopic growth will activate at a lower supersaturation than a CCN of constant surface tension equivalent to the pure-water value, since the former activates at a larger diameter, as is evident from the examples of the red and green Köhler curves shown in Fig. 1b. This predicted size effect indicates that it is not generally valid to assume that all activating CCN will have a surface tension equivalent to or close to that of pure water, nor is it appropriate to use a single measurement of the surface tension of a multicomponent CCN of known dry composition at its activation size (only) to determine its Köhler curve, as also noted in previous studies (Prisle et al., 2010, 2008; Sorjamaa et al., 2004). Furthermore, these model predictions also suggest that measurements of the surface tension of larger CCN particles (e.g., >150 nm dry diameter) may not allow for conclusions about the surface tension of much smaller CCN, e.g., of 50 nm dry diameter.

4 Identifying surface tension effects from critical supersaturation

Although the LLPS-based and compressed film models of CCN activation have had some success in capturing surface tension effects, there remain substantial challenges in developing a generalized theory. One challenge is that CCN techniques do not measure surface tension directly but instead observe the effects of changes in surface tension, which may often be attributed to other factors. In order to identify surface tension effects using these techniques, experiments must be performed to maximize the scope of surface tension effects while minimizing changes in other variables that might influence observations. Here, we propose new experiments, using a model system as an example, which allows surface tension effects to be identified in the absence of other complicating factors.

Using a cloud condensation nucleus counter (CCNC; Droplet Measurement Technologies), we measured the supersaturation required to activate mixed suberic acid and ammonium sulfate particles. Suberic acid was chosen to represent the low-solubility oxygenated organic material typical of atmospheric secondary organic aerosol. It is not a traditional surfactant, but its role in suppressing surface tension and modifying the shape of the Köhler curve has been previously identified (Ruehl et al., 2016). Ammonium sulfate particles were generated using an atomizer and dried using silica gel and a Nafion drier with dry N₂ counter flow. The size distribution was measured and a size-selected seed was introduced into a flow tube containing suberic acid and housed within a furnace oven. The temperature was set to volatilize the organic material and allow it to condense onto the seed particles up to a desired thickness. The coated particles were size-selected again and introduced into a particle counter and a CCNC at a concentration of around 2000 cm⁻³. The activated fraction was measured as a function of saturation ratio, and the critical supersaturation was determined from the half-rise times of a sigmoid fit to the data. A range of dry particle sizes and organic volume fractions (f_org) were selected for measurements under humidified conditions at room temperature (∼20 ^∘C). Notably, the coated particle (i.e., total size) of the aerosol in its dry state was kept constant across a dataset spanning a range of organic volume fractions. The CCNC was calibrated with ammonium sulfate particles at room temperature at regular intervals, although typically the calibration remained stable during continued usage.

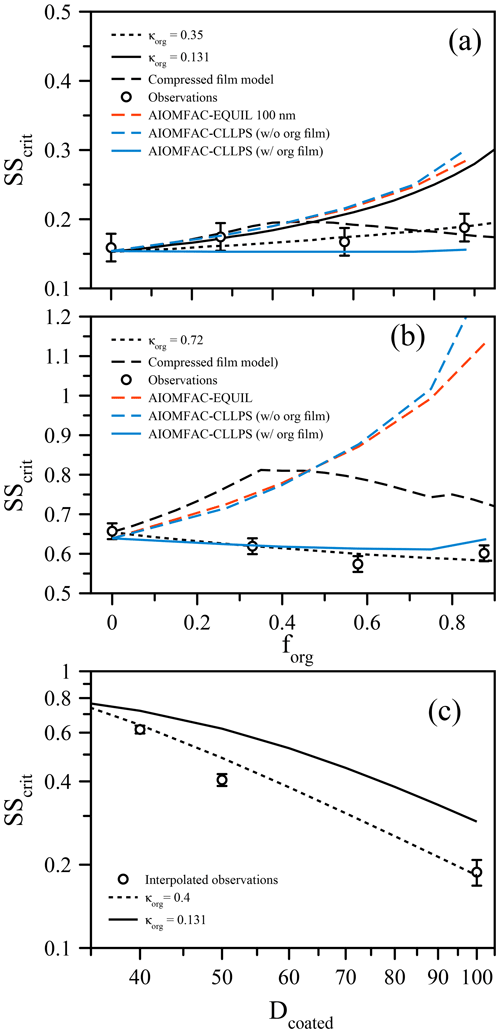
Figure 2 (a) Measured critical supersaturation (SS_crit) of size-selected ammonium sulfate particles coated with suberic acid (points) to a set dry diameter of 100 nm at T≈293 K. The curves show predictions from the compressed film model of Ruehl et al.. (2016), a simple κ-Köhler model with constant surface tension, and model variants from the AIOMFAC-based framework (see text). (b) Analogous to (a) but for particles of ammonium sulfate coated to 40 nm dry diameter by suberic acid. (c) Using the data from (a) and (b), SS_crit is shown as a function of coated diameter with a fixed inorganic seed of 33 nm (points). The lines indicate the κ-Köhler model with constant surface tension using different but constant values of κ_org.

The organic volume fraction (f_org) was varied while maintaining fixed dry particle sizes (Prisle et al., 2010; Wittbom et al., 2018), ensuring that any surface tension effect would not be masked by changes in the overall size, in contrast to other studies that allow both coated particle size and organic volume fraction to vary simultaneously (e.g., Hings et al., 2008; Nguyen et al., 2017). Figure 2a shows the critical supersaturation as a function of f_org for 100 nm (dry diameter) mixed ammonium sulfate and suberic acid particles. Remarkably, despite the much lower hygroscopicity of suberic acid relative to ammonium sulfate, there is very little increase in the required supersaturation as the organic volume fraction increases (while the ammonium sulfate volume fraction is reduced accordingly). In fact, considering a fixed surface tension of pure water, a κ_org value of 0.35 for the organic fraction is required to explain these data (using κ=0.62 for ammonium sulfate). This κ_org value is lower than that reported by Ruehl et al. (2016) (where κ_org=0.5), although those measurements were performed on 150 nm particles at f_org=0.963. If we apply the compressed film model (using the parameters established in Ruehl et al. (2016) for 150 nm particles at f_org=0.963) to predict the critical supersaturation as a function of f_org, we obtain a dependence that shows a peak SS_crit at f_org=0.4 (Fig. 2), followed by a decrease towards higher f_org. This shape is consistent with the lower value of SS_crit reported by Ruehl et al. (2016) at f_org=0.963. If we use the ideal molar-volume-derived κ_org value of 0.131 and a constant surface tension of σ=σ_w, the bulk solubility prediction significantly overestimates SS_crit for f_org>0.5. It must be noted here that without prior knowledge that suberic acid is inherently of very low hygroscopicity and exhibits low water solubility, the prediction using κ_org=0.35 could be mistaken as the correct answer. However, a κ_org value of this magnitude is unphysical when considering the original definition of κ. One could ignore the physical meaning of κ and simply use it as an all-encompassing parameter to describe activation efficiency. In this case, the generality of the parameter to interpret observations in different conditions is lost. The compressed film model decouples the water activity component from the surface tension component and thus should better represent the physical processes at work. However, the agreement for all these models breaks down further when looking at differently sized particles. For example, Fig. 2b shows the same system of ammonium sulfate and suberic acid, this time using 40 nm dry diameter particles. In this case, the required supersaturation decreases with increasing organic fraction, suggesting that suberic acid is more hygroscopic than ammonium sulfate (requiring κ_org=0.72). For the ultrafine aerosol size reported here, the compressed film model does a worse job at predicting the behavior, suggesting that it too suffers from a lack of generality in its applicability. What is clear, however, is that a specific suberic acid hygroscopicity alone cannot explain the observations across a range of particle sizes and compositions.

These observations are obscured when the data are reported with a fixed inorganic seed size with an increasing organic fraction achieved through an increase in the coated diameter. The data as a function of f_org with a fixed total diameter were used to plot SS_crit as a function of f_org with a fixed inorganic seed size, shown in Fig. 2c with an arbitrarily chosen inorganic seed size of 33 nm dry diameter. The value of SS_crit for coated diameters 40, 50, and 100 nm was found by linear interpolation of the data in Fig. 2a and b (and the 50 nm case in Fig. 3). The data are compared against a bulk κ-Köhler prediction, which exhibits a similar trend, although with a slightly smaller slope when κ_org=0.15. These data are brought to agreement using κ_org=0.4. However, we have already shown that for the 40 nm case, a value of κ_org greater than that of AS is required to explain the data as a function of f_org with a fixed dry diameter. Specifically, in Fig. 2c, the organic volume fractions are distinctly different for the three points shown: f_org=0.40, 0.70, and 0.96 for the 40, 50, and 100 nm coated diameter cases, respectively. Thus, the choice of experimental procedure or data presentation can impact the interpretation of experimental observations, and we suggest caution when presenting such data. When composition and particle size are coupled in D_coated, the sensitivity to surface tension effects is diminished, as smaller particles will contain a lower volume fraction of organic material.

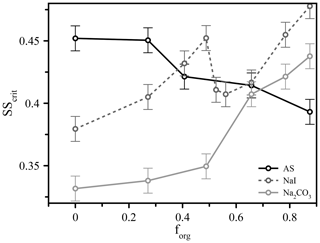
Figure 3 The measured critical supersaturation for 50 nm dry diameter particles comprised of different salts (ammonium sulfate, sodium iodide, and sodium carbonate) and variable volume fractions of suberic acid (f_org) at T≈293 K.

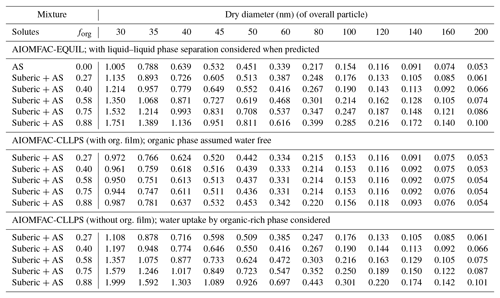
For both sets of measurements, we also applied three model predictions based on the AIOMFAC (Zuend et al., 2008, 2011) model with LLPS and a phase-specific surface tension mixing rule considered. The full equilibrium calculation, labeled as AIOMFAC-EQUIL in Fig. 2, considers the potential existence of a bulk liquid–liquid equilibrium, resulting in two liquid phases of distinct compositions yet each containing some amounts of all three components. The chemical compositions affect the surface tensions of the individual phases and, using a core–shell morphology assumption and minimum phase (film) thickness, that of the overall droplet. For the calculations performed, suberic acid is assumed to be in a liquid state at high water activity. This model predicts an LLPS for the aqueous suberic acid + ammonium sulfate system, but only up to a certain water activity level <0.99, beyond which a single liquid phase is the stable state. The upper limit of LLPS predicted increases with the fraction of suberic acid in the system: LLPS onset a_w≈0.942 for f_org=0.27 to a_w≈0.983 for f_org=0.88. This results in the absence of LLPS at supersaturated conditions prior to CCN activation for both dry particle diameters considered. Therefore, the AIOMFAC-EQUIL prediction does not lead to a significant surface tension reduction here, which explains why the predicted SS_crit in Fig. 2 is similar to that of an iso-σκ-Köhler model with κ_org≈0.13. The two AIOMFAC-CLLPS variants represent simplified model calculations in which the assumption is made that dissolved aqueous electrolytes and organics always reside in separate phases regardless of water content. In the variant labeled AIOMFAC-CLLPS (with org. film), all organic material is assumed to reside in a water-free organic shell phase (an organic film) at the surface of the aqueous droplet. This assumption leads to a maximum possible surface tension lowering up to relatively large droplet sizes (for intermediate to high f_org), yet a reduced solute effect, especially for high f_org. The variant labeled AIOMFAC-CLLPS (without org. film) in Fig. 2 differs by allowing water to partition to the organic-rich shell phase (in equilibrium with the target water activity), which may affect the surface tension of that phase. Due to a significant water uptake by suberic acid, predicted to occur for a_w>0.99, the resulting surface tension prior to and near activation is that of pure water and the SS_crit prediction resembles that of the AIOMFAC-EQUIL case. Physical parameters used in these simulations are presented in Table 1 and a schematic representation of these cases is shown in Fig. A1. A comparison of predicted Köhler curves from these model variants is shown in Fig. A2 for the case of f_org=0.58. The AIOMFAC-based predictions of critical dry diameters and SS_crit are listed in Table 2 for a range of dry diameters. A comparison of the different models with experimental data in Fig. 2 indicates that for f_org>0.3, the simplified organic film model variant AIOMFAC-CLLPS (with org. film) offers the best agreement with the measurements. This observation is consistent with the results of Prisle et al. (2011), who applied a similar simple model to droplets containing ionic surfactants and hint at a significant suppression of surface tension by suberic acid, which is likely highly enriched at the droplet surface.

Table 1 Values of physical parameters used in AIOMFAC calculations. Density of mixtures were calculated as a linear (additive) combination of the apparent molar volumes of the contributions of water, ammonium sulfate (AS), and suberic acid.

^a Value taken from measurements for adipic acid (Riipinen et al., 2007) on the basis of structural similarity to suberic acid. ^b Assumption of no influence on droplet surface tension compared to water here (since highly dilute).

Table 2 Critical supersaturation SS_crit (%) for given dry diameters (D_dry,crit) and organic volume fractions (f_org) in dry particles at T=293.15 K; predicted by the different AIOMFAC-based models.

Unfortunately, neither of the models fully captures the observed behavior at all f_org and size regimes, and is suggestive that additional factors that have yet to be fully identified may influence the activation process. As discussed by Ovadnevaite and coworkers (Ovadnevaite et al., 2017), the AIOMFAC-EQUIL and AIOMFAC-CLLPS (with org. film) calculations may provide upper and lower bounds on the prediction of SS_crit for a given system, which is roughly in agreement with the data in Fig. 2. In reality, it is likely that some portion of suberic acid dissolves into the aqueous droplet bulk at high relative humidity, itself contributing to the water uptake of the droplet, as predicted by AIOMFAC-EQUIL, while a significant organic enrichment prevails at the surface, lowering the surface tension and consequently SS_crit. Such behavior could explain the data and the increasing model–measurement deviations towards higher f_org. Improvements of the AIOMFAC-based models with more sophisticated bulk–surface partitioning treatments in individual liquid phases seem to offer a way forward to address some of the observed shortcomings in future work. At this point, it remains intriguing that the simplified organic film model provides the best description of these experimental data, even though its restrictive assumptions about phase separation and organic water content seem to make it a less physically realistic model variant.

Table 3 Experimentally measured critical supersaturation for given dry diameter, inorganic particle core, and organic volume fraction.

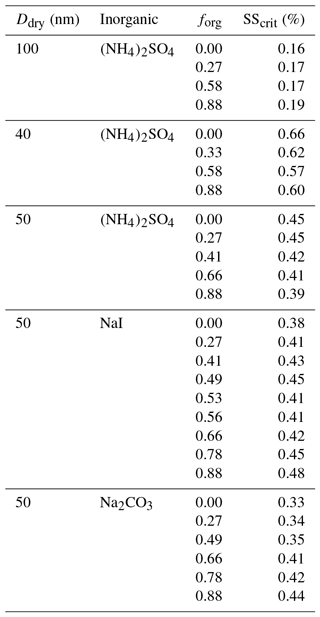
These types of experiment also expose further factors that influence CCN activation, possibly through modification to surface partitioning, such as the role of inorganic ions. We performed additional measurements using different inorganic seed particles coated with suberic acid and observed vastly different behavior across three different salts (ammonium sulfate, sodium iodide, and sodium carbonate), shown in Fig. 3 for 50 nm dry diameter particles. We see for ammonium sulfate the same qualitative behavior as for the other two sizes already discussed; in contrast, the responses of the systems containing the other salts (all with suberic acid as the organic component) are very different. Sodium carbonate exhibits an increase in the required critical supersaturation across the range of compositions, a trend that could reasonably be predicted without invoking surface tension effects. The trend with sodium iodide is more complex and appears to show a sharp discontinuity near f_org=0.5, which was highly reproducible across multiple repeat experiments over multiple days. These salts were chosen to span the range of the Hofmeister series, which describes the propensity of inorganic ions to salt in or salt out organic molecules (proteins in particular). Sulfate and carbonate are the best salting-out ions, while iodide has a relatively weak salting-out effect due to its own surface propensity (Santos et al., 2010). It is interesting to note the differences between carbonate and sulfate, despite their similar position on the Hofmeister scale. The role of the cation is generally considered to be much smaller than that of the anion, and thus these differences are nontrivial. These results serve to further highlight a key conclusion of this work – that we currently lack a robust molecular model that is capable of describing and therefore accurately predicting CCN hygroscopicity and activation even in a relatively simple model system. We hope to prompt further discussions and experimental studies to explore these observations and bulk–surface composition effects on surface tension and CCN activation in more detail.

5 Summary and conclusions

Surface tension effects can lead to significant differences from classic, hygroscopicity mixing rule mechanisms for CCN activation (Hansen et al., 2015; Kristensen et al., 2014). While it has already been made clear that the activation diameter can be significantly different from that determined by an iso-σ Köhler curve, in this work we reveal the potential for more subtle changes in CCN activity (both increases and decreases relative to pure ammonium sulfate particles) as a result of the organics-influenced surface tension evolution during droplet growth. These changes were captured by measuring particles at a fixed diameter with a range of organic volume fractions. Ultimately, to derive an accurate picture of CCN activity across the relevant ranges of chemical compositions and size distributions, the effects of surface tension variability must be taken into account. It should be noted, however, that there are many situations in which using simple mixing rules with inferred values for κ_org can lead to sufficiently accurate predictions without the need for more complex analyses or simulations. It is therefore of key importance to constrain the conditions under which simple approaches are justified – and to know when they may be inappropriate. Taking the activation model based on Köhler theory forward will require a more rigorous interrogation of the role of co-solutes in partitioning and ultimately an assessment of its effect in real-world simulations of cloud formation.

In the meantime, it is important for environmental scientists to recognize the conditions under which surface effects may be influencing cloud droplet formation, e.g., low solubility or insoluble organics mixed with inorganic salts, high-RH phase separation, small particle sizes with critical supersaturations close to the peak supersaturations experienced in clouds, etc. We suggest, if possible, that experimental data be explored as a function of organic volume fraction while keeping the overall dry particle size the same, as from our laboratory experiments this dependence shows the most clear indicator of an unexplained size effect that may be attributed to bulk–surface partitioning. In experiments in which both size and composition vary, the contribution from each is less clear and the effect of the organic component due to bulk–surface partitioning could be hidden. Further fundamental laboratory and modeling studies being performed will allow for in-depth testing and refinements of the proposed models and mechanisms that describe bulk–surface partitioning and surface tension, ultimately achieving a robust and universal mechanism that allows both hygroscopicity and surface tension effects to be coupled into a practical framework.

Appendix A

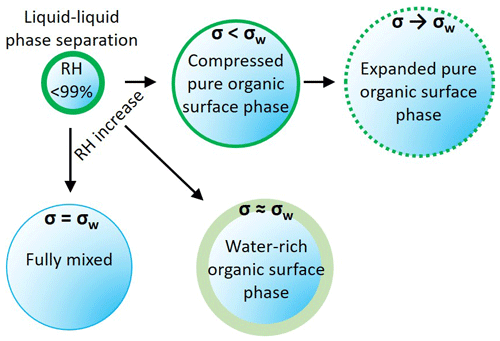
Figure A1 Schematic representation of the three model variants. AIOMFAC-EQUIL treats the droplets as a fully mixed single phase, with the surface tension of the wet droplet sharply approaching σ_w. The phase-separated variants considered a surface phase that is water rich, with surface tension close to σ_w, and a surface phase that excludes water, behaving as an organic surface film, with σ<σ_w. The output from these scenarios is shown in Fig. A2.

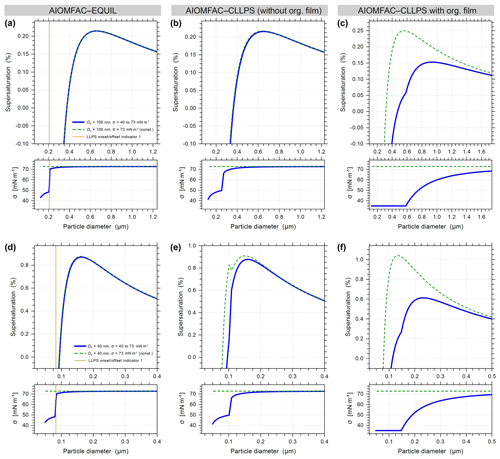
Figure A2 Predicted Köhler curves and associated droplet surface tensions for 100 nm (a, b, c) and 40 nm (d, e, f) dry diameter particles of ammonium sulfate with suberic acid at f_org=0.58 using the AIOMFAC models described in the main text. The AIOMFAC-CLLPS with org. film gives the closest predictions to the experimental observations and predicts similar-shaped curves to those measured experimentally by Ruehl et al. (2016).