the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Rate enhancement in collisions of sulfuric acid molecules due to long-range intermolecular forces
Evgeni Zapadinsky
Theo Kurtén
Hanna Vehkamäki
Bernhard Reischl
Collisions of molecules and clusters play a key role in determining the rate of atmospheric new particle formation and growth. Traditionally the statistics of these collisions are taken from kinetic gas theory assuming spherical noninteracting particles, which may significantly underestimate the collision coefficients for most atmospherically relevant molecules. Such systematic errors in predicted new particle formation rates will also affect large-scale climate models. We studied the statistics of collisions of sulfuric acid molecules in a vacuum using atomistic molecular dynamics simulations. We found that the effective collision cross section of the H2SO4 molecule, as described by an optimized potentials for liquid simulation (OPLS). OPLS all-atom force field, is significantly larger than the hard-sphere diameter assigned to the molecule based on the liquid density of sulfuric acid. As a consequence, the actual collision coefficient is enhanced by a factor of 2.2 at 300 K compared with kinetic gas theory. This enhancement factor obtained from atomistic simulation is consistent with the discrepancy observed between experimental formation rates of clusters containing sulfuric acid and calculated formation rates using hard-sphere kinetics. We find reasonable agreement with an enhancement factor calculated from the Langevin model of capture, based on the attractive part of the atomistic intermolecular potential of mean force.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(3061 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(3061 KB) - Full-text XML
- Corrigendum
- BibTeX
- EndNote
New particle formation from condensable vapours provides an important contribution to the composition of aerosols in the atmosphere which affects air quality as well as the Earth's climate. The positive and negative contributions of atmospheric aerosols to the planet's radiative balance are still not fully understood, and currently constitute one of the largest uncertainties in climate modelling. The earliest stage of new particle formation involves the collisions of individual molecules leading to the appearance of a new molecular complex. In many theoretical approaches, the statistics of such collisions are simply taken from kinetic gas theory, i.e. the molecules are considered to be noninteracting hard spheres, and a collision occurs when the impact parameter, i.e. the perpendicular distance between the spheres' trajectories, is smaller than the sum of the hard spheres' radii. The hard-sphere collision cross section is independent of the relative velocity of the colliding bodies, and the collision rate coefficient for hard spheres of identical radii is customarily expressed as
where kB is the Boltzmann constant, T is the temperature, μ is the reduced mass, and R is the radius of the spheres.
It is well known that acid–base clusters, in particular clusters containing sulfuric acid and ammonia, or amines, are very relevant in nucleation and growth of particles that can serve as cloud condensation nuclei (Almeida et al., 2013). However, such molecules are not necessarily spherical and, despite being charge neutral, exhibit long-range attraction due to interactions between permanent dipoles, permanent and induced dipoles, or induced dipoles (Israelachvili, 2011). Therefore, it is reasonable to expect that particle growth rates or cluster size distributions predicted using collision coefficients from kinetic gas theory will have a systematic error, which needs to be accounted for. In fact, systematic discrepancies have been found between experimental particle formation rates and values predicted from kinetic modelling and cluster dynamics simulations, where hard-sphere collisions are assumed. Kürten et al. (2014) measured the kinetic formation rate of sulfuric acid dimers and found that an enhancement factor of 2.3 needed to be applied to the formation rate obtained from a kinetic model. Lehtipalo et al. (2016) and Kürten et al. (2018) have studied particle formation rates in systems containing sulfuric acid, dimethylamine, and water and concluded that a respective enhancement factor of 2.7 and 2.3 was needed to match experimental particle formation rates.
The effect of long-range interactions between neutral polar molecules on the capture rate constant has been studied by classical trajectory integration (Maergoiz et al., 1996c). The interaction potential between the colliding parties has been approximated by two terms: first, an anisotropic interaction between permanent dipoles proportional to r−3, where r is the distance between the centres of mass of the molecules. Second, an isotropic term due to the interaction between permanent dipoles and induced dipoles, and the interaction between induced dipoles, proportional to r−6. However, such an approximation is inaccurate when the distance between the colliding particles is comparable to their size. Rate coefficients for ion–molecule capture processes have also been studied theoretically in both classic and quantum regimes (Moran and Hamill, 1963; Su and Bowers, 1973; Su et al., 1978; Chesnavich et al., 1980; Clary, 1985; Troe, 1987) or by using trajectory calculations (Dugan and Magee, 1967; Chesnavich et al., 1980; Su and Chesnavich, 1982; Maergoiz et al., 1996a, b). Atomistic simulations have been used to study collisions of Lennard-Jones clusters and atmospherically relevant molecules, but these studies did not analyse or report thermal collision rate coefficients (Napari et al., 2004; Loukonen et al., 2014). Recently, Yang et al. (2018) studied the condensation rate coefficients for Au and Mg clusters at various gas temperatures using molecular dynamics (MD) calculations. The influence of van der Waals forces on the collision rate has also been considered in Brownian coagulation models of ultrafine aerosol particles (Marlow, 1980; Sceats, 1986, 1989).
In the present work, we use atomistic molecular dynamics simulations to study the statistics of collisions between sulfuric acid molecules in a vacuum, determine the collision rate coefficient, and calculate the enhancement factor over kinetic gas theory. Here, we focus on “reactive” collisions, defined by the formation of one or more hydrogen bonds between the molecules. Detailed modelling of e.g. proton transfer processes related to hydrogen bond formation in such reactive collisions would require first-principle simulations (Loukonen et al., 2014); however, the need to simulate a large number of individual trajectories to cover a representative range of impact parameters and relative velocities makes this impossible. In the present study we model the collision rate enhancement due to long-range interactions, which can be decently described by empirical force fields.
In Sect. 2 we discuss technical matters regarding the choice of the force field and the simulation set-up and give a brief overview of the theoretical background of collisions of atmospheric particles. In Sect. 3, simulation results are presented, discussed within the theoretical framework, and compared to analytical and experimental results.
2.1 Force field benchmark
We considered two force fields to describe the sulfuric acid molecules in the present study. The first choice was the force field by Ding et al. (2003), fitted specifically to reproduce DFT structures and energies of small clusters of sulfuric acid, bisulfate, and water, in a vacuum. The second choice was the force field by Loukonen et al. (2010), who fitted interaction parameters for sulfuric acid, bisulfate, and dimethylammonium according to the OPLS all-atom procedure (Jorgensen et al., 1996). Both force fields are fitted to reproduce the C2 geometry of the isolated H2SO4 molecule in a vacuum, and the atoms' partial charges create dipole moments of 3.52 and 3.07 debyes, for Ding et al. (2003) and Loukonen et al. (2010), respectively, which is in agreement with experiments (2.7–3.0 debyes) and ab initio calculations (2.7–3.5 debyes) (Sedo et al., 2008). In both force fields intermolecular interactions are described by the sum of Lennard-Jones potentials between atoms i and j separated by a distance rij, with distance and energy parameters σij and εij, and Coulomb interactions between the partial charges qi and qj,
However, in the force field by Ding et al. (2003), the geometry of the individual molecule is simply constrained by harmonic potentials with force constants kij between all pairs of atoms,
whereas in OPLS the intramolecular interactions consist of the usual sum of two, three, and four-body potentials, i.e. harmonic bonds between covalently bonded atoms, harmonic angles θ between atoms separated by two covalent bonds, and torsion (dihedral angles ϕ) between atoms separated by three covalent bonds,
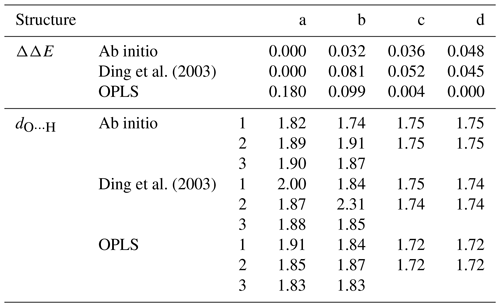
To validate the force fields, we compare the structures and energies of four stable configurations of the sulfuric acid dimer illustrated in Fig. 1a–d to ab initio structures and energies at the RI-MP2/CBS//6-31+G* level of theory calculated by Temelso et al. (2012). The results of the benchmark are summarized in Table 1. The force field by Ding et al. (2003) correctly predicts the lowest energy for dimer structure “a”, and the relative energy differences ΔΔE between optimized structures are closer to those obtained in the ab initio calculation than for the OPLS force field; the OPLS force field assigns the lowest energy to structure “d”, which is the highest energy structure in the ab initio calculation. The geometries of the structures agree well with the ab initio result for both force fields, with the OPLS force field reproducing the ab initio hydrogen bond lengths slightly better than the force field by Ding et al. (2003). The binding energies at T=0 K are slightly lower for the force fields (−0.64 and −0.67 eV for OPLS and Ding et al., 2003, respectively) compared with the ab initio value of −0.72 eV. Overall, the force field by Ding et al. (2003) performs slightly better in terms of energetics.
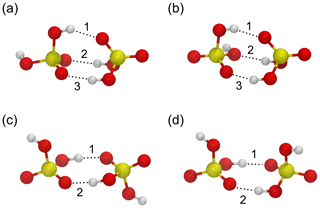
Figure 1Four minimum energy structures for the sulfuric acid dimer (a–d) used to benchmark the force fields by Ding et al. (2003) and Loukonen et al. (2010) against ab initio calculations by Temelso et al. (2012). Sulfur atoms are yellow, oxygen atoms are red, and hydrogen atoms are white. Hydrogen bonds are indicated by dotted lines and enumerated according to Table 1.
Table 1Relative energies ΔΔE (eV) and hydrogen bond distances dO⋯H (Å) for the sulfuric acid dimer structures (a)–(d) in Fig. 1 obtained from ab initio calculations by Temelso et al. (2012) and with the force fields by Ding et al. (2003) and Loukonen et al. (2010), following the OPLS doctrine.
Energy unit conversion: 1 eV ≈96.49 kJ mol kcal mol at
T=300 K.
However, the vibrational spectra, calculated from the Fourier transform of the velocity autocorrelation functions of an isolated H2SO4 molecule in a vacuum exhibit strong differences: the force field by Loukonen et al. (2010) is able to reproduce the experimental and ab initio spectra very well (Hintze et al., 2003; Chackalackal and Stafford, 1966; Miller et al., 2005), whereas the force field by Ding et al. (2003) is not, as shown in Fig. 2. Intramolecular vibrations are relevant in the context of molecular collisions, e.g. when studying energy transfer between different internal degrees of freedom during and after the collision. Also, the OPLS all-atom procedure allows for transferable potentials, as opposed to the Ding et al. (2003) force field which cannot easily be extended to other chemical compounds in future studies. For these two reasons, we decided to use the OPLS force field by Loukonen et al. (2010) for the collision simulations.
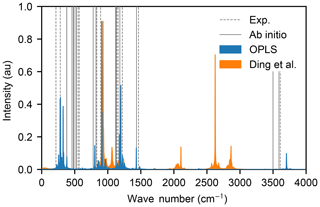
Figure 2Vibrational spectra of the sulfuric acid molecule obtained with OPLS (Loukonen et al., 2010) (blue area) and the force field by Ding et al. (2003) (orange area). The spectra of Ding et al. (2003) has its highest frequency mode at 6565 cm−1 outside of the range of the figure. The positions of the peaks in the experimental spectra (Hintze et al., 2003; Chackalackal and Stafford, 1966; Miller et al., 2005) and ab initio calculations (Miller et al., 2005) are indicated by dashed and solid grey lines, respectively.
2.2 Potential of mean force of two sulfuric acid molecules
We first calculated the binding free energy of two sulfuric acid molecules in a vacuum as described by the force fields of Loukonen et al. (2010) and Ding et al. (2003)
The potential of mean force (PMF) as a function of the sulfur–sulfur distance was calculated from a well-tempered metadynamics simulation (Barducci et al., 2008), using the plumed plug-in (Tribello et al., 2014) for lammps (Plimpton, 1995). We used a velocity Verlet integrator with a time step of 1 fs, to correctly resolve the motion of the hydrogen atoms. The Lennard-Jones interactions were cut off at 14 Å and electrostatic interactions were only evaluated in direct space, with a cut-off at 40 Å. We employed 24 random walkers, and Gaussians with a width of 0.1 Å and initial height of kBT were deposited every 500 steps along the collective variable; a harmonic wall was used to restrict the collective variable to values below 35 Å. A bias factor of 5 was chosen, and a Nosé–Hoover chain thermostat of length 5 with a time constant of 0.1 ps was used to maintain a temperature of T=300 K. The combined length of the trajectories was 120 ns for each force field. Both PMFs, shown in Fig. 3, exhibit a minimum at r=4.1 Å, and the binding free energies are and −0.27 eV for Loukonen et al. (2010), and Ding et al. (2003), respectively. This is in excellent agreement with the ab initio value of eV obtained from Boltzmann-averaging over the four minimum energy dimer structures by Temelso et al. (2012) at 298.15 K, and more recent calculations at a higher level of theory, which predict slightly weaker binding (−0.23 to −0.26 eV) (Elm et al., 2016; Myllys et al., 2017).
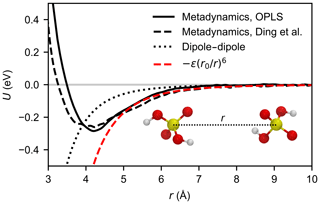
Figure 3Potential of mean force between two H2SO4 molecules as a function of the sulfur–sulfur distance calculated by metadynamics simulation for the OPLS force field (Loukonen et al., 2010) (solid black line) and the force field by Ding et al. (2003) (dashed black line) at 300 K. For comparison, the Keesom (thermally averaged permanent dipole–permanent dipole) interaction between two point dipoles (see Eq. A11) of 3.07 debyes is depicted by the dotted line. The dashed red line shows the attractive potential (Eq. 8) based on the calculated PMF curve of the OPLS force field.
2.3 Collision simulation set-up
Molecular dynamics simulations were performed with the lammps code, using a velocity Verlet integrator with a time step of 1 fs. The Lennard-Jones interactions were cut off at 14 Å and electrostatic interactions were only evaluated in direct space, with a cut-off at 120 Å. The simulations were carried out in the NVE ensemble, as the colliding molecules constitute a closed system (under atmospheric conditions collisions with the carrier gas are rare on the timescale of collisions between sulfuric acid molecules). In order to determine the molecules' collision probability as a function of impact parameter and relative velocity, the following set-up was used: first, two sulfuric acid molecules were placed in the simulation box, separated by 100 Å along x and the impact parameter b was set along the z direction, ranging from 0 to 17.5 Å in steps of 0.5 Å.
Atomic velocities were randomly assigned from a Maxwell–Boltzmann distribution at T=300 K, and the centre of mass motion of each molecule was removed separately.
Then the system was evolved for 50 ps, to randomize the intermolecular orientation and ensure equipartition of energy along the intramolecular degrees of freedom.
At t=50 ps, each molecule received a translational velocity along the x direction, , where v denotes the relative velocity, to set them on a potential collision course. The simulation was continued for another 250 ps, to ensure the possibility of a collision, even at the smallest relative velocities.
For a collision of two identical molecules with molecular mass m, the relative velocities follow the Maxwell–Boltzmann distribution with reduced mass .
We sampled relative velocities between 50 and 800 m s−1, in steps of 50 m s−1. A total of 99 % of the distribution lies within this range at T=300 K.
For each value of the impact parameter b and the relative velocity v, 1000 simulations were carried out starting with different initial atomistic velocities, to ensure good sampling. The simulation set-up is very similar to the one recently used by Yang et al. (2018).
Sulfuric acid molecules bind to each other via the formation of one or more hydrogen bonds. However, even if a collision course leads to an attachment of the two molecules, a portion of the kinetic energy will be redistributed on the degrees of freedom of the formed complex, and this excess energy can lead to a rapid dissociation in the absence of a thermalizing medium. To automate the analysis of over half a million individual trajectories, we define a collision as a trajectory during which the electrostatic energy (ECoul) is lower than a threshold value of −0.25 eV in at least 10 consequent frames (100 fs), indicative of the formation of one or more hydrogen bonds. Three examples of simulated trajectories with a relative velocity closest to the mean velocity at 300 K (350 m s−1) and an impact parameter of 8.5 Å are illustrated in Fig. 4.
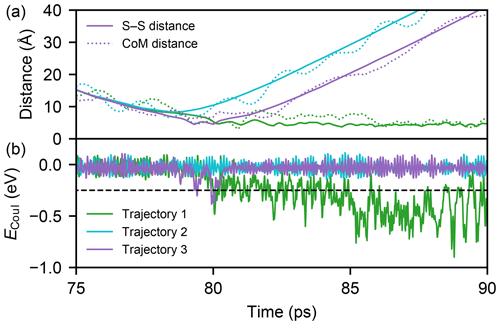
Figure 4Three example MD trajectories with a relative velocity of 350 m s−1 and an impact parameter of 8.5 Å after 50 ps of energy relaxation and the first 25 ps of collision simulation. Panel (a) shows both the distance between the two sulfur atoms (solid lines) and the centre-of-mass distance of the molecules (dotted lines) during the simulations. The electrostatic energies ECoul, which is used to determine the possible collision event, for successful (1), unsuccessful (2), and successful but instantly evaporating (3, continuously 0.18 ps below the threshold) trajectories are shown in panel (b) with the threshold value (dashed black line).
The results from the atomistic simulations will be compared to different theoretical models described in the following.
2.4 Classical model of capture in a field of force
As the collision rate in the context of atomistic simulations is defined as the reaction rate of hydrogen bonding, the related theoretical models are often based on the assumption that if the trajectory of the colliding molecules is able to surmount a centrifugal barrier the reaction is certain. This is known as the capture approximation; to emphasize this conceptual difference between simulations and theoretical models, we use the word capture instead of collision to refer to theory-based results.
The interaction between two identical polar molecules is usually written as
where d1 and d2 are the dipole moment vectors of the molecules, n is the unit vector along the distance vector r connecting the centres of mass of the molecules, and U(r) is a spherically symmetric potential, usually proportional to r−6. The capture rate constant for such a potential can only be calculated numerically (Maergoiz et al., 1996c). In the present section we consider only the isotropic part U(r) of the interaction described by Eq. (5), the effect of the anisotropic part (first term in Eq. 5) is discussed in Appendix A. Then, the Langevin model of capture (Langevin, 1905) can be used to calculate the critical impact parameter beyond which point-like colliding particles in a vacuum will escape from each other. Here, the motion of the two colliding molecules is reduced to a one-body problem in an external central field by using an effective potential containing dispersion and centrifugal terms (Landau and Lifshitz, 1976):
where r is the distance of the colliding body from the centre of the field, and L is the angular momentum. Both the total energy of the system (which equals the initial translational energy μv2∕2 at r→∞) and the angular momentum are conserved. The centrifugal term introduces an energy barrier, and for a successful capture at the barrier (r=rmax) the translational energy has to be positive. As the angular momentum equals L=μvb, the condition for b2 to ensure a capture is
In case of a simple attractive potential (repulsive forces can be neglected, as the studied velocities are relatively low),
the square of the critical impact parameter can be written as
It is preferable to consider the squared value of b, as the capture cross section is calculated as . It is important to note that in the Langevin model, the total energy is divided strictly to the translational and potential energy, the internal degrees of freedom of the two bodies are considered to be completely decoupled, i.e. exchange of translational energy to rotations and vibrations that will occur in a real molecule is completely neglected.
2.5 Brownian model of aerosol coagulation
In the study by Kürten et al. (2014), a model of Brownian coagulation in a field of force (Sceats, 1986, 1989) was used to estimate the collision enhancement factor for neutral cluster formation involving sulfuric acid in a free molecule regime (Chan and Mozurkewich, 2001). The model is based on solving the Fokker–Planck equation for a pair of Brownian particles whose motion is determined by a thermal random force (Sceats, 1986). In the paper by Chan and Mozurkewich (2001), the Hamaker constant describing the strength of the van der Waals interaction was fitted to experiments with uncharged H2SO4∕H2O particles with diameters of 49–127 nm, yielding a collision enhancement factor value of 2.3 at 300 K. Although the Hamaker constant is usually considered to be size-independent, there may be enhanced interaction for very small particle sizes, with radii of the order of 1 nm (Pinchuk, 2012).
For the attractive potential described by Eq. (8), the collision enhancement factor over the kinetic gas theory rate, , from the Brownian coagulation model in the free molecule limit can be written as (Sceats, 1989)
To compare the Brownian and the Langevin models to atomistic simulation results using the OPLS force field, we have determined the attractive potential parameters ϵ and r0 to be equal to −2ΔF and the sulfur-sulfur distance at which the PMF reaches its minimum, respectively.
It should be noted that the model of Brownian coagulation does not describe the correct transport physics of collisions of molecules in the gas phase. For a discussion on the transition from the free molecular (ballistic) regime to the continuum (diffusive) regime, see e.g. Ouyang et al. (2012).
The statistics of the collision probabilities as a function of the impact parameter and relative velocity, P(b,v), obtained from the atomistic simulations are shown as a heat map in Fig. 5 where white indicates a certain collision event (defined by the formation of one or more hydrogen bonds) and black indicates zero collision probability. The critical impact parameter (above which a collision unlikely occurs) has a negative exponential dependency on the relative velocity, which corresponds well with the Langevin model. A more detailed plot is provided in Fig. B1, where the sigmoidal probability curves are shown for each velocity separately. Predominantly, the collision probability approaches unity with a lower relative velocity and a shorter impact parameter. However, the collision probability decreases slightly at high relative velocities where rapid re-dissociation of the complex can be caused by high kinetic energy and slow redistribution of the energy to vibrational modes of the formed cluster. At the slowest velocity of 50 m s−1, and small values of the impact parameter, the collision probability is also reduced. This happens because in some cases the fluctuations in the intermolecular energy, just as they come within interaction range, are sufficient to exceed the very small initial translational energies of the colliding molecules, effectively repelling them (see Appendix C for a more detailed discussion).
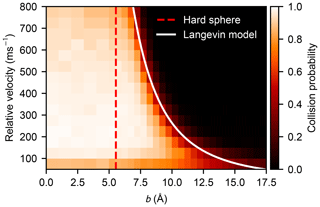
Figure 5Heat map of the collision probability of sulfuric acid molecules plotted as a function of impact parameter b and relative velocity v obtained from molecular dynamics simulation. The impact parameter equivalent to the hard-sphere collision area (b=2R) and the critical impact parameter obtained from the Langevin capture model (Eq. 9) are indicated by the dashed red and the solid white lines, respectively.
The dynamical collision cross section, obtained from the integral over the collision probability functions,
is consistently decreasing with relative velocity v. Even though it can be seen in Fig. 5, and especially in Fig. B1, that values of σd are smaller than the corresponding Langevin capture cross sections σc, the velocity dependence of the change in σd is in very close agreement with the Langevin model solution
where v0 is a reference velocity, as shown in Fig. 6. The importance of contributions from long-range interactions to the collision cross section is evident, as σc is proportional to , for interactions decaying with r−n. Furthermore, as can be seen in Fig. B1, the critical impact parameters from the Langevin model match rather well with the tails of the simulated collision probability curves, the intersection is located without exception at .
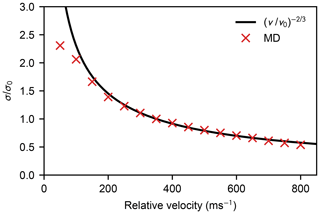
Figure 6Ratio between the collision cross section σ and a reference value σ0 as a function of relative velocity. Here the reference value σ0 is the cross section corresponding to a relative velocity v0=350 m s−1. The red crosses show the ratio of dynamical cross sections obtained from MD simulations, and the solid black line shows the relation predicted by the Langevin model in Eq. (12).
The discrepancy between σd and σc is the result of the assumptions made in the Langevin model, where the capture is considered to be orientation-independent and the particles do not have any internal structure. If the anisotropy of the dipole–dipole potential is taken into account, as in Eq. (5), the capture cross section will be reduced (this has been estimated in Appendix A using a numerical approach provided by Maergoiz et al., 1996c). However, if two molecules are able to move rather close to each other, translational energy can be transferred to rotational and vibrational modes; therefore, the motion over the centrifugal barrier is hindered, and the critical impact parameter is effectively reduced. Additionally, steric hindrance caused by intermolecular orientations incompatible with the formation of hydrogen bonds will also lower the collision probability. Due to coupling, steric hindrance, and other dynamical effects, the ratio between the cross sections σd and σc is 0.82 on average for the collision of two sulfuric acid molecules.
The canonical collision rate coefficient can be calculated in a similar fashion to Eq. (1), but as the collision probabilities P(b,v) obtained from the atomistic simulations depend on both the velocity and the impact parameter, the MD-based collision rate coefficient is calculated by integrating over both the relative velocity distribution f(v) and b2 as
While the thermal velocity distribution f(v) of the colliding molecules can be altered freely to correspond with an arbitrary temperature, the effect of the internal motion to the collision probability function is not necessarily temperature-invariant. However, in Appendix B it is shown that a moderate change (simulations carried out at 250 and 400 K) in the internal kinetic energy does not effect the collision probabilities significantly. Therefore, we used the collision probability distributions calculated at 300 K to compute the collision rate coefficients for the atmospherically relevant temperature range T=225–425 K (see Fig. 7).
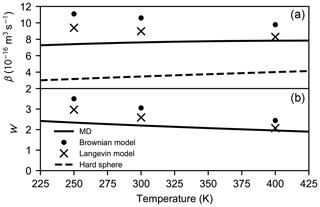
Figure 7Collision rate coefficient β (a) and the enhancement factor W (b) as a function of temperature calculated for the hard-sphere, MD, Langevin, and Brownian approaches.
For the Langevin model (Eq. 9) the expression for the canonical capture rate coefficient can be simplified to
As the potential of mean force is required for the Langevin model, the coefficients are only calculated at 250, 300, and 400 K (see Appendix B for further details).
In addition to the coefficients obtained by different approaches, we examine the enhancement factor W relative to the kinetic gas theory rate expressed in Eq. (1), where a hard-sphere radius R=2.77 Å was calculated from the bulk liquid density of sulfuric acid, ρ=1830 kg m−3, assuming a volume fraction of one. Thus, after performing the integration, the enhancement factor obtained using the Langevin model can be expressed analytically as
where Γ(x) denotes the Gamma function, and ϵ and r0 are the parameters based on the potential of mean force between two sulfuric acid molecules in a vacuum, using the functional form in Eq. (8). The enhancement factor from the Brownian model of aerosol coagulation, WB, was calculated analytically from Eq. (10).
We find that WMD≈2.20, WL≈2.59, and WB≈3.06 at 300 K. Both the collision rate coefficients and the enhancement factors are shown in Fig. 7. As the hard-sphere collision rate increases linearly as the molecular velocity is proportional to , the rate coefficient based on atomistic simulations only slightly increases with temperature due to the exponential narrowing of the collision cross section as the relative velocity increases. However, the dependency is different in case of the Langevin model as the rate coefficient decreases with increasing temperature. This is due to the neglect of the anisotropy of the dipole–dipole interactions in the Langevin model: at higher temperatures, the effect of anisotropy becomes less important; therefore, the model overestimates the collision rate less, compared with lower temperatures. The same effect can be observed in the Brownian coagulation model. Indeed, as seen in Fig. 7, the enhancement factors based on the theoretical models reach better agreement with the factor obtained from atomistic simulations as the temperature rises. As a result of the above-mentioned reasons, the enhancement factor over the hard-sphere collision rate coefficient is lower at higher temperatures regardless of the approach chosen.
The enhancement factor obtained by atomistic simulations is in very good agreement with the kinetic modelling on the recent experimental results of the formation of atmospheric sulfuric acid dimers (Kürten et al., 2014) and small clusters of sulfuric acid, dimethylamine, and water (Lehtipalo et al., 2016; Kürten et al., 2018). In these studies, the enhancement factor was estimated to be 2.3–2.7 using the Brownian coagulation model and van der Waals interactions fitted to experimental data, as mentioned earlier, whereas according to our molecular model of long-range interaction the basic Brownian model using the attractive part of the potential of mean force overestimates the rate enhancement factor by about 40 %.
In summary, we have benchmarked two classical force fields against experimental and ab initio data and determined that the OPLS force field by Loukonen et al. (2010) was able to describe the geometry and vibrational spectra of the isolated sulfuric acid molecule, as well as the geometry and binding free energy of the sulfuric acid dimer. We studied the statistics of collisions of sulfuric acid molecules in a vacuum using molecular dynamics simulations and compared our results against simple theoretical models. We found that the effective collision cross section of two H2SO4 molecules, as described by the OPLS force field, is significantly larger than the hard-sphere diameter assigned to the molecule based on the liquid density of sulfuric acid. As a consequence, we find that the collision coefficient for sulfuric acid molecules is enhanced by a factor of 2.2, compared with kinetic gas theory at 300 K. This enhancement factor obtained from atomistic simulation is consistent with the discrepancy observed between experimental formation rates of clusters containing sulfuric acid and rates calculated using hard-sphere kinetics. At a temperature range from 250 to 400 K, the rate enhancement factor is monotonously decreasing with increasing temperature, however the drop is less than 20 %. The velocity dependence of the simulated dynamical collision cross section is in good agreement with the Langevin model solution. We also note that the enhancement factor obtained from the Langevin model using the attractive part of the intermolecular potential is slightly overestimated due to the imperfect treatment of the dipole–dipole interaction; nevertheless, in the atmospherically relevant temperature range the factor is within 30 % of the result from the atomistic simulation, at a fraction of the computational cost.
In the future, the atomistic collision modelling approach presented in this work can be applied to other atmospherically relevant molecules, clusters, or ions, exhibiting dipoles of varying magnitudes – and in some cases several times larger than that of the sulfuric acid molecule – to help understand the effect of long-range interactions in cluster formation rates. However, before we can quantitatively assess the influence of collision rate enhancement on atmospherical new particle formation rates obtained from cluster dynamics models (for example, Atmospheric Cluster Dynamics Code; McGrath et al., 2012), it is necessary to obtain the enhancement factors for all of the relevant collisions between clusters of different sizes and composition, as the pathway for growth may change – a formidable task, even if only the simplest acid–base clusters were considered. Thus, future work should also be aimed at finding simple models for predicting approximate rate enhancements, based on just a few physico-chemical properties, such as molecular structures, dipole moments, or charge distributions, of the interacting molecules and/or clusters.
Simulation data and input files can be made available upon request from the corresponding author.
Maergoiz et al. (1996c), using classical trajectory integration, calculated the capture rate constant when two identical polar molecules interact via a potential containing anisotropic () and isotropic () terms:
where d1 and d2 are the dipole moment vectors of the molecules, n is the unit vector along the distance vector r connecting the centres of mass of the molecules, and C is the isotropic interaction constant.
As in Eq. (1), the capture rate coefficient in an anisotropic field is given by
where the thermal capture cross section can be calculated using a fitting function κ(θ,M) as
where d is the molecular dipole moment (for the OPLS model of sulfuric acid, debyes). Maergoiz et al. (1996c) use two dimensionless parameters in their model:
and
Based on our MD simulations using the OPLS force field, the average moment of inertia I of a vibrating sulfuric acid molecule is 100.04 amuÅ2, which deviates slightly from the values of 100.66 and 104.94 amuÅ2 obtained experimentally (Kuczkowski et al., 1981) and from quantum chemical calculations (Zapadinsky et al., 2019), respectively. The fitting function is obtained from classical trajectory calculations and is expressed as
where
The reported fitting parameters according to Maergoiz et al. (1996c) are
As all different long-range interactions are included in the attractive part of the potential of mean force between two sulfuric acid molecules (Eq. 8), to exclude the dipole–dipole interaction from the isotropic interaction, the constant C is written as
where f is a factor denoting the relative magnitude of the anisotropic interaction between permanent dipoles with respect to the total interaction. Thus, the rate coefficient is controlled by the relative dipole–dipole interaction and the enhancement factor over the kinetic gas theory can be written as
Figure A1 shows the rate enhancement as a function of the interaction factor f at 300 K. As the anisotropic part does not contribute, i.e. f=0, the enhancement factor is less than 4 % higher than the value obtained from the Langevin model (the statistical error of the thermal capture cross section is about 2 %; Maergoiz et al., 1996c).
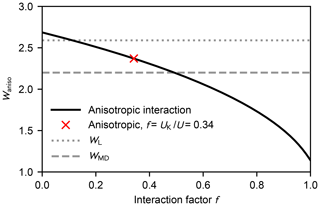
Figure A1Enhancement factor Waniso over the kinetic gas theory calculated from the anisotropic dipole–dipole collision cross section as a function of the interaction factor f at 300 K (black solid line). The red cross denotes the case where the dipole–dipole contribution of the total interaction equals the Keesom equation Eq. (A11) (Waniso=2.41). The enhancement factors obtained from the Langevin model and the MD simulations are shown as the dotted and dashed grey lines, respectively.
As we were unable to distinguish the actual dipole–dipole interaction from the total attractive potential, we estimated the interaction using the Keesom equation (see Fig. 3):
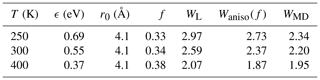
According to Eqs. (8) and (A11), about one-third of the attractive potential is due to dipole–dipole interaction; consequently, the enhancement factor is lower than for the isotropic field. The estimated rate enhancement factors at 250, 300, and 400 K are shown in Table A1. Thus, by taking the anisotropy of the intermolecular potential into account, the estimated capture rate is in better agreement with the result obtained using atomistic simulations.
Table A1The attractive potential parameters ϵ and r0 for H2SO4–H2SO4 interaction based on the PMF calculations with the estimated anisotropic interaction factor and the corresponding enhancement factors calculated by the Langevin model WL, the anisotropic approach Waniso(f), and the atomistic simulations WMD.
The canonical collision rate coefficient can be calculated from the collision probabilities obtained from atomistic simulation at arbitrary temperatures by shifting the Maxwell–Boltzmann relative velocity distribution, provided that changes in the internal motion of the molecules do not affect the collision probabilities. We tested the effect of the different rotational and vibrational motion on the collision statistics in an atmospherically relevant temperature range by carrying out MD collision simulations for a subset of impact parameters b where the molecules' atomistic velocities were drawn from Maxwell–Boltzmann distributions corresponding to 250 and 400 K, instead of 300 K. As shown in Fig. B1, such a moderate change in temperature does not affect the collision probabilities between two sulfuric acid molecules.
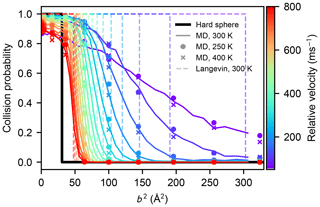
Figure B1Collision probabilities of sulfuric acid molecules, as a function of the impact parameter squared, for different values of the relative velocity, obtained from molecular dynamics simulations at 300 K (solid coloured lines), at 250 K (coloured dots), and at 400 K (coloured crosses). The step-like collision probabilities for a hard-sphere model (b2=(2R)2), or those obtained from the Langevin capture model (Eq. 9), are indicated by the solid black, and dashed coloured lines, respectively.
In order to vary temperature in calculating the thermal collision rate coefficient using the Langevin approach, the potential of mean force between two sulfuric acid molecules was calculated at 250, 300, and 400 K, and the parameters describing the attractive intermolecular interaction (Eq. 8) are reported in Table A1.
As shown in Figs. 5 and B1, for small values of the impact parameter and the initial relative velocity between two colliding molecules in the atomistic simulations, the collision probability can be considerably smaller than unity, which seems counter-intuitive at first. This is due to the fact that the intermolecular interaction is anisotropic and the molecules are rotating, which can lead to instantaneous repulsion even at distances where the intermolecular potential of mean force is slightly attractive. If the initial translational kinetic energy is low enough, the temporary fluctuations in intermolecular energy can alter the translational motion and eventually lead to a definitive separation of the molecules.
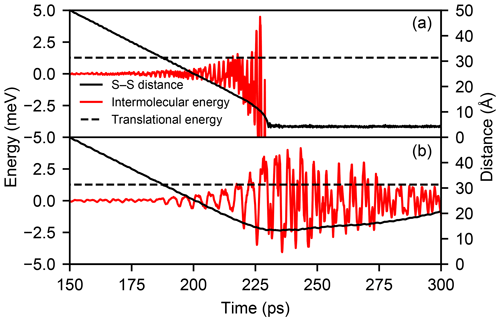
Figure C1Time evolution of the intermolecular energy (red line) and the sulfur–sulfur distance (solid black line) in one MD trajectory with relative velocity v=50 m s−1 and b=0 Å where a collision occurs (a) and one where the molecules are repelled at range (b). The initial translational kinetic energy of the molecules (1.27 meV) is indicated by the dashed black line.
This process is illustrated in Fig. C1, which shows the evolution of the intermolecular energy and distance in one trajectory with b=0 Å and v=50 m s−1 where a collision occurs and a second one where the molecules are repelled at range. While the fluctuation of the intermolecular energy exceeds the initial translational energy of 1.27 meV in both cases, in the trajectory exhibiting a repulsion, the large positive energy fluctuations are longer lived and dominate the interaction.
RH and BR planned the simulation set-up and performed benchmark calculations. BR carried out collision and metadynamics simulations and wrote the first draft of the paper. RH and EZ provided the theoretical framework. RH analysed the simulation data. TK and HV helped plan the project. All authors contributed to writing the final paper.
The authors declare that they have no conflict of interest.
Computational resources were provided by the CSC–IT Center for Science Ltd., Finland.
This research has been supported by the European Research Council (DAMOCLES; grant no. 692891), the Academy of Finland (grant nos. 266388 and 285067), and the University of Helsinki, Faculty of Science (ATMATH project).
Open access funding was provided by Helsinki University Library.
This paper was edited by Fangqun Yu and reviewed by two anonymous referees.
Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S.,d Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurtén, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppä, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petäjä, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamäki, H., and Kirkby, J.: Molecular understanding of sulphuric acid–amine particle nucleation in the atmosphere, Nature, 502, 359–363, https://doi.org/10.1038/nature12663, 2013. a
Barducci, A., Bussi, G., and Parrinello, M.: Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method, Phys. Rev. Lett., 100, 020603, https://doi.org/10.1103/PhysRevLett.100.020603, 2008. a
Chackalackal, S. M. and Stafford, F. E.: Infrared Spectra of the Vapors above Sulfuric and Deuteriosulfuric Acids, J. Am. Chem. Soc., 88, 723–728, 1966. a, b
Chan, T. W. and Mozurkewich, M.: Measurement of the coagulation rate constant for sulfuric acid particles as a function of particle size using tandem differential mobility analysis, J. Aerosol Sci., 32, 321–339, 2001. a, b
Chesnavich, W. J., Su, T., and Bowers, M. T.: Collisions in a noncentral field: a variational and trajectory investigation of ion–dipole capture, J. Chem. Phys., 72, 2641–2655, 1980. a, b
Clary, D.: Calculations of rate constants for ion-molecule reactions using a combined capture and centrifugal sudden approximation, Mol. Phys., 54, 605–618, 1985. a
Ding, C. G., Taskila, T., Laasonen, K., and Laaksonen, A.: Reliable potential for small sulfuric acid-water clusters, Chem. Phys., 287, 7–19, 2003. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r
Dugan Jr., J. V. and Magee, J. L.: Capture collisions between ions and polar molecules, J. Chem. Phys., 47, 3103–3112, 1967. a
Elm, J., Jen, C. N., Kurtén, T., and Vehkamäki, H.: Strong Hydrogen Bonded Molecular Interactions between Atmospheric Diamines and Sulfuric Acid, J. Phys. Chem. A, 120, 3693–3700, 2016. a
Hintze, P. E., Kjaergaard, H. G., Vaida, V., and Burkholder, J. B.: Vibrational and electronic spectroscopy of sulfuric acid vapor, J. Phys. Chem. A, 107, 1112–1118, 2003. a, b
Israelachvili, J. N.: Intermolecular and Surfaces Forces, 3rd edn., Academic Press, Elsevier, Waltham, Massachusetts, USA, 2011. a
Jorgensen, W. L., Maxwell, D. S., and Tirado-Rives, J.: Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 118, 11225–11236, 1996. a
Kuczkowski, R. L., Suenram, R. D., and Lovas, F. J.: Microwave spectrum, structure, and dipole moment of sulfuric acid, J. Am. Chem. Soc., 103, 2561–2566, 1981. a
Kürten, A., Jokinen, T., Simon, M., Sipilä, M., Sarnela, N., Junninen, H., Adamov, A., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Donahue, N. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hakala, J., Hansel, A., Heinritzi, M., Hutterli, M., Kangasluoma, J., Kirkby, J., Laaksonen, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Mathot, S., Onnela, A., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schobesberger, S., Seinfeld, J. H., Steiner, G., Tomé, A., Tröstl, J., Winkler, P. M., Williamson, C., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K. S., Kulmala, M., Worsnop, D. R., and Curtius, J.: Neutral molecular cluster formation of sulfuric acid–dimethylamine observed in real time under atmospheric conditions, P. Natl. Acad. Sci. USA, 111, 15019–15024, 2014. a, b, c
Kürten, A., Li, C., Bianchi, F., Curtius, J., Dias, A., Donahue, N. M., Duplissy, J., Flagan, R. C., Hakala, J., Jokinen, T., Kirkby, J., Kulmala, M., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Onnela, A., Rissanen, M. P., Simon, M., Sipilä, M., Stozhkov, Y., Tröstl, J., Ye, P., and McMurry, P. H.: New particle formation in the sulfuric acid–dimethylamine–water system: reevaluation of CLOUD chamber measurements and comparison to an aerosol nucleation and growth model, Atmos. Chem. Phys., 18, 845–863, https://doi.org/10.5194/acp-18-845-2018, 2018. a, b
Landau, L. D. and Lifshitz, E. M.: Mechanics, vol. 1, Course of Theoretical Physics, 3rd edn., Butterworth-Heinemann, Nauka, Moscow, Russia, 1976. a
Langevin, P.: A fundamental formula of kinetic theory, Ann. Chim. Phys., 5, 245–288, 1905. a
Lehtipalo, K., Rondo, L., Kontkanen, J., Schobesberger, S., Jokinen, T., Sarnela, N., Kürten, A., Ehrhart, S., Franchin, A., Nieminen, T., Riccobono, F., Sipilä, M., Yli-Juuti, T., Duplissy, J., Adamov, A., Ahlm, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Downard, A. J., Dunne, E. M., Flagan, R. C., Guida, R., Hakala, J., Hansel, A., Jud, W., Kangasluoma, J., Kerminen, V.-M., Keskinen, H., Kim, J., Kirkby, J., Kupc, A., Kupiainen-Määttä, O., Laaksonen, A., Lawler, M. J., Leiminger, M., Mathot, S., Olenius, T., Ortega, I. K., Onnela, A., Petäjä, T., Praplan, A., Rissanen, M. P., Ruuskanen, T., Santos, F. D., Schallhart, S., Schnitzhofer, R., Simon, M., Smith, J. N., Tröstl, J., Tsagkogeorgas, G., Tomé, A., Vaattovaara, P., Vehkamäki, H., Vrtala, A. E., Wagner, P. E., Williamson, C., Wimmer, D., Winkler, P. M., Virtanen, A., Donahue, N. M., Carslaw, K. S., Baltensperger, U., Riipinen, I., Curtius, J., Worsnop, D. R., and Kulmala, M.: The effect of acid–base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 7, 11594, https://doi.org/10.1038/ncomms11594, 2016. a, b
Loukonen, V., Kurtén, T., Ortega, I. K., Vehkamäki, H., Pádua, A. A. H., Sellegri, K., and Kulmala, M.: Enhancing effect of dimethylamine in sulfuric acid nucleation in the presence of water – a computational study, Atmos. Chem. Phys., 10, 4961–4974, https://doi.org/10.5194/acp-10-4961-2010, 2010. a, b, c, d, e, f, g, h, i, j, k
Loukonen, V., Bork, N., and Vehkamäki, H.: From collisions to clusters: first steps of sulphuric acid nanocluster formation dynamics, Mol. Phys., 112, 1979–1986, 2014. a, b
Maergoiz, A., Nikitin, E., Troe, J., and Ushakov, V.: Classical trajectory and adiabatic channel study of the transition from adiabatic to sudden capture dynamics. I. Ion–dipole capture, J. Chem. Phys., 105, 6263–6269, 1996a. a
Maergoiz, A., Nikitin, E., Troe, J., and Ushakov, V.: Classical trajectory and adiabatic channel study of the transition from adiabatic to sudden capture dynamics. II. Ion–quadrupole capture, J. Chem. Phys., 105, 6270–6276, 1996b. a
Maergoiz, A., Nikitin, E., Troe, J., and Ushakov, V.: Classical trajectory and adiabatic channel study of the transition from adiabatic to sudden capture dynamics. III. Dipole–dipole capture, J. Chem. Phys., 105, 6277–6284, 1996c. a, b, c, d, e, f, g
Marlow, W. H.: Derivation of aerosol collision rates for singular attractive contact potentials, J. Chem. Phys., 73, 6284–6287, 1980. a
McGrath, M. J., Olenius, T., Ortega, I. K., Loukonen, V., Paasonen, P., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 12, 2345–2355, https://doi.org/10.5194/acp-12-2345-2012, 2012. a
Miller, Y., Chaban, G., and Gerber, R.: Ab Initio Vibrational Calculations for H2SO4 and H2SO4⋅H2O: Spectroscopy and the Nature of the Anharmonic Couplings, J. Phys. Chem. A, 109, 6565–6574, 2005. a, b, c
Moran, T. F. and Hamill, W. H.: Cross Sections of Ion–Permanent-Dipole Reactions by Mass Spectrometry, J. Chem. Phys., 39, 1413–1422, 1963. a
Myllys, N., Olenius, T., Kurtén, T., Vehkamäki, H., Riipinen, I., and Elm, J.: Effect of Bisulfate, Ammonia, and Ammonium on the Clustering of Organic Acids and Sulfuric Acid, J. Phys. Chem. A, 121, 4812–4824, 2017. a
Napari, I., Vehkamäki, H., and Laasonen, K.: Molecular dynamic simulations of atom–cluster collision processes, J. Chem. Phys., 120, 165–169, 2004. a
Ouyang, H., Gopalakrishnan, R., and Hogan Jr., C. J.: Nanoparticle collisions in the gas phase in the presence of singular contact potentials, J. Chem. Phys., 137, 064316, https://doi.org/10.1063/1.4742064, 2012. a
Pinchuk, A. O.: Size-dependent Hamaker constant for silver nanoparticles, J. Phys. Chem. C, 116, 20099–20102, 2012. a
Plimpton, S.: Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comp. Phys., 117, 1–19, 1995. a
Sceats, M. G.: Brownian coagulation in a field of force, J. Chem. Phys., 84, 5206–5208, 1986. a, b, c
Sceats, M. G.: Brownian coagulation in aerosols–the role of long range forces, J. Colloid Interf. Sci., 129, 105–112, 1989. a, b, c
Sedo, G., Schultz, J., and Leopold, K. R.: Electric dipole moment of sulfuric acid from Fourier transform microwave spectroscopy, J. Mol. Spectrosc., 251, 4–8, 2008. a
Su, T. and Bowers, M. T.: Theory of ion-polar molecule collisions. Comparison with experimental charge transfer reactions of rare gas ions to geometric isomers of difluorobenzene and dichloroethylene, J. Chem. Phys., 58, 3027–3037, 1973. a
Su, T. and Chesnavich, W. J.: Parametrization of the ion–polar molecule collision rate constant by trajectory calculations, J. Chem. Phys., 76, 5183–5185, 1982. a
Su, T., Su, E. C., and Bowers, M. T.: Ion–polar molecule collisions. Conservation of angular momentum in the average dipole orientation theory. The AADO theory, J. Chem. Phys., 69, 2243–2250, 1978. a
Temelso, B., Phan, T. N., and Shields, G. C.: Computational Study of the Hydration of Sulfuric Acid Dimers: Implications for Acid Dissociation and Aerosol Formation, J. Phys. Chem. A, 116, 9745–9758, 2012. a, b, c, d
Tribello, G. A., Bonomi, M., Branduardi, D., Camilloni, C., and Bussi, G.: Plumed 2: New feathers for an old bird, Comput. Phys. Commun., 185, 604–613, 2014. a
Troe, J.: Statistical adiabatic channel model for ion–molecule capture processes, J. Chem. Phys., 87, 2773–2780, 1987. a
Yang, H., Goudeli, E., and Hogan Jr., C. J.: Condensation and dissociation rates for gas phase metal clusters from molecular dynamics trajectory calculations, J. Chem. Phys., 148, 164304, https://doi.org/10.1063/1.5026689, 2018. a, b
Zapadinsky, E., Passananti, M., Myllys, N., Kurtén, T., and Vehkamäki, H.: Modeling on Fragmentation of Clusters inside a Mass Spectrometer, J. Phys. Chem. A, 123, 611–624, 2019. a
- Abstract
- Introduction
- Simulation details and theoretical models
- Results and discussion
- Conclusions
- Data availability
- Appendix A: Effect of anisotropy on the dipole–dipole capture rate
- Appendix B: The temperature dependence of collision probabilities and interaction parameters
- Appendix C: Intermolecular repulsion at low velocities in MD simulations
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(3061 KB) - Full-text XML
- Abstract
- Introduction
- Simulation details and theoretical models
- Results and discussion
- Conclusions
- Data availability
- Appendix A: Effect of anisotropy on the dipole–dipole capture rate
- Appendix B: The temperature dependence of collision probabilities and interaction parameters
- Appendix C: Intermolecular repulsion at low velocities in MD simulations
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References





