the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The ice-nucleating ability of quartz immersed in water and its atmospheric importance compared to K-feldspar
Katherine Lever
Alberto Sanchez-Marroquin
Mark A. Holden
Thomas F. Whale
Mark D. Tarn
James B. McQuaid
Benjamin J. Murray
Mineral dust particles are thought to be an important type of ice-nucleating particle (INP) in the mixed-phase cloud regime around the globe. While K-rich feldspar (K-feldspar) has been identified as being a particularly important component of mineral dust for ice nucleation, it has been shown that quartz is also relatively ice-nucleation active. Given quartz typically makes up a substantial proportion of atmospheric desert dust, it could potentially be important for cloud glaciation. Here, we survey the ice-nucleating ability of 10 α-quartz samples (the most common quartz polymorph) when immersed in microlitre supercooled water droplets. Despite all samples being α-quartz, the temperature at which they induce freezing varies by around 12 ∘C for a constant active site density. We find that some quartz samples are very sensitive to ageing in both aqueous suspension and air, resulting in a loss of ice-nucleating activity, while other samples are insensitive to exposure to air and water over many months. For example, the ice-nucleation temperatures for one quartz sample shift down by ∼2 ∘C in 1 h and 12 ∘C after 16 months in water. The sensitivity to water and air is perhaps surprising, as quartz is thought of as a chemically resistant mineral, but this observation suggests that the active sites responsible for nucleation are less stable than the bulk of the mineral. We find that the quartz group of minerals is generally less active than K-feldspars by roughly 7 ∘C, although the most active quartz samples are of a similar activity to some K-feldspars with an active site density, ns(T), of 1 cm−2 at −9 ∘C. We also find that the freshly milled quartz samples are generally more active by roughly 5 ∘C than the plagioclase feldspar group of minerals and the albite end member has an intermediate activity. Using both the new and literature data, active site density parameterizations have been proposed for freshly milled quartz, K-feldspar, plagioclase and albite. Combining these parameterizations with the typical atmospheric abundance of each mineral supports previous work that suggests that K-feldspar is the most important ice-nucleating mineral in airborne mineral dust.
- Article
(11903 KB) - Full-text XML
- BibTeX
- EndNote
The formation of ice in supercooled clouds strongly affects hydrometeor size, which in turn impacts cloud lifetime, precipitation and radiative properties (Kanji et al., 2017). There are a number of primary and secondary mechanisms through which ice can form in clouds. Homogeneous freezing of cloud droplets becomes increasingly important below −33 ∘C (Herbert et al., 2015), but clouds commonly glaciate at much warmer temperatures (Kanitz et al., 2011; Ansmann et al., 2009). Freezing at these warmer temperatures can occur through secondary ice production (Field et al., 2017) or heterogeneous freezing on ice-nucleating particles (INPs) (Murray et al., 2012; Hoose and Möhler, 2012). The presence of INPs, which tend to comprise only a small fraction of cloud condensation nuclei and can dramatically reduce the lifetime of shallow clouds (Vergara-Temprado et al., 2018), alter the development of deep convective clouds through, for example, the release of latent heat, which invigorates the updraught thus altering cloud structure (Lohmann, 2017; Rosenfeld et al., 2011). It is also recognized that an accurate representation of cloud phase is important for assessments of climate sensitivity (Tan et al., 2016; Ceppi et al., 2017). However, our understanding of which type of aerosol particles serve as effective INPs is incomplete (Vergara-Temprado et al., 2017; Kanji et al., 2017).
Mineral dust has been inferred to be an effective INP in the atmosphere from field, model and laboratory studies (Hoose and Möhler, 2012; Vergara-Temprado et al., 2017). Observations of aerosol within ice crystals have shown that mineral dust is often present, suggesting they act as INPs within mixed-phase clouds (Iwata and Matsuki, 2018; Eriksen Hammer et al., 2018; Pratt et al., 2009). Laboratory studies also demonstrate that mineral dusts are relatively effective at nucleating ice (Hoose and Möhler, 2012; Murray et al., 2012; DeMott et al., 2015). Atmospheric mineral dusts are composed of several components. Clay is a major component of airborne mineral dust and is sufficiently small that its atmospheric lifetime is relatively long. Hence, historically ice-nucleation studies have focused on the clay group of minerals (e.g. Broadley et al., 2012; Murray et al., 2011; Wex et al., 2014; Mason and Maybank, 1958; Pinti et al., 2012; Roberts and Hallett, 1968; Hoose and Möhler, 2012). However, more recent work shows that K-rich feldspars (K-feldspars) are very effective INPs when immersed in supercooled water (Whale et al., 2017; Zolles et al., 2015; Tarn et al., 2018; Peckhaus et al., 2016; DeMott et al., 2018; Reicher et al., 2018; Harrison et al., 2016; Niedermeier et al., 2015; Atkinson et al., 2013). However, there are other minerals present in the atmosphere, many of which are relatively poorly characterized in terms of their ice-nucleating activity.
Quartz is a major component of aerosolized atmospheric mineral dust (Perlwitz et al., 2015; Glaccum and Prospero, 1980) and studies have shown that it can be active as an INP (Zolles et al., 2015; Atkinson et al., 2013; Isono and Ikebe, 1960; Holden et al., 2019; Kumar et al., 2019a; Losey et al., 2018). Boose et al. (2016b) showed a correlation between the INP activity of nine desert dusts and the concentration of K-feldspar at temperatures of −20 ∘C. However, at lower temperatures (−35 to −28 ∘C) the ice-nucleating activity of the dusts correlated with the combined concentration of quartz and K-feldspar. Boose et al. (2016b) thus emphasized the importance of understanding quartz and feldspars present in the atmosphere for the modelling of INPs. Recently, Kumar et al. (2018) investigated five milled quartz samples (two synthetic, three naturally occurring) for their ice-nucleating activity, demonstrating the activity of milled quartz. Very recently, Holden et al. (2019) demonstrated that nucleation on quartz is indeed site specific through repeated freezing experiments with high-speed cryomicroscopy and found that micron sized defects tended to be co-located with the nucleation sites. While our understanding of ice nucleation by quartz has improved recently, it is still unclear how variable quartz samples are in their ice-nucleating ability, which prevents an assessment of its atmospheric importance as an ice-nucleating particle relative to other minerals.
When designing experiments focused on understanding the ice-nucleating activity of atmospheric mineral dusts, we must consider the processes that lead to the production of dust in the atmosphere (these processes are illustrated in Fig. 1). It is common practice to mill relatively pure samples to fine powders that can be studied in the laboratory (Atkinson et al., 2013; Harrison et al., 2016; Peckhaus et al., 2016; Zolles et al., 2015; DeMott et al., 2018; Kumar et al., 2018; Niedermeier et al., 2015) for the purposes of characterizing the ice-nucleating ability of individual minerals, but the relevance of this mechanical milling process to natural airborne mineral dusts needs some discussion. Ultimately, atmospheric mineral dust is derived from bulk rocks, which are mechanically broken down to finer particles through erosion processes (Blatt et al., 1980). The finer material that results can be transported by rivers or wind and forms soils in deserts or fertile regions. The particles in these soils undergo complex ageing chemistry (and biology), which converts certain minerals into clay minerals (Wilson, 2004). Minerals such as pyroxenes and amphiboles are relatively readily converted to clays over geological timescales, but quartz and, to a lesser extent, feldspars are relatively inert and therefore persist in soils (Goldich, 1938; Wilson, 2004). However, the ageing state of the surfaces of these minerals is unclear. While ageing processes may modify the surfaces relative to the original fresh surfaces, these aged materials are continually exposed to aeolian processes that involve grains mechanically abrading against one another, resulting in rounding of grains and the break-up of aggregates (Bagnold, 1941; Pye, 1994). These vigorous aeolian processes result in the generation of small airborne dust particles which most likely have fresh surfaces. Hence, the commonly applied practice of mechanically milling rock samples for laboratory characterization has some justification, but it would be wise to test how sensitive the active sites on these surfaces are to exposure to air and water. Previous studies indicate that K-feldspars tend to be relatively insensitive to exposure to water and air (Harrison, 2016; Whale et al., 2017), although acids can deactivate K-feldspars (Kumar et al., 2018). Hence, in the absence of strong acids, freshly milled K-feldspar is thought to be relevant for atmospheric mineral dust. Quartz, on the other hand, has been shown to be very sensitive to exposure to water and re-milling these samples appears to readily expose or create new active sites (Zolles et al., 2015; Kumar et al., 2019a).
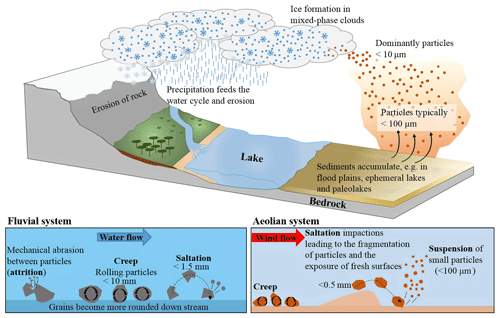
Figure 1Illustration of the geological processes that lead to the creation of a mineral dust and its emission to the atmosphere. Saltation and creep occur both in fluvial and aeolian systems and are processes responsible for the movement of material. There is typically more energy in a fluvial system, and hence the particle sizes moved in these systems are larger. Attrition between particles causes them to fragment and to become more rounded on transport, with small particles becoming suspended in water or air. The particles smaller than ∼10 µm in air can be transported for long distances and may interact with clouds, serving as INP, many hundreds or thousands of kilometres away from the source regions.
In this study we present a survey of the ice-nucleating ability of 10 naturally occurring quartz samples and demonstrate the variability in ice-nucleating ability within natural quartz. We also explore the stability of a subset of these samples to time spent in water or exposed to air, confirming that the activity of some quartz samples is very sensitive to ageing, in contrast to K-feldspars. Then, in order to compare the potential contribution of quartz to the atmospheric INP population to that of other minerals we have generated a parameterization for freshly milled quartz based on the experimental work in this study. In addition we present new parameterizations for K-feldspar, plagioclase feldspar and albite feldspar based on datasets available in the literature. This allows us to compare the potential contribution of quartz, albite, plagioclase and K-feldspar to the atmospheric INP population.
Quartz is the second most abundant mineral in the Earth's crust after the feldspar group of minerals. Its hardness (Mohs scale 7) and chemical nature, along with its lack of cleavage planes, mean it is also a common constituent of sands and soils, as it is resistant to weathering processes. Although quartz does not have cleavage planes, it does exhibit conchoidal fracturing, meaning particles tend to have smoothly curving surfaces as a result of fracturing (Deer et al., 1966), rather than planes with steps that might be expected on a cleavage plane. As it is a common constituent to soils, including desert soils, it can be lofted into the atmosphere and is found within transported mineral dusts (Caquineau et al., 1998; Avila et al., 1997; Kandler et al., 2009, 2011).
The silica minerals are composed of SiO2 tetrahedra with each silicon being bonded to four oxygen atoms and these tetrahedra form a 3-D framework, which can be in six-membered or eight-membered loops (Deer et al., 1992). There are three principal crystalline types of SiO2: quartz, cristobalite and tridymite, with stishovite and coesite being other high-pressure polymorphs. The polymorph that is present depends on the temperature and pressure during formation (Koike et al., 2013; Swamy et al., 1994). All three crystalline silica types (quartz, cristobalite and tridymite) can exist in two polymorphs, both a high-temperature (β) and low-temperature (α) state. α-quartz is most commonly found at or near the Earth's surface due to it being the most stable at atmospheric conditions and thus is the dominant polymorph of quartz found in soils and in atmospheric desert dust aerosol (Deer et al., 1992). In fact, α-quartz is so common that by convention it is referred to simply as quartz.
Generally, quartz samples tend to be close to 100 % SiO2, although it is common to find small amounts of oxides as inclusions or liquid infillings within cavities (Deer et al., 1966). The substitution of Al3+ for Si4+ allows for the introduction of alkali ions such as Li+ and Na+. These subtle impurities can lead to a variety of colours. If quartz with impurities (for example Al) is exposed to low levels of naturally occurring radiation, then one pair of electrons from an oxygen adjacent to Al can be emitted, leaving unpaired electrons otherwise known as “hole defects” (Nassau, 1978). This forms the basis for colour centres, which cause the colouration of amethyst. Amethyst is typically violet in colour and differs from standard α-quartz in that it has a larger proportion of Fe2O3 inclusions and marginally more TiO2 and Al2O3 in its structure (Deer et al., 1966). Rose quartz generally contains higher amounts of alkali oxides, Fe2O3, TiO2 and MnO2 (Deer et al., 1966). It has a pinkish colour, which is thought to be attributed to the presence of a fibrous mineral that was first suggested to be dumortierite (Kibar et al., 2007; Applin and Hicks, 1987) but has been suggested to be a different, unclassified type of mineral (Goreva et al., 2001). Smoky quartz has a black colour, which is caused by colour centres created by the irradiation of iron (Nassau, 1978). Chalcedony is a form of cryptocrystalline or microcrystalline α-quartz (Deer et al., 1966). It has been suggested that it is also commonly intergrown with another polymorph of quartz known as moganite (Heaney and Post, 1992; Götze et al., 1998). Moganite has a monoclinic crystal structure as opposed to the trigonal crystal system of quartz. Chalcedony often includes micropores within its structure due to its microcrystalline nature (Deer et al., 1966).
3.1 Samples and preparation
A total of 10 α-quartz samples were tested for their ice-nucleating ability. These included four typical α-quartz, two amethysts, two microcrystalline quartz (chalcedony), one rose quartz and one Smoky quartz, as summarized in Table 1. Photographs of the samples are presented in Fig. 2. These samples were selected to investigate the natural variability of the ice-nucleating ability of α-quartz.

Figure 2Pictures of the various quartz samples explored in this study showing their varying appearances and characteristics. Samples supplied in a milled state are not shown.
Table 1Table showing the relative concentrations of different minerals within each sample and the respective BET-specific surface area of the ground sample and derived spherical equivalent average surface area. The uncertainty in the XRD analysis is on the order of 0.1 %; therefore, the identification of some trace constituents in some samples is tentative. The mineral density was assumed to be 2.6 g cm−3 for the calculation of spherical equivalent diameter.
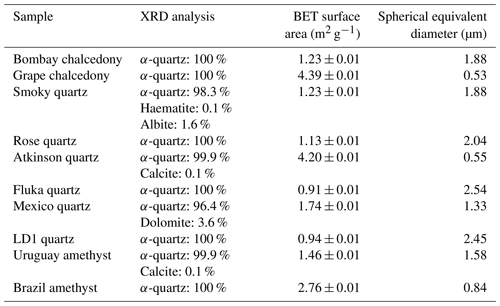
These samples were sourced from various gem sellers. The minerals were visually inspected, using their colour, crystal habit, lustre and cleavage to confirm whether the mineral was quartz and, if so, what type of quartz. Rietveld refinement of powder X-ray diffraction (XRD) patterns was then used to verify the silica polymorph and identify any significant crystalline impurities. The results of this process are presented in Table 1. Raman spectroscopy was used in conjunction with XRD to test for the presence of moganite within the two chalcedony samples, based on the work of Götze et al. (1998). However, both methods indicated that no moganite was present above the limit of detection (∼1 wt %).
Eight of the samples were prepared from bulk rock or crystal samples by first rinsing the rock surface with isopropanol and pure water and placing it into a clean, sealed plastic bag, before chipping off fragments and then grinding them into a powder with an agate mortar and pestle. The mortar and pestle were cleaned before use by scrubbing them with quartz sand (Fluka) and rinsing thoroughly with pure deionized water and isopropanol. A similar method was employed by Harrison et al. (2016), who investigated less ice-active minerals (plagioclase feldspars) and found that contamination from the cleaning process was not observed. Atkinson quartz (the same quartz sample as used by Atkinson et al., 2013) and Fluka quartz were supplied as a powder, although Atkinson quartz was originally ground via the same milling process (Atkinson et al., 2013).
These samples were reground to ensure all samples initially had freshly exposed surfaces for ice-nucleation experiments. The milling process was used to break down mineral crystals and powders to a sufficient size so that they may be suspended in water. We argue that these freshly milled samples are relevant in that they represent the fresh surfaces that are likely produced by mechanical processes in nature as rocks are broken down and particles aerosolized through the saltation process (see Fig. 1 and discussion in the introduction). We therefore suggest that the results from these freshly ground samples of quartz represent an upper limit to the ice-nucleating ability of quartz in atmospheric mineral dust since ageing processes may reduce this activity.
The specific surface areas of the quartz samples were measured using the Brunauer–Emmett–Teller (BET) N2 adsorption method with a Micromeritics TriStar 3000 instrument (Table 1). Heating of the sample overnight at 100 ∘C was performed under a steady flow of dry nitrogen to evaporate any moisture in the sample before the surface area measurement. After BET analysis, 1 wt % suspensions for all the samples were prepared gravimetrically by suspending a known amount of material in purified water (18.2 MΩ cm at 25 ∘C) in a 10 mL glass vial. In some instances, we had only small amounts of the sample, and therefore the sample used for BET analysis was subsequently used for the succeeding ice-nucleation experiments. As quartz is a hard mineral, the use of magnetic stirrer bars was avoided when suspending the material as preliminary experiments showed the potential for the Teflon coating to abrade off the stirrer bars and become mixed with the suspension. We also chose not to use glass stirrer bars, partly because glass is softer than quartz and partly because we have noted in the past that it can be a source of contamination. Therefore, particles were suspended by vortexing for 5 min prior to ice-nucleation experiments. Only small amounts of sample were available for Mexico quartz and Uruguay amethyst and so the powder used for BET analysis was then used to prepare the suspensions for ice-nucleation experiments. The BET analysis and subsequent suspension in water was carried out within a week of grinding the sample.
3.2 Ice-nucleation experiments
The microlitre Nucleation by Immersed Particle Instrument (µL-NIPI) was employed to test the ice-nucleating ability of the various quartz samples in the immersion mode (Whale et al., 2015). This technique has been used in several previous ice-nucleation studies (e.g. Atkinson et al., 2013; O'Sullivan et al., 2014; Harrison et al., 2016). In brief, 1 µL droplets of a suspension were pipetted onto a hydrophobic glass cover slip atop a cold plate (EF600, Asymptote, UK). During pipetting, the suspension was vigorously shaken manually every 10 droplets (with roughly 40 droplets per experiment) to keep the quartz particles suspended and to ensure that the amount of mineral in each droplet was similar. The cold plate and glass slide were then enclosed within a Perspex chamber and a digital camera was used to image the droplets. The temperature of the cold plate was decreased at a rate of 5 ∘C min−1 to 0 ∘C (from room temperature), then at 1 ∘C min−1 until all the droplets were frozen. Whilst cooling the system, a gentle flow of zero-grade dry nitrogen (<0.2 L min−1) was passed across the cold plate to reduce condensation onto the glass slide, which can cause interference between freezing droplets and the surrounding unfrozen droplets (Whale et al., 2015). As the droplets were cooled, images were recorded with the digital camera and freezing events identified in post-analysis to calculate the fraction of droplets frozen as a function of temperature ±0.4 ∘C. A second run for each sample suspension, with a fresh array of droplets, was performed immediately after the first experiment, with approximately 1 h between the two runs. Prior to the start of each experimental day droplets of pure water (no dust) were used to determine the background freezing signal. Umo et al. (2015) compiled a large collection of background freezing results to create a fit which represents the variability of the background in the μL-NIPI instrument. The background signal measured in this study was in line with the lower bound set by Umo et al. (2015).
We assume that nucleation on quartz occurs at specific active sites, as supported by the work of Holden et al. (2019), who showed that nucleation occurs preferentially at specific sites on α-quartz and feldspar using high-speed cryomicroscopy of ice crystal growth on thin sections of mineral. The cumulative ice-nucleating active site density ns(T), on cooling from 0 ∘C to a temperature, T, was determined for each quartz sample. Standardizing the active site density to the surface area of the nucleant allows for comparison of the ice-nucleating ability of different materials (Connolly et al., 2009; Vali et al., 2015). It should be noted that this model neglects the time dependence of nucleation, which can have some influence on the nucleation temperature (Herbert et al., 2014; Holden et al., 2019). ns(T) is calculated using
where n(T) is the cumulative number of frozen droplets upon cooling to temperature T, N is the total number of droplets in the experiment. A is the surface area of nucleant per droplet calculated based on the mass of quartz per droplet (assumed to be the same as in the bulk suspension) and the specific surface area determined via BET analysis.
We conducted Monte Carlo simulations to estimate the error in ns(T) as a result of the randomness of the distribution of active sites in the droplet freezing experiments. These simulations consider the possible distribution of active sites throughout the droplets that explain each fraction frozen and quantify this uncertainty, which is then combined with the uncertainty in the pipetting and BET measurements. This methodology was based on the work of Wright and Petters (2013).
4.1 The variable ice-nucleating ability of α-quartz
The cumulative fraction of droplets frozen (n(T)∕N) on cooling is shown in Fig. 3a for arrays of droplets containing the quartz samples. Comparison of these curves with the fraction frozen curves for droplets without added particles in the µL-NIPI system (Umo et al., 2015) shows that all quartz samples heterogeneously nucleate ice, since the freezing temperatures for droplets containing quartz are always much higher than the pure water droplets. These fraction frozen curves are then translated into ns(T) in Fig. 3b and c. In Fig. 3b we show ns for freshly prepared samples, where the particles were suspended in water for ∼10 min before carrying out an experiment. The variability in the ice-nucleating ability of these α-quartz samples is striking. Bombay chalcedony and Atkinson quartz are substantially more active than the other samples, with the activity spanning roughly 10 ∘C at ns(T)=10 cm−2. While the overall spread is large, it is also notable that the droplet freezing temperatures of 8 out of 10 of the samples falls between −17 and −20 ∘C at ns(T)=10 cm−2.
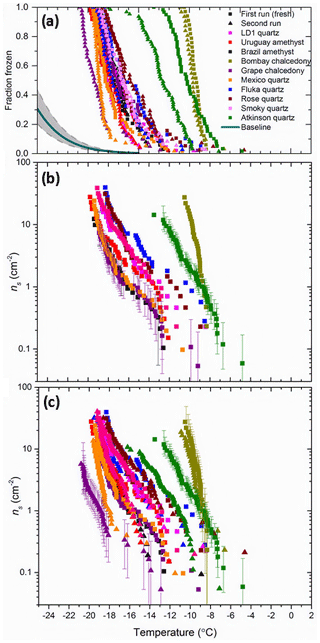
Figure 3Fraction frozen and active site densities for 10 quartz suspensions (1 wt %). (a) The fraction frozen versus temperature for the different quartz samples investigated in this study. The range of freezing for the baseline is highlighted in the grey-shaded region (Umo et al., 2015). (b) The active site density (ns) for the range of quartz samples in this study. In this plot only the first run of each sample is displayed. These samples are considered to be fresh as they have only spent roughly 10 min in suspension. (c) The active site density (ns) versus temperature for the quartz samples on their initial runs and their corresponding second runs. The second runs were carried out roughly an hour after the first run. A sample of the error bars is shown in Fig. 3b and c.
In Fig. 3c we show ns for both the first (fresh) run and a subsequent run performed approximately 1 h after the first experiment for each quartz sample. In the cases of Bombay chalcedony, Brazil amethyst and Smoky quartz, the first and second runs were identical within the uncertainties, whereas in the other cases there was a systematic decrease in freezing temperature. For example, the temperature at which Atkinson quartz had an ns(T) of 1 cm−2 decreased by ∼3 ∘C between the first experiment and the second experiment run. In the past, using this technique with mineral particles of a similar grain size has mostly resulted in consistent results from run to run (e.g. Atkinson et al., 2013; Whale et al., 2015). This suggests that the decrease in activity seen for some quartz samples is a real change in the activity of the quartz rather than artefacts such as, for example, the settling of particles out of suspension leading to less surface area in each droplet. The finding that the activity of many of the α-quartz samples decreases with time spent in water is perhaps surprising given quartz is typically regarded as an inert material. We come back to this issue of ageing of active sites in water and air in Sect. 4.2, where we describe a dedicated set of experiments to explore this topic.
The Bombay chalcedony sample stands out as being one of the most active quartz samples. For ns=1 cm−2 the Bombay chalcedony nucleates ice at −9 ∘C, which is comparable to K-feldspar (see Sect. 5.1 for a comparison with other minerals). As described in Sect. 2, chalcedony is a microcrystalline form of α-quartz and commonly has micropores. A sample of the error bars is shown in Fig. 3b and c. It is possible that these micropores contain ice-nucleation active sites or create zones of weakness that allow defects to be created when ground. In order to test if the superior ice-nucleating ability of Bombay chalcedony is inherent to chalcedony, we located, characterized and tested a second chalcedony sample. Grape chalcedony has a similar microcrystalline form to Bombay chalcedony but behaves more like the other quartz samples we have tested, both in having a lower ice-nucleating activity but also in the decrease in its activity with time spent in water. One possibility is that the Bombay chalcedony sample is contaminated with another very active ice-nucleating component. The X-ray diffraction results suggest that there is not enough inorganic crystalline material, for example, K-feldspar, to account for the result. In addition, we washed a ∼2 g sample of unground Bombay chalcedony in 10 mL pure water (shaking vigorously for ∼2 min) and tested the water. A droplet freezing assay with this washing water indicated that there was no significant detachable contamination. This suggests that the ice-nucleating activity of the Bombay chalcedony is inherent to the material rather than associated with an impurity, although the presence of an ice-nucleating impurity cannot be categorically excluded. These results suggest that a subtle difference between the two chalcedony samples causes the Bombay chalcedony to be much more active.
The second-most active quartz sample, fresh Atkinson quartz, does not have any obvious differences with the other less active quartz samples that might explain its activity. It is almost entirely pure α-quartz with only a minor component of calcite (0.2 %). It is unlikely that the calcite component is responsible for nucleation, since Uruguay amethyst (which is much less ice active) contains the same percent impurity of calcite.
Overall, the results in Fig 3 show a surprising diversity in ice-nucleation behaviour. As mentioned above, quartz is a relatively uniform material that is chemically and physically stable, hence we might have expected its ice-nucleating ability to be uniform and insensitive to ageing processes (in fact, this was our original hypothesis when we started this project). However, the results clearly demonstrate neither of these expectations is correct. Since all these quartz samples are α-quartz, we might have expected all of these quartz samples to exhibit similar nucleating properties. This variability indicates that these quartz samples do not nucleate through a lattice-matching mechanism. This is consistent with the recent observation that nucleation on quartz occurs at active sites (Holden et al., 2019). Our results suggest that these active sites have diverse properties, with different activities, different site densities and some being sensitive to ageing processes where others are not. In the next section we present a set of experiments designed to further probe the ageing of the ice-nucleation sites on quartz samples.
4.2 The sensitivity of ice-nucleating activity with time spent in water and air
The results presented in Fig. 3 clearly indicate that the activity of many of the samples of quartz decreases by several degrees within an hour (Fig. 3b). In initial experiments we also showed that the quartz powder used by Atkinson et al. (2013) had lost its activity since it was initially tested. The sample had been stored in air within a sealed glass vial under dark conditions for ∼5 years. However, milling of the powder dramatically increased its activity, which suggests that milling can (re)expose surfaces with the most effective active sites. This observation is similar to that described by Zolles et al. (2015), who noted that two out of three quartz samples increased in activity by up to 5 ∘C on milling. This supports the hypothesis that fresh surfaces are often key to maximizing a quartz sample's ice-nucleating ability. Very recently, Kumar et al. (2018) have also observed that milling quartz increases its ice-nucleation activity and suggest that this may be a result of defects created during the process.
In order to further explore the stability of active sites, we tested how the activity of three samples of quartz varied when exposed for a range of times to water and air. For this investigation we tested: (i) Smoky quartz, as it is a representative quartz in terms of its ice-nucleating ability, lying within the middle of the spread of ns(T); (ii) Bombay chalcedony, as it was the most active sample; and (iii) Atkinson quartz, since initial experiments indicated it was highly sensitive to ageing in both water and air. The dry powder and suspension samples were stored at room temperature in a dark cupboard in sealed glass vials. Prior to the droplet freezing experiment, wet samples were agitated to re-suspend the particles and the dry powders were added to water in the standard manner described above. The ns(T) of the various quartz samples aged in both water and in air for varying times are displayed in Fig. 4.
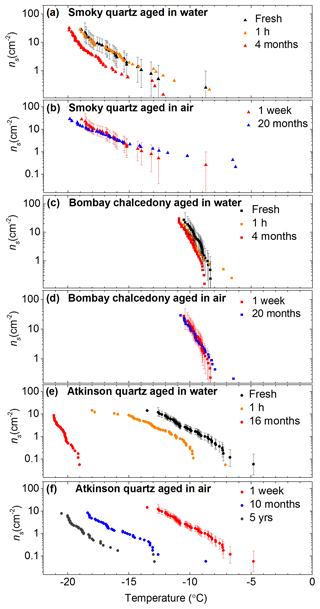
Figure 4Plots showing the sensitivity of quartz activity, expressed as ns, to time spent in water and air. Data are shown for (a, b) Smoky quartz, (c, d) Bombay chalcedony and (e, f) Atkinson quartz. Error bars for the first run of each time series are shown but omitted for the other datasets for clarity. The ns values for the fresh (∼10 min) and 1 h suspensions were taken from Fig. 3.
Each of the three samples responded in a distinct manner to time spent in water. Inspection of Fig. 4a, c and e reveals that while the ice-nucleating ability of Smoky quartz did not significantly decrease after ∼1 h, its activity decreased by about 3 ∘C after 4 months in water, which is well outside the uncertainties of the experiment. Bombay chalcedony was far more stable in water, with no substantial change in the ns(T) curve after 4 months, being within 1 ∘C of the fresh sample (close to the uncertainties of the experiment). In contrast, the activity of Atkinson quartz decreased dramatically on exposure to water. Even after only ∼1 h in suspension the ns(T) curve decreased by 2 ∘C, but after 16 months in water the activity decreased by 12 ∘C. These results point to populations of very different active sites on these three different quartz samples.
We also found that the activity of some quartz samples decreased even when they were stored in air (Fig. 4b, d and e). Dry Smoky quartz and Bombay chalcedony powders were tested after being left in a glass vial for 20 months and showed no decrease in activity. In contrast, the activity of Atkinson quartz decreased by ∼5 ∘C in half of this time period (10 months). Figure 4f also shows the initial freezing temperatures obtained using the same sample from the Atkinson et al. (2013) study, which had been stored for ∼5 years in a glass vial. This sample was ∼10 ∘C less active compared to the freshly ground powder.
4.3 Discussion of the nature of active sites on quartz
These results paint a complex picture of the properties of the active sites on quartz samples. Not only is the absolute activity of the samples variable, but the sensitivity of the sites to time spent in water and air is also highly variable. The active sites of the Atkinson quartz are far more susceptible to ageing in water and air than both the Smoky quartz and Bombay chalcedony. The sites on the Bombay chalcedony are stable in both air and water, whereas those on Smoky quartz are somewhat intermediate in stability, being sensitive to water only after an extended period of time beyond 1 h.
Very recently, Kumar et al. (2018) also described the deactivation of quartz in suspension over a period of 5 d. However, they noted that time series experiments carried out within glass vials showed deactivation of quartz in pure water, whereas experiments within polypropylene falcon tubes did not. They suggested that silicic acid leached from the glass vial walls allows the quartz fragments to slowly grow and the active sites to be lost during the process. The explanation of Kumar et al. (2018) is consistent with our observation that the nucleating ability of many samples decreases with time spent in water. However, it is inconsistent with the stability of Bombay chalcedony and it cannot explain the loss of activity seen for Atkinson quartz when aged in air.
The physical and chemical characteristics which lead to the large variability in the properties of the ice-nucleation sites on quartz are challenging to define. Classical nucleation theory suggests that ice critical clusters at the nucleation temperatures observed in this study are likely to be on the order of several nanometres across (Pummer et al., 2015). It therefore seems reasonable to think that the relevant ice-nucleation sites will be on a similar scale, but the nature of these sites remains unclear. A molecular dynamics study by Pedevilla et al. (2017) suggested that surfaces with strong substrate–water interaction and high densities of OH groups (or other H-bonding groups) give rise to effective sites for ice nucleation. However, sites with high densities of surface OH groups are also inherently thermodynamically unstable and will have a tendency to either react with, for example, moisture in air, or rearrange to a more stable configuration. Hence, it may be at defects in the crystal structure where such sites become stabilized when the thermodynamic cost of having a nanoscale region with a high density of H-bonding groups is outweighed by the gain from relaxing strain in a structure. For example, in K-feldspar, it has been suggested that active sites are related to strain induced by exsolution into K-rich and Na-rich regions, which is known to result in an array of nanoscale topographical features (Whale et al., 2017). Consistent with this idea, Kiselev et al. (2016) reported that nucleation on K-feldspar was related to exposed patches of the high-energy surface plane (100), and Holden et al. (2019) demonstrated that nucleation on K-feldspar always occurs within micrometre-scale surface imperfections. Holden et al. (2019) reports that topographic features were observed on quartz, at some of the nucleation sites, but they have not been further characterized.
Larger nanoscale patches of surface H-bonding groups should be better at nucleating ice, but these larger high-energy patches will also be less energetically stable. Hence, one might expect that the sites responsible for nucleation at the highest temperatures would also be the least stable and most sensitive to time spent in water or air. But, this does not hold for Bombay chalcedony, which is the most active quartz we studied and also the most insensitive to exposure to water and air (Fig. 4). This indicates that the sites in this case are either of a completely different chemistry (perhaps a different high-energy crystal plane), or the topography and strain associated with a defect imparts a greater stability on these sites. The fact that Bombay chalcedony is distinct from the bulk of the samples, being a microcrystalline quartz, may be related to this; however, grape chalcedony also has a similar morphology and does not possess the population of very active sites.
The increased ice nucleation associated with milling may be caused by the mechanical fracturing of the quartz, leading to exposure of high energy but unstable sites, which decay away through a structural rearrangement process when exposed to air or liquid water. Alternatively, milling may simply result in the removal of reaction products to leave exposed active sites. Kumar et al. (2018) suggest the milling process causes the breakage of Si–O bonds that act as high-energy sites for ice nucleation. Quartz does not exhibit a preferential plane of weakness (cleavage) to break along and it therefore fractures. The presence of small impurities distributed throughout the lattice, as described in Sects. 2 and 3, may influence the nature of fracturing and hence create differing defects and high-energy sites. Gallagher (1987) classified impurities as a form of structural weakness. The impurities can create zones of weakness and stress within the crystal structure and therefore act as a pathway of least resistance, resulting in the breakage of bonds and development of microtexture. Alternatively, in some instances the impurities may create areas of greater strength and so fracturing occurs around these zones. Hence, it is possible that the presence of impurities influences the way in which individual quartz samples fracture and therefore influence the presence of active sites.
Inherently, quartz is rather simple in terms of naturally occurring defects compared to other minerals, such as feldspar. In fact, in the past quartz has been considered to be in the “perfect crystal class”, i.e. lacking imperfections. However, quartz does have defects, albeit at a lower density than other minerals (Spencer and Smith, 1966). Quartz minerals can be subject to varying conditions and stresses after their formation and so the geological history of the quartz may also influence the degree of microtexture. For example, a quartz sample that has undergone stress at a fault boundary is more likely to exhibit microtextural features than one that has not (Mahaney et al., 2004). It may be these microtextural differences that lead to the observed variability in ice-nucleating ability. This hypothesis might be tested in the future if quartz samples could be obtained with well-characterized geological histories.
It has also been observed in the past that, for other minerals, the specifics of the mineral formation mechanism are critical for determining its ice-nucleating ability. Whale et al. (2017) demonstrated that a sample of K-feldspar, which had cooled sufficiently quickly during its formation that it did not undergo exsolution and therefore lacked the associated microtextures, had very poor ice-nucleation properties. This was in contrast to the more common K-feldspars that do have exsolution microtexture and nucleate ice very effectively. Despite having very different ice-nucleating properties, their crystal structures and compositions are very similar. A similar formation pathway dependence may be true for quartz, such as strain introduced in geological fault systems. But one thing is clear: while bulk mineralogy is a guide to ice-nucleating activity, in some cases details of the formation pathway may be more important.
5.1 Comparison to the literature data for quartz and feldspar
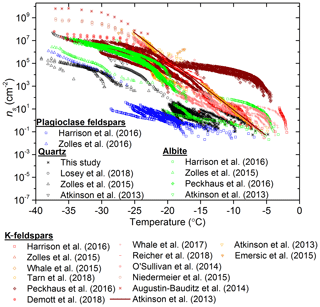
The data from the present study are contrasted with literature active site density data for quartz (Zolles et al., 2015; Atkinson et al., 2013; Losey et al., 2018) in Fig. 5. These data were also compared with ns(T) parameterizations for desert dust samples (Niemand et al., 2012; Ullrich et al., 2017) and K-feldspar (Atkinson et al., 2013). The variability within the α-quartz samples that we report is also reflected in the literature data for quartz. It is striking that two of the quartz samples in this study, Bombay chalcedony and Atkinson quartz, have an activity approaching or equal to K-feldspar. Nevertheless, it is apparent that quartz is never substantially more active than K-feldspar or desert dust in terms of ns(T).
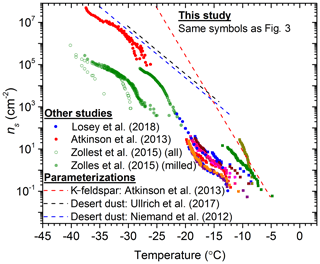
Figure 5Plot of ns versus temperature for the available literature data for quartz compared to the data collected in this study. The symbols for this study's data are displayed the same as in Fig. 2 and only the first runs (fresh samples) from this study are plotted. The data from Zolles et al. (2015) have been split into quartz samples that were milled for fresh surfaces and all the combined data (both milled and unmilled quartz).
Since one of our objectives is to determine how effective quartz is at nucleating ice in comparison to feldspars, we contrast the literature active site density data for feldspars and quartz in Fig. 6. The feldspars have been colour-coded into the plagioclase (blue), albite (green) and the K-feldspar (orange-reds) groups. We note that, by convention, albite is considered part of the plagioclase solid solution series. However, Harrison et al. (2016) demonstrated that albites had a distinct nucleating activity, and therefore we plot them here as a separate group. The K-feldspars presented here represent the K-rich samples from the alkali feldspar group (i.e. >10 % K). Overall, there is a general trend in that plagioclase feldspars are the least active of the four mineral groups and K-feldspar is the most active. Both albite and quartz show similar, intermediate, activities. K-feldspars from Whale et al. (2017) that did not exhibit the common phase separation were excluded from this plot as they are unrepresentative of common K-feldspars and are rare in nature. Although quartz is an ice active mineral, Fig. 6 supports the consensus that it is the K-feldspars that are the most active mineral for ice nucleation that is commonly found in mineral dusts in the atmosphere.
5.2 New parameterizations for the ice-nucleating activity of quartz, K-feldspar, plagioclase and albite
In order to be able to determine which mineral is most important in the atmosphere we need the activity of each mineral (expressed as ns(T)) in combination with estimates of the abundance of each mineral in the atmosphere. In this section we produce new ns(T) parameterizations for quartz, K-feldspar, plagioclase and albite using data from the present study in addition to literature data.
The new set of parameterizations is shown in Fig. 7. In order to derive these parameterizations we compiled data for representative samples of quartz, K-feldspar, plagioclase and albite. To create these parameterizations we binned the data within each dataset into 1 ∘C intervals and then fitted a polynomial line through the log averages of the data. We binned the data in an attempt to remove bias towards datasets with relatively high data density. In addition, we only applied a fit in the temperature range where multiple datasets were present (with the exception of plagioclase, where the available data is so sparse in some temperature regimes that we had to relax this criterion in order to produce a parameterization). We used polynomial fits to represent the data since the data are quite complex and alternatives such as a straight line would produce a very poor representation of the data. These fits were constrained at the warmest and coldest temperatures in order to obtain a reasonable representation of the data at these limits. We stress that these fits must not be extrapolated to higher and lower temperatures. The standard deviation for each parameterization was calculated by taking the average of the standard deviations of the log ns(T) values for each 1 ∘C temperature interval. The corresponding value was then used to approximate the standard deviation from each fit, which is represented by the dashed lines and shaded area in Fig. 7.
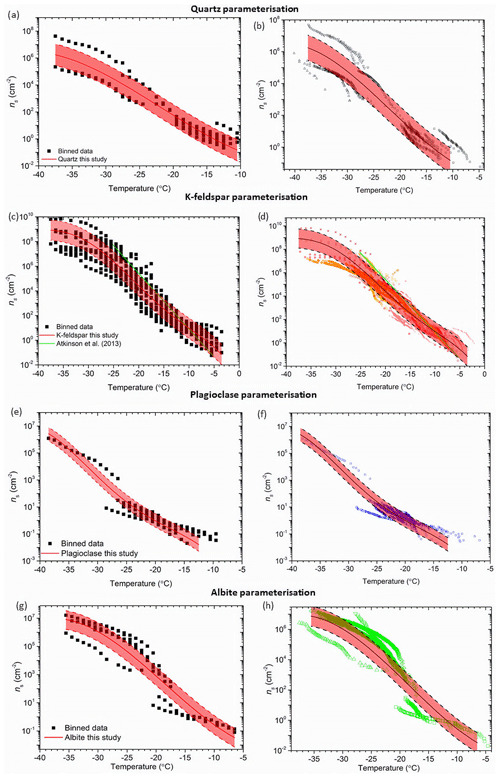
Figure 7Parameterizations developed for various silicate minerals. Panels (a), (c), (g) and (e) show the temperature-binned ns data used to derive the parameterizations. Panels (b),(d), (f), and (g) show the new parameterizations plotted with the original non-binned data. The standard deviation is highlighted in the red-shaded area for each parameterization. The green line in panel (d) indicates the K-feldspar parameterization from Atkinson et al. (2013). See Fig. 6 for the sources of the raw data. The new parameterizations (validity T ranges and standard deviation for log(ns(T)), where ns is in units of cm−2, are as follows. Quartz: log(ns(T)) = −1.709 + () + () + (), (−10.5 to −37.5 ∘C; 0.8); K-feldspar: log(ns(T)) = −3.25 + (−0.793T) + () + () + () + (), (−3.5 to −37.5 ∘C; 0.8); plagioclase feldspar: log(ns(T)) = () + () + (−0.106T2) + (−1.71T) −12, (−12.5 to −38.5 ∘C; 0.5); albite: log(ns(T)) = () + () + () −2.29, (−6.5 to −35.5 ∘C; 0.7).
For the quartz fit, the chalcedony samples were excluded given these microcrystalline minerals are unrepresentative of most quartz in nature and that they are therefore likely to be in negligible abundances in the atmosphere. We also only include the runs with freshly made quartz suspensions in the parameterization since the second runs often showed signs of deactivation in suspension. By only using the relatively fresh suspension data, our parameterization is representative of freshly milled quartz dust. The new parameterization can be seen in Fig. 7a and b and covers a temperature range of −10.5 to −37.5 ∘C and 9 orders of magnitude in ns(T). This is the first robust ns(T) parameterization developed for this mineral that can be used to determine its role as an INP in the atmosphere.
The K-feldspar parameterization developed by Atkinson et al. (2013) has been used extensively within the ice-nucleation community. However, this parameterization was created with data from one K-feldspar sample and does not reflect the variability we now know to exist. The parameterization developed as part of this study can be seen in Fig. 7c and d. We excluded K-feldspar samples which did not exhibit phase separation from the Whale et al. (2017) study from this parameterization as these types of alkali feldspar are rare and unlikely to be found in significant quantities in the atmosphere. The data included in these plots includes all three polymorphs of K-feldspar (microcline, orthoclase and sanidine), although most of the data is for microcline. The strongly hyperactive TUD #3, examined by Harrison et al. (2016) and Peckhaus et al. (2016), was excluded as it exhibited extremely high activity and appears to be an exceptional case that is generally unrepresentative of the K-feldspar group of minerals. With this in mind we have developed a parameterization that represents K-feldspars that possess exsolution microtexture. It should be noted that all of the studies used BET-derived surface areas for the calculation of ns(T), other than DeMott et al. (2018) and Augustin-Bauditz et al. (2014), who used geometric surface areas. However, while the difference between BET and geometric surface areas is substantial for clay samples (Hiranuma et al., 2015), the discrepancy is much smaller for materials with larger grain sizes like feldspar (Atkinson et al., 2013). When the new K-feldspar parameterization is compared to the literature data (Fig. 7d) it represents the variability of K-feldspar, as well as the curvature in the datasets. In particular, the new parameterization captures the observed plateau in ns(T) below about −30 ∘C. In addition, the new parameterization produces higher ns(T) values at temperatures warmer than −10 ∘C relative to that of Atkinson et al. (2013). Below −10 ∘C this new parameterization gives lower values of ns(T). The temperature range of the parameterization is also extended, covering −3.5 to −37.5 ∘C.
The parameterization proposed here to represent plagioclase feldspar is shown in Fig. 7e and f. The parameterization spans a temperature range of −12.5 to −38.5 ∘C. Only one dataset was available to represent the plagioclase feldspars in the lowest temperature regime (Zolles et al., 2015), hence this parameterization needs to be used cautiously, but it is nonetheless a best estimate at present given the current data available. A similar caution must be accepted when using the albite parameterization displayed in Fig. 6g and h, which spans a range of −6.5 to −35.5 ∘C. For the albite parameterization, the hyperactive Amelia albite from the Harrison et al. (2016) study was excluded due to its exceptional ice-nucleating ability making it unrepresentative of the other five albite samples. Hence, this parameterization is representative of the non-hyperactive albites.
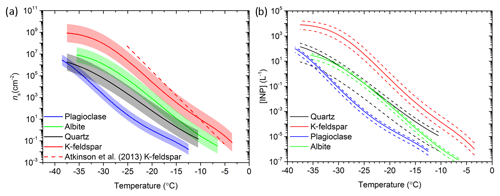
Figure 8Comparison of the newly developed parameterizations. (a) ns versus temperature for the four newly created parameterizations from this study and the K-feldspar parameterization proposed by Atkinson et al. (2013). The standard deviation of each parameterization is shown by the shaded regions. (b) INP per litre predictions using the quartz, K-feldspar, albite and plagioclase parameterizations. The solid lines represent the predicted INP concentration associated with the average mineral proportion and the dashed lines represent the upper and lower proportions based on the variability of mineral proportions of atmospheric desert dust (see Sect. 5.2 for details). An aerosol surface area concentration of 50 µm2 cm−3 and an external mixing assumption were used.
The parameterizations are summarized in Fig. 8a and are then combined with a typical abundance of each mineral to estimate the INP concentration ([INP]T) associated with each of the four minerals in Fig. 8b. On average, roughly 3±6 % (by mass) of atmospheric transported mineral dust particles are K-feldspar, whereas 16±15 % are quartz and 8±3 % are plagioclase (see compilations of measurements in Atkinson et al., 2013, which are consistent with more recent measurements; Boose et al., 2016b). Albite is often grouped with plagioclase feldspars when determining the mineralogy of atmospheric mineral dusts rather than being reported on its own. For the purposes of this estimate we have assumed that albite has a concentration equal to 10 % of that of plagioclase. [INP]T was derived from the ns(T) parameterizations, assuming a surface area concentration of mineral dust of 50 µm2 cm−3 (a moderately dusty environment) and that the mass fraction of each mineral is equivalent to its surface area fraction. In order to approximate the size distribution of dust, a lognormal size distribution centred around particles of 1 µm in diameter with a standard deviation of 0.3 µm was used. We have also assumed that each mineral is externally mixed (see Atkinson et al., 2013, for details of how to treat the mixing state of mineral dust), which is the assumption that has been made when modelling the global distribution of INPs in the past (Atkinson et al., 2013; Vergara-Temprado et al., 2017). In reality, desert dust aerosol will be somewhat internally mixed. The opposing assumption of full internal mixing produces 1–2 orders more INPs at the lowest temperatures but produces the same INP concentration above about −25 ∘C (Atkinson et al., 2013). The upper and lower bounds for each line in Fig. 8b are derived from the range of mineral mass concentrations.
The [INP]T curves in Fig. 8b confirm that, under most atmospheric situations, K-feldspar has the main contribution to the ice-nucleating particle population in desert dust. Quartz is the next most important mineral, with plagioclase the least important. The contribution of pure albite is rather uncertain given the amount of pure albite in desert dust is poorly constrained, but it is unlikely to compete with K-feldspar. Nevertheless, while K-feldspar is the most important contributor to the INP population, the estimates in Fig. 8b do suggest that quartz may make a non-negligible contribution to the INP budget at temperatures between about −20 and −12.5 ∘C. This is particularly so when we consider the variability in the ice-nucleating ability of the K-feldspar and quartz groups. It is possible that in a desert dust aerosol that if the K-feldspar was at the bottom end of the activity, whereas the quartz was at the top end of its activity range, then the quartz would contribute more INP than K-feldspar. However, it should also be considered that the estimated [INP]T curves in Fig. 8b are based on the assumption that quartz has the activity of fresh quartz. We know from the work presented above that the activity of quartz is sensitive to ageing processes. We cannot quantify ageing of atmospheric quartz, but the parameterization we present here probably represents an upper limit to its activity. In contrast, the activity of K-feldspar does not decrease with time spent in water or air (Kumar et al., 2018; Harrison et al., 2016; Whale et al., 2017). Overall, we conclude that K-feldspar contributes the bulk of the INPs associated with desert dust because it is more active and it is less sensitive to ageing processes. However, we should not rule out quartz making a significant contribution to the INP population in a minority of cases.
5.3 Testing the new parameterizations against literature laboratory and field measurements of the ice-nucleating ability of desert dust
We now test the quartz and K-feldspar parameterizations to see if they are consistent with literature data of the ice-nucleating ability of desert dust (Fig. 9). In Fig. 9a we contrast the predicted ns(T) values, based on the quartz and K-feldspar parameterizations, against a variety of literature datasets for desert dust. For the K-feldspar based prediction, we have presented lines where 20 %, 1 % and 0.1 % of the surface area of dust is made up of K-feldspar. For the 20 % prediction, which is consistent with measurements in Cabo Verde (Kandler et al., 2011), we have also shown the natural variability in K-feldspar activity as the shaded region. The line for assuming quartz is the dominant ice-nucleating mineral in desert dust is for 12 % quartz, which again is consistent with measurements made in Cabo Verde (Kandler et al., 2011).
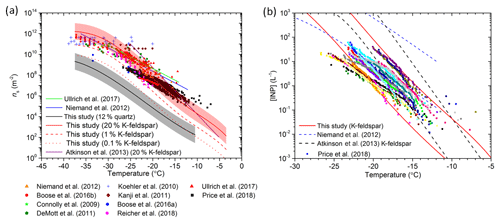
Figure 9Testing of the newly developed K-feldspar and quartz parameterizations against literature data for desert dust. (a) Comparison of ns versus temperature for mineral dust from laboratory and field studies against the K-feldspar and quartz parameterizations. The red lines are ns values where 0.1 %, 1 % and 20 % of the aerosol surface area is assumed to be K-feldspar. The standard deviation of the K-feldspar parameterization from this study is represented as the shaded area around the 20 % K-feldspar prediction; this is to show the natural variability in mineral activity. The prediction for 12 % quartz is shown using a black line, with the natural mineral variability of freshly milled quartz highlighted by the shaded region. Literature data and parameterizations have been plotted from Niemand et al. (2012), Boose et al. (2016a, b), Connolly et al. (2009), DeMott et al. (2011), Koehler et al. (2010), Kanji et al. (2011), Reicher et al. (2018), Ullrich et al. (2017), Price et al. (2018). (b) Comparison of the INP concentrations predicted by several parameterizations with the INP concentrations measured in the dusty eastern tropical Atlantic region by Price et al. (2018). The predictions were made assuming that 20 % of the dust was K-feldspar, consistent with Kandler et al. (2011). For this calculation we assumed that the dust is externally mixed in terms of its mineralogy, although in this regime an internal versus external mixing state assumption makes very little difference (see Atkinson et al., 2013). The upper and lower bounds of the predicted INP concentrations are based on the lowest and highest aerosol surface area concentrations corresponding to the INP data in Price et al. (2018). Note that the measured INP concentrations from Price et al. (2018) have been corrected downwards by a factor of 2.5 based on the work presented by Price et al. (2018) and Sanchez-Marroquin et al. (2019).
From Fig. 9a it is clear that quartz does not account for the ns(T) measurements of desert dusts sampled directly from the atmosphere and suspended in laboratory studies. However, the new K-feldspar parameterization is consistent with the ice-nucleating activity of dusts over a wide range of temperatures. The K-feldspar parameterization reasonably represents the majority of mineral dust measurements when taking into account that typically ∼1 % to 25 % of atmospheric desert dust can be attributed to K-feldspar (Atkinson et al., 2013) and that there is a natural variability in the ice-nucleating ability of K-feldspar (as represented by the shaded area around the 20 % K-feldspar prediction). The shape of the parameterization represents the bulk of the data well and plateaus at the lowest temperatures in agreement with the observations.
Figure 9b shows INP concentrations measured from an aircraft in the eastern tropical Atlantic (Price et al., 2018) plotted with the predicted INP concentrations based on the K-feldspar parameterization developed by Atkinson et al. (2013) (dashed black lines), the parameterization for desert dust by Niemand et al. (2012) (dashed blue lines) and the K-feldspar parameterization proposed here (solid red lines). The parameterizations were calculated assuming an externally mixed scenario (although both internal and external mixing assumptions produce a similar result in the regime where the measurements were made). The upper and lower bounds were calculated by incorporating the maximum and minimum in the aerosol surface area concentrations corresponding to the various aircraft measurements (23.8 to 1874 µm2 cm−3) (Price et al., 2018). K-feldspar was assumed to represent 20 % of the aerosol surface area, based on measurements by Kandler et al. (2011). Note that the small number of data points above ∘C have a very high uncertainty due to Poisson counting issues and should be regarded as upper limits. Price et al. (2018) and Sanchez-Marroquin et al. (2019) have described a sub-isokinetic sampling bias in the aircraft inlet, which results in an enhancement of aerosol surface area by roughly a factor of 2.5 for the used sampling conditions. We have therefore corrected the Price et al. (2018) data downwards by a factor of 2.5 (although on the log scale this makes a relatively small difference).
We can see that the Atkinson et al. (2013) parameterization is a relatively poor predictor of the INP concentration, especially at temperatures colder than about −15 ∘C. The parameterization by Niemand et al. (2012) tends to over-predict INP concentrations relative to the Price et al. (2018) data by about 1 order of magnitude. The K-feldspar parameterization proposed here better represents the magnitude, range and slope of the aircraft data. Overall, the new K-feldspar parameterization provides a good representation of the ice-nucleating activity of dust from field and laboratory studies and it further makes clear that quartz is of second-order importance for desert dust's ice-nucleating ability.
We have studied 10 quartz samples for their ice-nucleating ability in order to better understand and define the ice-activity of this abundant mineral. The chosen samples were all α-quartz, the most common silica polymorph found at the Earth's surface but included a variety of α-quartz types with varying degrees of impurities and different crystal habits. We found that the ice-nucleating activity of these samples is surprisingly variable, spanning about 10 ∘C. A total of 8 out of 10 of the quartz samples lay within −17 to −20 ∘C at ns(T)=10 cm−2, with two quartz samples, Bombay chalcedony and Atkinson quartz, being much more active (as active as K-feldspar). Overall, the quartz group of minerals tends to be less active than the K-feldspars, slightly less active than albite but more active than the plagioclase feldspars. In the future it would be interesting to probe the nature of the active sites on the two most active samples and to try to contrast these sites to those on the less active samples in order to further understand the nature of active sites and why they have such strongly contrasting characteristics.
Although quartz is regarded as a relatively chemically inert mineral the activity of some samples decreases with time spent in air and water. Most of the samples were sensitive to time spent in water but, interestingly, the most active sample activity did not change significantly even after many months in water. We note that the sensitivity to time in water displayed by most of the quartz samples studied here is in strong contrast to K-feldspars, which tend to be much more stable. Related to this, we also note that solutes can alter the ice-nucleating ability of mineral samples (Whale et al., 2018; Kumar et al., 2018, 2019a, b). Sensitivity to these ageing processes and solutes could be very important in determining the dominant INP types globally (Boose et al., 2019). Hence, we suggest further studies aim to build a better understanding of the relationship between the experimental observations and field-collected samples to determine the role of ageing in the atmosphere.
To investigate the relative importance of quartz to feldspars in the atmosphere we have proposed new active site density parameterizations for quartz, K-feldspar, plagioclase and albite. These parameterizations are based on a combination of the data presented here for quartz along with data available in the literature. Sparse data sets available for the albite and plagioclase mineral groups lead to lower confidence when creating parameterizations for these mineral groups. It is suggested that future studies expand on the current datasets of the ice-nucleating behaviour of minerals to improve these parameterizations. When using the newly developed parameterizations to predict INP concentrations in combination with typical atmospheric abundances of minerals, it is found that K-feldspar typically produces more INPs than milled quartz (or any other mineral). Also note that the parameterization for quartz is for freshly milled quartz and the ageing results presented here and elsewhere (Zolles et al., 2015; Kumar et al., 2019a) suggest that the active sites on quartz are removed upon exposure to air and water. Therefore, the parameterization for milled quartz should be regarded as an upper limit. Even with this upper limit, quartz is of secondary importance relative to K-feldspars, which appear to be less sensitive to ageing processes. In addition, we find that the newly developed K-feldspar parameterization is consistent with ns(T) literature measurements on desert dusts and better represents field measurements of INP concentrations in the dusty tropical Atlantic compared to the parameterizations by Atkinson et al. (2013) and Niemand et al. (2012). We hereby propose the use of this new K-feldspar parameterization when predicting INP concentrations related to mineral dusts.
Data for the various quartz samples presented in this paper are available at https://doi.org/10.5285/171726739bb54d0ba84cdde15c5b17ae (Harrison et al., 2019).
ADH designed the experiments with help from scientific discussions with BJM, TFW and JBM. Both KL and ADH performed the experiments. AS completed the calculations for the external mixing assumption used in Figs. 8b and 9a and assisted in the calculation of errors for the active site density measurements. MAH carried out Raman analysis of the chalcedony samples, and MDT helped in the assembly of the literature data. ADH prepared the manuscript with contributions from all co-authors.
We would like to take the opportunity to thank Lesley Neve for her contribution in the XRD analysis.
This research has been supported by the Natural Environment Research Council (grant no. NE/M010473/1), the European Research Council (ERC, MarineIce: grant no. 648661), Engineering and Physical Sciences Research Council (EPSRC, grant no. EP/M003027/1), and the Natural Environment Research Council (NERC, grant no. NE/M010473/1), along with Asymptote Ltd. (now part of GE Healthcare).
This paper was edited by Hinrich Grothe and reviewed by two anonymous referees.
Ansmann, A., Tesche, M., Seifert, P., Althausen, D., Engelmann, R., Fruntke, J., Wandinger, U., Mattis, I., and Müller, D.: Evolution of the ice phase in tropical altocumulus: SAMUM lidar observations over Cape Verde, J. Geophys. Res.-Atmos., 114, D17208, https://doi.org/10.1029/2008jd011659, 2009.
Applin, K. R. and Hicks, B. D.: Fibers of dumortierite in quartz, Am. Mineral., 72, 170–172, 1987.
Atkinson, J. D., Murray, B. J., Woodhouse, M. T., Whale, T. F., Baustian, K. J., Carslaw, K. S., Dobbie, S., O'Sullivan, D., and Malkin, T. L.: The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds, Nature, 498, 355–358, https://doi.org/10.1038/nature12278, 2013.
Avila, A., Queralt-Mitjans, I., and Alarcón, M.: Mineralogical composition of African dust delivered by red rains over northeastern Spain, J. Geophys. Res.-Atmos., 102, 21977–21996, https://doi.org/10.1029/97jd00485, 1997.
Bagnold, R. A.: The Physics of blown sand and desert dunes, Dover publicationsm Inc., New York, 10–37, 1941.
Blatt, H., Middleton, G., and Murray, R.: Origin of sedimentary rocks, Prentice-Hall, Inc., New Jersey, 245–275, 1980.
Boose, Y., Sierau, B., Garcia, I. M., Rodriguez, S., Alastuey, A., Linke, C., Schnaiter, M., Kupiszewski, P., Kanji, Z. A., and Lohmann, U.: Ice nucleating particles in the Saharan Air Layer, Atmos. Chem. Phys., 16, 9067–9087, https://doi.org/10.5194/acp-16-9067-2016, 2016a.
Boose, Y., Welti, A., Atkinson, J., Ramelli, F., Danielczok, A., Bingemer, H. G., Plötze, M., Sierau, B., Kanji, Z. A., and Lohmann, U.: Heterogeneous ice nucleation on dust particles sourced from nine deserts worldwide – Part 1: Immersion freezing, Atmos. Chem. Phys., 16, 15075–15095, https://doi.org/10.5194/acp-16-15075-2016, 2016b.
Boose, Y., Baloh, P., Plötze, M., Ofner, J., Grothe, H., Sierau, B., Lohmann, U., and Kanji, Z. A.: Heterogeneous ice nucleation on dust particles sourced from nine deserts worldwide – Part 2: Deposition nucleation and condensation freezing, Atmos. Chem. Phys., 19, 1059–1076, https://doi.org/10.5194/acp-19-1059-2019, 2019.
Broadley, S. L., Murray, B. J., Herbert, R. J., Atkinson, J. D., Dobbie, S., Malkin, T. L., Condliffe, E., and Neve, L.: Immersion mode heterogeneous ice nucleation by an illite rich powder representative of atmospheric mineral dust, Atmos. Chem. Phys., 12, 287–307, https://doi.org/10.5194/acp-12-287-2012, 2012.
Caquineau, S., Gaudichet, A., Gomes, L., Magonthier, M.-C., and Chatenet, B.: Saharan dust: Clay ratio as a relevant tracer to assess the origin of soil-derived aerosols, Geophys. Res. Lett., 25, 983–986, https://doi.org/10.1029/98gl00569, 1998.
Ceppi, P., Brient, F., Zelinka, M. D., and Hartmann, D. L.: Cloud feedback mechanisms and their represenation in global climate models, WIREs Climate Change, 8, 1–21, https://doi.org/10.1002/wcc.465, 2017.
Connolly, P. J., Möhler, O., Field, P. R., Saathoff, H., Burgess, R., Choularton, T., and Gallagher, M.: Studies of heterogeneous freezing by three different desert dust samples, Atmos. Chem. Phys., 9, 2805–2824, https://doi.org/10.5194/acp-9-2805-2009, 2009.
Deer, W. A., Howie, R. A., and Zussman, J.: An introduction to thr rock forming minerals, Longman group limited, London, 340–355, 1966.
Deer, W. A., Howie, R. A., and Zussman, J.: An introduction to the rock forming minerals, 2nd Edn., Addison Wesley Longman, Harlow, UK, 457–472, 1992.
DeMott, P. J., Möhler, O., Stetzer, O., Vali, G., Levin, Z., Petters, M. D., Murakami, M., Leisner, T., Bundke, U., Klein, H., Kanji, Z. A., Cotton, R., Jones, H., Benz, S., Brinkmann, M., Rzesanke, D., Saathoff, H., Nicolet, M., Saito, A., Nillius, B., Bingemer, H., Abbatt, J., Ardon, K., Ganor, E., Georgakopoulos, D. G., and Saunders, C.: Resurgence in Ice Nuclei Measurement Research, B. Am. Meteorol. Soc., 92, 1623–1635, https://doi.org/10.1175/2011bams3119.1, 2011.
DeMott, P. J., Prenni, A. J., McMeeking, G. R., Sullivan, R. C., Petters, M. D., Tobo, Y., Niemand, M., Möhler, O., Snider, J. R., Wang, Z., and Kreidenweis, S. M.: Integrating laboratory and field data to quantify the immersion freezing ice nucleation activity of mineral dust particles, Atmos. Chem. Phys., 15, 393–409, https://doi.org/10.5194/acp-15-393-2015, 2015.
DeMott, P. J., Möhler, O., Cziczo, D. J., Hiranuma, N., Petters, M. D., Petters, S. S., Belosi, F., Bingemer, H. G., Brooks, S. D., Budke, C., Burkert-Kohn, M., Collier, K. N., Danielczok, A., Eppers, O., Felgitsch, L., Garimella, S., Grothe, H., Herenz, P., Hill, T. C. J., Höhler, K., Kanji, Z. A., Kiselev, A., Koop, T., Kristensen, T. B., Krüger, K., Kulkarni, G., Levin, E. J. T., Murray, B. J., Nicosia, A., O'Sullivan, D., Peckhaus, A., Polen, M. J., Price, H. C., Reicher, N., Rothenberg, D. A., Rudich, Y., Santachiara, G., Schiebel, T., Schrod, J., Seifried, T. M., Stratmann, F., Sullivan, R. C., Suski, K. J., Szakáll, M., Taylor, H. P., Ullrich, R., Vergara-Temprado, J., Wagner, R., Whale, T. F., Weber, D., Welti, A., Wilson, T. W., Wolf, M. J., and Zenker, J.: The Fifth International Workshop on Ice Nucleation phase 2 (FIN-02): laboratory intercomparison of ice nucleation measurements, Atmos. Meas. Tech., 11, 6231–6257, https://doi.org/10.5194/amt-11-6231-2018, 2018.
Eriksen Hammer, S., Mertes, S., Schneider, J., Ebert, M., Kandler, K., and Weinbruch, S.: Composition of ice particle residuals in mixed-phase clouds at Jungfraujoch (Switzerland): enrichment and depletion of particle groups relative to total aerosol, Atmos. Chem. Phys., 18, 13987–14003, https://doi.org/10.5194/acp-18-13987-2018, 2018.
Field, P. R., Lawson, R. P., Brown, P. R. A., Lloyd, G., Westbrook, C., Moisseev, D., Miltenberger, A., Nenes, A., Blyth, A., Choularton, T., Connolly, P., Buehl, J., Crosier, J., Cui, Z., Dearden, C., DeMott, P., Flossmann, A., Heymsfield, A., Huang, Y., Kalesse, H., Kanji, Z. A., Korolev, A., Kirchgaessner, A., Lasher-Trapp, S., Leisner, T., McFarquhar, G., Phillips, V., Stith, J., and Sullivan, S.: Chapter 7. Secondary Ice Production – current state of the science and recommendations for the future, Meteor. Mon., 58, 1–20, https://doi.org/10.1175/amsmonographs-d-16-0014.1, 2017.
Gallagher, J. J.: Fractography of sand grains broken by uniaxial compression, Clastic particles: scanning electron microscopy and shape analysis of sedimentary and volcanic clasts, edited by: Marshall, J. R., Van Nostrand Reinhold, New York, USA, 189–228, 1987.
Glaccum, R. A. and Prospero, J. M.: Saharan aerosols over the tropical North Atlantic – Mineralogy, Mar. Geol., 37, 295–321, https://doi.org/10.1016/0025-3227(80)90107-3, 1980.
Goldich, S. S.: A Study in Rock-Weathering, J. Geol., 46, 17–58, https://doi.org/10.1086/624619, 1938.
Goreva, J. S., Ma, C., and Rossman, G. R.: Fibrous nanoinclusions in massive rose quartz: The origin of rose coloration, Am. Mineral., 86, 466–472, https://doi.org/10.2138/am-2001-0410, 2001.
Götze, J., Nasdala, L., Kleeberg, R., and Wenzel, M.: Occurrence and distribution of “moganite” in agate/chalcedony: a combined micro-Raman, Rietvel and cathodoluminescence study, Contrib. Mineral. Petr., 133, 96–105, 1998.
Harrison, A. D., Whale, T. F., Carpenter, M. A., Holden, M. A., Neve, L., O'Sullivan, D., Vergara Temprado, J., and Murray, B. J.: Not all feldspars are equal: a survey of ice nucleating properties across the feldspar group of minerals, Atmos. Chem. Phys., 16, 10927–10940, https://doi.org/10.5194/acp-16-10927-2016, 2016.
Heaney, P. J. and Post, J. E.: The widespread distribution of a novel silica polymorph in microcrystalline quartz varieties, Science, 255, 441–443, https://doi.org/10.1126/science.255.5043.441, 1992.
Herbert, R. J., Murray, B. J., Whale, T. F., Dobbie, S. J., and Atkinson, J. D.: Representing time-dependent freezing behaviour in immersion mode ice nucleation, Atmos. Chem. Phys., 14, 8501–8520, https://doi.org/10.5194/acp-14-8501-2014, 2014.
Herbert, R. J., Murray, B. J., Dobbie, S. J., and Koop, T.: Sensitivity of liquid clouds to homogenous freezing parameterizations, Geophys. Res. Lett., 42, 1599–1605, https://doi.org/10.1002/2014gl062729, 2015.
Hiranuma, N., Augustin-Bauditz, S., Bingemer, H., Budke, C., Curtius, J., Danielczok, A., Diehl, K., Dreischmeier, K., Ebert, M., Frank, F., Hoffmann, N., Kandler, K., Kiselev, A., Koop, T., Leisner, T., Möhler, O., Nillius, B., Peckhaus, A., Rose, D., Weinbruch, S., Wex, H., Boose, Y., DeMott, P. J., Hader, J. D., Hill, T. C. J., Kanji, Z. A., Kulkarni, G., Levin, E. J. T., McCluskey, C. S., Murakami, M., Murray, B. J., Niedermeier, D., Petters, M. D., O'Sullivan, D., Saito, A., Schill, G. P., Tajiri, T., Tolbert, M. A., Welti, A., Whale, T. F., Wright, T. P., and Yamashita, K.: A comprehensive laboratory study on the immersion freezing behavior of illite NX particles: a comparison of 17 ice nucleation measurement techniques, Atmos. Chem. Phys., 15, 2489–2518, https://doi.org/10.5194/acp-15-2489-2015, 2015.
Holden, M. A., Whale, T. F., Tarn, M. D., O'Sullivan, D., Walshaw, R. D., Murray, B. J., Meldrum, F. C., and Christenson, H. K.: High-speed imaging of ice nucleation in water proves the existence of active sites, Sci. Adv., 5, eaav4316, https://doi.org/10.1126/sciadv.aav4316, 2019.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
Isono, K. and Ikebe, Y.: On the Ice-nucleating Ability of Rock-forming Minerals and Soil Particles&lowast, J. Meteorol. Soc. Jpn. Ser. II, 38, 213–230, https://doi.org/10.2151/jmsj1923.38.5_213, 1960.
Iwata, A. and Matsuki, A.: Characterization of individual ice residual particles by the single droplet freezing method: a case study in the Asian dust outflow region, Atmos. Chem. Phys., 18, 1785–1804, https://doi.org/10.5194/acp-18-1785-2018, 2018.
Kandler, K., Schütz, L., Deutscher, C., Ebert, M., Hofmann, H., Jäckel, S., Jaenicke, R., Knippertz, P., Lieke, K., Massling, A., Petzold, A., Schladitz, A., Weinzierl, B., Wiedensohler, A., Zorn, S., and Weinbruch, S.: Size distribution, mass concentration, chemical and mineralogical composition and derived optical parameters of the boundary layer aerosol at Tinfou, Morocco, during SAMUM 2006, Tellus B, 61, 32–50, https://doi.org/10.1111/j.1600-0889.2008.00385.x, 2009.
Kandler, K., SchüTz, L., JäCkel, S., Lieke, K., Emmel, C., MüLler-Ebert, D., Ebert, M., Scheuvens, D., Schladitz, A., šEgviĆ, B., Wiedensohler, A., and Weinbruch, S.: Ground-based off-line aerosol measurements at Praia, Cape Verde, during the Saharan Mineral Dust Experiment: microphysical properties and mineralogy, Tellus B, 63, 459–474, https://doi.org/10.1111/j.1600-0889.2011.00546.x, 2011.
Kanitz, T., Seifert, P., Ansmann, A., Engelmann, R., Althausen, D., Casiccia, C., and Rohwer, E. G.: Contrasting the impact of aerosols at northern and southern midlatitudes on heterogeneous ice formation, Geophys. Res. Lett., 38, L17802, https://doi.org/10.1029/2011gl048532, 2011.
Kanji, Z. A., DeMott, P. J., Möhler, O., and Abbatt, J. P. D.: Results from the University of Toronto continuous flow diffusion chamber at ICIS 2007: instrument intercomparison and ice onsets for different aerosol types, Atmos. Chem. Phys., 11, 31–41, https://doi.org/10.5194/acp-11-31-2011, 2011.
Kanji, Z. A., Ladino, L. A., Wex, H., Boose, Y., Burkert-Kohn, M., Cziczo, D. J., and Krämer, M.: Overview of Ice Nucleating Particles, Meteorol. Mon., 58, 1.1–1.33, https://doi.org/10.1175/amsmonographs-d-16-0006.1, 2017.
Kibar, R., Garcia-Guinea, J., Çetin, A., Selvi, S., Karal, T., and Can, N.: Luminescent, optical and color properties of natural rose quartz, Radiat. Meas., 42, 1610–1617, https://doi.org/10.1016/j.radmeas.2007.08.007, 2007.
Koehler, K. A., Kreidenweis, S. M., DeMott, P. J., Petters, M. D., Prenni, A. J., and Möhler, O.: Laboratory investigations of the impact of mineral dust aerosol on cold cloud formation, Atmos. Chem. Phys., 10, 11955–11968, https://doi.org/10.5194/acp-10-11955-2010, 2010.
Koike, C., Noguchi, R., Chihara, H., Suto, H., Ohtaka, O., Imai, Y., Matsumoto, T., and Tsuchiyama, A.: Infrared Spectra of Silica Polymorphs and the Conditions of Their Formation, Astrophys. J., 778, 1–12, https://doi.org/10.1088/0004-637x/778/1/60, 2013.
Kumar, A., Marcolli, C., Luo, B., and Peter, T.: Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 1: The K-feldspar microcline, Atmos. Chem. Phys., 18, 7057–7079, https://doi.org/10.5194/acp-18-7057-2018, 2018.
Kumar, A., Marcolli, C., and Peter, T.: Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 2: Quartz and amorphous silica, Atmos. Chem. Phys., 19, 6035–6058, https://doi.org/10.5194/acp-19-6035-2019, 2019a.
Kumar, A., Marcolli, C., and Peter, T.: Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 3: Aluminosilicates, Atmos. Chem. Phys., 19, 6059-6084, https://doi.org/10.5194/acp-19-6059-2019, 2019b.
Lohmann, U.: Anthropogenic Aerosol Influences on Mixed-Phase Clouds, Curr. Clim. Change Rep., 3, 32–44, https://doi.org/10.1007/s40641-017-0059-9, 2017.
Losey, D. J., Sihvonen, S. K., Veghte, D. P., Chong, E., and Freedman, M. A.: Acidic processing of fly ash: chemical characterization, morphology, and immersion freezing, Environ. Sci. Process Impacts, 20, 1581–1592, https://doi.org/10.1039/c8em00319j, 2018.
Mahaney, W. C., Dirszowsky, R. W., Milner, M. W., Menzies, J., Stewart, A., Kalm, V., and Bezada, M.: Quartz microtextures and microstructures owing to deformation of glaciolacustrine sediments in the northern Venezuelan Andes, J. Quaternary Sci., 19, 23–33, https://doi.org/10.1002/jqs.818, 2004.
Mason, B. J. and Maybank, J.: Ice-nucleating properties of some natural mineral dusts, Q. J. Roy. Meteor. Soc., 84, 235–241, 1958.
Murray, B. J., Broadley, S. L., Wilson, T. W., Atkinson, J. D., and Wills, R. H.: Heterogeneous freezing of water droplets containing kaolinite particles, Atmos. Chem. Phys., 11, 4191–4207, https://doi.org/10.5194/acp-11-4191-2011, 2011.
Murray, B. J., O'Sullivan, D., Atkinson, J. D., and Webb, M. E.: Ice nucleation by particles immersed in supercooled cloud droplets, Chem. Soc. Rev., 41, 6519–6554, https://doi.org/10.1039/C2CS35200A, 2012.
Nassau, K.: The origins of color in minerals, Am. Mineral., 63, 219–229, 1978.
Niedermeier, D., Augustin-Bauditz, S., Hartmann, S., Wex, H., Ignatius, K., and Stratmann, F.: Can we define an asymptotic value for the ice active surface site density for heterogeneous ice nucleation?, J. Geophys. Res.-Atmos., 120, 5036–5046, https://doi.org/10.1002/2014jd022814, 2015.
Niemand, M., Möhler, O., Vogel, B., Vogel, H., Hoose, C., Connolly, P., Klein, H., Bingemer, H., DeMott, P. J., Skrotzki, J., and Leisner, T.: A particle-surface-area-based parameterization of immersion freezing on desert dust particles, J. Atmos. Sci., 69, 3077–3092, https://doi.org/10.1175/jas-d-11-0249.1, 2012.
O'Sullivan, D., Murray, B. J., Malkin, T. L., Whale, T. F., Umo, N. S., Atkinson, J. D., Price, H. C., Baustian, K. J., Browse, J., and Webb, M. E.: Ice nucleation by fertile soil dusts: relative importance of mineral and biogenic components, Atmos. Chem. Phys., 14, 1853–1867, https://doi.org/10.5194/acp-14-1853-2014, 2014.
Peckhaus, A., Kiselev, A., Hiron, T., Ebert, M., and Leisner, T.: A comparative study of K-rich and Na∕Ca-rich feldspar ice-nucleating particles in a nanoliter droplet freezing assay, Atmos. Chem. Phys., 16, 11477–11496, https://doi.org/10.5194/acp-16-11477-2016, 2016.
Pedevilla, P., Fitzner, M., and Michaelides, A.: What makes a good descriptor for heterogeneous ice nucleation on OH-patterned surfaces, Phys. Rev. B, 96, 115441, https://doi.org/10.1103/PhysRevB.96.115441, 2017.
Perlwitz, J. P., Pérez García-Pando, C., and Miller, R. L.: Predicting the mineral composition of dust aerosols – Part 1: Representing key processes, Atmos. Chem. Phys., 15, 11593–11627, https://doi.org/10.5194/acp-15-11593-2015, 2015.
Pinti, V., Marcolli, C., Zobrist, B., Hoyle, C. R., and Peter, T.: Ice nucleation efficiency of clay minerals in the immersion mode, Atmos. Chem. Phys., 12, 5859–5878, https://doi.org/10.5194/acp-12-5859-2012, 2012.
Pratt, K. A., DeMott, P. J., French, J. R., Wang, Z., Westphal, D. L., Heymsfield, A. J., Twohy, C. H., Prenni, A. J., and Prather, K. A.: In situ detection of biological particles in cloud ice-crystals, Nat. Geosci., 2, 398–401, https://doi.org/10.1038/ngeo521, 2009.
Price, H. C., Baustian, K. J., McQuaid, J. B., Blyth, A., Bower, K. N., Choularton, T., Cotton, R. J., Cui, Z., Field, P. R., Gallagher, M., Hawker, R., Merrington, A., Miltenberger, A., Neely Iii, R. R., Parker, S. T., Rosenberg, P. D., Taylor, J. W., Trembath, J., Vergara-Temprado, J., Whale, T. F., Wilson, T. W., Young, G., and Murray, B. J.: Atmospheric Ice-Nucleating Particles in the Dusty Tropical Atlantic, J. Geophys. Res.-Atmos., 123, 2175–2193, https://doi.org/10.1002/2017jd027560, 2018.
Pummer, B. G., Budke, C., Augustin-Bauditz, S., Niedermeier, D., Felgitsch, L., Kampf, C. J., Huber, R. G., Liedl, K. R., Loerting, T., Moschen, T., Schauperl, M., Tollinger, M., Morris, C. E., Wex, H., Grothe, H., Pöschl, U., Koop, T., and Fröhlich-Nowoisky, J.: Ice nucleation by water-soluble macromolecules, Atmos. Chem. Phys., 15, 4077–4091, https://doi.org/10.5194/acp-15-4077-2015, 2015.
Pye, K.: Sediment transport and depositional processes, edited by: Pye, K., Blackwell scientific publications, Oxford, Boston, 1–58, 1994.
Reicher, N., Segev, L., and Rudich, Y.: The WeIzmann Supercooled Droplets Observation on a Microarray (WISDOM) and application for ambient dust, Atmos. Meas. Tech., 11, 233–248, https://doi.org/10.5194/amt-11-233-2018, 2018.
Roberts, P. and Hallett, J.: A laboratory study of the ice nucleating properties of some mineral particulates, Q. J. Roy. Meteor. Soc., 94, 25–34, https://doi.org/10.1002/qj.49709439904, 1968.
Rosenfeld, D., Yu, X., Liu, G., Xu, X., Zhu, Y., Yue, Z., Dai, J., Dong, Z., Dong, Y., and Peng, Y.: Glaciation temperatures of convective clouds ingesting desert dust, air pollution and smoke from forest fires, Geophys. Res. Lett., 38, L21804, https://doi.org/10.1029/2011gl049423, 2011.
Sanchez-Marroquin, A., Hedges, D. H. P., Hiscock, M., Parker, S. T., Rosenberg, P. D., Trembath, J., Walshaw, R., Burke, I. T., McQuaid, J. B., and Murray, B. J.: Characterisation of the filter inlet system on the BAE-146 research aircraft and its use for size resolved aerosol composition measurements, Atmos. Meas. Tech. Discuss., https://doi.org/10.5194/amt-2019-196, in review, 2019.
Spencer, W. J. and Smith, W. L.: Defects in Natural Quartz, J. Appl. Phys., 37, 2557–2563, https://doi.org/10.1063/1.1782083, 1966.
Swamy, V., Saxena, S. K., Sundman, B., and Zhang, J.: A thermodynamic assessment of silica phase diagram, J. Geophys. Res.-Sol., 99, 11787–11794, https://doi.org/10.1029/93jb02968, 1994.
Tan, I., Storelvmo, T., and Zelinka, M. D.: Observational constraints on mixed-phase clouds imply higher climate sensitivity, Science, 352, 224–227, https://doi.org/10.1126/science.aad5300, 2016.
Tarn, M. D., Sikora, S. N. F., Porter, G. C. E., O'Sullivan, D., Adams, M., Whale, T. F., Harrison, A. D., Vergara-Temprado, J., Wilson, T. W., Shim, J. U., and Murray, B. J.: The study of atmospheric ice-nucleating particles via microfluidically generated droplets, Microfluid. Nanofluid., 22, 52, https://doi.org/10.1007/s10404-018-2069-x, 2018.
Ullrich, R., Hoose, C., Möhler, O., Niemand, M., Wagner, R., Höhler, K., Hiranuma, N., Saathoff, H., and Leisner, T.: A New Ice Nucleation Active Site Parameterization for Desert Dust and Soot, J. Atmos. Sci., 74, 699–717, https://doi.org/10.1175/jas-d-16-0074.1, 2017.
Umo, N. S., Murray, B. J., Baeza-Romero, M. T., Jones, J. M., Lea-Langton, A. R., Malkin, T. L., O'Sullivan, D., Neve, L., Plane, J. M. C., and Williams, A.: Ice nucleation by combustion ash particles at conditions relevant to mixed-phase clouds, Atmos. Chem. Phys., 15, 5195–5210, https://doi.org/10.5194/acp-15-5195-2015, 2015.
Vali, G., DeMott, P. J., Möhler, O., and Whale, T. F.: Technical Note: A proposal for ice nucleation terminology, Atmos. Chem. Phys., 15, 10263–10270, https://doi.org/10.5194/acp-15-10263-2015, 2015.
Vergara-Temprado, J., Murray, B. J., Wilson, T. W., O'Sullivan, D., Browse, J., Pringle, K. J., Ardon-Dryer, K., Bertram, A. K., Burrows, S. M., Ceburnis, D., DeMott, P. J., Mason, R. H., O'Dowd, C. D., Rinaldi, M., and Carslaw, K. S.: Contribution of feldspar and marine organic aerosols to global ice nucleating particle concentrations, Atmos. Chem. Phys., 17, 3637–3658, https://doi.org/10.5194/acp-17-3637-2017, 2017.
Vergara-Temprado, J., Miltenberger, A. K., Furtado, K., Grosvenor, D. P., Shipway, B. J., Hill, A. A., Wilkinson, J. M., Field, P. R., Murray, B. J., and Carslaw, K. S.: Strong control of Southern Ocean cloud reflectivity by ice-nucleating particles, P. Natl. Acad. Sci. USA, 115, 2687–2692, https://doi.org/10.1073/pnas.1721627115, 2018.
Wex, H., DeMott, P. J., Tobo, Y., Hartmann, S., Rösch, M., Clauss, T., Tomsche, L., Niedermeier, D., and Stratmann, F.: Kaolinite particles as ice nuclei: learning from the use of different kaolinite samples and different coatings, Atmos. Chem. Phys., 14, 5529–5546, https://doi.org/10.5194/acp-14-5529-2014, 2014.
Whale, T. F., Murray, B. J., O'Sullivan, D., Wilson, T. W., Umo, N. S., Baustian, K. J., Atkinson, J. D., Workneh, D. A., and Morris, G. J.: A technique for quantifying heterogeneous ice nucleation in microlitre supercooled water droplets, Atmos. Meas. Tech., 8, 2437–2447, https://doi.org/10.5194/amt-8-2437-2015, 2015.
Whale, T. F., Holden, M. A., Kulak, A. N., Kim, Y. Y., Meldrum, F. C., Christenson, H. K., and Murray, B. J.: The role of phase separation and related topography in the exceptional ice-nucleating ability of alkali feldspars, Phys. Chem. Chem. Phys., 19, 31186–31193, https://doi.org/10.1039/c7cp04898j, 2017.
Whale, T. F., Holden, M. A., Wilson, T. W., O'Sullivan, D., and Murray, B. J.: The enhancement and suppression of immersion mode heterogeneous ice-nucleation by solutes, Chem. Sci., 9, 4142–4151, https://doi.org/10.1039/c7sc05421a, 2018.
Wilson, M. J.: Weathering of the primary rock-forming minerals: processes, products and rates, Clay Miner., 39, 233–266, https://doi.org/10.1180/0009855043930133, 2004.
Wright, T. P., Petters, M. D., Hader, J. D., Morton, T., and Holder, A. L.: Minimal cooling rate dependence of ice nuclei activity in the immersion mode, J. Geophys. Res.-Atmos., 118, 10535–10543, https://doi.org/10.1002/jgrd.50810, 2013.
Zolles, T., Burkart, J., Häusler, T., Pummer, B., Hitzenberger, R., and Grothe, H.: Identification of Ice Nucleation Active Sites on Feldspar Dust Particles, J. Phys. Chem. A, 119, 2692–2700, https://doi.org/10.1021/jp509839x, 2015.