Core and margin in warm convective clouds – Part 2: Aerosol effects on core properties

The effects of aerosol on warm convective cloud cores are evaluated using single cloud and cloud field simulations. Three core definitions are examined: positive vertical velocity (W_core), supersaturation (RH_core), and positive buoyancy (B_core). As presented in Part 1 (Heiblum et al., 2019), the property $B_{\mathrm{core}}\subseteq {\mathrm{RH}}_{\mathrm{core}}\subseteq W_{\mathrm{core}}$ is seen during growth of warm convective clouds. We show that this property is kept irrespective of aerosol concentration. During dissipation core fractions generally decrease with less overlap between cores. However, for clouds that develop in low aerosol concentrations capable of producing precipitation, B_core and subsequently W_core volume fractions may increase during dissipation (i.e., loss of cloud mass). The RH_core volume fraction decreases during cloud lifetime and shows minor sensitivity to aerosol concentration.

It is shown that a B_core forms due to two processes: (i) convective updrafts – condensation within supersaturated updrafts and release of latent heat – and (ii) dissipative downdrafts – subsaturated cloudy downdrafts that warm during descent and “undershoot” the level of neutral buoyancy. The former process occurs during cloud growth for all aerosol concentrations. The latter process only occurs for low aerosol concentrations during dissipation and precipitation stages where large mean drop sizes permit slow evaporation rates and subsaturation during descent.

The aerosol effect on the diffusion efficiencies plays a crucial role in the development of the cloud and its partition to core and margin. Using the RH_core definition, it is shown that the total cloud mass is mostly dictated by core processes, while the total cloud volume is mostly dictated by margin processes. Increase in aerosol concentration increases the core (mass and volume) due to enhanced condensation but also decreases the margin due to evaporation. In clean clouds larger droplets evaporate much slower, enabling preservation of cloud size, and even increase by detrainment and dilution (volume increases while losing mass). This explains how despite having smaller cores and less mass, cleaner clouds may live longer and grow to larger sizes.

1 Introduction

Aerosols remain one of the largest sources of uncertainty in climate predictions, mainly via their effects on clouds (IPCC, 2013). Here we focus on the aerosol effects on warm clouds. Aerosols act as cloud condensation nuclei (CCN) during heterogeneous nucleation of cloud droplets (Köhler, 1936; Mason and Chien, 1962). The number, size, and composition of an aerosol distribution determine the initial cloud droplet size distribution (DSD). Polluted clouds (i.e., more aerosols) have more but smaller droplets and a narrower DSD compared to clean clouds (Andreae et al., 2004; Twomey, 1977). Changes in the initial DSD drive various effects and feedbacks on the cloud's evolution and key processes, such as droplet mobility, condensation–evaporation budgets, collision–coalescence, and entrainment (Jiang et al., 2006; Koren et al., 2015; Small et al., 2009; Xue and Feingold, 2006).

It is well known that an abundance of small droplets in a cloud (a narrow DSD) reduces the efficiency of the collision–coalescence process (Squires, 1958; Twomey, 1977; Warner, 1968), prolongs the diffusional growth time (Khain et al., 2005; Wang, 2005), and delays or even completely suppresses the initiation of precipitation (Albrecht, 1989; Hudson and Mishra, 2007; Hudson and Yum, 2001; L'Ecuyer et al., 2009). Moreover, in-cloud condensational growth is more efficient in consuming supersaturation because of the larger surface-area-to-volume ratio of droplets (Dagan et al., 2015a, b; Mordy, 1959; Pinsky et al., 2013; Reutter et al., 2009; Seiki and Nakajima, 2014). We note that throughout this work the word efficient will be used to describe both the rate and the total change of mass attributed to a microphysical process. The processes described above enable the more polluted cloud to condense more water and intensify its growth via increased release of latent heat (Kogan and Martin, 1994; Koren et al., 2014; Saleeby et al., 2015; Sheffield et al., 2015). The smaller droplets are also pushed higher in the atmosphere due to larger droplet mobility (Koren et al., 2014, 2015).

However, the increase in aerosol amount yields suppressing effects as well. An opposite effect should take place in the subsaturated regions of the cloud, where more numerous and smaller droplets increase the evaporation rate and loss of cloud mass (Grant and van den Heever, 2015; Saleeby et al., 2015; Storer and van den Heever, 2013). Henceforth evaporation will be referred to as a process (i.e., change of mass per unit of time) rather than complete evaporation of a water drop. Increased evaporation can promote entrainment mixing, which in turn mixes more subsaturated air into the cloud and further promotes evaporation (Jiang et al., 2006; Small et al., 2009; Xue and Feingold, 2006), effectively initiating a positive feedback between evaporation and mixing with the eventual suppression of cloud growth. This effect may also be accompanied by a suppressing effect of the larger water loading in polluted clouds, which contain more liquid water mass.

The competition between those opposing processes that are driven by enhanced aerosol loading determines the net aerosol effect on cloud properties such as cloud fraction, lifetime, albedo, mass, size, and precipitation amount. However, the sign and magnitude of such effects are non-trivial (Jiang and Feingold, 2006). Previous studies report opposing findings regarding the total aerosol effects on warm clouds (Altaratz et al., 2014). Some studies suggest cloud invigoration by aerosols (bigger and deeper clouds; Dey et al., 2011; Kaufman et al., 2005; Koren et al., 2014; Yuan et al., 2011), while some suggest cloud suppression or no effect at all (Jiang and Feingold, 2006; Li et al., 2011; Savane et al., 2015; Xue et al., 2008). Moreover, other work has shown that the precipitation susceptibility (i.e., quantifies the sensitivity of precipitation to the aerosol increase) has a non-monotonic behavior that reaches its maximum at intermediate liquid water path (LWP) values (Sorooshian et al., 2009), implying that the resultant aerosol effects are heavily dependent on cloud type and environmental conditions (Khain et al., 2008).

A different approach to aerosol effects suggests that cloud systems can be buffered to microphysical effects (Stevens and Feingold, 2009). Several studies have shown that given enough time for the cloud system to reach steady state, cloud macrophysical parameters (e.g., cloud fraction and rain yield) show similar results for various aerosol concentrations (Carrió and Cotton, 2014; Glassmeier and Lohmann, 2018; Seifert et al., 2015). Based on the idea that clouds can be partitioned to aerosol-limited, updraft-limited, or aerosol- and updraft-sensitive regimes (Reutter et al., 2009), a unified theory for the contradicting results regarding aerosol effects was suggested (Dagan et al., 2015b). Given an aerosol range that covers all three regimes, the competition between opposite processes leads to an optimum value of aerosol concentration regarding various cloud properties like total mass, cloud top, or rain (Dagan et al., 2015b). A cloud that develops under low aerosol concentration is aerosol limited, as it does not have enough collective droplet surface area to consume the available water vapor. On the other side of the trend, a cloud that develops in polluted environment (with more aerosols than the optimum) is influenced significantly by enhanced entrainment and larger water loading, causing suppression of cloud development. The optimal concentration is a function of the thermodynamic conditions (temperature and humidity profiles) and cloud size.

Environments that support larger cloud development will have larger cloud cores that are positively affected by aerosol increase and can be regarded as aerosol limited (i.e., on the ascending branch of the aerosol trend) up to a higher optimal aerosol concentration. Environmental conditions that support small clouds are more strongly affected by cloud suppression processes at the cloud margins (due to higher cloud surface-area-to-volume ratio) and would have a lower optimal aerosol concentration. This can explain why studies biased to smaller clouds (mostly numerical modeling studies) report cloud suppression and studies biased to larger clouds (mostly observational studies) report cloud invigoration. Similar conclusions were reached for the cloud field scale as well (Dagan et al., 2017).

In addition, it was shown that clouds impact differently the environmental thermodynamics according to the aerosol level in the field (Dagan et al., 2016; Seifert and Heus, 2013; Seifert et al., 2015). For example changes in aerosol loading impact the amount of precipitation reaching the surface and subsequently the evaporative cooling below cloud base and the organization patterns (Seifert and Heus, 2013; Seigel, 2014; Xue et al., 2008). Moreover, an increase in aerosol loading may increase evaporation rates around the margins and tops of clouds (Seigel, 2014; Stevens, 2007; Xue and Feingold, 2006), cooling the upper cloudy layer and increasing the convective instability. Therefore aerosol effects on phase changes and precipitation result in vertical redistribution of heat and moisture, which may either stabilize or destabilize the environment in which subsequent clouds grow (Seifert and Heus, 2013).

Irrespective of the definition chosen, the cloud's core and margin are dominated by different processes (Dagan et al., 2015b). These processes often compete with each other, with the dominant one changing along the cloud's evolution. For example, at the initial stage of cloud formation, a cloud is more adiabatic and is controlled by the core's processes (condensation), and when it dissipates the margin processes are more dominant (entrainment and evaporation). Aerosols affect each of these processes and thus each stage in the cloud's lifetime. As a continuation of Part 1 (Heiblum et al., 2019) of this work (hereafter PT1), in this part we analyze aerosol effects on the cloud's partition to core and margin throughout the lifetime of a cloud. We report the consequences that these effects have on evolution of a cloud in terms of volume, mass, and lifetime. As opposed to other works that typically focus on a single cloud core definition, here three different definitions are used (see Sect. 2), with emphasis placed on the sensitivity of each core definition to aerosol concentration. Moreover, the combination of single cloud with large-eddy simulations enables us to gain process-level understanding and test the robustness of our findings.

2 Methods

The analyses performed here are to the most part identical to those described in PT1 of this work. In this section we shall thus only give a brief review of the methods used. For single cloud simulations we use the Tel Aviv University axisymmetric cloud model (TAU-CM; Reisin et al., 1996), and for cloud field simulations we use the System for Atmospheric Modeling (SAM) model (version 6.10.3; for details see the following web page: http://rossby.msrc.sunysb.edu/~marat/SAM.html, last access: 10 October 2018; Khairoutdinov and Randall, 2003).

Both models utilize explicit bin-microphysics schemes (Khain et al., 2004; Tzivion et al., 1987), solving nucleation, diffusion (i.e., condensation and evaporation), collisional coalescence, breakup, and sedimentation microphysical processes. The single cloud model is initialized using a Hawaiian thermodynamic profile based on the 91285 PHTO Hilo radiosonde at 00:00 Z on 21 August 2007. The cloud field model is set up based on the BOMEX case study, including an initialization setup (sounding, surface fluxes, and surface roughness) and large-scale forcing setup (Siebesma et al., 2003). More details on the model setups and definitions can be found in PT1.

To study the effects of aerosols on the cloud cores we run each model setup with three different aerosol concentrations: clean – 25 cm⁻³, intermediate – 250 cm⁻³, and polluted – 2000 cm⁻³. The model domain is initialized using an oceanic size distribution (Altaratz et al., 2008; Jaenicke, 1988), maintaining a constant mixing ratio with height. The aerosol budget includes removal by nucleation and regeneration upon evaporation, while wet scavenging by precipitation removes aerosols from the domain. Thus, the aerosol concentration may be depleted by 20 %–40 % (depending on the precipitation amount) during the simulation. More on the treatment of aerosols in the cloud field model can be found in previous work (Heiblum et al., 2016a). As defined in PT1, all pixels with at least 0.01 g kg⁻¹ of liquid water are considered cloudy. Cloud cores are defined using three definitions: (1) RH_core : relative humidity >100 %, (2) B_core : buoyancy >0, and (3) W_core : vertical velocity >0. Relative humidity (RH) and vertical velocity (W) are standard outputs of the model, while the buoyancy (B) is calculated based on Eq. (1) in PT1, where each cloudy pixel is compared with the mean non-cloudy thermodynamic reference state per height.

In order to reduce the problem's dimensionality and distill signals in a cloud field system governed by high variance, we use the center of gravity vs. mass (CvM) phase space in combination with an automated 3-D cloud tracking algorithm (Heiblum et al., 2016a). The CvM phase space enables a compact view of all clouds in the simulation by projecting only their center-of-gravity (COG) height and mass at each output time step. Using the cloud tracking, it was shown that the lifetime of a cloud can be described by a trajectory on this phase space. Hence, the different locations in the CvM space are associated with different stages in a cloud's lifetime (i.e., growing, precipitating, and dissipating). For an in-depth explanation of the CvM space, the reader is referred to Sect. 2.4 in PT1 (see schematic illustration – Fig. 1, PT1).

3 Results – single cloud simulations

3.1 Sensitivity of different core types to aerosol concentration

Figure 1 presents time series of single cloud core volume fractions (f_vol) and cores' properties for three aerosol concentrations (clean, intermediate, and polluted). Also included are time series of instantaneous rain rates (mm h⁻¹) at the domain surface. For all aerosol concentrations and during most of the clouds' lifetimes, the volume fraction of W_core tends to be the largest and the volume fraction of B_core the smallest. Exceptions to this finding are seen either at the initial time step for the polluted cloud or in the later stages of cloud lifetime for the lower-concentration clouds. In addition, we find that RH_core⊆W_core for all stages of cloud lifetime while B_core⊆W_core, RH_core for all stages of the polluted cloud, but this only applies to the growing stages of lower-concentration clouds before precipitation production. Thus, the main finding from PT1 (i.e., $B_{\mathrm{core}}\subseteq {\mathrm{RH}}_{\mathrm{core}}\subseteq W_{\mathrm{core}}$) generally applies to all aerosol concentrations during the pre-precipitation stages of the clouds' lifetimes.

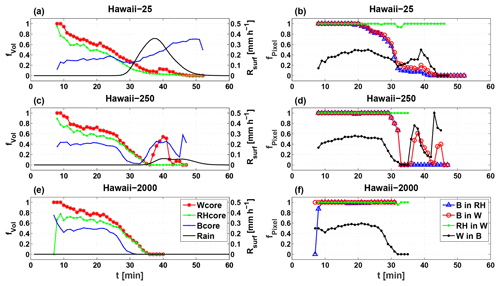
Figure 1 (a, c, e) Time series of core volume fractions (f_vol in %; left axis) and surface rain rate (R_surf in mm h⁻¹; right axis) for the clean (a), intermediate (c), and polluted (e) single cloud simulations. (b, d, f) Time series of pixel fractions (f_pixel in %) of one core type within another, for the respective simulation types. Core volume and pixel fractions are indicated by different line colors (see legends).

Lower-aerosol-concentration simulations produce more rain and at earlier stages of cloud lifetime due to efficient collision coalescence. The increase in the B_core volume fraction at later stages of cloud lifetime in those simulations (clean and intermediate) coincides with initiation of precipitation production followed by a consequent increase in the W_core volume fraction as well (more so for the intermediate concentration). This dissipating W_core is mostly contained within the B_core. The possible mechanism behind the increase in prevalence of buoyant parcels during precipitation is explored in Sect. 3.2. The lack of RH_core pixels at these stages indicates that the W_core is composed of pixels with small vertical velocities, insufficient for supersaturation production. The RH_core is the only one which is not sensitive to rain and monotonically decreases during all clouds' lifetimes. Another clear aerosol effect seen in Fig. 1 is an increase in cloud lifetime with a decrease in aerosol concentration. This point will be further explored in Sect. 3.3.

3.2 Mechanisms governing positive buoyancy

The theoretical arguments in PT1 showed that B_core should be the smallest of the three. This was shown for both the adiabatic cloud column case and also the non-adiabatic case, where entrainment mixing and consequent evaporation have a strong net negative effect on cloud buoyancy. Despite this fact, results show (see Fig. 1 and Fig. 2 in PT1) that pockets of positive buoyancy may form independently of the other cores during dissipation and precipitation stages, even though evaporation is to be expected then. Since positive buoyancy is the result of either higher temperature or vapor content (or both) than the surrounding environment, we choose to analyze these two terms during different stages of the single clouds' lifetimes. The liquid water content (LWC) buoyancy term (not shown here) is always negative and typically increases (in absolute value) with an increase in vertical velocity or total buoyancy.

Figure 2 shows the values of the temperature (B_T) and humidity (B_Qv) buoyancy terms in pixel buoyancy vs. pixel vertical velocity phase space. The scatterplots include all cloudy pixels during all time steps for the three different aerosol concentration simulations. The distribution of points for the polluted simulation shows a positive linear dependence of buoyancy on vertical velocity. Negative vertical velocity is associated with negative buoyancy, and positive vertical velocity shows a transition from negative to positive buoyancy with an increase in magnitude. For this case both B_T and B_Qv increase with an increase in vertical velocity, as is generally expected in convective clouds. The sign of pixel buoyancy is mostly dependent on B_T, since all pixels have positive B_Qv and a negative water loading term. This behavior is also seen for lower aerosol concentrations, where the sign of buoyancy is for the most part determined by B_T. Hereafter, we refer to positive buoyancy (both B_T and B_Qv) production within updrafts as updraft buoyancy.

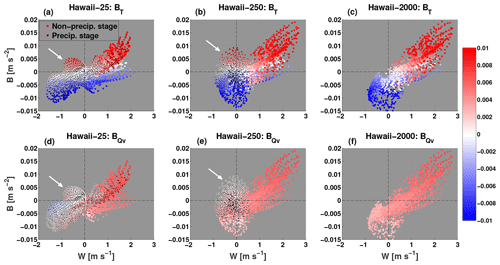
Figure 2 Scatterplots of pixel total buoyancy (m s⁻²) vs. pixel vertical velocity (m s⁻¹) for the clean (a, d), intermediate (b, e), and polluted (c, f) simulations. Data include all cloudy pixels during all time steps. Colors represent magnitude of buoyancy temperature term (B_T; a, b, c) and humidity term (B_Qv; d, e, f), where red (blue) shades indicate positive (negative) values. Markers with superimposed black dots represent temporal stages with non-zero surface precipitation. White arrows indicate outlier scatter of pixels with positive buoyancy and negative vertical velocity.

The clean and intermediate simulations show a similar dependence of buoyancy on vertical velocity; however, it is apparent that these simulations also include an outlier scatter region of pixels with positive buoyancy and weak negative vertical velocity which is absent in the polluted simulation (see white arrows; Fig. 2). Consistent with the rest of the cloudy pixels, these outlier pixels have positive B_T but differ in that they show neutral B_Qv. It can also be seen that these pixels are only attributed to the stages after surface precipitation has commenced (indicated by black dots in markers). Precipitation is indicative of both downdraft motion and abundance of large drop sizes.

Although not usually the focus of studies, the existence of positively buoyant downdrafts in convective clouds has been reported in both observations (Igau et al., 1999; Wei et al., 1998) and simulations (Xu and Randall, 2001; Zhao and Austin, 2005a, b). A possible explanation for this can be deduced from previous theoretical studies predicting mixing-induced downdrafts in cumulus clouds (Betts and Silva Dias, 1979; Betts, 1982). It was shown that in some cases cloud–environment mixtures are negatively buoyant (while still containing liquid water), and the consequent downdrafts can sometimes descend only partway down to the cloud base before reaching neutral buoyancy. Similar to convective overshooting, parcels with negative vertical momentum may then undershoot the downdraft equilibrium level and turn positively buoyant while the downdraft weakens. One can therefore expect the magnitude of positive buoyancy within the downdraft to reach a maximum when the velocity approaches zero. Hereafter we refer to positive buoyancy production within downdrafts as downdraft buoyancy.

Downdraft buoyancy production occurs frequently in cumulus fields because the negatively buoyant downdrafts follow a warming lapse rate which is more unstable than the environmental one, which is typically between the dry adiabat and moist adiabat (as is the case for the Hawaiian and BOMEX profiles simulated in this work). On one extreme, a descending parcel is least buoyant (i.e., coolest) when evaporation (after mixing) keeps it just barely saturated (Paluch and Breed, 1984, also PT1) so that the lapse rate of descent tends to be moist adiabatic and may remain negatively buoyant. On the other extreme, if little to no evaporation of liquid water occurs, the descent will follow the dry adiabat and switch to neutral (and then positive) buoyancy rapidly. Thus, the ability of a negatively buoyant cloudy downdraft to sustain itself depends on continuous inflow of liquid water (by mixing) and its consequent evaporation (Knupp and Cotton, 1985).

Indeed, the results in Fig. 2 match the hypothesis explained above, where positively buoyant downdrafts are warmer than the environment and tend to show larger buoyancy values for weaker downdraft velocities (especially for the intermediate case). Further analysis also shows that the more unsaturated the downdrafts (indicated also by low B_Qv), the larger the positive buoyancy. Moreover, the occurrence during precipitating stages and for lower aerosol concentrations indicates that slow evaporation due to larger drop sizes is crucial for downdraft buoyancy production, enabling a near-dry adiabatic lapse rate during descent.

3.3 The dependency of cloud characteristics on core and margin's processes

Here we evaluate how aerosol effects within the core and margin (using the three core definitions) affect the cloud characteristics, focusing on two main parameters: size (or volume) and mass. In Fig. 3 we follow the evolution of cloud, core, and margin mass and volume for different aerosol concentrations, using only the RH_core definition. We choose the RH_core, since it is the most stable out the core types, generally decreasing monotonically (see Fig. 1). A non-monotonic dependency of total cloud mass on aerosol concentration is seen, showing a maximum for the intermediate concentration. This type of dependency has been previously reported for warm cumulus clouds (Dagan et al., 2015b; Savane et al., 2015).

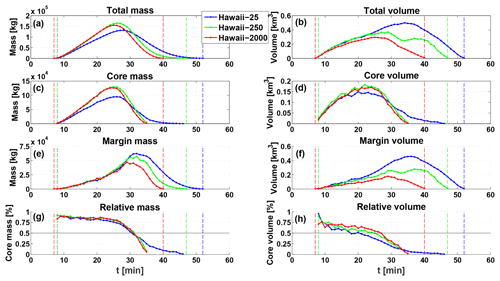
Figure 3 Time series of cloud mass (kg; a, c, e, g) and cloud volume (km³; b, d, f, h) for the different aerosol concentrations simulations (see legend). The total (a, b), core (c, d), margin (e, f), and relative fraction (g, h) values are shown for each parameter, as indicated by panel titles. The core here is defined according to RH > 100 % definition.

One can generally expect an increase in diffusion and decrease in collision–coalescence processes efficiency with an increase in aerosol concentration (Hudson and Yum, 2001; Jiang et al., 2009; L'Ecuyer et al., 2009; Pinsky et al., 2013), affecting both condensation and evaporation processes. The intermediate concentration shows the highest total mass as a result of being an optimal case, with higher condensation efficiency than the clean case and lower evaporation efficiency than the polluted case. It is convenient to represent the condensation and evaporation efficiencies by the RH_core and RH_margin mass, respectively. The intermediate cloud has almost identical core mass as the polluted cloud but retains higher mass in its margin as well. The clean cloud shows the lowest core mass but manages to accumulate the largest mass in its margin that dissipates slowly in subsaturated conditions. By comparing the total cloud mass evolution with the core and margin mass evolutions, it becomes clear that the total mass is primarily dependent on the cloud core. Another way to see this is by plotting the core mass fraction (Fig. 3g), which shows that clouds are core dominated (core fraction >0.5) with respect to mass for most of their lifetimes and for all aerosol concentrations.

With respect to cloud total volume, the lower the concentration, the larger the total cloud volume. We note that the cloud volume here excludes regions of precipitation below the initial cloud base height. By separating to core and margin regions, one can see that the total cloud volume is primarily dependent on the volume of the margin, which increases significantly with decreasing concentration. This is especially true during the dissipating stages of cloud lifetime, when the cloud is margin dominated. Although increasing the aerosol concentration does initially yield an increase in core volume (as was seen for the mass), the extents of the core size are typically smaller than those of the margin. There are large differences in the relative core volume percentage for the different clouds. The clean (polluted) cloud is margin (core) dominated with respect to volume for most of its lifetime. Excluding time of formation, the clean cloud shows the lowest core volume fractions but manages to maintain its core for the longest time span.

These results with respect to cloud volume can be attributed to the smaller drop sizes and higher diffusion efficiencies with an increase in aerosol concentration. Additionally, lower collision–coalescence efficiencies also maintain a narrow droplet spectrum of small droplets in the polluted cloud. During the growing stage a higher aerosol concentration may permit the cloud to condense more water, release more latent heat, and promote cloud growth. This explains the larger core volume sizes. However, after the cloud exhausts its convective potential (i.e., the growth of the convective core terminates and reaches its peak in mass), its main method of expansion is by mixing with the environment (i.e., detrainment and dilution). We note that precipitation can also be considered a method of expansion; however our choice to focus on volume above initial cloud base excludes this effect. Detrainment and mixing with the environment result in subsaturation conditions and evaporation of LWC. A clear indication for dilution is seen in Fig. 3, where between 30 and 35 min of simulation time, both the clean and polluted clouds lose total mass but only the clean cloud increases in total volume. The polluted cloud is composed of small drops, evaporates its margin regions efficiently, and is thus limited in horizontal growth by detrainment. The clean cloud is composed of larger drops, less efficient in evaporating its margins, and hence can grow by dilution of its LWC upon a larger volume. This large margin “shields” the core during dissipation stages and enables it to the live for a longer time.

The mechanism behind the results in Fig. 3 is demonstrated in Fig. 4, where horizontal cross-sections of mean (taken in the vertical dimension) cloud RH are shown for different stages during the clouds' lifetimes. For the polluted cloud, supersaturated or subsaturated conditions are rare. The RH throughout the cloud is near 100 % (almost always between 99.8 % and 100.2 %) except for a few pixels at its far edges which are a bit below 99 %. The polluted cloud resembles what one would expect to see using a moist adiabatic approximation (i.e., saturation adjustment), where all excess water vapor above saturation is converted to liquid water, mimicking infinitely efficient condensation (and evaporation).

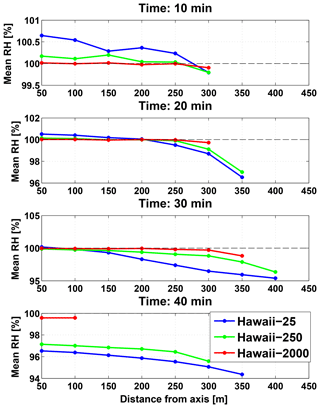
Figure 4 Four snapshots of horizontal cross-sections of RH (%; see panel titles for times). Panels include the results of different aerosol concentrations (see legend). Cross-sections are obtained by taking the mean RH of all vertical levels for each horizontal distance from the cloud center axis.

The clean cloud shows opposite behavior, with extremes of large supersaturation during cloud growth (initial stages) and large subsaturation during cloud dissipation (final stages). The large supersaturation can be explained by slow diffusional growth, but the large subsaturation also takes into consideration the larger drop sizes, which take more time to evaporate. This enables the clean cloud to expand to larger horizontal extents (by dilution and mixing with the environment without fully evaporating) and live for longer times. The intermediate aerosol concentration shows a midway scenario, where the supersaturation is consumed more efficiently than the clean case and at the same time much larger values of subsaturation may exist than those seen for the polluted case.

4 Results – cloud field simulations

In the following section we expand our analyses of aerosol effects on cloud core and margin from the single cloud scale to the cloud field scale. A cloud field can be considered to be composed of many individual clouds and thus can serve to test the robustness of the aerosol effects seen for a single cloud. Moreover, cloud fields include the added complexity of interactions between clouds and the clouds' effects on their thermodynamic environment.

4.1 Sensitivity of different core types to aerosol concentration

Here CvM space representations (see Sect. 2) are used to observe the core volume fractions of all clouds in BOMEX cloud field simulations. The rows in Fig. 5 represent different aerosol concentrations, while the columns represent different core type definitions. Different aerosol concentrations produce a vastly different scatter of clouds in the CvM space, as was previously discussed in depth (Heiblum et al., 2016b). The clean simulation (25 cm⁻³) shows two disconnected regions of cloud scatter: one which is adjacent to the adiabatic approximation and one of mainly small mass and high-COG clouds. The former region includes both clouds during their growth stages (smaller masses, LWP < 10 g m⁻²) and large precipitating entities (larger masses, LWP > 10 g m⁻²) which form due to merging processes (Heiblum et al., 2016b). The latter region (small mass and high COG) includes clouds at their dissipating stage, which form by the shedding mechanism off the large cloud entities. We note also the existence of small-mass elements well below the adiabat, representing precipitation cloud segments which shed off large precipitating clouds.

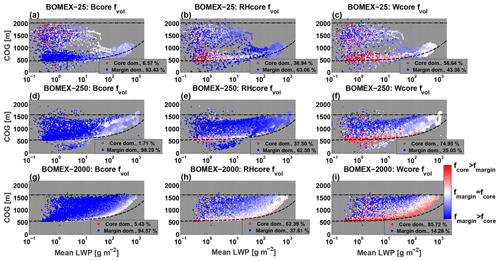
Figure 5 CvM phase-space diagrams of B_core (a, d, g), RH_core (b, e, h), and W_core (c, f, i) volume fractions (f_vol) for all clouds between 3 and 8 h in the BOMEX simulations. The rows correspond to the clean (a, b, c), intermediate (d, e, f), and polluted (g, h, i) aerosol cases. The red (blue) colors indicate a core f_vol above (below) 0.5. The size of each point in the scatter is proportional to the cloud mean area, where the smallest (largest) point corresponds to an area of 0.01 km² (11.4 km²). The percentage of clouds that are core dominated (f_vol>0.5) is included in panel legends. For an in-depth description of CvM space characteristics, the reader is referred to Sect. 2.4 in PT1.

The polluted simulation (2000 cm⁻³) shows a much more homogeneous scatter of clouds. The lower part of the scatter (closest to the adiabat) represents the cloud growing branch, while the rest of the scatter represents dissipating clouds, either by the gradual process of rising cloud base or by an immediate process of shedding off larger cloud entity (see Fig. 1, PT1). Precipitating cloud segments below the adiabat are absent from this simulation. The intermediate simulation (250 cm⁻³) shows a scatter which generally resembles the polluted case. However, the existence of relatively disconnected (from the main cloud scatter) small-mass cloud segments below the adiabat and near the inversion base height resembles the clean simulation as well. It should be noted that horizontal dashed lines in Fig. 5 represent the inversion base height after 5 h of simulation (approximately middle of simulation), where an increase in the inversion base height is seen with a decrease in aerosol concentration. This is due to increased net warming in the upper cloudy layer (i.e., release of latent heat during condensation with reduced local evaporation) with an increase in precipitation (Dagan et al., 2016; Heiblum et al., 2016b), which raises the inversion base.

The results in Fig. 5 show a consistent behavior of the core volume fractions for all aerosol concentrations, where the W_core type shows the largest fractions and the B_core type shows the smallest fractions. The W_core and RH_core generally show a decrease in core fractions along the growing branch, while the B_core fraction initially increases with cloud growth and then decreases for the large-mass growing clouds. The percentages in the panel legends (Fig. 5) indicate the fraction of clouds (out of the scatter) which are core dominated with respect to volume (f_vol > 0.5). For all concentrations, less than 7 % of clouds are B_core dominated, while more than 55 % are W_core dominated (with RH_core percentages somewhere in between). The B_core typically occupies a small portion of a typical cloud volume, while the W_core typically occupies most of the cloud. The mean cloud area (proportional to scatter point size) shows an increase with the increase in mean cloud LWP.

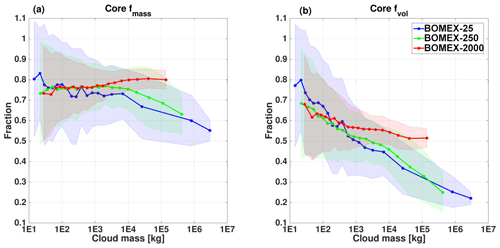
Figure 6 Average core mass fraction (a) and volume fraction (b) values for different aerosol concentrations, as indicated in the legend. The average only includes growing branch clouds from within the CvM space (i.e., clouds located in proximity to the adiabat). The core here is defined according to RH > 100 % definition.

These results are consistent with PT1 and the single cloud simulations in Sect. 3.1. Nevertheless, some significant aerosol effects on the partition to core types can be seen. Focusing on the growing branch first (i.e., clouds located near the adiabat), we note the following:

1. For the RH_core type, the core volume fractions of clouds after formation (i.e., with small mass) increase with decreasing aerosol concentration. This effect was also seen for the single cloud simulations and can be explained by the reduced efficiency of supersaturation consumption for fewer aerosols.

2. The B_core volume fraction increases at smaller mass values (or earlier in cloud's lifetime) and to higher values for increasing aerosol concentration. This effect is complementary to the previous one, since efficient consumption of supersaturation should result in more latent heat release and positive buoyancy.

3. The core volume fractions of the largest mass clouds increase with increasing aerosol concentration for all core types.

4. The mean area of large-mass clouds increases significantly with a decrease in aerosol concentration.

We also note a general increase in the fraction of clouds that are W_core or RH_core dominated with an increase in aerosol concentration, meaning adding aerosols shift a cloud from being mostly margin to being mostly core. The B_core is an exception, since the clean case shows the highest fraction of B_core-dominated clouds, and both the clean and polluted cases are more B_core dominated than the intermediate case. This can be explained by the different mechanisms of buoyancy production (see Sects. 3.2 and 4.2), where the polluted case is positively influenced by updraft buoyancy production and a larger core volume fraction, while the frequently precipitating clean case is positively influenced by downdraft buoyancy production. For the dissipating branch clouds, a highly variable pattern of core volume fractions can be seen, especially for the small-mass clouds. For all aerosol concentrations, these small cloud fragments can be either core dominated, margin dominated, or equally partitioned. One can assume that these differences can be related to the different mechanisms by which cloud fragments form, either by gradual dissipation of a large cloud or by instantaneous shedding of a large cloud. As for aerosol effects on the dissipating clouds, we see the following:

1. Higher RH_core- and W_core-volume fractions for gradually dissipating clouds (by rising cloud base) with an increase in aerosol concentration. This is manifested by a slower transition from red to blue colors in Fig. 5. It can be explained by the fact that more aerosols increase the convective intensity and extend the core size, while efficiently losing the margins, yielding a higher-core-volume fraction out of the total cloud.

2. The likelihood of finding dissipating cloud fragments with a B_core increases with a decrease in aerosol concentration. For the polluted case most of the dissipating clouds lack a B_core. This effect was seen in Fig. 1 and explained in Sect. 3.2, showing that downdrafts promote heating and positive buoyancy in low aerosol concentration cases where evaporation efficiency (and hence cooling) is limited. This effect is checked for the cloud field scale in Sect. 4.2.

As opposed to the single cloud simulations (Sect. 3) where cloud lifetime can be easily defined, in cloud field simulations (especially the cleaner cases) many clouds do not live as individual clouds from formation to dissipation but rather split and merge with other clouds continuously (Heiblum et al., 2016b). Thus, in order to evaluate the lifetime evolution of cores in cloud fields, we focus on the growing branch and use cloud mass (kg) as a proxy for the cloud lifetime during its initial and mature stages. We assume that in the vicinity of the growing branch a larger mass corresponds to a later stage in its lifetime.

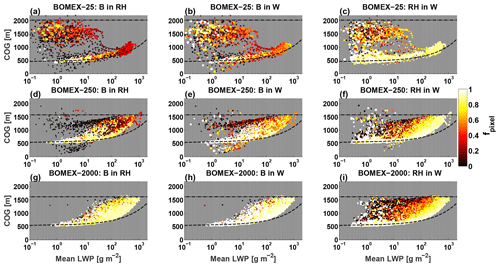
Figure 7 CvM space diagrams showing the pixel fractions (f_pixel) of B_core within RH_core (a, d, g), B_core within W_core (b, e, h), and RH_core within W_core (c, f, i) for the clean (top row, a, b, c), intermediate (middle row, d, e, f), and polluted (bottom row, g, h, i) simulations. Bright colors indicate high-pixel fractions (large overlap between two core types), while dark colors indicate low-pixel fractions (little overlap between two core types). The differences in the scatter density and location for different panels are due to the fact that only clouds which contain a core fraction above zero (for the core in question) are considered.

In Fig. 6 the core mass and volume fractions (f_mass and f_vol, using the RH definition) of all growing branch clouds are sorted by mass for the three aerosol concentrations. We note that the higher cloud masses reached by lower-aerosol-concentration simulation can be explained by cloud field organization effects due to precipitation (i.e., increased merging of clouds) rather than increased cloud condensation (Heiblum et al., 2016b; Seigel, 2014). The clean case starts off with the highest core fractions (both mass and volume), which decrease steadily with an increase in mass (or increase in lifetime). For all concentrations, most of the cloud mass is concentrated in the core region. The polluted case shows a slight increase in core mass fractions with increase in mass, while the other two cases show decreases in core mass fractions.

The core volume fractions show lower values than the mass fractions. The clean clouds are margin dominated for most masses, and the polluted clouds are core dominated for all masses. The intermediate case is generally confined to values between the other two cases. Figure 6 can be considered comparable with the lower panels in Fig. 3g and h, but excluding the dissipating part of those time series. The similar findings in both figures indicate the robustness of the aerosol effects on core properties in clouds.

Following the analyses of Sect. 3.1, we next test how aerosol concentration affects the subset properties of one core type within another for all clouds in a field (Fig. 7). We focus only on the typically smaller-sized cores (B_core, RH_core) within larger-sized cores. Out of the three permutations, the RH_core inside W_core shows the lowest sensitivity to aerosol. All three growing branches (for the different aerosol concentrations) consistently show that the RH_core is a subset of W_core (i.e., RH_core⊆W_core), while the dissipation branches show much lower overlap fraction between the two cores.

For the dissipating clouds in general, the lower the mass and the higher the COG, the smaller the overlap. The dissipating branches do include a scatter of small cloud for which RH_core⊆W_core, comprised of small cloud segments which shed off the main core regions of larger clouds. These findings slightly differ from those of the single cloud simulations that show RH_core⊆W_core for their entire lifetimes, while for cloud fields this property breaks down during dissipation. This difference highlights the importance of cloud interactions (i.e., splitting and merging) and cloud field air flow patterns (i.e., organized advection, updrafts, and downdrafts) in determining the relationships between core types, enabling supersaturation and downdrafts to coincide in small dissipating clouds.

The other two permutations (i.e., B_core inside RH_core, W_core) show significant changes due to aerosol. For the polluted case, B_core⊆W_core for nearly all clouds, including clouds at initial stages of dissipation. Similar results are seen for B_core inside RH_core, but with slightly lower pixel fractions. The polluted case thus illustrates the case of buoyancy production due to convective updraft. For the lower aerosol concentrations, two main aerosol effects are seen:

1. The lower the concentration, the lower the chance that B_core is a proper subset of the other cores for large growing branch clouds.

2. The lower the concentration, the more prevalent the independent dissipating branch B_core that has little to no overlap with the other cores.

For the case of B_core within RH_core, the lower concentrations show an almost-binary scenario where either B_core⊆RH_core or B_core∉RH_core. These results bear similarity to the single cloud simulations, where a quick transition (in time) from B_core⊆RH_core to B_core∉RH_core was seen. These results imply the existence of two different buoyancy production processes (more in Sect. 4.2), one associated with supersaturation and the other with subsaturation. In contrary, pixels fractions of B_core inside W_core span the entire range of values (i.e., partial overlaps between the core types), as seen for both single clouds and cloud fields during dissipation. This is to be expected due to a more direct physical link and feedbacks between the B_core and W_core.

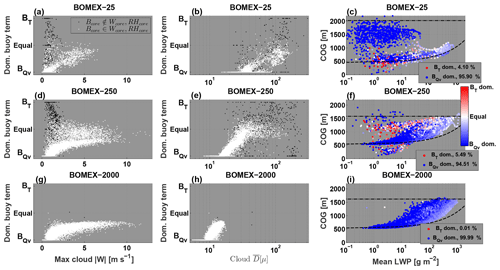
Figure 8 Analyses of dominant buoyancy term within B_core of clouds (see text for details). As seen in previous figures, rows represent clean (top, a, b, c), intermediate (middle, d, e, f), and polluted (bottom, g, h, i) simulations. Columns represent dependence on maximum absolute vertical velocity within cloud (a, d, g), dependence on partition of total cloud mass to cloud droplets and rain drops (b, e, h), and CvM space diagrams of all clouds with B_core, where red (blue) shades indicate temperature (humidity) buoyancy terms that dominate the cloud (c, f, i). Legends include percentage of clouds that are B_T or B_Qv dominated (see text for explanation).

4.2 Analysis of cloud field buoyancy

In Sect. 3.2 it was seen that for single clouds, positive buoyancy results from two main mechanisms: (i) convective updrafts – where updrafts promote supersaturation and latent heat release, and thus always positive B_Qv and frequently positive B_T – and (ii) dissipative downdrafts – where subsaturated cloudy downdrafts promote a positive B_T and neutral B_Qv. The latter case is dependent on low evaporation efficiency and hence seen mostly for precipitating stages of low aerosol concentration simulations. In Fig. 8 we perform a similar test for the cloud field scale. Instead of analyzing pixel by pixel, we check whether each buoyancy core within a cloud is B_T or B_Qv dominated. To quantify this we use a normalized buoyancy dominance parameter $\frac{\mathrm{\Sigma }{\mathrm{pixel}}_{B_{\mathrm{T}}>\mathrm{0}}-\mathrm{\Sigma }{\mathrm{pixel}}_{B_{\mathrm{Qv}}>\mathrm{0}}}{\mathrm{\Sigma }{\mathrm{pixel}}_{B>\mathrm{0}}}$, where a core comprised of only B_T>0 (B_Qv>0) pixels yields 1 (−1). Hence, we expect negative (positive) values to indicate dominance of updraft buoyancy (downdrafts buoyancy).

Analysis of the buoyancy components in the CvM space (Fig. 8c, f, and i) shows that the large majority of clouds are B_Qv dominated. For all concentrations, clouds initiate with all pixels showing B_Qv>0. As clouds develop along the growing branch the B_core becomes more abundant with B_T>0 pixels. This is expected with increasing release of latent heat during cloud growth. During dissipation B_Qv again becomes the dominant component for the majority of clouds. The polluted simulation shows an extreme case where all buoyancy cores in the simulation are B_Qv dominated, while for the lower concentrations a portion of the dissipating and precipitating clouds are B_T dominated.

Thus, we hypothesize that the polluted simulation only permits buoyancy cores of the updraft type which intersect with the other core types (i.e., B_core∈RH_core, W_core), while the lower concentrations also permit buoyancy cores of the downdraft type which do not intersect with the other core types (i.e., B_core∉RH_core, W_core). We test this by observing the relation of cloud maximum absolute vertical velocity (Fig. 8a, d, and g) and mean drop size (Fig. 8b, e, and h) with the relative dominance of the buoyancy terms. Absolute vertical velocity is chosen to represent both updrafts and downdrafts. The data are further separated into independent (B_core∉RH_core, W_core) and dependent (B_core∈RH_core, W_core) buoyancy subsets of the data by that separating to buoyant cores within updrafts and downdrafts. Clear aerosol effects are seen on cloud mean drop size and maximal $\left|W\right|$. As expected, there is a decrease in drop size with increase in aerosol concentration and increase in maximal velocity. Regarding cloud field buoyancy, as predicted, the independent buoyancy cores are more frequently B_T dominated than the dependent buoyancy cores.

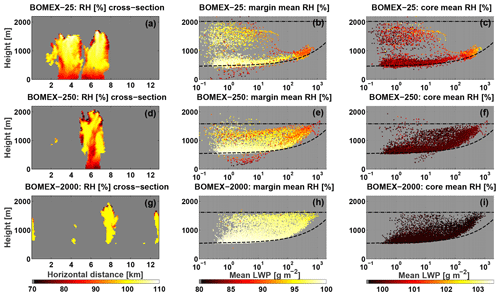
Figure 9 (a, g, g) Relative humidity (RH; %) vertical cross-sections slicing through the center of gravity of the most massive cloud in each simulation. (b, e, h) and (c, f, i) display CvM space diagrams of mean cloud margin RH and mean cloud core RH, respectively, using the RH_core definition. The upper (a, b, c), middle (d, e, f), and lower (g, h, i) panels correspond to the clean, intermediate, and polluted aerosol cases. Notice that the different color bar ranges for margin and core mean RH panels.

The polluted case is populated with dependent cores (white scatter) and shows a classic pre-precipitation convective growth scenario, where relative dominance of the B_T term increases linearly with increase in cloud mean drop size. A logarithmic dependence of B_T dominance on maximal $\left|W\right|$ is seen, which saturates at high maximal $\left|W\right|$. This can be explained by the fact that increased convection mainly increases the abundance of pixels with B_T>0, but without changing the fact that the entire cloud is B_Qv>0, so that B_T is unlikely to become the dominant term. The lower concentrations show a more complex scenario. These simulations show a superposition of dependent core convective growth behavior (i.e., the scatter pattern seen for the polluted case) and additional populations of both dependent (other white scatter points) and independent (black scatter) cores.

The independent cores span all the range of possibilities of B_T and B_Qv relative dominance. They tend to have larger cloud mean drop sizes, and a near-zero maximum $\left|W\right|$, indicating that they only form at late non-convective stages of cloud development. Furthermore, a trend is seen for the subset of scatter that is B_T dominated, where a positive (negative) correlation between mean drop size (maximal $\left|W\right|$) and B_T dominance is seen. This again stresses the importance of drop size on the formation of positive buoyancy within downdrafts and highlights the fact that B_T should be largest (and most abundant) below the downdraft equilibrium level, when the $\left|W\right|$ approaches zero. The independent cores that are B_T dominated thus fulfill the characteristics of the downdraft buoyancy production process, while the independent cores that are B_Qv dominated may originate from larger clouds (shedding mechanism) with high humidity content, have weak $\left|W\right|$, and are slow to evaporate.

The intermediate simulation shows an additional scatter area of dependent core clouds with increasing B_T relative dominance for lower maximal $\left|W\right|$, located between the independent core clouds and the convective growth core clouds. These clouds may represent a gradual transition from B_Qv dominance to B_T dominance during dissipation which is only possible in the intermediate simulation. This scatter area is absent from the clean and polluted simulation, in the former case due to absence of the gradual dissipation pathway and in the latter case due to efficient evaporation eliminating B_core during dissipation. We note that the intermediate case shows a slightly higher percentage of clouds that are B_T dominated (see legends in Fig. 8) than the clean case. This can be due to stronger convection in this simulation (i.e., increased $\left|W\right|$ range), which favors increased mixing with the dry environment (see Fig. 9) and the formation of unsaturated strong downdrafts that descend below the level of neutral buoyancy.

4.3 Aerosol effects on cloud relative humidity

From Fig. 3 it was demonstrated that a large part of the differences in single cloud characteristics (such as mass, volume, and the partition of these to core and margin regions) due to aerosols can be attributed to differences in vapor diffusion efficiencies. In Fig. 9 we check how these aerosol effects are manifested in the cloud field scale (using the CvM space) by observing the mean RH in the cloud core and margin of all clouds, where the core (margin) mean RH can be taken as a proxy for condensation (evaporation) efficiency. To gain additional intuition regarding the distribution of RH values within the clouds, vertical cross-sections (parallel to the prevailing wind direction) of the most massive clouds from each simulation are shown.

The vertical cross-sections demonstrate the large differences in the massive clouds for each of the simulations. In addition to the increase in precipitation production, lower aerosol concentrations yield much larger horizontal extents of clouds. The clean, intermediate, and polluted most massive clouds have a maximum radius of ∼3, ∼1, and ∼ 0.5 km, respectively. It is clear from the cross-section that the clean cloud is actually composed of two large clouds which merge together. For the clean case, the highest RH values are reached slightly below the cloud top. The edges of the clouds show subsaturation conditions, with the lowest RH values observed below the lifting condensation level (LCL; precipitation regions) and at the upper interface of the cloud with the environments.

The intermediate-case cloud shows lower maximal and minimal RH values and an increased dominance of the margin region. This cloud penetrates the inversion layer and entrains dry air into the cloud. In addition, the cloud produces significant precipitation which initiates downdrafts of dry entrained air through the cloud center. It can be seen that the increased vertical development of the intermediate-case cloud in comparison with the clean case increases the mixing with the environment. Thus, the dynamic effect of increased mixing and reduction in cloud RH overcomes the microphysical effect of increased evaporation and increase in cloud RH. The polluted-case cloud, on the other hand, shows a homogeneous RH pattern, with most of the cloud showing around 100 % RH and only a thin layer at the cloud edges (mainly at the upper regions) showing lower RH values. The polluted cloud penetrates the inversion layer as well, but this case lacks precipitation, and the microphysical effect of evaporation overcomes the dynamical effect of mixing.

Keeping in mind the insights obtained from comparisons of individual cloud, we move on to compare the RH characteristics of all clouds within the field. Looking first at core mean RH, a robust decrease is seen with increase in aerosol concentration. This decrease is seen for all cloud types and locations within the CvM space. The polluted case displays the most homogeneous pattern, with all clouds showing core mean RH values around 100 %, indicating efficient consumption of the supersaturation. The intermediate case displays a slightly less homogeneous pattern, with values ranging from 100 % to 101 % and with the higher values occurring along the growing cloud branch, especially for the largest clouds. The clean case shows the largest variance in core mean RH, ranging from 100 % for some cloud fragments that soon start to dissipate to 103 % in the cores of the large cloud entities. In addition to the low efficiency in consuming supersaturation, the high RH values in clean large clouds are due to the “protection” by large margin regions surrounding the core region.

The CvM patterns of mean margin RH show significant differences between the polluted case and the other two. The mean margin RH values of the polluted case are only marginally lower than 100 %, since subsaturated conditions within the cloud are quickly adjusted by efficient evaporation. Only the largest clouds in the polluted case permit lower mean margin RH values (∼95 %) due to the entrainment of very dry environmental pixels near the cloud tops (as seen in the vertical cross-section as well). The intermediate and clean cases show similar patterns. The smaller mass clouds (both growing and dissipating) show values above 95 %, while the larger mass clouds show values as low as 85 %. The larger clouds are most likely to reach low-RH areas near the inversion base and below the LCL (i.e., sub-cloudy layer) and entrain dry air and by that reduce the cloud margin RH.

As seen in the vertical cross-section examples, the largest clouds in the intermediate case have even lower margin RH values than for the clean case. This can be explained by the increased development of the large intermediate clouds to heights with lower RH and by more intense downdrafts for these large clouds. The lowest RH values in the domain are seen for the precipitating fragments (i.e., located below the adiabat). These fragments typically contain low concentrations of large drop sizes (precipitation drops) which are slow to evaporate and capable of surviving in low-RH conditions within the sub-cloudy layer.

5 Summary

In this work we explored how the aerosol effects on warm convective clouds are reflected in their partition to core and margin regions. Following Part 1 of this work (PT1), we evaluated three types of core definitions: positive buoyancy (B_core), supersaturation (RH_core), and positive vertical velocity (W_core). Both single cloud and cloud field models have been used. For all aerosol concentrations (clean, intermediate, and polluted), it is shown that the self-contained property of different core types (i.e., $B_{\mathrm{core}}\subseteq {\mathrm{RH}}_{\mathrm{core}}\subseteq W_{\mathrm{core}}$) is maintained for clouds during their growing and mature stages. This is especially robust for the RH_core⊆W_core subset. The W_core and RH_core volume fractions decrease monotonically during cloud growth, while B_core initially increases and then decreases after convection ceases. During growth, the RH_core (B_core) volume fractions are largest for clean (polluted) clouds. This is due to low (high) diffusion efficiencies, respectively, where efficient condensation promotes B_core at the expense of the RH_core.

During dissipation stages cores frequently cease to be subsets of one another and may either increase or decrease in their volume fractions. In cloud fields we also observe small cloud fragments which shed off larger cloud entities. This shedding increases for the lower-concentration simulations which produce long-lived large cloud entities due to cloud merging. These fragments show large variance in volume fraction (for all core types) magnitudes without any consistent behavior. This is due to the fact that they shed off various locations of the cloud. The polluted, non-precipitating cases are unique in that can one expect the B_core to decrease monotonically and remain the smallest and a proper subset of the other cores.

For low aerosol concentrations, a B_core may form during dissipation and exist independently of the other core types. These cores are typically located at the periphery of large clouds or throughout small precipitation or dissipating cloud fragments. The increase in B_core during dissipation typically coincides with large drop sizes and precipitation production. The fluctuations in B_core for low concentrations may also create a subsequent W_core but not of sufficient strength to also create a RH_core. Hence, the RH_core can be considered the most “well-behaved” and indicative of cloud lifetime, generally monotonically decreasing in volume fraction irrespective of aerosol concentration.

We show that the B_core in the warm convective cases considered here may form by two main processes:

1. Convective updrafts. Adiabatic cooling within updrafts promotes supersaturation, condensation, and release of latent heat. These cores are characterized by both positive temperature (B_T>0) and humidity (B_Qv>0) buoyancy terms.

2. Dissipative downdrafts. Subsaturated cloudy downdrafts follow a lapse rate which is unstable relative to the environmental one. These downdrafts undershoot the equilibrium level and become positively buoyant. These cores are characterized by positive temperature (B_T>0) but neutral humidity (B_Qv∼0) buoyancy terms.

The updraft buoyancy type is seen for all aerosol concentrations, while the dissipation buoyancy type is only seen for lower aerosol concentrations. The fact that the downdraft B_core is absent from polluted clouds highlights the importance of drop size and its effect on evaporation rate. The high (low) diffusion (collision coalescence) efficiencies in polluted clouds maintain a small mean drop size and enable rapid evaporation during entrainment, causing a negative effect on buoyancy. For lower concentrations, clouds with a downdraft B_core that only exist during late mature, dissipation, and precipitating stages after drop size have grown considerably. The larger mean drop sizes reduce evaporation rates, and the cloudy downdrafts may thus descend nearly dry adiabatically and become positively buoyant.

Focusing on cores using the RH definition, a cloud's mass (volume) is dependent primarily on the processes in its core (margin). The core increases cloud mass by condensation while the margin increases the cloud's volume by mixing with the environment or dilution. The magnitude of the effects in each region of the cloud is strongly dependent on the aerosol concentration. Polluted clouds are core dominated both in terms of mass and volume, since they can hardly maintain their margins. Clean clouds are also core dominated in terms of mass but to a lesser degree. Clean clouds tend to be margin dominated in terms of volume for most their lifetimes. Thus, despite weaker convection in the clean clouds, their large, slow evaporating margins enable their cores (and the entire cloud) to exist for longer time spans by applying a large protecting shield around the core.

The different diffusion efficiencies are demonstrated by observing the relative humidity (RH) values in clouds. Cleaner clouds show larger variance in RH values. During their growing stages large supersaturation in the core and subsaturation in the margin can be seen. During their dissipation stages clouds may exist for minutes without any cloud core, with the entire cloud at subsaturation. Polluted clouds show the opposite, with RH values nearing 100 % throughout the cloud at all stages. Hence, above a certain aerosol concentration, the saturation adjustment approximation (i.e., instant condensation of all supersaturation) can be considered valid. However, the transition from clean to polluted is not always linear. For example, the largest clouds in the intermediate case have a lower margin RH value than both the clean and polluted cases. This is due to the fact that the intermediate case manages to develop taller (than the clean case) clouds with stronger updrafts and downdrafts, which entrain drier air from above the inversion layer base, but at the same time is less efficient in evaporating (than the polluted case) water and adjusting the RH to 100 %.