Kinetics of the OH + NO₂ reaction: rate coefficients (217–333 K, 16–1200 mbar) and fall-off parameters for N₂ and O₂ bath gases

The radical terminating, termolecular reaction between OH and NO₂ exerts great influence on the NO_y∕NO_x ratio and O₃ formation in the atmosphere. Evaluation panels (IUPAC and NASA) recommend rate coefficients for this reaction that disagree by as much as a factor of 1.6 at low temperature and pressure. In this work, the title reaction was studied by pulsed laser photolysis and laser-induced fluorescence over the pressure range 16–1200 mbar and temperature range 217–333 K in N₂ bath gas, with experiments at 295 K (67–333 mbar) for O₂. In situ measurement of NO₂ using two optical absorption set-ups enabled generation of highly precise, accurate rate coefficients in the fall-off pressure range, appropriate for atmospheric conditions.

We found, in agreement with previous work, that O₂ bath gas has a lower collision efficiency than N₂ with a relative collision efficiency to N₂ of 0.74. Using the Troe-type formulation for termolecular reactions we present a new set of parameters with k₀(N₂) = $\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, k₀(O₂) = $\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, m=3.6, $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, and F_c=0.39 and compare our results to previous studies in N₂ and O₂ bath gases.

1 Introduction

The capacity of the atmosphere to oxidize trace gases and thus cleanse itself of pollutant emissions depends on the availability of OH radicals, which initiate the degradation of many organic and inorganic trace gases (Lelieveld et al., 2004; Lelieveld et al., 2016). Two reactions, the photolysis of ozone in the presence of water vapour (Reactions R1 and R2) and the reaction of HO₂ radicals with NO (Reaction R3), are responsible for a large fraction of atmospheric OH production.

$$\begin{array}{}\text{(R1)}& {\displaystyle }& {\displaystyle }{\mathrm{O}}_{\mathrm{3}}+h\mathit{\nu }\to \mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{O}}_{\mathrm{2}}\text{(R2)}& {\displaystyle }& {\displaystyle }\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \mathrm{2}\mathrm{OH}\text{(R3)}& {\displaystyle }& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}+\mathrm{NO}\to \mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}\end{array}$$

NO₂ is a key component in controlling atmospheric oxidation as it contributes via its photolysis (Reaction R4) to formation of tropospheric O₃ but also, via the title reaction (Reaction R5), leads to removal of OH.

$$\begin{array}{}\text{(R4)}& {\mathrm{NO}}_{\mathrm{2}}+h\mathit{\nu }\left({\mathrm{O}}_{\mathrm{2}}\right)\to \mathrm{NO}+{\mathrm{O}}_{\mathrm{3}}\end{array}$$

$$\begin{array}{}\text{(R5a)}& {\displaystyle }\mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}+M& {\displaystyle }\to {\mathrm{HNO}}_{\mathrm{3}}+M\text{(R5b)}& {\displaystyle }& {\displaystyle }\to \mathrm{HOONO}+M\end{array}$$

Atmospheric HO_x levels (HO_x = OH + HO₂) and NO_x levels (NO_x = NO + NO₂), from the boundary layer to the stratosphere, are strongly influenced by the radical terminating reaction (Reaction R5) between the hydroxyl radical (OH) and nitrogen dioxide (NO₂). Reaction R5 is complex, with its rate coefficient displaying both a pressure and temperature dependence and two different reaction pathways, leading to either nitric acid (HNO₃) or pernitrous acid (HOONO). HNO₃ is the dominant product under atmospheric conditions and its long lifetime with respect to reformation of OH and NO₂ (via reaction with OH or photolysis) and rapid deposition to surfaces in the boundary layer mean that Reaction R5 is effectively a sink of both OH and NO₂. The yield of HOONO increases as a function of pressure, with a value of ∼14 % at atmospheric pressure (T=298 K) (Golden et al., 2003; Hippler et al., 2002; Mollner et al., 2010). The fate of HOONO is thought to be dominated by thermal decomposition at temperatures typical of the mid-latitude boundary layer, with the reaction with OH and photolysis potentially contributing at higher altitudes and lower temperatures where its thermal lifetime is longer. The impact of the title reaction as a HO_x and NO_x sink thus depends on the relative efficiency of formation of HNO₃ and HOONO and the fate of HOONO, investigation of which is beyond the scope of this study.

Whilst the importance of the reaction between OH and NO₂ has been recognized for a long time, and is reflected in the numerous studies of the kinetics of this process (see e.g. evaluations of the kinetic data; Atkinson et al., 2006; Burkholder et al., 2015; IUPAC, 2019), a recent modelling study has indicated that uncertainties in the rate coefficient have a great impact on the simulated chemical composition of the atmosphere (Newsome and Evans, 2017). The recommended parameterizations of the independent, expert evaluation panels, IUPAC (IUPAC, 2019) and NASA (Burkholder et al., 2015), for the rate coefficient (k₅) of the title reaction deviate to an unacceptable extent given the importance of this reaction. Figure 1 illustrates how the ratio of the rate coefficients recommended by IUPAC and NASA ($k_{\mathrm{5}}^{\mathrm{IUPAC}}/k_{\mathrm{5}}^{\mathrm{NASA}}$) varies with altitude, and thus pressure and temperature. Up to the tropopause (∼10 km at mid-latitudes), the difference between $k_{\mathrm{5}}^{\mathrm{IUPAC}}$ and $k_{\mathrm{5}}^{\mathrm{NASA}}$ is about 10 % but this increases to 60 % at an altitude of 30 km where the pressure and temperature of the stratosphere are low. The lack of consensus between the IUPAC and NASA panels (drawing from the same laboratory-derived datasets) reflects, in part, the complexity of the reaction, the study of which requires coverage of parameter space (pressure and temperature) that demands the use of different experimental methods. Reaction R5 is an association reaction (termolecular process) and the pressure and temperature dependence stems from stabilization of the initially formed association complex, which can dissociate back to reactants at low pressure or proceed to formation of products at high pressure. These types of reactions are generally parameterized using so-called fall-off curves (Troe, 1983, 2012), which require measurement of the rate coefficients at the low- and high-pressure limits, k₀ and k_∞ respectively. The form of the transition between the low-pressure limit, at which the rate coefficient is roughly proportional to pressure, and the high-pressure limit, at which the association complex is fully stabilized, is characterized by a broadening parameter, F_c. The low- and high-pressure limits have to be characterized experimentally, whereas the broadening factor can be estimated (Cobos and Troe, 2003). The IUPAC and NASA evaluation panels take different approaches to the broadening factor, with IUPAC quoting values that vary between ∼0.3 and 0.6 and NASA taking the more pragmatic approach of fixing F_c at 0.6, which may be justified in many circumstances given the uncertainties associated with k_∞ (see below). We show later that, for the OH + NO₂ reaction, the data are better parameterized using a value of F_c close to the theoretical value of 0.39.

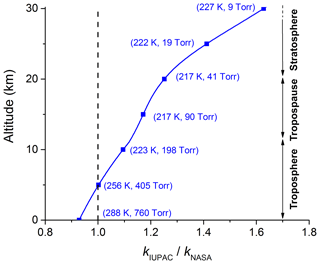
Figure 1 Ratio of the parameterized IUPAC and NASA rate coefficients (k₅) at various altitudes (temperatures and pressures).

The difficulty in parameterizing the rate coefficient for the reaction between OH and NO₂ lies in the fact that, across the range of temperatures and pressures that prevail in our atmosphere, the reaction is in the fall-off regime, yet the high-pressure limit is not accessible with standard methods. We show later that experiments conducted at pressures as high as 500 bar He are still below the high-pressure limit and that experiments at pressures as low as 5 Torr N₂ (1 Torr = 1.33 mbar = 133 Pa) are already impacted by fall-off. Only three previous studies (Anastasi and Smith, 1976; D'Ottone et al., 2001; Mollner et al., 2010) have determined the rate coefficient at pressures close to 1 bar. Further complexity is added by the fact that the efficiency of collisional deactivation of the association complex is, in contrast to the overwhelming majority of termolecular reactions of atmospheric relevance, different for N₂ and O₂, the major atmospheric “third-body” bath gases (M in Reaction R5).

The overall aim of this research was to reduce the uncertainty associated with the rate coefficient in N₂ and O₂ by generating an additional highly accurate dataset over a wide range of pressures and temperatures relevant for the atmosphere. To do this we have used the pulsed laser photolysis and laser-induced-fluorescence technique coupled with in situ measurement of NO₂ concentrations. We note that the rate coefficients we obtain represent the total loss rate coefficient (k₅) for OH loss (i.e. the sum of k_5a and k_5b).

2 Experimental details

2.1 PLP-LIF technique

Rate coefficients for the title reaction were measured using pulsed laser photolysis (PLP) for generation of OH and laser-induced fluorescence (LIF) to detect it in real time. The details of the experimental set-up have been published previously (Wollenhaupt et al., 2000) and only a brief description is given here. The experiments were carried out in a quartz reactor of volume ∼ 500 cm³, which was thermostatted to the desired temperature by circulating a 60:40 mixture of ethylene glycol ∕ water or ethanol through an outer jacket. The pressure in the reactor was monitored with 100 and 1000 Torr capacitance manometers (MKS). For all experiments, the axial flow velocity in the reactor was kept roughly constant at ∼10 cm s⁻¹ by adjusting the flow rate from 270 and 9900 cm³ (STP) min⁻¹ (sccm). As the ∼8 mm wide laser beam was normal to the direction of flow, this ensured that a fresh gas sample was available for photolysis at each laser pulse (laser frequency = 10 Hz). We additionally carried out some experiments at a lower repetition rate (5 Hz) to help rule out any influence of product build-up on the measured rate coefficient.

Pulses of 248 nm laser light (∼20 ns) for OH generation from HNO₃ andH₂O₂ precursors were provided by an excimer laser (Compex 205 F, Coherent) operated using KrF.

$$\begin{array}{}\text{(R6)}& {\displaystyle }& {\displaystyle }{\mathrm{HNO}}_{\mathrm{3}}+h\mathit{\nu }\left(\mathrm{248}\mathrm{nm}\right)\to \mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}\text{(R7)}& {\displaystyle }& {\displaystyle }{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+h\mathit{\nu }\left(\mathrm{248}\mathrm{nm}\right)\to \mathrm{2}\mathrm{OH}\end{array}$$

Laser fluences were measured using a calibrated joule meter located behind the exit window of the reactor.

The concentrations of H₂O₂ and HNO₃ were typically in the range 5–10×10¹³ and 5–10×10¹⁴ molecule cm⁻³ respectively, which, when combined with laser fluences of 5–40 mJ cm⁻² per pulse, resulted in initial OH concentrations of ∼1–12×10¹¹ molecule cm⁻³. We show later that variation in the initial radical concentration in this range had no effect on the results obtained, as expected for this chemical system.

OH fluorescence was detected using a photomultiplier tube screened by a 309 nm interference filter and a BG 26 glass cut-off filter following excitation of the OH $A^{\mathrm{2}}\mathrm{\Sigma }(v^{\prime }=\mathrm{1})\leftarrow X^{\mathrm{2}}\mathrm{\Pi }(v^{\prime \prime }=\mathrm{0}$) transition (Q11(1)) at 281.997 nm using a YAG-pumped dye laser (Quantel Brilliant B and Lambda Physik Scanmate). The time-dependent fluorescence signal was accumulated using a boxcar integrator triggered at different delay times between OH formation and excitation.

A second fluorescence detection axis was set up to enable detection of NO₂ in the same volume as OH. NO₂ was excited at ∼564 nm (Rhodamine 6G dye pumped by a frequency-doubled YAG at 532 nm) and the resulting fluorescence emission was detected using a multi-alkali photomultiplier tube screened by a 605 nm long-pass filter. The boxcar gate was timed to discriminate laser-scattered light from the NO₂ fluorescence. The NO₂ LIF signal was normalized to laser power using a photodiode sampling a fraction of the excitation pulse.

2.2 Online absorption measurement of NO₂ concentration

The experiments to determine the rate coefficient of the title reaction were performed under pseudo-first-order conditions (i.e. [NO₂]₀ ≫ [OH]₀). As a result, the overall uncertainty in k₅ was determined largely by the accuracy with which the NO₂ concentration was measured. Depending on the experimental conditions (T, p, and bath gas), the NO₂ concentration was varied from 1 to 45×10¹⁴ molecule cm⁻³.

The NO₂ concentration was continuously measured using two optical absorption cells at room temperature. In the first, upstream of the reactor, absorption of light (405–440 nm) from the collimated output from a halogen lamp transversed a 110 cm long absorption cell before being dispersed with a 0.5 m monochromator (B & M Spektronik BM50, 600 grooves per millimetre, blaze at 500 nm) and detected by a diode-array detector (Oriel InstaSpec 2). The effective spectral resolution (δλ=0.19 nm) of the monochromator–detector set-up was obtained by measuring the width and line shape (Gaussian) of the 404.66 nm Hg line from a low-pressure Hg lamp. NO₂ concentrations were determined by fitting optical densities (ODs) from 405 to 440 nm to a reference spectrum (Vandaele et al., 2002) (see Sect. 3.1), which was degraded to the resolution of our spectrometer. The second optical absorption cell (dual beam for simultaneous measurement of transmitted and reference light intensity, 43.8 cm long) was located downstream of the reactor. Here the extinction of 365 nm light from a low-pressure Hg lamp screened using a 365±5 nm interference filter was used to continuously monitor NO₂ at this wavelength.

The effective NO₂ cross section at 365 nm (σ₃₆₅; see Sect. 3.2) was determined by simultaneously monitoring the NO₂ concentration in the first absorption cell and measuring 365 nm extinction in the second absorption cell. σ₃₆₅ was calculated using the Beer–Lambert law:

$$\begin{array}{}\text{(1)}& {\mathrm{OD}}_{\mathrm{365}}=\ln \left({\displaystyle \frac{I_{\mathrm{0}}}{I}}\right)={\mathit{\sigma }}_{\mathrm{365}}\left[{\mathrm{NO}}_{\mathrm{2}}\right]l,\end{array}$$

where l is the optical path length (43.8 cm) and I₀ and I are the transmitted light intensities at 365 nm in the absence and in the presence of NO₂ respectively. The limit of detection of NO₂ (defined as 2σ of the signal in the absence of absorbent) was determined to be $\sim \mathrm{1}\times {\mathrm{10}}^{\mathrm{13}}$ molecule cm⁻³ for both the single wavelength (365 nm) and broadband (405–440 nm) absorption measurements. Drifts in zero measurements result in the smallest measurable OD in the 365 nm cell of $\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$, which is equivalent to 4.0×10¹² molecule cm⁻³ NO₂.

A third optical absorption cell (λ=184.95 nm, l=40.0 cm) was also used to measure optical extinction by NO₂ in experiments in which we explored the effect of pressure on ${\mathit{\sigma }}_{{\mathrm{NO}}_{\mathrm{2}}}$. Light at 184.95 nm was provided by a low-pressure Hg lamp screened by a 185±5 nm interference filter and was detected using a dual-beam set-up similar to that operated at 365 nm.

2.3 Chemicals

N₂ and O₂ (Westfalen 99.999 %) were used without further purification. H₂O₂ (AppliChem, 50 wt %) was concentrated to >90 % (wt) by vacuum distillation. Anhydrous nitric acid was prepared by mixing KNO₃ (Sigma Aldrich, 99 %) and H₂SO₄ (Roth, 98 %), and condensing HNO₃ vapour into a liquid nitrogen trap. NO₂ was generated via the reaction of NO with a large excess of O₂. The NO₂ thus was trapped in liquid N₂ and the excess O₂ was pumped out. The resulting NO₂ was stored as a mixture of ∼0.5 % NO₂ in N₂ or ∼5.5 % NO₂ in He. NO (3.5 Air Liquide) was purified of higher NO_x compounds by fractional vacuum distillation.

3 Results and discussion

3.1 NO₂ concentration measurement

As NO₂ concentrations were monitored in situ by optical absorption at 365 nm, the cross section determination was centrally important for derivation of the rate coefficient and considerable effort was dedicated to its accurate determination, with special attention paid to its pressure dependence.

3.1.1 Pressure dependence of the NO₂ absorption cross section at 365 nm

NO₂ has a complex and highly structured absorption spectrum in the UV–visible region with band shapes and line intensities depending on both temperature and pressure (Atkinson et al., 2004; IUPAC, 2019). The atomic Hg lines, used to determine [NO₂] in this work, are very narrow and therefore pressure broadening of NO₂ lines around 365 nm could affect the retrieved concentration. We performed two experiments (at room temperature) that indicate that, from 20 to 800 Torr of N₂, any pressure dependence in the NO₂ absorption cross section at 365 nm can safely be neglected.

In the first experiment, we simultaneously monitored optical extinction due to a flowing sample of NO₂ in N₂ at 184.95 and 365 nm. Whereas the NO₂ spectrum around 365 nm is highly structured (corresponding to excitation from the ground electronic state to the (1)²B₂ state), in the vacuum UV (180–220 nm) the spectrum obtained following excitation to the (2)²B₂ electronic state is largely continuous in nature (Au and Brion, 1997). It is highly unlikely that any pressure broadening effects for these two transitions/spectral regions will be identical. Figure 2a displays the result of a series of experiments in which the optical density (OD) observed for NO₂ concentrations between 2×10¹⁴ and 4×10¹⁵ molecule cm⁻³ at three different pressures (20, 255, and 610 Torr N₂) was recorded simultaneously in the two optical absorption cells. The ODs were corrected for a slight pressure (and thus concentration) difference between the two optical absorption cells and normalized to an optical path length of 1 cm to obtain the parameters OD${}_{\mathrm{365}}^{\mathrm{cor}}$ and OD${}_{\mathrm{185}}^{\mathrm{cor}}$. The linear regression of a plot of OD${}_{\mathrm{365}}^{\mathrm{cor}}$ versus OD${}_{\mathrm{185}}^{\mathrm{cor}}$ yields a value of OD${}_{\mathrm{365}}^{\mathrm{cor}}/$OD${}_{\mathrm{185}}^{\mathrm{cor}}=\mathrm{0.282}\pm \mathrm{0.004}$ (uncertainty is 2σ) and, within 1 %, is independent of pressure.

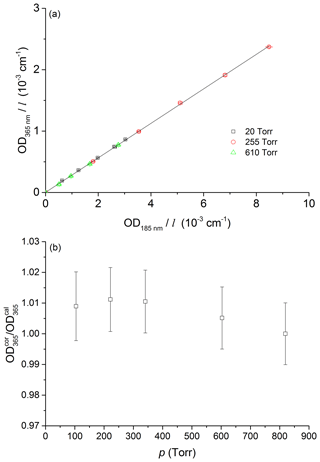
Figure 2 Pressure dependence of the relative NO₂ absorption cross section, σ_365 nm∕σ_185 nm, at 185 and 365 nm. The solid line is a linear regression for all three datasets giving a slope of 0.281±0.002 (uncertainty is 2σ, statistical only). Panel (b) shows the slopes obtained at 20, 255, and 610 Torr plotted versus pressure. The measurements were performed at room temperature.

In a second set of experiments, the optical density at 365 nm (OD₃₆₅) from 2.1×10¹⁶ molecule cm⁻³ NO₂ in 820 Torr of N₂ was initially recorded. The optical absorption cell was then evacuated stepwise to 100 Torr and OD₃₆₅ recorded at each pressure. The NO₂ samples contained N₂O₄ in equilibrium with NO₂ (Reactions R8 and R9).

$$\begin{array}{}\text{(R8)}& {\displaystyle }& {\displaystyle }{\mathrm{NO}}_{\mathrm{2}}+{\mathrm{NO}}_{\mathrm{2}}+M\to {\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}+M\text{(R9)}& {\displaystyle }& {\displaystyle }{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}+M\to \mathrm{2}{\mathrm{NO}}_{\mathrm{2}}+M\end{array}$$

Using the equilibrium coefficient of $\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{19}}$ cm³ molecule⁻¹ (average from IUPAC and NASA panels at 298 K) we calculated a N₂O₄∕NO₂ ratio that changed from $\mathrm{5.9}\times {\mathrm{10}}^{-\mathrm{3}}$ at 820 Torr ([NO₂] = 2.1×10¹⁶ molecule cm⁻³) to $\mathrm{7.0}\times {\mathrm{10}}^{-\mathrm{4}}$ at 100 Torr (NO₂ = 2.56×10¹⁵ molecule cm⁻³). OD₃₆₅ was thus corrected (<0.3 %) for the absorption of N₂O₄ at 365 nm (σ_365 nm (N₂O₄) = $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molecule⁻¹, Burkholder et al., 2015) and for the small change in [NO₂] resulting from the shift in equilibrium as the pressure and thus NO₂ concentration were reduced. We also corrected for NO₂ depletion due to photolysis (to NO and O(³P), Φ=1) caused by absorption of the 365 nm light. The photolytic loss rate constant of NO₂ was determined in a separate experiment to be $\mathrm{8}\times {\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, which requires a correction in [NO₂] of <0.2 % on the timescale of the experiment. Altogether, the corrections outlined above accounted for less than 2 % of the measured optical density.

In the absence of a pressure dependence of the effective absorption cross section of NO₂ at 365 nm, the ratio of measured optical density (OD${}_{\mathrm{365}}^{\mathrm{cor}}$) to that calculated directly (OD${}_{\mathrm{365}}^{\mathrm{calc}}$) from the initial concentration at 820 Torr and the subsequent changes in pressure should not deviate from unity. Figure 2b plots OD${}_{\mathrm{365}}^{\mathrm{cor}}/$OD${}_{\mathrm{365}}^{\mathrm{cal}}$ (normalized to the measurement at 820 Torr) against pressure and indicates that within an experimental uncertainty of 2 %, no pressure dependence in the NO₂ absorption cross section at 365 nm is observed.

The two sets of experiments described above show that there is no significant (<2 %) pressure dependence in the effective cross section of NO₂ at 365 nm.

3.1.2 Comparison of NO₂ literature spectra

The NO₂ visible spectra have already been reviewed (Orphal, 2003) and we extend this to include the more recent high-resolution work by Nizkorodov et al. (2004) as it was used as a reference in a recent kinetic study of OH + NO₂ (Mollner et al., 2010). At ultra-high resolution, rovibrational lines in the NO₂ spectrum broaden at higher pressures and the two more recent studies by Vandaele et al. (2002) and Nizkorodov et al. (2004) reported pressure broadening factors γ (γ being the half width at half maximum of a Lorentzian) in air of 0.081 and 0.116 cm⁻¹ atm⁻¹ respectively, corresponding to ∼0.0013 and ∼0.0019 nm at 1 atm and 405 nm respectively. Using the broadening factors above, one can generate spectra at any pressure by convoluting a pressure-dependent Lorentzian line width to a NO₂ spectrum obtained at low pressure and then degrading it (using a Gaussian slit function) to the resolution of the spectrometer. When applying these convolutions to the Vandaele et al. (2002) dataset, we found no difference in cross sections when using their spectra obtained at higher pressure or when using a calculated, pressure-broadened spectrum obtained at low pressure.

We also fitted our experimental measurement of NO₂ optical density (405 to 440 nm) using the lower-resolution spectra reported by Merienne et al. (1995) and Yoshino et al. (1997). Use of these reference spectra resulted in excellent agreement with those from Vandaele et al. (2002). This reflects the fact that although line widths increase at increasing pressure, once degraded to our spectral resolution, there is no discernible change in the cross sections in the 410–440 nm range. The same conclusion can be drawn when working with the spectra of Nizkorodov et al. (2004) that were obtained at pressures of <75 Torr. In contrast, using the NO₂ spectra of Nizkorodov et al. (2004), which were recorded at pressures ≥ 75 Torr, resulted in an overestimation of the NO₂ concentration by up to 20 % (at 596 Torr) when compared to those listed above. For these reasons, we use the spectrum reported by Vandaele et al. (2002) measured at 80 Torr as a reference spectrum throughout this work. We emphasize that use of any other spectrum (including the Nizkorodov spectrum obtained at low pressure and subsequently broadened (using their parameters) to any other pressure would have no significant impact ($<\sim \mathrm{3}$ %) on the cross section we derived at 365 nm.

3.1.3 Effective absorption cross section at 365 nm

The effective cross section of NO₂ at 365 nm was determined by measuring its concentration in the 110 cm optical cell using the spectrum of Vandaele et al. (2002) between 400 and 450 nm and simultaneously monitoring the optical density at 365 nm. An example of data used to retrieve the NO₂ concentration using the measured optical density (405 to 440 nm) and the spectrum of Vandaele et al. (2002) is given in Fig. 3a.

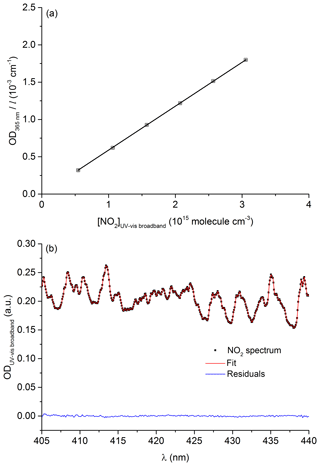
Figure 3 (a) Beer–Lambert plot of OD_365 nm∕l as a function of [NO₂] (determined using the long-path UV–vis broadband cell) used to determine the NO₂ effective cross section at 365 nm, ${\mathit{\sigma }}_{\mathrm{365}\mathrm{nm}}=(\mathrm{5.89}\pm \mathrm{0.24}){\mathrm{10}}^{-\mathrm{19}}$ċm² molecule⁻¹. (b) Example of a NO₂ spectrum (squares) recorded using the long-path UV–vis broadband cell. The red line shows the fit to the reference spectrum. The blue line is the residual. The experiments were performed at 297 K and 185 Torr.

Figure 3b shows the Beer–Lambert plot used to determine the 365 nm NO₂ absorption cross section at room temperature and 190 Torr of N₂. The effective cross section derived from the slope is $(\mathrm{5.89}\pm \mathrm{0.35})\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molecule⁻¹. The total uncertainty (6 % at 2σ) takes into account the spread in absorption cross sections (400–450 nm) reported in the literature (Merienne et al., 1995; Yoshino et al., 1997; Vandaele et al., 1998, 2002). Our effective cross section at 365 nm is in excellent agreement with previous values of $(\mathrm{5.75}\pm \mathrm{0.17})\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molecule⁻¹ reported by Wine et al. (1979) and D'Ottone et al. (2001), also obtained using low-pressure Hg lamps as emission-line sources.

3.1.4 Detection of NO₂ by LIF and NO₂ dimerization at low temperatures

At low temperatures and/or high NO₂ concentration, NO₂ partially dimerizes to N₂O₄ (Reactions R8 and R9), which will lead to differences in the NO₂ concentrations derived from the optical absorption measurements at room temperatures with respect to those in the reactor where the OH + NO₂ reaction is investigated. Indeed, at very low temperature, a plot of first-order OH loss constant versus NO₂ concentration as measured by optical absorption flattens at high [NO₂] due to the overestimation of the NO₂ concentration in the reactor. This is illustrated in Fig. S1 of the Supplement.

The NO₂ concentration in the cold reactor may be calculated using the following expression (Brown et al., 1999).

$$\begin{array}{}\text{(2)}& \left[{\mathrm{NO}}_{\mathrm{2}}\right]={\displaystyle \frac{\left(\sqrt{\mathrm{8}{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}{K}_{\mathrm{8}}+\mathrm{1}}\right)-\mathrm{1}}{\mathrm{4}{K}_{\mathrm{8}}}},\end{array}$$

where [NO₂]₀ is the measured concentration in the absorption cells at room temperature and K₈ is the equilibrium constant for Reactions R8 and R9.

At 217 K, K₈ is associated with an uncertainty of >50 % (Atkinson et al., 2004; Burkholder et al., 2015; IUPAC, 2019) with the value given by IUPAC ∼ 65 % smaller than that given by NASA. At 217 K and [NO₂] = 5×10¹⁴ molecule cm⁻³, the different recommendations would lead to a ∼13 % difference in NO₂. Even if K₈ were accurately known, thermal gradients along the length of the reactor and between the walls and the centre of the reactor (where we monitor OH kinetics) could potentially lead to concentration gradients of NO₂ and thus to a difference between the concentrations derived from the optical absorption measurements. For these reasons, we checked the validity and the magnitude of the correction that needed to be applied to [NO₂] at low temperatures by performing series of measurements where [NO₂] was measured simultaneously by in situ LIF and UV absorption ([NO₂]_UV) at different temperatures from 218 to 320 K and constant density (1.65×10¹⁸ molecule cm⁻³; corresponding to 50 Torr at 292 K).

Figure 4 displays the NO₂ LIF signal at six different temperatures (218, 234, 257, 274, 292, and 320 K) as a function of the NO₂ concentration measured by ex situ optical absorption at room temperature. For the three highest temperatures, where N₂O₄ formation is negligible at the concentrations used, there is a strictly linear dependence of the LIF signal on [NO₂] and no measurable change in the LIF sensitivity with temperature. The latter indicates that any dependence of the LIF efficiency on temperature is very weak. As far as we are aware, none of the previous studies of NO₂ fluorescence quenching have reported a temperature dependence of the fluorescence quenching rate constant for N₂ (Keil et al., 1980). Only Schurath et al. (1981) report a weak negative T dependence (T^−0.42) on the fluorescence quenching rate constant for NO₂* (formed in the NO + O₃ reaction) in N₂ between 285 and 446 K, but acknowledge that the T dependence might be erroneous due to the large scatter in their dataset.

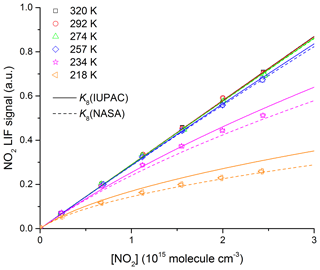
Figure 4 NO₂ LIF signal (following excitation at 564 nm) as a function of NO₂ concentration at six different temperatures from 218 to 320 K. The experiments were performed in N₂ bath gas ([N₂] = 1.65×10¹⁸ molecule cm⁻³). The lines were derived using the equilibrium constants (K₈) for NO₂ dimerization to N₂O₄ preferred by IUPAC (solid lines) and NASA (dashed lines).

The NO₂ LIF signals obtained at low temperatures (218 and 234 K) show deviation from linearity as expected if significant amounts of NO₂ dimerize to N₂O₄. In Fig. 4 we plot the expected dependence of the LIF signal from NO₂ in the cold reactor on the ex situ NO₂ concentration as calculated using Eq. (2) and the equilibrium constant K₈ recommended by IUPAC (solid lines) or NASA (dashed lines). The predicted dependence reproduces the measurements within ∼20 % confirming that the literature values of equilibrium coefficient are appropriate for correcting NO₂ concentrations in kinetic experiments at low temperatures. As our LIF signals at low temperatures lie broadly between those predicted using the equilibrium constants preferred by IUPAC and NASA, we have used an average value of K₈ for correcting NO₂ concentrations in the kinetic experiments. We note here that the corrections applied are small and do not impact significantly on the accuracy of the rate coefficient we derive (see later for details).

3.2 Rate coefficients for OH + NO₂ (k₅)

In this section, we present our measurements of k₅ in N₂ and O₂ bath gases and compare the results to previous datasets and the parameterizations presently preferred by evaluation panels. The PLP-LIF studies were carried out under pseudo first-order conditions with [NO₂] ≫ [OH], so that the OH profiles are described by

$$\begin{array}{}\text{(3)}& [\mathrm{OH}{]}_t=[\mathrm{OH}{]}_{\mathrm{0}}\exp (-k^{\prime }t),\end{array}$$

where [OH]_t is the concentration (molecule cm⁻³) at time t after the laser pulse. k^′ is the pseudo-first-order rate coefficient and is defined as

$$\begin{array}{}\text{(4)}& k^{\prime }=k_{\mathrm{5}}\left[{\mathrm{NO}}_{\mathrm{2}}\right]+k_{\mathrm{d}},\end{array}$$

where k₅ is the bimolecular rate coefficient (cm³ molecule⁻¹ s⁻¹) for the reaction between OH and NO₂. k_d (s⁻¹) accounts for OH loss due to diffusion out of the reaction zone and reaction with HNO₃ or H₂O₂. Figures 5 and 6 display representative datasets obtained in N₂ bath gas at 295 K and at four different pressures (100, 300, 500, and 900 Torr). OH decays are exponential over >2 orders of magnitude and the plots of k^′ versus [NO₂] are straight lines as expected from Eq. (4). Values of k₅ derived from these datasets typically have statistical uncertainty (2σ) of less than 5 %.

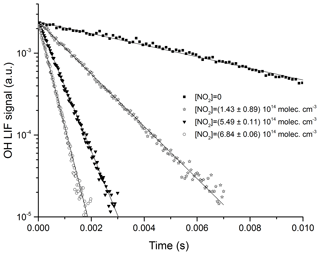
Figure 5 Exponential decay of the OH LIF signal in 100 Torr N₂, at 293 K, and at four different NO₂ concentrations. OH was generated by the photolysis (at time = 0 s) of H₂O₂ at 248 nm. The solid lines are fits to the datasets using Eq. (3).

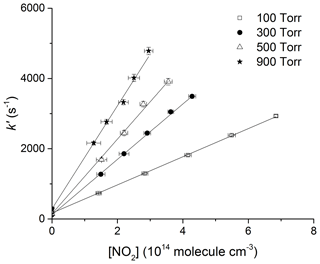
Figure 6 Plots of k^′ versus [NO₂] at four different pressures in N₂ and at 295 K. The lines are least-squares fits to the data using Eq. (4). Error bars are 2σ statistical only.

The overall uncertainty in k₅ is dominated by uncertainty in the NO₂ concentration, the origin of which is uncertainty in the NO₂ absorption cross sections and in the correction for NO₂ dimerization to N₂O₄. The NO₂ concentration used to determine the rate coefficient was the average of those determined by analysing the optical density between 405 and 450 nm in the 110 cm absorption cell located upstream of the reactor and the optical density at 365 nm measured in the 43.8 nm optical absorption cell located downstream of the reactor. The two concentrations generally agreed to better than 2 %. The optical absorption measurements of NO₂ were made at room temperature. However, when the reactor is operated at low temperatures some NO₂ is converted to N₂O₄ via the equilibrium (R8) and a correction must be made to account for the difference in [NO₂] between the optical absorption measurement and that present in the reactor (see Sect. 3.1.4). At temperatures above 273 K, no correction to [NO₂] was necessary, but amounted to 0.5 % to 3.5 % at 245 K, 4 % to 26 % at 229 K and 6 % to 29 % at 217 K, with the largest corrections being associated with the highest NO₂ concentrations. The total uncertainty associated with each value of k₅ is listed in Table 1 and considers uncertainty in NO₂ concentration measurement (i.e. uncertainty associated with NO₂ cross sections and the equilibrium constant for NO₂ dimerization) as well as statistical error on the fits to derive k^′ (Fig. 6). The expression used to calculate the total overall uncertainty for each value of k₅ is given in the Supplement and results in ∼8 % at T>240 K and ∼16 % for measurements at 217 and 229 K.

Table 1 Measurements of k₅ in N₂ and O₂ bath gases.

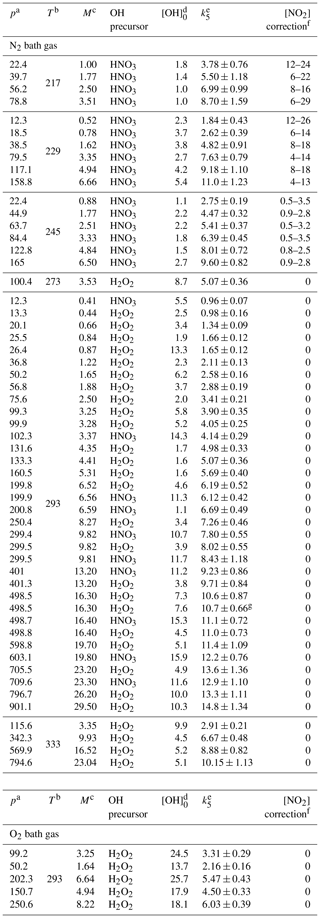
^a In torr. ^b In kelvin. ^c In 10¹⁸ molecules per cubic centimetre. ^d In 10¹¹ molecules per cubic centimetre, the OH concentration was calculated from the 248 nm laser fluence, H₂O₂ or HNO₃ concentrations and the respective quantum yield for OH production. ^e In 10⁻¹² cubic centimetres per molecule per second (errors are total uncertainty, 2σ). ^f As a percentage; due to dimerization of NO₂ to N₂O₄, which is insignificant at temperatures > 273 K. ^g Experiment performed at a laser repetition rate of 5 Hz (instead of the usual 10 Hz).

Apart from the use of different OH precursors (values of k₅ derived when using photolysis of either H₂O₂ or HNO₃ were not significantly different), experiments were carried out to investigate the effect of different initial OH concentrations. In two sets of experiments, at total pressures of either 200 or 500 Torr N₂, the 248 nm laser fluence was varied by a factor of 7 (from ∼5 to 35 mJ cm⁻²) and the H₂O₂ and HNO₃ concentrations by 4 and 6 respectively, resulting (at 200 Torr) in a factor of 10 change in [OH]₀ (from ∼10¹¹ to 10¹² molecule cm⁻³) (see Table 1). Reducing the laser repetition rate from 10 to 5 Hz had no discernible effect on the value of k₅ retrieved ($\mathrm{10.6}\pm \mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{12}}$ cm³ molecule⁻¹ s⁻¹ at 10 Hz and $\mathrm{10.7}\pm \mathrm{0.1}\times {\mathrm{10}}^{-\mathrm{12}}$ cm³ molecule⁻¹ s⁻¹ at 5 Hz; see Table 1, rate coefficients at 293 K and 498.5 Torr).

The results indicate that, within the range of OH mentioned above, there is no significant influence of secondary reactions of OH on the determination of k₅. For the OH + NO₂ reaction, the use of OH concentrations as high as 10¹² molecule cm⁻³ is not expected to have a significant impact on the OH decay rates because the major product, HNO₃, reacts only slowly with OH, with k(OH + HNO₃) = $\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{13}}$ cm³ molecule⁻¹ s⁻¹ at 296 K and 250 Torr (Dulitz et al., 2018). Even if the minor product, HOONO, were to react with OH with a rate coefficient of $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{10}}$ cm³ molecule⁻¹ s⁻¹ (i.e. close to collision frequency), this would still have an impact of less than 2 % on the first-order OH decay rate coefficient at 750 Torr pressure.

The self-reaction of OH at an initial concentration of 1×10¹² molecule cm⁻³ results in a loss rate of ∼15 s⁻¹, which is negligible compared to typical decay constants of ∼1000 to 10 000 s⁻¹ due to reaction with NO₂. Photolysis of NO₂ is inefficient as the cross section of NO₂ is low at 248 nm ($\mathrm{1}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹; IUPAC, 2019) but can result in approximately equivalent initial O(³P) and OH concentrations. However, the presence of O(³P) has a negligible impact as its fate is mainly reaction with NO₂ to form NO, which also reacts only slowly with OH.

3.2.1 Measurements of k₅ in N₂ bath gas and comparison with literature

Our measurements of k₅ in N₂ bath gas (12–900 Torr, 217–333 K) are summarized in Fig. 7 and listed in Table 1.

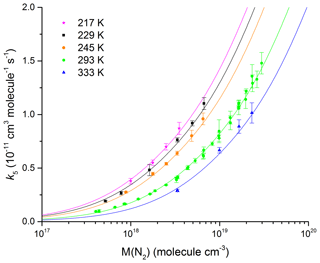
Figure 7 Rate coefficient, k₅, as a function of N₂ density in the fall-off range for five different temperatures. The error bars represent 2σ statistical uncertainty. The solid line fits to the data are described by Eq. (5) with $k_{\mathrm{0}}=\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, m=3.6, n=0, $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, and F_c=0.39 (fixed).

The solid lines in Fig. 7 are fits according to the Troe formalism for termolecular reactions (Troe, 1983) as adopted by the IUPAC panel:

$$\begin{array}{}\text{(5)}& k_{\mathrm{5}}(p,T)={\displaystyle \frac{\mathit{\beta }{k}_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}M{k}_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}{\mathit{\beta }{k}_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}M+k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}}\log F,\end{array}$$

where k₀ is the low-pressure limit rate coefficient in cm⁶ molecule⁻² s⁻¹, k_∞ is the high-pressure limit rate coefficient in cm³ molecule⁻¹ s⁻¹, T is the temperature in kelvin, M is the density in molecules per cubic metre, and m and n are dimensionless temperature exponents. β takes into account the overall collision efficiency for energy transfer from the initially formed OH–NO₂ association complex to the bath gases, with

$$\begin{array}{}\text{(6)}& \mathit{\beta }=\sum {\mathit{\beta }}_i{x}_i,\end{array}$$

where β_i and x_i are the collision efficiency and the mixing ratio of bath gas i respectively.

The broadening factor, F, is defined as

$$\begin{array}{}\text{(7)}& \log F={\displaystyle \frac{\log F_{\mathrm{c}}}{\mathrm{1}+{\left[\log \left(\frac{\mathit{\beta }{k}_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}M}{k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}\right)/N\right]}^{\mathrm{2}}}},\end{array}$$

where $N=[\mathrm{0.75}-\mathrm{1.27}\log F_{\mathrm{c}}]$ and F_c is the broadening factor at the centre of the fall-off curve.

Accurate representation of termolecular rate coefficients using this expression requires data on the low- and high-pressure limiting rate coefficients, k₀ and k_∞, and their temperature dependence. Data close to the low-pressure limit have generally been obtained using low-pressure flow tubes (Howard, 1979; Keyser, 1984), whereas measurements close to the high-pressure limit required equipment capable of operation at several hundred bar or the use of a different approach in which the rate coefficient for relaxation of vibrationally excited OH in collision with NO₂ is equated to the high-pressure limit of the association reaction.

In the case of the title reaction, several measurements have been performed close to the low-pressure limit (0.5 to 10 Torr) (Anderson and Kaufman, 1972; Anderson et al., 1974; Anderson, 1980; Burrows et al., 1983; Howard and Evenson, 1974), while only one group has carried out experiments at pressures approaching the high-pressure limit (Hippler et al., 2002, 2006). Even at 500 bar He, the reaction of OH with NO₂ is still not at the high-pressure limit, and at pressures as low as 10 Torr of He, there is already evidence for significant fall-off. The two determinations (D'Ottone et al., 2005; Smith and Williams, 1985) of the rate constant for vibrational relaxation of OH in collision with NO₂ deviate in their value of k_∞ by ∼25 %. For many termolecular reactions, limitations in data quality mean that k₀ or k_∞ is often derived by fitting to multiple datasets that span a large range of pressures and fixing F_c to either a theoretical value (IUPAC, 2019) or to a value of 0.6 (Burkholder et al., 2015). To analyse our data we used a similar approach to that of IUPAC with the broadening factor fixed to 0.39 (Cobos and Troe, 2003). In order to further reduce the number of variables when fitting data to expression (Eq. 7) we also make the assumption that k_∞ is independent of temperature (n=0). This assumption is reasonable as the value of n is expected to be much smaller than that of m and the data at high pressures are not of sufficient quality to constrain this parameter.

By fitting our data (217, 229, 245, 273, 293, and 333 K) to expression (Eq. 7) and allowing k₀, m, and k_∞ to vary, we derive values of $k_{\mathrm{0}}=\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, and m=3.6. These parameters accurately reproduce the pressure and temperature dependence of k₅, which we observe in N₂ bath gas (see Fig. 7) with most of the individual rate coefficients measured agreeing to better than 5 % of the parametrization. This is highlighted in Fig. S2, which shows the percentage deviation of each data point from the value derived using the values of k₀, k_∞, n, m, and F_c listed above.

We now compare our value of k₀ to those reported from low-pressure flow-tube studies of the title reaction. We note that, in low-pressure flow tubes operated at pressures greater than a few torr of N₂, mixing effects and OH losses to walls severely impede accurate kinetic measurements of OH rate coefficients, especially at low temperatures (Brown, 1978; Howard, 1979). In their study of the reaction between OH and NO₂, Howard and Evenson (1974) do not report rate coefficients at pressures greater than 2 Torr N₂ because of the large uncertainty resulting from the corrections applied. In low-pressure flow-tube studies of the OH + NO₂ reaction, the loss rate constant for OH (k^′) is a composite term (Eq. 8), with contributions from the association reaction (k₅[NO₂], slow at low pressures), the loss of OH to the bare flow-tube wall (k_w, experimentally derived in the absence of NO₂), and the heterogeneous loss of OH due to reaction with surface-adsorbed NO₂ (k_s[NO₂]_s), which depends on the rate coefficient for the surface reaction (k_s) and the availability of surface-adsorbed NO₂ ([NO₂]_s), with the latter dependent in a non-linear manner (via a gas-surface partition coefficient) on the gas-phase NO₂ concentration.

$$\begin{array}{}\text{(8)}& k^{\prime }=k_{\mathrm{5}}\left[{\mathrm{NO}}_{\mathrm{2}}\right]+k_{\mathrm{w}}+k_{\mathrm{s}}{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{s}}\end{array}$$

In low-pressure flow-tube studies, correction is rarely made for the surface-reaction-induced heterogeneous loss of OH, in this case k_s[NO₂]_s, the manifestation of which is often a positive intercept in plots of k_bi as a function of molecular density (Anderson et al., 1974; Howard and Evenson, 1974).

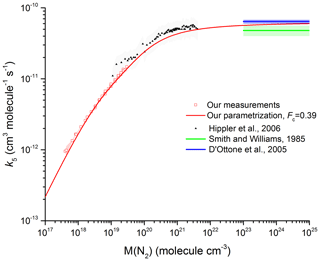
Figure 8 Comparison between our results in N₂ with the measurements by Hippler et al. (2006) (He bath gas; the grey shaded area represents total uncertainty) and the high-pressure limits derived by Smith and Williams (1985) and D'Ottone et al. (2005). All measurements are close to 298 K. The red line was obtained using Eq. (5) with $k_{\mathrm{0}}=\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, m=3.6, n=0, $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, and F_c=0.39 (fixed).

For the reaction of OH + NO₂ in N₂, low-pressure flow-tube studies report values of k₀ between 2.0 and $\mathrm{2.9}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹ close to room temperature. Although this range is consistent with the value we derive ($\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹), the agreement is to some extent fortuitous for reasons outlined above and also because the low-pressure flow-tube studies of the reaction between OH and NO₂ report values of k₀ that were derived by assuming a linear dependence of the rate coefficient on pressure. Our precise dataset and the parameterization with broad fall-off behaviour indicate significant deviation from linear behaviour at pressures of 2 Torr of N₂. In order to estimate the size of the error made by assuming linear behaviour, we calculated rate coefficients for the pressure range of 0.5 to 10 Torr of N₂ using fall-off curves with F_c=0.39, $k_{\mathrm{0}}=\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹ and $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹. Unweighted linear fitting of the rate coefficients thus obtained resulted in a value of $k_{\mathrm{0}}=\mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, an underestimation of 15 % (when fitted up to 2 Torr), which increases to 25 % when the fit is extended to 10 Torr. The values of k₀ obtained in the low-pressure flow-tube studies are thus likely to be biased to lower values, especially those that extend to pressures above 2 Torr N₂, though the effects of fall-off may not be evident in the highly scattered original datasets. The two low-pressure flow-tube studies (Anderson, 1980; Howard and Evenson, 1974) (both up to 2 Torr N₂) that reported rate coefficients at various pressures and the value of k₀ derived are compared to our parameterization in Fig. S3. The data of Anderson (1980) are limited in number and display large scatter. The reported value (at 300 K) of $k_{\mathrm{0}}=\mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹ appears to have been obtained from a linear fit with the intercept fixed to zero. The original rate coefficients by Howard and Evenson (1974) display better precision, but indicate a large intercept at zero pressure of $\mathrm{1.8}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molecule⁻¹ s⁻¹. The data simply corrected by subtracting a pressure-independent offset still lie ∼20 % above our parametrization. We conclude that the low-pressure flow-tube studies of the rate coefficient for OH + NO₂ are not of sufficient precision or accuracy to define k₀ for the purpose of obtaining an accurate parameterization of the rate coefficient, k₅.

We now compare our value of k_∞ ($\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹) to literature values. Figure 8 shows our data at 293 K (open symbols) along with values of k_∞ (blue- and green-shaded areas) derived from the vibrational relaxation of OH (D'Ottone et al., 2005; Smith and Williams, 1985). The height of the shaded areas indicates the reported overall uncertainty. We also plot the rate coefficients of Hippler et al. (2006) obtained at high pressure in He. To compare our measurements in N₂ with the high-pressure data in He, we scaled the He pressure by a factor of 0.39 (determined in our laboratory). We recognize that this is not a rigorous treatment of the relative collision efficiency of N₂ and He data close to the high-pressure limit, but note that using a more complex approach (i.e. using a density-dependent correction and bath-gas-dependent values of F_c) would lead to only insignificant changes in the equivalent N₂ pressure. The solid red line is our parameterization with the values of k₀, k_∞, and F_c given above and is seen to reproduce the trend in k₅ with pressure between 16 mbar and 190 bar N₂. Our value for k_∞ of $(\mathrm{6.3}\pm \mathrm{0.4})\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹ (error given at 2σ statistical only) is consistent within combined uncertainty with those of $(\mathrm{6.4}\pm \mathrm{0.3})\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹ obtained by D'Ottone et al. (2005) and $(\mathrm{4.8}\pm \mathrm{0.8})\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹ obtained by Smith and Williams (1985).

In this section, we compare our values of k₀ and k_∞ to those obtained in previous experiments at pressures in the fall-off regime, in which OH was generated photolytically. First, we note that values of k₀ and k_∞ and m obtained by fitting pressure-dependent datasets are strongly dependent on the choice of F_c and (to a lesser extent) whether an asymmetric (IUPAC) or symmetric (NASA) broadening factor has been used. In order to make a meaningful comparison between our values of k₀, k_∞, and m and those previously reported in the literature, we have therefore re-fitted the existing datasets using Eq. (5) with F_c fixed to 0.39. The results, presented in Table 2, show a variation of larger than a factor of 2 for both k₀ (1.8 to $\mathrm{3.8}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹) and k_∞ (3.4 to $\mathrm{7.9}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹) even though similar experimental procedures were used. Our value of 3.60 for m (describing the temperature dependence of k₀) is lower than those obtained from re-analysis of the datasets of Anastasi and Smith (1976), Wine et al. (1979), and Brown et al. (1999), which lie between 4.5 and 4.9. When the extensive dataset of Brown et al. (1999) is examined more closely, we find that excluding their room temperature data (the discrepancy at room temperature between our two works is discussed below) and only fit their four lowest temperatures (from 220 to 250 K) we would obtain a m of 3.9, in agreement with our dataset. We note that the IUPAC and NASA evaluation panels recommend different values for m. While IUPAC have m=4.5 for both reaction channels, NASA suggest use of 3 and 3.9 for HNO₃ and HOONO forming Reaction R5a and R5b respectively.

Table 2 Re-analysis of previous datasets using F_c=0.39.

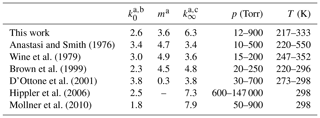
^a Values listed may deviate from those previously reported owing to use of F_c=0.39 to re-analyse data. ^b Units are 10⁻³⁰ cm⁶ molecule⁻² s⁻¹. ^c Units are 10⁻¹¹ cm³ molecule⁻¹ s⁻¹.

In a series of figures (Figs. S4–S10), we compare values of k₅ derived from our parameterization with those presented in previous studies of k₅ in N₂ bath gas over a similar pressure range. There are five previous flash/laser photolysis studies of the title reaction in N₂ bath gas (Anastasi and Smith, 1976; Brown et al., 1999; D'Ottone et al., 2001; Mollner et al., 2010; Wine et al., 1979). Three of these studies (Brown et al., 1999; D'Ottone et al., 2001; Wine et al., 1979) measured NO₂ concentrations in situ at 365 nm using a cross section that deviated by less than 3 % from that reported in the present study (see Sect. 3.1.3).

Anastasi and Smith (1976) reported values of k₅ (Fig. S4) over a wide range of temperatures (220 to 550 K) and pressures (10 to 500 Torr) using flash photolysis of H₂O or HNO₃ as OH precursor with the detection of OH by resonance absorption. The NO₂ concentration was obtained manometrically and no details pertaining to corrections for NO₂ dimerization at low temperatures were given. Our parametrization reproduces most of their data within their experimental uncertainty (reported to be 36 % at 2σ).

Wine et al. (1979) reported temperature-dependent values of k₅ (Fig. S5) in a more limited pressure range (up to ∼200 Torr in N₂) using laser photolysis of HNO₃ to generate OH and resonance fluorescence to detect it. Our parameterization is in good agreement (better than 10 %) with most of their data apart from at higher pressures points where the difference is >30 % and greater than the combined quoted uncertainties.

Figure S6 compares our parameterization to the data of Brown et al. (1999) whose methods (PLP-LIF) were very similar to the present study. Their data are however limited to pressures of less than 250 Torr N₂. At molecular densities of less than $\sim \mathrm{7}\times {\mathrm{10}}^{\mathrm{18}}$ molecule cm⁻³ there is good agreement (<10 % deviation) but this increases to ∼20 % at their highest pressures ($M=\mathrm{1}\times {\mathrm{10}}^{\mathrm{19}}$ molecule cm⁻³) and is largest at room temperature where it increases to 40 %. Compared to the present study, Brown et al. (1999) worked at lower concentrations of NO₂ ($<\mathrm{2}\times {\mathrm{10}}^{\mathrm{14}}$ molecule cm⁻³) in order to limit the formation of N₂O₄ at low temperatures. N₂O₄ formation is however not significant at 298 K and cannot explain the poor agreement at this temperature.

The dataset of D'Ottone et al. (2001) was also obtained using PLP-LIF and also covered a similar range of pressures (100 to 700 Torr N₂ at 298 and 273 K) to the present study. At room temperature, most of their measurements agree within 10 % with our parameterization (Fig. S7); however their values for k₅ obtained at 273 K are consistently lower by ∼25 %. In fact, their measurements at 273 and 298 K are indistinguishable and thus do not display the temperature dependence observed by all previous studies

The most recent dataset (Mollner et al., 2010) was also obtained using PLP-LIF and covered pressures up to 900 Torr N₂ at 298 K. Mollner et al. (2010) monitored NO₂ in situ via UV–visible broadband absorption using reference spectra from Vandaele et al. (2002) and Nizkorodov et al. (2004), though it is not clear how these two spectra were used or combined.

In Sect. 3.1.2, we indicated that using the spectra of Nizkorodov et al. (2004) that were obtained at pressures > 75 Torr could lead to an overestimation of the NO₂ concentration, which would result in an underestimation of k₅. We are unable to assess the extent to which this may have influenced the Mollner et al. (2010) values of k₅. On average, our parametrization overestimates their measurement of k₅ by ∼15 % (Fig. S8).

Values of k₅ in the fall-off regime have also been obtained using a high-pressure laminar flow-tube set up (Donahue et al., 1997; Dransfield et al., 1999) with OH detection by LIF and NO₂ concentrations derived by recording the concentration of a passive tracer (CF₂Cl₂) using FTIR and UV absorption in mixtures of NO₂ and CF₂Cl₂. Figures S9 and S10 indicate poor agreement between this dataset and our parameterization, the disagreement being most significant (factor 2) at room temperature. The discrepancy is smaller at low temperature with our parametrization predicting rates ∼5 % to 25 % faster in the 212.5 and 265 K temperature range.

The comparison of the various datasets reveals differences in the rate coefficients measured in N₂ that cannot be easily explained. All studies worked under pseudo-first-order conditions. Any discrepancy in k₅ between two independent studies is most likely related to the accuracy with which the concentration of NO₂ was measured, with secondary chemistry or reaction of OH with impurities unlikely to be important for reasons already discussed. The PLP-LIF studies used online measurement of NO₂ with almost identical absorption cross sections at 365 nm, or NO₂ reference spectra with absorption cross sections that agree to within a few percent (more details in Sect. 3.1.2). In our work, we recorded the NO₂ concentration using both methods (i.e. 365 nm and UV broadband absorption) and found no evidence for systematic bias in the NO₂ concentration. Also, we showed that the NO₂ cross sections are not influenced significantly by pressure. We have not identified the origin of discrepancies between these datasets but note that the plots of k₅ versus pressure in the present study are generally less scattered than in most other studies, and thus provide better constraint when deriving values for k₀ and k_∞ (Figs. 7, 10, S4–S8).

In Fig. 9, we compare our parametrization to those of IUPAC and NASA at four different temperatures in N₂. At pressures close to 1 bar and 300 K ($M\sim \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{19}}$ molecule cm⁻³), the IUPAC parameterization underpredicts k₅ slightly ($k_{\mathrm{5}}^{\mathrm{this}\mathrm{work}}/k_{\mathrm{5}}^{\mathrm{IUPAC}}\sim \mathrm{1.11}$) whereas the NASA parameterization is in good agreement ($k_{\mathrm{5}}^{\mathrm{this}\mathrm{work}}/k_{\mathrm{5}}^{\mathrm{NASA}}\sim \mathrm{1.01}$). At molecular densities and temperatures typical of the mid-latitude upper troposphere of 230 K and $M=\mathrm{8}\times {\mathrm{10}}^{\mathrm{18}}$ molecule cm⁻³ (∼250 mbar) the situation reverses with IUPAC accurately predicting our measured values ($k_{\mathrm{5}}^{thiswork}/k_{\mathrm{5}}^{\mathrm{IUPAC}}\sim \mathrm{1.00}$) and NASA overpredicting slightly ($k_{\mathrm{5}}^{\mathrm{this}\mathrm{work}}/k_{\mathrm{5}}^{\mathrm{NASA}}\sim \mathrm{1.10})$. As we move up to higher altitudes the discrepancy between measurement and the NASA recommendation increases: taking a typical value of $M\sim \mathrm{2}\times {\mathrm{10}}^{\mathrm{18}}$ molecule cm⁻³ for the lower stratosphere (20 km altitude) and a temperature of 215 K, we calculate ($k_{\mathrm{5}}^{\mathrm{this}\mathrm{work}}/k_{\mathrm{5}}^{\mathrm{IUPAC}}\sim \mathrm{0.95}$) and ($k_{\mathrm{5}}^{\mathrm{this}\mathrm{work}}/k_{\mathrm{5}}^{\mathrm{NASA}}\sim \mathrm{1.20}$). Moving up to 35 km altitude ($M\sim \mathrm{2}\times {\mathrm{10}}^{\mathrm{17}}$ molecule cm⁻³, T=230 K) deviation becomes substantial for both sets of recommendations with ($k_{\mathrm{5}}^{\mathrm{this}\mathrm{work}}/k_{\mathrm{5}}^{\mathrm{IUPAC}}\sim \mathrm{0.75}$) and ($k_{\mathrm{5}}^{\mathrm{this}\mathrm{work}}/k_{\mathrm{5}}^{\mathrm{NASA}}\sim \mathrm{1.35}$).

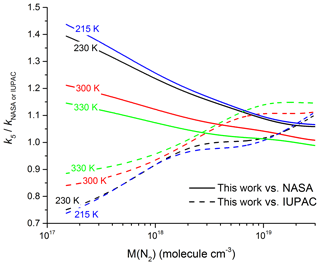
Figure 9 Ratio of our parametrized rate coefficient k₅ versus those calculated from the parameters recommended by IUPAC (dashed lines) and NASA (solid lines) for four different temperatures.

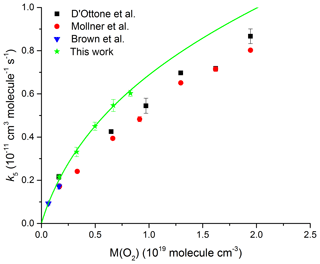
Figure 10 Rate coefficient k₅ as a function of O₂ density at T=293 K. The green data points are from the present study; the solid line represents a fit using Eq. (5) with $k_{\mathrm{0}}=\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹ (fixed), F_c=0.39 (fixed), and m=3.6 (fixed).

The great discrepancy between the IUPAC and NASA recommendations at low pressures and temperatures has its origin in the treatment of the low-pressure limit rate coefficient, k₀. In the IUPAC approach, the parametrization was constrained to the low-pressure datasets (Troe, 2012), extrapolating reported values of k₀ to a higher value assuming the data were in a pure third-order regime; however, as shown above this assumption results in an overestimation of k₀. By fixing F_c to 0.6 and constraining the fit to the high-pressure measurements of Hippler et al. (2006), the NASA parametrization will tend to underestimate k₀.

In order to test this, we fitted our data to the expression used by NASA (Eq. 9) with F_c fixed at 0.6. This resulted in values of k₀(N₂) = $\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹ and $k_{\mathrm{\infty }}=\mathrm{3.6}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹ (m stayed unchanged with a fitted value of 3.6), which are not consistent with either the high- or low-pressure data.

$$\begin{array}{}\text{(9)}& k_{\mathrm{NASA}}(p,T)={\displaystyle \frac{k_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}M}{\mathrm{1}+\frac{k_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}M}{k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}}}{\mathrm{0.6}}^{{\left\{\mathrm{1}+{\left[\log \left(\frac{k_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}M}{k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}\right)\right]}^{\mathrm{2}}\right\}}^{-\mathrm{1}}}\end{array}$$

3.2.2 Measurements of k₅ in O₂ bath gas and comparison with literature

Brown et al. (1999) were the first to recognize that the third-body collision efficiency of O₂ was lower than N₂ and, as a consequence, k₅ would be lower in air than in pure N₂. This was confirmed in subsequent measurements by D'Ottone et al. (2001) and Mollner et al. (2010).

We have also performed a series of measurements, displayed in Fig. 10, in pure O₂ bath gas (50–250 Torr, 295 K). The solid line is a fit to the data using expression (Eq. 5) whereby only k₀ was varied with k_∞, F_c, and m fixed as $\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, 0.39, and 3.6 respectively. The rate coefficients obtained in pure O₂ bath gas are in good agreement with the single low-pressure data point of Brown et al. (1999) but are systematically higher (by on average 10 % and 30 % respectively) than those reported by D'Ottone et al. (2001) and Mollner et al. (2010). As for the experiments in N₂, the reason for this discrepancy is not obvious.

Our analysis results in a low-pressure limit of k₀(O₂) = $\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹ and thus a relative collision efficiency of 0.74 for O₂ compared to N₂. This result is in excellent agreement with the results by Brown et al. (1999) (0.70), D'Ottone et al. (2001) (0.67), and Mollner et al. (2010) (0.67) and results in a collision efficiency in air (∼80 % N₂ and ∼20 % O₂) of 0.94 relative to N₂. The impact of the lower efficiency for collisional deactivation of O₂ compared to N₂ will be largest close to the low-pressure limit and tends to zero as we approach the high-pressure limit. At low pressures, we calculate a rate coefficient that will be lower by 5 % in air compared to N₂, while at 1 atm, the reduction in k₅ will be ∼3 %. To date, the NASA evaluation panel has incorporated this effect into its recommendations, whereas the IUPAC panel has not. We have not investigated the temperature dependence of the low-pressure rate coefficient (m) in O₂ but note that previous studies of k₅ close to the low-pressure limit indicate the same values of m for He, N₂, and Ar even though the third-body efficiencies of these three bath gases are very different (Anderson et al., 1974). There is no reason to expect that this would be different for O₂ and therefore do not consider the assumption of the same value of m for N₂ and O₂ to be a source of uncertainty in deriving rate coefficients for atmospheric conditions (i.e. a mixture of N₂ and O₂). We emphasize that, for use in atmospheric models, both the lower third body of efficiency of air compared to N₂ and the branching ratio to HNO₃ or HOONO formation need to be considered.

4 Conclusion

We report a new set of measurements of the rate coefficient (k₅) for the reaction of OH with NO₂ between 217 and 333 K and over a wide range a pressures in the fall-off regime in N₂ and O₂ bath gases. In order to measure NO₂ concentrations as accurately as possible we used three different optical absorption set-ups at different wavelengths/wavelength ranges as well as in situ, laser-induced-fluorescence detection of NO₂. The highly accurate and precise dataset obtained, combined with a theoretical value for the fall-off factor, enabled a more accurate assessment of the limiting low-pressure (k₀) rate coefficient than previous studies, including low-pressure flow-tube measurements. The rate coefficients we derive in the fall-off range are slightly larger than some previous studies using similar methods and the values for k_∞ are consistent with previous reports of this parameter based on experiments in high pressures of He and vibrational deactivation of OH in collision with NO₂.

We derive a parameterization of the overall rate coefficient and show that present divergent evaluations of k₅ result in significant differences, both underestimating and overestimating the rate coefficient in different parts of the atmosphere. Further study of the temperature and pressure dependence of the branching ratios on HNO₃ and HOONO formation as well as of the atmospheric fate of HOONO are required to fully understand and model the atmospheric impact of the title reaction.