the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Calculating the aerosol asymmetry factor based on measurements from the humidified nephelometer system
Gang Zhao
Chunsheng Zhao
Yuxuan Bian
Jiangchuan Tao
Chuanyang Shen
Yingli Yu
The aerosol asymmetry factor (g) is one of the most important factors for assessing direct aerosol radiative forcing. However, little attention has been paid to the measurement and parameterization of g. In this study, the characteristics of g are studied based on field measurements over the North China Plain (NCP) using the Mie scattering theory. The results show that calculated g values for dry aerosol can vary over a wide range (between 0.54 and 0.67). Furthermore, when ambient relative humidity (RH) reaches 90 %, g is significantly enhanced by a factor of 1.2 due to aerosol hygroscopic growth. For the first time, a novel method of calculating g based on measurements from the humidified nephelometer system is proposed. This method can constrain the uncertainty of g to within 2.56 % for dry aerosol populations and 4.02 % for ambient aerosols, providing that aerosol hygroscopic growth is taken into account. Sensitivity studies show that aerosol hygroscopicity plays a vital role in the accuracy of predicting g.
- Article
(3067 KB) - Full-text XML
-
Supplement
(1524 KB) - BibTeX
- EndNote
In addition to aerosol optical depth and aerosol single-scattering albedo, the aerosol phase function is the most important factor for assessing direct aerosol radiative forcing (DARF) (Andrews et al., 2006; Russell et al., 1997). The Henyey–Greenstein phase function (PFHG) is a widely used method to parameterize the phase function (Toublanc, 1996; Boucher, 1998; Pandey and Chakrabarty, 2016) because it uses the aerosol asymmetry factor (g) as the only free parameter. The PFHG is expressed as
where θ is the angle between the incident light direction and the scattered light direction. In this respect, the free parameter g can reflect the angular aerosol scattering energy distribution. g is defined as follows:
where P(θ) is the normalized scattering phase function. As a result, g can be a computationally efficient parameter to replace the phase function in the study of aerosol radiative transfer properties (Toublanc, 1996; Hansen, 1969; Boucher, 1998). This replacement proves to be useful and has been widely accepted in previous studies (Hansen, 1969; Wiscombe and Grams, 1976; Sagan and Pollack, 1967; Andrews et al., 2006); however significant bias may arise in g-related PFHG when estimating photo-dissociation rates (Toublanc, 1996) and aerosol radiative forcing effects (Boucher, 1998). In the past, few studies have assessed the deviation when replacing the ambient phase function with the g-related PFHG (Pandey and Chakrabarty, 2016; Boucher, 1998; Wiscombe and Grams, 1976), and there are no known studies that use field measurements of aerosol optical properties to estimate the bias. Moreover, variations in g can influence the evolution of the atmospheric vertical structure by effecting the atmospheric radiative distribution. Kudo et al. (2016) also found that the vertical profile of the asymmetry factor plays an important role in altering vertical variations in the solar heating rate. Marshall et al. (1995) reported that a 10 % overestimation of g can systematically reduce aerosol climatic forcing by 12 % or more. Furthermore, Andrews et al. (2006) found that a 10 % reduction in g would result in a 19 % overestimation of atmosphere radiative forcing at the top of atmosphere (TOA). Therefore, an accurate estimation of g has the potential to greatly improve the assessment of the aerosol radiative effect.
There are several methods available to derive the g of aerosol particles under dry and ambient conditions, respectively. Horvath et al. (2016) measured the phase function of aerosols, calculated the g of aerosols, and found that the g-related PFHG can be used as a good approximation of the measured phase function. Many studies have used the Mie model (Bohren and Huffman, 2007) to calculate the phase function and have proven its reliability (Andrews et al., 2006; Marshall et al., 1995; Bian et al., 2017). Comprehensive attempts have been made to relate g to the hemispheric backscatter fraction (b). The value of b is the ratio of light scattered into the backward hemisphere compared to total light scattered in all directions (Wiscombe and Grams, 1976; Andrews et al., 2006; Horvath et al., 2016), and is defined as follows:
The main advantage of the backscatter ratio is that it can be measured with an integrating nephelometer equipped with a backscatter shutter (Charlson et al., 1974).
The free parameter g varies significantly for different aerosol types and different seasons. In previous studies, the g values have mainly been examined using the Mie scattering theory and the measured aerosol particle numbers size distribution (PNSD). D'Almeida et al. (1991) suggested that g ranges from 0.64 to 0.83 at a wavelength of 500 nm depending on the aerosol type and the season; their study also found a mean g value of 0.67 at an ambient relative humidity (RH). Furthermore, Hartley and Hobbs (2001) reported a median g value of 0.7 for aerosols along the east coast of the United States. Formenti et al. (2000) measured Saharan dust aerosol and found that the aerosol g values ranged from 0.72 to 0.73. Biomass burning aerosols in Brazil were found to have a low g value of 0.54 (Ross et al., 1998).
Some studies have examined the impacts of aerosol hygroscopic growth on the parameter g (Hartley and Hobbs, 2001; Kuang et al., 2015; Andrews et al., 2006) and found that variations in g with RH can have significant influences on aerosol radiative effects (Kuang et al., 2015, 2016; Andrews et al., 2006). Therefore, a parameterization scheme of g, which takes RH and aerosol hygroscopic growth into account, is necessary.
When exposed to the ambient atmosphere, aerosols can grow by taking up water, which causes their corresponding optical properties to change considerably. The κ-Köhler theory (Petters and Kreidenweis, 2007) is widely used to describe the hygroscopic growth of aerosol particles using a single aerosol hygroscopic growth parameter (κ) and the κ-Köhler equation, which is described as follows:
where Dd is the dry particle diameter; gf(RH) is the aerosol growth factor, defined as the ratio of the aerosol diameter at a given RH to the dry aerosol diameter (DRH∕Dd); T is the temperature; σs∕a is the surface tension of the solution; Mwater is the molecular weight of water; R is the universal gas constant; and ρw is the density of water. The aerosol hygroscopic growth parameter κ can be further used to investigate the influence of aerosol hygroscopic growth on aerosol optical properties (Tao et al., 2014; Kuang et al., 2015; Zhao et al., 2017) and aerosol liquid water contents (Bian et al., 2014).
According to the Mie theory, g is associated with aerosol particle number size distribution, the particle complex refractive index, the aerosol mixing state and ambient RH. At the same time, the aerosol morphology has a significant influence on g. Datasets from the humidified nephelometer system can partially account for all of these factors. The humidified nephelometer system consists of two parallel nephelometers, one of which measures dry aerosol scattering properties whilst the other measures aerosol scattering properties under well-controlled RH conditions. This system can give the light scattering enhancement factor (fRH), which is defined as , or the ratio of the aerosol scattering coefficient under given RH conditions to that under dry conditions. Each nephelometer can provide a scattering coefficient (σsca) and a back-scattering coefficient (βsca) at three wavelengths (450, 525, and 635 nm). σsca can be used to calculate the aerosol scattering Ångstrom index, which reflects the aerosol PNSD to some extent. In general, a larger value for the Ångstrom index always corresponds to a smaller predominant aerosol size. Variations in βsca and σsca can be used to deduce the aerosol black carbon (BC) mixing state (Ma et al., 2012). At the same time, datasets from the humidified nephelometer system can also be used alone to measure the aerosol hygroscopicity and provide an overall hygroscopic parameter κ (Kuang et al., 2017). In conclusion, measurements from the humidified nephelometer system might be used for estimating g under given RH conditions. However, there is no clear relationship between the measured datasets from the humidified nephelometer and g. Furthermore, the nonlinear influence of the above listed factors on g also makes it difficult to parameterize the g.
The random forest machine learning model is a powerful technique that can be used for classification and nonlinear regression (Huttunen et al., 2016; Breiman, 2001; Hu et al., 2017). This model is a widely used nonparametric machine learning algorithm that has several strengths. First, it involves fewer assumptions regarding the dependence between observations and outcomes when compared with traditional parametric regression models. Second, strict relationships among variables are not needed before implementing the model. Third, this learning model requires far less computing resources than deep learning. Finally, this model has very low risk of over fitting by averaging over an ensemble of decision trees. Thus, the random forest machine learning model is used in this work to study the calculation of g based on the datasets of the humidified nephelometer system.
In this study, the Mie scattering theory and field measurements over the North China Plain (NCP) are used to study the characteristics of g. Section 2 describes the related datasets used in this study. Details of the study on the characteristics of g and the impacts of aerosol hygroscopic growth on g are shown in Sect. 3.1. A new method, which is based on a random forest machine learning model, is introduced to calculate g in Sect. 3.2. We also discuss the impacts of g variations on the uncertainties of DARF in Sect. 3.3, and the corresponding results are presented in Sect. 4.3. Section 4.1 gives the calculated characteristics of g and Sect. 4.2 proves the feasibility of using the machine learning model to calculate g. At the same time, this method is validated by the ambient aerosol phase function measured with a charge-coupled device–laser aerosol detective system (CCD–LADS). Conclusions are given in Sect. 5.
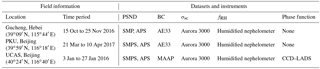
Datasets used in this study come from three field campaigns, which were conducted at three different sites in the NCP. These three field measurements were conducted at Gucheng in Hebei Province (Gucheng, 39∘09′ N, 115∘44′ E) from 15 October to 25 November in 2016, at the AERONET Beijing PKU station in Beijing (PKU, 39∘59′ N, 116∘18′ E) from 21 March to 10 April in 2017, and at the Yanqi Campus of the University of Chinese Academy of Sciences (UCAS, 40∘24′ N, 116∘40′ E) in the Huairou district in Beijing from 3 January to 27 January in 2016. Details of these locations are shown in Fig. S1 in the Supplement. The PKU station is located in the northwest of Beijing, between the 4th and 5th ring road. It is 11 km from the center of the megacity of Beijing, which is adjacent to Hebei Province and the megacity of Tianjin. In the abovementioned three areas, industrial manufacturing has led to heavy air pollution. Datasets for the PKU station are representative of urban aerosols in the NCP. Gucheng is located between two megacities (120 km from Beijing and 190 km from Shijiazhuang) in the NCP; therefore, the pollution conditions of Gucheng are a good representation of the continental background in the NCP. Details regarding the Gucheng station can be found in a study by Kuang et al. (2017). The UCAS station is 60 km away from the center of Beijing and is at the edge of the NCP, which makes it suitable for measuring the regional pollution properties of the NCP (Ma et al., 2016). More details about the measurement sites are available in Sect. S1 of the Supplement.
Table 1 lists the information for the field campaigns and the datasets used in this study. During the campaigns, sampled aerosols that had an aerodynamic diameter of less than 10µm are selected by an impactor (Mesa Labs, Model SSI2.5) at the inlet. These aerosols are then dried to below 30 % RH with a Nafion drying tube and lead to each instrument. Aerosol PNSDs ranging from 3 nm to 10 µm are measured using a scanning mobility particle sizer spectrometer (SMPS, TSI Inc., model 3936) and an aerodynamic particle sizer spectrometer (APS, TSI Inc., model 3321) with a temporal resolution of 5 min. Black carbon (BC) mass concentrations are measured by a multi-angle absorption photometer (MAAP model 5012, Thermo, Inc., Waltham, MA USA) at UCAS and by an Aethalometer (AE33)(Hansen et al., 1984; Drinovec et al., 2015) at PKU and Gucheng. The aerosol σsca is measured at wavelengths of 450, 525, and 635 nm by an Aurora 3000 nephelometer and the corresponding values are recorded every minute (Müller et al., 2011).
The fRH is measured by a self-constructed humidified nephelometer system. In this system, a humidifier is used to control the RH of the sample aerosol and σsca is measured for each of the controlled RH levels. The sample aerosol is humidified through a Gore-Tex tube, which is surrounded by a circulating water layer in a stainless steel tube. The RH is changed by changing the temperature of the circulating water, which is controlled by a water bath and software. For each cycle, the RH points are set to range from about 50 to about 90 % over 45 min. For most of the cases, the aerosol PNSDs are consistent over the cycle. These cycles of fRH values are abandoned when either the measured maximum or the minimum σsca values are beyond the range of 1.4 and 0.6 times the mean measured scattering coefficient of each cycle. The humidified nephelometer is described in detail by Kuang et al. (2017).
An ambient aerosol phase function with a time resolution of 5 min is measured at UCAS using a CCD–LADS. This system consists of a continuous laser, two charge-coupled device cameras, and corresponding fish eye lenses. The wavelength of the laser is 532 nm and a quarter-wave plate was mounted in front of the laser emitter to change the polarization state of the laser from linear to circular. The CCD–LADS can measure the ambient aerosol phase function at a wide angular range of 10–170∘ with a high resolution of 0.1∘. More details of the measurement system can be found in Bian et al. (2017).
3.1 Calculating characteristics of g based on the Mie scattering theory (gMie)
The Mie model (Bohren and Huffman, 2007) is applied to calculate the characteristics of gMie. When running the Mie model, aerosol PNSD, aerosol complex refractive index, BC mixing state, and BC mass concentration are essential. Its results include the aerosol phase function, and gMie can be calculated using Equation 2.
Mixing states of the BC come from field measurements. In the work by Ma et al. (2012), the mixing states of BC in the NCP are presented as both core-shell mixed and externally mixed. Ma et al. (2012) also provides the ratio of BC mass concentrations under an externally mixed state, Mext_BC, to total BC mass concentration, MBC as follows:
The mean value of rext_BC=0.51 (Ma et al., 2012) is used in this study. The size-resolved distribution of the BC mass concentration is the same as that used by Ma et al. (2012). The κ-Köhler theory and the Mie scattering model are employed to calculate gMie under different RH conditions. When the aerosol grows by taking up water, the BC is treated as a non-hygroscopic and insoluble core. The real time value κ, which is derived from the measurement of fRH, is used to account for aerosol hygroscopic growth. For each RH value, the growth factor can be calculated based on Equation 4. The corresponding ambient aerosol PNSD at a given RH can also be determined by applying the κ and Equation 4. The refractive index (), which accounts for water content in the particle, is derived as a volume mixture between the dry aerosol and water (Wex et al., 2002):
where fv, dry is the ratio of the dry aerosol volume to the total aerosol volume under a given RH condition; is the refractive index for dry ambient aerosols; and is the refractive index of water.
The refractive indices of BC, non-light-absorbing aerosols, and water, which are used in this study, are 1.8+0.54i (Kuang et al., 2015), (Wex et al., 2002), and , respectively. Then, the corresponding g values under the given RH and PNSD can also be calculated. More details on using the Mie model to calculate the aerosol phase function for different RH conditions can be found in Zhao et al. (2017).
3.2 Calculating g using the random forest machine learning model (gML)
In this study, the random forest machine learning model from the scikit-learn machine learning library (Hu et al., 2017; Pedregosa et al., 2011) was used to calculate g. The random forest model has two parameters: the number of input variables (npre) and the number of trees grown (ntree). In this study, the npre and ntree are determined by minimizing the relative difference of the gML and gMie. Details of choosing the values of npre and ntree are shown in Sect. S2. The npre and ntree are set as eight and thirty-two in this study, respectively. The eight input parameters include the three dry scattering coefficients, the three dry backscattering coefficients, the RH, and κ.
The measured datasets are divided into two parts: the training data for the random forest model and the testing data. All training datasets come from field measurements at Gucheng station, whereas the datasets from PKU are employed to test the accuracy of the model. With split datasets from different sites, the feasibility of the random forest model in the NCP can be guaranteed. Before calculating gMie, we compare the measured σsca from the dry nephelometer and calculate σsca from the Mie scattering model. These data, where the relative difference between the measured and calculated σsca is within 30 %, are used for the following analyses; therefore, instrument measurement inaccuracy can be avoided to some extent. More details regarding the data used is shown in Sect. S3.
To further avoid measurement uncertainties when training the random forest machine learning model, both the required input parameters and the predictors (g values) come from the calculations of the Mie scattering model. The Mie scattering model used aerosol PNSD and BC measurements from the field campaign in Gucheng. For each measured PSND and BC, the corresponding σsca and βsca under dry conditions at 450, 525, and 635 nm are modeled based on the Mie theory. With the concurrently measured κ values from the humidified nephelometer, the gMie values under different RH can also be determined. Then the modeled σsca, βsca under dry condition, the κ values, and the RH are used as the input data for the model and the corresponding gMie values are used as the prediction data.
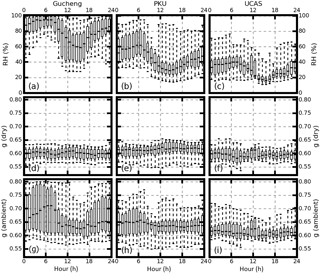
Figure 1Average diurnal pattern of RH (a, b, c), g values calculated from dry aerosols (d, e, f), and g values from ambient aerosols (g, h, i). Panels (a, d, g) are the results from Gucheng. Panels (b, e, h) are the results from PKU. Panels (c, f, i) are the results from UCAS. The box and whisker plots represent the 5th, 25th, 75th, and 95th percentiles.
3.3 Aerosol DARF estimations
Earth–atmosphere systems can be significantly influenced by aerosols through the scattering and absorption of energy. In this study, the Santa Barbara DISORT (discrete ordinates radiative transfer) Atmospheric Radiative Transfer (SBDART) model (Ricchiazzi et al., 1998) is employed to estimate the DARF. The characteristics of DARF relating to variations in g are studied.
The instantaneous DARF is calculated at the TOA for cloud-free conditions. DARF is defined as the difference between radiative flux at the TOA under present aerosol conditions and aerosol-free conditions:
where is the downward radiative irradiance flux with given aerosol distributions and is the radiative irradiance flux under aerosol-free conditions. The DARF at 50 km is calculated because almost all of the aerosols are distributed within the height of 50 km in the parameterization scheme (Liu et al., 2009). Wavelengths in the range of 0.25 to 4 µm are calculated for irradiance in this study.
Input data for the SBDART are as follows: vertical profiles of the aerosol optical properties, which include the aerosol extinction coefficient (σext), aerosol single scattering albedo (SSA), and g. All data have a vertical resolution of 50 m and come from the results of the Mie scattering model and the parameterized aerosol vertical distributions. Methods for parameterization and calculation of the aerosol optical profiles can be found in Sect. S4 or in Kuang et al. (2016) and Zhao et al. (2017). Atmospheric meteorological parameter profiles come from the results of the intensive radiosonde observations at the Meteorological Bureau of Beijing (39∘48′ N, 116∘28′ E) at 13:30 LT from July to September in 2008. Kuang et al. (2016) studied these measured profiles and found that the vertical distributions of these parameters, which include profiles for water vapor, pressure, and temperature, can be used as a good representation of the meteorological parameter profiles in the NCP during summer. The corresponding measured mean results during field measurement are used in this study and the details of these profiles are shown in Sect. S4. Surface albedo values are obtained from the Moderate Resolution Imaging Spectroradiometer (MODIS) V005 Climate Modeling Grid (CMG) Albedo Product (MCD43C3). The mean results of the surface albedo of Beijing from July to September in 2008 are used. The remaining input data for the SBDART are set to their default values (Ricchiazzi et al., 1998).
4.1 Characteristics of gMie
4.1.1 Characteristics of gMie at different sites
Figure 1 gives the statistical results for the calculated g properties at Gucheng, PKU, and UCAS. The RH values at the three sites show almost the same diurnal variation pattern (Fig. 1a, b, and c). The RH reaches a peak in the morning at approximately 06:00 LT , and then reaches its lowest value at approximately 16:00 LT in the afternoon. However, the mean values of RH are 77.7 % ± 20.9 % at Gucheng, 47.8 % ± 20.8 % at PKU, and 33.49 % ± 15.22 % at UCAS. The gMie values under dry conditions that are calculated by the measured PNSD have almost no diurnal patterns. The gMie values at PKU (0.614 ± 0.025) are slightly lower than those at Gucheng (0.601 ± 0.021) and UCAS (0.595 ± 0.023) (Fig. 1d, e, and f). The difference in the gMie values results from different aerosol properties at these sites. From Fig. S6, it can be noted that the peak diameter of the mean and median PNSD at Gucheng is located around 150 nm. However, the peak diameter of the mean and median PNSD at PKU is located at around 100 nm. The peak values of the mean and median diameter of the aerosol PNSD at UCAS is located at around 60 nm. At the same time, there are large partitions of small particles that are lower than 60 nm at PKU and UCAS. However, these particles, which are lower than 100 nm, do not really contribute to the total aerosol scattering. The aerosol PNSD at PKU is more dispersed than that at the Gucheng and UCAS sites, which corresponds to a larger variation in the g values. From Fig. S6g, h, and i, the size distribution of the aerosol scatter coefficient at around 500 nm contributes less to the scatter coefficient at PKU than to the scatter coefficients at Gucheng and UCAS. Thus these particles with a diameter larger than 500 nm contribute more to the aerosol scattering coefficient. As gMie increases with the aerosol diameter, the aerosol gMie under dry conditions at PKU tends to be larger than that at Gucheng and UCAS.
However, ambient gMie values have different patterns at different sites, as shown in Fig. 1g, h and i. The gMie values have an RH-related diurnal pattern at Gucheng, with a mean value of 0.668 ± 0.073; although gMie values show no diurnal variation at PKU and UCAS, where the mean values of gMie are 0.639 ± 0.049 and 0.618 ± 0.033, respectively. The variations in ambient gMie values mainly result from the variation in the aerosol hygroscopic growth under ambient conditions, which is highly related to the ambient RH. The gMie value is significantly influenced by RH when the RH is higher than 80 %, which is be detailed in Sect. 4.1.2. Ambient gMie values at Gucheng, PKU, and UCAS can vary from 0.57 to 0.8, 0.55 to 0.76, and 0.56 to 0.72, respectively; this makes them comparable to gMie values from Andrews et al. (2006), which range from 0.59 to 0.72.
4.1.2 Influence of RH on g
To assess the influence of RH on g, the gMie values are calculated under different RH conditions for each aerosol PNSD. The statistical results of gMie versus RH are shown in Fig. 2. The gMie value has a wide variation, ranging between 0.54 and 0.67 with the mean value located at 0.61, under dry conditions. However, the mean gMie value can change from 0.65 to 0.8 when the RH reaches 90 %. The gMie enhancement factor, which is defined as the ratio of gMie at a given RH and gMie under dry conditions, can reach a mean value of 1.2 at an RH of 90 %, which means that the gMie value under wet conditions is approximately 20 % higher than that under the dry conditions. This finding is consistent with that of Hartley and Hobbs (2001), who found that g is highly related to RH.
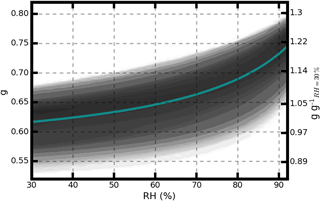
Figure 2Probability distributions of g under different RH conditions. The left y axis shows g values at different RH values and the right y axis shows the g enhancement factor, which is defined as the ratio of g at a given RH to the g value at dry conditions (RH = 30 %). The solid line (cyan) shows the mean result of the g values and the enhancement factor at different RH values.
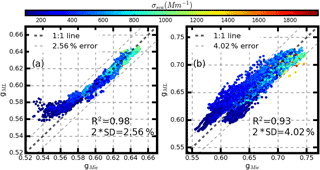
Figure 3Comparison of calculated g values (gMie) from the Mie model and predicted g values (gML) from the random forest model under (a) dry conditions and (b) ambient conditions at the PKU site. Colored dots represent the concurrently measured σsca corresponding to the time of g.
Contrary to RH, the aerosol complex refractive index has little influence on g and the uncertainties for g are less than 0.004 based on the Monte Carlo simulation of the g at different complex refractive index values. More details regarding the influence of the aerosol complex refractive index on g can be found in Sect. S6.
4.2 Calculating gML using the machine learning model
4.2.1 Feasibility of using the random forest model
We establish two independent random forest machine learning models to predict gML values under dry conditions and under ambient RH conditions, respectively.
When the random forest machine learning model is run for g values under dry conditions, σsca and βsca are used as the input for independent variables at three different wavelengths. The other two input parameters, RH and κ, are set to zero. The predictor g values come from the results of the Mie scattering model. Figure 3a shows the calculated and the predicted gML values from the random forest machine learning model under dry conditions at the PKU site. The results show that the gMie values and gML values have good consistency, with an R2 value of 0.98. Therefore, in 95 % of the cases, the relative difference between gMie and gML is within 2.56 %.
Figure 3b shows the comparison of the predicted gML values under different RH conditions and gMie values calculated by the Mie scattering model. The correlation coefficient between gMie and gML reaches 0.93, and 95 % of the relative differences are within 4.02 %. The random forest model has the potential to be a good method to predict g values under different RH conditions with high accuracy; the uncertainties of predicting g values using the random forest machine learning model is estimated to be 4.02 %.
The fill colors of the dots in Fig. 3 represent the concurrently measured σsca. It is shown that g values tend to be larger with an increase in σsca, which is in accordance with the particle scattering properties. When a particle has a larger diameter the σsca of the particle is higher, and there tends to be a larger partition of forward scattering light.
The reliability of the previous parameterization of the g using b is tested here. Wiscombe and Grams (1976) studied the relationship between b and g and gave the expression between them as follows:
This equation is widely used to calculate g from b (Andrews et al., 2006; Horvath et al., 2016; Kassianov et al., 2007). We use the field measurement results to test its reliability. The comparison results between calculated g values from the Mie scattering model and parameterized g values from Eq. (6) are shown in Fig. S9. From Fig. S9, we can see that the parameterized g values are prevalently larger than the calculated g values by approximately 10 %. When the σsca is smaller, the deviations become larger. Some other empirical relationships between b and g (Moosmüller and Ogren, 2017) are also tested. This parameterization scheme almost has the same result as Wiscombe and Grams (1976), which means that the previously established parameterization scheme is not applicable in the NCP
4.2.2 Sensitivity of the random forest model
Sensitivity studies are carried out to assess the influence of each input variable on gML. Based on the work of Müller et al. (2011), the uncertainties in total scattering are 4 % (450 nm), 2 % (525 nm), and 5 % (635 nm) for experiments with ambient air and laboratory generated white particles. For backscattering, the differences are higher and amount to 7 % (450 nm), 3 % (525 nm), and 11 % (635 nm). The uncertainty of the RH measured by the RH sensors is 1.7 % for RH ranges from 0 to 90 % (Kuang et al., 2017) and the uncertainty of the derived κ values is 6 % (Kuang et al., 2017). Monte Carlo simulations are conducted to study the sensitivity of the gML to the input parameters in three steps. First, the mean results of the measured dry σsca, dry βsca, RH, and κ values are used to predict the g value. Second, the dry σsca at 450 nm is randomly changed with a mean value of 0 and standard deviation of 4 % and the other inputs remain unchanged. The corresponding standard deviation of the predicted g value is used as the sensitivity of the gML to the σsca at 450 nm. Lastly, the sensitivity is determined for each input parameter and the uncertainties of the gML values to the input parameters are estimated. The total uncertainties of predicting g RH are derived when all of the input parameters are randomly changed with their corresponding uncertainties. For each test, the Monte Carlo simulations are carried out 20 000 times.
Table 2 gives the error to two standard deviations of the gML values corresponding to the uncertainties of the input parameters. From Table 2, it can be noted that the uncertainty of the measured σsca has little influence on the gML with g value uncertainties of 0.487, 0.492, and 0.486 % for 450, 525, and 635 nm, respectively. However, the measurement of the three βsca have larger uncertainties and lead to greater influence on predicting gML with uncertainties of 0.651, 0.486, and 0.710 %. The uncertainty of the RH (0.487 %) has little influence on predicting gML. However, the uncertainty of the derived κ values (6 %) influence the g values the most with a g value uncertainty of 1.92 %. The total uncertainty of predicting g due to uncertainties in the measurement parameters is 1.95 %. All in all, the total uncertainty of predicting the gML is estimated to be 4.47 %, considering the 4.02 % uncertainty of the random forest machine learning model from Sect. 4.2.1.
4.2.3 Validation of the random forest machine learning model
Datasets of the UCAS campaign are also used to validate the random forest machine learning model. On one hand, the gML values are calculated by using the random forest machine learning model with the measurements of the humidified nephelometer. On the other hand, ambient g values are calculated by using the measured phase function from the CCD–LADS gCCD according to the definition shown in Equation 2. The g values are then calculated, and the two methods are compared.
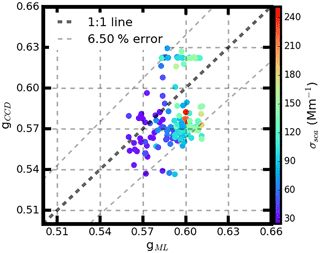
The results of the comparison of these two kinds of g values are shown in Fig. 4. As seen in Fig. 4, the values of gML and gCCD show good consistency. In 95 % of cases the relative differences between the gML and gCCD are within an acceptable range of 6.5 %, which is a little higher than the relative difference of the g values (4.02 %) between the machine learning method and the Mie scattering method. During the study period, the σsca ranged from 30 to 260 Mm−1, which led to cleaner conditions in UCAS than in Gucheng and PKU. Correspondingly, most of the gMie values are small and located in the 0.54 to 0.62 range, which is obviously lower than the range of values from other campaigns. At the same time, the surrounding conditions at UCAS during winter are relative dry, which results in small g values. These conditions may partially explain the higher difference between the gML and gCCD. With this validation, we conclude that the random forest machine learning model can give a reasonable g value based on the measurements of the humidified nephelometer system.
4.3 Estimating the impacts of g on DARF
4.3.1 Uncertainties of replacing the calculated phase function with the PFHG
When the PFHG is used to parameterize the calculated phase function using the Mie theory (PFMie), there are some deviations and the influence of these deviations should be estimated. The relative difference between the DARF from the PFMie and from the PFHG is used to estimate uncertainties when using the PFHG. First, the PFMie profiles are used as inputs to estimate DARFs. The PFMie is then replaced with the g-related PFHG, which is parameterized by gMie from the PFMie, and the DARFs are calculated again. These relative differences between the DARFs from the above two steps are recorded and compared. The relative differences at different zenith angle conditions are calculated to comprehensively estimate the influence of the PFHG.
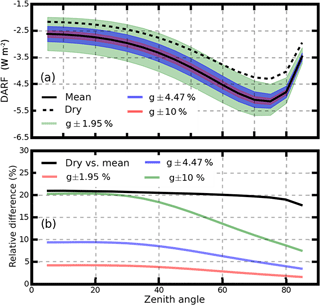
Figure 5 shows the estimated DARFs at different zenith angles. In Fig. 5a, DARF at the TOA can vary from −2.55 to −4.8 W m−2. When the PFMie is replaced by the PFHG, the calculated DARF ranges from −2.6 to −5.1 W m−2. The relative difference of the DARFs between the two methods ranges from 1.3 to 7.1 %, as shown in Fig. 5b. It is concluded that using the g-related PFHG to replace the PFMie to estimate aerosol radiative effects is applicable in the NCP, with a deviation of less than 7 %.
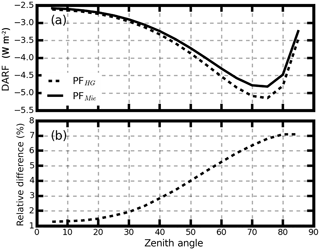
Figure 5(a) Estimated DARFs at different zenith angles using the g-related PFHG (dotted line) and the phase function calculated using the Mie scattering theory (solid line). (b) The relative difference between the DARFs in (a).
4.3.2 Impacts of g variations on DARF estimation
Variations in g can lead to significant changes in the estimated DARF (Kuang et al., 2016; Andrews et al., 2006; Mccomiskey et al., 2008). In this study, the uncertainty of the g value due to the uncertainty of the input parameters is estimated to be 1.95 % and the total variation in running the random forest machine learning model is estimated to be 4.47 %. At the same time, the g can vary about 10 % for different aerosol PNSD and can be enhanced by 20 % by an increase of the RH from 30 to 90 %. It is very important to know the extent of the variation in DARF corresponding to the uncertainties from g.
The variation in DARF from the uncertainties of g is calculated by increasing or decreasing g by 1.95, 4.47, and 10 % of the original g values, and then comparing the corresponding DARFs with the original values. To study the influence of RH on g and DARF, the DARF with the g values calculated from the dry parameterized aerosol population profile, is estimated.
Figure 6 shows the estimated DARFs with different variations in g and the corresponding variations in the estimated DARF. The results show that when g varies by 1.95 %, the DARF can vary by 4 %. However, variations of 4.47 and 10 % in g values can lead to variations of 9.4 and 21 % in the estimated DARF, respectively.
The estimated DARF using the parameterized aerosol profile, which considers the aerosol hygroscopic growth, is smaller than the DARF using the g profiles from the dry aerosol population. The g values under dry conditions are smaller than those under wet ambient conditions. Thus, there is larger partition of energy that is scattered forward which leads to less outgoing backscattering energy and a larger value of the estimated DARF.
When the DARF are estimated ignoring the impacts of aerosol hygroscopic growth on g, the relative difference can be as high as 20 % for all of the zenith angles. Thus, it is necessary to consider the aerosol hygroscopic growth when calculating the g values.
The characteristics of g in the NCP are studied based on the Mie scattering theory and field measurements from the Gucheng and PKU study sites. The results show that gMie values are 0.604 ± 0.025 at Gucheng and 0.615 ± 0.021 at PKU. The ambient gMie values at Gucheng show obvious diurnal variations due to variations in RH. When the ambient RH reaches 90 %, gMie can be enhanced by 20 % and the g values from different aerosol population can vary by 10 %. Comparison of the calculated gMie values from the Mie scattering model and the parameterized g values from the Wiscombe and Grams (1976) method shows that the parameterized g is overestimated by approximately 10 % and that the deviations become larger when the measured σsca is below 200 Mm−1.
The random forest machine learning model and datasets from the humidified nephelometer are employed to calculate gML values. The input data of the random forest model contain measured σsca and βsca at three wavelengths, RH, and the hygroscopic parameter κ. Except for RH, all input data came from measurements from the humidified nephelometer system (Kuang et al., 2017). The random forest model can significantly improve the accuracy of gML prediction. The uncertainties of the predicted gML values are constrained within 2.56 % under dry conditions and 4.02 % under ambient conditions and the uncertainties from the measurement of the humidified nephelometer can lead to a variation of 1.95 % in g, which mainly results from the inaccuracy of the derived κ. The total uncertainty of the g calculation using the random forest machine learning model is 4.47 %. This is the first time that a machine learning model and datasets from the humidified nephelometer system have been combined to study g. Additionally, this method can account for the influence of aerosol hygroscopic growth on g.
This new method for calculating g is validated by comparing the gML values from the random forest machine learning model and the gCCD values from the measured phase function by using the CCD–LADS. The g values from these two methods show good consistency, with 95 % of the data within a relative difference of 6.5 %.
The SBDART model is used to study the impacts of g on DARF. We first studied the relative differences between the estimated DARFs using the PFHG and the calculated phase function using the Mie theory, the measured mean aerosol PNSD, and BC mass concentration at the Gucheng and PKU study sites. The results show that the relative differences in DARF can be contained within 7.1 % of the mean when replacing the PFMie with the g-related PFHG. The PFHG has the potential to be a feasible parameterization scheme to study DARF in the NCP.
The sensitivity study shows that the maximum uncertainties of DARF are 4, 9.4, and 21 %, which correspond to the uncertainties of the g from instrument measurements, the machine learning model, and the variation of aerosol PNSD. However, when the DARF are estimated ignoring the effects of aerosol hygroscopic growth on g, the relative differences of the DARF are as large as 20 % for all zenith angles. It is necessary to parameterize the g accounting for the effect of aerosol hygroscopic growth.
This work furthers our understanding of the role of g in influencing aerosol radiative effects and can help reduce uncertainties in estimating DARF.
The measurement data involved in this study are available upon request to the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-9049-2018-supplement.
The authors declare that they have no conflict of interest.
This work is supported by the National Natural Science Foundation of China
(41590872) and the National Key R&D Program of China
(2016YFC020000: task 5).
Edited by: Armin Sorooshian
Reviewed by: two anonymous referees
Andrews, E., Sheridan, P. J., Fiebig, M., McComiskey, A., Ogren, J. A., Arnott, P., Covert, D., Elleman, R., Gasparini, R., Collins, D., Jonsson, H., Schmid, B., and Wang, J.: Comparison of methods for deriving aerosol asymmetry parameter, J. Geophys. Res., 111, D05S04, https://doi.org/10.1029/2004jd005734, 2006.
Bian, Y., Zhao, C., Xu, W., Zhao, G., Tao, J., and Kuang, Y.: Development and validation of a CCD-laser aerosol detective system for measuring the ambient aerosol phase function, Atmos. Meas. Tech., 10, 2313–2322, https://doi.org/10.5194/amt-10-2313-2017, 2017.
Bian, Y. X., Zhao, C. S., Ma, N., Chen, J., and Xu, W. Y.: A study of aerosol liquid water content based on hygroscopicity measurements at high relative humidity in the North China Plain, Atmos. Chem. Phys., 14, 6417–6426, https://doi.org/10.5194/acp-14-6417-2014, 2014.
Bohren, C. F. and Huffman, D. R.: Absorption and Scattering by a Sphere, in: Absorption and Scattering of Light by Small Particles, Wiley-VCH Verlag GmbH, 82–129, 2007.
Boucher, O.: On Aerosol Direct Shortwave Forcing and the Henyey–Greenstein Phase Function, J. Atmos. Sci., 55, 128–134, https://doi.org/10.1175/1520-0469(1998)055<0128:OADSFA>2.0.CO;2, 1998.
Breiman, L.: Random Forests, Machine Learning, 45, 5–32, https://doi.org/10.1023/a:1010933404324, 2001.
Charlson, R. J., Porch, W. M., Waggoner, A. P., and Ahlquist, N. C.: Background aerosol light scattering characteristics: nephelometric observations at Mauna Loa Observatory compared with results at other remote locations, Tellus, 26, 345–360, 1974.
D'Almeida, G. A., Koepke, P., and Shettle, E. P.: Atmospheric Aerosols: Global Climatology and Radiative Characteristics, J. Med. Microbiol., 54, 55–61, 1991.
Drinovec, L., Močnik, G., Zotter, P., Prévôt, A. S. H., Ruckstuhl, C., Coz, E., Rupakheti, M., Sciare, J., Müller, T., Wiedensohler, A., and Hansen, A. D. A.: The “dual-spot” Aethalometer: an improved measurement of aerosol black carbon with real-time loading compensation, Atmos. Meas. Tech., 8, 1965–1979, https://doi.org/10.5194/amt-8-1965-2015, 2015.
Formenti, P., Andreae, M. O., and Lelieveld, J.: Measurements of aerosol optical depth above 3570 m asl in the North Atlantic free troposphere: results from ACE-2, Tellus B, 52, 678–693, 2000.
Hansen, A. D. A., Rosen, H., and Novakov, T.: The aethalometer – An instrument for the real-time measurement of optical absorption by aerosol particles, Sci. Total Environ., 36, 191–196, https://doi.org/10.1016/0048-9697(84)90265-1, 1984.
Hansen, J. E.: Exact and Approximate Solutions for Multiple Scattering by Cloudy and Hazy Planetary Atmospheres, J. Atmos. Sci., 26, 478–487 https://doi.org/10.1175/1520-0469(1969)026<0478:eaasfm>2.0.co;2, 1969.
Hartley, W. S. and Hobbs, P. V.: An aerosol model and aerosol-induced changes in the clear-sky albedo off the east coast of the United States, J. Geophys. Res., 106, 9733–9748, https://doi.org/10.1029/2001jd900025, 2001.
Horvath, H., Kasahara, M., Tohno, S., Olmo, F. J., Lyamani, H., Alados-Arboledas, L., Quirantes, A., and Cachorro, V.: Relationship between fraction of backscattered light and asymmetry parameter, J. Aerosol Sci., 91, 43–53, https://doi.org/10.1016/j.jaerosci.2015.09.003, 2016.
Hu, X., Belle, J. H., Meng, X., Wildani, A., Waller, L. A., Strickland, M. J., and Liu, Y.: Estimating PM2.5 Concentrations in the Conterminous United States Using the Random Forest Approach, Environ. Sci. Technol., 51, 6936–6944, https://doi.org/10.1021/acs.est.7b01210, 2017.
Huttunen, J., Kokkola, H., Mielonen, T., Mononen, M. E. J., Lipponen, A., Reunanen, J., Lindfors, A. V., Mikkonen, S., Lehtinen, K. E. J., Kouremeti, N., Bais, A., Niska, H., and Arola, A.: Retrieval of aerosol optical depth from surface solar radiation measurements using machine learning algorithms, non-linear regression and a radiative transfer-based look-up table, Atmos. Chem. Phys., 16, 8181–8191, https://doi.org/10.5194/acp-16-8181-2016, 2016.
Kassianov, E. I., Flynn, C. J., Ackerman, T. P., and Barnard, J. C.: Aerosol single-scattering albedo and asymmetry parameter from MFRSR observations during the ARM Aerosol IOP 2003, Atmos. Chem. Phys., 7, 3341–3351, https://doi.org/10.5194/acp-7-3341-2007, 2007.
Kuang, Y., Zhao, C. S., Tao, J. C., and Ma, N.: Diurnal variations of aerosol optical properties in the North China Plain and their influences on the estimates of direct aerosol radiative effect, Atmos. Chem. Phys., 15, 5761–5772, https://doi.org/10.5194/acp-15-5761-2015, 2015.
Kuang, Y., Zhao, C. S., Tao, J. C., Bian, Y. X., and Ma, N.: Impact of aerosol hygroscopic growth on the direct aerosol radiative effect in summer on North China Plain, Atmos. Environ., 147, 224–233, 2016.
Kuang, Y., Zhao, C., Tao, J., Bian, Y., Ma, N., and Zhao, G.: A novel method for deriving the aerosol hygroscopicity parameter based only on measurements from a humidified nephelometer system, Atmos. Chem. Phys., 17, 6651–6662, https://doi.org/10.5194/acp-17-6651-2017, 2017.
Kudo, R., Nishizawa, T., and Aoyagi, T.: Vertical profiles of aerosol optical properties and the solar heating rate estimated by combining sky radiometer and lidar measurements, Atmos. Meas. Tech., 9, 3223–3243, https://doi.org/10.5194/amt-9-3223-2016, 2016.
Liu, P., Zhao, C., Zhang, Q., Deng, Z., Huang, M., Xincheng, M. A., and Tie, X.: Aircraft study of aerosol vertical distributions over Beijing and their optical properties, Tellus B, 61, 756–767, 2009.
Ma, N., Zhao, C. S., Müller, T., Cheng, Y. F., Liu, P. F., Deng, Z. Z., Xu, W. Y., Ran, L., Nekat, B., van Pinxteren, D., Gnauk, T., Müller, K., Herrmann, H., Yan, P., Zhou, X. J., and Wiedensohler, A.: A new method to determine the mixing state of light absorbing carbonaceous using the measured aerosol optical properties and number size distributions, Atmos. Chem. Phys., 12, 2381–2397, https://doi.org/10.5194/acp-12-2381-2012, 2012.
Ma, N., Zhao, C., Tao, J., Wu, Z., Kecorius, S., Wang, Z., Größ, J., Liu, H., Bian, Y., Kuang, Y., Teich, M., Spindler, G., Müller, K., van Pinxteren, D., Herrmann, H., Hu, M., and Wiedensohler, A.: Variation of CCN activity during new particle formation events in the North China Plain, Atmos. Chem. Phys., 16, 8593–8607, https://doi.org/10.5194/acp-16-8593-2016, 2016.
Marshall, S. F., Covert, D. S., and Charlson, R. J.: Relationship between asymmetry parameter and hemispheric backscatter ratio: implications for climate forcing by aerosols, Appl. Optics, 34, 6306–6311, https://doi.org/10.1364/AO.34.006306, 1995.
Mccomiskey, A., Schwartz, S. E., Schmid, B., Guan, H., Lewis, E. R., Ricchiazzi, P., and Ogren, J. A.: Direct aerosol forcing: Calculation from observables and sensitivities to inputs, J. Geophys. Res., 113, D09202, https://doi.org/10.1029/2007JD009170, 2008.
Moosmüller, H. and Ogren, J. A.: Parameterization of the Aerosol Upscatter Fraction as Function of the Backscatter Fraction and Their Relationships to the Asymmetry Parameter for Radiative Transfer Calculations, Atmosphere, 8, 133, https://doi.org/10.3390/atmos8080133, 2017.
Müller, T., Laborde, M., Kassell, G., and Wiedensohler, A.: Design and performance of a three-wavelength LED-based total scatter and backscatter integrating nephelometer, Atmos. Meas. Tech., 4, 1291–1303, https://doi.org/10.5194/amt-4-1291-2011, 2011.
Pandey, A. and Chakrabarty, R. K.: Scattering directionality parameters of fractal black carbon aerosols and comparison with the Henyey-Greenstein approximation, Opt. Lett., 41, 3351–3354, https://doi.org/10.1364/OL.41.003351, 2016.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion,B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg,V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, E.: Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 12, 2825–2830, 2011.
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007.
Ricchiazzi, P., Yang, S., Gautier, C., and Sowle, D.: SBDART: A Research and Teaching Software Tool for Plane-Parallel Radiative Transfer in the Earth's Atmosphere, B. Am. Meteorol. Soc., 79, 2101–2114, https://doi.org/10.1175/1520-0477(1998)079<2101:sarats>2.0.co;2, 1998.
Ross, J. L., Hobbs, P. V., and Holben, B.: Radiative characteristics of regional hazes dominated by smoke from biomass burning in Brazil: Closure tests and direct radiative forcing, J. Geophys. Res., 103, 31925–31941, 1998.
Russell, P. B., Kinne, S. A., and Bergstrom, R. W.: Aerosol climate effects: Local radiative forcing and column closure experiments, J. Geophys. Res., 102, 9397–9407, 1997.
Sagan, C. and Pollack, J. B.: Anisotropic nonconservative scattering and the clouds of Venus, J. Geophys. Res., 72, 469–477, https://doi.org/10.1029/JZ072i002p00469, 1967.
Tao, J. C., Zhao, C. S., Ma, N., and Liu, P. F.: The impact of aerosol hygroscopic growth on the single-scattering albedo and its application on the NO2 photolysis rate coefficient, Atmos. Chem. Phys., 14, 12055–12067, https://doi.org/10.5194/acp-14-12055-2014, 2014.
Toublanc, D.: Henyey-Greenstein and Mie phase functions in Monte Carlo radiative transfer computations, Appl. Optics, 35, 3270–3274, https://doi.org/10.1364/ao.35.003270, 1996.
Wex, H., Neusüß, C., Wendisch, M., Stratmann, F., Koziar, C., Keil, A., Wiedensohler, A., and Ebert, M.: Particle scattering, backscattering, and absorption coefficients: An in situ closure and sensitivity study, Journal of Geophysical Research: Atmospheres, 107, LAC 4-1-LAC 4-18,, https://doi.org/10.1029/2000JD000234, 2002.
Wiscombe, W. J. and Grams, G. W.: The Backscattered Fraction in two-stream Approximations, J. Atmos. Sci., 33, 2440–2451, https://doi.org/10.1175/1520-0469(1976)033<2440:TBFITS>2.0.CO;2, 1976.
Zhao, G., Zhao, C., Kuang, Y., Tao, J., Tan, W., Bian, Y., Li, J., and Li, C.: Impact of aerosol hygroscopic growth on retrieving aerosol extinction coefficient profiles from elastic-backscatter lidar signals, Atmos. Chem. Phys., 17, 12133–12143, https://doi.org/10.5194/acp-17-12133-2017, 2017.