the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Errors in nanoparticle growth rates inferred from measurements in chemically reacting aerosol systems
Peter H. McMurry
In systems in which aerosols are being formed by chemical transformations, individual particles grow due to the addition of molecular species. Efforts to improve our understanding of particle growth often focus on attempts to reconcile observed growth rates with values calculated from models. However, because it is typically not possible to measure the growth rates of individual particles in chemically reacting systems, they must be inferred from measurements of aerosol properties such as size distributions, particle number concentrations, etc. This work discusses errors in growth rates obtained using methods that are commonly employed for analyzing atmospheric data. We analyze “data” obtained by simulating the formation of aerosols in a system in which a single chemical species is formed at a constant rate, R. We show that the maximum overestimation error in measured growth rates occurs for collision-controlled nucleation in a single-component system in the absence of a preexisting aerosol, wall losses, evaporation or dilution, as this leads to the highest concentrations of nucleated particles. Those high concentrations lead to high coagulation rates that cause the nucleation mode to grow faster than would be caused by vapor condensation alone. We also show that preexisting particles, when coupled with evaporation, can significantly decrease the concentration of nucleated particles. This can lead to decreased discrepancies between measured growth rate and true growth rate by reducing coagulation among nucleated particles. However, as particle sink processes become stronger, measured growth rates can potentially be lower than true particle growth rates. We briefly discuss nucleation scenarios in which the observed growth rate approaches zero while the true growth rate does not.
- Article
(3758 KB) - Full-text XML
- BibTeX
- EndNote
Aerosol systems undergo transformations by processes that include coagulation, convection, deposition on surfaces, source emissions, nucleation, growth, etc. The aerosol general dynamic equation (GDE) (Friedlander, 2000; Gelbard and Seinfeld, 1979, 1980) describes the time rate of change of size-dependent particle concentration and composition by such processes. Recent work has focused on understanding processes that affect growth rates (GRs) of freshly nucleated atmospheric nanoparticles (Smith et al., 2008, 2010; Riipinen et al., 2012; Hodshire et al., 2016; Kontkanen et al., 2016; Tröstl et al., 2016). This is important because a particle's survival probability increases with GRs (McMurry and Friedlander, 1979; Weber et al., 1997; Kerminen and Kulmala, 2002; Kuang et al., 2010). Nucleated particles are more likely to form cloud condensation nuclei and affect climate when survival probabilities are high.
Following established conventions long used in modeling aerosol dynamics (Friedlander, 2000; Gelbard and Seinfeld, 1979, 1980), we define the particle GR as the net rate of change in diameter of individual particles due to the addition or removal of molecular species. (If evaporation exceeds addition, the GR would be negative.) While most work to date has focused on condensation and evaporation, chemical processes such as acid–base reactions, organic salt formation, liquid-phase reactions and the accretion of two or more organic molecules to form a larger compound with lower volatility may also contribute to growth (McMurry and Wilson, 1982; Barsanti et al., 2009; Riipinen et al., 2012; Lehtipalo et al., 2014). In a chemically reacting system, the total diameter GR is given by the sum of all such processes:
The effect of growth on the aerosol distribution function is given by (Heisler and Friedlander, 1977)
where the aerosol number distribution n(dp,t) is defined such that the number concentration of particles between dp and dp+ddp is equal to n(dp,t)ddp. Coagulation, including the coagulation of a molecular cluster with a larger particle, can also lead to particle growth. It is worthwhile, however, to treat coagulation and growth separately. The extent to which the coagulation of freshly nucleated molecular clusters contributes to measured GRs can be accurately determined only if the entire number distribution down to clusters of size 2 is accurately measured. In the absence of such data, the contributions of cluster coagulation to growth could erroneously be attributed to vapor uptake. Coagulation is accounted for with the coagulation integrals in the GDE and is a relatively well-understood process that can be described with reasonable confidence in models (Kürten et al., 2018; Chan and Mozurkewich, 2001). Growth involves processes that are not well understood for chemically complex aerosol systems, such as the atmosphere (Barsanti et al., 2009; Riipinen et al., 2012; Hodshire et al., 2016).
Progress towards understanding growth can be achieved through efforts to reconcile GRs that are observed experimentally with values predicted by models. Such work requires that size- and time-dependent GRs be accurately determined from observations. The literature includes many reports of observed GRs (Stolzenburg et al., 2005; Wang et al., 2013; Riccobono et al., 2012; Tröstl et al., 2016), but uncertainties in reported values are typically not well understood. Because it is usually not possible to measure the growth of individual particles as they undergo chemical transformations, GRs are calculated indirectly using time-dependent observations of aerosol properties such as number distributions or number concentrations larger than a given size. Those properties are typically affected by many processes, some poorly understood, that can affect reported GRs to an unknown extent.
A variety of approaches have been used to extract GRs from observations. We refer to these values as GRm, where the subscript “m” designates “measured”. Methods that we discuss include the following.
-
Maximum concentration method (Kulmala et al., 2012). During a nucleation event, particle concentrations in a given size bin increase from their initial values, passing through a peak before they eventually decrease. This technique involves noting the times that this maximum occurred in different size bins. The GR is obtained by first fitting a linear function of particle diameter (corresponding to the size bins) vs. time, and then calculating the slope of the fitted function.
-
Appearance time method (Lehtipalo et al. 2014). This approach has been used to analyze data from condensation particle counter (CPC) batteries (Riccobono, 2014), particle size magnifier (PSM) (Lehtipalo et al. 2014), etc. In brief, GRm is determined by the differences in concentration rise times (typically, either 5 or 50 % of the maximum) measured by the instruments with differing minimum detection sizes. A variation of this approach was reported by Weber et al. (1997), who estimated GRs from the observed time delay in measurements of sulfuric acid vapor and particles measured with a CPC with a minimum detectable size of about 3 nm.
-
Lognormal distribution function method (Kulmala et al., 2012). Lognormal distributions are fit to the growing mode of nucleated particles. GRm is defined as the GR of the geometric mean size of these distributions.
While these methods do not account for the effects of coagulation on measured changes in particle size, the literature includes approaches that explicitly account for such effects (Lehtinen et al., 2004; Verheggen and Mozurkewich, 2006; Kuang et al., 2012; Pichelstorfer et al., 2018). Other work has applied the above techniques after confirming that coagulation has an insignificant effect for the analyzed data (Kulmala et al., 2012) or explicitly accounting for the effects of coagulation on GRm (Stolzenburg et al., 2005; Lehtipalo et al., 2016).
This paper assesses errors of using GRm calculated using techniques commonly employed in the literature to infer particle GRs. Our results are especially germane to GR of freshly nucleated particles ranging in size from molecular clusters to about 40 nm. We use time-dependent distribution functions calculated numerically by McMurry and Li (2017) as “data”. The only process contributing to the addition or removal of molecular species in that work (i.e., to particle GRs as defined above) are condensation and evaporation. Because we understand this model system perfectly, GRtrue (i.e., the net GR due to molecular exchange through condensation and evaporation) can be calculated exactly. Errors in GRm due to coagulation, wall deposition, scavenging by preexisting particles or dilution are given by the difference between GRtrue and GRm. We do not examine errors associated with convection, source emission, etc.
We are not the first to examine factors that cause GRm to differ from GRtrue. For example, Kontkanen et al. (2016) used simulations to show that discrepancies between measured GR based on appearance time (AGR) and GR based on irreversible vapor condensation (CGR) can be significant. (Note that GRtrue used in this paper differs from CGR in that GRtrue also incorporates evaporation.) Our approach, which uses the nondimensional formulation described by McMurry and Li (2017), provides results that are generally applicable to nucleation and growth of a single chemical species, so long as it is being produced by chemical transformations at a constant rate, R. We show that the upper limit for overestimation of GRtrue by GRm occurs when nucleation takes place in the absence of preexisting aerosols and is collision controlled (i.e., when evaporation rates from even the smallest clusters occur at rates that are negligible relative to vapor condensation rates). Collision-controlled nucleation is an important limiting case because there is growing evidence that atmospheric nucleation of sulfuric acid with stabilizing species is well described as a collision-controlled process (Almeida et al., 2013; Kürten et al., 2018; McMurry, 1980). Because cluster evaporation, scavenging by preexisting aerosol, etc., all diminish the number of particles formed by nucleation, overestimation of GRtrue due to coagulation decreases as these processes gain in prominence. We do not explicitly study the effect of growth by processes other than condensation or evaporation, such as heterogeneous growth pathways that take place on or within existing particles. If such processes were to contribute significantly to growth, they would lead to higher GRs and therefore smaller relative errors in GRm due to coagulation. Additionally, we point out when particle sink processes consume nucleated particles at a fast rate (e.g., strong effects of dilution or scavenging by preexisting particles), GRm may not be used to estimate GRtrue. Our results help to inform estimates of uncertainties for systems with a single condensing species, or systems that can be modeled in a similar way to a single species system (Kürten et al., 2018).
2.1 Discrete-sectional model
We utilize the dimensionless discrete-sectional model described by McMurry and Li (2017) to simulate evolution of particle size distribution for a system with a single condensing species. We assume that the condensing species is produced at a constant rate by gas-phase reaction. Our code uses 200 discrete bins and 250 sectional bins, with a geometric volume amplification factor of 1.0718 for neighboring sections.
Physical processes that affect particle growth, including wall deposition, loss to preexisting particles, cluster evaporation and dilution, can be characterized by dimensionless parameters in this model. In the present study, however, not all aforementioned processes are discussed. Our previous work shows that wall losses, scavenging by preexisting particles and dilution have qualitatively similar effects on aerosol dynamics. Therefore, in this work we focus on preexisting aerosols and dilution to illustrate factors that contribute to errors in measured GRs and do not explicitly discuss wall deposition. A single dimensionless parameter, , is used to indicate the abundance of preexisting particles, with larger values representing a higher concentration of preexisting particles (or, equivalently, a slower rate at which the nucleating species is produced by chemical reaction). is calculated with the equation
where AFuchs is the Fuchs surface area concentration (Fuchs and Sutugin, 1971), kb is the Boltzmann constant, m1 is the mass of the monomer, R is the condensing species production rate and β11 fm is the monomer collision frequency function. The loss rate for particles containing k monomers is . This size dependence is included when solving the coupled differential equations for time-dependent cluster concentrations. Similarly, the dimensionless quantity M that characterizes dilution is given by the expression
where Qdil is the dilution flow rate and V is the volume of the system. Note the fractional dilution loss is independent of particle size. In addition to loss to preexisting particles and dilution, we consider the effect of cluster evaporation on particle growth with the assumption that evaporation follows the classical liquid droplet model. Two dimensionless parameters, E and Ω, are needed to fully describe the evaporation process. The dimensionless evaporation parameter, E, is proportional to the saturation vapor concentration of the nucleating species, while Ω is the dimensionless surface tension (Rao and McMurry, 1989; McMurry and Li, 2017). The evaporation rate for particles containing k monomers, Ek, is calculated with a discretized equation of the form
where c(i,k) is the dimensionless collision frequency between a monomer and a particle containing k monomers. To simplify our discussion, Ω is fixed to be 16 throughout this work (a representative value for the surface tension of sulfuric acid aqueous solutions), while the value of E is varied.
The solution to the GDE for a constant rate system (R = constant) depends on dimensionless time, cluster size and the dimensionless variables , M, E, Ω, etc., but is independent of the rate at which condensing vapor is produced by chemical reaction. That rate is required to transform the computed nondimensional solutions to dimensional results using simple multiplicative expressions given by McMurry and Li (2017):
In the above equations, is the dimensionless concentration of particle-containing k monomers, τ is the dimensionless time, is the dimensionless particle size and v1 is the monomer volume. Assuming a monomer volume of cm3 (volume of one sulfuric acid plus one dimethylamine molecule with a density of 1.47 g cm−3), would be equivalent to a dimensional particle size of 16.4 nm.
2.2 Evaluation of measured growth rate (GRm)
At time t1 and t2, if two particle sizes dp,t1 and dp,t2 are used to represent the particle size distribution, the measured GR can be calculated using the following equation as a first-order approximation:
If is available for a time series , GR can also be obtained by derivatizing a fitting function dp=dp(t) to obtain GR at any time ta:
To implement Eqs. (7) or (8), it is necessary to choose a particle size that is representative of the particle size distribution at a given time. The choice of this representative size varies among publications and can depend on the types of available data. Based on previous studies (Kulmala et al., 2012; Lehtipalo et al., 2014; Stolzenburg et al., 2005; Yli-Juuti et al., 2011), we have selected four representative sizes for discussion: , , and . At a given time τ, is the particle size at which reaches its local maximum. If the shape of the mode is lognormal, is equal to the geometric mean of the distribution. As suggested by Kulmala et al. (2012), the lognormal distribution method involves calculating GRs from observed time-dependent trends of . The maximum concentration method is based on the time when particles in a given size bin, , pass through their maximum (100 %) concentration (Lehtinen and Kulmala, 2003). The appearance time method is based on the time when particle concentrations in a bin, , pass through a specified percentage of its maximum (we have used 50 %). GRs are sometimes based on total concentrations of particles larger than a specified size. We refer to the particle size above, for which the total number concentration of particles reaches 50 % of its maximum value as . This approach is especially useful when measurements are carried out with a battery of CPCs with differing cutoff sizes. For simplicity, in this paper we assume that CPC detection efficiencies increase from 0 to 100 % at a given cutoff size. In practice, measured size-dependent detection efficiencies are typically used when analyzing CPC battery data. Figure 1 shows the location of these representative sizes at τ=20, 60 and 100 for two nucleation scenarios in the absence of preexisting particles. , , and are marked as points, with their y coordinates representing particle concentrations at corresponding sizes.
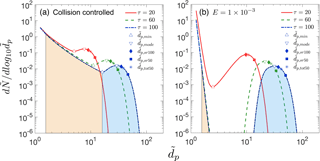
Figure 1Particle size distributions at dimensionless times τ=20, 60 and 100 (a) for collision-controlled nucleation (E=0) and (b) when evaporation is included with . Division of the distribution into monomer, cluster and nucleation mode is displayed for τ=100, with beige and light blue indicating the range of clusters and nucleation mode. Clusters and nucleation mode are separated by , where is at a local minimum. Characteristic sizes , , and are marked for each time. The relationship between symbols and characteristic sizes is shown only for τ=100.
As will be shown later, values of GRm obtained with , , or are not equal. To differentiate these cases, GRm are notated as GRm,mode, GRm,sr100, GRm,sr50 and GRm,tot50 accordingly.
2.3 Evaluation of true growth rate (GRtrue)
The true GR (GRtrue) defined in this paper follows the Lagrangian approach (Olenius et al., 2014), i.e., tracking the volume change of individual particles, and only including molecular species exchange by condensation and evaporation. It is calculated with the following expression:
where is the representative size, is the concentration of monomers and Ek is the particle evaporation rate given by Eq. (5).
If evaporation is negligible (E=0) and is constant, Eq. (9) leads to a higher GR for smaller particles, mainly because of the increased monomer collision frequency relative to particle size (Tröstl et al., 2016). Throughout this work Eq. (9) is used to evaluate true particle GR. Note GRtrue is calculated from dimensionless size and time, and is therefore dimensionless. Since we focus on relative values of true and measured GRs, our conclusions are unaffected by the dimensionality of GR. However, dimensionless GRs can be converted to dimensional values with Eq. (6).
3.1 Error of using GRm,mode as GRtrue
As mode diameter () is often employed to derive particle GR, in this section we discuss the error of using GRm,mode as a substitute for GRtrue in the absence of preexisting particles. The effect of preexisting particles is discussed in Sect. 3.3.
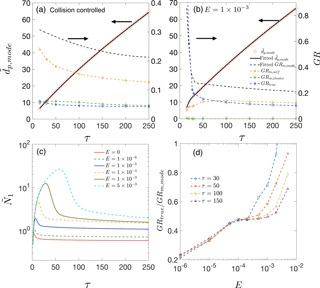
Figure 2(a) and various growth rates as functions of time for collision-controlled nucleation. Dashed black lines show the value of GRm,mode. Yellow, green and blue dashed lines represent GRm,self, GRm,cluster and GRtrue, respectively. (b) The same quantities as are shown in panel (a) but with the evaporation constant set to . For both panels (a) and (b), the left axis shows values for the solid lines and the right axis shows values for the dashed lines. (c) Monomer concentration as functions of time for different values of E. (d) GRtrue ∕ GRm,mode for different values of E at τ=30, 50, 100 and 150.
Both condensation and coagulation lead to growth of . To understand their relative importance, we attribute GRm,mode to three processes: monomer condensation minus evaporation (GRtrue), coagulation of the mode with clusters (GRm,cluster) and self-coagulation of the mode (GRm,self). The last two processes are the main causes of the discrepancy between GRm,mode and GRtrue. To evaluate GRm,cluster and GRm,self, the range of “clusters” and “mode” are defined as illustrated in Fig. 1 by the two shaded regions at τ=100: clusters (beige) and nucleation mode (light blue). Clusters and nucleation mode are separated by , where is at a local minimum. Stolzenburg et al. (2005) assumed the nucleation mode is lognormal and calculated GRtrue and GRm,self with the method of moments. In this work, since the mode for collision-controlled nucleation deviates significantly from lognormal (see Fig. 1a), no assumption regarding the shape of the nucleation mode is made. Instead, GRm,cluster and GRm,self are calculated with the first-order numerical approximation method outlined in Appendix A.
The calculation results are summarized by Fig. 2. We first consider collision-controlled nucleation (E=0). For this nucleation scenario, Fig. 2a shows on the left y axis and GR values on the right. A third-order polynomial is used for fitting and is plotted as a solid black line. Differentiating the fitted polynomial with respect to time gives the value of GRm,mode. It is clear that GRtrue only accounts for a small fraction (17–20 %) of GRm and is on par with the contribution of GRm,cluster (15–22 %). Self-coagulation is the major contributor (62–78 %) to GRm. Thus, using GRm,mode as a substitute for GRtrue leads to an overestimation by as much as a factor of about 6. We believe collision-controlled nucleation (E=0) in the absence of other particle loss mechanisms such as wall deposition (W=0) and scavenging by preexisting particles () provides an upper limit for overestimation of GRtruefor a constant rate system (R = constant). This is because these conditions lead to the maximum number of particles that can be produced by nucleation. High concentrations lead to high coagulation rates, and it is coagulation that is primarily responsible for errors in GRm. Furthermore, as is discussed below, the absence of evaporation and scavenging by nucleated particles keeps monomer concentrations low relative to values achieved when E≠0 (see Fig. 2a). Low monomer concentrations reduce the value of GRtrue, thereby increasing relative errors in GRm.
Distinctive features of particle growth emerge when cluster evaporation is included by setting . Figure 2b shows results for this nucleation scenario. Most noticeably, particles grow considerably faster at early stages of simulation. This occurs because evaporation depletes clusters and correspondingly increases monomer concentration. In the absence of preexisting particles, monomer concentration accumulates until the supersaturation is high enough for nucleation to take place (see Fig. 2c). The accumulated monomers then rapidly condense on the nucleated particles, leading to the rapid particle growth shown in Fig. 2b. To capture this rapid growth, two third-order polynomials are used to fit values for τ<40 and τ>35, respectively, with an overlapping region for . Furthermore, in comparison to collision-controlled nucleation, contribution of GRm,cluster to GRm,mode becomes negligible, due to decreased cluster concentration by evaporation. For τ>30, GRtrue accounts for about 40–55 % of GRm,mode, larger than that of collision-controlled nucleation; for τ<25, GRtrue almost entirely accounts for GRm,mode and even exceeds GRm,mode at the very beginning of the nucleation. GRtrue ∕ GRm,mode > 1 indicates a rapidly forming nucleation mode, in which freshly nucleated particles enter the mode and skew the mode distribution toward smaller sizes, slowing down the shift of the mode peak towards larger values.
Increase of GRtrue ∕ GRm,mode by evaporation is explained by the elevated monomer concentration due to particle volatility and the smaller number of particles formed by nucleation: the former increases GRtrue, and the latter decreases GRm,self and GRm,cluster. Figure 2c plots monomer concentration as a function of time for several values of E. Noticeably, monomer concentration increases with E since higher cluster evaporation rates require higher monomer concentrations (i.e., higher supersaturation) to overcome the energy barrier of nucleation. Once nucleation takes place, high monomer concentration leads to rapid nanoparticle GRs.
Figure 2d shows GRtrue ∕ GRm,mode at τ=30, 50, 100 and 150 for several E values. At a given time, GRtrue ∕ GRm,mode clearly increases with E: when evaporation rates are not negligible (i.e., E≠0), GRm,mode is closer to GRtrue than occurs when E=0. Again, this is because the elevated monomer concentrations increase GRtrue and the lowered concentrations of clusters and nucleated particles decrease GRm,cluster and GRm,self. As E approaches 0, the value of GRtrue ∕ GRm,mode converges to that of the collision-controlled nucleation (∼ 0.2). One data point, corresponding to and τ=30, with a value of 1.8, is not shown in Fig. 2d. It has a value significantly greater than unity because of the large quantities of nucleated particles entering the mode, skewing the mode peak toward smaller sizes.
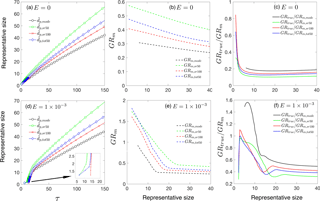
Figure 3(a) , , and as functions of time. (b) Measured growth rates GRm,mode, GRm,sr50, GRm,sr100 and GRm,tot50 as functions of representative sizes. (c) Ratio of true growth rate to measured growth rate, GRtrue ∕ GRm. Panels (a)–(c) are for collision-controlled nucleation with E=0. Panels (d)–(f) show the same quantities as are shown in panels (a)–(c) but with .
3.2 Comparison of representative sizes
In this section we examine how observed GR depends on the choice of a representative size. The application of GRm,mode to deduce GRtrue, though convenient in practice, depends on the existence of a nucleation mode. However, the nucleation mode is usually not well defined in the early stage of nucleation. In contrast, GRs based on other representative sizes (, and ) are not dependent on mode formation and are available for all particle sizes. In light of this, GRm,sr100, GRm,sr50 and GRm,tot50 have often been employed to describe the GR of small particles (< 5 nm). The effects of preexisting particles are neglected in this section (i.e., ) but are discussed in Sect. 3.3.
For collision-controlled nucleation, , , and are plotted as functions of time in Fig. 3a. The magnitude of the representative sizes follow < < < , as was previously illustrated in Fig. 1a. < indicates that a certain measurement bin first reaches its maximum concentration and becomes a local maximum at a later time. This is true for collision-controlled nucleation with a decreasing peak concentration but is not necessarily true for other nucleation scenarios. The observed GRs (i.e., slope of curves in Fig. 3a) are shown in Fig. 3b as a function of representative size, with a clear relationship GRm,mode < GRm,sr100 < GRm,tot50 < GRm,sr50. Note that GRm,mode is not available for small sizes, indicating the nucleation mode is yet to form at the early stage of nucleation. Figure 3c shows GRtrue ∕ GRm as a function of representative size, with GRtrue calculated with Eq. (9). Clearly GRtrue accounts for the highest percentage of GRm at the start of nucleation. This is partly due to higher monomer concentrations (see red solid curve in Fig. 2c) and partly due to Eq. (9), which leads to higher true GR for smaller particles: the addition of a monomer leads to a bigger absolute as well as fractional diameter growth for small particles.
Figure 3d–f are counterparts of Fig. 3a–c, but with evaporation constant E set to . Figure 3d shows that and increase relatively slowly at the start of the simulation (see the amplified figure at the lower right corner of Fig. 3d; for reference, the dimensionless sizes of monomer, dimer and trimer are 1.24, 1.56 and 1.79, respectively). Subsequently, a marked change slope of the curve is observed, indicating accelerated particle growth. This reflects that nucleation occurs with a burst of particle formation following a process of monomer and cluster accumulation. The slow growth of the smallest clusters is an indication that the accumulation process is slow due to the strength of the Kelvin effect.
Figure 3e shows GRm obtained by curve fitting after the nucleation burst and Fig. 3f shows the corresponding GRtrue ∕ GRm values. Different from collision-controlled nucleation, there is a sharp rise in the GRtrue ∕ GRm value at the start of nucleation. This is due to the sharp decrease in the evaporation term in Eq. (9), causing the value of GRtrue to increase sharply. As nucleation progresses, the ratio of GRtrue to GRm,sr100, GRm,tot50 and GRm,sr50 comes close to 1, with GRm,mode not yet available. Eventually, GRtrue ∕ GRm for all representative sizes decreases and falls into the range of 30–50 %, with GRm,mode giving the best estimate of GRtrue. Note the value of GRtrue ∕ GRm,mode significantly exceeds unity for due to the distortion of the mode toward smaller sizes by the high flux of freshly nucleated particles into the mode.
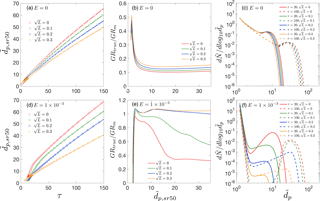
Figure 4Effect of preexisting particles on particle growth rate. (a) as a function of time. (b) Ratio of true growth rate to measured growth rate, GRtrue ∕ GRm,sr50. (c) Particle size distributions at τ=20 and τ=100. Panels (a)–(c) are for collision-controlled nucleation with E=0 and , 0.1, 0.2, 0.3. Panels (d)–(f) show the same quantities as are shown in panels (a)–(c) but with .
3.3 Effect of preexisting particles
Preexisting particles act as particle sinks to decrease the intensity of nucleation. Similarly, in chamber experiments, though loss to preexisting particles is often eliminated by using air that is initially particle free, loss of particles to chamber walls is inevitable. Since wall loss and loss to preexisting particles have a qualitatively similar effect on nucleation (McMurry and Li, 2017), we selectively examine the effect of preexisting particles on GR measurements to qualitatively illustrate the effects of all of these processes. To probe the initial stage of nucleation, we use as the basis for our analysis, with a comparison of representative sizes presented at the end of this section. As to the magnitude of , we choose based on previous work. It was shown in Fig. 2b in McMurry and Li (2017) that as exceeds 0.1, particle size distributions begin to deviate discernably from the collision-controlled case. In addition, was observed in the ANARChE field campaign carried out in Atlanta for nucleation events with sulfuric acid as the major nucleating species (Kuang et al., 2010).
The influence of preexisting particles on the discrepancy between true and measured GR (GRtrue ∕ GRm) is twofold. On the one hand, preexisting particles can decrease monomer concentration, which leads to a smaller GRtrue. On the other hand, preexisting particles reduce coagulation by scavenging nucleated particles, which could result in a narrower gap between GRtrue and GRm. Therefore, the response of GRtrue ∕ GRm to depends on the relative magnitude of these two competing effects. Figure 4a shows as a function of time for several values and Fig. 4b displays the corresponding GRtrue ∕ GRm values. It can be seen that GRtrue ∕ GRm positively correlates with , indicating preexisting particles are more effective in removing nucleated particles than reducing monomer concentrations. In fact, as further demonstrated by Fig. 4c, monomer concentrations (leftmost point of all the curves) are barely affected: scavenging of monomers by preexisting particles is offset by less condensation of monomers onto nucleated particles. Note that for the range of values examined, the presence of preexisting particles alter GRtrue ∕ GRm values by no more than 50 % for collision-controlled nucleation.
Figure 4d–f show the same quantities as are shown in Fig. 4a–c, but with E set to instead of zero. In contrast to collision-controlled nucleation, preexisting particles significantly affect the nucleation process when cluster evaporation is taken into account. As increases, Fig. 4e shows GRtrue ∕ GRm converges to a value slightly larger than unity. This indicates that the contribution of coagulation to measured GR approaches zero as becomes large; or equivalently, the concentration of nucleated particles is severely decreased by preexisting particles. Values of GRtrue ∕ GRm,sr50 slightly exceed unity for large sizes (Fig. 4f) due to the slightly higher condensational GRs of smaller particles in the nucleation mode. This shifts values of towards smaller sizes than would occur if all particles were to grow at the same rate, causing GRm,sr50 to be smaller than GRtrue.
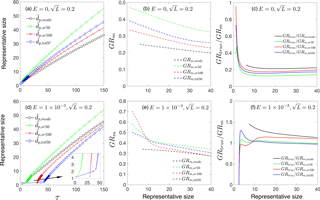
Figure 5(a) , , and as functions of time. (b) Measured growth rate GRm,mode, GRm,sr50, GRm,sr100 and GRm,tot50 as functions of representative sizes. (c) Ratio of true growth rate to measured growth rate, GRtrue ∕ GRm. Panels (a)–(c) are for collision-controlled nucleation with E=0 and . Panels (d)–(f) show the same quantities as are shown in panels (a)–(c) but with .
The decrease in nucleated particle concentration is further demonstrated in Fig. 4f. From to , the peak concentration of nucleated particles dropped by about 3 orders of magnitude. Such a decrease in concentration of nucleated particles results from the limiting effect of on monomer concentration. If preexisting particles are absent, then no major loss mechanisms for monomers exist prior to the nucleation burst. Monomers would accumulate until the nucleation energy barrier could be overcome: the higher the energy barrier, the higher the monomer concentration prior to nucleation, as shown in Fig. 2c. The elevated monomer concentration then leads to rapid growth of freshly nucleated particles immediately following the nucleation burst. However, in the presence of preexisting particles (i.e., ), monomer concentration can only increase to the point at which its production and consumption by preexisting particles reach balance, prohibiting its concentration from reaching a high value even prior to the nucleation burst. To facilitate comparison with experimental results, in Appendix B we provide an example of conversion from dimensionless distributions and GRs to dimensional ones.
Finally, Fig. 5 examines the difference between representative sizes used to calculate GRm when loss to preexisting particles is accounted for. Two cases are presented: (1) collision-controlled nucleation (E=0) with (Fig. 5a–c) and (2) nucleation accounting for both cluster evaporation and scavenging by preexisting particles ( and ; Fig. 5d–f). For collision-controlled nucleation with , the preexisting particles change nucleation only slightly, although GRm decreases and GRtrue ∕ GRm increases to a minor extent compared to collision-controlled nucleation in the absence of a preexisting aerosol (compare Figs. 5a–c to 3a–c). The analysis made in the discussion of Fig. 3a–c still stands for Fig. 5a–c. For nucleation with evaporation and preexisting particles coupled together (Fig. 5d–f), three features are worthy of attention. First, compared to evaporation-only nucleation, GRm is significantly decreased for small particle sizes. For , GRm is no larger than 0.7 with preexisting particles but can be greater than 1.5 without (refer to Fig. 3e). Second, as shown in Fig. 5f, GRtrue ∕ GRm,sr50 and GRtrue ∕ GRm,tot50 come close to unity due to negligible coagulation effects. Third, GRtrue ∕ GRm,mode is between 1.2 and 1.5 and GRtrue ∕ GRm,sr100 is between 1.1 and 1.2 for , indicating the true growth will be slightly underestimated if or is used to infer GRtrue.
3.4 Underestimation of GRtrue
In previous sections, mainly overestimation of the GRtrue by measured GR, GRm, has been discussed. Though we do not quantitatively study underestimation of GRtrue by GRm, in this section we show that in a constant rate system in which particle sink processes (i.e., dilution and loss to preexisting particles) strongly decrease the concentration of nucleated particles, GRm can approach zero and cannot be utilized to estimate GRtrue. Figure 6 shows such nucleation scenarios for (a) collision-controlled nucleation with M = 0.1 and (b) collision-controlled nucleation with . In both cases other sink processes were set equal to zero. As shown in both Fig. 6a and b, particle size distributions approach steady state after τ=100. As a result, GRm approaches zero beyond τ=100. At the same time, GRtrue remains finite since monomer concentration remains at steady state after τ=20. Therefore, other methods have to be utilized to infer GRtrue in such situations.
We used a discrete-sectional model to solve a dimensionless form of aerosol population balance equation for a single-species system. True GR and various “measured” GRs were examined for a variety of nucleation scenarios. Based on the simulation results, we draw the following conclusions.
-
Simulated data show that for collision-controlled nucleation without preexisting particles, GRs inferred from the modal size of nucleated particles (GRm,mode) is as much as 6 times greater than true GRs due to vapor condensation (GRtrue).
-
In the absence of preexisting particles or other sink processes, comparison of different GRs based on different representative sizes indicates the relationship GRm,mode < GRm,sr100 < GRm,tot50 < GRm,sr50 holds true for collision-controlled nucleation. If clusters evaporate, the nucleation process is characterized by rapid particle growth following the nucleation burst.
-
Both evaporation and scavenging by preexisting particles can reduce the concentration of particles formed by nucleation. Lower particle concentrations reduce the effect of coagulation on GRm, so overestimation of GRtrue by GRm is lower than is found in the absence of these processes.
-
Preexisting particles have dramatically different effects on collision-controlled nucleation and nucleation with cluster evaporation. For , collision-controlled nucleation is only slightly affected. However, if preexisting particles are coupled with evaporation, the number of nucleated particles can drop significantly, thus reducing the contribution of coagulation to measure GRs.
-
GRm can underestimate GRtrue in a system with strong dilution or other particle sink processes. Particle size distributions in such nucleation scenarios can approach a steady state that leads to a GRm close to 0, which underestimates GRtrue.
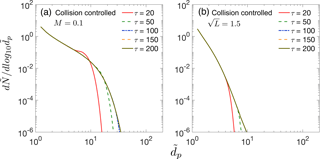
Figure 6Particle size distribution at different dimensionless times for collision-controlled nucleation with (a) M=0.1 and (b) . In both cases, sink processes not indicated in the figure were set to zero in the simulations. Particle size distributions at certain times are not visible in the figure since they overlap with the particle size distribution at a later time.
No data sets were used in this article.
To evaluate the contribution of self-coagulation of the mode (GRm,self) and cluster coagulation (GRm,clsuter) to measured GR based on mode diameter (GRm,mode), we used the following first-order numerical approximation method.
-
Find particle size distribution at a given time τ. k is the number of monomers in a particle and is the concentration of particles that contains k molecules. Since the simulation code only reports discrete particle concentration for each bin, an interpolation is performed using MATLAB function griddedInterpolant.m.
-
Find the value at which is locally maximized. A pre-factor 3log (10)k is multiplied by to convert the particle size distribution to . The mode diameter is then given by .
-
Use the following integration equations to obtain number distribution of the mode at time τ+Δτ assuming only one process causes the distribution to shift.
For self-coagulation,
For coagulation with clusters,
In the above equations, L and H are the lower and upper boundaries of the mode, Lc and Hc are the lower and upper boundary of clusters, c(ij) is the collision frequency function, H(x) is the Heaviside step function. Δτ is typically set between 0.1 and 1.
-
Find the k values at which and are locally maximized. The corresponding diameters are and .
-
The GR due to self-coagulation and coagulation with clusters are then given by
To facilitate comparison between dimensionless simulation results and experimental results, or previous dimensional simulation results, we convert selected dimensionless simulation results to dimensional quantities using Eq. (6). Specifically, we assume the monomer production rate is cm−3 s−1 and the monomer has a volume of cm3 and a density of 1.47 g cm−3. The collision frequency function for monomers, β11 fm, is cm−3s−1, calculated at atmospheric pressure and 300 K. We consider two nucleation scenarios. The first is collision-controlled nucleation in the presence of preexisting particles, with set to 0.2. The second scenario is nucleation with evaporation in the presence of preexisting particles. The evaporation constant in this case is and is 0.2. Both these cases are discussed in Sect. 3.3. The converted dimensional results are shown in Fig. B1, with relevant dimensional quantities displayed in the figure.
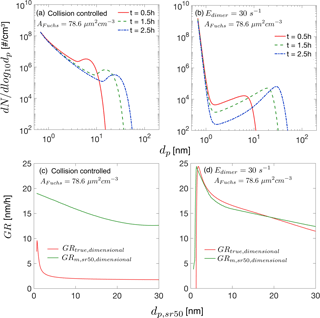
Figure B1Dimensional particle size distribution and growth rates. The quantities shown in this figure are converted from the dimensionless solution using Eq. (6). The dimensional quantities involved in the conversions are cm−3 s−1, cm−3 s−1 and cm3. The Fuchs surface area is 78.6 µm2 cm−3, corresponding to . (a) Particle size distribution for collision-controlled nucleation at t=0.5, 1.5 and 2.5 h. (b) Particle size distribution for nucleation with evaporation at t=0.5, 1.5 and 2.5 h. Monomer evaporation rate from the dimer is 30 s−1, corresponding to a dimensionless evaporation constant . (c) The dimensional particle growth rates for collision-controlled nucleation as is shown in panel (a). (d) The dimensional particle growth rates for nucleation with evaporation as is shown in panel (b).
| Collision-controlled nucleation | A limiting case for nucleation in which all collisions among condensing (nucleating) vapor occur at the rate predicted by kinetic theory and particles stick with 100 % efficiency. Vapor does not subsequently evaporate from particle surfaces, nor are particles scavenged by preexisting particles or the chamber wall. |
| Particle size corresponding to the local minimum in a representation of particle size distribution. | |
| Particle size corresponding to the local maximum in a representation of particle size distribution. | |
| Particle size of a measurement bin in which particle concentration reaches 50 % of its maximum value. | |
| Particle size of a measurement bin in which particle concentration reaches maximum value. | |
| Particle size above which total particle concentration reaches 50 % of its maximum value. | |
| GRm,mode | Measured dimensionless growth rate based on . |
| GRm,sr50 | Measured dimensionless growth rate based on . |
| GRm,sr100 | Measured dimensionless growth rate based on . |
| GRm,tot50 | Measured dimensionless growth rate based on . |
| GRtrue | True dimensionless particle growth rate attributed to the net flux of condensing vapors onto particle surface (i.e., the condensation rate minus the evaporation rate). |
| GRm,clsuter | Measured dimensionless particle growth rate attributed to coagulation with clusters. |
| GRm,self | Measured dimensionless growth rate attributed to self-coagulation of particles in the nucleation mode. |
| E, Ω | Dimensionless parameters characterizing evaporation rates of particles, derived from the liquid droplet model. E can be regarded as a dimensionless form of saturation vapor pressure of the condensing molecules and Ω a dimensionless form of surface tension. Ω assumes a constant value of 16 in this work. |
| Dimensionless parameter characterizing fractional loss rate of monomer or nucleated particles to preexisting particles. | |
| Dimensionless concentration of particles containing k monomers (i.e., k molecules of condensed vapor). |
The authors declare that they have no conflict of interest.
This research was supported by the U.S. Department of Energy's Atmospheric
System Research, an Office of Science, Office of Biological and
Environmental Research program, under grant number DE-SC0011780.
Edited by: Hang Su
Reviewed by: two anonymous referees
Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurtén, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppä, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petäjä, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamäki, H., and Kirkby, J.: Molecular understanding of sulphuric acid–amine particle nucleation in the atmosphere, Nature, 502, 359–363, https://doi.org/10.1038/nature12663, 2013.
Barsanti, K. C., McMurry, P. H., and Smith, J. N.: The potential contribution of organic salts to new particle growth, Atmos. Chem. Phys., 9, 2949–2957, https://doi.org/10.5194/acp-9-2949-2009, 2009.
Chan, T. W. and Mozurkewich, M.: Measurement of the coagulation rate constant for sulfuric acid particles as a function of particle size using tandem differential mobility analysis, J. Aerosol Sci., 32, 321–339, https://doi.org/10.1016/S0021-8502(00)00081-1, 2001.
Friedlander, S. K.: Smoke, dust, and haze: fundamentals of aerosol dynamics, 2nd ed., Oxford University Press, New York, USA, 2000.
Fuchs, N. A. and Sutugin, A. G.: HIGH-DISPERSED AEROSOLS A2 – HIDY, G. M, in: Topics in Current Aerosol Research, edited by: Brock, J. R., Pergamon, 1, Oxford, UK, 1971.
Gelbard, F. and Seinfeld, J. H.: The general dynamic equation for aerosols. Theory and application to aerosol formation and growth, J. Colloid Interf. Sci., 68, 363–382, https://doi.org/10.1016/0021-9797(79)90289-3, 1979.
Gelbard, F. and Seinfeld, J. H.: Simulation of multicomponent aerosol dynamics, J. Colloid Interf. Sci., 78, 485–501, https://doi.org/10.1016/0021-9797(80)90587-1, 1980.
Heisler, S. L. and Friedlander, S. K.: Gas-to-particle conversion in photochemical smog: Aerosol growth laws and mechanisms for organics, Atmos. Environ., 11, 157–168, https://doi.org/10.1016/0004-6981(77)90220-7, 1977.
Hodshire, A. L., Lawler, M. J., Zhao, J., Ortega, J., Jen, C., Yli-Juuti, T., Brewer, J. F., Kodros, J. K., Barsanti, K. C., Hanson, D. R., McMurry, P. H., Smith, J. N., and Pierce, J. R.: Multiple new-particle growth pathways observed at the US DOE Southern Great Plains field site, Atmos. Chem. Phys., 16, 9321–9348, https://doi.org/10.5194/acp-16-9321-2016, 2016.
Kerminen, V. M. and Kulmala, M.: Analytical formulae connecting the “real” and the “apparent” nucleation rate and the nuclei number concentration for atmospheric nucleation events, J. Aerosol Sci., 33, 609–622, 2002.
Kontkanen, J., Olenius, T., Lehtipalo, K., Vehkamäki, H., Kulmala, M., and Lehtinen, K. E. J.: Growth of atmospheric clusters involving cluster–cluster collisions: comparison of different growth rate methods, Atmos. Chem. Phys., 16, 5545–5560, https://doi.org/10.5194/acp-16-5545-2016, 2016.
Kuang, C., Riipinen, I., Sihto, S.-L., Kulmala, M., McCormick, A. V., and McMurry, P. H.: An improved criterion for new particle formation in diverse atmospheric environments, Atmos. Chem. Phys., 10, 8469–8480, https://doi.org/10.5194/acp-10-8469-2010, 2010.
Kuang, C., Chen, M., Zhao, J., Smith, J., McMurry, P. H., and Wang, J.: Size and time-resolved growth rate measurements of 1 to 5 nm freshly formed atmospheric nuclei, Atmos. Chem. Phys., 12, 3573–3589, https://doi.org/10.5194/acp-12-3573-2012, 2012.
Kulmala, M., Petäjä, T., Nieminen, T., Sipilä, M., Manninen, H. E., Lehtipalo, K., Dal Maso, M., Aalto, P. P., Junninen, H., Paasonen, P., Riipinen, I., Lehtinen, K. E. J., Laaksonen, A., and Kerminen, V.-M.: Measurement of the nucleation of atmospheric aerosol particles, Supplement, Nat. Protoc., 7, 1651, https://doi.org/10.1038/nprot.2012.091, 2012.
Kürten, A., Li, C., Bianchi, F., Curtius, J., Dias, A., Donahue, N. M., Duplissy, J., Flagan, R. C., Hakala, J., Jokinen, T., Kirkby, J., Kulmala, M., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Onnela, A., Rissanen, M. P., Simon, M., Sipilä, M., Stozhkov, Y., Tröstl, J., Ye, P., and McMurry, P. H.: New particle formation in the sulfuric acid–dimethylamine–water system: reevaluation of CLOUD chamber measurements and comparison to an aerosol nucleation and growth model, Atmos. Chem. Phys., 18, 845–863, https://doi.org/10.5194/acp-18-845-2018, 2018.
Lehtinen, K. E. J. and Kulmala, M.: A model for particle formation and growth in the atmosphere with molecular resolution in size, Atmos. Chem. Phys., 3, 251–257, https://doi.org/10.5194/acp-3-251-2003, 2003.
Lehtinen, K. E. J., Rannik, U., Petaja, T., Kulmala, M., and Hari, P.: Nucleation rate and vapor concentration estimations using a least squares aerosol dynamics method, J. Geophys. Res.-Atmos., 109, D21209, https://doi.org/10.1029/2004JD004893, 2004.
Lehtipalo, K., Leppa, J., Kontkanen, J., Kangasluoma, J., Franchin, A., Wimnner, D., Schobesberger, S., Junninen, H., Petaja, T., Sipila, M., Mikkila, J., Vanhanen, J., Worsnop, D. R., and Kulmala, M.: Methods for determining particle size distribution and growth rates between 1 and 3 nm using the Particle Size Magnifier, Boreal Environ. Res., 19, 215–236, 2014.
Lehtipalo, K., Rondo, L., Kontkanen, J., Schobesberger, S., Jokinen, T., Sarnela, N., Kürten, A., Ehrhart, S., Franchin, A., Nieminen, T., Riccobono, F., Sipilä, M., Yli-Juuti, T., Duplissy, J., Adamov, A., Ahlm, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Downard, A. J., Dunne, E. M., Flagan, R. C., Guida, R., Hakala, J., Hansel, A., Jud, W., Kangasluoma, J., Kerminen, V.-M., Keskinen, H., Kim, J., Kirkby, J., Kupc, A., Kupiainen-Määttä, O., Laaksonen, A., Lawler, M. J., Leiminger, M., Mathot, S., Olenius, T., Ortega, I. K., Onnela, A., Petäjä, U., Praplan, A., Rissanen, M. P., Ruuskanen, T., Santos, F. D., Schallhart, S., Schnitzhofer, R., Simon, M., Smith, J. N., Tröstl, J., Tsagkogeorgas, G., Tome, A. n., Vaattovaara, P., Hanna Vehkamäki, Vrtala, A. E., Wagner, P. E., Williamson, C., Wimmer, D., Winkler, P. M., Virtanen, A., Donahue, N. M., Carslaw, K. S., Baltensperger, U., Riipinen, I., Curtius, J., Worsnop, D. R., and Kulmala, M.: The effect of acid-base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 7, 11594, https://doi.org/10.1038/ncomms11594, 2016.
McMurry, P. H.: Photochemical aerosol formation from SO2: A theoretical analysis of smog chamber data, J. Colloid Interf. Sci., 78, 513–527, https://doi.org/10.1016/0021-9797(80)90589-5, 1980.
McMurry, P. H. and Friedlander, S. K.: New particle formation in the presence of an aerosol, Atmos. Environ., 13, 1635–1651, 1979.
McMurry, P. H. and Li, C.: The dynamic behavior of nucleating aerosols in constant reaction rate systems: Dimensional analysis and generic numerical solutions, Aerosol Sci. Tech., 51, 1057–1070, https://doi.org/10.1080/02786826.2017.1331292, 2017.
McMurry, P. H. and Wilson, J. C.: Growth laws for the formation of secondary ambient aerosols: Implications for chemical conversion mechanisms, Atmos. Environ., 16, 121–134, https://doi.org/10.1016/0004-6981(82)90319-5, 1982.
Olenius, T., Riipinen, I., Lehtipalo, K., and Vehkamäki, H.: Growth rates of atmospheric molecular clusters based on appearance times and collision–evaporation fluxes: Growth by monomers, J. Aerosol Sci., 78, 55–70, https://doi.org/10.1016/j.jaerosci.2014.08.008, 2014.
Pichelstorfer, L., Stolzenburg, D., Ortega, J., Karl, T., Kokkola, H., Laakso, A., Lehtinen, K. E. J., Smith, J. N., McMurry, P. H., and Winkler, P. M.: Resolving nanoparticle growth mechanisms from size- and time-dependent growth rate analysis, Atmos. Chem. Phys., 18, 1307–1323, https://doi.org/10.5194/acp-18-1307-2018, 2018.
Rao, N. P. and McMurry, P. H.: Nucleation and Growth of Aerosol in Chemically Reacting Systems: A Theoretical Study of the Near-Collision-Controlled Regime, Aerosol Sci. Tech., 11, 120–132, https://doi.org/10.1080/02786828908959305, 1989.
Riccobono, F.: Oxidation products of biogenic emissions contribute to nucleation of atmospheric particles, Science, 344, 717–721, 2014.
Riccobono, F., Rondo, L., Sipilä, M., Barmet, P., Curtius, J., Dommen, J., Ehn, M., Ehrhart, S., Kulmala, M., Kürten, A., Mikkilä, J., Paasonen, P., Petäjä, T., Weingartner, E., and Baltensperger, U.: Contribution of sulfuric acid and oxidized organic compounds to particle formation and growth, Atmos. Chem. Phys., 12, 9427–9439, https://doi.org/10.5194/acp-12-9427-2012, 2012.
Riipinen, I., Yli-Juuti, T., Pierce, J. R., Petäjä, T., Worsnop, D. R., Kulmala, M., and Donahue, N. M.: The contribution of organics to atmospheric nanoparticle growth, Nat. Geosci., 5, 453–458, https://doi.org/10.1038/ngeo1499, 2012.
Smith, J., Dunn, M., VanReken, T., Iida, K., Stolzenburg, M., McMurry, P., and Huey, L.: Chemical composition of atmospheric nanoparticles formed from nucleation in Tecamac, Mexico: Evidence for an important role for organic species in nanoparticle growth, Geophys. Res. Lett., 35, L04808, https://doi.org/10.1029/2007GL032523, 2008.
Smith, J. N., Barsanti, K. C., Friedli, H. R., Ehn, M., Kulmala, M., Collins, D. R., Scheckman, J. H., Williams, B. J., and McMurry, P. H.: Observations of aminium salts in atmospheric nanoparticles and possible climatic implications, P. Natl. Acad. Sci., 107, 6634–6639, 2010.
Stolzenburg, M. R., McMurry, P. H., Sakurai, H., Smith, J. N., Mauldin, R. L., Eisele, F. L., and Clement, C. F.: Growth rates of freshly nucleated atmospheric particles in Atlanta, J. Geophys. Res.-Atmos., 110, D22S05, https://doi.org/10.1029/2005JD005935, 2005.
Tröstl, J., Chuang, W. K., Gordon, H., Heinritzi, M., Yan, C., Molteni, U., Ahlm, L., Frege, C., Bianchi, F., Wagner, R., Simon, M., Lehtipalo, K., Williamson, C., Craven, J. S., Duplissy, J., Adamov, A., Almeida, J., Bernhammer, A.-K., Breitenlechner, M., Brilke, S., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Gysel, M., Hansel, A., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Keskinen, H., Kim, J., Krapf, M., Kürten, A., Laaksonen, A., Lawler, M., Leiminger, M., Mathot, S., Möhler, O., Nieminen, T., Onnela, A., Petäjä, T., Piel, F. M., Miettinen, P., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Sipilä, M., Smith, J. N., Steiner, G., Tomè, A., Virtanen, A., Wagner, A. C., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Carslaw, K. S., Curtius, J., Dommen, J., Kirkby, J., Kulmala, M., Riipinen, I., Worsnop, D. R., Donahue, N. M., and Baltensperger, U.: The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 533, 527–531, https://doi.org/10.1038/nature18271, 2016.
Verheggen, B. and Mozurkewich, M.: An inverse modeling procedure to determine particle growth and nucleation rates from measured aerosol size distributions, Atmos. Chem. Phys., 6, 2927–2942, https://doi.org/10.5194/acp-6-2927-2006, 2006.
Wang, J., McGraw, R. L., and Kuang, C.: Growth of atmospheric nano-particles by heterogeneous nucleation of organic vapor, Atmos. Chem. Phys., 13, 6523–6531, https://doi.org/10.5194/acp-13-6523-2013, 2013.
Weber, R. J., Marti, J. J., McMurry, P. H., Eisele, F. L., Tanner, D. J., and Jefferson, A.: Measurements of new particle formation and ultrafine particle growth rates at a clean continental site, J. Geophys. Res.-Atmos., 102, 4375–4385, https://doi.org/10.1029/96JD03656, 1997.
Yli-Juuti, T., Nieminen, T., Hirsikko, A., Aalto, P. P., Asmi, E., Hõrrak, U., Manninen, H. E., Patokoski, J., Dal Maso, M., Petäjä, T., Rinne, J., Kulmala, M., and Riipinen, I.: Growth rates of nucleation mode particles in Hyytiälä during 2003–2009: variation with particle size, season, data analysis method and ambient conditions, Atmos. Chem. Phys., 11, 12865–12886, https://doi.org/10.5194/acp-11-12865-2011, 2011.





