Errors in nanoparticle growth rates inferred from measurements in chemically reacting aerosol systems

In systems in which aerosols are being formed by chemical transformations, individual particles grow due to the addition of molecular species. Efforts to improve our understanding of particle growth often focus on attempts to reconcile observed growth rates with values calculated from models. However, because it is typically not possible to measure the growth rates of individual particles in chemically reacting systems, they must be inferred from measurements of aerosol properties such as size distributions, particle number concentrations, etc. This work discusses errors in growth rates obtained using methods that are commonly employed for analyzing atmospheric data. We analyze “data” obtained by simulating the formation of aerosols in a system in which a single chemical species is formed at a constant rate, R. We show that the maximum overestimation error in measured growth rates occurs for collision-controlled nucleation in a single-component system in the absence of a preexisting aerosol, wall losses, evaporation or dilution, as this leads to the highest concentrations of nucleated particles. Those high concentrations lead to high coagulation rates that cause the nucleation mode to grow faster than would be caused by vapor condensation alone. We also show that preexisting particles, when coupled with evaporation, can significantly decrease the concentration of nucleated particles. This can lead to decreased discrepancies between measured growth rate and true growth rate by reducing coagulation among nucleated particles. However, as particle sink processes become stronger, measured growth rates can potentially be lower than true particle growth rates. We briefly discuss nucleation scenarios in which the observed growth rate approaches zero while the true growth rate does not.

1 Introduction

Aerosol systems undergo transformations by processes that include coagulation, convection, deposition on surfaces, source emissions, nucleation, growth, etc. The aerosol general dynamic equation (GDE) (Friedlander, 2000; Gelbard and Seinfeld, 1979, 1980) describes the time rate of change of size-dependent particle concentration and composition by such processes. Recent work has focused on understanding processes that affect growth rates (GRs) of freshly nucleated atmospheric nanoparticles (Smith et al., 2008, 2010; Riipinen et al., 2012; Hodshire et al., 2016; Kontkanen et al., 2016; Tröstl et al., 2016). This is important because a particle's survival probability increases with GRs (McMurry and Friedlander, 1979; Weber et al., 1997; Kerminen and Kulmala, 2002; Kuang et al., 2010). Nucleated particles are more likely to form cloud condensation nuclei and affect climate when survival probabilities are high.

Following established conventions long used in modeling aerosol dynamics (Friedlander, 2000; Gelbard and Seinfeld, 1979, 1980), we define the particle GR as the net rate of change in diameter of individual particles due to the addition or removal of molecular species. (If evaporation exceeds addition, the GR would be negative.) While most work to date has focused on condensation and evaporation, chemical processes such as acid–base reactions, organic salt formation, liquid-phase reactions and the accretion of two or more organic molecules to form a larger compound with lower volatility may also contribute to growth (McMurry and Wilson, 1982; Barsanti et al., 2009; Riipinen et al., 2012; Lehtipalo et al., 2014). In a chemically reacting system, the total diameter GR is given by the sum of all such processes:

$$\begin{array}{ll}{\displaystyle \frac{\mathrm{d}{d}_{\mathrm{p}}}{\mathrm{d}t}}=& {\displaystyle }\mathrm{GR}={\mathrm{GR}}_{\mathrm{condensation}/\mathrm{evaporation}}+{\mathrm{GR}}_{\text{acid–base\hspace{0.17em} reactions}}\\ \text{(1)}& {\displaystyle }& {\displaystyle }+{\mathrm{GR}}_{\mathrm{accretion}}+{\mathrm{GR}}_{\mathrm{other}}.\end{array}$$

The effect of growth on the aerosol distribution function is given by (Heisler and Friedlander, 1977)

$$\begin{array}{}\text{(2)}& {\left.{\displaystyle \frac{\partial n}{\partial t}}\right|}_{\mathrm{Growth}}=-{\displaystyle \frac{\partial }{\partial d_{\mathrm{p}}}}\left[n(d_{\mathrm{p}},t){\displaystyle \frac{\mathrm{d}{d}_{\mathrm{p}}}{\mathrm{d}t}}\right],\end{array}$$

where the aerosol number distribution n(d_p,t) is defined such that the number concentration of particles between d_p and d_p+dd_p is equal to n(d_p,t)dd_p. Coagulation, including the coagulation of a molecular cluster with a larger particle, can also lead to particle growth. It is worthwhile, however, to treat coagulation and growth separately. The extent to which the coagulation of freshly nucleated molecular clusters contributes to measured GRs can be accurately determined only if the entire number distribution down to clusters of size 2 is accurately measured. In the absence of such data, the contributions of cluster coagulation to growth could erroneously be attributed to vapor uptake. Coagulation is accounted for with the coagulation integrals in the GDE and is a relatively well-understood process that can be described with reasonable confidence in models (Kürten et al., 2018; Chan and Mozurkewich, 2001). Growth involves processes that are not well understood for chemically complex aerosol systems, such as the atmosphere (Barsanti et al., 2009; Riipinen et al., 2012; Hodshire et al., 2016).

Progress towards understanding growth can be achieved through efforts to reconcile GRs that are observed experimentally with values predicted by models. Such work requires that size- and time-dependent GRs be accurately determined from observations. The literature includes many reports of observed GRs (Stolzenburg et al., 2005; Wang et al., 2013; Riccobono et al., 2012; Tröstl et al., 2016), but uncertainties in reported values are typically not well understood. Because it is usually not possible to measure the growth of individual particles as they undergo chemical transformations, GRs are calculated indirectly using time-dependent observations of aerosol properties such as number distributions or number concentrations larger than a given size. Those properties are typically affected by many processes, some poorly understood, that can affect reported GRs to an unknown extent.

A variety of approaches have been used to extract GRs from observations. We refer to these values as GR_m, where the subscript “m” designates “measured”. Methods that we discuss include the following.

1. Maximum concentration method (Kulmala et al., 2012). During a nucleation event, particle concentrations in a given size bin increase from their initial values, passing through a peak before they eventually decrease. This technique involves noting the times that this maximum occurred in different size bins. The GR is obtained by first fitting a linear function of particle diameter (corresponding to the size bins) vs. time, and then calculating the slope of the fitted function.

2. Appearance time method (Lehtipalo et al. 2014). This approach has been used to analyze data from condensation particle counter (CPC) batteries (Riccobono, 2014), particle size magnifier (PSM) (Lehtipalo et al. 2014), etc. In brief, GR_m is determined by the differences in concentration rise times (typically, either 5 or 50 % of the maximum) measured by the instruments with differing minimum detection sizes. A variation of this approach was reported by Weber et al. (1997), who estimated GRs from the observed time delay in measurements of sulfuric acid vapor and particles measured with a CPC with a minimum detectable size of about 3 nm.

3. Lognormal distribution function method (Kulmala et al., 2012). Lognormal distributions are fit to the growing mode of nucleated particles. GR_m is defined as the GR of the geometric mean size of these distributions.

While these methods do not account for the effects of coagulation on measured changes in particle size, the literature includes approaches that explicitly account for such effects (Lehtinen et al., 2004; Verheggen and Mozurkewich, 2006; Kuang et al., 2012; Pichelstorfer et al., 2018). Other work has applied the above techniques after confirming that coagulation has an insignificant effect for the analyzed data (Kulmala et al., 2012) or explicitly accounting for the effects of coagulation on GR_m (Stolzenburg et al., 2005; Lehtipalo et al., 2016).

This paper assesses errors of using GR_m calculated using techniques commonly employed in the literature to infer particle GRs. Our results are especially germane to GR of freshly nucleated particles ranging in size from molecular clusters to about 40 nm. We use time-dependent distribution functions calculated numerically by McMurry and Li (2017) as “data”. The only process contributing to the addition or removal of molecular species in that work (i.e., to particle GRs as defined above) are condensation and evaporation. Because we understand this model system perfectly, GR_true (i.e., the net GR due to molecular exchange through condensation and evaporation) can be calculated exactly. Errors in GR_m due to coagulation, wall deposition, scavenging by preexisting particles or dilution are given by the difference between GR_true and GR_m. We do not examine errors associated with convection, source emission, etc.

We are not the first to examine factors that cause GR_m to differ from GR_true. For example, Kontkanen et al. (2016) used simulations to show that discrepancies between measured GR based on appearance time (AGR) and GR based on irreversible vapor condensation (CGR) can be significant. (Note that GR_true used in this paper differs from CGR in that GR_true also incorporates evaporation.) Our approach, which uses the nondimensional formulation described by McMurry and Li (2017), provides results that are generally applicable to nucleation and growth of a single chemical species, so long as it is being produced by chemical transformations at a constant rate, R. We show that the upper limit for overestimation of GR_true by GR_m occurs when nucleation takes place in the absence of preexisting aerosols and is collision controlled (i.e., when evaporation rates from even the smallest clusters occur at rates that are negligible relative to vapor condensation rates). Collision-controlled nucleation is an important limiting case because there is growing evidence that atmospheric nucleation of sulfuric acid with stabilizing species is well described as a collision-controlled process (Almeida et al., 2013; Kürten et al., 2018; McMurry, 1980). Because cluster evaporation, scavenging by preexisting aerosol, etc., all diminish the number of particles formed by nucleation, overestimation of GR_true due to coagulation decreases as these processes gain in prominence. We do not explicitly study the effect of growth by processes other than condensation or evaporation, such as heterogeneous growth pathways that take place on or within existing particles. If such processes were to contribute significantly to growth, they would lead to higher GRs and therefore smaller relative errors in GR_m due to coagulation. Additionally, we point out when particle sink processes consume nucleated particles at a fast rate (e.g., strong effects of dilution or scavenging by preexisting particles), GR_m may not be used to estimate GR_true. Our results help to inform estimates of uncertainties for systems with a single condensing species, or systems that can be modeled in a similar way to a single species system (Kürten et al., 2018).

2 Methods

2.1 Discrete-sectional model

We utilize the dimensionless discrete-sectional model described by McMurry and Li (2017) to simulate evolution of particle size distribution for a system with a single condensing species. We assume that the condensing species is produced at a constant rate by gas-phase reaction. Our code uses 200 discrete bins and 250 sectional bins, with a geometric volume amplification factor of 1.0718 for neighboring sections.

Physical processes that affect particle growth, including wall deposition, loss to preexisting particles, cluster evaporation and dilution, can be characterized by dimensionless parameters in this model. In the present study, however, not all aforementioned processes are discussed. Our previous work shows that wall losses, scavenging by preexisting particles and dilution have qualitatively similar effects on aerosol dynamics. Therefore, in this work we focus on preexisting aerosols and dilution to illustrate factors that contribute to errors in measured GRs and do not explicitly discuss wall deposition. A single dimensionless parameter, $\sqrt{L}$, is used to indicate the abundance of preexisting particles, with larger $\sqrt{L}$ values representing a higher concentration of preexisting particles (or, equivalently, a slower rate at which the nucleating species is produced by chemical reaction). $\sqrt{L}$ is calculated with the equation

$$\begin{array}{}\text{(3)}& \sqrt{L}={\displaystyle \frac{\frac{\mathrm{1}}{\mathrm{4}}{\left(\frac{\mathrm{8}{k}_{\mathrm{b}}T}{\mathit{\pi }{m}_{\mathrm{1}}}\right)}^{\mathrm{1}/\mathrm{2}}{A}_{\mathrm{Fuchs}}}{\sqrt{R{\mathit{\beta }}_{\mathrm{11}\mathrm{fm}}}}},\end{array}$$

where A_Fuchs is the Fuchs surface area concentration (Fuchs and Sutugin, 1971), k_b is the Boltzmann constant, m₁ is the mass of the monomer, R is the condensing species production rate and β_11 fm is the monomer collision frequency function. The loss rate for particles containing k monomers is $\sqrt{L}/k^{\mathrm{1}/\mathrm{2}}$. This size dependence is included when solving the coupled differential equations for time-dependent cluster concentrations. Similarly, the dimensionless quantity M that characterizes dilution is given by the expression

$$\begin{array}{}\text{(4)}& M={\displaystyle \frac{Q_{\mathrm{dil}}/V}{\sqrt{R{\mathit{\beta }}_{\mathrm{11}\mathrm{fm}}}}},\end{array}$$

where Q_dil is the dilution flow rate and V is the volume of the system. Note the fractional dilution loss is independent of particle size. In addition to loss to preexisting particles and dilution, we consider the effect of cluster evaporation on particle growth with the assumption that evaporation follows the classical liquid droplet model. Two dimensionless parameters, E and Ω, are needed to fully describe the evaporation process. The dimensionless evaporation parameter, E, is proportional to the saturation vapor concentration of the nucleating species, while Ω is the dimensionless surface tension (Rao and McMurry, 1989; McMurry and Li, 2017). The evaporation rate for particles containing k monomers, E_k, is calculated with a discretized equation of the form

$$\begin{array}{}\text{(5)}& E_k=E{c}_{\mathrm{1}k}\exp \left[{\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}\mathrm{\Omega }\left(k^{\frac{\mathrm{2}}{\mathrm{3}}}-{\left(k-\mathrm{1}\right)}^{\frac{\mathrm{2}}{\mathrm{3}}}\right)\right],\end{array}$$

where c(i,k) is the dimensionless collision frequency between a monomer and a particle containing k monomers. To simplify our discussion, Ω is fixed to be 16 throughout this work (a representative value for the surface tension of sulfuric acid aqueous solutions), while the value of E is varied.

The solution to the GDE for a constant rate system (R = constant) depends on dimensionless time, cluster size and the dimensionless variables $\sqrt{L}$, M, E, Ω, etc., but is independent of the rate at which condensing vapor is produced by chemical reaction. That rate is required to transform the computed nondimensional solutions to dimensional results using simple multiplicative expressions given by McMurry and Li (2017):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{N}_k={\left({\displaystyle \frac{R}{{\mathit{\beta }}_{\mathrm{11}\mathrm{fm}}}}\right)}^{\mathrm{1}/\mathrm{2}}{\stackrel{\mathrm{̃}}{N}}_k;t={\left({\displaystyle \frac{\mathrm{1}}{R{\mathit{\beta }}_{\mathrm{11}\mathrm{fm}}}}\right)}^{\mathrm{1}/\mathrm{2}}\mathit{\tau };\\ \text{(6)}& {\displaystyle }& {\displaystyle }{d}_{\mathrm{p}}=\left(v_{\mathrm{1}}^{\mathrm{1}/\mathrm{3}}\right){\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}.\end{array}$$

In the above equations, ${\stackrel{\mathrm{̃}}{N}}_k$ is the dimensionless concentration of particle-containing k monomers, τ is the dimensionless time, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}$ is the dimensionless particle size and v₁ is the monomer volume. Assuming a monomer volume of $\mathrm{1.62}\times {\mathrm{10}}^{-\mathrm{22}}$ cm³ (volume of one sulfuric acid plus one dimethylamine molecule with a density of 1.47 g cm⁻³), ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}=\mathrm{30}$ would be equivalent to a dimensional particle size of 16.4 nm.

2.2 Evaluation of measured growth rate (GR_m)

At time t₁ and t₂, if two particle sizes d_p,t1 and d_p,t2 are used to represent the particle size distribution, the measured GR can be calculated using the following equation as a first-order approximation:

$$\begin{array}{}\text{(7)}& {\mathrm{GR}}_{\mathrm{m}}\left({\displaystyle \frac{d_{\mathrm{p},t_{\mathrm{1}}}+d_{\mathrm{p},t_{\mathrm{2}}}}{\mathrm{2}}},{\displaystyle \frac{t_{\mathrm{2}}+t_{\mathrm{1}}}{\mathrm{2}}}\right)={\displaystyle \frac{d_{\mathrm{p},t_{\mathrm{2}}}-d_{\mathrm{p},t_{\mathrm{1}}}}{t_{\mathrm{2}}-t_{\mathrm{1}}}}.\end{array}$$

If $d_{\mathrm{p},t_i}$ is available for a time series $\mathit{\{}{t}_i{\mathit{\}}}_{i=\mathrm{1},\mathrm{2},\mathrm{\dots }}$, GR can also be obtained by derivatizing a fitting function d_p=d_p(t) to obtain GR at any time t_a:

$$\begin{array}{}\text{(8)}& {\mathrm{GR}}_{\mathrm{m}}\left(d_{\mathrm{p}},t_{\mathrm{a}}\right)={\left.{\displaystyle \frac{\mathrm{d}{d}_{\mathrm{p}}\left(t\right)}{\mathrm{d}t}}\right|}_{t=t_{\mathrm{a}}}.\end{array}$$

To implement Eqs. (7) or (8), it is necessary to choose a particle size that is representative of the particle size distribution at a given time. The choice of this representative size varies among publications and can depend on the types of available data. Based on previous studies (Kulmala et al., 2012; Lehtipalo et al., 2014; Stolzenburg et al., 2005; Yli-Juuti et al., 2011), we have selected four representative sizes for discussion: ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$. At a given time τ, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$ is the particle size at which $\mathrm{d}\stackrel{\mathrm{̃}}{N}\left(\mathit{\tau }\right)/\mathrm{d}{\log }_{\mathrm{10}}{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}$ reaches its local maximum. If the shape of the mode is lognormal, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$ is equal to the geometric mean of the distribution. As suggested by Kulmala et al. (2012), the lognormal distribution method involves calculating GRs from observed time-dependent trends of ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$. The maximum concentration method is based on the time when particles in a given size bin, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$, pass through their maximum (100 %) concentration (Lehtinen and Kulmala, 2003). The appearance time method is based on the time when particle concentrations in a bin, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$, pass through a specified percentage of its maximum (we have used 50 %). GRs are sometimes based on total concentrations of particles larger than a specified size. We refer to the particle size above, for which the total number concentration of particles reaches 50 % of its maximum value as ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$. This approach is especially useful when measurements are carried out with a battery of CPCs with differing cutoff sizes. For simplicity, in this paper we assume that CPC detection efficiencies increase from 0 to 100 % at a given cutoff size. In practice, measured size-dependent detection efficiencies are typically used when analyzing CPC battery data. Figure 1 shows the location of these representative sizes at τ=20, 60 and 100 for two nucleation scenarios in the absence of preexisting particles. ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$ are marked as points, with their y coordinates representing particle concentrations at corresponding sizes.

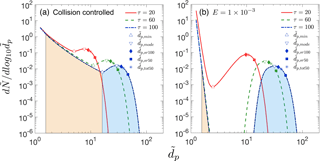
Figure 1 Particle size distributions at dimensionless times τ=20, 60 and 100 (a) for collision-controlled nucleation (E=0) and (b) when evaporation is included with $E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$. Division of the distribution into monomer, cluster and nucleation mode is displayed for τ=100, with beige and light blue indicating the range of clusters and nucleation mode. Clusters and nucleation mode are separated by ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\min }$, where $\mathrm{d}\stackrel{\mathrm{̃}}{N}/\mathrm{d}{\log }_{\mathrm{10}}{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}$ is at a local minimum. Characteristic sizes ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$ are marked for each time. The relationship between symbols and characteristic sizes is shown only for τ=100.

As will be shown later, values of GR_m obtained with ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$ or ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$ are not equal. To differentiate these cases, GR_m are notated as GR_m,mode, GR_m,sr100, GR_m,sr50 and GR_m,tot50 accordingly.

2.3 Evaluation of true growth rate (GR_true)

The true GR (GR_true) defined in this paper follows the Lagrangian approach (Olenius et al., 2014), i.e., tracking the volume change of individual particles, and only including molecular species exchange by condensation and evaporation. It is calculated with the following expression:

$$\begin{array}{ll}{\displaystyle }{\mathrm{GR}}_{\mathrm{true}}& {\displaystyle }={\displaystyle \frac{\mathrm{d}{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}}{\mathrm{d}\mathit{\tau }}}={\displaystyle \frac{\mathrm{2}}{\mathit{\pi }{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{d}\stackrel{\mathrm{̃}}{V}}{\mathrm{d}\mathit{\tau }}}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{2}}{\mathit{\pi }{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}^{\mathrm{2}}}}\cdot {\displaystyle \frac{\stackrel{\mathrm{̃}}{V}+c\left(i,k\right){\stackrel{\mathrm{̃}}{N}}_{\mathrm{1}}\cdot \mathrm{d}\mathit{\tau }-E_k\cdot \mathrm{d}\mathit{\tau }-\stackrel{\mathrm{̃}}{V}}{\mathrm{d}\mathit{\tau }}}\\ \text{(9)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{2}\left(c\left(i,k\right){\stackrel{\mathrm{̃}}{N}}_{\mathrm{1}}-E_k\right)}{\mathit{\pi }{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}^{\mathrm{2}}}},\end{array}$$

where ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}$ is the representative size, ${\stackrel{\mathrm{̃}}{N}}_{\mathrm{1}}$ is the concentration of monomers and E_k is the particle evaporation rate given by Eq. (5).

If evaporation is negligible (E=0) and ${\stackrel{\mathrm{̃}}{N}}_{\mathrm{1}}$ is constant, Eq. (9) leads to a higher GR for smaller particles, mainly because of the increased monomer collision frequency relative to particle size (Tröstl et al., 2016). Throughout this work Eq. (9) is used to evaluate true particle GR. Note GR_true is calculated from dimensionless size and time, and is therefore dimensionless. Since we focus on relative values of true and measured GRs, our conclusions are unaffected by the dimensionality of GR. However, dimensionless GRs can be converted to dimensional values with Eq. (6).

3 Results and discussion

3.1 Error of using GR_m,mode as GR_true

As mode diameter (${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$) is often employed to derive particle GR, in this section we discuss the error of using GR_m,mode as a substitute for GR_true in the absence of preexisting particles. The effect of preexisting particles is discussed in Sect. 3.3.

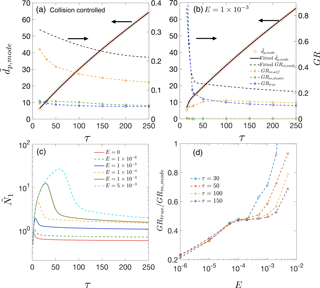
Figure 2 (a) ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$ and various growth rates as functions of time for collision-controlled nucleation. Dashed black lines show the value of GR_m,mode. Yellow, green and blue dashed lines represent GR_m,self, GR_m,cluster and GR_true, respectively. (b) The same quantities as are shown in panel (a) but with the evaporation constant set to $E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$. For both panels (a) and (b), the left axis shows values for the solid lines and the right axis shows values for the dashed lines. (c) Monomer concentration as functions of time for different values of E. (d) GR_true ∕ GR_m,mode for different values of E at τ=30, 50, 100 and 150.

Both condensation and coagulation lead to growth of ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$. To understand their relative importance, we attribute GR_m,mode to three processes: monomer condensation minus evaporation (GR_true), coagulation of the mode with clusters (GR_m,cluster) and self-coagulation of the mode (GR_m,self). The last two processes are the main causes of the discrepancy between GR_m,mode and GR_true. To evaluate GR_m,cluster and GR_m,self, the range of “clusters” and “mode” are defined as illustrated in Fig. 1 by the two shaded regions at τ=100: clusters (beige) and nucleation mode (light blue). Clusters and nucleation mode are separated by ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\min }$, where $\mathrm{d}\stackrel{\mathrm{̃}}{N}/\mathrm{d}{\log }_{\mathrm{10}}{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}$ is at a local minimum. Stolzenburg et al. (2005) assumed the nucleation mode is lognormal and calculated GR_true and GR_m,self with the method of moments. In this work, since the mode for collision-controlled nucleation deviates significantly from lognormal (see Fig. 1a), no assumption regarding the shape of the nucleation mode is made. Instead, GR_m,cluster and GR_m,self are calculated with the first-order numerical approximation method outlined in Appendix A.

The calculation results are summarized by Fig. 2. We first consider collision-controlled nucleation (E=0). For this nucleation scenario, Fig. 2a shows ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$ on the left y axis and GR values on the right. A third-order polynomial is used for fitting ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}={\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}\left(\mathit{\tau }\right)$ and is plotted as a solid black line. Differentiating the fitted polynomial with respect to time gives the value of GR_m,mode. It is clear that GR_true only accounts for a small fraction (17–20 %) of GR_m and is on par with the contribution of GR_m,cluster (15–22 %). Self-coagulation is the major contributor (62–78 %) to GR_m. Thus, using GR_m,mode as a substitute for GR_true leads to an overestimation by as much as a factor of about 6. We believe collision-controlled nucleation (E=0) in the absence of other particle loss mechanisms such as wall deposition (W=0) and scavenging by preexisting particles ($\sqrt{L}=\mathrm{0}$) provides an upper limit for overestimation of GR_truefor a constant rate system (R = constant). This is because these conditions lead to the maximum number of particles that can be produced by nucleation. High concentrations lead to high coagulation rates, and it is coagulation that is primarily responsible for errors in GR_m. Furthermore, as is discussed below, the absence of evaporation and scavenging by nucleated particles keeps monomer concentrations low relative to values achieved when E≠0 (see Fig. 2a). Low monomer concentrations reduce the value of GR_true, thereby increasing relative errors in GR_m.

Distinctive features of particle growth emerge when cluster evaporation is included by setting $E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$. Figure 2b shows results for this nucleation scenario. Most noticeably, particles grow considerably faster at early stages of simulation. This occurs because evaporation depletes clusters and correspondingly increases monomer concentration. In the absence of preexisting particles, monomer concentration accumulates until the supersaturation is high enough for nucleation to take place (see Fig. 2c). The accumulated monomers then rapidly condense on the nucleated particles, leading to the rapid particle growth shown in Fig. 2b. To capture this rapid growth, two third-order polynomials are used to fit ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$ values for τ<40 and τ>35, respectively, with an overlapping region for $\mathrm{35}<\mathit{\tau }<\mathrm{40}$. Furthermore, in comparison to collision-controlled nucleation, contribution of GR_m,cluster to GR_m,mode becomes negligible, due to decreased cluster concentration by evaporation. For τ>30, GR_true accounts for about 40–55 % of GR_m,mode, larger than that of collision-controlled nucleation; for τ<25, GR_true almost entirely accounts for GR_m,mode and even exceeds GR_m,mode at the very beginning of the nucleation. GR_true ∕ GR_m,mode > 1 indicates a rapidly forming nucleation mode, in which freshly nucleated particles enter the mode and skew the mode distribution toward smaller sizes, slowing down the shift of the mode peak towards larger values.

Increase of GR_true ∕ GR_m,mode by evaporation is explained by the elevated monomer concentration due to particle volatility and the smaller number of particles formed by nucleation: the former increases GR_true, and the latter decreases GR_m,self and GR_m,cluster. Figure 2c plots monomer concentration ${\stackrel{\mathrm{̃}}{N}}_{\mathrm{1}}$ as a function of time for several values of E. Noticeably, monomer concentration increases with E since higher cluster evaporation rates require higher monomer concentrations (i.e., higher supersaturation) to overcome the energy barrier of nucleation. Once nucleation takes place, high monomer concentration leads to rapid nanoparticle GRs.

Figure 2d shows GR_true ∕ GR_m,mode at τ=30, 50, 100 and 150 for several E values. At a given time, GR_true ∕ GR_m,mode clearly increases with E: when evaporation rates are not negligible (i.e., E≠0), GR_m,mode is closer to GR_true than occurs when E=0. Again, this is because the elevated monomer concentrations increase GR_true and the lowered concentrations of clusters and nucleated particles decrease GR_m,cluster and GR_m,self. As E approaches 0, the value of GR_true ∕ GR_m,mode converges to that of the collision-controlled nucleation (∼ 0.2). One data point, corresponding to $E=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ and τ=30, with a value of 1.8, is not shown in Fig. 2d. It has a value significantly greater than unity because of the large quantities of nucleated particles entering the mode, skewing the mode peak toward smaller sizes.

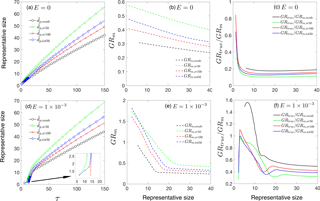
Figure 3 (a) ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{bin}\mathrm{50}}$ as functions of time. (b) Measured growth rates GR_m,mode, GR_m,sr50, GR_m,sr100 and GR_m,tot50 as functions of representative sizes. (c) Ratio of true growth rate to measured growth rate, GR_true ∕ GR_m. Panels (a)–(c) are for collision-controlled nucleation with E=0. Panels (d)–(f) show the same quantities as are shown in panels (a)–(c) but with $E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$.

3.2 Comparison of representative sizes

In this section we examine how observed GR depends on the choice of a representative size. The application of GR_m,mode to deduce GR_true, though convenient in practice, depends on the existence of a nucleation mode. However, the nucleation mode is usually not well defined in the early stage of nucleation. In contrast, GRs based on other representative sizes (${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$) are not dependent on mode formation and are available for all particle sizes. In light of this, GR_m,sr100, GR_m,sr50 and GR_m,tot50 have often been employed to describe the GR of small particles (< 5 nm). The effects of preexisting particles are neglected in this section (i.e., $\sqrt{L}=\mathrm{0}$) but are discussed in Sect. 3.3.

For collision-controlled nucleation, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$ are plotted as functions of time in Fig. 3a. The magnitude of the representative sizes follow ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$ < ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{bin}\mathrm{100}}$ < ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$ < ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{bin}\mathrm{50}}$, as was previously illustrated in Fig. 1a. ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$ < ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{bin}\mathrm{100}}$ indicates that a certain measurement bin first reaches its maximum concentration and becomes a local maximum at a later time. This is true for collision-controlled nucleation with a decreasing peak concentration but is not necessarily true for other nucleation scenarios. The observed GRs (i.e., slope of curves in Fig. 3a) are shown in Fig. 3b as a function of representative size, with a clear relationship GR_m,mode < GR_m,sr100 < GR_m,tot50 < GR_m,sr50. Note that GR_m,mode is not available for small sizes, indicating the nucleation mode is yet to form at the early stage of nucleation. Figure 3c shows GR_true ∕ GR_m as a function of representative size, with GR_true calculated with Eq. (9). Clearly GR_true accounts for the highest percentage of GR_m at the start of nucleation. This is partly due to higher monomer concentrations (see red solid curve in Fig. 2c) and partly due to Eq. (9), which leads to higher true GR for smaller particles: the addition of a monomer leads to a bigger absolute as well as fractional diameter growth for small particles.

Figure 3d–f are counterparts of Fig. 3a–c, but with evaporation constant E set to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$. Figure 3d shows that ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$ increase relatively slowly at the start of the simulation (see the amplified figure at the lower right corner of Fig. 3d; for reference, the dimensionless sizes of monomer, dimer and trimer are 1.24, 1.56 and 1.79, respectively). Subsequently, a marked change slope of the ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}={\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}\left(\mathit{\tau }\right)$ curve is observed, indicating accelerated particle growth. This reflects that nucleation occurs with a burst of particle formation following a process of monomer and cluster accumulation. The slow growth of the smallest clusters is an indication that the accumulation process is slow due to the strength of the Kelvin effect.

Figure 3e shows GR_m obtained by curve fitting after the nucleation burst and Fig. 3f shows the corresponding GR_true ∕ GR_m values. Different from collision-controlled nucleation, there is a sharp rise in the GR_true ∕ GR_m value at the start of nucleation. This is due to the sharp decrease in the evaporation term in Eq. (9), causing the value of GR_true to increase sharply. As nucleation progresses, the ratio of GR_true to GR_m,sr100, GR_m,tot50 and GR_m,sr50 comes close to 1, with GR_m,mode not yet available. Eventually, GR_true ∕ GR_m for all representative sizes decreases and falls into the range of 30–50 %, with GR_m,mode giving the best estimate of GR_true. Note the value of GR_true ∕ GR_m,mode significantly exceeds unity for ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}\in [\mathrm{5},\mathrm{11}]$ due to the distortion of the mode toward smaller sizes by the high flux of freshly nucleated particles into the mode.

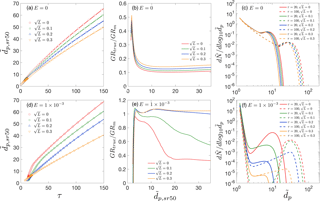
Figure 4 Effect of preexisting particles on particle growth rate. (a) ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$ as a function of time. (b) Ratio of true growth rate to measured growth rate, GR_true ∕ GR_m,sr50. (c) Particle size distributions at τ=20 and τ=100. Panels (a)–(c) are for collision-controlled nucleation with E=0 and $\sqrt{L}=\mathrm{0}$, 0.1, 0.2, 0.3. Panels (d)–(f) show the same quantities as are shown in panels (a)–(c) but with $E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$.

3.3 Effect of preexisting particles

Preexisting particles act as particle sinks to decrease the intensity of nucleation. Similarly, in chamber experiments, though loss to preexisting particles is often eliminated by using air that is initially particle free, loss of particles to chamber walls is inevitable. Since wall loss and loss to preexisting particles have a qualitatively similar effect on nucleation (McMurry and Li, 2017), we selectively examine the effect of preexisting particles on GR measurements to qualitatively illustrate the effects of all of these processes. To probe the initial stage of nucleation, we use ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{bin}\mathrm{50}}$ as the basis for our analysis, with a comparison of representative sizes presented at the end of this section. As to the magnitude of $\sqrt{L}$, we choose $\sqrt{L}\in [\mathrm{0},\mathrm{0.3}]$ based on previous work. It was shown in Fig. 2b in McMurry and Li (2017) that as $\sqrt{L}$ exceeds 0.1, particle size distributions begin to deviate discernably from the collision-controlled case. In addition, $\sqrt{L}\approx \mathrm{0.2}$ was observed in the ANARChE field campaign carried out in Atlanta for nucleation events with sulfuric acid as the major nucleating species (Kuang et al., 2010).

The influence of preexisting particles on the discrepancy between true and measured GR (GR_true ∕ GR_m) is twofold. On the one hand, preexisting particles can decrease monomer concentration, which leads to a smaller GR_true. On the other hand, preexisting particles reduce coagulation by scavenging nucleated particles, which could result in a narrower gap between GR_true and GR_m. Therefore, the response of GR_true ∕ GR_m to $\sqrt{L}$ depends on the relative magnitude of these two competing effects. Figure 4a shows ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$ as a function of time for several $\sqrt{L}$ values and Fig. 4b displays the corresponding GR_true ∕ GR_m values. It can be seen that GR_true ∕ GR_m positively correlates with $\sqrt{L}$, indicating preexisting particles are more effective in removing nucleated particles than reducing monomer concentrations. In fact, as further demonstrated by Fig. 4c, monomer concentrations (leftmost point of all the curves) are barely affected: scavenging of monomers by preexisting particles is offset by less condensation of monomers onto nucleated particles. Note that for the range of $\sqrt{L}$ values examined, the presence of preexisting particles alter GR_true ∕ GR_m values by no more than 50 % for collision-controlled nucleation.

Figure 4d–f show the same quantities as are shown in Fig. 4a–c, but with E set to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$ instead of zero. In contrast to collision-controlled nucleation, preexisting particles significantly affect the nucleation process when cluster evaporation is taken into account. As $\sqrt{L}$ increases, Fig. 4e shows GR_true ∕ GR_m converges to a value slightly larger than unity. This indicates that the contribution of coagulation to measured GR approaches zero as $\sqrt{L}$ becomes large; or equivalently, the concentration of nucleated particles is severely decreased by preexisting particles. Values of GR_true ∕ GR_m,sr50 slightly exceed unity for large sizes (Fig. 4f) due to the slightly higher condensational GRs of smaller particles in the nucleation mode. This shifts values of ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$ towards smaller sizes than would occur if all particles were to grow at the same rate, causing GR_m,sr50 to be smaller than GR_true.

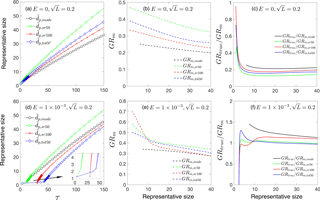
Figure 5 (a) ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$, ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{bin}\mathrm{50}}$ as functions of time. (b) Measured growth rate GR_m,mode, GR_m,sr50, GR_m,sr100 and GR_m,tot50 as functions of representative sizes. (c) Ratio of true growth rate to measured growth rate, GR_true ∕ GR_m. Panels (a)–(c) are for collision-controlled nucleation with E=0 and $\sqrt{L}=\mathrm{0.2}$. Panels (d)–(f) show the same quantities as are shown in panels (a)–(c) but with $E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$.

The decrease in nucleated particle concentration is further demonstrated in Fig. 4f. From $\sqrt{L}=\mathrm{0}$ to $\sqrt{L}=\mathrm{0.3}$, the peak concentration of nucleated particles dropped by about 3 orders of magnitude. Such a decrease in concentration of nucleated particles results from the limiting effect of $\sqrt{L}$ on monomer concentration. If preexisting particles are absent, then no major loss mechanisms for monomers exist prior to the nucleation burst. Monomers would accumulate until the nucleation energy barrier could be overcome: the higher the energy barrier, the higher the monomer concentration prior to nucleation, as shown in Fig. 2c. The elevated monomer concentration then leads to rapid growth of freshly nucleated particles immediately following the nucleation burst. However, in the presence of preexisting particles (i.e., $\sqrt{L}\ne \mathrm{0}$), monomer concentration can only increase to the point at which its production and consumption by preexisting particles reach balance, prohibiting its concentration from reaching a high value even prior to the nucleation burst. To facilitate comparison with experimental results, in Appendix B we provide an example of conversion from dimensionless distributions and GRs to dimensional ones.

Finally, Fig. 5 examines the difference between representative sizes used to calculate GR_m when loss to preexisting particles is accounted for. Two cases are presented: (1) collision-controlled nucleation (E=0) with $\sqrt{L}=\mathrm{0.2}$ (Fig. 5a–c) and (2) nucleation accounting for both cluster evaporation and scavenging by preexisting particles ($E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$ and $\sqrt{L}=\mathrm{0.2}$; Fig. 5d–f). For collision-controlled nucleation with $\sqrt{L}=\mathrm{0.2}$, the preexisting particles change nucleation only slightly, although GR_m decreases and GR_true ∕ GR_m increases to a minor extent compared to collision-controlled nucleation in the absence of a preexisting aerosol (compare Figs. 5a–c to 3a–c). The analysis made in the discussion of Fig. 3a–c still stands for Fig. 5a–c. For nucleation with evaporation and preexisting particles coupled together (Fig. 5d–f), three features are worthy of attention. First, compared to evaporation-only nucleation, GR_m is significantly decreased for small particle sizes. For ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}<\mathrm{10}$, GR_m is no larger than 0.7 with preexisting particles but can be greater than 1.5 without (refer to Fig. 3e). Second, as shown in Fig. 5f, GR_true ∕ GR_m,sr50 and GR_true ∕ GR_m,tot50 come close to unity due to negligible coagulation effects. Third, GR_true ∕ GR_m,mode is between 1.2 and 1.5 and GR_true ∕ GR_m,sr100 is between 1.1 and 1.2 for ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}>\mathrm{10}$, indicating the true growth will be slightly underestimated if ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$ or ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$ is used to infer GR_true.

3.4 Underestimation of GR_true

In previous sections, mainly overestimation of the GR_true by measured GR, GR_m, has been discussed. Though we do not quantitatively study underestimation of GR_true by GR_m, in this section we show that in a constant rate system in which particle sink processes (i.e., dilution and loss to preexisting particles) strongly decrease the concentration of nucleated particles, GR_m can approach zero and cannot be utilized to estimate GR_true. Figure 6 shows such nucleation scenarios for (a) collision-controlled nucleation with M = 0.1 and (b) collision-controlled nucleation with $\sqrt{L}=\mathrm{1.5}$. In both cases other sink processes were set equal to zero. As shown in both Fig. 6a and b, particle size distributions approach steady state after τ=100. As a result, GR_m approaches zero beyond τ=100. At the same time, GR_true remains finite since monomer concentration remains at steady state after τ=20. Therefore, other methods have to be utilized to infer GR_true in such situations.

4 Conclusions

We used a discrete-sectional model to solve a dimensionless form of aerosol population balance equation for a single-species system. True GR and various “measured” GRs were examined for a variety of nucleation scenarios. Based on the simulation results, we draw the following conclusions.

1. Simulated data show that for collision-controlled nucleation without preexisting particles, GRs inferred from the modal size of nucleated particles (GR_m,mode) is as much as 6 times greater than true GRs due to vapor condensation (GR_true).

2. In the absence of preexisting particles or other sink processes, comparison of different GRs based on different representative sizes indicates the relationship GR_m,mode < GR_m,sr100 < GR_m,tot50 < GR_m,sr50 holds true for collision-controlled nucleation. If clusters evaporate, the nucleation process is characterized by rapid particle growth following the nucleation burst.

3. Both evaporation and scavenging by preexisting particles can reduce the concentration of particles formed by nucleation. Lower particle concentrations reduce the effect of coagulation on GR_m, so overestimation of GR_true by GR_m is lower than is found in the absence of these processes.

4. Preexisting particles have dramatically different effects on collision-controlled nucleation and nucleation with cluster evaporation. For $\sqrt{L}\in [\mathrm{0},\mathrm{0.3}]$, collision-controlled nucleation is only slightly affected. However, if preexisting particles are coupled with evaporation, the number of nucleated particles can drop significantly, thus reducing the contribution of coagulation to measure GRs.

5. GR_m can underestimate GR_true in a system with strong dilution or other particle sink processes. Particle size distributions in such nucleation scenarios can approach a steady state that leads to a GR_m close to 0, which underestimates GR_true.

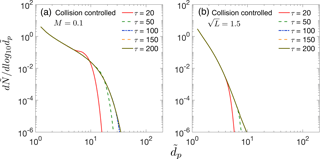
Figure 6 Particle size distribution at different dimensionless times for collision-controlled nucleation with (a) M=0.1 and (b) $\sqrt{L}=\mathrm{1.5}$. In both cases, sink processes not indicated in the figure were set to zero in the simulations. Particle size distributions at certain times are not visible in the figure since they overlap with the particle size distribution at a later time.

Appendix A

To evaluate the contribution of self-coagulation of the mode (GR_m,self) and cluster coagulation (GR_m,clsuter) to measured GR based on mode diameter (GR_m,mode), we used the following first-order numerical approximation method.

1. Find particle size distribution $\stackrel{\mathrm{̃}}{n}=\stackrel{\mathrm{̃}}{n}\left(k,\mathit{\tau }\right)$ at a given time τ. k is the number of monomers in a particle and ${\stackrel{\mathrm{̃}}{n}}_k$ is the concentration of particles that contains k molecules. Since the simulation code only reports discrete particle concentration for each bin, an interpolation is performed using MATLAB function griddedInterpolant.m.

2. Find the value $k=k_{max}$ at which $\mathrm{3}\log \left(\mathrm{10}\right)k\stackrel{\mathrm{̃}}{n}\left(k,\mathit{\tau }\right)$ is locally maximized. A pre-factor 3log (10)k is multiplied by $\stackrel{\mathrm{̃}}{n}\left(k,\mathit{\tau }\right)$ to convert the particle size distribution to $\mathrm{d}\stackrel{\mathrm{̃}}{N}/\mathrm{d}{\log }_{\mathrm{10}}{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}$. The mode diameter is then given by ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}\left(\mathit{\tau }\right)={\left(\frac{\mathrm{6}{k}_{max}}{\mathit{\pi }}\right)}^{\mathrm{1}/\mathrm{3}}$.

3. Use the following integration equations to obtain number distribution of the mode at time τ+Δτ assuming only one process causes the distribution to shift.

   For self-coagulation,

   $$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\stackrel{\mathrm{̃}}{n}}_{\mathrm{self}}\left(k,\mathit{\tau }+\mathrm{\Delta }\mathit{\tau }\right)=\stackrel{\mathrm{̃}}{n}\left(k\right)+\mathrm{0.5}\times \mathrm{\Delta }\mathit{\tau }\\ {\displaystyle }& {\displaystyle }\times \underset{L}{\overset{k}{\int }}c\left(x,k-x\right)\stackrel{\mathrm{̃}}{n}\left(x,\mathit{\tau }\right)\stackrel{\mathrm{̃}}{n}\left(k-x,\mathit{\tau }\right)\mathrm{d}x\\ \text{(A1)}& {\displaystyle }& {\displaystyle }-\underset{L}{\overset{H}{\int }}c\left(x,k\right)\stackrel{\mathrm{̃}}{n}\left(k,\mathit{\tau }\right)\stackrel{\mathrm{̃}}{n}\left(x,\mathit{\tau }\right)\mathrm{d}x.\end{array}$$

   For coagulation with clusters,

   $$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\stackrel{\mathrm{̃}}{n}}_{\mathrm{cluster}}\left(k,\mathit{\tau }+\mathrm{\Delta }\mathit{\tau }\right)=\stackrel{\mathrm{̃}}{n}\left(k,\mathit{\tau }\right)+\mathrm{0.5}\cdot \mathrm{\Delta }\mathit{\tau }\\ {\displaystyle }& {\displaystyle }\cdot \underset{L_{\mathrm{c}}}{\overset{H_{\mathrm{c}}}{\int }}c\left(x,k-x\right)\stackrel{\mathrm{̃}}{n}\left(x,\mathit{\tau }\right)\stackrel{\mathrm{̃}}{n}\left(k-x,\mathit{\tau }\right)H\left(H_{\mathrm{c}}-k+x\right)\mathrm{d}x+\mathrm{\Delta }\mathit{\tau }\\ {\displaystyle }& {\displaystyle }\cdot \underset{L_{\mathrm{c}}}{\overset{H_{\mathrm{c}}}{\int }}c\left(x,k-x\right)\stackrel{\mathrm{̃}}{n}\left(x,\mathit{\tau }\right)\stackrel{\mathrm{̃}}{n}\left(k-x,\mathit{\tau }\right)H\left(k-x-H_{\mathrm{c}}\right)\mathrm{d}x-\mathrm{\Delta }\mathit{\tau }\\ \text{(A2)}& {\displaystyle }& {\displaystyle }\cdot \underset{L_{\mathrm{c}}}{\overset{H_{\mathrm{c}}}{\int }}c\left(x,k\right)\stackrel{\mathrm{̃}}{n}\left(x,\mathit{\tau }\right)\stackrel{\mathrm{̃}}{n}\left(k,\mathit{\tau }\right)\mathrm{d}x.\end{array}$$

   In the above equations, L and H are the lower and upper boundaries of the mode, L_c and H_c are the lower and upper boundary of clusters, c(ij) is the collision frequency function, H(x) is the Heaviside step function. Δτ is typically set between 0.1 and 1.

4. Find the k values at which $\mathrm{3}\log \left(\mathrm{10}\right)k{\stackrel{\mathrm{̃}}{n}}_{\mathrm{self}}\left(k,\mathit{\tau }+\mathrm{\Delta }\mathit{\tau }\right)$ and $\mathrm{3}\log \left(\mathrm{10}\right)k{\stackrel{\mathrm{̃}}{n}}_{\mathrm{cluster}}\left(k,\mathit{\tau }+\mathrm{\Delta }\mathit{\tau }\right)$ are locally maximized. The corresponding diameters are ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{self}}\left(\mathit{\tau }+\mathrm{\Delta }\mathit{\tau }\right)$ and ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{cluster}}\left(\mathit{\tau }+\mathrm{\Delta }\mathit{\tau }\right)$.

5. The GR due to self-coagulation and coagulation with clusters are then given by

   $$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{GR}}_{\mathrm{m},\mathrm{self}}={\displaystyle \frac{{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{self}}\left(\mathit{\tau }+\mathrm{\Delta }\mathit{\tau }\right)-{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}\left(\mathit{\tau }\right)}{\mathrm{\Delta }\mathit{\tau }}};\\ \text{(A3)}& {\displaystyle }& {\displaystyle }{\mathrm{GR}}_{\mathrm{m},\mathrm{cluster}}={\displaystyle \frac{{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{cluster}}\left(\mathit{\tau }+\mathrm{\Delta }\mathit{\tau }\right)-{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}\left(\mathit{\tau }\right)}{\mathrm{\Delta }\mathit{\tau }}}.\end{array}$$

Appendix B

To facilitate comparison between dimensionless simulation results and experimental results, or previous dimensional simulation results, we convert selected dimensionless simulation results to dimensional quantities using Eq. (6). Specifically, we assume the monomer production rate is $R=\mathrm{1}\times {\mathrm{10}}^{\mathrm{6}}$ cm⁻³ s⁻¹ and the monomer has a volume of $\mathrm{1.62}\times {\mathrm{10}}^{-\mathrm{22}}$ cm³ and a density of 1.47 g cm⁻³. The collision frequency function for monomers, β_11 fm, is $\mathrm{4.27}\times {\mathrm{10}}^{-\mathrm{10}}$ cm⁻³s⁻¹, calculated at atmospheric pressure and 300 K. We consider two nucleation scenarios. The first is collision-controlled nucleation in the presence of preexisting particles, with $\sqrt{L}$ set to 0.2. The second scenario is nucleation with evaporation in the presence of preexisting particles. The evaporation constant in this case is $E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$ and $\sqrt{L}$ is 0.2. Both these cases are discussed in Sect. 3.3. The converted dimensional results are shown in Fig. B1, with relevant dimensional quantities displayed in the figure.

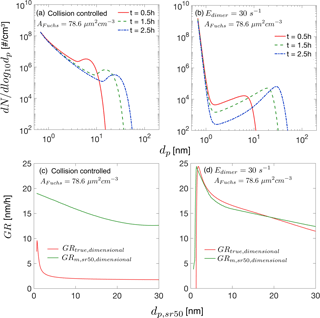
Figure B1 Dimensional particle size distribution and growth rates. The quantities shown in this figure are converted from the dimensionless solution using Eq. (6). The dimensional quantities involved in the conversions are $R=\mathrm{1}\times {\mathrm{10}}^{\mathrm{6}}$ cm⁻³ s⁻¹, ${\mathit{\beta }}_{\mathrm{11}\mathrm{fm}}=\mathrm{4.27}\times {\mathrm{10}}^{-\mathrm{10}}$ cm⁻³ s⁻¹ and $v_{\mathrm{1}}=\mathrm{1.62}\times {\mathrm{10}}^{-\mathrm{22}}$ cm³. The Fuchs surface area is 78.6 µm² cm⁻³, corresponding to $\sqrt{L}=\mathrm{0.2}$. (a) Particle size distribution for collision-controlled nucleation at t=0.5, 1.5 and 2.5 h. (b) Particle size distribution for nucleation with evaporation at t=0.5, 1.5 and 2.5 h. Monomer evaporation rate from the dimer is 30 s⁻¹, corresponding to a dimensionless evaporation constant $E=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$. (c) The dimensional particle growth rates for collision-controlled nucleation as is shown in panel (a). (d) The dimensional particle growth rates for nucleation with evaporation as is shown in panel (b).

Appendix C: Nomenclature

Collision-controlled nucleation	A limiting case for nucleation in which all collisions among condensing (nucleating) vapor occur at the rate predicted by kinetic theory and particles stick with 100 % efficiency. Vapor does not subsequently evaporate from particle surfaces, nor are particles scavenged by preexisting particles or the chamber wall.
${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\min }$	Particle size corresponding to the local minimum in a $\mathrm{d}\stackrel{\mathrm{̃}}{N}/\mathrm{d}{\log }_{\mathrm{10}}{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}$ representation of particle size distribution.
${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$	Particle size corresponding to the local maximum in a $\mathrm{d}\stackrel{\mathrm{̃}}{N}/\mathrm{d}{\log }_{\mathrm{10}}{\stackrel{\mathrm{̃}}{d}}_{\mathrm{p}}$ representation of particle size distribution.
${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$	Particle size of a measurement bin in which particle concentration reaches 50 % of its maximum value.
${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$	Particle size of a measurement bin in which particle concentration reaches maximum value.
${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$	Particle size above which total particle concentration reaches 50 % of its maximum value.
GRm,mode	Measured dimensionless growth rate based on ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{mode}}$.
GRm,sr50	Measured dimensionless growth rate based on ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{50}}$.
GRm,sr100	Measured dimensionless growth rate based on ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{sr}\mathrm{100}}$.
GRm,tot50	Measured dimensionless growth rate based on ${\stackrel{\mathrm{̃}}{d}}_{\mathrm{p},\mathrm{tot}\mathrm{50}}$.
GRtrue	True dimensionless particle growth rate attributed to the net flux of condensing vapors onto particle surface (i.e., the condensation rate minus the evaporation rate).
GRm,clsuter	Measured dimensionless particle growth rate attributed to coagulation with clusters.
GRm,self	Measured dimensionless growth rate attributed to self-coagulation of particles in the nucleation mode.
E, Ω	Dimensionless parameters characterizing evaporation rates of particles, derived from the liquid droplet model. E can be regarded as a dimensionless form of saturation vapor pressure of the condensing molecules and Ω a dimensionless form of surface tension. Ω assumes a constant value of 16 in this work.
$\sqrt{L}$	Dimensionless parameter characterizing fractional loss rate of monomer or nucleated particles to preexisting particles.
${\stackrel{\mathrm{̃}}{N}}_k$	Dimensionless concentration of particles containing k monomers (i.e., k molecules of condensed vapor).