Experimental study of H₂SO₄ aerosol nucleation at high ionization levels

One hundred and ten direct measurements of aerosol nucleation rate at high ionization levels were performed in an 8 m³ reaction chamber. Neutral and ion-induced particle formation from sulfuric acid (H₂SO₄) was studied as a function of ionization and H₂SO₄ concentration. Other species that could have participated in the nucleation, such as NH₃ or organic compounds, were not measured but assumed constant, and the concentration was estimated based on the parameterization by Gordon et al. (2017). Our parameter space is thus [H₂SO₄] $=\mathrm{4}\times {\mathrm{10}}^{\mathrm{6}}-\mathrm{3}\times {\mathrm{10}}^{\mathrm{7}}$ cm⁻³, [NH₃+ org] = 2.2 ppb, T=295 K, RH = 38 %, and ion concentrations of 1700–19 000 cm⁻³. The ion concentrations, which correspond to levels caused by a nearby supernova, were achieved with gamma ray sources. Nucleation rates were directly measured with a particle size magnifier (PSM Airmodus A10) at a size close to critical cluster size (mobility diameter of ∼ 1.4 nm) and formation rates at a mobility diameter of ∼ 4 nm were measured with a CPC (TSI model 3775). The measurements show that nucleation increases by around an order of magnitude when the ionization increases from background to supernova levels under fixed gas conditions. The results expand the parameterization presented in Dunne et al. (2016) and Gordon et al. (2017) (for [NH₃+org] = 2.2 ppb and T=295 K) to lower sulfuric acid concentrations and higher ion concentrations. The results make it possible to expand the parameterization presented in Dunne et al. (2016) and Gordon et al. (2017) to higher ionization levels.

1 Introduction

Secondary aerosol particles, which are formed by nucleation processes in the atmosphere, play an important role in atmospheric chemistry and in the Earth's climate system. They affect the Earth's radiation balance by scattering solar radiation back to space and can also act as cloud condensation nuclei (CCN) and thereby affect the amount of cloud and its radiative properties. Clouds have a net cooling effect on the Earth's radiation budget of about −27.7 W m⁻² (Hartmann, 1993). Thus, a small change in cloud properties can have significant effect on the climate system. Results by Merikanto et al. (2009) and Yu and Luo (2009) have shown that a significant fraction (ranging between 31 and 70 %) of cloud-forming aerosol particles in the atmosphere are secondary particles that originate from nucleation. Therefore, understanding nucleation is crucial in order to fully understand the atmospheric and climatic effects of aerosols.

Sulfuric acid (H₂SO₄) is the primary ingredient in the production of secondary aerosols because of its low vapour pressure and its ability to bond with water, which is ubiquitous in the atmosphere (Curtius, 2006). H₂SO₄ is primarily produced in the atmosphere from sulfur dioxide (SO₂) via oxidation by the OH radical, produced photochemically with ultraviolet light coming from the Sun. When H₂SO₄ collides with other molecules, it starts forming small clusters of molecules that can grow into new stable aerosols. If only H₂O and H₂SO₄ take part, the process is termed binary homogeneous nucleation. Nucleation can be significantly enhanced by other substances, the dominant ones being ammonia (NH₃) and organic molecules (Zhang et al., 2004; Kirkby et al., 2011, 2016; Ehn et al., 2014; Dunne et al., 2016). These processes are termed ternary and organic-mediated nucleation, respectively. Recent results show that in low H₂SO₄ environments nucleation also happens by condensation of highly oxygenated organic molecules alone (Bianchi et al., 2016). Further, ions enhance the nucleation process by stabilizing the molecular clusters. This process is termed ion-induced nucleation. The fraction of ion-induced nucleation of total particle formation was observed in various environments by Manninen et al. (2010). This study found that the fraction was in the range 1–30 % being highest in environments with generally low nucleation rates.

The typical concentration range of gas-phase H₂SO₄ in the atmosphere is 10⁶–10⁷ cm⁻³. The concentrations vary with location, time of day and emission of SO₂, which can be both anthropogenic and natural. Ions are ubiquitous in the lower atmosphere and are mainly produced by galactic cosmic rays (GCRs), forming 1–40 ion pairs cm⁻³ s⁻¹. The formation rate depends on factors such as altitude, latitude, and the solar cycle. Ionization is higher above land than above ocean due to natural radioactivity from soils, and the maximum ionization is at altitudes of ∼ 13 km (Bazilevskaya et al., 2008). In addition to the natural variations in ionization, an event such as a nearby supernova would significantly increase the atmospheric ionization in the time following the event. There exists strong indications of a supernova at a relatively close distance of ∼ 50 pc from the solar system ∼ 2.2 million years ago (Knie et al., 2004; Kachelrieß et al., 2015; Savchenko et al., 2015; Fimiani et al., 2016). According to Melott et al. (2017) the increase in GCR from such an event would cause an increase in tropospheric ionization of up to a factor of 50 during the first few hundred years following the event.

Few measurements exist that quantify parameters affecting and assisting nucleation (e.g. Berndt et al., 2006; Svensmark et al., 2007; Sipilä et al., 2010; Benson et al., 2011; Kirkby et al., 2011; Enghoff et al., 2011; Yu et al., 2017). Recent laboratory measurements made in the European Organization for Nuclear Research CLOUD (Cosmics Leaving Outdoor Droplets) chamber were presented in Dunne et al. (2016) and showed the dependence on temperature, trace gas and ion concentrations. Based on the measurements a parameterization that can be incorporated into climate models was developed and this parameterization was improved by Gordon et al. (2017). These and other measurements, (e.g. Svensmark et al., 2007; Enghoff et al., 2011; Kirkby et al., 2011) have verified that ionization helps the nucleation process. In this work we expand on these results by measuring nucleation at ion production rates (q), ranging from background levels to 560 cm⁻³ s⁻¹ and corresponding to those following a nearby supernova, and atmospherically relevant H₂SO₄ concentrations (4×10⁶–3×10⁷ cm⁻³).

2 Experimental methods

The measurements presented in this work were performed in an 8 m³ reaction chamber (SKY2). The set-up is shown schematically in Fig. 1. The chamber is made of electro-polished stainless steel and has one side fitted with a Teflon foil to allow UV light (253.7 nm) to illuminate the chamber and start the photochemical reaction to generate H₂SO₄. Dry purified air (20 L min⁻¹) from a compressor with an active charcoal, citric acid, and particle filter was passed through a humidifier and added to the chamber to reach a relative humidity of 38 %. 5 L min⁻¹ of dry air from the same compressor went through an ozone generator where O₂ is photolysed by a UV lamp to produce O₃. Sulfur dioxide (3.5 mL min⁻¹) was added from a pressurized bottle (5 ppm SO₂ in air, AGA). The resulting concentrations of O₃ (20–30 ppb) and SO₂ (0.6–0.9 ppb) were measured by a Teledyne T400 analyser and with a Thermo 43 CTL analyser, respectively. The H₂SO₄ concentration was measured with a chemical ionization atmospheric pressure interface time-of-flight (CI-API-ToF) mass spectrometer (Jokinen et al., 2012). The chamber is also equipped with instruments to measure temperature, differential and absolute pressure, humidity, and UV intensity. The pressure was held at a standard pressure of ∼ 1 bar with a slight (0.1 mbar) overpressure relative to the surroundings, the temperature was at 295 K, and the UV intensity was varied as part of the experiments.

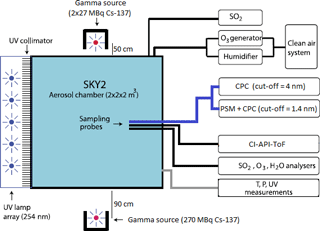
Figure 1 A schematic of the SKY2 reaction chamber and the instruments used for the experiment. The figure is an edited version of the schematic from Svensmark et al. (2013).

Two different condensation particle counters (CPCs) and a particle size magnifier (PSM) were used to count the aerosols formed in the experiments. A TSI model 3775 CPC was used to determine the aerosol particle concentration above a cut-off diameter of 4 nm ($d_{\mathrm{p},\mathrm{cut}-\mathrm{off}}=\mathrm{4}$ nm). A TSI 3776 CPC ($d_{\mathrm{p},\mathrm{cut}-\mathrm{off}}=\mathrm{2.5}$ nm) was used in series with the PSM Airmodus A10, developed and described by Vanhanen et al. (2011) to detect particles above a cut-off diameter of ∼ 1.4 nm. The cut-off diameter is defined as the mobility diameter of particles, of which 50 % are counted, and it depends on the saturator flow rate and the chemical composition of the particles. For the PSM, the saturator flow rate was set to 1.3 L min⁻¹, which corresponds to a cut-off diameter of 1.4 nm for tungsten oxide particles. The cut-off for H₂SO₄ aerosols is not known exactly. The cut-off diameter of the PSM is very close to the critical size of ∼ 1.5 nm (Kirkby et al., 2011), which allows for direct measurements of nucleation rate, thereby avoiding extrapolations of the nucleation rate from larger sizes (Kürten et al., 2018). Both instruments (PSM and CPC) sampled from the same line and had identical sampling pathways as illustrated in Fig. 1. The CPC with the larger cut-off diameter was used on its own to achieve a larger size span between the instruments, which enables the determination of the particle growth rate (GR).

2.1 Ionization of air by gamma sources

The air in the 8 m³ reaction chamber was ionized by gamma sources. Enghoff et al. (2011) have shown that the nature of the ionizing particles is not important for the nucleation of aerosols. Therefore, even though particles from an accelerator beam can have energies closer to GCR, gamma radiation, which is more accessible, can be used to study the ion-induced nucleation. Three Cs-137 sources were used in the set-up: two 27 MBq and one 270 MBq. To achieve a homogeneous irradiation of the chamber, the 270 MBq source was placed on one side of the chamber at a ∼ 90 cm distance, and the two 27 MBq sources were placed close to each other on opposite sides of the chamber at ∼ 50 cm distance. The set-up is illustrated in Fig. 1. Ions are also produced in the chamber by naturally occurring GCR and background radiation from Radon at a rate of ∼ 3 cm⁻³ s⁻¹. In order to perform measurements at different ionization levels, lead shielding of varying thickness was placed in front of the sources. Four ionization levels were achieved by using either 0, 1.5, 3.5, or 8.5 cm lead shielding.

The uniformity and level of the ionization caused by the sources were estimated from simulations in Geant 4, with the G4beamline programme (CMS Groupware, 2017). Figure 2 shows the ionization rates (q) in the chamber caused by the gamma sources, for minimum and maximum shielding thickness. The graphs show the chamber as seen from opposite the UV lamps. Thus, the 270 MBq source is on the left side of the graphs. From the simulation results in Fig. 2, it is clear that when the gamma sources were fully exposed the 270 MBq source created more ion pairs than the two weaker sources on the opposite side of the chamber. The variation from highest to lowest ionization is around a factor of 2, which translates into a factor of 1.4 in ion concentration. There is some circulation of the air in the chamber and the air is sampled from approximately midway between the sources as seen in Fig. 1. Therefore it is assumed that the average ionization for the entire chamber is a good representation of the ionization of the sampled air.

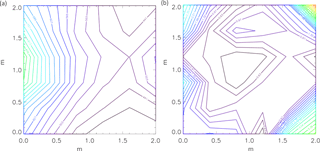
Figure 2 Geant 4 simulations of ionization rate, q [cm⁻³ s⁻¹], in the chamber with 0 cm (a) and 8.5 cm (b) lead shielding. The average ionization for the entire chamber is presented in Table 1.

Table 1 Average ionization rate for the entire chamber (q) achieved with the gamma sources at various thicknesses of lead shielding calculated with Geant 4. N is the ion density including the ions produced by naturally occurring radiation.

^∗ Approximate values calculated with $N=\sqrt{q_{\mathrm{total}}/\mathit{\alpha }}$, where $\mathit{\alpha }=\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{6}}$ is the recombination coefficient and q_total is the sum of the natural ionization (3 cm⁻³ s⁻¹) and the enhanced ionization caused by the sources.

2.2 Design of experiments

The experiments were conducted by turning on the UV lamps for 20 min to generate H₂SO₄. The [H₂SO₄] depends on the intensity of the UV light; thus by varying the intensity between experiments, the H₂SO₄ concentration was varied. Once sufficient H₂SO₄ was present, nucleation started and continued until the H₂SO₄ was used up and/or lost to the chamber walls. The aerosol formation rate was measured at the respective cut-off diameters with the PSM and CPC. The procedure lasted 6 to 14 h for a single run under fixed gas conditions, depending on the sulfuric acid concentration, because the system had to return to its initial conditions (PSM concentration < 2 cm⁻³) before a new experiment was started. In between experiments, the ionization conditions were varied by changing the amount of lead shielding in front of the gamma sources. At least 1 h before each experiment the lead shielding was put in the right position to allow the ionization level to stabilize before the nucleation started.

The upper limit to the H₂SO₄ concentrations was chosen based on time constraints, because too high concentrations yielded a particle count which took a long time to decay to initial conditions (< 2 cm⁻³). The lower limit of the H₂SO₄ concentrations was chosen based on the particle detection limit of the CPC model 3775, which was the limiting instrument because the majority of the particles are lost during the growth from 1.4 to 4 nm. On average, 25 % of the particles survive the growth. The survival is only 10 % for low H₂SO₄ concentrations since the GR is slower in this case.

Every fifth measurement was performed as a reference experiment with a standard ion concentration (N=2900 cm⁻³ s⁻¹) and UV intensity (20 %) to avoid unnoticed drifts in parameters or instruments. The reference experiments showed that the [H₂SO₄] varied despite the identical UV setting, because the O₃ concentration decreased during the measurement series. This drift was caused by the O₃ generator, in which a UV lamp was replaced immediately prior to the measurements series. The lamp intensity decreased with time, causing smaller H₂SO₄ concentrations for a given UV setting. A list of settings and the number of measurements at each setting is presented in Table 2.

Table 2 The range of UV and radiation level settings that were used through the measurement series. The radiation levels are 0: N = 1700 cm⁻³, 1: N = 2900 cm⁻³, 2: N = 8400 cm⁻³, 3: N = 19 000 cm⁻³. The last column shows the number of measurements at each setting. The reference measurements were performed at 20 % UV and radiation level 1.

3 Data processing

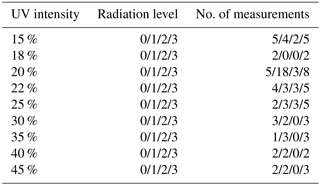
Figure 3 shows an example of a run sequence (for 22 % UV and N=8400 [cm⁻³]) as a function of time. The UV lamps were turned on for 20 min from 02:26:10 to 02:46:12. The top panel shows the temperature in the chamber during the experiment. It shows that the temperature increased by ∼ 0.1 K when the UV lamps were turned on. When the UV was on the highest setting (45 %) the temperature increased by 0.2 K. This slight increase in temperature is negligible with regards to the nucleation rate (5 % change for a 0.2 K increase at the highest [H₂SO₄] based on Dunne et al., 2016). Therefore, a constant temperature of 295.4 K was used in the further analysis. The second panel shows the H₂SO₄ concentration in units of 10⁷ [cm⁻³]. The red line is the 50-point boxcar moving average. Immediately after the UV lamps were turned on, the H₂SO₄ concentration started to increase. When the UV was turned off, the H₂SO₄ was lost to scavenging by aerosol particles and to the chamber walls. The third panel shows the aerosol particle concentration measured with the PSM and CPC without any corrections for the wall losses. The red lines represent the 50-point boxcar moving average, which is used for further data analysis to avoid artefacts from noise. Corrections for particle loss to chamber walls are presented further down and the data analysis was performed on the corrected version of the moving average.

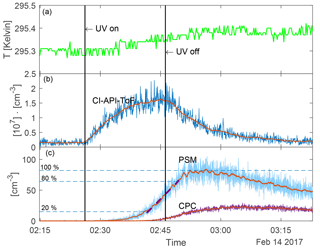
Figure 3 Run sequence for an experiment with 22 % UV and N=8400 [cm⁻³]. The vertical lines show when the UV lamps were turned on and off. (a) Temperature in the chamber. (b) H₂SO₄ concentration measured with the CI-API-ToF and 50-point moving average shown in red. (c) Aerosol particle concentration measured with PSM and CPC (before the loss correction). The 50-point moving average is shown in red. The purple dashed line on top of the PSM data shows the linear fit between 20 and 80 of the maximum concentration. The gradient of this fit (on the loss-corrected data) was used as the nucleation rate.

3.1 Sulfuric acid measurements

The CI-API-ToF mass spectrometer was used to determine the concentration of H₂SO₄. The CI-API-ToF spectrometer used in the set-up was calibrated with the calibration system presented in Kürten et al. (2012). We use the calibration coefficient, C, as defined in Eq. (1) in Jokinen et al. (2012):

$$\begin{array}{}\text{(1)}& {\displaystyle }\left[{\text{H}}_{\mathrm{2}}{\text{SO}}_{\mathrm{4}}\right]={\displaystyle \frac{{\text{HSO}}_{\mathrm{4}}^{-}+{\text{HSO}}_{\mathrm{4}}^{-}\cdot {\text{HNO}}_{\mathrm{3}}}{{\text{NO}}_{\mathrm{3}}^{-}+{\text{NO}}_{\mathrm{3}}^{-}{\text{HNO}}_{\mathrm{3}}+{\text{NO}}_{\mathrm{3}}^{-}({\text{HNO}}_{\mathrm{3}}{)}_{\mathrm{2}}}}\cdot C.\end{array}$$

The resulting calibration coefficient was $C=\mathrm{9.86}\times {\mathrm{10}}^{\mathrm{9}}\pm \mathrm{4.22}\times {\mathrm{10}}^{\mathrm{8}}$ molec cm⁻³. Values in the literature vary from 5×10⁹ to 1.89×10¹⁰ molec cm⁻³ (Kürten et al., 2012).

The concentrations measured directly by the mass spectrometer are integrated concentrations of masses over a small region (±0.5 AMU) of the spectrum. This means that the concentrations are overestimated because they include noise around the actual peak. This was also taken into account and corrected for using the results from Hansen (2016), where a relation between the analysis of the ±0.5 AMU data was found from the API-ToF and data analysed using Tofware (Stark et al., 2015).

The H₂SO₄ concentration is determined from the peak value of the 50-point boxcar moving average (the red line in Fig. 3). This method introduces a statistical uncertainty in addition to the uncertainty in the calibration factor. The statistical uncertainty arises from the fluctuations in the non-smoothed data and was calculated from the standard error of the difference between the non-smoothed and the smoothed data for the 50 points around the peak.

The CI-API-ToF mass spectrometer broke down during the measurement series. Therefore, 60 out of 110 experiments do not include direct measurements of the H₂SO₄ concentration. For these experiments, the concentration was interpolated from a linear relation between the H₂SO₄ concentration, in the 50 direct measurements, and the GR of the aerosol particles; see Sect. 3.2. Previously, linear relations between GR and H₂SO₄ have been demonstrated by Kulmala et al. (2001).

3.2 Determination of growth rate

The different cut-off diameters of the PSM A10 (1.4 nm) and TSI model 3775 CPC (4 nm) allow for the GR to be calculated from the time difference, Δt, between measurements in the two instruments. A percentage limit (50 % of the maximum concentration) was used instead of absolute numbers to take particle losses during growth into account. The difference in the cut-off diameters of the two instruments is 2.6 nm. The GR is therefore defined as

$$\begin{array}{}\text{(2)}& {\displaystyle }\text{GR}={\displaystyle \frac{\mathrm{2.6}\mathrm{nm}}{\mathrm{\Delta }t}}.\end{array}$$

The calculated GRs were in the interval 14–34 nm h⁻¹ at H₂SO₄ concentration, ranging from 7.2×10⁶ to 2.7×10⁷ cm⁻³. These GR values are reasonable compared to atmospheric GR (∼ 1–20 nm⁻¹) (Kulmala et al., 2004). We note that, although the GR are higher than expected from pure sulfuric acid condensation at the kinetic limit, indicating the participation of other vapours in the early growth (Tröstl et al., 2016), we still find a linear relationship between sulfuric acid and the GR. These other vapours can also contribute to the observed nucleation rates (see Sect. 4 Results and Discussion).

3.3 Determination of nucleation rate

Nucleation rates, J_D, were measured at a mobility diameter of D ∼ 1.4  nm with the PSM A10. The particle diameter of 1.4 nm comes close to the critical cluster size, and therefore the PSM allows for direct measurements of the nucleation rate. The PSM measures the concentration of particles with diameters above the cut-off, N_1.4.

The nucleation rate is defined as $J=\mathrm{d}N/\mathrm{d}t$, where $N=N_{\mathrm{1.4}}/\exp (-k\cdot t)$. Here k is a loss term that represents loss to the chamber walls and t is the time after the particles reached the critical size. From Svensmark et al. (2013) we have the size-dependent loss term k, which is an approximation of particle loss to the chamber walls:

$$\begin{array}{}\text{(3)}& {\displaystyle }k=\mathit{\lambda }/r_i^{\mathit{\gamma }}.\end{array}$$

The term γ is determined experimentally in Svensmark et al. (2013) to $\mathit{\gamma }=\mathrm{0.69}\pm \mathrm{0.05}$ and $\mathit{\lambda }=\mathrm{6.2}\times {\mathrm{10}}^{-\mathrm{4}}$ nm^γ s⁻¹. The average radius r_i that the particles have at a certain time is given by the critical radius (0.7 nm), the growth rate, and the time they took to grow. This is multiplied by 0.5 to get the average size:

$$\begin{array}{}\text{(4)}& {\displaystyle }{r}_i=\mathrm{0.7}\mathrm{nm}+\text{GR}\cdot \mathrm{0.5}\cdot \mathrm{\Delta }{t}_i.\end{array}$$

The loss term is used to correct the particle count from the PSM at any time and the result is seen in Fig. 4.

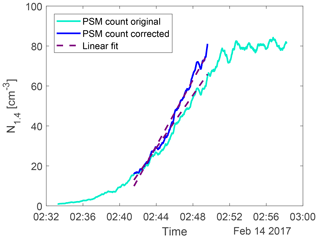
Figure 4 An example of the particle count from the PSM (light blue) and the loss-corrected data (dark blue). The dashed lines show the linear fit between 20 and 80 % of the maximum count. The gradient of the fit on the corrected data was used as the nucleation rate J_1.4.

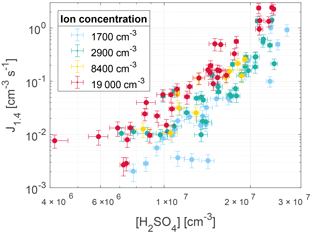
The nucleation rate J_1.4 was determined by calculating the gradient of the area between 20 and 80 % of each corrected peak of particle concentration. This is illustrated by the dashed lines in Fig. 3 and 4. The nucleation rates as a function of H₂SO₄ and ion concentrations are seen in Fig. 5 with error bars. The error bars on the nucleation rate are the 95 % confidence interval of the gradient. The error bars on the H₂SO₄ are the statistical standard errors. The Poisson counting uncertainty for the PSM ($\sqrt{N}$, see Sect. 3.4) and the calibration uncertainty for the mass spectrometer (∼ 5 % measurement error + additional errors from calibration parameters; ∼ 30 %, Kürten et al., 2012) are not shown.

Figure 5 Nucleation rates as a function of sulfuric acid concentration and ion concentration. The error bars represent 1σ standard deviation on the [H₂SO₄] and the 95 % confidence interval on the nucleation rate.

3.4 Additional uncertainties

Additional uncertainties in the particle concentration measurement arise, for example, from low particle counting statistics, from chemical-composition-dependent variation in the cut-off diameter of the particle counters, and from loss of particles in the sampling system. According to Kangasluoma and Kontkanen (2017) particle sampling and counting is a Poisson process and the statistical uncertainty is determined from the Poisson counting uncertainty, $\sqrt{N}$, which describes the standard deviation, σ, of the counted particles, N.

Aerosols are lost to the walls of the sampling system due to diffusion. This type of loss is size dependent and was estimated using the particle loss calculator (PLC) developed by von der Weiden et al. (2009). The loss function estimates that the losses of the 1.4 nm particles in the sampling system are ∼ 50 % and only ∼ 15 % for the 4 nm particles. Since we do not measure the particle size distribution diffusion losses are not included directly in the data analysis. This means that we could have underestimated the concentration of the smallest aerosols and thereby the nucleation rates.

4 Results and discussion

As the measurements presented here are an extension of the measurements presented in Dunne et al. (2016), at the given conditions, it is natural to compare the two. Therefore, the results shown in Fig. 5 are compared to Gordon et al. (2017), which presents the parameterization of the CLOUD experiments to the highest precision. In their work nucleation is represented as a sum of binary (b), ternary (t), neutral (n), ion-induced (i), and organic nucleation (org). The term representing the organic nucleation rate is not used in the following, as our study does not intentionally add or measure organic molecules. However, as deduced from the high GR, there might be traces of organic species that can also contribute to the nucleation rate. The concentration of organics is considered constant and is included in the ternary nucleation rate. Thus, a nucleation rate given by the sum of the four contributions is considered:

$$\begin{array}{}\text{(5)}& {\displaystyle }J=J_{\mathrm{b},\mathrm{n}}+J_{\mathrm{t},\mathrm{n}}+J_{\mathrm{b},\mathrm{i}}+J_{\mathrm{t},\mathrm{i}}.\end{array}$$

At the temperatures and gas concentrations used in this study, ternary nucleation is expected to dominate, as binary clusters are unstable (Hanson and Lovejoy, 2006). The model of binary nucleation presented in Ehrhart et al. (2016) shows good agreement with measurements performed in the European Organization for Nuclear Research CLOUD (Cosmics Leaving Outdoor Droplets) chamber at lower temperatures (< 273 K). However at tropospheric temperatures (> 273 K) the binary nucleation rate cannot explain the nucleation rates that are observed in either of these studies at the given sulfuric acid concentrations. Since the sulfuric acid concentration is lower in our study, this is particularly important here. Ehrhart et al. (2016) attributes the differences to contamination which is more important in providing stabilization for the pre-nucleating clusters when the temperature (and thereby the evaporation) is high. Nevertheless, we have included the binary term for the sake of completeness.

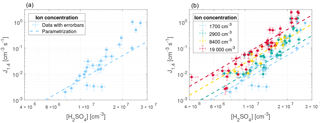
Figure 6 Parameterization from Gordon et al. (2017) with [NH₃] = 2.2 ppb (dashed lines) and nucleation rate measurements from this study at T=295 K, RH = 38 %, N = 1700 cm⁻³ (a) and all N (b).

Ammonia (NH₃) is filtered from the air that enters the chamber with a citric acid filter. However, trace amounts (which can originate from incomplete filtering or introduction through the humidifier or the bottled SO₂ in air) are still present in the chamber and contribute to the production of stable clusters together with organic molecules. As the concentrations of neither NH₃ nor organic molecules are measured, an ammonia equivalent concentration [NH₃ + org] that represents both species is estimated by comparing the results from the two studies under the same conditions (including T = 295 K, RH = 38 %, and N = 1700 cm⁻³).

Figure 6 shows the parameterization from Gordon et al. (2017) (dashed lines) on top of the data from our experiments with the [NH₃] concentration set to 5.5×10¹⁰ cm⁻³ (2.2 ppbv) for N=1700 cm⁻³ (left) and all ionization levels (right). Since $\left[{\mathrm{NH}}_{\mathrm{3}}\right]=\mathrm{5.5}\times {\mathrm{10}}^{\mathrm{10}}$ cm⁻³ is the value that gives the best match between the data and the extrapolated parameterization, it is assumed to represent the concentration of NH₃ and organic species, [NH₃ + org]. Atmospherically observed NH₃ concentrations are typically at the sub-ppbv and ppbv levels (Erupe et al., 2010; Nowak et al., 2006). Since the air is filtered before entering the chamber, we would expect a concentration that is lower than in the atmosphere. Once again, this is an indication of the presence of other nucleation-enhancing species in our chamber.

We note that nucleation rates were reported for a mobility diameter of 1.7 nm in Dunne et al. (2016), meaning that the rates measured in this study should be slightly overestimated since we measure at a mobility diameter of ∼ 1.4 nm (see Sect. 2).

As seen from Fig. 6 the parameterization presented in Gordon et al. (2017) matches the nucleation rates from this study, when extrapolated to the same region, especially at $\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\right]<\mathrm{2}\times {\mathrm{10}}^{\mathrm{7}}$ cm⁻³. At higher values of [H₂SO₄] the nucleation rates from this study are higher than expected from the parameterization. The resulting parameterization shows that at an atmospherically relevant H₂SO₄ concentration of 1×10⁷ cm⁻³, the increase in ions from background levels to the highest measured levels causes an increase in nucleation rate of around an order of magnitude.

The disagreement between the data and the expected parameterization could be caused by the narrow range of [H₂SO₄] in this study, which are all within 1 order of magnitude. Another explanation could be that the detection efficiency of the PSM is ∼ 50 % for particles close to the critical size of 1.4 nm. Since we use a percentage region instead of a fixed time interval when calculating the nucleation rate (see Sect. 3.3), it is possible that the dependence on [H₂SO₄] was overestimated due to the lower detection efficiency of PSM for particles smaller than 2 nm. At higher [H₂SO₄], more particles could grow into sizes that are detected more efficiently by the PSM compared to at lower [H₂SO₄]. This was taken into account by verifying that the regions between 20 and 80 % of each peak of particle concentration were linear. If the detection efficiency was dependent on [H₂SO₄], these regions would not be linear but the gradient would increase with time for a given peak. However, we still note that the detection efficiency of the PMS could have affected the results in another way. Likewise, it is worth noting that the effect of ions on the detection efficiency of the PSM is unknown, but ions may be more efficiently detected (Winkler et al., 2008).

It can be complicated to compare different experimental studies, even under similar conditions, because it is unclear how experimental techniques and parameters affect the results. Four studies (Kirkby et al., 2011; Almeida et al., 2013; Duplissy et al., 2016; Kürten et al., 2016), all performed in the CLOUD chamber, are most relevant for intercomparison, because they were made in a reaction chamber analogous to this study. The experiments presented in Sipilä et al. (2010) were performed in a flow tube. Yet, we include these in the comparison, because in it nucleation was measured directly at the critical cluster size with a PSM instrument. Table 3 gives an overview of the studies and conditions that were compared. Some studies consist of several experiments using varying parameters. Table 3 only shows the measurements made under the conditions that were closest to the parameters of this study. The experiments from this study with lowest ionization are used for comparison, because this ionization level (4.4 cm⁻³ s⁻¹) is close to the cosmic ray background ionization (GCR ∼ 3 cm⁻³ s⁻¹).

Table 3 Comparison of similar nucleation rate experiments. The numbers refer to the different studies: 1 is this study, 2 is Kirkby et al. (2011), 3 is Almeida et al. (2013), 4 is Duplissy et al. (2016), 5 is Kürten et al. (2016), and 6 is Sipilä et al. (2010). The fifth parameter, D, is the mobility diameter. GCR corresponds to the background GCR (galactic cosmic ray) ionization (∼ 3 cm⁻³ s⁻¹). Cells with a dash mean that the value was not measured or reported.

^a The nucleation rates were read from the figures in the respective papers and are therefore only approximate values. ^b The observed growth rate in this study was close to that from pure sulfuric acid.

From Table 3 it is clear that experiments conducted under the exact same conditions as in this study do not exist. Nevertheless, the nucleation rates in this study lie slightly below or within the range of the nucleation rates obtained in the experiments performed in the CLOUD chamber (studies 2–5). Except for study 3, which was made under lower temperatures, these studies have sulfuric acid concentrations that are 1 to 2 orders of magnitude higher than is the case for this study. As with the parameterization this indicates the existence of other nucleating species within our chamber. By comparing studies 2 and 5 made under almost identical conditions the effect on nucleation of an increase in NH₃ concentration is evident (e.g. at $\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\right]=\mathrm{2}\times {\mathrm{10}}^{\mathrm{8}}$ cm⁻³, which is the lower limit for study 2 and the upper limit for study 5).

The temperature used in this paper is only relevant to the boundary layer of the troposphere. At this high temperature evaporation of pre-nucleation clusters is very important and the stabilization provided by ions can have a strong effect (Lovejoy et al., 2004), as is also seen in this study. Higher in the troposphere where temperatures are lower the importance of evaporation decreases. However ions can still have a strong effect on the nucleation rates. Kirkby et al. (2011) showed that ions can affect pure binary nucleation rates at mid-troposphere conditions (∼ 250 K). An even higher increase in ionization, as used in this work, would increase the nucleation rates even more – by about 1 order of magnitude according to the parameterization used here. The concentrations of ternary gases are also expected to be lower in the free troposphere, which increases the effect of the ions.

In order to fully account for the variables in nucleation processes observed in this study, direct measurement of NH₃ and organic substances would have been preferred. Nonetheless, the results show that the nucleation increases linearly with ion concentration, even at the highest ionization. Also, consistency with the results from Dunne et al. (2016) and Gordon et al. (2017) is shown.

5 Conclusions

The nucleation of H₂SO₄/H₂O aerosols was studied under near-atmospheric conditions in an 8 m³ reaction chamber. Sulfuric acid was produced in situ in the range $\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\right]=\mathrm{4}\times {\mathrm{10}}^{\mathrm{6}}$–3×10⁷ cm⁻³ and the ionization of the air in the chamber was increased from background levels of ∼ 4 up to 560 cm⁻³ s⁻¹ (ion concentrations $=\mathrm{1700}-\mathrm{19}\mathrm{000}$ cm⁻³) using gamma sources. Such levels of ionization are relevant for a nearby (∼ 50 pc) supernova which is thought to have occurred ∼ 2.2 million years ago. The experiments were performed at T=295 K and RH = 38 %. The study shows that nucleation increases linearly with ion concentration over the full range of ion concentrations. We find that nucleation increases by an order of magnitude, when the ion concentration is increased from background to maximum levels. We have not measured the concentration of nucleating species other than sulfuric acid, so the nucleation pathways are unclear. Based on comparisons with other studies we conclude that ternary nucleation involving ammonia or organics is required to explain the observed nucleation rates. Still, this study is a novel contribution to the experimental studies of nucleation rates for the ammonia/organic-mediated H₂SO₄/H₂O system because of the direct measurements of nucleation rates at sizes close to the critical cluster size at high ion concentrations. This work expands the measurements presented in Dunne et al. (2016) for $[{\mathrm{NH}}_{\mathrm{3}}+\text{org}]=\mathrm{2.2}$ ppb, RH = 38 % and T=295 K. Based on the presented experiments we find it possible to expand the parameterization from Gordon et al. (2017) to higher ion concentrations.