the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Nanoparticle growth by particle-phase chemistry
Michael J. Apsokardu
The ability of particle-phase chemistry to alter the molecular composition and enhance the growth rate of nanoparticles in the 2–100 nm diameter range is investigated through the use of a kinetic growth model. The molecular components included are sulfuric acid, ammonia, water, a non-volatile organic compound, and a semi-volatile organic compound. Molecular composition and growth rate are compared for particles that grow by partitioning alone vs. those that grow by a combination of partitioning and an accretion reaction in the particle phase between two organic molecules. Particle-phase chemistry causes a change in molecular composition that is particle diameter dependent, and when the reaction involves semi-volatile molecules, the particles grow faster than by partitioning alone. These effects are most pronounced for particles larger than about 20 nm in diameter. The modeling results provide a fundamental basis for understanding recent experimental measurements of the molecular composition of secondary organic aerosol showing that accretion reaction product formation increases linearly with increasing aerosol volume-to-surface-area. They also allow initial estimates of the reaction rate constants for these systems. For secondary aerosol produced by either OH oxidation of the cyclic dimethylsiloxane (D5) or ozonolysis of β-pinene, oligomerization rate constants on the order of 10−3 to 10−1 M−1 s−1 are needed to explain the experimental results. These values are consistent with previously measured rate constants for reactions of hydroperoxides and/or peroxyacids in the condensed phase.
- Article
(1824 KB) - Full-text XML
-
Supplement
(1806 KB) - BibTeX
- EndNote
Atmospheric aerosols influence Earth's energy balance either directly by scattering incoming solar radiation or indirectly through cloud formation (Charlson et al., 1992; Kerminen et al., 2012; Lohmann and Feichter, 2005). A significant fraction of airborne particles originate from gas-to-particle conversion during new particle formation (NPF; Bzdek and Johnston, 2010). Volatile compounds emitted into the atmosphere from biogenic and anthropogenic sources are oxidized to produce semi-volatile and non-volatile products. Particle formation begins when these products, in combination with other gas-phase species, come together to form clusters on the order of 1–2 nm in diameter that are able to spontaneously grow to much larger sizes (Bzdek and Johnston, 2010; Dusek et al., 2006; Kulmala et al., 2013; Zhang et al., 2012). Depending on chemical composition, once the particles have grown to a size of 50–100 nm in diameter, they are able to serve as cloud condensation nuclei (CCN). The probability that a newly formed nanoparticle will grow to a CCN-relevant size depends on its growth rate relative to the loss rate from, e.g., coagulation or scavenging by pre-existing aerosols (Kuang et al., 2010). Uncertainties in predicting the conditions that favor CCN formation make it challenging to accurately predict future impacts of radiative forcing (Carslaw et al., 2013).
The three main chemical species that contribute to ambient nanoparticle growth are sulfuric acid, a neutralizing base (typically ammonia), and organic matter. The growth rate due to sulfuric acid along with neutralizing base is accurately predicted by experimental measurements of gas-phase mixing ratio and particle-phase composition using a condensational growth model (Bzdek et al., 2013; Pennington et al., 2013; Smith et al., 2008; Stolzenburg et al., 2005), though sulfuric acid represents only a minor fraction of the total growth rate of ambient particles (Kuang et al., 2010, 2012; Weber et al., 1996; Wehner et al., 2005). Nanoparticle composition and growth rate are dominated by organic matter (Bzdek et al., 2011, 2012, 2013, 2014a, b; Pennington et al., 2013; Riipinen et al., 2012; Smith et al., 2008), and though significant molecular insight has been gained (Bianchi et al., 2016; Ehn et al., 2014; Kulmala et al., 2013; Riccobono et al., 2014), current growth models for organic matter appear to be incomplete (Hallquist et al., 2009; Tröstl et al., 2016).
Gas-phase oxidation of volatile organic compounds occurs through a complex set of reaction pathways involving both the gas and particle phases to yield particle-phase products that often number in the hundreds or thousands based on accurate mass measurements (Bateman et al., 2008; Mentel et al., 2015; Reinhardt et al., 2007; Tu et al., 2016). Absorptive partitioning (Barsanti et al., 2017; Pankow, 1994) of gas-phase products to the particle phase forms secondary organic aerosol (SOA), which includes both non-volatile (NVOCs) and semi-volatile (SVOCs) organic compounds (Kroll and Seinfeld, 2008; Riipinen et al., 2012). NVOCs have a negligible evaporation rate after partitioning to the particle phase, and therefore cause particles to grow at a rate given by the condensation rate. SVOCs have a significant evaporation rate from the particle phase, and therefore grow particles at a slower rate than the condensation rate. Recent advances in measurement technology have greatly improved our molecular understanding of NVOC (Ehn et al., 2012, 2014; Jokinen et al., 2015). More broadly, the complex distribution of molecular products and their associated wide range of volatilities can be represented by a volatility basis set (VBS) distribution where products are binned according to their gas-phase saturation concentrations (Donahue et al., 2006, 2011, 2012).
Molecular analysis of SOA has shown the presence of compounds that were produced by a reaction within the particle phase. Some examples include oligomers in biogenic SOA formed by accretion reactions (Barsanti and Pankow, 2004; Kalberer et al., 2004; Tolocka et al., 2004a), imine related species formed by the reaction of dicarbonyls with ammonia or amines (Galloway et al., 2014; De Haan et al., 2011; Lee et al., 2013; Stangl and Johnston, 2017), and organosulfates (Riva et al., 2016; Surratt et al., 2007; Wong et al., 2015; Xu et al., 2015). Reactions such as these increase the aerosol yield by forming additional SOA beyond what would be expected from partitioning alone, if they form non-volatile products from semi-volatile reactants in the particle phase (Lopez-Hilfiker et al., 2016; Shiraiwa et al., 2014). Experimental measurements have shown that oligomers can constitute up to about 50 % of the mass of SOA produced from biogenic precursors in laboratory reactors, though it is not clear how much of the oligomeric matter is produced from semi-volatile vs. non-volatile precursors (Hall IV and Johnston, 2011).
The role of particle-phase oligomerization in SOA formation has been the focus of several modeling studies. Owing to the high molecular weight and corresponding low volatility of oligomer products (Shiraiwa et al., 2014), early work assumed an irreversible process (Vesterinen et al., 2007), which proved effective for predicting the yields of freshly formed aerosol in chamber experiments and estimating the magnitude of the oligomerization rate constant needed for the process to impact yields. More recent models have included reversibility (Roldin et al., 2014; Trump and Donahue, 2014), which is needed to reproduce perturbations of freshly formed SOA such as changes induced by isothermal dilution, thermal degradation, and/or aging. Regional air quality models show that oligomerization has the potential to significantly increase the SOA mass concentration (Aksoyoglu et al., 2011; Lemaire et al., 2016), and accurately representing this chemistry in these models is perhaps the greatest uncertainty for predicting SOA formation (Shrivastava et al., 2016).
The influence of particle size, or more precisely the relative roles of particle volume and surface area, on oligomer formation in SOA has received relatively little attention though these effects are implicit in all of the models. Particle size has been discussed primarily in the context of accumulation mode particles greater than 100 nm in diameter (Roldin et al., 2014; Shiraiwa et al., 2013; Vesterinen et al., 2007). The Vesterinen study did report aerosol yield functions from simulations starting with 20 nm diameter seed particles, and the results suggested that particle-phase chemistry could enhance growth rates under atmospherically relevant conditions.
In the work described here, we explore computationally the impact of particle-phase chemistry on both the growth rate and composition of nanoparticles (defined here as particles smaller than 100 nm in diameter). This work was inspired by recent composition studies of laboratory-generated secondary aerosol spanning several tens of nanometers in diameter, which showed systematic changes in composition with increasing particle size (Tu and Johnston, 2017; Wu and Johnston, 2017). In the first set of calculations, chemical composition and growth rate are determined for particles between 2 and 100 nm assuming that growth occurs by partitioning alone. These results are compared to a second set of calculations where semi-volatile molecules in the particle phase are allowed to undergo an accretion reaction to produce a non-volatile product. Together, the two sets of calculations give insight into the reaction conditions and particle size range where particle-phase chemistry is most likely to alter nanoparticle composition and accelerate the growth rate. The modeling approach is similar to that used in previous studies, though the reaction conditions used here more closely resemble those of an “open” laboratory reactor where aerosol flows into and out of the reactor (i.e., flow reactor), as opposed to a “closed” batch reactor which was the main focus of previous modeling work. The results are discussed in the context of recent size-resolved molecular composition measurements (performed with flow reactors) and the potential atmospheric impact of particle-phase chemistry.
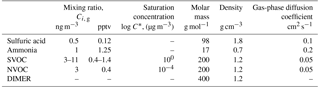
The growth model used in this work includes sulfuric acid, ammonia, and organic matter since these are the major components found in ambient nanoparticles during NPF (Bzdek et al., 2011, 2014a; Pennington et al., 2013; Smith et al., 2008; Stolzenburg et al., 2005). Water is also included as predicted by the Extended Aerosol Inorganics Model (E-AIM; Wexler and Clegg, 2002), and then corrected to account for the effects of particle surface curvature (Kreidenweis et al., 2005; Yli-Juuti et al., 2013). For simplicity, the gas-phase precursors to SOA formation are represented by two specific organic compounds, one non-volatile (NVOC) and the other semi-volatile (SVOC). Particle-phase chemistry involves a generic accretion reaction between two SVOC (or NVOC) molecules to give a dimer. Table 1 gives relevant molecular parameters and gas-phase mixing ratios. The gas-phase mixing ratios are assumed to be constant over time (steady state) as might be achieved in a flow reactor, and the values chosen are typical of what might be observed during NPF in a boreal forest (Vestenius et al., 2014). Molecular volatility is expressed in terms of the saturation concentration, C*, which is the equilibrium vapor pressure in units of µg m−3 (Donahue et al., 2006). Diffusion coefficients are obtained from the procedure described in the Supplement (Poling et al., 2001).
Calculations begin with a 2 nm diameter particle consisting of sulfuric acid and ammonia at a 2 : 1 ratio of base to acid. From there, gas-phase species partition to the particle phase based on their volatilities and gas-phase mixing ratios, causing the particle to grow. The growth calculation is iterative. Starting from an initial particle of a given composition and volume (Vp, n), the increase in particle volume (and corresponding change in composition) is determined over a short time period for each molecular species separately, and the increases for the individual components are summed to give the total volume of the particle at the end of the time period ( along with its composition. The end point for the first time period is used as the start point for the second time period, and the process repeats. A schematic of calculation work flow is given in Fig. S1 in the Supplement along with additional aspects of the approach.
2.1 Partitioning
The extent to which a compound formed in the gas-phase partitions to the particle phase is determined by its saturation ratio (Sd), which is the ratio of the gas-phase mixing ratio to the saturation mixing ratio. The subscript “d” refers to the particle diameter and acknowledges that the saturation ratio depends in part on the radius of curvature of the particle surface. Accordingly, the first step in the calculation is to determine the Kelvin effect modified vapor pressure (KEMPd) for all species based on the initial particle diameter. For the conditions used in this study, sulfuric acid and NVOCs have Sd≫1 for all particle diameters investigated, and as discussed previously, grow particles at their condensation rates. Ammonia, water, and SVOCs have Sd≪1 and grow particles at rates slower than their condensation rates.
The collision rate for species i determines the number of condensing molecules that can be taken into the particle during time period dt, thereby incrementing the particle volume by dVi:
where ci is the mean thermal velocity, γ is the uptake coefficient, d is the particle diameter, Ci, g is the gas-phase mixing ratio of species i, βd is the Loyalka correction factor for mass transport to a spherical particle with diameter d, and VM, i is the molar volume of species i. The equation for βd is given in the Supplement. Values of dVi for condensational growth by sulfuric acid and NVOC are calculated from Eq. (1), with the inherent assumption that the surface accommodation coefficient is 1.
Equation (1) can also be used to calculate the uptake of semi-volatile species provided that the total amount taken into the particle does not exceed the equilibrium end point. Ammonia uptake is determined from the number of sulfuric acid molecules that have condensed. For a given time period dt, once the number of ammonia molecules that have been taken into the particle equals twice the number of sulfuric acid molecules that were taken during the same time period, no further ammonia uptake occurs. While dissolution of ammonia into water is possible, the amount is negligible in comparison to ammonia uptake associated with condensation of sulfuric acid (Clegg et al., 1998; Wexler and Clegg, 2002). Under the conditions used in this study, the condensation rate of ammonia is about 25 times greater than that of sulfuric acid, so the model assumes that stoichiometric uptake of ammonia is instantaneous with sulfuric acid. Water uptake is determined from E-AIM based on the combined amounts of sulfuric acid, ammonia, and NVOC that have been added during time period dt. Since the gas-phase mixing ratio of water is very high, equilibrium is assumed to be achieved instantaneously during the time period.
Individual volume increments dVi for sulfuric acid, NVOC, ammonia, and water are summed to give the total volume increment. Because the volume of particle phase has increased, SVOC is no longer in equilibrium between the gas and particle phases, and a net migration of SVOC from the gas phase to the particle phase must occur. SVOC molecules are taken into the particle at a rate described by Eq. (1) to re-establish equilibrium. The equilibrium point (Pankow, 1994) expressed as the volume ratio of SVOC in the particle phase ( is
where i in this case refers to SVOC, ζi is the activity coefficient for SVOC in the particle phase (assumed to be 1 in this study), and VM, i and VM, p are the respective molar volumes of SVOC and the particle phase. The incremental increase of SVOC over time period dt is determined by evaluating Eq. (2) before and after the increases due to sulfuric acid, NVOC, ammonia, and water. For the conditions used in this study, the condensation rate of gas-phase SVOC is generally greater than the uptake rate needed to maintain equilibrium when particle growth is restricted to partitioning. The ratio of the two rates is dependent on the volume-to-surface-area ratio of the particle, ranging from several orders of magnitude for a 2 nm diameter particle to a factor of 200 for a 100 nm diameter particle. Because the condensation rate is generally much greater than the uptake rate needed for partitioning, no evaporation rate of particle-phase SVOC was included in the current study. The one situation where condensation is not sufficient for partitioning occurs when particle-phase chemistry is included and will be discussed later.
2.2 Particle-phase chemistry
Particle-phase chemistry is modeled as an irreversible accretion reaction where two monomers come together to produce a non-volatile dimer (DIMER). While all combinations of SVOC and NVOC molecules were considered, most calculations involved the reaction between two SVOC molecules:
where kDIMER is the second-order rate constant, and [SVOC] is the particle-phase concentration established by partitioning between the gas and particle phases. Since the reaction consumes particle-phase SVOC molecules, additional SVOC must be taken from the gas phase into the particle phase to re-establish equilibrium. The rate at which additional SVOC molecules are taken into the particle is determined by the rate of particle-phase reaction. When particle-phase reaction is included in the growth calculation, the change in particle volume from Vp, n to with respect to SVOC is the sum of the volume increase from unreacted SVOC molecules needed to re-establish partitioning equilibrium, and the volume increase from additional SVOC uptake to form dimers. SVOC continues to partition to the particle phase at each iteration, resulting in a continuous supply of reactant molecules for dimerization.
Dimerization rate constants in the range of 10−3 to 10−1 M−1 s−1 were studied, with most calculations at 10−2 M−1 s−1, which is the rate constant reported for dimerization of glyoxal in a bulk aqueous solution (Ervens and Volkamer, 2010). Ziemann and Atkinson (2012) have reviewed thermodynamic and kinetic data for several types of reactions relevant to biogenic SOA. The reaction of a hydroperoxide with a carbonyl to give a peroxyhemiacetal, and the reaction of a peroxyacid with a carbonyl to form an acyl peroxyhemiacetal, have reported rate constants in the 10−4 to 10−2 M−1 s−1 range depending on reaction conditions, and are relevant to the modeling results presented here. Reactions such as aldol condensation of carbonyls and ester formation from an acid and alcohol are much slower and unlikely to be atmospherically relevant based on both kinetics (Casale et al., 2007) and thermodynamics (DePalma et al., 2013). The effects of dimer decomposition (reaction reversibility), particle-phase diffusion coefficient, and phase separation are not considered in this work, though we note that all would have the effect of reducing the impact of particle-phase chemistry on composition and growth rate.
3.1 Particle growth by partitioning
The first set of calculations includes particle growth by partitioning, but no particle-phase reaction. Figure 1a shows the diameter growth rate and Fig. 1b the dry mass fraction for each chemical species as a function of particle diameter. For sulfuric acid and NVOC, where partitioning to the particle phase occurs at the collision limit, the growth rates for these species are independent of particle diameter. A constant growth rate for non-volatile species has been noted previously (Weber et al., 1996) and can be understood by rewriting Eq. (1) in terms of the diameter growth rate:
Since γ is independent of d for a surface-limited process such as condensation (Smith et al., 2003; Tolocka et al., 2004a), dd∕dt also becomes independent of d as a first approximation, provided that the precursor gas-phase mixing ratio (Ci, g) does not change. In practice, dd∕dt decreases slightly with increasing particle diameter owing to the effect of molecular diffusion on transport of vapor molecules to the particle surface (βd becomes less than 1). Ammonia uptake is driven by sulfuric acid uptake, and therefore follows the same particle diameter dependence.
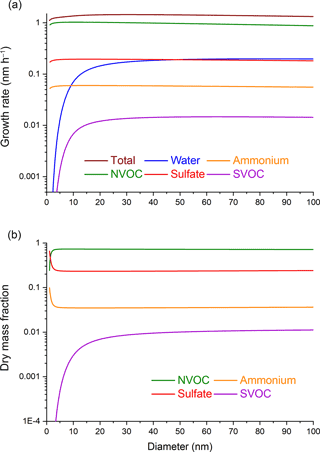
Figure 1Particle diameter dependence of (a) growth rates and (b) dry mass fractions of chemical species under the conditions where the gas-phase mixing ratios are constant and growth occurs by partitioning alone.
Water and SVOC show greater increases in their growth rates with increasing particle diameter than sulfuric acid and NVOC because they have Sd≪1. In principle, semi-volatile species are subject to two particle size-dependent effects: βd in Eq. (1) and KEMPd in Eq. (2). For the conditions studied here, the βd term has a negligible effect on the uptake rates of water and SVOC, since uptake is determined by the equilibrium endpoint rather than the condensation rate. Instead, the difference between the semi-volatile species and non-volatile species in Fig. 1a are driven by the particle size dependence of KEMPd, which alters the equilibrium point for absorptive partitioning.
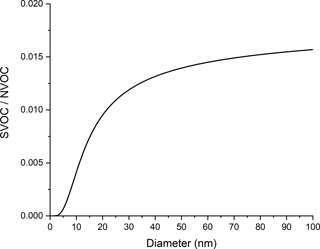
In Fig. 1b, the dry particle mass fractions of sulfuric acid, NVOC, and ammonia show very little change with increasing d since their relative growth rates are independent of d. Small changes just above 2 nm are due to the choice of starting composition of the 2 nm diameter particle. In contrast, the SVOC mass fraction increases quickly with increasing particle size owing to the dependence of KEMPd on d. Figure 2 shows the mass fraction ratio of SVOC to NVOC as a function of particle size. The ratio increases quickly at the smallest particle sizes and then more slowly thereafter. This plot is consistent with experimental measurements of molecular composition across a similar range of particle diameters, which show that lower volatility species are preferentially detected in smaller particles (Winkler et al., 2012; Zhao et al., 2013).
3.2 Particle growth by a combination of partitioning and particle-phase chemistry
When particle-phase reaction is included in the growth calculation, both the growth rate and chemical composition change. Figure 3a and b show diameter growth rates and dry mass fractions, respectively, when particle-phase reaction is included. Comparing Fig. 3a to Fig. 1a shows that particle-phase chemistry causes the diameter growth rate to continue increasing with increasing particle size above 10 nm. This diameter dependence is different from the growth rate due to partitioning alone where dd∕dt becomes independent of particle size above 10 nm. The size dependence of particle growth at larger particle sizes can be understood by expressing the uptake coefficient in terms of particle diameter:
In Eq. (5), the uptake coefficient is proportional to d, which is characteristic of a volume-limited process (Saul et al., 2006; Tolocka et al., 2004b). Inserting Eq. (5) into Eq. (4), shows that dd∕dt also increases linearly with d. The number of SVOC molecules that react to form DIMER is proportional to the total volume of the particle, and therefore the SVOC uptake rate needed to maintain partitioning equilibrium is also volume (and hence diameter) dependent. Note that the SVOC and DIMER diameter growth rates are both proportional to d in Fig. 3a. Growth by condensation of NVOC and sulfuric acid remain surface-limited, and therefore these diameter growth rates are unaffected by dimer formation.
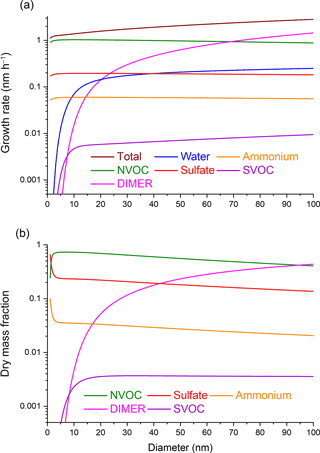
Figure 3Particle diameter dependence of (a) growth rates and (b) dry mass fractions of chemical species under the conditions where both partitioning and particle-phase chemistry (SVOC–SVOC dimer formation) are included.
Figure 3b shows the dry mass fractions as a function of particle diameter when particle-phase chemistry is included. Below about 10 nm, the plots in Fig. 3b are identical to those in Fig. 1b where partitioning alone is considered. Particle-phase chemistry has minimal impact on the growth and composition of small particles for two reasons. First, the ratio of particle volume to surface area is very small, which favors surface-limited processes (condensational growth by NVOC and sulfuric acid) over volume-limited processes (accretion reaction). Second, the dependence of KEMPd on d causes the equilibrium concentration of SVOC in the particle phase to be very low for small particles, which decreases the reaction rate (Eq. 3). As a result, particle-phase chemistry has little impact on the diameter growth rate or molecular composition below about 10 nm. Above 10 nm, DIMER mass starts to accumulate in the particle, causing the mass fractions of NVOC, sulfuric acid, and ammonia to decrease.
Figure 4a shows the mass fraction ratio of SVOC to NVOC as a function of particle diameter. Below 10 nm, where particle-phase chemistry has minimal impact, the ratio in Fig. 4a for particle-phase reaction is equivalent to that in Fig. 2 for partitioning alone. The plots in Figs. 2 and 4a diverge above about 10 nm because the DIMER mass fraction increases, causing the NVOC mass fraction to decrease.
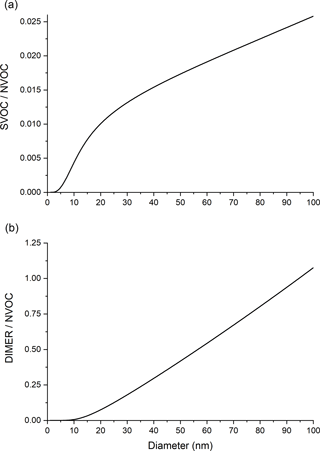
Figure 4Mass ratio vs. particle diameter for (a) SVOC to NVOC and (b) DIMER to NVOC, under conditions where both partitioning and particle-phase chemistry (SVOC–SVOC dimer formation) are included.
Figure 4b shows the mass fraction ratio of DIMER to NVOC. Below about 10 nm, hardly any dimer is produced. Above 10 nm, the dimer to NVOC ratio increases approximately linearly with increasing d as expected for a volume-limited process relative to a surface-limited process. Figures 3 and 4 show, for the conditions studied, that particle size dependencies of the growth rate and composition above 10 nm are driven mainly by particle-phase chemistry rather than partitioning alone. Figure 4b illustrates how the impact of an accretion reaction might be observed experimentally through organic molecular composition measurements. If a systematic increase in the concentration of non-volatile dimers and higher-order oligomers is observed with increasing particle diameter, then particle-phase chemistry is likely to have contributed to the formation of these molecules.
3.3 Factors that influence growth by particle-phase chemistry
Additional calculations were performed to investigate the roles of SVOC gas-phase mixing ratio and particle-phase reaction rate constant on growth rate and composition. In Fig. S2, diameter growth rates are shown for SVOC gas-phase mixing ratios between 0.35 and 1.4 pptv and compared to the partitioning calculation in Fig. 1a (the 1.4–NR plot for no reaction in Fig. S2). Above about 10 nm, the growth rates increase linearly with increasing d, and the slope of the increase scales by approximately [SVOC]2 as expected by Eq. (3). The actual dependence is slightly less than [SVOC]2 owing to the change in particle density that is associated with the changing DIMER mass fraction.
Figure 5a shows the effect of reaction rate constant on diameter growth rate. The rate constants investigated range over 2 orders of magnitude from 10−3 to 10−1 M−1s−1 while keeping the SVOC mixing ratio constant at 1.4 pptv. NR in Fig. 5a represents no reaction and is equivalent to the plot in Fig. 1a for growth by partitioning alone. For a reaction rate constant of 10−3 M−1 s−1, particle growth rate is only slightly larger than growth by partitioning only. In this case, DIMER production is slow, so there is only minor enhancement of the overall growth rate. Increasing the rate constant 1 order of magnitude to 10−2 M−1 s−1 causes a substantial enhancement of the growth rate above 10 nm. For a rate constant of 10−1 M−1 s−1, a complex plot is observed. Volume-limited particle growth occurs up to ∼ 40 nm, where the growth rate increases approximately linearly with d. Above ∼ 40 nm, the reaction rate becomes so fast that particle growth is limited by the condensation rate of SVOC, a surface-limited process, as reflected by the particle diameter dependence. Since the calculation methodology used in our study did not include an evaporation rate for SVOC, the transition from volume-limited to surface-limited kinetics is abrupt in Fig. 5a. In practice, one would expect a more gradual transition from one to the other. The lack of a particle size dependence on SOA growth in the limit of a fast reaction rate has also been suggested in a modeling study of SOA produced by α-pinene ozonolysis (Gatzsche et al., 2017). It is also consistent with the work of Vesterinen et al. (2007), who showed a linear increase of particle diameter with time when the reaction rate constant was sufficiently large.
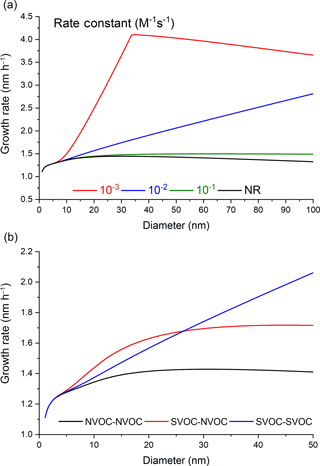
Figure 5Growth rate vs. particle diameter. (a) Comparison of growth rates with different dimer formation rate constants for the SVOC–SVOC reaction. (b) Comparison of growth rates for SVOC–SVOC, NVOC–NVOC, and SVOC–NVOC reactions having a dimer formation rate constant of 10−2 M−1 s−1. In these plots, the black line is equivalent to the particle diameter dependence in Fig. 1a.
Accretion chemistry is not necessarily restricted to SVOC molecules. If two NVOC molecules react in the particle phase to form DIMER, then the diameter growth rate will not change with increasing particle diameter since NVOC uptake remains unaffected, though the molecular composition will change with increasing diameter. A calculation demonstrating this principle is shown in Fig. S3 (growth rate vs. particle diameter) and Fig. S4 (DIMER ∕ NVOC mass ratio vs. particle diameter). If one SVOC molecule reacts with one NVOC molecule to form DIMER, both the growth rate and molecular composition change with increasing particle diameter. A calculation demonstrating this principle is shown in Fig. 5b, where growth rate vs. particle diameter are compared for SVOC–SVOC, NVOC–NVOC, and SVOC–NVOC dimer formation reactions. The SVOC–NVOC reaction enhances the particle growth rate at a much smaller particle diameter than the SVOC–SVOC reaction. This enhancement arises from KEMPd of SVOC, which favors formation of the SVOC–NVOC dimer over the SVOC–SVOC dimer at small particle sizes. Because of the greater potential of the SVOC–SVOC reaction to transform semi-volatile matter into non-volatile matter, its contribution to growth rate eventually overcomes that of the SVOC–NVOC reaction as the particle size increases.
Taken together, Figs. S2–S4 show that the observation of a change in dimer-to-monomer ratio with increasing particle diameter does not necessarily indicate an enhancement of the particle growth rate by accretion chemistry. On the other hand, Fig. 5b shows that the lack of a particle size-dependent change in the growth rate does not necessarily mean that particle growth rate is unaffected by accretion chemistry. Nonetheless, these results illustrate how experimental measurements of particle size-dependent changes in molecular composition and growth rate can supplement traditional measures, such as the concentration dependence of the aerosol yield and perturbations due to, e.g., isothermal dilution, to better constrain SOA formation models with regard to particle-phase chemistry.
3.4 Comparison to recent experimental measurements and atmospheric implications
For the modeling conditions studied here, particle-phase chemistry influences both the molecular composition and growth rate of sub-100 nm diameter particles under atmospherically relevant conditions, provided that the rate constant is above about 10−3 M−1 s−1 for semi-volatile reactants having a saturation concentration on the order of 1 µg m−3 and gas-phase mixing ratios on the low pptv level. Based on the condensed-phase concentration dependence of reactants on the reaction rate, a rate constant on the order of 10−1 M−1 s−1 would be required for semi-volatile reactants having saturation concentrations on the order of 10 µg m−3. These rate constants (Ziemann and Atkinson, 2012) and saturation concentrations (Trump and Donahue, 2014) are in the range of those expected for, e.g., monoterpene accretion chemistry. The overall conclusion that accretion chemistry may contribute to nanoparticle growth and/or composition under atmospherically relevant conditions is similar to that reached by Vesterinen et al. (2007). The current work provides an additional, fundamental basis for interpreting recent experimental measurements of molecular composition as a function of particle size in the case of monodisperse aerosols (Tu and Johnston, 2017), or more generally, volume-to-surface-area ratio for polydisperse aerosols (Wu and Johnston, 2017). In each study, the relative concentration of accretion products increased approximately linearly with particle size (or volume-to-surface-area ratio) as predicted by Fig. 4b. Below, we estimate the magnitudes of the reaction rate constants needed to reproduce the experimental results.
In the Wu study (Wu and Johnston, 2017), decamethylcyclopentasiloxane (D5) reacted with OH in the gas phase to produce secondary aerosol having three types of products: ring-opened species, oxidized monomers containing OH and/or CH2OH functionalities in place of CH3, and dimers of D5 and/or its monomer oxidation products. The dimer concentration in the particle phase (as indicated by the signal intensities of corresponding ions produced by electrospray ionization) increased linearly with increasing volume-to-surface-area ratio of the aerosol relative to the (non-volatile) ring-opened products. This dependence suggested that ring-opened products were formed in the gas phase and subsequently condensed onto the particles, while dimers were produced directly in the particle phase from monomers. Monomer gas-phase mixing ratios in these experiments were on the order of a few ppbv, which is similar in magnitude to the levels measured in a university lecture hall (Tang et al., 2015). Using these values in conjunction with the basic model described above, we estimate the dimerization rate constant had to be in the 10−3 to 10−1 M−1 s−1 range to achieve the level of dimerization observed, given that most of the monomers expected to participate in the reaction had estimated saturation concentrations in the 102 to 103 µg m−3 range. Smaller rate constants would have been unable to produce a sufficient amount of dimers, while higher rate constants would not have shown a volume-to-surface-area ratio dependence of the dimer concentration since the reaction rate would have been limited by transport of reacting monomer to the particle surface.
In the Tu study (Tu and Johnston, 2017), β-pinene ozonolysis produced SOA having systematic changes in molecular composition as a function of particle size. The relative concentrations (as indicated by the signal intensities of ions produced by electrospray ionization) of higher-order oligomers, i.e., trimers and tetramers, increased linearly with increasing particle size, similar to Fig. 4b. The total oligomer signal intensity was comparable to our previous study of α-pinene SOA formed under similar reaction conditions, where the oligomer content was experimentally determined to be about 50 % of the total SOA mass (Hall IV and Johnston, 2011). For the Tu study, we estimate the NVOC mixing ratio to be approximately 2 ppbv based on the yield estimate of Ehn et al. (2014) for β-pinene ozonolysis. We estimate the mixing ratios for the 10 and 100 µg m−3 saturation concentration bins to be approximately 30 and 40 ppbv, respectively, based on the volatility basis set (VBS) parameterization of Donahue and colleagues for α-pinene ozonolysis (Donahue et al., 2012; Trump and Donahue, 2014). For these conditions, condensational growth and/or partitioning of molecular species alone are able to explain the overall growth of particles to about 80–100 nm in diameter during the ∼ 20 s residence time of the flow reactor, though the modeling results are extremely sensitive to the mixing ratios and VBS parameterization used. However, condensational growth and partitioning cannot explain the high abundance of accretion reaction products that were measured. We estimate that the reaction rate constants needed to form dimers and higher-order oligomers in sufficient amounts had to be at least on the order of 10−3 M−1 s−1 (the required rate constant is dependent on SVOC volatility, with a larger rate constant needed for saturation concentrations above 10 µg m−3). Together, the modeling work performed here and the experimental measurements in the Wu and Tu studies suggest that reaction rate constants on the order of 10−3 to 10−1 M−1 s−1 are needed for accretion chemistry to be relevant to SOA formation and growth.
While systematic changes in molecular composition with increasing particle size and/or aerosol volume-to-surface-area ratio have been established experimentally, an enhancement of the particle growth rate in the sub-100 nm diameter range is less clear. Recent measurements by Kourtchev et al. (2016) of accretion oligomers in ambient aerosol from a boreal forest suggest that oligomer formation increases with increasing SOA mass concentration, an observation that is consistent with the molecular composition results reported here. More importantly, the authors noted that aerosols enriched with oligomers were strongly correlated with higher CCN activity, and they suggested that this correlation could indicate that oligomers may speed up particle growth. The modeling results presented here suggest that particle-phase reactions are indeed capable of enhancing growth rates in a size range relevant to CCN activity.
The work presented here suggests that experimental measurements of molecular composition as a function of particle size and/or aerosol volume-to-surface-area ratio can supplement traditional measurements (concentration-dependent aerosol mass yields, perturbations caused by isothermal dilution, etc.) for constraining aerosol formation models. Future modeling of size-dependent molecular composition should include physico-chemical parameters such as diffusion, phase separation, and reaction reversibility (Liu et al., 2014; Mai et al., 2015; Riipinen et al., 2012; Shiraiwa et al., 2012; Song et al., 2015; Trump and Donahue, 2014; Zaveri et al., 2014) that may influence the contribution of particle-phase chemistry to nanoparticle growth.
The code for the model developed in this work and the data calculated from it can be obtained from author Michael Apsokardu (maps@udel.edu).
Four figures (Figs. S1–S4) plus additional description of the particle growth model.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-1895-2018-supplement.
The authors declare that they have no conflict of interest.
This research was supported by the United States National Science Foundation
under grant nos. CHE-1408455 and AGS-1649719. The authors thank Pauli
Paasonen for helpful discussions on molecular transport
dynamics.
Edited by: Frank
Keutsch
Reviewed by: two anonymous referees
Aksoyoglu, S., Keller, J., Barmpadimos, I., Oderbolz, D., Lanz, V. A., Prévôt, A. S. H., and Baltensperger, U.: Aerosol modelling in Europe with a focus on Switzerland during summer and winter episodes, Atmos. Chem. Phys., 11, 7355–7373, https://doi.org/10.5194/acp-11-7355-2011, 2011.
Barsanti, K. C. and Pankow, J. F.: Thermodynamics of the formation of atmospheric organic particulate matter by accretion reactions-Part 1: aldehydes and ketones, Atmos. Environ., 38, 4371–4382, https://doi.org/10.1016/j.atmosenv.2006.03.013, 2004.
Barsanti, K. C., Kroll, J. H., and Thornton, J. A.: The Formation of Low-Volatility Organic Compounds in the Atmosphere: Recent Advancements and Insights, J. Phys. Chem. Lett., 8, 1503–1511, https://doi.org/10.1021/acs.jpclett.6b02969, 2017.
Bateman, A. P., Walser, M. L., Desyaterik, Y., Laskin, J., Laskin, A., Nizkorodov, S. A., and Bateman, A. P.: The Effect of Solvent on the Analysis of Secondary Organic Aerosol Using Electrospray Ionization Mass Spectrometry, Environ. Sci. Technol., 42, 7341–7346, https://doi.org/10.1021/es801226w, 2008.
Bianchi, F., Junninen, H., Frege, C., Henne, S., Hoyle, C. R., Molteni, U., Herrmann, E., Adamov, A., Bukowiecki, N., Chen, X., Duplissy, J., Gysel, M., Hutterli, M., Kangasluoma, J., Kontkanen, J., Manninen, H. E., Rondo, L., Williamson, C., Curtius, J., Worsnop, D. R., Kulmala, M., Dommen, J., and Baltensperger, U.: New particle formation in the free troposphere: A question of chemistry and timing, Science, 352, 1109–1112, https://doi.org/10.1126/science.aad5456, 2016.
Bzdek, B. R. and Johnston, M. V: New Particle Formation and Growth in the Troposhere, Anal. Chem., 82, 7871–7878, https://doi.org/10.1021/ac100856j, 2010.
Bzdek, B. R., Zordan, C. A., Luther, G. W., and Johnston, M. V: Nanoparticle Chemical Composition During New Particle Formation, Aerosol Sci. Tech., 45, 1041–1048, https://doi.org/10.1080/02786826.2011.580392, 2011.
Bzdek, B. R., Zordan, C. A., Pennington, M. R., Luther III, G. W., and Johnston, M. V.: Quantitative Assessment of the Sulfuric Acid Contribution to New Particle Growth, Environ. Sci. Technol., 46, 4365–4373, https://doi.org/10.1021/es204556c, 2012.
Bzdek, B. R., Horan, A. J., Pennington, M. R., DePalma, J. W., Zhao, J., Jen, C. N., Hanson, D. R., Smith, J. N., McMurry, P. H., and Johnston, M. V: Quantitative and time-resolved nanoparticle composition measurements during new particle formation, Faraday Discuss., 165, 25–43, https://doi.org/10.1039/c3fd00039g, 2013.
Bzdek, B. R., Lawler, M. J., Horan, A. J., Pennington, M. R., DePalma, J. W., Zhao, J., Smith, J. N., and Johnston, M. V.: Molecular constraints on particle growth during new particle formation, Geophys. Res. Lett., 41, 6045–6054, https://doi.org/10.1002/2014GL060160, 2014a.
Bzdek, B. R., Horan, A. J., Pennington, M. R., Janechek, N. J., Baek, J., Stanier, C. O., and Johnston, M. V.: Silicon is a frequent component of atmospheric nanoparticles, Environ. Sci. Technol., 48, 11137–11145, https://doi.org/10.1021/es5026933, 2014b.
Carslaw, K. S., Lee, L. A., Reddington, C. L., Mann, G. W., and Pringle, K. J.: The magnitude and sources of uncertainty in global aerosol, Faraday Discuss., 165, 495–512, https://doi.org/10.1039/c3fd00043e, 2013.
Casale, M. T., Richman, A. R., Elrod, M. J., Garland, R. M., Beaver, M. R., and Tolbert, M. A.: Kinetics of acid-catalyzed aldol condensation reactions of aliphatic aldehydes, Atmos. Environ., 41, 6212–6224, https://doi.org/10.1016/j.atmosenv.2007.04.002, 2007.
Charlson, R. J., Schwartz, S. E., Hales, J. M., Cess, R. D., Coakley, J. A., Hansen, J. E., and Hofmann, D. J.: Climate Forcing by Anthropogenic Aerosols, Science, 255, 423–430, 1992.
Clegg, S. L., Brimblecombe, P., and Wexler, A. S.: Thermodynamic Model of the System H+-NH-Na+-SO-NO-Cl−-H2O at 298.15 K, J. Phys. Chem., 5639, 2155–2171, 1998.
DePalma, J. W., Horan, A. J., Hall IV, W. A., and Johnston, M. V.: Thermodynamics of oligomer formation: implications for secondary organic aerosol formation and reactivity, Phys. Chem. Chem. Phys., 15, 6935, https://doi.org/10.1039/c3cp44586k, 2013.
Donahue, N. M., Robinson, A. L., Stanier, C. O., and Pandis, S. N.: Coupled Partitioning, Dilution, and Chemical Aging of Semivolatile Organics, Environ. Sci. Technol., 40, 2635–2643, https://doi.org/10.1021/es052297c, 2006.
Donahue, N. M., Epstein, S. A., Pandis, S. N., and Robinson, A. L.: A two-dimensional volatility basis set: 1. organic-aerosol mixing thermodynamics, Atmos. Chem. Phys., 11, 3303–3318, https://doi.org/10.5194/acp-11-3303-2011, 2011.
Donahue, N. M., Kroll, J. H., Pandis, S. N., and Robinson, A. L.: A two-dimensional volatility basis set – Part 2: Diagnostics of organic-aerosol evolution, Atmos. Chem. Phys., 12, 615–634, https://doi.org/10.5194/acp-12-615-2012, 2012.
Dusek, U., Frank, G. P., Hildebrandt, L., Curtius, J., Schneider, J., Walter, S., Chand, D., Drewnick, F., Hings, S., Jung, D., Borrmann, S., and Andreae, M. O.: Size Matters More Than Chemistry Aerosol Particles, Science, 312, 1375–1378, https://doi.org/10.1126/science.1125261, 2006.
Ehn, M., Kleist, E., Junninen, H., Petäjä, T., Lönn, G., Schobesberger, S., Dal Maso, M., Trimborn, A., Kulmala, M., Worsnop, D. R., Wahner, A., Wildt, J., and Mentel, Th. F.: Gas phase formation of extremely oxidized pinene reaction products in chamber and ambient air, Atmos. Chem. Phys., 12, 5113–5127, https://doi.org/10.5194/acp-12-5113-2012, 2012.
Ehn, M., Thornton, J. A., Kleist, E., Sipila, M., Junninen, H., Pullinen, I., Springer, M., Rubach, F., Tillmann, R., Lee, B., Lopez-Hilfiker, F., Andres, S., Acir, I. H., Rissanen, M., Jokinen, T., Schobesberger, S., Kangasluoma, J., Kontkanen, J., Nieminen, T., Kurten, T., Nielsen, L. B., Jorgensen, S., Kjaergaard, H. G., Canagaratna, M., Dal Maso, M., Berndt, T., Petaja, T., Wahner, A., Kerminen, V. M., Kulmala, M., Worsnop, D. R., Wildt, J., and Mentel, T. F.: A large source of low-volatility secondary organic aerosol, Nature, 506, 476–479, https://doi.org/10.1038/Nature13032, 2014.
Ervens, B. and Volkamer, R.: Glyoxal processing by aerosol multiphase chemistry: towards a kinetic modeling framework of secondary organic aerosol formation in aqueous particles, Atmos. Chem. Phys., 10, 8219–8244, https://doi.org/10.5194/acp-10-8219-2010, 2010.
Galloway, M. M., Powelson, M. H., Sedehi, N., Wood, S. E., Millage, K. D., Kononenko, J. A., Rynaski, A. D., and De Haan, D. O.: Secondary organic aerosol formation during evaporation of droplets containing atmospheric aldehydes, amines, and ammonium sulfate, Environ. Sci. Technol., 48, 14417–14425, https://doi.org/10.1021/es5044479, 2014.
Gatzsche, K., Iinuma, Y., Tilgner, A., Mutzel, A., Berndt, T., and Wolke, R.: Kinetic modeling studies of SOA formation from α-pinene ozonolysis, Atmos. Chem. Phys., 17, 13187–13211, https://doi.org/10.5194/acp-17-13187-2017, 2017.
De Haan, D. O., Hawkins, L. N., Kononenko, J. A., Turley, J. J., and Jimenez, J. L.: Formation of Nitrogen-Containing Oligomers by Methylglyoxal and Amines in Simulated Evaporating Cloud Droplets, Environ. Sci. Technol., 45, 984–991, https://doi.org/10.1021/es102933x, 2011.
Hall IV, W. A. and Johnston, M. V: Oligomer Content of α-Pinene Secondary Organic Aerosol, Aerosol Sci. Tech., 45, 37–45, https://doi.org/10.1080/02786826.2010.517580, 2011.
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009.
Jokinen, T., Berndt, T., Makkonen, R., Kerminen, V.-M., Junninen, H., Paasonen, P., Stratmann, F., Herrmann, H., Guenther, A. B., Worsnop, D. R., Kulmala, M., Ehn, M., and Sipilä, M.: Production of extremely low volatile organic compounds from biogenic emissions: Measured yields and atmospheric implications, P. Natl. Acad. Sci. USA, 112, 7123–7128, https://doi.org/10.1073/pnas.1423977112, 2015.
Kalberer, M., Paulsen, D., Sax, M., Steinbacher, M., Dommen, J., Prevot, AS. H., Fisseha, R., Weingartner, E., Frankevich, V., Zenobi, R., and Baltensperger, U.: Identification of polymers as major components of atmospheric organic aerosols, Science, 303, 1659–1662, https://doi.org/10.1126/science.1092185, 2004.
Kerminen, V.-M., Paramonov, M., Anttila, T., Riipinen, I., Fountoukis, C., Korhonen, H., Asmi, E., Laakso, L., Lihavainen, H., Swietlicki, E., Svenningsson, B., Asmi, A., Pandis, S. N., Kulmala, M., and Petäjä, T.: Cloud condensation nuclei production associated with atmospheric nucleation: a synthesis based on existing literature and new results, Atmos. Chem. Phys., 12, 12037–12059, https://doi.org/10.5194/acp-12-12037-2012, 2012.
Kourtchev, I., Giorio, C., Manninen, A., Wilson, E., Mahon, B., Aalto, J., Kajos, M., Venables, D., Ruuskanen, T., Levula, J., Loponen, M., Connors, S., Harris, N., Zhao, D., Kiendler-Scharr, A., Mentel, T., Rudich, Y., Hallquist, M., Doussin, J.-F., Maenhaut, W., Bäck, J., Petäjä, T., Wenger, J., Kulmala, M., and Kalberer, M.: Enhanced Volatile Organic Compounds emissions and organic aerosol mass increase the oligomer content of atmospheric aerosols, Sci. Rep., 6, 35038, https://doi.org/10.1038/srep35038, 2016.
Kreidenweis, S. M., Koehler, K., DeMott, P. J., Prenni, A. J., Carrico, C., and Ervens, B.: Water activity and activation diameters from hygroscopicity data – Part I: Theory and application to inorganic salts, Atmos. Chem. Phys., 5, 1357–1370, https://doi.org/10.5194/acp-5-1357-2005, 2005.
Kroll, J. H. and Seinfeld, J. H.: Chemistry of secondary organic aerosol: Formation and evolution of low-volatility organics in the atmosphere, Atmos. Environ., 42, 3593–3624, https://doi.org/10.1016/j.atmosenv.2008.01.003, 2008.
Kuang, C., Riipinen, I., Sihto, S.-L., Kulmala, M., McCormick, A. V., and McMurry, P. H.: An improved criterion for new particle formation in diverse atmospheric environments, Atmos. Chem. Phys., 10, 8469–8480, https://doi.org/10.5194/acp-10-8469-2010, 2010.
Kuang, C., Chen, M., Zhao, J., Smith, J., McMurry, P. H., and Wang, J.: Size and time-resolved growth rate measurements of 1 to 5 nm freshly formed atmospheric nuclei, Atmos. Chem. Phys., 12, 3573–3589, https://doi.org/10.5194/acp-12-3573-2012, 2012.
Kulmala, M., Kontkanen, J., Junninen, H., Lehtipalo, K., Manninen, H. E., Nieminen, T., Petäjä, T., Sipilä, M., Schobesberger, S., Rantala, P., Franchin, A., Jokinen, T., Järvinen, E., Äijälä, M., Kangasluoma, J., Hakala, J., Aalto, P. P., Paasonen, P., Mikkilä, J., Vanhanen, J., Aalto, J., Hakola, H., Makkonen, U., Ruuskanen, T., Mauldin, R. L., Duplissy, J., Vehkamäki, H., Bäck, J., Kortelainen, A., Riipinen, I., Kurtén, T., Johnston, M. V, Smith, J. N., Ehn, M., Mentel, T. F., Lehtinen, K. E. J., Laaksonen, A., Kerminen, V.-M., and Worsnop, D. R.: Direct observations of atmospheric aerosol nucleation, Science, 339, 943–946, https://doi.org/10.1126/science.1227385, 2013.
Lee, A. K. Y., Zhao, R., Li, R., Liggio, J., Li, S. M., and Abbatt, J. P. D.: Formation of light absorbing organo-nitrogen species from evaporation of droplets containing glyoxal and ammonium sulfate, Environ. Sci. Technol., 47, 12819–12826, https://doi.org/10.1021/es402687w, 2013.
Lemaire, V., Coll, I., Couvidat, F., Mouchel-Vallon, C., Seigneur, C., and Siour, G.: Oligomer formation in the troposphere: from experimental knowledge to 3-D modeling, Geosci. Model Dev., 9, 1361–1382, https://doi.org/10.5194/gmd-9-1361-2016, 2016.
Liu, A. T., Zaveri, R. A., and Seinfeld, J. H.: Analytical solution for transient partitioning and reaction of a condensing vapor species in a droplet, Atmos. Environ., 89, 651–654, https://doi.org/10.1016/j.atmosenv.2014.02.065, 2014.
Lohmann, U. and Feichter, J.: Global indirect aerosol effects: a review, Atmos. Chem. Phys., 5, 715–737, https://doi.org/10.5194/acp-5-715-2005, 2005.
Lopez-Hilfiker, F. D., Mohr, C., D'Ambro, E. L., Lutz, A., Riedel, T. P., Gaston, C. J., Iyer, S., Zhang, Z., Gold, A., Surratt, J. D., Lee, B. H., Kurten, T., Hu, W. W., Jimenez, J., Hallquist, M., and Thornton, J. A.: Molecular Composition and Volatility of Organic Aerosol in the Southeastern U.S.: Implications for IEPOX Derived SOA, Environ. Sci. Technol., 50, 2200–2209, https://doi.org/10.1021/acs.est.5b04769, 2016.
Mai, H., Shiraiwa, M., Flagan, R. C., and Seinfeld, J. H.: Under What Conditions Can Equilibrium Gas-Particle Partitioning Be Expected to Hold in the Atmosphere?, Environ. Sci. Technol., 49, 11485–11491, https://doi.org/10.1021/acs.est.5b02587, 2015.
Mentel, T. F., Springer, M., Ehn, M., Kleist, E., Pullinen, I., Kurtén, T., Rissanen, M., Wahner, A., and Wildt, J.: Formation of highly oxidized multifunctional compounds: autoxidation of peroxy radicals formed in the ozonolysis of alkenes – deduced from structure–product relationships, Atmos. Chem. Phys., 15, 6745–6765, https://doi.org/10.5194/acp-15-6745-2015, 2015.
Pankow, J. F.: An Absorption Model of Gas/Particle Partitioning of Organic Compounds in the Atmosphere, Atmos. Environ., 28, 185–188, https://doi.org/10.1016/1352-2310(94)90093-0, 1994.
Pennington, M. R., Bzdek, B. R., DePalma, J. W., Smith, J. N., Kortelainen, A.-M., Hildebrandt Ruiz, L., Petäjä, T., Kulmala, M., Worsnop, D. R., and Johnston, M. V.: Identification and quantification of particle growth channels during new particle formation, Atmos. Chem. Phys., 13, 10215–10225, https://doi.org/10.5194/acp-13-10215-2013, 2013.
Poling, B. E., Prausnitz, J. M., and O'Connell, J. P.: The properties of gases and liquids, 5th Edn., McGraw-Hill, New York, USA, 2001.
Reinhardt, A., Emmenegger, C., Gerrits, B., Panse, C., Dommen, J., Baltensperger, U., Zenobi, R., and Kalberer, M.: Ultrahigh mass resolution and accurate mass measurements as a tool to characterize oligomers in secondary organic aerosols, Anal. Chem., 79, 4074–4082, https://doi.org/10.1021/ac062425v, 2007.
Riccobono, F., Schobesberger, S., Scott, C. E., Dommen, J., Ortega, I. K., Rondo, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Downard, A., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hansel, A., Junninen, H., Kajos, M., Keskinen, H., Kupc, A., Kurten, A., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Petaja, T., Praplan, A. P., Santos, F. D., Schallhart, S., Seinfeld, J. H., Sipila, M., Spracklen, D. V., Stozhkov, Y., Stratmann, F., Tome, A., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Wimmer, D., Carslaw, K. S., Curtius, J., Donahue, N. M., Kirkby, J., Kulmala, M., Worsnop, D. R., Baltensperger, U., Kürten, A., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Petäjä, T., Praplan, A. P., Santos, F. D., Schallhart, S., Seinfeld, J. H., Sipilä, M., Spracklen, D. V., Stozhkov, Y., Stratmann, F., Tomé, A., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Wimmer, D., Carslaw, K. S., Curtius, J., Donahue, N. M., Kirkby, J., Kulmala, M., Worsnop, D. R., and Baltensperger, U.: Oxidation Products of Biogenic Emissions Contribute to Nucleation of Atmospheric Particles, Science, 344, 717–721, https://doi.org/10.1126/science.1243527, 2014.
Riipinen, I., Yli-Juuti, T., Pierce, J. R., Petäjä, T., Worsnop, D. R., Kulmala, M., and Donahue, N. M.: The contribution of organics to atmospheric nanoparticle growth, Nat. Geosci., 5, 453–458, https://doi.org/10.1038/ngeo1499, 2012.
Riva, M., Budisulistiorini, S. H., Chen, Y., Zhang, Z., D'Ambro, E. L., Zhang, X., Gold, A., Turpin, B. J., Thornton, J. A., Canagaratna, M. R., and Surratt, J. D.: Chemical Characterization of Secondary Organic Aerosol from Oxidation of Isoprene Hydroxyhydroperoxides, Environ. Sci. Technol., 50, 9889–9899, https://doi.org/10.1021/acs.est.6b02511, 2016.
Roldin, P., Eriksson, A. C., Nordin, E. Z., Hermansson, E., Mogensen, D., Rusanen, A., Boy, M., Swietlicki, E., Svenningsson, B., Zelenyuk, A., and Pagels, J.: Modelling non-equilibrium secondary organic aerosol formation and evaporation with the aerosol dynamics, gas- and particle-phase chemistry kinetic multilayer model ADCHAM, Atmos. Chem. Phys., 14, 7953–7993, https://doi.org/10.5194/acp-14-7953-2014, 2014.
Saul, T. D., Tolocka, M. P., and Johnston, M. V.: Reactive uptake of nitric acid onto sodium chloride aerosols across a wide range of relative humidities, J. Phys. Chem. A, 110, 7614–7620, https://doi.org/10.1021/jp060639a, 2006.
Shiraiwa, M., Pfrang, C., Koop, T., and Pöschl, U.: Kinetic multi-layer model of gas-particle interactions in aerosols and clouds (KM-GAP): linking condensation, evaporation and chemical reactions of organics, oxidants and water, Atmos. Chem. Phys., 12, 2777–2794, https://doi.org/10.5194/acp-12-2777-2012, 2012.
Shiraiwa, M., Yee, L. D., Schilling, K. A., Loza, C. L., Craven, J. S., Zuend, A., Ziemann, P. J., and Seinfeld, J. H.: Size distribution dynamics reveal particle-phase chemistry in organic aerosol formation, P. Natl. Acad. Sci. USA, 110, 11746–11750, https://doi.org/10.1073/pnas.1307501110, 2013.
Shiraiwa, M., Berkemeier, T., Schilling-Fahnestock, K. A., Seinfeld, J. H., and Pöschl, U.: Molecular corridors and kinetic regimes in the multiphase chemical evolution of secondary organic aerosol, Atmos. Chem. Phys., 14, 8323–8341, https://doi.org/10.5194/acp-14-8323-2014, 2014.
Shrivastava, M. K., Zhao, C., Easter, R. C., Qian, Y., Zelenyuk, A., Fast, J. D., Liu, Y., Zhang, Q., and Guenther, A.: Sensitivity analysis of simulated SOA loadings using a variance based statistical approach, J. Adv. Model. Earths Syst., 8, 499–519, https://doi.org/10.1002/2015MS000554, 2016.
Smith, G. D., Woods III, E., Baer, T., and Miller, R. E.: Aerosol Uptake Described by Numerically Solving the Diffusion-Reaction Equations in the Particle, J. Phys. Chem. A, 107, 9582–9587, https://doi.org/10.1021/jp021843a, 2003.
Smith, J. N., Dunn, M. J., VanReken, T. M., Iida, K., Stolzenburg, M. R., McMurry, P. H., and Huey, L. G.: Chemical composition of atmospheric nanoparticles formed from nucleation in Tecamac, Mexico: Evidence for an important role for organic species in nanoparticle growth, Geophys. Res. Lett., 35, 2–6, https://doi.org/10.1029/2007GL032523, 2008.
Song, M., Liu, P. F., Hanna, S. J., Li, Y. J., Martin, S. T., and Bertram, A. K.: Relative humidity-dependent viscosities of isoprene-derived secondary organic material and atmospheric implications for isoprene-dominant forests, Atmos. Chem. Phys., 15, 5145–5159, https://doi.org/10.5194/acp-15-5145-2015, 2015.
Stangl, C. M. and Johnston, M. V.: Aqueous Reaction of Dicarbonyls with Ammonia as a Potential Source of Organic Nitrogen in Airborne Nanoparticles, J. Phys. Chem. A, 121, 3720–3727, https://doi.org/10.1021/acs.jpca.7b02464, 2017.
Stolzenburg, M. R., McMurry, P. H., Sakurai, H., Smith, J. N., Mauldin, R. L., Eisele, F. L., and Clement, C. F.: Growth rates of freshly nucleated atmospheric particles in Atlanta, J. Geophys. Res.-Atmos., 110, 1–10, https://doi.org/10.1029/2005JD005935, 2005.
Surratt, J. D., Lewandowski, M., Offenberg, J. H., Kleindienst, T. E., Edney, E. O., Seinfeld, J. H., and Surratt, J. D.: Effect of Acidity on Secondary Organic Aerosol Formation from Isoprene Effect of Acidity on Secondary Organic Aerosol Formation from Isoprene, Environ. Sci. Technol., 41, 5363–5369, https://doi.org/10.1021/es0704176, 2007.
Tang, X., Misztal, P. K., and Goldstein, A. H.: Emitted from Engineering Students in a Classroom, Environ. Sci. Tech. Let., 2, 303–307, https://doi.org/10.1021/acs.estlett.5b00256, 2015.
Tolocka, M. P., Jang, M., Ginter, J. M., Cox, J., Kamens, R. M., Johnston, M. V., and Tolocka, M. P.: Formation of Oligomers in Secondary Organic Aerosol, 1428–1434, 38, 1428–1434, https://doi.org/10.1021/es035030r, 2004a.
Tolocka, M. P., Saul, T. D., and Johnston, M. V: Reactive uptake of nitric acid into aqueous sodium chloride particles using real-time single-particle mass spectrometry, J. Phys. Chem. A, 108, 2659–2665, https://doi.org/10.1021/jp036612y, 2004b.
Tröstl, J., Chuang, W. K., Gordon, H., Heinritzi, M., Yan, C., Molteni, U., Ahlm, L., Frege, C., Bianchi, F., Wagner, R., Simon, M., Lehtipalo, K., Williamson, C., Craven, J. S., Duplissy, J., Adamov, A., Almeida, J., Bernhammer, A.-K., Breitenlechner, M., Brilke, S., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Gysel, M., Hansel, A., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Keskinen, H., Kim, J., Krapf, M., Kürten, A., Laaksonen, A., Lawler, M., Leiminger, M., Mathot, S., Möhler, O., Nieminen, T., Onnela, A., Petäjä, T., Piel, F. M., Miettinen, P., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Sipilä, M., Smith, J. N., Steiner, G., Tomè, A., Virtanen, A., Wagner, A. C., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Carslaw, K. S., Curtius, J., Dommen, J., Kirkby, J., Kulmala, M., Riipinen, I., Worsnop, D. R., Donahue, N. M., and Baltensperger, U.: The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 533, 527–531, https://doi.org/10.1038/nature18271, 2016.
Trump, E. R. and Donahue, N. M.: Oligomer formation within secondary organic aerosols: equilibrium and dynamic considerations, Atmos. Chem. Phys., 14, 3691–3701, https://doi.org/10.5194/acp-14-3691-2014, 2014.
Tu, P. and Johnston, M. V.: Particle size dependence of biogenic secondary organic aerosol molecular composition, Atmos. Chem. Phys., 17, 7593–7603, https://doi.org/10.5194/acp-17-7593-2017, 2017.
Tu, P., Hall, W. A., and Johnston, M. V.: Characterization of Highly Oxidized Molecules in Fresh and Aged Biogenic Secondary Organic Aerosol, Anal. Chem., 88, 4495–4501, https://doi.org/10.1021/acs.analchem.6b00378, 2016.
Vestenius, M., Hellén, H., Levula, J., Kuronen, P., Helminen, K. J., Nieminen, T., Kulmala, M., and Hakola, H.: Acidic reaction products of monoterpenes and sesquiterpenes in atmospheric fine particles in a boreal forest, Atmos. Chem. Phys., 14, 7883–7893, https://doi.org/10.5194/acp-14-7883-2014, 2014.
Vesterinen, M., Lehtinen, K. E. J., Kulmala, M., and Laaksonen, A.: Effect of particle phase oligomer formation on aerosol growth, Atmos. Environ., 41, 1768–1776, https://doi.org/10.1016/j.atmosenv.2006.10.024, 2007.
Weber, R. J., Marti, J. J., and McMurry, P. H.: Measured Atmospheric New Particle Formation Rates: Implications for Nucleation Mechanisms, Chem. Eng. Commun., 151, 53–64, 1996.
Wehner, B., Petäjä, T., Boy, M., Engler, C., Birmili, W., Tuch, T., Wiedensohler, A., and Kulmala, M.: The contribution of sulfuric acid and non-volatile compounds on the growth of freshly formed atmospheric aerosols, Geophys. Res. Lett., 32, 3–6, https://doi.org/10.1029/2005GL023827, 2005.
Wexler, A. S. and Clegg, S. L.: Atmospheric aerosol models for systems including the ions H+, NH, Na+, SO, NO, Cl−, Br−, and H2O, J. Geophys. Res., 107, 1–14, https://doi.org/10.1029/2001JD000451, 2002.
Winkler, P. M., Ortega, J., Karl, T., Cappellin, L., Friedli, H. R., Barsanti, K., McMurry, P. H., and Smith, J. N.: Identification of the biogenic compounds responsible for size-dependent nanoparticle growth, Geophys. Res. Lett., 39, 1–6, https://doi.org/10.1029/2012GL053253, 2012.
Wong, J. P. S., Lee, A. K. Y., and Abbatt, J. P. D.: Impacts of Sulfate Seed Acidity and Water Content on Isoprene Secondary Organic Aerosol Formation, Environ. Sci. Technol., 49, 13215–13221, https://doi.org/10.1021/acs.est.5b02686, 2015.
Wu, Y. and Johnston, M. V.: Aerosol Formation from OH Oxidation of the Volatile Cyclic Methyl Siloxane (cVMS) Decamethylcyclopentasiloxane, Environ. Sci. Technol., 51, 4445–4451, https://doi.org/10.1021/acs.est.7b00655, 2017.
Xu, L., Guo, H., Boyd, C. M., Bougiatioti, A., Cerully, K. M., Hite, J. R., Isaacman-vanwertz, G., Kreisberg, N. M., Olson, K., Koss, A., Goldstein, A. H., Susanne, V., Gouw, J. De, Baumann, K., Lee, S., Nenes, A., Weber, R. J., and Ng, N. L.: Effects of anthropogenic emissions on aerosol formation from isoprene and monoterpenes in the southeastern United States, P. Natl. Acad. Sci. USA, 112, 37–42, https://doi.org/10.1073/pnas.1512277112, 2015.
Yli-Juuti, T., Barsanti, K., Hildebrandt Ruiz, L., Kieloaho, A.-J., Makkonen, U., Petäjä, T., Ruuskanen, T., Kulmala, M., and Riipinen, I.: Model for acid-base chemistry in nanoparticle growth (MABNAG), Atmos. Chem. Phys., 13, 12507–12524, https://doi.org/10.5194/acp-13-12507-2013, 2013.
Zaveri, R. A., Easter, R. C., Shilling, J. E., and Seinfeld, J. H.: Modeling kinetic partitioning of secondary organic aerosol and size distribution dynamics: representing effects of volatility, phase state, and particle-phase reaction, Atmos. Chem. Phys., 14, 5153–5181, https://doi.org/10.5194/acp-14-5153-2014, 2014.
Zhang, R., Khalizov, A., Wang, L., Hu, M., and Xu, W.: Nucleation and growth of nanoparticles in the atmosphere, Chem. Rev., 112, 1957–2011, https://doi.org/10.1021/cr2001756, 2012.
Zhao, J., Ortega, J., Chen, M., McMurry, P. H., and Smith, J. N.: Dependence of particle nucleation and growth on high-molecular-weight gas-phase products during ozonolysis of α-pinene, Atmos. Chem. Phys., 13, 7631–7644, https://doi.org/10.5194/acp-13-7631-2013, 2013.
Ziemann, P. J. and Atkinson, R.: Kinetics, products, and mechanisms of secondary organic aerosol formation, Chem. Soc. Rev., 41, 6582, https://doi.org/10.1039/c2cs35122f, 2012.