The relative impact of cloud condensation nuclei and ice nucleating particle concentrations on phase partitioning in Arctic mixed-phase stratocumulus clouds

This study investigates the interactions between cloud dynamics and aerosols in idealized large-eddy simulations (LES) of Arctic mixed-phase stratocumulus clouds (AMPS) observed at Oliktok Point, Alaska, in April 2015. This case was chosen because it allows the cloud to form in response to radiative cooling starting from a cloud-free state, rather than requiring the cloud ice and liquid to adjust to an initial cloudy state. Sensitivity studies are used to identify whether there are buffering feedbacks that limit the impact of aerosol perturbations. The results of this study indicate that perturbations in ice nucleating particles (INPs) dominate over cloud condensation nuclei (CCN) perturbations; i.e., an equivalent fractional decrease in CCN and INPs results in an increase in the cloud-top longwave cooling rate, even though the droplet effective radius increases and the cloud emissivity decreases. The dominant effect of ice in the simulated mixed-phase cloud is a thinning rather than a glaciation, causing the mixed-phase clouds to radiate as a grey body and the radiative properties of the cloud to be more sensitive to aerosol perturbations. It is demonstrated that allowing prognostic CCN and INPs causes a layering of the aerosols, with increased concentrations of CCN above cloud top and increased concentrations of INPs at the base of the cloud-driven mixed layer. This layering contributes to the maintenance of the cloud liquid, which drives the dynamics of the cloud system.

1 Introduction

Arctic mixed-phase stratocumulus clouds (AMPS) play a unique role in climate by producing a net warming at the Earth's surface over the annual cycle. This warming is due to the limited amount of incoming solar radiation at high latitudes, causing downward longwave radiative effects to dominate surface cloud forcing in the Arctic. AMPS are characterized by a liquid cloud layer with ice crystals that precipitate from cloud base even at temperatures well below freezing (Hobbs and Rangno, 1998; Intrieri et al., 2002; McFarquhar et al., 2007). The magnitude of the cloud-forced surface warming is primarily a function of the liquid water content of the AMPS and the properties of the cloud droplets (Curry and Ebert, 1992; Curry et al., 1993; Zhang et al., 1996). However, different from warm clouds, the magnitude and properties of cloud liquid in mixed-phase clouds are closely connected to the formation of cloud ice, which limits the availability of water vapor for droplet formation and growth (the Wegener–Bergeron–Findeisen, WBF, mechanism, Wegener, 1911; Bergeron, 1935; Findeisen, 1938) and acts as a sink for water vapor through the growth and sedimentation of frozen precipitation.

Cloud ice in AMPS must form through heterogeneous nucleation, since temperatures are too warm for homogenous ice nucleation (approximately >36 ^∘C). Heterogeneous ice nucleation can occur by a number of modes: either in the presence of supercooled droplets, when an aerosol comes into contact with a droplet (contact freezing) and is immersed in a droplet followed by freezing (immersion freezing), or in the absence of droplets through vapor deposition on aerosol (deposition freezing) or liquid forming on aerosol (condensation freezing) (Pruppacher and Klett, 1997). The efficiency of any of these modes in a given environmental state is a function of aerosol properties, which determine whether an aerosol can serve as an ice nucleating particle (INP), cloud condensation nuclei (CCN), or both. Based on measurements from in situ instrumentation and the reduced concentration of ice crystals relative to liquid droplets (Murray et al., 2012), it is believed that only a small fraction of aerosols can serve as INPs. For example, in the Indirect and Semi-Direct Aerosol Campaign (ISDAC) (McFarquhar et al., 2011) that took place off the coast of Utqiaġvik, (Barrow) Alaska, in the spring of 2008, the number of INPs available were observed to be 4 orders of magnitude smaller than the number of aerosols serving as CCN. However, it is important to note that only a few INPs are needed to glaciate a cloud (see discussion in DeMott et al., 2010).

The impact of CCN variability on warm cloud structure has been the subject of numerous papers. For a fixed liquid water path (LWP), an increase in CCN in warm clouds will increase the number of droplets and reduce the droplet size. This causes an increase in cloud albedo (the Twomey effect; Twomey, 1977) and potentially suppresses precipitation (the Albrecht effect; Albrecht, 1989). Suppressing precipitation can increase cloud thickness/coverage and cloud-driven turbulence, which increases the entrainment of dry air at cloud top, thereby thinning the cloud (Pincus and Baker, 1994; Stevens et al., 1998). This thinning of the cloud as a response to an increase in aerosols is an example of a buffering feedback that limits the impact of a CCN perturbation on the cloud structure (Stevens and Feingold, 2009). For LWPs greater than approximately 50 g m⁻², AMPS emit as blackbodies (Shupe and Intrieri, 2004) and an increase in CCN has minimal impact on longwave emissivity (Morrison et al., 2008). However, smaller droplets can also reduce the ice water path (IWP) through a reduction in collision–coalescence and riming of snow by droplets (Morrison et al., 2008) as well as make ice nucleation less efficient (Lance et al., 2011). These are only a few examples of buffering feedbacks that exist in mixed-phase clouds.

An increase in INPs in AMPS is known to produce a “glaciation effect”, i.e., a rapid depletion of cloud liquid, in part due to the WBF mechanism and the acceleration of frozen precipitation (Murray et al., 2012). However, the efficacy of this effect is dependent upon the chemical composition of the INPs. In cases where INPs are transported over long distances and coated in sulfate or organic materials, an increased concentration of INPs may actually be linked to a “deactivation effect”. This is because coated particles generally freeze at colder temperatures (Cziczo et al., 2009; Sullivan et al., 2010; Girard and Sokhandan, 2014), changing the number, size, and fall speeds of nucleated ice crystals and increasing cloud lifetime. The deactivation effect can cause a significant increase in surface warming, since a decrease in droplet size in optically thin clouds for constant LWP can produce a significant increase in cloud longwave emissivity (Garrett and Zhao, 2006).

Given the uncertainty in measurements of INPs (DeMott et al., 2015; Garimella et al., 2017), it has been challenging to study the manifestation of aerosol–cloud interactions in mixed-phase cloud conditions. This study investigates these interactions and their dependence on aerosol partitioning in idealized large-eddy simulations (LES) of AMPS observed at Oliktok Point, Alaska, 05:00–17:00 Z on 17 April 2015. In order to isolate the impact of these interactions on longwave cloud forcing, shortwave radiation is neglected in the simulations. The microphysics used in Solomon et al. (2015) have been modified to include prognostic CCN in addition to prognostic INPs. This allows for a more realistic representation of aerosols advected over the Oliktok Point site. In order to identify aerosol indirect effects in these simulations, aerosol chemistry is specified and, due to the in-cloud temperatures for this case, all cloud ice forms through immersion freezing. The focus on immersion freezing is supported by studies demonstrating that liquid droplets typically form prior to ice formation in mixed-phase cloud environments (e.g., de Boer et al., 2011; Westbrook and Illingworth, 2013).

This study is focused on the following research questions:

1. What is the relative impact of CCN versus INP perturbations on the phase partitioning between cloud liquid and cloud ice in AMPS? Specifically, what is the impact on cloud dynamics?

2. Are there buffering feedbacks in AMPS that limit the impact of CCN–INP perturbations?

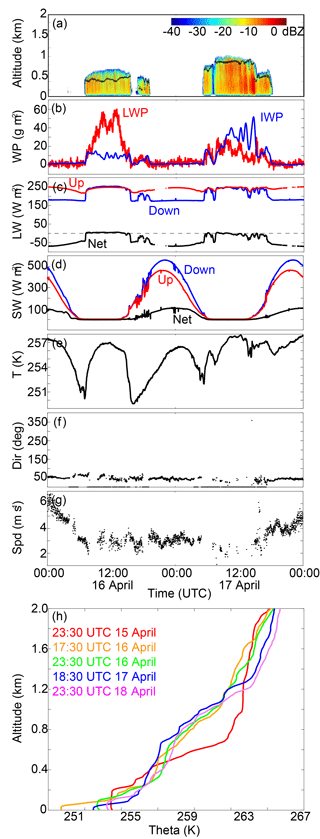
Figure 1 Measurements at Oliktok Point, Alaska, 15–17 April 2015. (a) Ceilometer (black dots) and Ka-band cloud radar reflectivity (colored shading). (b) LWP and IWP, in units of g m⁻². (c) LW and (d) SW surface radiation measurements, in units of W m⁻². (e) Surface air temperatures. (f) Surface wind direction, in units of degrees. (g) Surface wind speed, in units of m s⁻¹. (h) Radiosondes at approximately 23:30 UTC on 15 April, 17:30 and 23:30 UTC on 16 April, and 18:30 and 23:30 UTC on 17 April.

2 Case description

Simulations are set up to recreate conditions observed by the US Department of Energy (DOE) Atmospheric Radiation Measurement (ARM) program third mobile facility (AMF-3) at Oliktok Point, Alaska, on and around 17 April 2015 (Fig. 1). During this time period, Oliktok Point was situated in a relatively quiet regime synoptically, with surface high pressure to the northwest over the Chukchi Sea and a weak area of low pressure over central Alaska. This resulted in steadily increasing surface air pressure from around 1008 hPa at 00:00 Z on 16 April to around 1021 hPa at 00:00 Z on 18 April and relatively light (2–5 m s⁻¹) near-surface winds (U_10 m) from the east-northeast over this entire 2-day window (Fig. 1f, g). Near-surface air temperatures (T_2 m) varied dramatically (Fig. 1e), depending on time of day and cloud cover, with the coldest temperatures around 250 K during late evening and early morning clear periods on 16 April and the warmest temperatures being around 258 K during cloudy periods during local nighttime on 17 April. Near-surface relative humidity (RH_2 m) showed a weak diurnal signature, ranging from around 80 % during local daytime hours and 86 %–88 % during nighttime hours.

Radiosonde launches conducted at approximately 23:30 UTC on 15 April, 17:30 and 23:30 UTC on 16 April, and 18:30 and 23:30 UTC on 17 April reveal the evolution of the lower troposphere at Oliktok Point (Fig. 1h). The 23:30 UTC sounding from 15 April reveals a well-mixed surface layer extending up to around 200 m, a stable layer from 200 to 700 m, and then an elevated layer that is generally well mixed from 700 to 2000 m. By 17:30 UTC a strong inversion formed from 30 to 300 m above the surface where there is a residual mixed layer from the previous night's cloud cover between 300 and 600 m. Above this layer, there is a weakly stable layer from 600 m to around 1000 m. A similar vertical structure persists through the rest of the sampling period, with the strength of the near-surface inversion and depth of the overlying mixed layer evolving with time, and general warm-air advection occurring above 1000 m. With the exception of a very dry layer between 200 and 350 m in the 23:30 UTC sounding on 17 April and a saturated layer around 200 m in the 17:30 UTC sounding on 16 April, the lower atmosphere (0–700 m) features relative humidity between 70 % and 90 %. Above this, RH values feature variability between 30 % and 60 %, with the height at which this drop-off occurs increasing with time. The last two soundings are substantially drier between 1200 and 2000 m, with RH values around 20 %.

On both 16 and 17 April, low-level mixed-phase stratocumulus cloud layers were observed to develop during local nighttime (∼ 06:00–18:00 UTC). Surface radiation measurements (Fig. 1c, d) clearly demonstrate the presence of these clouds, with the net longwave radiation (LW_NET) increasing to around 0 W m⁻² as a result of increased downwelling longwave (LW_DOWN) during cloudy periods. An increase in downwelling shortwave radiation may be playing a role in the dissipation of the cloud layer. The presence of cloud is also detected by active remote sensors (Fig. 1a), with ceilometer cloud base (black dots) and Ka-band cloud radar reflectivity (colored shading) measurements clearly showing the nighttime appearance of liquid-containing cloud layers between 450 and 700 m (on 16 April) and between 800 and 1000 m (on 17 April) above the surface, with the cloud on 17 April starting and ending with lower cloud bases and tops. Both radar and surface precipitation gauges indicated weak snowfall associated with these clouds, and shortwave irradiance measurements reveal that the surface was snow covered during this time, with surface albedo around 80 %.

3 Model description

Simulations are completed using the large-eddy simulation mode of the Advanced Research WRF model (WRFLES) version 3.3.1 (Yamaguchi and Feingold, 2012) with the RRTMG longwave radiation parameterization (Mlawer et al., 1997) and the Morrison two-moment microphysical scheme (Morrison et al., 2009). Collision–coalescence was found to be important in CCN perturbation studies during the Fall 2004 Mixed-Phase Arctic Cloud Experiment (M-PACE; Morrison et al., 2008); however tests with and without riming and collision–coalescence indicated that these processes are not significant for this case and have been neglected in the simulations. Shortwave radiation is neglected given the nighttime occurrence of these clouds and to be able to focus on longwave indirect aerosol effects. Surface fluxes are calculated using the modified MM5 similarity scheme, which calculates surface exchange coefficients for heat, moisture, and momentum following Webb (1970) and uses Monin–Obukhov with Carlson–Boland viscous sublayer and standard similarity functions following Paulson (1970) and Dyer and Hicks (1970). The land surface is simulated with the unified Noah land-surface model (Tewari et al., 2004). Initial surface pressure is 1020 hPa. The initial surface temperature is 255 K.

All simulations are run on a domain of $\mathrm{3.6}\times \mathrm{3.6}\times \mathrm{1.4}$ km with a horizontal grid spacing of 50 m and vertical spacing of 10 m. The domain has $\mathrm{72}\left(x\right)\times \mathrm{72}\left(y\right)\times \mathrm{140}\left(z\right)$ grid points and is periodic in both the x and y directions. The top of the domain is at 1.4 km. The model time step is 0.5 s.

3.1 Initial atmospheric profiles

Initial profiles of temperature, moisture, and horizontal wind components are based on radiosonde measurements taken at Oliktok Point at 23:30 Z on 16 April 2015 (Fig. 1h). Soundings are not available during the cloudy period (05:00–18:00 Z), seen in the Ka-band ARM zenith radar (KAZR) reflectivity (Fig. 1a). Therefore, the model is initialized with a cloud-free sounding and the cloud forms in response to the radiative cooling, rather than starting the stimulation with a “cloudy” profile and requiring the cloud ice and liquid to adjust to the initial state. The potential temperature and water vapor mixing ratio from the radiosonde and the initial profiles used in the simulations are shown in Fig. 2. Initial water vapor is increased in the region where cloud liquid water was observed after 05:00 Z in order to produce cloud liquid water at the start of the integration. Initial temperature and subgrid turbulent kinetic energy (TKE) are perturbed below the top of the mixed layer with pseudo-random fluctuations with amplitude of 0.1 K and 0.1 m² s⁻², respectively.

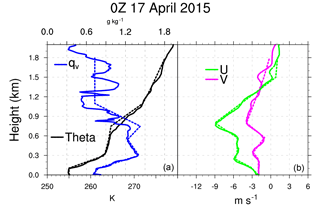
Figure 2 Sounding measured at 00:00 UTC on 17 April 2015 at Oliktok Point, Alaska. (a) Water vapor mixing ratio (q_v) and potential temperature (theta), in units of g kg⁻¹ and K, respectively. (b) Zonal wind (U) and meridional wind (V), in units of m s⁻¹. The dashed lines show the initial profiles used in the WRFLES experiments. The dashed line overlying the water vapor mixing ratio is the initial profile for the total water mixing ratio.

3.2 Large-scale forcing

Large-scale subsidence is specified by integrating the prescribed horizontal wind divergence from the surface upward. Divergence is assumed to be equal to $\mathrm{1.8}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{s}}^{-\mathrm{1}}$ below the inversion and 0 above, following the Solomon et al. (2015) study. This gives a linear increase in large-scale subsidence from 0 at the surface to 1.5 mm s⁻¹ at the base of the initial inversion (z=805 m), above which the large-scale vertical wind is constant. Large-scale subsidence is accounted for via a source term for any prognostic variable other than wind components.

Temperature and moisture profiles are nudged to the initial profiles in the top 100 m of the domain with a timescale of 1 h. Horizontal winds are nudged to the initial profiles at and below the initial inversion base with a timescale of 2 h. Nudging of the horizontal wind components, temperature, and moisture profiles is performed by adding a source term to the prognostic equations for potential temperature, water vapor, and horizontal wind components.

3.3 Droplet number concentration and CCN properties

Because CCN measurements were not available from Oliktok Point during this time, initial CCN size distributions at every grid point are based on springtime measurements taken during ISDAC (Earle et al., 2011). The accumulation mode observed during ISDAC had a concentration of less than 200 cm⁻³ (165 cm⁻³ used in this study), a modal diameter of 0.2 µm, and a geometric standard deviation of 1.4. Sensitivity studies vary initial CCN concentration with an arbitrary multiplication factor C (referred to as the CCN factor). CCN mean concentration is then treated as a prognostic variable. A prognostic equation for CCN number concentration has been added to WRFLES,

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\partial \mathrm{CCN}}{\partial t}}+\mathrm{ADV}+\mathrm{DIFF}={\left.{\displaystyle \frac{\mathit{\delta }\mathrm{CCN}}{\mathit{\delta }t}}\right|}_{\mathrm{condensation}}\\ \text{(1)}& {\displaystyle }& {\displaystyle }+{\left.{\displaystyle \frac{\mathit{\delta }\mathrm{CCN}}{\mathit{\delta }t}}\right|}_{\mathrm{evaporation}},\end{array}$$

where ADV represents advection and DIFF represents turbulent diffusion. Condensation is a sink of CCN and evaporation is a source of CCN. Evaporation (condensation) of one droplet produces (removes) one CCN.

Cloud droplets are activated using resolved and subgrid vertical motion (Morrison and Pinto, 2005) and a log-normal aerosol size distribution (assumed to be ammonium bisulfate and 30 % insoluble by volume) to derive cloud condensation nuclei spectra following Abdul-Razzak and Ghan (2000). As noted in Solomon et al. (2015), because the aerosol number size distribution peaks at a relatively large diameter of 0.2 µm, the majority of CCN activate into droplets at low supersaturation (at or below SS_w=0.15 %) for a reasonable range of aerosol composition assumptions. Since such supersaturations can be generated even by slow updrafts, the sensitivity of droplet number concentration to aerosol composition is expected to be weak. We therefore only include simulations that test the sensitivity to mean CCN concentrations.

3.4 Ice nucleation

Following Solomon et al. (2015), a prognostic equation for INP number concentration (N_INP) has been added to WRFLES,

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\partial N_{\mathrm{INP}}}{\partial t}}+\mathrm{ADV}+\mathrm{DIFF}={\left.{\displaystyle \frac{\mathit{\delta }{N}_{\mathrm{INP}}}{\mathit{\delta }t}}\right|}_{\mathrm{activation}}\\ \text{(2)}& {\displaystyle }& {\displaystyle }+{\left.{\displaystyle \frac{\mathit{\delta }{N}_{\mathrm{INP}}}{\mathit{\delta }t}}\right|}_{\mathrm{sublimation}},\end{array}$$

where ADV represents advection and DIFF represents turbulent diffusion. Activation is also referred to as ice nucleation and sublimation represents a source of INPs, supporting the recycling of these particles.

Eight prognostic equations are integrated for N_INP in equally spaced temperature intervals with nucleation thresholds spanning the range of the in-cloud temperatures (−20.15 to −14.55 ^∘C). Therefore, additional INPs become available for activation with decreasing temperature and as the cloud layer cools. INP number concentrations are initially specified at 1.3 L⁻¹ in each bin to produce IWP close to observations for this case. Sensitivity studies vary initial INP concentration with an arbitrary multiplication factor F (referred to as the INP factor).

It is assumed that 50 % of the INPs available in a bin nucleate if the in situ temperature is below the threshold temperature and the local conditions exceed water saturation. Therefore, initial N_INP's are a function of the nucleation threshold temperatures and are independent of the in situ temperature. The in situ temperature in regions of water saturation determines how many INPs are activated. Due to the pristine dendritic nature of the observed crystals and the limited number of INPs, ice shattering and aggregation are neglected in the simulations and sublimation returns one INP per sublimated crystal.

N_INP (in units of L⁻¹) integrated over the domain in each temperature bin k at time t is equal to

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }{\stackrel{\mathrm{‾}}{N}}_{\mathrm{INP}}\left(k,t\right)=\int \int \int N_{\mathrm{INP}}\left(x,y,z,k,t\right)\mathrm{d}x\mathrm{d}y\mathrm{d}z.\end{array}$$

Upon sublimation, the modification of activation thresholds that can occur for previously nucleated INPs, i.e., preactivation (Roberts and Hallett, 1968), is not considered and N_INP's are returned to each bin k with weighting:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }{\mathrm{W}}_k=\left[{\stackrel{\mathrm{‾}}{N}}_{\mathrm{INP}}\left(k,\mathrm{0}\right)-{\stackrel{\mathrm{‾}}{N}}_{\mathrm{INP}}\left(k,t\right)\right]/{\stackrel{\mathrm{‾}}{N}}_{\mathrm{INP}}\left(k,\mathrm{0}\right),\end{array}$$

where W_k is normalized such that $\sum {\mathrm{W}}_k=\mathrm{1}$. The W_k's are recalculated each time step. In this way, INPs are recycled preferentially to each of the eight temperature bins from which they originated (Feingold et al., 1996).

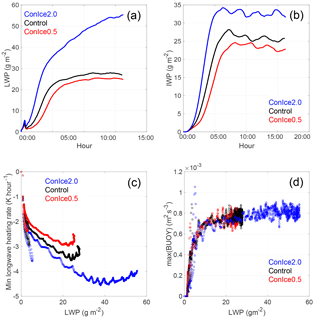
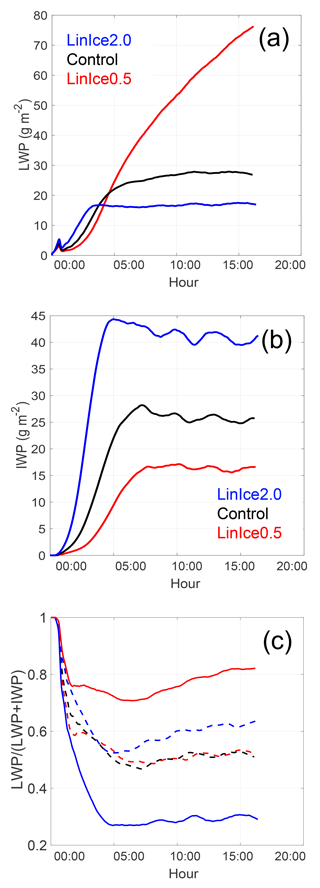
Figure 3 Time series from runs varying CCN concentrations with “constant” ice formation. (a) LWP, in units of g m⁻². (b) IWP, in units of g m⁻². (c) Scatterplot of minimum longwave heating rate vs. LWP, in units of K h⁻¹ and g m⁻², respectively. (d) Scatterplot of integrated buoyancy vs. LWP, in units of m³ s⁻³ and g m⁻², respectively. For INP factors equal to 1.0 and CCN factors 2.0 (blue), 1.0 (black), and 0.5 (red).

4 Simulations completed

Simulations completed for this study are listed in Table 1. A simulation with INP and CCN factors equal to 1.0 is referred to as the Control. To isolate the impact of CCN perturbations on mixed-phase clouds without a change in ice formation, three simulations were run with CCN factors 1∕2, 1, and 2 and INP factors equal to 1.0 (runs ConIce0.5, Control, and ConIce2.0). To identify the impact of CCN perturbations on mixed-phase clouds when ice formation is a linear function of the CCN number concentration, two runs were done with INP and CCN factors equal to 2, one with fixed CCN (FixedCCN2.0) and one with prognostic CCN (LinIce2.0), as well as one run with INP and CCN factors equal to 1∕2 (LinIce0.5).

Table 1 Description of simulations completed and discussed in the paper.

5 Model results

5.1 Control simulation

The control simulation (CCN and INP factors equal to 1) has IWP and LWP consistent with observations on 17 April 2015 (Figs. 1b and 3a) and a cloud system that reaches a steady state after 5 h with liquid water fractions close to 0.5. The cloud-driven mixed-layer depth slowly increases over the 16 h integration, with both cloud top rising and cloud base lowering at a rate of ∼5 m h⁻¹. However, the cloud system remains decoupled from the surface layer and a surface inversion of ∼180 m in depth is maintained throughout the integration.

Rain forms in the liquid layer (with concentrations less than 0.02 cm⁻³) and evaporates within 200 m of cloud base. Therefore, the production and impact of rain on this simulation can be neglected. This is true for the sensitivity studies discussed below as well but would not be the case for runs with more limited CCN, which would produce significant precipitation.

Snow does reach the surface during the steady state with a relatively constant flux of $\mathrm{6}\times {\mathrm{10}}^{-\mathrm{4}}$ g m⁻² s⁻¹. Sublimation at the base of the cloud-driven mixed layer reduces the snow water content by $\mathrm{6}\times {\mathrm{10}}^{-\mathrm{6}}$ g m⁻³ s⁻¹. In terms of number concentration, this causes the recycling of approximately 1 L⁻¹ h⁻¹ of INPs back into the cloud-driven mixed layer. Since total ice crystal number concentrations are 1–2 L⁻¹ in the mixed layer over the integration, this indicates that recycling of INPs is playing a significant role in the maintenance of cloud ice in this cloud system (e.g., Solomon et al., 2015).

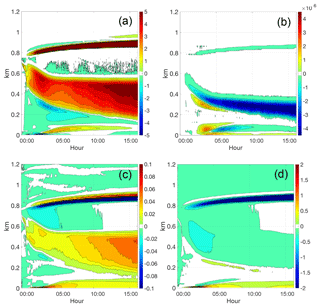
Figure 4 Impact of increasing CCN by 2× (ConIce2.0 minus ConIce1.0) on (a) relative humidity, (b) sublimation rate, (c) water vapor mixing ratio, and (d) temperature, in units of percent, g m⁻³ s⁻¹, g kg⁻¹, and ^∘C, respectively.

While the cloud system is maintaining a steady state in cloud ice and liquid, longwave cooling continually cools the cloud-driven mixed layer, contributing to the maintenance of the phase partitioning by increased activation of INPs within the liquid cloud layer and depletion of water vapor within the mixed layer. This cooling is required to maintain the cloud liquid because of the continuous depletion of water vapor and to maintain the cloud ice, since ∼2 L⁻¹ of INPs is lost to the surface through precipitation each hour.

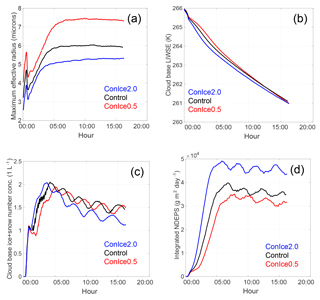
Figure 5 Time series from runs varying CCN concentrations with constant ice formation. (a) Maximum effective radius, in units of microns. (b) Cloud mixed-layer liquid–ice water static energy, in units of K. (c) Cloud base ice plus snow number concentration, in units of L⁻¹. (d) Vertically integrated net deposition rate, in units of g m⁻² day⁻¹. For INP factors equal to 1.0 and CCN factors 0.5 (red), 1.0 (black), and 2.0 (blue).

5.2 Impact of CCN perturbations with constant ice formation

The first set of simulations completed for this study tests the sensitivity of the cloud to perturbations in CCN concentrations, while keeping INP concentrations fixed (ConIce simulations). Simulations involved increasing and decreasing the initial CCN concentrations by a factor of 2. These runs provide insight into the impact of CCN perturbations in an Arctic environment with stable stratification near the surface and a weak inversion at cloud top with relatively moist air. Figure 3a shows that increasing the CCN concentrations has the expected effect at the beginning of the integrations when the cloud layer is optically thin – smaller droplets increase the cloud emissivity and thereby longwave cooling at cloud top, increasing turbulence, supersaturation, and droplet formation. The opposite result is found with decreasing CCN concentrations. For these optically thin cases, radiative cooling is a contribution from the full physical depth of the cloud and the increased cooling rate is therefore an expression of increased total emission of the cloud. Figure 3b shows that this also results in faster vapor deposition rates, resulting in increased ice mass given an increase in CCN. However, this increase in IWP plateaus and slowly decreases after hours 5–6 as ice crystals fall out of the cloud layer and are lost from the system. Decreasing CCN results in slower deposition rates and reduced IWP.

What is unexpected is that the minimum longwave heating rate (or maximum cooling rate) is not exclusively a function of LWP, even after the clouds become optically thick (Fig. 3c). The larger longwave cooling rate associated with a cloud forming in conjunction with elevated CCN concentrations causes increased total water in the cloud-driven mixed layer (indicating that liquid water increases faster than ice mass), which increases the water vapor mixing ratio below the liquid layer, increasing relative humidity in the mixed layer below the liquid layer (see Fig. 4a). The IWP shows larger temporal variability than the LWP, potentially due to larger sensitivity to small perturbations in relative humidity.

Increasing CCN causes the cloud top to rise and the cloud base to lower faster while keeping the maximum buoyancy relatively unchanged; the maximum buoyancy as a function of LWP is similar for ConIce2.0 and Control, with Control approximately $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ less than ConIce2.0 for LWP less than 17 g m⁻² (Fig. 3d). The deepening of the cloud layer for an increase in CCN causes the impact of CCN on maximum droplet size to persist throughout the integration (Fig. 5a), even though LWP is increasing more rapidly (Fig. 3a).

The ConIce set of simulations was designed to identify the impact of CCN variability on phase partitioning and cloud dynamics for a relatively constant magnitude of cloud ice number concentration. This is seen to be the case in Fig. 5c; however, interestingly, processes such as sublimation cause ConIce2.0 to have less total cloud ice number concentration than the other two runs (see Fig. 4a–d), since a reduction in sublimation causes more INPs to fall out of the mixed layer and less recycling of INPs in the cloud layer. However, the differences in relative humidity also play a role here and therefore the sublimation rate is not just a function of the ice present. Increasing CCN causes more rapid mixed-layer cooling (Figs. 4b and 5b) and deeper mixed-layer depths, and therefore larger net deposition rates (Fig. 5d) and larger IWPs (Fig. 3b).

Figure 6 Time series from runs varying CCN concentrations with “linear” ice formation. (a) LWP, in units of g m⁻². (b) IWP, in units of g m⁻². (c) Liquid water fraction for ConIce (solid) and LinIce (dashed). For CCN and INP factors 0.5 (red), 1.0 (black), and 2.0 (blue).

5.3 Impact of CCN perturbations with linear ice formation

A second set of simulations was completed adding an additional degree of realism to the simulations by scaling INP concentrations with the CCN concentration, i.e., equal INP and CCN factors (LinIce simulations). This was done in order to represent the case of a polluted air mass with equal relative increases in CCN and INPs. The fraction of INPs to CCN evolves in time as cloud ice forms and precipitates, sublimates below the cloud base, and advects back into the cloud layer with the cloud-driven vertical motions.

Figure 6 shows the sensitivity of the LWP and IWP to an increase and decrease in CCN and INPs by a factor of 2. Similar to the ConIce runs, the increase in LWP begins to slow when IWP exceeds 20 g m⁻². Before hour 5 the ConIce and LinIce runs have similar trajectories. After hour 5 these runs diverge; decreasing CCN and INP factors in LinIce results in larger LWP because of the dominating effect of INP variability on water vapor availability. Increasing CCN and INP factors from 0.5 to 1.0 results in a 63 % decrease in LWP at hour 15.

The LinIce runs highlight the extreme sensitivity of phase partitioning between cloud liquid and ice to very small changes in INP concentrations. For these simulations, there is a 5-orders-of-magnitude difference between CCN and INP concentrations, with the scaling done on a percentage basis relative to the absolute amount. In other words, a change in INPs from 1 to 2 L⁻¹ has a substantially larger effect on cloud phase than a change in CCN from 10 000 to 20 000 L⁻¹, despite the latter change obviously being much more extreme from the perspective of aerosol number concentration. The CCN variability in the LinIce runs causes a 50 % increase in droplet effective radius for a decrease in CCN by a factor of 2 (Fig. 7a). These changes are of the same sign as the ConIce runs but are larger due to the additional impact of INP variability on water vapor available for condensation. Similarly, the reduction of cloud droplet size related to the presence of elevated aerosol concentrations is exacerbated when both INP and CCN concentrations increase due to the combination of more nucleated droplets (on CCN) and increased water vapor deposition (on ice crystals generated by the elevated INP concentrations). However, the impact of the changes in droplet effective radius is small relative to the impact of INP variability on the dynamics of the cloud-driven mixed layer after approximately hour 4. For example, after hour 7 the LinIce0.5 run has a colder cloud-driven mixed layer than the Control and LinIce2.0 runs (Fig. 7b), whereas ConIce2.0 had a colder cloud-driven mixed layer than ConIce0.5 (Fig. 5b).

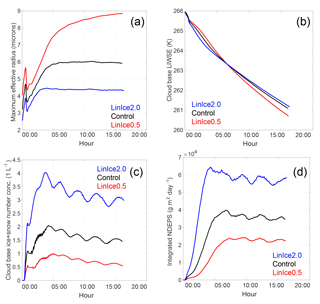
Figure 7 Time series from runs varying CCN concentrations with linear ice formation. (a) Maximum effective radius, in units of microns. (b) Cloud mixed-layer liquid–ice water static energy, in units of K. (c) Cloud base ice plus snow number concentration, in units of L⁻¹. (d) Vertically integrated net deposition rate, in units of g m⁻² day⁻¹. For CCN and INP factors 0.5 (red), 1.0 (black), and 2.0 (blue).

The ratio of INPs among the LinIce runs stays relatively constant for the 16 h integrations (Fig. 7c), indicating that differences in sublimation (INP recycling) and ice fall speeds do not produce appreciably different ice crystal number concentrations in the cloud-driven mixed layer. However, larger deposition rates in the cloud-driven mixed layer due to increased ice number concentrations (Fig. 7d) result in larger ice water mixing ratios (a 31 % increase between ConIce2.0 and LinIce2.0), even though mixed-layer temperatures are warmer for an increase in CCN and INP factors, indicating that vapor deposition on snow (NDEPS) is dominant relative to ice number in controlling IWP.

Allowing both prognostic CCN and INPs reveals interesting layering of aerosol distributions that results from differential liquid and ice processes. This is seen in Fig. 8, where the turbulent advection of droplets into the cloud-top inversion causes larger CCN concentrations above the liquid cloud layer than below (Fig. 8a). The opposite result is found for INPs, where gravitational settling of ice crystals and the subsequent sub-cloud sublimation produces locally elevated INP concentrations in the lowest 200 m (Fig. 8b). This layering of aerosols causes larger entrainment of CCN at cloud top and larger entrainment of INPs at the mixed-layer base as the mixed layer deepens. As was demonstrated in Solomon et al. (2015), the increase in INPs at the base of the mixed layer contributed to the maintenance of the phase partitioning by making more INPs available for activation as ice crystals as the mixed layer deepens.

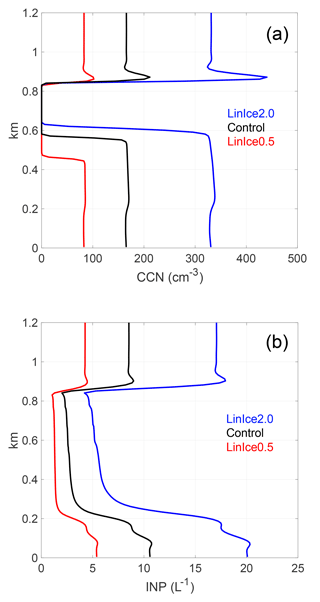
Figure 8 (a) CCN and (b) INPs in linear ice runs at hour 10, in units of cm⁻³ and L⁻¹, respectively. For CCN and INP factors 0.5 (red), 1.0 (black), and 2.0 (blue).

This layering of aerosols, with increased CCN above the liquid layer and increased INPs below the cloud-driven mixed layer, causes interesting differences between runs with and without prognostic CCN (Fig. 9). The increase in CCN above the liquid layer causes increased entrainment of CCN at cloud top (Fig. 9a), decreasing the droplet effective radius, increasing the longwave cooling (Fig. 9b), and increasing the deposition rate and ice water mixing ratio (Fig. 9c). Ultimately, these differences result in stronger buoyancy with the cloud layer (Fig. 9d), where buoyancy is increased by up to 10 %.

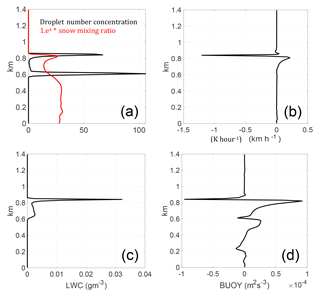
Figure 9 Impact of prognostic CCN (LinIce2.0–FixCCN2.0) over hour 10. (a) Droplet number concentration (black) and snow mixing ratio (red), in units of cm⁻³ and 1×10⁴ g kg⁻¹, respectively. (b) Longwave radiative heating rate, in units of K h⁻¹. (c) Liquid water content, in units of g m⁻³. (d) Buoyancy, in units of m² s⁻³.

6 Summary and discussion

In this study we use idealized large-eddy simulations to quantify the relative impact of CCN and INP perturbations on the phase partitioning and dynamics of AMPS. The modeling framework developed in Solomon et al. (2015) to study the recycling of INPs has been extended to include prognostic CCN. The first set of simulations was designed to investigate the impact of relatively small perturbations in CCN compared to studies such as Morrison et al. (2008) and Kravitz et al. (2014) in mixed-phase conditions with essentially constant INPs on phase partitioning and cloud dynamics. It is found that increasing CCN by a factor of 2 increases LWP by 60 %–100 %, while decreasing CCN by a factor of 2 reduces LWP by less than 8 %, i.e., the impact is highly nonlinear. This change stems primarily from an increase in cloud longwave emissivity and associated increase in cloud-top cooling rates, connected to a decrease in droplet size. This elevated cooling rate causes the cloud-driven mixed layer to cool and deepen more rapidly. However, interestingly, this difference persists even when the cloud radiates as a blackbody, highlighting the influence of early changes to the system.

The sensitivity to CCN in this study is significantly larger than that found in the M-PACE case study by Morrison et al. (2008) and the ISDAC case study by Kravitz et al. (2014). The M-PACE and ISDAC case studies are useful as examples of the extreme range of conditions under which mixed-phase clouds exist. M-PACE took place in October over open water with large fluxes of heat and momentum from the surface into the cloud layer, while ISDAC took place during the spring when the Arctic Ocean was essentially ice covered and the cloud layer was decoupled from the surface layer.

In the M-PACE case study, increasing CCN by a factor of 5–6 resulted in an increase in LWP by 20 % and a decrease in IWP by 60 %. In the ISDAC case study, increasing CCN by a factor of 4 resulted in similar LWP and IWP until hour 12 when the more pristine cloud collapsed. A very interesting difference between this study and the two previous studies is that both the M-PACE and ISDAC studies found IWP to decrease when CCN was increased, while this study finds an increase in IWP due to increased longwave cooling and larger deposition rates. For the ISDAC case study this may be due to the continuous decrease in droplet number concentration, which would cause the cloud dynamics to spin down. This study also finds a significantly larger sensitivity to INPs than the M-PACE case study. The M-PACE case study found that a 10× increase in INPs resulted in a 120 % increase in IWP and a 23 % decrease in LWP, while this study finds increasing INPs by 2× results in a 60 % increase in IWP and a 36 % decrease in LWP. These differences need to be investigated further to identify the relative impact of different environmental conditions and model physics.

The differences between this study and the M-PACE and ISDAC studies are due in part to the different environmental conditions but the different sensitivities to both CCN and INPs are also due to the different parameterizations used in these models. Both the M-PACE and ISDAC studies essentially hold INPs fixed, while this study does not constrain INPs other than specifying an initial value. This allows for the vertical redistribution of particles throughout the domain, resulting in feedbacks between ice and droplet properties and cloud dynamics not included in the two previous case studies and in many climate and weather-scale models.

Additionally, the inclusion of prognostic CCN and INPs reveals a number of feedbacks that buffer the cloud system from collapsing. The first buffering feedback is the recycling of INPs, which was the focus of the Solomon et al. (2015) study. The IWP, and therefore phase partitioning between cloud ice and liquid, cannot be maintained without this feedback. However, the reservoir of INPs below the mixed layer would be depleted if cloud-driven mixed layer became coupled to the surface layer. The second interesting buffering feedback is the layering of the aerosols, with increased concentrations of CCN above cloud top and increased concentrations of INPs at the base of the mixed layer. As demonstrated in this paper, this layering contributes to the maintenance of the cloud liquid, which ultimately drives the dynamics of the cloud system. A third buffering feedback is the thinning of the liquid layer when INP concentrations are increased. The occurrence of this thinning does not produce complete glaciation, but instead causes the mixed-phase clouds to radiate as grey bodies and the radiative properties of the clouds to be more sensitive to aerosol perturbations.

Ultimately, enhanced observations of the vertical structure of cloud microphysics and aerosol properties are required. Recent work by the DOE ARM program to operate unmanned aircraft and tethered balloons has provided new perspectives on these quantities and the dynamic and thermodynamic conditions supporting these cloud systems (de Boer et al., 2018). Such observational efforts should continue to be pursued further to help constrain the sensitivities demonstrated by numerical studies as presented here.